Hydrate Phase Transition Kinetic Modeling for Nature and Industry–Where Are We and Where Do We Go?

Abstract

Hydrate problems in industry have historically motivated modeling of hydrates and hydrate phase transition dynamics, and much knowledge has been gained during the last fifty years of research. The interest in natural gas hydrate as energy source is increasing rapidly. Parallel to this, there is also a high focus on fluxes of methane from the oceans. A limited portion of the fluxes of methane comes directly from natural gas hydrates but a much larger portion of the fluxes involves hydrate mounds as a dynamic seal that slows down leakage fluxes. In this work we review some of the historical trends in kinetic modeling of hydrate formation and discussion. We also discuss a possible future development over to classical thermodynamics and residual thermodynamics as a platform for all phases, including water phases. This opens up for consistent thermodynamics in which Gibbs free energy for all phases are comparable in terms of stability, and also consistent calculation of enthalpies and entropies. Examples are used to demonstrate various stability limits and how various routes to hydrate formation lead to different hydrates. A reworked Classical Nucleation Theory (CNT) is utilized to illustrate that nucleation of hydrate is, as expected from physics, a nano-scale process in time and space. Induction times, or time for onset of massive growth, on the other hand, are frequently delayed by hydrate film transport barriers that slow down contact between gas and liquid water. It is actually demonstrated that the reworked CNT model is able to predict experimental induction times.

1. Introduction

While problems related to formation of hydrate in pipelines and process equipment dominated funding of hydrate research for at least four decades since around 1940, the focus is now much more varied. The need for new unconventional energy sources is a strong driver for massive investments in the development of technologies for making use of the huge resources of natural gas trapped in the form of hydrate. Japan and China are two examples of countries that are conducting full-scale production tests for the evaluation of different production technologies. There is a need for accurate models that are not only able to model stability limits of hydrate but also able to predict the kinetics of hydrate formation and dissociation. Injection of carbon dioxide in natural gas hydrate reservoirs for combined storage of carbon dioxide in the form of hydrate, and simultaneous release of methane gas for energy, is a novel and interesting concept that will also briefly be discussed later in this paper as an illustration of the theory.

The globally increasing interest for storage of carbon dioxide in aquifers will in some cases also involve conditions favorable for the formation of carbon dioxide hydrate. Even if this hydrate may not be unconditionally stable (see discussion under Section 3) it may slow down vertical transport and as such be positive for storage integrety. Hydrate formation in a horizontal direction from the injection pipe, on the other hand, will be negative for the spreading of the carbon dioxide plume in the aquifer reservoir.

Depleted hydrocarbon reservoirs have proven sealing structures (cap rock, shale) and are also interesting as candidates for carbon dioxide storage, Worldwide there are quite a number of these reservoirs that are in cold regions and have favorable conditions for carbon dioxide hydrate.

Historically, much of hydrate stability modeling has been focused around simplified thermodynamic models in which the differences in chemical potentials between liquid water and water in an empty hydrate structure have been treated as empirical fitting functions. Stability of guest molecules in hydrate and separate phases (gas, liquid, fluid) has typically been treated by fugacity formulations rather than classical thermodynamic formulations (chemical potentials).

The primary objective of this work is to present what we see as some important aspects in the development of hydrate phase transition kinetic models. We do not claim that the models that we propose and discuss here are the only ways forward. However, if this work can contribute to stimulating a modern debate on the complexity of hydrate phases in multiphase systems, then much is achieved. Hopefully, this can lead to more collaboration on solving important challenges in the modern understanding of hydrates in nature and industry.

Frequently, only temperature and pressure projections of hydrate stability limits are used in analysis of hydrate risk analysis in industry, or in analysis of natural gas hydrates in nature. A second objective of this work is to illustrate some other hydrate stability limits of importance for industrial systems and hydrates in nature.

A third motivation for this work is related to the balance between all independent thermodynamic variables in a multiphase system and the associated constraints. In addition to temperature and pressure, these independent thermodynamic variables also involve concentrations of all components in all phases. A multiphase system can only establish thermodynamic equilibrium if the number of independent variables can be solved using conservation laws and conditions of equilibrium. Whether we list all independent variables, and constraining equations, discretely and find how many variables we must specify for equilibrium to be possible, or we use the Gibbs phase rule is not the most critical. The important aspect is that we have to be aware if the system can reach equilibrium or not and what the possible consequences are. For the simplest of all systems with one hydrate former in a separate phase, liquid water and one hydrate phase, it is well known that we can at maximum define, or fix, one independent thermodynamic variable. Practically all systems of methane and liquid inside hydrate formation conditions in nature or industry are therefore non-equilibrium systems. The question is therefore what the consequences are of only using temperature and pressure to define hydrate stability.

The fourth motivation is to stimulate a development towards more proper use of classical thermodynamics in hydrate stability analysis rather than projection of hydrate stability limits in independent variables such as temperature and pressure. Super saturation is a commonly used term in hydrate phase transition kinetics. A typical example is sub-cooling temperature, defined by a temperature lower than a hydrate stability temperature for a given pressure. The problem is that temperature and pressure are both independent thermodynamic variables and not phase transition related properties such as chemical potentials and free energy.

Finally, we also hope that the kinetic models presented in this work, which are simple to use and numerically fast, can be useful to other researchers as model platforms for various applications.

A brief overview of the relationship between fugacity and classical thermodynamics is provided in Section 2 along with modeling of some important hydrate stability limits in Section 3. The classical thermodynamics is needed for Section 5.

In Section 4 we give a brief overview of the historical development of kinetic models for hydrate growth and dissociation. Many of these models are based on semi-empirical concepts and phenomenological models. One of the reasons might be that models and concepts from physics contain properties that were not easily available five decades ago. In Section 5 we give a brief overview of one of the simplest models, the classical nucleation theory (CNT), along with some possible modifications that make it possible to also utilize these types of approaches. This section is one of the most important sections of this paper, since one of the intentions is to illustrate that classical thermodynamics combined with molecular modeling opens up for kinetic modeling of any route to hydrate phase transition. This section is therefore the largest section.

Some possible directions in future research on hydrate phase transition dynamics are discussed in Section 6. Our conclusions are presented in Section 7.

2. Classical Thermodynamics, Statistical Mechanics and Fugacity

In classical thermodynamics, phase stability is related to Gibbs free energy in systems controlled by pressure and temperature, and Helmholtz free energy for systems controlled by volume and temperature. Chemical potentials involved determine distributions of components in various co-existing phases. Industrial use of cubic equations of state has motivated the use of fugacity rather than chemical potentials. Rigorously, the equilibrium conditions between two phases (gas and liquid as example) are derived from the combined first and second laws under constraints of conservation laws:

$$T^{(liquid)}=T^{(gas)}.$$

(1)

$$P^{(liquid)}=P^{(gas)}.$$

(2)

$${\mu }_i^{(liquid)}(T^{(liquid)},P^{(liquid)},{\overrightarrow{x}}^{(liquid)})={\mu }_i^{(gas)}(T^{(gas)},P^{(gas)},{\overrightarrow{y}}^{(gas)}).$$

(3)

T is temperature, and P is pressure and superscripts denote phase. The chemical potential ${\mu }_i^{(p)}$ is the chemical potential for component i in phase p. x denotes mole-fractions in liquid and y denotes mole-fractions in gas. The arrow on these denotes vector of mole-fractions. The fugacity of a component is defined as:

$$d{\mu }_i^{(p)}(T_{}^{(p)},P_{}^{(p)},{\overrightarrow{x}}^{(p)})=RTd\ln f_i^{(p)}(T_{}^{(p)},P_{}^{(p)},{\overrightarrow{x}}^{(p)}).$$

(4)

$$\frac{d{\mu }_i^{(p)}(T_{}^{(p)},P_{}^{(p)},{\overrightarrow{x}}^{(p)})}{RT}=d\ln f_i^{(p)}(T_{}^{(p)},P_{}^{(p)},{\overrightarrow{x}}^{(p)}).$$

(5)

Integration of right hand side under the assumption of thermal equilibrium (Equation (1)) and same integration limit for gas and liquid leads to the following replacement of (3) in a fugacity formulation:

$$f_i^{(liquid)}(T^{(liquid)},P^{(liquid)},{\overrightarrow{x}}^{(liquid)})=f_i^{(gas)}(T^{(gas)},P^{(gas)},{\overrightarrow{y}}^{(gas)}).$$

(6)

It might be useful at this stage to shed some light on the information that was lost in replacing Equation (3) with the fugacity expression. If we now return to the first law for an open system we can consider one of the phases. The liquid will be open towards gas and vice versa, and for simplicity we might consider the two phases as isolated. This is not needed, but is easier for illustration purposes.

$$d{\underset{-}{U}}^{(liquid)}=d{Q}^{(liquid)}-P^{(liquid)}d{\underset{-}{V}}^{(liquid)}+{\displaystyle \sum _{i=1}^n{\mu }_i^{(liquid)}d{N}_i^{(liquid)}}.$$

(7)

U is internal energy and the line beneath denotes extensive energy with the unit Joule. The line under the volume V denotes extensive volume in m³. N is number of moles and index i is a counter on components. The two first two terms are easy to understand and visualize. The first term is the added heat and the second term is delivered mechanical work. The last term is frequently denoted as the chemical work. In short, the work is needed to release (negative dN_i) molecules from the actual phase, and the opposite for positive dN_i. The chemical potential ${\mu }_i^{(liquid)}$ is the driving force for this release; this driving force consists of a necessary energy to release the molecules from attractions to surrounding molecules, and an entropy contribution related to rearrangements of the remaining molecules. The use of Equation (6) rather than Equation (7) removes this information from the calculation of phase distributions and phase equilibrium.

Classical thermodynamics is generally defined by differences in energy states and requires reference states. One specific reference state has a convenient connection to classical statistical mechanics. In the classical limit the momentum space (ideal gas) and configurational spaces (molecular interactions) are orthonormal. The associated canonical partition function is then:

$$\begin{array}{l}{\underset{-}{A}}^{(p)}=-N^{(p)}R\cdot T\cdot \ln Q^{(p)}=-N^{(p)}R\cdot T\cdot \ln Q_M^{(p)}{Q}_C^{(p)}\\ =-N^{(p)}R\cdot T\cdot \ln Q_M^{(p)}-N^{(p)}R\cdot T\cdot \ln Q_C^{(p)}\\ ={\underset{-}{A}}^{(p,idea\lg as)}(T,{\underset{-}{V}}^{(p)}){\underset{-}{+A}}^{(p,residual)}(T,{\underset{-}{V}}^{(p)})\end{array}$$

(8)

For each of the phases p the relationship between Helmholtz free energy A (line under denote extensive) and the canonical partition function Q is then given by Equation (8) below. Subscript M denotes canonical partition function in momentum space and subscript C denotes canonical partition function in configurational space. N is the number of moles. The orthonormal formulation in the last term on the right hand side is the classical limit. In terms of temperatures and pressures for hydrate formation, almost all conditions of hydrates in nature and industry fall into this category. Even hydrates formed at low temperatures down to −30 °C are in the classical regime.

Equation (8) can either be reformulated to Gibbs free energy, or the temperature, and volume dependence can be reformulated into a temperature/density dependency. In the latter case the density is calculated from an appropriate equation of state for the given condition of temperature and pressure (and Equations (1) and (2)). For rigid molecules, there are analytical solutions for molecular translation and rotation and integrals that can be easily solved for intramolecular movements. Interatomic vibrations are frequently small enough to be neglected while intramolecular rotations need to be accounted for. The second term in the final formulation is the effect of molecular interactions and is denoted as residual, as in residual thermodynamics.

We can now be more specific in the integrations of Equation (4) under the constraints of Equations (1) and (2). The ideal gas limit is reached when the partial pressure goes to the limit of zero. Since free energy-related properties depend on the entropy of mixing we need to integrate Equation (4) in two steps. Starting with pure components as ideal gas we then first integrate to a mixture of ideal gases and then integrate from ideal gas mixture to real phase (gas, liquid, fluid). In

Table 1. Residual thermodynamic integration scheme for chemical potential and fugacity.

Property	Pure Component Ideal Gas at T, P	Ideal Gas Mix $\mathbf{T}, \mathbf{P}, \overrightarrow{\mathit{x}}$	Real Fluid $\mathbf{T}, \mathbf{P}, \overrightarrow{\mathit{x}}$
${\mu }_i^{(p)}(T_{}^{(p)},P_{}^{(p)},{\overrightarrow{x}}^{(p)})$	${\mu }_i^{(p,pure)}(T_{}^{(p)},P_{}^{(p)})$	$\begin{array}{l}{\mu }_i^{(p,pure)}(T_{}^{(p)},P_{}^{(p)})\\ +RT\ln x_i\end{array}$	$\begin{array}{l}{\mu }_i^{(p,pure)}(T_{}^{(p)},P_{}^{(p)})\\ +RT\ln x_i\\ +RT\ln {\varphi }_i^{(p)}(T_{}^{(p)},P_{}^{(p)},{\overrightarrow{x}}^{(p)})\end{array}$
$f_i^{(p)}(T_{}^{(p)},P_{}^{(p)},{\overrightarrow{x}}^{(p)})$	$P_{}^{(p)}$	$P_{}^{(p)}{x}_i$	$P_{}^{(p)}{x}_i{\varphi }_i^{(p)}(T_{}^{(p)},P_{}^{(p)},{\overrightarrow{x}}^{(p)})$

we list the various steps towards the final result for fugacity as used in Equations (3) and (6) respectively. ${\varphi }_i^{(p)}$ is the fugacity coefficient for component i in phase p, which is defined as the fugacity of component I divided by the partial pressure of component i in the mixture. This is trivially given by any equation of state.

The same reference state is utilized for chemical potential as for fugacity, but the ideal gas difference between components is lost in the fugacity formulation.

Ideal gas as reference state is of course convenient and the closest reference for gas phase. From the first publication of the original van der Waal equation of state, numerous cubic equations of state have been published. In the oil and gas industry, the Soave-Redlich-Kwong [1] and Peng-Robinson [2] are among the most popular since these models have proven accurate enough also for liquid hydrocarbons in term of mole-fraction ratios (mole-fraction of i in gas divided by mole-fraction of i in liquid). Two other integration limits for (4) will be useful for the rest of this work. For complex liquids, such as, for instance, water containing additives and/or impurities, pure liquid water may be more appropriate. In

Table 2. Symmetric excess integration scheme for chemical potential and fugacity.

Property	Pure Component Liquid at T, P	Ideal Liquid Mix $\mathbf{T}, \mathbf{P}, \overrightarrow{\mathit{x}}$	Real Fluid $\mathbf{T}, \mathbf{P}, \overrightarrow{\mathit{x}}$
${\mu }_i^{(p)}(T_{}^{(p)},P_{}^{(p)},{\overrightarrow{x}}^{(p)})$	${\mu }_i^{(p,pure)}(T_{}^{(p)},P_{}^{(p)})$	$\begin{array}{l}{\mu }_i^{(p,pure)}(T_{}^{(p)},P_{}^{(p)})\\ +RT\ln x_i\end{array}$	$\begin{array}{l}{\mu }_i^{(p,pure)}(T_{}^{(p)},P_{}^{(p)})\\ +RT\ln x_i\\ +RT\ln {\gamma }_i^{(p)}(T_{}^{(p)},P_{}^{(p)},{\overrightarrow{x}}^{(p)})\end{array}$
$f_i^{(p)}(T_{}^{(p)},P_{}^{(p)},{\overrightarrow{x}}^{(p)})$	$\begin{array}{l}{f}_i^{(p,pure)}(T_{}^{(p)},P_{{}_i^{}}^{(p)})\\ ={\varphi }_i^{(p,pure)}(T_{}^{(p)})\\ \cdot P_{{}_i^{}}^{(p,saturated)}(T_{}^{(p)})\\ \cdot {\mathrm{e}}^{{\displaystyle \underset{P_{{}_i^{}}^{(p,saturated)}}{\overset{P}{\int }}\frac{V_i^{p,pure}}{RT}dP}}\end{array}$	$\begin{array}{l}{f}_i^{(p,pure)}(T_{}^{(p)},P_{{}_i^{}}^{(p)})x_i\\ =x_i{\varphi }_i^{(p,pure)}(T_{}^{(p)})\\ \cdot P_{{}_i^{}}^{(p,saturated)}(T_{}^{(p)})\\ \cdot {\mathrm{e}}^{{\displaystyle \underset{P_{{}_i^{}}^{(p,saturated)}}{\overset{P}{\int }}\frac{V_i^{p,pure}}{RT}dP}}\end{array}$	$\begin{array}{l}{f}_i^{(p)}(T_{}^{(p,pure)},P_{{}_i^{}}^{(p)})x_i{\gamma }_i(T_{}^{(p)},P_{{}_i^{}}^{(p)},\overrightarrow{x})\\ =x_i{\varphi }_i^{(p,pure)}(T_{}^{(p)})\\ \cdot P_{{}_i^{}}^{(p,saturated)}(T_{}^{(p)})\\ \cdot {\mathrm{e}}^{{\displaystyle \underset{P_{{}_i^{}}^{(p,saturated)}}{\overset{P}{\int }}\frac{V_i^{p,pure}}{RT}dP}}\\ \cdot {\gamma }_i(T_{}^{(p)},P_{{}_i^{}}^{(p)},\overrightarrow{x})\end{array}$

we list a similar comparison.

${\gamma }_i^{(p)}(T_{}^{(p)},P_{}^{(p)},{\overrightarrow{x}}^{(p)})$ is the activity coefficient for component i in the liquid mixture. Asymptotic value of the activity coefficient is 1.0 for component i when mole-fraction of i approaches 1.0. In this scheme the saturation pressure for the actual temperature is used as a reference point in the fugacity formulation. This is not generally needed in the chemical potential formulation since pure component chemical potentials for liquids can be calculated from molecular simulations using verified models for interactions. One example for this can be found from Kvamme and Tanaka [3]. Kvamme and Tanaka [3] utilized the TIP4P [4] interaction potential for water to calculate chemical potentials for water as ice and water in empty hydrates of structure I and II. Experimental data for enthalpy of water dissociation at zero °C, and specific heat capacity for liquid water were utilized to calculate also chemical potentials for liquid water. These chemical potentials are for 1 bar pressure, but are trivially corrected to higher pressures by a simple Poynting correction, since the density of water is almost constant. The fugacity scheme utilizes saturation pressure for the actual temperature as a “helping point”. The fugacity coefficient for the gas phase for a pure component is equal to the fugacity coefficient for pure liquid at the saturation curve, and the recalculation of fugacity back to the real pressure, from the “helping point”, is frequently a factor close to unity except for high pressures. Examples of the use of this scheme can be found elsewhere for water containing various amounts of methanol [5]. In principle also the fugacity scheme can be used without utilization of the “helping point” at saturation curve if an accurate equation of state is available for pure water.

Yet another scheme is useful in this work. Many hydrate formers have very limited solubility in water. In

Table 3. Asymmetric excess integration scheme for chemical potential and fugacity.

Property	Pure Component Liquid at T, P	Ideal Liquid Mix $\mathbf{T}, \mathbf{P}, \overrightarrow{\mathit{x}}$	Real Fluid $\mathbf{T}, \mathbf{P}, \overrightarrow{\mathit{x}}$
${\mu }_i^{(p,\infty )}(T_{}^{(p)},P_{}^{(p)},{\overrightarrow{x}}^{(p)})$	${\mu }_i^{(p,\infty )}(T_{}^{(p)},P_{}^{(p)})$	$\begin{array}{l}{\mu }_i^{(p,\infty )}(T_{}^{(p)},P_{}^{(p)})\\ +RT\ln x_i\end{array}$	$\begin{array}{l}{\mu }_i^{(p,\infty )}(T_{}^{(p)},P_{}^{(p)})\\ +RT\ln x_i\\ +RT\ln {\gamma }_i^{(p,\infty )}(T_{}^{(p)},P_{}^{(p)},{\overrightarrow{x}}^{(p)})\end{array}$
$f_i^{(p)}(T_{}^{(p)},P_{}^{(p)},{\overrightarrow{x}}^{(p)})$	$f_i^{(p,\infty )}(T_{}^{(p)},P_{{}_i^{}}^{(p)})$	$f_i^{(p,\infty )}(T_{}^{(p)},P_{{}_i^{}}^{(p)})x_i$	$f_i^{(p)}(T_{}^{(p)},P_{{}_i^{}}^{(p)})x_i{\gamma }_i^{p,\infty }(T_{}^{(p)},P_{{}_i^{}}^{(p)},\overrightarrow{x})$

we list chemical potential formulation and fugacity formulation for a component i in a solvent p (such as, for instance, water). A more appropriate reference state may therefore be infinite dilution in liquid water. The symbol ∞ in the superscript denotes infinite dilution in the solvent. For the activity coefficient, the asymptotic limit is 1.0 for infinite dilution of I in the solvent. Infinite symbol in superscript on volume denotes molar volume at infinite dilution in solvent. Chemical potential for i at infinite dilution in solvent can be estimated from model systems in molecular simulations but has to be verified towards experimental solubility data in a similar way as a fugacity formulation has to be verified towards experimental data.

Since the compressibility of liquid water is small, the fugacity formulation may be reformulated as:

$$\begin{array}{l}{f}_i^{(p)}(T_{}^{(p)},P_{{}_i^{}}^{(p)})x_i{\gamma }_i^{p,\infty }(T_{}^{(p)},P_{{}_i^{}}^{(p)},\overrightarrow{x})\\ =f_i^{(p,\infty )}(T_{}^{(p)},P_{{}_i^0}^{(p)})\cdot {\mathrm{e}}^{{\displaystyle \underset{P_{{}_i^0}^{(p)}}{\overset{P}{\int }}\frac{V_i^{p,\infty }}{RT}dP}}\\ \cdot x_i\cdot {\gamma }_i^{p,\infty }(T_{}^{(p)},P_{{}_i^{}}^{(p)},\overrightarrow{x})\\ \approx f_i^{(p,\infty )}(T_{}^{(p)},P_{{}_i^0}^{(p)})\cdot {\mathrm{e}}^{{\displaystyle \underset{P_{{}_i^0}^{(p)}}{\overset{P}{\int }}\frac{V_i^{p,\infty }}{RT}dP}}\\ \cdot x_i\cdot {\gamma }_i^{p,\infty }(T_{}^{(p)},P_{{}_i^0}^{(p)},\overrightarrow{x})\end{array}$$

(9)

The latest approximation reflects the activity coefficient for the solute in an almost incompressible liquid, such as water.

3. Hydrate Stability Limits and Sub-Cooling

Stability limits are always the maximum possible limits that can be achieved, and there are many such stability limits since hydrate can form in many ways in a real system in nature, or in an industrial situation related to multiphase flow with a separate water phase or water dissolved in a hydrate forming gas (or liquid). The most typical stability limits are related to heterogeneous hydrate formation on water/gas interface.

The first step in any stability limit analysis is to find out how many degrees of freedom there are in the system. This can be trivially counted by listing all the independent thermodynamic variables and then subtracting both conservation laws and conditions of equilibrium. For water and methane, as a simple example, we end up with 12 independent thermodynamic variables and 11 constraints (conservation laws and conditions of equilibrium). This means that only one independent variable can be defined. When this variable is defined the equations for conservation and thermodynamic equilibrium can be solved for all other independent variables. The Gibbs phase rule expresses the same net summation in a more compressed form but the advantage of doing the summation in more generally is the analysis of relevant phases that can lead to hydrate formation, and also of components that do not participate in phase transitions. An example of the latter is ions in water. Within reasonable accuracy they stay in water permanently and affect the thermodynamics of water involved in the hydrate formation (or dissociation). Ions can upconcentrate, but unless they form solid salts they do not participate in any hydrate phase transitions and cannot enter hydrate cavities. In real natural hydrate systems, and in experiments using saline water, pockets of water with high concentrations of ions can be encapulated by hydrate.

In the classical thermodynamic formulation we the use chemical potentials directly. The chemical potential of water in hydrate can be expressed according to Kvamme and Tanaka [3] as:

$${\mu }_{H_{2}O}^H={\mu }_{H_{2}O}^{O,H}-{\displaystyle \sum }_{k=1,2}RT{v}_k\ln \left(1+{\displaystyle \sum }_i{h}_{ki}\right)$$

(10)

${\mu }_{H_{2}O}^{O,H}$ denotes water chemical potential in an empty clathrate. Number of cavities is ν. Subscript k denotes large and small cavities respectively. Structure I is the main focus in this overview on thermodynamics and for this structure ν_øarge = 3/24 and ν_small = 1/24. Within the scope of this work it is assumed that only one guest molecule can enter a cavity. The harmonic oscillator approach model can be expressed as:

$$h_{ki}=e^{\beta \left[{\mu }_{ki}-\Delta g_{ki}\right]}$$

(11)

${\mu }_{ki}$ is the chemical potential for molecule type i in cavity type k. It is assumed that small and large cavities are at equilibrium, such that:

$${\mu }_{l\arg e_i}={\mu }_{smal{l}_i}$$

(12)

i.e., for a system at equilibrium the chemical potential for a guest molecule in a cavity is equal to the chemical potential for the same molecule in the other cavities in the hydrate. Δg_k1 is the free energy change for inclusion for guest molecule i in a cavity of type k.

The most typical example is a hydrate former phase (gas, liquid, supercritical) in contact with liquid (or ice) water. Under favorable conditions hydrate will form heterogeneously on the interface. For these three phases there are 12 independent thermodynamic variables, 3 conservation laws and 8 conditions of equilibrium. We can then fix only one independent thermodynamic variable. The most common choices are T or P. For this particular case equation of equilibrium we have:

$$h_{ki}=e^{\beta \left[{\mu }_i^{gas}(T,P,\overrightarrow{x})-\Delta g_{ki}\right]}$$

(13)

for the equilibrium between the gas and the hydrate, the chemical potential for the guest that enters hydrate is the same as in the original phase. The expression can be found in the last column of Table 1 for chemical potential as well as for fugacity needed in the more common formulations.

The formulation due to van der Waal and Platteeuw [6] ends up with the same result as (10) but only for a rigid water lattice in the hydrate. The approach by Kvamme and Tanaka [3] have results based on rigid hydrate water lattice as well as dynamic water lattice, in which distortions for large guest molecules movements can be accounted for in an appropriate way by sampling frequecies of molecular movements that interferes with librational frequencies for water in the lattice. See Kvamme and Tanaka [3] and Kvamme et al. [7] for a more detailed discussion. The fugacity formulation for the cavity partition function can be written as:

$$h_{ki}=f_i^{gas}(T,P,\overrightarrow{x})C_{ki}(T)=x_i{\varphi }_i(T,P,\overrightarrow{x})P{C}_{ki}(T)$$

(14)

The Langmuir constant $C_{ki}(T)$ for a molecule i in cavity k is given below as Equation (15). In the simplest case of monoatomic spherical guest molecules, the Langmuir constant is a simple integral over the Boltzmann factors of interaction energies between the guest molecule and surrounding waters:

$$C_{ki}(T)=\frac{1}{k_{B}T}{\displaystyle \iiint e^{\beta \left[{\phi }_{iw}(x,y,z)\right]}}dxdydz$$

(15)

For non-linear, multi-atomic representations of guest molecules, the integration will involve rotational degrees of freedom. Guest-guest interactions, between guests in different cavities, are also significant [8]. Polar guest molecules, such as, for instance, H₂S, will also obtain extra stabilization from coulumbic interactions between the partial charges in H₂S and water molecules in the cavity lattice [9]. For CO₂, on the other hand, the quadropole moment will result in a destabilization effect [10]. However, for now Equation (13) serves as sufficient illustration. Various simplifications of (13) can be found in [11].

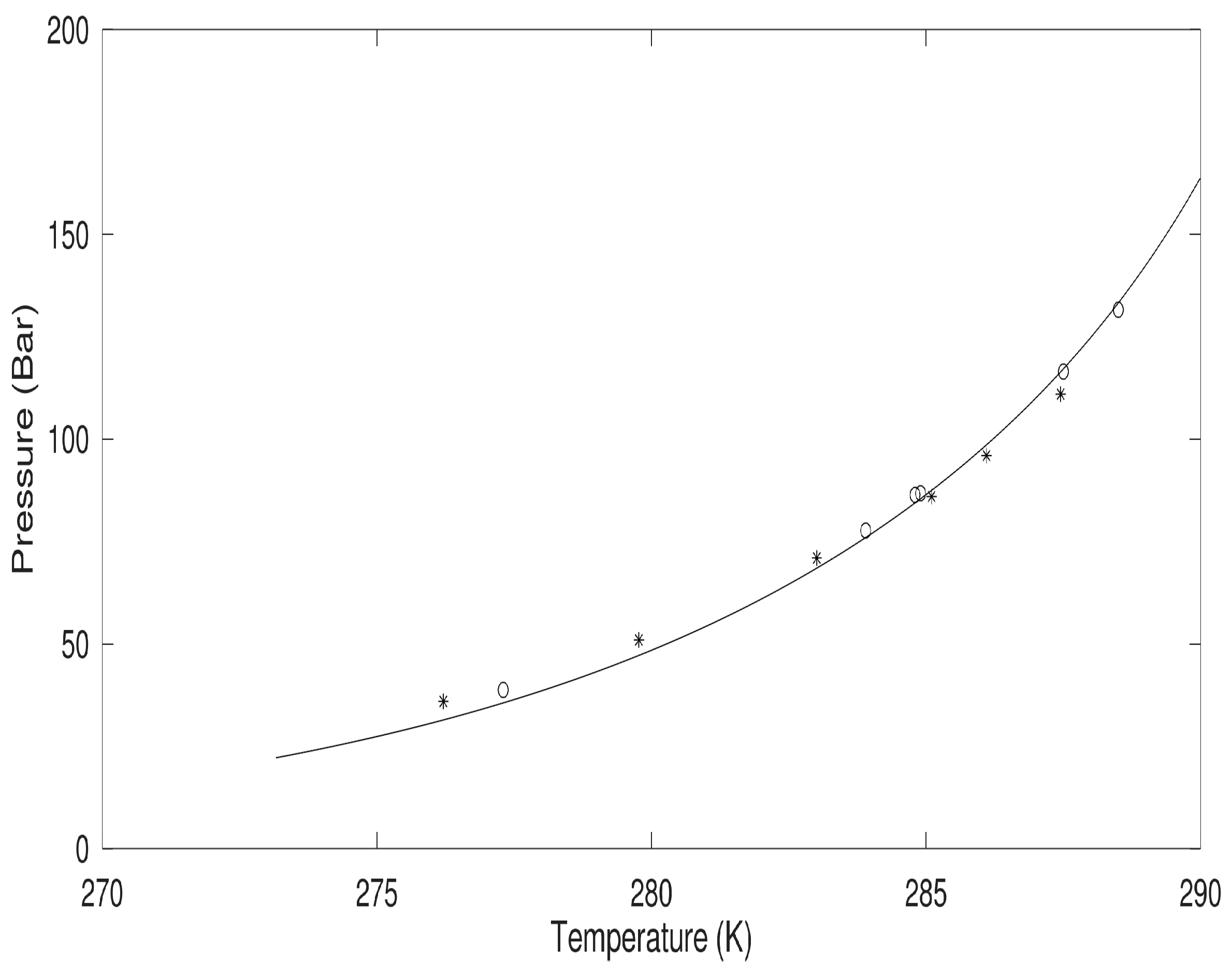
As mentioned above, we use the classical thermodynamic approach to illustrate the stability limit in temperature and pressure for methane hydrate. This is accomplished by setting the chemical potential of water in hydrate, according to Equation (10), equal to chemical potential for pure water according to the last column in Table 2. For pure water, the activity coefficient is 1 and mole-fraction water is 1. The actual values of empty hydrate in Equation (10) are calculated based on Kvamme and Tanaka [3] and so also for liquid water chemical potential. With gas chemical potential equal to chemical potential in large and small cavities of the hydrate it ends up with one equation in the unknown pressure for defined temperatures. The solution is given in Figure 1 below. This figure is actually a verification of the free energy model since chemical potentials for water and guests are used in the solutions that resulted in Figure 1. The chemical potentials and hydrate free energy are plotted in Figure 2.

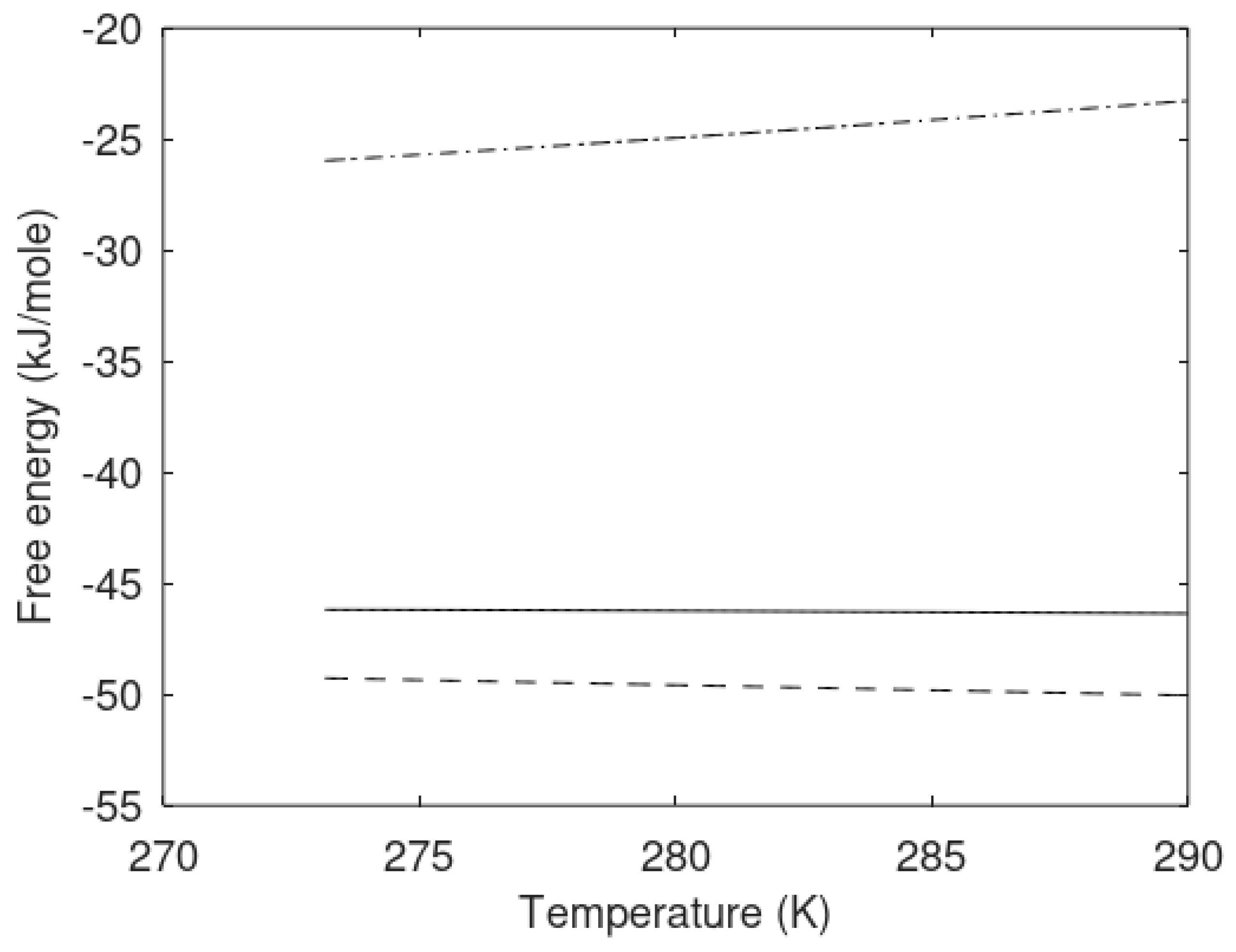
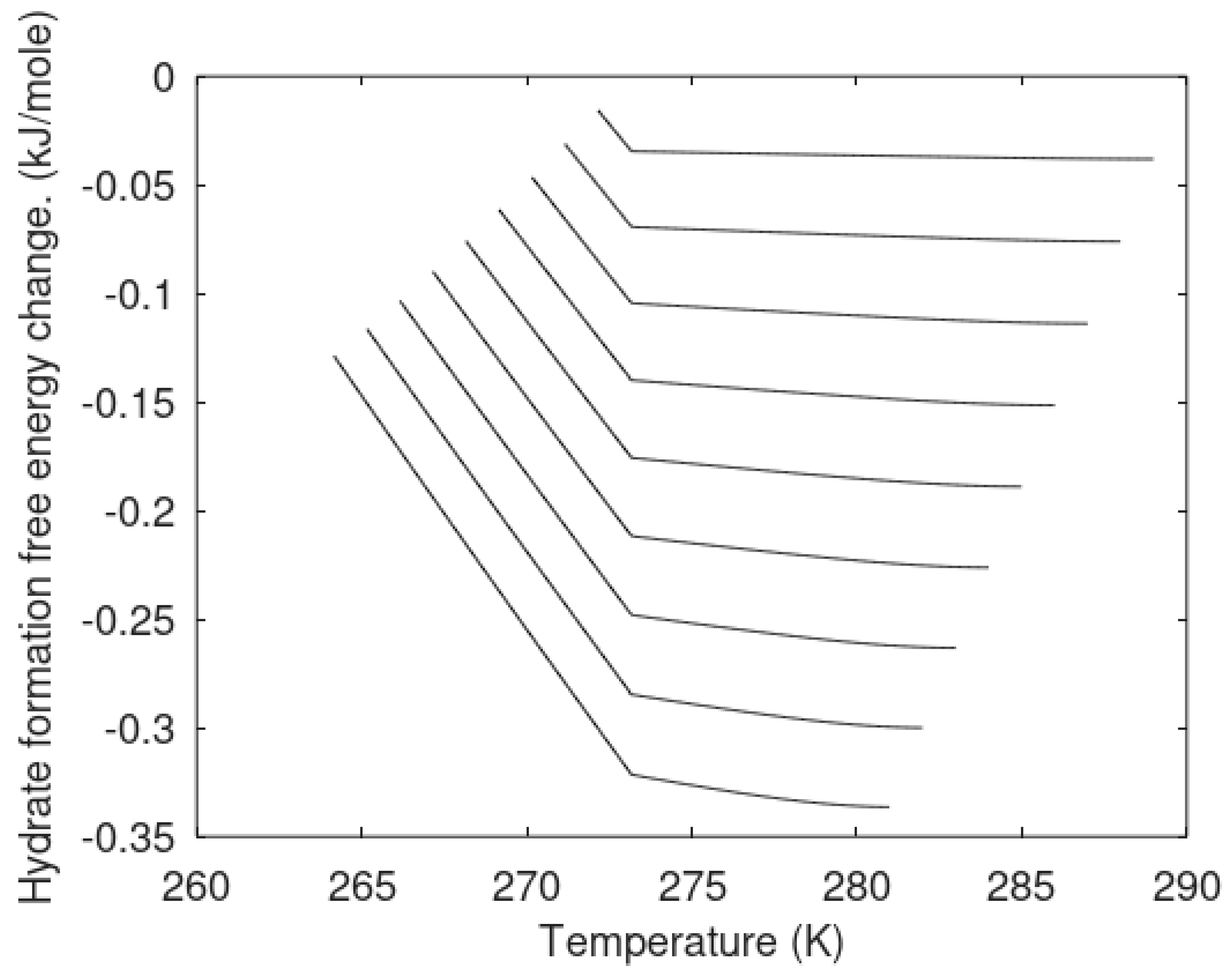
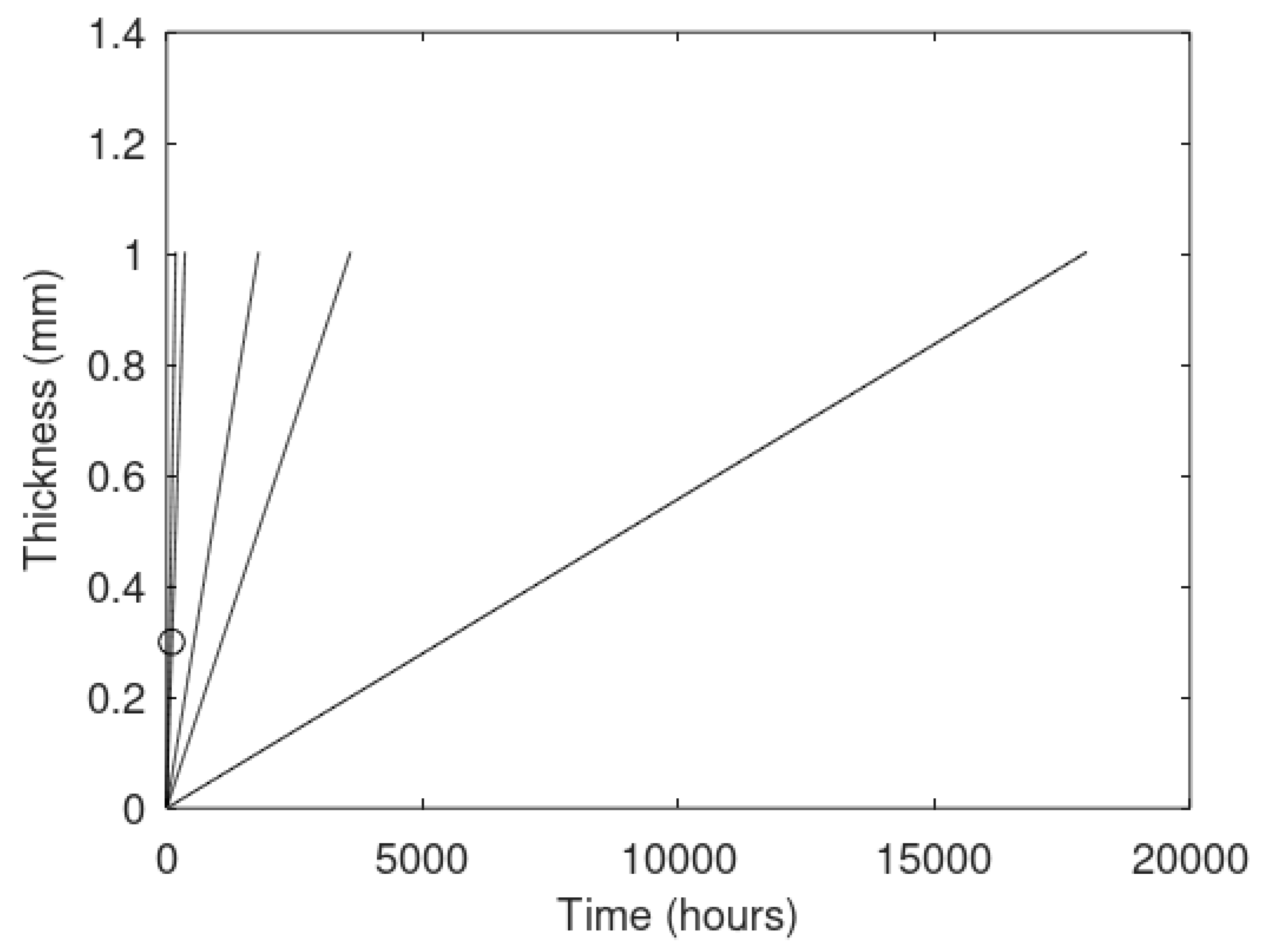
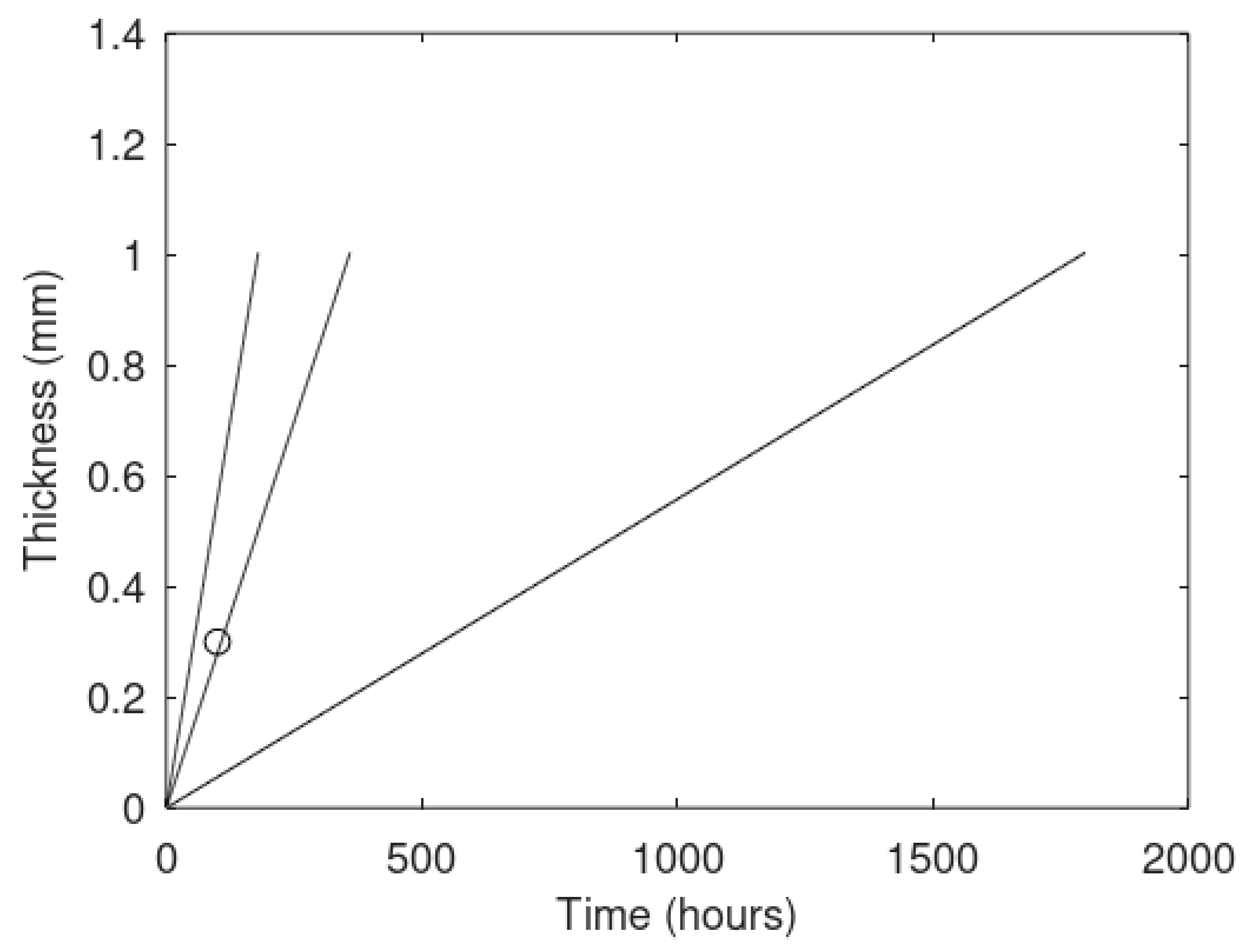
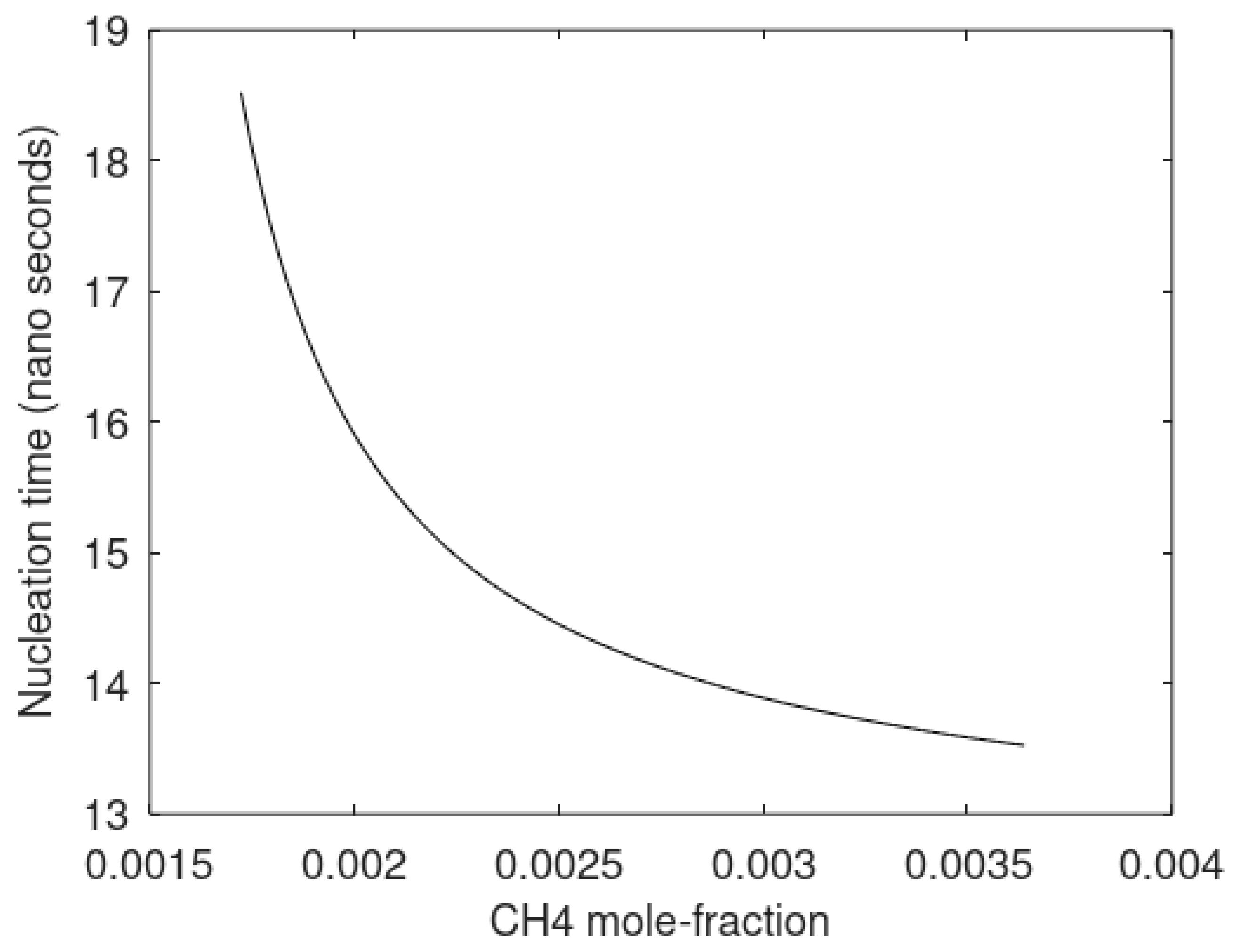
The primary focus of this work is modeling of the kinetics of hydrate formation and dissociation and choice of thermodynamic platform. Driving forces for hydrate formation are typically plotted in terms of sub-cooling temperature. However, temperature and pressure are independent thermodynamic variables and it is therefore relevant to also illustrate what specific sub-cooling temperatures actually mean in terms of thermodynamic driving force. In Figure 3 we therefore plot free energy differences for hydrate minus liquid water (or ice) for specific sets of sub-cooling temperatures for the pressures from Figure 1.

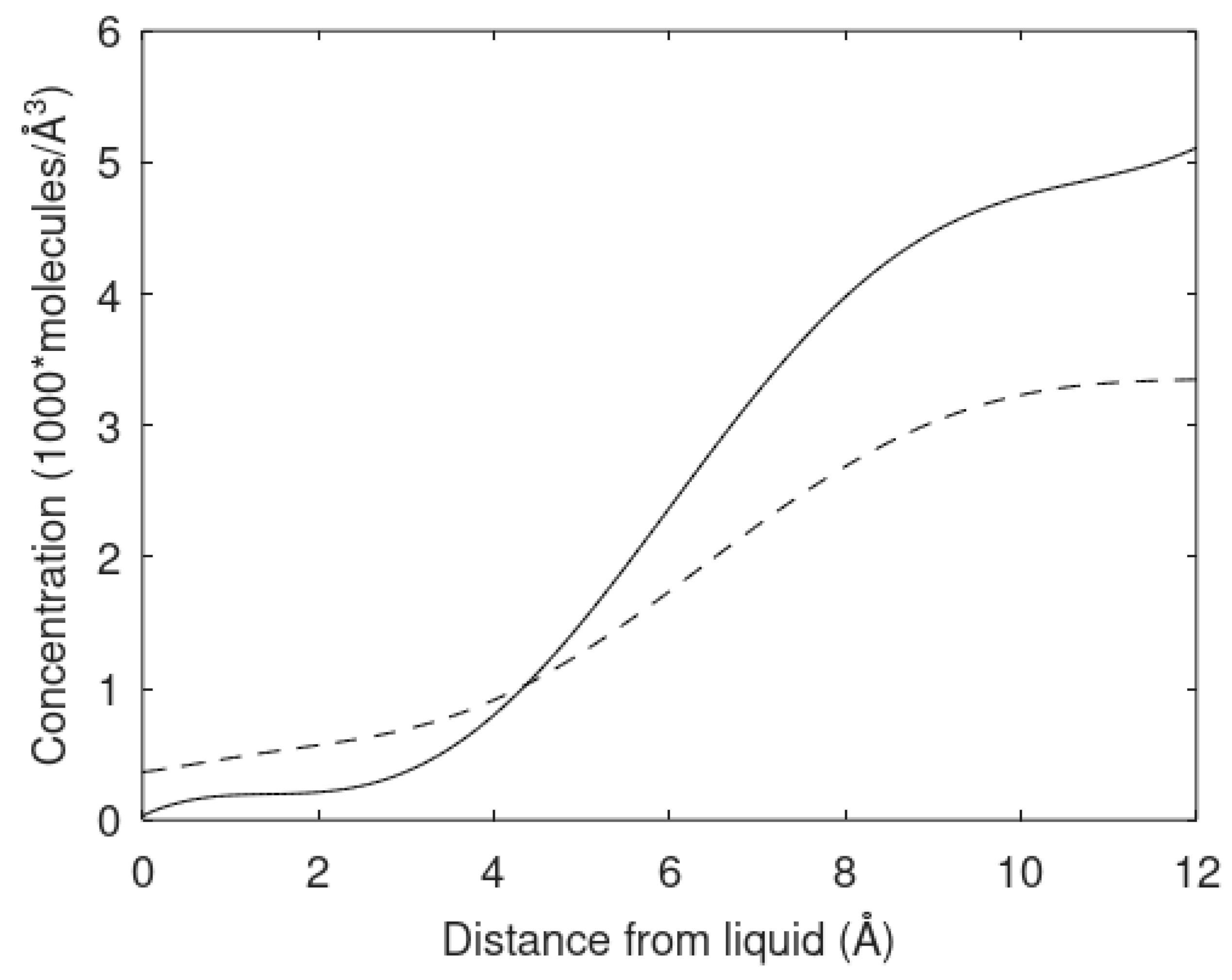
There are several other hydrate stability limits. As discussed elsewhere [10], mineral surfaces can stimulate hydrate nucleation by direct and indirect adsorption of hydrate formers. However, hydrate cannot remain close to mineral surfaces. There are two ways to argue for this. The partial charges of mineral atoms in the surface will never be compatible with average charge distribution of water molecules on the hydrate. From a thermodynamic point of view the chemical potential of adsorbed water in the range of the first two-to-three density maximums from the mineral surface are substantially lower than what is possible for hydrate water. In this respect a mineral surface is a thermodynamic hydrate inhibitor. Mineral surfaces will therefore be separated from hydrate with minimum distances in the range of 3 to 4 nm as minimum. However, due to molecular transport (diffusion) and other transport processes (hydrodynamics) the separation between hydrate and minerals will normally be substantially larger. Even in permafrost hydrates it is rare to find concentrations of hydrates higher than 85 per cent of pore volume.

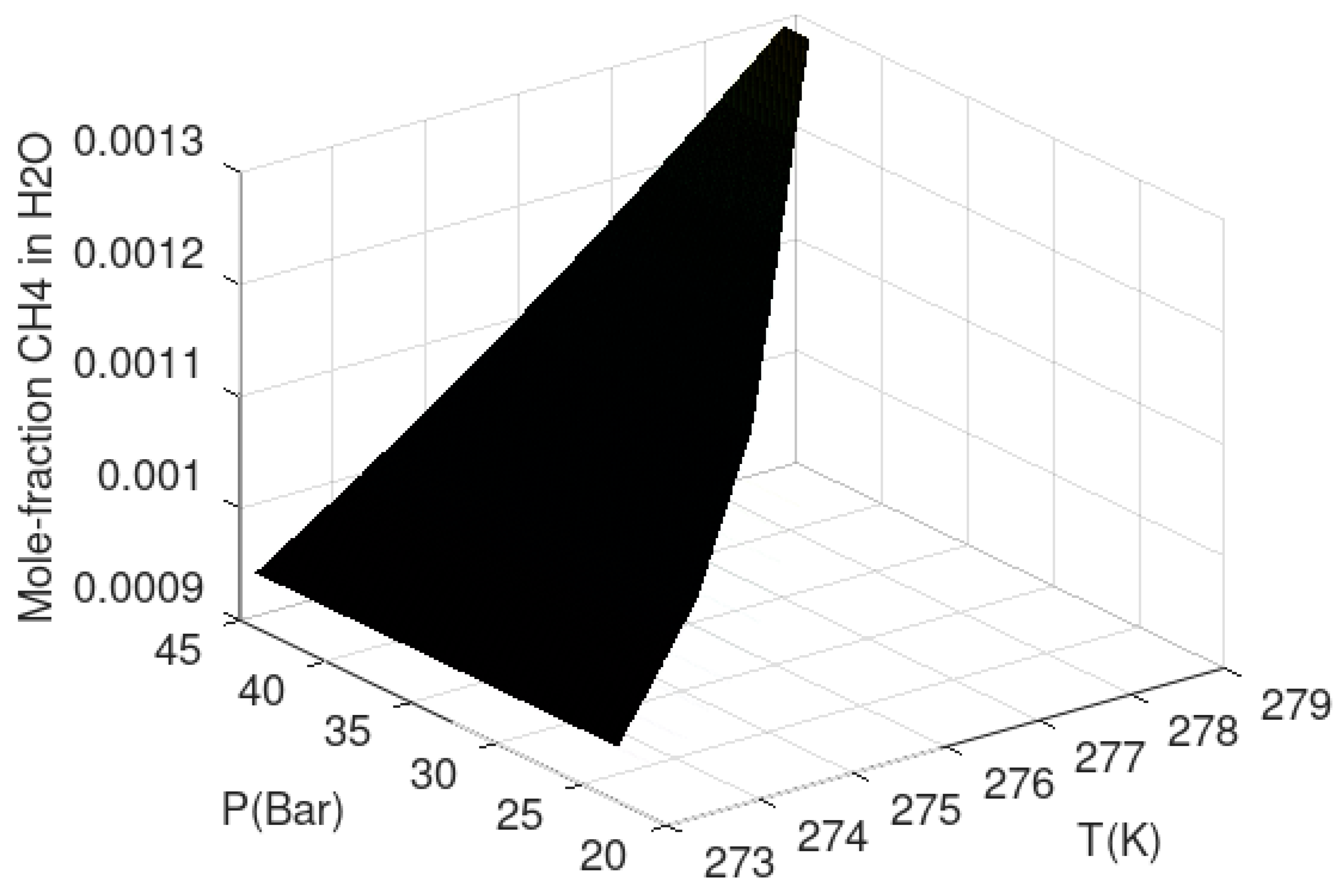
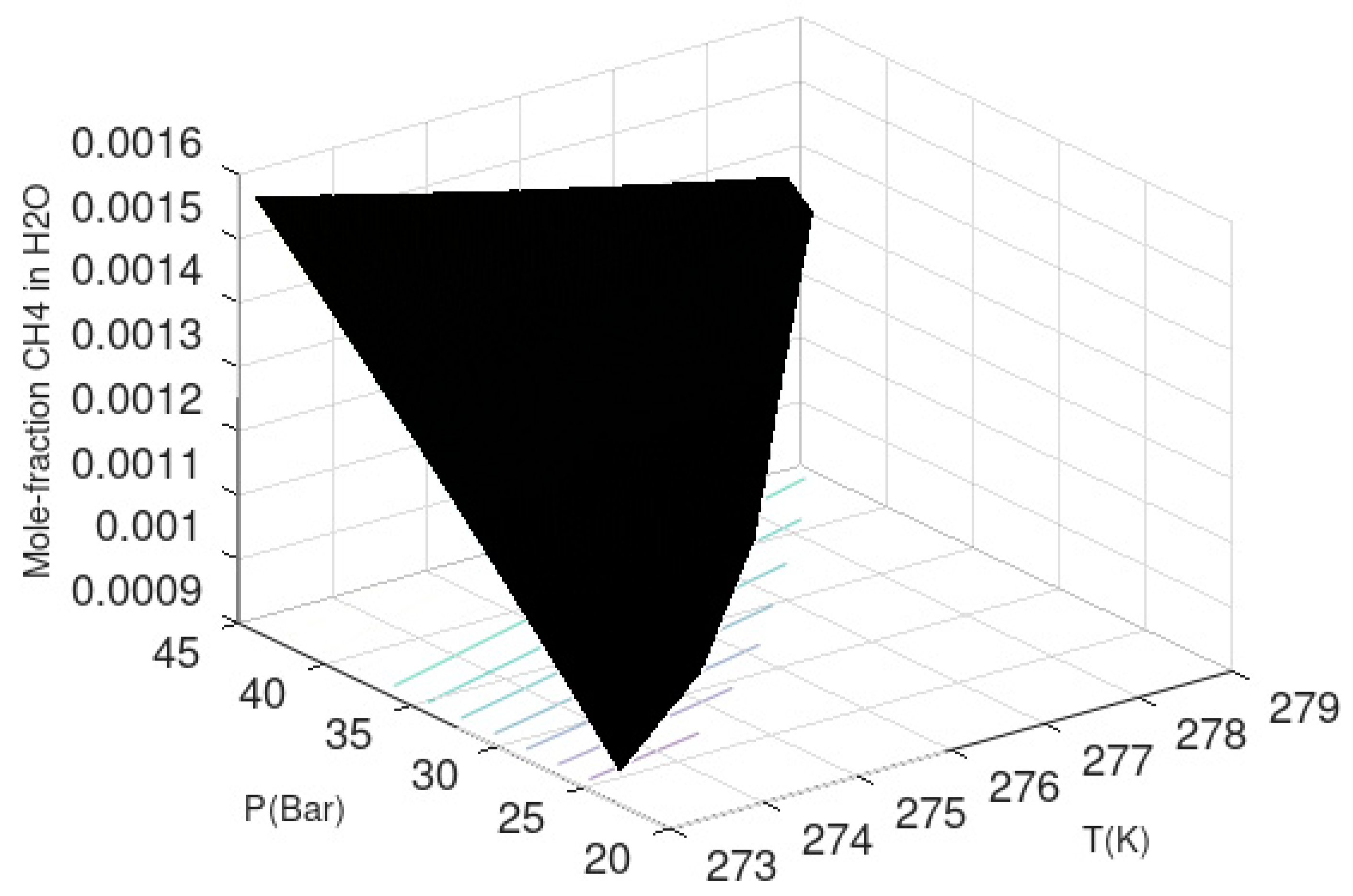
Yet another hydrate stability limit is related to the concentration of hydrate former in the contacting liquid water phase. This limit is often related to solubility in the hydrate region since it can be experimentally observed as a lower liquid water concentration in the hydrate formation region than in the regions outside hydrate formation. In thermodynamic terms these lower concentrations inside hydrate formation condition of temperature and pressure are hydrate stability limit concentration. The fact that hydrates form is because it is a more stable phase for water than liquid water. Hydrate will therefore dominate the concentration of hydrate former in the connecting liquid water phase. There are two practical consequences of this. Hydrate can form homogeneously from dissolved hydrate former if the concentration is higher than the hydrate stability concentration and lower than the liquid solubility concentrations. For offshore natural gas hydrate, fracture systems can lead to inflow of seawater from above. The incoming seawater has normally limited hydrocarbon content–typically almost infinite dilution. The chemical potential for methane at infinite dilution is lower than the chemical potential for methane in the hydrate and the hydrate dissociated. Visible evidences of this type of stability limit can be found all over the world in the form of methane fluxes from hydrate reservoirs. Most offshore hydrates are in a dynamic balance between formation of new hydrate from upcoming hydrocarbons and dissociation of hydrate towards incoming seawater. A more representative hydrate stability limit graph for natural gas hydrates in porous media is plotted in Figure 4 below. A 3D graph is not easy to read quantitatively. The plot is, however, intended as an illustration in the context of this work. This curve is constructed using chemical potential for methane in water according to the asymmetric convention (last column in Table 3) instead of the chemical potential for methane gas. For each set of temperature and pressure the mole-fraction methane in water is solved iteratively to satisfy equal chemical potential for water in hydrate and liquid water.

See Kvamme et al. [7] and Kvamme [14] for model parameters and further details.

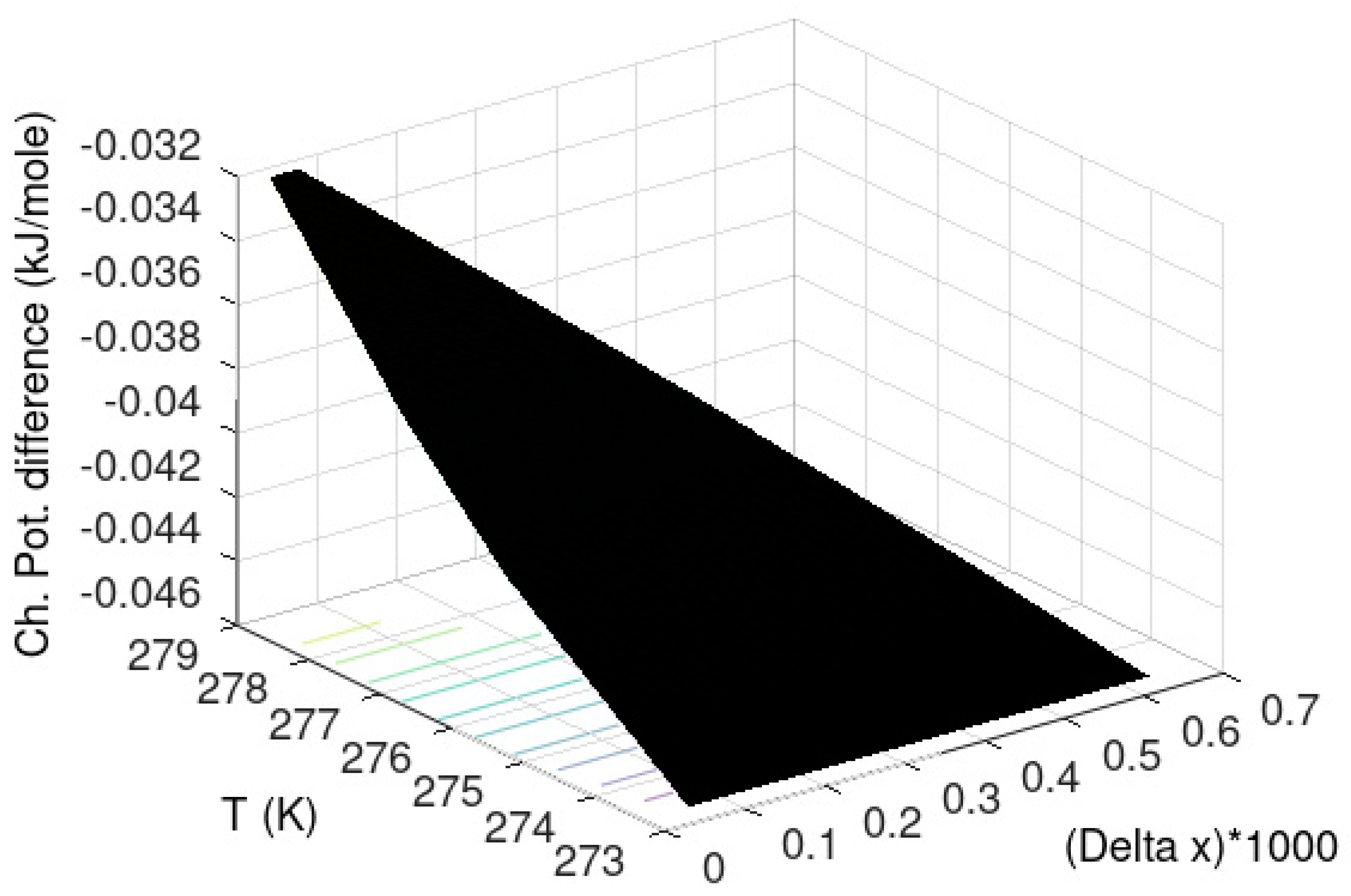
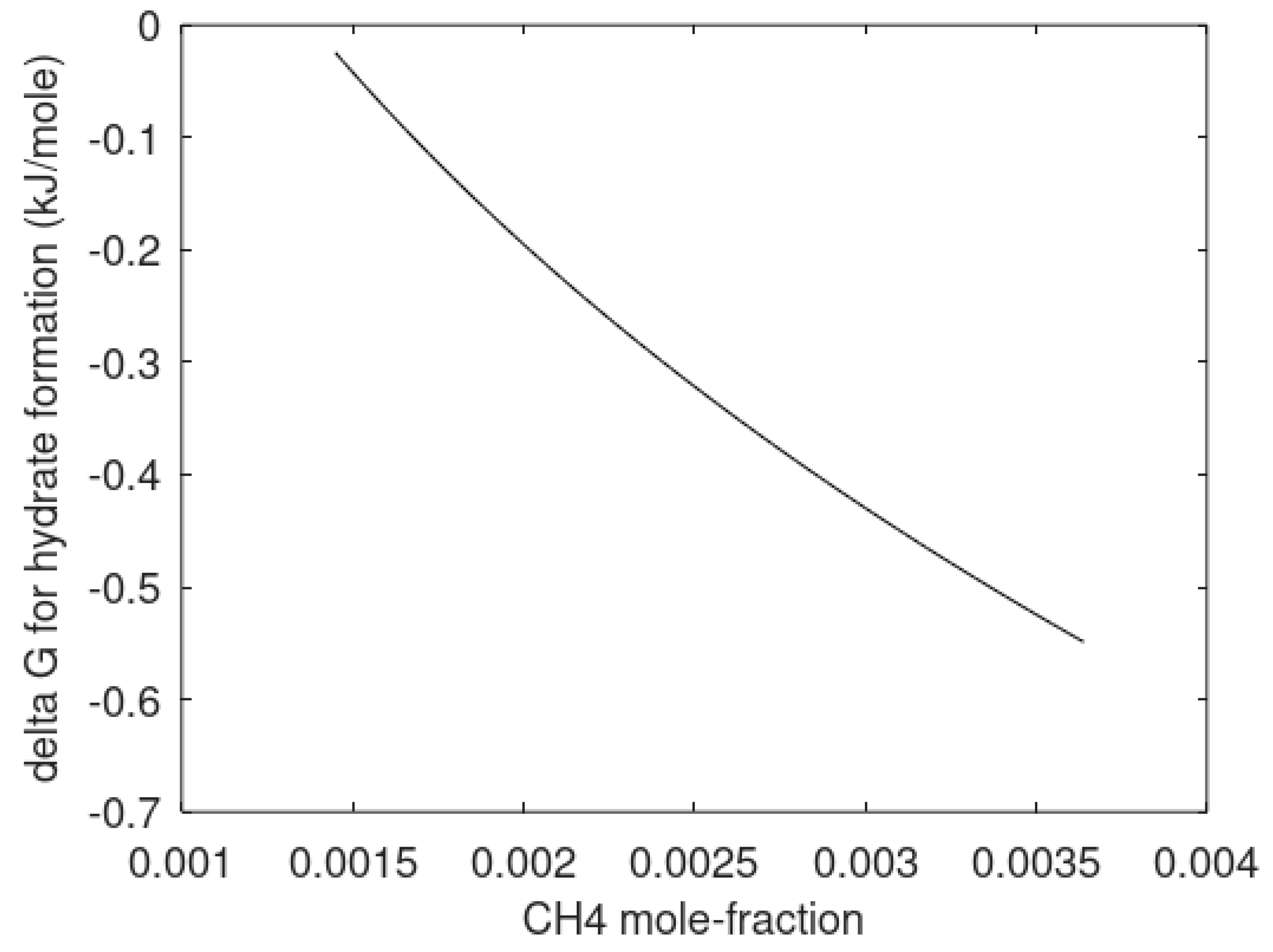
The maximum supersaturation possible for homogeneous hydrate formation is the difference between the liquid solubility of methane and the hydrate stability limit concentration. This is calculated for any defined P and T by solving iteratively for same chemical potential of methane in gas (last column in Table 1) as chemical potential of methane in water (last column in Table 3). This is plotted in Figure 5 for the same conditions of P and T as Figure 4. Hydrate can form for all mole-fraction of methane solubility which are higher that hydrate stability limits in Figure 4 but here we only plot results for maximum supersaturation. These are plotted in the form of chemical potential difference between water in hydrate and water in liquid and plotted for all the same temperatures and pressures as in Figure 4 and Figure 5.

The calculated results plotted in Figure 4 and Figure 5 have been verified towards experimental data elsewhere [7,14,15,16].

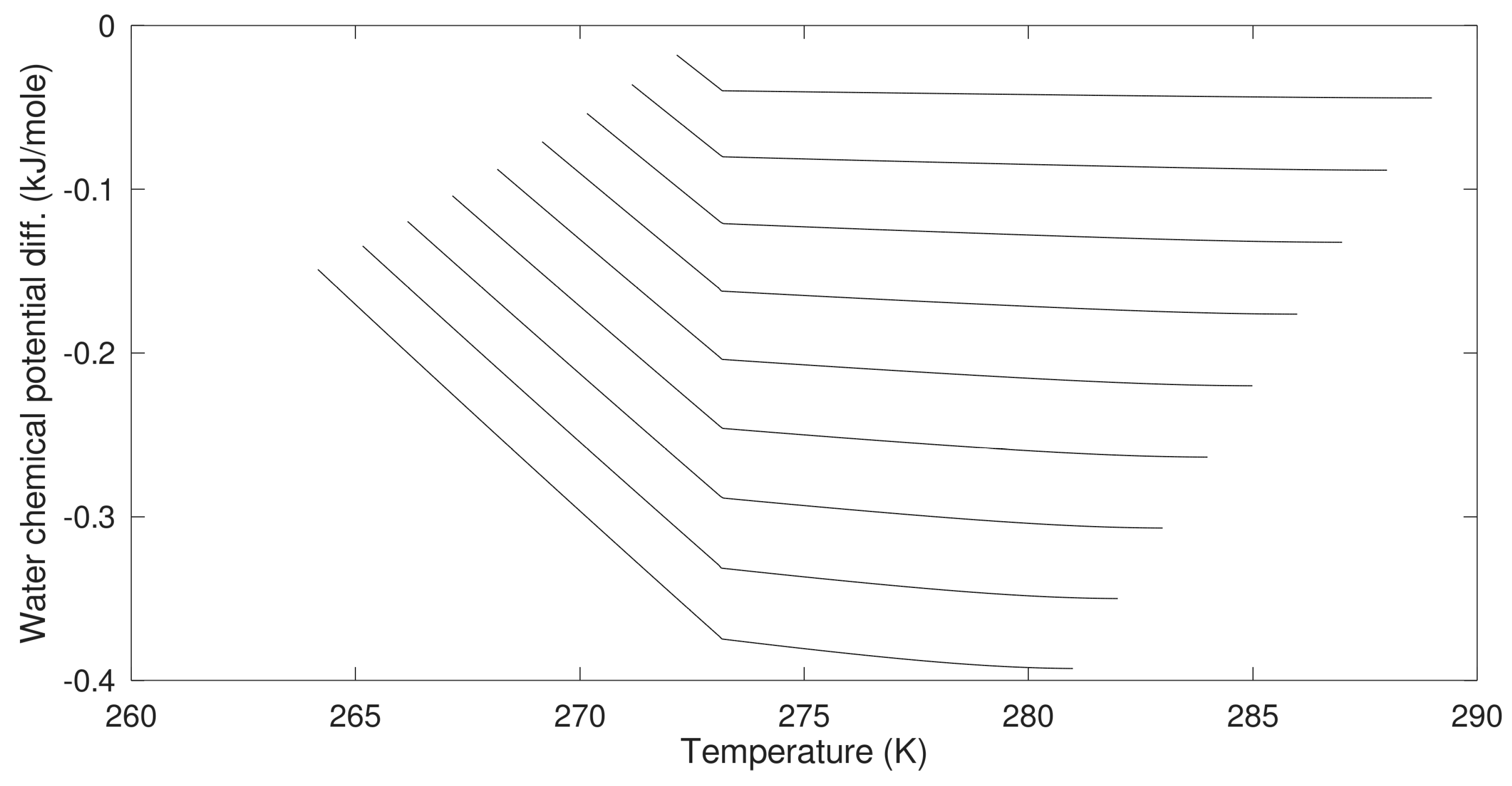
In Figure 6 we plot the difference in chemical potential for water in hydrate and liquid water as the supersaturation in thermodynamic formulation.

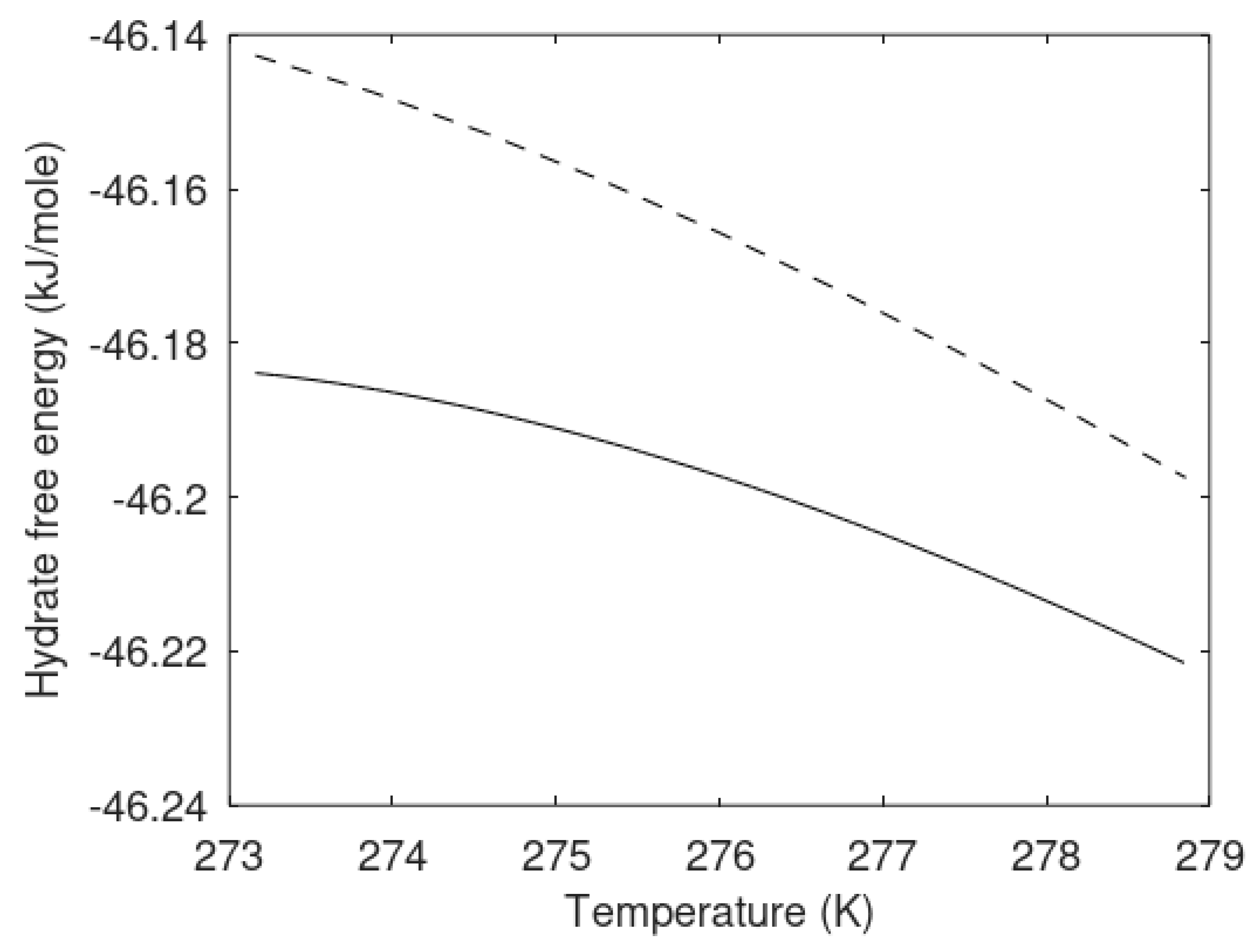
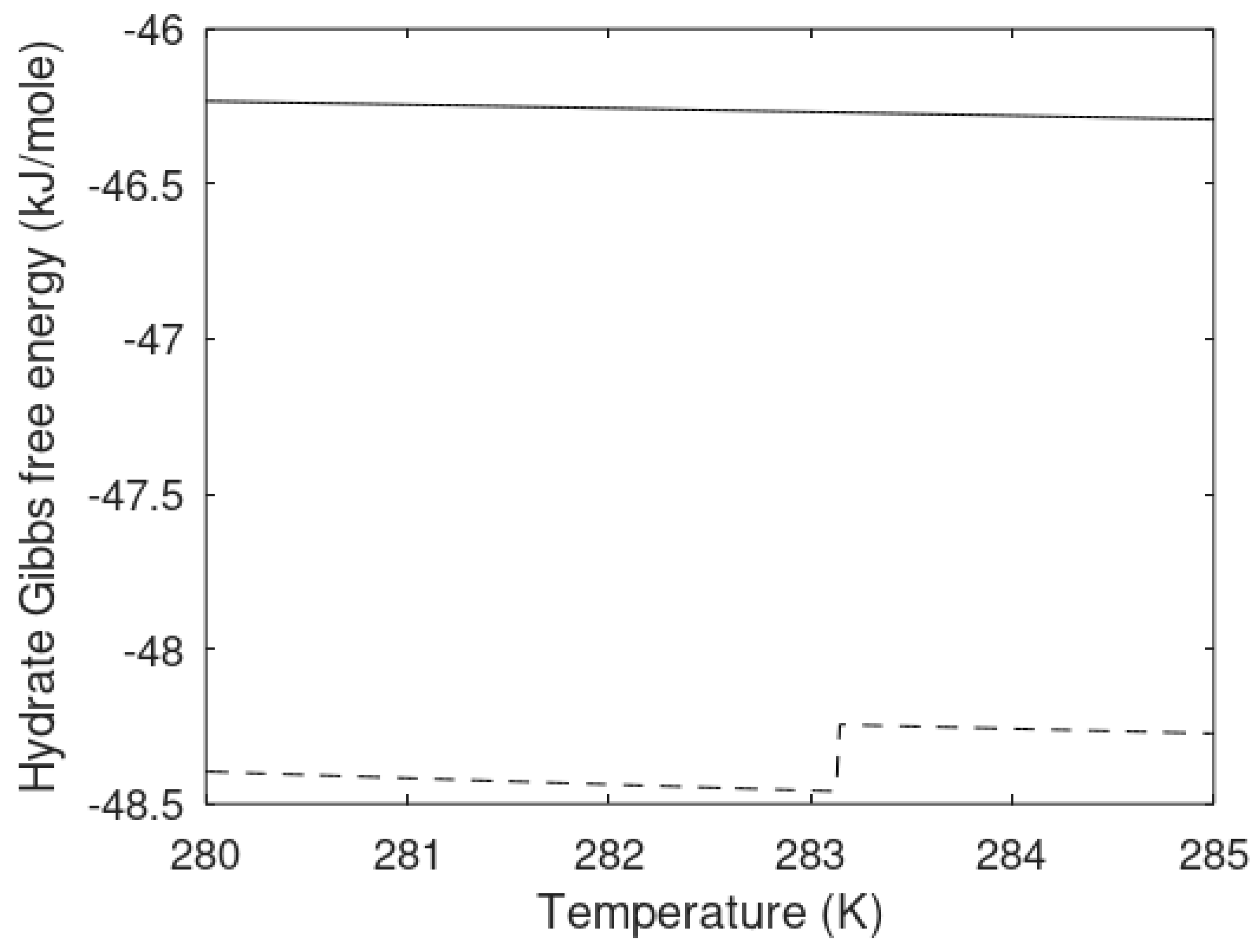
Another important issue is that the free energy of the hydrates formed heterogeneously and homogeneously are different. In a non-equilibrium situation there are no general constraints that dictate the chemical potentials to be the same in all phases. There are simply too many constraints compared to the number of independent variables. Additionally, if we assume thermal and mechanical equilibrium then it is not possible to also fulfill equal chemical potentials. See, for instance, Kvamme et al. [10] for more details. Instead, the combined first and second laws of thermodynamics direct the system towards minimum free energy, in a balance between mole-fraction distributions and phase distributions. Figure 7 illustrates that the homogeneously formed hydrate and the heterogeneously formed hydrates are different phases. Temperatures and pressures are the same but hydrate compositions, densities and free energies are different. They are by thermodynamic definition different phases. Heterogeneously formed hydrate is slightly more stable than the homogeneously formed hydrate.

As mentioned before, the heterogeneous hydrate is trapping gas molecules in cavities. The corresponding cavity partition function is then directly given by Equation (13). The system is not an equilibrium system when two independent thermodynamic variables are defined but only one is permitted mathematically by counting numbers of independent thermodynamic variables minus constraints (conservation laws and equilibrium conditions). Chemical potential for methane in gas is not equal to the chemical potential for methane dissolved in water. For the homogeneous case the chemical potential for dissolved methane in water results in different cavity partition functions when the chemical potential from Table 3 is inserted into Equation (13). Practically, this means that degree of freedom in Gibbs phase rule is 0 rather than 1 with one when counting only one hydrate. The iteration for stability limit concentration is the same as for the heterogeneous hydrate with cavity partition functions containing dissolved methane chemical potential in (13) and then inserted in (10). Equal water chemical potentials for hydrate and liquid water (Table 1) for defined temperature and pressure results in the solutions plotted in Figure 6.

The differences in hydrate compositions between heterogeneous hydrate (Figure 1) and homogeneous hydrate (Figure 6) are available from:

$${\theta }_{ki}=\frac{h_{ki}}{1+{\displaystyle \sum _j{h}_{ki}}}$$

(16)

${\theta }_{ki}$ is the filling fraction of component i in cavity type k. In addition:

$$x_{i,l\arg e}^H=\frac{{\theta }_{l\arg e,i}{\nu }_{l\arg e}}{1+{\theta }_{l\arg e,i}{\nu }_{l\arg e}+{\theta }_{small,i}{\nu }_{small}}$$

(17)

$$x_{i,small}^H=\frac{{\theta }_{small,i}{\nu }_{small}}{1+{\theta }_{l\arg e,i}{\nu }_{l\arg e}+{\theta }_{small,i}{\nu }_{small}}$$

(18)

where ν is the fraction of cavity per water for the actual cavity type, as indicated by subscripts. The corresponding mole-fraction water is then given by:

$$x_{H_{2}O}^H=1-{\displaystyle \sum _i{x}_{i,l\arg e}^H}-{\displaystyle \sum _i{x}_{i,small}^H}$$

(19)

and the associated hydrate free energy (Figure 7 for the two types of hydrate) is then:

$$G^{(H)}=x_{H_{2}O}^H{\mu }_{H_{2}O}^H+{\displaystyle \sum _i{x}_i^H{\mu }_i^H}$$

(20)

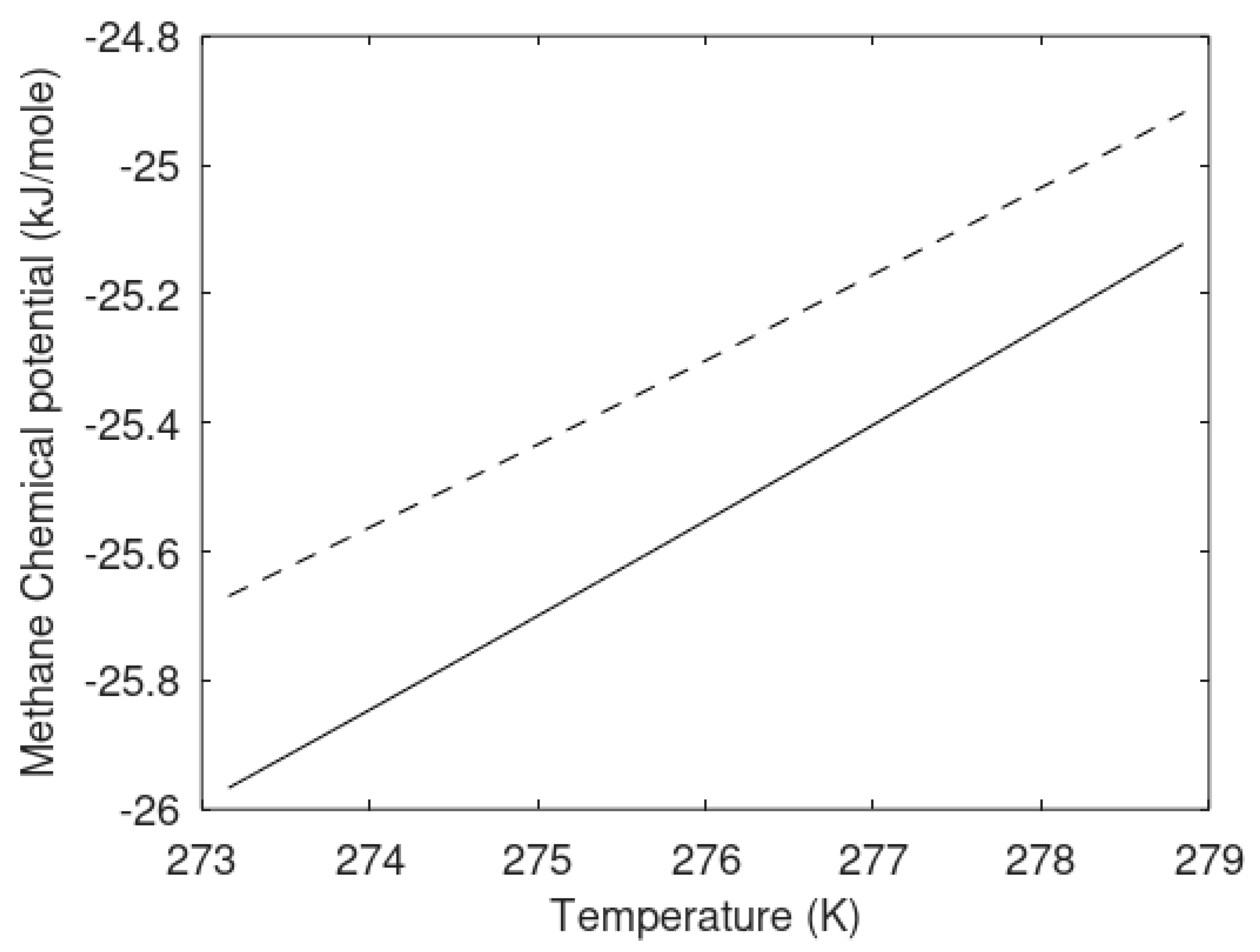
The chemical potential differences for the guest molecules in the two types of hydrate are plotted in Figure 8 below, and the hydrate compositions are plotted in Figure 9 in terms of methane mole-fractions in hydrate.

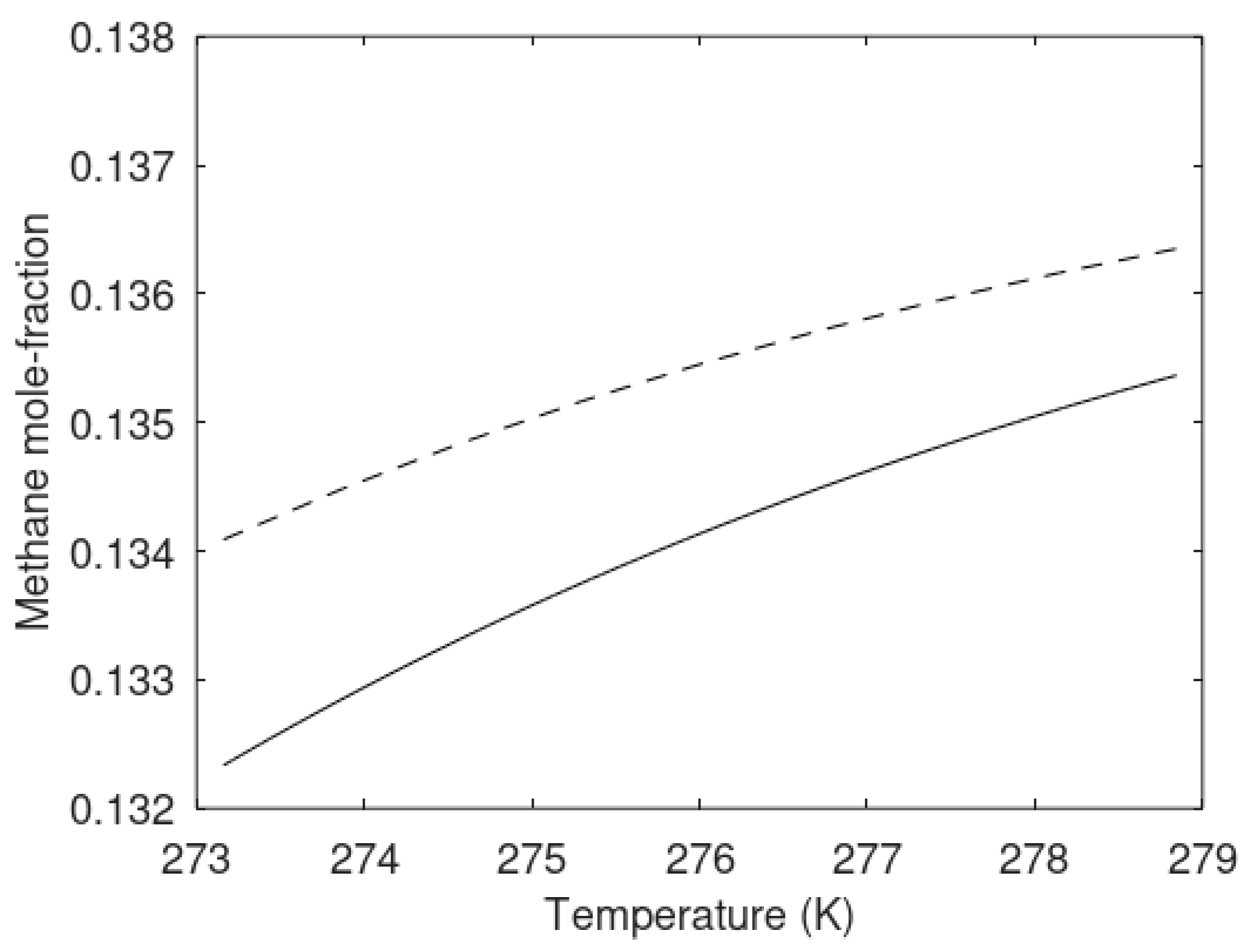
The calculated methane mole-fractions in hydrate illustrate that the filling of methane in the two types of hydrate is different. The net result is, however that the heterogeneous hydrate is more stable as illustrated by Figure 7. There are also differences in the small and large cavity fillings between the two hydrates that give further details on the differences, but this is not needed in the context of this work.

4. Hydrate Kinetic Modeling Review

Gas hydrates have been known to man since the nineteenth century; however, experimental and numerical attempts at studying the intrinsic kinetics of gas hydrate growth and dissociation have their roots in the late twentieth century. During this time period the number of publications with the keywords “gas hydrates” and “kinetics” has increased dramatically from 1, or fewer, publications per year between 1965 and 1983 to 232 in both 2019 and 2020. Of these works, the earliest attempt at quantifying the rate of hydrate growth came in 1965 when Pinder [17] formed hydrates from THF. While these early experiments were performed at atmospheric pressure and with very simple equipment (a beaker, a thermometer and a refractometer), Pinder [17] was able to conclude the observed rate of hydrate growth was diffusion limited. Pinder [17] did not present any attempts to extract a rate constant but he did make indirect reference to the temperature difference being the driving force for the growth of hydrate particles. Following Pinder’s work [17] with THF hydrates, Miller and Smythe [18] and Falabella [19] formed hydrates in the presence of CO₂ and CH₄, but at temperatures between 152 to 183 K. At these extremely low temperatures, hydrates can form at pressures only slightly above atmospheric conditions. It is worth noting that in modelling their results, both Miller and Smythe [18] and Falabella [19] used a pressure difference as the driving force.

In the early 1980s, the laboratory of P.R.Bishnoi, at the Uninversity of Calgary, became the first group to study hydrate growth kinetics at significantly elevated pressures and in the presence of a synthetic natural gas. The group’s initial foray into gas hydrate growth kinetics was the study of Maini and Bishnoi [20] which examined the formation of synthetic natural gas hydrates on gas bubbles suspended in flowing salt water. In this study, which was motivated by the desire to track gas plumes in underwater well blowouts, a high pressure water tunnel was built to allow for direct observation of a hydrate layer on a stabilized bubble of gas. By means of direct observation, Maini and Bishnoi [20] were able to observe that the formation of gas hydrates requires a supersaturated solution and that, at a constant temperature, the rate of reaction was a strong function of pressure.

Parallel to the work of Maini and Bishnoi [20], Vysniauskus and Bishnoi [21] formed gas hydrates with pure methane, pure ethane and a synthetic natural gas mixture in a semi-batch stirred reactor. From measurements of temperature and pressure, it was possible to track the number of moles of gas that had been consumed in the formation of hydrates and then subsequently to regress a rate constant. The data for the reaction rate was then fit to the following equation:

$$r=A{e}^{-\Delta E_a/RT}{e}^{-a/\Delta T^b}{p}^{\gamma }$$

(21)

where r is the reaction rate, A is the pre-exponential constant, ΔE_a is the activation energy, γ is the overall rate of reaction with pressure and a and b are constants. In formulating Equation (21), Vysniauskus and Bishnoi [21] assumed that the formation of gas hydrates was a homogeneous reaction that consisted of three steps: (i) clustering of sub-critical nuclei, (ii) formation of a nucleus of critical radius and (iii) hydrate crystal growth around a stable nucleus.

In addition to the significance of the experimental results, the two aforementioned studies from Professor Bishnoi’s group made equally significant contributions to the design of gas hydrate kinetics apparatus. Being the first studies of their kind, it was not possible to purchase equipment and thus, the equipment had to be designed and manufactured in-house. However, as will be seen, many of the basic elements of Vysniauskus and Bishnoi’s [21] reactor have become standard features in present day hydrate formation apparatus.

Following the seminal work of Vysniauskus and Bishnoi [21], the next significant step towards understanding gas hydrate formation came in 1987 from Englezos et al. [22]. Following Vysniauskus, it became apparent that viewing hydrate formation as a homogeneous reaction precludes a full understanding of the process. In particular, Englezos et al. [22] regarded hydrate formation as a heterogeneous reaction in which the observed reaction rate depends on the surface area available for reaction. In 1987, Englezos et al. [22] did not have access to a particle size analyser that could operate at high pressure, and thus the transient particle size distribution was estimated solely from the population balance equation. The other significant insight of Englezos et al. [22] was the use of the fugacity difference as the driving force, as seen in Equation (22). As will be seen, many subsequent studies of gas hydrate growth kinetics interpret their data using versions of the model of Englezos et al. [22] in which the estimation of surface area and/or the definition of the driving force has been changed.

$${\left(\frac{dn}{dt}\right)}_p=K^{*}{A}_p\left(f-f_{eq}\right)$$

(22)

where ƒ is the fugacity, A_P is the surface area of a hydrate particle and K* is the reaction rate constant. The second of Englezos’ works from 1987 [23] extended Equation (22) to describing the rate of formation of multi-component gas hydrate formation. In their formulation, the rate of growth of hydrates is simply the sum of the rate of growth for each individual component, and thus there was no need to regress additional parameters. When applied to the formation of methane-ethane mixed hydrates, the model of Englezos et al. [23] performed well. However, Englezos only considered gas mixtures of two very similar molecules. Subsequent studies [24,25] have shown that this approach needs to be modified in the case of gas mixtures of dissimilar molecules.

Just as the work of Englezos et al. [22] became a standard for studying gas hydrate growth kinetics, the work of Kim et al. [26] has become a standard for studying gas hydrate dissociation kinetics. Both works used the same apparatus and, as seen in Equation (3), both models write the rate of reaction as being proportional to the product of the surface area times a fugacity difference. However, the model of Kim et al. [26] computes fugacity in the gas phase whereas Englezos’ model [22] requires a value for the fugacity in the liquid solution. Kim et al. [26] also incorporated the hydrate particle surface area into the kinetic model. However, in order to estimate the surface area at the onset of dissociation, Kim et al. [26] measured the settling time of hydrate particles. Note that in both Equation (22) and Equation (23) the rate constants, K* and K_d, are global rate constants, which are affected by both the intrinsic rate of hydrate growth, or dissociation, as well as the rate of mass transfer.

$$-{\left(\frac{d{n}_H}{dt}\right)}_p=K_d{A}_p\left(f_{eq}-f\right)$$

(23)

In looking back at the evolution of the understanding of gas hydrate kinetics up to the end of the 1980s, one can see a shrinking of scale; initially hydrate growth kinetics were deduced solely from temperature and pressure measurements, whereas by the end of the 1980s it was becoming accepted that a full understanding of gas hydrate growth kinetics also required a knowledge of the size distribution of micron-sized particles. However, it would be another ten years before it would become possible to make measurements of hydrate particle size distributions. During the 1990s, population balance-based modelling was used in several studies [27,28,29,30], however, there were also several prominent works that disputed the model of Englezos et al. [22] or the notion that hydrate formation was a heterogeneous process.

In particular, the work of Skovborg and Rasmussen [31] disagreed that the values of K* obtained by Englezoes et al. [22] were the true intrinsic rate constant. Skovborg and Rasmussen [31] examined the Englezos’ data and concluded that mass transfer from the gas phase to the bulk water phase was the rate limiting step. Specifically, Skovborg and Rasmussen [31] noted that the model of Englezos et al. [22] is extremely sensitive to the number of moles of hydrate former absorbed in the liquid, prior to hydrate formation. Under these assumptions, the fugacity difference is replaced with a mole fraction difference and the population balance is removed completely, as seen in Equation (24):

$$\frac{d{n}_H}{dt}=k_L{A}_{(g-L)}\left(x_{\mathrm{int}}-x_b\right)$$

(24)

where x is the liquid phase mole fraction, A_(g-L) is the gas-liquid surface area and k_L is the reaction rate constant. At roughly the same time as Skovborg and Rasmussen [31], a handful of groups [32,33,34,35] modelled gas hydrate growth kinetics as a multi-step reaction-diffusion process. Of these four works, three of them [33,34,35] were specific to the hydrate formation kinetics in the presence of liquid CO₂. In the reaction-diffusion approach, the rates of the reaction and the diffusion steps depend on either concentrations or concentration gradients, which results in a set of equations with multiple parameters. As an example of this class of models, the model of Lund et al. [34] is presented in Equation (25). In addition to two adjustable parameters, k_f and k_d, application of Equation (25) also requires knowledge of the concentration of water in liquid CO₂, in the clathrate phase and in sea water. As a result of having multiple adjustable parameters and requiring values of concentrations that are not easily measured, this class of models has never seen wide-scale application in the gas hydrates community.

$$r=[\begin{array}{l}-k_d{C}_{clath}^{\beta }\left(1-\frac{C_{C{O}_2}}{C_{C{O}_2}^{sat}}\right)\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{0.17em}Water\hspace{0.17em}phase\\ k_f{C}_{water}^{\alpha }-k_d{C}_{clath}^{\beta }\left(1-\frac{C_{C{O}_2}}{C_{C{O}_2}^{sat}}\right)\hspace{1em}\hspace{1em}\hspace{0.17em}Hydrate\hspace{0.17em}film\\ k_f{C}_{water}^{\alpha }\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}Liquid\hspace{0.17em}C{O}_2\hspace{0.17em}phase\end{array}$$

(25)

where C is the concentration, r is the net rate of reaction and k_f and k_d are formation and dissociation reaction rate constants. By the start of the new millennium, experimental instrumentation had developed to the point where it was now possible to measure hydrate particle size distributions during growth or dissociation. The first such formation experiments were those of Herri et al. [36], whereas the first such dissociation experiments were those performed by Clarke and Bishnoi [37,38,39]. The apparatus of Herri et al. [36] used a turbidimetric sensor to monitor the attenuation of a beam of light after it had passed through gas hydrates suspended in water. From knowledge of the attenuation, Herri et al. [36] were able to estimate the population density of particles with diameters from (10 to 150) μm. This was conceptually similar to what had been done by Parent and Bishnoi [40]; however, they did not attempt to extract a population density function from their light scattering data. For their analysis, Herri et al. [36] stated that they agreed with Skovborg and Rasmussen’s conclusion that the hydrate formation process was mass transfer limited; however, they also added that it was necessary to add a term to Skovborg and Rasmussen’s model [31], to account for the particulate nature of the problem.

For their dissociation experiments, Clarke and Bishoi [37,38] modified the apparatus of Kim et al. [26] by adding a continuously circulating sample stream that was connected to a high-pressure optical cell, which was housed inside of an external particle size analyser. The particle size analyser that was used by Clarke and Bishnoi [37,38] could only measure particle sizes down to 1 μm in diameter and could not distinguish gas bubbles from gas hydrates. Thus, reliable hydrate particle size distributions could only be measured immediately prior to the onset of dissociation. Once measured, the particle size distribution information was subsequently incorporated into the model of Kim et al. [26] by use of the population balance.

Clarke and Bishnoi [39] also addressed the dissociation of hydrates formed from gas mixtures of methane and ethane. Similar to the work of Englezos et al. [22], Clarke and Bishnoi [39] assumed that the rate of dissociation of a mixed hydrates is the sum of the dissociation rates of the individual components. This proved sufficient for mixtures of methane and ethane but was will later be shown, by Girlado and Clarke [41], that it is insufficient for gas mixtures consisting of dissimilar molecules.

Shortly after Clarke and Bishnoi’s studies on dissociation kinetics, Kashchiev and Firoozabadi [42], addressed the definition of the driving force for gas hydrate formation. In their formulation a chemical potential difference, also known as the supersaturation, was postulated as the driving force for hydrate crystal growth. The supersaturation, which is shown in Equation (7), is the difference in the chemical potential, μ of the new phases (hydrate) minus the old phases dissolved gas + water). Kashchiev and Firoozabadi [42] noted that the evaluation of Equation (26) will depend upon whether or not a state of chemical equilibrium has been achieved.

$$\Delta \mu ={\mu }_{gs}+n_w{\mu }_w-{\mu }_h$$

(26)

Following their earlier work, Clarke and Bishnoi [37,38,39] gained the capability to make in situ measurements of gas hydrate particle sizes during formation [43] and at the onset of dissociation [44]. For both of the studies of Clarke and Bishnoi [43,44], the consumption, or production, of gas was correlated with the model of Englzos et al. [22], or Kim et al. [22], modified in a manner so as to incorporate the data from the in situ particle size analyser. The in situ particle size analyser was a Lasentec D600L and it allowed Clarke and Bishnoi to measure particle chord lengths as small as 0.5 μm. While this was still not sufficient to allow for direct observation of critical-sized nuclei, it did allow Clarke and Bishnoi [43] to directly observe the presence of a large number of micron-sized bubbles. In later experiments with the same apparatus [25,41,45,46] the mixer was modified so as to significantly reduce the number of bubbles measured by the particle size analyzer.

The presence of background noise in the data of Clarke and Bishnoi [43] was noted by Hashemi et al. [47] who independently examined the data of Clarke and Bishnoi [43]. Hashemi et al. [47] suggested that the background noise was caused by foreign particles, which may be acting as nucleation sites. Thus, Hashemi et al. [47] claimed that it is not possible to extract an intrinsic rate constant value from the data of Clarke and Bishnoi [43]. Additionally, Hashemi et al. [47] argued that because hydrate formation is an exothermic process there has to be a temperature gradient across the liquid-hydrate interface and thus, the driving force for hydrate formation should be in terms of two-phase equilibrium conditions, instead of three-phase equilibrium conditions (Equation (27)). The resulting system of equations, which can be found elsewhere [46], resembled the model of Englezos et al. [22] except with concentrations in place of fugacities.

A year later, another study from Servio’s group at McGill University [48] measured propane hydrate formation kinetics with the aid of an externally connected zeta-sizer. The zeta-sizer was capable of measuring particle diameters from 0.6 nm to 6.0 μm and a mean diameter of 118 nm was observed at the onset of growth. The data was subsequently analyzed using a modified form of the model of Hashemi et al. [47], which is seen in Equation (27). In Equation (26), the mole fractions are that of the hydrate former at two-phase liquid-vapour (L-V) equilibrium conditions and at two-phase hydrate-vapour (H-V) equilibrium conditions.

$$\frac{d{n}_H}{dt}=\frac{C_{w0}\left(x_{L-V}^i-x_{H-L}^i\right)}{\frac{1}{A_p{k}_r}+\frac{1}{k_{L-V}^l{A}_{L-V}}}$$

(27)

In 2012, Herri and Kwaterski [24] adopted a non-equilibrium approach for modelling the formation kinetics of gas hydrates formed from gas mixtures. During the process of hydrate growth, it was assumed that hydrate particles were surrounded by a transition layer, in which solid changes to liquid, and a diffusion layer. In the resulting model, the mole fraction gradient across the transition layer is the driving force for hydrate growth. As a result of the postulated mechanism, the linear growth rate and the hydrate composition are both strong functions of the intrinsic rate constant, except in cases where hydrate growth is known to be diffusion limited. This contrasts with the approach taken by Englezos et al. [23] in which the overall rate of each is the direct sum of the constituent rates.

Giraldo et al. [25] also questioned Englezos’ [23] assumption that the rate of formation of a mixed hydrate is the direct sum of the constituent rates; however, their approach was quite different to that adopted by Herri and Kwaterski [24]. Rather than postulating a completely new mechanism, Giraldo et al. [25] proposed that the overall rate of formation is equal to the weighted sum of constituent rates and that the weights could be given as the ratio of the stoichiometric coefficient of component j to that of a reference component. Due to the stoichiometry, the resulting model had the advantage that it only required knowledge of the rate constant of the reference component and it also reduced the number of ordinary differential equations that would have had to be solved with Englezos’ model [23]. When applied to systems of CH₄ + CO₂, the model was seen to be in fair agreement with the experimental data.

Following the early studies on hydrate kinetics in the presence of ice [18,19], ice-gas-hydrate systems were not studied again until 2020. Zhao et al. [49] used XCT to monitor the formation of xenon gas hydrates on the surface of a sphere of ice. It was observed that the hyrate layer that was formed on the outside of the ice sphere was porous, as well as that the diffusivity of xenon in the hydrate layer was observed to change with time. Unlike previous kinetic studies of ice-hydrate-gas systems [18,19], Zhao et al. [49] also proposed a kinetic model. The kinetic model was based on a shrinking core model in which the concentration difference is the driving force. This model can be explicitly arranged to for the rate constant of hydrate formation, k_r, as seen in Equation (28):

$$k_r=\frac{{\rho }_i}{n\left(C_{eq}-C_i\right)}\frac{d{R}_i}{dt}$$

(28)

Over the course of approximately the last 50 years, experimental capabilities and theoretical understandings of the kinetics of gas hydrates formation and dissociation have evolved tremendously. The scale at which the phenomena can be observed has shrunk from the visual range, in the 1980s, to the micron range, in the early 2000s, to the nano-meter range, in the 2010s. Along with this change of scale of observations, the idea of the driving force has also changed. As can be seen in

Table 4. Summary of proposed driving forces for gas hydrate formation.

Phases in Equilibrium	Driving Source for Hydrate Growth	Source
Ice-gas-hydrate	ΔP	[18,19]
Ice-gas-hydrate	ΔC	[49]
Water-gas-hydrate	ΔT	[21]
Water-gas-hydrate	Δƒ	[22,23,25,27,30,43,45,46]
Water-gas-hydrate	Δx	[31,36,47,48]
Water-gas-hydrate	Δμ	[42]

, there have been more than a half-dozen different driving forces proposed for gas hydrate growth kinetics. On the other hand, there have been relatively few attempts at quantifying the kinetics of hydrate dissociation, all of which are at least 15 years in the past. The relatively small amount of attention that has been paid to dissociation kinetics should not be taken as a sign that it is less important than the formation kinetics. Nor should it be taken as a sign that the phenomenon is perfectly understood. Rather, it is most likely that dissociation has not been extensively studied because it requires additional equipment beyond that which is required for formation kinetics.

While there have been many different interpretations of the driving force for gas hydrate formation, all of the intrinsic kinetic models, except for [47,48], define the driving force relative to a three-phase equilibrium condition. However, as noted in the previous sections, it is unlikely that the chemical potential of water on the surface of the hydrate is exactly equal to the chemical potential at the three-phase equilibrium conditions. Thus, the actual driving hydrate growth and for hydrate dissociation is expected to be smaller than that predicted by the models that were reviewed in this section, although it is not clear at the present moment if the difference between the actual driving force and the driving force based on the three-phase conditions is significant.

In addition to the aforementioned uncertainties in the driving force for formation and dissociation, the reviewed intrinsic kinetic models present nucleation in a very simplified form and they also neglect particle agglomeration and breakage. Since the time of Englezos’ pioneering works the understanding of crystallization has, however, increased significantly. Wohlgemuth and Schembecker [50] noted that in a crystallizing system, the change in the total particle is the sum of simultaneous changes in particle counts due to nucleation, growth, agglomeration and breakage. Thus, it is not possible to de-couple the four processes, as has been done in the intrinsic hydrate kinetic models. Additionally, each of the four processes consists of several sub-mechanisms.

In particular, Wohlgemuth and Schembecker [50] noted that the change in particle numbers due to nucleation consists of contributions from primary, secondary and induced nucleation. Primary and secondary nucleation are well known and they will be discussed further in a later section. Induced nucleation, on the other hand, can be due to bubbles acting as nucleation sites [51]. This is especially relevant in the context of gas hydrate formation, given the presence of dissolved gases. Clarke and Bishnoi [43] even noted that the non-zero base-line reading, for particle size analysis, was likely due to the presence of gas bubbles, although they [43] did not speculate that the bubbles could be inducing nucleation.

5. Hydrate Phase Transition Dynamics

In this section we will mainly focus on a single hydrate former which is very well known to the hydrate community, CH₄. There is nothing in the theories presented that is limited to a single hydrate former and the references provide many examples of mixtures and structure I as well as structure II applications of the approach described. Many aspects will be simpler and easier to follow with only one hydrate former. Aspects such as selective adsorption on water surface and impact on hydrate non-equilibrium, effects of mineral surfaces on hydrate nucleation from mixtures, and homogeneous formation of hydrates from dissolved hydrate formers are just three of many concepts that make the discussion more complex and might overshadow the general principles that we want to illustrate.

Hydrate phase transitions are by physical nature nano-scale phenomena that are controlled by implicit couplings between mass transport, heat transport and thermodynamic control. The range of the phase transition dynamics depends on the interface thickness between hydrate and the “parent” phases. For heterogeneous hydrate formation between a single hydrate former and water, a lot of information can be achieved from Molecular Dynamics simulations (MD) of verified model systems. By verified, we mean that the interaction models for water and hydrate former have been used to calculate relevant properties for hydrate and have been able to reproduce these properties to acceptable accuracy. The most critical is the model for water. We know from our original MD studies [3] and subsequent publications [6,7,14,15,16,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71] that the TIP4P [4] interaction model along with verified interaction models for various guest molecules are able to predict hydrate stability limits for heterogeneous hydrate formation. A simple example is illustrated here in the form of Figure 1 which is constructed on the basis of chemical potentials for liquid water, water in empty hydrate and chemical potential for methane. These types of verifications are valuable for the thermodynamic control of the phase transition dynamics but also for the hydrate/water interface. Based on MD studies of methane hydrate/liquid water systems and carbon dioxide hydrate/liquid water systems and samplings of interface structures, we find that a realistic interface thickness is roughly 1.2 nm. These studies have been part of different projects but the most important references in the context of this work are [62,63,64,65], because these studies are directly linked to the use of these interface properties in meso-scale modeling of phase transition dynamics. A substantial number of publications using Phase Field Theory (PFT) modeling utilizing these interfaces are included in Svandal’s Ph.D. thesis [63] and the theses of Buanes [66] Quasim [67] and Baig [68]. The hydrate/liquid water interface thickness does not vary significantly between methane hydrate and carbon dioxide hydrate. The interface smoothed concentration profiles for methane hydrate and carbon dioxide hydrates from MD simulations are plotted in Figure 10 below.

Calculations of diffusivity coefficient from MD simulations across a thin interface divided into sections is a very demanding task, in terms of accuracy and the need for very long simulations. For that reason we present samplings based on a similar MD approach as utilized by Kvamme and Tanaka [3] without any rigor and details behind the calculations here. As such it may be considered as empirical until we have conducted more rigorous simulations and published these with proper computational details. Nevertheless, for the time being it is the best we have available for the moment and the profiles in Figure 10 and Figure 11 have been successfully utilized in studies of hydrate induction times [69].

With reference to Figure 11 and Figure 12 it should be noted that the values are reasonable in view of the released heat during water restricting to hydrate at interface thickness, which will temporarily destabilize hydrogen bonds in the surface layers of the original nucleus. “Cold” diffusivities as applied in Monte Carlo studies of diffusivities based on guest molecule “cavity jumping” are typically significantly lower. Diffusivity coefficient gradients for CH₄ across the interface between liquid water and the hydrate surface cannot be measured experimentally. In a dynamic situation of hydrate growth or diffusion, the diffusivity coefficient gradient is also highly dynamic. Theoretical estimates for transport of CH₄ through the solid hydrate are available from various open sources but the relevance is questionable. These are mainly estimates of “cold” transport through a hydrate cell. Hydrate nucleation and growth involves restructuring of water that releases heat locally. Most estimated diffusivity coefficients are based on Monte Carlo studies for model systems of hydrate and guest molecules jumping between cavities [70,71,72]. Typically, these studies are conducted at constant temperature. The assumption is that a solid-state diffusion occurs when the hydrate guest jumps from an occupied cage to the neighboring empty cage through a hexagonal or pentagonal faces of water ring of structure I or II hydrate [71,72]. There is no verified mechanism involved in this cavity jumping mechanism. Molecular Dynamics simulations [3] indicate that water molecules between filled and empty cavities have larger vibration amplitudes from minimum energy positions. These less-stable boundary water molecules may be easier pushed temporarily out of position to let molecules pass from a filled cavity to the empty cavity.

In Section 5.1 we summarize briefly the basic physics related to the two physically well-defined stages in hydrate formation (as in any other phase transition). A third stage is frequently defined by induction time, or, what might be a more precise term: “time for onset of massive growth”. Monitoring this stage is highly sensitive to monitoring method.

In Section 5.2 we propose some changes to the original Classical Nucleation Theory by bringing in results from MD studies, and other results from a combination of statistical mechanics and classical thermodynamics.

5.1. Hydrate Nucleation and Growth

In Classical Nucleation Theory (CNT) the total free energy involved in a phase transition consists of the free energy change related to the phase transition itself and a penalty term which is the work needed to push away the old phases. For the heterogeneous formation of hydrate on the liquid water/gas interface, this involves a push work towards liquid water on one side and gas phase on the other side. During the nucleation period the clusters are fairly small, typically less than 3 nm [16,69], and it is fair to assume that the hydrate cluster is facing water on all sides due to capillary forces.

$$\Delta {\underset{\_}{G}}^{Total}=\Delta {\underset{\_}{G}}^{Phasetransition}+\Delta {\underset{\_}{G}}^{Pushwork}$$

(29)

For the simplest possible geometry of a crystal, which is a sphere, with radius R we then get:

$$\Delta {\underset{\_}{G}}^{Total}=\frac{4}{3}\pi R^3{\rho }_N^H\Delta G^{Phasetransition}+4\pi R^2\gamma$$

(30)

${\rho }_N^H$ is the molar density of the hydrate core, and in the first term the difference in molar density between hydrate and liquid water is neglected. $\Delta G^{Phasetransition}$ is the molar Gibbs free energy change for the phase transition. $\gamma$ is interface free energy. Frequently, interfacial tension $\sigma$ is used instead of $\gamma$. Interfacial tension is related to interfacial stress and is one-dimensional, while interface free energy is the work needed to create an interface. The two are related by:

$$\sigma =\gamma +A_s\frac{d\gamma }{d{A}_s}$$

(31)

$A_s$ is contact surface area between the phases. For non-polar gas/liquid interfaces the difference between $\sigma$ and $\gamma$ is limited for low to moderate pressures. For solid/liquid the difference is generally significant. The interface free energy between hydrate and liquid water is not known and as approximation we use the experimental value for ice/liquid water, equal to 29.1 × 10⁻³ Joule/m² [73].

The nucleation stage is a period of unstable growth and decay due to the competition between the free energy gain and the penalty of pushing away the old phases. Mathematically this appears as a maximum in total free energy in Equation (30). The cluster size for maximum is called critical nuclei size. See for instance Kvamme et al. [16]. Within the simple CNT this is the transition over to stable growth. Limitations in supply of mass, and/or limitations related to transport of released heat, require a different approach, such as, for instance, PFT [62,63,64,65,66,67,68]. For a simple sphere the critical radius is then given by:

$$R^{*}=-\frac{2\gamma }{{\rho }_N^H\Delta G^{Phasetransition}}$$

(32)

in which the * indicates critical radius. The critical radius is also a turning point for Gibbs free energy and opens up for the possibility of an additional shape factor to describe a non-spherical shape. See for instance Kvamme and Kuznetsova [74].

5.2. Reworking Classical Nucleation Theory

The kinetics of a phase transition are implicit functions of thermodynamic control and related mass and heat transport. Heat transport through condensed (ice, liquid water, hydrate) water phases are normally two-to-three orders of magnitudes faster than mass transport [75]. There are certainly exceptions to that. Hydrate formation from water dissolved in gas is thermodynamically feasible [76]. The actual hydrate formation through this route will, however, be limited by mass transport, which makes formation very slow. Structuring of the water towards hydrate will release heat that needs to be transported away though a heat insulating phase (CH₄ and CO₂ as examples in this paper).

Classical Nucleation Theory (CNT) can be expressed by:

$$J=J_0{e}^{-\beta \Delta G^{Total}}$$

(33)

where J₀ is the mass transport flux supplying building blocks for the hydrate growth. For the heterogeneous hydrate phase formation it will be the supply of methane to the interface growth. For homogeneous hydrate formation it will be the diffusion rate for dissolved methane to hydrate crystal growth from aqueous solution. The original CNT is limited by a classical pre-factor J₀ for single pure component transport. It was utilized by Kvamme [77,78] in Multicomponent Diffuse Interface Theory [MDIT]. Looking forward, we need an approach that can be developed also for multicomponent mixtures. This is needed since hydrate will not form from “bulk” hydrate formers but rather from hydrate formers adsorbed on water interface, and correspondingly a super-saturated water interface. Selective adsorption of water surface is therefore important in the composition of the hydrate and transport of different molecules through the interface. See Kvamme [79] for an example related to a mixture of CO₂ and N₂.

5.2.1. Mass Transport Kinetics

A mathematical fit of the profile in Figure 11 and Figure 12 is given by Equation (34) below with parameters in

Table 5. Parameters for Equation (34).

I	Parameter	i	Parameter	I	Parameter
1	0.979242	4	171.673	7	−9649.96
2	15.5427	5	6.76975	8	14,779.7
3	−88.5112	6	1939.55	9	−7496.15

. At this stage, Equation (34) is considered as semi-empirical since the samplings of diffusivities from MD are fairly uncertain. For the same reason, no computational details are given on these samplings. Work is in progress for establishing a new research project for this. In addition, note that the parameters in Table 5 are the same for CH₄ and CO₂. There might be significant differences beyond difference in diffusivity on the liquid side of the interface.

$$\left[\frac{D{(z)}_j}{D_{liquid,j}}\right]=9.5\cdot {10}^{-{\displaystyle \sum _{i=1}^9{a}_i{\left(a\tan \left[(0.5z\frac{\pi }{2})/12\right]\right)}^{i-1}}}$$

(34)

The time for a methane molecule to cross the interface can be found by integrations of the second order Fick’s law:

$$t(R=12\AA )-t(R=0\AA )={\displaystyle {\int }_{C_{C{H}_4}(R=0)}^{C_{C{H}_4}(R=12)}\frac{\partial C_{C{H}_4}(z)}{\left[-D_{C{H}_4}(z)\frac{{\partial }^2{C}_{C{H}_4}(z)}{\partial z^2}\right]}}$$

(35)

The liquid water/hydrate interface is constantly reproducing itself on nano-scales in time. The mass transport is dynamically limited by the very low diffusivity close to the hydrate surface. A fair approximation is therefore:

$$\frac{dR}{dt}\approx \frac{\Delta R}{\Delta t}=\frac{\Delta R}{{\displaystyle {\int }_{C_{C{H}_4}(R=12-\Delta )}^{C_{C{H}_4}(R=12)}\frac{\partial C_{C{H}_4}(z)}{\left[-D_{C{H}_4}(z)\frac{{\partial }^2{C}_{C{H}_4}(z)}{\partial z^2}\right]}}}$$

(36)

For hydrate growth beyond interface thickness, Equation (35) is used as a constant value for film thickness growth. The corresponding mass transport dynamics in CNT, J₀, is then given by:

$$J_0=\left[\frac{T}{273.15}\right]{\rho }^H\frac{dR}{dt}\approx \left[\frac{T}{273.15}\right]{\rho }^H\frac{\Delta R}{{\displaystyle {\int }_{C_{C{H}_4}(R=12-\Delta R)}^{C_{C{H}_4}(R=12)}\frac{\partial C_{C{H}_4}(z)}{\left[-D_{C{H}_4}(z)\frac{{\partial }^2{C}_{C{H}_4}(z)}{\partial z^2}\right]}}}$$

(37)

${\rho }^H$ is the molar density of the hydrate. This is trivial to calculate from the volume of the hydrate (unit cell dimension) and filling of the cavities. Diffusivities based on auto velocity correlation samplings scale proportionally to square velocities. The relationship between kinetic energy and temperature per degree of freedom for movement gives the temperature scaling relative to the MD simulations that were conducted at 273.15 K. Within other uncertainties this scaling is not very significant. Values estimated from Equation (36) using the profiles for CH₄ diffusivity and concentration gives the mass transport flux plotted in Figure 13 below.

As will be discussed later, hydrate nucleation is a nano-scale process in time and scale. A second is a very long time and more representative for induction times, which in time scale typically range from seconds to hours. To illustrate the meaning of the numbers in Figure 13, a one-second transport of mass to a spherical hydrate core with radius of 10 Ångsrøms would involve the transport of 5 × 10⁷ molecules. Corresponding numbers for spherical hydrate particles of radius 20 Ångstrøms and 30 Ångstrøm are 2 × 10⁸ molecules and 4.5 × 10⁸ molecules, respectively.

While the kinetic prefactor is the most important modification of CNT in this work, the use of residual thermodynamics derived from Molecular Dynamics simulations [3,6,14] is also unique and provides a consistent thermodynamic description of the phase transition thermodynamic control (Gibbs free energy change) and associated enthalpy change (Section 5.2.3). Chemical potentials for ice, liquid water and water in empty hydrate [3] have been utilized for more than 25 years and verified towards experimental data. This is critically important since hydrates in natural sediments cannot reach thermodynamic equilibrium [10] and as a consequence guest chemical potentials of hydrate formers in different phases are not the same because there are no unique solutions for constraints on the total system (conservation laws and equilibrium conditions) and all the independent thermodynamic variables. The total system is simply mathematically undetermined and hydrates in natural sediments reside in stationary balance. One way to model nucleation sites that we have utilized in the past goes via a 2D adsorption theory in which the associated flux of hydrate formin molecules towards the liquid water surface is modeled by kinetic gas theory [79]. In very simplified language, the selective adsorption depends on the interaction energy between liquid water and hydrate formers and the distance from condensation for the various molecues in the mixture. For more details the reader is directed to Kvamme [79]. The liquid side of the water is approximated to be in quasi equilibrium with the adsorbed layer and the interface water concentration is calculated according to the model for chemical potential of methane in liquid form, Table 2, and the adsorbed methane gas chemical potential [79]. It appears, however, that the mass transport involved in supplying the water with methane is much faster than the transport of molecules across structured water on a growing hydrate cluster. For all the illustrations in this work, the creation of adsorption sites and associated solvation of hydrate formers into the liquid water side is not kinetically limiting. Liquid side concentration and concentration profiles as well as diffusivity profiles across the interface dominates totally. The diffusivity of hydrate former close to the hydrate side of interface is less that 10⁻¹² m²/s. This is also illustrated by Figures 20 and 21 that predict experimentally observed induction times without empirical parameters.

5.2.2. Thermodynamic Control

The thermodynamic control of the phase transition in CNT is the Boltzmann factor in Equation (33). For heterogeneous hydrate formation molar free energy change of hydrate formation as function of sub-cooling is plotted in Figure 14 below. Total free energy change, Equations (29) and (30), will be discussed later in terms of examples.

5.2.3. Heat Transport Kinetics

The final part of the kinetic model is the heat transport. In general it can be written as:

$$\dot{Q}\sim \Delta {\underset{\_}{H}}^{Total}$$

(38)

in which the proportionality is a detailed heat transport mechanism. Heat conduction, heat convection and radiation may be the most important for hydrates in sediments. The dot on Q denotes heat transport in Joule per time. Due to general uncertainties, it is common to use a heat conductivity model that also includes “lumped” contributions for other effects. For the simple spherical nucleus the heat transport is simply given by:

$$\dot{Q}=k\cdot (4\pi R^2)\cdot \frac{dT}{dR}=\Delta H^{Total}\cdot J_0\cdot (4\pi R^2)$$

(39)

in which it is assumed that heat transport kinetics is substantially faster than mass transport as discussed above. $\Delta H^{Total}$ is the molar free enthalpy of the phase transition. A consistent way to calculate $\Delta H^{Total}$ is given by the general thermodynamic relationship:

$$\frac{\partial {\left[\frac{\Delta G^{Total}}{RT}\right]}_{P,\overrightarrow{N}}}{\partial T}=-\left[\frac{\Delta H^{Total}}{R{T}^2}\right]$$

(40)

The route to enthalpy changes, from the residual thermodynamic scheme described in this work, is fairly straightforward, utilizing Equation (10) for hydrate water and the liquid water chemical potential from Table 2. We now use H₁ to denote heterogeneous hydrate formation from liquid water (or ice) and methane gas. The same proportionality as in (40) applies to the relationship between chemical potential and partial molar enthalpy:

$$\frac{\partial {\left[\frac{\Delta {\mu }_{H_{2}O}^{{}^{(H_1),Phasetransition}}}{RT}\right]}_{P,\overrightarrow{N}}}{\partial T}=-\left[\frac{\Delta {\overline{H}}_{H_{2}O}^{{}^{(H_1),Phasetransition}}}{R{T}^2}\right]$$

(41)

in which $\Delta {\overline{H}}_{H_{2}O}^{{}^{(H_1),Phasetransition}}$ is the partial molar enthalpy change for water during the phase transition.

Differentiation of Equation (10) gives the following results for partial molar enthalpy of water in hydrate [60,80,81]:

$${\overline{H}}_{H_{2}O}^H=-R{T}^2\frac{\partial {\left[\frac{{\mu }_{H_{2}O}^{0,H}}{RT}\right]}_{P,\overrightarrow{N}}}{\partial T}+\left[{\displaystyle \sum }_{k=1,2}{v}_k\frac{{\displaystyle {\displaystyle \sum }_i}{h}_{ki}\left[({\mu }_{ki}-\Delta g_{ki})-T(\frac{\partial {\mu }_{ki}}{\partial T}-\frac{\partial \Delta g_{ki}}{\partial T})\right]}{\left(1+{\displaystyle {\displaystyle \sum }_i}{h}_{ki}\right)}\right]$$

(42)

and from Table 2 for liquid water:

$${\overline{H}}_{H_{2}O}^{water}=-R{T}^2\frac{\partial {\left[\frac{{\mu }_{H_{2}O}^{pure,H_{2}O}}{RT}\right]}_{P,\overrightarrow{N}}}{\partial T}--R{T}^2{x}_{H_{2}O}^{water}{\frac{\partial \ln {\gamma }_{H_{2}O}^{water}}{\partial T}|}_{P,\overrightarrow{N}}$$

(43)

and the enthalpy of hydrate formation is then:

$$\Delta {\overline{H}}_{H_{2}O}^{{}^{(H_1),Phasetransition}}=x_{H_{2}O}^{{}^{(H_1)}}\left[{\overline{H}}_{H_{2}O}^{H_1}-{\overline{H}}_{H_{2}O}^{water}\right]+{\displaystyle \sum _{i=1}^n{x}_i^{{}^{(H_1)}}\left[{\overline{H}}_i^{H_1}-{\overline{H}}_i^{gas}\right]}$$

(44)

The last term in the last brackets on right hand side is the partial molar enthalpy of the guest molecules in the gas (or liquid) hydrate former phase. This is directly available using any equation of state. Formally, the relationship is the same as that in Equation (41) for each component in each hydrate former phase. Equations (40) and (41) apply to each phase as well as phase transition differences. Using the equation for chemical potential for methane from Table 1 and utilizing Equation (41) gives the desired result. For the SRK [1] equation of state, this term is available from engineering handbooks and does not need any space here. The partial molar enthalpy of each guest molecule in the hydrate, ${\overline{H}}_i^{H_1}$, is described below.

The ideal gas enthalpy for a guest molecule depends only on temperature. It will be the same for the guest molecule inside the cavities and in the gas mixture. We therefore only need the residual contributions for these two contributions. Entropy-related properties such as chemical potentials and free energies are sensitive to possible interactions between water movements and guest movements. Average interaction energy, on the other hand, is less sensitive to these effects. We have utilized a Monte Carlo approach [8,9] to evaluate average interaction energies between guest and water for the two types of cavities in structure I. Efficient volume for the guest in the cavity is also sampled. This is used to calculate compressibility factors for guest molecules inside the two types of cavities.

$$z_{ki}=\frac{P{V}_{ki}}{RT}$$

(45)

where V_kl is the sampled molar volume of guest molecule i in cavity type k.

$$H_{ki}^R=U_{ki}^R+(z_{ki}-1)RT$$

(46)

$$\begin{array}{l}{x}_i^{H_1}{\overline{H}}_i^{H_1}-x_i^{H_1}{\overline{H}}_i^{gas}=x_i^{H_1}{\overline{H}}_i^{H_1,R}-x_i^{H_1}{\overline{H}}_i^{gas,R}\\ =x_{l\arg e,i}^{H_1}{\overline{H}}_{l\arg e,i}^{H_1,R}+x_{lsmall,i}^{H_1}{\overline{H}}_{small,i}^{H_1,R}-x_i^{H_1}R{T}^2\frac{\partial \ln {\varphi }_i^{gas}(T,P,{\overrightarrow{x}}^{gas})}{\partial T}|\end{array}$$

(47)

The heat flux based on a total mass transport limitation, $\Delta H^{Total}\cdot J_0$, is plotted in Figure 15 below for CH₄ hydrate formation at 150 bar pressure and four different temperatures.

As with the previous section, it is important to keep in mind the nano-scale nature of hydrate nucleation and growth. As will be discussed in more detail later, growth is controlled by the nano-scale transport of guest molecules across liquid water/hydrate interfaces. Stirring in experimental apparatus can break hydrate films and continuously expose new contact between gas and liquid water. Stirring can also hydro-dynamically transport in gas in the form of dispersed bubbles in water. These can be in the visible range and all the way down to nano-bubbles and increase the overall rate of heterogeneous hydrate formation.

To our knowledge, the model for enthalpy of hydrate formation in Equations (40)–(47) is the only model for hydrate formation and dissociation which is general for mixtures of hydrate formers, and it is thermodynamically consistent since the enthalpy and Gibbs free energy are linked by fundamental thermodynamic relationships. Practically this mean that as long as the Gibbs free energy calculations are correct (verified by Figure 1) and enthalpies are verified elsewhere [61,80,81], the entropy of the formed hydrate should be reasonable as well. With reference to statistical mechanics and the couplings between structure and thermodynamics, this implies that the calculated formed hydrate has a reasonable structure.

Another important feature of the model is that it can be applied to homogeneous hydrate formation as well [60] by replacing properties of guests as gas with appropriate properties for guests dissolved in water. Of course, this also applies to hydrate formed partly from guests in gas and other guests from water solution. This is particularly important for various concepts for hydrate capture and storage of hydrogen. These are all based on the use of different help components that stabilize the large cavity of either structure I or II without being able to enter small cavities. Since structure II has a ratio of 2:1 for small to large cavities, then this is more attractive than structure I for capture of hydrogen in the small cavities. Tetrahydrofuran (THF) is just one of many examples of water-soluble hydrate formers which have been studied intensively for this purpose. A recent paper [82] contains many references to this approach.

There are actually no formal limitations in the use of this model, as long as partial molar enthalpies for guests and water in “parent” phases that give rise to the hydrate formation. Our next goal is related to various routes to hydrate formation that involve the impact of solid surfaces [10].

5.3. Heterogeneous Nucleation, Growth and Induction

In Figure 16 we plot the total Gibbs free energy as function of pressure and radius of hydrate core, i.e., Equation (30), for CH₄. As expected, the pressure sensitivity of critical radius is limited since it is dominated by condensed phases (liquid water and hydrate). After the maximum in Gibbs free energy, Gibbs free energy goes rapidly negative and soon the benefit totally outcompetes the penalty term. For the growth phase it is therefore fair to neglect the penalty term as an approximation.

Critical nuclei size as function of temperature for CH₄ for hydrate nucleation is plotted in Figure 17 and corresponding nucleation times are plotted in Figure 18.

Figure 17 and Figure 18 illustrate that nucleation of hydrates are nano-scale processes in time and space. This is in accordance with general physical understanding of phase transition nucleation. Critical sizes and nucleation times are in accordance with many similar systems.

In open literature, hydrate induction times are often misinterpreted as nucleation times because hydrate cores or hydrate films in the sizes of Figure 17 are not visible to the human eye. Monitoring technologies such as Magnetic Resonance Imaging (MRI) (see for instance Kvamme et al. [64]) have a resolution of 100 microns at best. Transport through hydrate films is very slow and can delay observable hydrate substantially, as discussed below.

After the critical core size, the hydrate will grow steadily if mass supply is readily available and heat can be distributed away from the core rapidly enough. After the turning point at maximum (see Figure 16) there is still a region of positive Gibbs free energy. In this region the Boltzmann factor in Equation (33) is less than unity but the gradient in free energy is negative, as also seen in Figure 16. The very small range of crystal size used in visualization of the nucleation process will not show the asymptotic values of the thermodynamic control of the growth process. See Figure 19 for a plot of the Boltzmann factor for thermodynamic control up to a crystal radius of 5 nm and temperatures between 274 K and 285 K. See also Kvamme et al. [16] for illustration of Boltzmann factors for larger hydrate cores.

Many experiments on hydrate phase transition are conducted with stirring. The drawback of this is the implicit couplings of dynamics on the phase transition level (nano-scale), meso-scale effects and hydrodynamic effects (micro-scale). The phase transition is on the molecular-dynamics scale and the ideal is to conduct experiments without included effects on a higher level as a reference state for the phase transition dynamics. Induced hydrodynamic effects can be included in subsequent experiments. The ideal is gradual increase and also connected to hydrodynamic modeling. This underscores the importance of a mathematically simple, and numerically fast, model. The MDIT model mentioned earlier is as numerically fast and the reworked CNT has the advantage of direct connection to properties that can be modeled using molecular simulations. This includes both selective adsorption of guest molecules on the interface and transport of more than one type of guest molecules through the interface. This transport is thermodynamically driven by the difference in chemical potential of each type of molecule in the hydrate and on the liquid side of the interface. This type of driving force can be incorporated in molecular simulations of model systems. We utilized the TIP4P [4] in studies of the thermodynamic properties of water phases (ice, liquid, empty hydrate) [3] and also the rough estimates of diffusivity profile in Equation (34). There are certainly alternative models for water that can be evaluated for both thermodynamic estimates and capability to model transport properties. Nevertheless, in Figure 1 we plot estimates of induction times for CH₄ for some different values of diffusivity for CH4 on the liquid side of the interface in Equation (33) ranging from 1.0 × 10⁻⁷ m²/s to 1.0 × 10⁻⁹ m²/s. Both of these are extreme values since the fastest of these is even close to “bulk” liquid water and the lowest is unreasonable slow. These are, however included as illustrations of the sensitivity of diffusivity on induction times. The experiment was conducted in a plastic compartment with equal volumes of liquid water and methane gas at 4 °C and 83 bar [64,66] without any external hydrodynamic forces. Hydrate induction time was monitored with Magnetic Resonance Imaging (MRI). Resolution was approximately 300 micron in the actual set-up. Calculated results are plotted in Figure 20 and Figure 21 below.

An interesting aspect of the calculated results is that the match between experimental value for induction time and estimated result is achieved without any adjustable parameters and for a very reasonable value of liquid side of interface diffusivity. Similar good predictions for CO₂ hydrate are also reported by Kvamme et al. [69].

5.4. Homogenous Nucleation and Growth

Hydrates can nucleate and grow in between the solubility of CH₄ in water, Figure 5, and the lower limit for hydrate stability, Figure 4, and, as discussed before, the composition of this hydrate is different than heterogeneous hydrate discussed in the previous section. There is actually the possibility of many hydrates depending on the specific concentration in between Figure 4 and Figure 5, and each will produce a different hydrate because the chemical potential of methane in water solution varies with concentration and the canonical partition function for guest, Equation (13) with dissolved CH_4, chemical potential instead of gas chemical potential varies accordingly, and then also for water hydrate, the chemical potential varies.

For the purpose of illustration it is sufficient to use one condition of temperature and pressure. Quite randomly, we examine hydrate nucleation and growth for a temperature of 280 K and a pressure of 180 bar. The minimum mole-fraction in water for hydrate stability is then 1.381 × 10⁻³. In Figure 22 we plot free energy change for hydrate formation as function of mole-fraction CH₄ in water. The critical radius for maximum driving force (saturated CH₄ in liquid water before hydrate formation) is 2.04 nm.

For mole-fractions very close to the hydrate stability limit, the thermodynamic driving force for hydrate formation is very small and the critical nuclei radius will be very large. For the lowest mole-fraction, CH₄ in Figure 22, the critical nuclei radius is 46.7 nm and corresponding nucleation time is 61.4 ns. Even for a mole-fraction CH₄ equal to 0.00172, the critical radius is 10.6 nm and nucleation time is 18.9 ns. Critical nucleation sizes and corresponding nucleation times are plotted in Figure 23 and Figure 24, respectively.

Hydrate growth from solution depends very much on the situation. If there is continuous supply of new dissolved CH₄ then that is one extreme. Another extreme is that the liquid water phase is trapped by hydrate films. Then, hydrate can grow from the specific trapped volume of water until the concentration has reached the hydrate stability limit. The latter is just approximately true and assumes extremely slow diffusion of new CH₄ through hydrate films surrounding the liquid water volume. With all the possible variations, and the illustrations of hydrate growth in the previous section, we skip the growth illustrations here.

Finally, there are even two heterogeneous routes to hydrate formation from CH₄ dissolved in water. The first of these goes through CH₄ adsorbed in structured water at the liquid water/hydrate interface. CH₄ hydrate has lower density than liquid water and will float to the surface. Of course, there can already be a hydrate film from heterogeneous hydrate formation on gas/liquid water surface. A second route goes via the surrounding boundaries. It could be a steel container. If that is stainless steel it is neutral to water. If it is rusty it will structure contacting water and promote hydrate nucleation [6,83,84,85,86,87,88,89]. For experimental evidence on water structuring on mineral oxides, the paper by Geissbühler et al. [90] is a representative study that we have reproduced theoretically using Molecular Dynamics simulation with verified models for water [91]. See also references [52,53,54,55,56,57,58] for the impact of rust on water drop-out from water dissolved in gas.

6. Future Directions

A fundamental problem in past modeling of hydrate was the assumption of one hydrate stability limit related to the pressure temperature projection of the total multivariable dependency of hydrate stability. These include concentrations (and corresponding chemical potentials) of all relevant components in all co-exiting phases. Even for the simple case of one hydrate former and liquid water as a basis for hydrate formation, we have illustrated that as a minimum there are four phases when homogeneous hydrate formation is also included. The Gibbs phase rule can be utilized. Detailed counting of independent thermodynamic variables and comparison to constraints (conservation laws and conditions for equilibrium) is better since it might be easier to add other phases of relevance, such as, for instance, adsorption on mineral surfaces. Whatever approach is chosen, the result is the same [10]. There are no degrees of freedom and no thermodynamic variables can be fixed for the system to establish full equilibrium. The picture is more complicated in real life since solid surfaces act as hydrate promotors. We should actually use detailed counting when moving to hydrate forming mixtures because the complexity increases. If one uses the Gibbs phases rule without reflection it seems easy to obtain equilibrium systems with one or two fixed thermodynamic variables, but the problem is that several more hydrates may form. Selective adsorption [79], and the combined first and second laws of thermodynamics, will lead to a variety of hydrates even for a binary gas mixture.

The first message from this work is that hydrates in nature and industry can never reach full thermodynamic equilibrium. There are many important implications of this. Hydrates in offshore natural sediments are normally in a stationary balance between up-coming (though fracture systems) hydrate formers and incoming water from seafloor through fracture systems. The average hydrate saturation varies widely depending on these incoming fluxes of hydrate formers and water that dissociate hydrate. It is critically important to understand these systems in order predict what will happen during changes related to hydrocarbon production from hydrates in sediments.

A second message, related to the first one, is that we need a thermodynamic model system that makes it transparent to evaluate the relative stability of co-existing phases. The only way to achieve this is to establish a universal reference system for all components in all phases. Fortunately, the world has moved substantially in terms of computational resources and interaction models for water and hydrate formers. Molecular dynamics simulations are therefore capable of estimating thermodynamic variables for ice, liquid water and hydrates based on residual thermodynamics. The simulations provide ideal gas properties through samples of velocities and kinetic energies, while impact of interactions is residual properties. We have demonstrated these features during almost three decades and a significant number of papers based on the TIP4P [4] model for water using water properties derived from MD simulations [3]. It is not our intention that other groups should have to use over values. If they want to use them, then the data are conveniently organised in several of our papers, but the message is that residual thermodynamic schemes for all phases of relevance to hydrates should be developed in order to be able to minimize free energy for solution of mass distribution in the different co-existing phases, and that we need more complete stability limit mapping.

Temperature and pressure dominate in discussion of hydrate stability, but these are only two of many thermodynamic independent variables. Hydrate stability cannot be discussed in terms of independent thermodynamic variables. Stability boundaries in a projection of two independent thermodynamic variables do not say anything about phase stability. For stability evaluation we need to compare free energy responses on the independent variables. A very typical example in this respect is that many publications state that methane hydrate is more stable that carbon dioxide hydrate beyond a certain temperature (it is a temperature for a phase transition for carbon dioxide). This is illustrated in Figure 25 and Figure 26 below. One practical consequence of this is that injection of CO₂ into CH₄ hydrate-filled sediments will lead to the formation of a new CO₂ hydrate with free water in the pores. The extraction of water will lead to higher ion concentration in the remaining water. The first hydrate that will start to dissociate from the increased ion concentration is the CH₄ hydrate.

Yet another aspect of moving to classical thermodynamics in hydrate kinetic modeling is that fugacity may be a convenient engineering formulation but it does not distinguish between components in the reference state in residual thermodynamics. All components have total pressure as an ideal gas reference state while a reference state in classical thermodynamics can be calculated from statistical mechanics based on translational degrees of freedom, rotational degrees of freedom and intramolecular degrees of freedom.

Finally, there is a need for a consistency between descriptions of Gibbs free energy and enthalpy for the different phases in order to ensure that reasonable structures for the formed hydrates are calculated. This will have impact for the reverse processes of dissociating hydrates as well. If the hydrate entropy (and related structure) is wrong, then the final phases after dissociation will also be wrong.

6.1. Nano- to Meso-Scale Modeling Approaches

It has been a goal in this work, as well as in the work reported in many of the papers referred to, to develop a numerically simple approach which can easily be incorporated in various modeling tools for industrial and natural purposes. For that purpose, the reworked version of CNT is considered as useful and, within all other uncertainties in macro-scale modeling of hydrate systems, accurate enough. The flexibility of also using a shape factor in the geometrical model for the hydrate nuclei and the also using the criteria that critical core size is also a turning point will result in an expected core shape which depends on the driving force. The simplest modification of shape is replacing a sphere with an ellipsoid [74].

We have spent close to two decades on various meso-scale modeling tools such as Phase Field Theory (PFT). While these are extremely useful tools that can assist in verification of simpler approaches, they do have size limitations if used properly. By this, we mean that the hydrate phase transitions are the core of the problem and these are nano-scale. Keeping treatment of the phase transitions rigorously correct will limit the range of integrations in time and volume to maybe a single pore with boundary conditions of inflow and outflow of mass and heat. PFT modeling of a whole hydrate section of a real reservoir will have to make serious compromises on the phase-transition dynamic descriptions. We propose the use of PFT and also Density Functional Theory in the classical regime just as tools for exploring specific phenomena that at maxim reach the pore-scale level in hydrate-filled sediments. Similarly, there will be many examples where PFT can assist in industrial modeling. One example is multiphase pipeline transport containing hydrocarbon gas and liquid with various water cuts. For this example, combinations of PFT and Molecular Dynamics simulations can assist in exploring the impact of rust on adsorption of water, structuring of water and trapping of hydrate forming molecules as direct adsorption on rust surface [85,86,87] or trapped in structured water [6,83,84,88]. There are numerous examples in which PFT can assist in adding information to a simpler model but with present generation of computers it is not possible to incorporate PFT in macro-scale modeling tools directly if the phase transition dynamics is to be kept at a sufficient rigorous level.

6.2. Multi-Scale Approaches

CNT, as we have illustrated here, is numerically efficient enough to enter as sub-routines in hydrodynamic modeling tools for pipeline flow and simulations of equipment in process industry. This can be accomplished in various ways–either by full CNT model incorporation of through generated hydrate stability limit functions and associated functions for nucleation and growth.

Similarly for hydrate phase transitions in simulations of hydrate reservoirs. We have developed the first hydrate reservoir simulator for non-equilibrium treatment. By non-equilibrium, we then do not mean only distance from hydrate stability but a system that cannot reach thermodynamic equilibrium because there is not a balance between number of independent thermodynamic variables and number of constraints (conservation laws and equilibrium conditions). We therefore utilize a free energy minimization scheme in out reservoir simulator. This is accomplished by treating hydrate phase transitions and starting with a reactive transport simulator. We used the hydrogeological simulator RetrasoCodeBright as basis since it has a free energy minimization method inside in order to evaluate the result of competing reactions. Every hydrate phase transition is treated as a pseudo reaction with associated kinetic model as derived from CNT [92,93,94,95,96,97,98]. There are five PhD theses [92,95,96,97,98] and a significant number of publications from this project, most of these included in the PhD theses.

7. Discussion

Huge experimental and theoretical efforts have been put into development of understanding the kinetics of hydrate formation and dissociation during the last five decades. Many models have been developed and are in current use in industrial flow simulators and pipeline flow models, as well as in reservoir modeling of hydrate phase transitions. We have made a review of some of these to indicate a trend. We do not claim to have captured all significant contributions.

During the same five decades, there has been a huge development in computational resources and the way modern software can even use the powers of graphical cards for molecular dynamics simulations and other types of numerical modeling. Parallel to this, the development of models for molecular interactions has moved rapidly forward. Numerical algorithms have improved, and many properties that seemed impossible to calculate five decades ago are now a reality through combinations of quantum mechanics, classical statistical mechanics and simulations.

In this work we have illustrated some possible directions forward in moving from fugacity-dominated models over to models based on classical thermodynamics and the use of results from Molecular Dynamics (MD) simulations to arrive at a model scheme with a uniform reference state for all components in all phases. Residual thermodynamics is the natural choice for hydrocarbon systems, but MD modeling has also made this into a feasible choice for water phases (ice, liquid water, water in empty clathrate). Unlike the reference method that treats the difference in chemical potential for water in liquid (or ice) state and empty clathrate, the use of residual thermodynamics results in calculated phases that can be directly compared for stability, and new routes to hydrate formation can be explored. As a consequence, we are now able to compare stabilities of various hydrates that form in real situations. Deliberately we have used a single hydrate former as example so as to make it simple to follow, and CH₄ hydrate is likely the hydrate former that has been most extensively studies in modern times. The same approach has been used on numerous mixtures that covers both structure I and structure II, as can be found in the references.

For systems that can reach thermodynamic equilibrium it is trivial to solve for same temperatures and pressures in all phases and then solve for equal chemical potentials of all components in all phases in combination with mass balances, such as what would be called a multiphase “Flash” calculation.

However, as we have discussed here, there are too many phases in natural gas hydrate systems. These include also mineral surfaces and adsorption. According to the first and second laws of thermodynamics, the equilibrium equations are replaced by:

$$\min \left[{\displaystyle \sum _{m=1}^{phases}{\underset{-}{-S}}^{(m)}d{T}^{(m,surr.)}+{\underset{-}{V}}^{(m)}d{P}^{(m)}+{\displaystyle \sum _{i=1}^{n.m}{\mu }_i^{(m)}d{N}_i^{(m)}}}\le 0\right]$$

(48)

Under the constraints of mass and heat transport. A constrained version of the first law also follows from the combined law as:

$$d{\underset{-}{H}}^{total}\le {\displaystyle \sum _{m=1}^{phases}d{Q}^{(m)}+{\underset{-}{V}}^{(m)}d{P}^{(m)}+{\displaystyle \sum _{i=1}^{n.m}{\mu }_i^{(m)}d{N}_i^{(m)}}}$$

(49)

Minimization of (48) under constraints of (49) gives the most likely distribution of phases and associated compositions. It does not imply that the resulting phases are unconditionally stable. For this to be the case then the additional constraints must be also be fulfilled:

$${\left[\frac{\partial {\underset{\_}{G}}^{(m)}}{\partial L}\right]}_{K\ne M}\delta L\le 0$$

(50)

for any possible range of changes of an independent variable L. One of many examples here is that hydrate may form due to T and P being inside a hydrate formation region but it may also dissociate again because another independent variable, such as concentration of methane in surrounding water, is too low for hydrate to remain stable. This example is seen all over the world in the form of hydrate mounds on top of leaking hydrocarbon sources.

A reworked version of Classical Nucleation theory actually predicts induction times without any empirical parameters at all. This opens up for a simple modeling tool which is numerically fast enough for implementation in flow modeling. There are many possible directions for this, as briefly mentioned in the previous section. Toru Sato and his group have used Computational Fluid Dynamics [99,100] for various applications related to hydrate dissociation and leakage from reservoirs. The same group also utilized Boltzmann flow combined with simplified models for hydrate phase transition kinetics to simulate sediment blocks containing hydrate in model pore structures constructed from fundamental measurements [101,102]. The list of examples on the use of flow modeling and hydrate phase transition models is very long and far too extensive to include here. However, the message is that the CNT model with classical thermodynamics is very feasible and can address more hydrate phase transitions, and corresponding kinetics, than what has been common up to now.

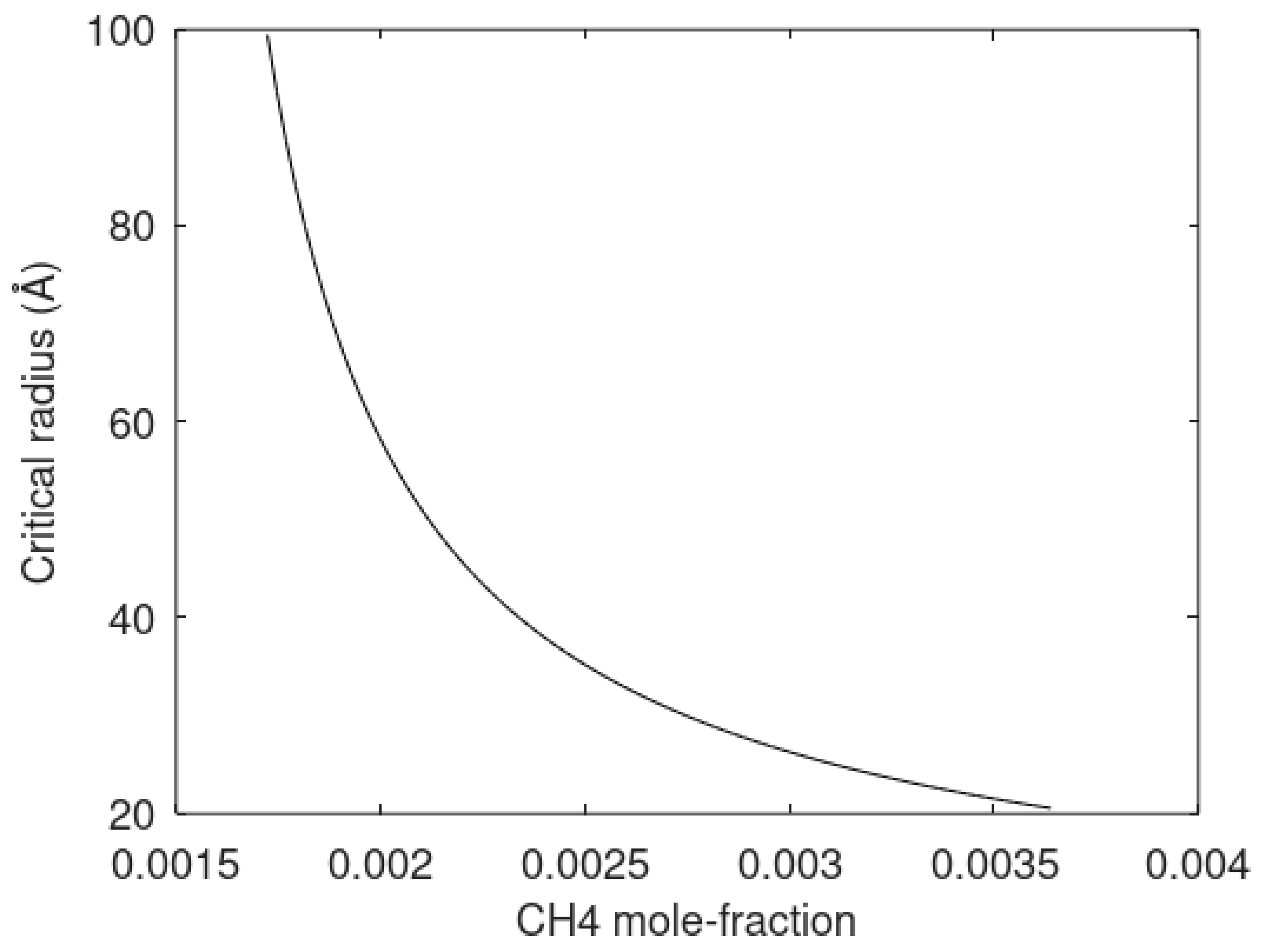
A recent interesting work on experimental measurements of nucleation rates by Maeda [103] is definitely a very valuable contribution to the progress in understanding hydrate nucleation better. A challenge in the interpretation of the results is that the critical radius of the hydrate cannot be measured. As such it is not clear how much of the observations are related to particles in a stable growth phase. As mentioned in Section 5, we have also undertaken efforts in modeling heterogeneous hydrate nucleation using a 2D adsorption model for selective surface adsorption, and kinetic gas theory for associated flux for gas supply to the water surface. Kinetic rates of gas supply, and average adsorption appeared to be very fast compared to the limitations of mass transport across liquid water/hydrate interface. Another challenge in interpretation of the experimental data from Maeda is the selective adsorption of propane and methane on the water. Propane will dominate the initial adsorption and also dominate first hydrates. It is therefore expected that there will be a high degree of non-uniform hydrate formation. In a more recent paper, Maeda and Shen [104] discuss various scaling laws for hydrate induction times. One of the challenges with these experiments relative to real pipelines is the impact of solid surfaces on hydrate nucleation. Rusty pipelines act in one way as providing hydrate nucleation sites dues to the structuring effect on water [6,52,53,54,56,57,58,76,87,88,89,90,91]. However, hydrate can never stick to the mineral surfaces and hydrate will either be bridged to the mineral surfaces by structured water, or release and grow elsewhere. Stainless steel is neutral to water.

There is also a very interesting modeling paper on hydrate nucleation from Kashiev and Firoozobadi [105]. There are three important differences from the nucleation calculation conducted in this work. The first difference is in the thermodynamic description of the phase transition. The use of classical thermodynamics rather than fugacity based thermodynamics is that also the ideal gas term reflects component differences, and the total free energy change due to hydrate formation will include changes in both water and hydrate formers. This is in contrast to the formulation of Kashiev and Firoozobadi [105] in their equation numbers (2) and (8). The use of residual thermodynamics for all phases makes it transparent to compare free energies of different hydrate phasesIn a non-equilibrium system, chemical potentials for hydrate formers from different phases (gas, water solution, adsorbed on mineral surfaces) are different. This has also been experimentally verified, as discussed by Sloan [106] during a hydrate workshop in New Zealand. He presented experimental measurements of two methane hydrates in the same system of water and methane. The first hydrate was measured from the gas side and down while the other hydrate was measured from water side and up. The two hydrates had different compositions. Examples of the same here can be found in Figure 7, Figure 8 and Figure 9. Different compositions arise from different guest chemical potentials in the different phases that results in different cavity canonical partition functions. As also discussed in this work, there is a significant difference between interface free energy and interfacial tension. It is also unclear what they [105] mean by specific surface energy. There are many other differences as well, such as the use of the geometrical shapes of the different hydrate particles on the water/gas interface. Our experiences during three decades of hydrate modeling using nano-scale methods (mainly Molecular Dynamics simulations) and meso-scale methods (Phase Field Theory) shows that water will cover surface particles (Figure 1c) in [105]) on all sides due to capillary forces and strong water hydrogen bonds. A follow-up paper on induction times [107] contains several assumptions and model approximations that make it hard to relate it to physics. We do not know if their [107] results can be extrapolated. Nucleation times are extremely rapid (nano-seconds) and rapidly build up mass transport barriers between liquid water and hydrate former phases. The predictions that we have presented here are reasonable. Hydrodynamic shear forces will break hydrate films and create new hydrate films which, in summary, increases hydrate in the system with time as function of hydrodynamics. Added surfactants reduce interface hydrate blocking films but also increase interface thickness and can increase hydrate formation rates due to faster transport of hydrate formers into liquid side of liquid water interface [5,108,109,110]. In summary, these are just two examples in which it is possible to work on the physics of the hydrate system and extend the models presented here also over to hydrodynamic systems.

Even if we have made approximate calculations of adsorption and associated and found that it was not at all kinetically limiting relative to mass transport limitations at water/hydrate interface we also need to discuss the dynamics of liquid water interfaces. There are no stationary flat surfaces with well-defined nucleation sites. Liquid water is highly dynamic and the capillary waves detach clusters of water, which subsequently reside back to the liquid water, and the resulting average capillary waves are just one of the aspects that make it hard to define nucleation sites. It is more a dynamic situation that supplies the liquid water side of the interface with supersaturation of hydrate formers that distribute dynamically in time and space. In Figure 27 below we show a snapshot from a Molecular Dynamics (MD) study of methane and water at 275 K and 65 bar pressure using TIP4P [4] for water and the same methane model [111] that we have utilized in our thermodynamic calculations [112]. The white atoms are oxygen and the red are hydrogen. The simulation system is a rectangular box with a liquid water slab embedded inside methane on all sides with periodic boundary conditions in all dimensions. The surface water contours are drawn in actual molecular scale while the rest are “pin and ball” representations. Both sides of the water slab illustrate some of the dynamics. The left one illustrates an average surface shape for a snapshot, while the right one illustrates the liquid water gas dynamics and distribution of water and methane across the dynamic interface. This is just a snapshot of a whole movie that illustrates even more how irregular and dynamic the system is. Removing all the dynamics and creating artificial flat surfaces with adsorption sites does not give any justice to the real system. The computational details of this example are of no interest in the context of this paper and would enhance the size of this paper far beyond what is reasonable. There are 2500 TIP4P water and 144 methane molecules with a system size 42Å x42Å x82Å. NPT-dynamics with Nosé-Hoover thermostat and thermostat masses according to Kuznetsova and Kvamme [112,113,114]. What is important, on the other hand, is how these simulations are used in our modeling. Equation (31) provides the relationship between interface free energy and interfacial tension. Interface free energy is the relevant and correct quantity involved in phase transition penalty terms. Interfacial tension is related to interface stress in hydrodynamics. It is unclear what interface energy means in the context of references [105,107]. It seems at best unprecise in thermodynamic terms but if it is only an interface energy then it is even less optimal than using interfacial tensions, since the entropy contribution to the interface dynamics is absolutely critical. It is quite clear from the snapshot in Figure 27 that there is no well-defined adsorprion or nucleation area, and it is most likely that the nucleation happens inside the liquid side of the interface [62,63,64,65,66,67,68], which makes the definition of nucleation sites even more diffuse.

Capillary wave theory can be expressed [116,117] by:

$$\gamma 4\pi {\sigma }^2=-k_{B}T\ln \left[\frac{1+f_u}{1+f_l}\right]$$

(51)

$$f_u={(\frac{2\pi l_c}{L_u})}^2,f_l={(\frac{2\pi l_c}{L_l})}^2,l_c={\left[\frac{\gamma }{g({\rho }_I-{\rho }_{\mathrm{II}})}\right]}^{\frac{1}{2}},$$

(52)

$\gamma$ is in this context interface free energy (and not to be confused with activity coefficients that are also using the same symbol). ${\sigma }^2$ is related to fluctuations in capillary height (see Equation (54). l_u and l_l are the upper and lower wavelengths. G is the gravity constant and $\rho$ is density. Subscripts I and II. denote the two phases. k_B is Boltzmann’s constant. A first order approximation to Equations (51) and (52) can be written as:

$${\sigma }^2=\frac{k_{B}T}{2\pi \gamma }\ln \frac{l_u}{l_l}$$

(53)

$${\sigma }^2={\displaystyle \sum {\displaystyle \sum \left[h_{ij}-\langle h_{ij}\rangle \right]}}$$

(54)

Equations (53) and (54) can be solved for the interface free energy. The capillary wave was included here to indicate that Molecular Dynamics simulations are also needed for this part of nucleation modelling.

8. Conclusions

In this work we have conducted a brief review of the historical development of kinetic models for hydrate phase transitions. The review is more intended to illustrate the trends in developments during the latest five decades and as such is not complete. Based on the historical development, we look towards future possibilities on the development of models based on classical thermodynamics and utilization of molecular modeling to establish residual thermodynamic models for all phases. As we have discussed here, this opens up for a new level of modeling non-equilibrium systems since the Gibbs free energy of all phases is based on the same reference level for all components in all phases. We have used a single hydrate former to illustrate the concept in order to make arguments easier to follow, and CH₄ hydrate is well known to the natural gas hydrate community. However, as we have discussed here, there are several ways that CH₄ hydrate can form in a real system, and all the different routes result in different hydrates. Included references illustrate the concept for many different real systems of hydrate-forming mixtures. Another important feature of the model is that the enthalpy of hydrate phase transitions can be consistently modelled within the same concept for mixtures and for many different routes to hydrate formation and dissociation. We have also shown that the use of classical thermodynamics opens up for the use of kinetic models from physics in a direct fashion without going through fugacity formulations. Specifically, we have reworked the Classical Nucleation Theory by replacing the mass transport term with a diffusivity model for the interface between liquid water and hydrate. We have used the model to discuss hydrate nucleation, growth and induction. Without any adjustable parameters, the model has been able to reproduce experimental induction times in a system without hydrodynamic forces. We therefore propose a future development based on implementation in fluid dynamic tools for pipeline flow, process equipment or sediment and then incorporate how fluid mechanics will change the macroscopic hydrate phase transition dynamics. This can be breaking of hydrate films and exposing new contact areas between water and hydrate former phase or it can be generation of gas bubbles distributed in water for increased gas/water contact area and many other effects cause by shear forces due to hydrodynamics in multi-phase flow. Effects of mineral surfaces are also within reach within the same concept.