On the Applicability of Two Families of Cubic Techniques for Power Flow Analysis
Abstract
:1. Introduction
1.1. Motivation
- Robustness: for effectively solving ill-conditioned systems, which are mainly encountered in presence of cascading failures, heavy loading conditions or badly initialization of the iterative procedure.
- Efficiency: this aspect is crucial for online applications, since it determines the ability of a PF solver for quickly finding the solution of the PF equations.
1.2. Literature Review
1.3. Contributions and Paper Organization
2. Background
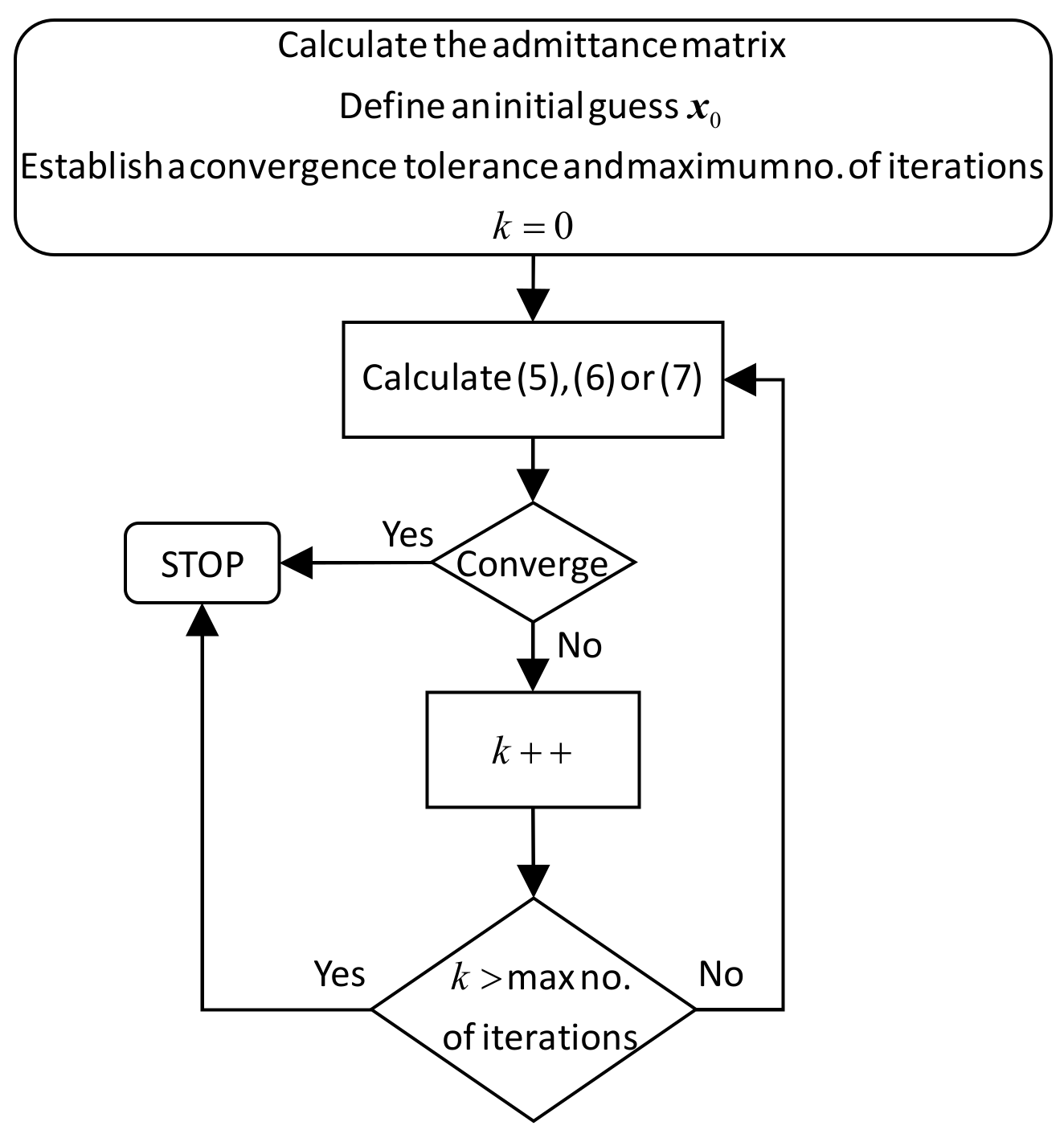
2.1. PF Solution Using NR
2.2. Weerakoon-Like Methods for PF Analysis
2.3. Darvishi-Like Methods for PF Analysis
3. Stability of the Considered Cubic Methodologies
- Sink: if all the eigenvalues of the Jacobian of have a negative real part.
- Source: if at least one of the eigenvalues of the Jacobian of has a positive real part.
3.1. Stability of 3OW
3.2. Stability of 3OD
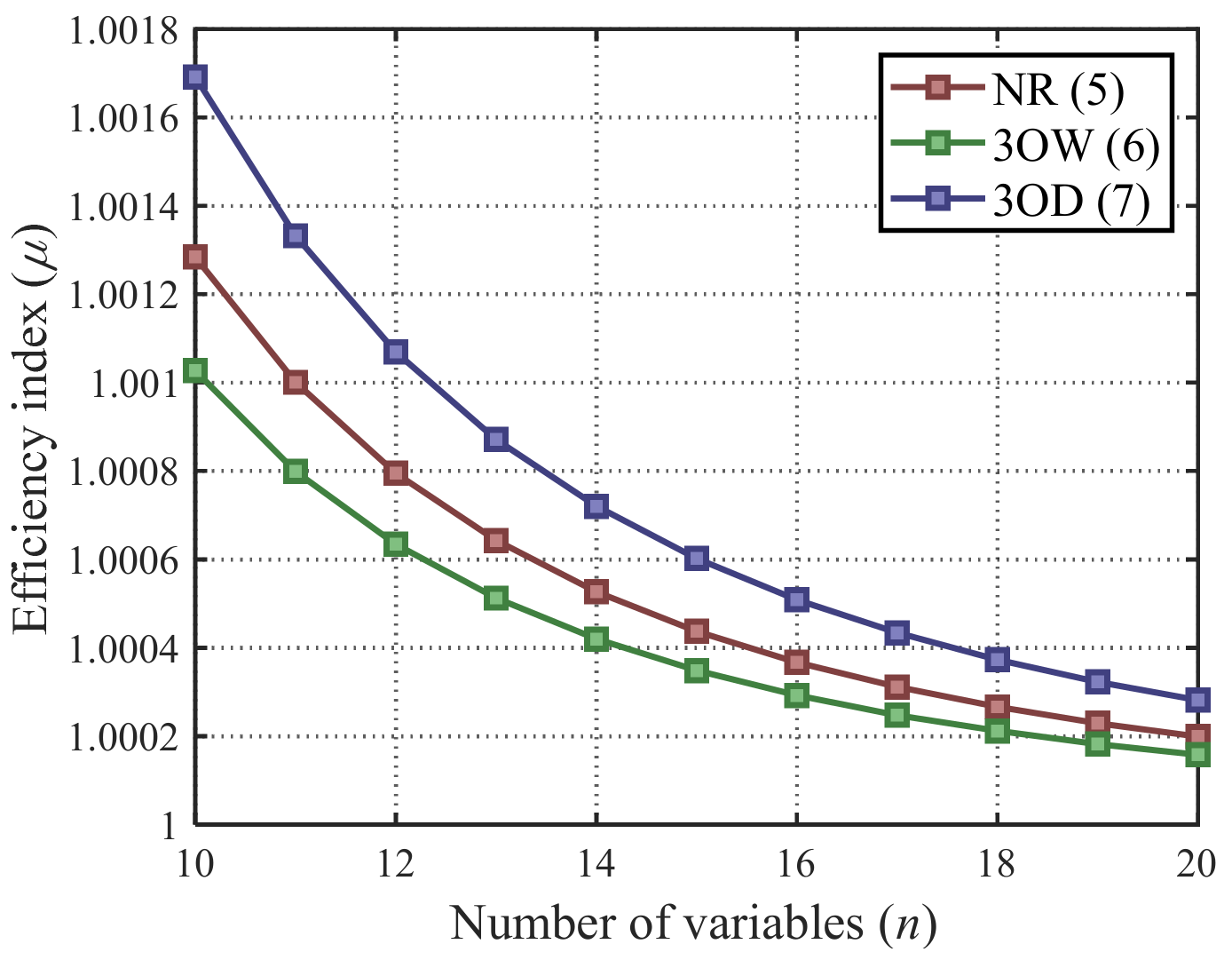
4. A Comparison of the Considered Cubic Techniques
5. Numerical Experiments
- The 2736-bus snapshot of the Polish Transmission System at summer 2004 peak [45].
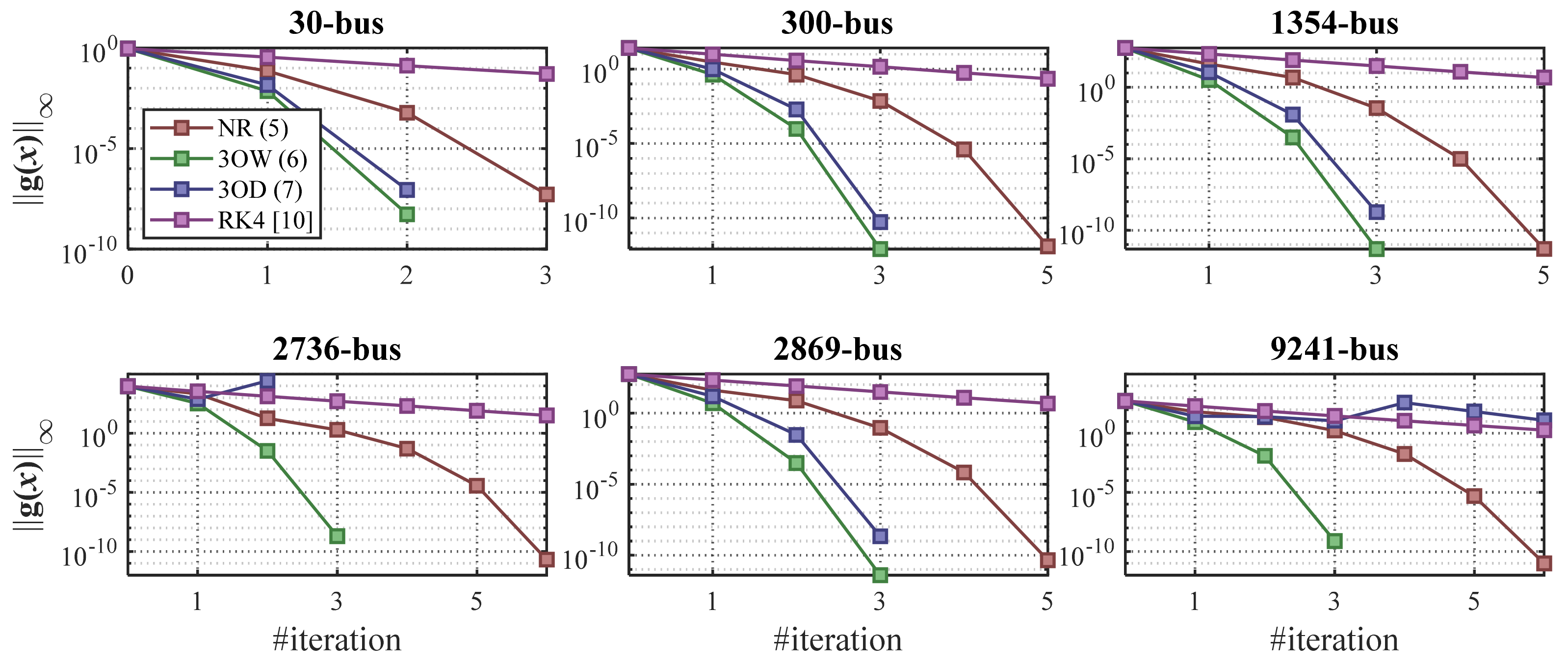
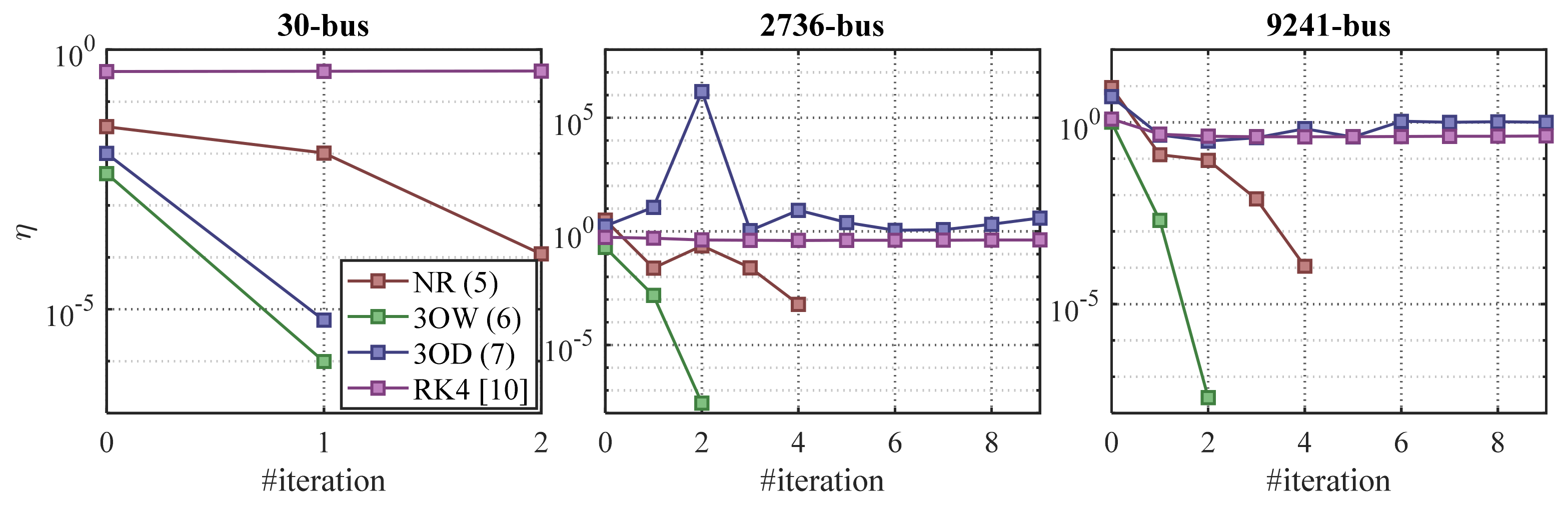
5.1. Convergence Rates
5.2. Solution Times
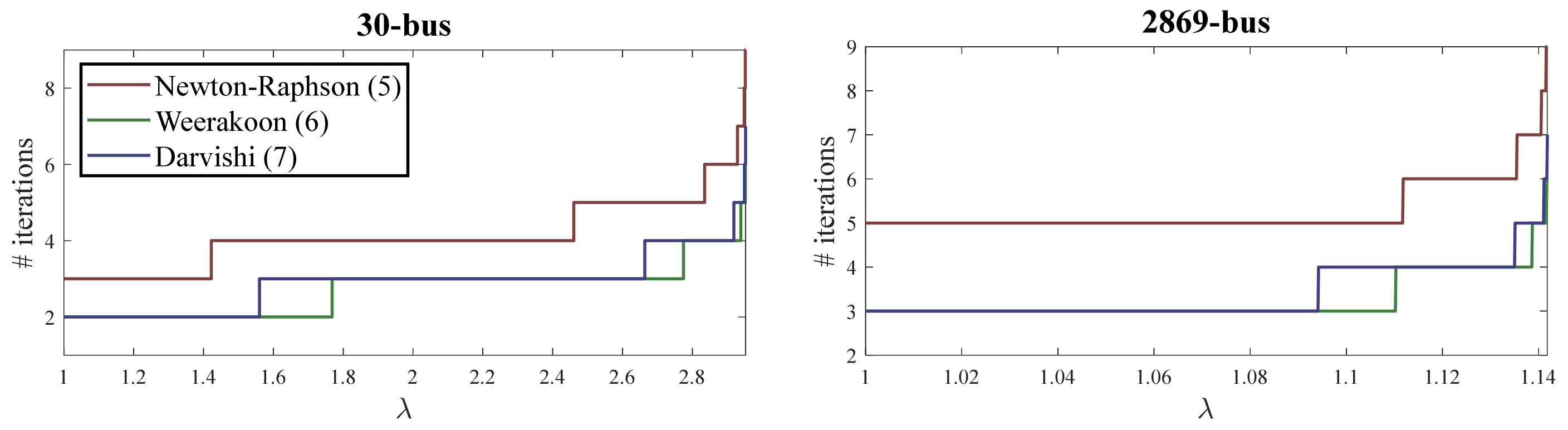
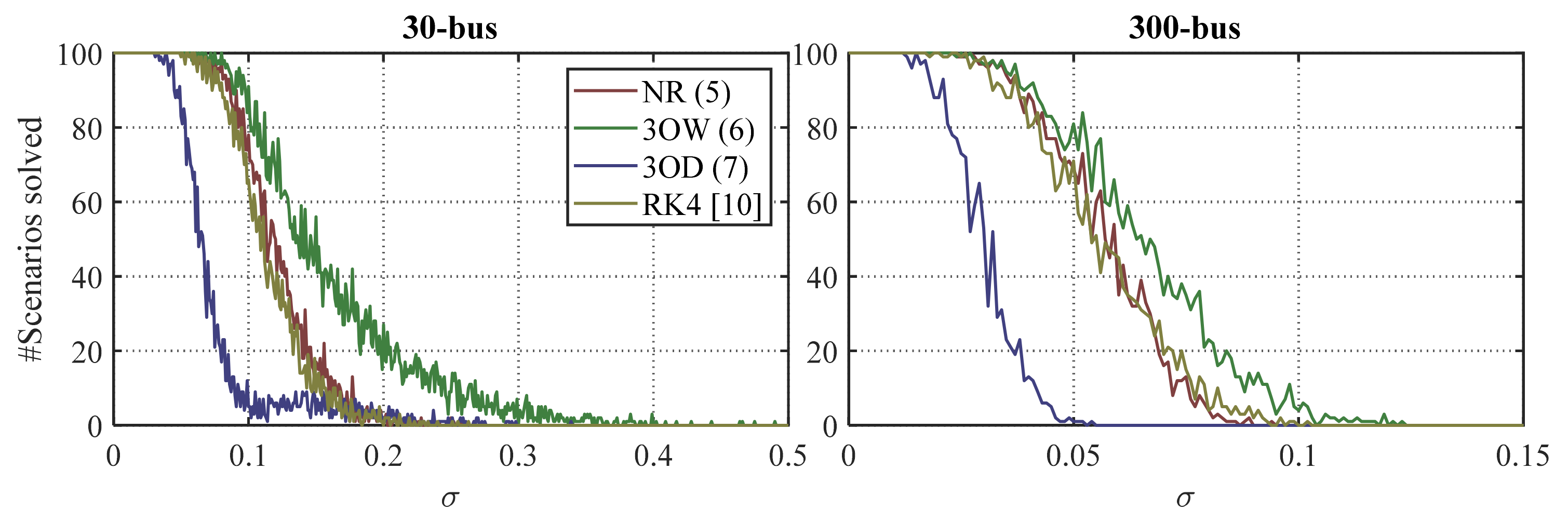
5.3. Influence of the Loading Level
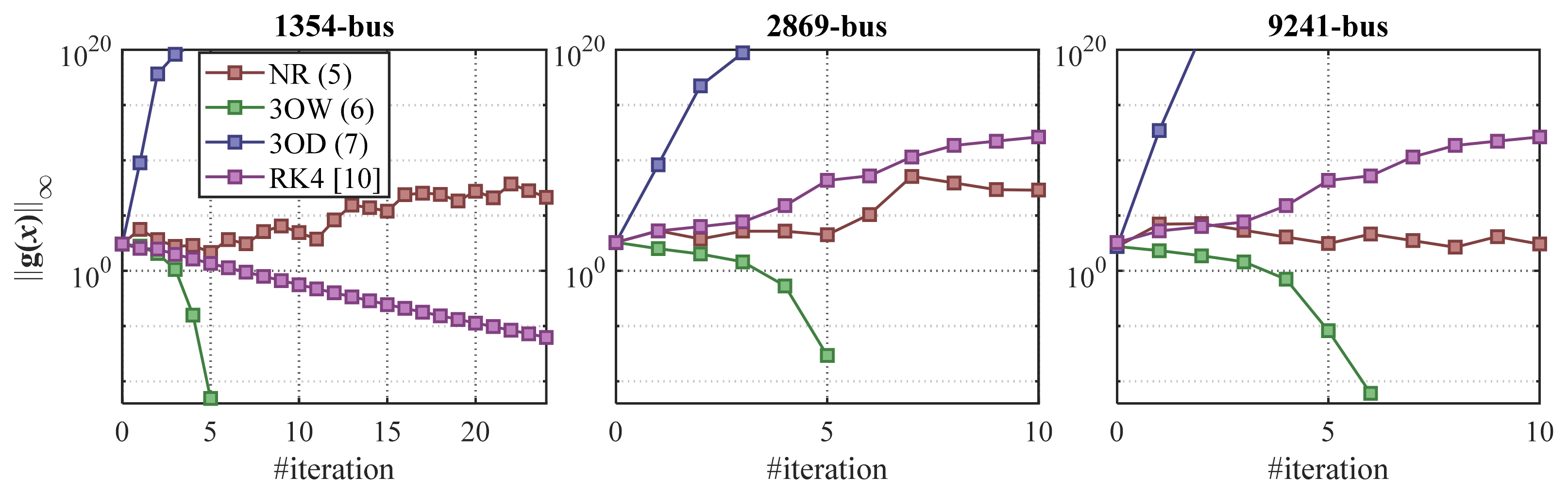
5.4. Contractive Properties
- Convergence of a mapping is ensured if the followingholds.
- Intuitively, one can guess that the lowest the highest degree of robustness and stability.
5.5. Influence of the Initial Guess
6. Concluding Remarks
Author Contributions
Funding
Institutional Review Board Statement
Conflicts of Interest
Abbreviations
| PF | Power-Flow |
| NR | Newton-Raphson |
| HONL | High-Order Newton-like |
| 3OW | Third-order Weerakoon method (3) |
| 3OD | Third-order Darvishi method (4) |
| LU | Lower-Upper |
| RK4 | 4th-order Runge-Kutta technique (see [10]) |
References
- Pourbagher, R.; Derakhshandeh, S.Y. Application of high-order newton-like methods to solve power flow equations. IET Gener. Transm. Distrib. 2016, 10, 1853–1859. [Google Scholar] [CrossRef]
- Tostado, M.; Kamel, S.; Jurado, F. Developed Newton-Raphson based predictor-corrector load flow approach with high convergence rate. Int. J. Electric. Power Energy Syst. 2019, 105, 785–792. [Google Scholar] [CrossRef]
- Tostado-Véliz, M.; Kamel, S.; Jurado, F. A novel family of efficient power-flow methods with high convergence rate suitable for large realistic power systems. IEEE Syst. J. 2021, 15, 738–746. [Google Scholar] [CrossRef]
- Tostado-Véliz, M.; Kamel, S.; Jurado, F. Two efficient and reliable power-flow methods with seventh order of convergence. IEEE Syst. J. 2021, 15, 1026–1035. [Google Scholar] [CrossRef]
- Tinney, W.F.; Hart, C.E. Power flow solution by Newton’s method. IEEE Trans. Power Appar. Syst. 1967, PAS-86, 1449–1460. [Google Scholar] [CrossRef]
- Wang, L.; Lin, X.R. Robust fast decoupled power flow. IEEE Trans. Power Syst. 2000, 15, 208–215. [Google Scholar] [CrossRef]
- Dasgupta, K.; Swarup, K.S. Distributed fast decoupled load flow analysis. In 2008 Joint International Conference on Power System Technology and IEEE Power India Conference; IEEE: New Delhi, India, 2008; pp. 1–6. [Google Scholar] [CrossRef]
- Gnanavignesh, R.; Shenoy, U.J. Parallel sparse LU factorization of power flow jacobian using GPU. In TENCON 2019—2019 IEEE Region. 10 Conference (TENCON); IEEE: Piscataway, NJ, USA, 2019; pp. 1857–1862. [Google Scholar] [CrossRef]
- Iwamoto, S.; Tamura, Y. A load flow calculation method for ill-conditioned power systems. IEEE Trans. Power Appar. Syst. 1981, PAS-100, 1736–1743. [Google Scholar] [CrossRef]
- Milano, F. Continuous newton’s method for power flow analysis. IEEE Trans. Power Syst. 2009, 24, 50–57. [Google Scholar] [CrossRef]
- Kersting, W.H. Distribution System Modeling and Analysis, 2nd ed.; CRC Press: Boca Raton, FL, USA, 2006. [Google Scholar]
- Farivar, M.; Low, S.H. Branch flow model: Relaxations and convexification-part I. IEEE Trans. Power Syst. 2013, 28, 2554–2564. [Google Scholar] [CrossRef]
- Kamel, S.; Abdel-Akher, M.; Jurado, F. Improved NR current injection load flow using power mismatch representation of PV bus. Int. J. Electr. Power Energy Syst. 2013, 53, 64–68. [Google Scholar] [CrossRef]
- Penido, D.R.R.; de Araujo, L.R.; Júnior, S.C.; Pereira, J.L.R. A new tool for multiphase electrical systems analysis based on current injection method. Int. J. Electr. Power Energy Syst. 2013, 44, 410–420. [Google Scholar] [CrossRef]
- Saleh, S.A. The formulation of a power flow using d-q reference frame components-part II: Unbalanced 3φ systems. IEEE Trans. Ind. Appl. 2018, 54, 1092–1107. [Google Scholar] [CrossRef]
- Xie, N.; Torelli, F.; Bompard, E.; Vaccaro, A. Dynamic computing paradigm for comprehensive power flow analysis. IET Gener. Transm. Distrib. 2013, 7, 832–842. [Google Scholar] [CrossRef]
- Tostado-Véliz, M.; Kamel, S.; Jurado, F. Development of different load flow methods for solving large-scale ill-conditioned systems. Int. Trans. Electr. Energy Syst. 2019, 29, e2784. [Google Scholar] [CrossRef]
- Tostado-Véliz, M.; Kamel, S.; Jurado, F. Comparison of various robust and efficient load-flow techniques based on Runge–Kutta formulas. Electr. Power Syst. Res. 2019, 174, 105881. [Google Scholar] [CrossRef]
- Tostado-Véliz, M.; Kamel, S.; Jurado, F. A robust power flow algorithm based on bulirsch–stoer method. IEEE Trans. Power Syst. 2019, 34, 3081–3089. [Google Scholar] [CrossRef]
- Tostado-Véliz, M.; Kamel, S.; Jurado, F. Development of combined Runge-Kutta Broyden’s load flow approach for well and ill-conditioned power systems. IET Gener. Transm. Distrib. 2018, 12, 5723–5729. [Google Scholar] [CrossRef]
- Xie, N.; Bompard, E.; Napoli, R.; Torelli, F. Widely convergent method for finding solutions of simultaneous nonlinear equations. Electr. Power Syst. Res. 2012, 83, 9–18. [Google Scholar] [CrossRef]
- Torelli, F.; Vaccaro, A. A second order dynamic power flow model. Electr. Power Syst. Res. 2013, 126, 12–20. [Google Scholar] [CrossRef]
- Milano, F. Analogy and convergence of Levenberg’s and Lyapunov-based methods for power flow analysis. IEEE Trans. Power Syst. 2016, 31, 1663–1664. [Google Scholar] [CrossRef]
- Tostado, M.; Kamel, S.; Jurado, F. An effective load-flow approach based on Gauss-Newton formulation. Int. J. Electr. Power Energy Syst. 2019, 113, 573–581. [Google Scholar] [CrossRef]
- Tostado-Véliz, M.; Kamel, S.; Jurado, F. An efficient and reliable power flow solution method for large scale Ill-Conditioned cases based on the Romberg’s integration scheme. Int. J. Electr. Power Energy Syst. 2020, 123, 106264. [Google Scholar] [CrossRef]
- Mehta, D.; Nguyen, H.D.; Turitsyn, K. Numerical polynomial homotopy continuation method to locate all the power flow solutions. IET Gener. Transm. Distrib. 2016, 10, 2972–2980. [Google Scholar] [CrossRef] [Green Version]
- Feng, Y.; Tylavsky, D.J. A Holomorphic embedding approach for finding the Type-1 power-flow solutions. Int. J. Electr. Power Energy Syst. 2019, 102, 179–188. [Google Scholar] [CrossRef]
- Karimi, M.; Shahriari, A.; Aghamohammadi, M.R.; Marzooghi, H.; Terzija, V. Application of Newton-based load flow methods for determining steady-state condition of well and ill-conditioned power systems: A review. Int. J. Electr. Power Energy Syst. 2019, 113, 298–309. [Google Scholar] [CrossRef]
- Tostado-Véliz, M.; Kamel, S.; Jurado, F. An efficient power-flow approach based on Heun and King-Werner’s methods for solving both well and ill-conditioned cases. Int. J. Electr. Power Energy Syst. 2020, 119, 105869. [Google Scholar] [CrossRef]
- Weerakoon, S.; Fernando, T.G.I. A variant of Newton’s method with accelerated third-order convergence. Appl. Math. Lett. 2000, 13, 87–93. [Google Scholar] [CrossRef]
- Darvishi, M.T.; Barati, A. A third-order Newton-type method to solve systems of nonlinear equations. Appl. Math. Comput. 2007, 187, 630–635. [Google Scholar] [CrossRef]
- Chun, C.; Neta, B. Developing high order methods for the solution of systems of nonlinear equations. Appl. Math. Comput. 2019, 342, 178–190. [Google Scholar] [CrossRef]
- Frontini, M.; Sormani, E. Some variant of Newton’s method with third-order convergence. Appl. Math. Comput. 2003, 140, 419–426. [Google Scholar] [CrossRef]
- Özban, A.Y. Some new variants of Newton’s method. Appl. Math. Lett. 2004, 17, 677–682. [Google Scholar] [CrossRef] [Green Version]
- Frontini, M.; Sormani, E. Third-order methods from quadrature formulae for solving systems of nonlinear equations. Appl. Math. Comput. 2004, 149, 771–782. [Google Scholar] [CrossRef]
- Cordero, A.; Torregrosa, J.R. Variants of Newton’s method for functions of several variables. Appl. Math. Comput. 2006, 183, 199–208. [Google Scholar] [CrossRef]
- Babajee, D.K.R.; Dauhoo, M.Z.; Darvishi, M.T.; Karami, A.; Barati, A. Analysis of two Chebyshev-like third order methods free from second derivatives for solving systems of nonlinear equations. J. Comput. Appl. Math. 2010, 233, 2002–2012. [Google Scholar] [CrossRef] [Green Version]
- Traub, J.F. Iterative Methods for the Solution of Equations, 2nd ed.; American Mathematical Society: New York, NY, USA, 1982. [Google Scholar]
- Lotfi, T.; Bakhtiari, P.; Cordero, A.; Mahdiani, K.; Torregrosa, J.R. Some new efficient multipoint iterative methods for solving nonlinear systems of equations. Int. J. Comput. Math. 2015, 92, 1921–1934. [Google Scholar] [CrossRef] [Green Version]
- Cordero, A.; Hueso, J.L.; Martínez, E.; Torregrosa, J.R. A modified Newton-Jarratt’s composition. Numer. Algorithms 2010, 5, 87–99. [Google Scholar] [CrossRef]
- Birchfield, A.B.; Xu, T.; Gegner, K.M.; Shetye, K.S.; Overbye, T.J. Grid structural characteristics as validation criteria for synthetic networks. IEEE Trans. Power Syst. 2017, 32, 3258–3265. [Google Scholar] [CrossRef]
- Peyghami, S.; Davari, P.; Fotuhi-Firuzabad, M.; Blaabjerg, F. Standard test systems for modern power system analysis: An overview. IEEE Ind. Electron. Mag. 2019, 13, 86–105. [Google Scholar] [CrossRef]
- Fliscounakis, S.; Panciatici, P.; Capitanescu, F.; Wehenkel, L. Contingency ranking with respect to overloads in very large power systems taking into account uncertainty, preventive, and corrective actions. IEEE Trans. Power Syst. 2013, 28, 4909–4917. [Google Scholar] [CrossRef] [Green Version]
- Josz, C.; Fliscounakis, S.; Maeght, J.; Panciatici, P. AC power flow data in MATPOWER and QCQP format: ITesla, RTE snapshots, and PEGASE. arXiv 2016, arXiv:1603.01533. Available online: http://arxiv.org/abs/1603.01533 (accessed on 22 June 2021).
- MATPOWER. Available online: http://www.pserc.cornell.edu/matpower/ (accessed on 22 June 2021).
- Zimmerman, R.D.; Murillo-Sánchez, C.E.; Thomas, R.J. MATPOWER: Steady-state operations, planning, and analysis tools for power systems research and education. IEEE Trans. Power Syst. 2011, 26, 12–19. [Google Scholar] [CrossRef] [Green Version]
- Ortega, J.M.; Rheinboldt, W.C. Iterative Solution of Nonlinear Equations in Several Variables; Society of Industrial Applied Mathematics: Philadelphia, PA, USA, 2000. [Google Scholar]
- Modified EU Pegase Systems. Available online: https://zenodo.org/record/3553615 (accessed on 22 June 2021).

| Computation | PF Solution Method | ||
|---|---|---|---|
| NR (5) | 3OW (6) | 3OD (7) | |
| Function evaluations () | 1 | 1 | 2 |
| Jacobian evaluations () | 1 | 2 | 1 |
| Factorizations () | 1 | 2 | 1 |
| Linear systems solved () | 1 | 2 | 2 |
| System | Buses | Branches | Generators | Load | ||
|---|---|---|---|---|---|---|
| MW | MVar | |||||
| 30-bus | 30 | 41 | 6 | 283.4 | 126.2 | 53 |
| 300-bus | 300 | 411 | 69 | 23,525.8 | 7788.0 | 530 |
| 1354-bus | 1354 | 1991 | 260 | 73,059.7 | 13,401.4 | 2447 |
| 2736-bus | 2736 | 3504 | 420 | 18,074.5 | 5339.5 | 5237 |
| 2869-bus | 2869 | 4582 | 510 | 132,437.3 | 29,007.8 | 5227 |
| 9241-bus | 9241 | 16,049 | 1445 | 312,354.1 | 73,581.6 | 17,036 |
| System | NR (5) | RK4 (10) | 3OW (6) | 3OD (7) |
|---|---|---|---|---|
| 30-bus | 3.30 | 70.50 | 3.84 | 2.56 |
| 300-bus | 11.48 | 185.26 | 12.66 | 8.72 |
| 1354-bus | 41.55 | 797.22 | 48.07 | 28.42 |
| 2736-bus | 100.69 | 1902.75 | 99.35 | |
| 2869-bus | 93.91 | 1860.29 | 110.59 | 62.38 |
| 9241-bus | 387.29 | 6052.44 | 384.23 |
| System | NR (5) | RK4 (10) | 3OW (6) | 3OD (7) |
|---|---|---|---|---|
| 30-bus | 3 | 64 | 4 | 2 |
| 300-bus | 5 | 80 | 6 | 3 |
| 1354-bus | 5 | 96 | 6 | 3 |
| 2736-bus | 6 | 112 | 6 | |
| 2869-bus | 5 | 96 | 6 | 3 |
| 9241-bus | 6 | 96 | 6 |
| Method | Total | Iteration |
|---|---|---|
| 3OW (6) | 40.15 | 8.03 |
| RK4 (10) | 804.26 | 33.51 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tostado-Véliz, M.; Kamel, S.; Jurado, F.; Ruiz-Rodriguez, F.J. On the Applicability of Two Families of Cubic Techniques for Power Flow Analysis. Energies 2021, 14, 4108. https://doi.org/10.3390/en14144108
Tostado-Véliz M, Kamel S, Jurado F, Ruiz-Rodriguez FJ. On the Applicability of Two Families of Cubic Techniques for Power Flow Analysis. Energies. 2021; 14(14):4108. https://doi.org/10.3390/en14144108
Chicago/Turabian StyleTostado-Véliz, Marcos, Salah Kamel, Francisco Jurado, and Francisco J. Ruiz-Rodriguez. 2021. "On the Applicability of Two Families of Cubic Techniques for Power Flow Analysis" Energies 14, no. 14: 4108. https://doi.org/10.3390/en14144108
APA StyleTostado-Véliz, M., Kamel, S., Jurado, F., & Ruiz-Rodriguez, F. J. (2021). On the Applicability of Two Families of Cubic Techniques for Power Flow Analysis. Energies, 14(14), 4108. https://doi.org/10.3390/en14144108









