An Effective Acoustic Impedance Imaging Based on a Broadband Gaussian Beam Migration
Abstract
:1. Introduction
2. The Principle of Gaussian Beam Migration
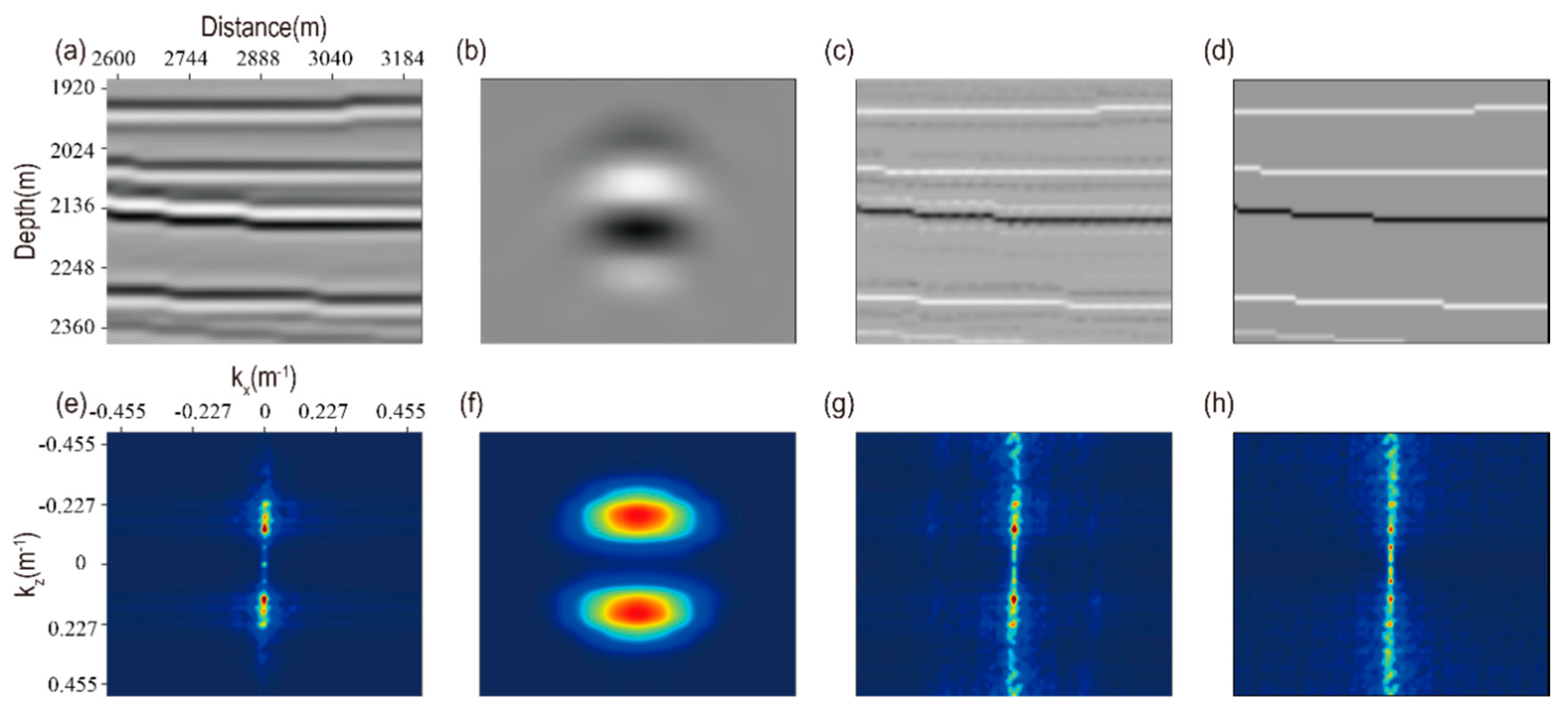
3. The Broadband Reflectivity Estimation Based on Point Spread Function
4. The Impedance Inversion Based on the Estimated Reflectivity
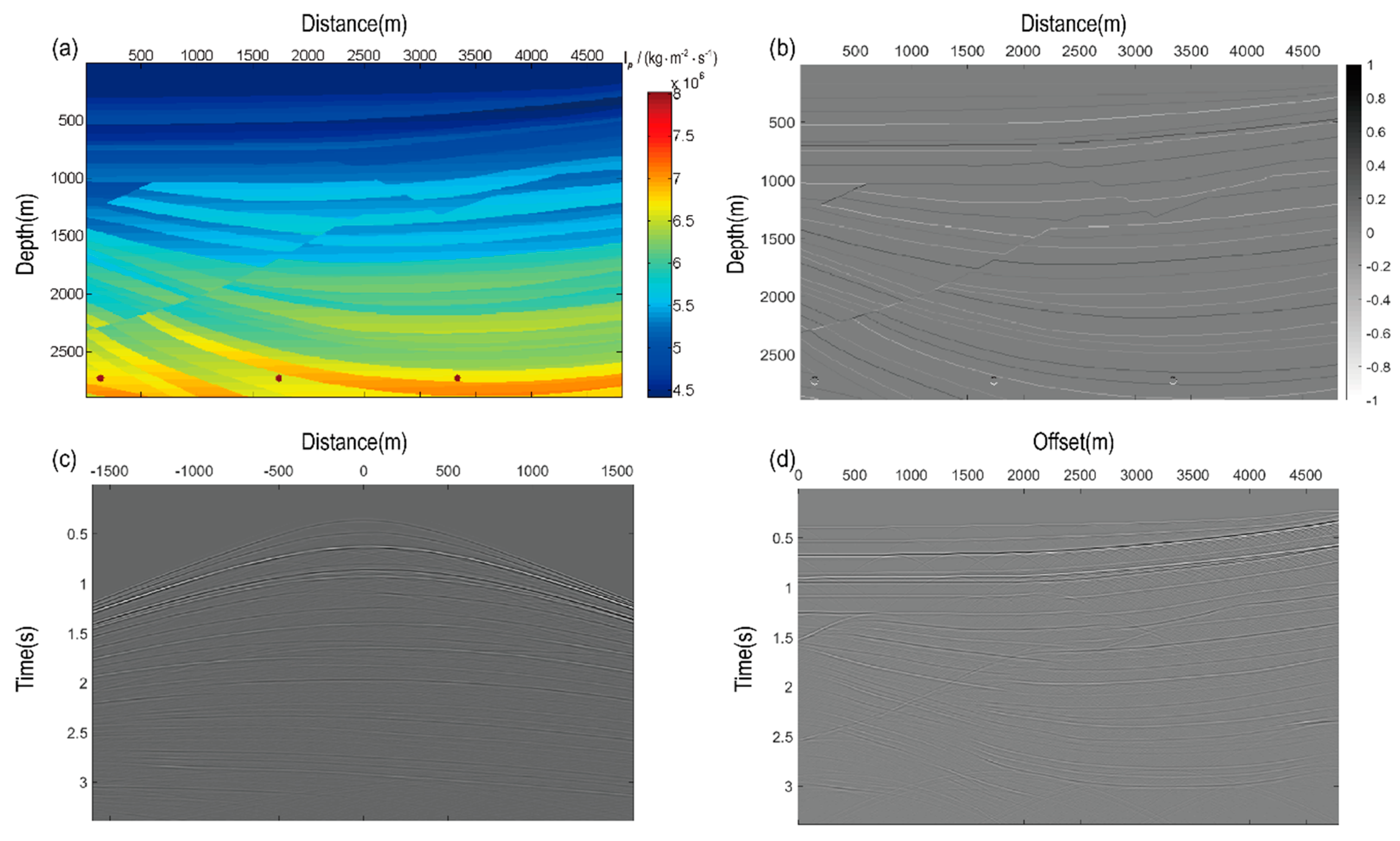
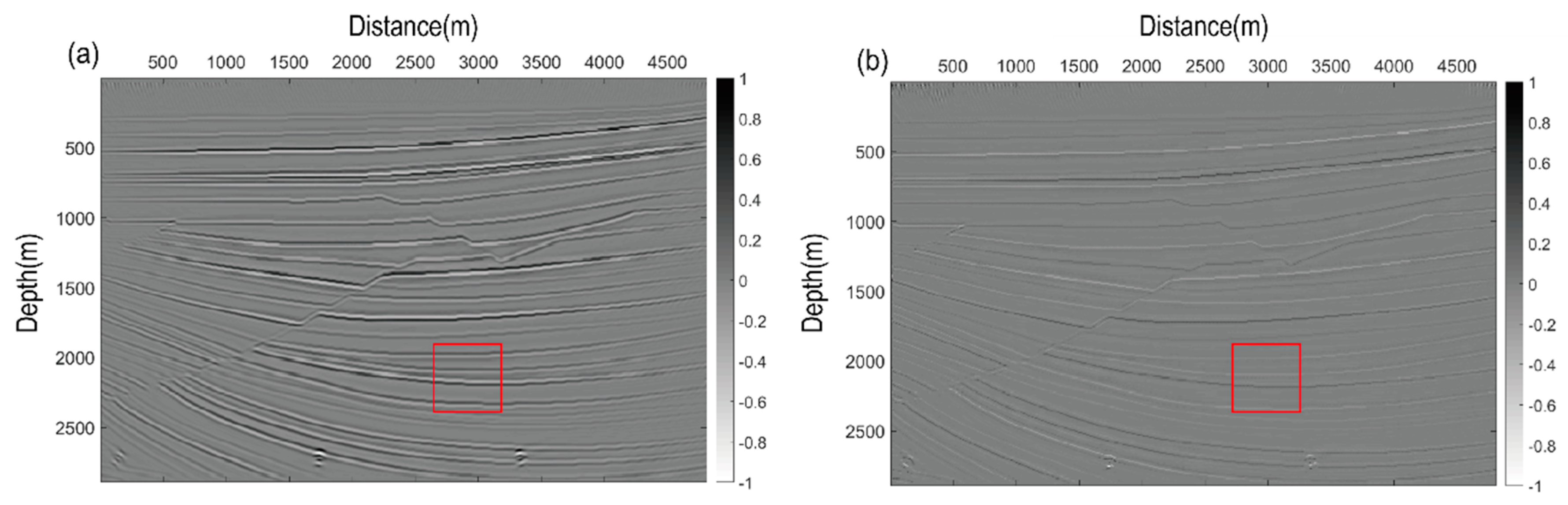
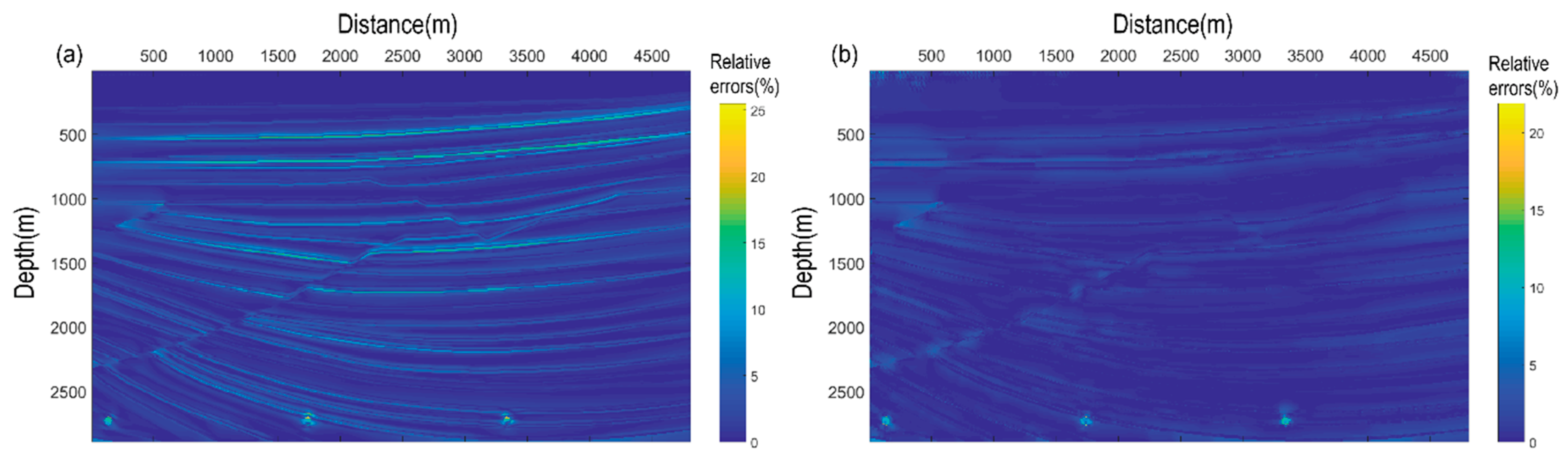
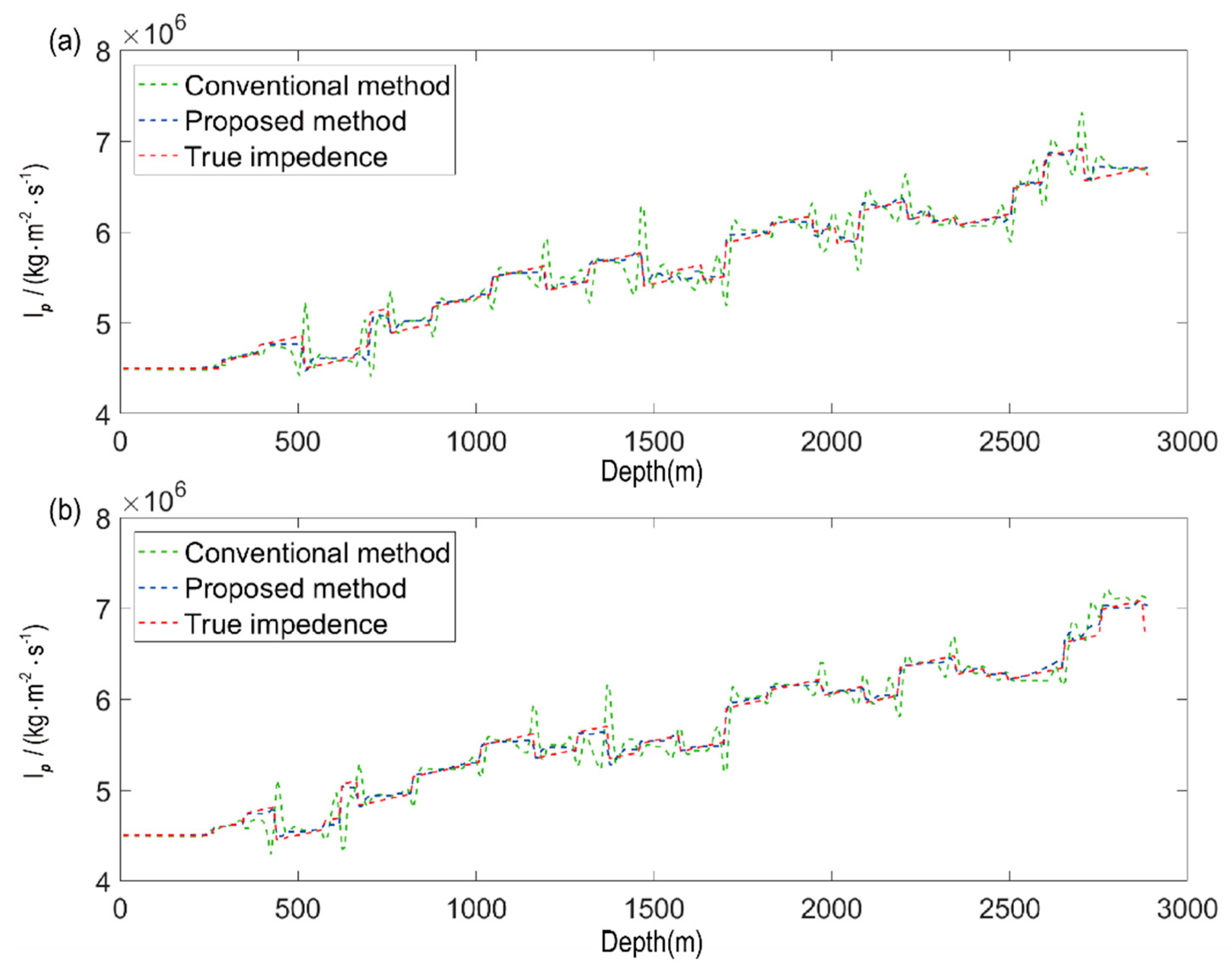
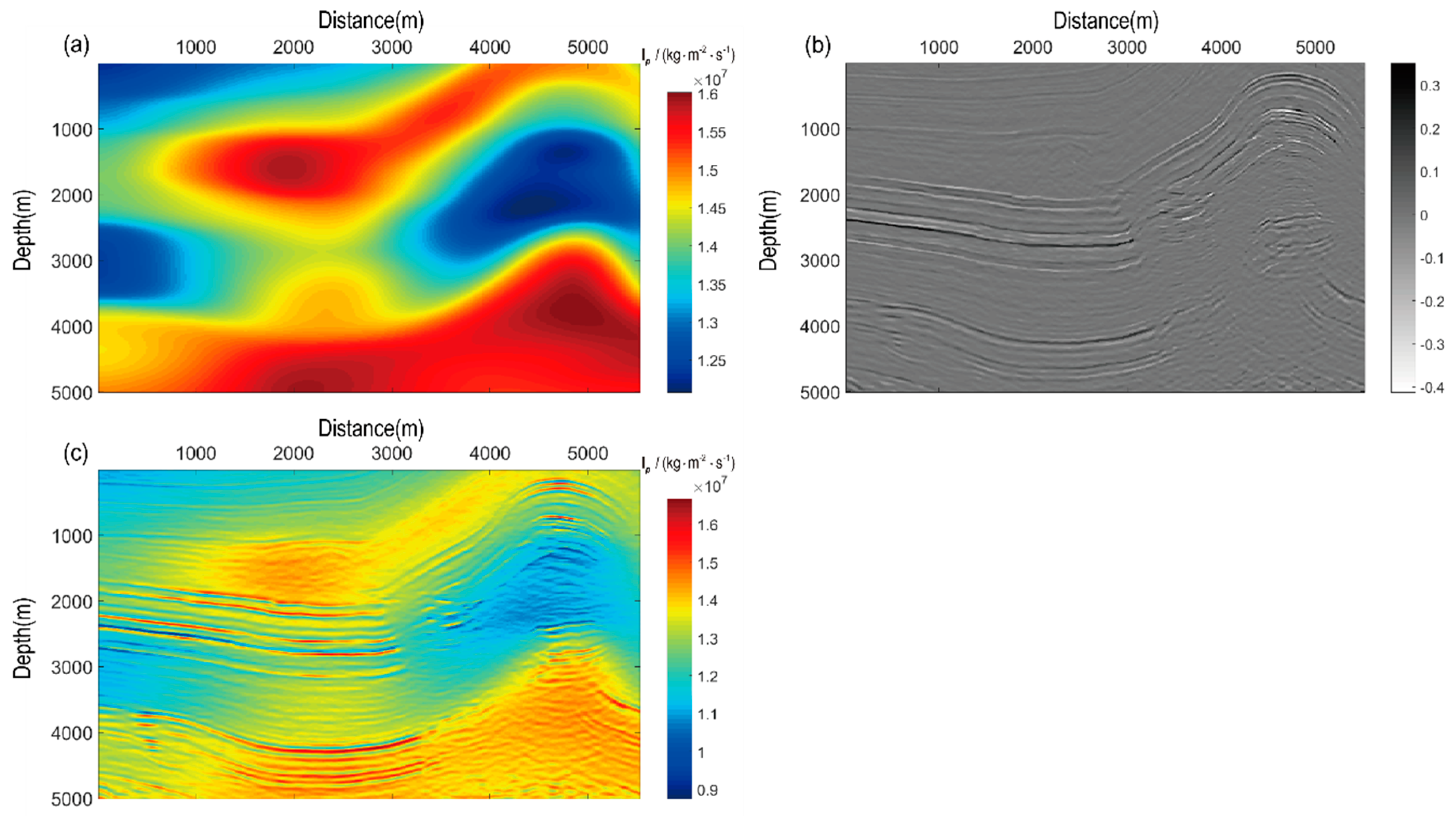
5. Numerical Examples
6. Discussions
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Wang, H.Z.; Guo, S.; Zhou, Y. Broadband Acoustic Impedance Model Building for Broadband, Wide-Azimuth, and High-Density Seismic Data. Geophys. Pros. Pet. 2019, 58, 1–8. [Google Scholar]
- Mabrouk, W.M. Acoustic Impedance Inversion Approach from Petrophysical Data. J. Pet. Sci. Eng. 2010, 73, 181–184. [Google Scholar] [CrossRef]
- Alves, F.; Almeida, J.A.; Silva, A.P. Simulation of acoustic impedance images by stochastic inversion of post-stack seismic reflection amplitudes and well data. J. Pet. Sci. Eng. 2014, 121, 52–65. [Google Scholar] [CrossRef]
- Zahmatkesh, I.; Kadkhodaie, A.; Soleimani, B.; Golalzadeh, A.; Azarpour, M. Estimating Vsand and Reservoir Properties from Seismic Attributes and Acoustic Impedance Inversion: A Case Study from the Mansuri Oilfield, SW Iran. J. Pet. Sci. Eng. 2018, 161, 259–274. [Google Scholar] [CrossRef]
- Wu, H.; Chen, Y.P.; Li, S.; Peng, Z.M. Acoustic Impedance Inversion Using Gaussian Metropolis–Hastings Sampling with Data Driving. Energies 2019, 12, 2744. [Google Scholar] [CrossRef] [Green Version]
- Walker, C.; Ulrych, T.J. Autoregressive Recovery of the Acoustic Impedance. Geophysics 1983, 48, 1338–1350. [Google Scholar] [CrossRef]
- Oldenburg, D.W.; Scheuer, T.; Levy, S. Recovery of the Acoustic Impedance from Reflection Seismograms. Geophysics 1983, 48, 1318–1337. [Google Scholar] [CrossRef]
- Berteussen, K.A.; Ursin, B. Approximate Computation of the Acoustic Impedance from Seismic Data. Geophysics 1983, 48, 1351–1358. [Google Scholar] [CrossRef]
- Gholami, A. Nonlinear Multichannel Impedance Inversion by Total-Variation Regularization. Geophysics 2015, 80, R217–R224. [Google Scholar] [CrossRef]
- Gholami, A. A Fast Automatic Multichannel Blind Seismic Inversion for High-Resolution Impe Dance Recovery. Geophysics 2016, 81, V357–V364. [Google Scholar] [CrossRef]
- Tarantola, A. Inversion of Seismic Reflection Data in the Acoustic Approximation. Geophysics 1984, 49, 1259–1266. [Google Scholar] [CrossRef]
- Lambaré, G.; Virieux, J.; Madariaga, R.; Jin, S. Iterative Asymptotic Inversion in the Acoustic Approximation. Geophysics 1992, 57, 1138–1154. [Google Scholar] [CrossRef]
- Pratt, R.G. Seismic Waveform Inversion in the Frequency Domain, Part 1: Theory and Verify Cation in a Physical Scale Model. Geophysics 1999, 64, 888–901. [Google Scholar] [CrossRef] [Green Version]
- Claerbout, J.F. Imaging the Earth's Interior; Blackwell Scientific Publications: Oxford, UK, 1985. [Google Scholar]
- Wang, Y.; Pratt, R.G. Sensitivities of Seismic Traveltimes and Amplitudes in Reflection Tomography. Geophys. J. Int. 1997, 131, 618–642. [Google Scholar] [CrossRef] [Green Version]
- Guo, S.; Wang, H. Seismic Absolute Acoustic Impedance Inversion with L1 Norm Reflectivity Constraint and Combined First- and Second-Order Total Variation Regularizations. J. Geophys. Eng. 2019, 16, 773–788. [Google Scholar] [CrossRef]
- Feng, B.; Xu, W.; Wu, R.S.; Xie, X.B.; Wang, H. Finite-Frequency Traveltime Tomography Using the Generalized Rytov Approximation. Geophys. J. Int. 2020, 221, 1412–1426. [Google Scholar] [CrossRef]
- Virieux, J.; Asnaashari, A.; Brossier, R.; Métivier, L.; Ribodetti, A.; Zhou, W. An Introduction to Full Waveform Inversion. In Encyclopedia of Exploration Geophysics; Society of Exploration Geophysicists: Tulsa, OK, USA, 2014; pp. R1-1–R1-40. [Google Scholar] [CrossRef]
- Liu, S.Y.; Wu, R.S.; Feng, B.; Wang, H.Z.; Guo, S. A True-Amplitude Imaging Method Based on Gaussian Beam Migration and Demigration. P. Appl. Geophys. 2020, 177, 4707–4718. [Google Scholar] [CrossRef]
- Beylkin, G. Imaging of Discontinuities in the Inverse Scattering Problem by Inversion of a Generalized Radon Transform. J. Mathe. Phys. 1985, 26, 99–108. [Google Scholar] [CrossRef]
- Bleistein, N. On the Imaging of Reflectors in the Earth. Geophysics 1987, 52, 931–942. [Google Scholar] [CrossRef]
- Bleistein, N.; Zhang, Y.; Xu, S.; Zhang, G.; Gray, S.H. Migration/Inversion: Think Image Point Coordinates, Process in Acquisition Surface Coordinates. Inverse Problems 2005, 21, 1715–1744. [Google Scholar] [CrossRef] [Green Version]
- Nemeth, T.; Wu, C.; Schuster, G.T. Least-Squares Migration of Incomplete Reflection Data. Geophysics 1999, 64, 208–221. [Google Scholar] [CrossRef]
- Duquet, B.; Marfurt, K.J.; Dellinger, K.J. Kirchhoff Modeling, Inversion for Reflectivity, and Subsurface Illumination. Geophysics 2000, 65, 1195–1209. [Google Scholar] [CrossRef]
- Dai, W.; Huang, Y.; Schuster, G.T. Least-Squares Reverse Time Migration of Marine Data with Frequency-Selection Encoding. Geophysics 2013, 78, S233–S242. [Google Scholar] [CrossRef] [Green Version]
- Ma, C.; Gao, Y.; Lu, C. Numerical Modeling of Elastic Wave in Frequency-Domain by Using Staggered Grid Fourth-Order Finite-Difference Scheme. Adv. Geo Energy Res. 2019, 3, 410–420. [Google Scholar] [CrossRef] [Green Version]
- Cerveny, V.; Popov, M.M.; Psencik, I. Computation of Wave Fields in Inhomogeneous Media—Gaussian Beam Approach. Geophys. J. Int. 1982, 70, 109–128. [Google Scholar] [CrossRef] [Green Version]
- Hill, N.R. Gaussian Beam Migration. Geophysics 1990, 55, 1416–1428. [Google Scholar] [CrossRef]
- Gray, S.H.; Bleistein, N. True Amplitude Gaussian Beam Migration. Geophysics 2009, 74, S11–S23. [Google Scholar] [CrossRef]
- Liu, S.Y.; Gu, H.M.; Han, B.K.; Yan, Z.; Liu, D.; Cai, J. Band-Limited Beam Propagator and Its Application to Seismic Migration. Geophysics 2018, 83, S311–S319. [Google Scholar] [CrossRef]
- Huang, X.; Sun, H.; Sun, J. Born Modeling for Heterogeneous Media Using the Gaussian Beam Summation Based Greens Function. J. Appl. Geophys. 2016, 131, 191–201. [Google Scholar] [CrossRef]
- Sun, H.; Gao, C.; Zhang, Z.; Liao, X.; Wang, X.; Yang, J. High-Resolution Anisotropic Prestack Kirchhoff Dynamic Focused Beam Migration. IEEE Sens. J. 2020, 20, 11753–11760. [Google Scholar] [CrossRef]
- Hu, H.; Liu, Y.; Zheng, Y. Least-Squares Gaussian Beam Migration. Geophysics 2016, 81, S87–S100. [Google Scholar] [CrossRef]
- Yue, Y.; Sava, P.; Qian, Z.; Yang, J.; Zou, Z. Least-Squares Gaussian Beam Migration in Elastic Media. Geophysics 2019, 84, S329–S340. [Google Scholar] [CrossRef]
- Schuster, G.; Liu, Z. Least Squares Migration: Current and Future Directions. In Proceedings of the 81st EAGE Conference and Exhibition 2019, London, UK, 3–6 June 2019; European Association of Geoscientists & Engineers: Houten, The Netherlands, 2019; pp. 1–5. [Google Scholar] [CrossRef]
- Wu, R.; Luo, M.; Chen, S.; Xie, X. Acquisition aperture correction in angle-domain and true-amplitude imaging for wave equation migration. Soc. Explor. Geophys. 2004, 23, 937–940. [Google Scholar] [CrossRef] [Green Version]
- Cao, J.; Wu, R.S. Amplitude Compensation of One-Way Wave Propagators in Inhomogeneous Media and Its Application to Seismic Imaging. Commun. Comput. Phys. 2008, 3, 203–221. [Google Scholar]
- Gelius, L.J.; Lecomte, I.; Tabti, H. Analysis of The Resolution Function in Seismic Prestack Depth Imaging. Geophys. Pros. 2002, 50, 505–515. [Google Scholar] [CrossRef]
- Lecomte, I. Resolution and Illumination Analyses in PSDM: A Ray-Based Approach. Lead. Edge 2008, 27, 650–663. [Google Scholar] [CrossRef]
- Yan, R.; Guan, H.; Xie, X.B.; Wu, R.S. Acquisition Aperture Correction in the Angle Domain toward True-Reflection Reverse Time Migration. Geophysics 2014, 79, S241–S250. [Google Scholar] [CrossRef] [Green Version]
- Yan, Z.; Xie, X.B. Full-Wave Seismic Illumination and Resolution Analyses: A Poynting-Vector- Based Method. Geophysics 2016, 81, S447–S458. [Google Scholar] [CrossRef] [Green Version]
- Xie, X.-B.; Wu, R.-S.; Fehler, M.; Huang, L. Seismic Resolution and Illumination: A Wave-Equation-Based Analysis. In Proceedings of the 75th Annual International Meeting; SEG Technical Program Expanded Abstracts; Society of Exploration Geophysicists: Tulsa, OK, USA, 2005; Volume 24, pp. 1862–1865. [Google Scholar] [CrossRef] [Green Version]
- Xie, X.B.; JIN, S.; Wu, R.S. Wave-Equation Based Seismic Illumination Analysis. Geophysics 2006, 71, S169–S177. [Google Scholar] [CrossRef]
- Liu, S.; Xie, X.; Wu, R.; Yan, Z.; Gu, H. An Effective True-Amplitude Gaussian Beam Migration via Illumination Compensation. In Proceedings of the EAGE 2020 Annual Conference & Exhibition Online 2020; European Association of Geoscientists & Engineers: Houten, The Netherlands, 2020; pp. 1–5. [Google Scholar] [CrossRef]
- Hill, N.R. Prestack Gaussian-Beam Depth Migration. Geophysics 2001, 66, 1240–1250. [Google Scholar] [CrossRef]
- Chen, B.; Xie, X.-B. An efficient method for broadband seismic illumination and resolution analyses. In SEG Technical Program Expanded Abstracts 2015; Society of Exploration Geophysicists: Tulsa, OK, USA, 2015; Volume 34, pp. 4227–4231. [Google Scholar] [CrossRef] [Green Version]
- Kang, W.; Willingham, B.; Kriseman, Z.; Yong, S.L. Statistical calibration of the point spread function for image-domain least-squares migration. In SEG Technical Program Expanded Abstracts 2019; Society of Exploration Geophysicists: Tulsa, OK, USA, 2019; Volume 38, pp. 4226–4230. [Google Scholar] [CrossRef]
- Wu, R.S.; Aki, K. Scattering Characteristics of Waves by an Elastic Heterogeneity. Geophysics 1985, 50, 582–595. [Google Scholar] [CrossRef]
- Malvic, T.; Prskalo, S. Significance of the Amplitude Attribute in Porosity Prediction, Drava Depression Case Study. Nafta 2008, 59, 39–51. [Google Scholar]
- Yang, Z.; Lu, J. Second-Order Approximation of the Seismic Reflection Coefficient in Thin Interbeds. Energies 2020, 13, 1465. [Google Scholar] [CrossRef] [Green Version]
- Foster, M. Transmission Effects in the Continuous One-Dimensional Seismic Model. Geophys. J. R. Astron. Soc. 1975, 42, 519–527. [Google Scholar] [CrossRef]
- Goldstein, T.; Osher, S. The Split Bregman Method for L1 Regularized Problems. Siam J. Imaging Sci. 2009, 2, 323–343. [Google Scholar] [CrossRef]
- Pan, S.; Yan, K.; Lan, H.; Badal, J.; Qin, Z. A Sparse Spike Deconvolution Algorithm Based on a Recurrent Neural Network and the Iterative Shrinkage-Thresholding Algorithm. Energies 2020, 13, 3074. [Google Scholar] [CrossRef]
- Paffenholz, J.; Stefani, J.; McLain, B.; Bishop, K. SIGSBEE_2A Synthetic Subsalt Dataset—Image Quality as Function of Migration Algorithm and Velocity Model Error. In 64th EAGE Conference & Exhibition; European Association of Geoscientists & Engineers: Houten, The Netherlands, 2002; p. cp-5. [Google Scholar] [CrossRef]
- Liu, S.Y.; Yan, Z.; Zhu, W.T.; Han, B.K.; Gu, H.M.; Hu, S.Z. An Illumination-Compensated Gaussian Beam Migration for Enhancing Subsalt Imaging. Geophys. Prospect. 2021. [Google Scholar] [CrossRef]
- Feng, B.; Wu, R.S.; Wang, H. A Generalized Rytov Approximation for Small Scattering-Angle Wave Propagation and Strong Perturbation Media. Geophys. J. Int. 2019, 219, 968–974. [Google Scholar] [CrossRef]
- Yuan, S.; Wang, S.; Luo, Y.; Wei, W.; Wang, G. Impedance Inversion by Using the Low-Frequency Full-Waveform Inversion Result as A Priori Model. J. Geophys. 2019, 84, 1–95. [Google Scholar] [CrossRef]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, S.; Zhu, W.; Yan, Z.; Xu, P.; Wang, H. An Effective Acoustic Impedance Imaging Based on a Broadband Gaussian Beam Migration. Energies 2021, 14, 4105. https://doi.org/10.3390/en14144105
Liu S, Zhu W, Yan Z, Xu P, Wang H. An Effective Acoustic Impedance Imaging Based on a Broadband Gaussian Beam Migration. Energies. 2021; 14(14):4105. https://doi.org/10.3390/en14144105
Chicago/Turabian StyleLiu, Shaoyong, Wenting Zhu, Zhe Yan, Peng Xu, and Huazhong Wang. 2021. "An Effective Acoustic Impedance Imaging Based on a Broadband Gaussian Beam Migration" Energies 14, no. 14: 4105. https://doi.org/10.3390/en14144105
APA StyleLiu, S., Zhu, W., Yan, Z., Xu, P., & Wang, H. (2021). An Effective Acoustic Impedance Imaging Based on a Broadband Gaussian Beam Migration. Energies, 14(14), 4105. https://doi.org/10.3390/en14144105




