Abstract
This paper examines the environmental Kuznets curve (EKC) in Vietnam between 1977 and 2019. Using the autoregressive distributed lag (ARDL) approach, we find an inverted N-shaped relation between economic growth and carbon dioxide emissions in both the long- and short-run. The econometric results also reveal that energy consumption and urbanization statistically positively impact pollution. The long-run Granger causality test shows a unidirectional causality from energy consumption and economic growth to pollution while there is no causal relationship between energy consumption and economic growth. These suggest some crucial policies for curtailing emissions without harming economic development. In the second step, we also employed the back-propagation neural networks (BPN) to compare the work of econometrics in carbon dioxide emissions forecasting. A 5-4-1 multi-layer perceptron with BPN and learning rate was set at 0.1, which outperforms the ARDL’s outputs. Our findings suggest the potential application of machine learning to notably improve the econometric method’s forecasting results in the literature.
1. Introduction
Vietnam is a developing country with notable economic growth during the last four decades. Since 1986, there have been some critical political and social reform milestones. The government has adopted open-door policies toward international trade and investment, and industrial activity in large cities has become increasingly active. As a result, Vietnam has risen from a low-income country to lower-middle-income status, with an average Gross Domestic Product (GDP) of US $ 2700 with more than 45 million people lifted out of poverty since 1986 [1]. Vietnam has also developed strategies to pursue economic growth associated with sustainable development. In particular, Vietnam has ratified international treaties, namely, the Kyoto Protocol (2002) and the Paris Agreement (2016), to adapt to climate change and reduce carbon emissions. Vietnam has amended the national law on environmental protection since 2014. The legislation focuses on three pillars, i.e., cap and trade, industrial emissions reporting provisions, and a database of all carbon and mitigation steps. For instance, cap and trade concentrate on creating a domestic carbon credit market where companies are limited in their emissions, so if they do not reach the cap, they could trade the surplus with other companies to optimize the cost of emissions. On the other hand, companies also regularly report their emissions to the authorized agency to monitor the quota.
Regarding renewable energies, the primary objective is to accelerate the production towards the maximal replacement of fossil energy sources. In particular, renewable electricity sources account for 15–20% of overall primary energy production in 2030 [2], biomass power, wind power, and solar power reach 6.3%, 2.7%, and 6% of total electricity output, respectively [3]. Furthermore, the government establishes a framework for fostering and attracting non-state investment in the nation’s power transmission system [2]. These steps are expected to create a free energy market and efficiently monitor environmental policies.
Although those attempts have been recognized to serve sustainable development, Vietnam faces the over fossil fuel consumption to hardly obtain the low carbon economy by 2030. Coal consumption accounts for between 65% and 75% of overall CO2 emissions from the entire electricity sector, and oil consumption increases an average of 2.73% from 1977 to 2013 [4]. The excessive demand for natural resources and fossil-fuel energy due to the significant economic transformation has increased air pollution, especially in big cities where traffic congestion and industrial issues have become more serious [5,6]. For example, according to Our World in Data [7] and Euromonitor Passport Database [8], the average increase in carbon dioxide (CO2) emissions reached 5.14%, along with the 6.53% increase in energy consumption and a 4.62% increase in real income for the period 1977 to 2019. Additionally, for the period 2007 to 2017, the total economic development by 6.1% resulted in a 9.3% growth of the industrial sector’s energy consumption (Electricity and Renewable Energy Authority in Vietnam and Danish Energy Agency-EREA and DEA [9]). The evidence suggests that economic expansion is related to a rise in Vietnam’s energy consumption and environmental deterioration. The CO2 emissions and economic growth were normalized and presented in Figure 1.
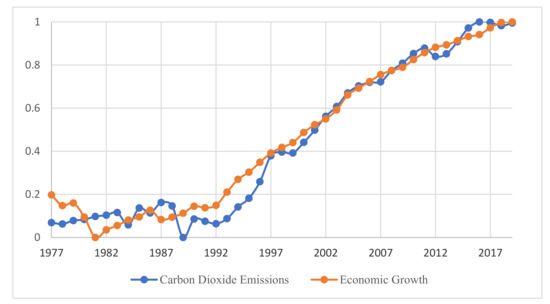
Figure 1.
Evolution of carbon dioxide emissions and economic growth (normalized values), 1977–2019.
As shown in Figure 1, the trend is not a linear relationship. While real income saw a steadily upward trend after 1981, the CO2 emissions line has fluctuated with several decreased points, for instance, 1983–1985, 2011–2013, and 2017–2018. In other words, these historical data suggest the possibility that an environmental Kuznets curve (EKC) hypothesis existed during the period 1977 to 2019. Although the EKC hypothesis has been widely examined in both developing and developed countries, few studies have been conducted in the context of Vietnam. Accordingly, we are interested in gaining insight into the EKC pattern for a specific developing economy since environmental issues have been seriously concerned in Vietnam recently.
Furthermore, recent studies have applied advanced techniques in environmental issues [10,11,12,13]. One primary reason is that forecasts of CO2 emissions are difficult due to nonlinear regression. Therefore, the econometric method may not accurately capture the complicated behavior of analyzed variables [10,14]. As a result, finding a reliable model that can predict CO2 emissions patterns could be used to formulate policies that will mitigate environmental problems [10]. Although previous studies have adopted artificial neural networks (ANN) on this topic, few studies test benchmarks between econometrics and machine-learning approaches. In this study, once the form of EKC trajectory is determined for the long run, we apply the back-propagation algorithm (BPN) to ANN to calculate the forecast results and compare them to the econometric results. We aim to fill this gap by adding to the literature an empirical study that presents the predictive effectiveness of BPN.
From the analysis above, the study’s first aim is to validate the EKC in Vietnam from 1977 to 2019. We employed the autoregressive distributed lag (ARDL) method to examine the cointegration between analyzed variables. We also investigate the long- and short-run estimations to ascertain the parameters of the EKC curve in the sample. We further analyze the Granger causality to determine the directional effects between variables to raise reliable policy implications. The second aim of the paper is to enhance the predictive results by the machine learning method. We suppose that a machine learning approach is suitable for the complex predictive task than the econometrics approach. To conduct the comparison, we employed BPN to show the CO2 emissions forecasting results and then compare the results to the ARDL’s by examining benchmarked indicators. We expect that the BPN has outperformed results due to capturing the complex behaviors between variables. Based on our findings, we add to the literature an improvement of CO2 emissions forecasting by BPN.
The rest of the paper is organized as follows: Section 2 provides a review of the EKC literature. Section 3 and Section 4 present the proposed model and data sources. Section 5 demonstrates the framework of ARDL, BPN, and comparative forecasting indicators between the ARDL and the BPN approaches. The empirical results and discussions are presented in Section 6, Section 7 and Section 8 discusses the conclusion and future research.
2. Related Literature
The fundamental idea of EKC is understandable and intuitive. The EKC reveals the inverted quadratic linkage between economic growth and environmental degradation, in which high economic growth initially leads to environmental deterioration due to scale effects. Then the economy reaches a certain level of average economic development when the environmental quality starts to improve because of the technical effects [15,16]. Since Grossman and Krueger [17] and Panayotou [18] had pioneering endeavors to investigate the EKC hypothesis, a considerable number of empirical studies have focused on this issue. The studies that tested the hypothesis of the EKC used multiple variables of environmental deterioration, i.e., CO2 [19,20,21], nitrous oxide (N2O) emission [22,23], ecological footprints [24,25,26], electronic waste [27], water quality [28,29,30], and chromium emissions [31]. Regarding explanatory variables, previous studies used a range of indicators, such as economic growth [20,31,32], energy consumption [33,34,35,36,37], trade openness [31,38,39], urban population [40,41,42], financial development [43,44,45], technological development [22,46], and education expenditure [47,48]. Regarding econometric approaches, several studies employed the semiparametric method as alternatives to the parametric method [49,50,51] because the results obtained from the semiparametric approach avoid the parametric functional form assumptions [50]. The summary of empirical studies published from 2015 to 2020 is presented in Appendix A. The review shows that 48% of studies find appropriate evidence while 52% of ones find mixed or no evidence of the EKC hypothesis in the analyzed sample. Therefore, the evidence has not converged [15].
The empirical evidence of the EKC hypothesis is found in developed economies in, for instance, the USA [49], the UK [52], the EU [25], Canada [53], Australia [48], and Singapore [31,45]. Whereas it is not widely supported in developing countries such as Cambodia [54], Malaysia [55], Myanmar [41], Sri Lanka [56], and African countries [39,57,58]. The differences in environmental awareness may explain the significant reason for this phenomenon. While awareness is driven mainly by environmental protection perceptions in developed countries, protections are lax in developing countries due to their primary focus on achieving economic growth [15,59]. In other words, developed countries have reached their turning point; they have passed the phase of using technological efficiency to enhance economic growth while keeping in place environmental protections, whereas developing countries are in the early stage of scale effects in economic development [15,16,18]. However, several empirical studies show the opposite trend. The presence of the EKC hypothesis is confirmed in developing countries such as Pakistan [32,43], Indonesia [60], South Africa [61], India [62,63], and China [40,64]. Meanwhile, several empirical studies provide no existence of the EKC hypothesis in developed countries, for example, the USA [50,65], Australia [66], the EU [67,68], and the OECD [16,69]. The main reasons behind the mixed results may be due to scaling factors employed in models [70], datasets, timespan, economic specifications in a country, and methods used to investigate the EKC hypothesis [12,30,71]. For these previous practical experiences, in this paper, we focus on studies that examine the EKC in developing countries which have similar conditions to Vietnam to find out the relationship between environmental deterioration and related explanatory factors.
Shahbaz et al. [72] employed the ARDL technique to examine the EKC trajectory of Pakistan from 1971 to 2009 and confirms the presence of EKC both in the long- and short-run. In addition, energy consumption also significantly increases CO2 emissions. The study emphasizes the country’s effort to mitigate CO2 emissions based on a national environmental law released in 2005 and suggests a green tax to support the law in protecting the environment. For China and India, Pal and Mitra [73] confirm the N-shaped pattern of the EKC hypothesis rather than the inverted U-curve. The N-shaped curve indicates that environmental degeneration will increase in both economies, increasing population growth, urban congestion, and industrial emissions. The results suggest that Indian policymakers could direct their efforts toward renewable energy sources such as hydropower, nuclear power, windmills, and solar power to replace coal in producing electric power. Meanwhile, the policymakers in China should consider the speed of urbanization to reduce the high electricity demand and encourage technological enhancement in the energy supply.
In Southeast Asia, Saboori and Sulaiman [74] find the EKC hypothesis for both long- and short-run in Malaysia. Moreover, the results also show the unidirectional causality from economic growth to CO2 emissions in the long run. As a result, the government could implement policies that reduce emissions without harming economic growth to obtain sustainable development in the long run. Similarly, Sugiawan and Managi [60] also confirm the EKC hypothesis in Indonesia, with the turning point occurring outside the period from 1971–2010. Energy consumption has a significantly positive effect on CO2 emissions, whereas electricity production from renewable energy is a statistically negative sign for both the long- and short-run. These indicate the necessity for switching to CO2 emission-free energy shortly. However, Ozturk and Al-Mulali [54] find no EKC hypothesis in Cambodia. Similarly, Al-Mulali et al. [75] find a monotonically positive relationship between income and environmental degradation in Vietnam. The EKC hypothesis does not exist because these economies are still in their early stages, so environmental degradation has not reached the turning point yet.
Meanwhile, Shahbaz et al. [76] found N-shaped EKC in the long run and suggest some policies to prevent the economy from reaching the second turning point. For developing countries, mixed results could raise arguments over the presence of the EKC hypothesis. The divergent results are found even in the same country, i.e., using the example of China, Jalil and Mahmud [77] find the inverted U-shaped EKC while Pal and Mitra [73] find the N-shaped EKC; in the case of Malaysia, Lau et al. [78] confirmed the EKC hypothesis whereas Gill, Viswanathan and Hassan [55] showed the monotonically increase of EKC. Therefore, our work investigates the existence of the EKC hypothesis in Vietnam, a country that has undergone notable changes in economic growth.
Regarding ANN application in the literature, Acheampong and Boateng [10] employed BPN to predict carbon emissions intensity with nine explanatory inputs and five nodes in the hidden layer. A 9-5-1 multilayer perceptron (MLP) system shows that the predictive errors are trivial. More specifically, the mean absolute deviations and the mean squared errors are close to zero. In addition, some factors such as urbanization, energy consumption, and population have the most significant impact on CO2 emissions, especially in the USA, India, and China. Aydin, Jang and Topal [11] also used BPN to establish a system of four attributes, i.e., population, GDP, exports, and imports, to forecast energy consumption in the top-10 highest energy-consuming countries. The 4-10-1 MLP shows that correlation coefficients in the training set and testing set are over 0.96 and 0.89, respectively. Meanwhile, the performance values such as mean absolute percentage error and root mean square error are insignificant. These indicate that the BPN adopted in this study could suggest adequate predicting results within the analyzed economies. Bildirici and Ersin [12] proposed the Markov-switching vector autoregressive MLP approach to investigate the nonlinear relationship between emissions, petrol prices, and economic growth in the USA and the UK. The proposed approach has values of Mean Squared Errors (MSE), Mean Absolute Error (MAE), and Root Mean Squared Error (RMSE) that are less than the approach without MLP in both expansion and recession regimes. These indicate that the complicated nonlinear connection between analyzed variables may be adequately explained using neural networks.
From the analysis of the related literature, few studies focus on this topic in Vietnam even though the EKC hypothesis could affect economic development for the last four decades. Second, we emphasize the importance of energy consumption and urbanization variables, which significantly affect CO2 emissions in developing countries like Vietnam. Third, finding a reliable model of CO2 emissions prediction is needed to formulate effective environmental protection policies. Therefore, in the first stage, we employed the ARDL to examine the presence of the EKC hypothesis in Vietnam by investigating the relationship between CO2 emissions and the explanatory variables. In the second stage, once the long run EKC form is determined, we applied the BPN method to predict CO2 emissions. We then compare the predicted outcome between BPN and ARDL by using the comparative indicators. Our work further analyzes the forecasting improvement of BPN and will show potential approaches for future studies.
3. Proposed Model
The shape of the EKC hypothesis has always varied. Some studies initially assumed the monotonic relationship between economic growth and CO2 emissions [75,79,80], some favored the quadratic function [55,64,65,71] to test the presence of the EKC hypothesis. This study initially examines the cubic form of the EKC hypothesis in Vietnam because this assumed function is the general form, including linear and quadratic functions. Based on some recent models such as Pal and Mitra [73], Onafowora and Owoye [81], and Neve and Hamaide [82], we propose a general cubic form that shows the relationship between CO2 emissions, economic growth, energy consumption, and urbanization. We transformed all variables into the natural logarithm before testing for less non-normality and heteroscedasticity (for a similar approach, see [44,73,83,84]). The proposed model is specified as:
where CO2 represents environmental degradation, GDP denotes economic growth. EC stands for energy consumption, UrB depicts urbanization, and ut is independent and identically distributed. The specific functional form is determined by the Beta coefficients [15,81,85] as follows:
- ≠ 0, = = 0: linear relationship between CO2 and growth
- < 0, > 0, = 0: U-shaped CO2-growth nexus
- > 0, < 0, = 0: inverted U-shaped CO2-growth nexus
- > 0, < 0, > 0: N-shaped CO2-growth nexus
- < 0, > 0, < 0: inverted N-shaped CO2-growth nexus
The only turning point is calculated by t* = exp(−/3) if the first derivative function of Equation (1) has one solution, or two turning points are computed by = exp([− ± ( − 3)1/2]/3) if the first derivative function of Equation (1) has two solutions (Appendix B).
4. Data Sources
We test the validating of the EKC hypothesis in Vietnam between 1977 and 2019. With data for analysis, CO2 emissions and energy consumption are collected from Our World in Data [7], real GDP data are compiled from Euromonitor Passport Database [8], and data on urbanization are collected from World Development Indicators [86]. CO2 emissions are measured by kilograms per capita. Energy consumption is measured by kilowatt-hours per capita and compiled from seven sources: oil, coal, gas, hydropower, solar, wind, nuclear, and other renewables. GDP refers to economic growth measured per capita in 1977 of constant Vietnam currency. Urbanization is measured by the population ratio in urban agglomerations of more than one million of the total population. The descriptive statistics for all the analyzed variables were presented in Table 1.

Table 1.
Descriptive Statistics of the data of Vietnam, 1977–2019.
5. Methodological Framework
5.1. Auto Regressive Distributed Lag Approach
In this study, we employ the ARDL, developed by Pesaran et al. [87], to determine CO2 behavior and other explanatory variables in the Vietnamese context. The ARDL method is widely applied compared to other cointegration approaches, such as those suggested by Engle and Granger [88], Johansen and Juselius [89]. The ARDL method is a good fit for our research purposes and the data we collected because the ARDL can be applied for integration at different orders whether the latent variables are a mixture of I(0) and I(1). Second, the ARDL distinguishes long- and short-run effects between independent and dependent variables. Third, this method eliminates endogenous problems by adding lags for independent and dependent variables and selecting the optimal lag length for each variable. Fourth, and more importantly, in applying the bounds testing proposed by Narayan [90], this approach allows the cointegration testing of small samples [75,91,92]. More specifically, our analyzed sample is relatively small, containing forty-two observations, so applying this method within this study is a reasonable choice. The relationship between environmental degradation, economic growth, energy consumption, and urbanization is presented in the cubic form as follows:
where CO2, GDP, EC, and UrB are represented for CO2 emissions, economic growth, energy consumption, and urbanization. , , and are the differenced operator, the intercept, and the white noise, respectively. The parameters , , , , , and represent the short-run dynamics while the parameters , , , , , and indicate the long-run relationship between these variables.
5.1.1. ARDL Bounds Testing for Cointegration Approach
In the ARDL bounds testing method, to examine long-run associations, the null hypothesis of no cointegration was examined, H0: = = = = = = 0 against the alternative of H1: 0. The F-statistic was compared with the upper critical bound (UCB) for the mixed of I(1) or/and I(0). This study used the UCB derived from Narayan [90] due to the small sample size. If the F-statistic is higher than the UCB, we reject the null hypothesis of no cointegration. The Akaike information criterion (AIC) was used to determine the optimal lag length before testing for cointegration [55,65,71]. We choose AIC(p) because of its ability to correctly determining the true lag length (refer to Liew [93] for seeing the experimental testing on those criteria). After confirming long-run cointegration, we then analyzed the function to identify the existing state of EKC in Vietnam. We also presented the short-run estimation to confirm the persistence of the proposed model. The robustness of the long run ARDL model could be investigated for both diagnostic and stability tests. More precisely, we employed the Jarque-Bera test for residual normality Jarque and Bera [94], the Breusch-Godfrey Lagrange multiplier test for serial correlation [95,96], the White test for heteroscedasticity [97], the Ramsey reset test for the correct form of the chosen model [98], the cumulative sum of recursive residuals (CUSUM), and the cumulative sum of squares of recursive residuals (CUSUMSQ) [99] (for similar approach see [32,45,48,60,100]). We also obtain the predicted CO2 emissions values by replacing the actual values of explanatory variables in the long-run form. We then compare the predicted CO2 values to actual CO2 values by applying three comparative indicators for ARDL’s and artificial neural networks’ results.
5.1.2. The VECM Granger Causality Analysis
The causal relationship between the variables determines the framework of policy analysis. We, therefore, applied the vector error correction model (VECM) to investigate the causality between CO2 emissions, energy consumption, economic growth, and urbanization in the context of Vietnam. The results derived from the VECM could suggest policies to reduce environmental degradation by increasing/decreasing determinant factors for both the short run and long run. Once the long-run relationship is confirmed, the lagged error correction term (LECTt−1) derived from the long-run relationship was added into the VECM to examine the long- and short-run Granger causality between these variables as follows:
The coefficient of LECTt − 1, which lies between −1 and 0, for each equation ( should be significantly negative to indicate the speed of adjustment to long-run equilibrium. Furthermore, the significant also implies the long-run Granger causality from independent variables to dependent variable in each equation. For the short-run relationship, the significance of the first difference for each variable confirms the short-run Granger causality between variables. For instance, if 0 is significant, energy consumption Granger-causes CO2 emissions, and vice versa for 0 [101].
5.2. Backpropagation Neural Networks Algorithm
The ARDL method could confirm the pattern of the EKC in Vietnam, and the ARDL could predict the CO2 emissions based on the relationship between analyzed variables. However, our aim is not to stop at the econometrics approach for predicting. We further investigate the ability of the machine learning technique in forecasting. We suppose that advanced techniques such as machine learning could enhance the forecasting results because those methods could capture the complicated fluctuation patterns between variables, especially nonlinear relationships. Recently, several previous studies have applied ANN to examine environmental problems [10,11,12,14]. ANN has several advantages in the regressing task. There is no need to determine mathematical relations between the inputs and corresponding outputs [14,102]. ANN is also free from statistical assumptions and captures complex nonlinear behavior in analyzed attributes [103,104,105]. Additionally, ANN does not require steady data and could learn from data [106]. These advantages motivate us to employ ANN as a valuable method compared to the econometrics approach. In this study, we implement the backpropagation neural networks algorithm (BPN), which is the essence of neural network training, developed by Rumelhart et al. [107], Werbos [108], Parker [109].
Generally, a predicted output is computed in a feed-forward procedure based on the chosen activation function, which transfers information from inputs to hidden nodes and then from hidden nodes to the predicted output. The output is then compared to the actual value to compute the error, which is calculated using a back-propagated procedure to update all weight-connected inputs. Afterward, the next iteration proceeds until the stop condition is met. In this study, the BPN we set up includes the framework of an MLP, which has one hidden layer between the input layer and the output layer. The five-neuron input denotes the five independent variables, and the one-neuron output represents the dependent variable, as shown in Figure 2.
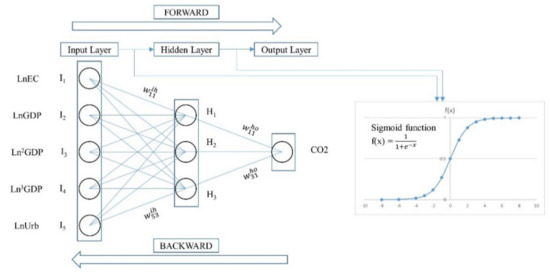
Figure 2.
Illustration for the BPN procedure with three hidden nodes.
The number of nodes in the hidden layer could affect the output error. The optimal number of nodes in the hidden layer should avoid overfitting and satisfy minimal error [110]. Additionally, the optimum number of hidden-layer neurons generally has to be found via trial and error [11,111], and the number of hidden layers changes depending on the complexity of data [112]. Several previous studies show the different optimal hidden nodes [10,110,113]. In other words, there is no theoretical assumption to expect the number of hidden nodes needed to obtain the specific performance of the model [114]. Therefore, we tested several hidden nodes according to previous studies [110,115,116,117,118].
To reduce computational consumption during training due to unstable later layers [119,120] and expedite the sigmoid function’s application for both hidden layer and output layer [10], we normalized data to feed into the neural networks. We also note that the sigmoid function was chosen due to better performance than the tanh function. In addition, data normalizing could eliminate the dominance of any large-scale variable [121] and improve the precision of consecutive numeric calculations [110]. We then de-normalized data to the original for analysis. The algorithm was coded by Python language. The BPN flowchart is shown in Figure 3.
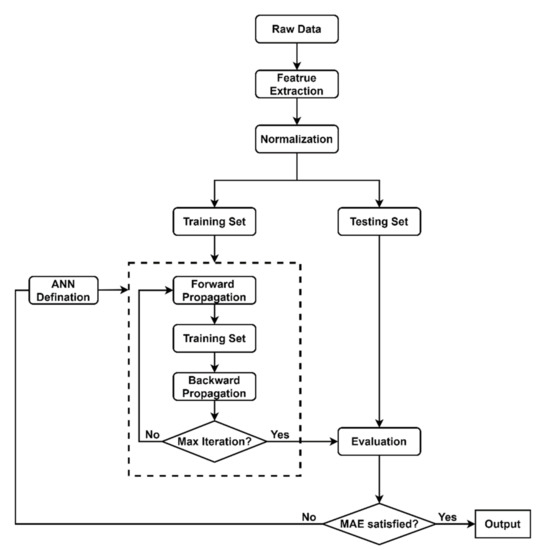
Figure 3.
Flowchart of back-propagation neural networks procedure.
5.3. Criteria for Comparison
To evaluate the accuracy for either the ARDL or BPN approach, we used comparative indicators such as Mean Relative Error (MRE), MSE, and MAE as the following formulas:
where n is the number of input data; At and Ft, are actual and forecasted values of CO2. All three indicators measure the performance of point forecasts; hence the smaller the values are, the better the forecasting is [110]. Additionally, the MAE indicator is used to reduce the effect of heavily weighted outliers [122].
Concerning the number of iterations, we set 200 epochs to converge on the minimum values of these indicators due to our small sample. Additionally, BPN randomly produces connecting weights until convergence, and the output value is also different for each whole procedure. This study tried five different numbers of hidden nodes introduced by [110,115,116,117,118] and three different learning rates, which are 0.01, 0.1, and 0.9. We ran each combination between hidden node and learning rate ten times to obtain stable results. Therefore, for each criterion of MSE, MRE, and MAE, we have a total of 10*3*5 = 150 cells for the training set (the period from 1977 to 2010, equal to 80% of the sample size) and also 150 cells for the testing set (the period between 2011 and 2019, equal to 20% of the sample size). We then select the minimum value of each MSE, MRE, and MAE indicator in the testing set for comparison with the ARDL method.
6. Empirical Results
6.1. Auto Regressive Distributed Lag approach
6.1.1. Unit Root Test
The first step aims to check the order of integration for each variable to confirm whether the data series is stationary. The ARDL bounds testing cointegration approach can be used to identify the possible long-run cointegration among the variables, which have mixed order I(0) and/or I(1). In this study, we employed the Zivot and Andrews [123] and the Perron [124] tests to examine the unit roots due to the probability of the presence of structural breakpoints in the analyzed variables [83,125]. More specifically, the Zivot and Andrews [123] test with a one-unknown structural break which allows for a one-time change in both intercept and trend function of the variables as the following equation:
where DUt is the intercept dummy, representing a mean shift; DUt = 1 if t ≥ Time break (Tb), and 0 otherwise. DTt is the slope dummy, which denotes a trend shift; DTt = t − Tb if t > Tb, and 0 otherwise. The Tb is determined by the minimum t-Statistic of the autoregressive variable (), and the Schwartz Information Criterion determines the lag length (k).
The Perron [124] test is based on Zivot and Andrews [123] except for the time shock dummy variable D(TB)t:
where the indicator D(TB) = 1 if t = TB + 1. The Perron test chooses the breakpoint where the t-statistic for testing = 1 is the minimum as explained for Zivot and Andrews [123] test.
The results from both tests with intercept and trend are presented in Table 2. Overall, the time break for the series is found about 1986–1992. The break also refers to the 1986–1990 transformation from centrally planned to the open-door economy. Due to the stagflation issue, i.e., hyperinflation (average of 497%) and high unemployment (13%) from 1986–1989 [126], the industrial sector dramatically decreased. As a result, the fuel fossil consumption and the emissions were reduced to approximately 19.12% and 14.46%, respectively, from 1986 to 1989 [7]. These facts explain why the computed CO2 emissions and economic growth results are consistent with the downward trend for 1986–1989, as shown in Figure 1.

Table 2.
Unit root test with structural break: Intercept and time trend included.
The results show that CO2 emissions and GDP are I(1) while energy consumption and urbanization are I(0). We note that all the series are stationary after the first difference. The result indicates the ARDL approach is appropriate for testing cointegration for mixed integrated variables. Readers may refer to Appendix D to extend the discussion about the breakpoint that existed within our data sample.
6.1.2. ARDL Bounds Testing for Cointegration Test
According to all of the criteria used and presented in Table 3, the maximum lag order is chosen at 2 to minimize the possible loss in degrees of freedom [61]. The optimal ARDL(p,q1,q2,q3,q4,q5) model for Equation (2) was then chosen by the Akaike information criteria (AIC) from (k + 1)n regressions, where k is the maximum number of lags, and n is the number of variables [127].

Table 3.
Selection of optimal lag order.
Table 4 reports the ARDL bounds testing approach. When CO2, GDP, and UrB are dependent variables, the F-statistics are 5.71, 8.23, and 3.75, respectively. These values are greater than the upper bounds testing developed by Narayan [90] at 5%, 1%, and 10% significance levels, respectively. In other words, the empirical evidence indicates the existence of cointegration between CO2 emissions, economic growth, energy consumption, and urbanization in the case of Vietnam between 1977 and 2019.

Table 4.
ARDL bounds test for cointegration.
6.1.3. Long- and Short-Run Estimations
The result of the long-run relationship between variables is reported in Table 5. The optimal ARDL bounds testing (1, 0, 0, 0, 0, 1) specification indicates that explanatory variables have a long-run relationship with CO2 emissions. Energy consumption positively affects CO2 at a 1% level of significance. This finding is in line with [74,75,81]. Overall, the increase in energy consumption at 1% increases CO2 by 0.5%. We also note that the energy consumption coefficient is larger in the long run than in the short run. In other words, Vietnam tends to consume more energy in the long run. Because fossil energy consumption accounts for 84.7% of total energy consumption in Vietnam, and fossil energy consumption is a well-known cause of CO2 emissions (especially coal consumption) and contributes 65% to 75% of total CO2 emissions [9]. Thus, our findings show that Vietnam may face an increase in CO2 emissions in the future if fossil energy consumption continues at the current rate.

Table 5.
Long run and short run estimations.
Second, CO2 emissions are positively associated with urbanization at a 10% level of significance. The elasticity of CO2 emissions related to urbanization is 1.338, which implies that with each 1% growth in urbanization, CO2 emissions increase by 1.338%. This finding is in line with Refs. [10,42,76,128]. The results are consistent with the reality of a developing country like Vietnam, where cities of more than a million people continue attracting migrants. The phenomenon may be because these cities have better hospitals, schools, and businesses than in other areas. This continuous flow of people into the cities inevitably leads to the rise in CO2 emissions because of either industrial activities or transportation [5,129,130,131,132].
Third, both linear and nonlinear coefficients of income support the presence of an inverted N-curve between CO2 emissions and economic growth. Specifically, the coefficient signs of GDP, GDP2, and GDP3 are negative, positive, and negative at 1% level of significance. The negative effect of the cubic coefficient validates the trend of environmental degradation decreasing when income is higher. Additionally, according to logarithms (see the calculation in Appendix B), the two estimated turning points are per capita incomes of 4.413 and 5.706, equal to 82.49 and 300.55 in exponential values. Both are between the sample minimum value (68.42) and the maximum value (642.29), as shown in Table 1. The values indicate that the monotonic increase in pollution appears when the income lies between the turning points, and pollution decreases to monotonic levels when the income exceeds the threshold level of the second turning point (5.706). These findings confirm that the CO2 and economic growth nexus in Vietnam is the inverted N-shaped function rather than the inverted U-shaped trajectory. However, the cubic form could probably support a bell-shaped performance for the CO2-GDP nexus if the income lies between the first and the second turning point [81]. In contrast to Al-Mulali, Saboori and Ozturk [75], this result shows the monotonic increase between CO2 emissions and economic growth in the context of Vietnam. Our finding is in line with previous studies for Iran [85], Tunisia [133,134], and South Korea [81].
The short-run dynamic relationship based on the ARDL cointegration is also presented in Table 5. The results show that the cubic form of EKC remains steady in the short run. In sum, the inverted N-shaped function exists for both long- and short-run in the context of Vietnam. It is notable that in the long run, the negative cubic term, which is the dominant factor of the EKC trend, is smaller than that of the short-run (−0.269 versus -0.202). Specifically, in the long run, 1% of income will decrease by every 0.269% of CO2 emissions while the ratio is 1:0.202 in the short run. The results indicate that the environment has improved over time along with incremental income. Additionally, energy consumption statistically affects CO2 emissions, whereas urbanization does not. This finding suggests that energy consumption is the cause of environmental degradation, while urbanization has an insignificant effect on the environment in the short run.
The diagnostic results of residual normality, serial correlation, and heteroscedasticity are shown in the lower part of Table 5. More precisely, the critical F-statistics are 2.664, 0.674, and 1.155, with all p-values greater than 10%. These results are failed to reject the null hypotheses. In other words, residuals are normality distributed, no serial correlation in the residuals, and the variances for the errors are equal. Regarding the stability test, the critical F-statistic of the Ramsey reset test is 1.432, with a p-value greater than 10%. This means the null hypothesis of no misspecification of functional form cannot be rejected.
Furthermore, Figure 4 shows the plot of CUSUM and CUSUMSQ converge between the boundary lines at the 5% level of significance. The results imply all the coefficients of the model are stable. In sum, the EKC curve in Vietnam is the inverted N-shaped form in both the long- and short-run.
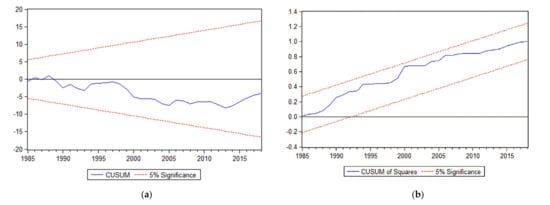
Figure 4.
(a) The cumulative sum of recursive residuals; (b) the cumulative sum of squares of recursive residuals.
6.1.4. Granger Causality Analysis
The long- and short-run Granger causalities based on VECM were shown in Table 6. In the long run, the coefficient of LECTt-1 when CO2 emissions as the dependent variable is −0.765 and statistically significant at the 1% level. The significant LECTt−1 confirms the long-run relationship of CO2 emissions with economic growth, energy consumption, and urbanization in Vietnam. Additionally, the result also indicates that 76.5% of changes in CO2 emissions are adjusted by deviations in the short run toward long-run equilibrium each year. In other words, short-run deviations in CO2 emissions converge with long-run equilibrium after approximately one year and four months.

Table 6.
Granger causality analysis.
In the long run, the results in Table 6 also suggest an existing bidirectional causal relationship between urbanization and CO2 emissions. We find that economic growth and energy consumption have a unidirectional causality relationship with CO2 emissions, and we also find that economic growth and energy consumption have a unidirectional causality relationship with urbanization. Our findings are supported by Shahbaz, Lean and Shabbir [72] and Onafowora and Owoye [81].
In the short run, the empirical evidence shows the bidirectional relationship between energy consumption and CO2 emissions. Meanwhile, the unidirectional causality relationship is found from CO2 emissions to urbanization, from urbanization to economic growth, and from economic growth to CO2 emissions. Our findings are consistent with Dogan and Turkekul [65] and Saboori and Sulaiman [74]. All the Granger causality test results are summarized in Figure 5.
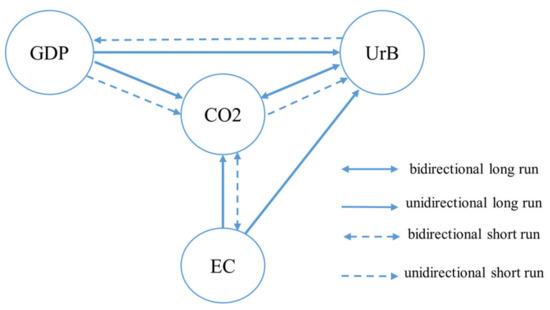
Figure 5.
Pairwise Granger causality flows.
6.2. Back-Propagation Neural Networks
Table 7 shows the minimum values of MSE, MRE, and MAE for all five hidden node approaches employed by BPN compared with the ARDL’s results. First, almost all values of MSE, MRE, and MAE in the testing set (approximately 86%) are lower than in the training set. The results indicate that the proposed model overcomes the overfitting problem, which occurs when the training data fits well, but the testing is poor [131]. The results also imply that the model is reliable to be an appropriate approach for forecasting CO2 emissions. Second, BPN generally outshines ARDL in predicting CO2 emissions. More precisely, with the MSE indicator, values ranged from 0.00356 to 0.00434, from 0.00676 to 0.00754 for the MRE indicator, and from 0.05081 to 0.056655 for the MAE indicator. These values are smaller than ARDL’s, which are 0.014639, 0.015693, 0.104254, respectively. The results show that the predictive errors of BPN’s are trivial than the ARDL’s. In other words, BPN’s approach is more precise than that of ARDL. Third, we find that the hidden nodes, as followed by Tamura and Tateishi [118], led to minimum MSE, MRE, and MAE compared with other approaches. Specifically, a 5-4-1 MLP has the better performance in which values of MSE, MRE, and MAE are 0.003565, 0.006761, and 0.050809, respectively. Fourth, concerning the learning rate, if the learning rate is set at 0.1, all the comparative criteria are the minimum compared to the others that are 0.01 and 0.9.

Table 7.
Criteria for comparison.
The predictive results for both the ARDL and the BPN approaches were shown in Figure 6. Specifically, the ARDL’s outputs are derived from the long-run form of EKC trajectory, while the BPN’s outputs are obtained by setting a 5-4-1 MLP with the learning rate at 0.1. Figure 6 also illustrates that the BPN’s results are closer to the actual outputs than the ARDL’s, especially for 2011–2019, represented for the testing set. We also present all the best predictive results of each combination between hidden nodes and learning rates in Appendix C.
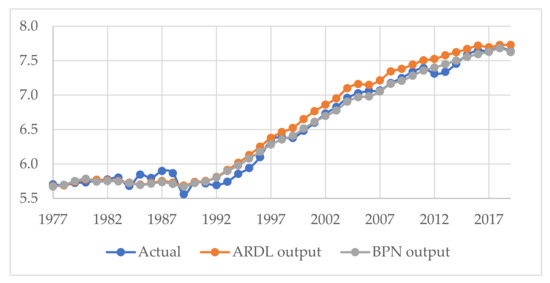
Figure 6.
CO2 emissions predicting results for both BPN and ARDL methods.
6.3. Sensitivity Analysis
The sensitivity analysis aims to analyze the extent of the crucial input variable of the model and quantify the effect of input instability [10,135,136]. We applied two approaches to examine the sensitivity analysis, i.e., partial Spearman’s rank correlation [137] and partial Kendall’s rank correlation [138], to test the sensitivity weight between CO2 emissions and each explanatory variable. The former is suitable for describing the degree of monotonicity instead of linear relationship [135,139], while the latter is appropriate for relaxing of normal distribution assumption [140] (the intuitive correlation between each pair of analyzed variables and the distribution of each variable are illustrated in Figure A5).
The partial Spearman’s rank correlation results show that energy consumption (0.951), urbanization (0.917), and economic growth (0.906) (refer to Figure 7a). The partial Kendall’s rank correlation results also reveal that energy consumption (0.852), urbanization (0.798), and economic growth (0.787) (refer to Figure 7b). To summarize, both methods indicate that energy consumption has the highest sensitivity weight with CO2 emissions, followed by urbanization and economic growth. The results are consistent with Granger causality when these explanatory variables statistically affect the CO2 emissions in the long run. On the other hand, the findings of the sensitivity analysis implied that each input variable had a substantial and different effect on the level of the CO2 emissions in the context of Vietnam. Therefore, in our proposed model, omitting these input variables could bias the actual CO2 emissions.
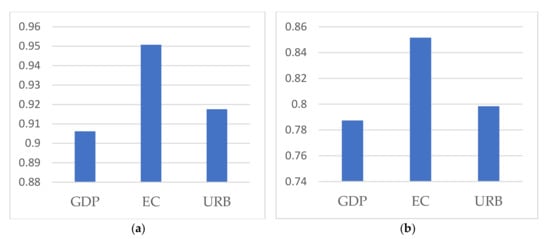
Figure 7.
The partial correlation coefficient between CO2 emissions and each input variable: (a) partial Spearman’s rank correlation; (b) partial Kendall’s rank correlation.
7. Discussion
First, the inverted N-shaped curve between CO2 and real income for both long- and short-run shows the recovery of environmental quality in the context of Vietnam. The results are strictly related to increasing renewable consumption in recent years. In particular, we record an upward trend in the use of renewable energy sources in Vietnam. Specifically, the average increase of renewable energy use from 1977 to 2019 is 5.66% compared to the average decrease of 0.24% of fossil consumption [7] (see Figure A4). The results are also consistent with the vision of national energy development strategies, in which replacing fossil consumption with renewable use as much as possible and towards the ratio of 25–30% renewable use in 2045. By 2030, Vietnam aims to enhance renewable energies, i.e., hydroelectricity, wind, biomass, and solar, account for 15.5%, 2.1%, 2.1%, and 3.3% in total electricity generation [141]. To obtain this target, Vietnam prioritizes wind and solar energy production for electricity generation and plans to create a renewable energy center in Ninh Thuan province with geographical advantages for wind and solar energies. At the end of 2020, the center contributed 2473 MW electricity, equal to 25.9% of total renewable energies in the nation [142]. The trend indicates the Vietnam government aims to reduce CO2 emissions and opens to eco-friendly environmental projects in the long run. The inverted N-shaped relationship between CO2 emissions and economic growth also indicates that Vietnam may currently benefit from a reduction in CO2 emissions. However, CO2 emissions could increase in a new cycle of the EKC when fossil fuel sources still account for approximately 84.53% of energy consumption [7] (see Figure A4). This fact poses a challenge to mitigate fossil fuel energy to help preserve the environment. Therefore, to keep the current flow for reducing CO2 emissions, lawmakers should keep the attractive price for buying electricity made from renewable sources. As a result, the policy could encourage private companies who invest capital to build the infrastructure served green electricity production.
Second, the Granger causality test shows a unidirectional causality relationship between energy consumption and CO2 emissions in the long run. Moreover, the sensitivity analysis also reveals that energy consumption is the most significant factor that affects CO2 emissions among analyzed variables. The result reinforces that the primary energy source in Vietnam is fossil fuels, which directly cause environmental degradation. Vietnam is an oil- and coal-producing country, and the national energy strategy serving economic development based on fossil fuels is understandable. Consequently, the environment is seriously degraded by industrial and residential activities. Another issue is that fossil fuels are non-renewable energy sources so that overexploitation will lead to depleting these sources, then the economic development scenarios based on fossil fuels will be failed. Thus, policymakers in Vietnam have set the goal of “roadmap to reduce the share of coal-fired power” and “reducing greenhouse gas emission from energy activities 15% by 2030” [2]. To obtain those objectives, lawmakers create and develop the carbon credit market to optimize emissions from economic activities (National Assembly of Vietnam—NAV [143]). Furthermore, research and development utilizing new technologies should be prioritized to replace fossil fuels producing in the future. Therefore, minimizing fossil fuel use will decrease CO2 emissions as expected.
On the other hand, energy consumption and economic growth do not have causal effects in the short and long run. One possible explanation for this finding is that the economy has relied on agricultural operations, which are only carried out with a small number of energy-consuming equipment [76]. Thus, Vietnam could encourage policies to lower fossil fuels, which account for most energy consumption ratio, without harming economic growth. In other words, Vietnam has a potential period to transform the economy based on fossil fuels into an economy that relied on renewable energies. As a result, Vietnam could achieve both goals of improving economic growth and reducing CO2 emissions.
Third, GDP has a unidirectional causality relationship to CO2 emissions in the long- and short-run. This finding is in line with Saboori and Sulaiman [74] for Malaysia. Our finding also indicates that CO2 emissions will not affect income in Vietnam in the long run. In other words, causing less pollution will not impair economic growth and could be a way for Vietnam to pursue sustainable development in the long run. These numbers may suggest that renewable energy can likely replace fossil fuel energy to achieve a more environmentally friendly form of energy without harming economic growth. This target is within reach since the government has developed policies for sustainable energy expansion based on four main pillars: energy efficiency, renewable energy, energy market, and climate change [9]. Our findings reconfirm that Vietnam has an opportunity to adopt renewable energy sources to reduce CO2 emissions without slowing down economic development.
Fourth, the urban population is an essential factor affecting CO2 emissions. Our findings imply that densely populated cities lead to increases in CO2 emissions in the long run. When CO2 emissions in certain regions rise, it can signal that economic opportunity and infrastructure in the bigger cities in these regions are more attractive than in other areas. The signal promotes migration to the larger cities in Vietnam. Only the impact of CO2 on urbanization is statistically significant in the short term. This empirical evidence may suggest that the government may focus on CO2 emissions reduction policies by disintegrating industrial activities [131], reducing private vehicles [6], and collecting carbon taxes on automobiles and motorbikes [76] in large cities in the short term. As a result, these urbanization restrictions will improve environmental quality in the long run.
Fifth, the results show BPN is a reliable method for reducing prediction errors compared with ARDL’s results. Moreover, the sensitivity reveals that all inputs have high sensitivity weights with CO2 emissions. Hence, these variables, i.e., energy consumption, economic growth, and urbanization, could be considered the most affecting factors to air pollution in Vietnam. Our findings suggest that the government could control the environmental degeneration by adjusting explanatory inputs based on the BPN framework. The forecasting improvement also makes the policy more practical, minimizing the overestimation or underestimation of the link between income and carbon emissions.
8. Conclusions and Future Research
In this study, we employed the ARDL method developed by Pesaran, Shin and Smith [87] to validate the EKC hypothesis from 1977 to 2019 in Vietnam. The cointegration result reveals the long-run relationship between CO2 emissions, real income, energy consumption, and urbanization. The long- and short-run results show an inverted N-curve with two-income turning points equal to 82 and 300 (constant 1977 Vietnam currency prices). The diagnostic tests confirm that our finding is stable. Furthermore, the independent variable’s coefficients in the short run are statistically smaller than those in the long run. The results indicate that if the economy reduces fossil fuel consumption, the environment shows signs of recovery. The possible reason, in our opinion, is the recent increase in the rate of renewable energy use in Vietnam. Several projects investing in renewable energies have been deployed in Ninh Thuan province, planned as a renewable energy center in Vietnam [142]. Overall, Vietnam may benefit from an inverse N-shaped relationship between CO2 emissions-economic growth nexus. However, we also note that, with the characteristics of the industrial based on fossil energy consumption, Vietnam may face a new cycle of the EKC curve, i.e., an upward emissions trend in the future without the successful transition to a renewable energy-based economy. Therefore, Vietnam needs to consistently pursue environmental objectives by 2030 as approved by legislation [2,141,143].
The long- and short-run estimations show that urbanization factors significantly positively influence CO2 emissions. The results are consistent with the densely populated cities phenomenon, which cause air pollution in Vietnam. To decrease the harmful effects of urbanization, Vietnam should consider redistribution of industrial factories to satellite towns. It could lessen citizens to free air pollution. Also, lawmakers could consider the carbon taxes on vehicles and encourage people to use public transportation to save the environment.
When CO2 emissions play the role of the dependent variable, the LECTt − 1 is statistically negative and less than −1, as expected. The coefficient confirms the cointegration between variables and shows the long-run Granger causality that ties income, energy consumption, and urbanization to CO2 emissions. The result of long-run Granger causality shows that energy consumption has a unidirectional effect on CO2 emissions. The result means that policies aiming to lessen energy consumption could reduce CO2 emissions. Additionally, the Granger analysis also reveals that economic growth and energy consumption have no causal relationship. Our findings suggest that Vietnam has a possible chance to transform the fossil fuel-based economy to the one based on renewable energies without diminishing income.
We also adopted BPN to compare the results of econometrics predictions. The comparative criteria show that the BPN method outperforms the ARDL approach in forecasting. Our experiment provides a practical approach to shed light on how to improve these forecasting results. More precisely, the econometrics approach provides the background of the relationship between analyzed variables while the BPN performs well on forecasting results. This combination could enhance the reliable model and the predicting accuracy. The results suggest that BPN and other machine-learning approaches could be applied as practical tools for predicting CO2 emissions in future studies, such as support vector regression (SVR). In particular, the SVR approach attempts to match the best line inside the threshold value, which is the distance from the hyperplane to the boundary line, instead of minimizing errors like the BPN procedure does within our study. Since the nonparametric method estimation has been considered [144], SVR combines the advantages of nonparametric and parametric methods, in which it could reflect complicated behaviors between variables, also avoid overfitting [145]. This approach is expected to provide more accurate predictions for the CO2 emission, thereby amending the environmental protection policies to avoid the under/over estimation of the practical situation.
Author Contributions
A.-T.N., Conceptualization, Methodology, Formal Analysis, Writing—Original draft preparation. P.T.T.N., Visualization, Software, Data curation. S.-H.L., Validation, Supervision, Writing—Review and Editing. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data presented in this study are openly available in Mendeley Data, V2, doi: 10.17632/dht8zxxv84.3 (accessed on 17 May 2021). The findings of this study, were obtained by using Eviews software and Python computer code, are available from the corresponding author upon reasonable request.
Acknowledgments
This paper has greatly benefitted from comments and suggestions received from anonymous referees. However, the authors are solely responsible for all remaining errors and/or omissions.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A

Table A1.
Summary of previous empirical studies on the EKC hypothesis.
Table A1.
Summary of previous empirical studies on the EKC hypothesis.
| No. | Author | Period | Country/Region | Methodologies | Dependent(s)/Explanatory Variables | Support the EKC Hypothesis? |
|---|---|---|---|---|---|---|
| Country-specific studies | ||||||
| 1 | [146] | 1960–2009 | Turkey | Dynamic OLS and Error Correction Model | CO2 emissions/energy consumption, income, tourism development | Yes |
| 2 | [125] | 1980–2009 | Tunisia | ARDL | CO2 emissions/income, energy consumption, population, exports, imports | No |
| 3 | [147] | 1911–2010 | South Africa | Co-summability | CO2 emissions/income | No |
| 4 | [148] | 2000–2012 | China | Generalized Least Square method of random effect | CO2 emissions/income, environmental regulation, technical progress, population, trade | Yes |
| 5 | [28] | 1985–2009 | South Korea | Fixed-effects | Water quality/income, trade, population | Mixed (Yes for Geum, Nakdong, and Yeongsan rivers. No for Han river) |
| 6 | [60] | 1971–2010 | Indonesia | ARDL | CO2 emissions/income, electricity production, energy consumption, total factor productivity | Yes |
| 7 | [40] | 1996–2012 | China | Generalized Method of Moments, ARDL | CO2, industrial waste water, industrial waste solid emissions/income, energy consumption, trade, urbanization | Yes |
| 8 | [43] | 1972–2013 | Pakistan | ARDL | CO2 emissions/income, trade, financial development | Yes |
| 9 | [44] | 1980–2011 | Qatar | ARDL | CO2 emissions, ecological footprint/income, energy consumption, financial development, trade | Mixed (Yes for ecological footprint. No for CO2 emissions) |
| 10 | [41] | 1970–2014 | Myanmar | ARDL | CO2, CH4, N20 emissions/income, trade, financial openness, urbanization | No |
| 11 | [83] | 1971–2011 | Saudi Arabia | ARDL | CO2 emissions/income, road energy consumption | No |
| 12 | [66] | 1960–2014 | Australia | Fully Modified OLS, and Non-nested tests | CO2 emissions/income | No |
| 13 | [63] | 1971–2015 | India | ARDL | CO2 emissions/income, trade, renewable energy generation, electric power consumption | Yes |
| 14 | [53] | 1990–2014 | Canada | Fixed-effects | Greenhouse Gas emissions/income, trade, dummy interaction between GDP and province/territory | Yes |
| 15 | [48] | 1950–2014 | Australia | ARDL | CO2 emissions/income, index of education | Yes |
| 16 | [21] | 1995–2014 | France | VECM | CO2 emissions/income, tourism | Yes |
| 17 | [33] | 1980–2011 | Peru | ARDL | CO2 emissions/income, renewable electricity, dry natural gas, and petroleum consumption | No |
| 18 | [45] | 1971–2011 | Singapore | ARDL | CO2 emissions/income, energy consumption, population density, financial development, trade | Yes |
| 19 | [20] | 2000–2018 | USA | Dynamic OLS | CO2 emissions/income, industrial production, renewable consumption | Yes |
| 20 | [32] | 1980–2015 | Pakistan | ARDL | CO2 emissions/income, biomass energy, foreign direct investment, trade | Yes |
| 21 | [31] | 1900–2017 | Singapore | Vector Error Correction model | Chromium emissions/income, foreign direct investment, trade, environmental regulation | Yes |
| 22 | [50] | 1988–2017 | USA | Partial linear semiparametric model | Total waste/real income | No |
| 23 | [49] | 1929–1994 | USA | Semiparametric partially linear model | Sulfur dioxide, nitrogen oxide/income | Yes |
| Multi-countries Studies | ||||||
| 24 | [149] | 1990–2011 | 14 Asian countries | Generalized Method of Moments | CO2 emissions/income, population density, industry share, political stability, government effectiveness, quality of regulation, and corruption | Yes |
| 25 | [150] | 1960–2010 | Arctic countries | ARDL | CO2 emissions/income, energy consumption | No |
| 26 | [30] | 2003–2008 | 149 countries, 30 OECD countries, & 48 US States | Generalized Least Square | Water withdrawals/income | Yes |
| 27 | [51] | 1981–1998 | 17 OECD countries | Semiparametric smooth coefficient model | CO2 emissions/income (deflator), labor, capital, energy consumption | Mixed |
| 28 | [151] | 1980–2008 | 93 countries | Fixed effects and Generalized Method of Moments | Ecological footprint/income, energy consumption, urbanization, trade openness, and financial development | Mixed (Yes for upper middle- and high-income countries. No for low- and lower middle-income countries) |
| 29 | [42] | 1992–2010 | 15 new European Union countries | Panel co-integration and Panel Causality tests | CO2 emissions/income, energy consumption, trade openness, urban population | Yes |
| 30 | [152] | 1998–2000 | 84 cities in both developed and developing countries | Panel co-integration | CO, VHC, and NOx/income, urbanization, population, fuel price | Yes |
| 31 | [153] | 2005–2013 | 34 developed and developing countries | Principal Component Analysis | CO2 emissions/income, tourism, energy consumption, health expenditure | Yes |
| 32 | [69] | 1990–2012 | 17 OECD countries | Fixed-effects | CO2 emissions/income, renewable energy consumption, public consumption for energy development | No |
| 33 | [154] | 1980–2011 | 5 African countries | Fully Modified OLS | CO2 emissions/income, energy intensity, energy structure, urbanization | No |
| 34 | [155] | 1990–2011 | 22 Latin American and Caribbean countries | Generalized Least Square | Energy consumption/income, agriculture employment | No |
| 35 | [156] | 1977–2010 | 17 OECD countries | Fully Modified OLS and Dynamic OLS | CO2 emissions/income, renewable energy consumption | Yes |
| 36 | [157] | 1990–2012 | 56 countries | Generalized Method of Moments | CO2 emissions/income, energy consumption, financial development, trade | Yes |
| 37 | [35] | 1970–2012 | 4 countries: India, Indonesia, China, Brazil | ARDL | CO2 emissions/income, energy consumption, trade | Mixed (Yes for Indonesia and Brazil. No for India) |
| 38 | [67] | 1995–2009 | 27 EU countries | Feasible Generalized Least Squares | Total, household, productive transport energy consumption/gross value added, energy prices | No |
| 39 | [23] | 1990–2015 | BRICS countries | Fixed-effects | N2O, Greenhouse gas emissions/income, finance, transport, renewable energy consumption | Yes |
| 40 | [58] | 1980–2012 | 25 African countries | Dynamic OLS, system GMM, Dynamic Fixed effects | CO2 emissions/income, oil consumption, electricity consumption, population growth | No |
| 41 | [158] | 1960–2010 | 50 US States | Augmented Mean Group, Common Correlated Effects Mean Group Estimator | CO2 emissions/income, energy consumption, population growth | Mixed (Yes for AMG method. No for CCEMG method) |
| 42 | [159] | 1980–2010 | 26 OECD and 52 emerging countries | Panel Data Estimation | CO2 emissions/income, energy consumption | No |
| 43 | [24] | 1975–2007 | 15 MENA countries | Fully Modified OLS, and Dynamic OLS | Ecological footprint/income, energy consumption, urbanization, political index, fertility, life expectancy at birth | Mixed (Yes for oil-exporting countries. No for non-oil-exporting ones) |
| 44 | [160] | 1970–2013 | ASEAN-4 | Fully Modified OLS and Dynamic OLS, panel VECM | CO2 emissions/income, renewable, non-renewable energy consumption, agricultural value added | No |
| 45 | [29] | 1996–2005 | 94 countries | OLS estimation | Water footprint/income, agriculture, income level binary, coastal country binary | No |
| 46 | [25] | 1980–2013 | EU countries | Fully Modified OLS, and Dynamic OLS | Ecological footprint/income, renewable and non-renewable energy consumption, trade openness | Yes |
| 47 | [46] | 1994–2012 | 74 countries | Quantile regression | CO2 emissions/income, renewable energy consumption, technological development, trade, institutional quality | No |
| 48 | [161] | 1970–2016 | 14 Asia-Pacific countries | Fully Modified OLS, and Augmented mean group | CO2 emissions/income, natural gas consumption | Yes |
| 49 | [162] | 1980–2017 | Gulf Cooperation Council | Fully Modified OLS, pooled mean group, and Dynamic common correlated effects | CO2 and SO2 emissions/income, electricity consumption, financial development, export | Mixed (No for Oman. Yes for other 5 countries) |
| 50 | [163] | 2005–2013 | 64 developing countries | Generalized Method of Moments | Ecological footprint, CO2 emissions/income, energy consumption, corruption, trade, foreign direct investment | No |
| 51 | [164] | 1990–2016 | 28 EU countries | Fixed-effects | Greenhouse gas emissions/income, energy consumption, renewable energy consumption | Mixed (Yes for 17/28 countries) |
| 52 | [165] | 1990–2014 | 86 countries | Generalized Method of Moments | CO2 emissions/income, energy consumption, forest area, agricultural area | Mixed (Yes for the whole sample and Africa. No for other groups) |
| 53 | [166] | 2000–2017 | 24 emerging countries | Generalized Method of Moments | CO2 emissions, fossil fuel energy consumption, and nitrous oxide emissions/income, industrial index, domestic credit, transport services, renewable energy consumption | Mixed (Yes for nitrous oxide emissions. No for carbon dioxide emissions and fossil fuel energy consumption) |
| 54 | [167] | 1960–2014 | 121 countries | Fixed-effects | CO2 intensity, CO2 permission per capita, CO2 in total/income | Mixed (Yes for 95/121 countries) |
| 55 | [34] | 1995–2014 | 14 countries | Fixed-effects | CO2 emissions/income, energy consumption, globalization index, international tourism arrivals | Yes |
| 56 | [168] | 1995–2015 | 27 EU countries | Fully Modified OLS, and Dynamic OLS | CO2 emissions/income, renewable energy consumption, biomass energy | Yes |
| 57 | [169] | 1995–2015 | 18 OECD countries | Fully Modified OLS, and Generalized Method of Moments | CO2 emissions/income, nuclear electricity output, non-renewable consumption, trade | Yes |
| 58 | [26] | 1970–2014 | G7 countries | Bootstrap panel causality test | Ecological footprint (carbon, cropland, grounds, forest products, and grazing land)/income | Mixed (Yes for USA and Japan. No for other 5 countries) |
| 59 | [68] | 1995–2011 | 27 EU countries and 12 major countries | Fixed-effects | CO2 emissions/income, energy efficiency, intermediate inputs, primary, secondary, and tertiary, trade | No |
| 60 | [22] | 1990–2015 | 16 APEC countries | Generalized Method of Moments | N2O emissions/income, technological development, population | No |
| 61 | [170] | 1995–2017 | 25 EU countries | Fully Modified OLS, and Dynamic OLS | CO2 emissions/economic complexity index, energy intensity | Mixed (Yes for the whole sample and 6 countries. No for the rest countries) |
| 62 | [27] | 2000–2016 | 30 EU countries | Generalized Method of Moments, Two-stage least square, and OLS | Electronic waste/income, ICT exports, population | Yes |
| 63 | [19] | 1992–2015 | 12 OPEC countries | Panel corrected standard errors | CO2 emissions/income, energy consumption, trade, oil prices | Yes |
| 64 | [47] | 1995–2015 | G7 countries | Random-effects | CO2 emissions/income, tourism, education expenditures, health expenditure, GINI index, foreign direct investment | Yes |
| 65 | [38] | 1990–2016 | 34 Annex I countries | Fully Modified OLS, and Dynamic OLS | CO2 emissions/income, trade, fossil fuel consumption | No |
| 66 | [39] | 1970–2017 | West African States | Panel Quantile regression | CO2 emissions/income, trade, financial development, trade, human capital, bio capacity. | No |
| 67 | [171] | 1990–2016 | 3 NAFTA countries | Vector Autoregression | CO2 emissions/income, fossil fuel consumption, exergetic renewable, exergy intensity, trade, human development | Mixed (Yes for USA and Mexico. No for Canada) |
| 68 | [172] | 1980–2014 | BRICST countries | Fully Modified OLS, Dynamic OLS, and Augmented Mean Group | Ecological footprint/income, energy structure, energy intensity, population | No |
| 69 | [173] | 1995–2013 | 98 developed and developing countries | Generalized Method of Moments, Pooled Mean Group | CO2 emissions/income, export diversification | Yes |
| 70 | [174] | 1980–2016 | USA, Mexico, and Canada | Moments Quantile Regression | Ecological footprint/income, trade, patents applied | Yes |
| 71 | [175] | 1990–2014 | 18 Sub-Saharan African countries | Panel cointegration | CO2 emissions/income, energy consumption, trade. | Yes |
Appendix B
The general cubic form is as follows:
In order to find out the turning points, we find the solution(s) for the first derivative of Equation (A1):
Equation (A2) is the quadratic function, so the solution(s) depends on the value of delta ():
If = 0: Equation (A2) has only one solution that is the turning point of equation (A1):
In this case, the variation of Equation (A1) as follows:

Table A2.
> 0.
Table A2.
> 0.
| X | |||||
| 0 | |||||
| Y | Y1 | ||||

Table A3.
< 0.
Table A3.
< 0.
| X | |||||
| 0 | |||||
| Y | Y2 | ||||
Figure A1.
The cubic shape when equation (A1) has one turning point: (a) < 0; (b) > 0.
If > 0: Equation (A2) has two solutions that are the turning points of Equation (A1):

Table A4.
< 0.
Table A4.
< 0.
| X | ||||||
| 0 | + | 0 | ||||
| F(X) | Y2 | |||||
| Y1 |

Table A5.
> 0.
Table A5.
> 0.
| X | ||||||
| 0 | 0 | |||||
| f(X) | Y1 | |||||
| Y2 |
Figure A2.
The cubic shape when Equation (A1) has two turning points: (a) < 0; (b) > 0.
In our study, from the long-run cubic form between GDP and CO2, we have:
where Y, X, and k represent CO2, GDP, and other variables, respectively.
Y = − 20.332387X + 4.085637X2 − 0.269191X3 + k
Hence, the two turning points are computed:
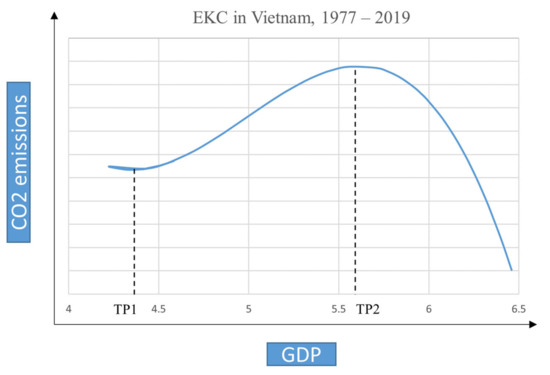
Figure A3.
The inverted N-shaped of the EKC in Vietnam, 1977–2019.
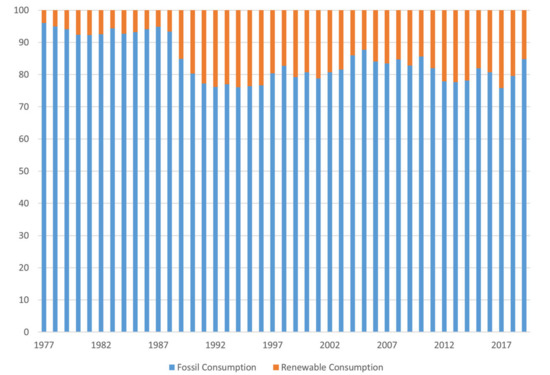
Figure A4.
The ratio of total energy consumption in Vietnam, 1977–2019.
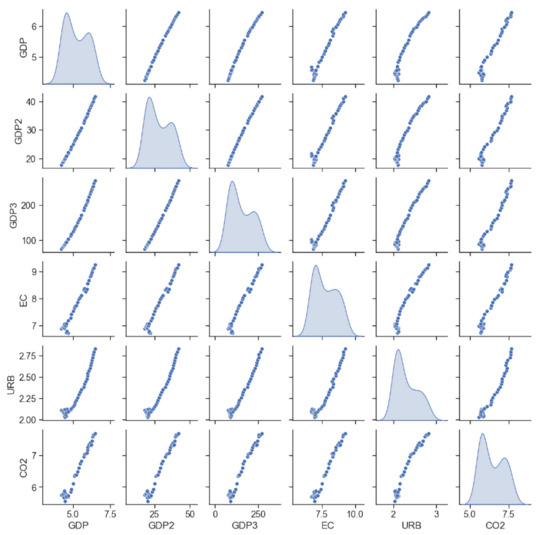
Figure A5.
The illustration of the correlation between each pair of analyzed variables and the distribution of each variable.
Appendix C
The ARDL’s outputs were calculated based on the long-run form between CO2 and independent variables. Meanwhile, the BPN was tested by five different numbers of hidden nodes and three different learning rates, which are 0.01, 0.1, and 0.9, respectively. We ran this procedure ten times and the best results were shown in Table A6.

Table A6.
The output values from the ARDL and BPN approaches.
Table A6.
The output values from the ARDL and BPN approaches.
| Year | CO2 (Actual) | ARDL (Output) | Artificial Neural Networks with Back-Propagation Algorithm—BPN (Output) | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Hecht-Nielsen [112] | Turban, Sharda, Delen, Aronson, Liang and King [113] | Zhang, Ma and Yang [114] | Tamura and Tateishi [115] | Sheela and Deepa [107] | |||||||||||||
| 0.01 | 0.1 | 0.9 | 0.01 | 0.1 | 0.9 | 0.01 | 0.1 | 0.9 | 0.01 | 0.1 | 0.9 | 0.01 | 0.1 | 0.9 | |||
| 1977 | 5.7025 | 5.6766 | 5.7068 | 5.6924 | 5.6107 | 5.6985 | 5.6780 | 5.6595 | 5.7485 | 5.6860 | 5.7470 | 5.8315 | 5.6701 | 5.6318 | 5.7830 | 5.6993 | 5.6325 |
| 1978 | 5.6899 | 5.6871 | 5.7104 | 5.7141 | 5.6736 | 5.7011 | 5.6993 | 5.6813 | 5.7373 | 5.6993 | 5.7399 | 5.7969 | 5.6965 | 5.6802 | 5.7366 | 5.7088 | 5.6891 |
| 1979 | 5.7223 | 5.7389 | 5.7605 | 5.7666 | 5.7406 | 5.7496 | 5.7545 | 5.6964 | 5.7833 | 5.7493 | 5.7538 | 5.8369 | 5.7514 | 5.7379 | 5.7717 | 5.7585 | 5.7525 |
| 1980 | 5.7324 | 5.7726 | 5.7668 | 5.7938 | 5.8152 | 5.7596 | 5.7789 | 5.7427 | 5.7642 | 5.7708 | 5.7478 | 5.7694 | 5.7841 | 5.8064 | 5.7229 | 5.7719 | 5.8243 |
| 1981 | 5.7621 | 5.7683 | 5.6969 | 5.7513 | 5.7844 | 5.6937 | 5.7229 | 5.8320 | 5.6760 | 5.7190 | 5.7311 | 5.6515 | 5.7426 | 5.8039 | 5.6086 | 5.7149 | 5.8035 |
| 1982 | 5.7745 | 5.7607 | 5.7173 | 5.7583 | 5.7890 | 5.7148 | 5.7357 | 5.7911 | 5.7012 | 5.7330 | 5.7344 | 5.6798 | 5.7493 | 5.7976 | 5.6522 | 5.7294 | 5.8050 |
| 1983 | 5.8003 | 5.7526 | 5.7221 | 5.7542 | 5.7751 | 5.7206 | 5.7343 | 5.7734 | 5.7094 | 5.7339 | 5.7367 | 5.6904 | 5.7446 | 5.7837 | 5.6750 | 5.7306 | 5.7913 |
| 1984 | 5.6799 | 5.7278 | 5.7135 | 5.7343 | 5.7345 | 5.7125 | 5.7165 | 5.7481 | 5.7094 | 5.7195 | 5.7370 | 5.7032 | 5.7227 | 5.7465 | 5.6940 | 5.7182 | 5.7520 |
| 1985 | 5.8438 | 5.6999 | 5.6946 | 5.7074 | 5.6881 | 5.6941 | 5.6899 | 5.7315 | 5.6976 | 5.6966 | 5.7345 | 5.7026 | 5.6937 | 5.7064 | 5.6976 | 5.6969 | 5.7082 |
| 1986 | 5.7959 | 5.7229 | 5.7241 | 5.7269 | 5.6979 | 5.7252 | 5.7129 | 5.7238 | 5.7288 | 5.7218 | 5.7455 | 5.7315 | 5.7131 | 5.7172 | 5.7453 | 5.7221 | 5.7183 |
| 1987 | 5.8970 | 5.7514 | 5.7282 | 5.7441 | 5.7440 | 5.7331 | 5.7278 | 5.7666 | 5.7144 | 5.7367 | 5.7432 | 5.6802 | 5.7338 | 5.7638 | 5.7158 | 5.7308 | 5.7648 |
| 1988 | 5.8644 | 5.7272 | 5.7111 | 5.7204 | 5.7038 | 5.7165 | 5.7042 | 5.7523 | 5.7032 | 5.7164 | 5.7408 | 5.6781 | 5.7085 | 5.7294 | 5.7176 | 5.7119 | 5.7270 |
| 1989 | 5.5589 | 5.6858 | 5.6831 | 5.6838 | 5.6417 | 5.6873 | 5.6675 | 5.7242 | 5.6878 | 5.6825 | 5.7359 | 5.6867 | 5.6688 | 5.6731 | 5.7167 | 5.6817 | 5.6671 |
| 1990 | 5.7374 | 5.7364 | 5.7395 | 5.7361 | 5.6988 | 5.7418 | 5.7238 | 5.7240 | 5.7455 | 5.7347 | 5.7530 | 5.7473 | 5.7220 | 5.7208 | 5.7732 | 5.7350 | 5.7202 |
| 1991 | 5.7161 | 5.7523 | 5.7542 | 5.7566 | 5.7330 | 5.7545 | 5.7446 | 5.7307 | 5.7576 | 5.7510 | 5.7548 | 5.7583 | 5.7438 | 5.7473 | 5.7710 | 5.7513 | 5.7513 |
| 1992 | 5.6922 | 5.8092 | 5.8086 | 5.8140 | 5.8053 | 5.8079 | 5.8047 | 5.7568 | 5.8065 | 5.8060 | 5.7727 | 5.7980 | 5.8035 | 5.8101 | 5.8085 | 5.8051 | 5.8198 |
| 1993 | 5.7413 | 5.9119 | 5.9079 | 5.9046 | 5.8868 | 5.9069 | 5.9005 | 5.8197 | 5.9082 | 5.8992 | 5.8271 | 5.9022 | 5.8949 | 5.8890 | 5.9180 | 5.8995 | 5.9011 |
| 1994 | 5.8540 | 6.0155 | 5.9984 | 5.9885 | 5.9607 | 5.9975 | 5.9865 | 5.9010 | 6.0029 | 5.9846 | 5.8973 | 6.0045 | 5.9785 | 5.9642 | 6.0214 | 5.9870 | 5.9769 |
| 1995 | 5.9383 | 6.1288 | 6.0938 | 6.0857 | 6.0657 | 6.0943 | 6.0858 | 6.0060 | 6.0925 | 6.0812 | 5.9802 | 6.0828 | 6.0778 | 6.0651 | 6.1056 | 6.0817 | 6.0813 |
| 1996 | 6.0992 | 6.2501 | 6.1923 | 6.1844 | 6.1659 | 6.1948 | 6.1848 | 6.1226 | 6.1896 | 6.1799 | 6.0925 | 6.1771 | 6.1771 | 6.1652 | 6.2035 | 6.1799 | 6.1827 |
| 1997 | 6.3493 | 6.3774 | 6.2942 | 6.2883 | 6.2734 | 6.2993 | 6.2884 | 6.2510 | 6.2887 | 6.2835 | 6.2263 | 6.2711 | 6.2817 | 6.2726 | 6.3023 | 6.2823 | 6.2913 |
| 1998 | 6.3859 | 6.4618 | 6.3633 | 6.3610 | 6.3508 | 6.3689 | 6.3608 | 6.3333 | 6.3566 | 6.3541 | 6.3186 | 6.3386 | 6.3552 | 6.3471 | 6.3635 | 6.3526 | 6.3681 |
| 1999 | 6.3762 | 6.5219 | 6.4135 | 6.4143 | 6.4071 | 6.4182 | 6.4134 | 6.3846 | 6.4092 | 6.4046 | 6.3873 | 6.3988 | 6.4087 | 6.4007 | 6.4092 | 6.4045 | 6.4240 |
| 2000 | 6.4798 | 6.6505 | 6.5158 | 6.5200 | 6.5152 | 6.5235 | 6.5164 | 6.5121 | 6.5118 | 6.5096 | 6.5364 | 6.5023 | 6.5139 | 6.5109 | 6.5129 | 6.5093 | 6.5338 |
| 2001 | 6.5980 | 6.7654 | 6.6090 | 6.6177 | 6.6170 | 6.6187 | 6.6127 | 6.6270 | 6.6029 | 6.6060 | 6.6568 | 6.5905 | 6.6119 | 6.6122 | 6.6000 | 6.6046 | 6.6358 |
| 2002 | 6.7308 | 6.8603 | 6.6875 | 6.7007 | 6.7038 | 6.6978 | 6.6951 | 6.7187 | 6.6794 | 6.6872 | 6.7457 | 6.6647 | 6.6957 | 6.6967 | 6.6688 | 6.6847 | 6.7218 |
| 2003 | 6.8263 | 6.9519 | 6.7656 | 6.7818 | 6.7859 | 6.7777 | 6.7725 | 6.8010 | 6.7620 | 6.7674 | 6.8349 | 6.7562 | 6.7752 | 6.7821 | 6.7543 | 6.7667 | 6.8056 |
| 2004 | 6.9576 | 7.0989 | 6.8942 | 6.9141 | 6.9184 | 6.9137 | 6.8982 | 6.9571 | 6.8939 | 6.9021 | 6.9597 | 6.8903 | 6.9042 | 6.9248 | 6.9042 | 6.9018 | 6.9423 |
| 2005 | 7.0257 | 7.1607 | 6.9563 | 6.9791 | 6.9851 | 6.9762 | 6.9608 | 7.0123 | 6.9600 | 6.9661 | 7.0138 | 6.9636 | 6.9682 | 6.9925 | 6.9697 | 6.9672 | 7.0093 |
| 2006 | 7.0605 | 7.1476 | 6.9689 | 6.9939 | 7.0031 | 6.9877 | 6.9701 | 6.9786 | 6.9891 | 6.9785 | 7.0381 | 7.0233 | 6.9798 | 7.0148 | 7.0020 | 6.9868 | 7.0297 |
| 2007 | 7.0656 | 7.2132 | 7.0402 | 7.0676 | 7.0785 | 7.0599 | 7.0424 | 7.0485 | 7.0620 | 7.0524 | 7.0975 | 7.0973 | 7.0531 | 7.0911 | 7.0752 | 7.0607 | 7.1050 |
| 2008 | 7.1747 | 7.3427 | 7.1469 | 7.1745 | 7.1822 | 7.1650 | 7.1543 | 7.1905 | 7.1545 | 7.1603 | 7.1735 | 7.1637 | 7.1631 | 7.1889 | 7.1576 | 7.1623 | 7.2048 |
| 2009 | 7.2462 | 7.3799 | 7.1890 | 7.2168 | 7.2246 | 7.2037 | 7.1976 | 7.2185 | 7.1977 | 7.2014 | 7.2129 | 7.2095 | 7.2060 | 7.2286 | 7.1923 | 7.2039 | 7.2456 |
| 2010 | 7.3385 | 7.4420 | 7.2657 | 7.2927 | 7.2985 | 7.2804 | 7.2731 | 7.2967 | 7.2749 | 7.2789 | 7.2810 | 7.2850 | 7.2813 | 7.3042 | 7.2751 | 7.2813 | 7.3193 |
| 2011 | 7.3913 | 7.5036 | 7.3420 | 7.3668 | 7.3689 | 7.3552 | 7.3481 | 7.3757 | 7.3496 | 7.3545 | 7.3494 | 7.3547 | 7.3553 | 7.3750 | 7.3536 | 7.3563 | 7.3888 |
| 2012 | 7.3110 | 7.5248 | 7.3884 | 7.4115 | 7.4127 | 7.3993 | 7.3932 | 7.4065 | 7.3995 | 7.3999 | 7.3982 | 7.4086 | 7.3999 | 7.4188 | 7.4039 | 7.4029 | 7.4319 |
| 2013 | 7.3362 | 7.5766 | 7.4390 | 7.4579 | 7.4548 | 7.4436 | 7.4433 | 7.4506 | 7.4455 | 7.4461 | 7.4446 | 7.4481 | 7.4478 | 7.4571 | 7.4406 | 7.4481 | 7.4717 |
| 2014 | 7.4534 | 7.6215 | 7.4954 | 7.5093 | 7.5015 | 7.4945 | 7.4975 | 7.4991 | 7.4989 | 7.4981 | 7.4963 | 7.4965 | 7.5000 | 7.5018 | 7.4911 | 7.4999 | 7.5166 |
| 2015 | 7.5867 | 7.6674 | 7.5531 | 7.5607 | 7.5472 | 7.5459 | 7.5522 | 7.5478 | 7.5528 | 7.5504 | 7.5468 | 7.5442 | 7.5523 | 7.5455 | 7.5426 | 7.5519 | 7.5604 |
| 2016 | 7.6457 | 7.7182 | 7.6006 | 7.6012 | 7.5816 | 7.5845 | 7.5966 | 7.5827 | 7.5943 | 7.5906 | 7.5859 | 7.5786 | 7.5939 | 7.5762 | 7.5745 | 7.5915 | 7.5925 |
| 2017 | 7.6406 | 7.6947 | 7.6376 | 7.6344 | 7.6146 | 7.6196 | 7.6300 | 7.5960 | 7.6393 | 7.6262 | 7.6243 | 7.6320 | 7.6270 | 7.6110 | 7.6269 | 7.6296 | 7.6255 |
| 2018 | 7.6933 | 7.7264 | 7.6988 | 7.6859 | 7.6588 | 7.6730 | 7.6856 | 7.6427 | 7.6964 | 7.6796 | 7.6687 | 7.6825 | 7.6795 | 7.6539 | 7.6870 | 7.6835 | 7.6681 |
| 2019 | 7.6343 | 7.7279 | 7.7329 | 7.7124 | 7.6794 | 7.6978 | 7.7157 | 7.6636 | 7.7238 | 7.7056 | 7.6900 | 7.7029 | 7.7070 | 7.6712 | 7.7042 | 7.7089 | 7.6867 |
Appendix D
To investigate the possible effect of the breakpoint on the outputs, we re-examined Equation (1) by adding the Dummy and the interactive variables:
where Dt is the dummy year variable (Dt = 1 for t = 1989, …2019, and Dt = 0 otherwise). Dt*GDPt and Dt*are the interactive variables representing the possible effect of economic growth and the breakpoint to CO2 emissions. ECt represents energy consumption, and UrBt denotes urbanization. The year 1989 was chosen for the breakpoint.
We separate the two terms Dt*GDPt and Dt* for each Equations (A9) and (A10) to investigate the possible effect of the dummy variable on the linear and the cubic forms. Meanwhile, the Equation (A11) shows the possible effect of the structural break on results based on the linear model assumption.
The cointegration tests are presented in Table A7, the long- and short-run estimations are shown in Table A8, and the cumulative sum of recursive residuals (CUSUM) and cumulative sum of squares of recursive residuals (CUSUMSQ) are depicted in Figure A6.

Table A7.
ARDL bounds test for cointegration.
Table A7.
ARDL bounds test for cointegration.
| Dependent Variable, Independent Variables. | Optimal ARDL Model | F-Statistic | Cointegration |
|---|---|---|---|
| Equation (A7) | |||
| CO2, GDP, GDP2, GDP3, EC, UrB, D , D*GDP | 1,0,0,0,0,0,2,0 | 4.70 a | Yes |
| Significant level | Lower Bound (I0 bound)l | Upper Bound (I1 bound) u | |
| 10% | 2.03 | 3.13 | |
| 5% | 2.32 | 3.50 | |
| 1% | 2.96 | 4.26 | |
| Equation (A8) | |||
| CO2, GDP, GDP2, GDP3, EC, UrB, D, D*GDP3 | 1, 0, 0, 0, 0, 0, 2, 0 | 4.71 a | Yes |
| Significant level | Lower Bound (I0 bound) l | Upper Bound (I1 bound) u | |
| 10% | 2.03 | 3.13 | |
| 5% | 2.32 | 3.50 | |
| 1% | 2.96 | 4.26 | |
| Equation (A9) | |||
| CO2, GDP, EC, UrB, D, D*GDP | 1, 0, 0, 0, 0, 0, 2, 0 | 3.87 b | Yes |
| Significant level | Lower Bound (I0 bound) l | Upper Bound (I1 bound) u | |
| 10% | 2.26 | 3.35 | |
| 5% | 2.62 | 3.79 | |
| 1% | 3.41 | 4.68 | |
a, b indicate significance at 1%, 5%. l, u The critical values are derived from case III: unrestricted intercept and no trend, k = 5, N = 40 in Narayan [90].
The results from Table A7 reveal that the cointegration between analyzed variables was confirmed at 5% level of significance.

Table A8.
The long- and short-run estimations.
Table A8.
The long- and short-run estimations.
| Variables | Equation (A7) | Equation (A8) | Equation (A9) | |||
|---|---|---|---|---|---|---|
| Coefficient | t-Statistic | Coefficient | t-Statistic | Coefficient | t-Statistic | |
| Long-run relationship (dependent variable CO2) | ||||||
| GDP | −18.807 b | −2.105 | −19.141 b | −2.048 | −0.432 0.565 k | −1.165 0.366 |
| GDP2 | 3.757 b | 2.183 | 3.776 b | 2.209 | − | − |
| GDP3 | −0.244 b | −2.282 | −0.241 b | −2.459 | − | − |
| EC | 0.822 a | 3.653 | 0.827 a | 3.627 | 0.738 a | 2.851 |
| UrB | 0.411 | 0.593 | 0.408 | 0.555 | 1.115 | 2.902 |
| D | 0.8 | 0.304 | 0.161 | 0.174 | −5.026 a | −2.885 |
| D*GDP | −0.223 | −0.384 | − | − | 1.026 b | 2.652 |
| D*GDP3 | − | − | −0.004 | −0.402 | − | − |
| Intercept | 30.065 b | 2.122 | 30.892 c | 2.015 | 4.959 b | 2.546 |
| Short-run relationship (dependent variable ΔCO2) | ||||||
| ΔGDP | −12.828 c | −1.866 | −13.058 c | −1.829 | −0.256 | −1.201 |
| ΔGDP2 | 2.563 c | 1.936 | 2.576 c | 1.959 | − | − |
| ΔGDP3 | −0.167 c | −2.028 | −0.165 c | −2.159 | − | − |
| ΔEC | 0.561 a | 3.416 | 0.564 a | 3.403 | 0.437 a | 3.02 |
| ΔUrB | 0.28 | 0.598 | 0.278 | 0.602 | 3.799 | 1.577 |
| ΔD | 0.419 | 0.234 | −0.017 | −0.027 | −3.035 a | −2.762 |
| ΔD*GDP | −0.152 | −0.381 | − | − | 0.608 b | 2.454 |
| ΔD*GDP3 | − | − | −0.003 | −0.399 | ||
| LECT(t-1) | −0.682 a | −5.311 | −0.682 a | −5.316 | −0.592 a | −5.155 |
| Residual Diagnostics | F-Statistic (Prob.) | F-Statistic (Prob.) | F-Statistic (Prob.) | |||
| Jarque-Berra | 2.833 (0.243) | 2.849 (0.240) | 1.466 (0.480) | |||
| Correlation LM | 0.419 (0.662) | 0.419 (0.661) | 0.649 (0.530) | |||
| Heteroscedasticity test (BPG) | 0.511 (0.869) | 0.532 (0.854) | 0.653 (0.743) | |||
| Stability Diagnostics | F-Statistic (Prob.) | F-Statistic (Prob.) | F-Statistic (Prob.) | |||
| Ramsey reset | 0.711 (0.406) | 0.815 (0.426) | 0.034 (0.085) | |||
| CUSUM | Portrayed by two lines b | Portrayed by two lines b | Cross two lines b | |||
| CUSUMSQ | Portrayed by two lines b | Portrayed by two line b | Cross two lines b | |||
a, b, c indicate significance at 1%, 5%, 10%. k implies the sub-sample (1989–2019).
The results from Table A8 show that in the context of the cubic form (Equations (A9) and (A10)), the terms of dummy time variables (D and D*GDP/D*GDP3) have a statistically insignificant effect on CO2 emissions. The diagnostic and stability tests (lower part of Table A8) confirm that the estimated results are stable. In other words, no difference between the two periods (before and after breakpoint—the year 1989) given the cubic form in the sample. Indeed, the cubic form could describe the change of slopes without breaking.
In the linear form context (Equation (A11)), the results reveal that the dummy time variables have a statistically significant effect on CO2 emissions. The results are as expected because the breakpoint separates two periods into two independent linearities with different slopes. The causality analysis (Table A9) shows the interactive variable positively affects emissions in the long- and short run, indicating that economic growth from 1989 to 2019 positively affects emissions. However, we also note that the GDP regressor is insignificant; the Ramsey reset test indicates the misspecification of the linear function (Table A8); the CUSUM and CUSUMSQ cross the boundaries (Figure A6). In other words, the linear form is not a good fit function to describe data in the sample.
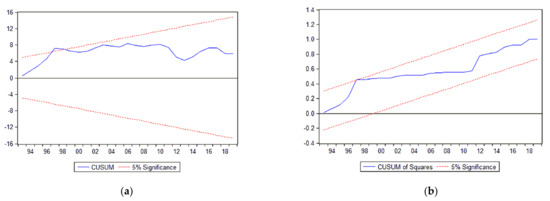
Figure A6.
The breakpoint testing for the linear form assumption: (a) CUSUM; (b) CUSUMSQ.

Table A9.
Granger causality analysis.
Table A9.
Granger causality analysis.
| Short-Run Granger Causality Wald Test (p-Value) | Long-Run Granger Causality | ||||||
|---|---|---|---|---|---|---|---|
| Variables | CO2 | EC | GDP | UrB | D | D*GDP | LECTt-1 (t-stats) |
| CO2 | - | 0.31 (0.080) c | −0.29 (0.20) | 2.79 (0.38) | −3.56 (0.03) b | 0.73 (0.046) b | −0.703 (−4.405) a |
| EC | 0.29 (0.031) b | - | 0.05 (0.805) | −2.34 (0.419) | −2.78 (0.071) c | 0.63 (0.063) c | - |
| GDP | -0.11 (0.298) | 0.03 (0.861) | - | 6.26 (0.010) b | −3.93 (0.000) a | 0.87 (0.000) a | −0.411 (−2.451) b |
| UrB | 0.01 (0.477) | 0.01 (0.922) | 0.06 (0.001) a | - | 0.14 (0.156) | −0.03 (0.180) | −0.004 (−0.234) |
| D | - | - | - | - | - | - | - |
| D*GDP | 0.14 (0.012) b | 0.15 (0.031) b | 0.62 (0.001) a | −2.36 (0.107) | 4.51 (0.001) a | - | - |
a, b, c indicate significance at 1%, 5%, 10%.
Therefore, the proposed cubic function interpreting the EKC in Vietnam could reflect the two distinct periods without breaking, while the structural change analysis is crucial for the linear assumption. In any given case, an econometric investigation should be carefully examined to describe data in the sample.
References
- WorldBank. Vietnam Overview; The World Bank: Washington, DC, USA, 2019; Available online: https://www.worldbank.org/en/country/vietnam/overview (accessed on 10 July 2020).
- Communist-Party-of-Vietnam. Resolution of the Politburo On Orientations of the Viet Nam’s National Energy Development Strategy to 2030 and outlook to 2045. Int. J. Econ. Bus. Adm. 2020, 8, 1023–1032. [Google Scholar]
- Kimura, S.; Phoumin, H. Energy Outlook and Energy Saving Potential in East Asia 2020; Economic Research Institute for ASEAN and East Asia: Jakarta, Indonesia, 2021; Available online: https://think-asia.org/handle/11540/13353 (accessed on 17 May 2021).
- WDI. Energy Use (Kg of oil Equivalent Per Capita); The World Bank: Washington, DC, USA, 2020; Available online: https://data.worldbank.org/indicator/EG.USE.PCAP.KG.OE (accessed on 5 December 2020).
- Tung, H.; Tong, H.; Hung, W.; Anh, N. Development of emission factors and emission inventories for motorcycles and light duty vehicles in the urban region in Vietnam. Sci. Total. Environ. 2011, 409, 2761–2767. [Google Scholar] [CrossRef]
- Ho, B.Q.; Vu, K.H.N.; Nguyen, T.T.; Nguyen, H.T.T.; Ho, D.M.; Nguyen, H.N.; Nguyen, T.T.T. Study loading capacties of air pollutant emissions for developing countries: A case of Ho Chi Minh City, Vietnam. Sci. Rep. 2020, 10, 1–12. [Google Scholar] [CrossRef]
- OWID. CO2 Emissions. 2020. Our World in Data. Available online: https://ourworldindata.org/co2-emissions (accessed on 5 December 2020).
- EPD. Global Market Information. 2020. Euromonitor Passport Database. Available online: https://www.portal.euromonitor.com/portal/account/login (accessed on 17 May 2021).
- EREA; DEA. Vietnam Energy Outlook Report 2019; Electricity and Renewable Energy Authority Danish Energy Agency: Hanoi, Vietnam, 2020; Available online: https://vietnam.um.dk/en/green-growth/vietnam-energy-outlook-report/ (accessed on 10 December 2020).
- Acheampong, A.O.; Boateng, E.B. Modelling carbon emission intensity: Application of artificial neural network. J. Clean. Prod. 2019, 225, 833–856. [Google Scholar] [CrossRef]
- Aydin, G.; Jang, H.; Topal, E. Energy consumption modeling using artificial neural networks: The case of the world’s highest consumers. Energ. Source Part. B. 2016, 11, 212–219. [Google Scholar] [CrossRef]
- Bildirici, M.; Ersin, Ö. Markov-switching vector autoregressive neural networks and sensitivity analysis of environment, economic growth and petrol prices. Environ. Sci, Pollut. R. 2018, 25, 31630–31655. [Google Scholar] [CrossRef]
- Pérez-Suárez, R.; López-Menéndez, A.J. Growing green? Forecasting CO2 emissions with environmental Kuznets curves and logistic growth models. Environ. Sci. Policy 2015, 54, 428–437. [Google Scholar] [CrossRef]
- Gallo, C.; Conto, F.; Fiore, M. A neural network model for forecasting CO2 emission. Agri. Paper. Econ. Infor. 2014, 6, 31–36. [Google Scholar] [CrossRef]
- Shahbaz, M.; Sinha, A. Environmental Kuznets curve for CO2 emissions: A literature survey. J. Econ. Stud. 2019. [Google Scholar] [CrossRef]
- Álvarez-Herránz, A.; Balsalobre, D.; Cantos, J.M.; Shahbaz, M. Energy innovations-GHG emissions nexus: Fresh empirical evidence from OECD countries. Energ. Policy 2017, 101, 90–100. [Google Scholar] [CrossRef]
- Grossman, G.M.; Krueger, A.B. Environmental impacts of a North American free trade agreement. Natl. Bur. Econ. Res. Bull. Aging Health 1991. Available online: http://www.nber.org/papers/w3914.pdf (accessed on 15 July 2020).
- Panayotou, T. Empirical tests and policy analysis of environmental degradation at different stages of economic development. Int. Labour Organ. 1993. Available online: http://www.ilo.org/public/libdoc/ilo/1993/93B09_31_engl.pdf (accessed on 5 July 2020).
- Moutinho, V.; Madaleno, M.; Elheddad, M. Determinants of the Environmental Kuznets Curve considering economic activity sector diversification in the OPEC countries. J. Clean. Prod. 2020, 271, 122642. [Google Scholar] [CrossRef]
- Bulut, U. Testing environmental Kuznets curve for the USA under a regime shift: The role of renewable energy. Environ. Sci. Pollut. R. 2019, 26, 14562–14569. [Google Scholar] [CrossRef] [PubMed]
- Bella, G. Estimating the tourism induced environmental Kuznets curve in France. J. Sustain. Tour. 2018, 26, 2043–2052. [Google Scholar] [CrossRef]
- Sinha, A.; Sengupta, T. Impact of energy mix on nitrous oxide emissions: An environmental Kuznets curve approach for APEC countries. Environ. Sci. Pollut. R. 2019, 26, 2613–2622. [Google Scholar] [CrossRef]
- Nassani, A.A.; Aldakhil, A.M.; Abro, M.M.Q.; Zaman, K. Environmental Kuznets curve among BRICS countries: Spot lightening finance, transport, energy and growth factors. J. Clean Prod. 2017, 154, 474–487. [Google Scholar] [CrossRef]
- Charfeddine, L.; Mrabet, Z. The impact of economic development and social-political factors on ecological footprint: A panel data analysis for 15 MENA countries. Renew. Sust. Energ. Rev. 2017, 76, 138–154. [Google Scholar] [CrossRef]
- Destek, M.A.; Ulucak, R.; Dogan, E. Analyzing the environmental Kuznets curve for the EU countries: The role of ecological footprint. Environ. Sci. Pollut. R. 2018, 25, 29387–29396. [Google Scholar] [CrossRef]
- Yilanci, V.; Ozgur, O. Testing the environmental Kuznets curve for G7 countries: Evidence from a bootstrap panel causality test in rolling windows. Environ. Sci. Pollut. R. 2019, 26, 24795–24805. [Google Scholar] [CrossRef]
- Boubellouta, B.; Kusch-Brandt, S. Testing the environmental Kuznets Curve hypothesis for E-waste in the EU28+ 2 countries. J. Clean. Prod. 2020, 277, 123371. [Google Scholar] [CrossRef]
- Choi, J.; Hearne, R.; Lee, K.; Roberts, D. The relation between water pollution and economic growth using the environmental Kuznets curve: A case study in South Korea. Water Int. 2015, 40, 499–512. [Google Scholar] [CrossRef]
- Paolo Miglietta, P.; De Leo, F.; Toma, P. Environmental Kuznets curve and the water footprint: An empirical analysis. Water. Environ. J. 2017, 31, 20–30. [Google Scholar] [CrossRef]
- Katz, D. Water use and economic growth: Reconsidering the Environmental Kuznets Curve relationship. J. Clean Prod. 2015, 88, 205–213. [Google Scholar] [CrossRef]
- Chen, Q.; Taylor, D. Economic development and pollution emissions in Singapore: Evidence in support of the Environmental Kuznets Curve hypothesis and its implications for regional sustainability. J. Clean Prod. 2020, 243, 118637. [Google Scholar] [CrossRef]
- Mahmood, N.; Wang, Z.; Yasmin, N.; Manzoor, W.; ur Rahman, A. How to bend down the environmental Kuznets curve: The significance of biomass energy. Environ. Sci, Pollut. R. 2019, 26, 21598–21608. [Google Scholar] [CrossRef]
- Zambrano-Monserrate, M.A.; Silva-Zambrano, C.A.; Davalos-Penafiel, J.L.; Zambrano-Monserrate, A.; Ruano, M.A. Testing environmental Kuznets curve hypothesis in Peru: The role of renewable electricity, petroleum and dry natural gas. Renew. Sust. Energ. Rev. 2018, 82, 4170–4178. [Google Scholar] [CrossRef]
- Saint Akadiri, S.; Lasisi, T.T.; Uzuner, G.; Akadiri, A.C. Examining the impact of globalization in the environmental Kuznets curve hypothesis: The case of tourist destination states. Environ. Sci. Pollut. R. 2019, 26, 12605–12615. [Google Scholar] [CrossRef]
- Alam, M.M.; Murad, M.W.; Noman, A.H.M.; Ozturk, I. Relationships among carbon emissions, economic growth, energy consumption and population growth: Testing Environmental Kuznets Curve hypothesis for Brazil, China, India and Indonesia. Ecol. Indic. 2016, 70, 466–479. [Google Scholar] [CrossRef]
- Luzzati, T.; Orsini, M. Investigating the energy-environmental Kuznets curve. Energy 2009, 34, 291–300. [Google Scholar] [CrossRef]
- Aruga, K. Investigating the energy-environmental Kuznets Curve hypothesis for the Asia-Pacific region. Sustainability 2019, 11, 2395. [Google Scholar] [CrossRef]
- Jin, T.; Kim, J. Investigating the environmental Kuznets curve for Annex I countries using heterogeneous panel data analysis. Environ. Sci. Pollut. R. 2020, 1–16. [Google Scholar] [CrossRef]
- Halliru, A.M.; Loganathan, N.; Hassan, A.A.G.; Mardani, A.; Kamyab, H. Re-examining the environmental Kuznets curve hypothesis in the Economic Community of West African States: A panel quantile regression approach. J. Clean. Prod. 2020, 276, 124247. [Google Scholar] [CrossRef]
- Li, T.; Wang, Y.; Zhao, D. Environmental Kuznets curve in China: New evidence from dynamic panel analysis. Energ. Policy 2016, 91, 138–147. [Google Scholar] [CrossRef]
- Aung, T.S.; Saboori, B.; Rasoulinezhad, E. Economic growth and environmental pollution in Myanmar: An analysis of environmental Kuznets curve. Environ. Sci. Pollut. R. 2017, 24, 20487–20501. [Google Scholar] [CrossRef] [PubMed]
- Kasman, A.; Duman, Y.S. CO2 emissions, economic growth, energy consumption, trade and urbanization in new EU member and candidate countries: A panel data analysis. Econ. Model. 2015, 44, 97–103. [Google Scholar] [CrossRef]
- Javid, M.; Sharif, F. Environmental Kuznets curve and financial development in Pakistan. Renew. Sust. Energ. Rev. 2016, 54, 406–414. [Google Scholar] [CrossRef]
- Mrabet, Z.; Alsamara, M. Testing the Kuznets Curve hypothesis for Qatar: A comparison between carbon dioxide and ecological footprint. Renew. Sust. Energ. Rev. 2017, 70, 1366–1375. [Google Scholar] [CrossRef]
- Zambrano-Monserrate, M.A.; Carvajal-Lara, C.; Urgiles-Sanchez, R. Is there an inverted U-shaped curve? Empirical analysis of the Environmental Kuznets Curve in Singapore. Asia-Pac. J. Account. E. 2018, 25, 145–162. [Google Scholar] [CrossRef]
- Allard, A.; Takman, J.; Uddin, G.S.; Ahmed, A. The N-shaped environmental Kuznets curve: An empirical evaluation using a panel quantile regression approach. Environ. Sci. Pollut. R. 2018, 25, 5848–5861. [Google Scholar] [CrossRef] [PubMed]
- Anser, M.K.; Yousaf, Z.; Nassani, A.A.; Abro, M.M.Q.; Zaman, K. International tourism, social distribution, and environmental Kuznets curve: Evidence from a panel of G-7 countries. Environ. Sci. Pollut. R. 2020, 27, 2707–2720. [Google Scholar] [CrossRef]
- Balaguer, J.; Cantavella, M. The role of education in the Environmental Kuznets Curve. Evidence from Australian data. Energy Econ. 2018, 70, 289–296. [Google Scholar] [CrossRef]
- Millimet, D.L.; List, J.A.; Stengos, T. The environmental Kuznets curve: Real progress or misspecified models? Rev. Econ. Stat. 2003, 85, 1038–1047. [Google Scholar] [CrossRef]
- Kasioumi, M.; Stengos, T. The Environmental Kuznets Curve with Recycling: A Partially Linear Semiparametric Approach. J. Risk. Fin. Man. 2020, 13, 274. [Google Scholar] [CrossRef]
- Kalaitzidakis, P.; Mamuneas, T.P.; Stengos, T. Greenhouse emissions and productivity growth. J. Risk. Fin. Man. 2018, 11, 38. [Google Scholar] [CrossRef]
- Sephton, P.; Mann, J. Compelling evidence of an environmental Kuznets curve in the United Kingdom. Environ. Resour. Econ. 2016, 64, 301–315. [Google Scholar] [CrossRef]
- Olale, E.; Ochuodho, T.O.; Lantz, V.; El Armali, J. The environmental Kuznets curve model for greenhouse gas emissions in Canada. J. Clean Prod. 2018, 184, 859–868. [Google Scholar] [CrossRef]
- Ozturk, I.; Al-Mulali, U. Investigating the validity of the environmental Kuznets curve hypothesis in Cambodia. Ecol. Indic. 2015, 57, 324–330. [Google Scholar] [CrossRef]
- Gill, A.R.; Viswanathan, K.K.; Hassan, S. A test of environmental Kuznets curve (EKC) for carbon emission and potential of renewable energy to reduce green house gases (GHG) in Malaysia. Environ. Dev. Sustain. 2018, 20, 1103–1114. [Google Scholar] [CrossRef]
- Gasimli, O.; Naradda Gamage, S.K.; Shihadeh, F.; Rajapakshe, P.S.K.; Shafiq, M. Energy, trade, urbanization and environmental degradation Nexus in Sri Lanka: Bounds testing approach. Energies 2019, 12, 1655. [Google Scholar] [CrossRef]
- Ben Jebli, M.; Ben Youssef, S.; Ozturk, I. The role of renewable energy consumption and trade: Environmental kuznets curve analysis for sub-saharan Africa countries. Afr. Dev. Rev. 2015, 27, 288–300. [Google Scholar] [CrossRef]
- Zoundi, Z. CO2 emissions, renewable energy and the Environmental Kuznets Curve, a panel cointegration approach. Renew. Sust. Energ. Rev. 2017, 72, 1067–1075. [Google Scholar] [CrossRef]
- Chen, X.; Huang, B.; Lin, C.-T. Environmental awareness and environmental Kuznets curve. Econ. Model. 2019, 77, 2–11. [Google Scholar] [CrossRef]
- Sugiawan, Y.; Managi, S. The environmental Kuznets curve in Indonesia: Exploring the potential of renewable energy. Energ. Policy. 2016, 98, 187–198. [Google Scholar] [CrossRef]
- Kohler, M. CO2 emissions, energy consumption, income and foreign trade: A South African perspective. Energ. Policy. 2013, 63, 1042–1050. [Google Scholar] [CrossRef]
- Boutabba, M.A. The impact of financial development, income, energy and trade on carbon emissions: Evidence from the Indian economy. Econ. Model. 2014, 40, 33–41. [Google Scholar] [CrossRef]
- Sinha, A.; Shahbaz, M. Estimation of environmental Kuznets curve for CO2 emission: Role of renewable energy generation in India. Renew. Energy 2018, 119, 703–711. [Google Scholar] [CrossRef]
- Ertugrul, H.M.; Cetin, M.; Seker, F.; Dogan, E. The impact of trade openness on global carbon dioxide emissions: Evidence from the top ten emitters among developing countries. Ecol. Indic. 2016, 67, 543–555. [Google Scholar] [CrossRef]
- Dogan, E.; Turkekul, B. CO2 emissions, real output, energy consumption, trade, urbanization and financial development: Testing the EKC hypothesis for the USA. Environ. Sci. Pollut. R. 2016, 23, 1203–1213. [Google Scholar] [CrossRef]
- Moosa, I.A. The econometrics of the environmental Kuznets curve: An illustration using Australian CO2 emissions. Appl. Econ. 2017, 49, 4927–4945. [Google Scholar] [CrossRef]
- Pablo-Romero, M.; Cruz, L.; Barata, E. Testing the transport energy-environmental Kuznets curve hypothesis in the EU27 countries. Energy Econ. 2017, 62, 257–269. [Google Scholar] [CrossRef]
- Jiang, L.; He, S.; Zhong, Z.; Zhou, H.; He, L. Revisiting environmental kuznets curve for carbon dioxide emissions: The role of trade. Struct. Change Econ. Dynam. 2019, 50, 245–257. [Google Scholar] [CrossRef]
- Lorente, D.B.; Álvarez-Herranz, A. Economic growth and energy regulation in the environmental Kuznets curve. Environ. Sci. Pollut. R. 2016, 23, 16478–16494. [Google Scholar] [CrossRef] [PubMed]
- Borghesi, S. The environmental Kuznets curve: A critical survey. Econ. Inst. Envr. Policy 2001, 2, 201–224. [Google Scholar]
- Ahmad, N.; Du, L.; Lu, J.; Wang, J.; Li, H.-Z.; Hashmi, M.Z. Modelling the CO2 emissions and economic growth in Croatia: Is there any environmental Kuznets curve? Energy 2017, 123, 164–172. [Google Scholar] [CrossRef]
- Shahbaz, M.; Lean, H.H.; Shabbir, M.S. Environmental Kuznets curve hypothesis in Pakistan: Cointegration and Granger causality. Renew. Sust. Energ. Rev. 2012, 16, 2947–2953. [Google Scholar] [CrossRef]
- Pal, D.; Mitra, S.K. The environmental Kuznets curve for carbon dioxide in India and China: Growth and pollution at crossroad. J. Pol. Modeling 2017, 39, 371–385. [Google Scholar] [CrossRef]
- Saboori, B.; Sulaiman, J. Environmental degradation, economic growth and energy consumption: Evidence of the environmental Kuznets curve in Malaysia. Energ. Policy. 2013, 60, 892–905. [Google Scholar] [CrossRef]
- Al-Mulali, U.; Saboori, B.; Ozturk, I. Investigating the environmental Kuznets curve hypothesis in Vietnam. Energ. Policy. 2015, 76, 123–131. [Google Scholar] [CrossRef]
- Shahbaz, M.; Haouas, I.; Van Hoang, T.H. Economic growth and environmental degradation in Vietnam: Is the environmental Kuznets curve a complete picture? Emerg. Mark. Rev. 2019, 38, 197–218. [Google Scholar] [CrossRef]
- Jalil, A.; Mahmud, S.F. Environment Kuznets curve for CO2 emissions: A cointegration analysis for China. Energ. Policy. 2009, 37, 5167–5172. [Google Scholar] [CrossRef]
- Lau, L.-S.; Choong, C.-K.; Eng, Y.-K. Investigation of the environmental Kuznets curve for carbon emissions in Malaysia: Do foreign direct investment and trade matter? Energ. Policy. 2014, 68, 490–497. [Google Scholar] [CrossRef]
- Tamazian, A.; Chousa, J.P.; Vadlamannati, K.C. Does higher economic and financial development lead to environmental degradation: Evidence from BRIC countries. Energ. Policy 2009, 37, 246–253. [Google Scholar] [CrossRef]
- Jaunky, V.C. The CO2 emissions-income nexus: Evidence from rich countries. Energ. Policy. 2011, 39, 1228–1240. [Google Scholar] [CrossRef]
- Onafowora, O.A.; Owoye, O. Bounds testing approach to analysis of the environment Kuznets curve hypothesis. Energy Econ. 2014, 44, 47–62. [Google Scholar] [CrossRef]
- Neve, M.; Hamaide, B. Environmental Kuznets curve with adjusted net savings as a trade-off between environment and development. Aust. Econ. Pap. 2017, 56, 39–58. [Google Scholar] [CrossRef]
- Alshehry, A.S.; Belloumi, M. Study of the environmental Kuznets curve for transport carbon dioxide emissions in Saudi Arabia. Renew. Sust. Energ. Rev. 2017, 75, 1339–1347. [Google Scholar] [CrossRef]
- Hdom, H.A.; Fuinhas, J.A. Energy production and trade openness: Assessing economic growth, CO2 emissions and the applicability of the cointegration analysis. Energy Strateg. Rev. 2020, 30, 100488. [Google Scholar] [CrossRef]
- Moghadam, H.E.; Dehbashi, V. The impact of financial development and trade on environmental quality in Iran. Empirical. Econ. 2018, 54, 1777–1799. [Google Scholar] [CrossRef]
- WDI. Population in Urban Agglomerations of More Than 1 Million; The World Bank: Washington, DC, USA, 2020; Available online: https://data.worldbank.org/indicator/EN.URB.MCTY.TL.ZS (accessed on 5 December 2020).
- Pesaran, M.H.; Shin, Y.; Smith, R.J. Bounds testing approaches to the analysis of level relationships. J. Appl. Econom. 2001, 16, 289–326. [Google Scholar] [CrossRef]
- Engle, R.F.; Granger, C.W. Co-integration and error correction: Representation, estimation, and testing. Econom. J. Econometric. Soc. 1987, 251–276. [Google Scholar] [CrossRef]
- Johansen, S.; Juselius, K. Maximum likelihood estimation and inference on cointegration—with appucations to the demand for money. Oxford Bull. Econ. Statist. 1990, 52, 169–210. Available online: https://digidownload.libero.it/rocco.mosconi/JohansenJuselius1990.pdf (accessed on 10 November 2020). [CrossRef]
- Narayan, P.K. The saving and investment nexus for China: Evidence from cointegration tests. Appl. Econ. 2005, 37, 1979–1990. [Google Scholar] [CrossRef]
- Sankaran, A.; Kumar, S.; Arjun, K.; Das, M. Estimating the causal relationship between electricity consumption and industrial output: ARDL bounds and Toda-Yamamoto approaches for ten late industrialized countries. Heliyon 2019, 5, e01904. [Google Scholar] [CrossRef]
- Ozturk, I.; Acaravci, A. Electricity consumption and real GDP causality nexus: Evidence from ARDL bounds testing approach for 11 MENA countries. ApEn 2011, 88, 2885–2892. [Google Scholar] [CrossRef]
- Liew, V.K.-S. Which lag length selection criteria should we employ? Econ. Bull. 2004, 3, 1–9. [Google Scholar]
- Jarque, C.M.; Bera, A.K. A test for normality of observations and regression residuals. Int. Stat. Rev. 1987, 163–172. [Google Scholar] [CrossRef]
- Breusch, T.S. Testing for autocorrelation in dynamic linear models. Aust. Econ. Pap. 1978, 17, 334–355. [Google Scholar] [CrossRef]
- Godfrey, L.G. Testing for higher order serial correlation in regression equations when the regressors include lagged dependent variables. Econometrica 1978, 1303–1310. Available online: https://www.jstor.org/stable/pdf/1913830.pdf (accessed on 10 November 2020).
- White, H. A heteroskedasticity-consistent covariance matrix estimator and a direct test for heteroskedasticity. Econometrica J. Econometric. Soc. 1980, 817–838. [Google Scholar] [CrossRef]
- Ramsey, J.B. Tests for specification errors in classical linear least-squares regression analysis. J. Roy. Stat. Soc. B. Met. 1969, 31, 350–371. Available online: https://www.jstor.org/stable/2984219 (accessed on 10 November 2020). [CrossRef]
- Brown, R.L.; Durbin, J.; Evans, J.M. Techniques for testing the constancy of regression relationships over time. J. Roy. Stat. Soc. B. Met. 1975, 37, 149–163. Available online: https://www.jstor.org/stable/2984889 (accessed on 10 November 2020). [CrossRef]
- Bölük, G.; Mert, M. The renewable energy, growth and environmental Kuznets curve in Turkey: An ARDL approach. Renew. Sust. Energ. Rev. 2015, 52, 587–595. [Google Scholar] [CrossRef]
- Shahbaz, M.; Loganathan, N.; Zeshan, M.; Zaman, K. Does renewable energy consumption add in economic growth? An application of auto-regressive distributed lag model in Pakistan. Renew. Sust. Energ. Rev. 2015, 44, 576–585. [Google Scholar] [CrossRef]
- Shahin, M.; Elchalakani, M. Neural networks for modelling ultimate pure bending of steel circular tubes. J. Constr. Steel Res. 2008, 64, 624–633. [Google Scholar] [CrossRef]
- Detienne, K.B.; Detienne, D.H.; Joshi, S.A. Neural networks as statistical tools for business researchers. Organ. Res. Methods 2003, 6, 236–265. [Google Scholar] [CrossRef]
- Li, Y.; Ma, W. Applications of artificial neural networks in financial economics: A survey. In Proceedings of the 2010 International Symposium on Computational Intelligence and Design, Hangzhou, China, 29–31 October 2010; pp. 211–214. [Google Scholar]
- Önder, E.; Bayır, F.; Hepsen, A. Forecasting macroeconomic variables using artificial neural network and traditional smoothing techniques. J. Appl. Financ. Bank. 2013, 3, 73–104. [Google Scholar] [CrossRef]
- Galeshchuk, S. Neural networks performance in exchange rate prediction. Neurocomputing 2016, 172, 446–452. [Google Scholar] [CrossRef]
- Rumelhart, D.E.; Hinton, G.E.; Williams, R.J. Learning representations by back-propagating errors. Nature 1986, 323, 533–536. [Google Scholar] [CrossRef]
- Werbos, P. Beyond Regression: New Tools for Prediction and Analysis in the Behavioral Sciences. Ph.D. Thesis, Harvard University, Cambridge, MA, USA, 1974. Available online: https://ci.nii.ac.jp/naid/10004070196/ (accessed on 5 December 2020).
- Parker, D.B. Learning Logic. Invention Report S81-64, File 1; Stanford University, Oce of Technology Licensing: Paolo Alto, CA, USA, 1982. [Google Scholar]
- Sheela, K.G.; Deepa, S.N. Review on methods to fix number of hidden neurons in neural networks. Math. Probl. Eng. 2013, 2013. [Google Scholar] [CrossRef]
- Maier, H.R.; Dandy, G.C. Neural network based modelling of environmental variables: A systematic approach. MComM 2001, 33, 669–682. [Google Scholar] [CrossRef]
- Dehuri, S.; Roy, R.; Cho, S.-B.; Ghosh, A. An improved swarm optimized functional link artificial neural network (ISO-FLANN) for classification. J. Syst. Software 2012, 85, 1333–1345. [Google Scholar] [CrossRef]
- Choi, B.; Lee, J.-H.; Kim, D.-H. Solving local minima problem with large number of hidden nodes on two-layered feed-forward artificial neural networks. Neurocomputing 2008, 71, 3640–3643. [Google Scholar] [CrossRef]
- Khemakhem, S.; Said, F.B.; Boujelbene, Y. Credit risk assessment for unbalanced datasets based on data mining, artificial neural network and support vector machines. J. Modell. Manage. 2018. [Google Scholar] [CrossRef]
- Hecht-Nielsen, R. Kolmogorov’s mapping neural network existence theorem. In Proceedings of the International Conference on Neural Networks, San Diego, CA, USA, 21–24 June 1987; pp. 11–14. [Google Scholar]
- Turban, E.; Sharda, R.; Delen, D.; Aronson, J.E.; Liang, T.-P.; King, D. Decision Support and Business Intelligent Systems, 9th ed.; Prentice Hall: New Jersey, NJ, USA, 2011. [Google Scholar]
- Zhang, Z.; Ma, X.; Yang, Y. Bounds on the number of hidden neurons in three-layer binary neural networks. Neural Netw. 2003, 16, 995–1002. [Google Scholar] [CrossRef]
- Tamura, S.i.; Tateishi, M. Capabilities of a four-layered feedforward neural network: Four layers versus three. ITNN 1997, 8, 251–255. [Google Scholar] [CrossRef]
- Moolayil, J. Learn Keras for Deep Neural Networks; Springer: New York, NY, USA, 2019. [Google Scholar]
- Aggarwal, C.C. Neural Networks and Deep Learning—A Textbook; Springer: Cham, Switzerland, 2018. [Google Scholar]
- Boateng, E.B.; Pillay, M.; Davis, P. Predicting the level of safety performance using an artificial neural network. In Proceedings of the International Conference on Human Systems Engineering and Design: Future Trends and Applications, Ardenne, France, 25–27 October 2018; pp. 705–710. [Google Scholar]
- Bermejo, S.; Cabestany, J. Oriented principal component analysis for large margin classifiers. Neural. Netw. 2001, 14, 1447–1461. [Google Scholar] [CrossRef]
- Zivot, E.; Andrews, D.W.K. Further evidence on the great crash, the oil-price shock, and the unit-root hypothesis. J. Bus. Econ. Stat. 2002, 20, 25–44. [Google Scholar] [CrossRef]
- Perron, P. Further evidence on breaking trend functions in macroeconomic variables. J. Econom. 1997, 80, 355–385. [Google Scholar] [CrossRef]
- Jebli, M.B.; Youssef, S.B. The environmental Kuznets curve, economic growth, renewable and non-renewable energy, and trade in Tunisia. Renew. Sust. Energ. Rev. 2015, 47, 173–185. [Google Scholar] [CrossRef]
- SBV. Bank of Vietnam Period 1986–1990: The Review; State Bank of Vietnam: Hanoi, Vietnam, 2008; Available online: https://bitly.com.vn/hatn9k (accessed on 17 May 2021).
- Ahmad, N.; Du, L. Effects of energy production and CO2 emissions on economic growth in Iran: ARDL approach. Energy 2017, 123, 521–537. [Google Scholar] [CrossRef]
- Martínez-Zarzoso, I.; Maruotti, A. The impact of urbanization on CO2 emissions: Evidence from developing countries. Ecol. Econ. 2011, 70, 1344–1353. [Google Scholar] [CrossRef]
- Ho, B.Q.; Clappier, A. Road traffic emission inventory for air quality modelling and to evaluate the abatement strategies: A case of Ho Chi Minh City, Vietnam. AtmEn 2011, 45, 3584–3593. [Google Scholar] [CrossRef]
- Bang, H.Q.; Khue, V.H.N.; Tam, N.T.; Lasko, K. Air pollution emission inventory and air quality modeling for Can Tho City, Mekong Delta, Vietnam. Air Qual. Atmos. Health 2018, 11, 35–47. [Google Scholar] [CrossRef]
- Huy, L.N.; Oanh, N.T.K. Assessment of national emissions of air pollutants and climate forcers from thermal power plants and industrial activities in Vietnam. Atmos. Pollut. Res. 2017, 8, 503–513. [Google Scholar] [CrossRef]
- Fan, P.; Ouyang, Z.; Nguyen, D.D.; Nguyen, T.T.H.; Park, H.; Chen, J. Urbanization, economic development, environmental and social changes in transitional economies: Vietnam after Doimoi. Landsc. Urban Plann. 2019, 187, 145–155. [Google Scholar] [CrossRef]
- Abdallah, K.B.; Belloumi, M.; De Wolf, D. Indicators for sustainable energy development: A multivariate cointegration and causality analysis from Tunisian road transport sector. Renew. Sust. Energ. Rev. 2013, 25, 34–43. [Google Scholar] [CrossRef]
- Fodha, M.; Zaghdoud, O. Economic growth and pollutant emissions in Tunisia: An empirical analysis of the environmental Kuznets curve. Energ. Policy. 2010, 38, 1150–1156. [Google Scholar] [CrossRef]
- Marino, S.; Hogue, I.B.; Ray, C.J.; Kirschner, D.E. A methodology for performing global uncertainty and sensitivity analysis in systems biology. JTBio 2008, 254, 178–196. [Google Scholar] [CrossRef] [PubMed]
- Saltelli, A. Sensitivity analysis for importance assessment. Risk Anal. 2002, 22, 579–590. [Google Scholar] [CrossRef] [PubMed]
- Spearman, C. The Proof and Measurement of Association between Two Things. Am. J. Psychol. 1904, 15, 72–101. [Google Scholar] [CrossRef]
- Kendall, M.G. Partial Rank Correlation. Biometrika 1942, 32, 277–283. [Google Scholar] [CrossRef]
- de Winter, J.C.; Gosling, S.D.; Potter, J. Comparing the Pearson and Spearman correlation coefficients across distributions and sample sizes: A tutorial using simulations and empirical data. Psychol. Methods 2016, 21, 273. [Google Scholar] [CrossRef]
- Schaeffer, M.S.; Levitt, E.E. Concerning Kendall’s tau, a nonparametric correlation coefficient. Psychol. Bull. 1956, 53, 338–346. [Google Scholar] [CrossRef] [PubMed]
- Prime-Minister. National electricity development planning for the period 2011–2020 with a vision to 2030. Energy Rep. 2016, 6, 19–24.
- Doan, V.B.; Bui, V.H. Developing the Renewable Energy Center in Ninh Thuan Province; Ban Kinh te Trung Uong Ha Noi: 2021. Available online: https://www.tapchicongsan.org.vn/web/guest/thuc-tien-kinh-nghiem1/-/2018/821654/phat-trien-trung-tam-nang-luong-tai-tao-tinh-ninh-thuan.aspx (accessed on 17 May 2021).
- NAV. Law on Environmental Protection. 55/2014/QH13 2014. Available online: https://www.ecolex.org/details/legislation/law-on-environmental-protection-no-552014qh13-lex-faoc168513/ (accessed on 17 May 2021).
- Sadik-Zada, E.R.; Loewenstein, W. Drivers of CO2-Emissions in Fossil Fuel abundant settings:(Pooled) mean group and nonparametric panel analyses. Energies 2020, 13, 3956. [Google Scholar] [CrossRef]
- Stuart, R.; Peter, N. Artificial Intelligence-A Modern Approach, 3rd ed.; Pearson: London, UK, 2016. [Google Scholar]
- De Vita, G.; Katircioglu, S.; Altinay, L.; Fethi, S.; Mercan, M. Revisiting the environmental Kuznets curve hypothesis in a tourism development context. Environ. Sci, Pollut. R. 2015, 22, 16652–16663. [Google Scholar] [CrossRef] [PubMed]
- Nasr, A.B.; Gupta, R.; Sato, J.R. Is there an environmental Kuznets curve for South Africa? A co-summability approach using a century of data. Energy Econ. 2015, 52, 136–141. [Google Scholar] [CrossRef]
- Yin, J.; Zheng, M.; Chen, J. The effects of environmental regulation and technical progress on CO2 Kuznets curve: An evidence from China. Energ. Policy. 2015, 77, 97–108. [Google Scholar] [CrossRef]
- Apergis, N.; Ozturk, I. Testing environmental Kuznets curve hypothesis in Asian countries. Ecol. Indic. 2015, 52, 16–22. [Google Scholar] [CrossRef]
- Baek, J. Environmental Kuznets curve for CO2 emissions: The case of Arctic countries. Energy Econ. 2015, 50, 13–17. [Google Scholar] [CrossRef]
- Al-Mulali, U.; Weng-Wai, C.; Sheau-Ting, L.; Mohammed, A.H. Investigating the environmental Kuznets curve (EKC) hypothesis by utilizing the ecological footprint as an indicator of environmental degradation. Ecol. Indic. 2015, 48, 315–323. [Google Scholar] [CrossRef]
- Liddle, B. Urban transport pollution: Revisiting the environmental Kuznets curve. Int. J. Sustain. Transp. 2015, 9, 502–508. [Google Scholar] [CrossRef]
- Zaman, K.; Shahbaz, M.; Loganathan, N.; Raza, S.A. Tourism development, energy consumption and Environmental Kuznets Curve: Trivariate analysis in the panel of developed and developing countries. Tourism. Manag. 2016, 54, 275–283. [Google Scholar] [CrossRef]
- Lin, B.; Omoju, O.E.; Nwakeze, N.M.; Okonkwo, J.U.; Megbowon, E.T. Is the environmental Kuznets curve hypothesis a sound basis for environmental policy in Africa? J. Clean. Prod. 2016, 133, 712–724. [Google Scholar] [CrossRef]
- Pablo-Romero, M.d.P.; De Jesús, J. Economic growth and energy consumption: The energy-environmental Kuznets curve for Latin America and the Caribbean. Renew. Sust. Energ. Rev. 2016, 60, 1343–1350. [Google Scholar] [CrossRef]
- Bilgili, F.; Koçak, E.; Bulut, Ü. The dynamic impact of renewable energy consumption on CO2 emissions: A revisited Environmental Kuznets Curve approach. Renew. Sust. Energ. Rev. 2016, 54, 838–845. [Google Scholar] [CrossRef]
- Youssef, A.B.; Hammoudeh, S.; Omri, A. Simultaneity modeling analysis of the environmental Kuznets curve hypothesis. Energy Econ. 2016, 60, 266–274. [Google Scholar] [CrossRef]
- Atasoy, B.S. Testing the environmental Kuznets curve hypothesis across the US: Evidence from panel mean group estimators. Renew. Sust. Energ. Rev. 2017, 77, 731–747. [Google Scholar] [CrossRef]
- Özokcu, S.; Özdemir, Ö. Economic growth, energy, and environmental Kuznets curve. Renew. Sust. Energ. Rev. 2017, 72, 639–647. [Google Scholar] [CrossRef]
- Liu, X.; Zhang, S.; Bae, J. The impact of renewable energy and agriculture on carbon dioxide emissions: Investigating the environmental Kuznets curve in four selected ASEAN countries. J. Clean. Prod. 2017, 164, 1239–1247. [Google Scholar] [CrossRef]
- Dong, K.; Sun, R.; Li, H.; Liao, H. Does natural gas consumption mitigate CO2 emissions: Testing the environmental Kuznets curve hypothesis for 14 Asia-Pacific countries. Renew. Sust. Energ. Rev. 2018, 94, 419–429. [Google Scholar] [CrossRef]
- Alsamara, M.; Mrabet, Z.; Saleh, A.S.; Anwar, S. The environmental Kuznets curve relationship: A case study of the Gulf Cooperation Council region. Environ. Sci. Pollut. R. 2018, 25, 33183–33195. [Google Scholar] [CrossRef] [PubMed]
- Masron, T.A.; Subramaniam, Y. The environmental Kuznets curve in the presence of corruption in developing countries. Environ. Sci. Pollut. R. 2018, 25, 12491–12506. [Google Scholar] [CrossRef]
- Sterpu, M.; Soava, G.; Mehedintu, A. Impact of Economic Growth and Energy Consumption on Greenhouse Gas Emissions: Testing Environmental Curves Hypotheses on EU Countries. Sustainability 2018, 10, 3327. [Google Scholar] [CrossRef]
- Parajuli, R.; Joshi, O.; Maraseni, T. Incorporating forests, agriculture, and energy consumption in the framework of the Environmental Kuznets Curve: A dynamic panel data approach. Sustainability 2019, 11, 2688. [Google Scholar] [CrossRef]
- Hove, S.; Tursoy, T. An investigation of the environmental Kuznets curve in emerging economies. J. Clean. Prod. 2019, 236, 117628. [Google Scholar] [CrossRef]
- Zhang, Y.; Chen, X.; Wu, Y.; Shuai, C.; Shen, L. The environmental Kuznets curve of CO2 emissions in the manufacturing and construction industries: A global empirical analysis. Environ. Impact Assess. Rev. 2019, 79, 106303. [Google Scholar] [CrossRef]
- Baležentis, T.; Streimikiene, D.; Zhang, T.; Liobikiene, G. The role of bioenergy in greenhouse gas emission reduction in EU countries: An Environmental Kuznets Curve modelling. Resour. Conserv. Recy. 2019, 142, 225–231. [Google Scholar] [CrossRef]
- Lau, L.-S.; Choong, C.-K.; Ng, C.-F.; Liew, F.-M.; Ching, S.-L. Is nuclear energy clean? Revisit of Environmental Kuznets Curve hypothesis in OECD countries. Econ. Model. 2019, 77, 12–20. [Google Scholar] [CrossRef]
- Neagu, O. The Link between Economic Complexity and Carbon Emissions in the European Union Countries: A Model Based on the Environmental Kuznets Curve (EKC) Approach. Sustainability 2019, 11, 4753. [Google Scholar] [CrossRef]
- Arango Miranda, R.; Hausler, R.; Romero Lopez, R.; Glaus, M.; Pasillas-Diaz, J.R. Testing the environmental kuznets curve hypothesis in North America’s free trade agreement (NAFTA) countries. Energies 2020, 13, 3104. [Google Scholar] [CrossRef]
- Dogan, E.; Ulucak, R.; Kocak, E.; Isik, C. The use of ecological footprint in estimating the Environmental Kuznets Curve hypothesis for BRICST by considering cross-section dependence and heterogeneity. Sci. Total. Environ. 2020, 138063. [Google Scholar] [CrossRef] [PubMed]
- Mania, E. Export diversification and CO2 emissions: An augmented environmental Kuznets curve. J. Int. Devel. 2020, 32, 168–185. [Google Scholar] [CrossRef]
- Gómez, M.; Rodríguez, J.C. The Ecological Footprint and Kuznets Environmental Curve in the USMCA Countries: A Method of Moments Quantile Regression Analysis. Energies 2020, 13, 6650. [Google Scholar] [CrossRef]
- Sun, H.; Enna, L.; Monney, A.; Tran, D.K.; Rasoulinezhad, E.; Taghizadeh-Hesary, F. The Long-Run Effects of Trade Openness on Carbon Emissions in Sub-Saharan African Countries. Energies 2020, 13, 5295. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).