Reliability and Economic Evaluation of Offshore Wind Power DC Collection Systems
Abstract
1. Introduction
1.1. Background
1.2. Different Collection System Options
1.3. The Requirement of Reliability and Economic Assessment
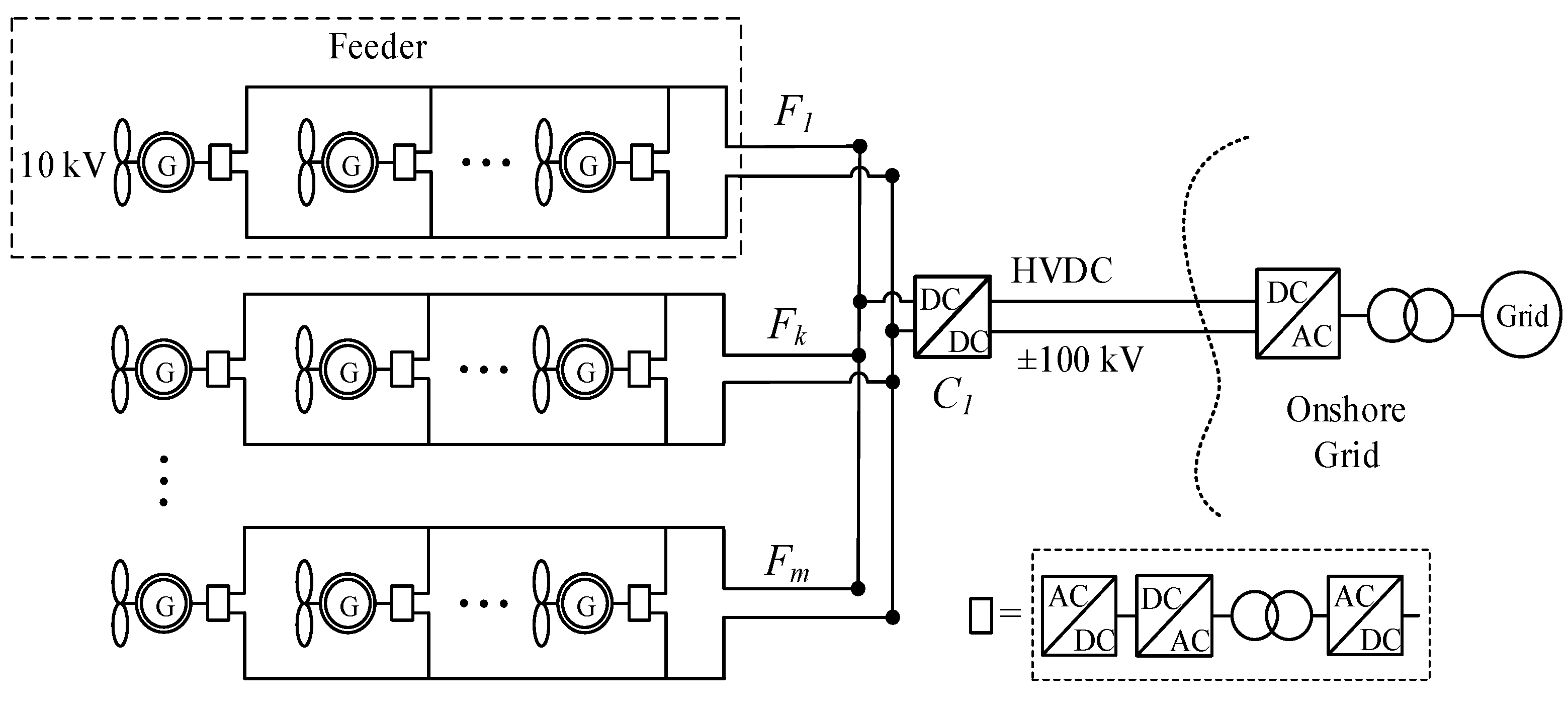
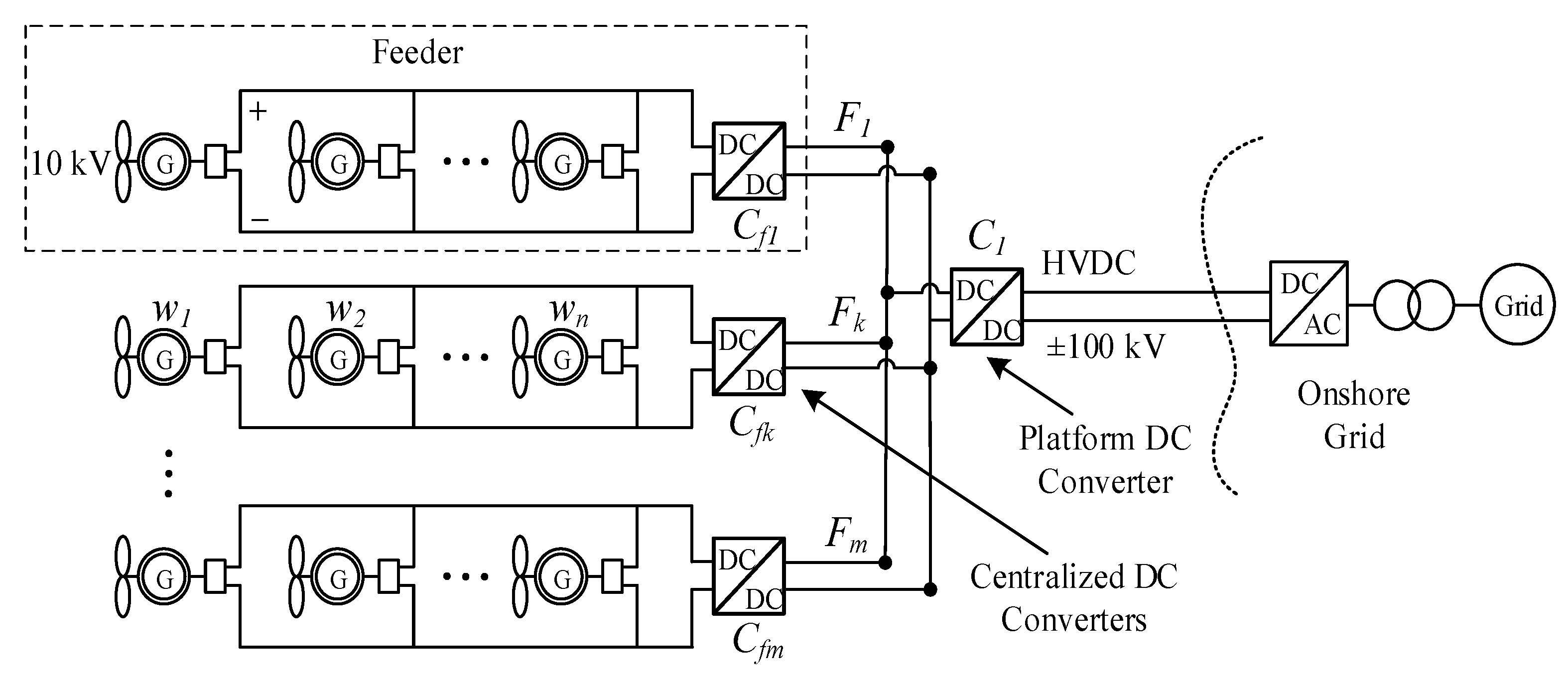
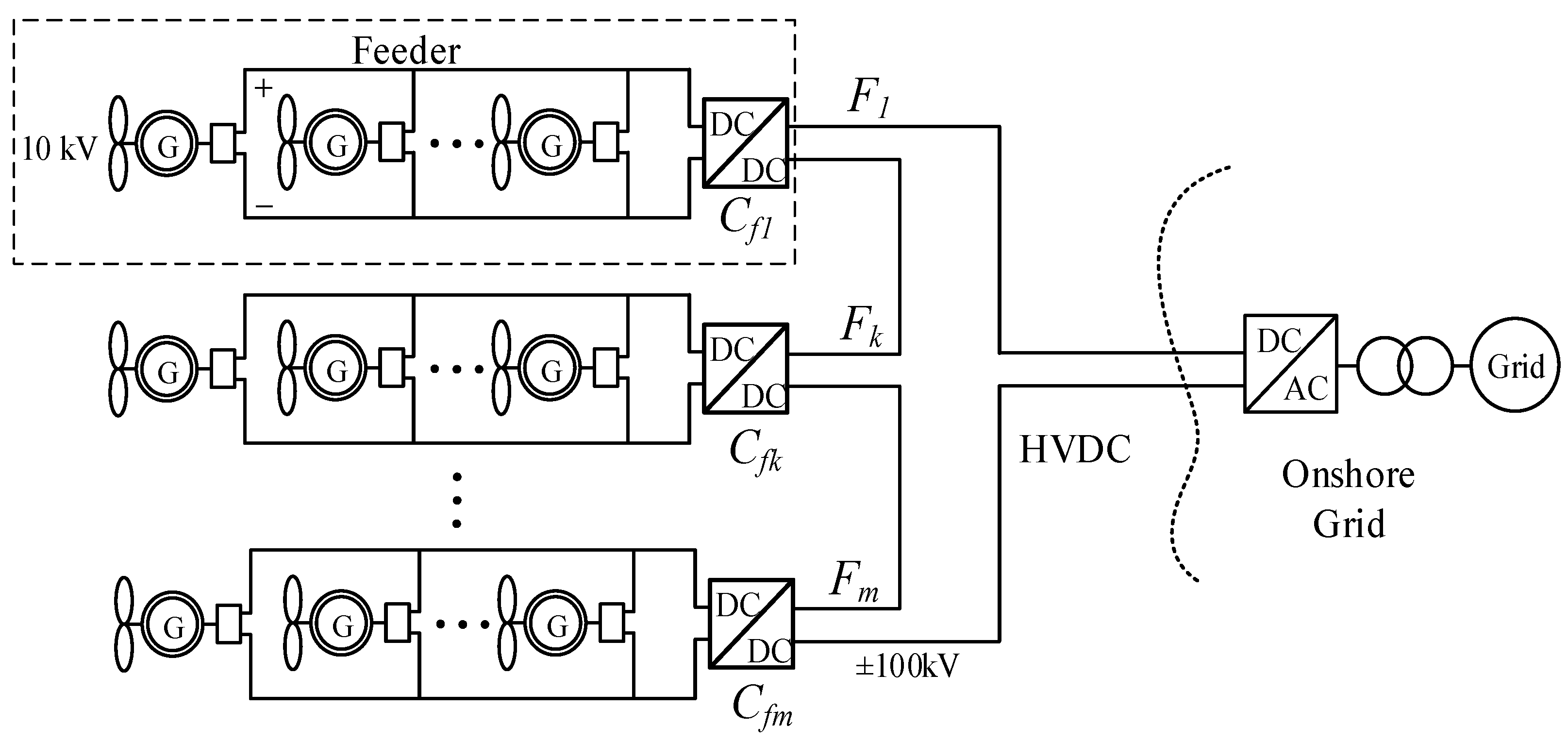
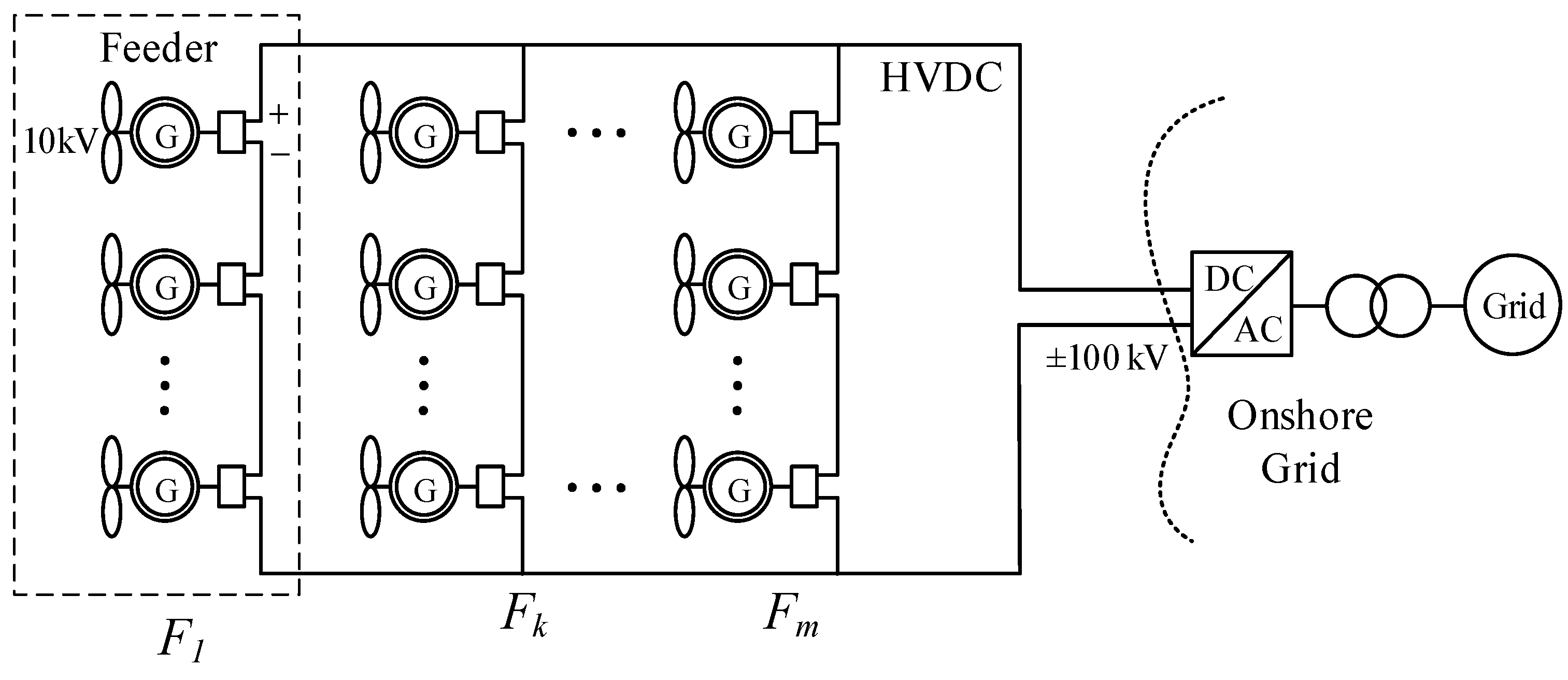
2. Network Topologies for DC Collection Systems
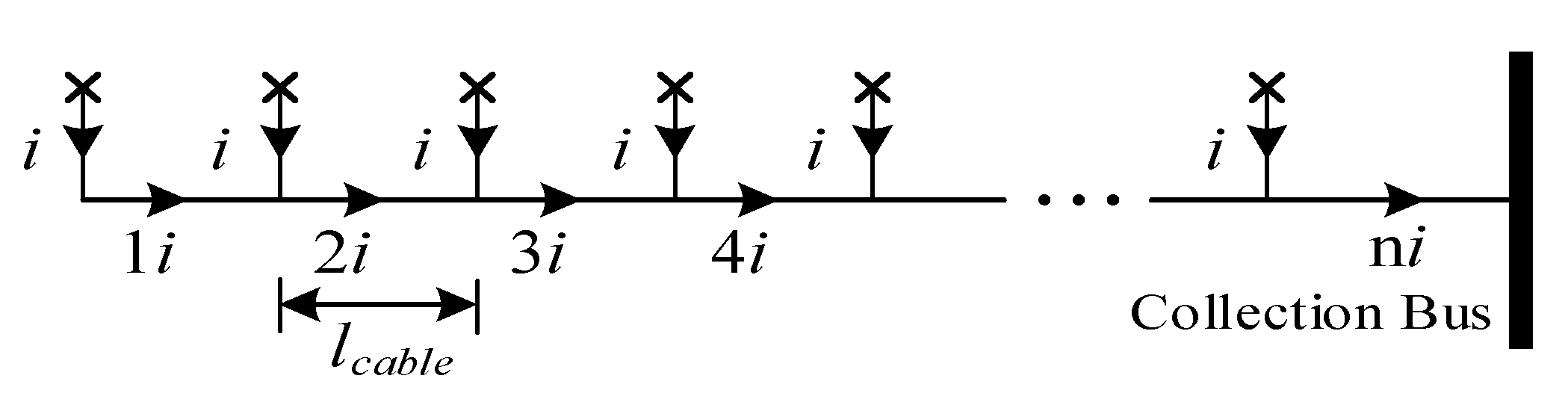
2.1. DC Radial Collection Systems
2.2. Series–Parallel Collection System
3. Methodology
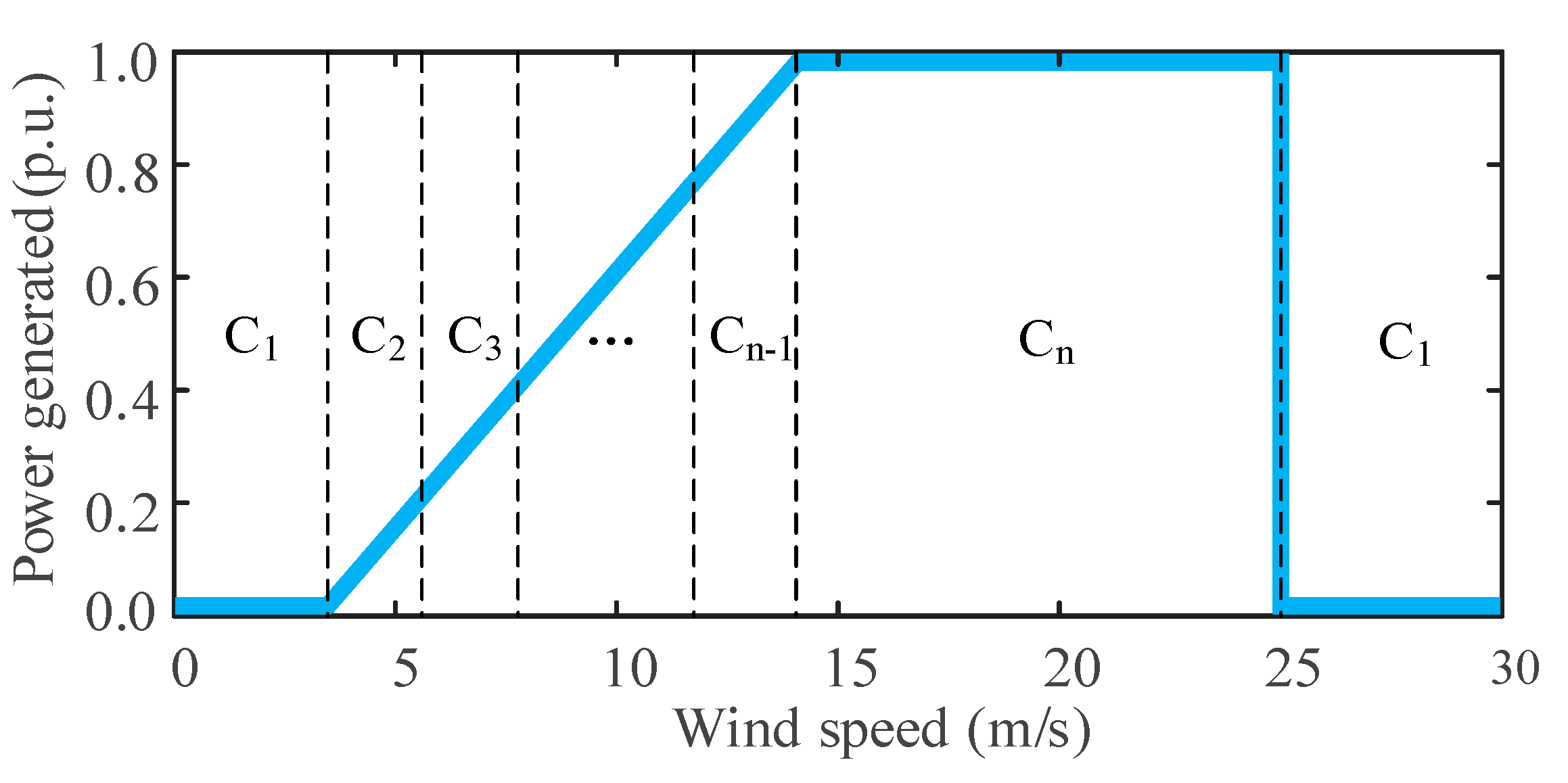
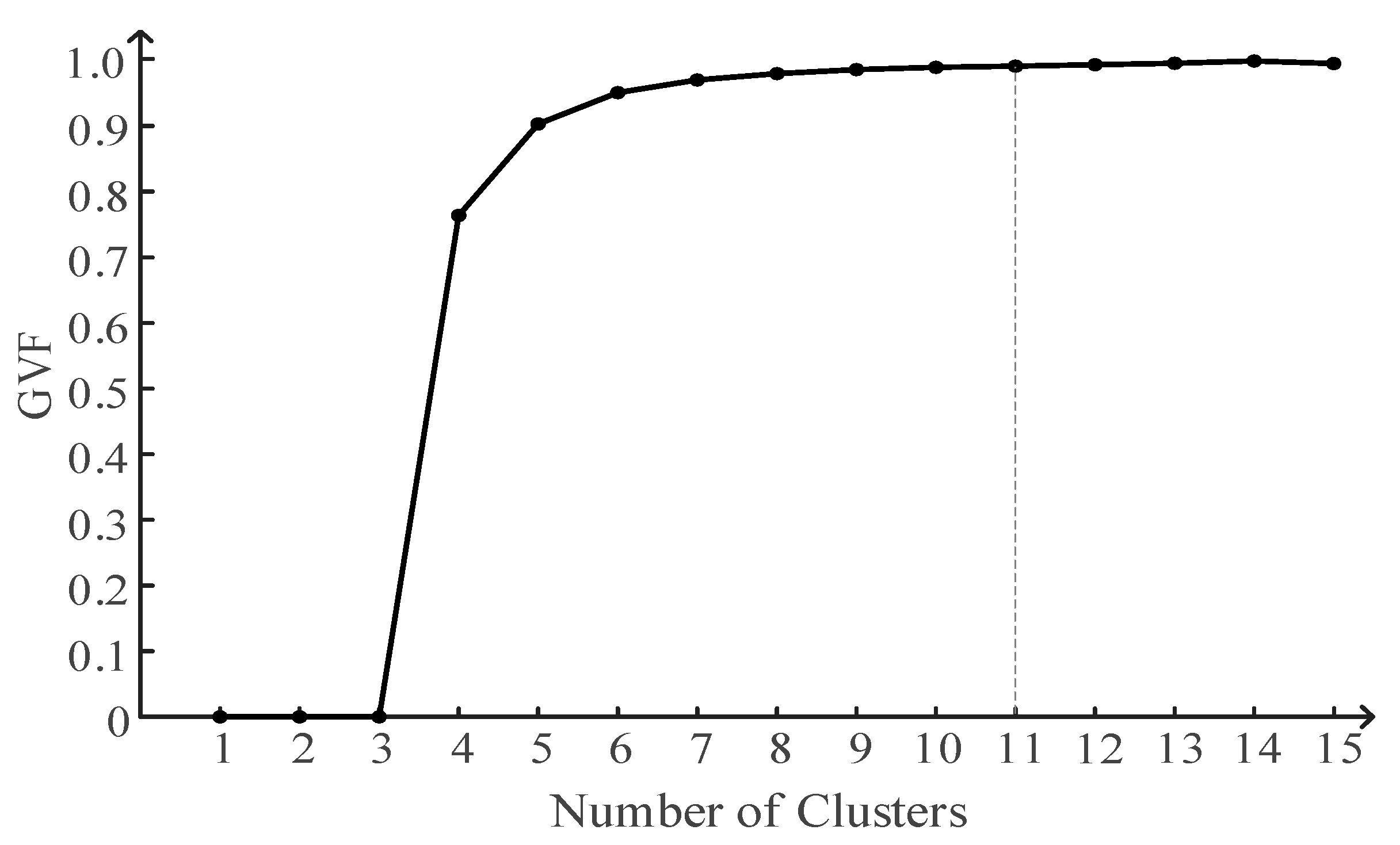
3.1. Clustering of Wind Turbine Power Output
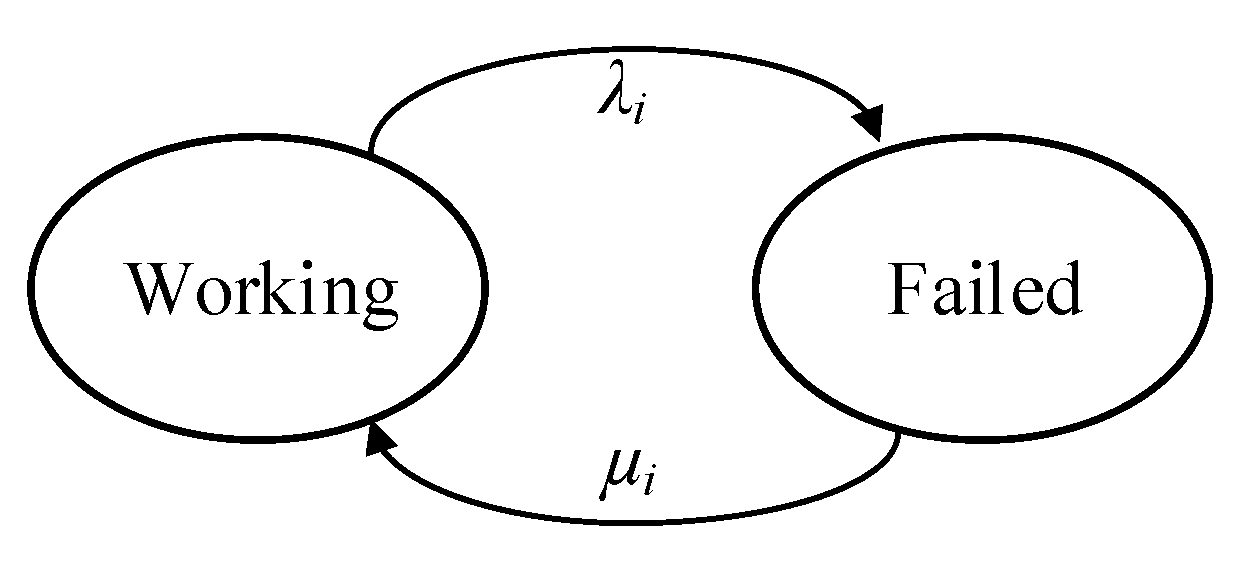
3.2. Reliability Modelling
3.2.1. Failure Rate Calculation of dcWT
3.2.2. The Universal Generating Function
UGF Model for Radial Topology
- Radial-1 Topology
- Radial-2 Topology
- Radial-3 Topology
- Determine the UGF (UCFk) of each feeder DC/DC converter as in Equation (18)
- Obtain the UGF of all m feeders (k = 1,2,…,m)
- Define the value of kmin, i.e., the minimum number of centralized DC/DC converters required for a successful operation of the OWF collection system.
- Obtain the new UGF by replacing all zknPx with z0 for k < kmin in Equation (25)
- Finally, combine Equation (26) with the UGF of the OWF collection system Ur1, which comprises m-feeders and n-WTs per feeder, as defined in Equation (19).
- The final UGF for ncl states can be obtained by referring to Equations (21) and (22).
UGF Model for Series-Parallel Structure
3.2.3. Reliability Indices
3.3. Lifetime Cost Estimation
3.3.1. Capital Investment
- WT Cost
- DC/DC Converter Costs
- DC Cable Cost
3.3.2. Costs Associated with Energy Losses
- Cable Losses (Radial Topology)
- Cable Losses (SP Topology)
- Converter Losses
- Cost of Losses
4. Case Study
4.1. Obtaining Optimal Number of Wind Power Output Clusters and Other Parameters
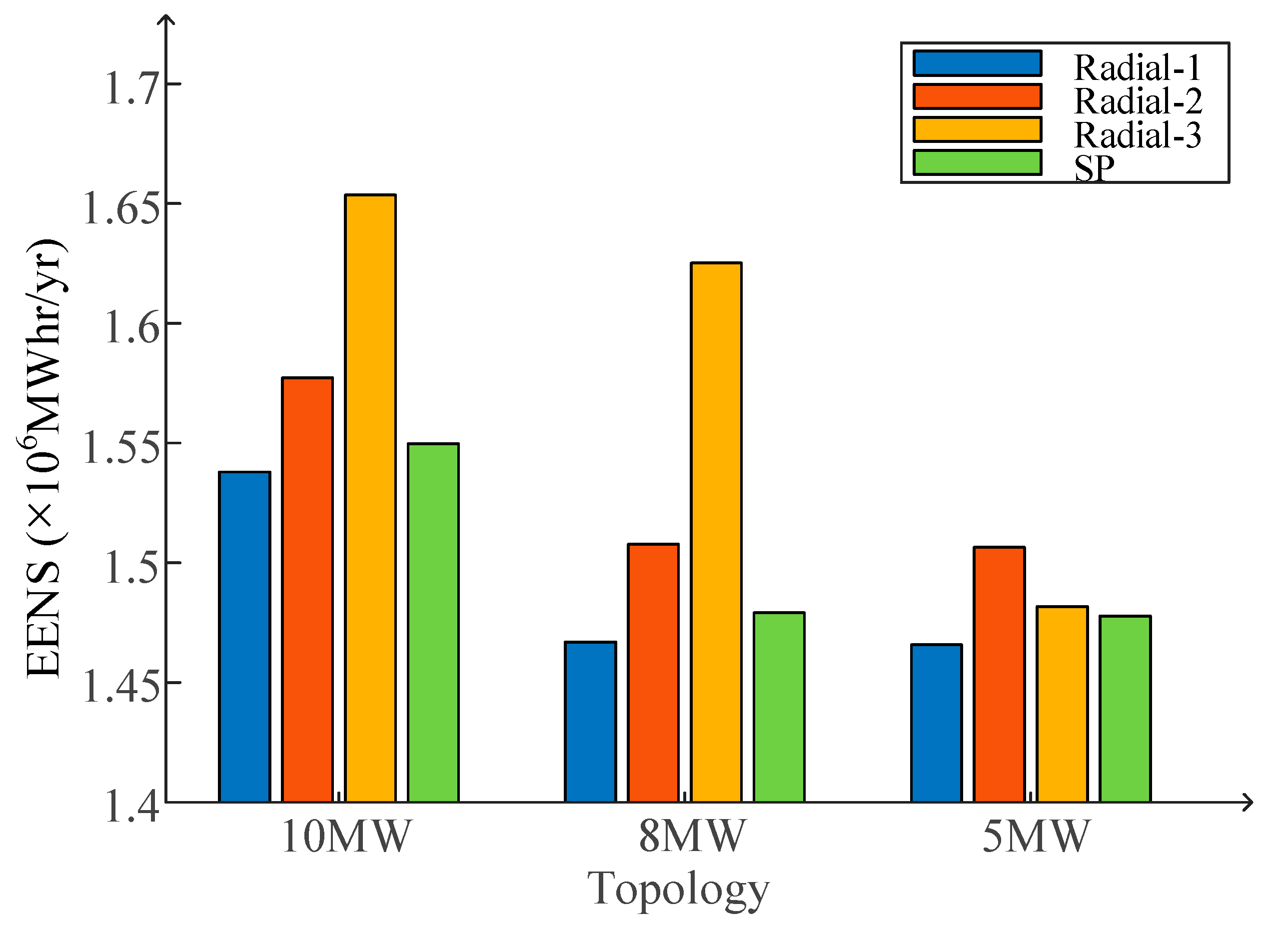
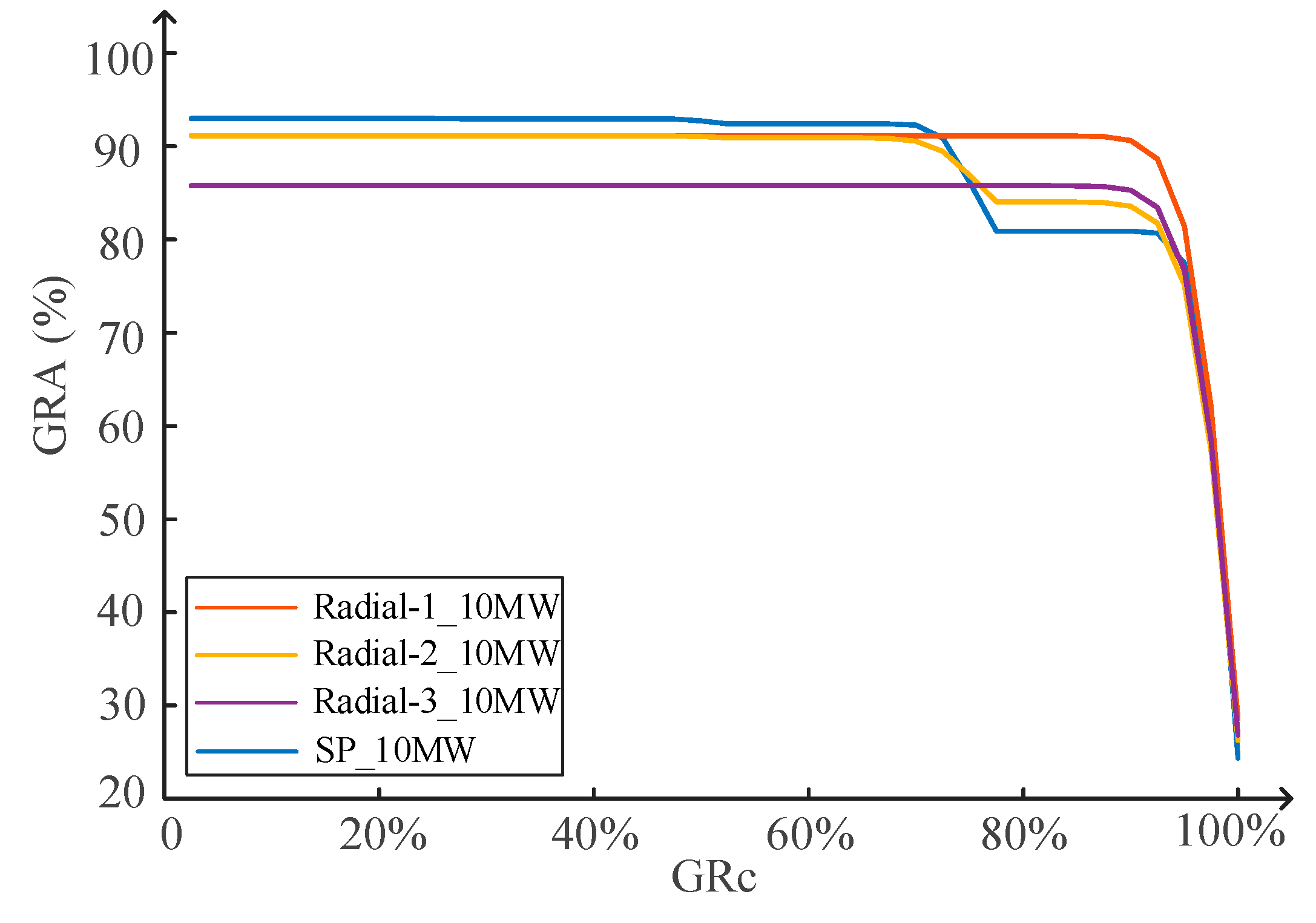
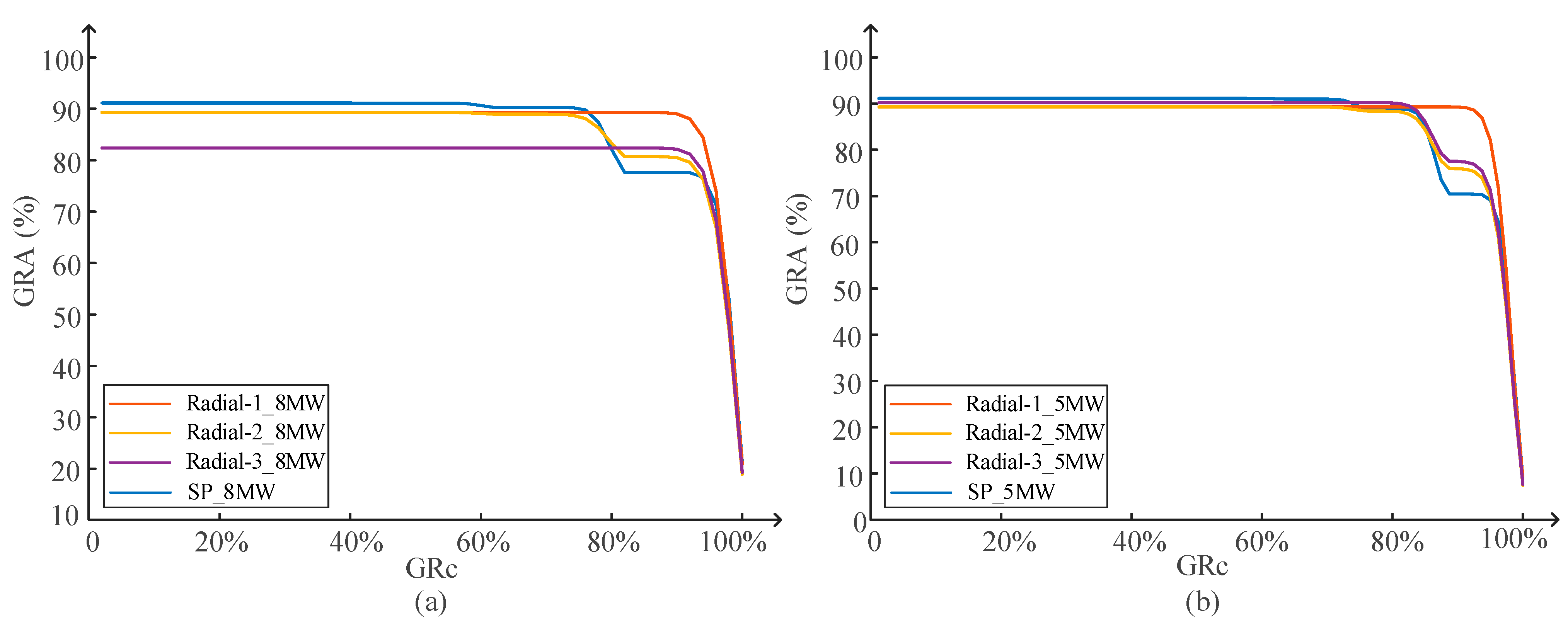
4.2. Reliability of DC Collection Systems
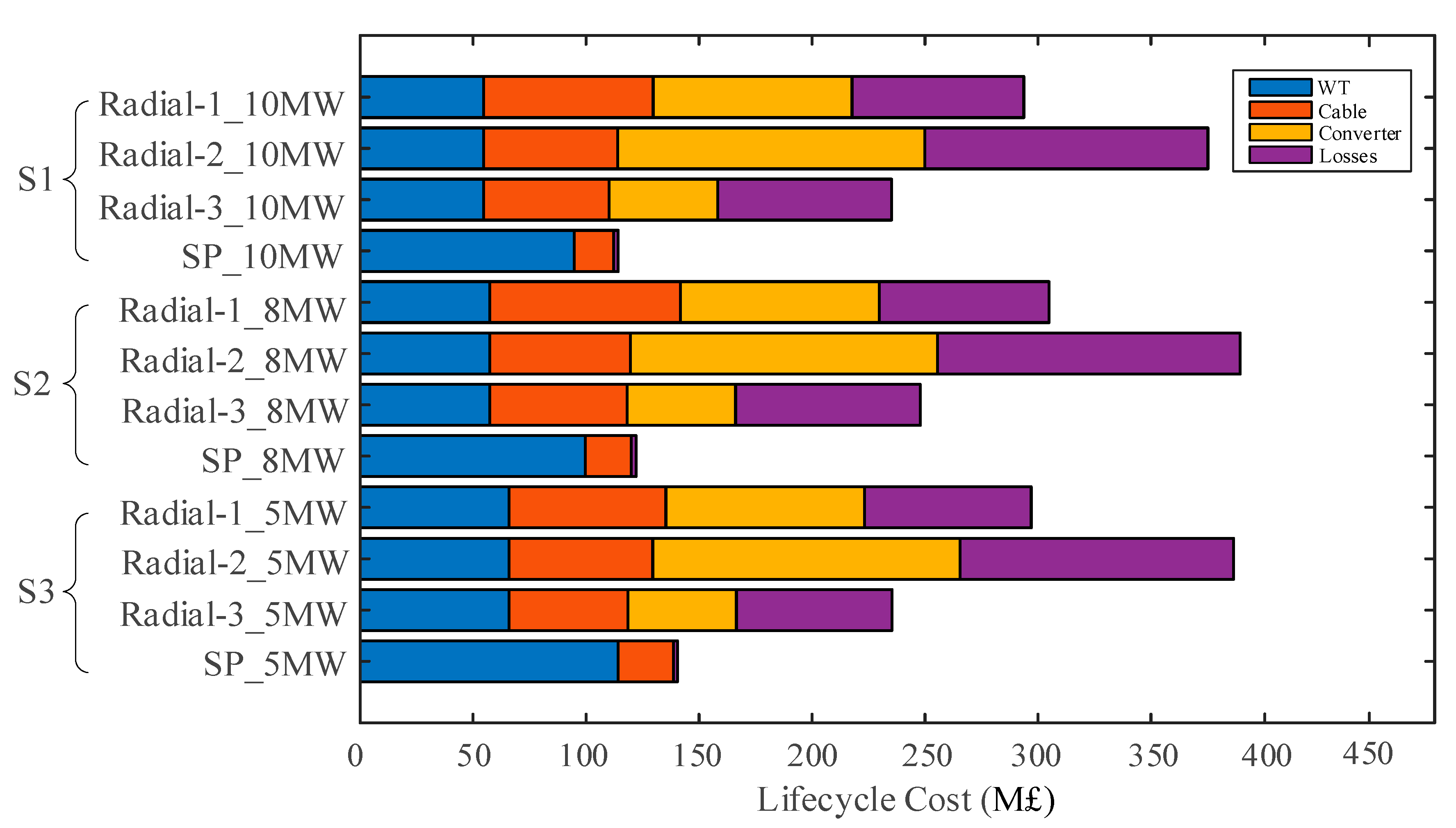
4.3. Economic Evaluation of Candidate DC Collection Systems
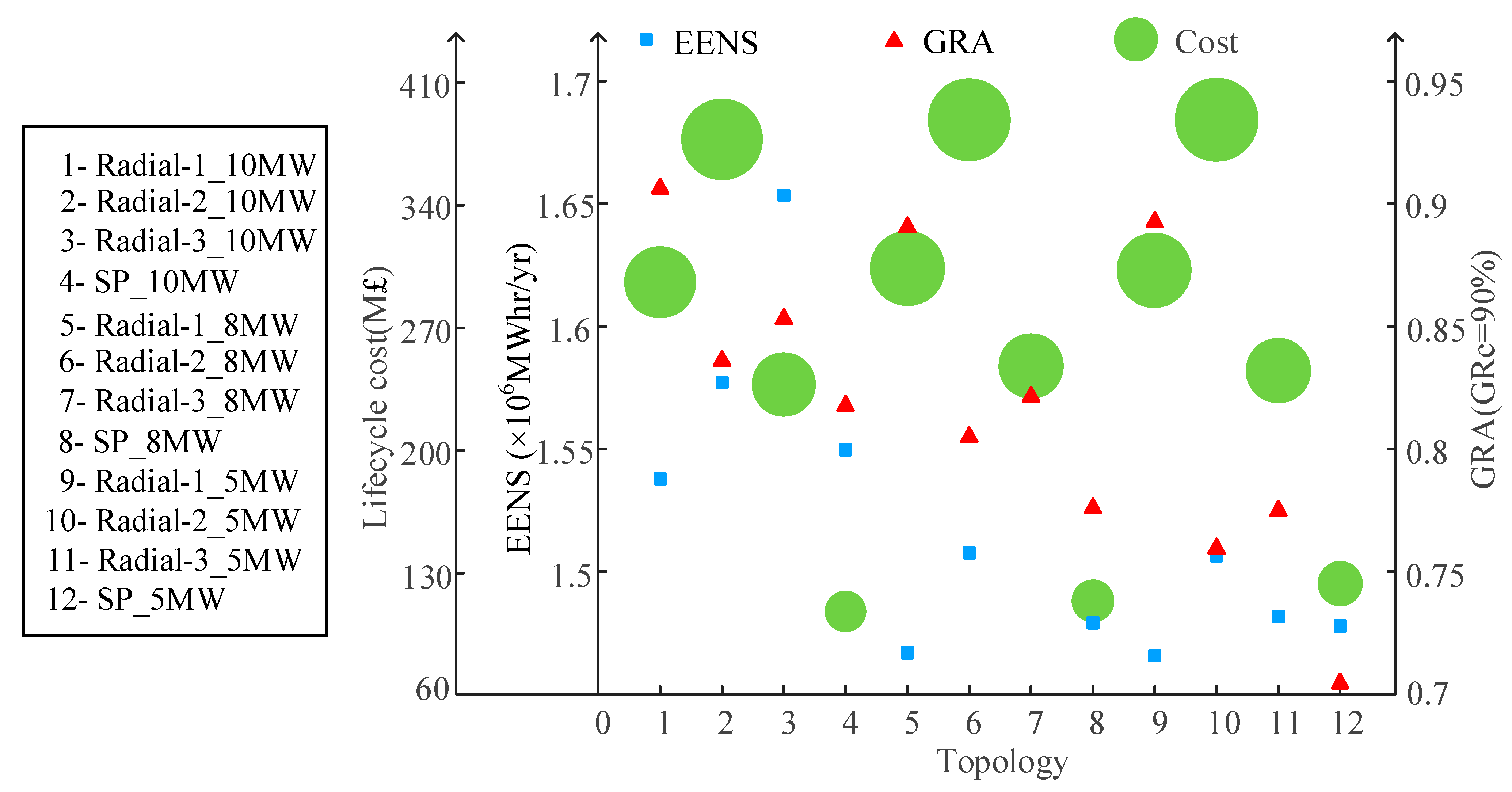
4.4. Overall Assessment of DC Collection System Options
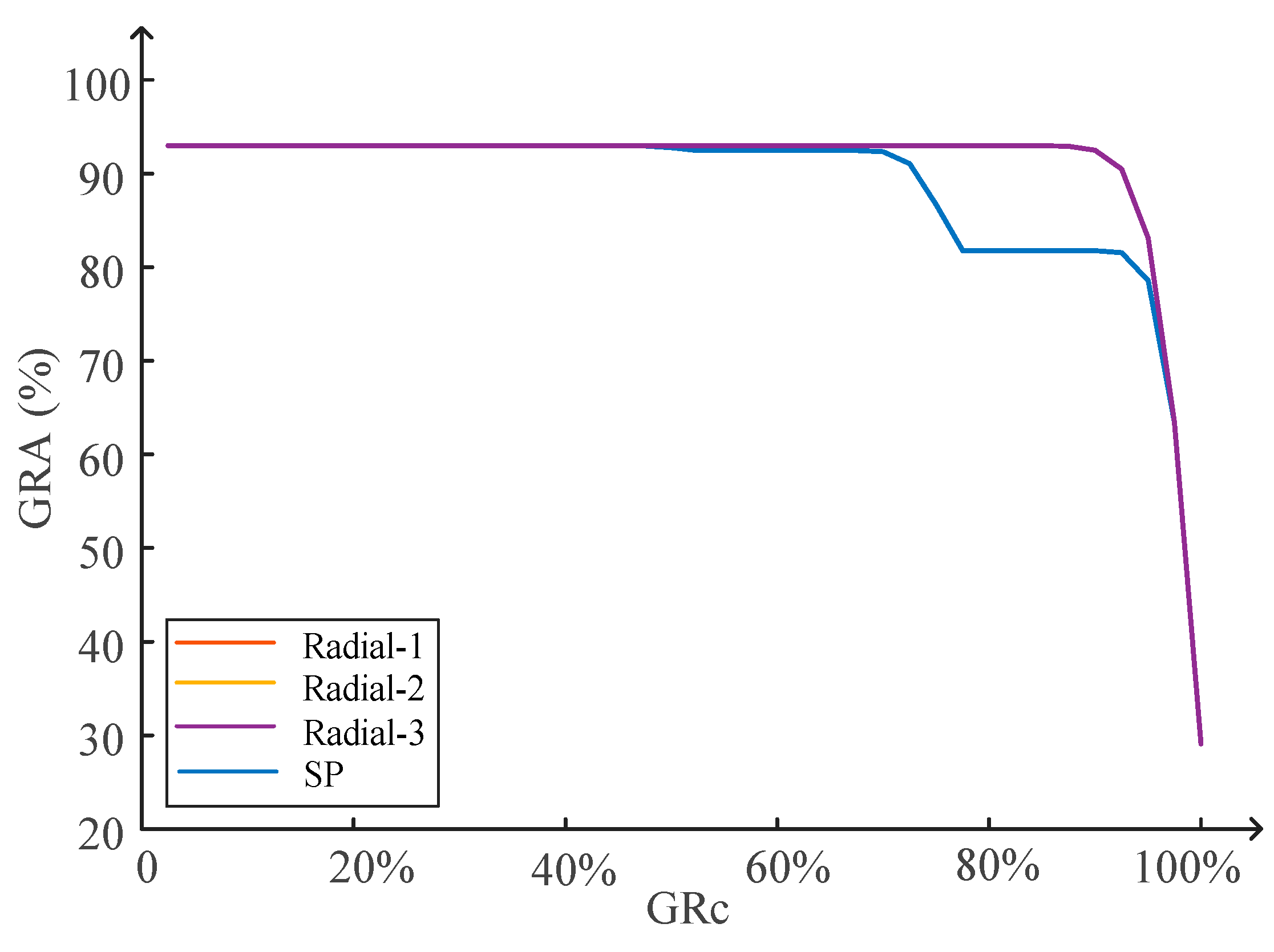
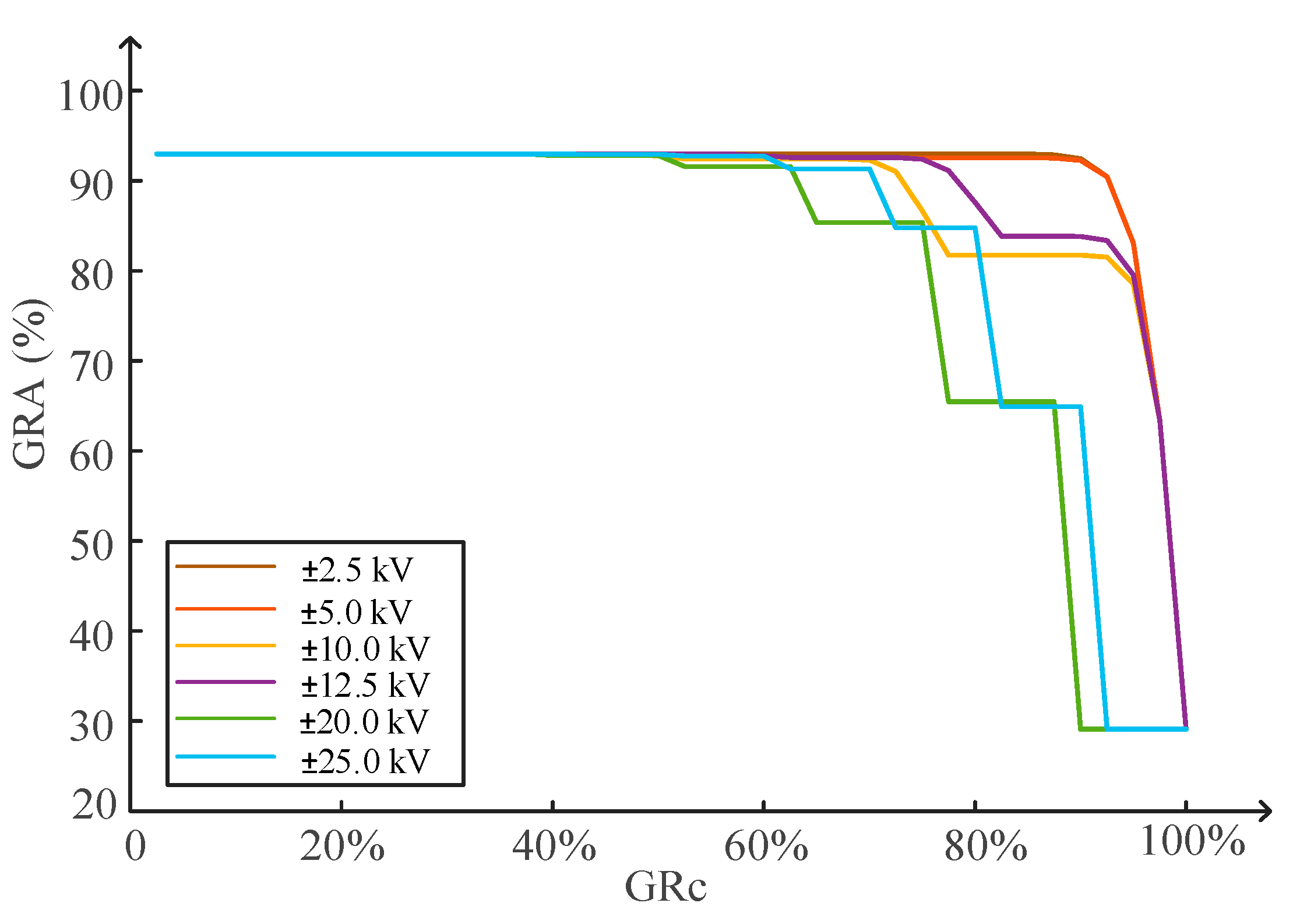
4.5. Impact of the DC Voltage Level for the Reliability of Series–Parallel Topology
4.6. Discussion of the Results
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
References
- UK Becomes First Major Economy to Pass Net-Zero Emissions Law. Available online: https://www.gov.uk/government/news/uk-becomes-first-major-economy-to-pass-net-zero-emissions-law (accessed on 10 February 2021).
- European Union. Going Climate-Neutral by 2050: A Strategic Long-Term Vision for a Prosperous, Modern, Competitive and Climate-Neutral EU Economy; Technical Report; European Union: Brussels, Belgium, 2019. [Google Scholar]
- Mallapaty, S. How China could be carbon neutral by mid-century. Nature 2020, 586, 482–483. [Google Scholar] [CrossRef] [PubMed]
- Ritchie, H.; Roser, M. How Much of Our Primary Energy Comes from Renewables? Available online: https://ourworldindata.org/renewable-energy (accessed on 15 February 2021).
- Wang, Q.; Yu, Z.; Ye, R.; Lin, Z.; Tang, Y. An Ordered Curtailment Strategy for Offshore Wind Power under Extreme Weather Conditions Considering the Resilience of the Grid. IEEE Access 2019, 7, 54824–54833. [Google Scholar] [CrossRef]
- Global Wind Energy Council. GWEC Global Wind Report 2019; Technical Report; Global Wind Energy Council: Brussels, Belgium, 2019. [Google Scholar]
- Global Wind Energy Council. Global Offshore Wind Report 2020; Technical Report; Global Wind Energy Council: Brussels, Belgium, 2020. [Google Scholar]
- News Release from Vestas Wind Systems A/S. Vestas Launches the V236-15.0 MW to Set New Industry Benchmark and Take Next Step towards Leadership in Offshore Wind. Available online: https://www.vestas.com/en/media/company-news?n=3886820 (accessed on 16 February 2021).
- Skopljak, N. 14 MW GE Haliade-X for Third Phase of World’s Largest Offshore Wind Farm. December 2020. Available online: https://www.offshorewind.biz/2020/12/18/14-mw-ge-haliade-x-for-third-phase-of-worlds-largest-offshore-wind-farm (accessed on 20 February 2021).
- Li, X.; Abeynayake, G.; Yao, L.; Liang, J. Recent Development and Prospect of Offshore Wind Power in Europe. J. Glob. Energy Interconnect. 2019, 2, 116–126. [Google Scholar]
- Pérez-Rúa, J.-A.; Cutululis, N.A. Electrical Cable Optimization in Offshore Wind Farms—A Review. IEEE Access 2019, 7, 85796–85811. [Google Scholar] [CrossRef]
- Amaral, L.; Castro, R. Offshore wind farm layout optimization regarding wake effects and electrical losses. Eng. Appl. Artif. Intell. 2017, 60, 26–34. [Google Scholar] [CrossRef]
- Banzo, M.; Ramos, A. Stochastic optimization model for electric power system planning of offshore wind farms. IEEE Trans. Power Syst. 2011, 26, 1338–1348. [Google Scholar] [CrossRef]
- Cerveira, A.; de Sousa, A.; Pires, E.J.S.; Baptista, J. Optimal cable design of wind farms: The infrastructure and losses cost minimization case. IEEE Trans. Power Syst. 2016, 31, 4319–4329. [Google Scholar] [CrossRef]
- Fischetti, M.; Pisinger, D. Optimizing wind farm cable routing considering power losses. Eur. J. Oper. Res. 2018, 270, 917–930. [Google Scholar] [CrossRef]
- Pérez-Rúa, J.A.; Lumbreras, S.; Ramos, A.; Cutululis, N.A. Closed-loop two-stage stochastic optimization of offshore wind farm collection system. J. Phys. Conf. Ser. 2020, 1618, 042031. [Google Scholar] [CrossRef]
- De Prada Gil, M.; Domínguez-García, J.L.; Díaz-González, F.; Aragüés-Peñalba, M.; Gomis-Bellmunt, O. Feasibility analysis of offshore wind power plants with dc collection grid. Renew. Energy 2015, 78, 467–477. [Google Scholar] [CrossRef]
- Lakshmanan, P.; Liang, J.; Jenkins, N. Assessment of collection systems for HVDC connected offshore wind farms. Electr. Power Syst. Res. 2015, 129, 75–82. [Google Scholar] [CrossRef]
- Abeynayake, G.; Li, G.; Liang, J.; Cutululis, N.A. A Review on MVdc Collection Systems for High-Power Offshore Wind Farms. In Proceedings of the 2019 14th Conference on Industrial and Information Systems (ICIIS), Kandy, Sri Lanka, 18–20 December 2019; pp. 407–412. [Google Scholar]
- Musasa, K.; Nwulu, N.I.; Gitau, M.N.; Bansal, R.C. Review on DC collection grids for offshore wind farms with high-voltage DC transmission system. Iet Power Electron. 2017, 10, 2104–2115. [Google Scholar] [CrossRef]
- Wei, S.; Feng, Y.; Liu, K.; Fu, Y. Optimization of Power Collector System for Large-scale Offshore Wind Farm Based on Topological Redundancy Assessment. E3S Web Conf. 2020, 194, 03025. [Google Scholar]
- Dahmani, O.; Bourguet, S.; Machmoum, M.; Guerin, P.; Rhein, P.; Josse, L. Optimization and Reliability Evaluation of an Offshore Wind Farm Architecture. IEEE Trans. Sustain. Energy 2017, 8, 542–550. [Google Scholar] [CrossRef]
- Shin, J.; Kim, J. Optimal Design for Offshore Wind Farm considering Inner Grid Layout and Offshore Substation Location. IEEE Trans. Power Syst. 2017, 32, 2041–2048. [Google Scholar] [CrossRef]
- Holtsmark, N.; Bahirat, H.J.; Molinas, M.; Mork, B.A.; Hoidalen, H.K. An All-DC Offshore Wind Farm with Series-Connected Turbines: An Alternative to the Classical Parallel AC Model? IEEE Trans. Ind. Electron. 2013, 60, 2420–2428. [Google Scholar] [CrossRef]
- Bahirat, H.J.; Kjølle, G.H.; Mork, B.A.; Høidalen, H.K. Reliability assessment of DC wind farms. In Proceedings of the 2012 IEEE Power and Energy Society General Meeting, San Diego, CA, USA, 22–26 July 2012; pp. 1–7. [Google Scholar]
- Abeynayake, G.; Li, G.; Joseph, T.; Ming, W.; Liang, J.; Moon, A.; Smith, K.; Yu, J. Reliability Evaluation of Voltage Source Converters for MVDC Applications. In Proceedings of the 2019 IEEE Innovative Smart Grid Technologies—Asia (ISGT Asia), Chengdu, China, 21–24 May 2019; pp. 2566–2570. [Google Scholar]
- Lisnianski, A.; Frenkel, I.; Ding, Y. Multi-State System Reliability Analysis and Optimization for Engineers and Industrial Managers; Springer: London, UK, 2010. [Google Scholar]
- Chuangpishit, S.; Tabesh, A.; Moradi-Shahrbabak, Z.; Saeedifard, M. Topology Design for Collector Systems of Offshore Wind Farms with Pure DC Power Systems. IEEE Trans. Ind. Electron. 2014, 61, 320–328. [Google Scholar] [CrossRef]
- Liu, H.; Dahidah, M.S.A.; Yu, J.; Naayagi, R.T.; Armstrong, M. Design and Control of Unidirectional DC-DC Modular Multilevel Converter for Offshore DC Collection Point: Theoretical Analysis and Experimental Validation. IEEE Trans. Power Electron. 2019, 34, 5191–5208. [Google Scholar] [CrossRef]
- Engel, S.P.; Stieneker, M.; Soltau, N.; Rabiee, S.; Stagge, H.; De Doncker, R.W. Comparison of the Modular Multilevel DC Converter and the Dual-Active Bridge Converter for Power Conversion in HVDC and MVDC Grids. IEEE Trans. Power Electron. 2015, 30, 124–137. [Google Scholar] [CrossRef]
- Meyer, C. Key Components for Future Offshore Dc Grids. Ph.D. Thesis, Institution of Power Generation and Storage Systems, RWTH Aachen University, Aachen, Germany, 2007. [Google Scholar]
- Lakshmanan, P.; Guo, J.; Liang, J. Energy curtailment of DC series-parallel connected offshore wind farms. IET Renew. Power Gener. 2018, 12, 576–584. [Google Scholar] [CrossRef]
- Dahmani, O.; Bourguet, S.; Machmoum, M.; Guerin, P.; Rhein, P. Reliability analysis of the collection system of an offshore wind farm. In Proceedings of the 2014 Ninth International Conference on Ecological Vehicles and Renewable Energies (EVER), Monte-Carlo, Monaco, 25–27 March 2014; pp. 1–6. [Google Scholar]
- Huang, L.; Fu, Y.; Mi, Y.; Cao, J.; Wang, P. A Markov-Chain-Based Availability Model of Offshore Wind Turbine Considering Accessibility Problems. IEEE Trans. Sustain. Energy 2017, 8, 1592–1600. [Google Scholar] [CrossRef]
- Ramezanzadeh, S.P.; Mirzaie, M.; Shahabi, M. Reliability assessment of different HVDC transmission system configurations considering transmission lines capacity restrictions and the effect of load level. Int. J. Electr. Power Energy Syst. 2021, 128, 106754. [Google Scholar] [CrossRef]
- MacIver, C.; Bell, K.R.W.; Nedić, D.P. A Reliability Evaluation of Offshore HVDC Grid Configuration Options. IEEE Trans. Power Deliv. 2016, 31, 810–819. [Google Scholar] [CrossRef]
- Chao, H.; Hu, B.; Xie, K.; Tai, H.; Yan, J.; Li, Y. A Sequential MCMC Model for Reliability Evaluation of Offshore Wind Farms Considering Severe Weather Conditions. IEEE Access 2019, 7, 132552–132562. [Google Scholar] [CrossRef]
- Leite, J.B.; Mantovani, J.R.S.; Dokic, T.; Yan, Q.; Chen, P.; Kezunovic, M. Resiliency Assessment in Distribution Networks Using GIS-Based Predictive Risk Analytics. IEEE Trans. Power Syst. 2019, 34, 4249–4257. [Google Scholar] [CrossRef]
- Abeynayake, G.; Van Acker, T.; Van Hertem, D.; Liang, J. Analytical Model for Availability Assessment of Large-Scale Offshore Wind Farms including their Collector System. IEEE Trans. Sustain. Energy 2021. [Google Scholar] [CrossRef]
- Sulaeman, S.; Benidris, M.; Mitra, J.; Singh, C. A wind farm reliability model considering both wind variability and turbine forced outages. IEEE Trans. Sustain. Energy 2017, 8, 629–637. [Google Scholar] [CrossRef]
- Zhao, M.; Chen, Z.; Blaabjerg, F. Generation Ratio Availability Assessment of Electrical Systems for Offshore Wind Farms. IEEE Trans. Energy Convers. 2007, 22, 755–763. [Google Scholar] [CrossRef]
- Wind Farm Costs, CATAPULT Offshore Renewable Energy, UK. Available online: https://guidetoanoffshorewindfarm.com/wind-farm-costs (accessed on 20 February 2021).
- Parker, M.A.; Anaya-Lara, O. Cost and losses associated with offshore wind farm collection networks which centralise the turbine power electronic converters. IET Renew. Power Gener. 2013, 7, 390–400. [Google Scholar] [CrossRef]
- Stamatiou, G. Techno-Economical Analysis of DC Collection Grid for Offshore Wind Parks. Master’s Thesis, University of Nottingham, Nottingham, UK, 2010. [Google Scholar]
- Lundberg, S. Performance Comparison of Wind Park Configurations; Technical Report; Department of Electric Power Engineering, Chalmers University of Technology: Göteborg, Sweden, 2003. [Google Scholar]
- Bahirat, H.J.; Mork, B.A.; Høidalen, H.K. Comparison of wind farm topologies for offshore applications. In Proceedings of the 2012 IEEE Power and Energy Society General Meeting, San Diego, CA, USA, 22–26 July 2012; pp. 1–8. [Google Scholar]
- de Prada, M.; Igualada, L.; Corchero, C.; Gomis-Bellmunt, O.; Sumper, A. Hybrid AC-DC Offshore Wind Power Plant Topology: Optimal Design. IEEE Trans. Power Syst. 2015, 30, 1868–1876. [Google Scholar] [CrossRef]
- Baring-Gould, I. Offshore Wind Plant Electrical Systems. In Proceedings of the BOEM Offshore Renewable Energy Workshop, Sacramento, CA, USA, 29–30 July 2014. [Google Scholar]
- Abeynayake, G.; Li, G.; Joseph, T.; Liang, J.; Ming, W. Reliability and Cost-oriented Analysis, Comparison and Selection of Multi-level MVdc Converters. IEEE Trans. Power Deliv. 2021. [Google Scholar] [CrossRef]
- Ørsted Offshore Operational Data Sharing: Anholt and Westermost Rough LiDAR Data Documentation. Available online: https://orsted.com/en/our-business/offshore-wind/wind-data (accessed on 5 March 2021).
- MHI Vestas Offshore V164-9.5 MW. Available online: https://en.wind-turbine-models.com/turbines/1605-mhi-vestas-offshore-v164-9.5-mw (accessed on 10 March 2021).
- MHI Vestas Offshore V164-8.0 MW. Available online: https://en.wind-turbine-models.com/turbines/1419-mhi-vestas-offshore-v164-8.0-mw (accessed on 12 March 2021).
- Saeki, M.; Tobinaga, I.; Sugino, J.; Shiraishiet, T. Development of 5-MW offshore wind turbine and 2-MW floating offshore wind turbine technology. Hitachi Rev. 2014, 63, 414. [Google Scholar]
- Bala, S.; Pan, J.; Das, D.; Apeldoorn, O.; Ebner, S. Lowering failure rates and improving serviceability in offshore wind conversion-collection systems. In Proceedings of the 2012 IEEE Power Electronics and Machines in Wind Applications, Denver, CO, USA, 16–18 July 2012; pp. 1–7. [Google Scholar]
- Rock, D. Guidance on the Offshore Transmission Owner Licence for Tender Round 5 (TR5); Ofgem: London, UK, 2017; pp. 1–39. [Google Scholar]
- International Renewable Energy Agency (IRENA). Renewable Power Generations Costs in 2018. Available online: https://www.irena.org/Publications (accessed on 15 March 2021).
| WT Capacity (MW) | Cost per WT (£) |
|---|---|
| 10 | 1,366,674 |
| 8 | 1,149,339 |
| 5 | 823,337 |
| Voltage Levels (kV) | A (×106) | B |
|---|---|---|
| ±10.0 | −0.32 | 0.0850 |
| ±12.5 | −0.32 | 0.0850 |
| ±20.0 | −0.314 | 0.0618 |
| ±25.0 | −0.314 | 0.0618 |
| ±40.0 | 0 | 0.0280 |
| ±100.0 | 0.079 | 0.0120 |
| Capacity (MW) | Model | Rated Wind Speed (m/s) | Cut-In Speed (m/s) | Cut-Out Speed (m/s) | Rotor Diameter (m) |
|---|---|---|---|---|---|
| 10 (S1) | V164-9.5 [51] | 14 | 3.5 | 25 | 164 |
| 8 (S2) | V164-8.0 [52] | 13 | 4.0 | 25 | 164 |
| 5 (S3) | HTW5.0-126 [53] | 13 | 4.0 | 25 | 126 |
| Cluster Number | Cluster Center (MW) | State Probability |
|---|---|---|
| 1 | 0.000 | 0.0700773 |
| 2 | 0.474 | 0.0422715 |
| 3 | 1.572 | 0.0756075 |
| 4 | 2.796 | 0.0811175 |
| 5 | 3.967 | 0.0929224 |
| 6 | 5.113 | 0.0934911 |
| 7 | 6.267 | 0.0968191 |
| 8 | 7.390 | 0.0924218 |
| 9 | 8.506 | 0.0869786 |
| 10 | 9.540 | 0.0664654 |
| 11 | 10.000 | 0.2018278 |
| WT Component | Failure Rate (occ/yr) | Repair Time (h) |
|---|---|---|
| Generator | 0.1000 | 240 |
| Transformer | 0.0131 | |
| AC breaker | 0.0250 | |
| DC breaker | 0.0250 | |
| Full power converter | 0.2000 | |
| AC/DC converter | 0.1000 | |
| DC/DC converter | 0.6132 |
| Rated Power (MW) | Converter Type and Scenario | Input and Output Voltage Levels (kV) | Percentage Losses |
|---|---|---|---|
| 40 | R-3 (Cf1); S2 | ±10/±20 | 1.79% |
| 40 | R-2 (Cf1); S2 | ±10/±40 | 1.88% |
| 50 | R-3 (Cf1); S3 | ±10/±12.5 | 1.53% |
| 50 | R-3 (Cf1); S1 | ±10/±25 | 1.68% |
| 50 | R-2 (Cf1); S2 | ±10/±40 | 1.65% |
| 400 | R-2 (C1); S1, S2, S3 | ±40/±100 | 1.31% |
| 400 | R-1 (C1); S1, S2, S3 | ±10/±100 | 1.44% |
| WT Capacity | Terminal Voltage (kV) | WTs per Feeder | EENS (MWhr/yr) |
|---|---|---|---|
| 10 MW | ±2.5 | 40 | 1.4980 × 106 |
| ±5.0 | 20 | 1.5015 × 106 | |
| ±10.0 | 10 | 1.5496 × 106 | |
| ±12.5 | 8 | 1.5292 × 106 | |
| ±20.0 | 5 | 1.7179 × 106 | |
| ±25.0 | 4 | 1.6653 × 106 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, R.; Abeynayake, G.; Liang, J.; Wang, K. Reliability and Economic Evaluation of Offshore Wind Power DC Collection Systems. Energies 2021, 14, 2922. https://doi.org/10.3390/en14102922
Sun R, Abeynayake G, Liang J, Wang K. Reliability and Economic Evaluation of Offshore Wind Power DC Collection Systems. Energies. 2021; 14(10):2922. https://doi.org/10.3390/en14102922
Chicago/Turabian StyleSun, Ruijuan, Gayan Abeynayake, Jun Liang, and Kewen Wang. 2021. "Reliability and Economic Evaluation of Offshore Wind Power DC Collection Systems" Energies 14, no. 10: 2922. https://doi.org/10.3390/en14102922
APA StyleSun, R., Abeynayake, G., Liang, J., & Wang, K. (2021). Reliability and Economic Evaluation of Offshore Wind Power DC Collection Systems. Energies, 14(10), 2922. https://doi.org/10.3390/en14102922







