Boundary Conditions for Transient and Robust Performance of a Reduced-Order Model-Based State Feedback Controller with PI Observer
Abstract
:1. Introduction
1.1. Literature Review
1.2. Proposed Analysis
- 1
- Introducing a trade-off that exists between transient state performance and disturbance rejection ability in an observer compensated ROMBC through a mathematical analysis and a simulation based validation.
- 2
- Presenting analysis that supports the break from the separation principle that exists for reduced-order model-based state feedback controller and observer.
- 3
- Presenting a stability boundary condition for the closed-loop system based on the ROMBC closed-loop pole and ROPIO gain.
- 4
- Proposing a relatively desirable performance region based on the values of closed-loop pole and observer gain for ROPIO compensated ROMBC.
2. Reduced-Order Model-Based State Feedback Control
3. Stability Conditions for an ROPIO Compensated ROMBC
3.1. Design of an ROPIO Compensated ROMBC
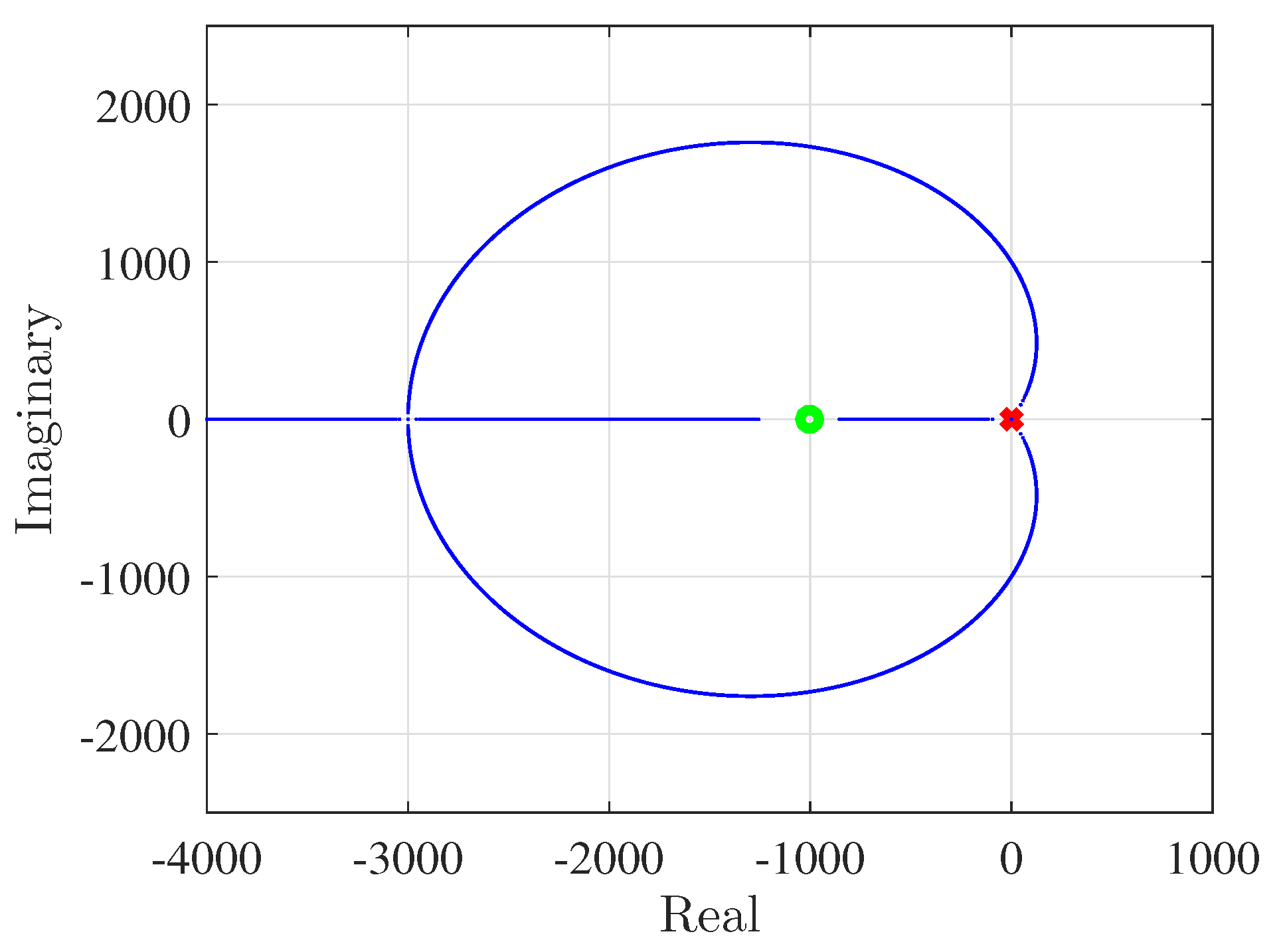
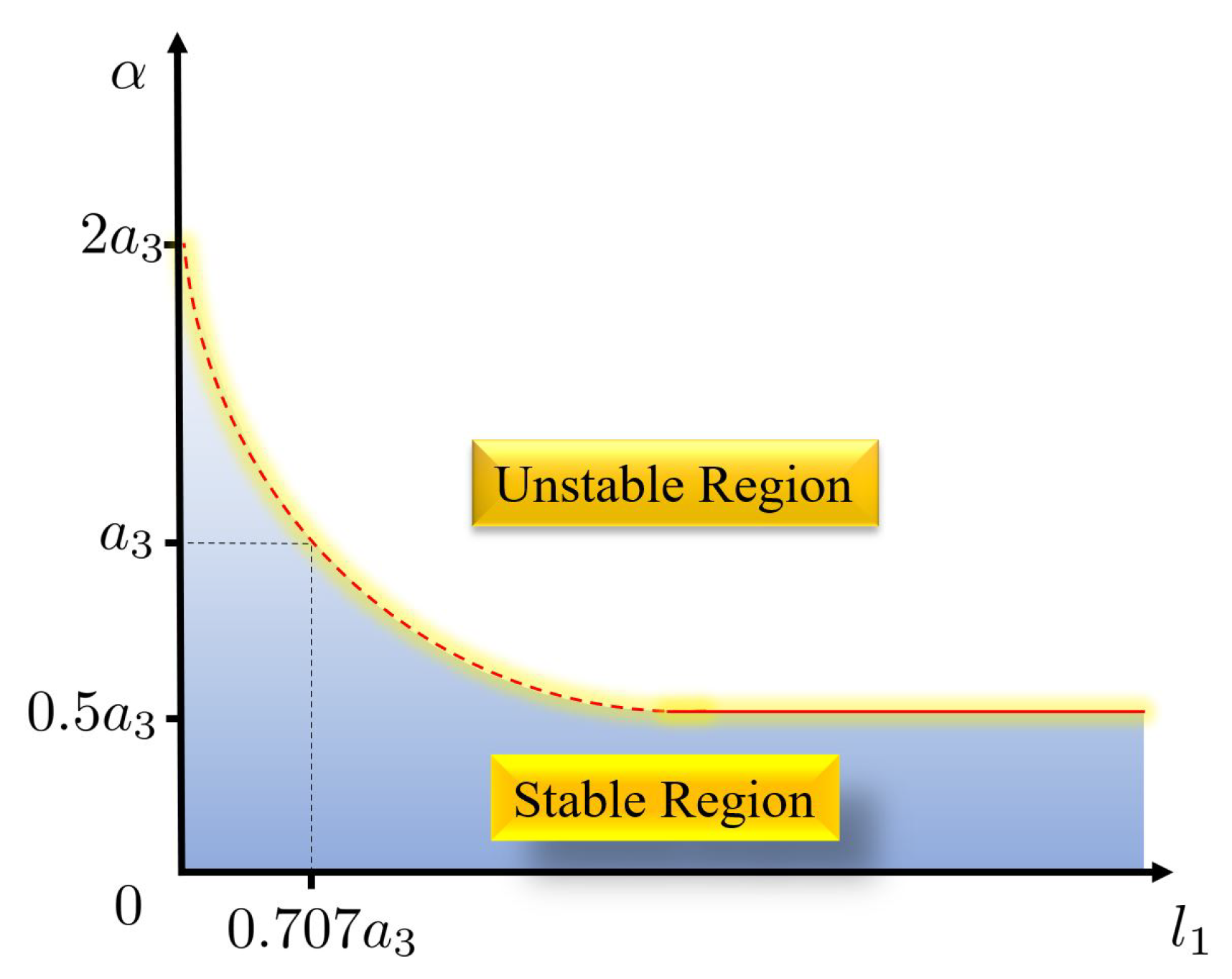
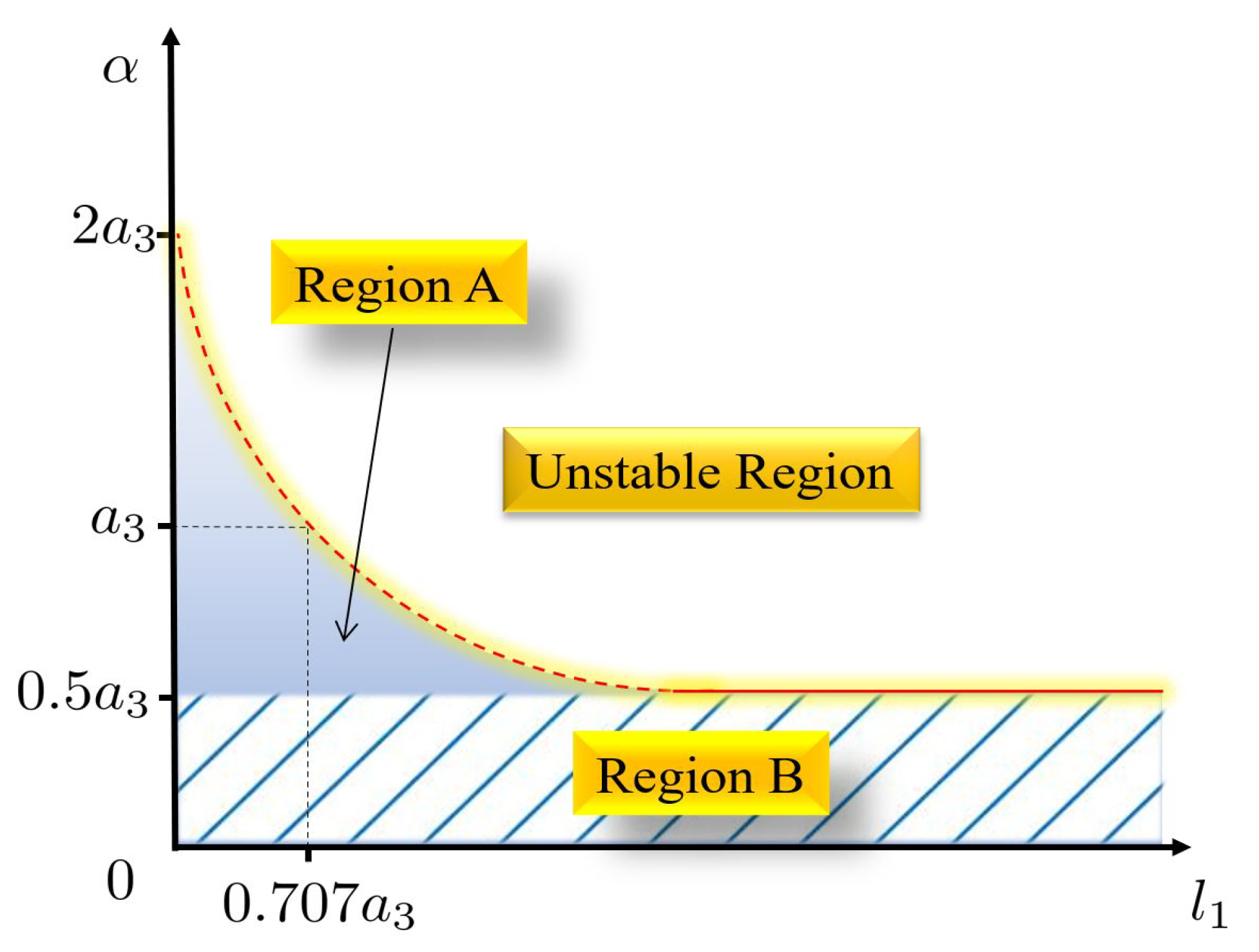
3.2. Stability Boundary for an ROPIO Compensated ROMBC
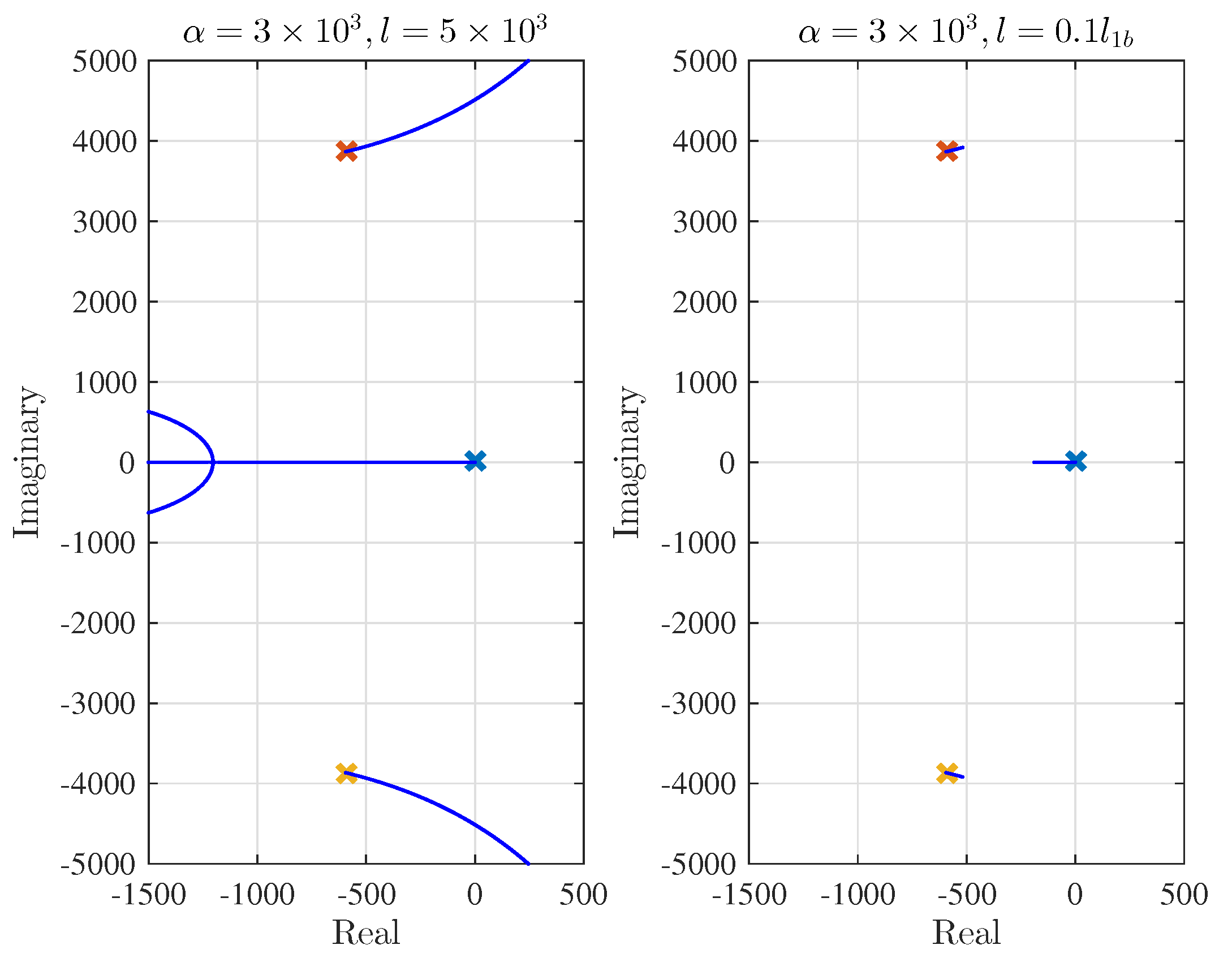
4. Further Analysis Using DC Motor Position Control System
4.1. Boundary Conditions for DC Motor Position Control
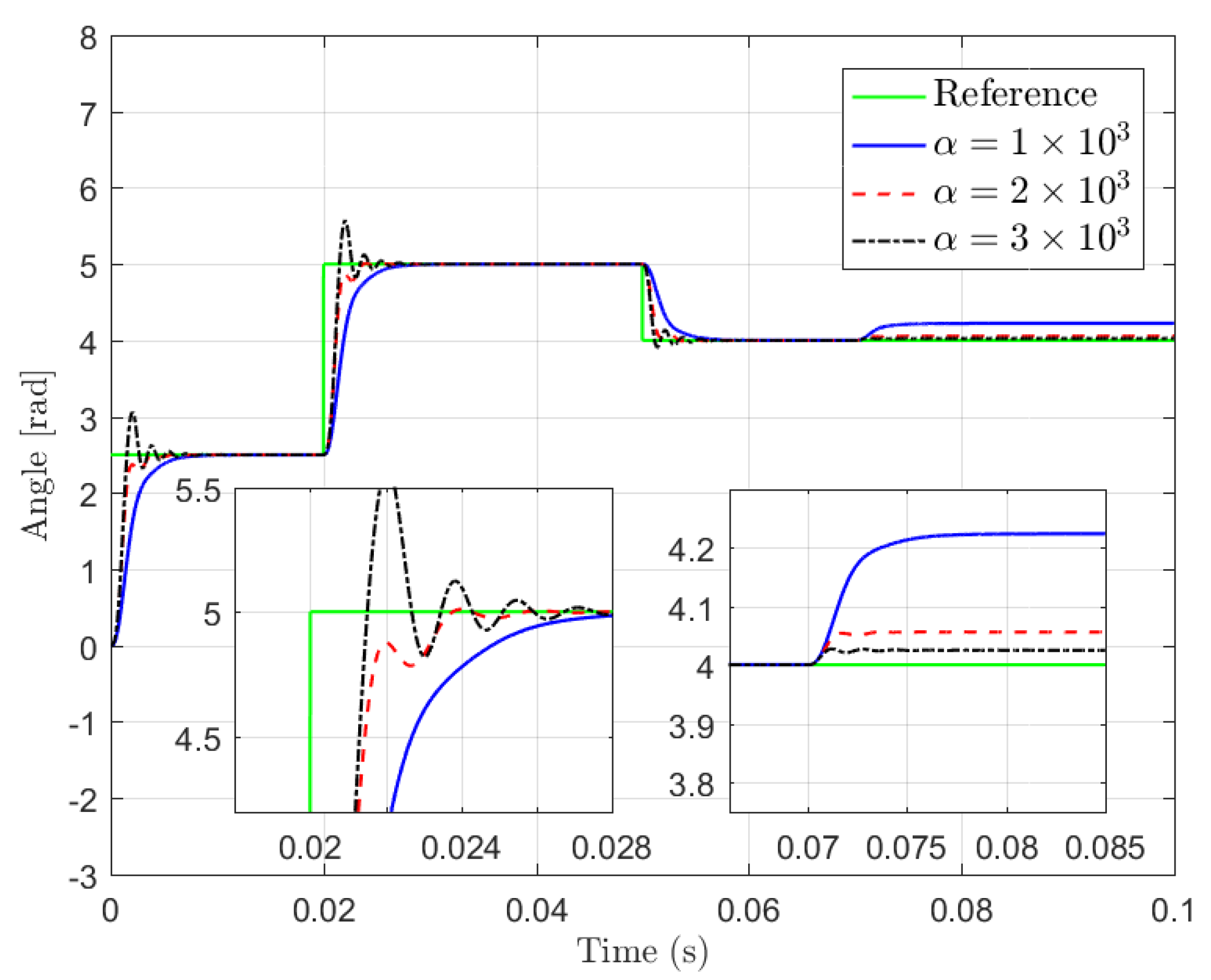
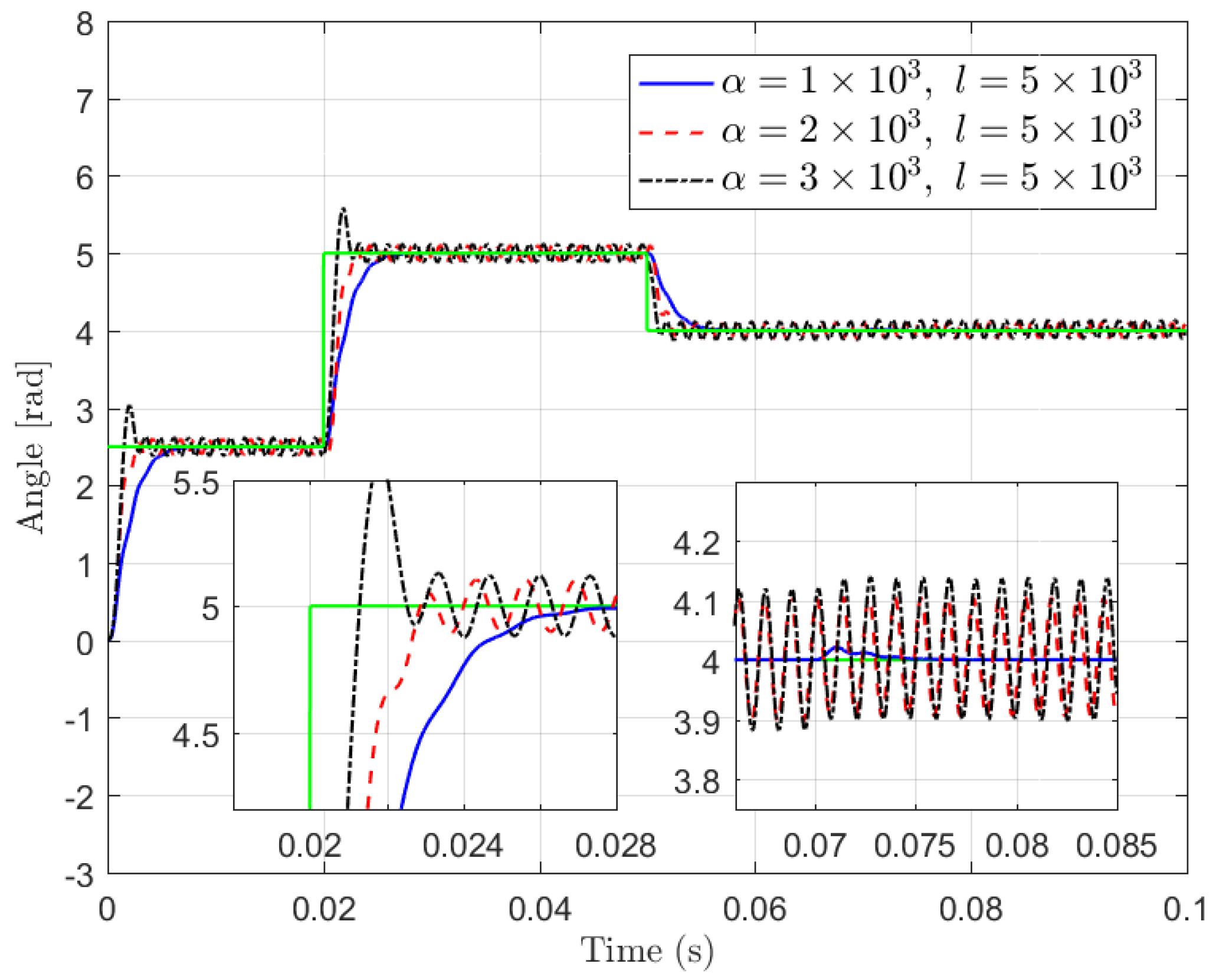
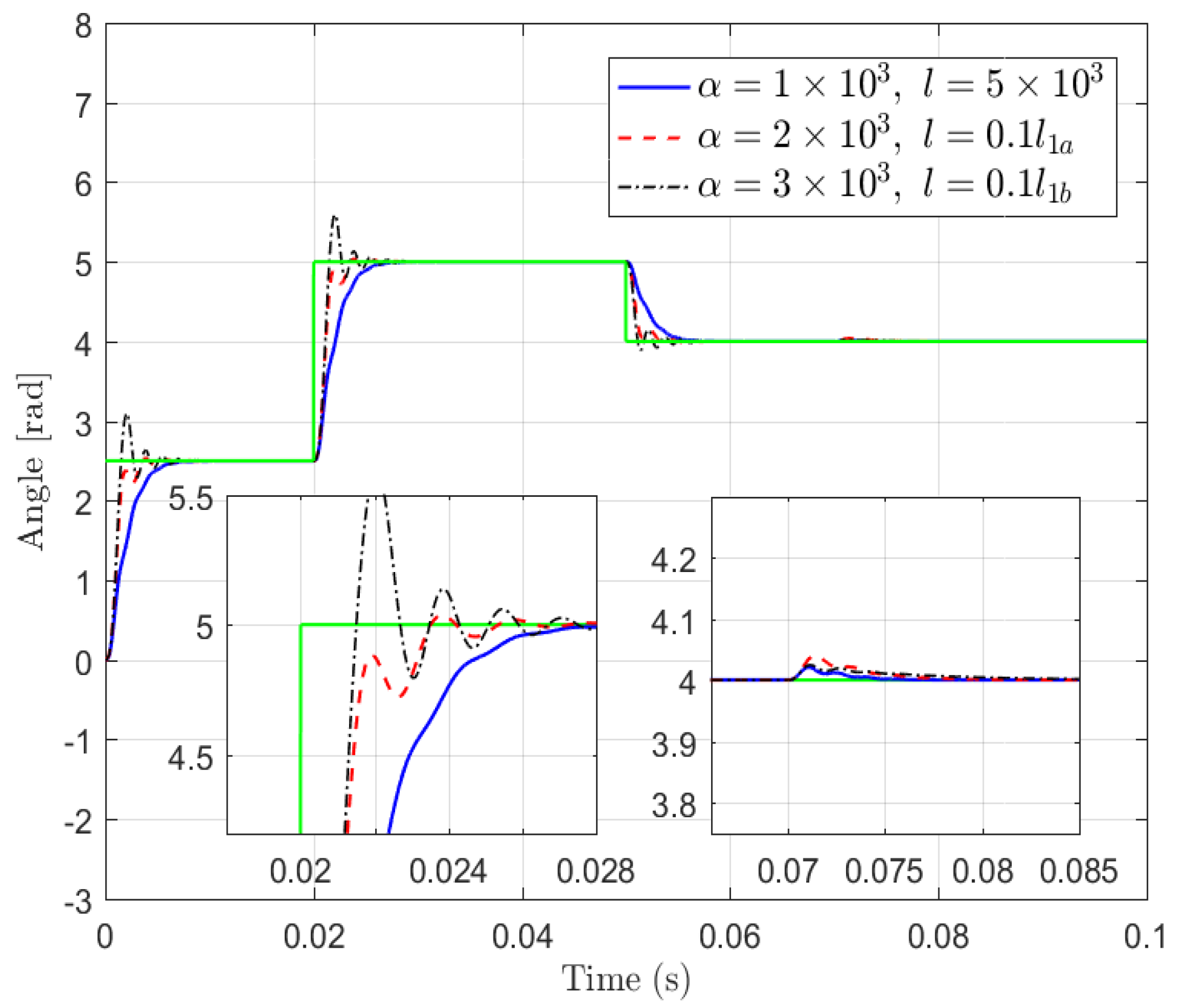
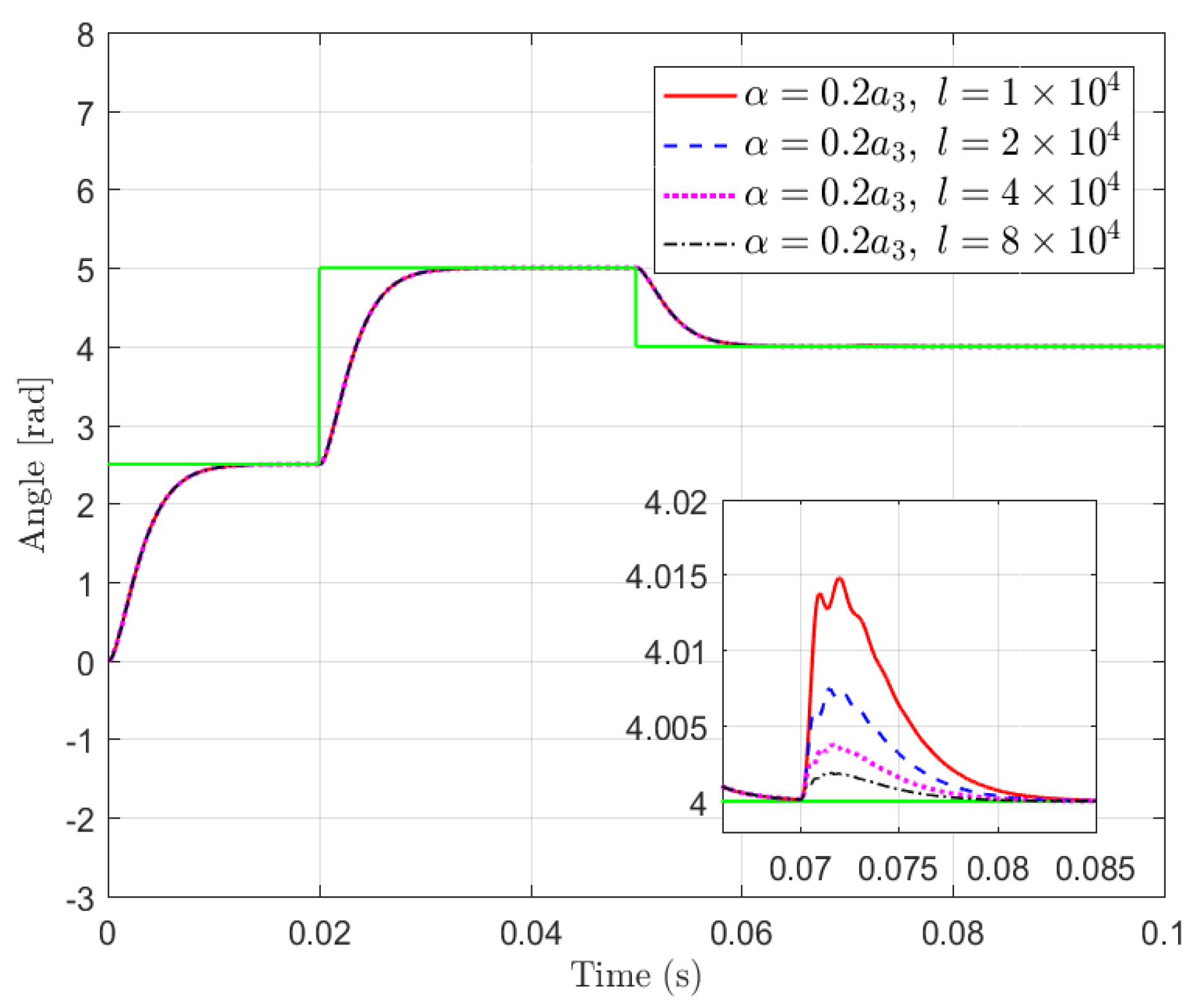
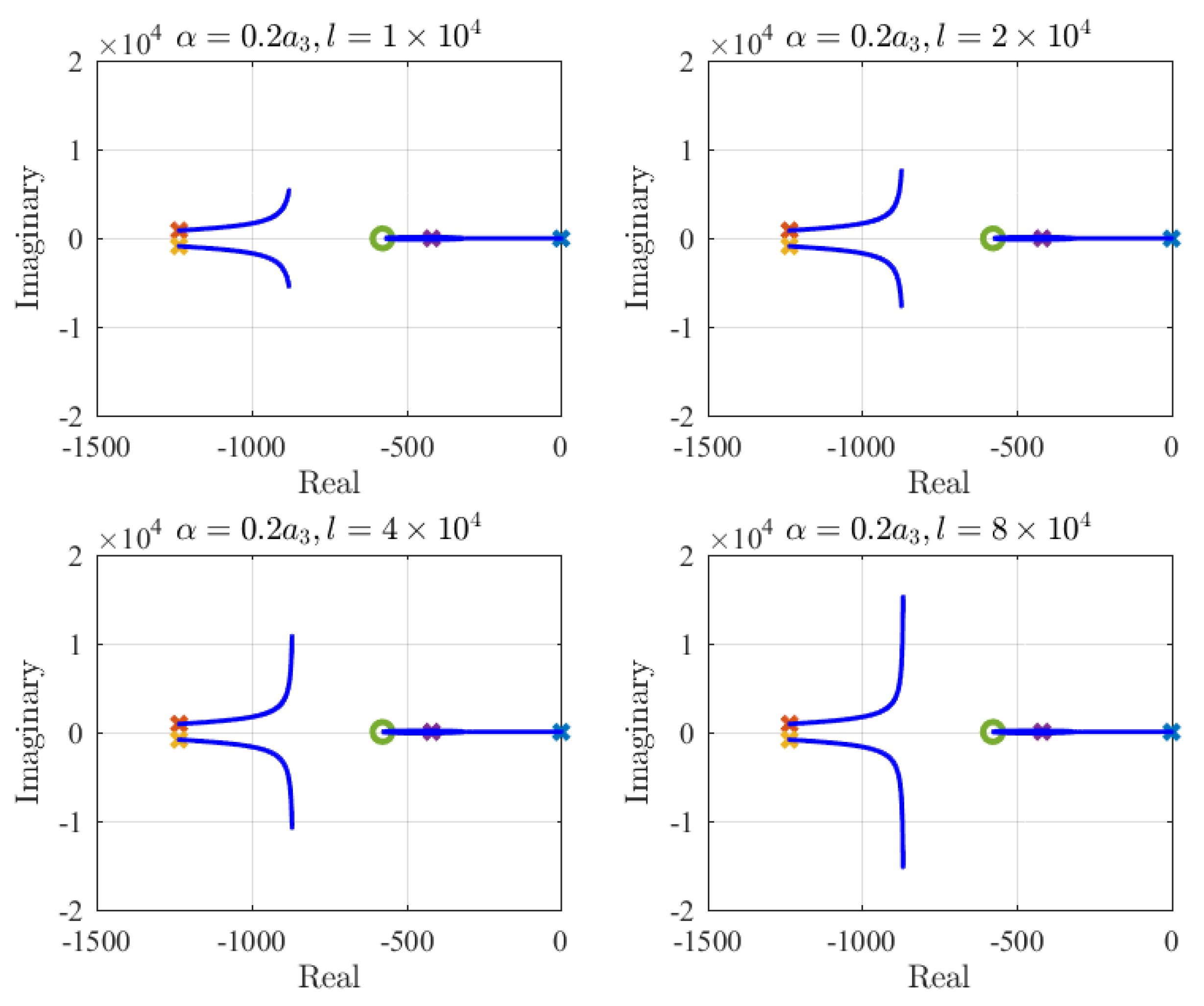
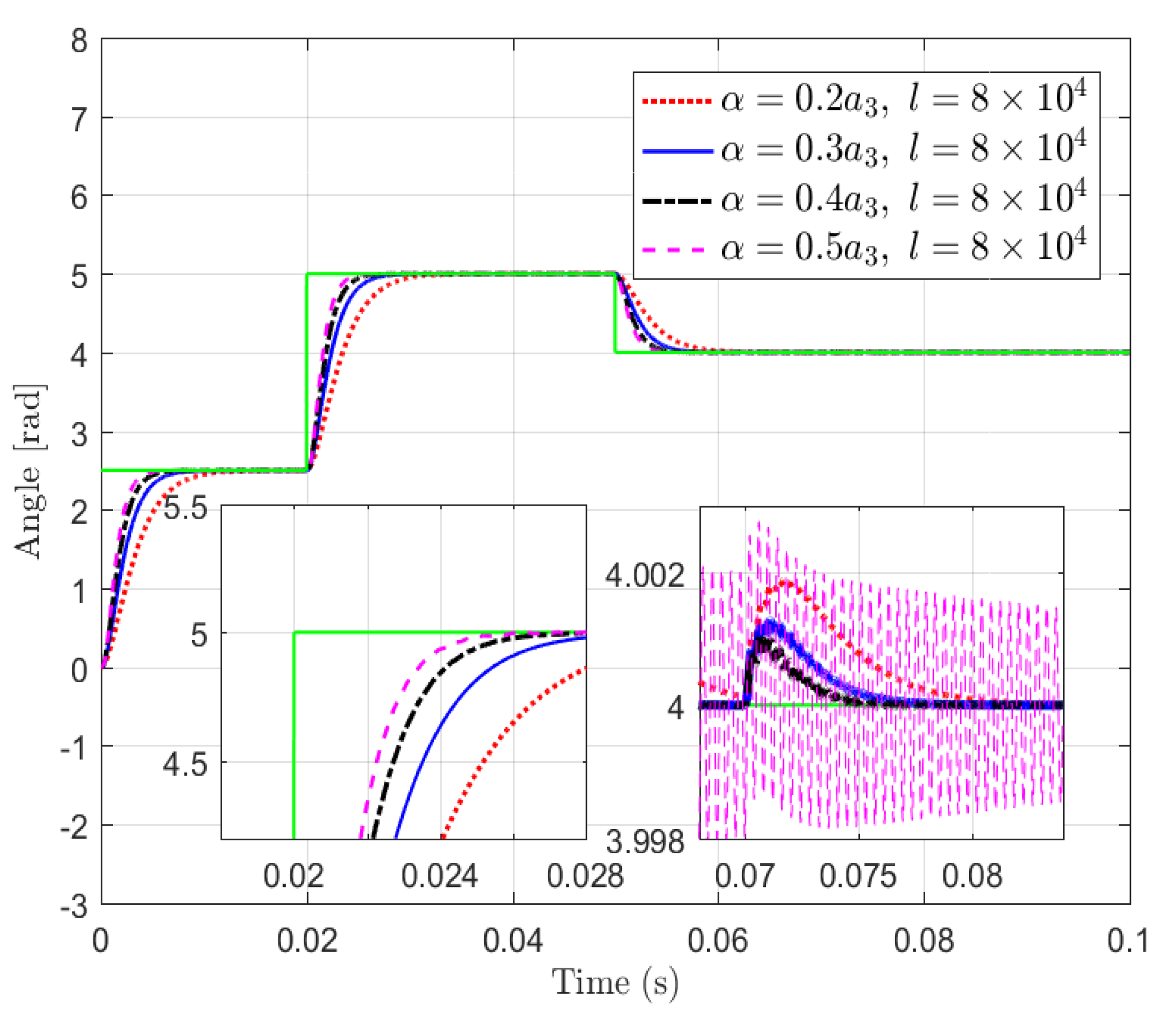
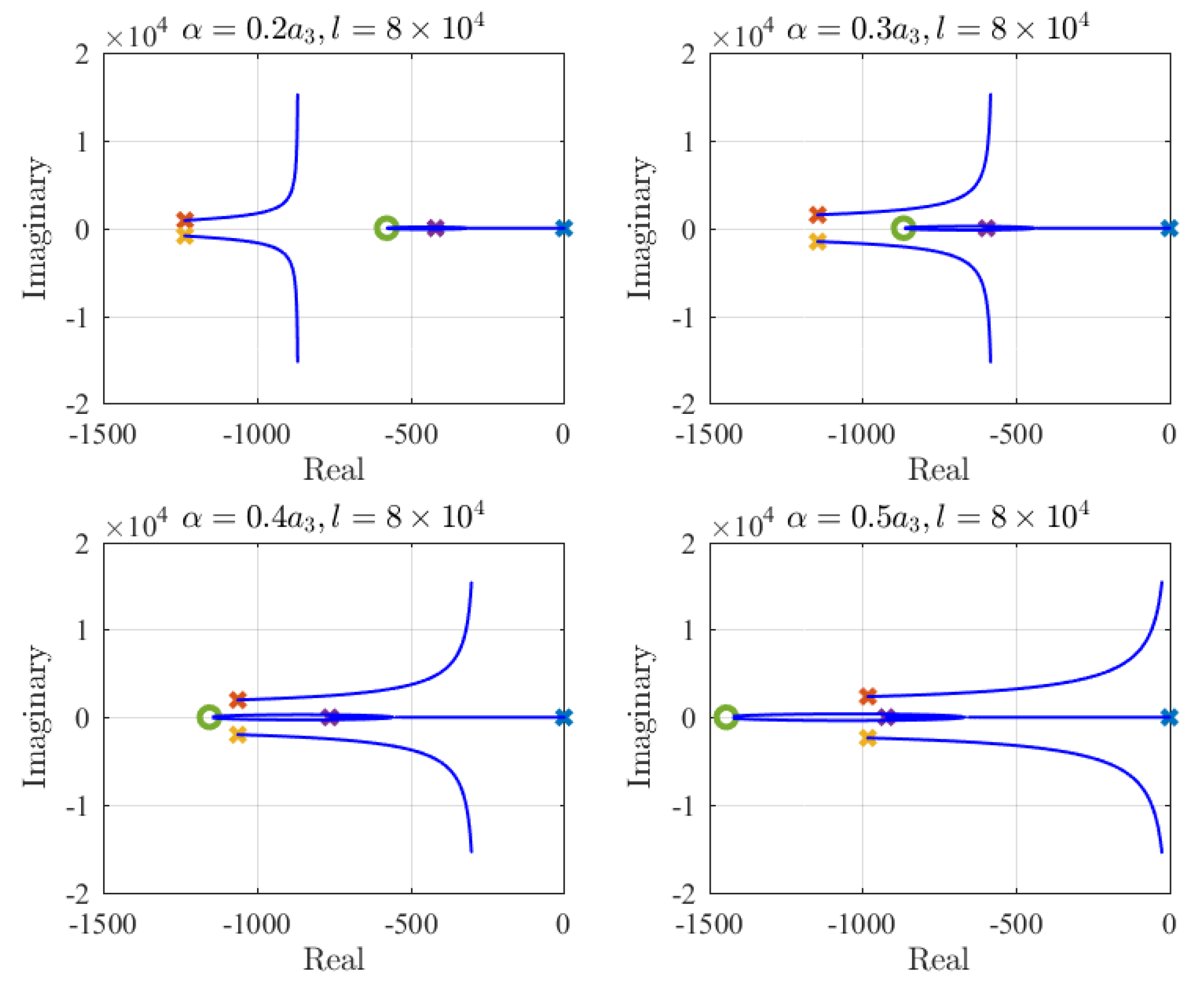
4.2. Simulation Studies for Improving Transient and Robust Performance
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
Abbreviations
| ROMBC | Reduced-Order Model-Based Controller |
| ROPIO | Reduced-Order Proportional-Integral Observer |
References
- Franklin, G.F.; Powell, J.D.; Emami-Naeini, A. Feedback Control of Dynamic Systems, 5th ed.; Prentice-Hall: Upper Saddle River, NJ, USA, 2005; pp. 20–454. [Google Scholar]
- Kokotović, P.; Khalil, H.K.; O’Reilly, J. Singular Perturbation Methods in Control: Analysis and Design; SIAM: Philadedlphia, PA, USA, 1999; pp. 1–43. [Google Scholar]
- Skogestad, S.; Postlethwaite, I. Multivariable Feedback Control: Analysis and Design; John Wiley & Sons, Inc.: New York, NY, USA, 2005; pp. 479–498. [Google Scholar]
- Khalil, H.K. Nonlinear Systems, 3rd ed.; Prentice-Hall: Upper Saddle River, NJ, USA, 2002; pp. 432–460. [Google Scholar]
- Li, C.; Du, Z.; Ni, Y.; Zhang, G. Reduced model-based coordinated design of decentralized power system controllers. IEEE Trans. Power Syst. 2016, 31, 2172–2181. [Google Scholar] [CrossRef]
- Yao, J.; Jiao, Z.; Ma, D. Adaptive robust control of DC motors with extended state observer. IEEE Trans. Ind. Electron. 2014, 61, 3630–3637. [Google Scholar] [CrossRef]
- Yook, J.H.; Kim, I.H.; Son, Y.I. Robustness improvement of DC motor speed control using communication disturbance observer under uncertain time delay. Electron. Lett. 2017, 53, 389–391. [Google Scholar] [CrossRef]
- Saha, S.; Amrr, S.M.; Nabi, M.U.; Iqbal, A.A. Reduced-order modeling and sliding mode control of active magnetic bearing. IEEE Access 2019, 7, 113324–113334. [Google Scholar] [CrossRef]
- Anandan, P.; Gagliano, S.; Bucolo, M. Computational models in microfluidic bubble logic. Microfluid. Nanofluid. 2015, 18, 305–321. [Google Scholar] [CrossRef]
- Li, S.; Yang, J.; Chen, W.H.; Chen, X. Disturbance Observer-Based Control: Methods and Applications; CRC Press: Boca Raton, FL, USA, 2014. [Google Scholar]
- Shim, H.; Jo, N.H. An almost necessary and sufficient condition for robust stability of closed-loop systems with disturbance observer. Automatica 2009, 45, 296–299. [Google Scholar] [CrossRef]
- Son, Y.I.; Kim, I.H.; Choi, D.S.; Shim, H. Robust cascade control of electric motor drives using dual reduced-order PI observer. IEEE Trans. Ind. Electron. 2015, 62, 3672–3682. [Google Scholar] [CrossRef]
- Chen, W.H.; Yang, J.; Guo, L.; Li, S. Disturbance-observer-based control and related methods-an overview. IEEE Trans. Ind. Electron. 2016, 63, 1083–1095. [Google Scholar] [CrossRef] [Green Version]
- Kim, I.H.; Son, Y.I. Regulation of a DC/DC boost converter under parametric uncertainty and input voltage variation using nested reduced-order PI observers. IEEE Trans. Ind. Electron. 2017, 64, 552–562. [Google Scholar] [CrossRef]
- Sariyildiz, E.; Oboe, R.; Ohnishi, K. Disturbance observer-based control and its application: 35th anniversary overview. IEEE Trans. Ind. Electron. 2020, 67, 2042–2053. [Google Scholar] [CrossRef] [Green Version]
- Kim, I.H.; Son, Y.I. Design of a low-order harmonic disturbance observer with applications to a DC motor position control. Energies 2020, 13, 1020. [Google Scholar] [CrossRef] [Green Version]
- Amare, N.D.; Son, Y.I.; Lim, S. Dual PIO-based controller design for robustness improvement of a magnetic levitation system. J. Electr. Eng. Technol. 2020, 15, 1389–1398. [Google Scholar] [CrossRef]
- Wu, M.; Gao, F.; Yu, P.; She, J.; Cao, W. Improve disturbance-rejection performance for an equivalent-input-disturbance-based control system by incorporating a proportional-integral observer. IEEE Trans. Ind. Electron. 2020, 67, 1254–1260. [Google Scholar] [CrossRef]
- Jo, N.H.; Joo, Y.J.; Shim, H. A study of disturbance observers with unknown relative degree of the plant. Automatica 2014, 50, 1730–1734. [Google Scholar] [CrossRef]

| Parameter | Value | Unit |
|---|---|---|
| 0.605 | [] | |
| 0.210 | [mH] | |
| 0.0234 | [Nm/A] | |
| 86.57 | [g-cm] | |
| 4.2167 × 10 | [mNm/(rad/s)] | |
| 0.0233 | [V/(rad/s)] |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Amare, N.D.; Kim, D.H.; Yang, S.J.; Son, Y.I. Boundary Conditions for Transient and Robust Performance of a Reduced-Order Model-Based State Feedback Controller with PI Observer. Energies 2021, 14, 2881. https://doi.org/10.3390/en14102881
Amare ND, Kim DH, Yang SJ, Son YI. Boundary Conditions for Transient and Robust Performance of a Reduced-Order Model-Based State Feedback Controller with PI Observer. Energies. 2021; 14(10):2881. https://doi.org/10.3390/en14102881
Chicago/Turabian StyleAmare, Nebiyeleul Daniel, Doe Hun Kim, Sun Jick Yang, and Young Ik Son. 2021. "Boundary Conditions for Transient and Robust Performance of a Reduced-Order Model-Based State Feedback Controller with PI Observer" Energies 14, no. 10: 2881. https://doi.org/10.3390/en14102881
APA StyleAmare, N. D., Kim, D. H., Yang, S. J., & Son, Y. I. (2021). Boundary Conditions for Transient and Robust Performance of a Reduced-Order Model-Based State Feedback Controller with PI Observer. Energies, 14(10), 2881. https://doi.org/10.3390/en14102881






