Distributed Energy-Resource Design Method to Improve Energy Security in Critical Facilities †
Abstract
1. Introduction
1.1. Literature Review
1.2. Novel Contribution and Paper Organization
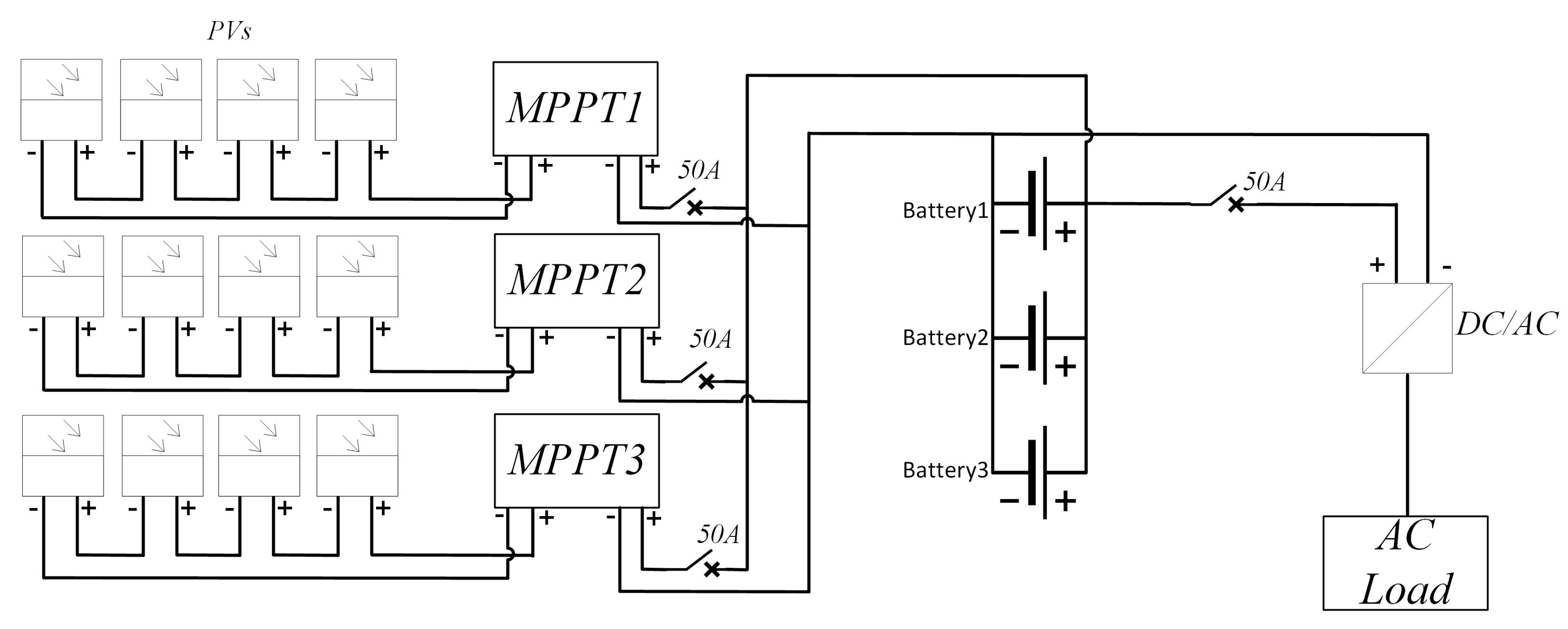
2. DER Design Methodology and Software Implementation
2.1. Design Methodology and Equations
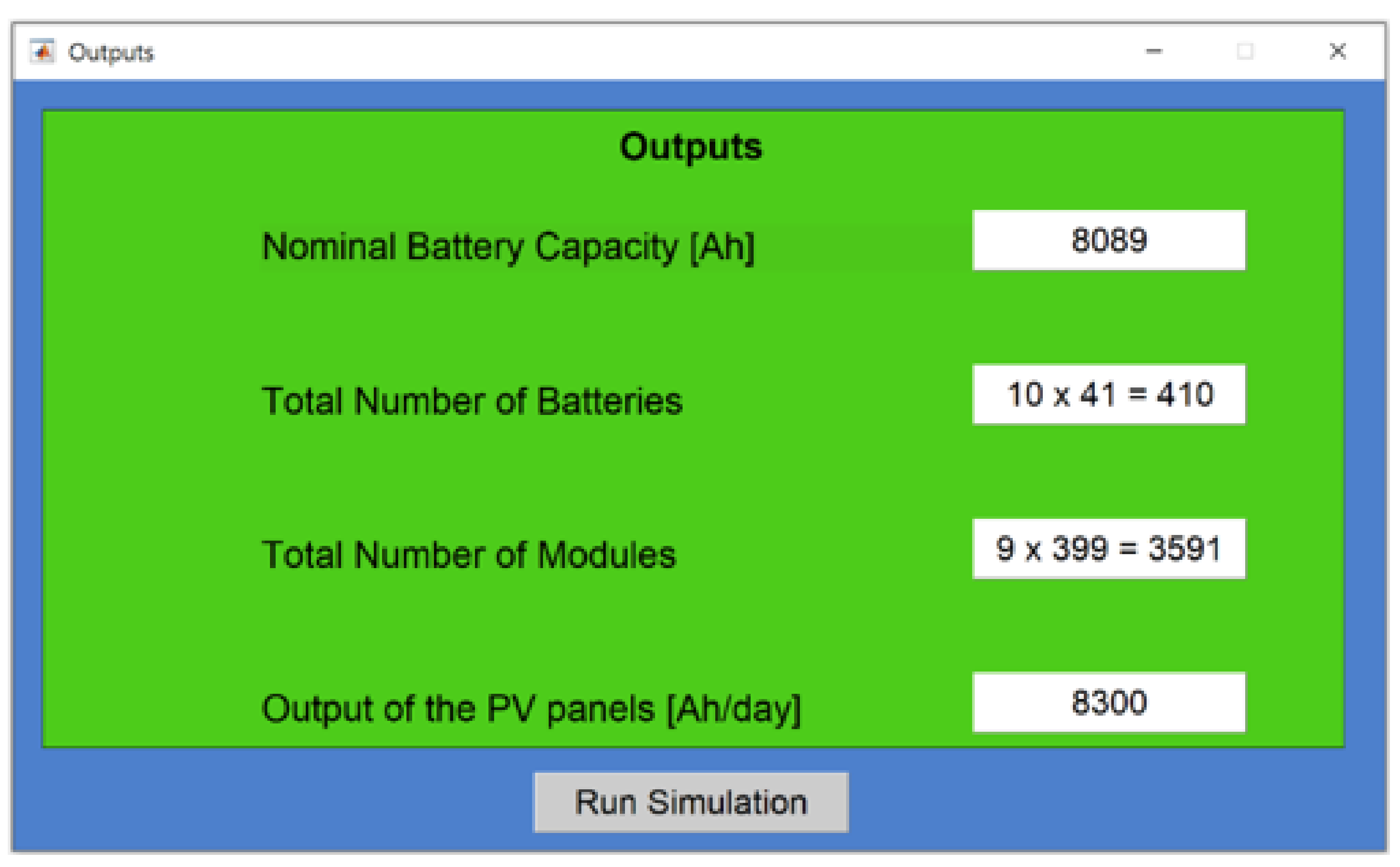
2.2. Design Software
3. Design Examples and Simulated Outputs
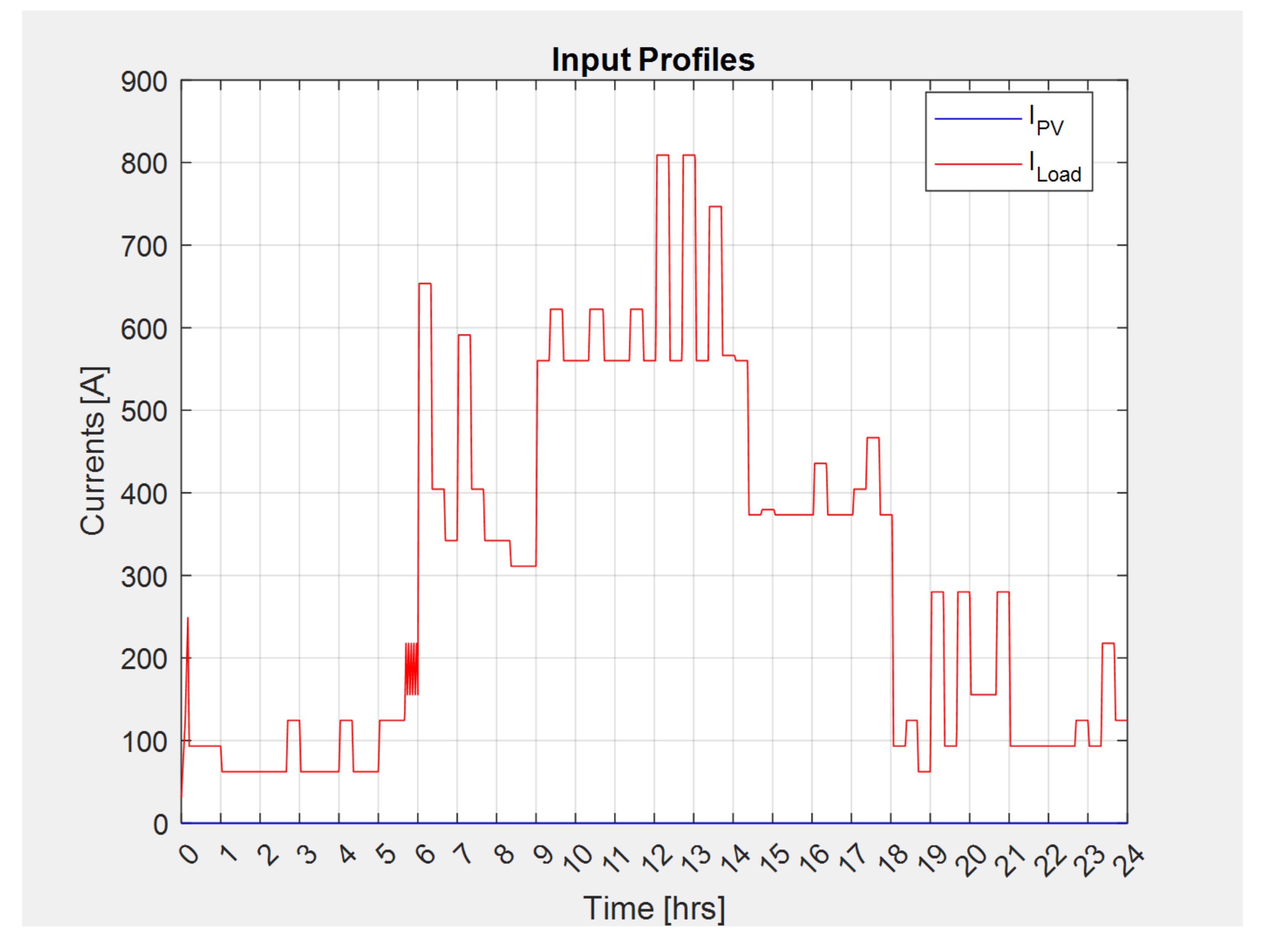
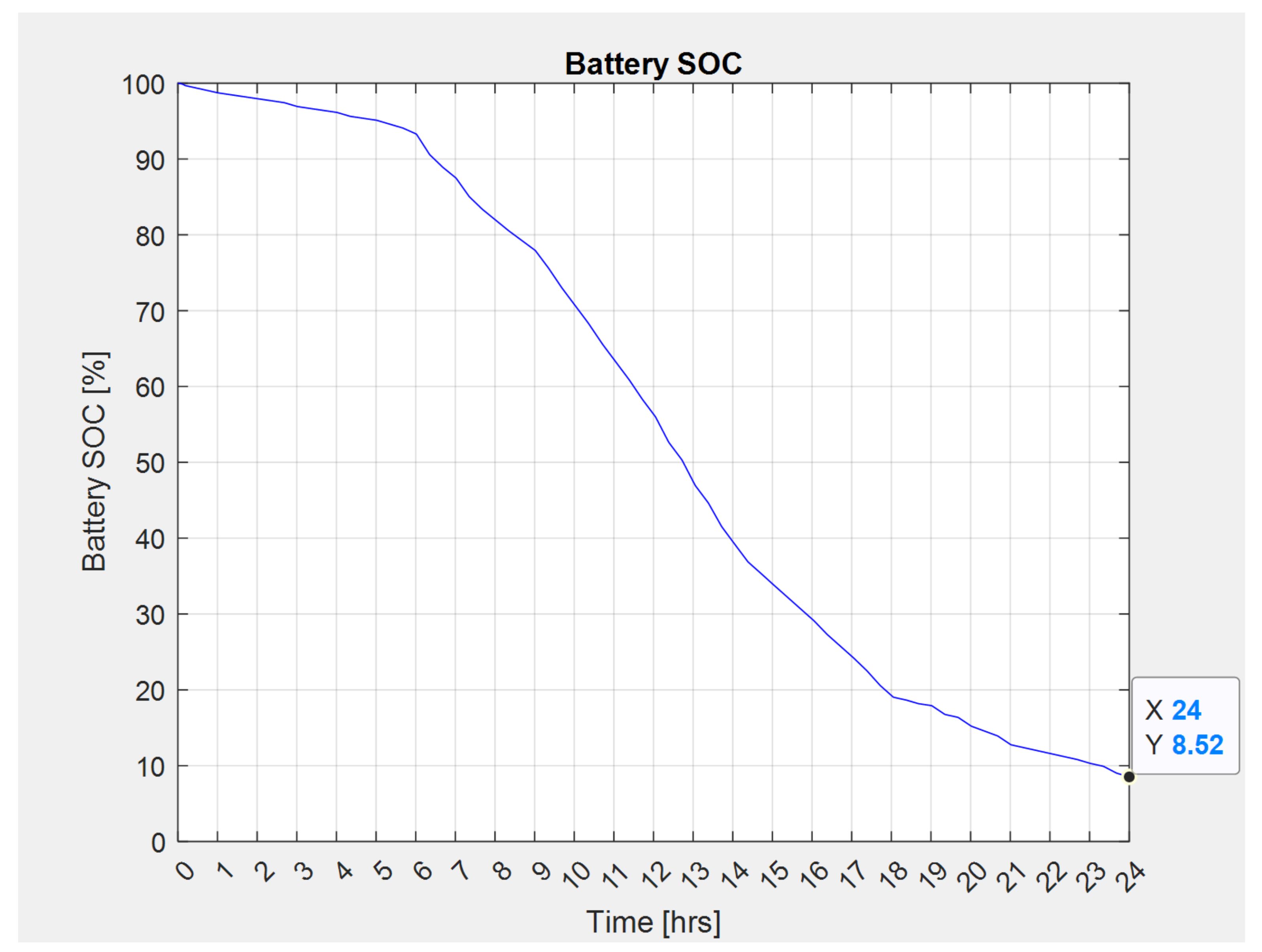
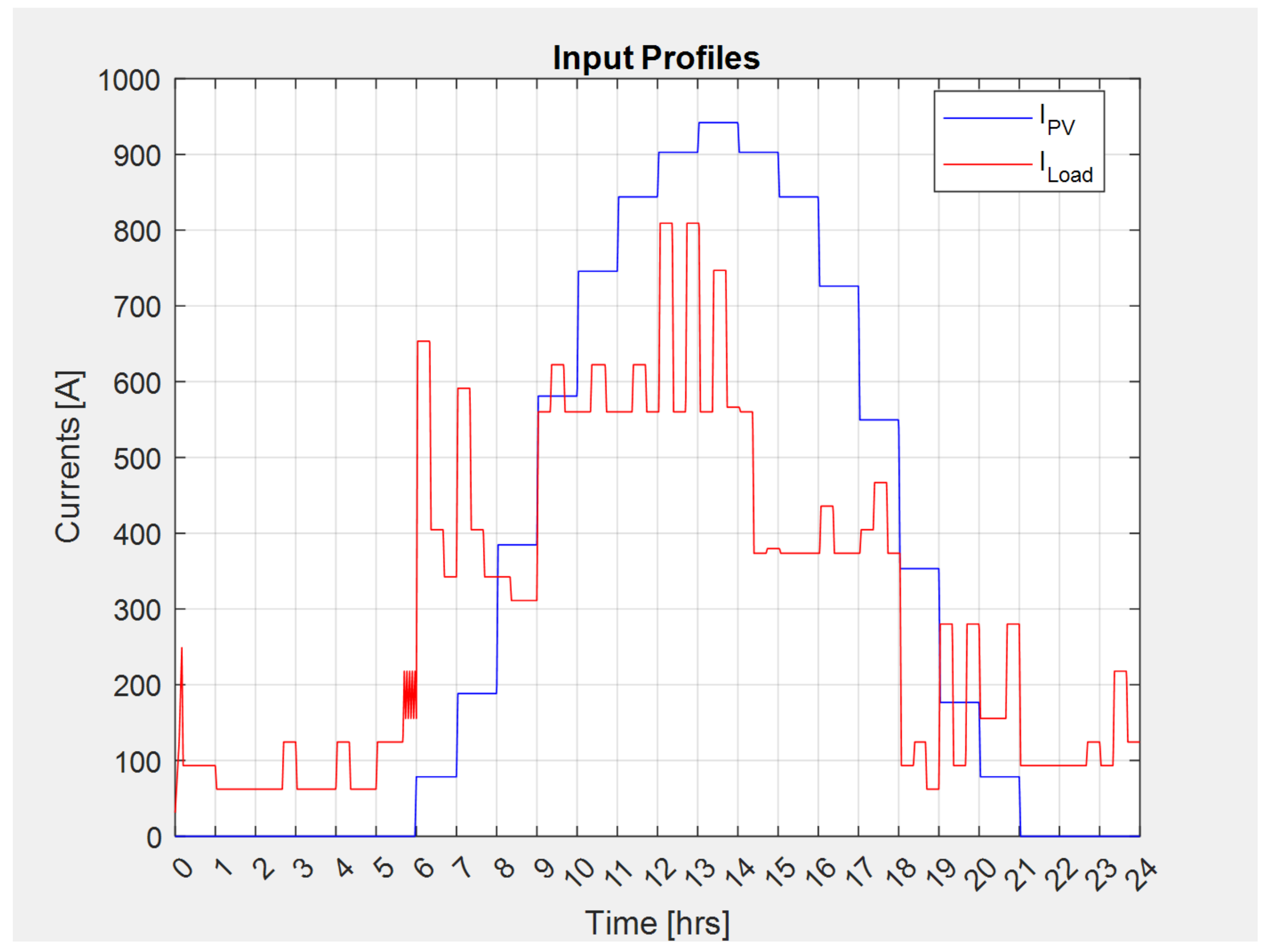
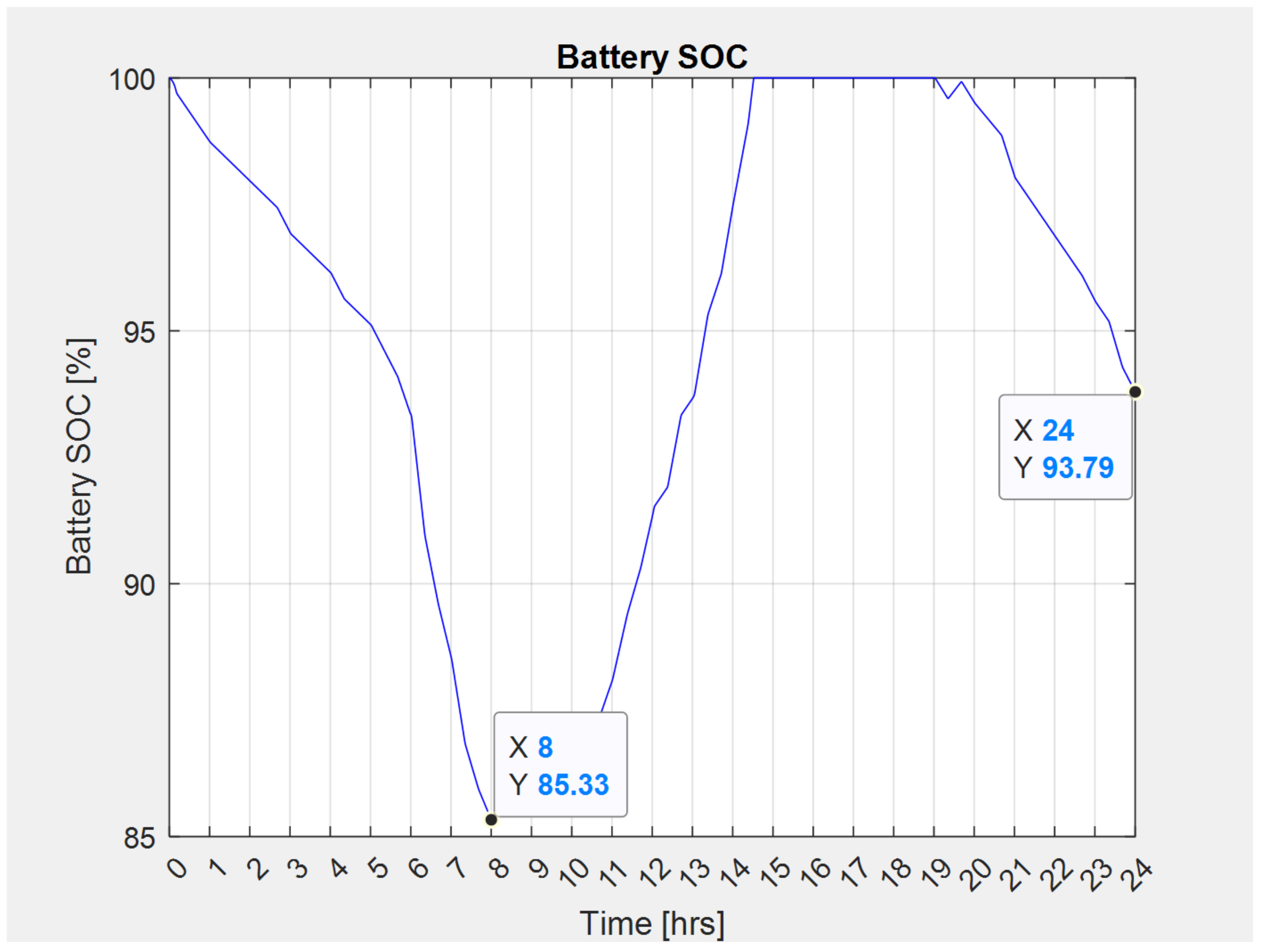
3.1. Design Example 1: 24 h Autonomy without Sunlight
3.2. Design Example 2: 24 h Autonomy with Sunlight
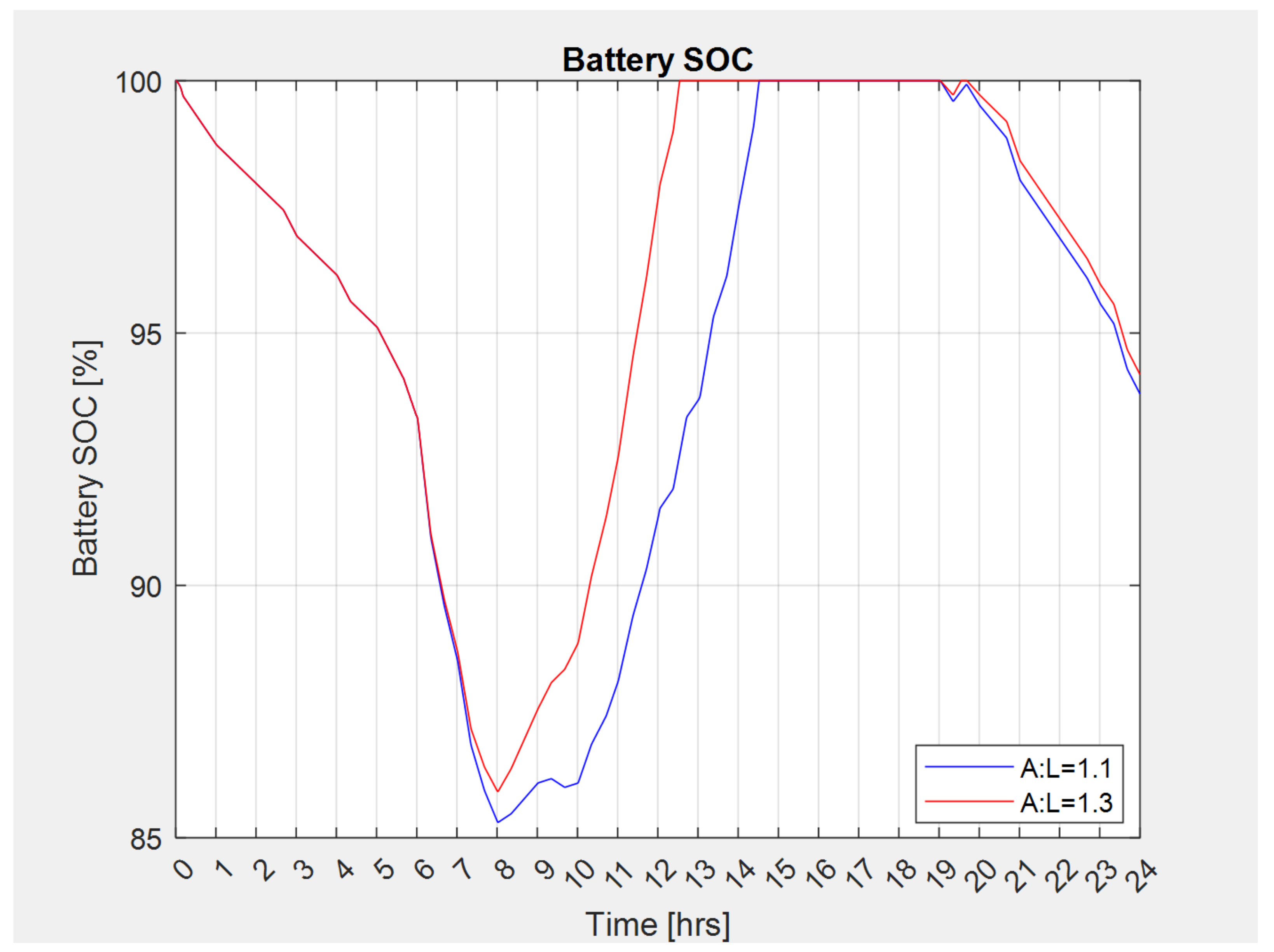
3.3. Design Example 3: Impact of A:L Parameter
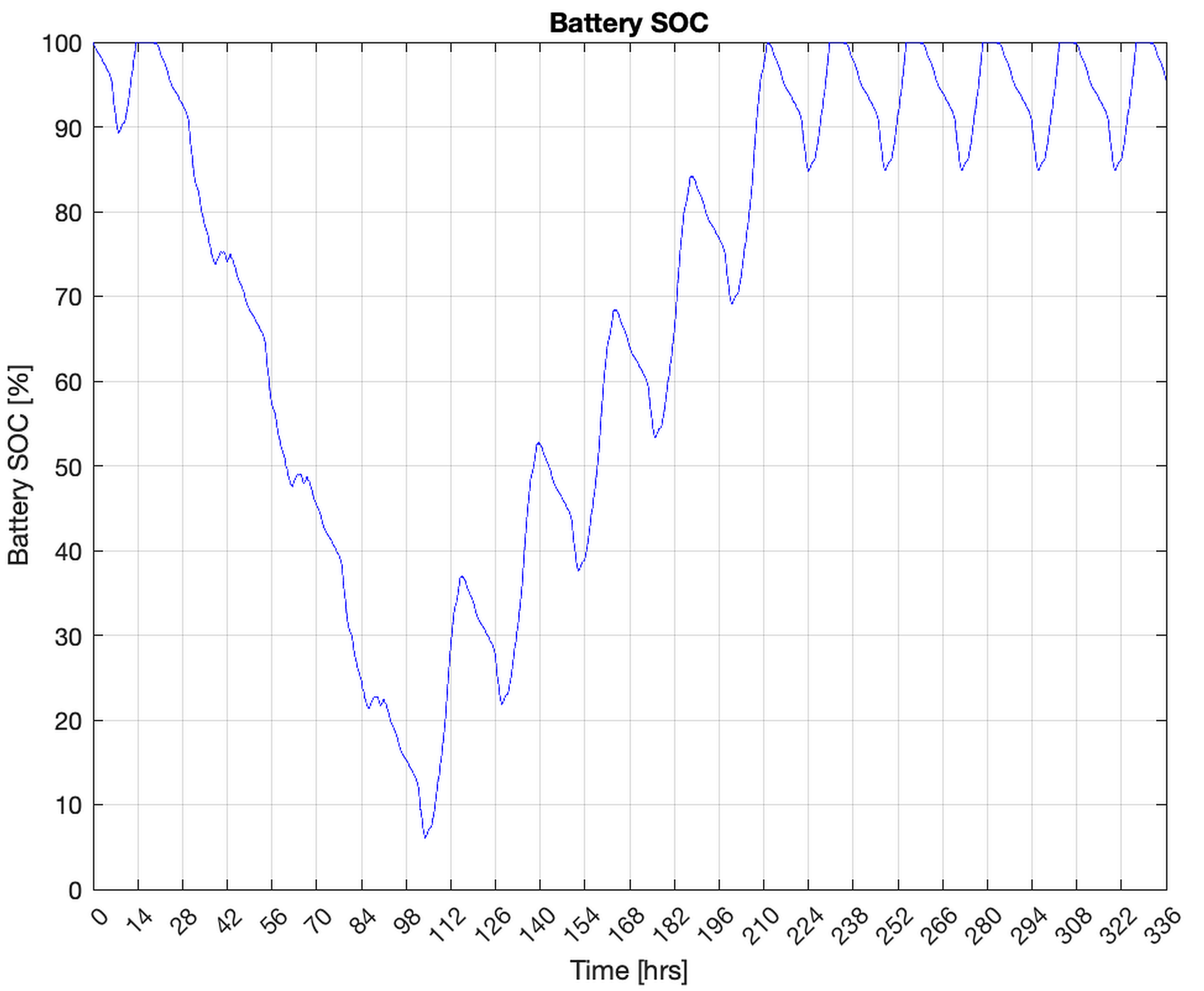
3.4. Design Example 4: 14 Day Autonomy with Prolonged Partial PV Disruption
3.5. Design Example 5: 14 Day Autonomy with Prolonged Partial PV Disruption and Increased A:L Ratio
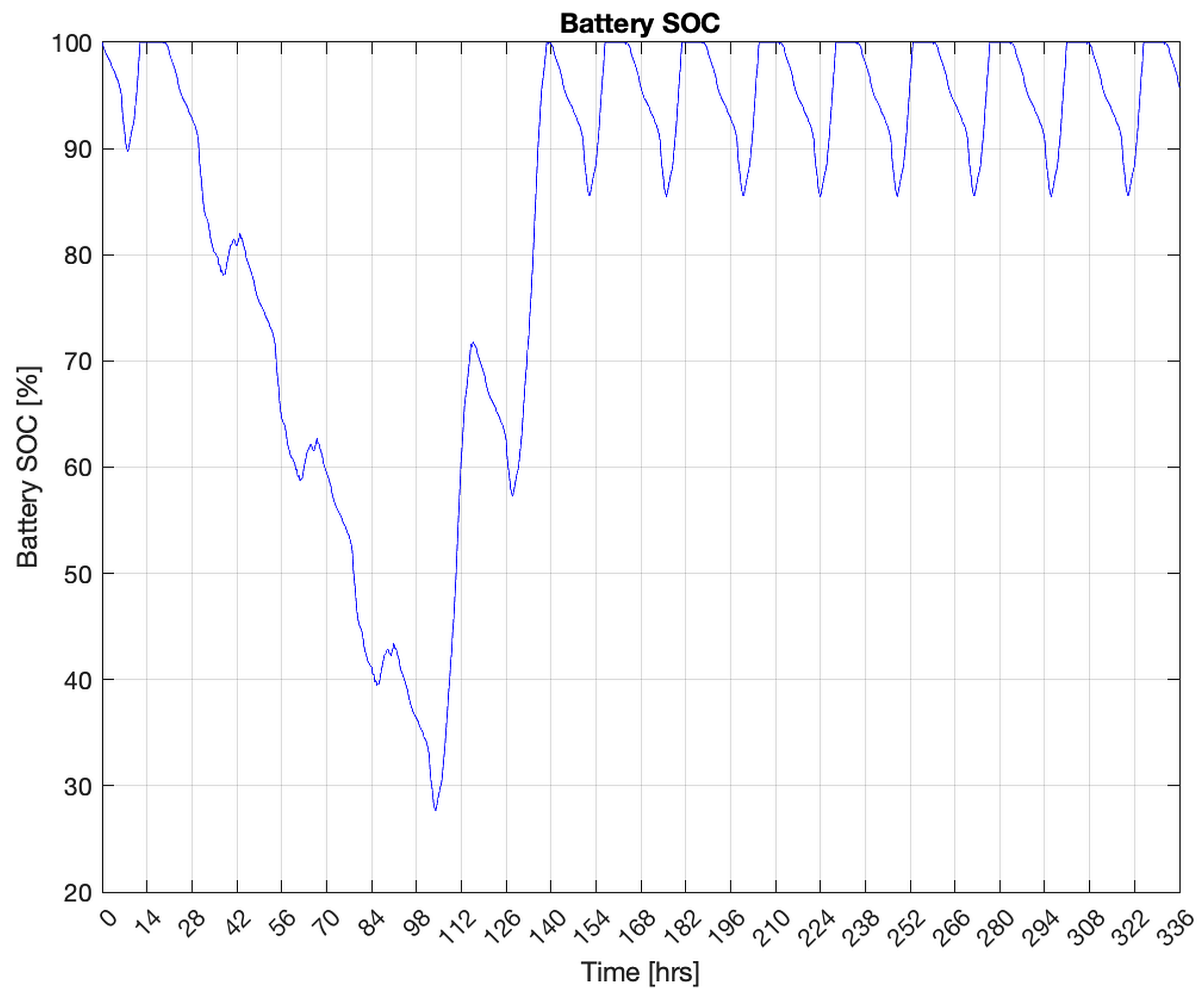
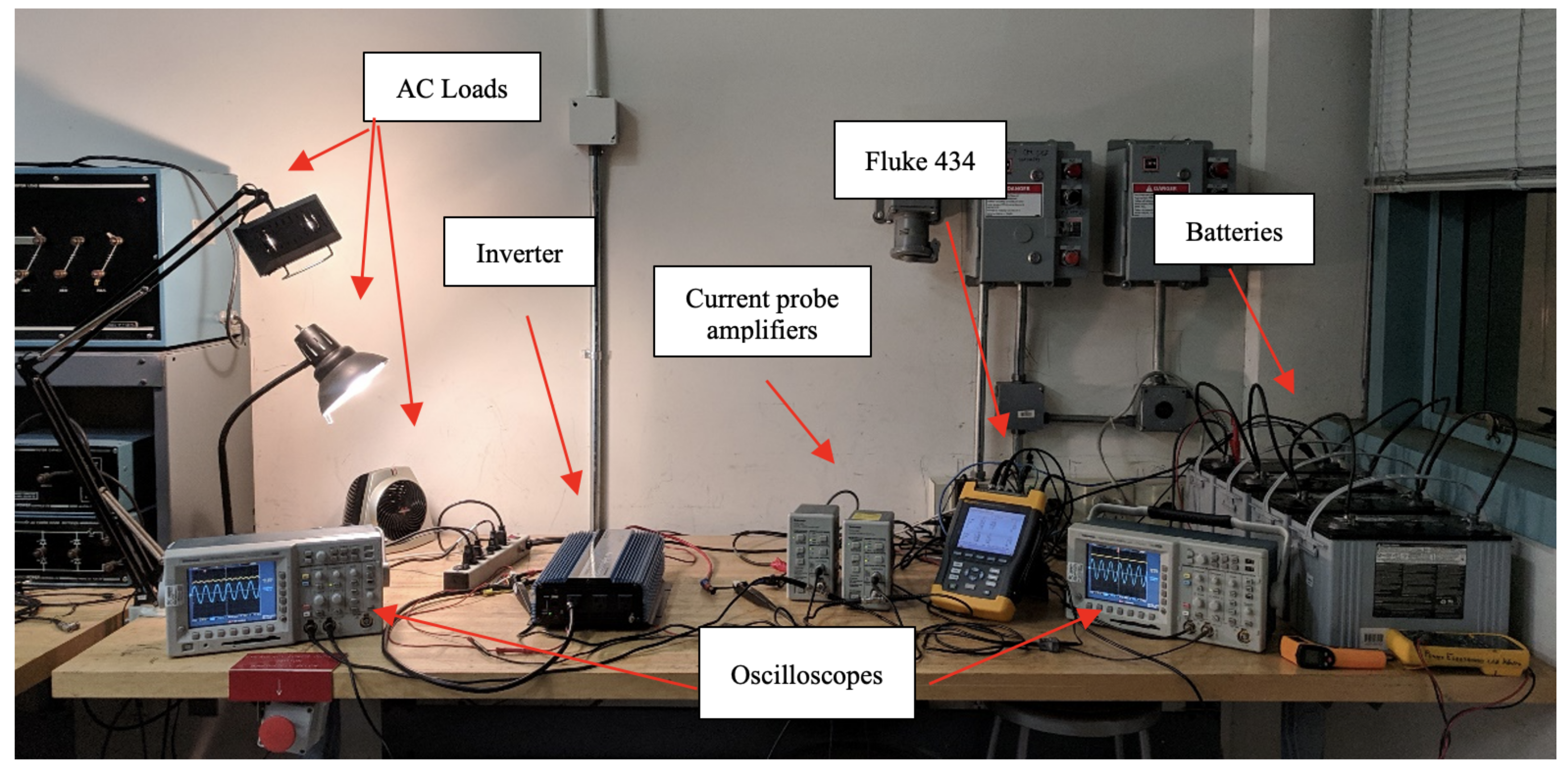
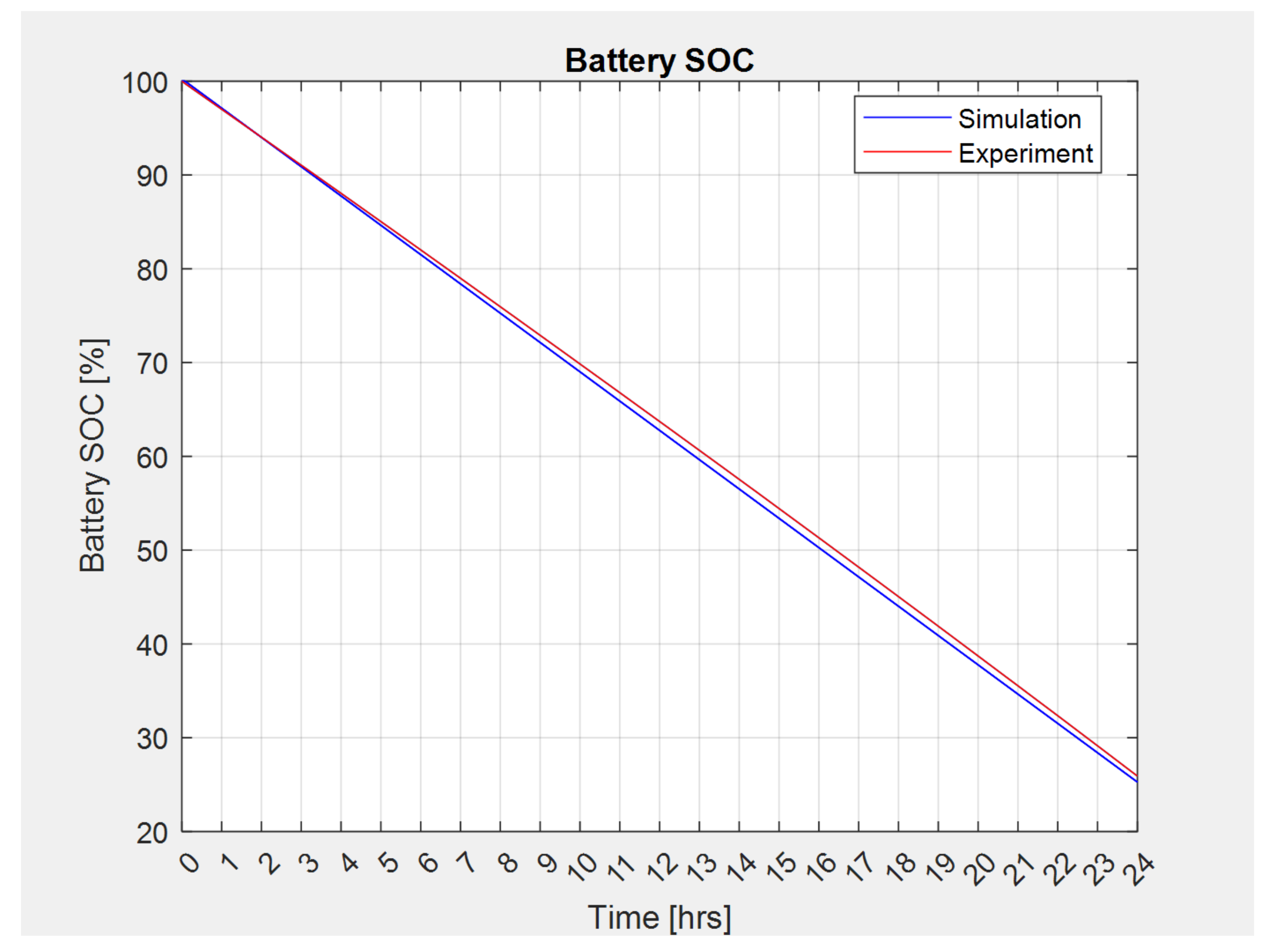
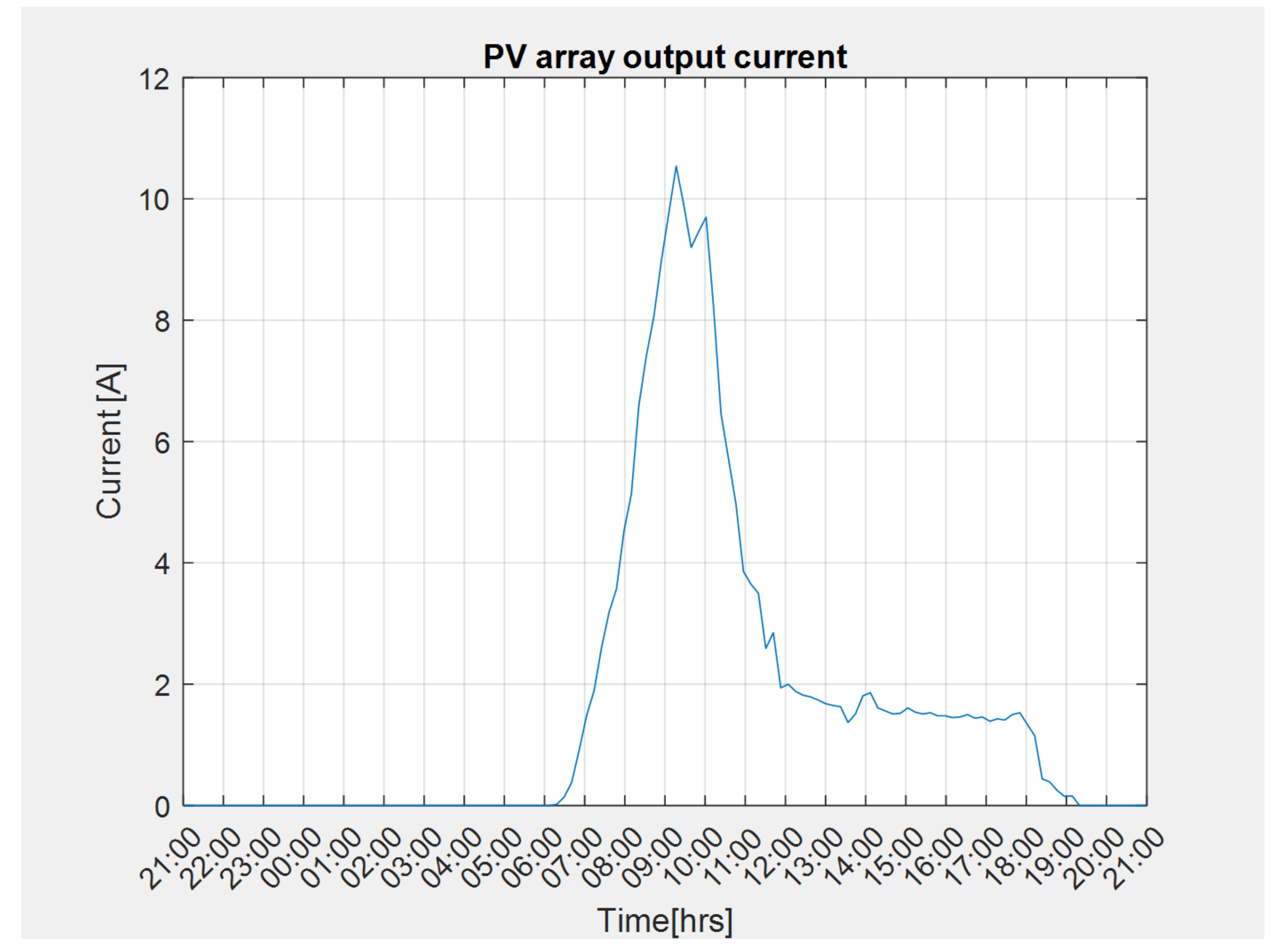
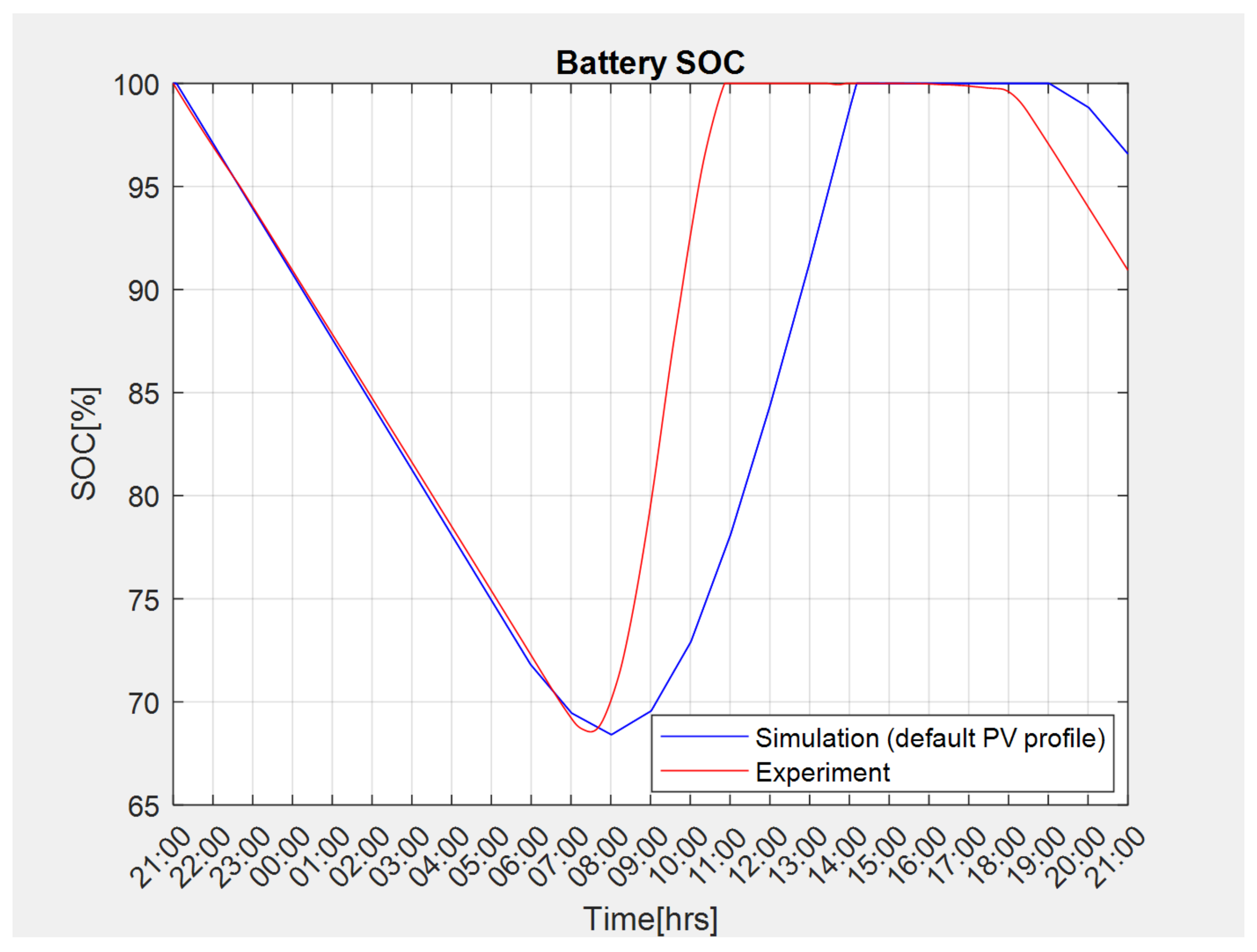
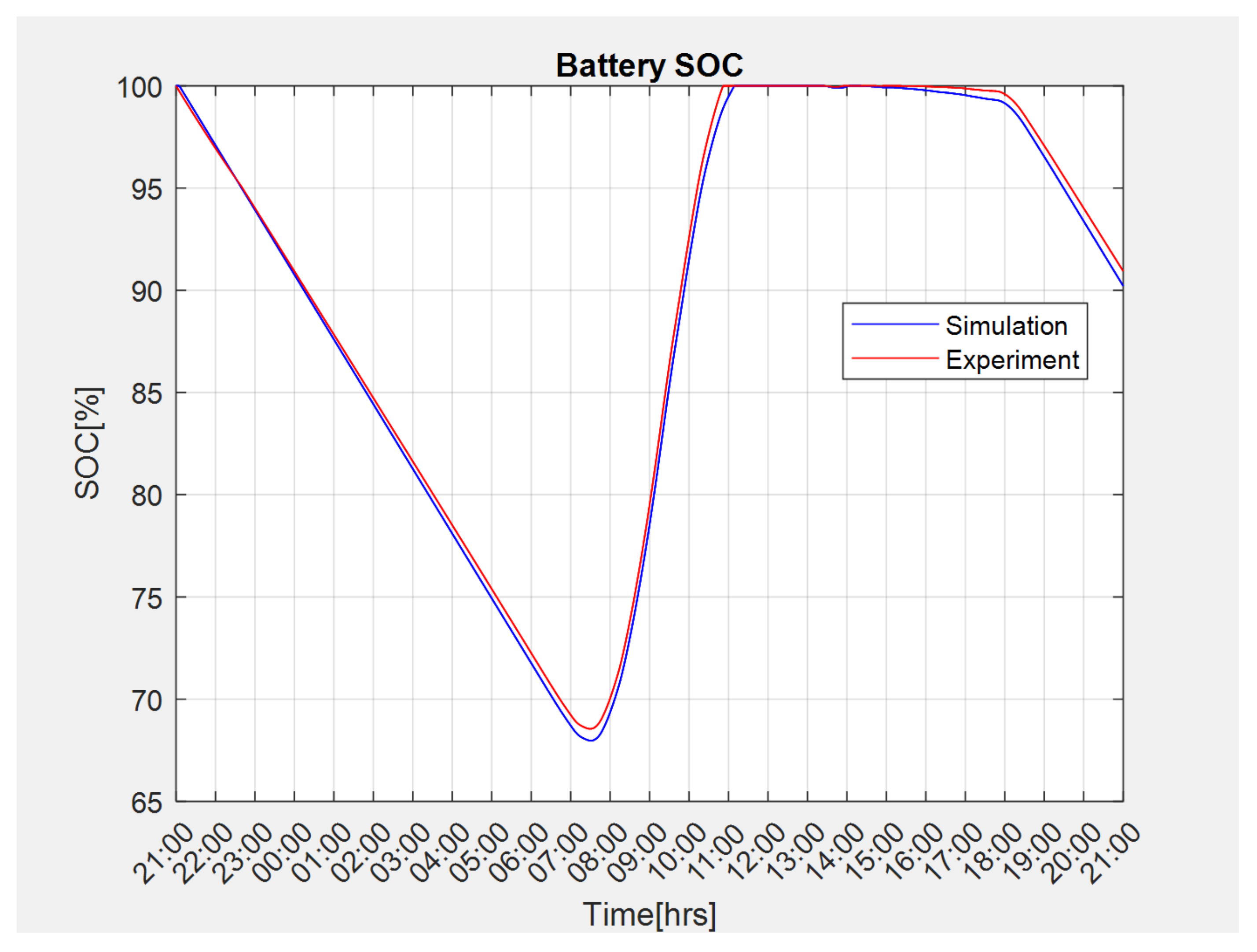
4. Experimental Validation of Design Method and Software
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Siritoglou, P. Distributed Energy Storage Design and Modeling to Improve the Energy Security of Naval Facilities. Master’s Thesis, Naval Postgraduate School, Monterey, CA, USA, 2019. [Google Scholar]
- Siritoglou, P.; Oriti, G. Distributed Energy Resources Design Method to Improve Energy Security in Critical Facilities. In Proceedings of the IEEE 2020 International Conference on Environment and Electrical Engineering and 2020 IEEE Industrial and Commercial Power Systems Europe (EEEIC/I and CPS Europe), Madrid, Spain, 9–12 June 2020. [Google Scholar]
- Paravantis, J.; Kontoulis, N.; Ballis, A.; Tsirigotis, D.; Dourmas, V. A geopolitical review of definitions, dimensions and indicators of energy security. In Proceedings of the 2018 9th International Conference on Information, Intelligence, Systems and Applications (IISA), Zakynthos, Greece, 23–25 July 2018; pp. 1–8. [Google Scholar]
- Van Broekhoven, S.; Judson, N.; Nguyen, S.; Ross, W. Microgrid Study: Energy Security for DoD Installations; Technical Report; Massachusetts Inst of Tech Lincoln Lab.: Lexington, MA, USA, 2012. [Google Scholar]
- Van Broekhoven, S.; Judson, N.; Galvin, J.; Marqusee, J. Leading the charge: Microgrids for domestic military installations. IEEE Power Energy Mag. 2013, 11, 40–45. [Google Scholar] [CrossRef]
- Strategy, D.E. Report of the Defense Science Board Task Force on DoD Energy Strategy “More Fight–Less Fuel”; Technical Report; Office of the Under Secretary of Defense For Acquisition, Technology, and Logistics: Washington, DC, USA, 2008. [Google Scholar]
- Peterson, C.J. Systems Architecture Design and Validation Methods for Microgrid Systems. Master’s Thesis, Naval Postgraduate School, Montere, CA, USA, 2019. [Google Scholar]
- Giachetti, R.E.; Peterson, C.J.; Van Bossuyt, D.L.; Parker, G.W. Systems Engineering Issues in Microgrids for Military Installations. In INCOSE International Symposium; Wiley Online Library: New York, NY, USA, 2020; Volume 30, pp. 731–746. [Google Scholar]
- Peters, J.W. In the Virgin Islands, Hurricane Maria Drowned What Irma Didn’t Destroy. New York Times, 27 September 2017. [Google Scholar]
- IEEE. IEEE Guide for Array and Battery Sizing in Stand-Alone Photovoltaic (PV) Systems; Standard IEEE Std 1562-2007; IEEE: Washington, DC, USA, 2008. [Google Scholar]
- IEEE. IEEE Recommended Practice for Sizing Lead-Acid Batteries for Stand-Alone Photovoltaic (PV) Systems; Standard IEEE Std 1013-2019; IEEE: Washington, DC, USA, 2019. [Google Scholar]
- Panagiotou, K.; Klumpner, C.; Sumner, M. Sizing guidelines for grid-connected decentralised energy storage systems: Single house application. J. Eng. 2019, 2019, 3802–3806. [Google Scholar] [CrossRef]
- Mehrtash, M.; Capitanescu, F.; Heiselberg, P.K.; Gibon, T.; Bertrand, A. An Enhanced Optimal PV and Battery Sizing Model for Zero Energy Buildings Considering Environmental Impacts. IEEE Trans. Ind. Appl. 2020, 56, 6846–6856. [Google Scholar] [CrossRef]
- Bandyopadhyay, S.; Mouli, G.C.; Qin, Z.; Elizondo, L.R.; Bauer, P. Techno-economical model based optimal sizing of pv-battery systems for microgrids. IEEE Trans. Sustain. Energy 2019, 11, 1657–1668. [Google Scholar] [CrossRef]
- Rodríguez-Gallegos, C.D.; Gandhi, O.; Yang, D.; Alvarez-Alvarado, M.S.; Zhang, W.; Reindl, T.; Panda, S.K. A siting and sizing optimization approach for PV–battery–diesel hybrid systems. IEEE Trans. Ind. Appl. 2017, 54, 2637–2645. [Google Scholar] [CrossRef]
- Nikhil, P.; Subhakar, D. Sizing and parametric analysis of a stand-alone photovoltaic power plant. IEEE J. Photovoltaics 2013, 3, 776–784. [Google Scholar] [CrossRef]
- Jain, D.; Sandeep, N.; Verma, A.K.; Yaragatti, U.R. A Simple Methodology for Sizing of Stand-Alone PV-Battery System. In Proceedings of the 2019 8th International Conference on Power Systems (ICPS), Jaipur, India, 20–22 December 2019; pp. 1–5. [Google Scholar]
- Diab, A.A.Z.; Sultan, H.M.; Mohamed, I.S.; Kuznetsov, O.N.; Do, T.D. Application of different optimization algorithms for optimal sizing of PV/wind/diesel/battery storage stand-alone hybrid microgrid. IEEE Access 2019, 7, 119223–119245. [Google Scholar] [CrossRef]
- Masters, G.M. Renewable and Efficient Electric Power Systems; John Wiley and Sons: Hoboken, NJ, USA, 2013. [Google Scholar]
- Keesee, C.W. Realizing Energy Security on a DoD Installation Using Photovoltaics with a Battery Energy Storage System. Master’s Thesis, Naval Postgraduate School, Monterey, CA, USA, 2018. [Google Scholar]
- Ali, W.; Farooq, H.; Rehman, A.U.; Awais, Q.; Jamil, M.; Noman, A. Design considerations of stand-alone solar photovoltaic systems. In Proceedings of the 2018 International Conference on Computing, Electronic and Electrical Engineering (ICE Cube), Quetta, Pakistan, 12–13 November 2018; pp. 1–6. [Google Scholar]
- Dong, J.; Zhu, L.; Su, Y.; Ma, Y.; Liu, Y.; Wang, F.; Tolbert, L.M.; Glass, J.; Bruce, L. Battery and backup generator sizing for a resilient microgrid under stochastic extreme events. IET Gener. Transm. Distrib. 2018, 12, 4443–4450. [Google Scholar] [CrossRef]
- Lai, K.; Wang, Y.; Shi, D.; Illindala, M.S.; Jin, Y.; Wang, Z. Sizing battery storage for islanded microgrid systems to enhance robustness against attacks on energy sources. J. Mod. Power Syst. Clean Energy 2019, 7, 1177–1188. [Google Scholar] [CrossRef]
- Zhang, B.; Dehghanian, P.; Kezunovic, M. Optimal allocation of PV generation and battery storage for enhanced resilience. IEEE Trans. Smart Grid 2017, 10, 535–545. [Google Scholar] [CrossRef]
- Chatterji, E.; Bazilian, M.D. Battery Storage for Resilient Homes. IEEE Access 2020, 8, 184497–184511. [Google Scholar] [CrossRef]
- Homer Energy LLC. Homer Grid. Available online: https://www.homerenergy.com/products/pro/docs/3.11/index.html (accessed on 1 August 2020).
- National Renewable Energy Laboratory (NREL). System Advisor Model (SAM). Available online: http://sam.nrel.org (accessed on 1 August 2020).
- Sandia National Laboratories. Microgrid Design Toolkit. Available online: https://www.sandia.gov/CSR/tools/mdt.html (accessed on 1 August 2020).
- XENDEE. XENDEE Microgrid Design Platform. Available online: https://www.xendee.com/ (accessed on 1 August 2020).
- Pajkic, N.; Kragh, M.; Yang, J.; Wijeratne Mudiyanselage, P.; Wijeratne Mudiyanselage, P.; Too, E.; Wakefield, R.; Eisenlohr, J.; Boddaert, S.; Bonomo, P.; et al. BIPV Design and Performance Modelling: Tools and Methods. 2019. Available online: https://repository.supsi.ch/12051/ (accessed on 1 August 2020).
- Lithium Battery Company. LiFePO4 vs. SLA-12V100AH testing report. Unpublished.
- National Renewable Energy Laboratory (NREL). National Solar Radiation Database. Available online: https://nsrdb.nrel.gov/ (accessed on 1 August 2020).
- Anglani, N.; Oriti, G.; Colombini, M. Optimized energy management system to reduce fuel consumption in remote military microgrids. IEEE Trans. Ind. Appl. 2017, 53, 5777–5785. [Google Scholar] [CrossRef]
- RELiON Batteries. RB 48V 200 Li-Ion battery. Available online: https://relionbattery.com/products/lithium/rb48v200 (accessed on 1 August 2020).
- SunPower Corporation. X-Series X22-360 Commercial Solar Panel, 514617. Available online: https://us.sunpower.com/ (accessed on 1 August 2020).
- Glavin, M.; Chan, P.K.; Armstrong, S.; Hurley, W. A stand-alone photovoltaic supercapacitor battery hybrid energy storage system. In Proceedings of the 2008 13th International Power Electronics and Motion Control Conference, Poznan, Poland, 1–3 September 2008; pp. 1688–1695. [Google Scholar]
- Bessani, M.; Massignan, J.A.D.; Fanucchi, R.Z.; Camillo, M.H.M.; London, J.B.A.; Delbem, A.C.B.; Maciel, C.D. Probabilistic Assessment of Power Distribution Systems Resilience Under Extreme Weather. IEEE Syst. J. 2019, 13, 1747–1756. [Google Scholar] [CrossRef]
- Mishra, S.; Anderson, K.; Miller, B.; Boyer, K.; Warren, A. Microgrid resilience: A holistic approach for assessing threats, identifying vulnerabilities, and designing corresponding mitigation strategies. Appl. Energy 2020, 264, 114726. [Google Scholar] [CrossRef]
- Billinton, R.; Fotuhi-Firuzabad, M.; Bertling, L. Bibliography on the application of probability methods in power system reliability evaluation 1996–1999. IEEE Trans. Power Syst. 2001, 16, 595–602. [Google Scholar] [CrossRef]
- Hosseini, S.; Barker, K.; Ramirez-Marquez, J.E. A review of definitions and measures of system resilience. Reliab. Eng. Syst. Saf. 2016, 145, 47–61. [Google Scholar] [CrossRef]
- Madni, A.M.; Jackson, S. Towards a Conceptual Framework for Resilience Engineering. IEEE Syst. J. 2009, 3, 181–191. [Google Scholar] [CrossRef]
- Mahzarnia, M.; Moghaddam, M.P.; Baboli, P.T.; Siano, P. A Review of the Measures to Enhance Power Systems Resilience. IEEE Syst. J. 2020, 14, 4059–4070. [Google Scholar] [CrossRef]
- Chang, W.Y. The state of charge estimating methods for battery: A review. Int. Sch. Res. Not. 2013, 2013, 953792. [Google Scholar] [CrossRef]
- Chiasson, J.; Vairamohan, B. Estimating the state of charge of a battery. In Proceedings of the 2003 American Control Conference, Denver, CO, USA, 4–6 June 2003; Volume 4, pp. 2863–2868. [Google Scholar]



| Time (h:min) | DC Current (A) | AC Current rms (A) | DC Voltage (V) | AC Voltage rms (V) |
|---|---|---|---|---|
| 1:20 | 11.23 | 0.999 | 12.54 | 119.8 |
| 9:30 | 11.56 | 0.999 | 12.29 | 119.8 |
| 19:00 | 12.04 | 0.999 | 11.88 | 119.6 |
| 23:00 | 12.24 | 1.002 | 11.70 | 119.9 |
| Time (h:min) | DC Current (A) | AC Current rms (A) | DC Voltage (V) | AC Voltage rms (V) |
|---|---|---|---|---|
| 21:23 | 8.90 | 0.752 | 12.68 | 119.8 |
| 06:56 | 8.96 | 0.760 | 12.45 | 119.7 |
| 11:19 | 8.60 | 0.753 | 14.44 | 120.0 |
| 16:05 | 8.73 | 0.756 | 13.88 | 119.9 |
| 18:38 | 8.82 | 0.753 | 12.91 | 119.5 |
| 21:07 | 8.90 | 0.755 | 12.76 | 119.7 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Siritoglou, P.; Oriti, G.; Van Bossuyt, D.L. Distributed Energy-Resource Design Method to Improve Energy Security in Critical Facilities. Energies 2021, 14, 2773. https://doi.org/10.3390/en14102773
Siritoglou P, Oriti G, Van Bossuyt DL. Distributed Energy-Resource Design Method to Improve Energy Security in Critical Facilities. Energies. 2021; 14(10):2773. https://doi.org/10.3390/en14102773
Chicago/Turabian StyleSiritoglou, Petros, Giovanna Oriti, and Douglas L. Van Bossuyt. 2021. "Distributed Energy-Resource Design Method to Improve Energy Security in Critical Facilities" Energies 14, no. 10: 2773. https://doi.org/10.3390/en14102773
APA StyleSiritoglou, P., Oriti, G., & Van Bossuyt, D. L. (2021). Distributed Energy-Resource Design Method to Improve Energy Security in Critical Facilities. Energies, 14(10), 2773. https://doi.org/10.3390/en14102773






