Improved IMPES Scheme for the Simulation of Incompressible Three-Phase Flows in Subsurface Porous Media
Abstract
1. Introduction
2. Mathematical Model
3. Standard IMPES Scheme
| Algorithm 1 Standard IMPES Scheme |
|
4. Improved IMPES Scheme
| Algorithm 2 Improved IMPES Scheme |
|
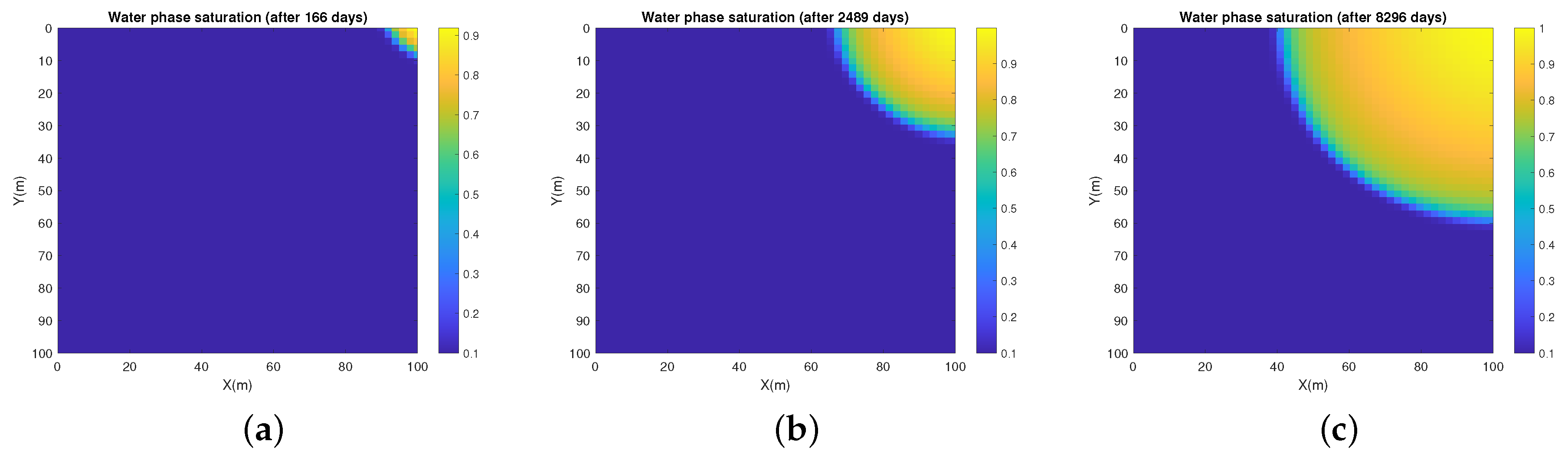
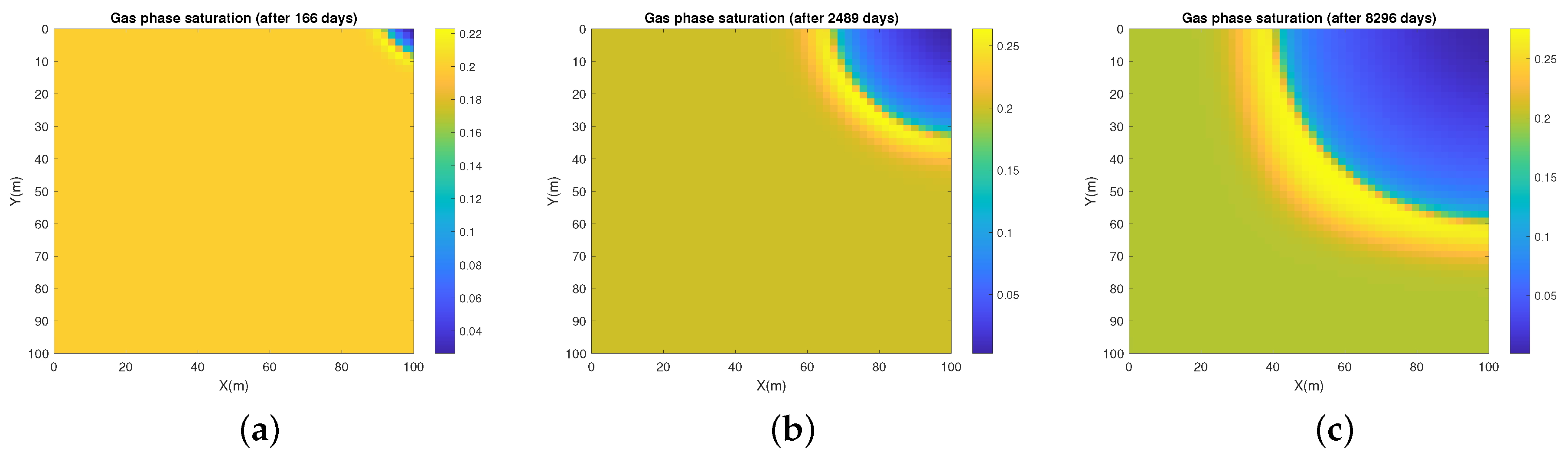
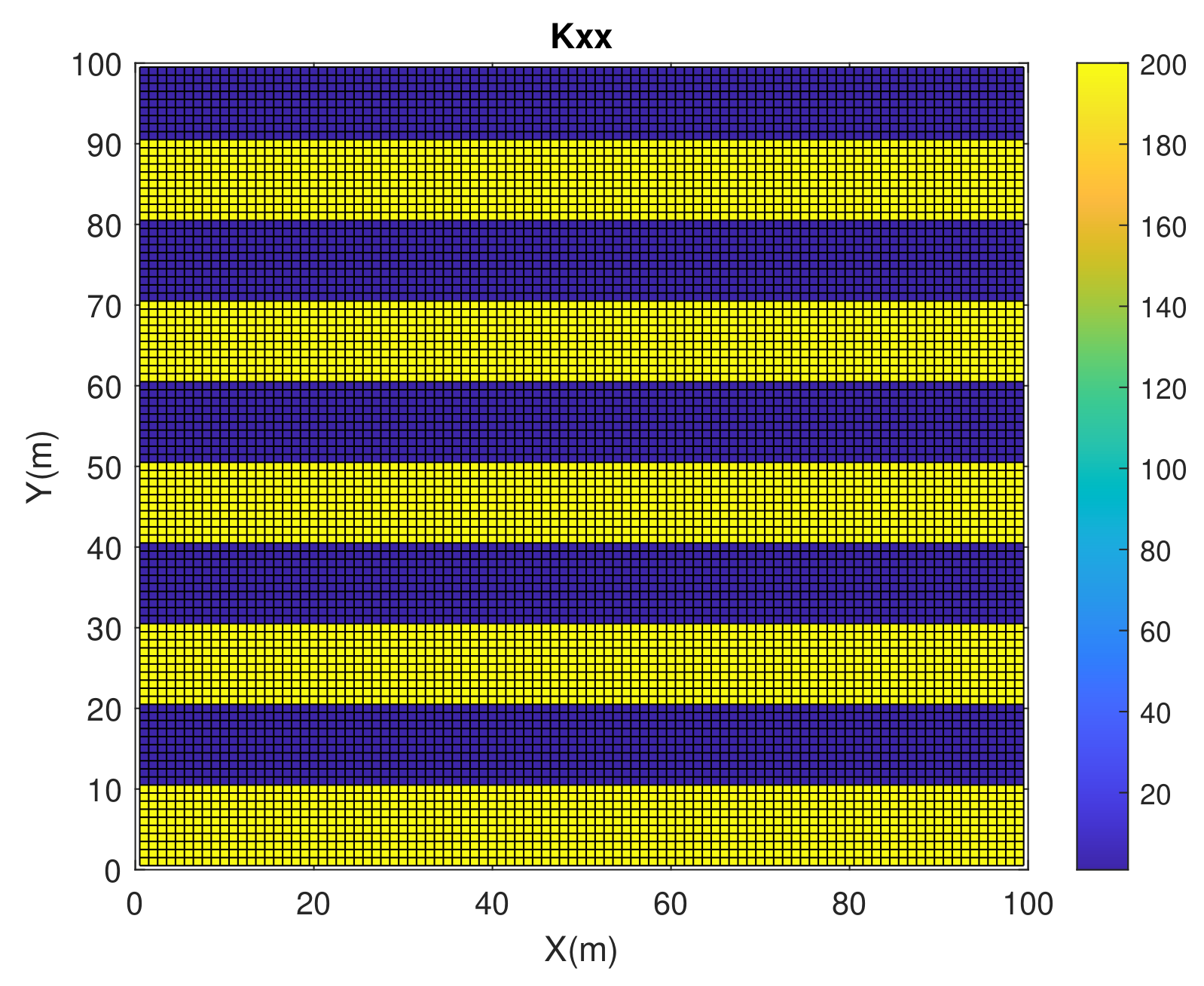
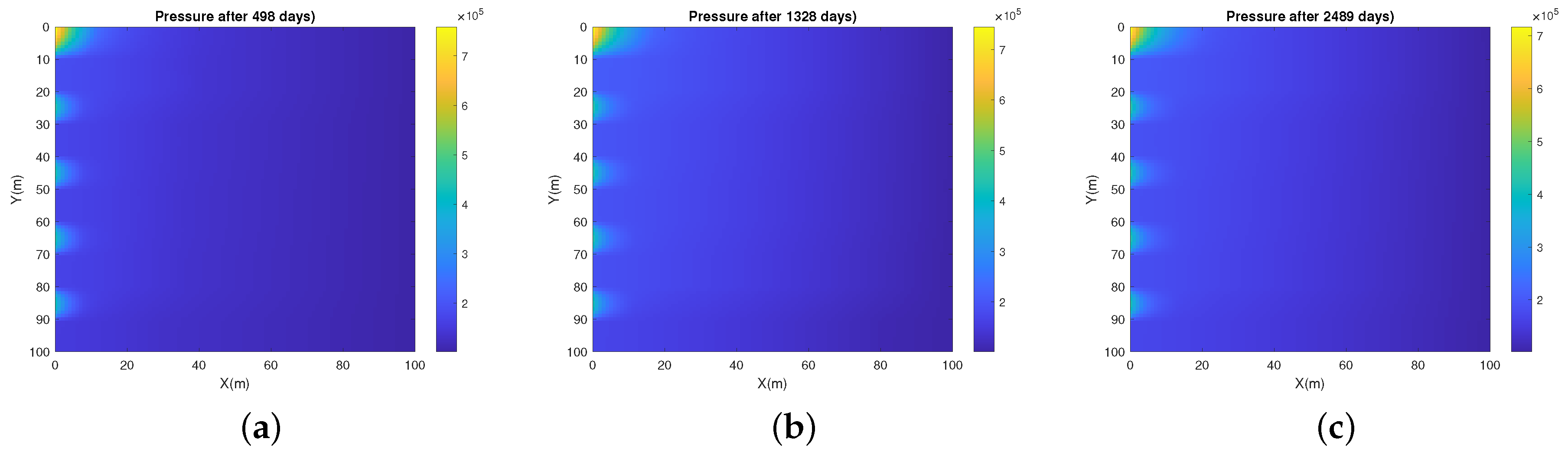
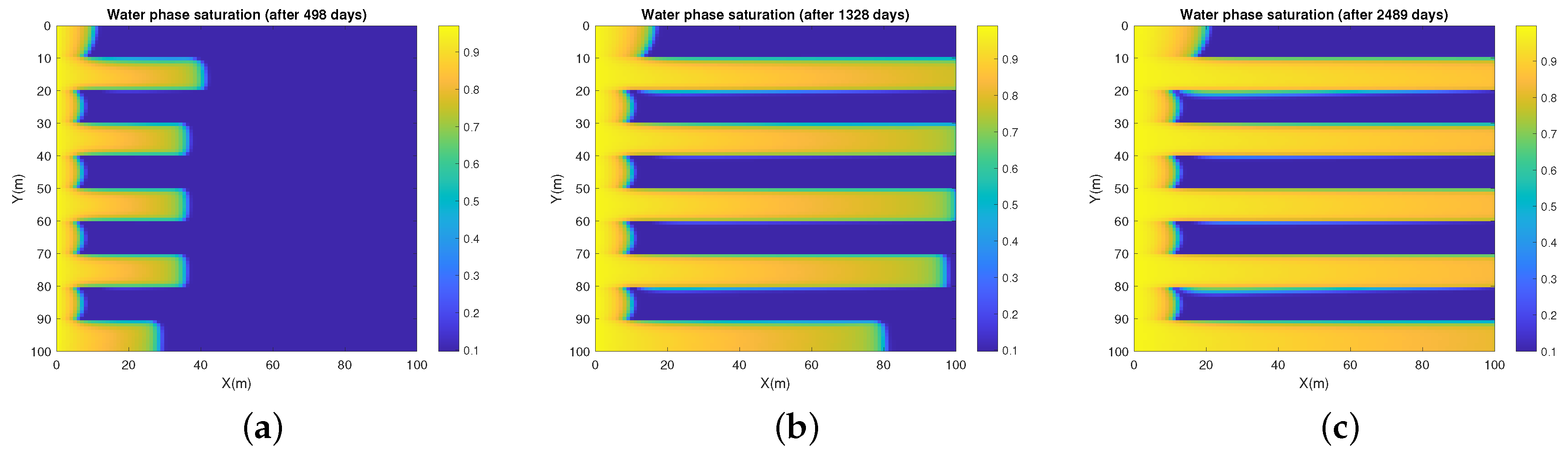
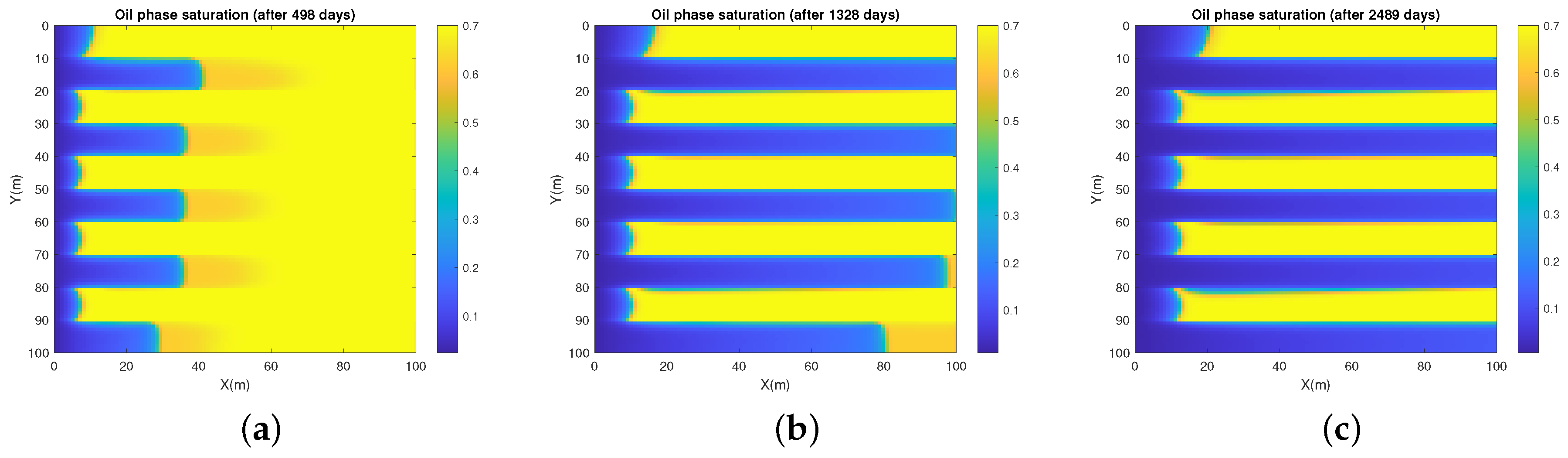
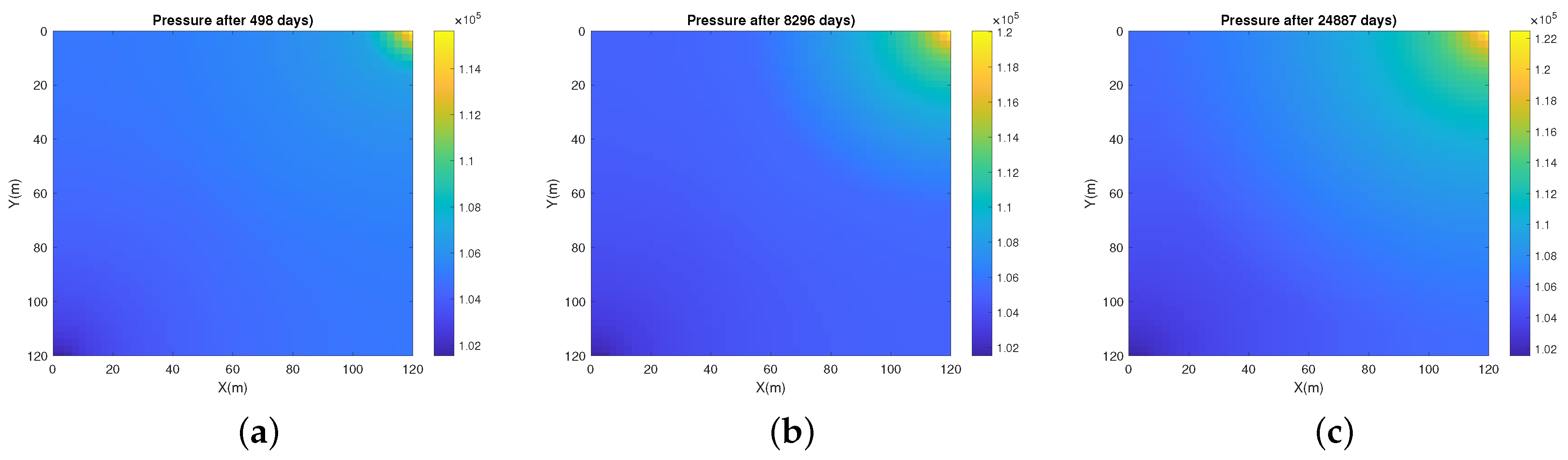
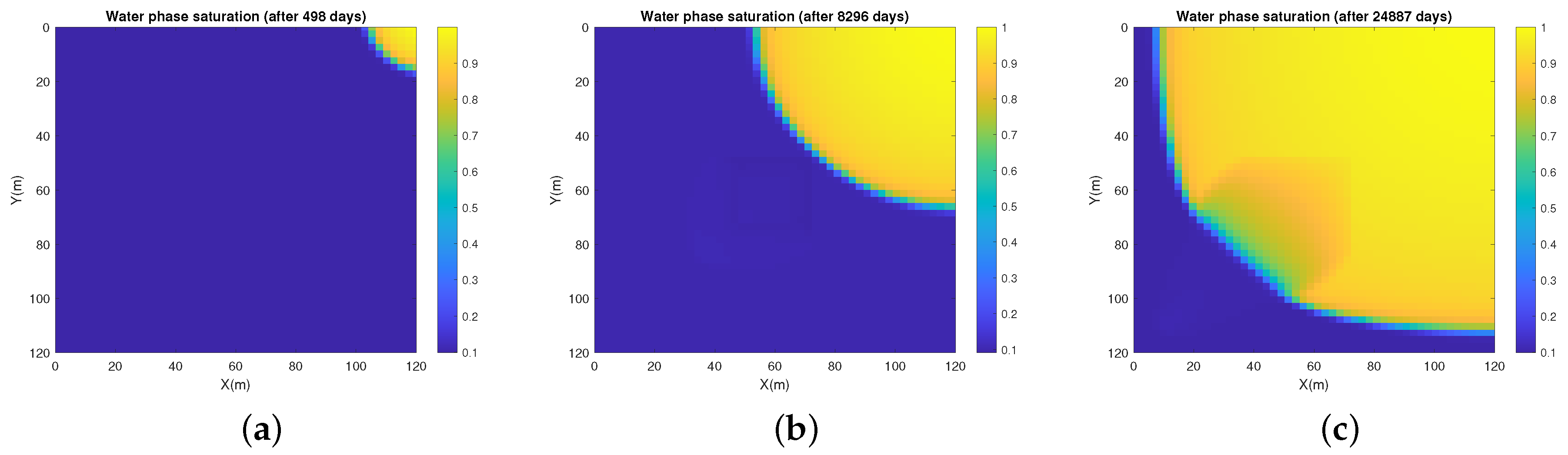
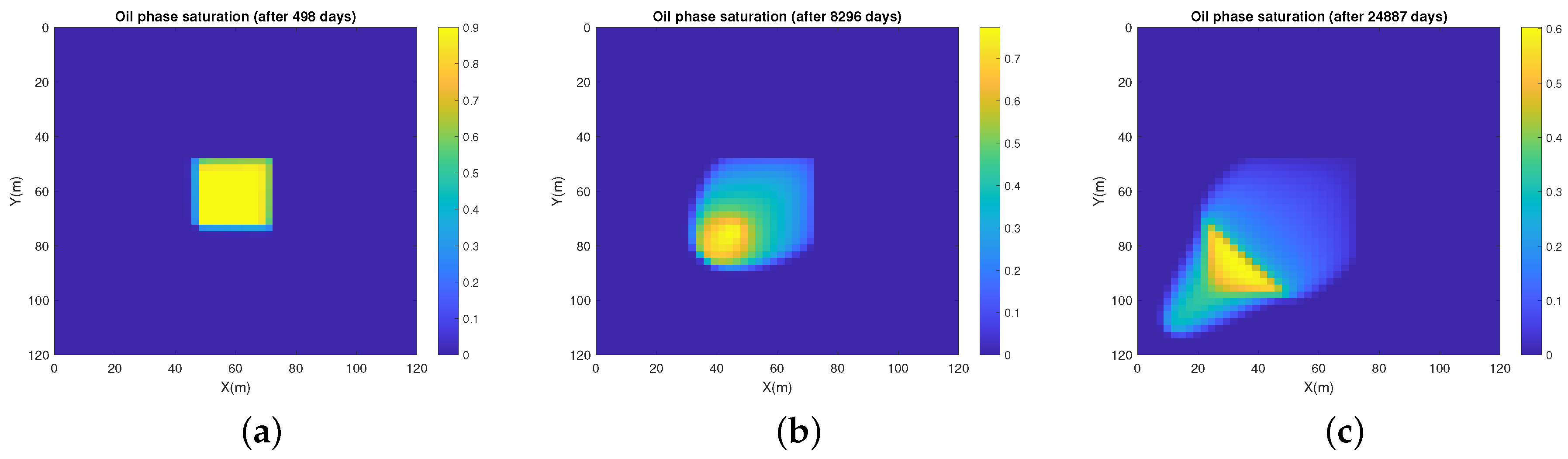
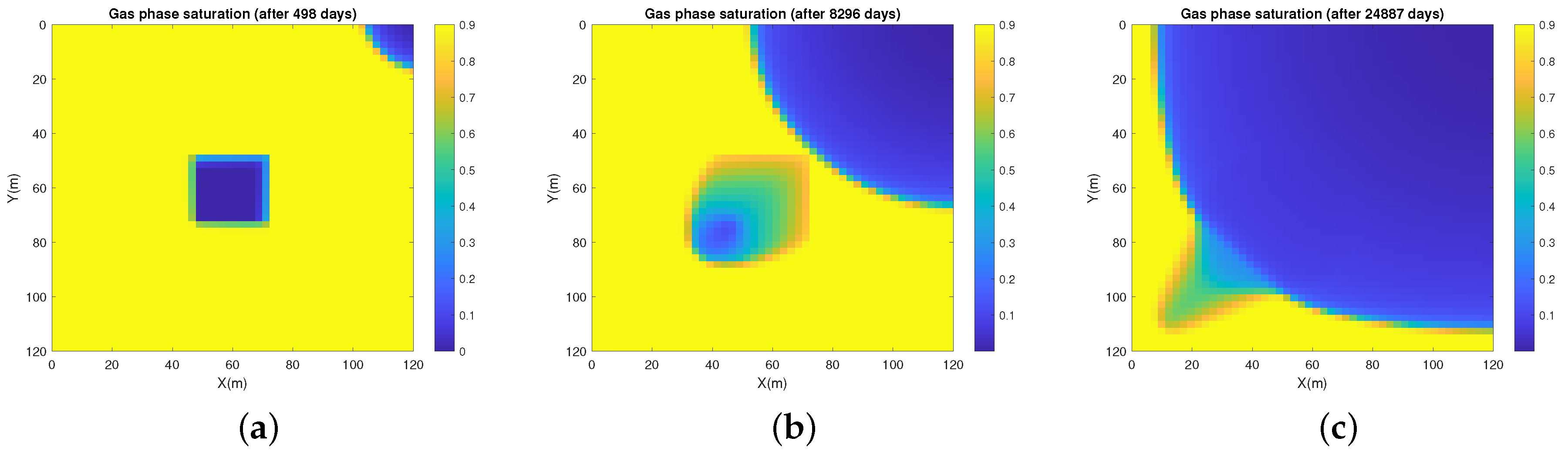
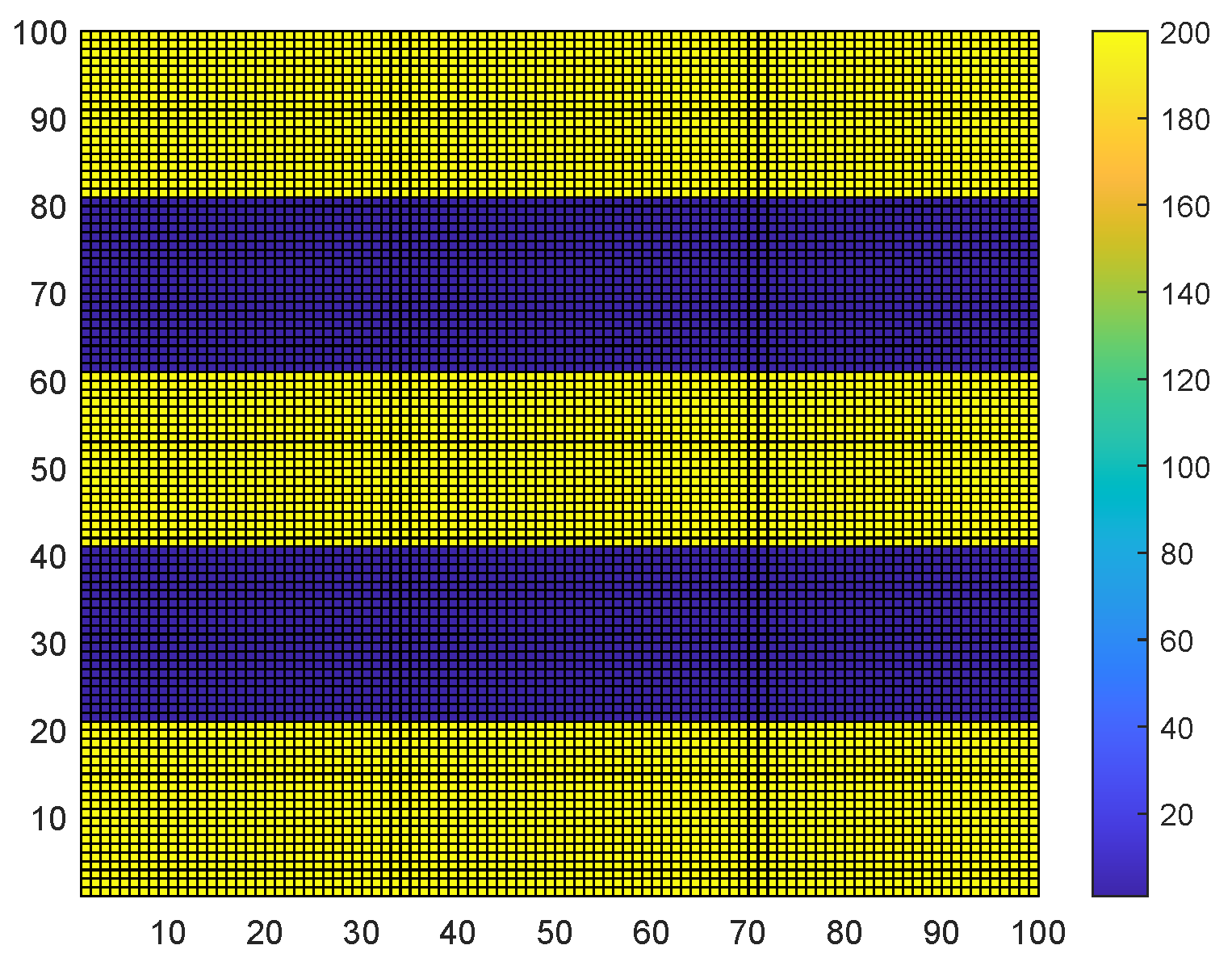
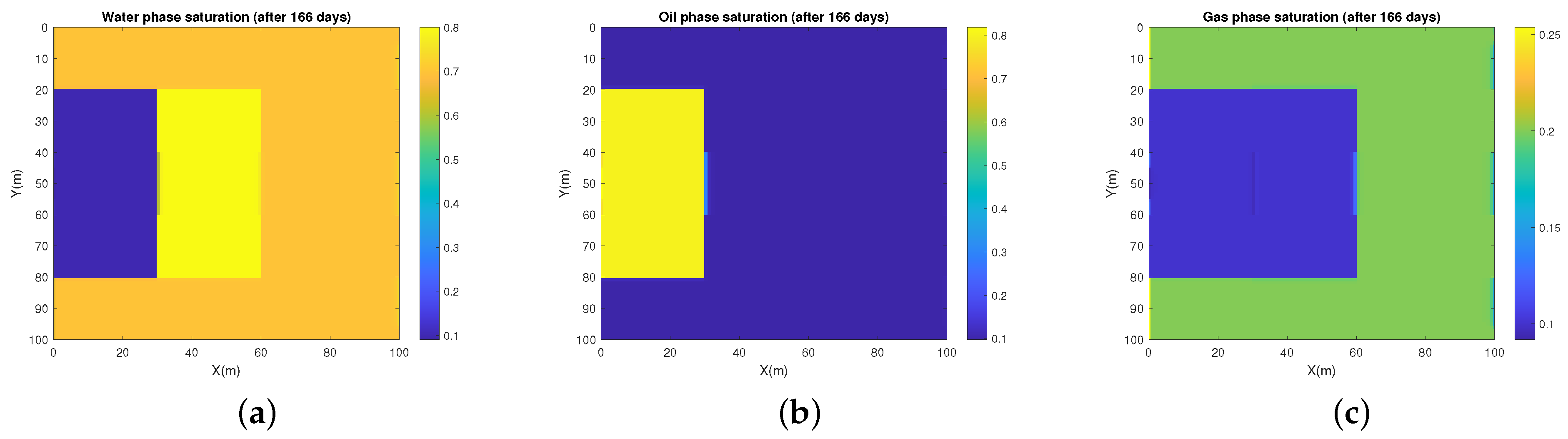
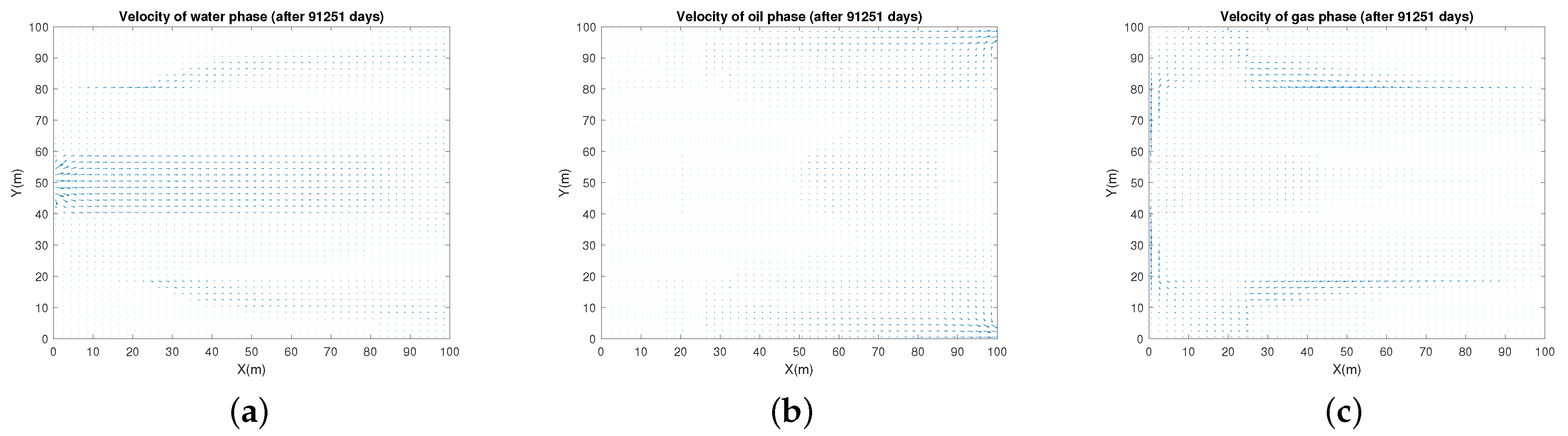
5. Numerical Experiments
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Chen, H.; Kou, J.; Sun, S.; Zhang, T. Fully mass-conservative IMPES schemes for incompressible two-phase flow in porous media. Comput. Methods Appl. Mech. Eng. 2019, 350, 641–663. [Google Scholar] [CrossRef]
- Chen, H.; Sun, S. A new physics-preserving IMPES scheme for incompressible and immiscible two-phase flow in heterogeneous porous media. J. Comput. Appl. Math. 2021, 381, 113035. [Google Scholar] [CrossRef]
- Redondo, C.; Rubio, G.; Valero, E. On the efficiency of the IMPES method for two phase flow problems in porous media. J. Pet. Sci. Eng. 2018, 164, 427–436. [Google Scholar]
- Hoteit, H.; Firoozabadi, A. Numerical modeling of two-phase flow in heterogeneous permeable media with different capillarity pressures. Adv. Water Resour. 2008, 31, 56–73. [Google Scholar] [CrossRef]
- Hoteit, H.; Firoozabadi, A. An efficient numerical model for incompressible two phase flow in fracture media. Adv. Water Resour. 2008, 31, 891–905. [Google Scholar] [CrossRef]
- Lux, J.; Anguy, Y. A study of the behavior of implicit pressure explicit saturation (IMPES) schedules for two-phase flow in dynamic pore network models. Transp. Porous Media 2012, 93, 203–221. [Google Scholar] [CrossRef]
- Chen, Z.; Ewing, R.E. Comparison of various formulations of three-phase flow in porous media. J. Comput. Phys. 1997, 132, 362–373. [Google Scholar] [CrossRef]
- Douglas, J., Jr. Finite difference methods for two-phase incompressible flow in porous media. SIAM J. Numer. Anal. 1983, 20, 681–696. [Google Scholar] [CrossRef]
- Rahman, N.A.; Lewis, R.W. Finite element modelling of multiphase immiscible flow in deforming porous media for subsurface systems. Comput. Geotech. 1999, 24, 41–63. [Google Scholar] [CrossRef]
- Allen, M.B., III. Numerical modelling of multiphase flow in porous media. Adv. Water Resour. 1985, 8, 162–187. [Google Scholar] [CrossRef]
- Yang, H.; Li, Y.; Sun, S. Nonlinearly preconditioned constraint-preserving algorithms for subsurface three-phase flow with capillarity. Comput. Methods Appl. Mech. Eng. 2020, 367, 113140. [Google Scholar] [CrossRef]
- Abreu, E.; Furtado, F.; Pereira, F. On the numerical simulation of three-phase reservoir transport problems. Transp. Theory Stat. Phys. 2004, 33, 503–526. [Google Scholar] [CrossRef]
- Stone, H.L. Probability model for estimating three-phase relative permeability. J. Pet. Technol. 1970, 22, 214–218. [Google Scholar] [CrossRef]
- Monteagudo, J.E.P.; Firoozabadi, A. Comparison of fully implicit and IMPES formulations for simulation of water injection in fractured and unfractured media. Int. J. Numer. Methods Eng. 2010, 69, 698–728. [Google Scholar] [CrossRef]
- Aziz, K.; Settari, A. Petroleum Reservoir Simulation, 3rd ed.; Applied Science Publishers: London, UK, 1979; pp. 135–139. [Google Scholar]
- Yang, H.; Sun, S.; Li, Y.; Yang, C. A fully implicit constraint-preserving simulator for the black oil model of petroleum reservoirs. J. Comput. Phys. 2019, 396, 347–363. [Google Scholar] [CrossRef]
- Gao, Y.; Mei, L. Implicit-explicit multistep methods for general two-dimensional nonlinear Schrödinger equations. Appl. Numer. Math. 2016, 109, 41–60. [Google Scholar] [CrossRef]
- Ascher, U.M.; Ruuth, S.J.; Wetton, B.T.R. Implicit-explicit methods for time-dependent partial differential equations. SIAM J. Numer. Anal. 1995, 32, 797–823. [Google Scholar] [CrossRef]
- Kou, J.; Sun, S. On iterative IMPES formulation for two-phase flow with capillarity in heterogeneous porous media. Int. J. Numer. Anal. Model. Ser. 2010, 1, 20–40. [Google Scholar]
- Ruuth, S.J. Implicit-explicit methods for reaction-diffusion problems in pattern formation. J. Math. Biol. 1995, 34, 148–176. [Google Scholar] [CrossRef]
- Negara, A.; El-amin, M.F.; Sun, S. Simulation of CO2 plume in porous media: Consideration of capillary and buoyancy effects. Int. J. Numer. Anal. Model. 2011, 2, 315–337. [Google Scholar]
- Fan, X.; Salama, A.; Sun, S. A locally and globally phase-wise mass conservative numerical algorithm for the two-phase immiscible flow problems in porous media. Comput. Geotech. 2020, 119, 103370. [Google Scholar] [CrossRef]
- Chen, Z.; Huan, G.; Li, B. An improved IMPES method for two-phase flow in porous media. Transp. Porous Media 2004, 54, 361–376. [Google Scholar] [CrossRef]
- Jo, J.; Kwak, D.Y. An IMPES scheme for a two-phase flow in heterogeneous porous media using a structured grid. Comput. Methods Appl. Mech. Eng. 2017, 317, 684–701. [Google Scholar] [CrossRef]
- Kou, J.; Sun, S. A new treatment of capillarity to improve the stability of IMPES two-phase flow formulation. Comput. Fluids 2010, 39, 1923–1931. [Google Scholar] [CrossRef]
- Sheldon, J.W.; Zondek, B.; Cardwell, W.T. One-dimensional, incompressible, noncapillary, two-phase fluid flow in a porous medium. Trans. AIME 1959, 207, 136–143. [Google Scholar] [CrossRef]
- Kou, J.; Sun, S. Upwind discontinuous Galerkin methods with conservation of mass of both phases for incompressible two-phase flow in porous media. Numer. Methods Partial. Differ. Equ. 2014, 30, 1674–1699. [Google Scholar] [CrossRef]
- Rui, H.; Pan, H. A block-centered finite difference method for the Darcy–Forchheimer model. SIAM J. Numer. Anal. 2012, 50, 2612–2631. [Google Scholar] [CrossRef]
- Weiser, A.; Wheeler, M.F. On convergence of block-centered fnite differences for elliptic problems. SIAM J. Numer. Anal. 1988, 25, 351–375. [Google Scholar] [CrossRef]
- Starnoni, M.; Berre, I.; Keilegavlen, E.; Nordbotten, J.M. Consistent MPFA discretization for flow in the presence of gravity. Water Resour. Res. 2019, 55, 10105–10118. [Google Scholar] [CrossRef]




Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liang, R.; Fan, X.; Luo, X.; Sun, S.; Zhu, X. Improved IMPES Scheme for the Simulation of Incompressible Three-Phase Flows in Subsurface Porous Media. Energies 2021, 14, 2757. https://doi.org/10.3390/en14102757
Liang R, Fan X, Luo X, Sun S, Zhu X. Improved IMPES Scheme for the Simulation of Incompressible Three-Phase Flows in Subsurface Porous Media. Energies. 2021; 14(10):2757. https://doi.org/10.3390/en14102757
Chicago/Turabian StyleLiang, Runhong, Xiaolin Fan, Xianbing Luo, Shuyu Sun, and Xingyu Zhu. 2021. "Improved IMPES Scheme for the Simulation of Incompressible Three-Phase Flows in Subsurface Porous Media" Energies 14, no. 10: 2757. https://doi.org/10.3390/en14102757
APA StyleLiang, R., Fan, X., Luo, X., Sun, S., & Zhu, X. (2021). Improved IMPES Scheme for the Simulation of Incompressible Three-Phase Flows in Subsurface Porous Media. Energies, 14(10), 2757. https://doi.org/10.3390/en14102757






