Semi-Analytical Solution to Assess CO2 Leakage in the Subsurface through Abandoned Wells
Abstract
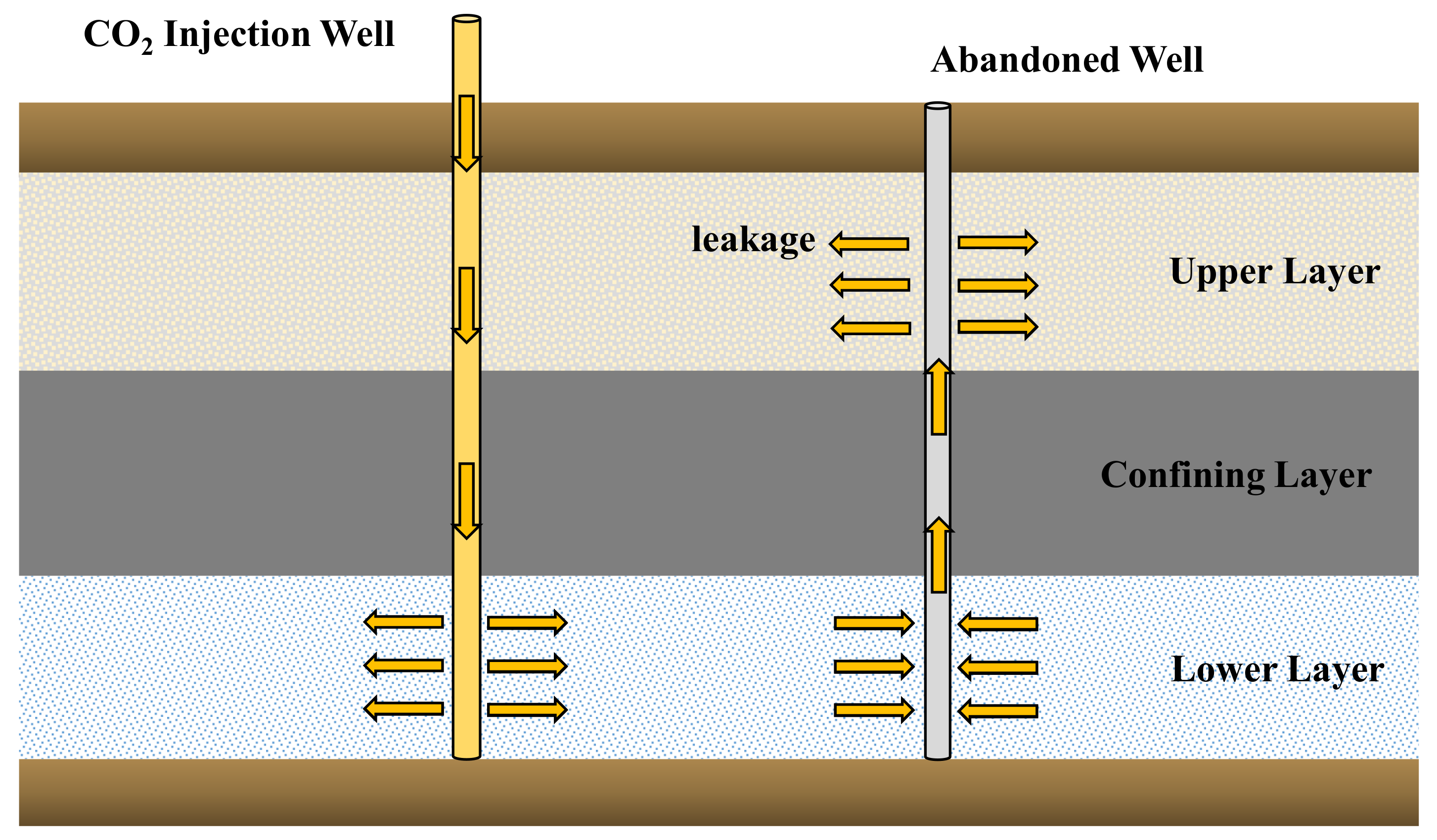
1. Introduction
2. Background
3. Governing Equations
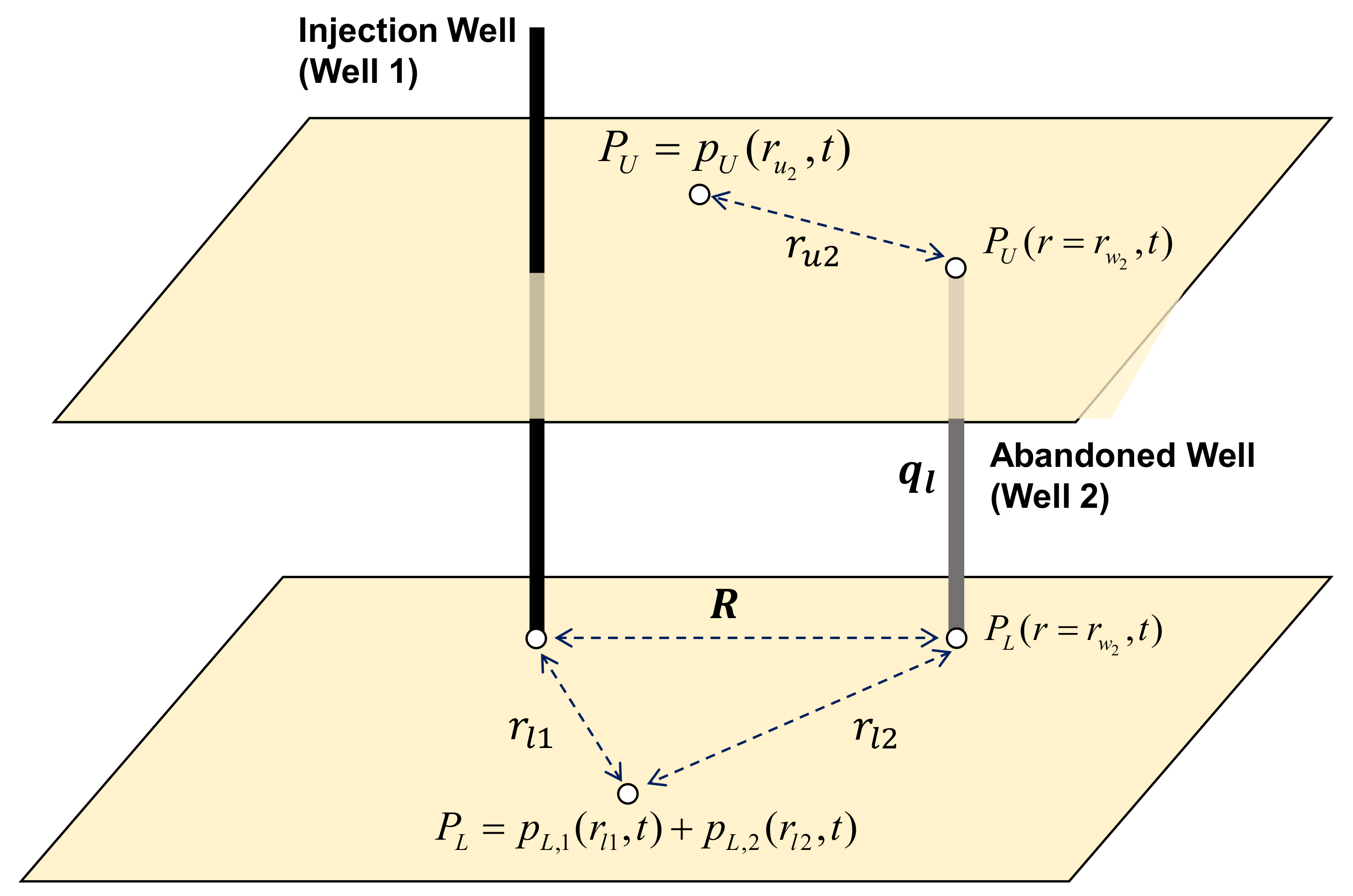
4. Proposed Solution
5. Solution with the Abandoned Well
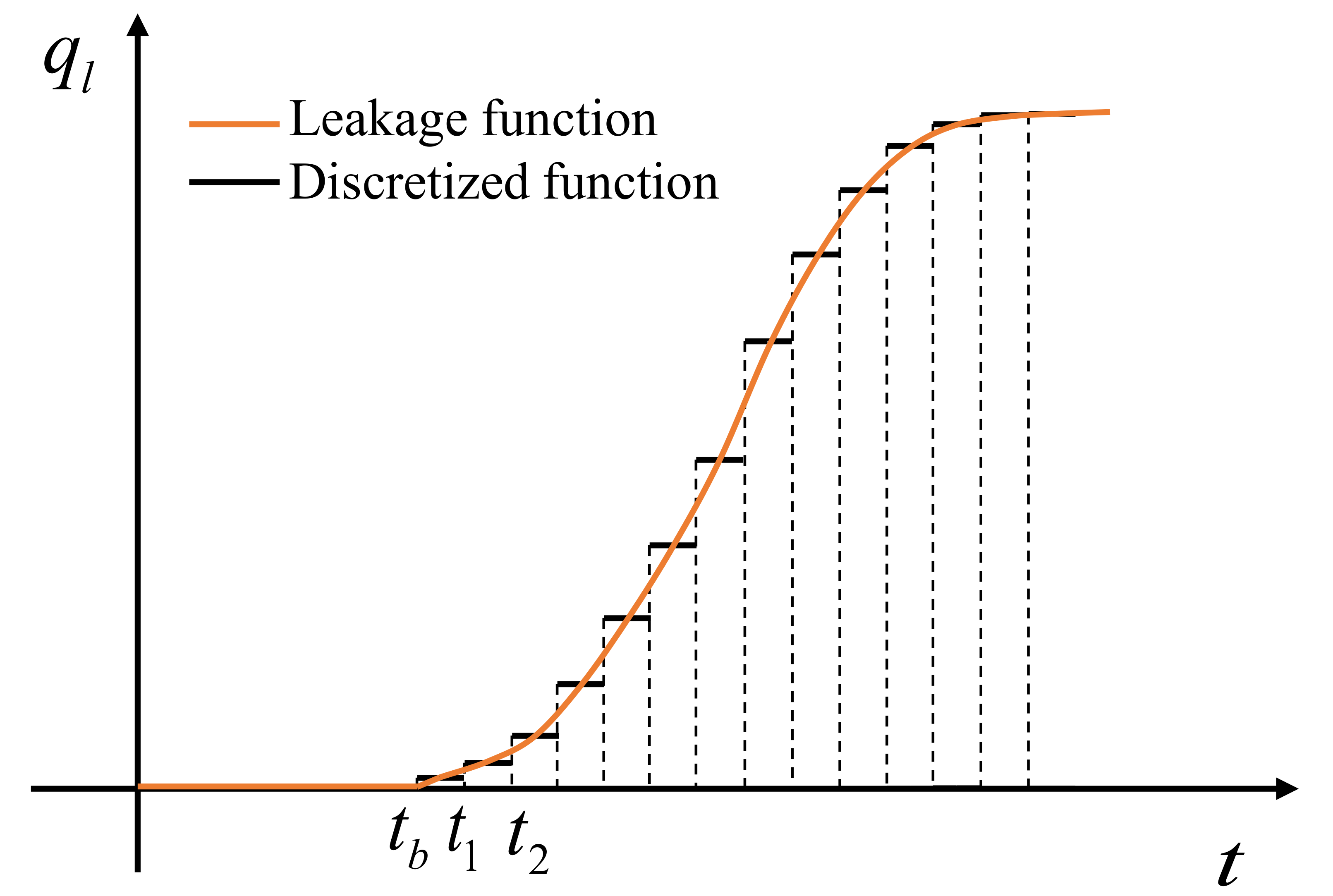
6. Total Pressure Change and Leakage Rate
- 1.
- Define the time intervals in terms of the total time.
- 2.
- Compute the pressure change caused by injection at the abandoned well location pL,1(rl1 = R) for all time intervals.
- 3.
- For the time intervals, when pressure change pL,1(rl1 = R, t = ti) is zero, the leakage rates ql (t = ti) are also recorded as zero.
- 4.
- From the time interval, when the pressure change pL,1 (rl1 = R, t = tb) is not zero, the rest of leakage rates can be solved based on the abandoned well constraint (Equation (8)).
- 5.
7. Results
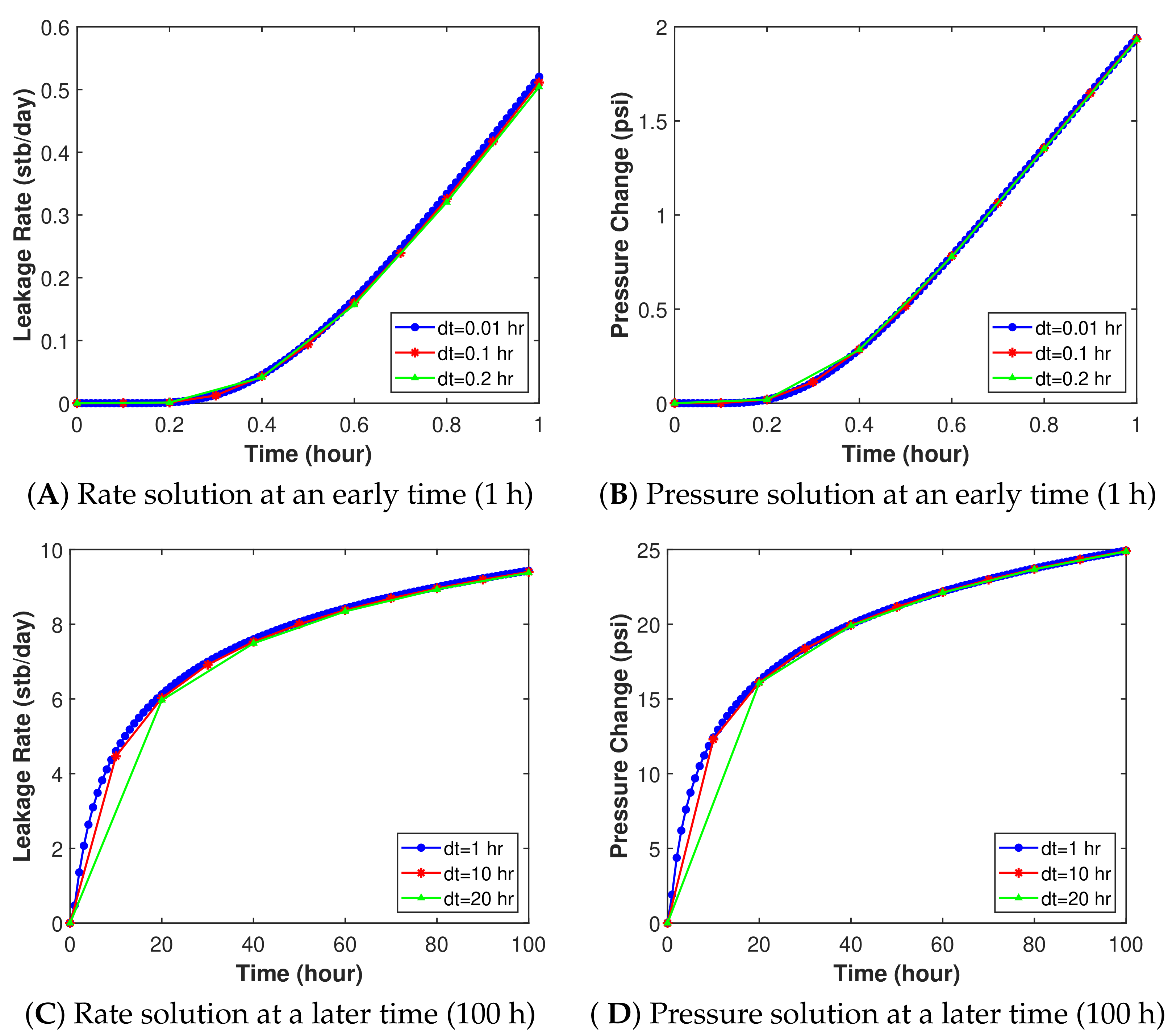
7.1. Sensitivity of Leakage Rate Discretization
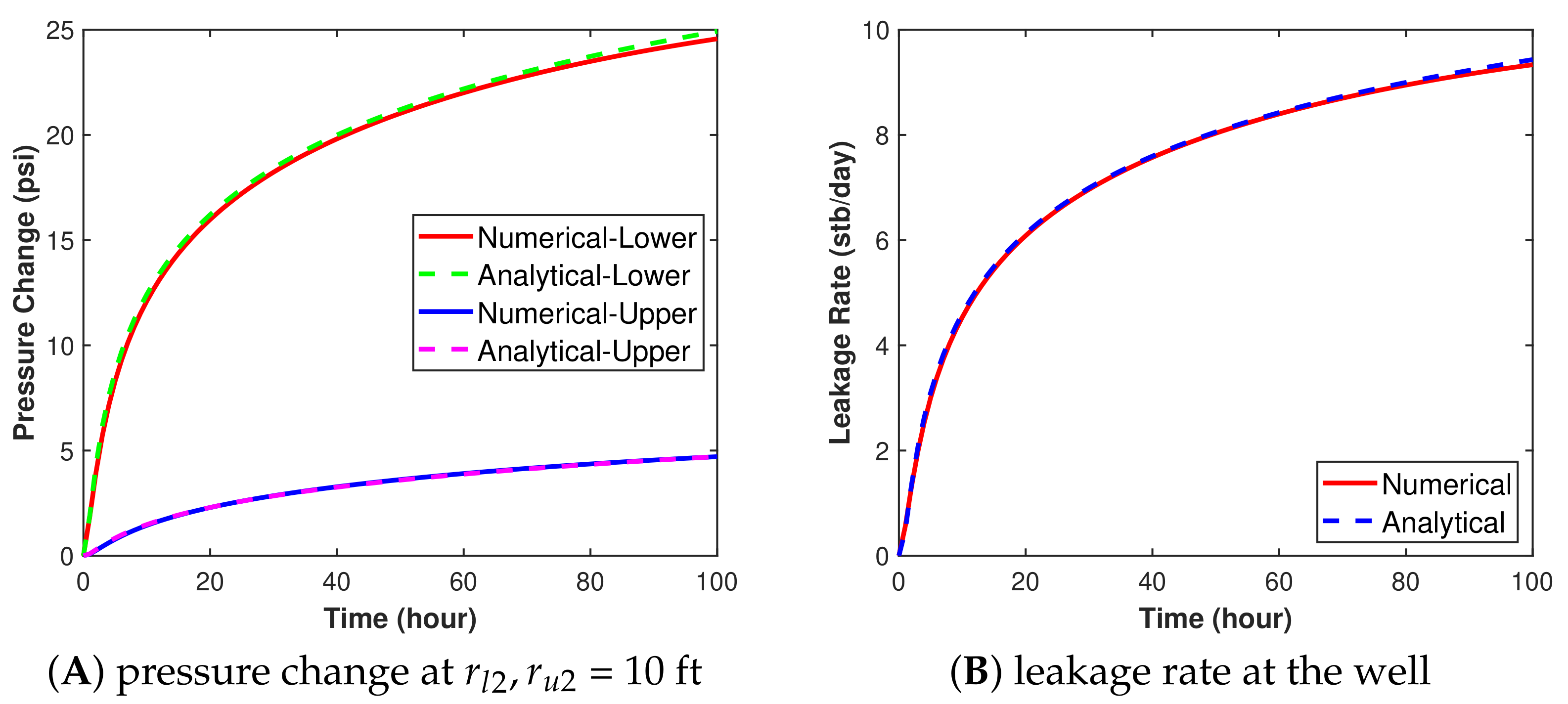
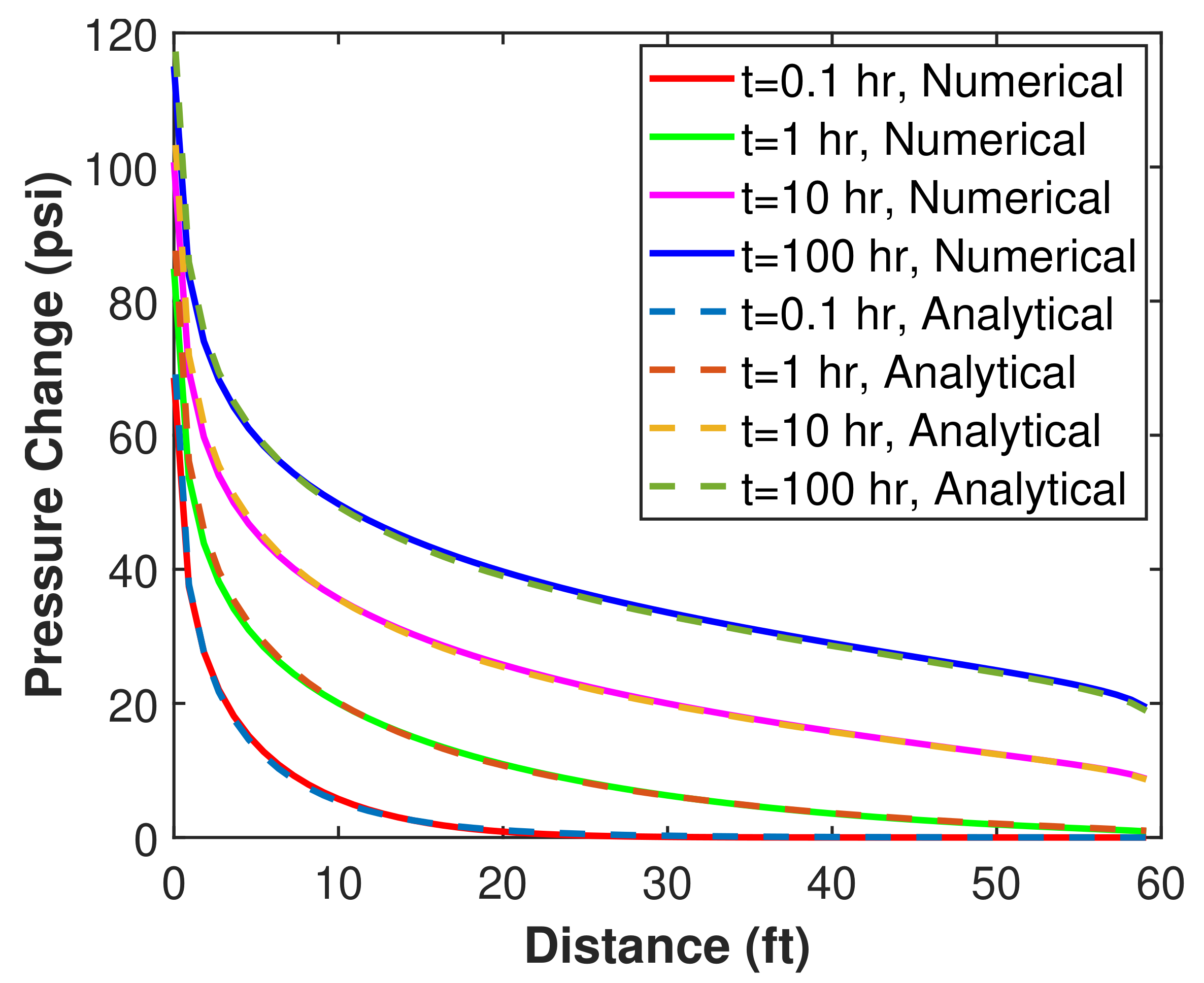
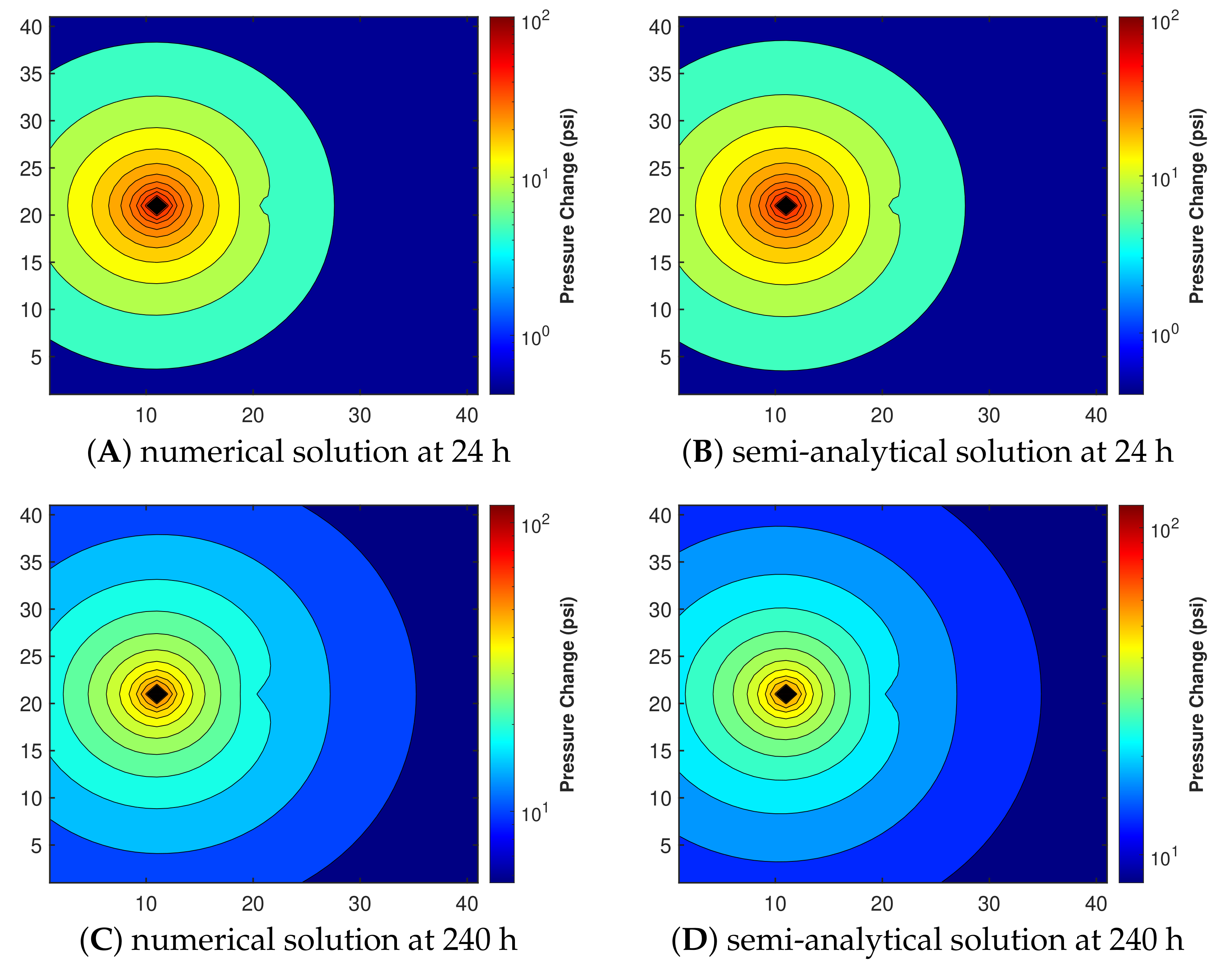
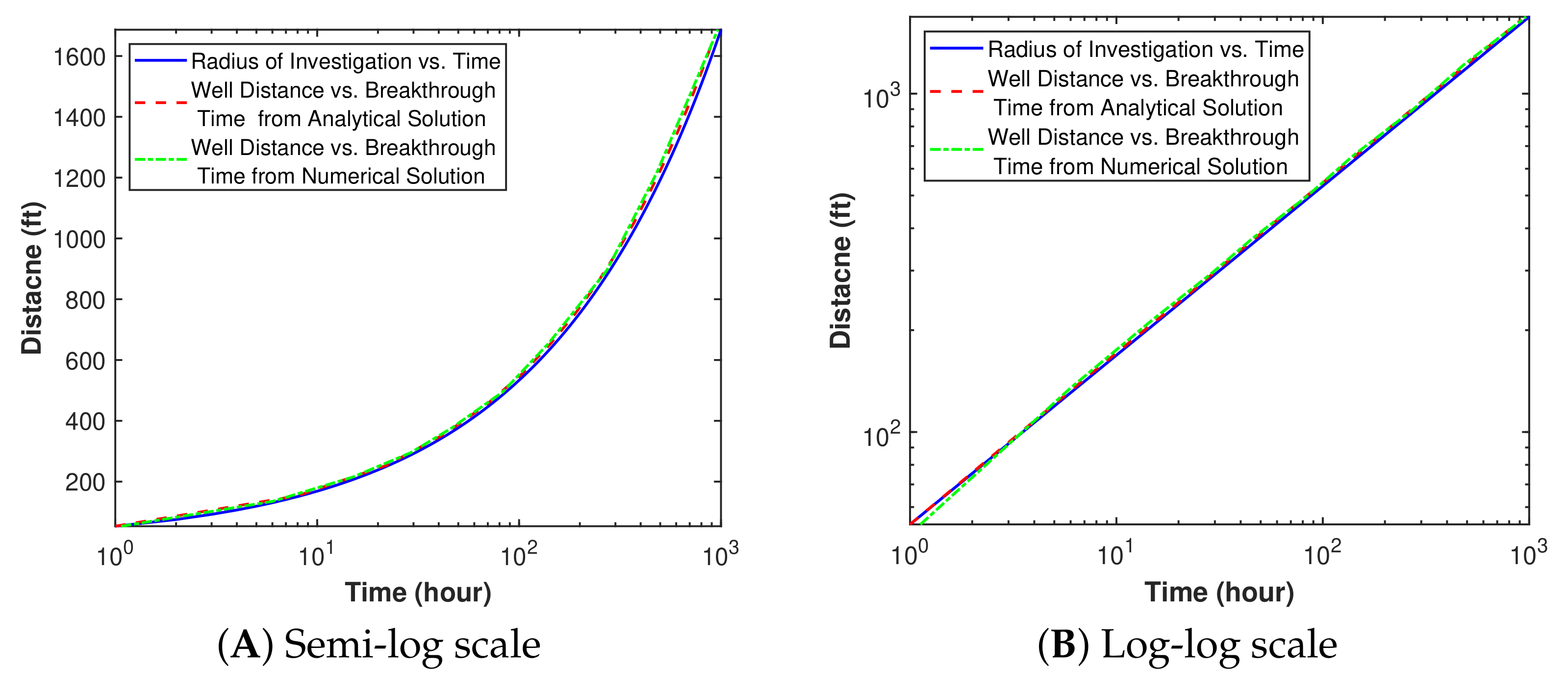
7.2. Solution Verification
7.3. Sensitivity Analysis
8. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| a | Constant parameters related to the reservoir and fluid properties |
| b | Constant parameters related to the reservoir and fluid properties |
| B | Volume formation factor |
| C | Rock/fluid compressibility |
| h | Layer thickness |
| k | Permeability |
| p | Fluid pressure |
| q | Fluid rate |
| r | Radial distance |
| t | Time |
| ϕ | Porosity |
| Ω | Flow resistance within the leaky well |
| α | Unit conversion constant |
| μ | Fluid viscosity |
References
- Dai, A. Drought under global warming: A review. Wiley Interdiscip. Rev. Clim. Chang. 2011, 2, 45–65. [Google Scholar] [CrossRef]
- Emanuel, K. Global warming effects on U.S. hurricane damage. Weather Clim. Soc. 2011, 3, 261–268. [Google Scholar] [CrossRef]
- Meehl, G.A.; Washington, W.M.; Collins, W.D.; Arblaster, J.M.; Hu, A.; Buja, L.E.; Strand, W.G.; Teng, H. How much more global warming and sea level rise? Science 2005, 307, 1769–1772. [Google Scholar] [CrossRef] [PubMed]
- Mousavi, M.E.; Irish, J.L.; Frey, A.E.; Olivera, F.; Edge, B.L. Global warming and hurricanes: The potential impact of hurricane intensification and sea level rise on coastal flooding. Clim. Chang. 2011, 104, 575–597. [Google Scholar] [CrossRef]
- Schiermeier, Q. Increased flood risk linked to global warming. Nature 2011, 470, 316. [Google Scholar] [CrossRef]
- Lashof, D.A.; Ahuja, D.R. Relative contributions of greenhouse gas emissions to global warming. Nature 1990, 344, 529–531. [Google Scholar] [CrossRef]
- Olivier, J.G.J.; Peters, J. Trends in Global CO2 and Total Greenhouse Gas Emissions: Report 2019; PBL Netherlands Environmental Assessment Agency: The Hague, The Netherlands, 2020; Volume 2020, p. 70. [Google Scholar]
- Bachu, S.; Bonijoly, D.; Bradshaw, J.; Burruss, R.; Holloway, S.; Christensen, N.P.; Mathiassen, O.M. CO2 storage capacity estimation: Methodology and gaps. Int. J. Greenh. Gas Control 2007, 1, 430–443. [Google Scholar] [CrossRef]
- IEA. CCUS in Clean Energy Transitions; IEA: Paris, France, 2020; Available online: https://www.iea.org/reports/ccus-in-clean-energy-transitions (accessed on 1 September 2020).
- Hoteit, H.; Fahs, M.; Soltanian, M.R. Assessment of CO2 injectivity during sequestration in depleted gas reservoirs. Geosciences 2019, 9, 199. [Google Scholar] [CrossRef]
- De Silva, P.N.K.; Ranjith, P.G. A study of methodologies for CO2 storage capacity estimation of saline aquifers. Fuel 2012, 93, 13–27. [Google Scholar] [CrossRef]
- Jia, B.; Tsau, J.S.; Barati, R. A review of the current progress of CO2 injection EOR and carbon storage in shale oil reservoirs. Fuel 2019, 236, 404–427. [Google Scholar] [CrossRef]
- Albattat, R.; Hoteit, H. A Semi-Analytical Approach to Model Drilling Fluid Leakage Into Fractured Formation. arXiv 2015, arXiv:2011.04746. [Google Scholar]
- Bachu, S.; Bennion, D.B. Experimental assessment of brine and/or CO2 leakage through well cements at reservoir conditions. Int. J. Greenh. Gas Control 2009, 3, 494–501. [Google Scholar] [CrossRef]
- Celia, M.A.; Bachu, S.; Nordbotten, J.M.; Gasda, S.E.; Dahle, H.K. Quantitative Estimation of CO2 Leakage from Geological Storage: Analytical Models, Numerical Models, and Data Needs; Elsevier Science Ltd.: Oxford, UK, 2005; pp. 663–671. [Google Scholar] [CrossRef]
- Koohbor, B.; Fahs, M.; Hoteit, H.; Doummar, J.; Younes, A.; Belfort, B. An advanced discrete fracture model for variably saturated flow in fractured porous media. Adv. Water Resour. 2020, 140. [Google Scholar] [CrossRef]
- Mehana, M.; Hosseini, S.A.; Meckel, T.A.; Viswanathan, H. Modeling CO2 plume migration using an invasion-percolation approach that includes dissolution. Greenh. Gases Sci. Technol. 2020, 10, 283–295. [Google Scholar] [CrossRef]
- Nicot, J.P.; Oldenburg, C.M.; Houseworth, J.E.; Choi, J.W. Analysis of potential leakage pathways at the Cranfield, MS, USA, CO2 sequestration site. Int. J. Greenh. Gas Control 2013, 18, 388–400. [Google Scholar] [CrossRef]
- Bielicki, J.M.; Pollak, M.F.; Deng, H.; Wilson, E.J.; Fitts, J.P.; Peters, C.A. The Leakage Risk Monetization Model for Geologic CO2 Storage. Environ. Sci. Technol. 2016, 50, 4923–4931. [Google Scholar] [CrossRef]
- Ran, X. Advanced Water Injection for Low Permeability Reservoirs: Theory and Practice; Gulf Professional Publishing: Oxford, UK, 2013. [Google Scholar]
- Syed, T.; Cutler, T. Well integrity technical and regulatory considerations for CO2 injection wells. In Proceedings of the SPE International Conference on Health, Safety and Environment in Oil and Gas Exploration and Production, Rio de Janeiro, Brazil, 12–14 April 2010; Volume 1, pp. 80–96. [Google Scholar] [CrossRef]
- Janiga, D.; Wojnarowski, P.; Stopa, J.; Czarnota, R. Technical conditions of well application for EOR-CCS project in Polish conditions. Int. Multidiscip. Sci. Geoconf. SGEM 2015, 1, 821. [Google Scholar]
- Dusseault, M.B.; Gray, M.N.; Nawrocki, P.A. Why Oilwells Leak: Cement Behavior and Long-Term Consequences. In Proceedings of the International Oil and Gas Conference and Exhibition in China, Beijing, China, 7–10 November 2000; pp. 623–630. [Google Scholar] [CrossRef]
- Gasda, S.E.; Bachu, S.; Celia, M.A. Spatial characterization of the location of potentially leaky wells penetrating a deep saline aquifer in a mature sedimentary basin. Environ. Geol. 2004, 46, 707–720. [Google Scholar] [CrossRef]
- Wisen, J.; Chesnaux, R.; Werring, J.; Wendling, G.; Baudron, P.; Barbecot, F. A portrait of wellbore leakage in northeastern British Columbia, Canada. Proc. Natl. Acad. Sci. USA 2020, 117, 913–922. [Google Scholar] [CrossRef]
- Guo, B.; Bandilla, K.W.; Doster, F.; Keilegavlen, E.; Celia, M.A. A vertically integrated model with vertical dynamics for CO2 storage. Water Resour. Res. 2014, 50, 6269–6284. [Google Scholar] [CrossRef]
- Busch, A.; Kampman, N. Migration and Leakage of CO2 From Deep Geological Storage Sites. In Geological Carbon Storage; American Geophysical Union (AGU): Washington, DC, USA, 2018; Chapter 14; pp. 283–303. [Google Scholar] [CrossRef]
- Humez, P.; Audigane, P.; Lions, J.; Chiaberge, C.; Bellenfant, G. Modeling of CO2 Leakage up Through an Abandoned Well from Deep Saline Aquifer to Shallow Fresh Groundwaters. Transp. Porous Media 2011, 90, 153–181. [Google Scholar] [CrossRef]
- Pawar, R.J.; Watson, T.L.; Gable, C.W. Numerical Simulation of CO2 Leakage through Abandoned Wells: Model for an Abandoned Site with Observed Gas Migration in Alberta, Canada. Energy Procedia 2009, 1, 3625–3632. [Google Scholar] [CrossRef]
- Hayek, M.; Mouche, E.; Mügler, C. Modeling vertical stratification of CO2 injected into a deep layered aquifer. Adv. Water Resour. 2009, 32, 450–462. [Google Scholar] [CrossRef]
- Hayek, M.; Younes, A.; Zouali, J.; Fajraoui, N.; Fahs, M. Analytical solution and Bayesian inference for interference pumping tests in fractal dual-porosity media. Comput. Geosci. 2018, 22, 413–421. [Google Scholar] [CrossRef]
- Shao, Q.; Fahs, M.; Hoteit, H.; Carrera, J.; Ackerer, P.; Younes, A. A 3-D Semianalytical Solution for Density-Driven Flow in Porous Media. Water Resour. Res. 2018, 54, 10094–10116. [Google Scholar] [CrossRef]
- Avci, C.B. Evaluation of flow leakage through abandoned wells and boreholes. Water Resour. Res. 1994, 30, 2565–2578. [Google Scholar] [CrossRef]
- Javandel, I.; Tsang, C.F.; Witherspoon, P.A.; Morganwalp, D. Hydrologic detection of abandoned wells near proposed injection wells for hazardous waste disposal. Water Resour. Res. 1988, 24, 261–270. [Google Scholar] [CrossRef]
- Nordbotten, J.M.; Celia, M.A.; Bachu, S. Analytical solutions for leakage rates through abandoned wells. Water Resour. Res. 2004, 40. [Google Scholar] [CrossRef]
- Nordbotten, J.M.; Celia, M.A.; Bachu, S.; Dahle, H.K. Semianalytical solution for CO2 leakage through an abandoned well. Environ. Sci. Technol. 2005, 39, 602–611. [Google Scholar] [CrossRef]
- Nordboiten, J.M.; Kavetski, D.; Celia, M.A.; Bachu, S. Model for CO2 leakage including multiple geological layers and multiple leaky wells. Environ. Sci. Technol. 2009, 43, 743–749. [Google Scholar] [CrossRef]
- Zeidouni, M.; Pooladi-Darvish, M. Leakage characterization through above-zone pressure monitoring: 2-Design considerations with application to CO2 storage in saline aquifers. J. Pet. Sci. Eng. 2012, 98–99, 69–82. [Google Scholar] [CrossRef]
- Zeidouni, M.; Vilarrasa, V. Identification of above-zone pressure perturbations caused by leakage from those induced by deformation. Environ. Earth Sci. 2016, 75. [Google Scholar] [CrossRef]
- Zeidouni, M.; Tran, N.H.; Munawar, M.D. Interpretation of above-zone pressure influence time to characterize CO2 leakage. Greenh. Gases Sci. Technol. 2017, 7, 1050–1064. [Google Scholar] [CrossRef]
- Ahmadi, M.A.; Chen, Z. Analytical Model for Leakage Detection in CO2 Sequestration in Deep Saline Aquifers: Application to ex Situ and in Situ CO2 Sequestration Processes. ACS Omega 2019, 4, 21381–21394. [Google Scholar] [CrossRef] [PubMed]
- Cihan, A.; Zhou, Q.; Birkholzer, J.T. Analytical solutions for pressure perturbation and fluid leakage through aquitards and wells in multilayered-aquifer systems. Water Resour. Res. 2011, 47, 1–17. [Google Scholar] [CrossRef]
- Cihan, A.; Birkholzer, J.T.; Zhou, Q. Pressure Buildup and Brine Migration During CO2 Storage in Multilayered Aquifers. GroundWater 2013, 51, 252–267. [Google Scholar] [CrossRef]
- Mu, L.; Liao, X.; Zhao, X.; Zhang, J.; Zou, J.; Chen, L.L.; Chu, H. Analytical model of leakage through an incomplete-sealed well. J. Nat. Gas Sci. Eng. 2020, 77, 103256. [Google Scholar] [CrossRef]
- Zeidouni, M. Analytical model of well leakage pressure perturbations in a closed aquifer system. Adv. Water Resour. 2014, 69, 13–22. [Google Scholar] [CrossRef]
- Oruganti, Y.D.; Bryant, S.L. Pressure build-up during CO2 storage in partially confined aquifers. Energy Procedia 2009, 1, 3315–3322. [Google Scholar] [CrossRef]
- Lee, J.; Rollins, J.B.; Spivey, J.P. Pressure Transient Testing; Henry, L., Ed.; Doherty Memorial Fund of AIME, Society of Petroleum Engineers: Richardson, TX, USA, 2003. [Google Scholar]
- Al-Kobaisi, M.; Ozkan, E.; Kazemi, H.; Ramirez, B. Pressure-Transient-Analysis of Horizontal Wells with Transverse, Finite-Conductivity Fractures. In Proceedings of the Canadian International Petroleum Conference, Calgary, AB, Canada, 13–15 June 2006. [Google Scholar] [CrossRef]
- Theis, C.V. The relation between the lowering of the piezometric surface and the rate and duration of discharge of a well using ground-water storage. EOS Trans. Am. Geophys. Union 1935, 16, 519–524. [Google Scholar] [CrossRef]
- Mao, Y.; Zeidouni, M.; Duncan, I. Temperature analysis for early detection and rate estimation of CO2 wellbore leakage. Int. J. Greenh. Gas Control 2017, 67, 20–30. [Google Scholar] [CrossRef]
- Stewart, G. Well Test Design & Analysis; PennWell Corporation: Tulsa, OK, USA, 2011. [Google Scholar]


| Porosity for both layers (dimensionless) | 0.3 |
| Rock compressibility (1/psi) | 9 × 10−6 |
| Fluid compressibility (1/psi) | 3 × 10−6 |
| Fluid density (lb/ft3) | 62 |
| Permeabilities of both layers (mD) | 10 |
| Viscosity (cp) | 1 |
| Injection rate (STB/D) | 100 |
| Well distance (ft) | 60 |
| Wellbore radius of the abandoned well (ft) | 0.5 |
| Resistance of abandoned well (psi/(STB/D)) | 1 |
| Layer thickness (ft) for both layers | 100 |
| Reservoir thickness (ft) | 300 |
| Reservoir length (ft) | 10,100 |
| Reservoir width (ft) | 10,100 |
| Number of grid blocks in the x-direction | 101 |
| Number of grid blocks in the y-direction | 101 |
| Number of grid blocks in the z-direction | 10 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qiao, T.; Hoteit, H.; Fahs, M. Semi-Analytical Solution to Assess CO2 Leakage in the Subsurface through Abandoned Wells. Energies 2021, 14, 2452. https://doi.org/10.3390/en14092452
Qiao T, Hoteit H, Fahs M. Semi-Analytical Solution to Assess CO2 Leakage in the Subsurface through Abandoned Wells. Energies. 2021; 14(9):2452. https://doi.org/10.3390/en14092452
Chicago/Turabian StyleQiao, Tian, Hussein Hoteit, and Marwan Fahs. 2021. "Semi-Analytical Solution to Assess CO2 Leakage in the Subsurface through Abandoned Wells" Energies 14, no. 9: 2452. https://doi.org/10.3390/en14092452
APA StyleQiao, T., Hoteit, H., & Fahs, M. (2021). Semi-Analytical Solution to Assess CO2 Leakage in the Subsurface through Abandoned Wells. Energies, 14(9), 2452. https://doi.org/10.3390/en14092452








