1. Introduction
The production of bioethanol is a current topic raised by scientists, technologists, and representatives of fuel companies in the European Union who are working on satisfying the percentage share of this biocomponent in conventional fuels. The policy of the European Union countries is aimed at the search for low-emission technology, which is sustainable and aimed at reducing CO2 production at relatively low cost of production lines. Taking this into account, research targeting the development of bioethanol preparation from the available lignocellulosic biomass, using the existing production lines or innovative pretreatment methods, is an important topic. The preparation of bioethanol is a complex procedure, the success of which hinges primarily on the use of raw material that is inexpensive, available in every region of Europe, and has effective and cost-efficient pretreatment, which will result in a high yield of fermenting sugars.
Numerous examples of the production of fermenting sugars from lignocellulose can be found in the literature. A large portion of these publications contain data on the impact of pretreatment on enzymatic hydrolysis of the biomass. The most common include treatments using ammonia fiber expansion (AFEX), steam explosion, ionic liquids (ILs) and other methods [
1,
2,
3,
4,
5]. There are numerous examples of conversion of rye, corn, rice, wheat straw, poplar, willow, and coniferous tree chips into bioethanol based on the method using pretreatment with ionic liquids and enzymatic hydrolysis [
6,
7,
8,
9,
10]. However, comparison of the majority of the data has proven to be difficult due to various amounts of substrates used for the process or other pretreatment parameters. Therefore, the use of literature data to design the bioethanol production process at a greater scale is very complicated and problematic. In this study, an attempt was made to create a model that would allow for the estimation or prediction of bioethanol concentration from various lignocellulosic raw materials. Such a model would allow the classification of biomass for bioethanol production on the basis of its chemical composition and facilitate choice of a suitable ionic liquid and enzyme preparation used for pretreatment. Such an approach would save time and costs in laboratory research, which is now a way to search for ideal production methods and an efficient source of lignocellulosic biomass.
Mathematical and statistical models provide essential information for understanding, analyzing, and predicting biological processes, and are necessary to optimize key parameters to improve process performance. Modeling and optimization of biofuel manufacturing processes will contribute to a better understanding of the process expenditures in order to obtain the optimum efficiency. The main purpose of modeling is to optimize the operations involved in their production in order to achieve efficiency improvement [
11,
12,
13].
Artificial intelligence tools have appeared as a promising method for modeling and optimizing bioprocesses. In the last decade, artificial neural networks (ANNs) were applied in multidimensional, nonlinear research and development of bioprocesses. They have been found effective in developing bioprocess models devoid of prior information on the kinetics and metabolic flows occurring in cells and cell surroundings [
14]. Furthermore, ANN are completely based on data, without prior knowledge on the events regulating the process [
15]. The appeal of ANN as a modeling tool derives from their unique functions of processing information that is assigned primarily—linearity, high parallelism, and error and noise acceptance—as well as their capability to learn and generalize. ANNs have gained much attention from significant soft computing tools that are not only limited to data processing and analysis, but can also be used to solve problems in multifaceted and nonlinear processes [
16].
For these reasons, the aim of this study was to collect the current data on the production of bioethanol from lignocellulosic biomass using ionic liquids and to create a model that can be used to predict ethanol concentration from lignocellulosic raw materials. For this purpose, machine learning (ML) methods were used. Increased interest in the use of ML procedures has been observed, e.g., artificial neural networks (ANNs) and random forests (RFs) in the context of bioethanol production from biomass [
17,
18,
19,
20]. With the use of these algorithms, it was assumed that on the basis of the results of laboratory tests obtained, it will be possible to predict the concentration of bioethanol in various biomass species based on their lignocellulosic composition. This would aid the classification of biomass type to the suitable ionic liquid or type of cellulolytic enzyme. This preliminary estimation in the case of laboratory studies is important because in this way the costs associated with the synthesis or purchase of ionic liquid and enzymes can be kept to the minimum. It would be possible to perform more rapid verification and grouping of plant types that are found in the given region. Such model could also inspire classification of other pretreatments, and ML data could be applied to a wider extent in scaling-up processes. In order to reduce the costs of the process, plants can be grouped in terms of similarities in their cellulose content, affinity for ionic liquids, and their influence on the exposure of cellulose fibers or the selection of cellulolytic enzymes for the appropriate type of biomass.
In the present study, the prognostic model was verified by empirical studies of bioethanol production from hemp (
Cannabis sativa L.) and mugwort (
Artemisia vulgaris L.). The stems of hemp contain high amounts of cellulose (up to 80%), with lignin content of about 15–20%. In addition, it is a plant that is increasingly commonly grown for the production of oil, fiber, essential oils, etc. The use of both plants properly fit in the criteria of sustainable development, especially considering their biological and agrotechnical properties, which makes them economically and environmentally favorable. The properties exhibited by this biomass source make them admirable for the development of multiprocessor systems by gradually separating the biomass into several useful components. This trait provides hemp with an advantage over other industrial crops, as they are usually used for extraction of one component [
21,
22]. As far as energy consumption is concerned, it is necessary to emphasize that the mean yield value of green hemp plants was 14.5 t/ha [
23] (by means of dry weight). It is possible to obtain about 10.5 t/ha of raw material, which can be potentially used for energy purposes [
24]. Parts of the stems that were considered waste or could be used for the production of solid fuel (pellets) were used to produce bioethanol. For contrast, mugwort was used, which is a plant commonly viewed as a weed, growing in arable land as well as boundary strips and agricultural wastelands. This plant possesses approximately 1–1.5 m stems with 35% cellulose content, 25% lignin, and approximately 20% hemicellulose. Mugwort is a native species to Poland. It was introduced to North America, where it has spread and is treated as an invasive species. The mugwort species found in Europe are typically weed and ruderal plants. Common mugwort is the most widespread species. It is characterized by high growth force and good regenerative abilities. New plants can emerge from even finely cut rhizome fragments [
25,
26].
The production of bioethanol from lignocellulose could become profitable if the costs associated with the production of biomass are very low. Each geographic region is distinguished by a great variety of flora. These can be found in many literature reports stating that the success of the bioethanol production process is influenced by the biomass composition: proportions of cellulose, hemicellulose, and lignin; and the type of fiber arrangement, and thus also the plant species and the degree of its maturity. Taking all these factors into account, it becomes very difficult to test all plant species that could potentially form a good source for the production of bioethanol. Therefore, it is easier to use energy crops for the production of bioethanol. A mathematical model based on experimental data can be a helpful tool in determining the suitability of a plant species for processing into bioethanol. The production of bioethanol is one of the biotechnological processes the complexity of which is high and difficult to present via ready-made algorithms. Therefore, in such situations it is perfect to use ML, including e.g., ANN or RF, as a prediction tool for future biomass samples. This publication attempts to create a model based on experimental data of the bioethanol production process from biomass on a laboratory scale and validate this model based on the results of the experiment—fermentation of hemp and mugwort stems.
2. Materials and Methods
2.1. Raw Materials
Two plant species were used for model validation: stems of hemp, cultivar Finola (plant collection of the Department of Agrobiotechnology, Koszalin University of Technology) and common mugwort stems collected from agricultural wastelands. Stems of mugwort were taken from two wastelands and hemp samples from two extreme cultivation sites within 30 km from Koszalin (N 54°11′26.11″, E 16°10′53.77″), and then the bioethanol production process was carried out for each sample separately in triplicate. The mean values of three replicates for four biomass samples are presented in
Table 1. The biomass was collected in late autumn (second half of October 2019). The stems were dried and ground, then the material was pretreated using different ionic liquids.
2.2. Ionic Liquids (ILs)
For the pretreatment of cellulose-rich material, five ILs from imidazolium and ammonium groups were chosen. Three were commercially available (Iolitech GmbH, Germany) imidazolium ILs: 1-ethyl-3-methylimidazolium acetate ([EMIM][OAc]), 1-butyl-3-methylimidazolium acetate ([BMIM][OAc]), and 1-ethyl-3-methylimidazolium diethyl phosphate ([EMIM][DEP]). The remaining two, belonging to the group of ammonium ILs, were synthesized for the study: butyl(cyclohexyl)dimethylammonium acetate (([CHDMA-C4][OAc]) and (cyclohexyl) hexyldimethylammonium acetate ([CHDMA-C6][OAc]).
2.3. Synthesis of [CHDMA-C4][OAc] and [CHDMA-C6][OAc] Ionic Liquids
Synthesis of [CHDMA-C4][OAc] and [CHDMA-C6][OAc], and its bromide precursors was conducted according to a previous work, where apart from the synthetic route, full characteristics and cellulose dissolution were also described [
27]. In that way, appropriate bromides were prepared in a quaternization reaction between cyclohexyldimethylamine and an appropriate 1-bromoalkane with 10% extension, in acetonitrile, at room temperature for 72 h. The crude product was obtained by evaporation of the reaction background in a rotary evaporator. After the ethyl acetate addition, the prepared bromides were filtered and dried at 40 °C under reduced pressure for 48 h (vacuum dryer). The product was then kept in a desiccator to avoid moisture uptake from the environment. The second step of the ILs preparation was the anion exchange reaction between quaternary bromide and acetic acid. An appropriate bromide (with hexyl or butyl substituent) was dissolved in methanol. To this solution, a previously prepared stoichiometric amount of KOH dissolved in methanol was added. The solutions were stirred for 3 h at ambient temperature. Partially precipitated side product (KBr) was filtrated and an appropriate (stoichiometric) amount of acetic acid was added to the reaction mixture. Solutions were further stirred at the same conditions for 1 h and the reaction background was evaporated in a rotary evaporator (40 °C). The crude product was purified with the addition of anhydrous acetone. The remaining potassium bromide was filtered, and solvent once again removed (rotary evaporator) to give the final product. The ILs obtained ([CHDMA-C4][OAc] and [CHDMA-C6][OAc] were finally dried for 48 h under reduced pressure in a vacuum dryer.
2.4. Pretreatment, Enzymatic Hydrolysis, and Alcoholic Fermentation
Imidazolium ILs, namely [EMIM][OAc], [BMIM][OAc], [EMIM][DEP], [CHDMA-C4][OAc], and [CHDMA-C6][OAc] were used for biomass purification. To achieve this, solutions of appropriate ground material (5 g) and a specific IL (50 mL) were prepared, which were further subjected to homogenization (2 min) and incubation at 120 °C for 2 h. Samples were afterwards left to cool to room temperature. In the next step, the cellulose fibers were isolated via thorough rinsing of the prepared mixture with deionized water. This was repeated at least three times, to the point of total IL removal. The solid fraction obtained was further dissolved in a 50 mM acetate buffer with a pH equal to 5.0 (100 mL). Enzymatic hydrolysis was then performed on the pretreated and nontreated lignocellulosic biomass.
For the enzymatic hydrolysis of hemp stems, Cellic CTec2 (Sigma-Merck, Darmstad, Germany) was used at the amount of 20 FPU/g of cellulose. Samples were incubated at 50 °C for 72 h. On the other hand, the mugwort samples were hydrolyzed using the following enzymatic preparations: Cellic CTec2, cellulase from Aspergillus sp., cellulase from T. reesei (Sigma-Merck, Darmstad, Germany). The incubation of biomass fractions mixed with Aspergillus sp. and T. reesei cellulases was performed for 72 h at 47 °C.
Before performing the alcoholic fermentation, the hydrolysate solutions were purified by means of filtration to get rid of any residual lignocellulose. The pH of the fermentation broth was kept constant at 5.0 for each sampling point. The pH control was performed by the adding a solution of H2SO4 (10 wt.%) or NaOH (20 wt.%). Freeze-dried distiller’s yeast Saccharomyces cerevisiae type II (purchased from Sigma-Aldrich) (5%, w/v) were used to initiate ethanol fermentation. This was afterwards allowed to proceed in anaerobic conditions for four days. After fermentation, the samples were further analyzed to establish the ethanol concentrations.
Control samples were hemp and mugwort stalks not pretreated with ionic liquids. Samples were dissolved in an acetate buffer, according to the protocol described for IL pretreated samples. The material was characterized to establish the cellulose, hemicellulose, and lignin content. Glucose content after the process of enzymatic hydrolysis and alcohol concentration after the fermentation process were also determined.
2.5. Analytical Techniques
An Ankom A200 fiber analyzer was used to determine the amounts of lignin/cellulose/hemicellulose in all biomass samples (with the use of filter bag encapsulation). Fiber test results were determined as neutral detergent fibers (NDF) with the use of Van Soest method, and acidic detergent fiber (ADF) and acidic detergent lignin (ADL) according to the standard [
28]. The difference between the ADF and ADL fractional share was the cellulose content, while the difference between NDF and ADF fractional share was the hemicellulose content. High performance liquid chromatography (HPLC) was used to determine the amounts of glucose and ethanol (Merck Hitachi, Darmstadt, Germany). For that purpose, the prepared samples were, in the first step, subjected to centrifugation (10 min, 4000×
g, 4 °C) with the use of a Multifuge 3SR (Darmstadt, Germany) and filtered in the second step using membrane filters with a pore diameter of 0.22 µm (Millex-GS, Millipore, Burlington, MA, USA). An Aminex HPX-87P column (Bio-Rad, Hercules, CA, USA) was used for the separation of glucose and ethanol with a 5 mM solution of H
2SO
4 (mobile phase) at a flow rate of 0.6 mL/min at 30 °C. The detection of glucose and ethanol was performed with a refractive index detector (Model L-7490, Merck Hitachi, Darmstadt, Germany).
4. Results and Discussion
Mugwort is an example of biomass obtained without the need for cultivation and fertilization, with an average cellulose content of 45%, hemicellulose 13.8%, and lignin 20.4%. For comparison, the conversion was also carried out on hemp stalks, which have recently become very popular for functional reasons. Finola hemp stalks had an average cellulose content of 62%, hemicellulose 17%, and lignin 19%. In this study, for the production of bioethanol, ground plant stalks were used and the process was carried out by performing a pretreatment with the use of various ionic liquids and various enzyme preparations. Glucose content in mugwort samples depended on the type of pretreatment and enzyme preparation used.
Table 1 presents glucose contents obtained after 72 h enzymatic hydrolysis, bioethanol content, and chemical composition of hemp and mugwort.
After the enzymatic hydrolysis of mugwort, the highest content of glucose was obtained in the samples where imidazolium ionic liquids ([EMIM][OAc] and [BMIM][OAc]), and Cellic CTec2 for enzymatic hydrolysis were used. A similar relationship was observed in the samples of hemp for reducing sugars, but the results were significantly higher as compared with common mugwort. The content of simple sugars after enzymatic hydrolysis with the use of Cellic CTec2 amounted to 12.27 g/L for material purified with [BMIM][OAc] and 11.32 g/L for biomass purified with [EMIM][OAc]. For comparison, in the sample of native hemp hydrolyzed with Cellic CTec2, 3.2 g/L glucose was obtained after 72 h.
In the experiments with the use of machine learning, including ANN and RF methods for the estimation of bioethanol concentration, results of experiments concerning the processing of hay, agricultural wastelands, and selected energy crops were utilized. The RF method exhibits different advantages than ANN. Each tree represents the learning process and each tree can select traits and samples at random [
33]. The final prediction is obtained by averaging the predictions concerning the trees. This enables efficient avoidance of excessive matching and the effect of single samples [
34]. On the other hand, ANN is characterized by singular correlation or learning process. Furthermore, many earlier studies show that the RF may give better predictions for the same problem [
35,
36].
Experimental data concerning bioethanol production from hemp and mugwort stems were used for the validation of the ANN model. The raw material is characterized by high cellulose content, low lignin content, and better structural properties after processing with ionic liquids; i.e., the material is more porous and there is more area free and available for cellulolytic enzymes; thus enzymatic hydrolysis is facilitated and more efficient. The situation is completely different when a raw material such as common mugwort is used, as its cellulose content is lower by 50% and it contains considerably higher amounts of lignin and hemicellulose. In addition, after dissolution in ionic liquids, common mugwort stems are not deprived of lignin with the same efficiency as for hemp stems. High amounts of lignin remaining in biomass samples directed for enzymatic hydrolysis may be linked to a poorer course of the process, because lignin is an enzyme inhibitor [
37]. In this case, the use of ML methods perfectly reflects the processes of pretreatment and enzymatic hydrolysis processes.
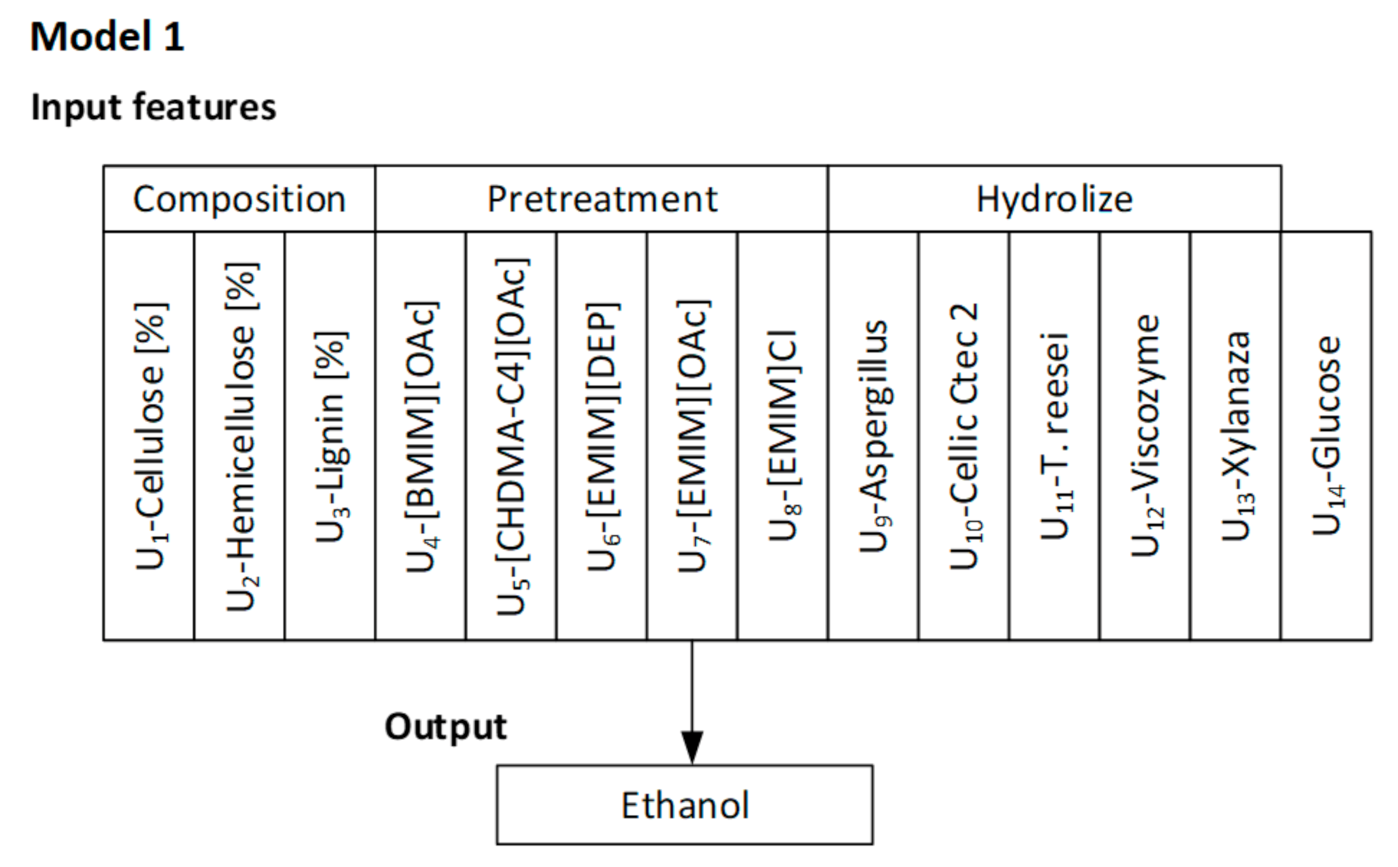
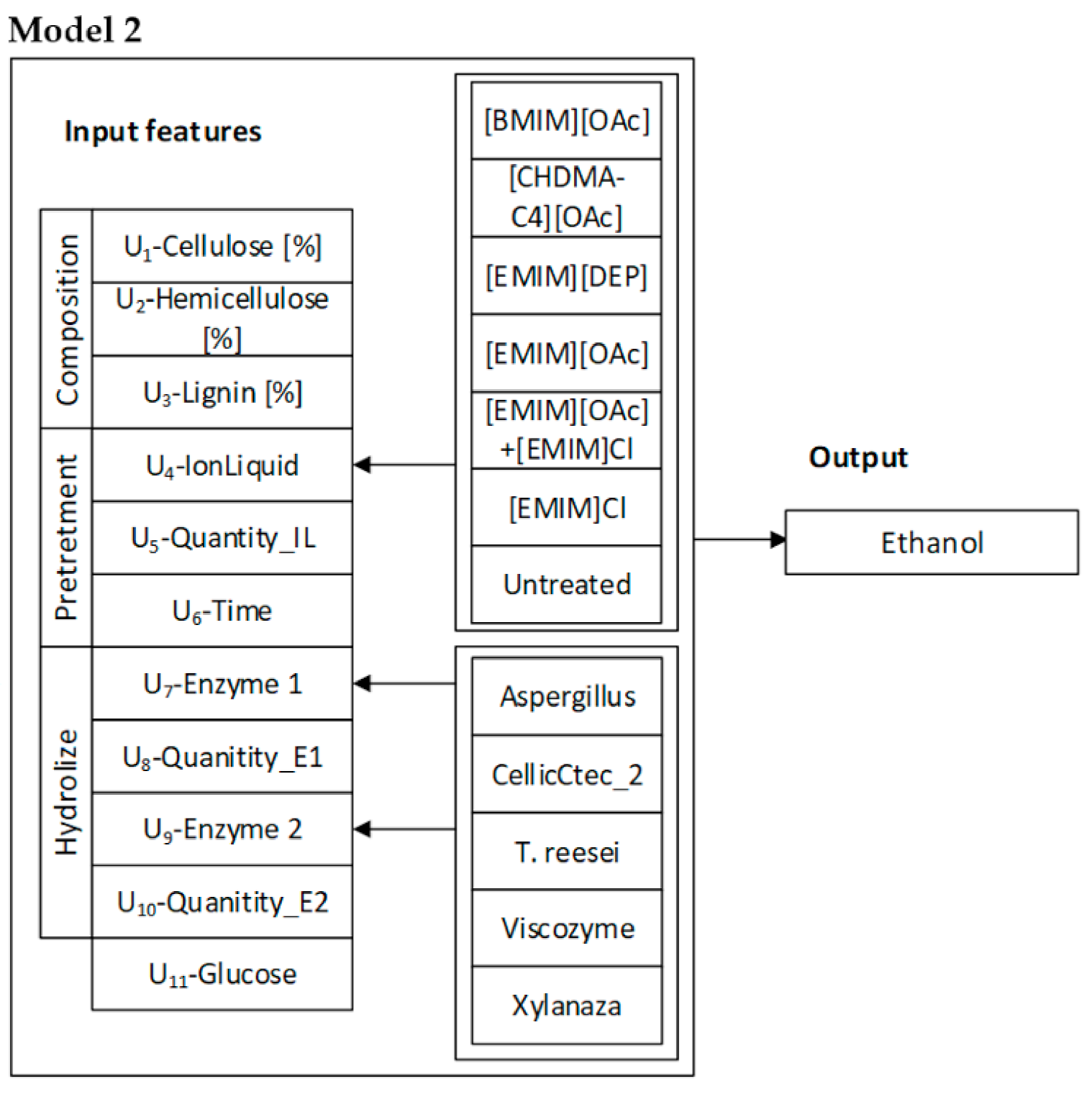
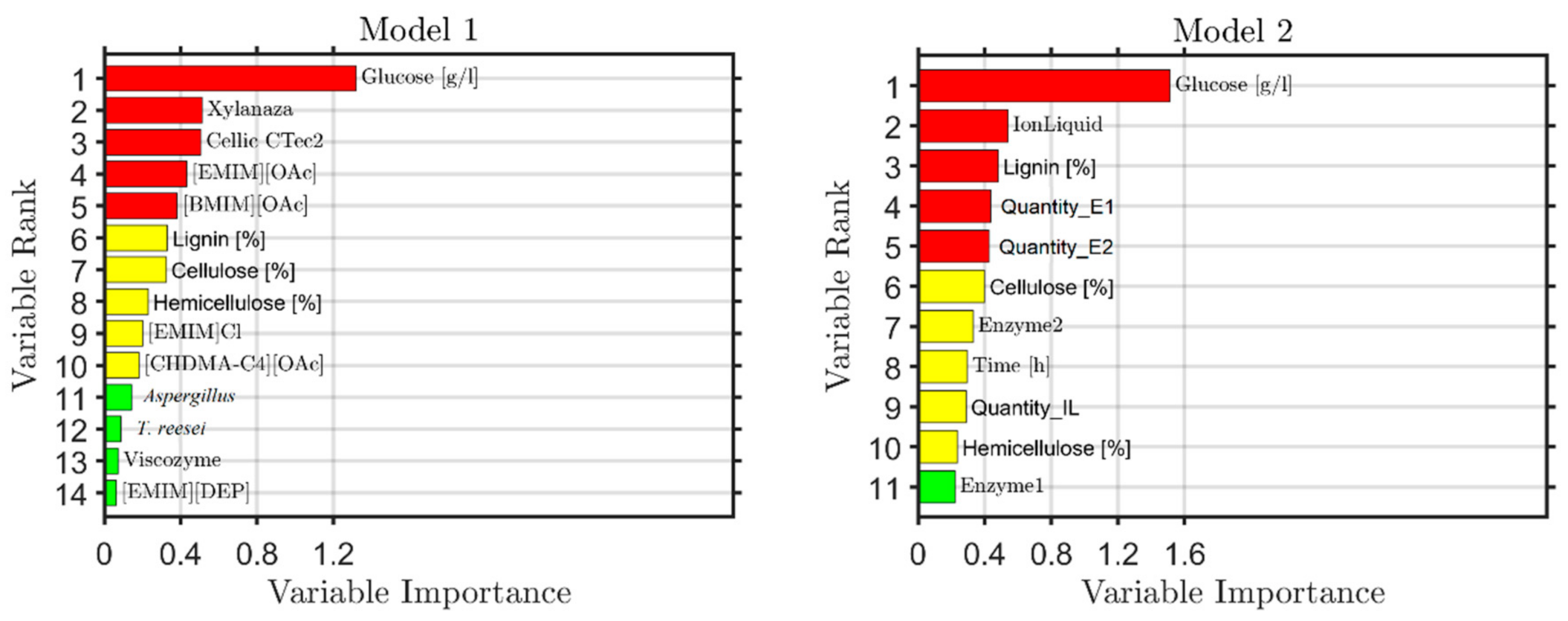
The type of biomass, as well as the contribution of cellulose in the composition of plants, has direct influence on the content of simple sugars, including glucose after enzymatic hydrolysis. Thus, the selection of biomass rich in cellulose, as was the case for hemp stems, should be linked to more efficient ethanol production (
Figure 4). For Model 1, the use of Cellic CTec2 in enzymatic hydrolysis was most important because, regardless of the type of biomass used, i.e., whether it was weed, woody plants, or energy crops, high concentrations of glucose were obtained when the enzyme was used for the hydrolysis. The pretreatment of biomass and type of ionic liquid applied were also significant for Model 1. More favorable results were obtained in the case of imidazolium liquids, and the most important was the use of [EMIM][OAc] and [BMIM][OAc], for both energy crops—hemp, as well as woody weed with higher lignin content. The content of lignin in the biomass composition is another significant factor affecting the reduction of bioethanol production efficiency. In Model 2, this variable is in the third place, whereas second place is taken by the use of ionic liquids as pretreatment type. Dependable variables that affect the described model are also E1 and E2 enzymes, that is,
T. reesei and Cellic CTec2 and their amounts, appropriately selected to the content of cellulose after pretreatment.
The use of xylanase as an additional enzyme in enzymatic hydrolysis resulted in increased content of simple sugars by decomposing hemicellulose, which is linked to cellulose. Enzymatic digestion of hemicellulose resulted in exposing cellulose fibers, which were then digested by cellulase. Therefore, the use of xylanase in such cases directly contributed to the increase of the content of glucose in the samples. Considering the costs of the process, the use of an additional enzyme (xylanase) is not valid.
Ahmadian-Moghadam et al. [
38] examined the influence of the initial concentration of the substrate (molasses), live yeast cells, and dead yeast cells as the input parameters of the process on the production of bioethanol via
Saccharomyces cerevisiae. An R
2 value equal to 0.93 was obtained, which shows that the model was suitable for pattern recognition into data and these patterns precisely predicted ethanol efficiency. In the latest research conducted by Betiku and Taiwo [
39], the influence of breadfruit hydrolysate concentration, hydraulic retention time, and pH on the production of bioethanol was assessed with ANN and response surface methodology (RSM). The ANN had an absolute mean deviation between the predicted and observed value of 0.09%, compared to 1.67% after RSM [
39]. These results further confirm the precision of ANN modeling in comparison with other techniques, such as RSM.
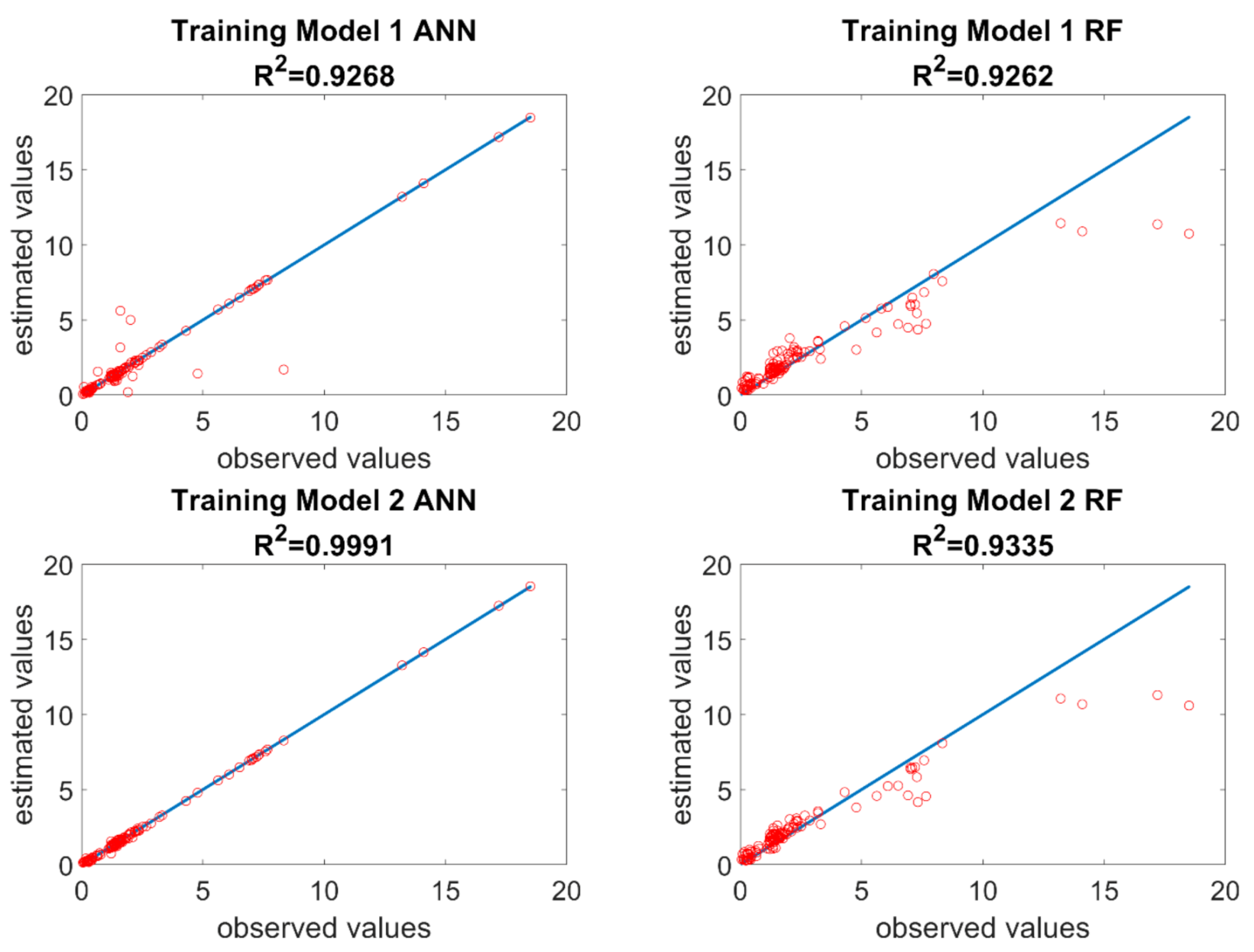
ANN and RF algorithms have a random training start point, thus they were repeated 11 times to ensure higher reliability of the results obtained. The following analyses present results of the iteration whose error was a median of error from 11 replications. In the learning process, the R
2 determination coefficient for Model 1 was 0.92 for ANN and 0.93 for RF. In Model 2, the R
2 coefficient increased to near 1 for ANN, whereas for RF it remained at the same level (
Figure 5).
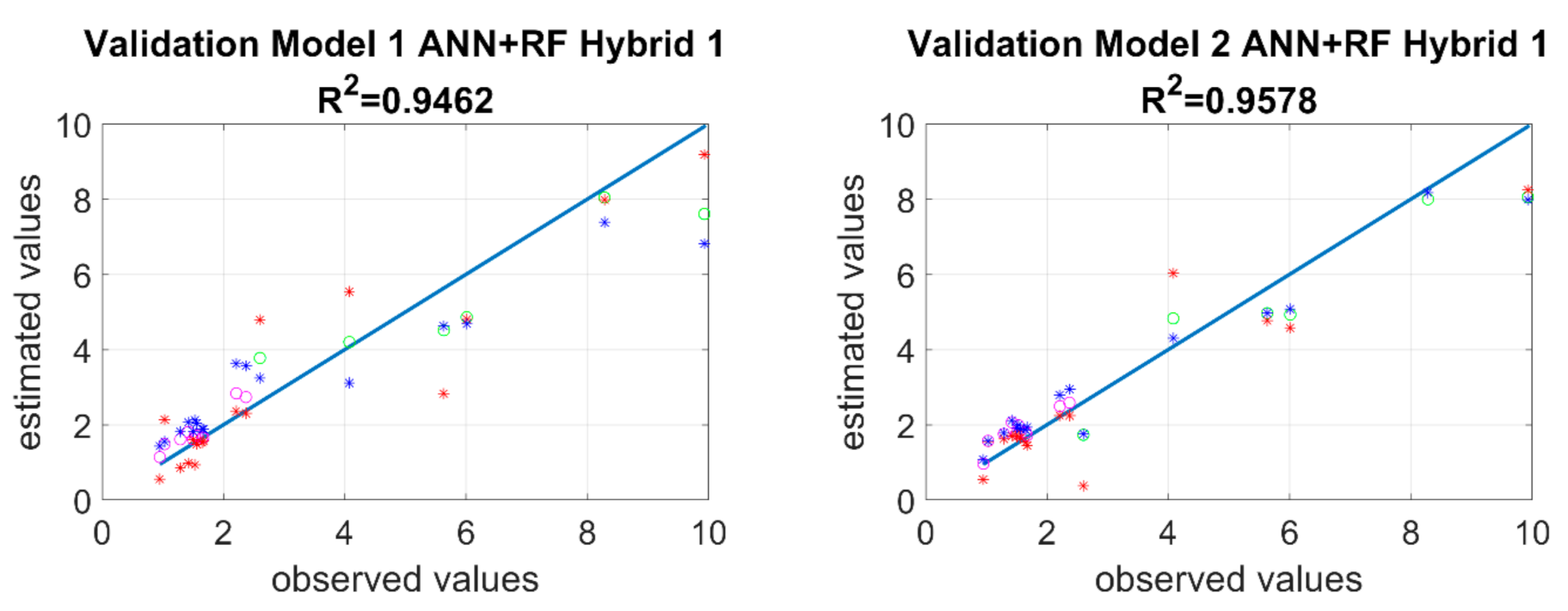
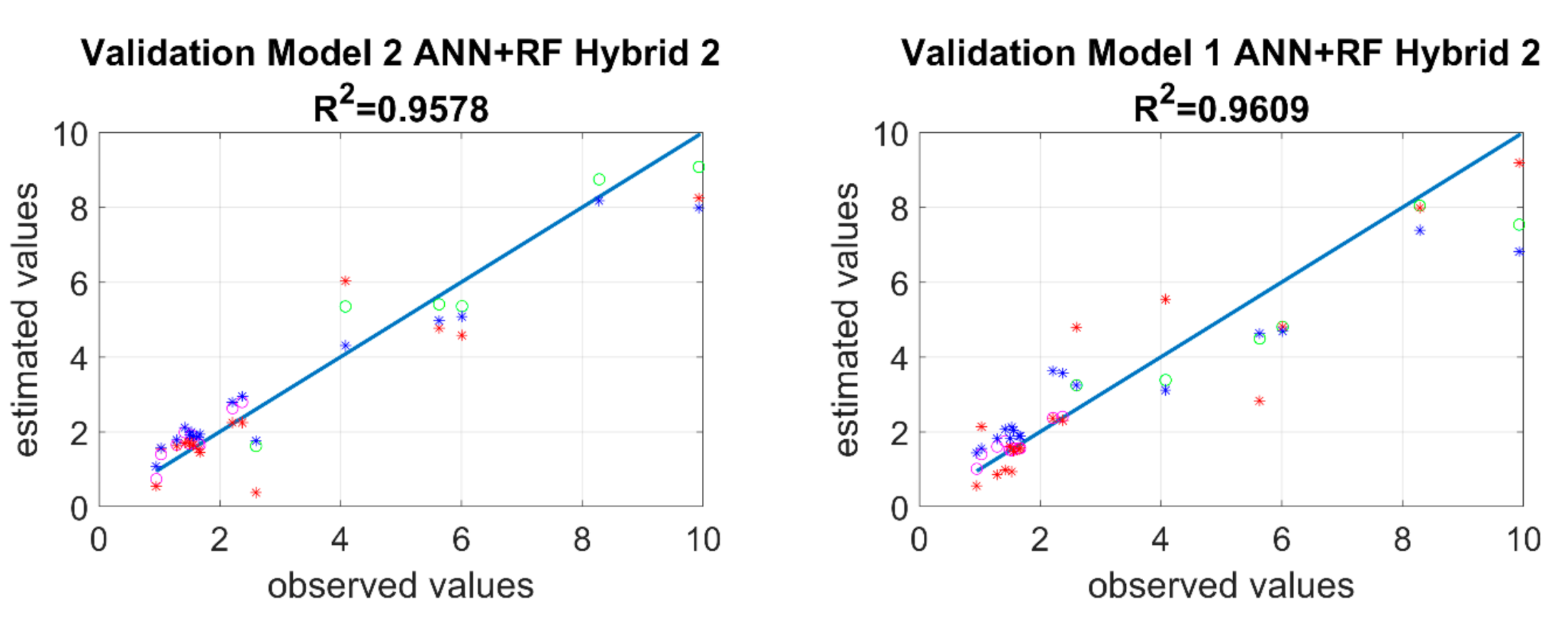
Data for mugwort and hemp were used for validation. In both models, the determination coefficient for neural networks >0.9, whereas for RF it oscillated around 0.95. In the RF training models, there were four wasteland samples whose observed values significantly differ from the estimated values. The ethanol content of these samples was significantly different from the others and due to the principle of operation of the RF algorithm, those samples could not be included. Considering the rather wide dispersion of the determination coefficient, two hybrid models were executed. The first hybrid model (Hybrid 1) consisted of assuming the median from the set of data estimated from 22 replications. The second hybrid model (Hybrid 2) assumed determination of a linear function describing the variables from the entire training set of 22 replications (11 ANN and 11 RF). Subsequently, median from the validation set was calculated, on the basis of which new estimated values were calculated. The last step of the process was to calculate the value closest to estimated values from the set of 22 values. During the calculation of these models, 70% of points in Model 1 from ANN were selected and 75% of points in Model 2 from ANN were selected. When both hybrid models were applied, a clear increase of determination coefficient can be observed with regards to ANN, and a considerable decrease of RMSE (root mean square error), ME (mean error), and MAE (mean absolute error) for mugwort and hemp. Furthermore, mean values (est_mean) and medians (est_median) of estimates were calculated for each model and algorithm.
Table 2 above describes the sum parameters concerning the presented models of bioethanol production from hemp and common mugwort. The R
2 determination coefficient depended on the type of applied model. The hybrid approach in the creation of models explaining this process of bioethanol production resulted in increased match of the model to R
2 = 0.961 for Hybrid 2. In the original calculations, R
2 reached about 0.96 match only for Model 2–RF. Precision of Model 1–Hybrid 2 for the prediction of ethanol production process from biomass is satisfactory and higher than the ANN and RF models. RMSE values for the RF algorithm in each case of validation sample analysis, that is, hemp and mugwort biomass, were lower, and the model was better matched than for ANN. Moreover, differences in R
2 and RMSE relative to the analyzed material can be observed. RMSE was lower for common mugwort samples, the results of which were predicted with the use of ANN. A reverse situation occurred for validation of the model utilizing hemp samples. In this case, lower RMSE with better match of the model (R
2 = 0.961) was obtained for Model 2–RF. Considering that the differences were significant and did not provide a clear answer, it was decided to use a hybrid model, which vastly improved the effects of predicting bioethanol concentrations from lignocellulosic materials and provided a better match of the hybrid model to experimental results–validation, presented in
Figure 6. The pink color in the
Figure 6 was used to mark experimental results of bioethanol concentration obtained from common mugwort stems, and green was used to mark bioethanol concentrations obtained from cannabis stems. The blue asterisk refers to RF values and the red asterisk to ANN values.
In the case of modeling such complex processes as bioethanol production from different lignocellulosic raw materials and taking into account numerous initial samples, the use of only one algorithm type results in difficulties. Due to the concerns that the use of ANN would result in flattening or not using all process conditions and mechanisms, scientists often refer to the comparison with such algorithms as random forest, adaptive neuro–fuzzy inference system, and support vector machine [
35,
36,
40]. The application of a hybrid approach to the discussed issues aimed for a more comprehensive inclusion of the mechanisms that are not yet discovered in bioethanol production, or have not yet been classified as of key importance on bioethanol concentration. In this study, the hybrid model is well matched to the process presented, and it further includes a very wide spectrum of lignocellulosic biomass, not including raw materials due to, e.g., an excessive amount of lignin. This may largely contribute to the expansion of knowledge in the field of bioethanol production from mixed types of lignocellulosic biomass with different chemical compositions, and acceleration of the selection of pretreatment type based only on several input variables.