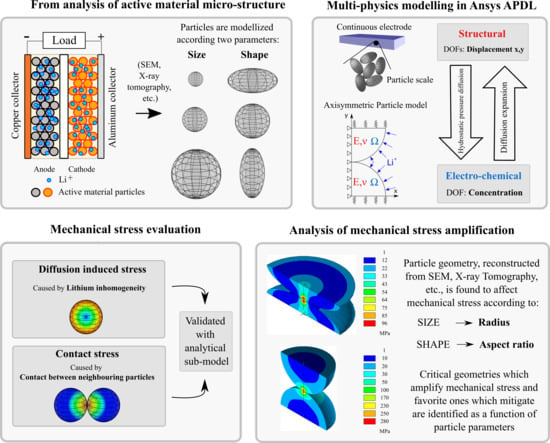
Shape Influence of Active Material Micro-Structure on Diffusion and Contact Stress in Lithium-Ion Batteries
Abstract
1. Introduction
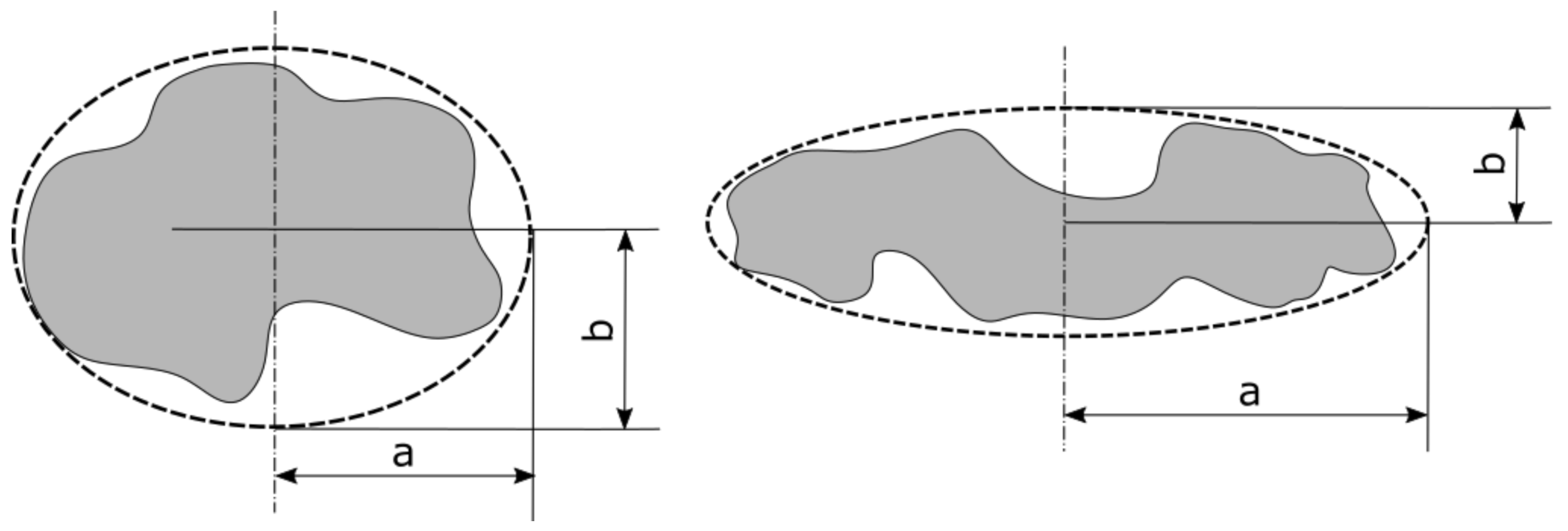
2. Equivalent Particle Shape
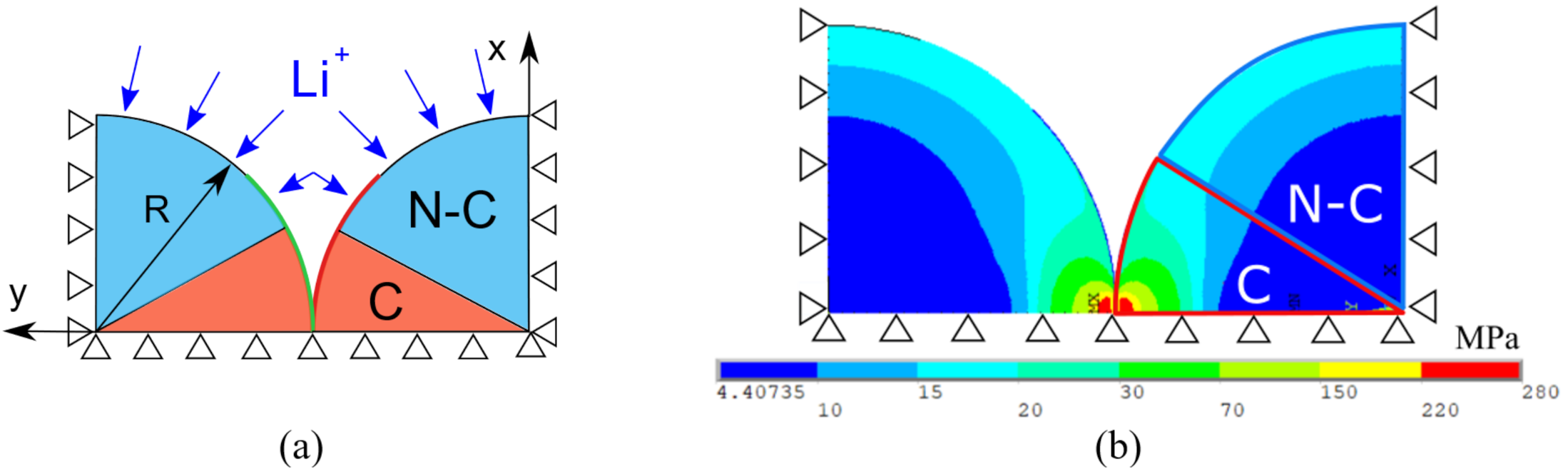
3. Multiphysics Modelling
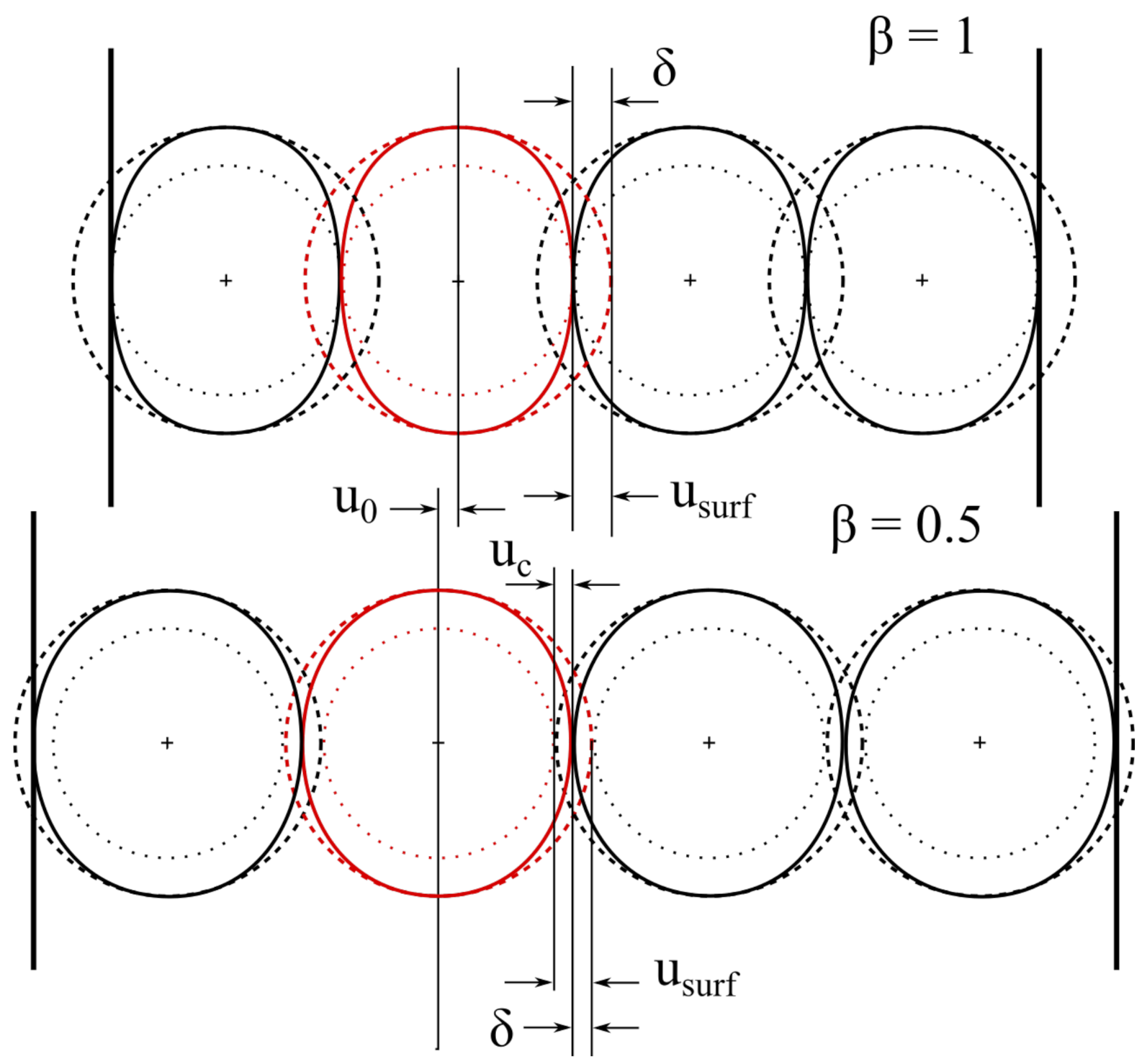
- Contact stress depends on the amount of inhibited displacement (), proportional to the amount of expansion which would occur if the particle was able to expand freely. The expansion of the particle surface does not depends on the distribution of the lithium concentration inside active material, but just on the amount of lithium stored in particle (K). Qualitatively, it is reasonable that higher lithium content causes greater particle expansion, and then the contact with neighbouring particles is stronger as a consequence.
- Diffusion induced stress depends uniquely on the concentration gradient: high differences in lithium content in the particle makes great differential strain which lead to high stress.
3.1. DIS Model
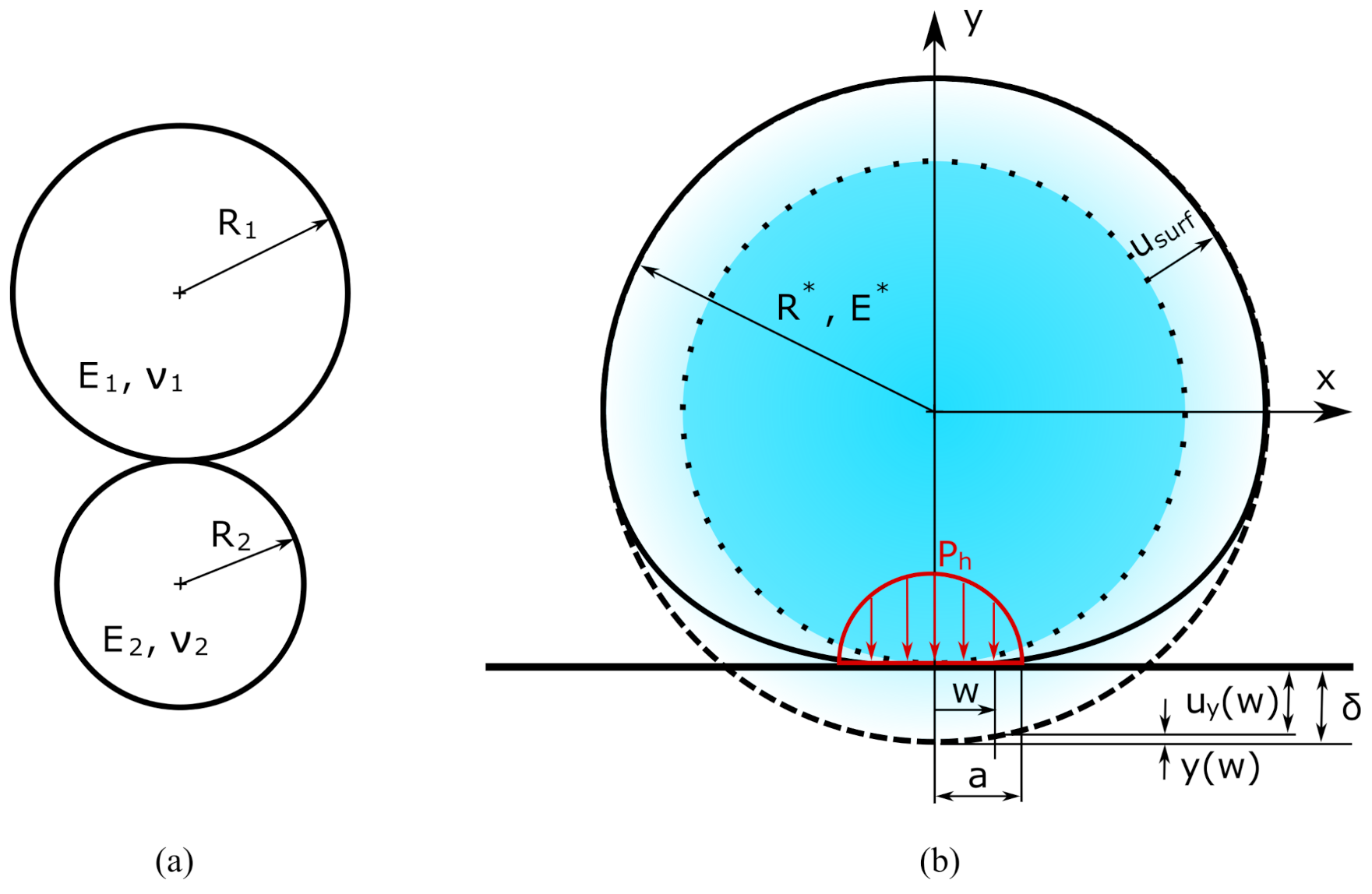
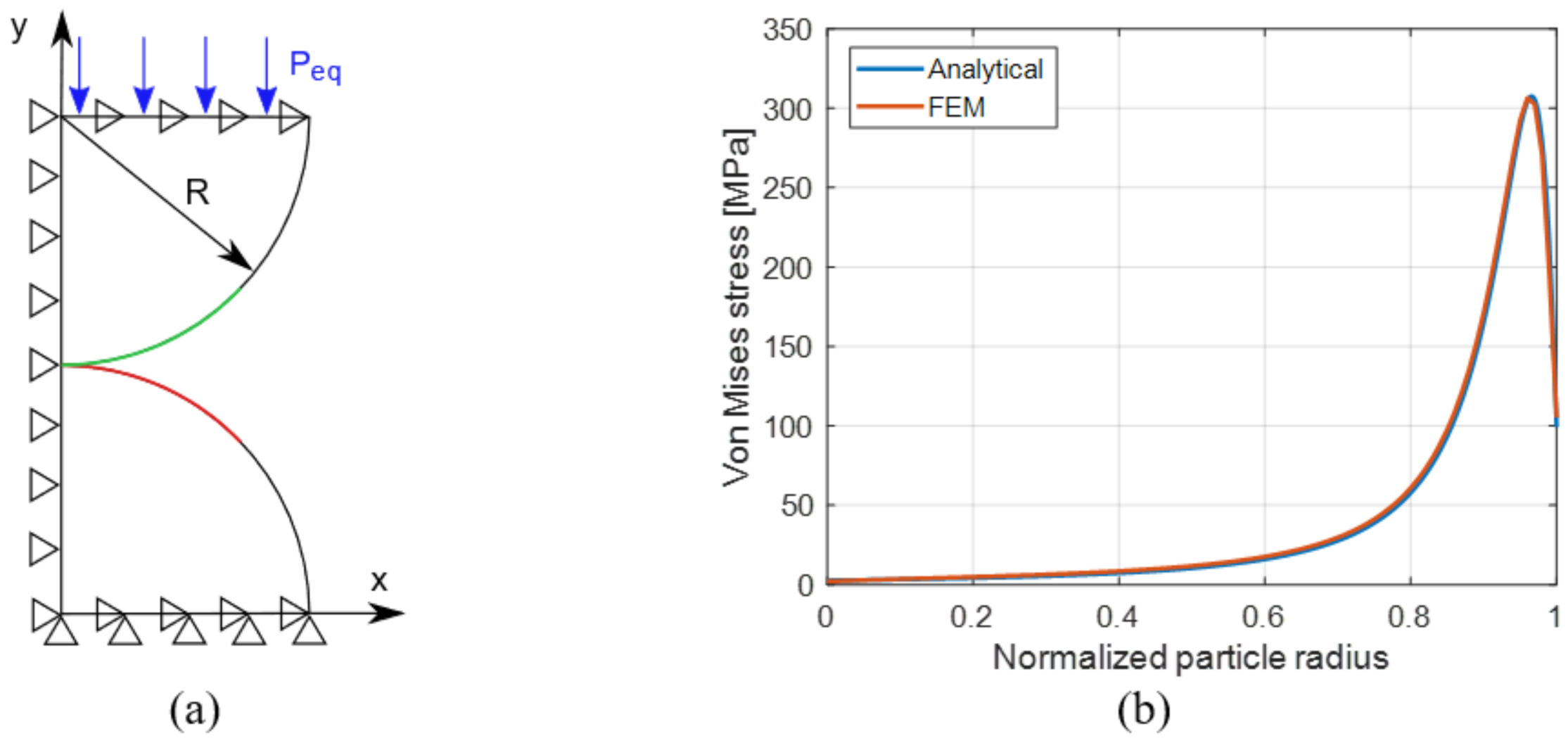
3.2. Hertz Model
3.3. FE Multiphysics Model
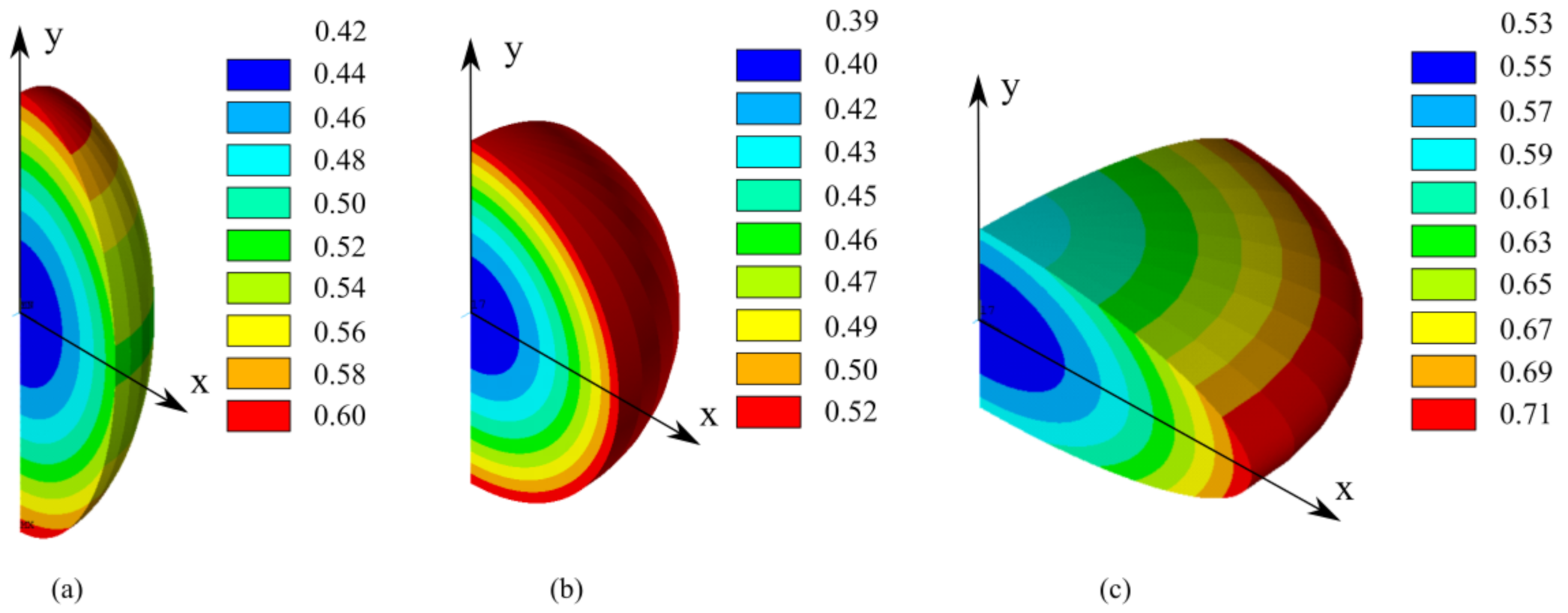
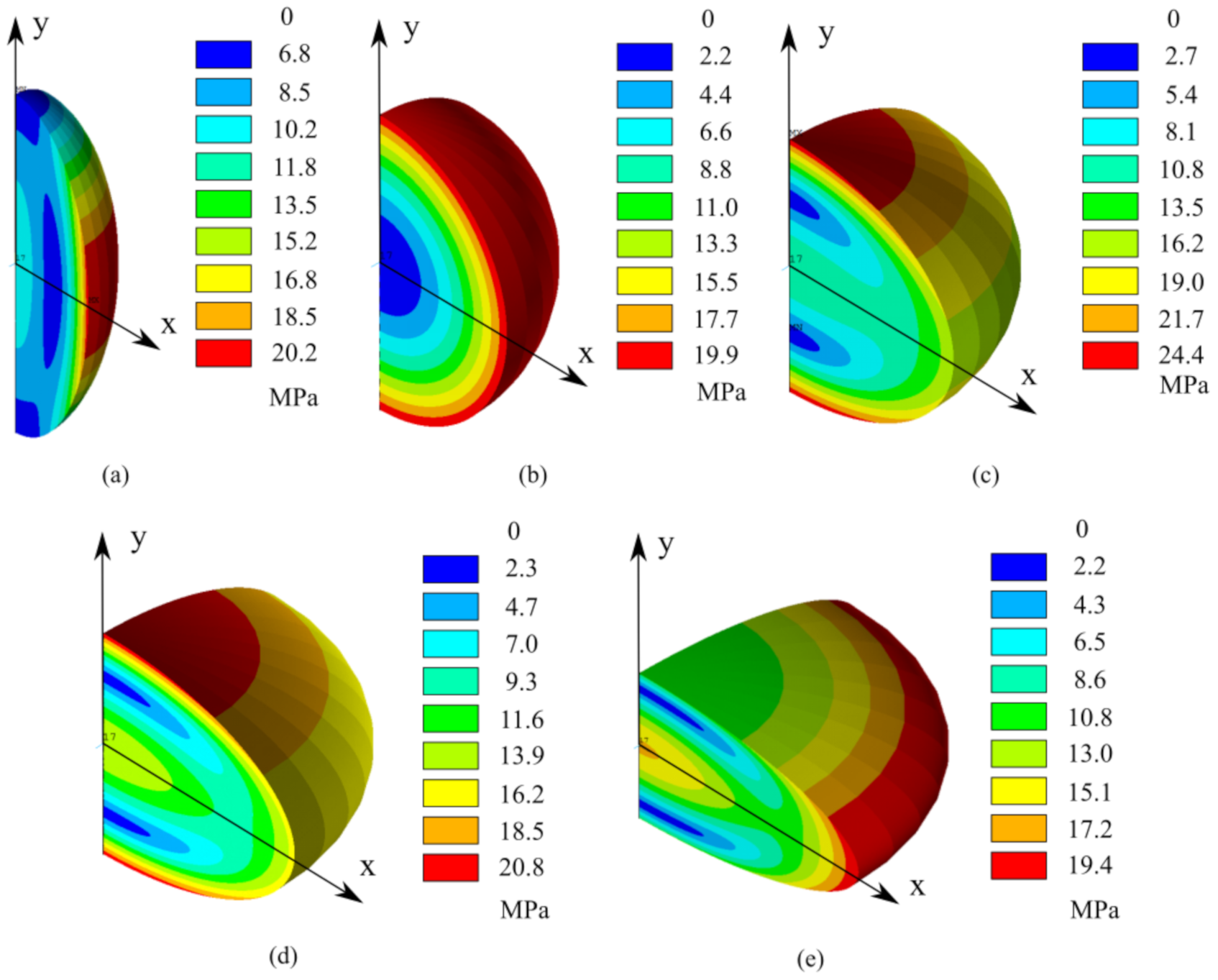
4. Results
4.1. FE Sub-Models Validation
- a
- The contact algorithm is validated by the analytical model of Section 3.2 as shown in Figure 6b, so the effectiveness of the model is confirmed and can be incorporated in the electrochemical-mechanical FE model which aims to compute diffusion induced and contact stress simultaneously.
- b
- The contact stress due to a specific electrochemical operation is computed, independently from diffusion induced stress.
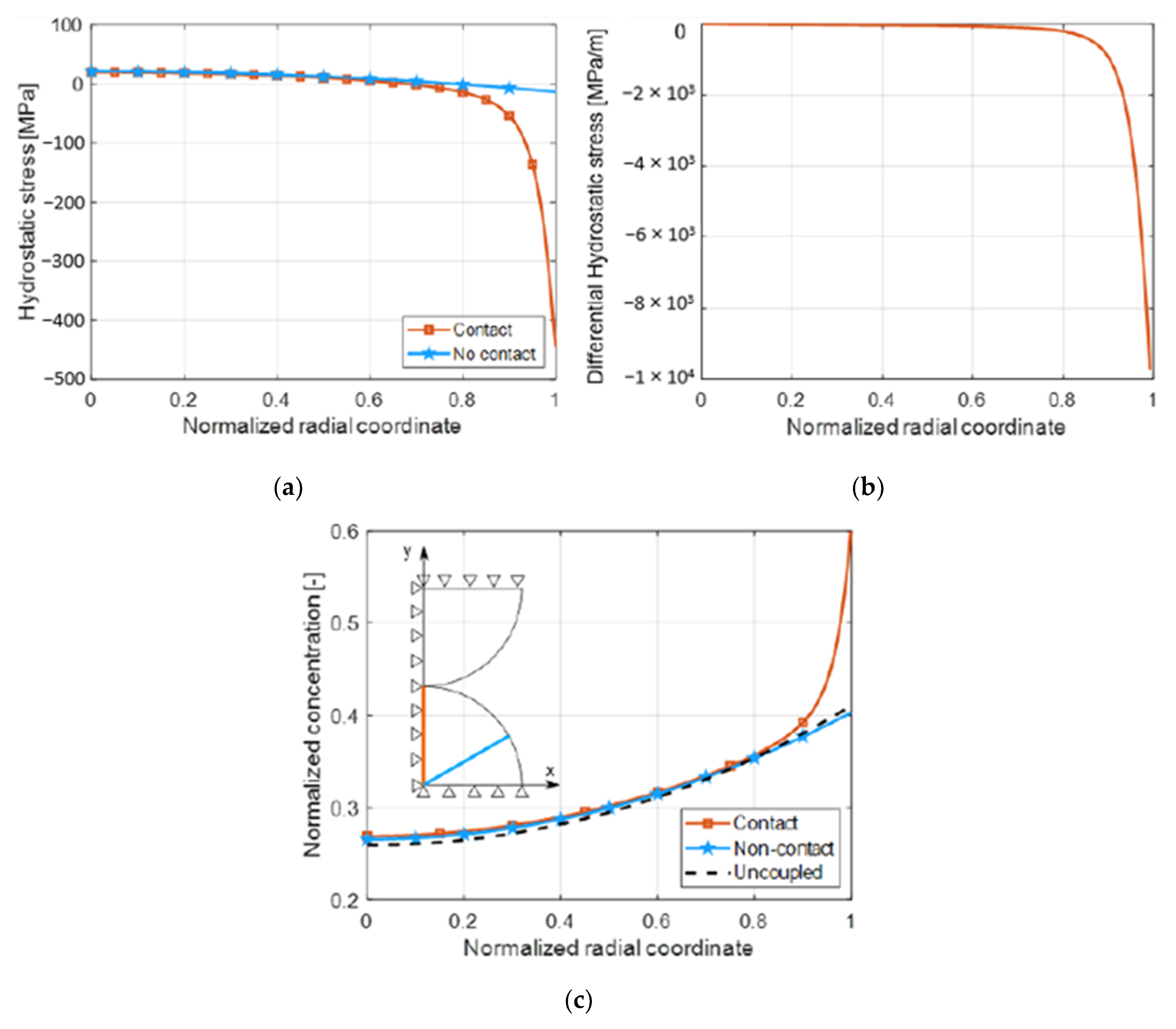
4.2. Coupling Effect
- Lithium diffuses from areas with higher concentration to areas with lower concentration. For this reason, lithium diffuses towards the core of the particle (negative lithium flux in Equation (23)) when the derivative of concentration is positive, according to Equation (23).
- Lithium diffuses from areas with low hydrostatic stress to areas with higher hydrostatic stress, assuming negative stress as compression and positive as tensile. Namely, the diffusion of lithium ions is enhanced from compression areas to tensile (or lower compression) areas. For this reason, a negative derivative of hydrostatic stress enhances lithium diffusion inside the particle (negative lithium flux) according to Equation (23).
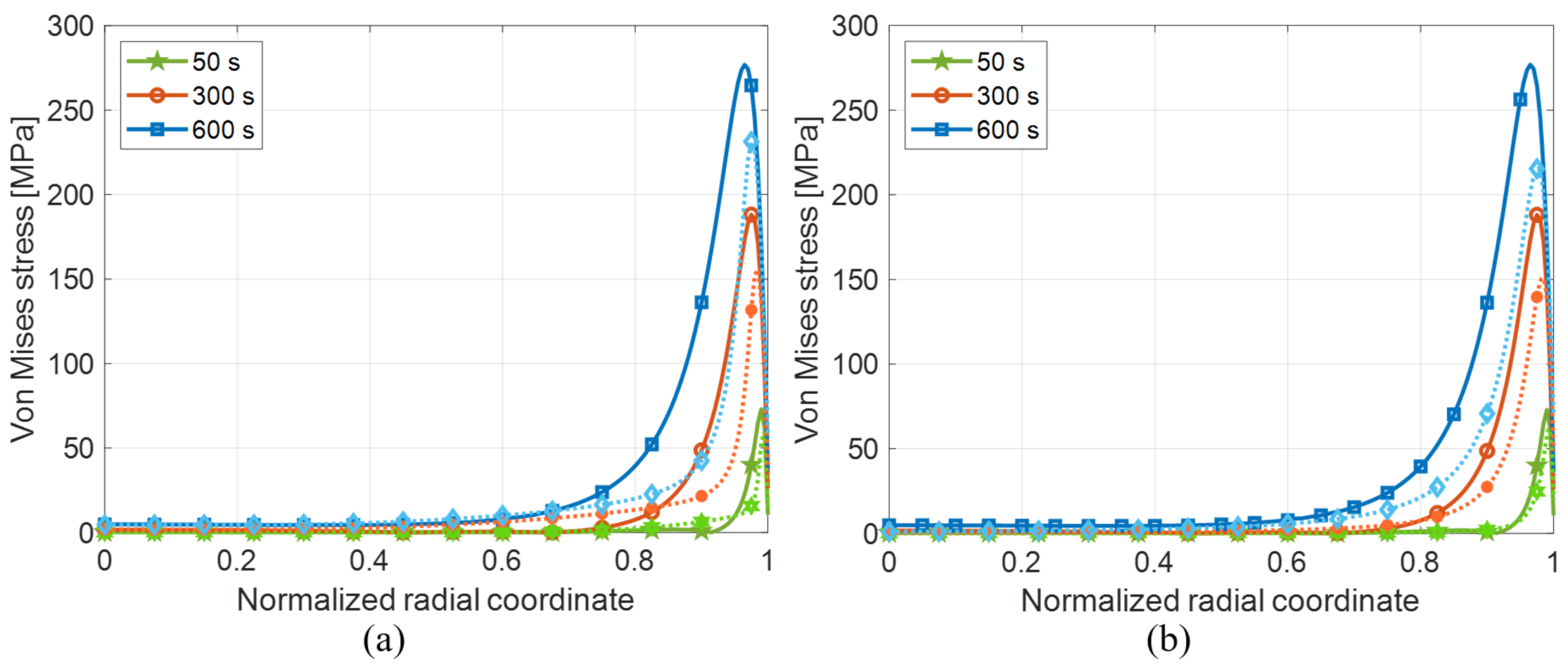
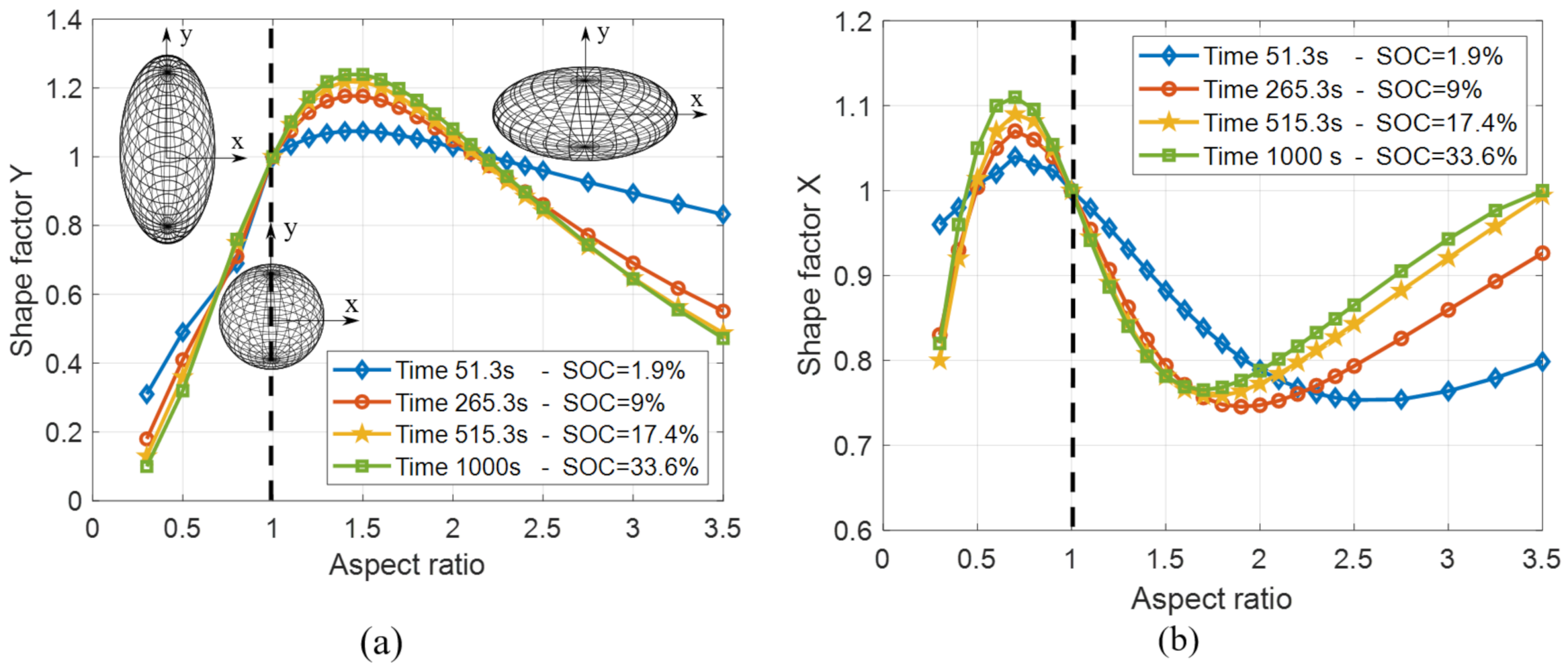
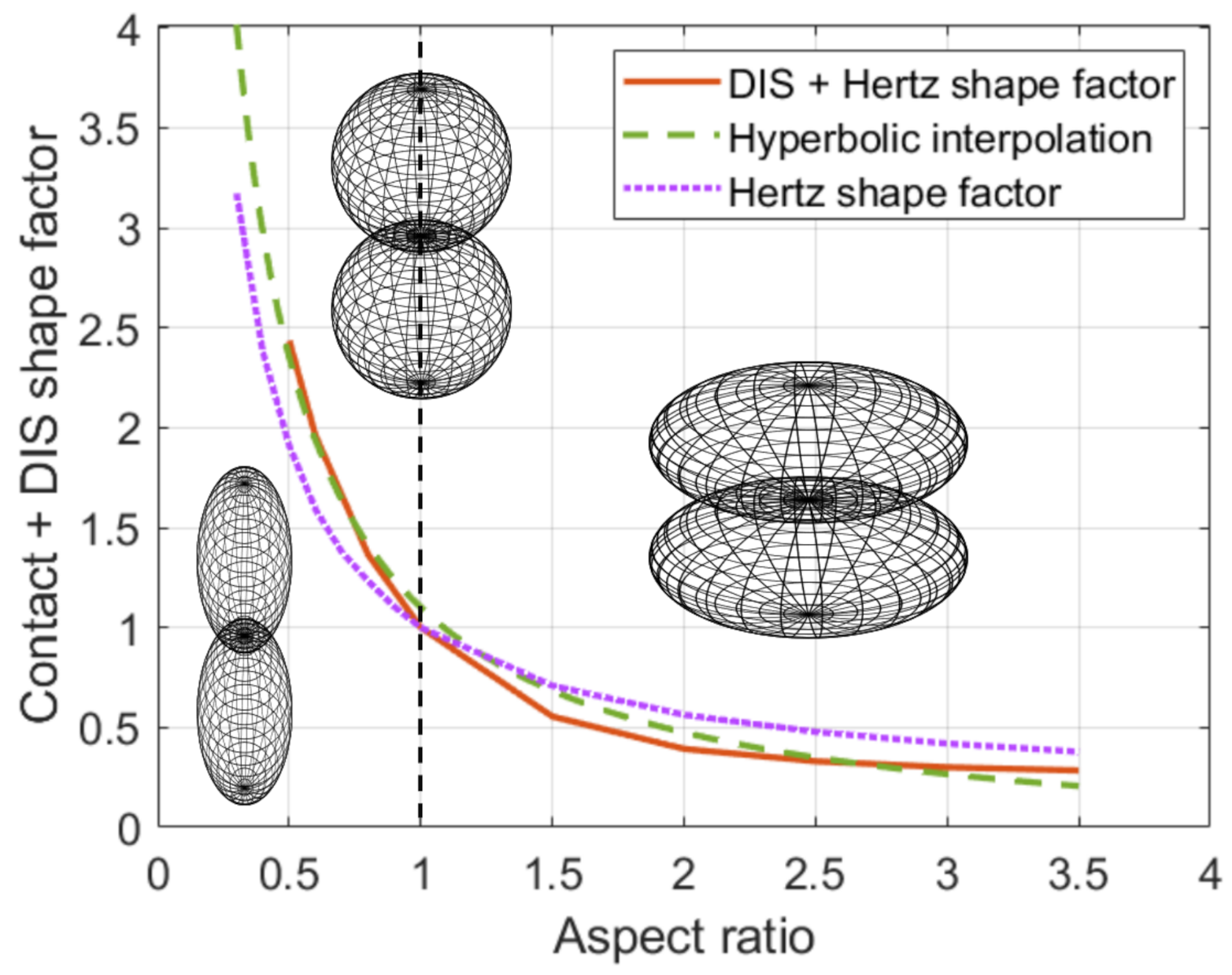
4.3. Shape Factor
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| a | Radius of contact area | m |
| c | Concentration | mol/m |
| Normalized concentration | - | |
| Initial concentration | mol/m | |
| Maximum concentration | mol/m | |
| D | Diffusion coefficient | m/s |
| E | Young Modulus | MPa |
| Young Modulus particle 1 in contact | MPa | |
| Young Modulus particle 2 in contact | MPa | |
| Equivalent young Modulus in contact analysis | MPa | |
| F | Contact force | N |
| Faraday constant | 96,485.332 As/mol | |
| I | Current density | A/m |
| J | Lithium flux | mol/ms |
| K | Percentage of lithium content | % |
| M | Mobility | mol·s/Kg |
| Equivalent pressure in contact analysis | MPa | |
| Maximum pressure in contact area | MPa | |
| r | Radial coordinate | m |
| Normalized radius | - | |
| R | Particle radius | m |
| Radius particle 1 in contact | m | |
| Radius particle 2 in contact | m | |
| Equivalent radius in contact analysis | m | |
| Gas constant | 8.3145 J/mol K | |
| Shape factor | - | |
| State of charge | - | |
| T | Temperature | 298 K |
| u | General displacement | m |
| Elastic displacement along y axis | m | |
| Displacement of particle centre | m | |
| Surface displacement | m | |
| Normalized x coordinate | - | |
| y | Original surface separation in contact area | m |
| Normalized y coordinate | - | |
| w | Radial coordinate in contact area | m |
| Aspect ratio | - | |
| constraint parameter | - | |
| prevented displacement in contact analysis | m | |
| Hoop strain | - | |
| Chemical strain | - | |
| Radial strain | - | |
| Chemical potential | J/mol | |
| Reference chemical potential | J/mol | |
| Poisson ratio | - | |
| Hoop stress | MPa | |
| Hydrostatic stress | MPa | |
| Radial stress | MPa | |
| Cartesian tensor | MPa | |
| Principal stresses | MPa | |
| Characteristic diffusion time | - | |
| Partial molar volume | m/mol | |
| Normalized contact depth | - |
References
- Somà, A.; Bruzzese, F.; Mocera, F.; Viglietti, E. Hybridization factor and performance of hybrid electric telehandler vehicle. IEEE Trans. Ind. Appl. 2016, 52, 5130–5138. [Google Scholar] [CrossRef]
- Mocera, F.; Vergori, E.; Somà, A. Battery Performance Analysis for Working Vehicle Applications. IEEE Trans. Ind. Appl. 2019, 56, 644–653. [Google Scholar] [CrossRef]
- Wang, Z.; Ni, J.; Li, L.; Lu, J. Theoretical Simulation and Modeling of Three-Dimensional Batteries. Cell Rep. Phys. Sci. 2020, 1, 100078. [Google Scholar] [CrossRef]
- Mocera, F.; Somà, A.; Clerici, D. Study of aging mechanisms in lithium-ion batteries for working vehicle applications. In Proceedings of the 2020 Fifteenth International Conference on Ecological Vehicles and Renewable Energies (EVER), MonteCarlo, Monaco, 10–12 September 2020; pp. 1–8. [Google Scholar] [CrossRef]
- Mukhopadhyay, A.; Sheldon, B.W. Deformation and stress in electrode materials for Li-ion batteries. Prog. Mater. Sci. 2014, 63, 58–116. [Google Scholar] [CrossRef]
- Blake, H.W.; Li, J. Electrode manufacturing for lithium-ion batteries—Analysis of current and next generation processing. J. Energy Storage 2019, 25, 100862. [Google Scholar]
- Clerici, D.; Mocera, F.; Somà, A. Analytical Solution for Coupled Diffusion Induced Stress Model for Lithium-Ion Battery. Energies 2020, 13, 1717. [Google Scholar] [CrossRef]
- Lu, B.; Zhao, Y.; Feng, J.; Song, Y.; Zhang, J. Mechanical contact in composite electrodes of lithium-ion batteries. J. Power Sources 2019, 440, 227115. [Google Scholar] [CrossRef]
- Deshpande, R.; Verbrugge, M.; Cheng, Y.T.; Wang, J.; Liu, P. Battery cycle life prediction with coupled chemical degradation and fatigue mechanics. J. Electrochem. Soc. 2012, 159, A1730. [Google Scholar] [CrossRef]
- Zhao, K.; Matt, P.; Vlassak, J.J.; Suo, Z. Fracture of electrodes in lithium-ion batteries caused by fast charging. J. Appl. Phys. 2010, 108, 073517. [Google Scholar] [CrossRef]
- Wilson, J.R.; Cronin, J.S.; Barnett, S.A.; Harris, S.J. Measurement of three-dimensional microstructure in a LiCoO2 positive electrode. J. Power Sources 2011, 196, 3443–3447. [Google Scholar] [CrossRef]
- Christensen, J.; Newman, J. Stress generation and fracture in lithium insertion materials. J. Solid State Electrochem. 2006, 10, 293–319. [Google Scholar] [CrossRef]
- Zhang, X.; Shyy, W.; Sastry, A.M. Numerical simulation of intercalation-induced stress in Li-ion battery electrode particles. J. Electrochem. Soc. 2007, 154, A910. [Google Scholar] [CrossRef]
- Cheng, Y.T.; Verbrugge, M.W. Evolution of stress within a spherical insertion electrode particle under potentiostatic and galvanostatic operation. J. Power Sources 2009, 190, 453–460. [Google Scholar] [CrossRef]
- Malavé, V.; Berger, J.; Zhu, H.; Kee, R.J. A computational model of the mechanical behavior within reconstructed LixCoO2 Li-ion battery cathode particles. Electrochim. Acta 2014, 130, 707–717. [Google Scholar] [CrossRef]
- Chung, M.; Seo, J.; Zhang, X.; Sastry, A. Implementing realistic geometry and measured diffusion coefficients into single particle electrode modeling based on experiments with single LiMn2O4 spinel particles. J. Electrochem. Soc. 2011, 158, A371. [Google Scholar] [CrossRef]
- Wiedemann, A.H.; Goldin, G.M.; Barnett, S.A.; Zhu, H.; Kee, R.J. Effects of three-dimensional cathode microstructure on the performance of lithium-ion battery cathodes. Electrochim. Acta 2013, 88, 580–588. [Google Scholar] [CrossRef]
- Mendoza, H.; Roberts, S.A.; Brunini, V.E.; Grillet, A.M. Mechanical and electrochemical response of a LiCoO2 cathode using reconstructed microstructures. Electrochim. Acta 2016, 190, 1–15. [Google Scholar] [CrossRef]
- Hun, J.; Chung, M.; Park, M.; Woo, S.; Zhang, X.; Marie, A. Generation of realistic particle structures and simulations of internal stress: A numerical/AFM study of LiMn2O4 particles. J. Electrochem. Soc. 2011, 158, A434. [Google Scholar] [CrossRef]
- Lim, C.; Yan, B.; Yin, L.; Zhu, L. Simulation of diffusion-induced stress using reconstructed electrodes particle structures generated by micro/nano-CT. Electrochim. Acta 2012, 75, 279–287. [Google Scholar] [CrossRef]
- Stershic, A.; Simunovic, S.; Nanda, J. Modeling the evolution of lithium-ion particle contact distributions using a fabric tensor approach. J. Power Sources 2015, 297, 540–550. [Google Scholar] [CrossRef]
- Xu, R.; Zhao, K. Mechanical interactions regulated kinetics and morphology of composite electrodes in Li-ion batteries. Extrem. Mech. Lett. 2016, 8, 13–21. [Google Scholar] [CrossRef]
- Stein, P.; Xu, B. 3D Isogeometric Analysis of intercalation-induced stresses in Li-ion battery electrode particles. Comput. Methods Appl. Mech. Eng. 2014, 268, 225–244. [Google Scholar] [CrossRef]
- Bucci, G.; Swamy, T.; Bishop, S.; Sheldon, B.W.; Chiang, Y.M.; Carter, W.C. The effect of stress on battery-electrode capacity. J. Electrochem. Soc. 2017, 164, A645. [Google Scholar] [CrossRef]
- Wu, B.; Lu, W. A battery model that fully couples mechanics and electrochemistry at both particle and electrode levels by incorporation of particle interaction. J. Power Sources 2017, 360, 360–372. [Google Scholar] [CrossRef]
- Mei, W.; Duan, Q.; Qin, P.; Xu, J.; Wang, Q.; Sun, J. A Three-Dimensional Electrochemical-Mechanical Model at the Particle Level for Lithium-Ion Battery. J. Electrochem. Soc. 2019, 166, A3319. [Google Scholar] [CrossRef]
- Huttin, M.; Kamlah, M. Phase-field modeling of stress generation in electrode particles of lithium ion batteries. Appl. Phys. Lett. 2012, 101, 133902. [Google Scholar] [CrossRef]
- Bohn, E.; Eckl, T.; Kamlah, M.; McMeeking, R. A model for lithium diffusion and stress generation in an intercalation storage particle with phase change. J. Electrochem. Soc. 2013, 160, A1638. [Google Scholar] [CrossRef]
- Miller, M.I.; Christensen, G.E.; Amit, Y.; Grenander, U. Mathematical textbook of deformable neuroanatomies. Proc. Natl. Acad. Sci. USA 1993, 90, 11944–11948. [Google Scholar] [CrossRef]
- Martin, E.; Chung, D.-W.; Edwin, G.R.; Vanessa, W. Tortuosity anisotropy in lithium-ion battery electrodes. Adv. Energy Mater. 2014, 4, 1301278. [Google Scholar]
- Zhao, Y.; Stein, P.; Bai, Y.; Al-Siraj, M.; Yang, Y.; Xu, B.X. A review on modeling of electro-chemo-mechanics in lithium-ion batteries. J. Power Sources 2019, 413, 259–283. [Google Scholar] [CrossRef]
- Johnson, K. Contact Mechanics; Cambridge University Press: Cambridge, UK, 1985; Volume 95, p. 365. [Google Scholar]

| Mechanical Equations | |
|---|---|
| Constitutive | |
| Congruence | |
| Equilibrium | |
| Diffusion Equation | |
| Chemical potential | |
| Flux | |
| Mass conservation | |
| Solutions | |
| Displacement | |
| Radial stress | |
| Hoop stress | |
| Concentration |
| Parameter | Symbol | Value | Unit |
|---|---|---|---|
| Diffusion coefficient | D | m/s | |
| Partial molar volume | m/mol | ||
| Maximum concentration | mol/m | ||
| Young modulus | E | 10 | GPa |
| Poisson ratio | 0.3 | - | |
| Particle radius (sphere) | R | m |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Clerici, D.; Mocera, F.; Somà, A. Shape Influence of Active Material Micro-Structure on Diffusion and Contact Stress in Lithium-Ion Batteries. Energies 2021, 14, 134. https://doi.org/10.3390/en14010134
Clerici D, Mocera F, Somà A. Shape Influence of Active Material Micro-Structure on Diffusion and Contact Stress in Lithium-Ion Batteries. Energies. 2021; 14(1):134. https://doi.org/10.3390/en14010134
Chicago/Turabian StyleClerici, Davide, Francesco Mocera, and Aurelio Somà. 2021. "Shape Influence of Active Material Micro-Structure on Diffusion and Contact Stress in Lithium-Ion Batteries" Energies 14, no. 1: 134. https://doi.org/10.3390/en14010134
APA StyleClerici, D., Mocera, F., & Somà, A. (2021). Shape Influence of Active Material Micro-Structure on Diffusion and Contact Stress in Lithium-Ion Batteries. Energies, 14(1), 134. https://doi.org/10.3390/en14010134