3.1. Electricity Market Costs Due to Forecasting Errors
The costs relate to the overall forecasting error of the total energy balance of the balance responsible party of the actor in the market. Thus, the load forecast of a consumer group segment is only one component of the total forecast. There are forecasts for different types of load and local generation. The different forecasts are not fully independent, because many of them may use the same weather forecasts and be subject to interactions between consumer group behavior. However, the errors of accurate forecasters tend to be independent and it is easy to check to what extent this assumption holds. Going to such details is complicated and outside the scope of this paper. Thus, for clarity of the analysis, we assume that the errors of different segment forecasts are independent. Then the contribution of the expected individual error component
e1 to the total expected forecast error
e is as follows.
where
e0 is the expected total error of all the other forecast components.
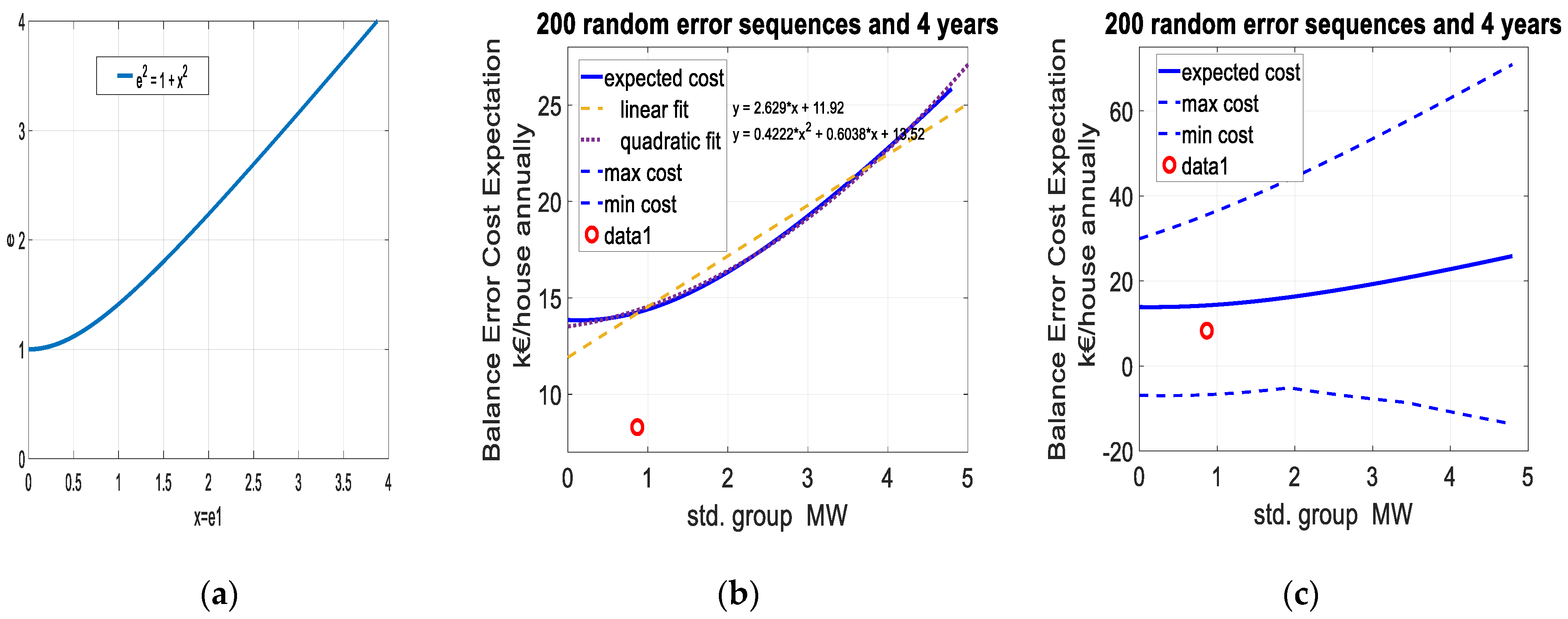
Figure 1a shows how the total error
e behaves as a function of
e1 when
e0 is set to 1. For small
e1, the increase in
e is quadratic.
The monetary cost of the total forecasting error needs to be assessed in the electricity market. For simplicity, we assume that the forecasting errors cause costs via the market balancing errors. The market rules for penalizing the balancing errors of loads vary from country to country. The Nordic power market applies the balancing market price as the cost of the balancing errors. In the Nordic countries, one price system is applied for errors in consumption (load) balance and, in addition, there is a small cost component proportional to the absolute balancing error (volume fee for imbalance power). Power generation plants below 1 MVA are included in the consumption balance.
The price of consumption imbalance power is the price for which Fingrid both purchases balance power from a balance responsible party and sells it to one. In the case of the regulating hour, the regulation price is used. If no regulation has been made, the Elspot FIN price is used as the purchase and selling price of consumption imbalance power. For an explanation, see [
13]. All the prices and fees are publicly available at the webpages of Fingrid and NordPool, such as [
14]. In addition, imbalance power in the consumption balance is subject to a volume fee. There is also a fee for actual consumption, but that depends only on the actual consumption and not on the forecasting errors. The volume fee of imbalance power for consumption during the whole study period was 0.5 €/MWh. See [
15] for the fees.
From an actual or simulated component load forecasting error, the resulting increase the forecasting error of the total energy balance can be calculated, and using this increase in error the resulting balancing cost increase was calculated based on the price of imbalance power and the volume fee of the power imbalance. In this way, we got an estimate for how much electricity market costs the forecasting error causes to the balance responsible actor. We do not know the forecasting errors of the balance responsible party. In the following study, we generated them as a normally distributed sequence that has standard deviation 3 MW. The actual errors may be bigger, but as we see later, that will not affect the conclusions. The price of imbalance price occasionally has very high peaks. Thus, the cost estimate will be very inaccurate, even when a very long simulation period is applied. It is necessary to check the contribution of the very highest price peaks to the cost in order to have a rough idea on the inaccuracy of the results. We avoided this challenge as follows. We made a short-term load forecast using a residual hybrid of physically based load control response models and a stacked booster network as explained in [
16] for a four-year-long test period. We found out that the forecasting errors were rather well normally distributed and bounded. We generated 200 random normally distributed bounded error sequences over the four–year period. With each one of these 200 normally distributed bounded random error sequences, we calculated the balancing error costs for the forecast group. Then, the standard deviation of the group errors was varied and the same cost calculation repeated. The variation of the costs between the error sequences was very large. The mean behaved as assumed in
Figure 1a and an actual measured and forecast case was clearly in the area where the quadratic dependency dominates (see
Figure 1b). The demand response aggregator considers the actual and forecast active loads as trade secrets and does not allow us to make them public information. Except for this one point, all data used for the simulations in
Figure 1 are publicly available.
The balancing error cost was very stochastic, because the impact of high balancing market price peaks dominated (see
Figure 1c). The balancing error cost over the whole four-year-long period mostly depended on the forecasting error during those few price peaks. The red circle represents the forecasting errors when an experimental short-term demand response forecasting algorithm was applied to the forecasting on the morning of the previous day. There, the aggregated controllable power was slightly over 18 MW. The results support the use of the quadratic error criteria std. and RMSE, rather than linear criteria such as MAPE etc. In this case, data driven forecasters that do not model the dynamic load control responses have so poor accuracy that the cost dependency approaches a linear dependency. Here, we have ignored the fact that especially large forecasting errors can affect the price of imbalance power significantly, thus increasing the balancing error cost much more than linearly.
Another observation is that with the good performance forecasting model, the forecasting errors increased the imbalance costs very little, only 0.53 € per controllable house annually. This suggests that the one price balancing error model gives only very weak incentives to improve the forecasting accuracy in normal situations. The one–price balance error cost model may not adequately reflect the situation from the power system point of view. A further study is needed to find out to what extent, how much and with which market mechanisms the power system can in the future benefit from improving the short-term forecasting accuracy. A conclusion of the H2020 SmartNet project [
17] was that improving the forecasting accuracy is critical for getting the benefits from the future ancillary service market architectures for enabling the provision of the ancillary services using distributed flexible energy resources.
Some other countries apply a two–price system for balancing error costs. That means that the price for the balancing errors is separately defined by the balancing market for both directions. Then the costs of load forecasting errors are much higher than in a one–price system. They may even exaggerate the related needs of power system, if the errors of the forecasts of the individual balancing are assumed to be independent from each other. When the share of distributed generation increases, the one price system may become problematic, because the consumption and distributed generation may not have enough incentives to minimize their balancing errors. This increases the need for balancing reserves in the system. The share of distributed generation is expected to increase much during the summertime, which means that also in the Nordic countries there may appear needs to change the market rules regarding the balancing costs somehow. Moving to two–price system may be one such possibility. Thus, it may be worthwhile to repeat the above study using the two–price system of the generation balance.
3.2. Distribution Network Costs Due to Forecasting Errors
Overloading of network components causes high losses that increase the temperature of the components. Overheating reduces the lifetime of the insulator materials in the network components rapidly. If the forecast underestimates the peak load, the operational measures to limit overload are not activated in time, energy losses increase and the component aging increases so much that the expected lifetime is reduced.
The losses in the network components are generally proportional to the square of the current. When the voltage is kept roughly constant and the reactive power, voltage unbalance and distortion are assumed to be negligible, the losses are roughly proportional to the square of the transferred power. In real networks, these assumptions are not accurate enough. Strbac et al. [
18] calculated losses using a complete model of three power distribution license areas in UK. The analysis highlighted that 36–47% of the losses are in low voltage (LV) networks, 9–13% are associated with distribution transformer load related losses, 7–10% are distribution transformer no-load losses and the remaining part in higher voltage levels. They [
18] (p. 43) showed the marginal transmission losses as a function of system loading. A 1 MWh reduction in load would reduce transmission losses by 0.11 MWh during peak load condition (100%). When system loading is 60%, reducing the load by 1 MWh will reduce transmission losses by 0.024 MWh. This corresponds to the dependency f(P) = P
2.98. The sample size is small, so the accuracy of this dependency is questionable. Nevertheless, the dependency is clearly different from f(P) = P
2 that results from assuming constant voltage at the purely active power load and transmission losses relative to the square of the current. Underestimating the peak loads causes much higher losses and related costs than other load forecasting errors. Thus, the impact of forecasting errors to the energy losses is very nonlinear and depends on the direction of the error and size of the load.
Ref. [
19] studied how transformer oil lifetime depends on temperature. Arrhenius’ law describes the observed aging rather well. Aging mechanisms of cable polymers were discussed in [
20]. The Arrhenius method is often used to predict the aging of cable insulation, although it is valid only in a narrow temperature range. For example, it is applicable only below the melting point of the insulator. For simplicity, we here model the aging using the Arrhenius method. According to it,
k the rate of chemical reaction (such as insulator aging) is an exponential function of the inverse of the absolute temperature
T.
where R is the gas constant, and the pre-exponential factor A and the activation energy E
a are almost independent from the temperature
T. In the steady state, the difference between the component or insulator temperature and the ambient temperature is linearly proportional to the losses. Components are normally operated much below their nominal or design capacity and the impact of forecasting errors on the losses and aging is small. When the component during peak load is operated at or above its nominal load and is subject to high ambient temperature and poor power quality high losses, fast component aging, or expensive operational measures result from under-forecasting the load.
Thus, the impact of forecasting errors to the costs is very nonlinear and depends on the direction of the error and size of the load. Most of the time, the network costs from short term load forecasting errors are small or even insignificant. However, the costs of forecasting errors increase rapidly when the load is at or above the nominal capacity of the network bottlenecks, if the actual load is higher than the forecast load.
3.3. A Consumer Cost Case Study: Load Forecasting Based Control of Domestic Energy Storage System
All the costs of the power supply are paid by the users of the electricity grid. The forecasting errors discussed in the other chapters increase the electricity prices and grid tariffs by increasing the costs of the electricity retailers, the aggregators and the grid operators. Here, we consider those costs that the consumer has possibilities to control more directly.
By using energy storage in a domestic building, a customer can get savings in the electricity bill [
21]. The amount of the savings depends on many factors. The load profile of the customer and the electricity pricing structure and price levels are the main variables that affect the savings, but the customer has very limited possibilities to change them. The size of the energy storage can be optimized for the customer’s load profile, but after that, controlling the energy storage and consumption is the only way to maximize the savings. Energy storage can be used, e.g., to increase the self-consumption of small-scale photovoltaic production, but it can also be used for minimizing costs from different electricity pricing components. If the energy retailer’s price is based on the market price of electricity, the customer can get savings by charging the energy storage during low price and discharging during high price as in [
21]. If electricity distribution price is based on the maximum peak powers, the customer can get savings by discharging the battery during peak hours, as in [
22].
Such electrical energy storage systems are still rare and typically installed to increase the self-consumption of small-scale photovoltaic power production. Although the battery technologies progress all the time, the profitability in such use is still typically poor, especially if there are loads that can be easily shifted in time. One can improve the profitability of the battery system significantly by having several control targets or a more holistic one. Such a possibility is minimizing the costs from different electricity pricing components, but that requires short–term load forecasting.
In this case study, it is assumed that every customer in the study group has a market price-based contract with an electricity retailer and the distribution price is partly based on the maximum peak powers as in [
23]. The energy retailer price is based on hourly day-ahead market prices of Finland’s area in Nord Pool electricity markets [
13]. The electricity retailer adds a margin of 0.25 c/kwh to the hourly prices. Distribution prices are based on the study in [
23], where the price components were calculated for the area of the same distribution system operator (DSO) as where the customers’ data of this study were measured. The price structure includes two consumption-based components: volumetric charge (0.58 c/kWh) and power charge (5.83 €/kW). The power charge is based on the monthly highest hourly average peak power. When value added tax (24%) is added to these charges, the prices which affect to customers’ costs are: volumetric charge 0.72 c/kWh and power charge: 7.23 €/kWh. The same prices were used in [
22].
Customers’ load data are from one Finnish DSO, whose license area is partly rural and partly small towns. The study group consists of 500 random customers. In simulations, each customer has 6 kWh with a 0.7 C-rate Lithium-ion battery. Battery type is lithium iron phosphate (LFP), because it has good safety for domestic use. The energy storage system is controlled firstly to decrease the monthly maximum peak power and secondly to decrease the electricity costs with market price-based control as in [
22]. The battery is discharged when power is forecast to increase over the monthly peak and charged during low prices. The market price-based control algorithm and battery simulation model were presented in [
21]. In previous studies, the controlling of energy storage was based on load forecasting. The load forecasts are based on a model, which utilizes customer’s historical load data and temperature dependence of load with temperature forecast [
24].
In the present study, the dependence between the accuracy of load forecasting and the customers’ savings achieved by using the energy storage are studied. The simulations are made for every customer with 11 different load forecasts each having a different load forecasting accuracy. The forecasting accuracy is varied by scaling the forecast error time series. The actual load forecast time series is nominated as the basic level (100%) and the real load data correspond to the ideal forecast (0%). The range of studied error scaling is selected linearly between 0% and 200%, with 20% step size in every hour. Customers’ yearly cost savings and different forecast accuracy criteria (SSE, RMSE, NRMSE, MAE and MAPE) have been calculated during simulations. Additionally, because most of the savings come from the decrease in monthly peak powers, the MAE of monthly peak powers (MAE
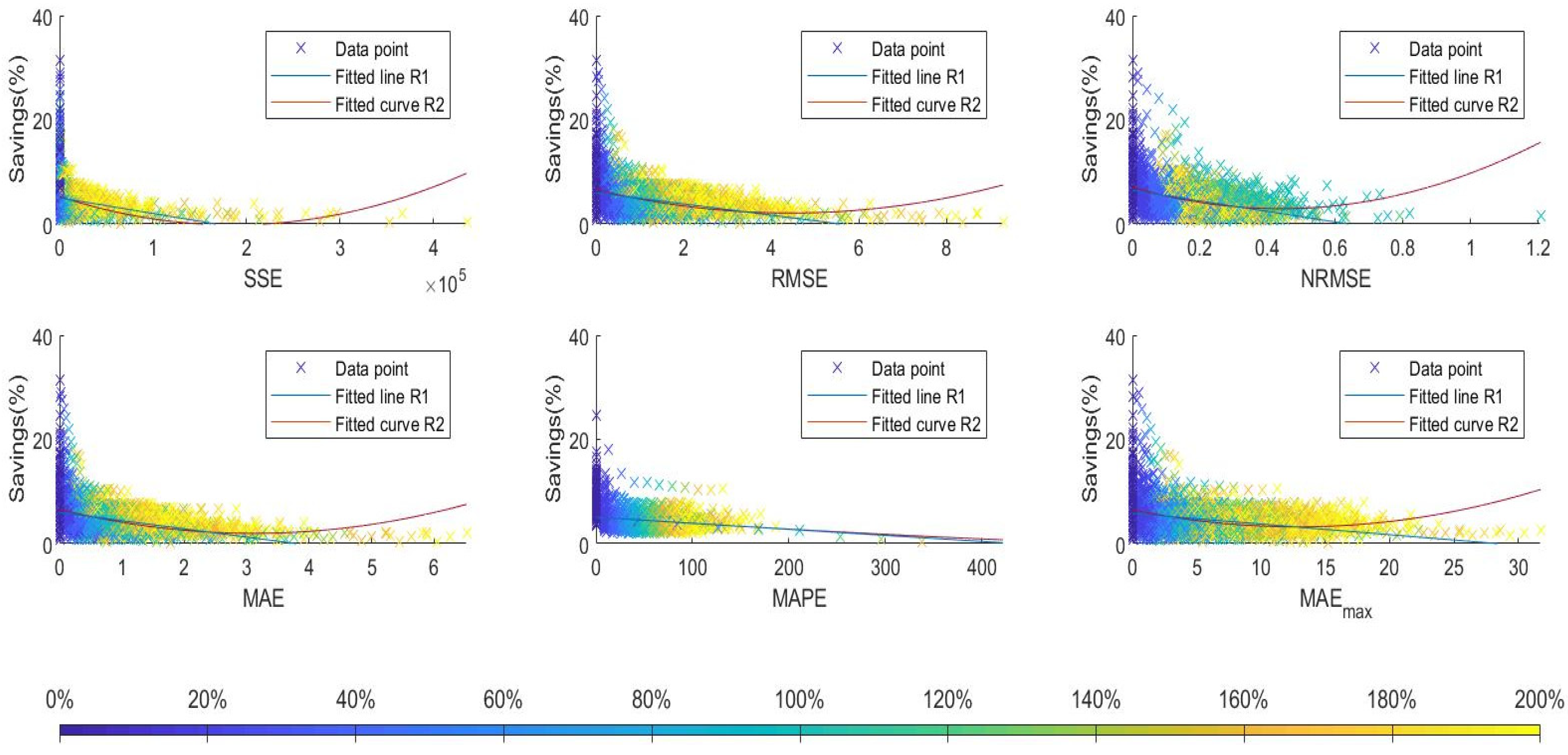
max) was calculated. The monetary value of the cost savings depends on the customer’s load profile, so the results are given as percentage values of cost savings. The results of the simulations are shown in
Figure 2. From the result points, we calculated least-squares fitted line (R1) and least-squares fitted second-order curve (R2).
From the results, we see that with ideal forecasts the savings of the customers vary a lot. This stems from the different load profiles of the customers. The customers, whose load profile includes high peaks during several months, can get very high savings. If customer’s load profile is very flat, the savings can be low. When the errors in the forecast start to increase, the savings drop very fast at first, but the decrease in the savings slows quickly and the decrease stays low until the end.
From the results of
Figure 2 and the results of least-squared fittings, we collected the main results and values for the
Table 1, which helps to compare different criteria. In
Table 1, data points mean the points (maximum 5500 points) which can be used and logical order means that the data points are in order, such that higher error gives lower savings.
The idea in the comparison is that good criteria predict as accurate as possible the cost savings of a customer. Fitted lines and curves predict the cost savings best with MAPE, but MAPE can be calculated only for a small part of the customers. For this reason, the values of MAPE seem better than they really are. With NRMSE, the order of points is not logical: the savings do not monotonically decrease as the NRMSE value increases. SSE gives the worst values in fittings. RMSE and MAE are almost equal, but MAE is in this case marginally the best criteria. Differences between the criteria are not large and selecting the most suitable criteria in this case requires accurate comparison.
Additionally, the MAE of the monthly peak powers is shown in
Figure 2. As we can see, MAE
max describe the effect of forecasting error for the savings almost as well as traditional forecast error criteria. This is logical when most of the savings come from the decrease in monthly peak powers. When the other forecast error criteria take into account all hours during the year (8760 h), this MAE
max is calculated only from one hour per month (12 h).
3.4. Comparison of Methods across Different Forecasting Cases
When the same method is used to forecast different aggregated loads the values of the same accuracy criteria can be very different. Humeau et al. [
25] analyzed the consumption of 782 households and found out how the values of the NRMSE decrease with the increase in the number of sites in clusters. They compared linear regression, support vector regression (SVR) and multilayer perceptron (MLP) in this respect. [
26] shows a typical short-term load forecasting accuracy dependence on the prediction time horizon. The weather forecasts and load forecasting methods have improved much so now the accuracy decreases somewhat later but the shape of the dependency is still similar. In addition to the number of sites, the value of criteria depends also on the size and type of sites, type of loads, the presence of active demand, etc.
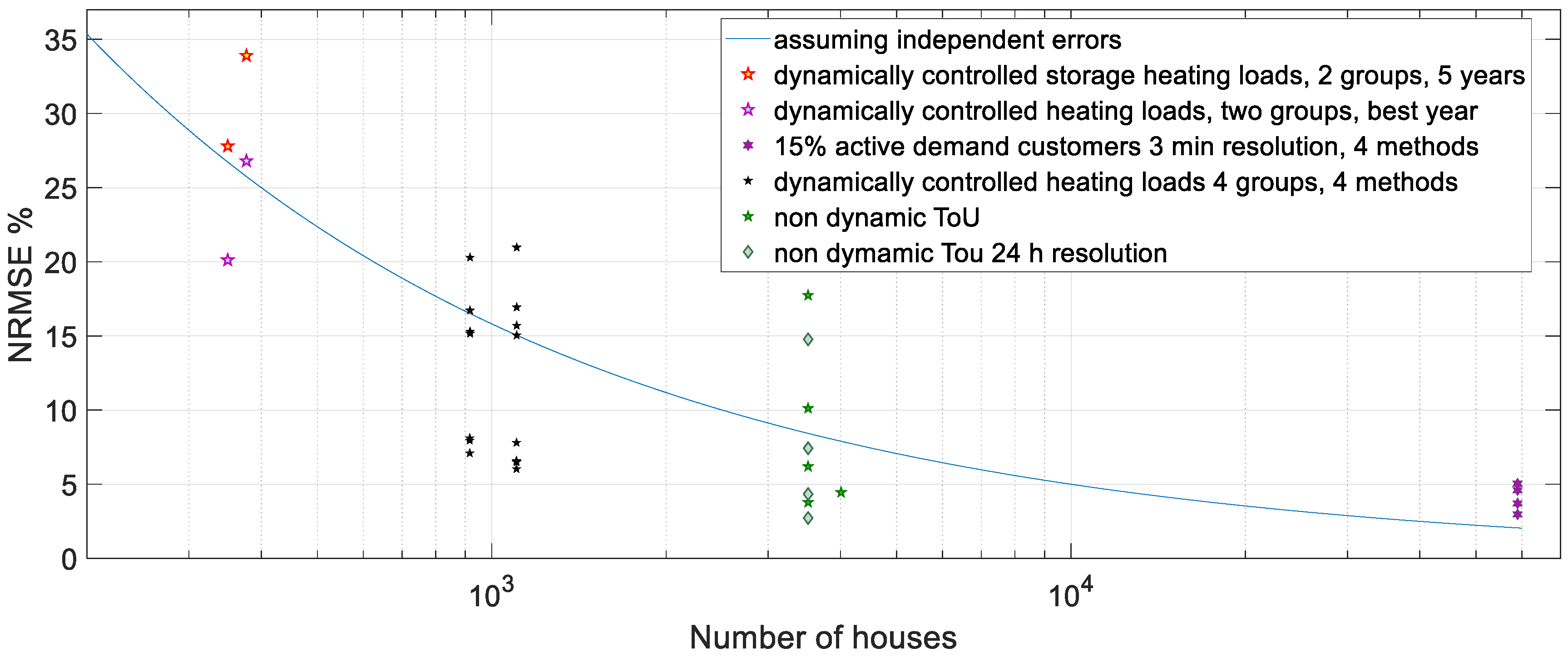
Figure 3 demonstrates some of the dependencies. It summarizes some results from our past publications between the years 2012 and 2020. All these publications can be found via [
11,
16]. All the most accurate methods in
Figure 3 are hybrids that combine several short-term forecasting methods and include both machine learning and physically based models. In the case with about 59,000 customers, the most accurate method includes also a similar day method. All of the most accurate methods use more than one hybridization approach, including residual hybrid, ensemble and range constraining.
In
Figure 3, the four markers on the right end represent different forecasting method applied to the exact same case. At about 1000 aggregated customers, there are combinations of four rather similar groups of about 1000 customers and two different methods in all eight combinations. The blue line in the figure shows how the forecasting accuracy measured in std. depends on the number of customers assuming completely independent forecasting errors. The expected behavior of uncorrelated forecasts is like that. The cases are not fully comparable and the amount of them is too small for making any reliable conclusions. Forecasting when active loads are not present is usually more accurate than when dynamic load control is applied. Load control also makes the load behavior strongly correlated, which also tends to increase the correlation of forecasting errors and thus reduce the NRMSE improvement stemming from increasing the number of aggregated customers. In the cases with 59,000 customers at the right side of
Figure 3, the forecasting time resolution was 3 min and in the other cases it was 1 h. In the lowest NRMSE case at about 3500 customers, it was 24 h. Using more accurate time resolution causes higher values of criteria. At about 3500 customers, the range of the values shows the impact of the improvement of the methods when the case remains the same. There, the outdated national load profiles had the highest NRMSE. In the four groups that have about 1000 customers, the controllable loads dominate. With two of these four groups, the forecasting performance is very good as compared to the blue line. The two leftmost groups, each having 350 to 380 customers, suffered from communication failures in the first third of the 5-year-long verification period. Selecting only the best year of the verification would have given NRMSE = 20.1% for group 1 and NRMSE = 26.8% for group 2 of that case.
One observation is that the results are not always very well comparable between different groups in the same case, nor between different years for the same group. Thus, meaningful comparison of methods across different individual forecasting cases does not seem feasible. The comparability was even worse when using MAPE instead of NRMSE. In addition, the results support the hypothesis that with the best forecasting methods in the studied cases the assumption of mutually independent forecasting errors may be justified if the number of houses is not very large. The amount of cases is too small for making firm conclusions. When the forecasting cases represent the same time and country the cross correlation can be calculated from the forecasts. We leave that now to further studies. The purpose here is only to show that (1) this kind of analysis may be useful when made with many more cases and (2) the comparison of forecasting methods between different cases is complex and gives only very rough results. Further research with many more cases is needed in order to get reliable quantitative results.
Figure 4 shows how the MAPE and NRMSE depended on each other in 38 short-term forecasts that we have produced in six different forecasting cases. All the forecasts have the same forecasting horizon. The differences in their behavior are rather small. This is the expected result for the errors of accurate forecasts. We expect that the results may be much more different if either low accuracy forecasts or more exceptional situations are included in the comparison. Further studies are needed regarding that.
All those six forecasts that have NRMSE between 15% and 17% are from the same group in the same case but use different forecasting methods. The group behavior in the verification was rather different from the identification. The low MAPE in one of the forecasts may indicate that MAPE there failed to adequately detect the rather large peak load errors caused by the behavior change. That may happen, because the statistical behavior of the errors was not any more normally distributed, as is the case with accurate forecasts.
3.5. Load Peak Sensitive Validation
The most valuable forecasts for peak load can be obtained by modeling the actual costs of forecasting errors in the electricity market, in the distribution grid or in both depending on the purpose of forecasting. For most comparisons, this is not practical, because of the complexity and stochastic nature of the costs as shown before. As the cost of the errors is the fundamental reason for the need for accurate forecasts, it is nevertheless important to have at least a general idea on how the costs form and use criteria that reflect the load peak sensitivity of the costs.
Conventional validation statistics cannot solely guarantee the performance of a model in load peak situations. For instance, the recent study on weather forecast-based short-term fault prediction using a neural network (NN) model [
27] showed some inherent limitations of the standard MAPE and mean absolute error (MAE) metrics. MAPE does not work due to existence of zero values, i.e., the absence of network faults. MAE does not properly reflect the model performance thoroughly, e.g., in rare peak events. The high fault rate periods are important to predict in order to temporarily increase preparedness to manage them. On the other hand, the results indicate that the index of agreement (IA) [
28] may provide a more robust metric for measuring the model performance, including peak events and for model evaluation and comparison in general:
where
,
is the true number of faults,
is the predictied number of faults,
,
,
is the sample size, and
IA , higher values of IA indicate better models.
The study [
27] also showed that the resampling/boosting of rare faults peaks in the training data can be used to enhance the ability of an NN model to forecast fault events.
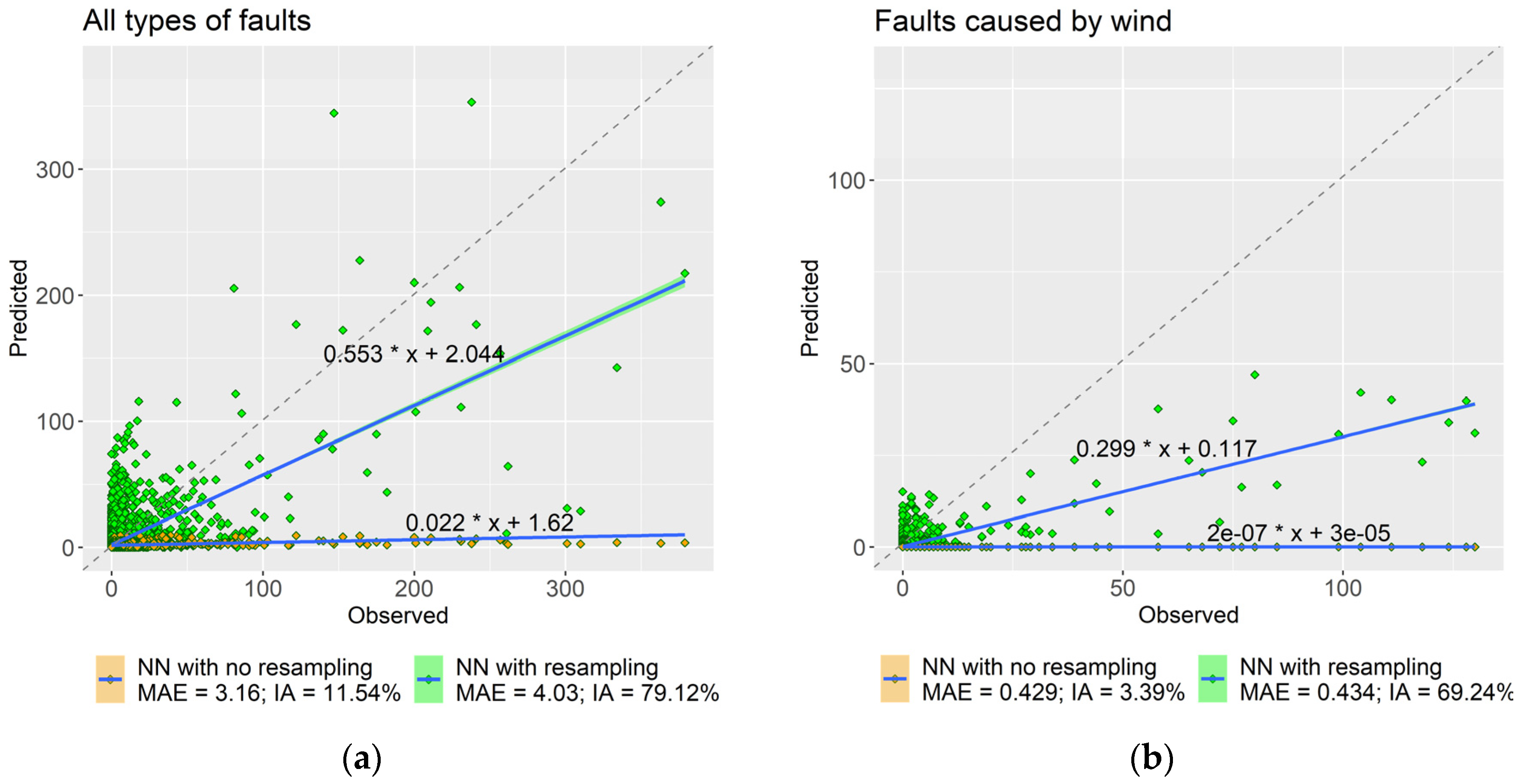
Figure 5 demonstrates the results of forecasting all types of faults and faults caused by wind, originally presented in [
27].
NN models without resampling do not predict peaks but have better MAE as they are more accurate for samples of fewer faults, which are prevalent in the data. On the contrary, NN models with resampling are less accurate for samples of fewer faults, which makes MAE higher. However, the models with resampling are able to predict large peaks, which is more valuable from the problem perspective. For the prediction of all the considered types of faults and wind faults, higher IA values correspond to models with oversampling, which are better at predicting peaks. Based on the given liner regression, we see that there is still a tendency to underestimate peaks. Anyway, the index of agreement may be useful as an additional criterion also in short term load forecasting that has similarly challenges in assessing the performance of forecasting the load peaks.
One option to the aforementioned standard evaluation metrics are categorical statistics i.e., to evaluate model’s performance in critical load peak situations by discriminating electric load to a category/class (e.g., low and high) and then apply some conventional index for each class separately or only to the peak loads. Discrimination can also be based on variables that affect the load such as the outdoor temperature and electricity market price. Evaluation of the accuracy of the daily peak load forecast is sometimes used as a peak load sensitive criterion.
Accurate peak load forecasting is so important that short term peak loads are often separately forecast, as in [
29,
30], for example. Peak load forecasting may be less sensitive to the choice of criterion than the forecasting of the full profile, but absolute maximum error (AME) was used in [
30] to complement MAPE when comparing forecasting methods. This seems justified although there both criteria rated the compared four methods clearly in the same order.
Based on the discrimination and the contingency table, a set of different standard metrics can be derived including:
The fraction of correct prediction (true positive rate, TPR)
the false positive rate, FPR
the Success Index (SI): SI = TPR − FPR
where TPR is the true positive rate representing the sensitivity of the model (the fraction of correct predictions) and FPR is the false positive rate, representing the specificity of the model. SI is limited to the range of −1, 1 and for a perfect model SI = 1 [
31,
32,
33]. With this approach, it is also necessary to have a category for too high predictions, because otherwise too high peak predictions would not be penalized.
Such categorical statistics including probability of detection (POD), critical success index (CSI) and false alarm ration (FAR) are used, e.g., in wind power ramp forecasting as measures of accuracy for forecasts of sudden and large power changes [
34,
35]. The detection and forecasting of those events is crucial with regard to power production and load balance. However, the ability of forecasting methods to predict those events remains relatively low for short term operation.
Probability of detection (POD): POD = TP/TP + FN
Critical success index (CSI): CSI = TP/(TP + FN + FP)
False alarms ratio (FAR): FAR = FP/(FP + TP).
A possible way to classify the load to suitable categories could be based on the gradient of the load duration curve. Also, proportions of the observed peak load or time could be considered; for example, those times could be used when the load is over 80% of the peak load or 20% of the highest loads measured.