Productivity-Index Behavior for a Horizontal Well Intercepted by Multiple Finite-Conductivity Fractures Considering Nonlinear Flow Mechanisms under Steady-State Condition
Abstract
1. Introduction
2. Model Assumption
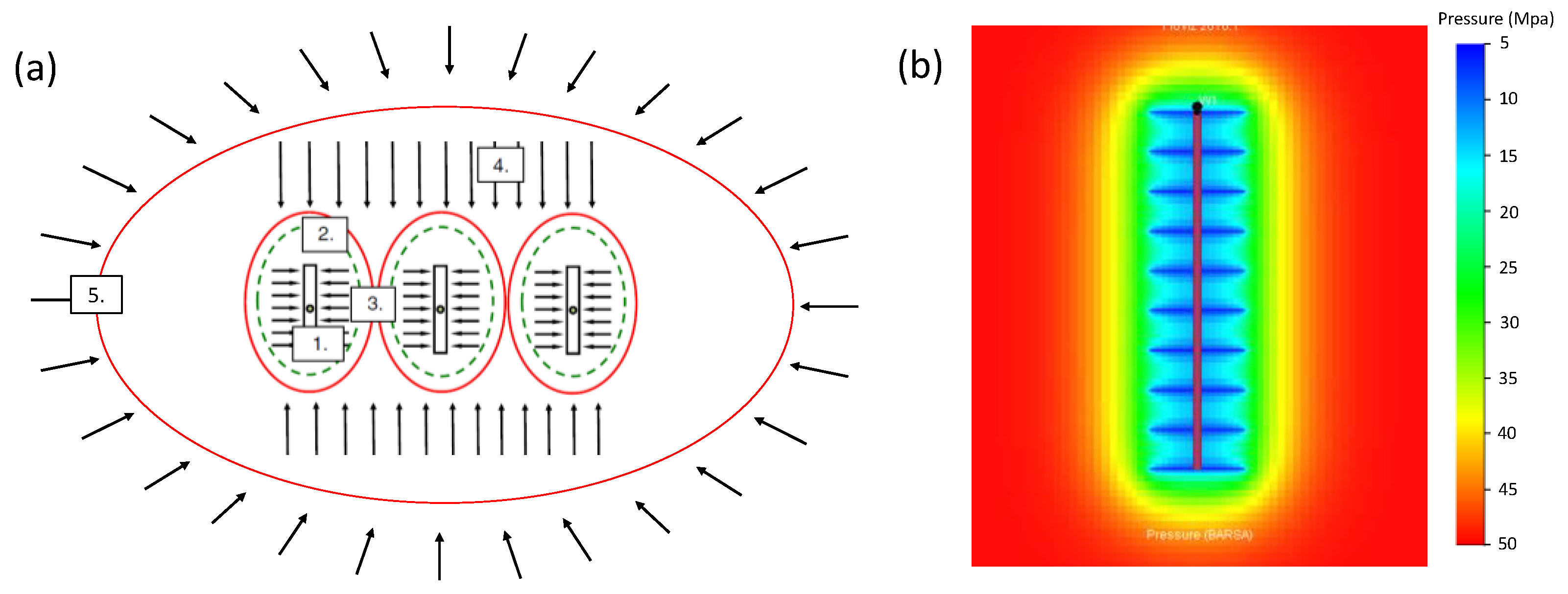
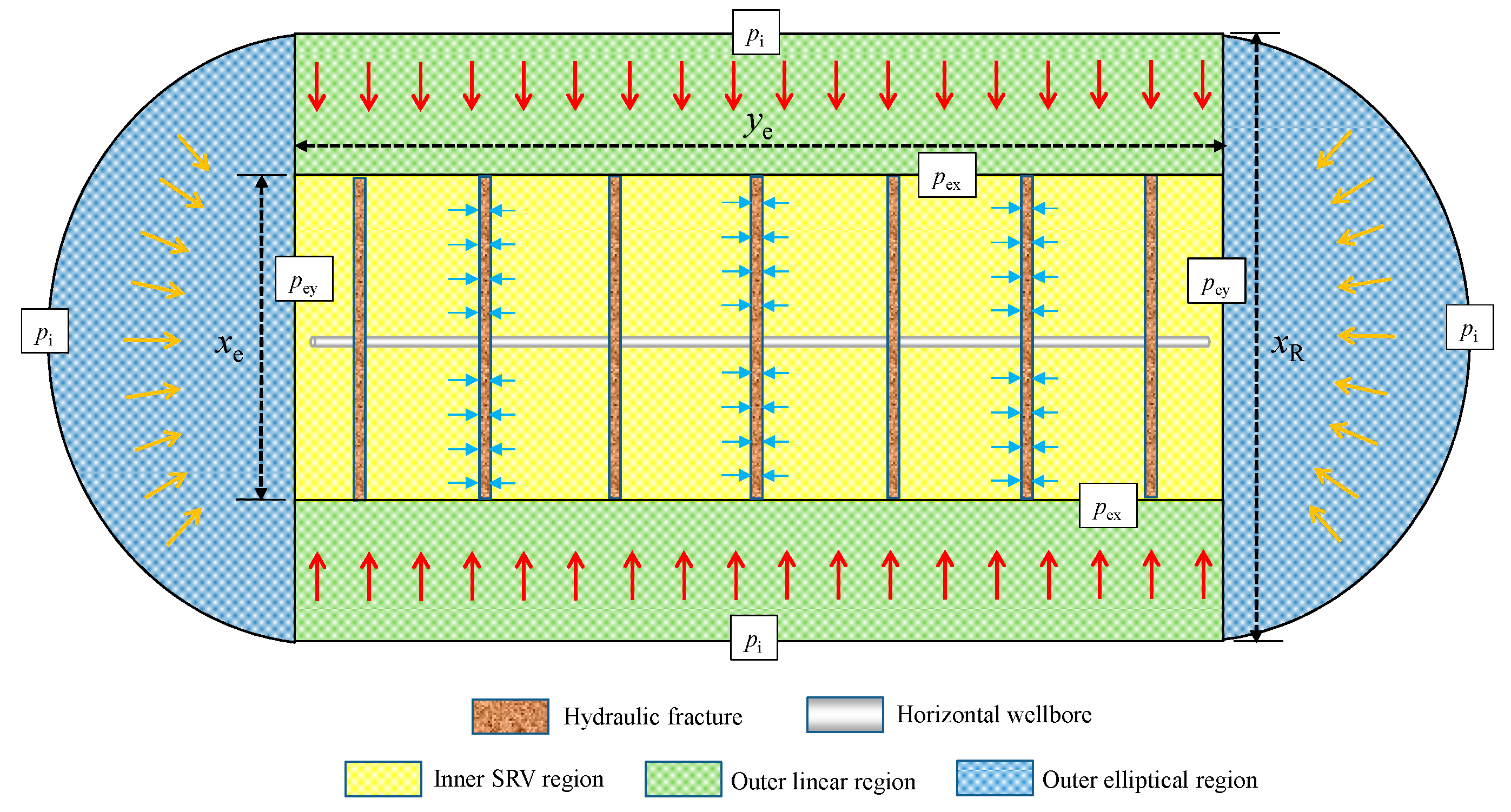
2.1. Physical Model
- The reservoir is horizontal and of uniform thickness, with impermeable lower and upper boundaries. The pressure on the outer boundary in the x–y plane keeps constant.
- Along the horizontal wellbore, multiple hydraulic fractures are evenly distributed. Hydraulic fractures are considered to be a finite conductivity.
- The wellbore is produced under constant-rate condition.
- Flow in the reservoir is assumed to be single-phase fluid (i.e., pure gas) with slight compressibility and constant viscosity.
- Fluid flowing in the fracture is assumed to be nonlinear.
- Fluids from the reservoir enter the wellbore only through hydraulic fractures, and the pressure loss in the wellbore is neglected.
2.2. Variables Definitions
3. Mathematical Model
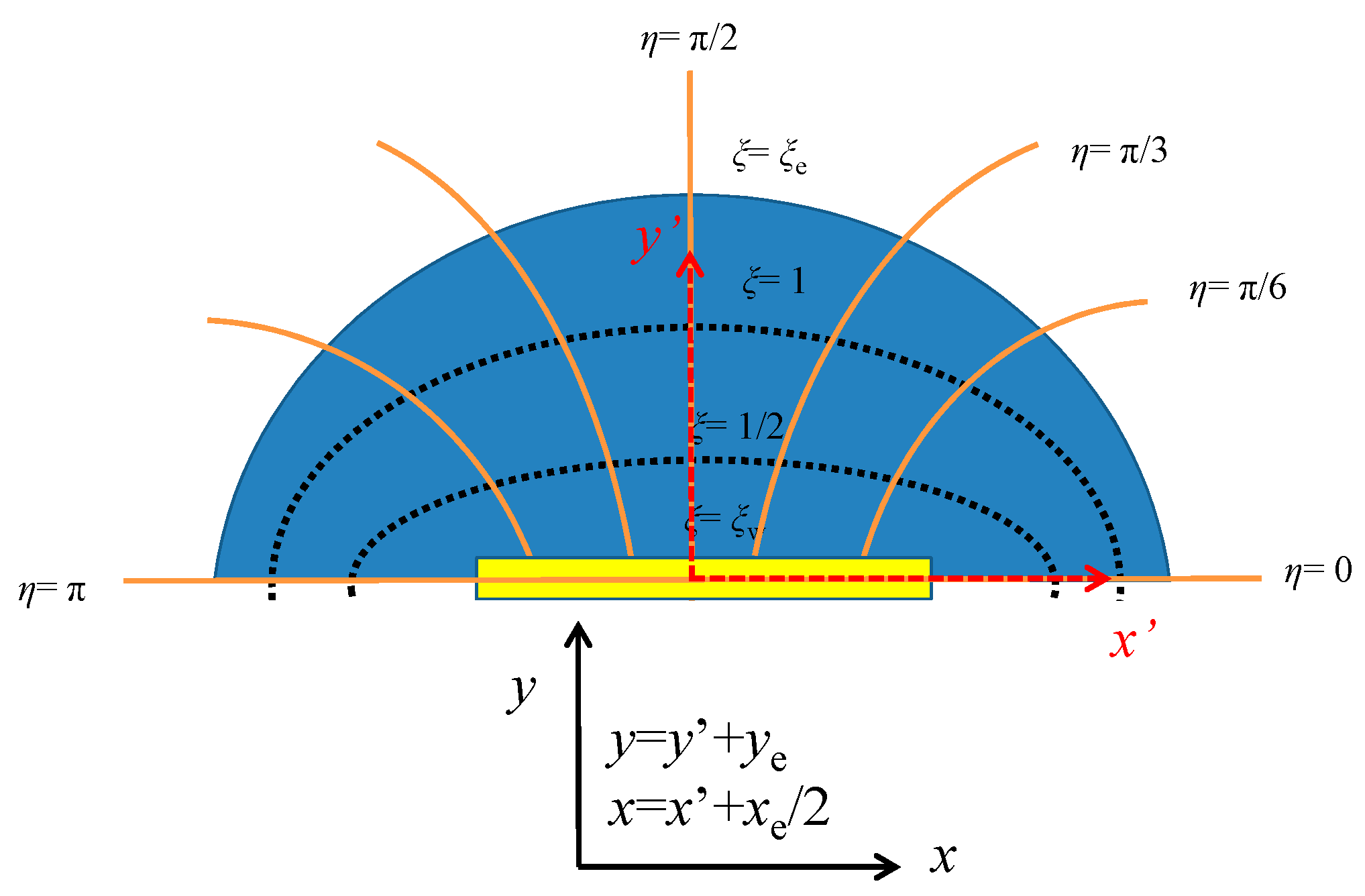
3.1. Fluid Flow in the Inner SRV Region
3.2. Fluid Flow in the Outer Region
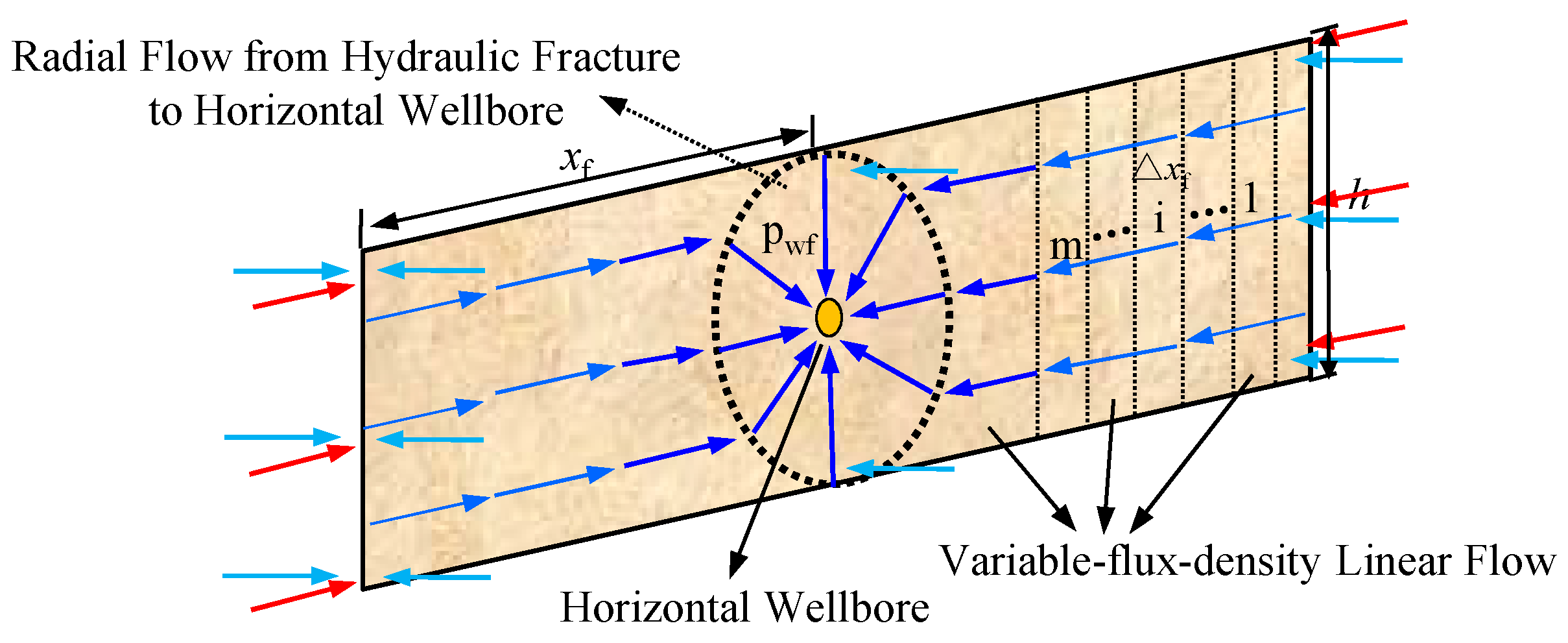
3.3. Fluid Flow in the Fracture
3.3.1. Model of a Conductivity Fracture with Non-Darcy Flow
3.3.2. Model of a Conductivity Fracture with Pressure Sensitivity Effect
4. Semi-Analytical Solution for Coupled Model
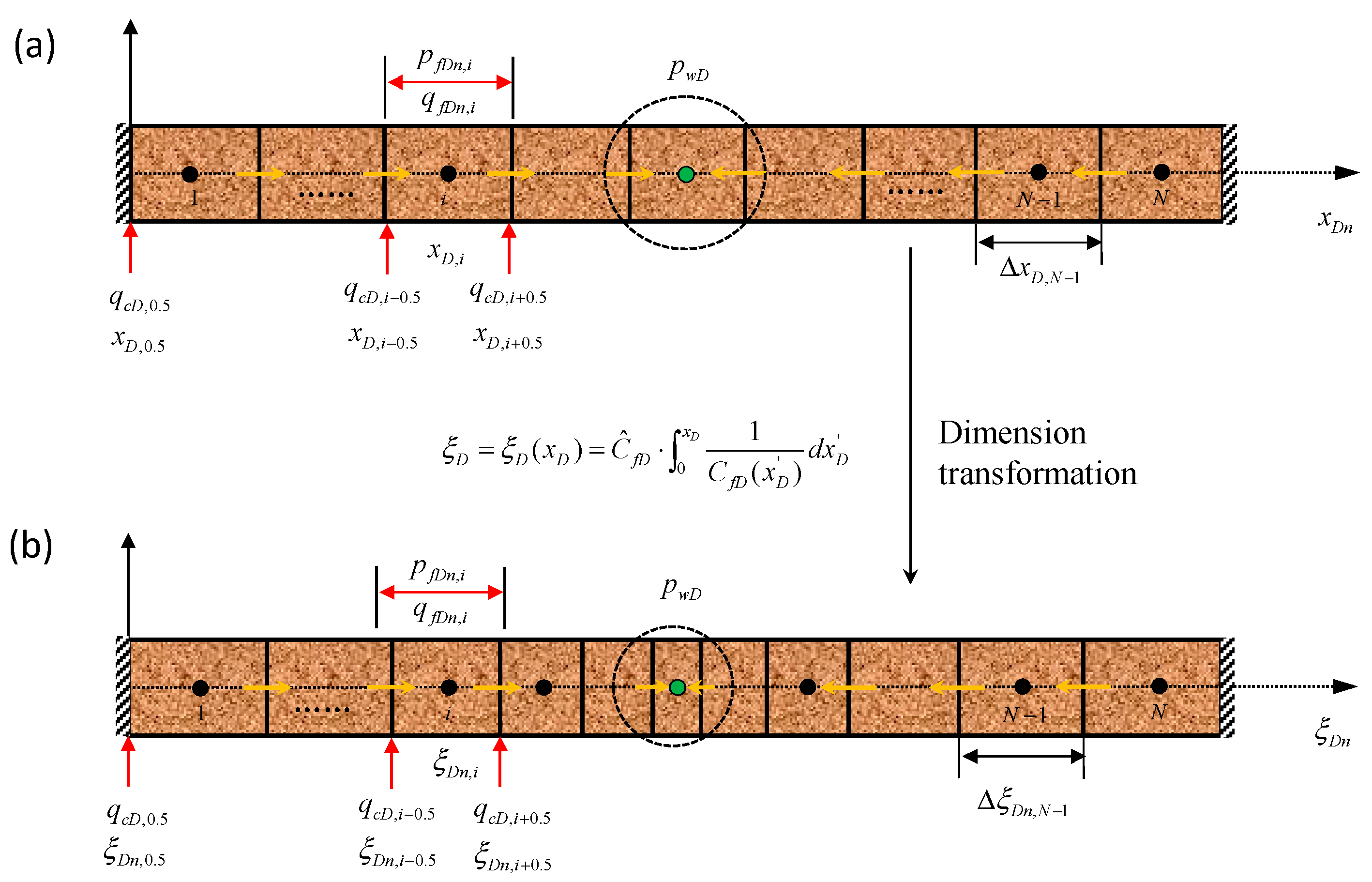
4.1. Dimension Transformation
4.2. Discretization
4.3. Computation Consideration
- Step 1: Initial calculation, with k = 0, the fracture is assumed to be uniform (Case 1 and Case 2). By combing through Equation (29) to Equation (32), we can obtain (qfDn)k. The fracture pressure (pfDn)k (Case 1) and flowing rate (qfDn)k (Case 2) would be then achieved from Equation (28).
- Step 2: Calculating the pressure-sensitive conductivity CfDn[(pfDn)k] (Case 1) and CfDn[(qcDn)k] (Case 2) along fracture, and then transforming xDn into ξDn based on Equation (26).
- Step 3: Solving Equation (33) with the updated CfDn[(pfDn)k] to achieve (pfDn)k+1 and (pwD)k+1 in Case 1; solving Equation (34) with the updated CfDn[(qcDn)k] to achieve (qcDn)k+1 and (pwD)k+1 in Case 2.
- Step 4: Terminate the iterative procedure if |(pwD)k+1 − (pwD)k|/(pwD)k < ε; otherwise, update pressure distribution along fracture by setting (pfDn)k = (pfDn)k+1 (Case 1) and flow distribution along fracture by setting (qcDn)k = (qcDn)k+1 (Case 2), and k = k + 1 back to step 2 until the convergence is achieved.
5. Results and Sensitivity Analysis
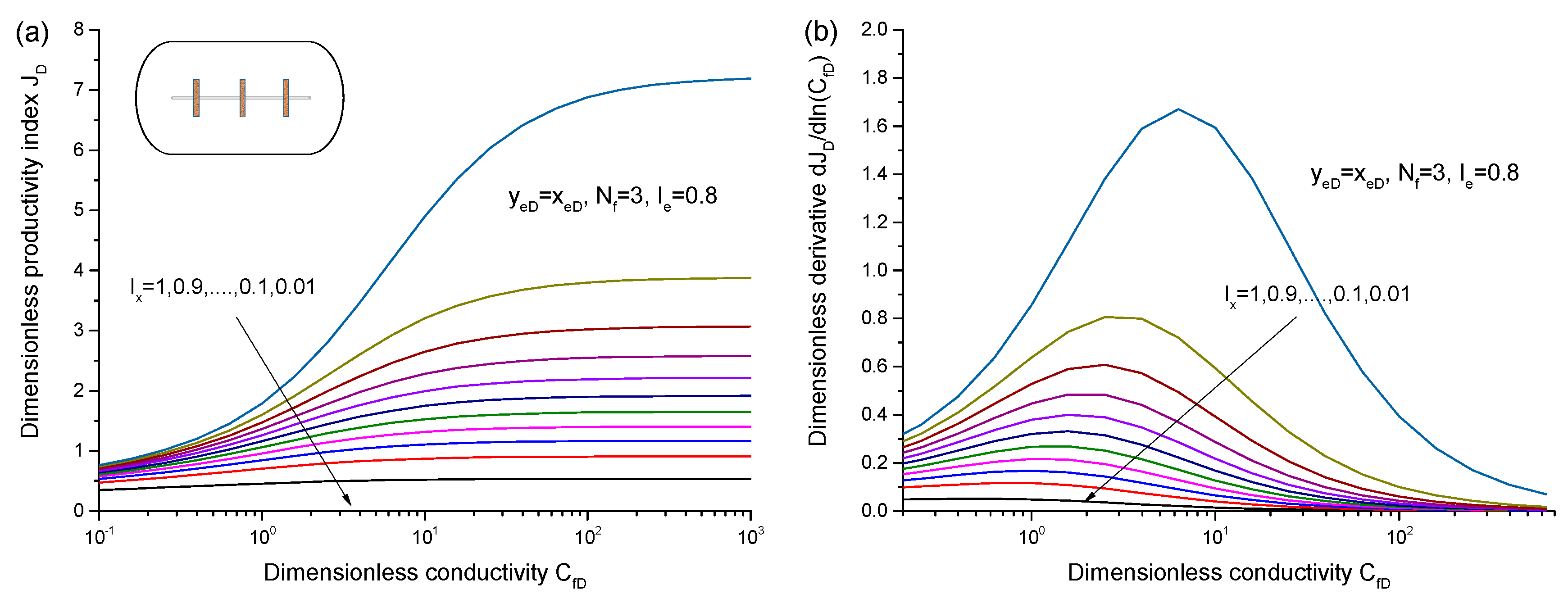
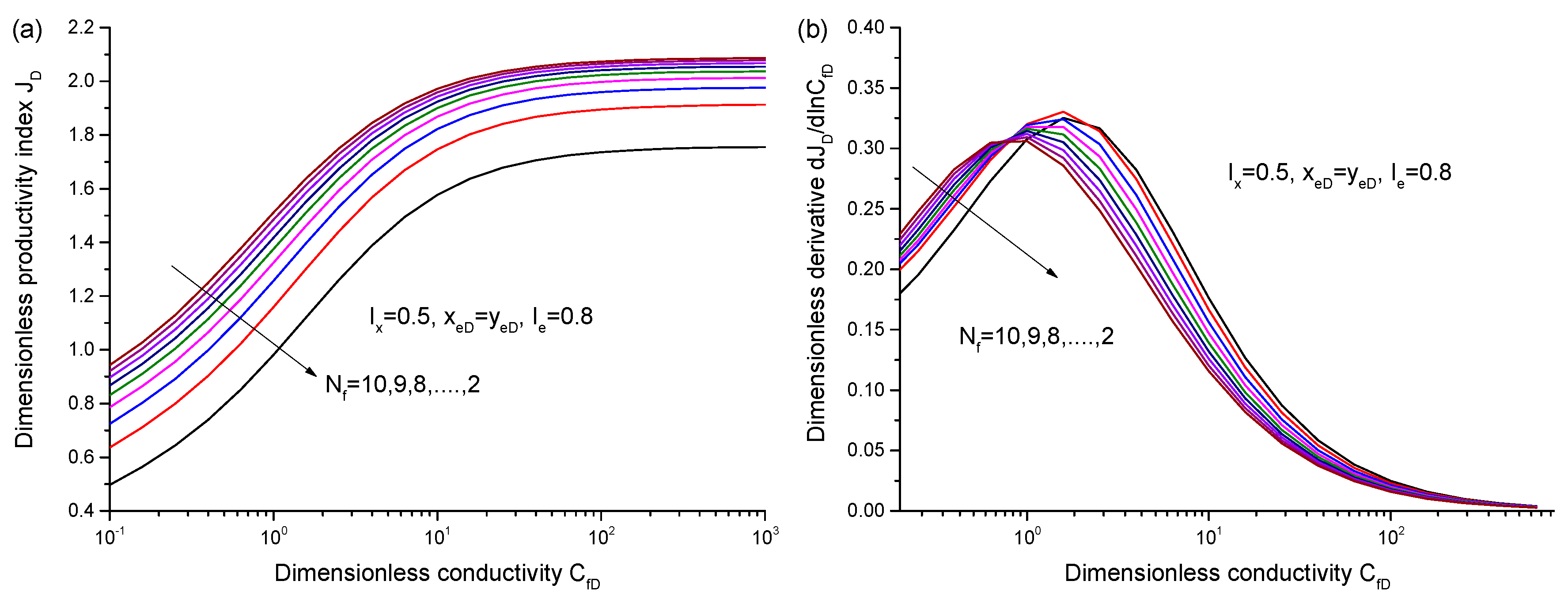
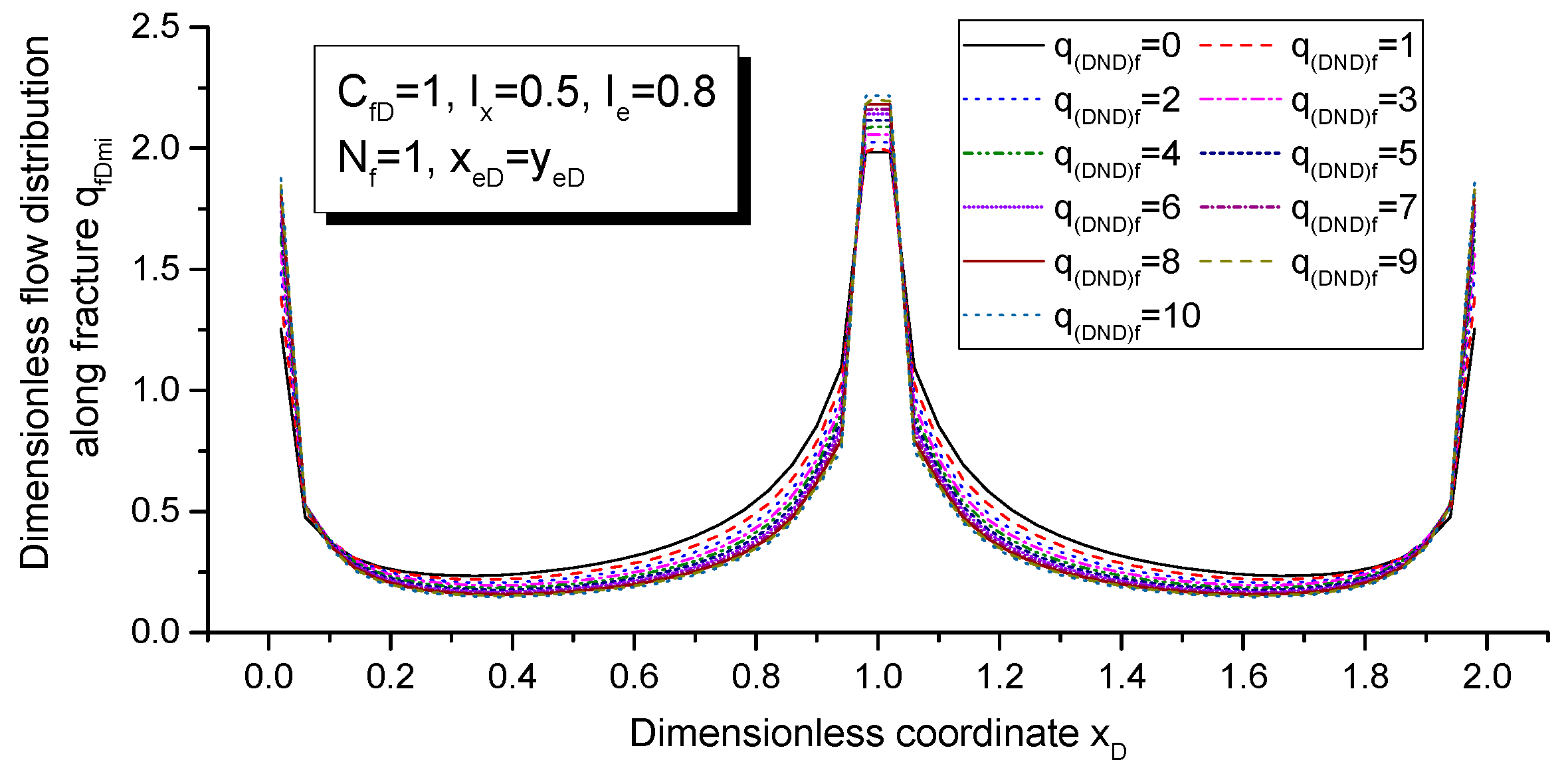
5.1. Influence of Fracture Properties on PI
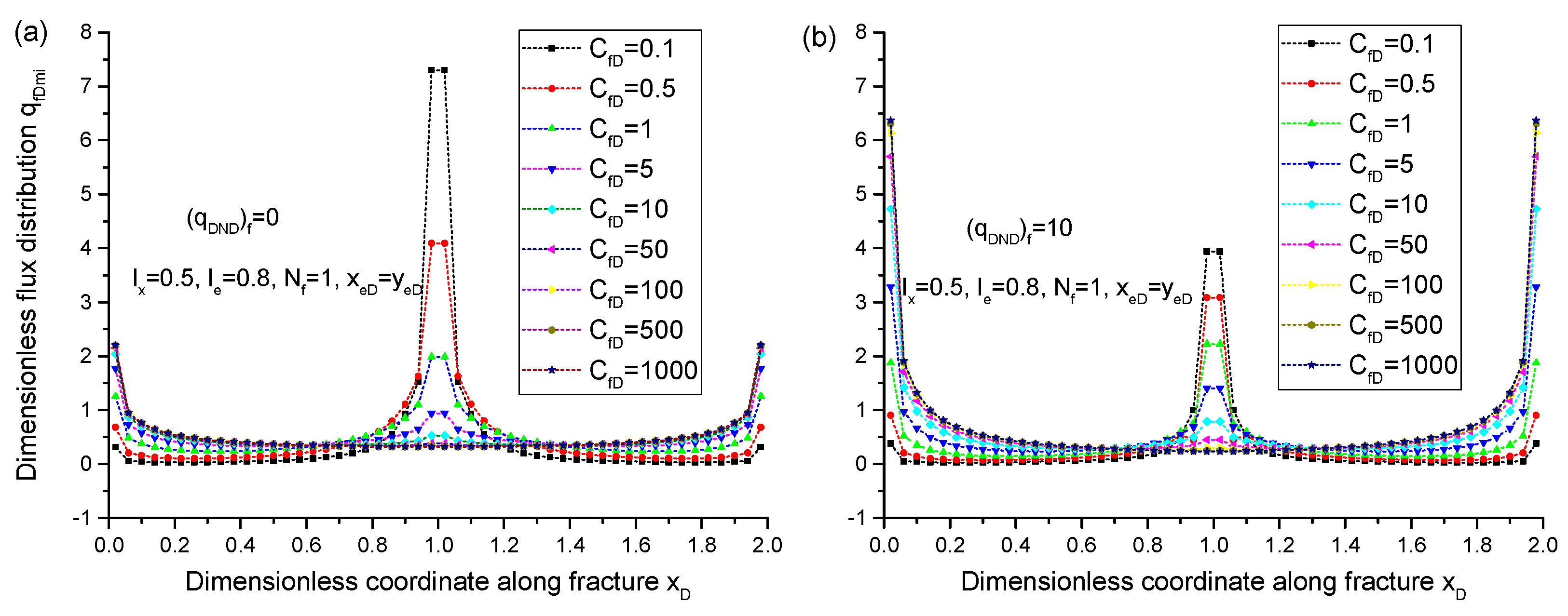
5.2. Influence of Non-Darcy Flow on PI
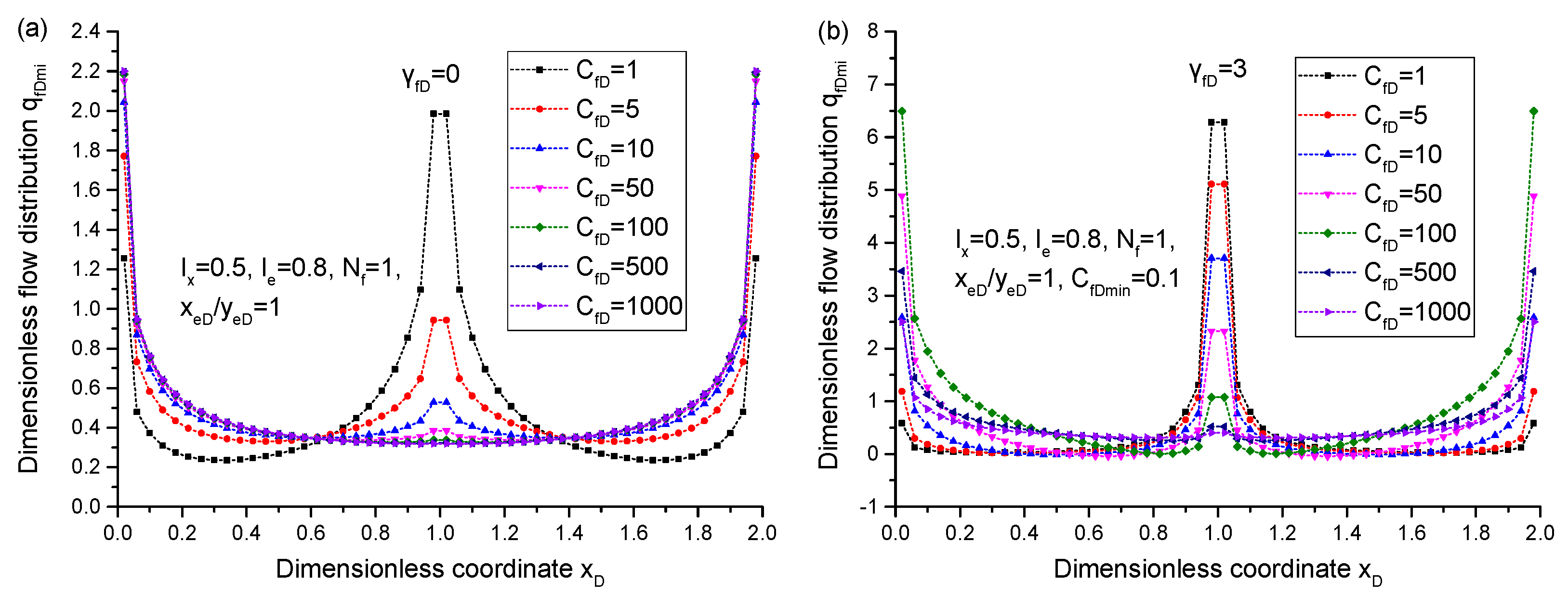
5.3. Influence of the Pressure-Sensitivity Effect on PI
6. Conclusions
- PI increases with the increase of CfD, until it reaches the maximum (JDmax) at CfD = 300.
- PI is deteriorated under the influence of nonlinear flow mechanisms. With the consideration of non-Darcy flow, for the small range of the penetration ratio of the inner SRV region with regard to whole drainage (Ie < 0.9), the relationship between Ie and PI exhibits an approximately linear behavior. When Ie > 0.9, PI is increased rapidly with the Ie.
- With the consideration of pressure sensitivity, the apparent fracture is degraded from the initial conductivity to the minimal conductivity, which is caused by fracture closure. As a result, an extra pressure drop is acquired to offset the conductivity degradation, and PI would be declined to the minimal PI.
- The disadvantage dimensions of fracture (such as small conductivity, penetration ratio, and less fractures) contribute to severe pressure depletion, while, in turn, the severe pressure depletion will strengthen the effect of the nonlinear flow mechanism on PI behavior.
- If the conductivity in the fracture reaches the level of infinite conductivity, the influence of nonlinear flow mechanism on PI could be neglected.
Author Contributions
Funding
Conflicts of Interest
Appendix A. Analytical Solution for the Inner SRV Region
Appendix B. Analytical Solution for the Outer Region
References
- Clarkson, C.R.; Bustin, R.M.; Seidle, J.P. Production-data analysis of single-phase (gas) coalbed-methane wells. SPE Reserv. Eval. Eng. 2007, 3, 312–341. [Google Scholar] [CrossRef]
- Wang, J.H.; Wang, X.D.; Dong, W.X. Rate decline curves analysis of multiple-fractured horizontal wells in heterogeneous reservoirs. J. Hydrol. 2017, 553, 527–539. [Google Scholar] [CrossRef]
- Deng, J.; Zhu, W.Y.; Ma, Q. A new seepage model for shale gas reservoir and productivity analysis of fractured well. Fuel 2014, 124, 232–240. [Google Scholar] [CrossRef]
- Clarkson, C.R. Production data analysis of unconventional gas wells: Review of theory and best practices. Int. J. Coal Geol. 2013, 109–110, 101–146. [Google Scholar] [CrossRef]
- Zhang, Q.; Su, Y.L.; Wang, W.D.; Lu, M.; Ren, L. Performance analysis of fractured wells with elliptical SRV in shale reservoirs. J. Nat. Gas Sci. Eng. 2017, 45, 380–390. [Google Scholar] [CrossRef]
- Wang, J.L.; Wei, Y.S.; Luo, W.J. A unified approach to optimize fracture design of a horizontal well intercepted by primary- and secondary-fracture networks. SPE J. 2019, 24, 1270–1287. [Google Scholar] [CrossRef]
- Al-Rbeawi, S. Productivity-index behavior for hydraulically fractured reservoirs depleted by constant production rate considering transient-state and semisteady-state conditions. SPE Prod. Oper. 2018, 33. [Google Scholar] [CrossRef]
- Warren, J.E.; Root, P.J. The behavior of naturally fractured reservoirs. SPE J. 1963, 3, 245–255. [Google Scholar] [CrossRef]
- Obinna, E.D.; Hassan, D. A model for simultaneous matrix depletion into natural and hydraulic fracture networks. J. Nat. Gas Sci. Eng. 2014, 16, 57–69. [Google Scholar]
- Stalgorova, E.; Mattar, L. Analytical model for unconventional multifractured composite systems. SPE Reserv. Eval. Eng. 2013, 16, 246–256. [Google Scholar] [CrossRef]
- Al-Ghamdi, A.; Chen, B.; Behmanesh, H.; Qanbari, F.; Aguilera, R. An improved triple-porosity model for evaluation of naturally fractured reservoirs. SPE Reserv. Eval. Eng. 2011, 8, 397–404. [Google Scholar] [CrossRef]
- Karimi-Fard, M.; Durlofsky, L.J. A general gridding, discretization, and coarsening methodology for modeling flow in porous formations with discrete geological features. Adv. Water Resour. 2016, 96, 354–372. [Google Scholar] [CrossRef]
- Xu, Y.; Cavalcante Filho, J.S.A.; Yu, W. Discrete-fracture modeling of complex hydraulic-fracture geometries in reservoir simulators. SPE Reserv. Eval. Eng. 2017, 20, 403–422. [Google Scholar] [CrossRef]
- Li, L.Y.; Lee, S.H. Efficient field-scale simulation of black oil in a naturally fractured reservoir through discrete fracture networks and homogenized media. SPE Reserv. Eval. Eng. 2008, 8, 750–758. [Google Scholar] [CrossRef]
- Cinco-Ley, H.; Samaniego, F.; Dominguez, N. Transient pressure behavior for a well with a finite-conductivity vertical fracture. Soc. Pet. Eng. J. 1978, 8, 254–265. [Google Scholar]
- Wang, J.L.; Jia, A.L.; Wei, Y.S.; Qi, Y.D. Approximate semi-analytical modeling of transient behavior of horizontal well intercepted by multiple pressure-dependent conductivity fractures in pressure-sensitive reservoir. J. Pet. Sci. Eng. 2017, 153, 157–177. [Google Scholar] [CrossRef]
- Wang, J.L.; Jia, A.L.; Wei, Y.S. A general framework model for simulating transient response of a well with complex fracture network by use of source and Green’s function. J. Nat. Gas Sci. Eng. 2018, 55, 254–275. [Google Scholar] [CrossRef]
- Zhou, W.T.; Banerjee, R.; Poe, B. Semianalytical production simulation of complex hydraulic-fracture networks. SPE J. 2013, 19, 6–18. [Google Scholar] [CrossRef]
- Kuchuk, F.; Biryukov, D. Pressure-transient behavior of continuously and discretely fractured reservoirs. SPE Reserv. Eval. Eng. 2014, 17, 82–97. [Google Scholar] [CrossRef]
- Al-Rbeawi, S. The optimal reservoir configuration for maximum productivity index of gas reservoirs depleted by horizontal wells under Darcy and non-Darcy flow conditions. J. Nat. Gas Sci. Eng. 2018, 49, 179–193. [Google Scholar] [CrossRef]
- Chen, Z.M.; Liao, X.W.; Zhao, X.L.; Lyu, S.; Zhu, L. A comprehensive productivity equation for multiple fractured vertical well with non-linear effects under steady-state flow. J. Pet. Sci. Eng. 2017, 149, 9–24. [Google Scholar] [CrossRef]
- Li, J.; Guo, B.; Gao, D.; Ai, C. The effect of fracture-face matrix damage on productivity of fractures with infinite and finite conductivities in shale-gas reservoirs. SPE Drill. Complet. 2012, 9, 347–353. [Google Scholar] [CrossRef]
- Prats, M.; Raghavan, R. Finite horizontal well in a uniform-thickness reservoir crossing a natural fracture normally. SPE J. 2013, 10, 982–992. [Google Scholar] [CrossRef]
- Tahmasebi, P.; Kamrava, S. A pore-scale mathematical modeling of fluid-particle interactions: Thermo-hydro-mechanical coupling. Int. J. Greenh. Gas Control 2019, 83, 245–255. [Google Scholar] [CrossRef]
- Zhang, X.M.; Tahmasebi, P. Effects of grain size on deformation in porous media. Transp. Porous Media 2019, 129, 321–341. [Google Scholar] [CrossRef]
- Zhang, X.M.; Tahmasebi, P. Micromechanical evaluation of rock and fluid interactions. Int. J. Greenh. Gas Control 2018, 76, 266–277. [Google Scholar] [CrossRef]
- Guppy, K.H.; Cinco-Ley, H.; Ramey, H.J. Effect of non-Darcy flow on the constant-pressure production of fractured wells. Soc. Pet. Eng. J. 1981, 12, 390–400. [Google Scholar] [CrossRef]
- Wu, Y.S.; Li, J.F.; Ding, D.; Wang, C.; Di, Y. A generalized framework model for simulation of gas production in unconventional gas reservoir. In Proceedings of the SPE Reservoir Simulation Symposium, The Woodlands, TX, USA, 18–20 February 2013. [Google Scholar]
- Lin, J.; Zhu, D. Predicting well performance in complex fracture systems by slab source method. In Proceedings of the SPE Hydraulic Fracturing Technology Conference, The Woodlands, TX, USA, 6–8 February 2012. [Google Scholar]
- Pedroso, C.A.; Correa, A.C. A new model of a pressure-dependent-conductivity hydraulic fracture in a finite reservoir: Constant rate production case. In Proceedings of the Latin American and Caribbean Petroleum Engineering Conference, Rio de Janeiro, Brazil, 30 August–3 September 1997. [Google Scholar]
- Zhang, Z.; He, S.L.; Liu, G.; Guo, X.; Mo, S. Pressure buildup behavior of vertically fractured wells with stress-sensitive conductivity. J. Pet. Sci. Eng. 2014, 122, 48–55. [Google Scholar] [CrossRef]
- Yao, S.S.; Zeng, F.H.; Liu, H. A semi-analytical model for hydraulically fractured wells with stress-sensitive conductivities. In Proceedings of the SPE Unconventional Resources Conference, Calgary, AB, Canada, 5–7 November 2012. [Google Scholar]
- Biryukov, D.; Kuchuk, F.J. Transient pressure behavior of reservoirs with discrete conductive faults and fractures. Transp. Porous Media 2012, 95, 239–268. [Google Scholar] [CrossRef]
- Rasoulzadeh, M.; Kuchuk, F.J. Pressure transient behavior of high-fracture-density reservoirs (dual-porosity models). Transp. Porous Media 2019, 127, 222–243. [Google Scholar] [CrossRef]
- Kuchuk, F.J.; Habashy, T. Pressure behavior of laterally composite reservoirs. SPE Form. Eval. 1997, 3, 47–56. [Google Scholar] [CrossRef]
- Luo, W.J.; Tang, C.F. A semianalytical solution of a vertical fractured well with varying conductivity under non-Darcy-flow condition. SPE J. 2015, 20, 1028–1040. [Google Scholar] [CrossRef]
- Luo, W.J.; Tang, C.F.; Feng, Y. Mechanism of fluid flow along a dynamic conductivity fracture with pressure-dependent permeability under constant wellbore pressure. J. Pet. Sci. Eng. 2018, 166, 465–475. [Google Scholar] [CrossRef]






© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cao, M.; Xiao, H.; Wang, C. Productivity-Index Behavior for a Horizontal Well Intercepted by Multiple Finite-Conductivity Fractures Considering Nonlinear Flow Mechanisms under Steady-State Condition. Energies 2020, 13, 2015. https://doi.org/10.3390/en13082015
Cao M, Xiao H, Wang C. Productivity-Index Behavior for a Horizontal Well Intercepted by Multiple Finite-Conductivity Fractures Considering Nonlinear Flow Mechanisms under Steady-State Condition. Energies. 2020; 13(8):2015. https://doi.org/10.3390/en13082015
Chicago/Turabian StyleCao, Maojun, Hong Xiao, and Caizhi Wang. 2020. "Productivity-Index Behavior for a Horizontal Well Intercepted by Multiple Finite-Conductivity Fractures Considering Nonlinear Flow Mechanisms under Steady-State Condition" Energies 13, no. 8: 2015. https://doi.org/10.3390/en13082015
APA StyleCao, M., Xiao, H., & Wang, C. (2020). Productivity-Index Behavior for a Horizontal Well Intercepted by Multiple Finite-Conductivity Fractures Considering Nonlinear Flow Mechanisms under Steady-State Condition. Energies, 13(8), 2015. https://doi.org/10.3390/en13082015



