On Distributional Effects in Local Electricity Market Designs—Evidence from a German Case Study
Abstract
1. Introduction
2. Background and Literature
3. Methodology
3.1. The Prosumer’s Problem
3.2. The Consumer’s Problem
3.3. The Independent Power Producer’s Problem
3.4. Local Balancing Mechanism
4. A Case Study in the German Regulatory Context
4.1. The Benchmark of a Market Design
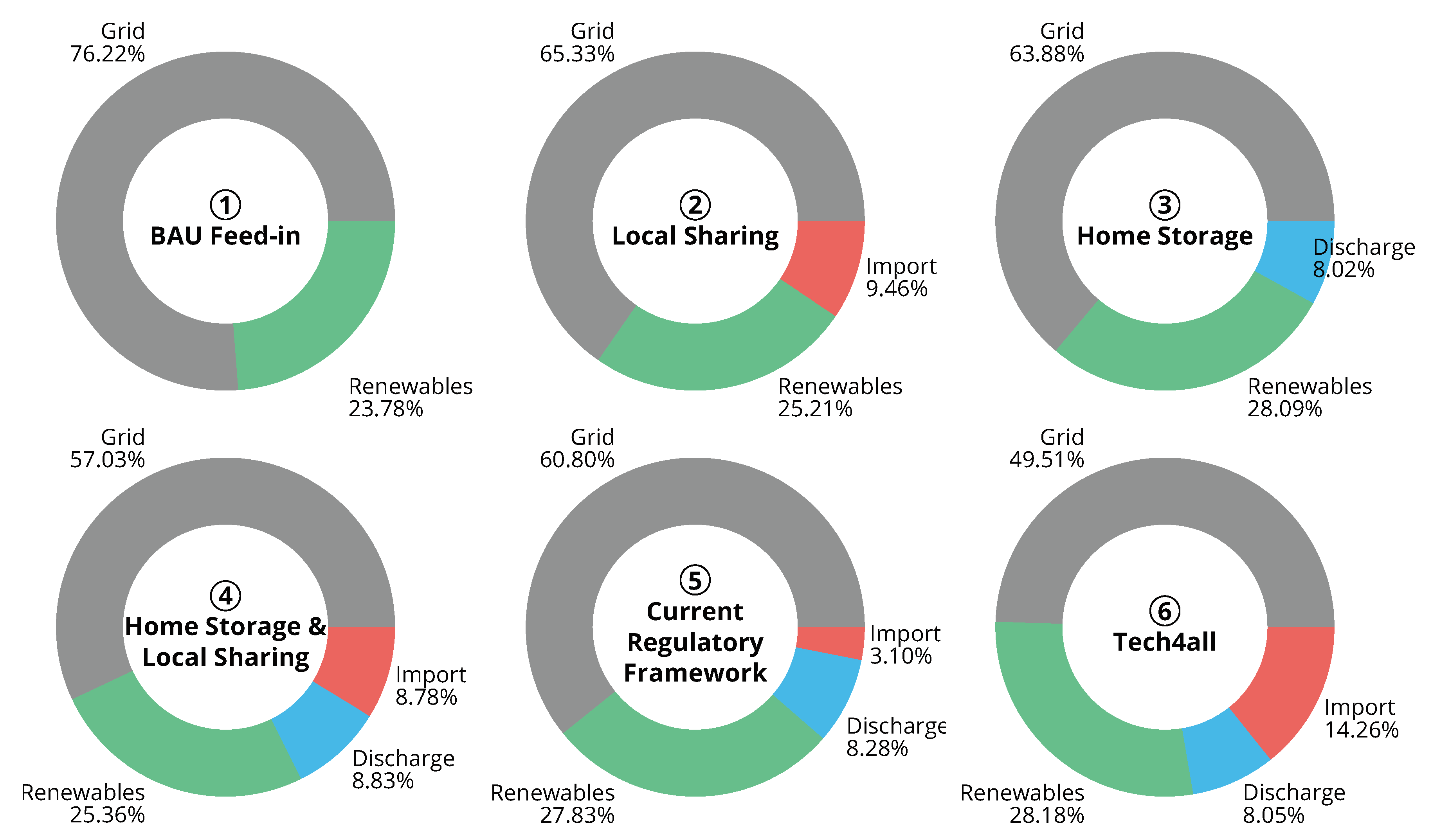
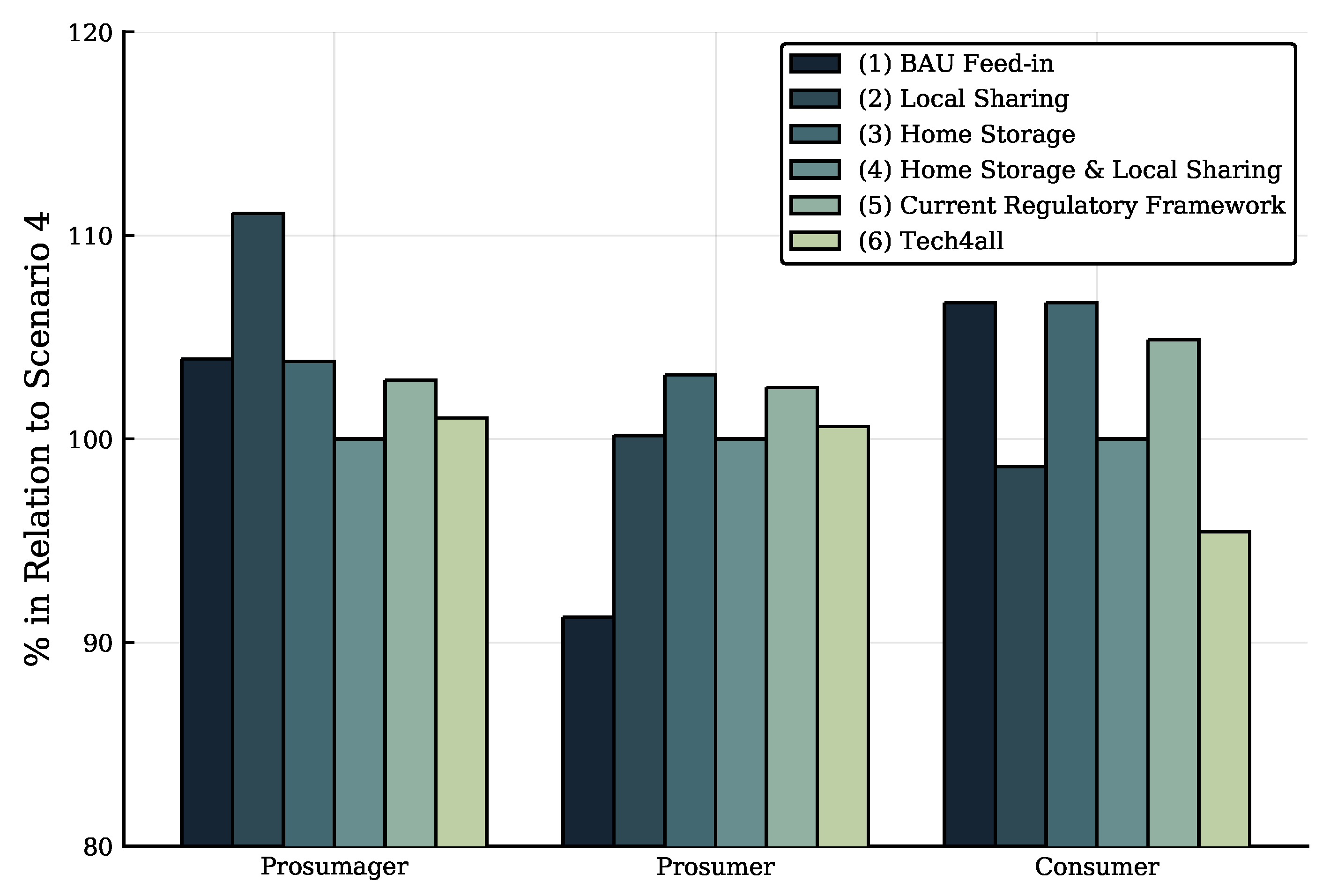
- the more features enabled within the community, the higher the monetary savings.
- prosumers profit most from owning both generation technologies and storage, and a pure consumer sees only a small decrease in costs.
- cheap rates in the local market can only be reached by avoiding grid fees, surcharges and/or levies, which is the main assumption for the local rate.
- the community’s self-sufficiency rate increases (see Figure 2) while the peak load remains rather constant.
4.2. Integration Into the German Regulatory Framework
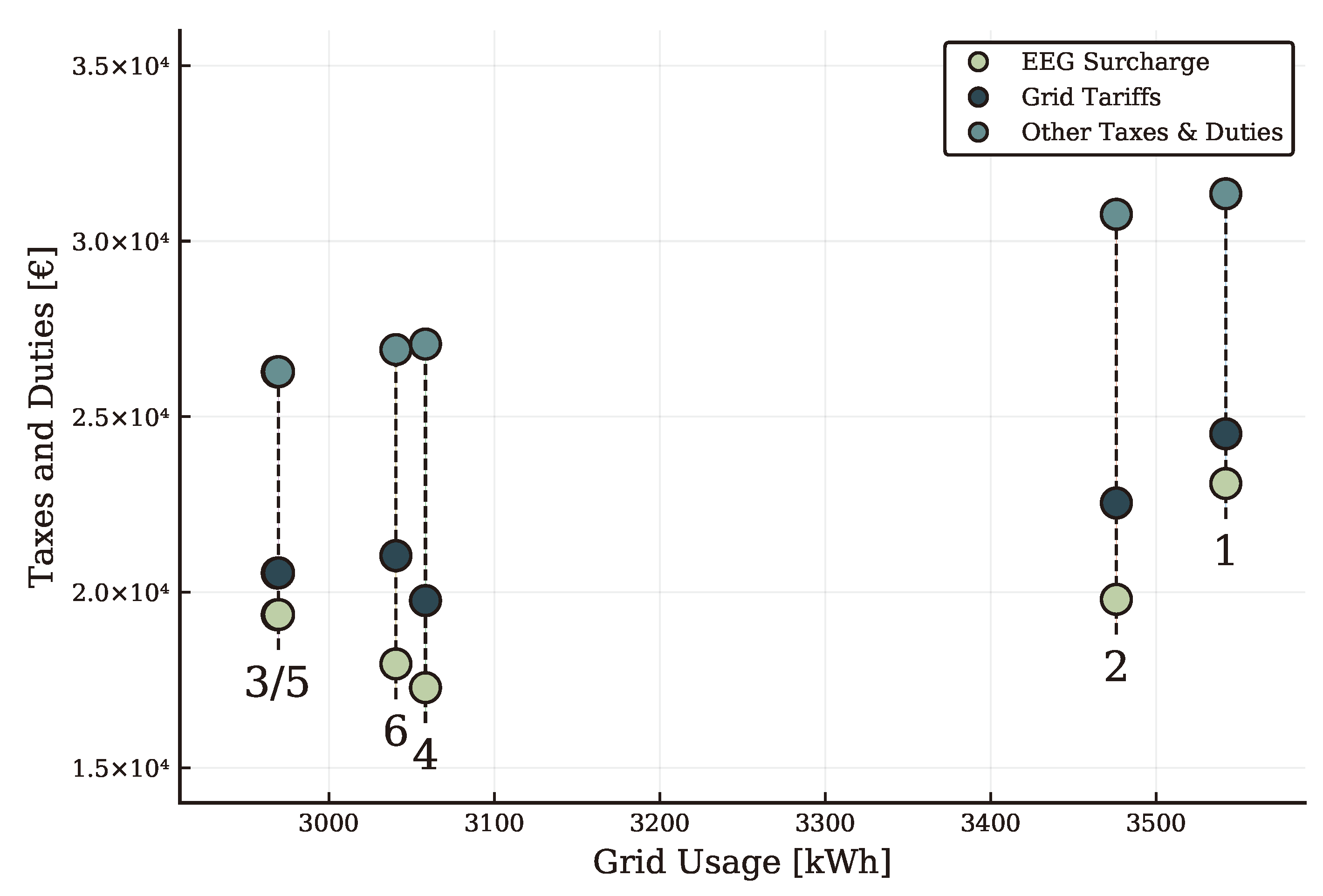
- The regulatory framework makes it unattractive for prosumers to trade locally when their marginal costs are higher than the electricity spot price.
- Under the framework, local trade is only economically viable for prosumers with fully written-off installations.
- Once more installations are written-off this model can become competitive under the current regulation if we disregard the administrative burden.
- With the first version of the German Renewable Energy Sources Act (EEG) in 2000, Germany started a series of laws on prioritising green energy in the electricity mix. Together with the Energy Industry Act (EnWG), the basic legal framework for the German electricity market is formed. (There are about 90 other acts, directives and regulations on European and national level that affect Germany’s energy supply system [56].) While the EEG handles mostly rules on renewable energy sources and their integration into the system, the EnWG defines also the regulatory framework for the overall energy—including the electricity—sector.
- From a legal perspective, the prosumer is end-user (§ 3 Nr. 33 EEG) and auto-producer (§ 3 Nr. 19 EEG). As of today, regulation allows prosumers with a capacity of up to 100 kWp to feed their electricity into the network but exempts them from regulatory duties and rewards them at a rate determined by the Federal Network Agency (Bundesnetzagentur, BNetzA) based on the overall installed capacity. The rate is transferred into consumers’ electricity bills by adding a reallocation charge (EEG-Umlage) on top of each kWh consumed. Thus, end-users pay a surcharge which in turn is paid to prosumers and operators of renewable energy installations for each kWh they feed in.
- If prosumers intend to bypass the fixed feed-in tariff and instead trade with a chosen, presumably locally circumjacent partner instead, they will need to perform some or all retailing duties depending on the prosumer’s intention. The EnWG declares in principle every participant feeding electricity into the grid as an energy utility. Thus, parties making use of the grid by sending electricity through the network have to pay a grid fee and perform a set of bureaucratic duties. These duties comprise accounting, billing, reporting and metering tasks [54]. While grid fees are usually passed on to the customers’ bills, these duties stay on the producers’ list of tasks, and generally exceed the average prosumer’s personal capacity of work load as the processes are matched with energy utilities’ businesses [54].
- Aside from the fixed feed-in tariff, other existing business models are difficult to implement for prosumers with small capacities. On the one hand, responsibilities increase to a large extent once electricity is directly sold to another customer. On the other hand, the economic potential is fairly unattractive [36]. Appendix C elaborates on the details.
- It is noteworthy at this point that fixed feed-in rates phase out 20 years after installation and will—as of today—not be given to new installations once an aggregated capacity of 52 GW of installed solar power is reached in Germany, despite recent political discussions.
4.3. New Market Design: Tech4all
- Consumers are allowed to participate in the energy transition.
- Most participants can lower their costs compared to today’s framework.
- The quantity financed by the EEG surcharge is lowered due to a separate rate for local trading.
- Players always pay full grid charges when the grid is used.
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| BMWi | German Federal Ministry of Economic Affairs and Energy |
| BNetzA | German Federal Network Agency |
| DER | Distributed Energy Resource |
| EEG | German Renewable Energy Sources Act |
| EnWG | German Energy Industry Act |
| IPP | Independent Power Producer |
| KKT | Karush–Kuhn–Tucker Condition |
| LCOE | Levelised Cost of Energy |
| LCOS | Levelised Costs of Storage |
| LEM | Local Electricity Market |
| LMP | Locational Marginal Pricing |
| MaStR | Markstammdatenregister |
| MCP | Mixed Complementarity Problem |
| OPSD | Open Power System Data |
| P2P | Peer-to-Peer |
Appendix A. Karush-Kuhn-Tucker Conditions
Appendix A.1. The Prosumer’s Problem
Appendix A.2. The Consumer’s Problem
Appendix A.3. The Independent Power Producer’s Problem
Appendix A.4. Local Balancing Mechanism
Appendix B. Data
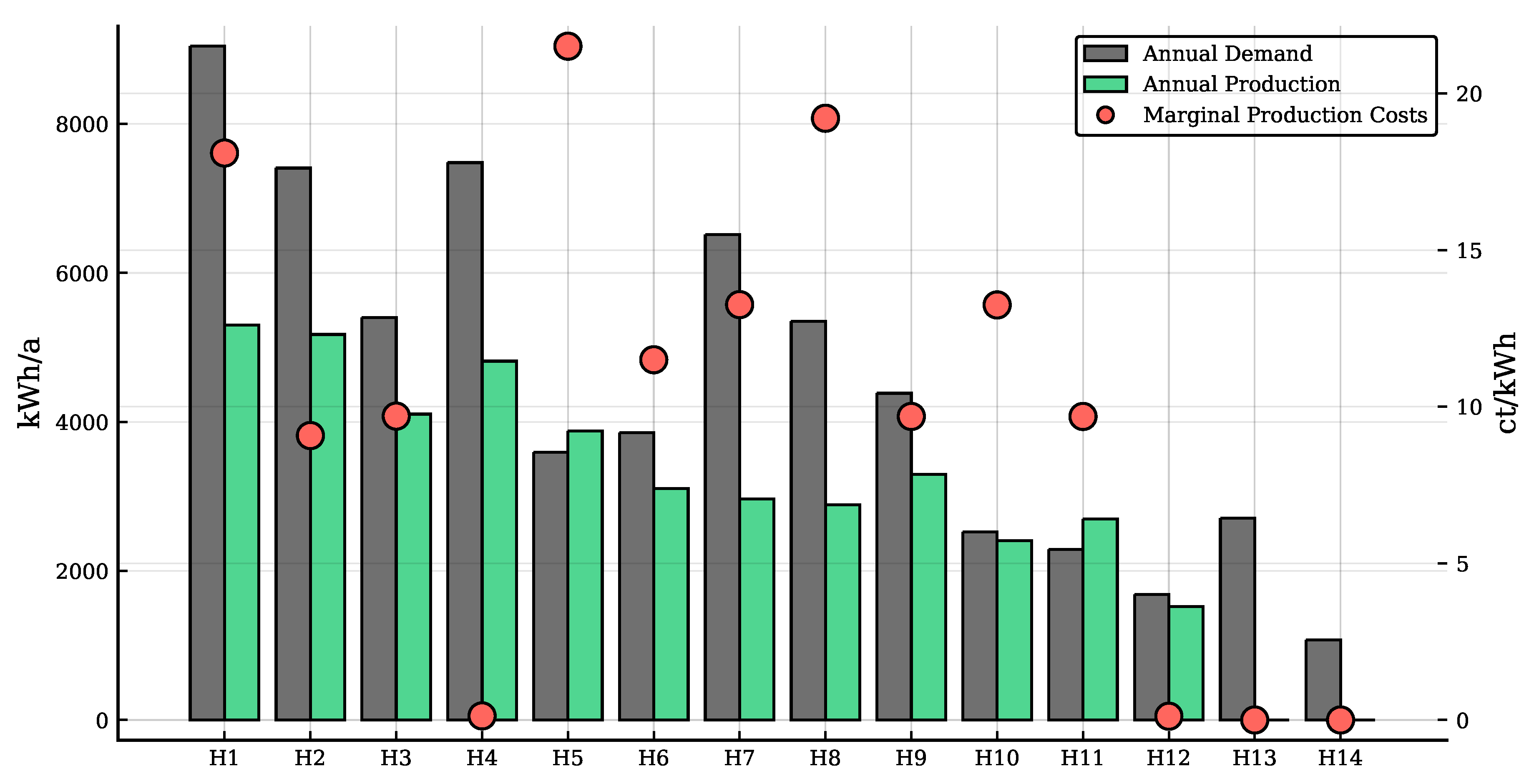
| Player | Annual Demand [kWh] | Annual Production [kWh] | Type | Installed Capacity [kWp] | Year of Installation | Feed-In Tariff [ct/kWh] | Marginal Prod. Cost [ct/kWh] | Storage Capacity [kWh] |
|---|---|---|---|---|---|---|---|---|
| H1 | 9043 | 5301 | Wind | 2.00 | 2011 | 8.97 | 18.10 | 6 |
| H2 | 7408 | 5174 | PV | 4.08 | 2019 | 11.11 | 9.08 | 4 |
| H3 | 5401 | 4104 | PV | 3.24 | 2017 | 12.20 | 9.70 | 4 |
| H4 | 7480 | 4816 | PV | 3.80 | 2006 | – | 0.13 | 4 |
| H5 | 3592 | 3880 | PV | 3.06 | 2010 | 33.03 | 21.51 | 4 |
| H6 | 3857 | 3106 | PV | 2.45 | 2015 | 12.47 | 11.50 | – |
| H7 | 6516 | 2966 | PV | 2.34 | 2012 | 24.43 | 13.26 | – |
| H8 | 5350 | 2890 | PV | 2.28 | 2011 | 28.74 | 19.21 | – |
| H9 | 4386 | 3294 | PV | 2.60 | 2017 | 12.30 | 9.69 | – |
| H10 | 2522 | 2409 | PV | 1.90 | 2012 | 24.43 | 13.25 | – |
| H11 | 2288 | 2698 | PV | 2.13 | 2017 | 12.20 | 9.69 | – |
| H12 | 1685 | 1521 | PV | 1.20 | 2004 | – | 0.12 | – |
| H13 | 2708 | 0/208 | – | –/2.00 | – | – | –/25.77 | – |
| H14 | 1073 | 0/104 | – | –/1.10 | – | – | –/25.77 | – |
| IPP | 0 | 0/10,419 | PV | –/100.00 | – | – | –/5.40 | – |
| Sum | 63,308 | 40,288/50,707 | – | 31.08/131.08 | – | – | – | 22 |
| sonnenBatterie | ||
|---|---|---|
| eco 8.0/4 | eco 8.0/6 | |
| usable battery capacity [kWh] | 4 | 6 |
| max. efficiency battery | 98 % | |
| max. efficiency inverter | 96 % | |
| max. charge rate [kW] | 2.5 | 3.0 |
| max. discharge rate [kW] | 2.5 | 3.0 |
| investment costs [EUR/kWh] | 400 | |
| lifetime [years] | 20 | |
| operating hours per year | 3300 | 4400 |
| discharge price [ct/kWh] | 1.21 | 1.36 |
Appendix C. Business Cases for Consumers and Prosumers
Appendix C.1. Electricity Consumption
| Self-Consumption | Direct Supply | Direct Marketing | |
|---|---|---|---|
| Tax/Levy | § 5 (1) StromStG: tax payment for electricity from the public grid § 9 (1) StromStG: exemption for installations <2 MW used for self-consumption § 61 (1) EEG: payment of EEG levy § 61 a, b EEG: exemption or reduction to 40% of EEG levy possible | § 2 (3) StromStG: obligation to disclose as small utility § 4 StromStG: request at the main Customs Office § 5 StromStG: supplier is subject to taxation § 60 EEG: full payment of EEG levy No exemption from fiscal coverage/supply obligations | Prosumer becomes energy utility – obligations are similar to direct supply Direct marketing can only be realised with the help of a service provider: Taxes, levy, reporting and notification duties as well as responsibilities are similar to self-supply, i.e., registration obligations to network operators and authorities, maintenance and repair work/costs Additional contractual obligations between the prosumer and the service provider who assumes the responsibilities of the energy supplier (GTC and contractual services) |
| Reporting and notification duties | § 6 EEG: registration of installation § 62b EEG: definition of production quantities § 71 EEG: reporting obligations to DSO: billing and tax exemption § 74a EEG: reporting obligations lapse from § 74a (1) S.3 for PV up to 7 kW and other installations to 1 kW § 76 EEG: reporting to BNetzA might be necessary | § 5 EnWG: Notification requirements towards BNetzA § 6 EEG: registration of installation § 74 EEG: reporting obligations to from § 61i, and annual statements § 75 EEG: Auditing § 76 EEG: Information to be provided to the Federal Network Agency § 4 (6) StromStG: reporting of tax exemptions to main customs office | |
| Responsi- bilities | Energiesammelgesetz: formal requirements of DSOs for reporting are to be respected Prosumer has obligation to stay informed | Obligation for utilities to report quantities to main customs office; applies for self-consumed and direct supply § 4 StromNZV: designation of balancing group pursuant | |
| Payment entitlements | § 19 EEG: entitled to claim 1. feed-in tariff/market premium from § 21 (1) and (2) EEG 2. surcharge from tenant electricity law § 21 (3) EEG | § 41 EnWG: Utilities need to conclude contracts for retail sale with customers (in conjunction with § 40, 42 EnWG) | Payment entitlements and obligations to service providers in accordance with contractual agreements |
Appendix C.2. Electricity Production
References
- European Commission; Directorate-General for Energy. Clean Energy for All Europeans; Publications Office of the European Union: Luxembourg, 2019. [Google Scholar] [CrossRef]
- European Parliament; European Council. Directive (EU) 2019/944 of the European Parliament and of the Council of 5 June 2019 on Common Rules for the Internal Market for Electricity and Amending Directive 2012/27/EU; Official Journal of the European Union: Brussels, Belgium, 2019. [Google Scholar]
- Caramizaru, A.; Uihlein, A. Energy Communities: An Overview of Energy and Social Innovation; JRC Science for Policy Report JRC119433; Publications Office of the European Union: Luxembourg, 2020. [Google Scholar] [CrossRef]
- Zhang, C.; Wu, J.; Long, C.; Cheng, M. Review of Existing Peer-to-Peer Energy Trading Projects. Energy Procedia 2017, 105, 2563–2568. [Google Scholar] [CrossRef]
- Kampman, B.; Blommerde, J.; Afman, M. The potential of energy citizens in the European Union; Technical Report; CE Delft: Delft, The Netherlands, 2016. [Google Scholar]
- Šajn, N. Electricity “Prosumers”; Briefing, European Parliamentary Research Service: Brussels, Belgium, 2016. [Google Scholar]
- Mathiesen, B.V.; David, A.; Petersen, S.; Sperling, K.; Hansen, K.; Nielsen, S.; Lund, H.; Neves, J.B. The Role of Photovoltaics towards 100% Renewable Energy Systems: Based on International Market Developments and Danish Analysis; Technical Report; Department of Development and Planning, Aalborg University: Aalborg, Denmark, 2017. [Google Scholar]
- Inderberg, T.H.J.; Tews, K.; Turner, B. Is there a Prosumer Pathway? Exploring household solar energy development in Germany, Norway, and the United Kingdom. Energy Res. Soc. Sci. 2018, 42, 258–269. [Google Scholar] [CrossRef]
- GfK Belgium Consortium. Study on “Residential Prosumers in the European Energy Union”; Technical Report JUST/2015/CONS/FW/C006/0127; European Commission: Brussels, Belgium, 2017. [Google Scholar]
- European Comission. Clean Energy for All: New Electricity Market Design: A Fair Deal for Consumers; EU COM(2016) 860 Final; European Commission: Brussels, Belgium, 2016. [Google Scholar]
- Park, C.; Yong, T. Comparative review and discussion on P2P electricity trading. Energy Procedia 2017, 128, 3–9. [Google Scholar] [CrossRef]
- Zhang, C.; Wu, J.; Cheng, M.; Zhou, Y.; Long, C. A Bidding System for Peer-to-Peer Energy Trading in a Grid-connected Microgrid. Energy Procedia 2016, 103, 147–152. [Google Scholar] [CrossRef]
- Zhang, C.; Wu, J.; Zhou, Y.; Cheng, M.; Long, C. Peer-to-Peer energy trading in a Microgrid. Appl. Energy 2018, 220, 1–12. [Google Scholar] [CrossRef]
- Khorasany, M.; Mishra, Y.; Ledwich, G. Market framework for local energy trading: A review of potential designs and market clearing approaches. IET Gener. Transm. Distrib. 2018, 12, 5899–5908. [Google Scholar] [CrossRef]
- Mengelkamp, E.; Diesing, J.; Weinhardt, C. Tracing local energy markets: A literature review. it-Inf. Technol. 2019, 61, 101–110. [Google Scholar] [CrossRef]
- Parag, Y.; Sovacool, B.K. Electricity market design for the prosumer era. Nature Energy 2016, 1, 16032. [Google Scholar] [CrossRef]
- Sorin, E.; Bobo, L.; Pinson, P. Consensus-Based Approach to Peer-to-Peer Electricity Markets with Product Differentiation. IEEE Trans. Power Syst. 2019, 34, 994–1004. [Google Scholar] [CrossRef]
- Mengelkamp, E.; Gärttner, J.; Rock, K.; Kessler, S.; Orsini, L.; Weinhardt, C. Designing microgrid energy markets: A case study: The Brooklyn Microgrid. Appl. Energy 2018, 210, 870–880. [Google Scholar] [CrossRef]
- Sousa, T.; Soares, T.; Pinson, P.; Moret, F.; Baroche, T.; Sorin, E. Peer-to-peer and community-based markets: A comprehensive review. Renew. Sustain. Energy Rev. 2019, 104, 367–378. [Google Scholar] [CrossRef]
- Moret, F.; Pinson, P. Energy Collectives: A Community and Fairness Based Approach to Future Electricity Markets. IEEE Trans. Power Syst. 2019, 34, 3994–4004. [Google Scholar] [CrossRef]
- Hahnel, U.J.; Herberz, M.; Pena-Bello, A.; Parra, D.; Brosch, T. Becoming prosumer: Revealing trading preferences and decision-making strategies in peer-to-peer energy communities. Energy Policy 2020, 137, 111098. [Google Scholar] [CrossRef]
- Morstyn, T.; Farrell, N.; Darby, S.J.; McCulloch, M.D. Using peer-to-peer energy-trading platforms to incentivize prosumers to form federated power plants. Nat. Energy 2018, 3, 94–101. [Google Scholar] [CrossRef]
- Lüth, A.; Zepter, J.M.; Crespo del Granado, P.; Egging, R. Local electricity market designs for peer-to-peer trading: The role of battery flexibility. Appl. Energy 2018, 229, 1233–1243. [Google Scholar] [CrossRef]
- Zepter, J.M.; Lüth, A.; Crespo del Granado, P.; Egging, R. Prosumer integration in wholesale electricity markets: Synergies of peer-to-peer trade and residential storage. Energy Build. 2019, 184, 163–176. [Google Scholar] [CrossRef]
- Long, C.; Wu, J.; Zhang, C.; Cheng, M.; Al-Wakeel, A. Feasibility of Peer-to-Peer Energy Trading in Low Voltage Electrical Distribution Networks. Energy Procedia 2017, 105, 2227–2232. [Google Scholar] [CrossRef]
- Mengelkamp, E.; Bose, S.; Kremers, E.; Eberbach, J.; Hoffmann, B.; Weinhardt, C. Increasing the efficiency of local energy markets through residential demand response. Energy Inform. 2018, 1, 11. [Google Scholar] [CrossRef]
- Ottesen, S.Ø.; Tomasgard, A.; Fleten, S.E. Prosumer bidding and scheduling in electricity markets. Energy 2016, 94, 828–843. [Google Scholar] [CrossRef]
- Correa-Florez, C.A.; Michiorri, A.; Kariniotakis, G. Robust optimization for day-ahead market participation of smart-home aggregators. Appl. Energy 2018, 229, 433–445. [Google Scholar] [CrossRef]
- Ottesen, S.Ø.; Tomasgard, A.; Fleten, S.E. Multi market bidding strategies for demand side flexibility aggregators in electricity markets. Energy 2018, 149, 120–134. [Google Scholar] [CrossRef]
- Olivella-Rosell, P.; Forsstrom, J.; Ottesen, S.Ø.; Villafafila-Robles, R.; Sumper, A.; Rulclan, F.; Lloret-Gallego, P.; Prieto-Araujo, E.; Ferrer-San-Jose, R.; Barja-Martinez, S.; et al. Centralised and Distributed Optimization for Aggregated Flexibility Services Provision. IEEE Trans. Smart Grid 2020. [Google Scholar] [CrossRef]
- Ableitner, L.; Meeuw, A.; Schopfer, S.; Tiefenbeck, V.; Wortmann, F.; Wörner, A. Quartierstrom— Implementation of a real world prosumer centric local energy market in Walenstadt, Switzerland. arXiv 2019, arXiv:1905.07242. [Google Scholar]
- Egerer, J.; Weibezahn, J.; Hermann, H. Two price zones for the German electricity market—Market implications and distributional effects. Energy Econ. 2016, 59, 365–381. [Google Scholar] [CrossRef]
- Morstyn, T.; Teytelboym, A.; Hepburn, C.; McCulloch, M.D. Integrating P2P Energy Trading with Probabilistic Distribution Locational Marginal Pricing. IEEE Trans. Smart Grid 2019. [Google Scholar] [CrossRef]
- Van Soest, H. Peer-to-peer electricity trading: A review of the legal context. Compet. Regul. Netw. Ind. 2019, 19, 180–199. [Google Scholar] [CrossRef]
- Eid, C.; Bollinger, L.A.; Koirala, B.; Scholten, D.; Facchinetti, E.; Lilliestam, J.; Hakvoort, R. Market integration of local energy systems: Is local energy management compatible with European regulation for retail competition? Energy 2016, 114, 913–922. [Google Scholar] [CrossRef]
- Scheller, F.; Johanning, S.; Seim, S.; Schuchardt, K.; Krone, J.; Haberland, R.; Bruckner, T. Legal Framework of Decentralized Energy Business Models in Germany: Challenges and Opportunities for Municipal Utilities. Z. Energiewirtschaft 2018, 42, 207–223. [Google Scholar] [CrossRef]
- Grimm, V.; Ambrosius, M.; Rückel, B.; Sölch, C.; Zöttl, G. Modellierung von liberalisierten Strommärkten—Herausforderungen und Lösungen. Perspekt. Wirtsch. 2017, 18, 2–31. [Google Scholar] [CrossRef]
- Gabriel, S.A.; Conejo, A.J.; Fuller, J.D.; Hobbs, B.F.; Ruiz, C. Complementarity Modeling in Energy Markets; International Series in Operations Research & Management Science; Springer: New York, NY, USA, 2013; Volume 180. [Google Scholar] [CrossRef]
- Schill, W.P.; Kemfert, C. Modeling Strategic Electricity Storage: The Case of Pumped Hydro Storage in Germany. Energy J. 2011, 32. [Google Scholar] [CrossRef]
- Egging, R.; Holz, F.; Gabriel, S.A. The World Gas Model. Energy 2010, 35, 4016–4029. [Google Scholar] [CrossRef]
- Huppmann, D.; Egging, R. Market power, fuel substitution and infrastructure—A large-scale equilibrium model of global energy markets. Energy 2014, 75, 483–500. [Google Scholar] [CrossRef]
- Egging-Bratseth, R.; Baltensperger, T.; Tomasgard, A. Solving oligopolistic equilibrium problems with convex optimization. Eur. J. Oper. Res. 2020, 284, 44–52. [Google Scholar] [CrossRef]
- Hall, L.M.; Buckley, A.R. A review of energy systems models in the UK: Prevalent usage and categorisation. Appl. Energy 2016, 169, 607–628. [Google Scholar] [CrossRef]
- Dirkse, S.P.; Ferris, M.C. The path solver: A nommonotone stabilization scheme for mixed complementarity problems. Optim. Methods Softw. 1995, 5, 123–156. [Google Scholar] [CrossRef]
- Ferris, M.C.; Munson, T.S. Complementarity problems in GAMS and the PATH solver. J. Econ. Dyn. Control. 2000, 24, 165–188. [Google Scholar] [CrossRef]
- Brown, D.; Hall, S.; Davis, M.E. Prosumers in the post subsidy era: An exploration of new prosumer business models in the UK. Energy Policy 2019, 135, 110984. [Google Scholar] [CrossRef]
- Friends of the Earth Europe. Unleashing the Power of Community Renewable Energy; Technical Report; Friends of the Earth Europe: Brussels, Belgium, 2019; Available online: www.foeeurope.org (accessed on 1 March 2020).
- Brown, C.; Poudineh, R.; Foley, B. Achieving a Cost-Competitive Offshore Wind Power Industry; Oxford Institute for Energy Studies: Oxford, UK, 2015. [Google Scholar] [CrossRef]
- Tegen, S.; Hand, M.M.; Maples, B.; Lantz, E.; Schwabe, P.; Smith, A. 2010 Cost of Wind Energy Review; Technical Report NREL/TP-5000-52920; National Renewable Energy Lab. (NREL): Golden, CO, USA, 2012. [CrossRef]
- Weniger, J.; Tjaden, T.; Quaschning, V. Solare Unabhängigkeitserklärung. Photovoltaik 2012, 5, 50–54. [Google Scholar]
- Crespo Del Granado, P.; Wallace, S.W.; Pang, Z. The value of electricity storage in domestic homes: A smart grid perspective. Energy Syst. 2014, 5, 211–232. [Google Scholar] [CrossRef]
- Pollitt, M.G. Electricity Network Charging in the Presence of Distributed Energy Resources: Principles, Problems and Solutions. Econ. Energy Environ. Policy 2018, 7. [Google Scholar] [CrossRef]
- Schäfer-Stradowsky, S.; Bachmann, S. Rechtspolitische Rahmenbedingungen für Prosumer: Status quo und aktuelle Entwicklungen: Schwerpunkt: Prosumer für die Energiewende. öKologisches Wirtsch. Fachz. 2016, 31, 21. [Google Scholar] [CrossRef]
- Von Oppen, M.; Streitmayer, A.; Huneke, F. Impulspapier Bürgerstromhandel; Technical Report; Energy Brainpool GmbH & Co. KG: Berlin, Germany, 2017. [Google Scholar]
- Mengelkamp, E.; Staudt, P.; Gärttner, J.; Weinhardt, C. Trading on local energy markets: A comparison of market designs and bidding strategies. In Proceedings of the 2017 14th International Conference on the European Energy Market (EEM), Dresden, Germany, 6–9 June 2017; pp. 1–6. [Google Scholar] [CrossRef]
- BMWi. Overview of Legislation Governing Germany’s Energy Supply System: Key Strategies, Acts, and Regulations/Ordinances; Technical Report; BMWi: Berlin, Germany, 2017.
- Tobiasson, W.; Jamasb, T. The Solution that Might Have Been: Resolving Social Conflict in Deliberations about Future Electricity Grid Development. Energy Res. Soc. Sci. 2016, 17, 94–101. [Google Scholar] [CrossRef]
- Staffell, I.; Pfenninger, S. Using bias-corrected reanalysis to simulate current and future wind power output. Energy 2016, 114, 1224–1239. [Google Scholar] [CrossRef]
- Pfenninger, S.; Staffell, I. Long-term patterns of European PV output using 30 years of validated hourly reanalysis and satellite data. Energy 2016, 114, 1251–1265. [Google Scholar] [CrossRef]
- Kost, C.; Schlegl, T.; Thomsen, J.; Nold, S.; Mayer, J. Studie Stromgestehungskosten Erneuerbare Energien; Technical Report; Fraunhofer ISE: Freiburg im Breisgau, Germany, 2018; Available online: https://www.ise.fraunhofer.de/de/veroeffentlichungen/studien/studie-stromgestehungskosten-erneuerbare-energien.html (accessed on 1 March 2020).
- Cole, W.J.; Frazier, A. Cost Projections for Utility-Scale Battery Storage; Technical Report; NREL/TP-6A20-73222; National Renewable Energy Laboratory (NREL): Golden, CO, USA, 2019. [CrossRef]
- Fraunhofer ISE. Studie zu Stromgestehungskosten: Photovoltaik und Onshore-Wind Sind GüNstigste Technologien in Deutschland; Technical Report; Fraunhofer ISE: Freiburg im Breisgau, Germany, 2018. [Google Scholar]
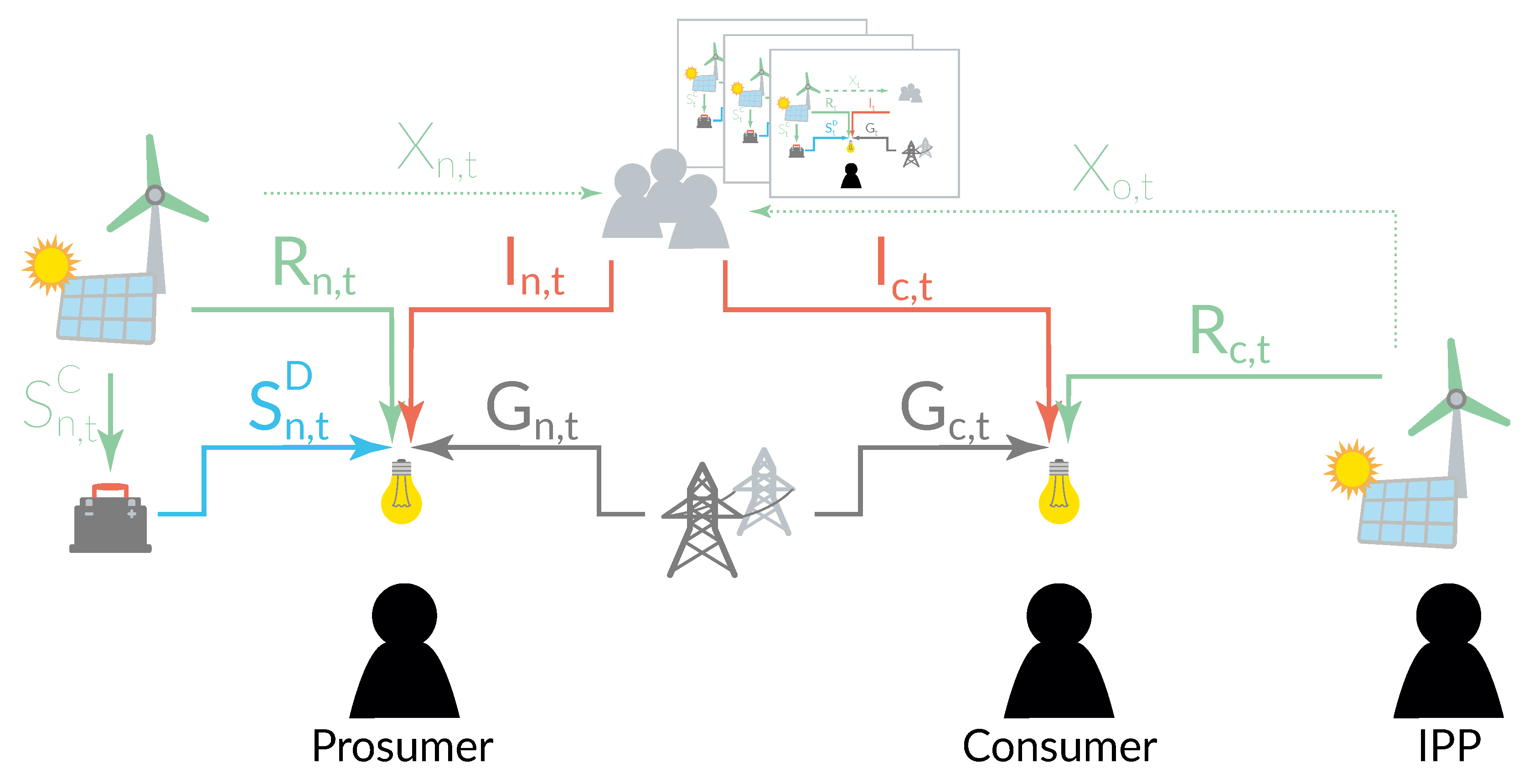
| Sets | |
| player a in community | |
| consumer c in community | |
| prosumer n in community | |
| independent producer o in community | |
| hour t in time horizon | |
| Scalars | |
| distribution grid tariff per kWh | |
| EEG reallocation charge per kWh | |
| wholesale electricity charge per kWh | |
| grid consumption tariff per kWh | |
| handling fee per kWh | |
| local balancing mechanism consumption tariff per kWh | |
| taxes and duties per kWh | |
| transmission grid tariff per kWh | |
| battery round trip efficiency | |
| Parameters | |
| demand of player a in time step t | |
| discharge penalty per kWh for player a | |
| feed-in tariff per kWh for player a | |
| marginal cost per kWh for player a | |
| price per kWh of electricity sold from player o to shareholder a | |
| marginal discharge costs per kWh for player a | |
| renewable energy production of player a in time step t | |
| upper bound of storage level in battery for player a | |
| lower bound of storage level in battery for player a | |
| initial storage level in battery for player a | |
| / | maximum charge/discharge rate of battery for player a |
| Primal Variables | |
| feed into the grid for player a in time step t | |
| consumption of energy from the grid for player a in time step t | |
| consumption from local balancing mechanism for player a in time step t | |
| consumption of renewable energy for player a in time step t | |
| battery storage level for player a in time step t | |
| battery storage charging for player a in time step t | |
| battery storage discharging for player a in time step t | |
| sale of renewable energy to local balancing mechanism for player a in time step t | |
| Dual Variables | |
| price of electricity in the local balancing mechanism in time step t | |
| price of electricity for player a in time step t | |
| price of electricity in the storage for player a in time step t | |
| price of curtailment for each player a in time step t | |
| price of storage lower bound for each player a in time step t | |
| price of storage upper bound for each player a in time step t | |
| price of storage charging for each player a in time step t | |
| price of storage discharging for each player a in time step t | |
| [ct/kWh] | [%] | |
|---|---|---|
| wholesale electricity charge () | 6.44 | 22.4 |
| distribution network charge () | 3.48 | 12.1 |
| transmission network charge () | 3.44 | 12.0 |
| EEG reallocation charge () | 6.52 | 22.7 |
| other taxes & duties () | 8.85 | 30.8 |
| total kilowatt-hour rate | 28.73 | 100.0 |
| Set-Up | Consumption from Grid | Consumption from LBM | Consumption from Storage | Feed-in into Grid | Feed-in into LBM |
|---|---|---|---|---|---|
| ① BAU Feed-in | — | — | — | ||
| ② Local Sharing | id. | — | — | ||
| ③ Home Storage | id. | — | — | — | |
| ④ Home Storage & Local Sharing | id. | — | |||
| ⑤ Current Regulatory Framework for ④ | id. | — | |||
| ⑥ Tech4all | id. | — |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lüth, A.; Weibezahn, J.; Zepter, J.M. On Distributional Effects in Local Electricity Market Designs—Evidence from a German Case Study. Energies 2020, 13, 1993. https://doi.org/10.3390/en13081993
Lüth A, Weibezahn J, Zepter JM. On Distributional Effects in Local Electricity Market Designs—Evidence from a German Case Study. Energies. 2020; 13(8):1993. https://doi.org/10.3390/en13081993
Chicago/Turabian StyleLüth, Alexandra, Jens Weibezahn, and Jan Martin Zepter. 2020. "On Distributional Effects in Local Electricity Market Designs—Evidence from a German Case Study" Energies 13, no. 8: 1993. https://doi.org/10.3390/en13081993
APA StyleLüth, A., Weibezahn, J., & Zepter, J. M. (2020). On Distributional Effects in Local Electricity Market Designs—Evidence from a German Case Study. Energies, 13(8), 1993. https://doi.org/10.3390/en13081993





