1. Introduction
The potentially catastrophic consequences of our reliance on fossil fuels have led to a world-wide effort to increase the share of renewables in the global energy mix. Most renewable energy sources, such as wind and solar power, are highly intermittent and should be coupled with energy storage devices that can save excess energy for use when the sun is not shining and the wind does not blow. Batteries are excellent for small- and medium-scale energy storage but are limited by cost for large-scale applications. A viable alternative is to use excess energy to produce hydrogen from water by electrolysis. The hydrogen can later be fed to a fuel cell to produce electricity on demand. However, gaseous hydrogen has a very low density even at high pressure, leading to low volumetric energy density for hydrogen gas-based energy storage systems. Moreover, gas compression itself is energy consuming and there are safety issues with storing large amounts of pressurized hydrogen, as demonstrated by the recent explosion in a Norwegian hydrogen filling station [
1].
Safer and much more compact hydrogen storage can be achieved in solid metal hydrides, but all investigated hydrogen storage materials come with drawbacks such as low gravimetric hydrogen content, poor hydrogen sorption kinetics, unfavorable stabilities and/or capacity loss on cycling [
2]. For instance, many LaNi
5-based alloys have excellent hydrogen absorption kinetics and cyclability at near-ambient conditions, but can only store about 1.3 wt% hydrogen. MgH
2 contains 7.6 wt% hydrogen but is very stable and must be heated above 300 °C to release it [
3,
4]. The EU project HyCare (
https://hycare-project.eu/) is currently developing a hydrogen storage tank based on TiFe-alloys with hydrogen capacities around 1.9 wt%. Complex hydrides generally have high hydrogen content but poor cyclability [
5,
6].
Body-centered cubic (BCC) alloys based on titanium and vanadium form hydrogen storage materials that do not excel in any particular aspect but have decent overall performance. They form face-centered cubic (FCC) hydrides that hold significantly more hydrogen than LaNi
5, up to around 3 wt% H, and the stability and kinetics are tuneable by varying the Ti/V ratio [
7] or by alloying with other transition elements. The alloying elements can be dissolved in the BCC phase [
8,
9] or give secondary phases, e.g., Laves phases, that enhance the hydrogen sorption properties [
10,
11]. Unfortunately, vanadium is prohibitively expensive for large scale applications. A workaround is to use much cheaper
ferrovanadium which contains 20%–50% Fe and other minor impurities. Several studies have shown that use of ferrovanadium rather than pure vanadium in BCC alloys can be beneficial for the hydrogen sorption kinetics, but it usually comes at the cost of reduced hydrogen capacity [
12,
13,
14,
15]. Intuitively, this might seem reasonable since Ti and V are both hydride-forming elements while Fe is not. However, there are many examples of intermetallic hydrides with hydrogen accommodating interstitial sites that are coordinated by several Fe or other non-hydride-forming elements. For instance, 80% of the hydrogen in Zr
2FeH
5 is situated in Zr
3Fe tetrahedra [
16] and solely Zr
2Fe
2 tetrahedral sites are occupied by hydrogen in ZrFe
2H
2.66 [
17]. Ti-V-based BCC alloys are solid solutions with the different metal atoms distributed over a single crystallographic site. A typical composition for hydrogen storage applications is Ti
0.7V
0.3. Substitution of pure vanadium with ferrovanadium would typically result in about 10 mol% Fe in the alloy. Assuming a random distribution of the elements in the solid solution, 99.6% of the tetrahedral sites would then be coordinated by at least two hydride-forming elements (Ti and/or V) and expected to be accessible for hydrogen occupation. Thus, the reported capacity losses with ferrovanadium [
12,
13,
14,
15] cannot be explained from the average crystal structure, which is obtained, e.g., from powder diffraction and Rietveld refinements (
Figure 1). To understand the capacity loss from a structural perspective, we need a technique that is sensitive to the
local structure. This study uses neutron total scattering, i.e., measurements of both Bragg and diffuse scattering, to investigate short-range metal-metal and metal-hydrogen correlations to explain the capacity loss induced by iron in a Ti-V BCC alloy. Since ferrovanadium also contains other impurities such as oxygen, we chose to make the samples from high purity (99% or more) Ti, V and Fe metals since the total scattering analyses benefits greatly from single phase samples and requires precise knowledge of elemental composition.
2. Materials and Methods
The Ti-V-Fe alloy with composition (Ti7V3)9Fe was synthesized by arc-melting of six smaller ingots, with a weight of about 2 g each, under argon atmosphere from Ti-granules (99.95%, Aldrich), V-turnings (99.7%, ABCR) and Fe-powder (99%, Alfa Aesar). To improve homogeneity the ingots were turned over after each time they were melted. At the same time the melting chamber was evacuated down to 10−2 mbar and refilled with argon to reduce oxidation. Re-melting of each ingot and flushing of the chamber were repeated at least three times. The surface of the ingots was polished to remove any oxide layers before being cut into smaller pieces with a hacksaw or crushed with a diamond mortar. All six crushed ingots were mixed together into one sample. No subsequent heat treatment was performed on the alloy in order to preserve the disordered BCC-structure.
Deuteration of the sample was performed in a stainless-steel autoclave connected to a homemade Sieverts apparatus. The materials were first activated under a dynamic vacuum of approximately 10−7 mbar at 400 °C for one hour. Subsequently, D2 gas was introduced into the autoclave while keeping the sample at 400 °C. The deuterium pressure of 9.1 bar was chosen so that absorption of all the gas would yield a deuteride with D/M = 0.5. Rapid absorption of almost all D2 occurred within a few minutes, which increased the temperature to around 420 °C inside the sample holder due to the heat of reaction. When the pressure had decreased below 1 bar the sample holder was cooled down to room temperature (RT) and kept there for around 15 h to further absorb any D2 gas present in the autoclave. When the pristine material first absorbed D2 it broke up into finer pieces increasing the reaction surface before a second and final deuteration at RT. A D2 pressure of 27.2 bar corresponding to D/M = 1.5 was introduced into the autoclave at 23.5 °C. The temperature inside the autoclave reached a maximum of 110 °C in about three minutes while at the same time the pressure decreased to 8.1 bar. The temperature then decreased slowly to RT in about one hour. The deuterated sample was kept at RT for 23 h to finalize the absorption process which ended at a final pressure of 0.3 bar. The now brittle hydride sample was removed from the autoclave under an Ar atmosphere in an MBraun glove box and crushed with a mortar into a fine powder.
The amount of absorbed D2 was determined with thermogravimetric analysis (TGA) on a Netsch STA 449 F3 Jupiter instrument under an argon atmosphere at a heating rate of 10 °C/min from 30 to 750 °C. A 70 μL alumina crucible was used to hold the sample, which weighed ~50 mg.
Synchrotron radiation powder X-ray diffraction (SR-PXD) measurements were performed at the BM01B station at the Swiss Norwegian beamline (SNBL) at ESRF, France. The samples were contained in 0.5 mm boronglas capillaries, which were spinning during data acquisition. The X-ray wavelength was 0.24815 Å. For each sample, 70 2D patterns, each with an exposure time of 5 sec, were collected with an air-cooled Dexela-Perkin Elmer 2923 CMOS pixel detector consisting of 3888 × 3072 pixels of 74.8 μm
2 [
18]. The images were corrected for dark current signal, summed and integrated to 1D diffraction patterns with the program Fit2D [
19].
Neutron total scattering was performed on the GEM diffractometer [
20] at ISIS, UK. The sample was contained in a 6-mm-diameter V-can. Additional measurements of an empty vanadium can, the empty instrument and a vanadium rod were performed in order to correct and normalize the data in the program Gudrun [
21] to obtain the total scattering structure factor, F(
Q). Gudrun was then used to obtain the pair distribution function (PDF), G(
r), by a Fourier transform of F(
Q). G(
r) is the weighted sum of the partial pair distribution functions, g
ij(
r), which shows the distribution of interatomic distances between atoms of type
i and
j:
where the summation is over the m different kinds of chemical species in the sample, c
i and c
j are the concentrations of the species i and j, b
i and b
j are their coherent neutron scattering lengths, and
where n
ij(
r) is the number for atoms of type
j at a distance between
r and
r + d
r from an atom of type
i, averaged over all atoms of type
i. ρ
j is the bulk atomic number density of atoms of type j.
Full definition of the scattering functions and the relationships between them are given in reference [
22].
Reverse Monte Carlo (RMC) structure modelling [
23] was performed by fitting the G(
r), F(
Q) and Bragg peak intensities calculated from a large structure model to the corresponding experimental functions using the program RMCProfile [
24]. In order to ensure physically sound structure models, the closest atom pair distances were determined from the neutron PDFs and set as limiting values in the RMC modelling.
RMCProfile uses the following minimization scheme for the total goodness-of-fit factor:
where
The σ’s are weighting terms and are normally fixed to a value for each of the functions in Equation (4) above, independent of the summation variables. Atom eye viewer [
25] was used to create graphical representations of the structure models.
Rietveld refinements were performed with the GSAS software package [
26] with the EXPGUI interface [
27]. The Bragg peaks from the GEM instrument were modelled with a Thomson-Cox-Hastings pseudo-Voigt function convoluted with a moderator pulse shape function (profile number 2 in GSAS). The background was modelled with a shifted Chebyschev polynomial with 12 terms.
Transmission electron microscopy (TEM) samples were made by making a solution with the powder and ethanol, and placing a drop of the sample onto a holey carbon film, supported by a Cu slot. The TEM used for the work was a JEOL JEM2100F microscope with an ultra-high-resolution pole piece and an Oxford X-Max-80 SDD Energy Dispersive X-ray detector (EDS).
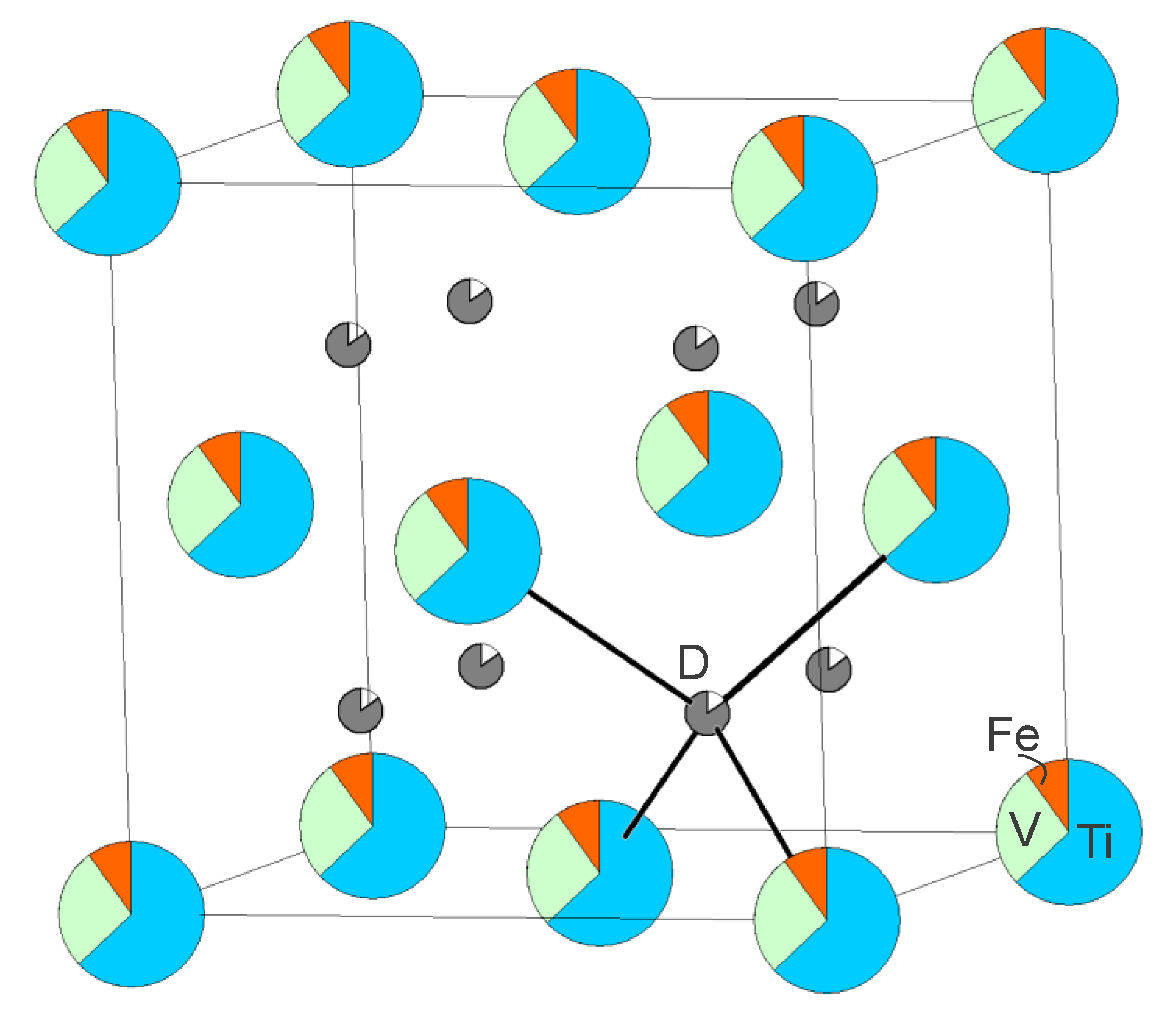
Density functional theory (DFT) calculations on the deuteride were carried out on a 3 × 3 × 3 FCC unit cell with the experimental FCC lattice parameter with 108 metal atoms (68 Ti, 29 V and 11 Fe atoms) distributed over the 4a-sites of the FCC lattice, and 187 H atoms distributed over the tetrahedral interstitial sites). The site occupation was chosen in two ways: (a) random (homogeneous) distribution; (b) distribution obtained by the RMC method.
Similar models for the deuterium-free BCC alloy, with and without short-range order, were constructed by transforming the 3 × 3 × 3 FCC models to body-centered tetragonal (BCT) symmetry (aBCT = bBCT = aFCC/√2; cBCT = aFCC) and then to BCC by compressing the c-axis. The models thus contain 54 BCC unit cells.
All the calculations were carried out within the framework of the plane-wave pseudo-potential DFT method using the Perdew–Burke–Ernzerhof generalized gradient approximation exchange and correlation potential as implemented in the Quantum Espresso package [
9]. Ion-electron interactions were described by the ultrasoft pseudopotentials introduced by Vanderbilt [
10]. The charge and kinetic energy cut-offs were equal to 45 Ry and 450 Ry, respectively. A Monkhorst-Pack mesh with a 2 × 2 × 2 k-point grid was used for geometry relaxations, followed by a total energy calculation at the optimal geometry using a 3 × 3 × 3 k-point grid for greater accuracy. Self-consistency was achieved with a tolerance of 0.1 mRy (0.13 kJ/mol) in total energy. To accelerate the convergence the Methfessel-Paxton Fermi-level smearing with a width of 0.13 eV was used.
3. Results
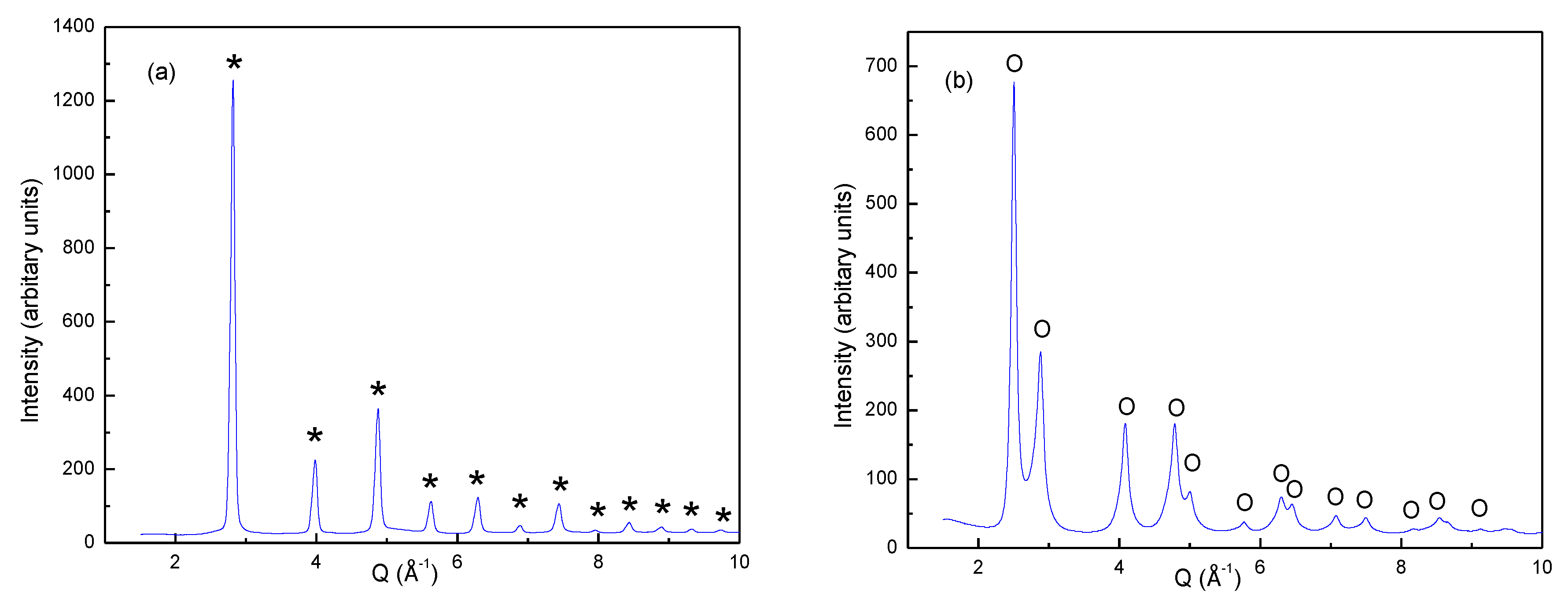
The as-cast alloy was too hard to crush sufficiently for powder diffraction measurements. The deuterated alloy was on the other hand easy to crush to a fine powder in a mortar. SR-PXD data of the deuteride are shown in
Figure 2a and the Bragg peaks can be indexed according to a single FCC phase. To investigate the state of the deuterium-free alloy, a small sample of crushed deuteride was heated to 900 °C under dynamic vacuum until all the deuterium was desorbed. SR-PXD measurement of the product revealed a single BCC phase (
Figure 2b). The lack of superstructure peaks confirms that there is no long-range ordering of Ti, V and/or Fe over the atom sites in either the deuteride or the alloy.
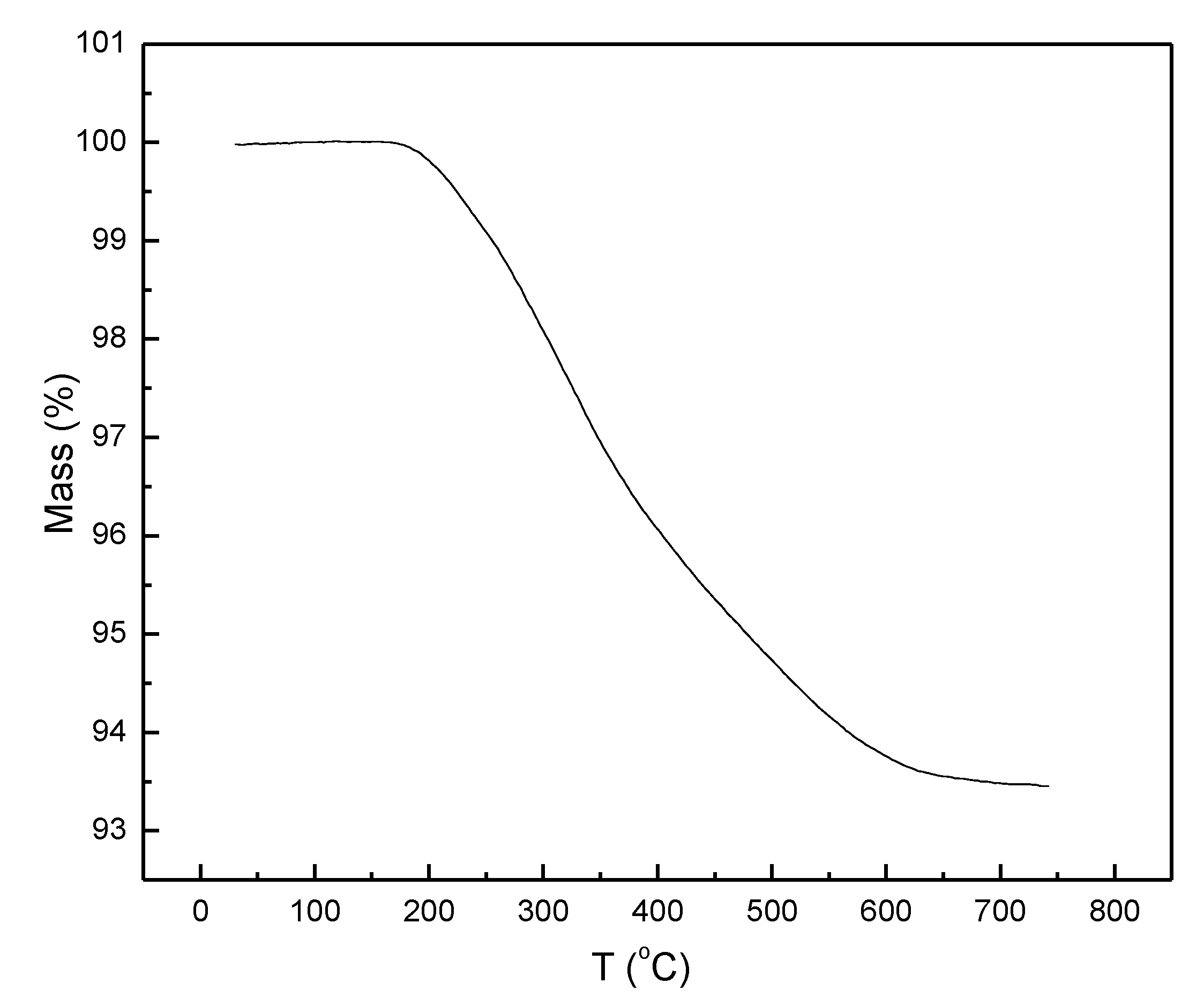
The mass loss of the deuteride upon heating to 750 °C in the TGA was 6.54 wt%, which corresponds to a deuterium-to-metal ratio of D/M = 1.73 and thus the composition Ti
0.63V
0.27Fe
0.10D
1.73 (
Figure 3)
. The desorption started at 175 °C and was complete at 650 °C.
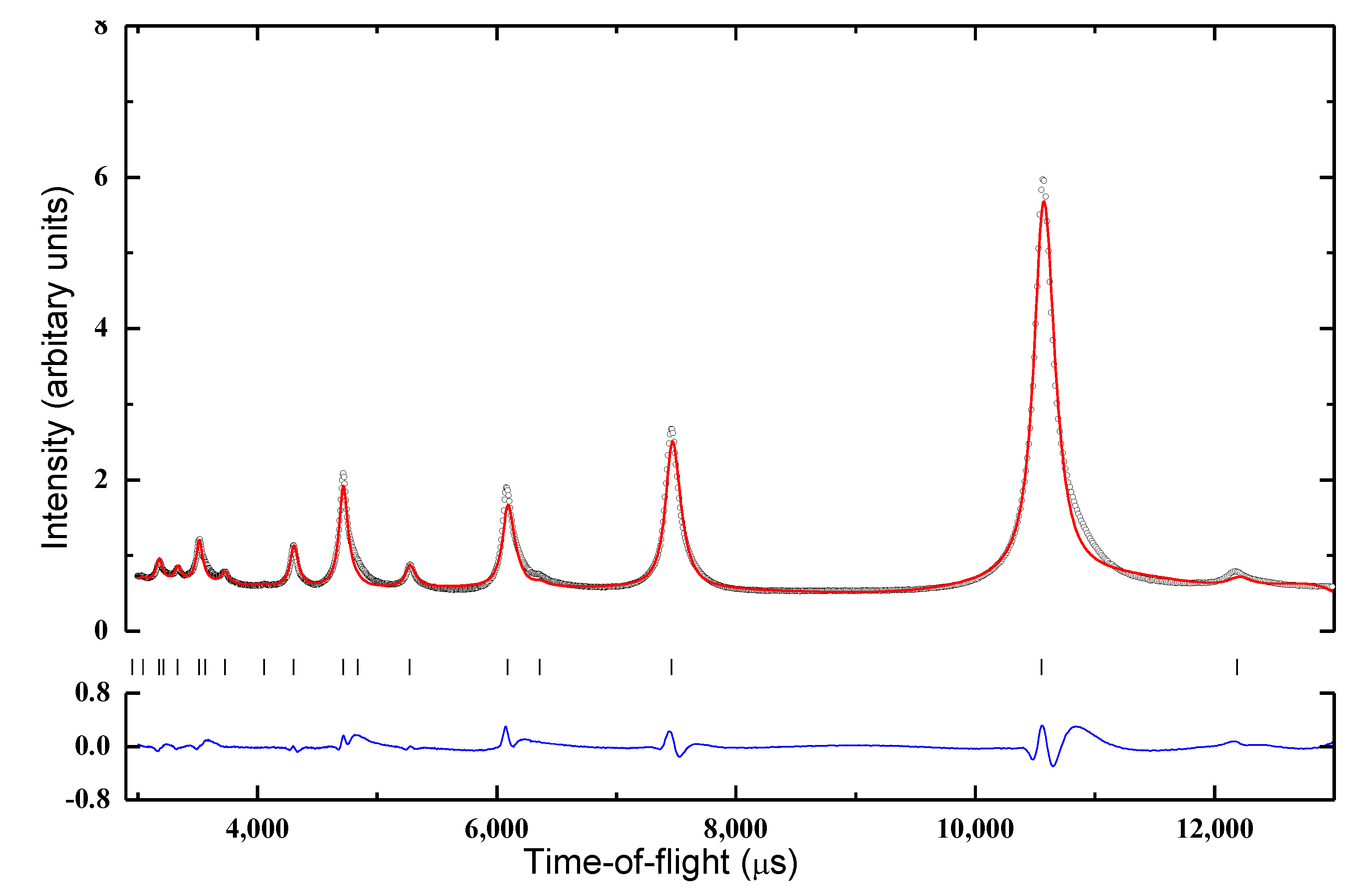
The FCC unit cell found by SR-PXD is confirmed with neutron scattering data from the GEM instrument by Rietveld refinement (
Figure 4). Refinement of the deuterium occupancy is not reliable since it correlates strongly with the isotropic displacement factors. Moreover, the Bragg scattering from the metal sublattice is weak, with an average scattering length of −1.3 fm for the metal site (b
Ti = −3.37 fm, b
v = −0.44 fm, b
Fe = 9.45 fm) according to the nominal composition, compared to 6.7 fm for deuterium. Even a small deviation from the nominal metal composition would significantly impact the average metal site scattering length and thus the refinement of the deuterium site occupancy. The Rietveld model was thus locked to the nominal composition and refinement showed good agreement with the data when all the D atoms are placed in tetrahedral sites, as expected. The refined unit cell parameter is a = 4.350(1) Å. The Bragg peaks contain no information about the typical local atomic configurations around the vacant tetrahedral sites. The Fourier transform of the total scattering, G(
r), as defined in Equation (1), is, however, sensitive to local deviations from the average structure.
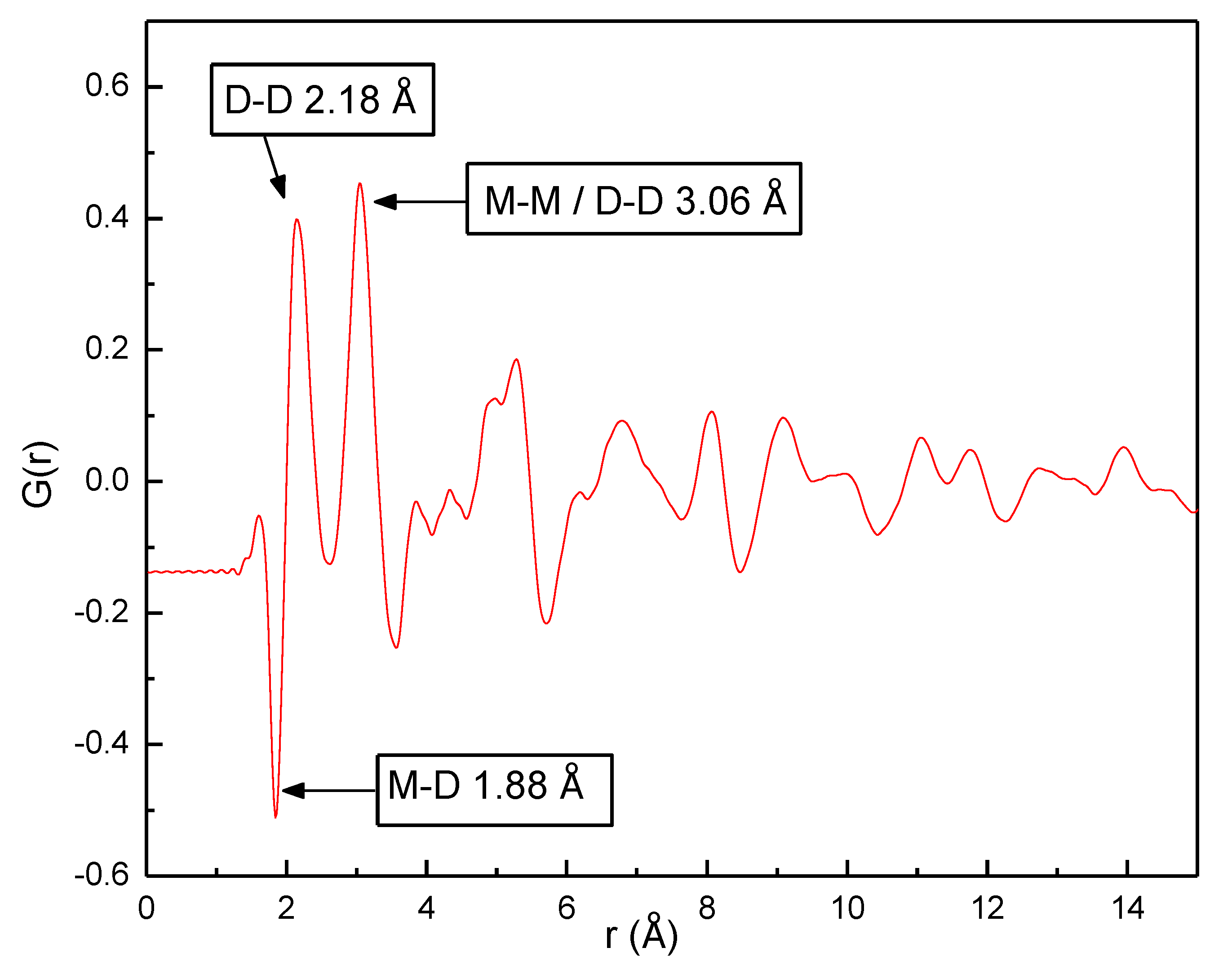
Figure 5 shows G(
r) obtained from the experimental total scattering data. The peaks in G(
r) correspond to distances between pairs of atoms in the sample, weighted by the product of the atoms’ scattering lengths and the elements’ overall concentrations in the material (Equations (1) and (2)). The first peak in G(
r) is at
r = 1.88 Å which corresponds to the distance from the metal atom site to the tetrahedral interstitial site in the unit cell, given by √3a
FCC/4. The peak thus corresponds to metal-deuterium pairs. The negative value of the peak means that it is dominated by Ti-D pairs, since the scattering length of Ti is negative, whereas it is positive for Fe and close to zero for V. The second peak is at 2.18 Å, which corresponds to the distance between tetrahedral sites in the FCC structure (½
aFCC) and is thus due to D-D pairs. The third peak at 3.06 Å corresponds to the shortest metal-metal distance and second-nearest D-D distance (average value
aFCC/√2). Thus, the local interatomic distances are in good agreement with those expected from the average structure. The small feature in G(
r) immediately before the first peak is at
r = 1.65 Å, which is significantly shorter than any reasonable distance between atoms that give a positive peak, i.e., atoms pair where both have positive or both have negative scattering lengths. This result is thus interpreted as an artefact from the data processing. More detailed information about the local structure is difficult to obtain from a mere inspection of G(
r).
The RMC method (see Experimental) was employed to build structure models from the total scattering data. The initial structure model was made from 10 × 10 × 10 FCC unit cells. 2520 Ti atoms, 1080 V atoms and 400 Fe atoms were randomly distributed over the 4000 metal atom positions in the supercell, and 6920 D atoms were randomly distributed over the 8000 tetrahedral sites, thus yielding a model with the composition Ti0.63V0.27Fe0.10D1.73 in agreement with the sample composition. In addition, 1080 particles with zero scattering length were placed in the remaining tetrahedral sites as reference points for vacancies. Three different kind of moves were used to optimize the model: swap moves, where two random metal atoms of different kind swap positions; swap moves, where a random deuterium atom and a random vacancy swap positions, and; displace moves, where a random metal or deuterium atom moves a random distance in a random direction. The metal atoms were allowed translations of up to 0.05 Å in one move while deuterium atoms were limited to 0.10 Å in one move. The two types of swap moves were used to model short-range order in the metal- and deuterium sublattices, respectively, while the displace moves model thermal and possible static displacements of atoms from their average, crystallographic positions. The modelling was constrained to not move atoms unphysically close together, i.e., M-M ≥ 2.64 Å, M-D/vac ≥ 1.73 and D-D/vac ≥ 1.73 Å. The RMC modelling was run until there was no further improvement in χ2 (Equation (3)), i.e., in the agreement between the experimental data and the corresponding signals.
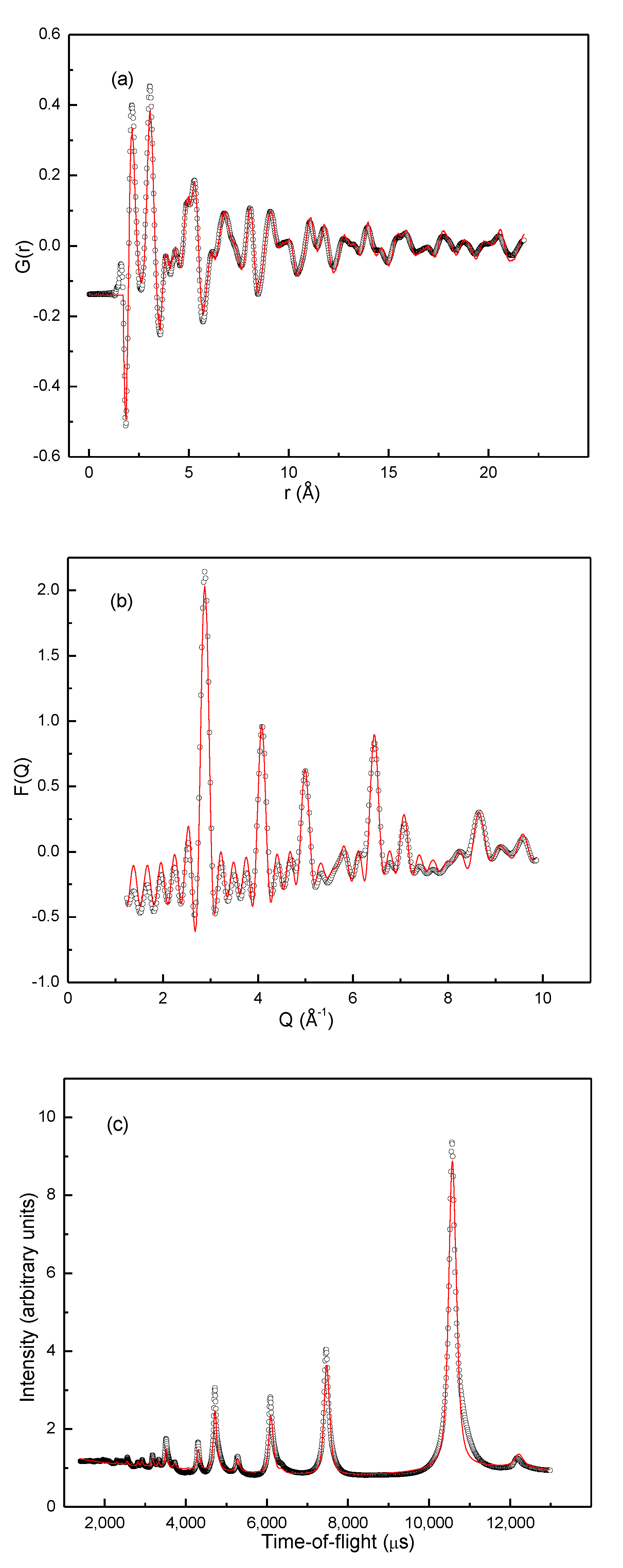
Figure 6 shows the final fits to G(
r), F(
Q) and the Bragg peaks. The good agreements mean that the final RMC model represents both the typical short- and long-range structural features of the Ti
0.63V
0.27Fe
0.10D
1.73 structure well. Partial pair distribution functions (g(
r)) can easily be calculated from the RMC model. Since the effect of Fe is the primary concern of the study, Fe-M (M = Fe, V, Ti) partial PDFs were considered first.
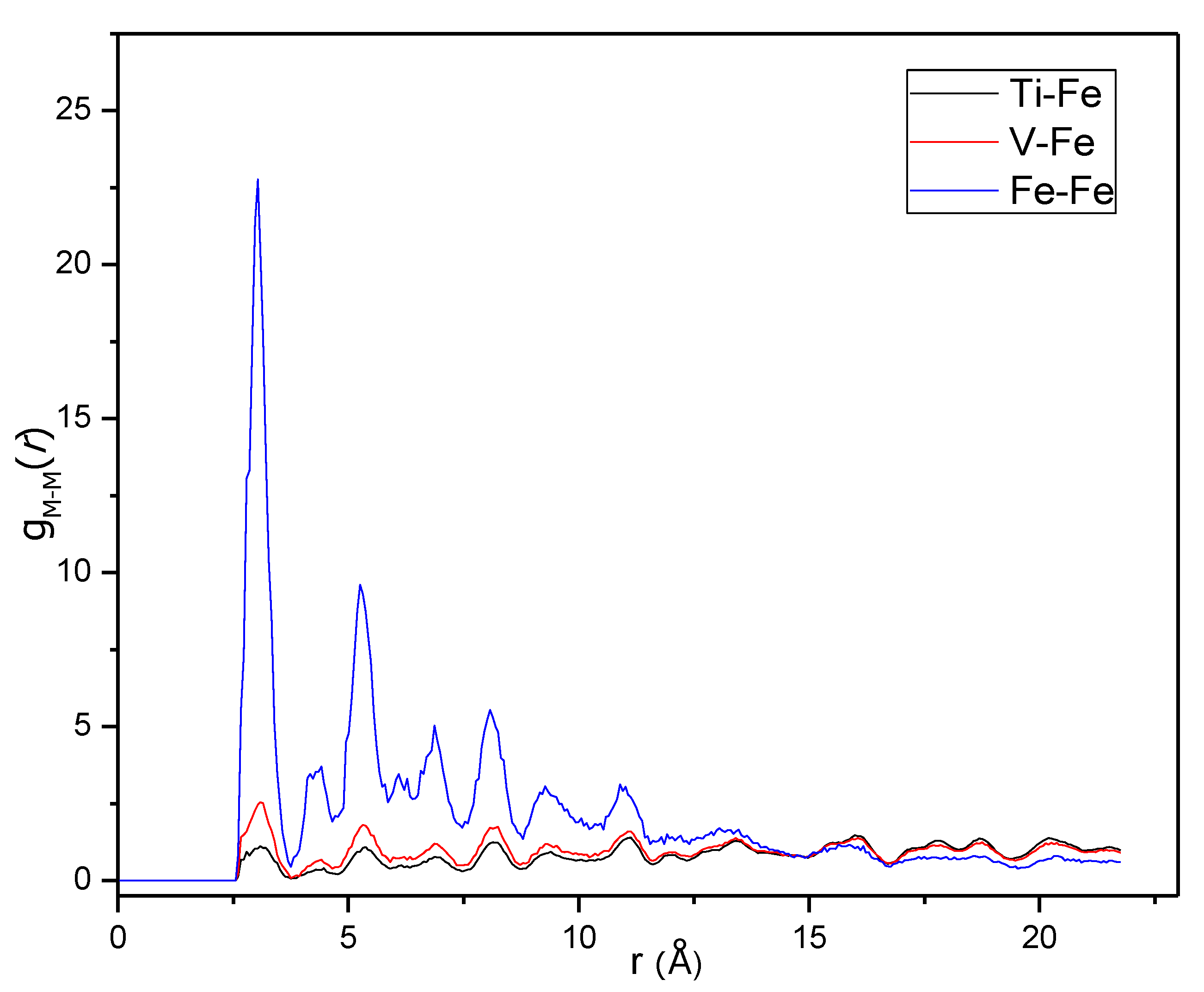
Figure 7 shows g
Fe-Fe(
r), g
Fe-Ti(
r) and g
Fe-V(
r) plotted together on the same scale. For a completely random elemental distribution over the metal sites, these curves would be similar since each is normalized to the overall density of the different elements. However, the curves are very different, indicating strong occupational short-range ordering in the metal lattice. The first peaks are clearly much stronger in g
Fe-Fe(
r) than in the two other functions, showing that the sites around Fe atoms are much more likely to be occupied by other Fe atoms compared to in a fully random distribution.
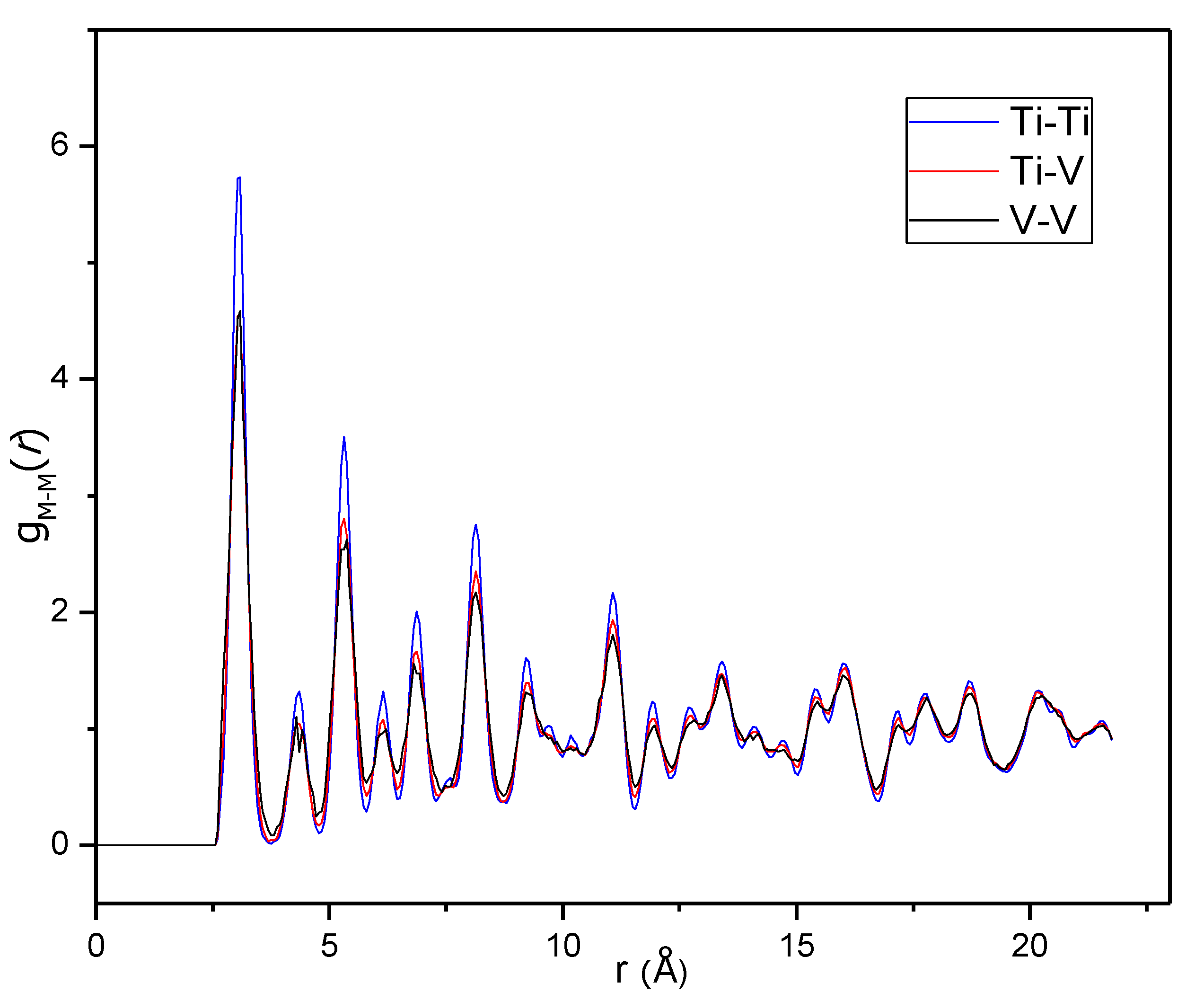
The remaining metal-metal partial PDFs, g
Ti-Ti(
r), g
Ti-V(
r) and g
V-V(
r), are, on the other hand, very similar (
Figure 8). The first peak of g
Ti-Ti appears as somewhat more intense than the other two, but this is mostly because it is slightly narrower. Fitting the first peak of each of the partial PDFs in
Figure 8 with a Gaussian, shows that the peak areas differ by only 6% from the highest (Ti-Ti) to the lowest (Ti-V) area, which is hardly significant. The overall picture from the metal-metal partial PDF is thus that Fe has a strong preference for being coordinated by Fe while the distribution of Ti and V is more or less random. This is different from an inelastic neutron scattering study of BCC Ti-V monohydrides, where an increased probability of metal atoms being coordinated by atoms of the same kind was found [
28].
The next step is to investigate short-range order in the distribution of deuterium atoms and vacancies.
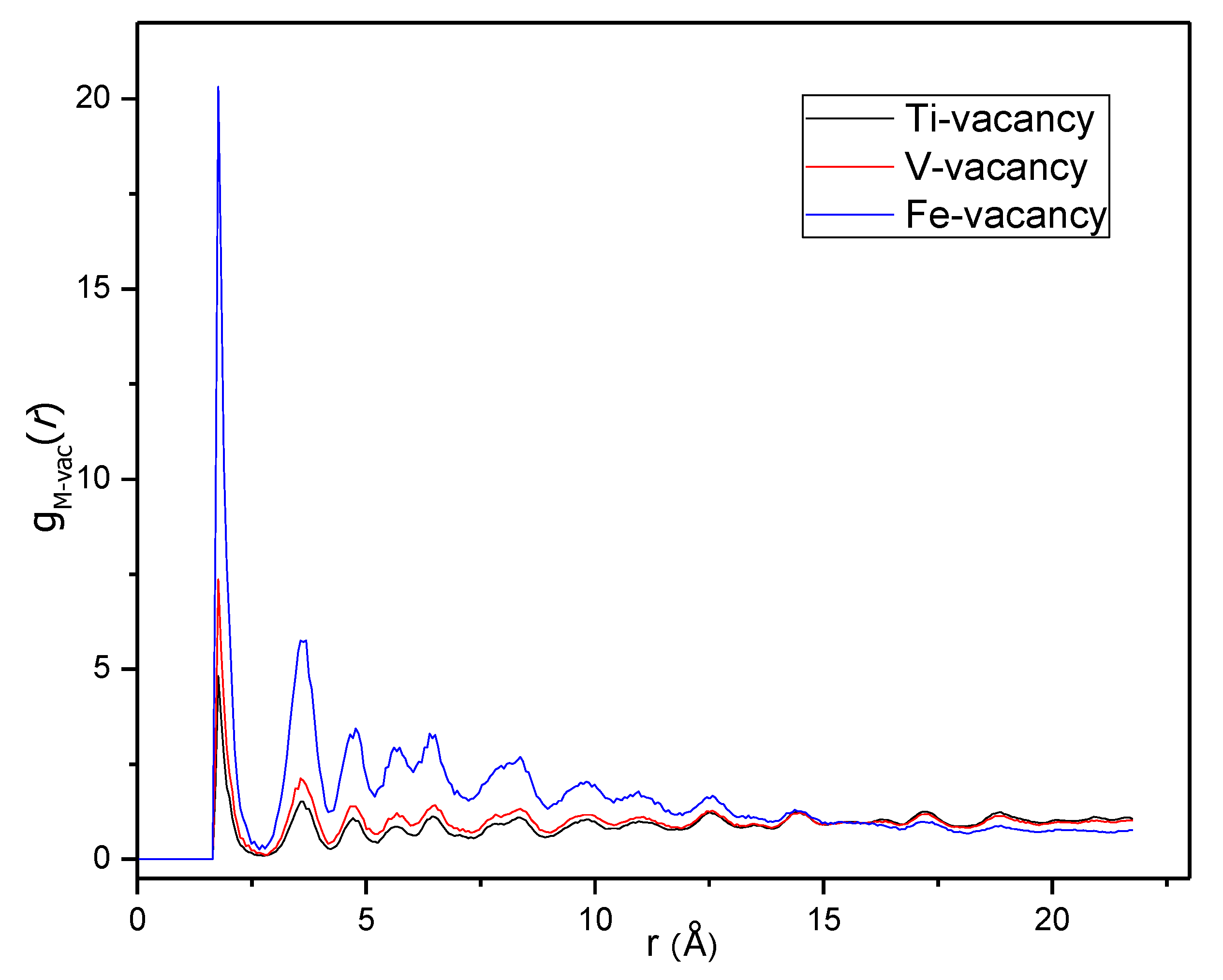
Figure 9 shows the vacancy-metal pair distribution functions. Again, a random distribution of vacancies, and thus of deuterium atoms, over the tetrahedral sites would give three similar g(
r)s, but g
Fe-vac(
r) has much stronger peaks than the other two, which means that the vacancies are much more likely to be coordinated by Fe than by Ti and V.
The reason for the Fe-induced capacity loss is emerging: Fe is not homogeneously distributed in the metal matrix but forms clusters and these Fe- or Fe-rich clusters hold the majority of vacant tetrahedral sites. It makes perfect sense that Fe-rich clusters will not accommodate deuterium since Fe is not a hydride- or deuteride-forming element. However, this chemical knowledge was not imposed on the model and the result comes entirely from fitting the functions derived from the experimental total scattering data.
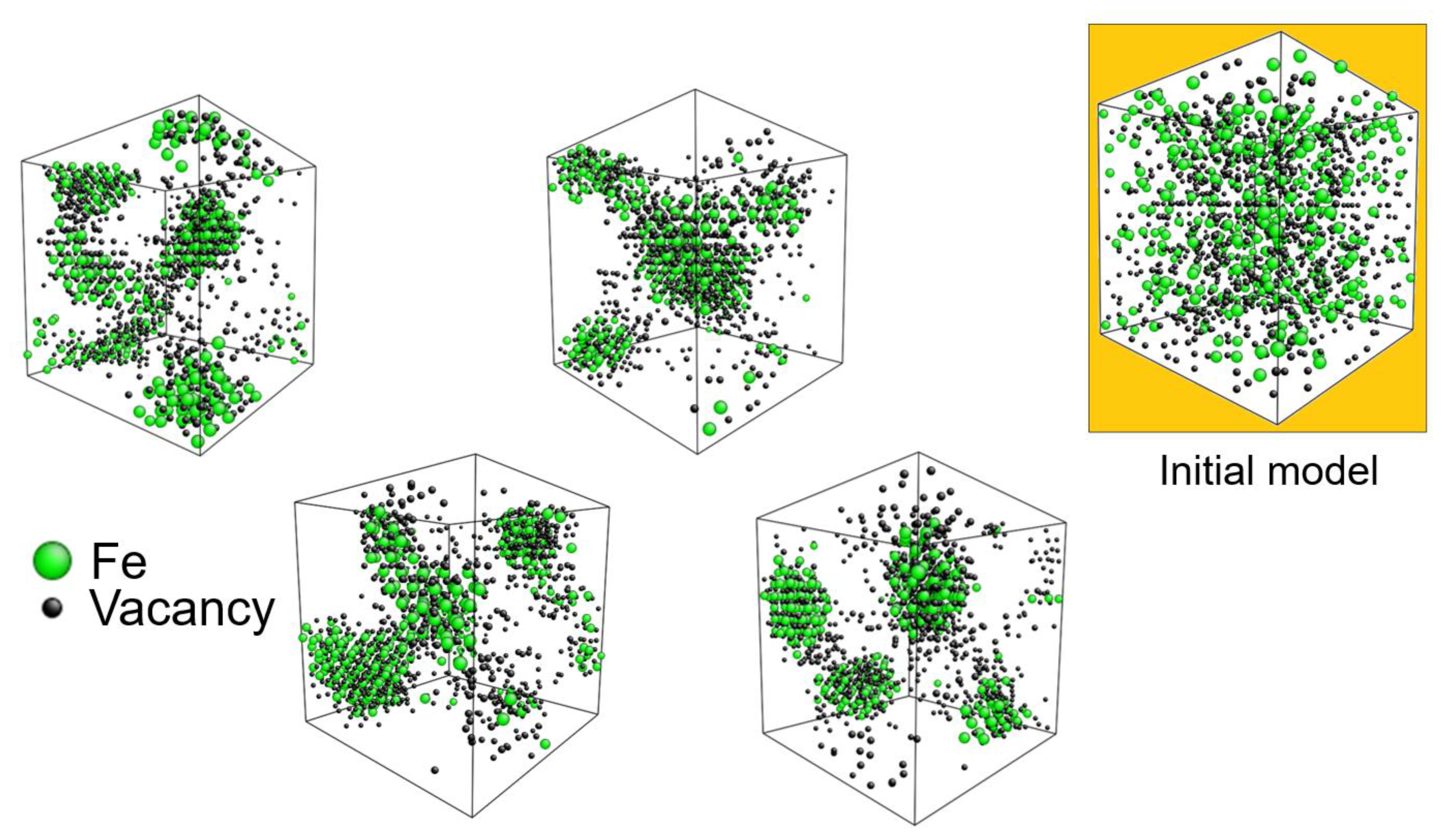
Plotting all the atoms in an RMC model makes a very busy and bewildering picture, but the main result is nicely visualized when displaying only the Fe atoms and vacancies. The green spheres in
Figure 10 are Fe atoms and the small black spheres are vacancies. Clustering of the Fe atoms is evident and it is clear that the majority of the vacancies reside in these clusters. RMC models are of course not unique [
29,
30], but several reruns of the RMC simulations with different starting models (i.e., with different distributions of the metal atoms over the metal sites and deuterium atoms/vacancies over the tetrahedral sites, while keeping the nominal composition) always gave similar fits, partial PDFs and hence similar models with Fe- and vacancy clusters.
The Fe clustering was supported by TEM/EDS.
Figure 11 shows the EDS signals of Ti, V and Fe from a ca. 100 × 100 nm
2 area of the sample. While Ti and V appears to be homogeneously distributed, Fe is mostly found in ribbon-like areas which are less than 10 nm wide and several tens of nanometers long. The fact that the V- and Ti signals are not notably weaker in the areas with strong Fe signal, indicate that thicknesses of these ribbons are small compared to the thickness of the sample in the probed area. All areas investigated by TEM/EDS showed similar features.
Since the Fe clusters result in hydrogen capacity loss, it would be interesting to know if they are caused by thermodynamics or due to kinetic limitations. In the latter case, they could be removed; e.g., by thermal annealing or higher-energy arc melting of the alloy. However, Fe has a lower melting point than Ti and V, which makes traces of unmelted Fe from the arc melting unlikely. Moreover, metallic Fe has a BCC structure with
aBCC = 2.866 Å [
31] and Fe-Fe distances down to ½√3a
BCC = 2.48 Å; significantly shorter than the first metal-metal peak in the experimental G(
r) at 3.08 Å (
Figure 5). Shorter Fe-Fe distances from BCC iron should be readily visible in G(
r) due to the high coherent scattering length of Fe. Finally, the Rietveld refinement shows no indication of a BCC phase. Thus, it is concluded that the Fe clusters have the same FCC structure as the rest of the metal matrix, and are not due to unreacted Fe from the synthesis.
The experimental findings of thermodynamically stable Fe clustering are also supported by atomistic DFT simulations. Since first-principles calculations on the 10 × 10 × 10 unit cell RMC model are too computationally demanding, a smaller 3 × 3 × 3 model derived from RMC was considered. This model also shows clear tendencies for Fe atom and D-vacancy clustering. Both the random 3 × 3 × 3 starting model and corresponding RMC model were relaxed using DFT formalism. The total energy of the relaxed RMC model was 2.14 kJ/(mole metal atoms) lower than the relaxed random model, thus indicating that the short-range ordering occurs due to a higher stability rather than inadequate synthesis conditions.
BCC models of similar size for DFT were made by first describing the FCC structure as body-centered tetragonal and then adjusting the tetragonal unit cell parameters to match the cubic lattice parameter of the deuterium-free alloy. The deuterium atoms and vacancies were removed. DFT relaxation did again show lower energy for the model with Fe-clustering than for the random model (derived from final and initial RMC models, respectively). The energy difference between the two models was 2.15 kJ/(mole metal atoms). This indicates that the clustering has taken place during the casting of the alloy and not as a result of the deuteration.