1. Introduction
For this paper, we searched for concentration-dependent resistance data of ion exchange membranes. We restricted our search to NaCl solutions and found 145 usable (i.e., with sufficient data at concentrations below 0.1 M) plots in 36 publications [
1,
2,
3,
4,
5,
6,
7,
8,
9,
10,
11,
12,
13,
14,
15,
16,
17,
18,
19,
20,
21,
22,
23,
24,
25,
26,
27,
28,
29,
30,
31,
32,
33,
34,
35,
36]. Some publications were not or only partially used because they list only resistance at higher concentrations (>0.1 M) [
37,
38], are missing detailed information about the method of resistance measurement [
39,
40], or describe the effect of extreme pretreatment methods [
34].
Ion exchange membranes (IEM) are applied in different fields of separation technology and power generation [
41,
42,
43]. Examples are electrodialysis, fuel cells, Donnan dialysis, capacitive mixing, and reverse electrodialysis. In most cases, low resistance, high permselectivity, and low water transport is needed. Other important aspects are mechanical strength, resistance to chemicals and high temperatures, selectivity for monovalent ions, and proton conductance. This paper is focused on one of these aspects: namely, membrane resistance. The term
resistance is usually used in the field of electrodialysis and reverse electrodialysis, whereas the inverse term
conductivity is more common in the energy world where ion-exchange membranes are used in fuel cells.
Ion exchange membranes are divided into different classes: (i) anion exchange membranes (AEM) are permeable to negative ions (anions) and the common fixed charge carriers are quaternary ammonium groups (approximately NR
3+); cation exchange membranes (CEM) are permeable to positive ions (cations) and the fixed charges are commonly sulfonate groups (approximately SO
3−); (ii) homogeneous membranes (HoM) contain a polymer (in most membranes cross-linked, except in Nafion type membranes) with covalent bonded fixed charges, whereas heterogeneous membranes (HeM) are solid mixtures of an uncharged thermoplastic polymer and a charge-containing compound (an ion exchange resin); (iii) monovalent selective membranes are mainly permeable for monovalent ions in contrast to ‘normal’ IEMs, which are also permeable to ions of higher valencies; (iv) moreover, there are special membranes for proton transport, for use at extreme pH conditions, for the chloralkali process, for desalination, and so on. A special class is formed by inorganic pseudo ion exchange membranes [
44].
The production of ion exchange membranes is performed via very different routes, depending on the desired properties and the available skills of the manufacturer. The principle of the ion transfer mechanism is globally understood and is mainly explained in terms of the Donnan exclusion theory. However, much is still unknown about the structure of the different membranes and the mechanism(s) governing of ion transport across them. This lack of knowledge is a barrier for the development of membranes for specific applications such as desalination, reverse electrodialysis, and so on.
In this paper, we focus on the membrane resistance. With data from the literature, we test some structural models of the involved membranes. To get more information while measuring the membrane resistance, some parameters should be varied in the same way as in spectroscopy where the structure of a compound can be elucidated from the spectrum. By analogy with spectroscopy where the frequency is varied, in membrane technology, the effect on the resistance of the following parameters are commonly studied:
Varying the frequency of the applied current, a method known as electrical impedance spectroscopy (EIS) provides information about the partial resistance of membrane, Stern layer, diffusion boundary layer, and bulk solution. However, no special information is retrieved about the internal membrane structure [
45].
Varying the current gives a I-U (current density-voltage) plot showing the limiting and over-limiting current in electrodialysis [
46].
Varying the kind of ion (e.g., measuring the resistance of a Neosepta CMX membrane in a MgCl
2, CaCl
2, SrCl
2, and BaCl
2 solution) provides knowledge about the transport mechanism and the role of ion hydration thereby [
7,
18].
Varying the membrane composition “step-by-step” gives direct information between production and resistance and some information about the transport mechanism [
6].
Varying the temperature makes it possible to derive the activation energy from the Arrhenius plot [
47,
48].
Varying the thickness of the membrane provides information about the contribution of liquid surface layers (Stern layer and diffusion boundary layer) to the total resistance [
49].
Varying the relative composition of the bulk solution gives insight into the particular effect of a given ion, for example different NaCl/MgCl
2 solutions with the same total concentration, to study the effect of bivalent ions on the resistance [
37,
50].
Varying the concentration of the bulk solution gives insight into the internal structure of the membrane [
1].
In this paper, the last method, the effect of the bulk salt concentration on the membrane resistance, is applied: in the scientific literature, most data are reported for NaCl solutions. Therefore, we have restricted ourselves to this salt. It should be emphasized that a good ion exchange membrane has a low resistance in combination with a high permselectivity and low water transport. In practice, membrane manufacturers make a trade-off between these contradictory properties.
In almost all applications, the ion exchange membrane under study separates two compartments containing solutions with different salt concentrations. For practical work, it is important to know the resistance of the membrane under these conditions. However, only a few papers indicate this aspect [
1,
4,
51]. This item is out of the scope of this publication and will not be discussed further.
During the analysis of the datasets, we found a broad spread of data of resistance measurements of commercial membranes. The large variances can be assigned to the supplied membranes, to pretreatment conditions, and to measurement techniques. The first cause may be important because the dataset extends to a period of 50 years, but it is difficult to quantify this effect. Pretreatment is normally restricted to conditioning some hours in solutions of the concerning salt (in our case NaCl), and we expect in most cases no significant contribution of different conditioning times to the observed variance. Distinct ways of pretreatment will be discussed in the text. We focus on the different measurement techniques and try to get insight into their usefulness and reliability.
Resuming, our first goal was to find the correlation between six membrane models and the experimental data reported in the literature. These models include three theoretically based models and three phenomenological constructions. Additionally, the different used measuring techniques were compared.
2. Model Development
All ion exchange membranes—including the homogeneous membranes—are heterogeneous on a small scale.
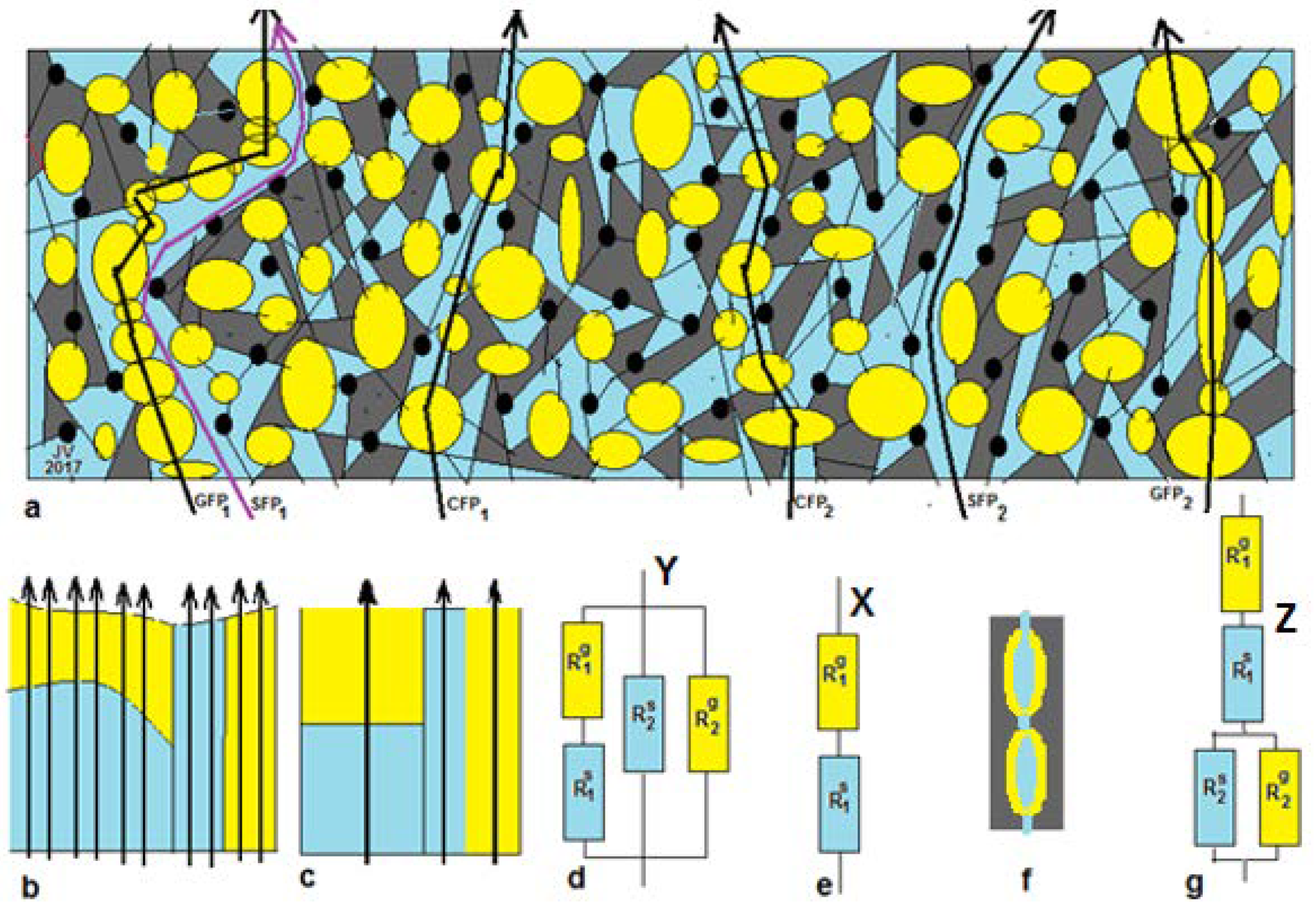
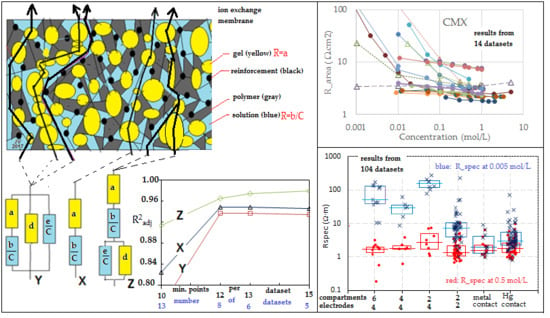
Figure 1a presents a summary of possible paths across both gel and solution phases as well as paths that cross solely gel or solely solution phases. By imaginary rearrangement of the different phases and omitting the non-conducting phases, we can construct
Figure 1b. Thus, there are three types of flow path: CFP (combination flow paths), GFP (gel flow paths), and SFP (solution flow paths).
2.1. Equivalent Circuit Models
The general expression for the total resistance of the model of
Figure 1b can be written according to the “resistances-in-series” approach as:
All resistances R are expressed in Ω∙cm2 and are formally called area resistances. From this expression, three physical models are derived:
Three-thread model Y. In this paper, we use data from the literature and unfortunately, most authors have shown only about 5 data points for each concentration-dependent resistance plot. Therefore, we have to simplify the model in the following manner: If the dimensions of the different phases are small with respect to the thickness of the membrane, then all CFP trajectories contain about the same amount gel phase and solution phase with a small standard deviation. The same holds for the GFP and the SFP. This system can be represented by
Figure 1c, and the concept is introduced by Gnusin et al. [
52] and later on elaborated by Zabolotsky and Nikonenko [
40]. This model is called the
3-thread model, and the equivalent circuit Y is shown in
Figure 1d. The 3-thread model includes 4 fitting parameters, and that is almost over the limit of feasibility if there are only 5 measurements. An additional complication may be the possible presence of pinholes in the studied membrane: their effect appears as SFPs.
One-thread model X.Figure 1a shows that the presence of single flow channels (solely gel or solution phase) is doubtful, and we can simplify the 3-thread model to a 1-thread model Y as depicted in
Figure 1e. Galama et al. showed this model to be successful in their work on the Neosepta CMX membrane [
1].
Gierke model Z. Gierke et al. [
53] concluded that a Nafion CEM contains vesicles with the negatively charged sulfonate groups pointing from the wall to the water clusters. Together with water and positively charged counter-ions, in this way, a gel layer is formed, whereas a solution phase is present within the vesicles. These vesicles are interconnected by small channels, partially as gel and partially as solution phase (
Figure 1f). The corresponding equivalent circuit Z is shown in
Figure 1g.
In addition to the physical models, we will also consider three phenomenological models E, P, and M. The assumption for the X, Y, and Z models was that inhomogeneities in the membrane structure are averaged. This is only true if they are small with respect to the membrane thickness. However, they are rather large in heterogeneous membranes and are much larger in reinforced membranes with nonwoven structures and very large in membranes containing woven structures. Such circumstances cause different parallel flow channels, and averaging the concentration-dependent resistance results in big standard deviations. Therefore, we introduce the models E, P, and M.
The
exponential model E is defined as:
where
R stands for the area resistance (Ω∙cm
2) and
C stands for the bulk concentration (mol/L), whereas
p,
q, and
r are fitting parameters.
The power model
p is proposed by Zhu et al. [
23] to explain the concentration-dependent resistance of ion exchange membranes inserted in different salt solutions (the chlorides of Na, K, Ca, Mg, and Al as well as HCl).
The mixed model is added to incorporate the effect of decreasing conductivity at high bulk concentrations due to membrane shrinking.
From all these models, the one-thread model X is the most simple with only two parameters. It will be shown that this model can be used with rather good values of R2 in most experiments to describe the membrane resistance. Moreover, due to the restricted number of data points in many published experiments, it is in most cases the only possible fit model. The value of the term a stands for the contribution of the gel and that of b stands for the solution part in the membrane. The values of a and b are derived from plots of Rarea (in Ω∙cm2) versus concentration (in mol/L) and are membrane properties with units Ω∙cm2 for a and Ω∙cm2.mol/L for b. For a thickness independent comparison between the different membranes, we will use the parameters a/δ and b/δ, where δ stands for the membrane thickness; these values are related to the specific resistance and are material properties.
2.2. Resistance of the Gel and Solution Phases
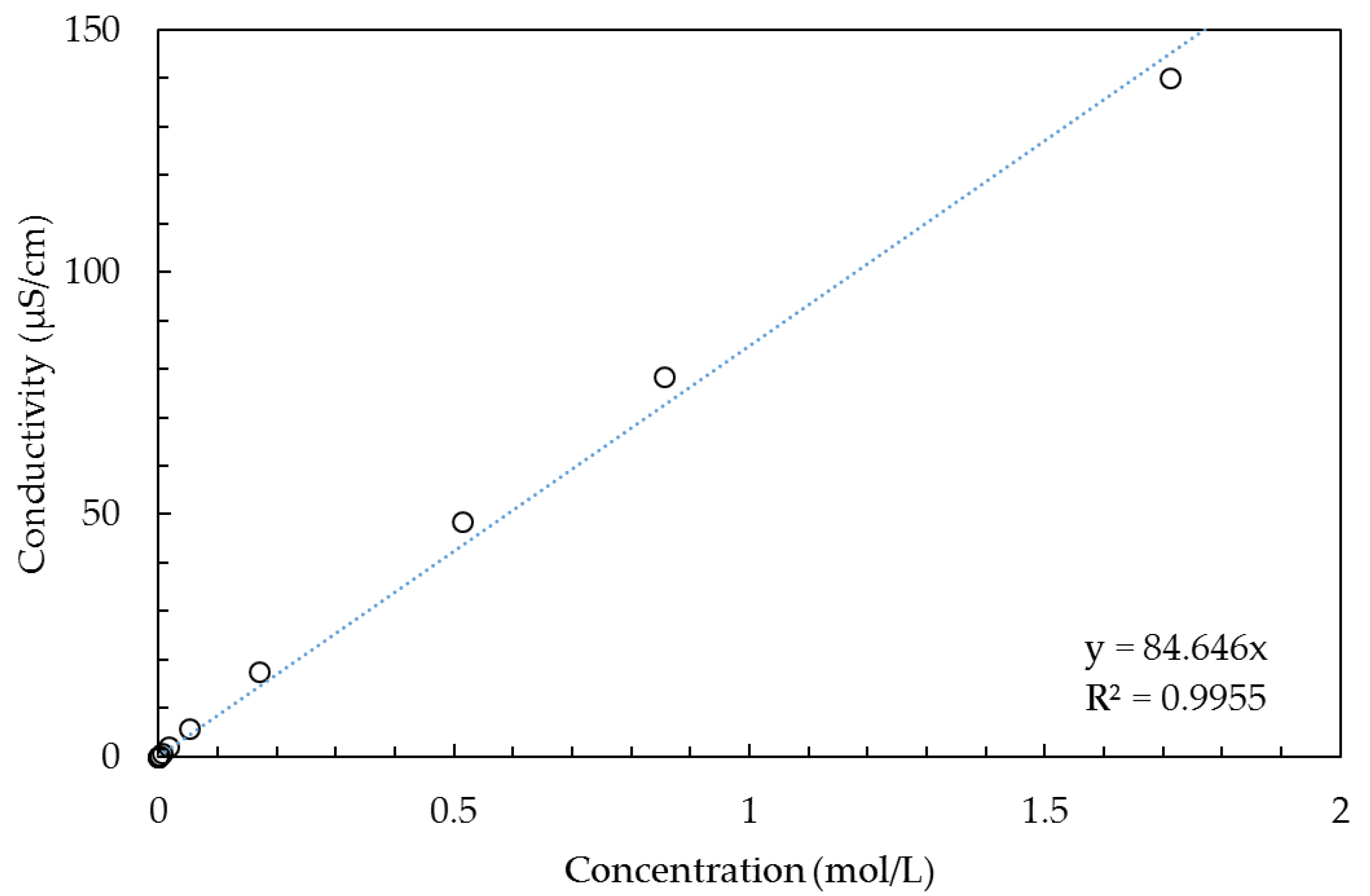
Solution phase. The resistance of the solution phase is strongly dependent on the salt concentration, and we assume there the same dependence as within the bulk solution outside the membrane. With the use of data from [
54], we constructed
Figure 2 and fitted the simple one parameter function
Κ = a∙C for concentrations below 2 mol/L (
Κ is the conductivity in µS/cm and
C the concentration in mol/L). The regression resulted in
a = 84.646 with a rather good coefficient of determination (R
2 = 0.9955). If the concentration range is restricted to a lower maximum, the coefficient of determination is better as depicted in
Table 1.
Although models with more fit parameters (e.g., parabolic equations with 3 parameters) result in better R2 values, it is important to restrict the number of fit parameters as much as possible. The number of data points in a single experiment in the scientific literature is often restricted to only 5 or less, and we use also fit parameters for the gel phase in the different models. Therefore, we will apply the simple function K = a∙C for the solution phase with only one fit parameter.
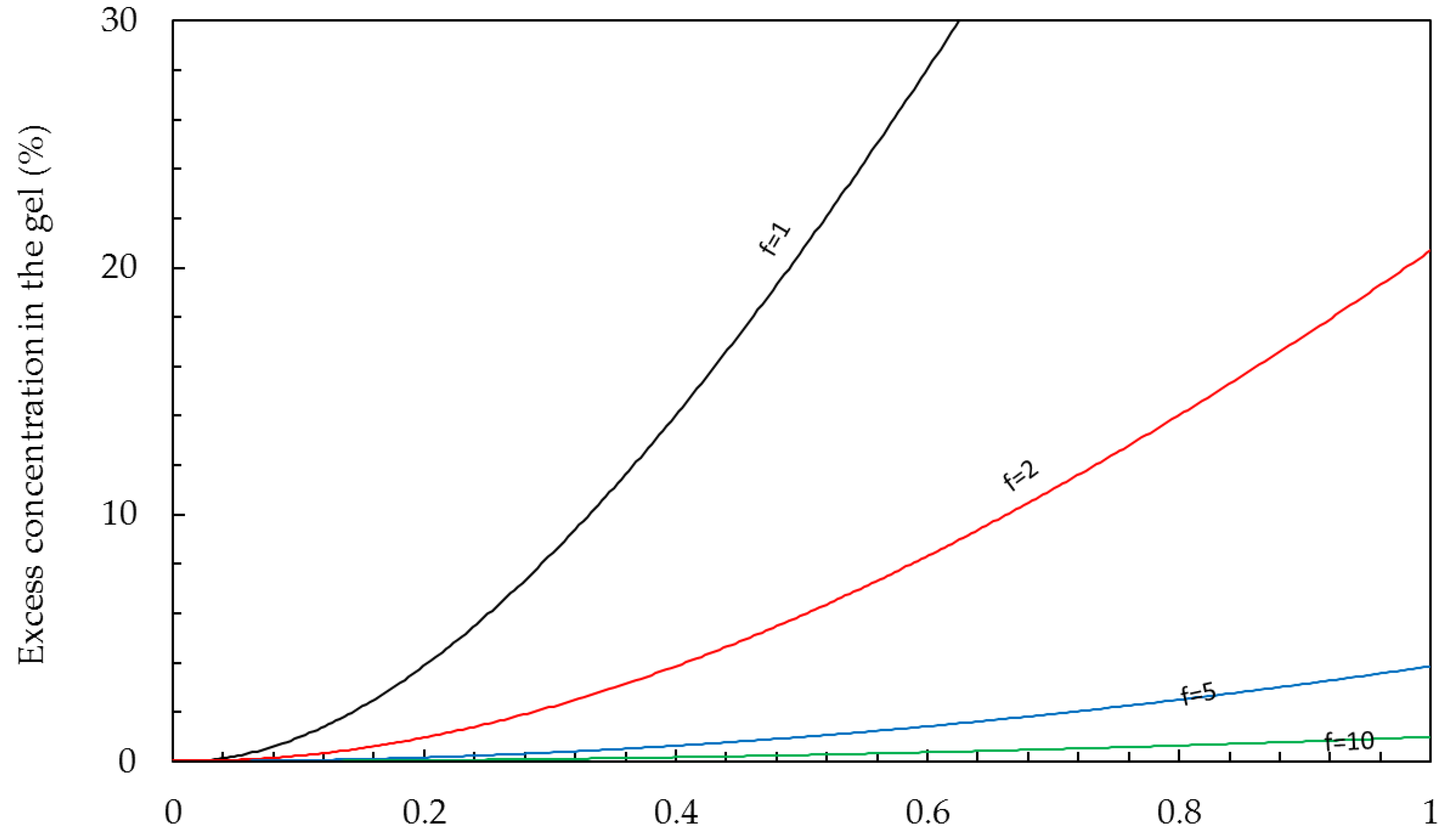
Gel phase. The conductivity of the gel phase is mainly ascribed to the presence of the counter-ions. The concentrations of counter-ions
(p) and co-ions
(q) are determined by the Donnan equations [
42]:
where
C is the bulk concentration (mol/L) and
f is the concentration of fixed charges in the membrane gel phase (‘charge density’). The charge density of most ion exchange membranes is in the range 5–10 mol/L. If an IEM is in equilibrium with pure water, there are no co-ions present. In this case, the concentration of the counter-ions is equal to the charge density, and these ions are called
condensed counter ions. In an IEM, immersed in a NaCl solution, there is a small concentration of co-ions and also the same excess of counter-ions. These ‘free ions’ are known as the ‘free salt’ and the concentration is the value
q in Equation (6).
Figure 3 shows this excess in percentage for different membranes in contact with NaCl solutions of up to 1 mol/L.
Membrane conduction is facilitated by the transport of (i) condensed counter-ions, (ii) excess counter-ions, and (iii) co-ions. Kamcev et al. suggest that the diffusion constant of condensed ions is about 2–2.5 times greater than those of the excess co-ions [
55]. This is explained by a facilitated transport of condensed ions via the charged backbone of the gel polymer. It is reasonable to assume that this factor holds also for ionic mobilities. Mobilities of Na
+ and Cl
− in free solution at 25 °C are respectively 5.19 and 7.91 (in units of∙10
−8 m
2s
−1V
−1). If we assume that these are also the mobilities of the free ions in the gel phase, it follows (applying the factor of 2.5) that the mobility of condensed Na
+ ions in a CEM is about 13 in the same units, which is almost equal to the sum of the two free ion mobilities. The consequence is that an excess of 1% results in an increase of the conductivity of 1%. In the case of an AEM, we expect a mobility of condensed Cl
− of 20 units, which is 1½ times the sum of the free ions. Thus, an excess of 1% in an AEM results in an increase of the conductivity of less than 1%.
It is worth mentioning that the discussed increase of co-ions in the gel phase at higher bulk electrolyte concentrations is the cause of reduced membrane permselectivity at these concentrations. Thus, plots describing the effect of bulk concentration on permselectivity can give more insight into the degree of excess. Unfortunately, there are very few papers that pay attention to this phenomenon.
Most commercial membranes have charge densities higher than 5 eq/L [
56], and most maximal bulk NaCl concentrations in the datasets are 0.5 mol/L. With these values, Equation (6) predicts an excess of 0.99% and therefore also a comparable increase of membrane conductivity. Therefore, we can conclude that the conductivity (and the resistance) is almost independent of the bulk concentration for commercial membranes at bulk concentrations beneath 0.5 mol/L NaCl.
Another complication in theoretical considerations about the effect of concentration on membrane resistance is swelling at low concentrations and shrinking of the membrane at high salt concentrations. The degree of volume change is influenced by the cross-linking density. This effect of swelling on the membrane area resistance is minimal for CMX membranes [
23] but may be considerable for non-cross-linked membranes.
2.3. Fitting the Models
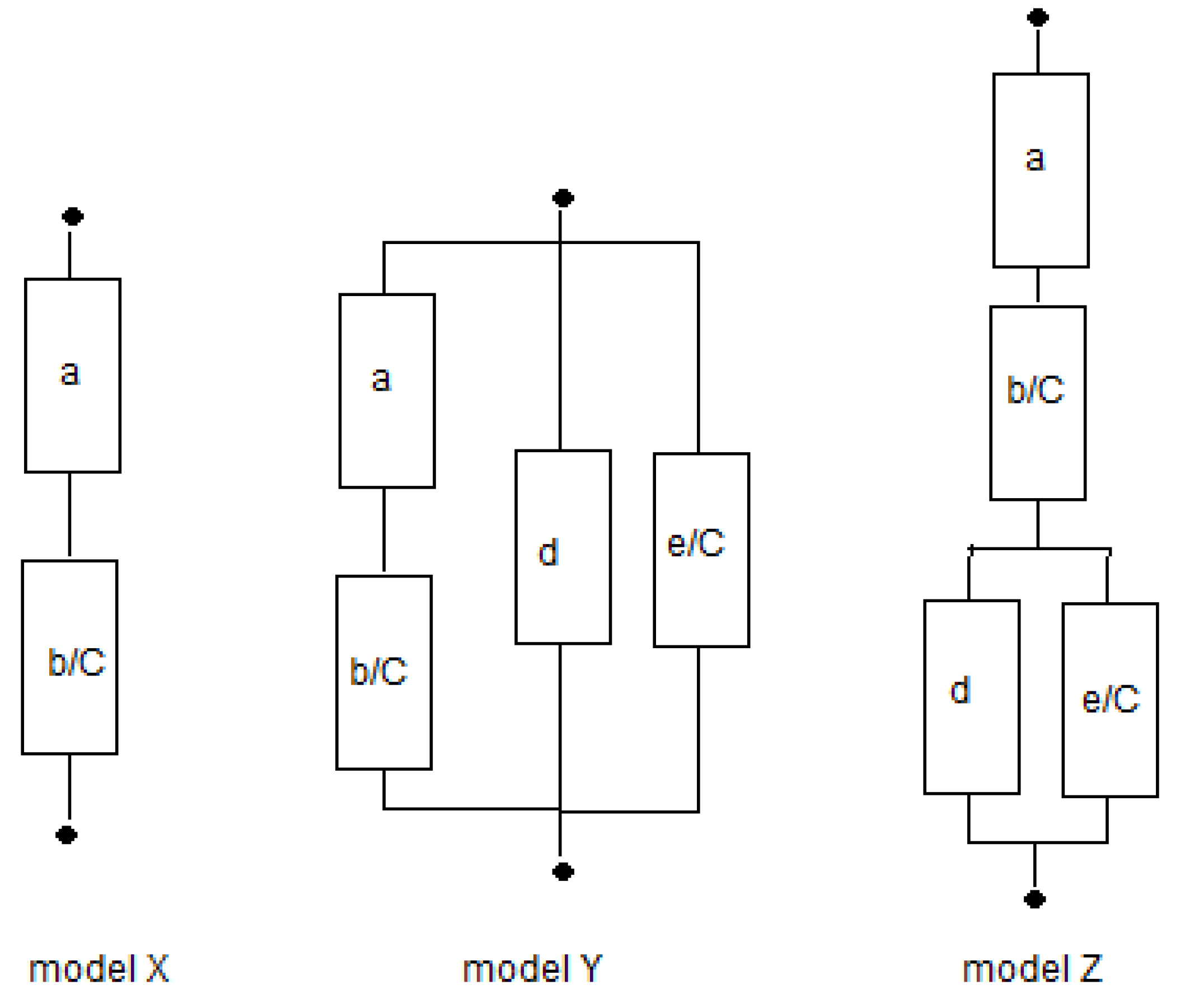
In the foregoing analysis, we have restricted the number of fit parameters for both the solution phase and the gel phase to only one. We will consider the three physical models
X,
Y, and
Z as shown in
Figure 4 and also the three phenomenological models
E,
P, and
M. The equations of the 6 studied models are summarized in
Table 2. Fits can be performed in the resistance or in the conductivity domain, as will be discussed further on.
The purpose of this study is to test the aforementioned models with data from published scientific literature and to get more knowledge about the internal structure of ion exchange membranes. Moreover, we want to compare data found with different measurement techniques. A complication is that the membrane resistance is dependent on the membrane material and its thickness, as well as the used salt and its concentration and temperature. Most published concentration-dependent resistance measurements were done with NaCl at 25 °C (sometimes 20 °C) with concentrations between 0.01 and 0.5 mol/L. A few experiments were done with other salts, such as NH4Cl and KCl, and we decided to focus on NaCl. Usually, measurements were done in 5 steps, and this restricted number of data points complicates a thorough statistical analysis.
Finally, we will give some short notes on the meaning of the membrane resistance for the application of these membranes: (i) In practice, all membranes work under direct current circumstances, and therefore it can be argued that direct current (DC) measurements are more realistic. (ii) Secondly, in all applications, the concentration at both membrane sides is different. Galama et al. [
1] and Geise et al. [
4] have shown that in this case, the lower concentration has the largest influence on the membrane resistance. In membrane specifications, normally the area resistance is listed for 0.5 mol/L NaCl solutions. However, in many applications, the lowest concentration is much lower than 0.5 mol/L and therefore an indication of the resistance at 0.1 mol/L or lower in membrane specifications would be very valuable. (iii) In practice, almost all membrane operations (except for Donnan dialysis) are performed with an electrical direct current (DC). Ion movement, osmosis, and electro-osmosis can influence the membrane behavior. (iv) Other ions—especially bivalent ions—have a large influence on the membrane resistance.
Comparisons between AC and DC methods for measuring membrane resistance and general comparisons between different measurement techniques are discussed by Galama et al. [
1,
20], Karpenko et al. [
22], Kamcev et al. [
21], Nouri et al. [
15], and Zabolotsky et al. [
40].
4. Results and Discussion
Our dataset contains 145 datasets of 60 different membranes from 36 publications and are listed in
Table 4. Not included are experiments with special pretreatments such as boiling and heating as performed by Berezina et al. [
34]. The most abundant membranes are CMX for the class of homogeneous CEMs (16x), AMX for the homogeneous AEMs (13x), MK-40 for the heterogeneous CEMs (10x), and MA-41 for the heterogeneous AEMs (6x). Perfluorinated CEMs can be considered as a special class because the common commercial membranes are not cross-linked; Nafion-117 is the most abundant (10x) representative in our dataset.
4.1. Dependence of the Resistance on the Bulk Concentration
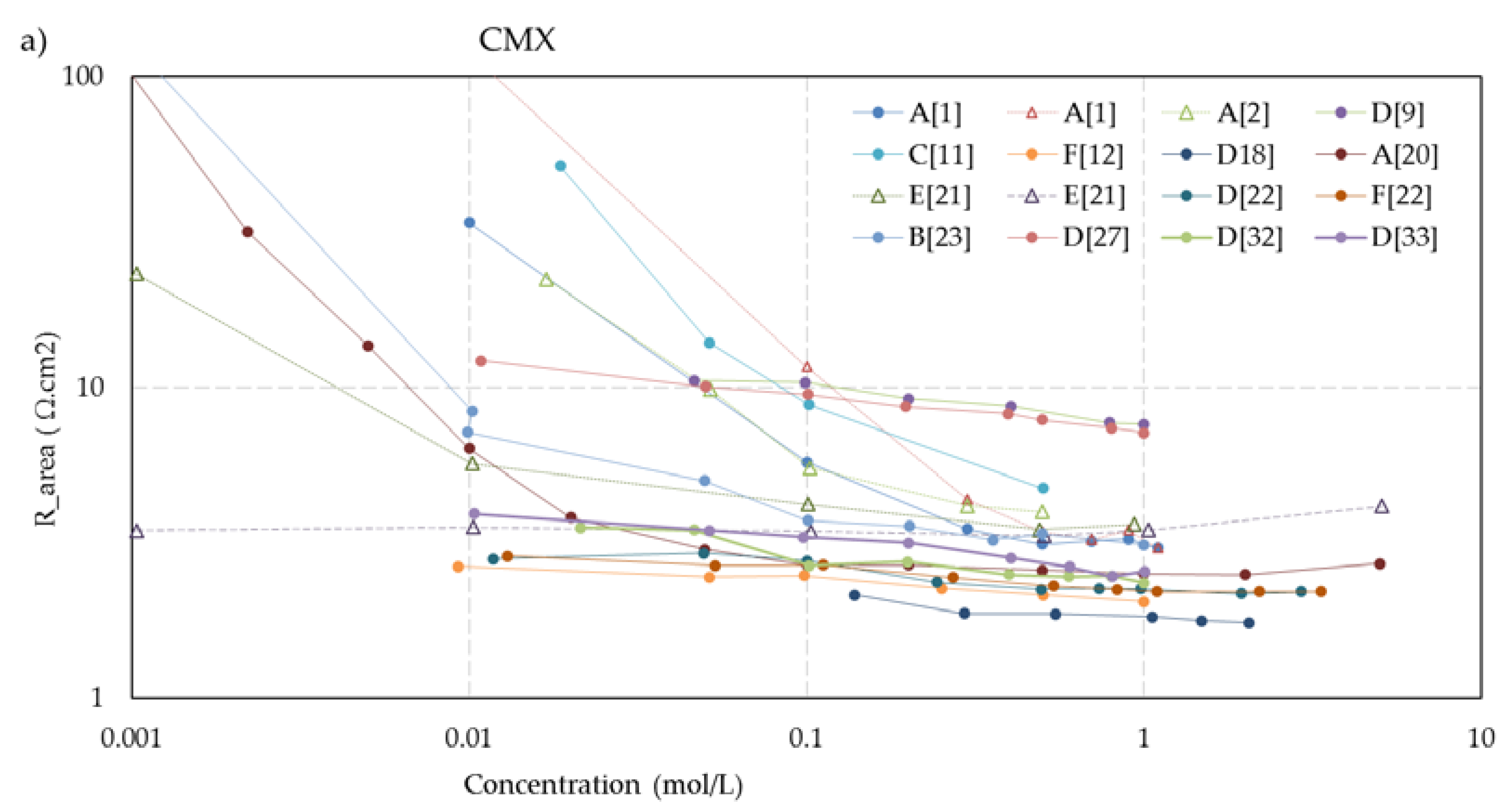
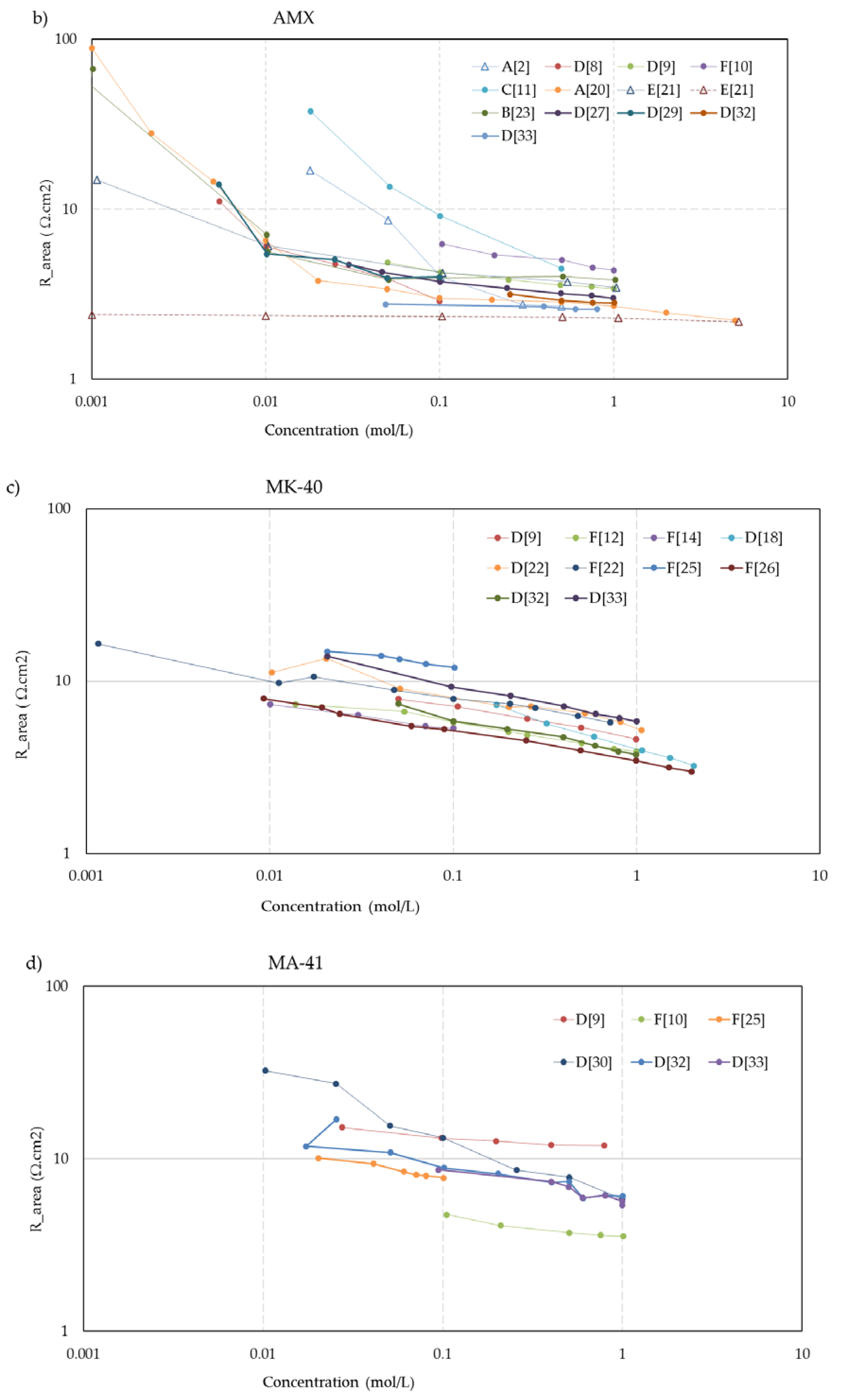
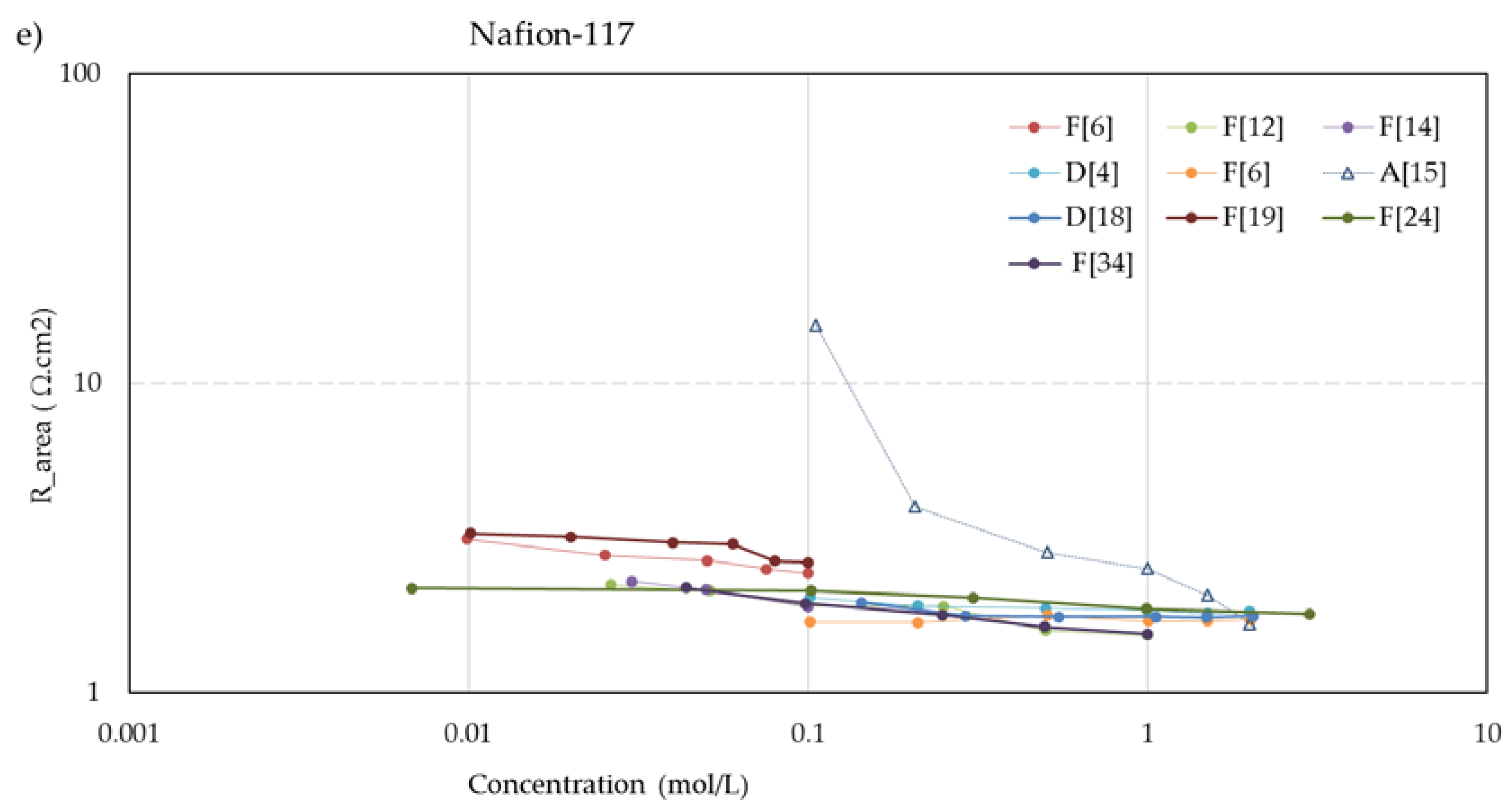
Figure 5 shows the concentration dependent resistance of these five membranes. The legend mentions the used measurement cell (A, B... F) as well as the source. To aid visual interpretation, the data points are interconnected by solid lines for experiments performed with alternating current (AC) and dotted lines for experiments performed with direct current (DC). An exception is the dashed lines in the CMX and AMX plots from the experiments of Kamcev et al. [
21], who used a short dip with the membranes in concentrated NaCl (5 M) before the measurement to prevent depletion layers between the electrodes and the membrane. Apart from these two datasets, the membrane resistance increased at lower concentrations in all cases of these five selected membranes. This suggests that the dip method as applied by Kamcev is not entirely optimal. The Nafion-117 plots (
Figure 5e) also show an outlier: the plot indicated as A [
15] from the experiments of Nouri et al. [
15]. In the collection of all Nafion-117 plots in this figure, the A [
15] plot is the only one performed with DC and the only one measured in a six-compartment cell with two pairs of electrodes. However, such deviations are not seen in the graphs of the other membranes in
Figure 5, and our conclusion is an error in the measurement or in the examined membrane.
The trend of higher resistance at lower bulk concentration is present in the whole dataset.
Exceptions are:
The
MF-4SK-1** and
MF-4SK-2** membranes in the paper of Falina et al. [
19]. These membranes have a very dense reinforcing fabric which makes swelling difficult. This results in membranes with little solution phase, leading to a relatively high resistance in a 0.5 M bulk solution and no remarkable increase of the resistance at dilution of this solution.
The membranes
CMX and
AMX in the experiments with a 5 M NaCl dip of Kamcev et al. [
21]. The authors used the metal contact method and argued that a short dip in a concentrated NaCl solution improves the contact between electrode and membrane. However, all other datasets show an increase of the resistance at dilution of the bulk, and it seems that the salt is diffused inside the membrane. Moreover, the authors applied a DC current with a superimposed AC current and therefore, the migration of salt ions into the membrane is conceivable.
The membranes
CM-1, CM-2, and
Nafion-117 in the experiments of Nouri et al. [
15] with the mercury contact method. However, with other measuring techniques, they found an increasing resistance at dilution of the bulk. Given the abundance of conflicting results with other methods and by other researchers, we regard these data as outliers.
4.2. Effect of the Method
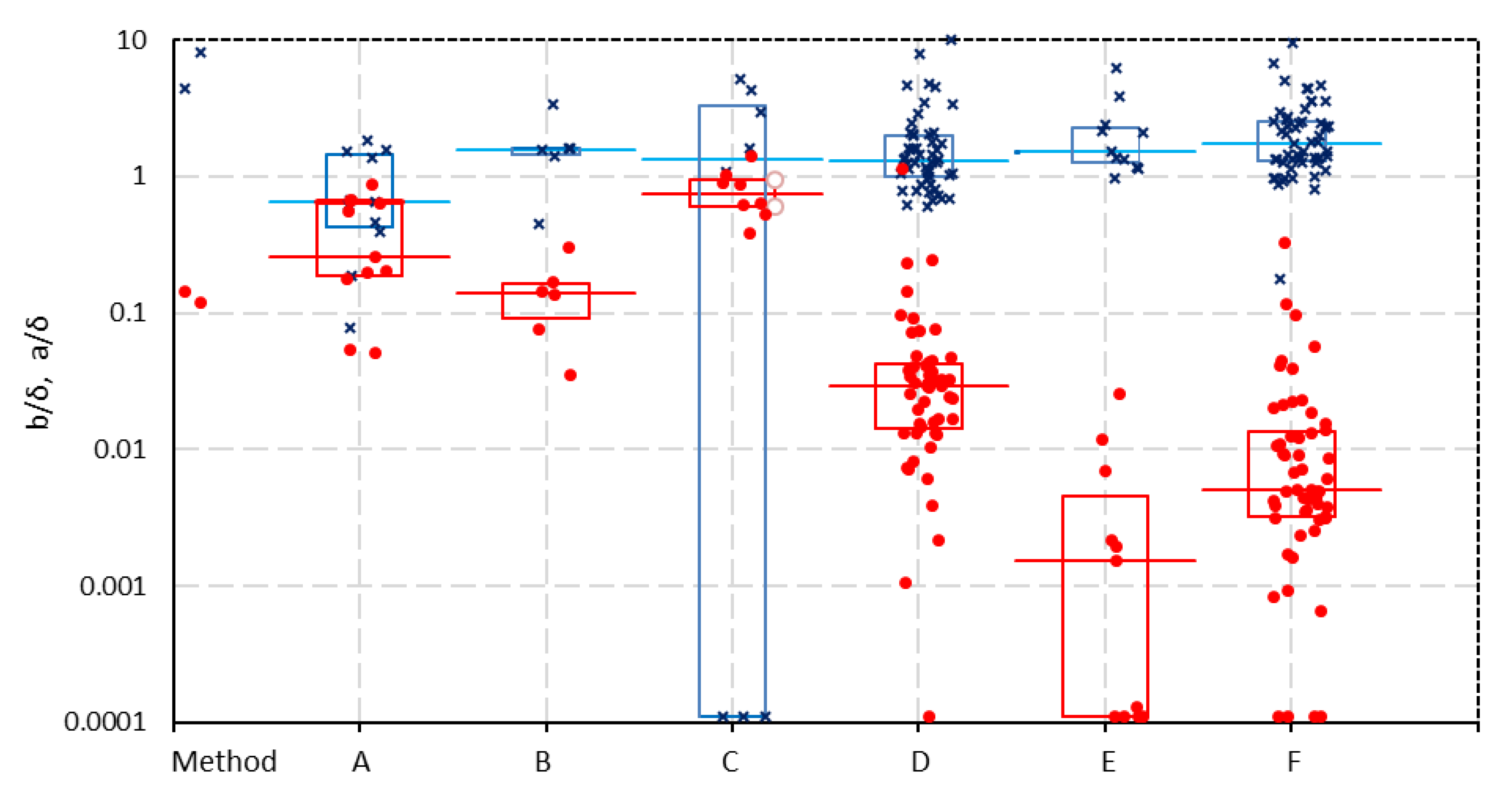
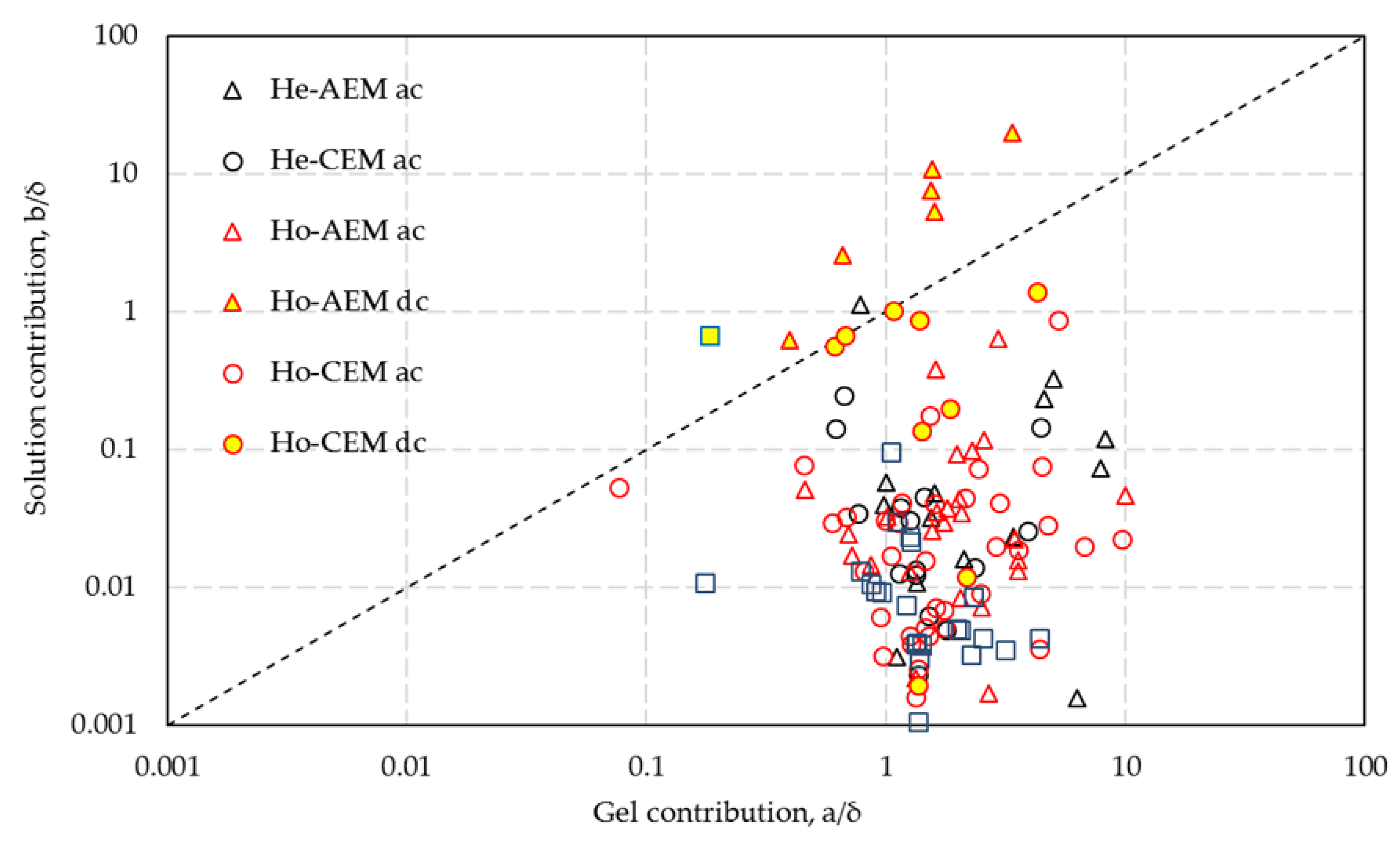
In
Figure 6, the corrected values a/
δ and b/
δ from the one-thread model of all the datasets are plotted according to the various measuring techniques. There are no significant differences for
a/δ with the different methods. However, remarkably large differences are seen for
b/δ between results on the one hand for
A, B and
C and on the other hand for
E and
F with an intermediate formed by D.
The same trend is seen in
Figure 7 where the specific resistance (the area resistance
Rarea divided by the membrane thickness
δ) at low concentrations (0.005 mol/L) of all membranes is plotted. These resistances are calculated using the values
a and
b from the fits of the 1-thread model (R
spec = (a + b/C)/
δ). The figure shows no large deviations between the methods at ‘normal’ bulk concentrations (0.5 mol/L). However, at low concentrations (0.005 mol/L), the resistances measured with methods A, B, and C are very increased, and with method D, the values are increased moderately. We will try to interpret these differences.
Use of reference electrodes. The difference between (
A, B, C) and (
D, E, F) is that in the first group (
A, B, C) of reference electrodes are used in the cell and in the other group (
D, E, F), the voltage is measured across the working electrodes. In most cases, these reference electrodes are Ag/AgCl electrodes connected with Luggin–Haber capillaries near the membrane surface. Capillaries near the membrane can obstruct the ionic current perpendicular on the membrane. An indication that the broad Luggin–Haber capillaries are the cause of the deviant behavior are the two datasets (for
AMX and
CMX) from Galama et al. [
20], who used thin platinum–iridium wires as reference electrodes in a 6-compartment cell; in these cases, the b/
δ values are rather small (respectively 0.051 and 0.053).
Applying blank correction. With direct contact methods between the membrane and electrodes (method E and F), no blank correction is used. However, possible effects of the blank correction on the resistance are unclear. Then, method D remains a separate problem: most measurements in our dataset are achieved with clip cells where a blank correction is applied. Here, the increase in resistance is significant but not as extreme as with the methods A, B, and C.
Nouri et al. [
15] compared three methods: the mercury cell, a clip cell (‘LMEI clip’), and a 6-compartment cell with reference electrodes (‘Guillou’s cell’). As stated before, the results with the mercury cell are very divergent from all other datasets with this cell type, and we shall ignore these measurements. However the comparison of the 6-compartment cell (method
A) and the clip cell (method
D) is very illustrative.
Table 5 shows again the same discrepancy for
b/δ if measured with different systems.
In all considerations about membrane resistance, the question is whether we are interested in membrane properties or material properties. Suppose that the mercury contact method is superior for determining the material resistance; then, it is possible that the water-contact methods give a better approach of the expected resistance of the membrane in real applications.
4.3. Choice of Fitting in the Resistance or in the Conductivity Domain
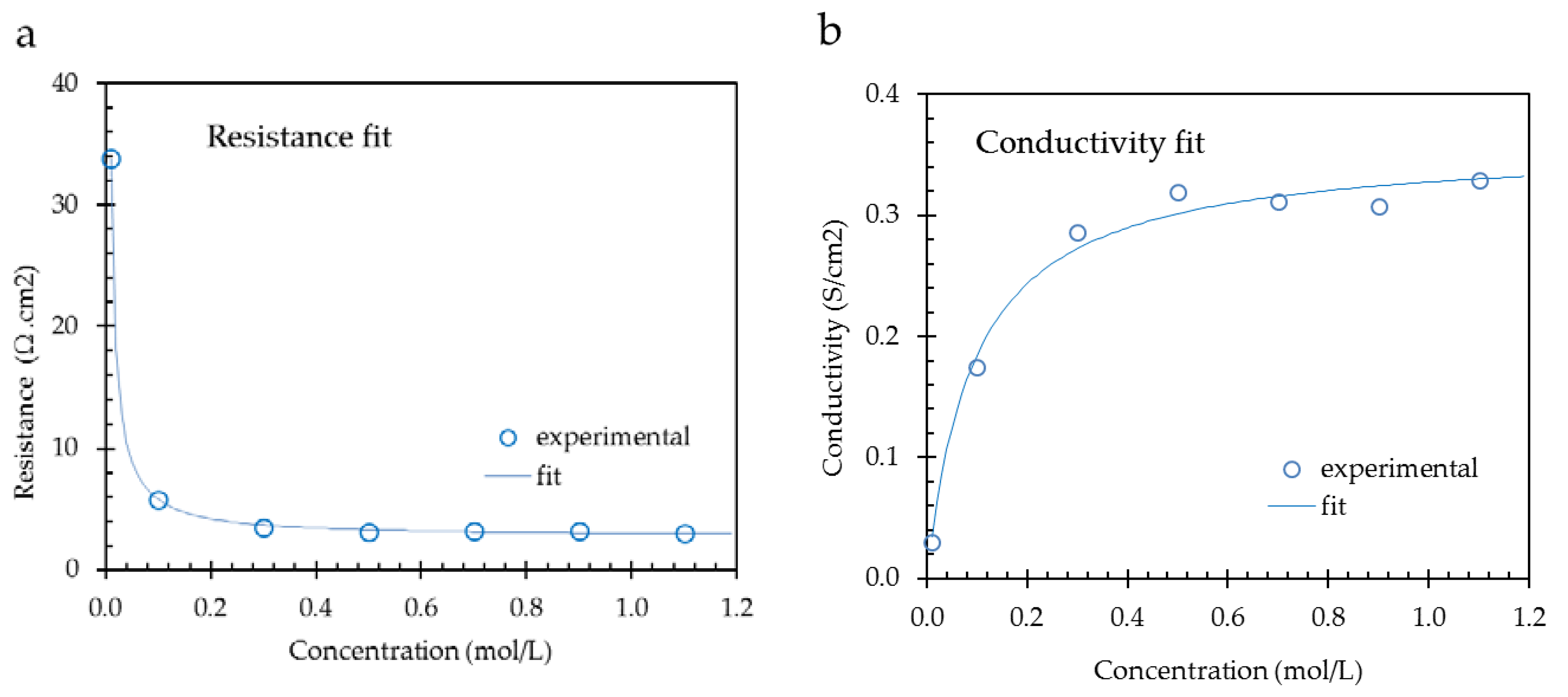
Figure 8 shows the results for a CMX membrane from a resistance fit (left) and a conductivity fit (right); data used from [
1]. The numerical results are listed in
Table 6. For the fits, the simple 1-thread (two parameter) model is applied.
With the resistance fit method, the fit values at low concentrations are high and influence the model more than the high concentration fit values. At low concentrations, the contribution of the solution phase is predominant. At these low concentrations, there is a danger of experimental errors in maintaining the bulk concentration constant, especially if metal contact methods are used. Otherwise, the assumptions of a linear conductivity of the bulk and a constant conductivity of the gel phase are better guaranteed at lower concentrations. Moreover, the published datasets cover usually the lower concentration range below 1 mol/L. The conclusion is that we expect that fitting the resistance is more reliable than fitting the conductivity, assuming that the experiments were carried out with great care.
In the example as presented in
Table 6, the best fits are obtained with the resistance method due to the higher R
2 value. However, this is only one example, and we fitted the 6 suggested models to each of the 145 datasets in two ways (resistance and conductivity). For each pair (resistance and conductivity plot), we compared the R
2 values. For each model,
Table 7 shows higher R
2 values with the resistance regression. The last row in the table indicates the
p-values as obtained with the binomial sign-test. For most models, these
p-values are less than the significance level of 0.05, indicating a significant improvement. Only for the 3-thread model do both fit methods seem to be statistically equivalent. Therefore, we will restrict ourselves to the following considerations to the resistance fit method.
4.4. Comparison between AC and DC Measurement
The simple model
R = a + b/C is fitted in the resistance domain for all datasets. The corrected parameters
a/δ (the contribution of the solution in the membrane vesicles) and
b/δ (the gel contribution) are shown in
Figure 9. It should be emphasized that the plot includes very different membranes (homo- and heterogeneous, anion and cation exchange, commercial and homemade) and measurement methods (AC and DC, metal or water contact, with or without reference electrodes, with 2, 4, or 6 compartments, different year of production).
The mean values for the two parameters are
= 2.00 and
= 0.111; thus, the contribution of the gel phase is about 20 times that of the solution phase or 25 times that of the solution phase when not normalizing the fitting parameters by the membrane thickness. No significant differences between the five membrane types are seen in this figure. However, with DC measurement, the
b/δ values are much higher than with AC measurement, while the
a/δ values are lower.
Table 8 shows also the ratio
)/(
), which is quite different for both methods. The reason is that with DC measurement, there is the effect of ion depletion outside one side of the membrane and perhaps also within the membrane vesicles.
4.5. Fitting the Six Different Models
The six membrane models from
Table 2 were fitted to the found datasets in the resistance (R) and conduction (Κ) domain. Calculated are the normal (R
2) and the adjusted coefficients of determination (R
2adj). Adjusted coefficients of determination are needed to compare methods with a different number of variables. From all individual coefficients of determination, the mean values are calculated.
Table 9 shows the results. R
2adj are calculated with [
63]:
where
n stands for the number of data points and
p stands for the number of fit parameters;
R2 is the normal coefficient of determination.
The following conclusions can be drawn from this table:
Very low values of R2adj are the result of the small number of data points in each experiment (in much cases less than 5). This can result in zero or negative values of R2adj.
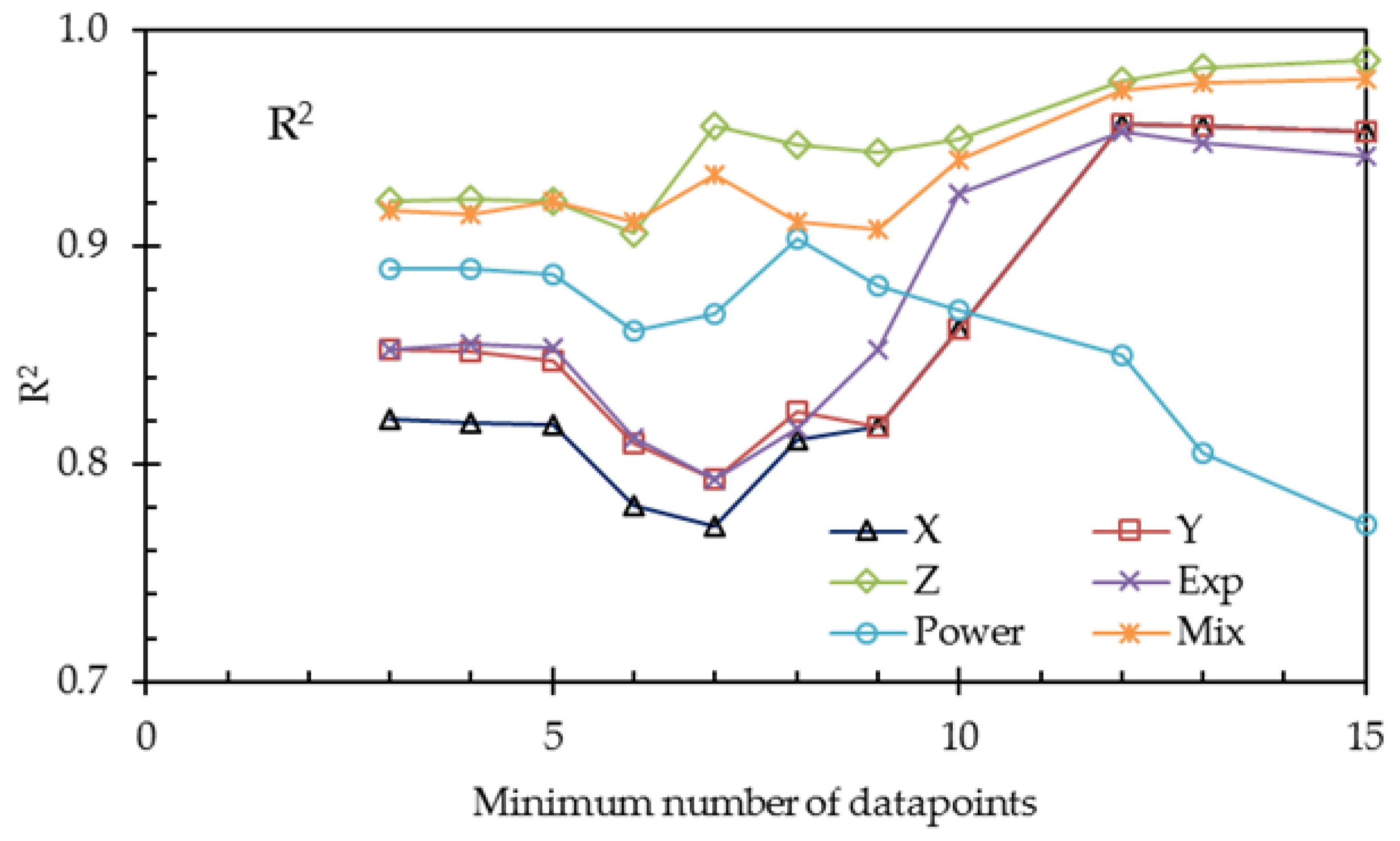
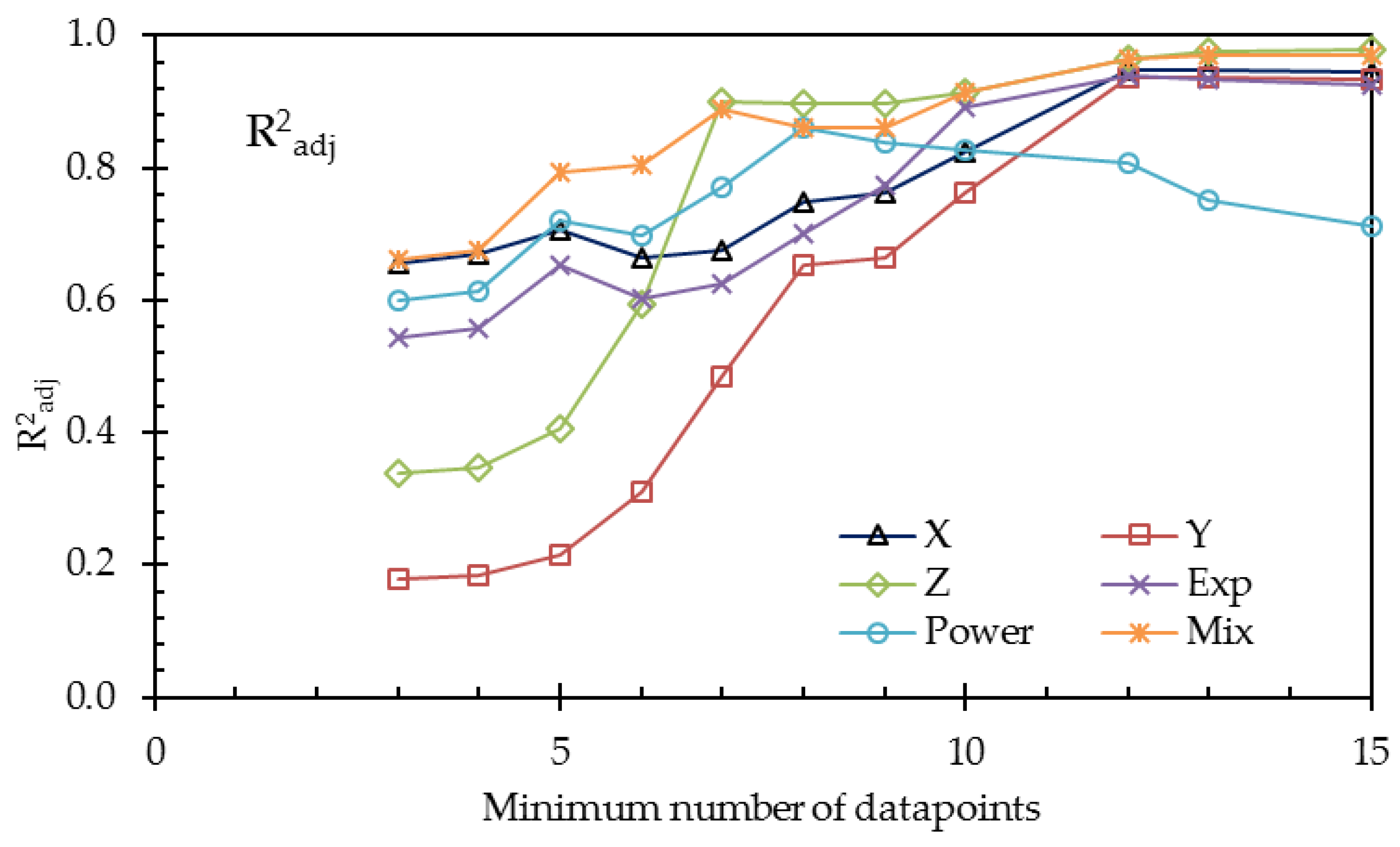
To overcome the problem of the small number of data points, we repeated the calculations with restricted numbers of datasets. The results are listed in
Table 10 and plotted in
Figure 10 and
Figure 11.
From
Table 10 and the last two figures, we can conclude, on the basis of the adjusted coefficients of determination, that the 3-thread model (
Y) is not an improvement of the 1-thread model
X. Although the value R
2 of
Y is a little higher, the improvement is due to the increased number of fit parameters, resulting in a decrease of the value of R
2adj. On the other hand, the refinement by using the Gierke model (
Z) is a real improvement, as seen in the larger R
2adj.
The exponential (Exp), the power (Power), and the mixed (Mix) phenomenological models—each with three fit parameters—can be compared with each other with the use of R2. The mixed model provides the best fit, which is probably because this model accounts for the nonlinear conductance of gel and solution.
5. Conclusions
Our goal was to compare different methods of measuring membrane resistance and to compare different fit models. We found differences between the different methods but could not clearly identify the causes. There are probably two main causes: the use of reference electrodes (especially thick Luggin–Haber capillaries) and the contact medium (water or metal/carbon) with the membrane. Complications are the great variety in apparatuses, protocols, blank correction methods, and EIS procedures. Moreover, commercial membranes are not chemical compounds with unchanging properties; different lot numbers, year of production, and storage conditions can influence their properties. This makes a straightforward comparison of the applied methods difficult.
For the structural elucidation of ion exchange membranes, concentration-dependent resistance measurement can be a useful tool if enough data points are available. Our first goal was to test three physical models—the 1-thread model, the 3-thread model, and the Gierke model—using the datasets as found in the scientific literature. Resistance measurements in most publications are limited to about 5 data points, which is far too few for models with 4 parameters. By limiting ourselves to only datasets with a larger number of data points, it was possible to investigate also the 4 parameter models, and we concluded that the Gierke model is an improvement of the 1-thread model in contrast to the 3-thread model.
We tested also three phenomenological models: an exponential model, a power model, and mixed model. The power model turned out to be very poor, while the exponential model performed better; however, the best fits were achieved with the mixed model, although these were not better than those of the Gierke model.