Abstract
The growth in the integration of converter interfaced renewable energy has reduced the system inertia, which threatens system stability due to high rate of change of frequency (RoCoF) and frequency nadir issues unless steps are taken to mitigate it. There is a need to provide sufficient fast frequency response to maintain adequate inertia in the system. This paper investigates the capabilities of a variable speed heat pump to provide an emulated inertial response. This paper presents a virtual synchronous machine control for a variable speed heat pump that provides support for grid frequency regulation over the inertial response time frame. A small-signal model with the transfer function of the variable speed heat pump is developed to analyse the effectiveness and feasibility of providing virtual inertia at the device and grid level, respectively. Furthermore, the small-signal model is validated using hardware in the loop simulation. Finally, the aggregated frequency response and virtual inertia contribution by a population of the heat pumps are evaluated and quantified in an urban distribution system.
1. Introduction
Europe has set an ambitious target to combat global warming by reducing the greenhouse gas emissions by at least 40% by 2030 and 80% by 2050 compared to the 1990 levels [1]. The emissions from the heating sector are about 600 Mt or 32% of Europe’s total emissions [2]. Electrification of heating combined with the increased use of renewable generation plays a vital role in reducing these emissions. Electric heat pumps are seen as a leading technology to provide a path towards a low carbon heating sector [3]. At the same time, increased use of variable renewable generation from wind and PV reduces power system inertia, as these generators are connected through a power electronics interface and do not provide inertia. The reduction in system inertia due to the increased penetration of renewable generation has the potential to cause cascading failures and blackouts due to the high rate of change of frequency (RoCoF) unless actions are taken to mitigate it. This paper investigates the role that heat pump technology can play in providing an emulated inertial and fast frequency response in the context of low inertia power systems. In particular, it investigates whether a controlled response from heat pumps can provide a virtual inertia-type response to the system.
The concept of using the demand-side response as a cost-effective solution to provide greater system flexibility in the context of growing variable renewable penetration is well known. Domestic appliances such as electric water and space heaters, air conditioners, and heat pumps make use of inherent thermal inertia and can be built to aid in the system frequency regulation [4] while minimising the impact on end-users. For example, in the U.K., domestic heat pumps have become common, and it has been estimated that they could provide a frequency regulation capacity of 2 GW by 2030 [5]. In California, thermostatically controlled loads (TCLs) such as air conditioners, heat pumps, water heaters, and refrigerators have a frequency regulation capacity of 0.6 GW [6]. In many European countries, the electrification of heating combined with increased renewable generation is seen as an important pathway to energy system decarbonization, so it is likely that heat pumps as a potential resource for frequency regulation will grow in the future.
The participation of heats pumps in frequency regulation has been investigated in previous works. However, most of these works have focused on the response to centrally dispatched direct load control signals (DLC). For example, the work in [7] investigated such a response, but only including the dynamics of a heat pump induction machine in the model. The work in [8] developed a dynamic model of the VSHP, which included the dynamics of a variable speed drive (VSD) controlled induction machine, a heat pump cooling cycle, and an experimental commercial building. This was used to estimate the effect of DLC application to the VSHP on the building indoor air temperature. The work in [5] presented a thermodynamic model of the entire population of localised load controlled heat pumps connected to the U.K. power system, but it only reflected the frequency response based on an on/off control of the heat pump. The works in [9,10] presented a hardware demonstration of VSHP participating in frequency response through a centralised control signal.
Although the concept of providing frequency response from direct centralised control of heat pumps has been studied, the provision of emulated inertia from heat pumps has received little attention. In contrast to previous studies, in this paper, the provision of a controlled inertial response from VSHP is investigated. In the power system, inertia is an inherent property of the synchronous machine, present due to energy stored in its large rotating mass and its electromechanical coupling to the grid. In low inertia systems, the main concern for systems operators is to ensure adequate frequency response that is effective in the first hundreds of milliseconds after an event, which is most likely to impact the system dynamics [11]. Consequently, an emulated inertial response should act on fast localised measurements and not rely on centralised communications. The key to an inertial response is that it is proportional to the rate of change of frequency (RoCoF) and not the frequency deviation.
The provision of emulated inertia from power electronics interfaced storage and generation has gained attention in recent years, through for example virtual synchronous machine-type controls [12,13] of the power electronics converters. Providing an inertial response typically requires short-term energy storage, and it has been investigated for energy storage systems (ESS) such as batteries, supercapacitors, and flywheel storage in [14,15,16,17,18,19] and for photo-voltaic systems operating off their maximum power point [20]. For wind turbines, the stored kinetic energy in the turbine rotor can be used in combination with VSMcontrol, as shown in [21,22,23].
The contribution of this paper is to develop a virtual inertia control for the variable speed heat pump (VSHP) and, using this, estimate the level of inertial response that can be contributed by increasing use of VSHP in a distribution system. To do this, a detailed dynamic model of the VSHP is first developed including the dynamics of the VSD controlled induction machine, heat pump cooling cycle, thermal model of a residential building, phase-locked loop (PLL), and virtual inertia control. The resulting small-signal model based on transfer functions is validated with measurements from hardware. Using this model, the virtual inertia control is designed, and the resulting inertial response is characterised. These results show that the inertial response is limited by the uni-directional nature of the typical VSHP drive topology. Consequently, to achieve increased response, a modification of the drive approach is investigated, which can extract the machine stored kinetic energy to provide maximum support for grid frequency regulation. Finally, simulation studies are performed to evaluate and quantify the aggregated frequency response and virtual inertia capability of a population of such heat pumps in an urban distribution system.
2. Modelling and Control Architecture
2.1. Overview
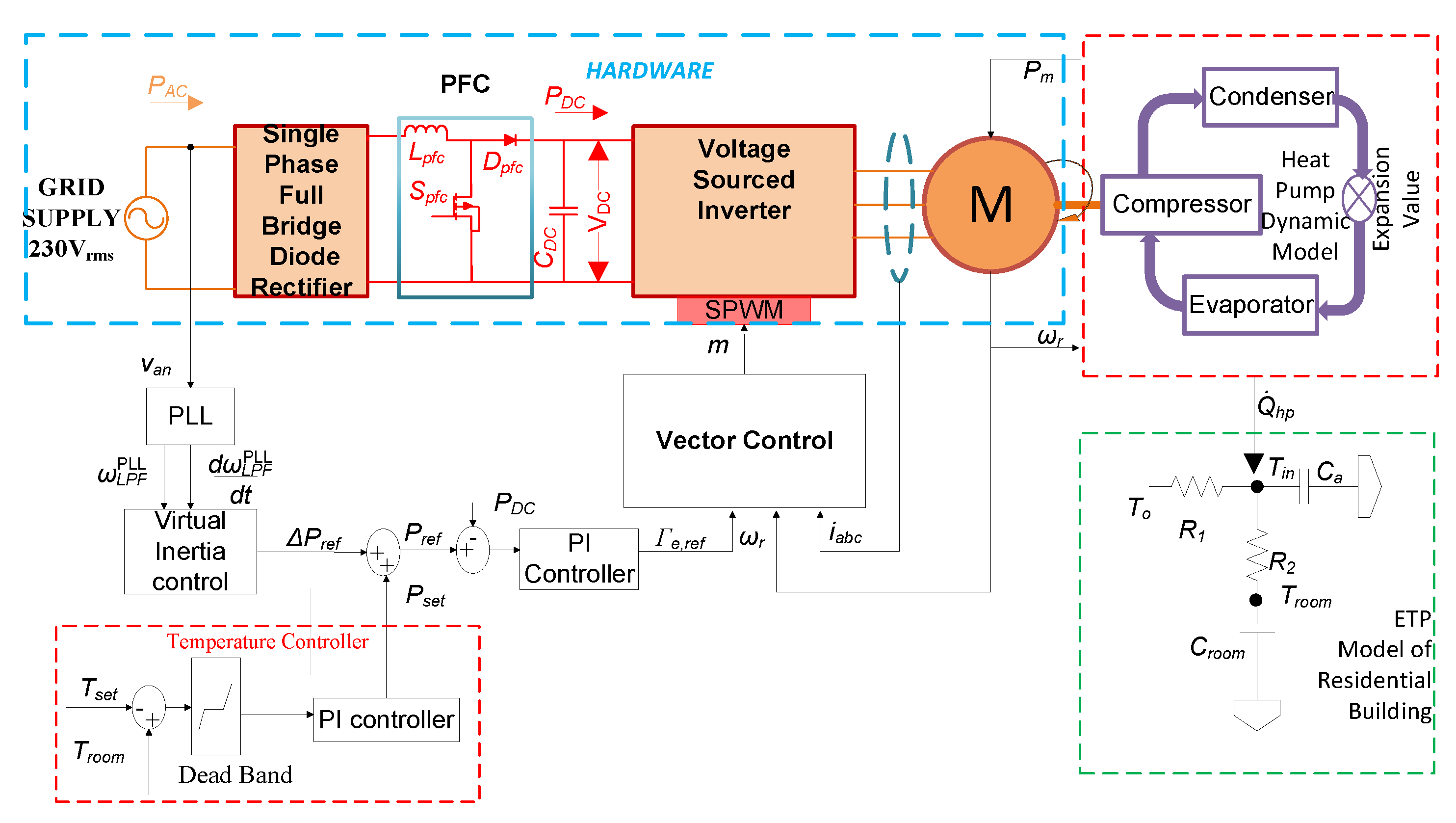
A simplified schematic of the air source heat pump, which is widely used in the residential sector to exchange heat from the outside air to the building, is shown in Figure 1. The figure shows the VSHP, its electrical drive, and its controls, including virtual inertia control and indoor air temperature control. The variable speed electrical drive consists of a single-phase full-bridge diode rectifier and active power factor correction (PFC) feeding a voltage source inverter driving an induction machine. The single-phase full-bridge rectifier with active boost converter based PFC is used to control the DC voltage to the inverter. The voltage source inverter acts as the variable speed drive for the induction machine and is used to control the power consumed by the machine. The heat pump itself contains an evaporator, a compressor, which is driven by the induction machine, a condenser, and an expansion valve. The evaporator exchanges the heat between the refrigerant and the outside air, then the refrigerant temperature and pressure are further raised using the compressor. The heat collected from the evaporator and the compressor is transferred to the ambient air using the condenser. Finally, the expansion valve reduces refrigerant pressure.
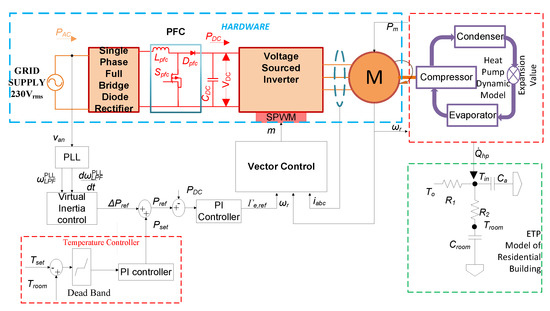
Figure 1.
A simplified schematic diagram of the VSHP model with VSMcontrol and indoor air temperature control. PFC, power factor correction; ETP, equivalent thermal parameter.
The heat pump heating cycle model is used to determine the operational characteristics in both steady-state and transient operation [8]. An equivalent thermal parameter (ETP) model of the building being heated is included to determine the power setpoints and indoor temperature variations. The power setpoint for the VSHP is usually provided by a temperature controller, which attempts to control the room temperature to the user input setpoint.
The frequency response control is achieved by an outer closed-loop power control of the induction machine, which drives the heat pump compressor. For this work, it is assumed that the induction machine has a 2 kW rated power and 230 V rated voltage. The induction machine has an inner vector controller such that the rotor flux is always maintained constant in the steady-state [24]. An enhanced phase-locked loop (EPLL) [25,26] is used to determine the frequency of the grid voltage. The temperature controller provides the power setpoint . The virtual inertia controller provides the modifying power to provide frequency response. The combination of temperature setpoint and modifying power from the virtual inertia control provides a reference to the outer power controller of the induction machine drive, which then determines a torque reference for the vector control of the induction machine. The vector control outputs the modulation index, and the inverter is controlled using the sinusoidal pulse width modulation (SPWM) technique.
The thermal model of a residential building, EPLL, and virtual inertia control are implemented as explained in the section below. The goal of the modelling is to determine the dynamics of the variation of the heat pump power consumption, which can be achieved in response to a system frequency and RoCoF change. In order to achieve this, the various parts of the system and their small-signal models are described in detail in the section below.
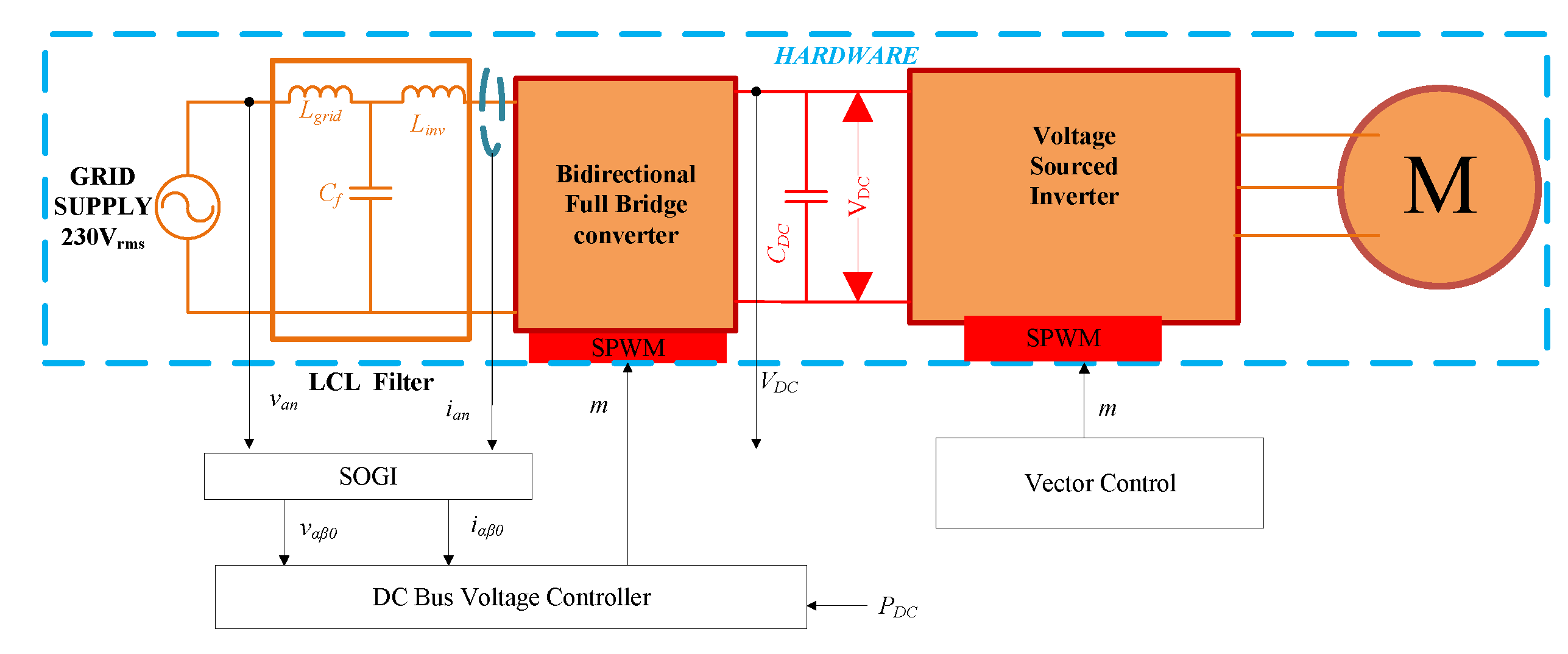
The electrical drive topology of the VSHP shown in Figure 1, although commonly used, does not allow for energy to be returned to the grid supply due to the use of the diode bridge rectifier. However, the stored kinetic energy from induction machine loads can be extracted and returned to the source by employing regenerative braking with the VSD [27]. Figure 2 presents a variation in design of the VSHP drive system, which replaces the diode bridge and power factor correction circuit with a bi-directional full-bridge converter and passive LCLfilter. This allows bidirectional power exchange with the grid so that kinetic energy stored in the induction machine can if required be returned to the grid. In this approach, the full bridge converter is controlled so as to maintain the DC link voltage constant. The indicated DC bus voltage controller regulates the DC bus voltage under variable load power , and the controller design is implemented as in [24]. The LCL filter is used to minimise the input current harmonics.
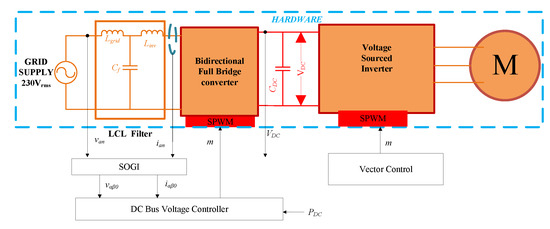
Figure 2.
A simplified schematic diagram of the modified VSHP model.
2.2. Thermal Model of a Residential Building
An equivalent thermal parameter (ETP) model of a residential building is used to provide the temperature feedback signal for the temperature controller. The ETP model of a residential building can be used to evaluate the thermal load capacities and the indoor air temperature variation due to the frequency responsive heating loads [28]. The evaluated thermal load capacities from the ETP model provides knowledge about how long the duration of the space heater power can be reduced to support frequency, without significantly changing the room temperature.
The ETP model is described by the following differential equations:
where is the heat flow into the building provided by the heat pump. are the building indoor air and mass heat capacity, respectively. are the thermal resistance between air to the ambient environment and air to the mass respectively. , and are the indoor air, building mass, and ambient temperature, respectively. Typically, the is very large, and the temperature variation is negligible, Hence, it is assumed that = and the equivalent heat capacity , and the equivalent model is reduced as shown in Equation (3).
Table 1 presents the parameters for a residential building used in the equivalent electric circuit of an equivalent thermal parameter model, as shown in Figure 1. The time constants , associated with the temperature controller, are much greater than the frequency response time constants, and hence, they do not interact, essentially meaning that reducing the space heater’s power for a few seconds has a negligible impact on the room temperature.

Table 1.
Building model parameters [5].
2.3. Dynamic Model of the Heat Pump
The dynamic model of the heat pump used follows the approach presented in [8], which developed a simplified dynamic model of a VSHP for real-time simulation studies. The characteristics of a VSHP (Equations (4) and (6)) in both steady-state and transient operation are extracted from the experimentally verified coupled nonlinear differential equation presented in [29,30], which relates the mass, momentum, and energy balances of all components in the refrigeration cycle [8]. From the data presented in [10], it is shown that the steady-state relationship between the compressor steady-state mechanical power and shaft speed , ambient temperatures , and indoor air temperatures can be very reasonably approximated as a linear one as described in Equation (4). Since in this work, the main purpose of this relationship is to determine the steady state operating point for different indoor and outdoor temperatures, it is not expected that minor deviations from the assumed linear relationship would have any significant impact on the dynamic response of interest. The four parameters , , , and were determined using a multiple polynomial regression algorithm applied to 94 different combinations of input variables and output data obtained from the work conducted in [31].
Perturbing (4) and eliminating the small-signal cross products, DC terms yield the small-signal variation in steady-state mechanical power, , for a small variation in , , and .
In terms of dynamics, the time constants associated with variations in temperature and are much larger than those associated with [8]. Hence, for the purposes of fast inertial response, these can be neglected.
The transient change in power, , resulting from a change in mechanical speed is of interested here. In [8], it was shown that this dynamic relationship could be accurately approximated by a second-order system as shown in Equation (6). The work in [8] showed that the dynamic response approximated by the second-order system was virtually indistinguishable from that obtained from the nonlinear differential equations. The four coefficients , , , and are estimated using the polynomial regression algorithm [8].
The mechanical power variation of the compressor with respect to speed variation and mechanical torque variation can be expressed as:
where and are the initial operating torque and speed of the compressor, respectively. Substituting Equation (7) in Equation (6) yields the small-signal transfer function of the compressor.
2.4. Enhanced Phase-Locked Loop
A vital component of this control architecture is the PLL, which is required to calculate the angle and frequency of the grid voltage waveform with reasonable accuracy. The method for the calculation of the rate of change of frequency (RoCoF) is based on the derivative of the frequency measurement from the PLL. When measuring the RoCoF, noise is a critical issue. This noise comes from the grid voltage and also from the harmonics of the grid voltage, which can give rise to large fluctuations in measured RoCoF unless appropriate filtering is used. There is thus a trade-off between the accuracy and time response in the measurement of RoCoF. In general, increasing accuracy requires filtering, which also increases the time response.
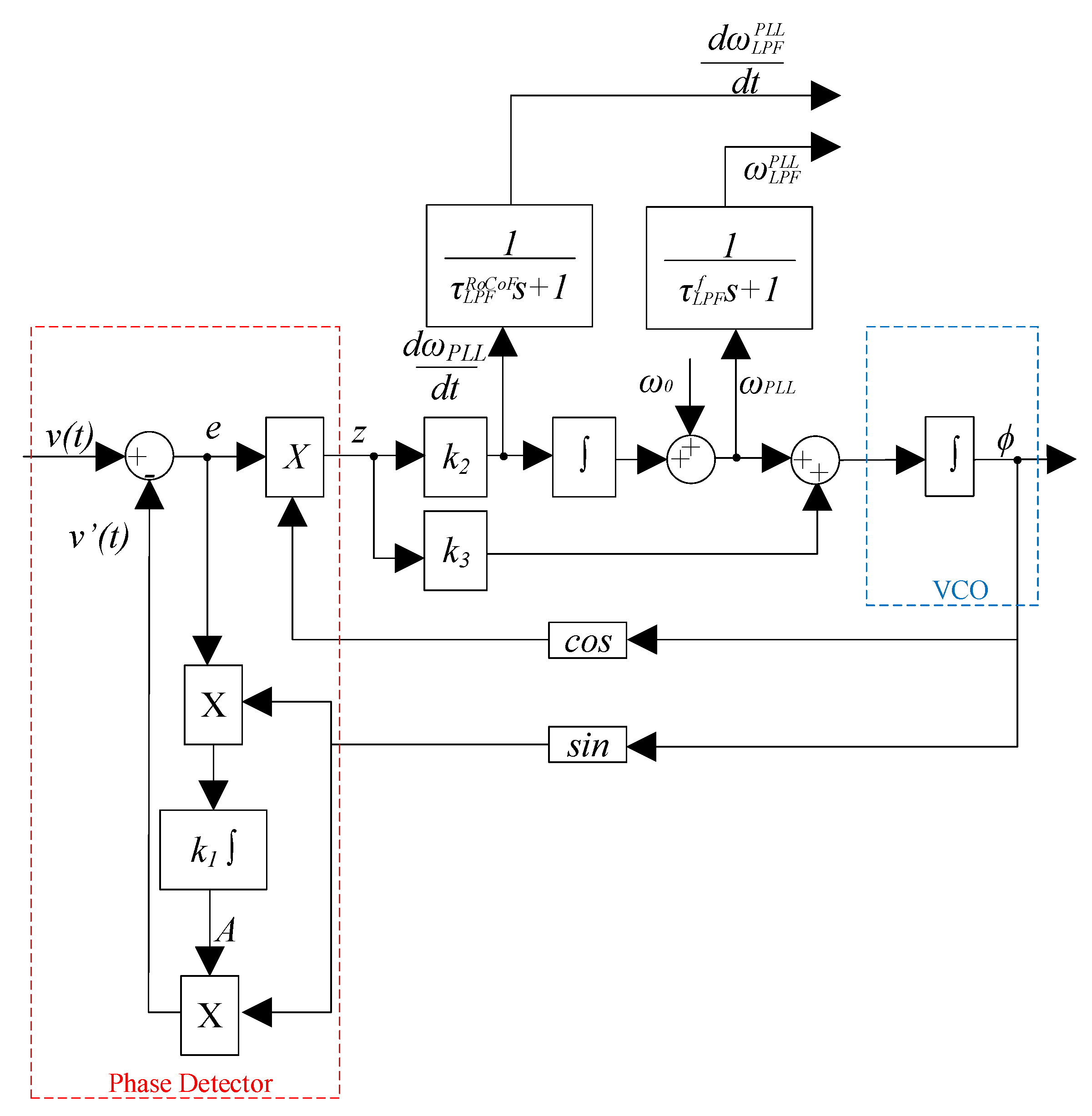
Here, the enhanced phase-locked loop (EPLL) introduced in [25] is used, which has been shown to be more suitable for single-phase measurement in frequency varying and harmonics conditions. An adaptive notch filter is used in the EPLL to eliminate the double frequency errors and to estimate the voltage amplitude [26]. Low pass filters with time constants and are used in the EPLL measuring frequency and RoCOF, respectively. The schematic representation of the EPLL is shown in Figure 3.
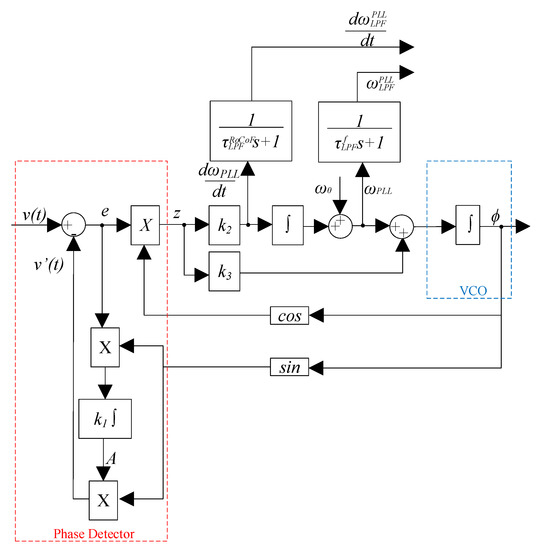
Figure 3.
Single-phase enhanced phase-locked loop (EPLL) system with a direct estimation of amplitude, phase, frequency, and the rate of change of frequency (RoCoF).
Small-Signal Model of EPLL
The EPLL differential equations and output of the EPLL phase detector were presented in [26], which are used to derive the small-signal model of EPLL.
The actual phase angle to actual frequency in the Laplace domain representation is:
Substituting Equation (13) in Equation (12) yields the closed loop transfer function of the EPLL without the added filter:
The outputs from the EPLL are further low pass filtered, before being used to calculate the power reference to remove the disturbances caused by the harmonics. The low pass filter associated with the EPLL measurement for frequency and RoCoF are taken as first-order filters with transfer functions given as:
where and are the time constant of the low pass filters used in the EPLL measuring frequency and RoCoF, respectively. The overall small-signal transfer functions of the EPLL including the low pass filter are given as:
The EPLL control parameter represents the time constant of the adaptive notch filter, whereas , represent the natural frequency and damping ratio of the EPLL, respectively. Higher values for the EPLL parameter () provide a faster response, but higher noise while measuring RoCoF. Lower gain values measure RoCoF without noise, but give a slower response. Hence, there is a trade-off between response time and noise attenuation while selecting the parameters. An appropriate set of EPLL parameters is selected using a trial and error approach in order to obtain a critically damped response, and the parameters obtained are as follows: , , and . The low pass filter time constants and are selected as 0.05 s and 0.1 s, respectively.
2.5. Virtual Inertia Control
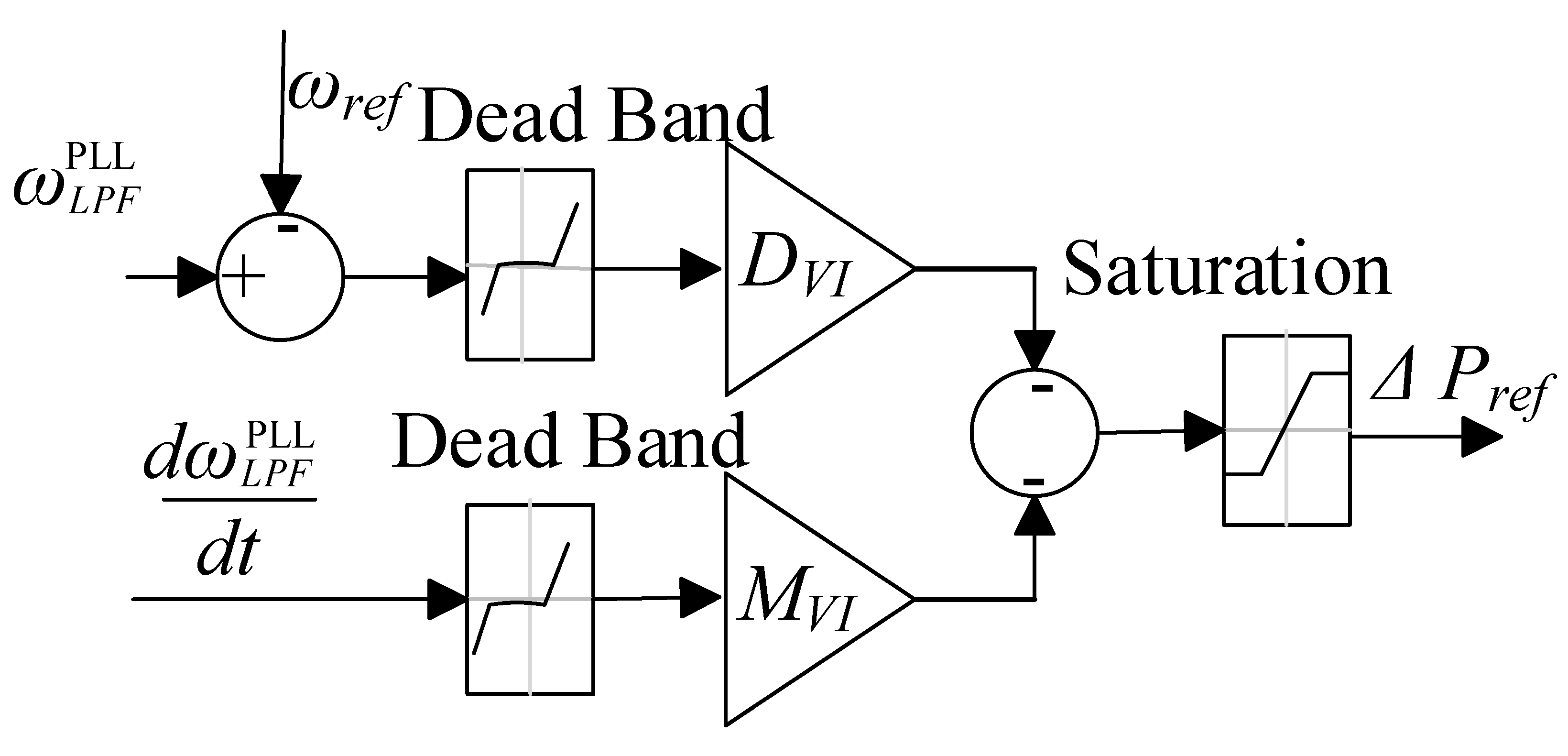
The virtual inertia control is a strategy that emulates the dynamics of the synchronous machine, including inertia emulation, and damping power, when used to control converter interfacing distributed generation or energy storage [14]. Here, the control is only used to provide the frequency response by emulating the inertial response and the damping power of a synchronous machine. The power control block is shown in Figure 4. The controller modulates the power reference with a component that is proportional to frequency deviation (droop) and a component that is proportional to RoCoF (inertial). The output power reference of the controller is given by Equation (19) [32].
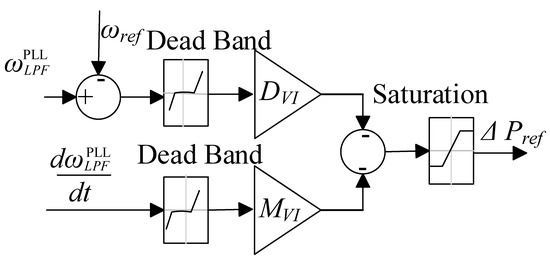
Figure 4.
Block diagram of the power control of the virtual inertia control.
Here, and represent the virtual inertia and droop factor of the virtual inertia control, respectively, is a measurement of the angular frequency of the grid, and is the reference grid frequency. Note that the parameter provides damping to the response during transients and also provides a steady-state response proportional to a frequency deviation. The saturation block limits the reference power to the rated power and maximum export power to the grid. Both components incorporate a dead-band, and if the frequency deviation and RoCoF are within this band, then no component is generated. The control receives its frequency and RoCoF measurement from the phase-locked loop (PLL) and then outputs the , which modifies the power setpoint from the temperature controller.
2.6. Induction Machine Power Control
The induction machine is operated with an outer power controller and an inner torque vector control. The outer power controller receives its reference from the temperature controller and the frequency response controller. It utilises a PI control to output a reference torque for the inner torque controller. Here, we assume that the power reference change results only from the frequency controller as described by Equation (19). The inner torque control uses a standard vector control technique, the details of which can be found in [24]. Since the main goal of this section is to determine the small-signal response for power consumption, the torque control is only very briefly reviewed. The PI power controller outputs the machine electrical torque reference according to the following relation:
where are the power controller proportional and integrator gain, power reference, and measured power in the DC bus, respectively. Making use of a rotating reference frame synchronised with the rotor field, the q-axis component of stator current reference can be taken to be linearly related to the machine electrical torque reference:
where , and are the rotor leakage factor, rotor inductance, magnetising inductance, and the magnetising current, and assuming that , the machine magnetising current is held constant. Thus, torque can be controlled using the q-axis component of stator current. With a properly designed current controller, the q-axis stator current can be made to follow its reference with a first-order lag, so that:
where is the time constant of the current controller. The electrical torque is linearly related to the q-axis component of stator current as:
The speed variation of the induction machine in response to a change in electrical torque and mechanical torque is given as:
where J and B are the inertia and friction coefficient of the induction machine, respectively. Rearranging Equation (30) yields:
Similarly, combining Equations (21)–(23), perturbing, and eliminating the small-signal cross products and DC terms yield:
Neglecting the losses in the AC/DC converter (single phase rectifier with the boost PFC), the power consumed by the induction machine is:
where and are the -axis stator voltages and and are the -axis stator currents. Assuming the power loss is negligible or constant and a system aligned with the rotor field, i.e., with set to zero, then the power consumed by the induction machine can be expressed as:
The q-axis stator voltage variation is given as [8]:
where = and = . In order to measure the DC power for feedback, a low pass filter is used to remove the disturbances while measuring the DC bus power. The measured power with the filter dynamics is given as:
where is the time constant of the low pass filter used in measuring power. Substituting Equations (32), (33), and (38) into Equation (37) yields the complete closed loop transfer function from commanded change in reference power to actual change.
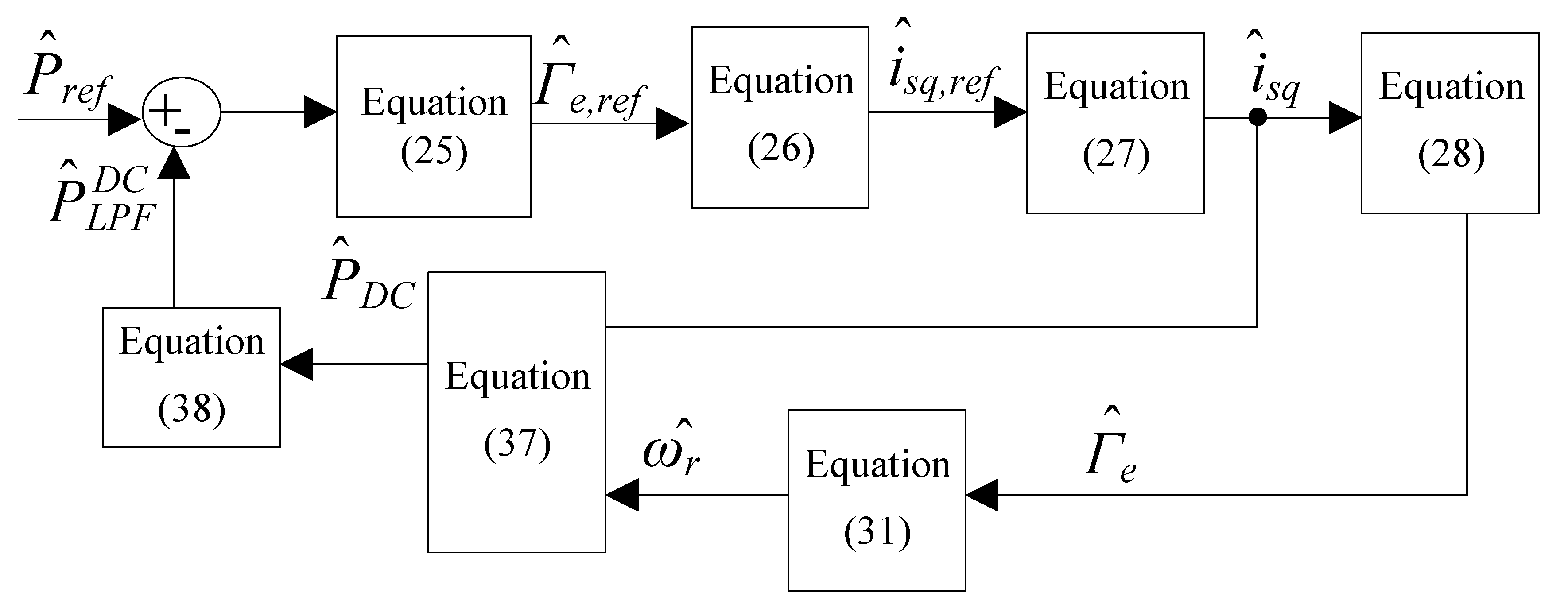
where , , and . is the compressor transfer function presented in Equation (8). Figure 5 now shows the complete small-signal frequency domain model of the induction machine power control with the main equations used summarised in Table 2.
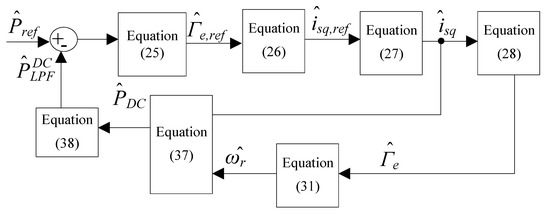
Figure 5.
Block diagram for the small-signal frequency domain analysis of the VSHP.

Table 2.
Summary of the equations.
2.7. Overall Small-Signal Model
2.8. Induction Motor Power Controller Design
Table 3 summarises the initial operating point and parameter values used for controller design studies. From Equation (37), the input power variation of the VSD controlled VSHP () has a dependence on the dynamics of the stator current and the motor speed . With the correct design of the current controller, can be made to change rapidly. The change in is limited by the compressor characteristics (inertia, friction, etc.). The term dominates the initial change so that the initial input power variation is similar for different compressor characteristics.

Table 3.
Initial operating point and parameter values used for controller design studies.
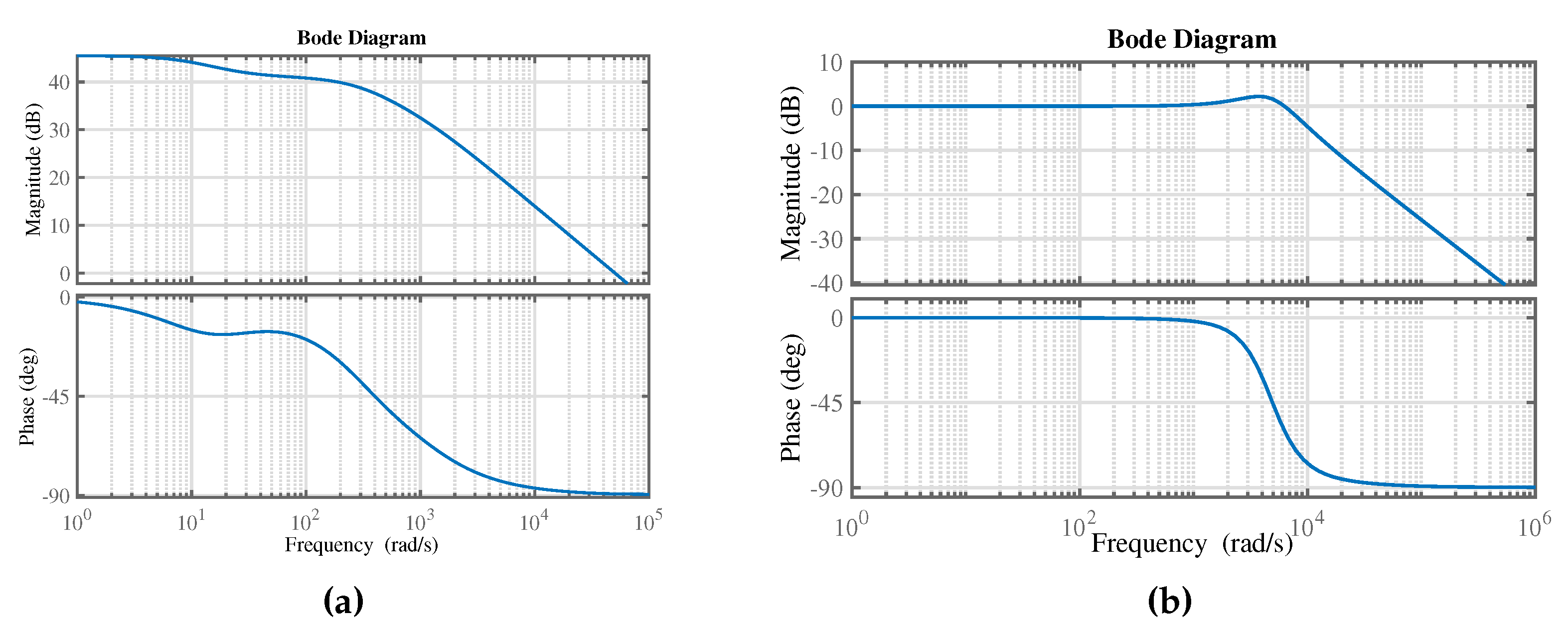
Figure 6a presents the Bode plot for the open loop transfer function from the change in to the resulting change in measured DC link power for the operating conditions in Table 3. It is inferred from Figure 6a that the input power of the VSD controlled VSHP can be actively controlled to follow the power reference with large PI controller gains. The cross-over frequency of the controlled system is chosen to be one decade less than the switching frequency (i.e., 1000 Hz) and a phase margin of 60°, which yields and equal to 0.103 and 455.67, respectively.
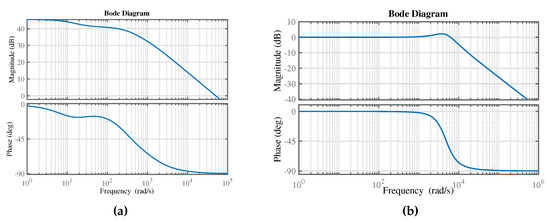
Figure 6.
Bode plot: (a) open loop transfer function from the change in to the resulting change in measured DC link power ; (b) closed loop transfer function from a change in to the resulting change in DC power .
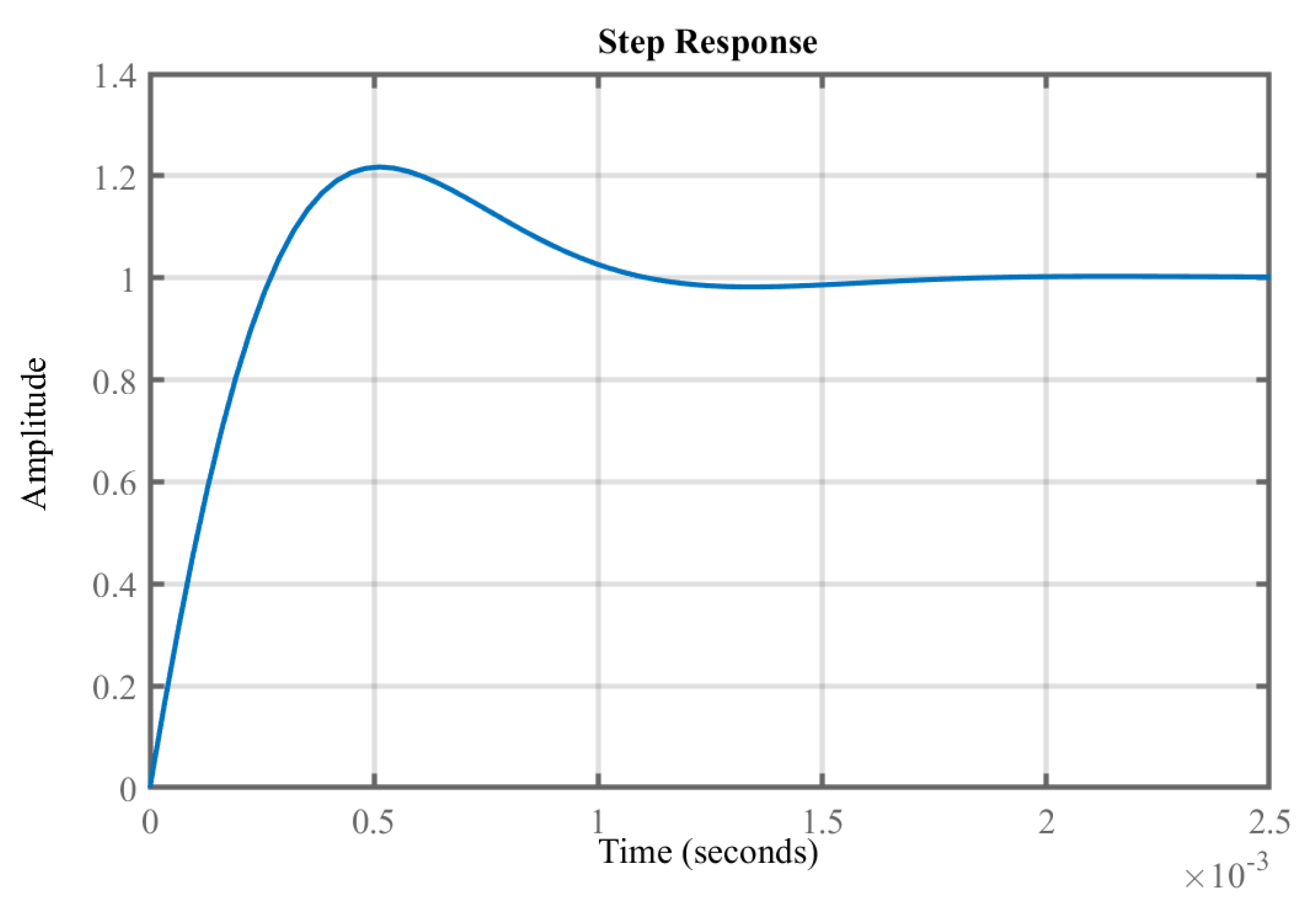
Figure 6b shows the resulting closed loop transfer function from a change in to the resulting change in DC power . It can be inferred that the closed loop system is stable. Figure 7 shows the step response of VSHP power consumption to 1 W variation in , which responds in 0.5 ms.
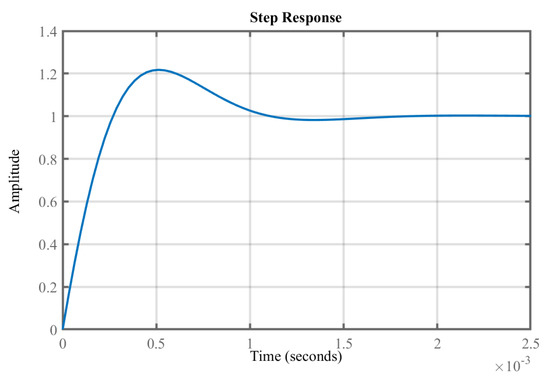
Figure 7.
Step response of VSHP power consumption to 1 W variation in .
2.9. Virtual Inertia Control Parameter Selection
In order to choose the virtual inertia controller parameters, and , some estimate of the quantity of response available is required. The quantity of demand response available from the VSHP obviously depends on its operating conditions. The speed setpoint for different ambient temperatures is determined from the thermal model of a residential building described in Section 2.2. Manufacturers recommend that the heat pump should not be turned off/on frequently and should operate at a minimum speed of (i.e., 1/3 of the rated speed). Hence, a constraint is introduced such that VSHP speed is always greater than or equal to its minimum speed. For this analysis, the VSHP minimum speed is set as 1/3 of its rated speed. The available demand response is constrained by speed variation , where is an operating speed for a particular ambient temperature, is the minimum speed of the VSHP, and is the maximum available speed variation. The maximum available demand response or the maximum power variation to maximum speed variation is determined using Equation (6).
The maximum released kinetic energy due to heat pump speed variation can be estimated as:
The estimated inertia for heat pump with rated power 0.9 kW and nominal speed 1500 rpm is J = 0.0127 kgm using the formula presented in [33]. Table 4 shows the calculated maximum available speed variation, demand response, and released kinetic energy for different ambient temperatures. These parameters can be used as a basis for setting the values of inertia and droop based on the worst case frequency variation scenario as described in the next section.

Table 4.
Determined power setpoint for different outdoor temperature.
Selection Based on the Worst Case Scenario
A constraint for the selection of the control parameter based on the worst case scenario is introduced such that the controller provides its entire available power plus the stored kinetic energy as estimated in the previous section, for the worst case scenario. The worst case scenario considered is a system with maximum RoCoF of 1 Hz/s and maximum frequency deviation of 1 Hz with all of the available kinetic energy released over 1 s. Substituting these constraints in Equations (19) yields:
A fixed droop of 4% is used, i.e., for a 4% change in frequency; the power change is 100%, which yields:
Based on these assumptions, Table 5 presents the selected control parameters for different outdoor temperatures.

Table 5.
The determined virtual inertia control parameters for different outdoor temperatures.
3. Hardware Validation and Single Device Characterisation
Hardware validation and device characterisation were performed using a VSHP emulator consisting of a 2 kW wound rotor induction machine mechanically coupled to a dynamometer with variable torque generator, which supplied the heat pump compressor load torque. The power conversion system consisted of three LabVolt IGBT Chopper/Inverter 8857-1 modules with the control implemented using the hardware in the loop system OP5600 from OPAL-RT.
3.1. Single Device Characteristics
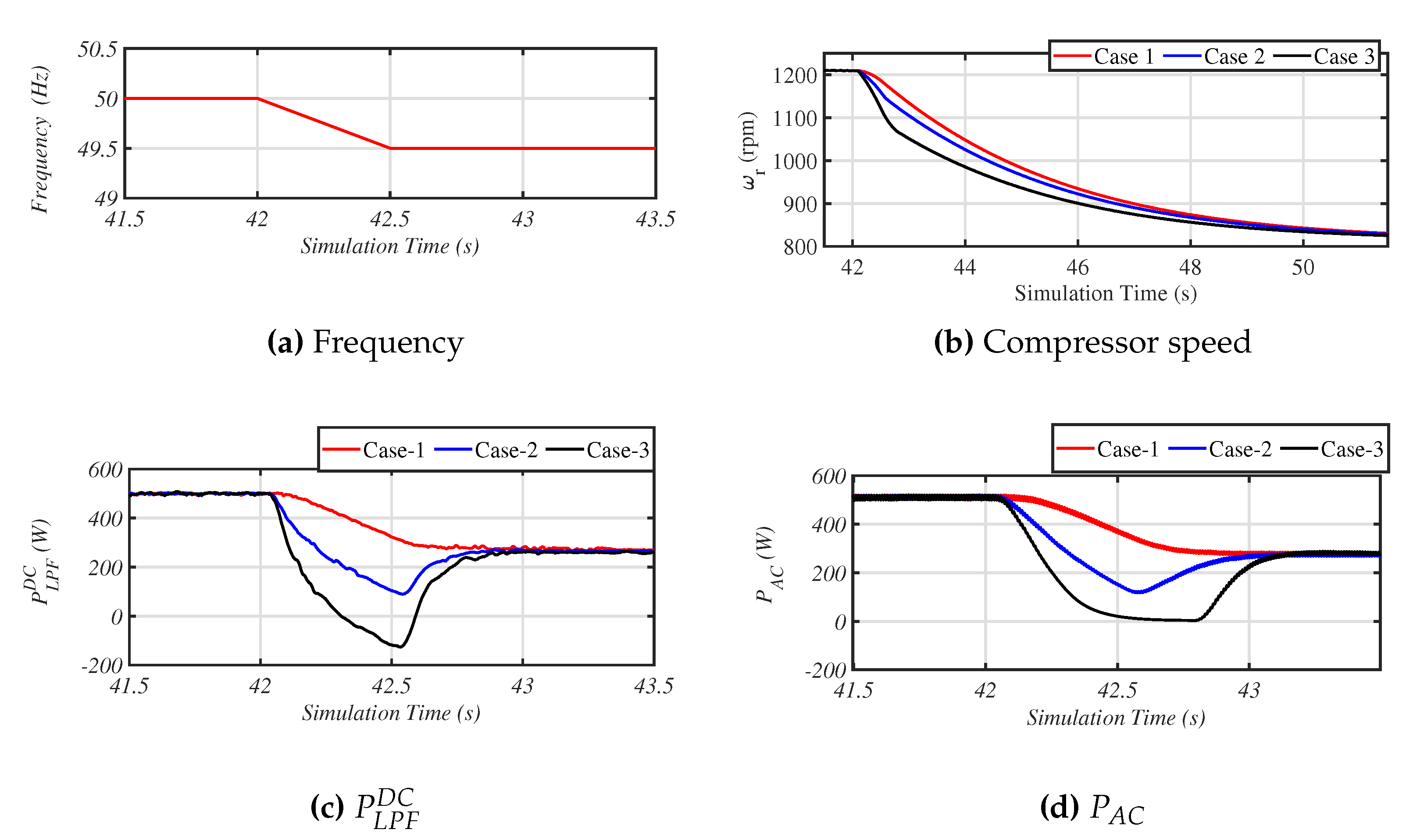
To determine the characteristics of the virtual inertia controlled VSHP, power hardware in the loop (PHIL) simulation was performed with the parameters summarised in Table 3 and for three different sets of virtual inertia control parameters (Case 1: = 0 Ws, = 500 Ws; Case 2 = 150 Ws, = 500 Ws; and Case 3 = 350 Ws, = 500 Ws). Initially, a supply voltage of 230 V and frequency of 50 Hz were supplied to the system. At time t = 42 s, a ramp change in frequency −1 Hz/s was introduced until the frequency reached 49.5 Hz. These initial tests were done with the uni-directional electrical drive containing the diode rectifier as shown in Figure 1.
Figure 8 shows the variation in the power demand and compressor speed of the VSHP’s system for a change in grid frequency. Figure 8b shows that the variation in compressor speed was smooth. The effect of the increased virtual inertia setting can be clearly observed from Figure 8c,d. In Case 1, the virtual inertia controller setting was set as a simple droop; hence, the change in power contained only a droop response that was proportional to the frequency deviation. In Case 2 and Case 3, the virtual inertia controller responded to the RoCoF of −1 Hz/s from simulation time t = 42 s to t = 42.5 s; hence, the change in power was larger compared to Case 1. After simulation time t = 42.5 s, the RoCoF was 0 Hz/s; hence, the virtual inertial response was zero, and contained only a droop response.
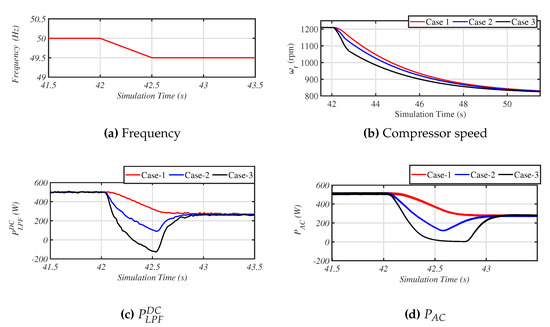
Figure 8.
VSHP measured test result.
In Figure 8c, for a high virtual inertia setting, i.e., for Case 3, it can be observed that the DC bus power was negative, indicating that the induction machine regenerated back to the supply in this situation. However, the power transferred from the grid to the DC bus was zero, as shown in Figure 8d, since the diode rectifier blocked the negative power being supplied to the grid. A simple replacement of the diode rectifier by the proposed bi-directional full-bridge converter as shown in Figure 2 would allow this extra inertial response to be transferred to the grid. Hence, for more effective virtual inertia support, we proposed this modification to replace the diode rectifier and PFC with a bidirectional full-bridge converter.
3.2. Modified VSHP System
Again, this system was set up in hardware as described previously, and the frequency of the VSHP’s supply voltage was varied at 42 s and for six different sets of virtual inertia control parameters:
- Case 4: = 300 Ws = 1000 Ws.
- Case 5: = 100 Ws = 1000 Ws.
- Case 6: = 0 Ws = 1000 Ws.
- Case 7: = 100 Ws = 250 Ws.
- Case 8: = 0 Ws = 250 Ws.
- Case 9: = 300 Ws = 250 Ws.
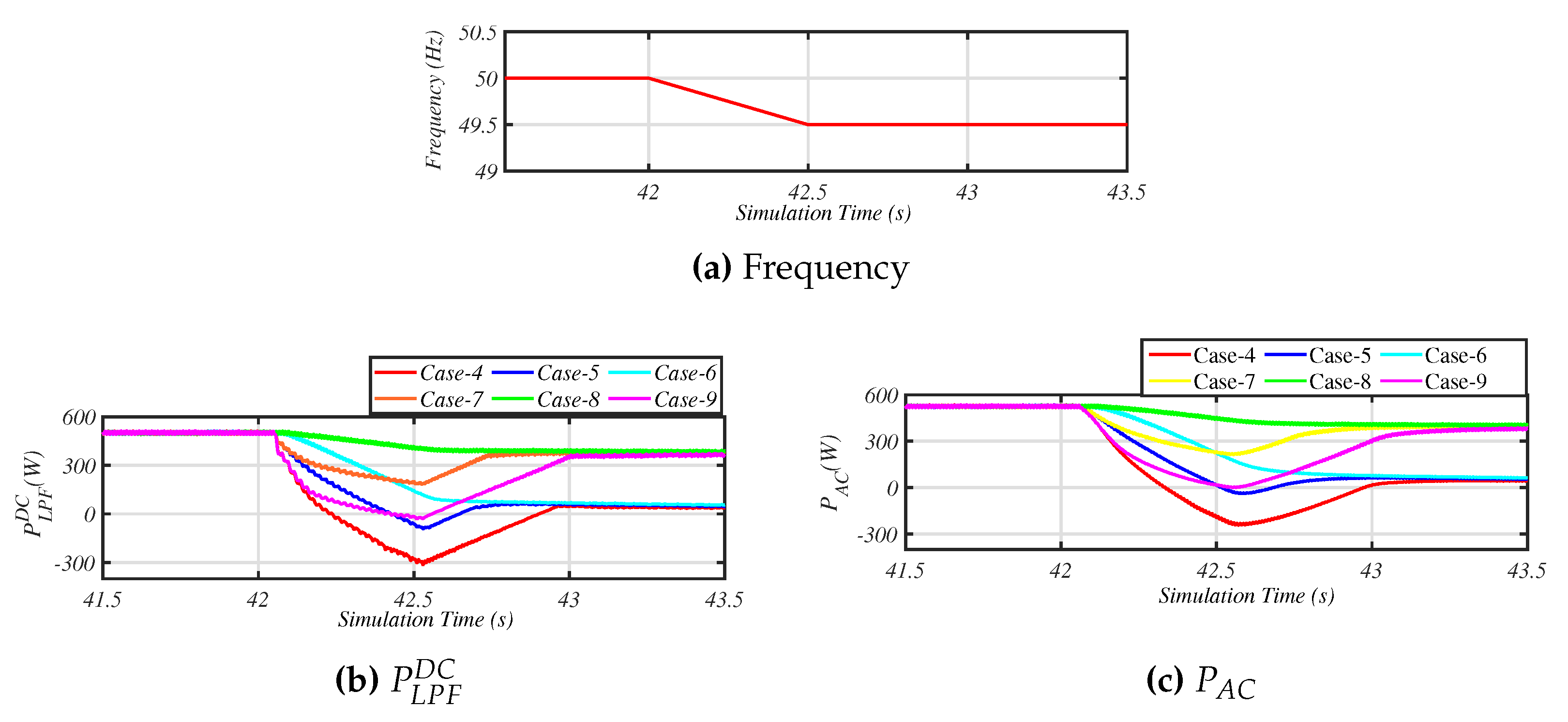
Figure 9 shows the variation in power demand of the VSHP’s system for different cases. Figure 9b,c shows that the modified VSHP system had the capability to reduce demand quickly, and in this case, for large virtual inertia settings, the system could transfer the negative power to the grid.
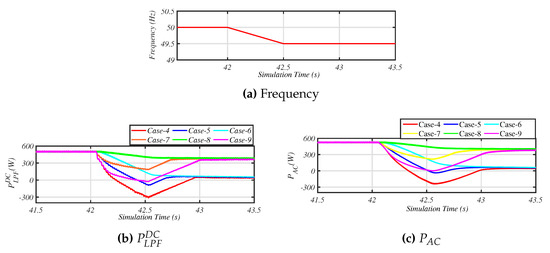
Figure 9.
Modified VSHP measured test result.
3.3. Validation of VSHP Small-Signal Model
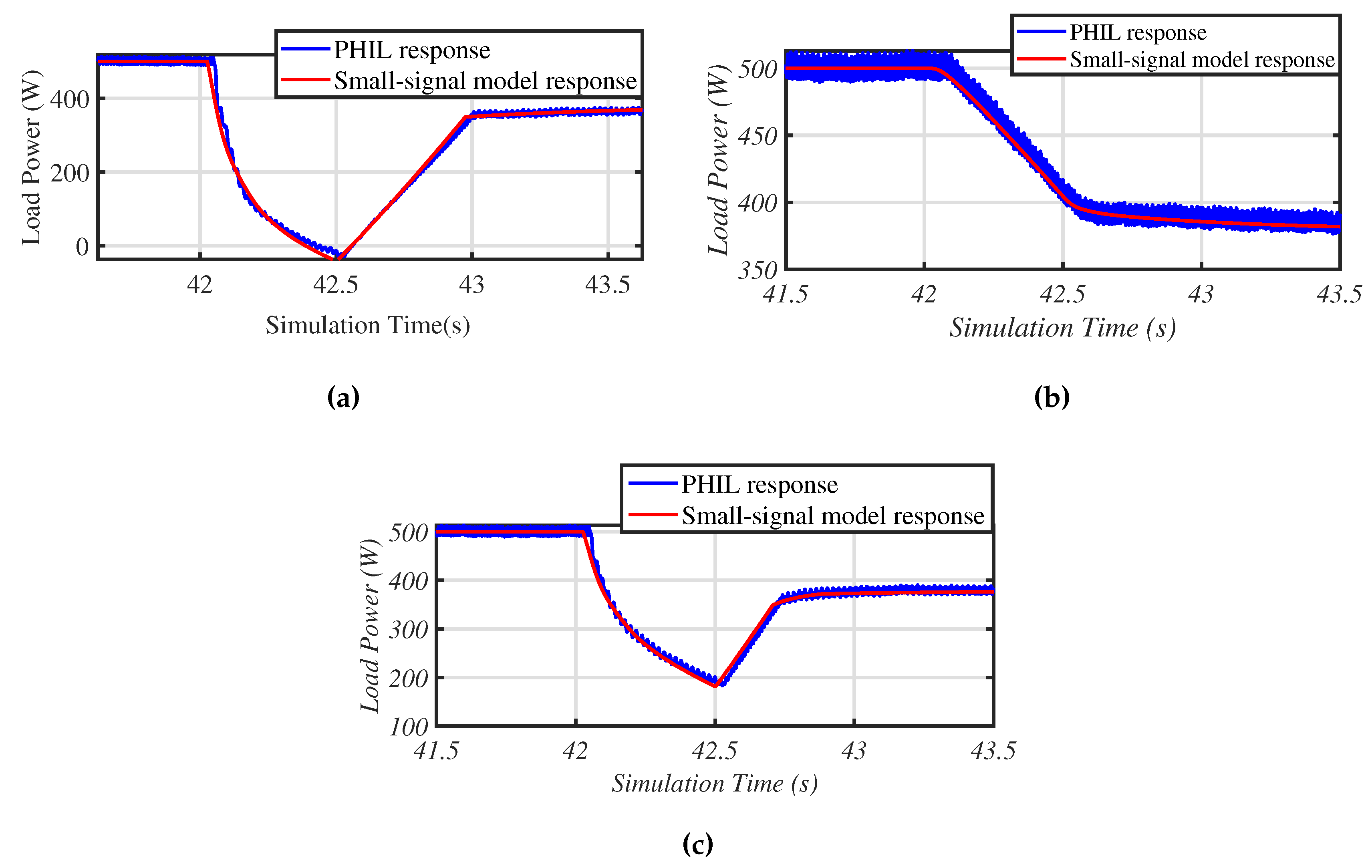
The small-signal model of the VSHP system was later used for determining the aggregated response of a large population of VSHP systems in Section 4. In order to validate the small signal model of the VSHP system as expressed by Equation (40), the predicted output from the model in terms of power variation in response to a change in frequency was compared to measured results from the hardware system. The system was set up in hardware as described previously, and the frequency of the VSHP’s supply voltage was varied at 42 s for four different sets of virtual inertia control parameters (Case 10: = 1000 Ws = 250 Ws, Case 11: = 0 Ws = 250 Ws, and Case 12: = 250 Ws = 250 Ws). Figure 10 shows the comparison between the response of the small signal model and hardware setup to a ramp change in frequency for the different cases. It can be seen from these results that the small signal model was a good representation of the hardware result, thus giving confidence that it could be used further in modelling studies.
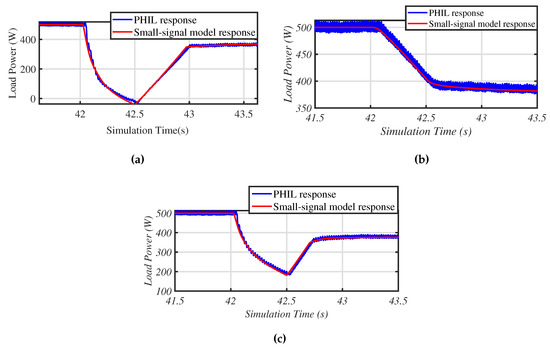
Figure 10.
Comparison of the small-signal model with the hardware setup. (a) Case 10. (b) Case 11. (c) Case 12. PHIL, power hardware in the loop.
4. Case Study: Aggregated Response from a Population of Heat Pumps
In order to understand the aggregate response and quantify the maximum attainable virtual inertia from a large population of VSHP embedded in the distribution grid, electromagnetic transient (EMT) simulations were performed on the real-time simulation platform [34]. For the simulations, each VSHP was represented by the validated transfer function in Equation (40) using the virtual inertia control settings derived using the worst case settings described earlier.
4.1. Simulation Results in the Test Distribution System
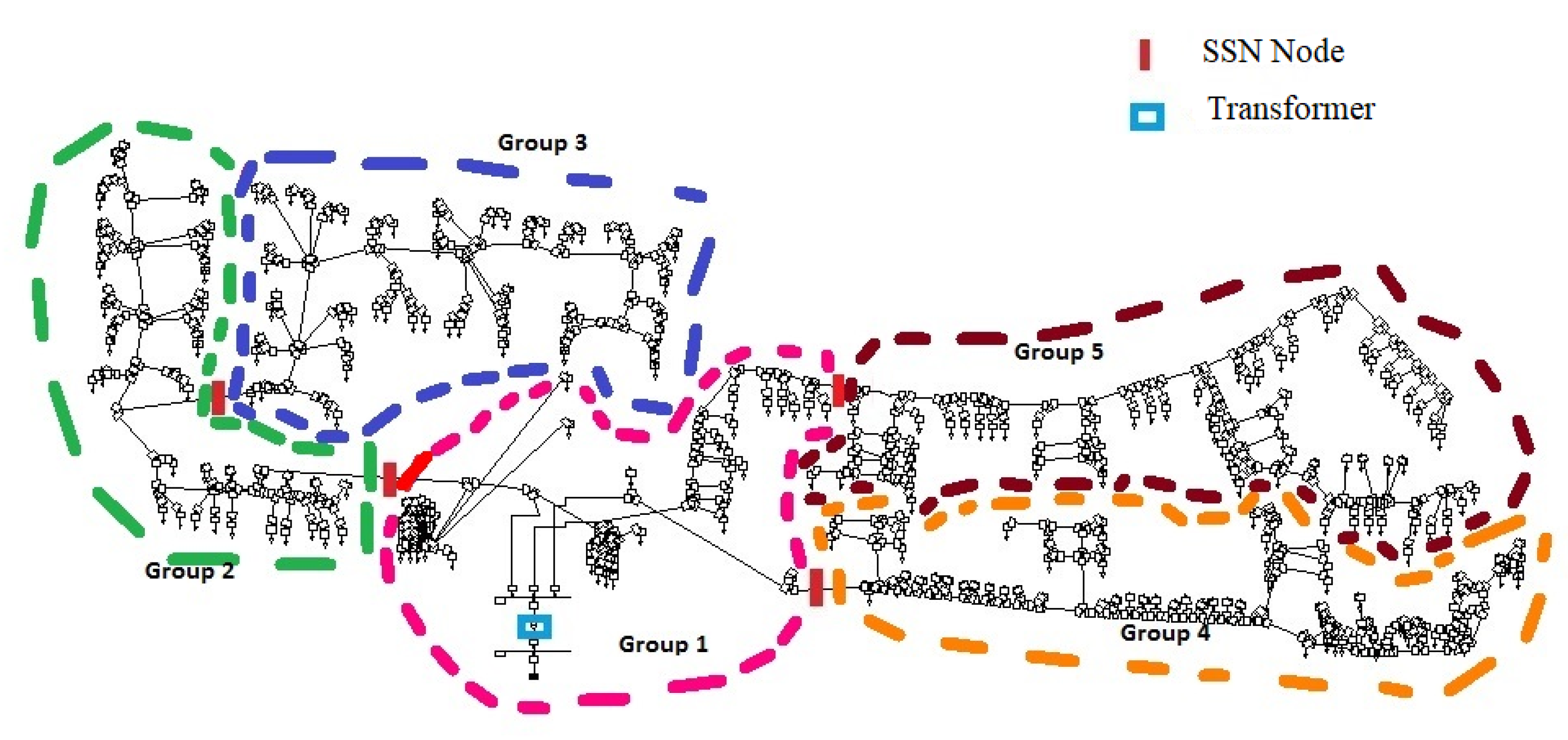
The distribution grid model used for real-time simulation was based on an urban LV distribution grid in the U.K. [35], a diagram of which is shown in Figure 11. The network contained three feeders with 330 houses, 6350 nodes, three phase, and four wire configuration distribution cables. The system frequency of the network was 50 Hz, and the voltage was fed to the network through an MV (13.8 kV) to an LV (400 V) delta-star transformer, as shown in Figure 11. The challenges and methodology used in modelling this network in the real-time platform were further described in [34]. The network was divided into five groups for parallel processing using the real-time simulator, and the colours illustrate how the network was split into the five groups.
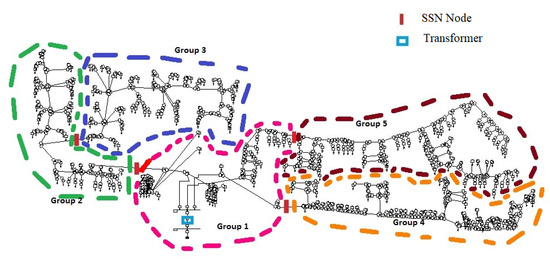
Figure 11.
ENWLdistribution network in Manchester.
The loads in the distribution system were modelled as per the recommendations by the IEEE Task Force on Load Representation for Dynamic Performance [36]. The load model consisted of ZIPterms plus two voltage-/frequency-dependent terms as shown in the following equations:
where and are the nominal active, reactive load powers, and load voltage, respectively. Table 6 provides the load data description and the values used for the load modelling.

Table 6.
Load data description and values.
In order to observe the effect of the virtual inertia controlled VSHPs, the distribution system was supplied by a synchronous generator with a steam turbine governor model, and a transient increase in load was implemented to perturb the frequency. The parameters of the synchronous generator model and load damping are presented in Table 7. Simulations were performed for a different number of houses with the droop and virtual inertia controller installations and different outdoor temperatures.

Table 7.
Parameters for the synchronous generator model and load damping.
is the nominal power of the synchronous machine. is the power base for per unit calculations. is the power consumed by the distribution network. D is the damping provided by the distribution network. M is the inertia of the synchronous machine. is the time constant of the synchronous machine turbine. is the time constant of the synchronous machine governor.
4.1.1. Droop vs. Virtual Inertia Controller
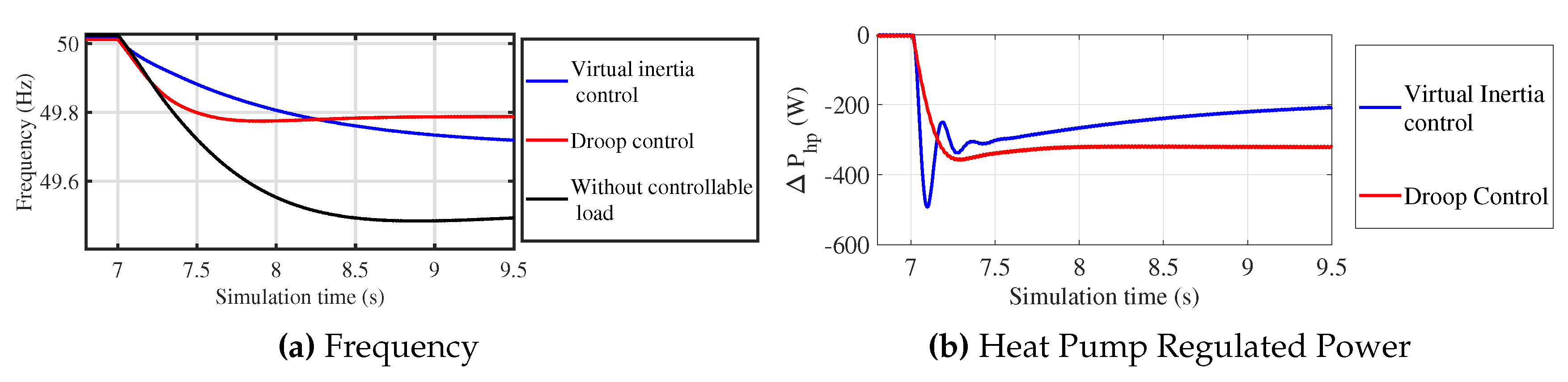
The time-domain simulations were performed on the distribution test grid with 300 installations of VSHP with the droop and virtual inertia controllers providing frequency response for an operating point at °C. At 7 s, a bulk three-phase load of 112.500 kW was connected to the network to produce a frequency perturbation. Figure 12a shows the frequency variation of the network for the 300 houses with the droop and virtual inertia controller installations. Note here that for “droop control”, the entire available power was provided as a droop response ( = 0 Ws = 1022 Ws), whereas for “virtual inertia control”, it was split between inertial and droop response. Clearly, the frequency control of the VSHP loads provided an improved frequency response compared to the case where no frequency control was implemented. Figure 12b shows the response from an individual heat pump with the droop and virtual inertia controller installation. It can be seen that the droop controller provided a better reduction in frequency nadir, whereas the virtual inertia controller provided a better reduction in RoCoF. There is potential scope to optimise the relative contribution of droop and inertial responses, depending on system requirements at any time. Dynamic tuning of the virtual inertia control parameter could be implemented to update settings so as to obtain a better trade-off between reduction in RoCoF and frequency nadir.
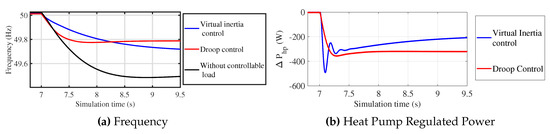
Figure 12.
Response of the distribution system for droop or virtual inertia controlled VSHP.
4.1.2. Increased Virtual Inertia Controller Installations
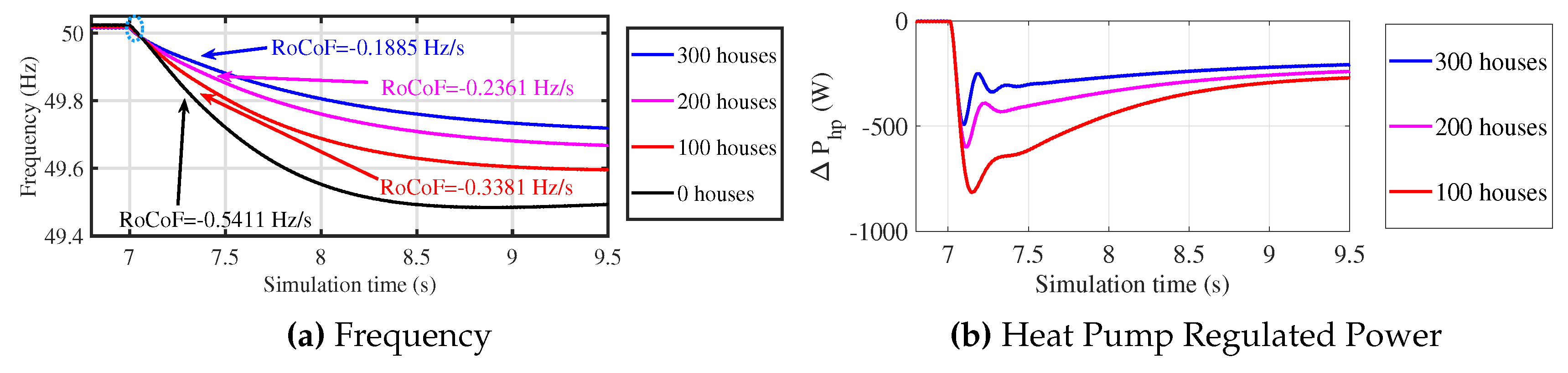
The time domain simulations were performed on the distribution test grid with different numbers of houses with virtual inertia controlled VSHP providing frequency response for an operating point at °C. At 7 s, a bulk three-phase load of 112.500 kW was connected to the network to produce a frequency perturbation. Figure 13 shows the frequency variation of the network for the different number of houses with the virtual inertia controlled VSHP. The RoCoF was calculated 0.300 s after the disturbance occurs, over a 1 ms time window, and the equivalent aggregated distribution system inertia in pu was calculated from Equation (49) [37].
where is the variation in power and is the RoCoF measured 0.300 s after the disturbance. The calculated total system inertia for the system without virtual inertia controller installations and with 100, 200, and 300 virtual inertia controller installations was 5.200 s, 8.320 s, 11.910 s, and 14.920 s, respectively. Hence, the added virtual inertia from 100, 200, and 300 virtual inertia controller installations was 3.120 s, 6.710 s, and 9.720 s, respectively.
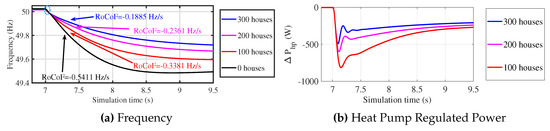
Figure 13.
Response of the distribution system for different virtual inertia controller installations.
Figure 13b shows the response from an individual heat pump for different virtual inertia controller installation. It can be seen that increasing the number of installations reduced the response from individual heat pumps, as they saw less frequency deviation and RoCoF.
4.1.3. Different Outdoor Temperatures
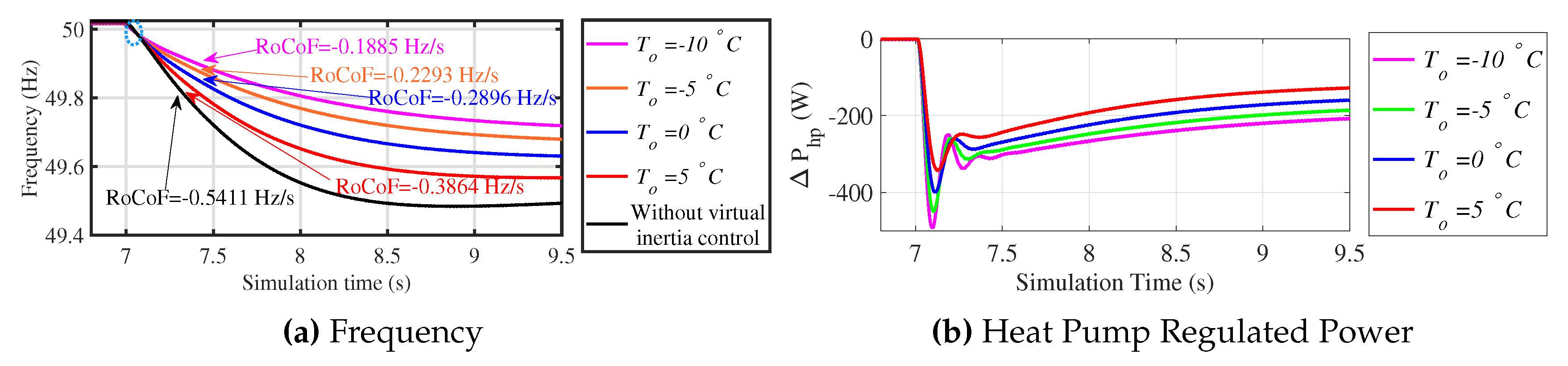
As indicted previously, the available response was dependent on outdoor temperature, and to investigate this, the time domain simulations were performed on the distribution test grid with 300 houses with virtual inertia controlled VSHP providing the frequency response for different operating points at = 5 °C, 0 °C, −5 °C, and −10 °C. At 7 s, a bulk three-phase load of 1112.500 kW was connected to the network to produce a frequency perturbation. Figure 14 shows the frequency variation of the network for different outdoor temperatures.
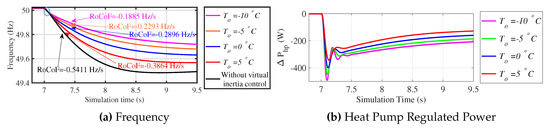
Figure 14.
Response of the distribution system for different outdoor temperatures.
The calculated system inertia for the system without virtual inertia controller installations and with 300 virtual inertia controller installations at operating point = 5 °C, 0 °C, − 5 °C, and −10 °C was 5.2 s, 7.280 s, 9.710 s, 12.260 s, and 14.920 s, respectively. Hence, the added virtual inertia from 300 virtual inertia controller installations at operating point = 5 °C, 0 °C, −5 °C, and −10 °C was 2.080 s, 4.510 s, 7.060 s, and 9.720 s, respectively.
Figure 14b shows the response from an individual heat pump for different outdoor temperatures. It can be seen that as for lower temperatures, the response from individual heat pumps was higher since the virtual inertia controller setting was set at a higher value and vice versa.
Clearly, the ability of VSHPs to deliver frequency support is not constant, but dependant on consumer behaviour in how they use their heat pumps and is also dependant on temperature. This makes the frequency support resource variable, but given a large population of such VSHPs, the available resource at any given time and for any conditions will be reasonably predictable. The availability and use of the resource would therefore need to be planned and coordinated with other sources of flexibility as part of a wider system operation strategy.
5. Conclusions
The paper presented the dynamic model of a variable speed heat pump providing frequency response with virtual inertia control. The hardware in the loop simulation studies showed that the heat pump could quickly change its power consumption and also provide power during regenerative braking. The paper presented a modification in variable speed heat pump design to provide power from the heat pump to the grid during regenerative braking; hence providing maximum frequency response during the inertial response time frame. A small signal model was developed and validated with hardware in the loop simulation results. The simulation studies performed on a test distribution grid verified that the virtual inertia controlled variable speed heat pump reduced the frequency nadir and RoCoF and provided significant virtual inertia to the system. The level of virtual inertia obtained from the heat pumps was quite significant, but obviously depended on ambient temperatures and the amount of penetration of these demand response controllers. To select the virtual inertia controller settings, there was a trade-off between virtual inertia gain, which helped in the reduction of RoCoF, and droop gain, which helped in the reduction of frequency nadir.
Author Contributions
Conceptualization, I.I. and T.O.; methodology, I.I.; software, I.I.; validation, I.I., C.O. and T.O.; formal analysis, I.I. and T.O.; investigation, I.I., C.O. and T.O.; resources, I.I., C.O. and T.O.; data curation, I.I., C.O. and T.O.; writing—original draft preparation, I.I. and T.O.; writing—review and editing, I.I. and T.O.; visualization, I.I.; supervision, T.O.; project administration, T.O.; funding acquisition, T.O. All authors have read and agreed to the published version of the manuscript.
Funding
This publication has emanated from research conducted with the financial support of Science Foundation Ireland under the SFI Strategic Partnership Programme Grant Number SFI/15/SPP/E3125.
Conflicts of Interest
The authors declare no conflict of interest.
References
- European Commission. A Roadmap for Moving to a Competitive Low Carbon Economy in 2050; European Commission: Brussel, Belgium, 2011. [Google Scholar]
- Connolly, D.; Mathiesen, B.V.; Østergaard, P.A.; Möller, B.; Nielsen, S.; Lund, H.; Persson, U.; Werner, S.; Grözinger, J.; Boermans, T.; et al. Heat Roadmap Europe 2050. In Second Pre-study for the EU27; Aalborg University: Aalborg, Denmark, 2013; p. 236. [Google Scholar]
- Davies, G.; Madden, C. Ireland’s Low Carbon Future–Dimensions of a Solution; Technical Report; ESB: Dublin, Ireland, 2017. [Google Scholar]
- Dehghanpour, K.; Afsharnia, S. Electrical demand side contribution to frequency control in power systems: a review on technical aspects. Renew. Sustain. Energy Rev. 2015, 41, 1267–1276. [Google Scholar] [CrossRef]
- Muhssin, M.T.; Cipcigan, L.M.; Jenkins, N.; Slater, S.; Cheng, M.; Obaid, Z.A. Dynamic frequency response from controlled domestic heat pumps. IEEE Trans. Power Syst. 2018, 33, 4948–4957. [Google Scholar] [CrossRef]
- Helman, U. Resource and transmission planning to achieve a 33% RPS in California–ISO modeling tools and planning framework. In Proceedings of the FERC Technical Conference on Planning Models and Software, Washington, DC, USA, 9–10 June 2010; Volume 2010, pp. 174–188. [Google Scholar]
- Masuta, T.; Yokoyama, A. Supplementary load frequency control by use of a number of both electric vehicles and water heaters. IEEE Trans. Smart Grid 2012, 3, 1253–1262. [Google Scholar] [CrossRef]
- Kim, Y.J.; Norford, L.K.; Kirtley, J.L. Modeling and analysis of a variable speed for frequency regulation through direct load control. IEEE Trans. Power Syst. 2015, 30, 397–408. [Google Scholar] [CrossRef]
- Su, L.; Norford, L.K. Demonstration of HVAC chiller control for power grid frequency regulation—Part 1: Controller development and experimental results. Sci. Technol. Built Environ. 2015, 21, 1134–1142. [Google Scholar] [CrossRef]
- Kim, Y.J.; Fuentes, E.; Norford, L.K. Experimental study of grid frequency regulation ancillary service of a variable speed heat pump. IEEE Trans. Power Syst. 2016, 31, 3090–3099. [Google Scholar] [CrossRef]
- Milano, F.; Dörfler, F.; Hug, G.; Hill, D.J.; Verbič, G. Foundations and challenges of low-inertia systems. In Proceedings of the 2018 Power Systems Computation Conference (PSCC), Dublin, Ireland, 11–15 June 2018; pp. 1–25. [Google Scholar]
- Zhong, Q.C.; Weiss, G. Synchronverters: Inverters that mimic synchronous generators. IEEE Trans. Ind. Electron. 2011, 58, 1259–1267. [Google Scholar] [CrossRef]
- Mo, O.; D’Arco, S.; Suul, J.A. Evaluation of virtual synchronous machines with dynamic or quasi-stationary machine models. IEEE Trans. Ind. Electron. 2017, 64, 5952–5962. [Google Scholar] [CrossRef]
- Liu, J.; Miura, Y.; Ise, T. Comparison of dynamic characteristics between virtual synchronous generator and droop control in inverter-based distributed generators. IEEE Trans. Power Electron. 2016, 31, 3600–3611. [Google Scholar] [CrossRef]
- Van Wesenbeeck, M.; De Haan, S.; Varela, P.; Visscher, K. Grid tied converter with virtual kinetic storage. In Proceedings of the 2009 IEEE Bucharest PowerTech, Bucharest, Romania, 28 June–2 July 2009; pp. 1–7. [Google Scholar]
- Driesen, J.; Visscher, K. Virtual synchronous generators. In Proceedings of the 2008 IEEE Power and Energy Society General Meeting-Conversion and Delivery of Electrical Energy in the 21st Century, Pittsburgh, PA, USA, 20–24 July 2008; pp. 1–3. [Google Scholar]
- Van Thong, V.; Woyte, A.; Albu, M.; Van Hest, M.; Bozelie, J.; Diaz, J.; Loix, T.; Stanculescu, D.; Visscher, K. Virtual synchronous generator: Laboratory scale results and field demonstration. In Proceedings of the 2009 IEEE Bucharest PowerTech, Bucharest, Romania, 28 June–2 July 2009; pp. 1–6. [Google Scholar]
- Albu, M.; Visscher, K.; Creanga, D.; Nechifor, A.; Golovanov, N. Storage selection for DG applications containing virtual synchronous generators. In Proceedings of the 2009 IEEE Bucharest PowerTech, Bucharest, Romania, 28 June–2 July 2009; pp. 1–6. [Google Scholar]
- Chen, J.; Liu, M.; O’Loughlin, C.; Milano, F.; O’Donnell, T. Modelling, simulation and hardware-in-the-loop validation of virtual synchronous generator control in low inertia power system. In Proceedings of the 2018 Power Systems Computation Conference (PSCC), Dublin, Ireland, 11–15 June 2018; pp. 1–7. [Google Scholar]
- Guo, Y.; Chen, L.; Li, K.; Zheng, T.; Mei, S. A novel control strategy for stand-alone photovoltaic system based on virtual synchronous generator. In Proceedings of the 2016 IEEE Power and Energy Society General Meeting (PESGM), Boston, MA, USA, 17–21 July 2016; pp. 1–5. [Google Scholar]
- Morren, J.; De Haan, S.W.; Kling, W.L.; Ferreira, J. Wind turbines emulating inertia and supporting primary frequency control. IEEE Trans. Power Syst. 2006, 21, 433–434. [Google Scholar] [CrossRef]
- Arani, M.F.M.; El-Saadany, E.F. Implementing virtual inertia in DFIG-based wind power generation. IEEE Trans. Power Syst. 2013, 28, 1373–1384. [Google Scholar] [CrossRef]
- Ma, J.; Qiu, Y.; Li, Y.; Zhang, W.; Song, Z.; Thorp, J.S. Research on the impact of DFIG virtual inertia control on power system small-signal stability considering the phase-locked loop. IEEE Trans. Power Syst. 2017, 32, 2094–2105. [Google Scholar] [CrossRef]
- Yazdani, A.; Iravani, R. Voltage-Sourced Converters in Power Systems; John Wiley & Sons: Hoboken, NJ, USA, 2010; Volume 34. [Google Scholar]
- Karimi-Ghartemani, M.; Ooi, B.T.; Bakhshai, A. Application of enhanced phase-locked loop system to the computation of synchrophasors. IEEE Trans. Power Deliv. 2010, 26, 22–32. [Google Scholar] [CrossRef]
- Karimi-Ghartemani, M. Linear and pseudolinear enhanced phased-locked loop (EPLL) structures. IEEE Trans. Ind. Electron. 2014, 61, 1464–1474. [Google Scholar] [CrossRef]
- Elizondo, J.; Zhang, R.Y.; Huang, P.H.; White, J.K.; Kirtley, J.L. Inertial and frequency response of microgrids with induction motors. In Proceedings of the 2016 IEEE 17th Workshop on Control and Modeling for Power Electronics (COMPEL), Trondheim, Norway, 27–30 June 2016; pp. 1–6. [Google Scholar]
- Lu, N. An evaluation of the HVAC load potential for providing load balancing service. IEEE Trans. Smart Grid 2012, 3, 1263–1270. [Google Scholar] [CrossRef]
- Rasmussen, B.P.; Alleyne, A.G. Dynamic Modeling and Advanced Control of Air Conditioning and Refrigeration Systems; Technical Report; Air Conditioning and Refrigeration Center, College of Engineering, University of Illinois at Urbana-Champaign: Champaign, IL, USA, 2006. [Google Scholar]
- He, X.D. Dynamic Modeling and Multivariable Control of Vapor Compression Cycles in Air Conditioning Systems. Ph.D. Thesis, Massachusetts Institute of Technology, Cambridge, MA, USA, 1996. [Google Scholar]
- Moradi, M.H.; Sohani, A.; Zabihigivi, M.; Wirbser, H. A comprehensive approach to find the performance map of a using experiment and soft computing methods. Energy Convers. Manag. 2017, 153, 224–242. [Google Scholar] [CrossRef]
- Shintai, T.; Miura, Y.; Ise, T. Oscillation damping of a distributed generator using a virtual synchronous generator. IEEE Trans. Power Deliv. 2014, 29, 668–676. [Google Scholar] [CrossRef]
- Delgado, J.; Martins, N.; Covas, D. Uncertainties in hydraulic transient modelling in raising pipe systems: Laboratory case studies. Procedia Eng. 2014, 70, 487–496. [Google Scholar] [CrossRef]
- Ibrahim, I.; Rigoni, V.; O’Loughlin, C.; Jasmin, S.; O’Donnell, T. Real Time Simulation Platform for Evaluation of Frequency Support from Distributed Demand Response. In Proceedings of the CIGRE International Symposium, Dublin, Ireland, 30 May 2017. [Google Scholar]
- ENWL. Low Voltage Networks Solutions. Available online: https://www.enwl.co.uk/zero-carbon/innovation/smaller-projects/low-carbon-networks-fund/low-voltage-network-solutions/ (accessed on 20 February 2020).
- Concordia, C.; Ihara, S. Load Representation in Power System Stability Studies. IEEE Trans. Power Appar. Syst. 1982, PAS-101, 969–977. [Google Scholar] [CrossRef]
- Ashton, P.M.; Saunders, C.S.; Taylor, G.A.; Carter, A.M.; Bradley, M.E. Inertia estimation of the GB power system using synchrophasor measurements. IEEE Trans. Power Syst. 2014, 30, 701–709. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).