Abstract
In the distribution system, customers have increasingly use renewable energy sources and battery energy storage systems (BESS), transforming traditional loads into active prosumers. Therefore, methodologies are needed to provide prosumers with tools to optimize their investments and increase business opportunities. In this paper, a stochastic mixed integer linear programming (MILP) formulation is proposed to solve for optimal sizes of prosumer assets, considering the use of a BESS and photovoltaic (PV) units. The objective is to minimize the total cost of the system, which is defined as the combination of a solar PV system investment, BESS investment, maintenance costs of assets, and the cost of electricity supplied by the grid. The developed method defines the optimal size of PV units, the power/energy capacities of the BESS, and the optimal value for initial energy stored in the BESS. Both deterministic and stochastic approaches were explored. For each approach, the proposed model was tested for three cases, providing a varying combination of the use of grid power, PV units, and BESS. The optimal values from each case were compared, showing that there is potential to achieve more economic plans for prosumers when PV and BESS technologies are taken into account.
1. Introduction
The world is heading towards an era where alternative energy sources will soon replace the use of non-renewable energy resources. Therefore, to address the inevitable depletion of the finite supply of non-renewable resources, renewable energy sources have emerged as a solution to a necessary reduction of carbon emissions [1]. Compared to non-renewable energy resources, renewable energy has an unlimited supply and is environmental beneficial. Although the generation of renewable energy is generally more expensive, recent works have been developed to prove that overall energy costs can be reduced by the adoption of alternative energy sources [2,3,4,5,6,7]. In addition, the adoption of renewable energy as a distributed generation (DG) has increased as technologies associated with photovoltaic (PV) generation and energy storage continue to evolve [8,9].
A prosumer is a customer capable of producing and consuming energy. Prosumers have the benefit of being able to share or sell excess energy produced by renewable energy sources to the grid [1]. A prosumer can achieve economic advantages by optimizing energy usage [10]. A key goal is to find the optimal schedules of energy flows of storage charge/discharge and load consumption. This occurs when the optimal size and configuration of generators and storage systems is determined by taking into account the prices of energy purchased from or sold to the grid.
One of the fastest expanding types of alternative energy sources is photovoltaic (PV) power [11]. The technology has advanced immensely over the years with PV generation available for anywhere from single homes to large commercial plants. Numerous countries have implemented initiatives to promote the growth of solar power. Due to the intermittent nature of PV energy production, battery energy storage systems (BESSs) have become a key element in improving PV production.
The combination of PV systems and BESSs are suitable for prosumers to optimize energy utilization [10]. The use of a BESS is quintessential for optimal energy utilization and efficiency [10]. Effective use of the BESS can be lucrative to the prosumer, e.g., energy produced during off-peak hours can be stored and later consumed during high-peak hours, reducing the cost of electricity significantly over time. In addition, some BESSs, such as lithium ion battery storage systems, have features including being environmentally friendly during operation, high efficiency, high energy density, small footprint, long life-cycle, and low maintenance [12,13]. The optimal scheduling of a BESS combined with a solar PV system can prolong the lifespan of the BESS. In addition, the usage of certain BESSs promotes less carbon-intensive, inexhaustible renewable energy sources (RES) that can also be economically beneficial and easily accessible [14]. At the same time, the utilization of BESSs can represent benefits to the grid as demand peaks can be reduced. In this context, prosumer asset planning is required to maximize economic benefits while meeting the needs of the prosumer. Considering one lifespan of the assets as the period for analysis, the prosumer assets can be optimized to minimize the overall cost of investment.
1.1. State of the Art
Many works have been done to prove the feasibility and economic benefits of integrating the use of energy storage systems (ESSs) with existing microgrids. For instance, authors in [15] determined the techno-economic feasibility of incorporating distributed energy sources (DER), such as a PV system, and ESSs into a virtual power plant. In this context, F. Berglund et al. presented a grid-connected PV system for a medium-scale swimming facility [2]. Authors demonstrated that the installation of a BESS into the existing microgrid is economically beneficial with net savings on the total cost of the system by optimal sizing and controlling of the BESS. A study on the reduction of life cycle carbon emissions and cost of electricity by the integration of a large-scale BESS has also been done [3].
Furthermore, previous studies were developed to demonstrate the potential of BESSs in residential microgrid applications. The aim of the study presented by J. Koskela et al. is to research the effect of electricity pricing on the profitability of a PV system and BESS in residential buildings, including detached homes and apartment buildings [4]. Given a set of asset sizes, the optimization of PV system and BESS sizing for a household load is presented in [16]. While the investment of incorporating a BESS was not proven to be profitable for a household load, the work presented by K. Kappner et al. [16] did not include an analysis of the profitability considering PV units and a BESS in a large entity capacity. Z. Iqbal et al. explore the potential reduction in electricity costs by implementing a smart home with an energy management system [17]. Although a combination of RESs and BESSs were considered to reduce electricity costs, the consideration of initial investment and net profitability were not accounted for. The work presented by the authors in [18] focuses on energy scheduling for a residential subdivision microgrid that includes renewable generations, electric vehicles, and vehicle-to-grid. L. Bhamidi et al. present an optimization model using mixed integer linear programming (MILP) techniques for the sizing and operation of a typical smart home with RESs and a BESS [19]. Solar irradiation and wind velocity data utilized in this optimization model are deterministic. The work presented by D. Hu et al. compares stochastic and deterministic approaches for addressing uncertainty in wind energy [20]. The results reinforce the benefits of using a stochastic approach over the latter.
In recent works, the optimization of energy scheduling in microgrids incorporating energy storage has been explored. T. Kerdphol et al. present a particle swarm optimization model to determine the optimal sizing of the BESS for a stand-alone microgrid by minimizing the total BESS cost [21]. This work excludes the optimization of the size of the PV system. Similarly, the work presented by Y. Hong et al. determines the optimal capacities of energy storage in an islanded microgrid while excluding the optimization of the size of the PV system and energy exchange between the grid and prosumer [22]. A genetic algorithm to optimize the charging and discharging scheduling of prosumer batteries by minimizing the amount of energy exchanged with the main grid was presented by F. Berglund et al. [2]. Moreover, several works present various approaches to optimize the energy scheduling of BESS in microgrid applications [23,24,25,26]. Previous works analyze the operation of microgrids including BESSs and present energy management strategies [27,28]. These works do not address optimal prosumer asset sizing. A.C. Luna et al. present a MILP deterministic optimization model to minimize the operating costs of a grid-connected microgrid with BESS [5]. This work is addressed as a deterministic model and excludes additional costs such as installation and maintenance costs. A MILP formulation solving for optimal sizing of BESS for microgrid applications is presented by I. Alsaidan et al., however this model does not incorporate the use of a PV system [29]. P. Yun et al. design a multi-objective hybrid optimization model for wind farm and ESS operation [30]. While this work excludes the use of a PV system, it develops an optimal operation strategy for a BESS, given the BESS capacity, upper and lower limits, and initial energy stored value. Tools like [6,7], which are available online, can be used to find the optimal sizing of a range of DER for commercial buildings. These tools are capable of optimizing energy resilience or financial savings but fail to use stochastic formulation to address the uncertainties associated with variable renewable energy. To the best of the authors’ knowledge, there are no existing works that presented a stochastic optimization tool for the sizing of prosumer assets including both PV units and BESS for industrial prosumers.
1.2. Contributions
Filling the void found in existing literature, this paper presents a novel algorithm for optimal asset planning of prosumers, taking into account PV generation and BESS with both deterministic and stochastic approaches. The proposed algorithm optimally sizes PV and BESS systems in combination with large (industrial or commercial) loads, while minimizing costs associated with energy consumption, PV and BESS investment, and PV and BESS maintenance, for a 25-year planning period. In addition, uncertainties associated to PV generation are considered, analyzing a large set of scenarios for solar generation. This set is later reduced using a scenario-reduction technique, obtaining a smaller set of scenarios with weighted probabilities. The algorithm is modeled as a MILP formulation, guaranteeing that the optimal solution is obtained.
The main contributions of this paper are two-fold:
- A novel optimization algorithm for prosumer asset planning that determines optimal sizes for PV generation, BESS maximum power, and BESS storage capacity, based on a MILP formulation which minimizes costs associated with investment, maintenance, and operation of the system over a 25-year period.
- A deterministic and stochastic MILP model which guarantees that the optimal solution is obtained and can cope with uncertainties associated with PV generation.
2. Optimal Prosumer Asset Planning
Optimal prosumer asset planning determines the requirements of equipment to minimize the costs of running a system. In this paper, the assets of the prosumer to be optimized consist of the solar PV system and the BESS. The asset sizes are optimized over one lifespan of the assets, measured in years. During analysis, each year is divided into four seasons due to the variance in the cost of electricity and solar radiance. Seasonal analyses in power systems were previously proposed in [31,32], proving to yield positive results. The deterministic model is run for one day for each of the four seasons. Furthermore, every hour of each day is considered to acquire accurate performance expectations from the assets.
The cost of electricity over the period of analysis is subject to the time-of-use periods for each season and their respective electricity rates for a specified location. The annual cost of electricity supplied by the grid is found as the cost of electricity for a day in each season, multiplied by the number of days per season.
All costs presented in this study are shown as present values. Given the annual cost of electricity, the total cost of electricity supplied by the grid over the period of analysis is brought to present value.
2.1. Solar PV
The estimated solar power generation of the PV system is based on the PV potential for a specified location. While the calculation of the PV potential is based on solar irradiance and temperature, tools and approaches [33,34,35] can be used to obtain the PV potential data to be used as an input. To combat the uncertainty of forecasting solar PV potential, a stochastic approach was proposed and the results are to be compared with the deterministic approach [36].
For the deterministic approach, historical data was collected for each individual day in a season and an average solar PV potential curve for each season was produced. The stochastic approach utilizes a scenario reduction technique to construct 10 scenarios (days) for each season with weighted probabilities from 1000+ scenarios. As opposed to the deterministic approach, the stochastic approach can better represent the uncertainties resulting from the variation in solar PV potential over a period of time. Given the respective solar generation profiles, the optimal size is determined by the optimization algorithm to minimize the total cost of the system.
2.2. Energy Storage
Optimal values for the power and energy capacities of the BESS are determined by the program. Moreover, the optimal value for initial energy stored in the BESS is set by the optimization program. Determining these values is critical to optimize the contribution of the BESS in the system [37]. The power and energy capacities of the BESS, and the initial energy stored are limited to be positive values. During analysis, the self-discharge effect of the BESS and the charging and discharging efficiencies were considered.
The total maintenance costs for the BESS and PV units are translated to present day values, given the annual maintenance costs. In this work, the sizes for the PV system and BESS capacities are assumed to be continuous variables, but the solutions can be later used to purchase commercially available sizes.
It is critical to define the economic optimal size of the power generators and storage capacity by using an optimization method where the objective function is the total cost of the system (including installation, operation, and maintenance) [38]. Moreover, the usage of advanced storage scheduling methods, for instance based on load and generation forecasts, have a vital role in allowing higher profitability results [39].
3. Mathematical Formulation
To solve the prosumer asset planning problem, this work proposes a MILP formulation. The goal is to determine the optimal size of the prosumer assets to minimize overall cost of energy and investment () over a period of time using both a deterministic and stochastic approach.
3.1. Deterministic Approach
Formulation for the deterministic model is presented below. The optimal sizes for the PV system and power and energy capacities of the BESS were determined by the algorithm.
3.1.1. Objective Function
The objective function (OF) for the deterministic MILP formulation is presented in Equation (1), representing the total cost as the combination of solar PV system investment, BESS investment, and cost of electricity supplied by the grid. This OF is subject to the set of constraints shown in Equations (2)–(19).
3.1.2. Load
Assuming a typical industrial demand curve, load power is computed for all hours in a day using Equation (2), where is the integer set from 1 to 24, representing each hour in a day, and is an array of percentages to indicate fluctuations from the peak demand through the course of a day. Given the peak load requirement () in MVA and the power factor (), the peak power requirement is calculated as shown in Equation (3).
3.1.3. Power Balance
To cover the demand, power is supplied from the solar PV system, the BESS, and the grid for all hours and all seasons. The power balance equation is presented in (4), where is the integer set from 1 to 4, representing each season in a year. In this work, excess power was not injected back into the grid, therefore grid power () was always greater or equal to zero.
3.1.4. PV Generators
The capital cost of the solar PV system is a function of the size of the PV. The optimal size of the PV system was determined by the optimization algorithm, subject to the following equations. Equation (5) represents the solar PV system investment () as the combination of the PV system capital cost, including installation costs, and PV system maintenance costs. Given a yearly PV system maintenance cost in CAD, the present value for maintenance costs over a period of time is computed as shown in Equation (6). The method for calculating the solar output was by multiplying the PV size, which was determined by the algorithm, by the PV potential of the location in which the solar PV would be implemented. As shown in Equation (7), the power from the solar PV system () is calculated given the PV potential () and the optimal size of the PV system (). Note that the power from the solar PV system () should be less or equal than the available PV power (); i.e., the PV system is able to curtail undesired excess of power in the case that PV generation is greater than the load consumption.
3.1.5. Energy Storage
Equation (8) represents the power supplied by the energy storage system () as the combination of the charging and discharging powers, which are limited by the power capacity of the BESS (), shown in Equations (9)–(11). The charging and discharging coefficients are binary variables representing whether the BESS is charging or discharging. To ensure that at any given time, power is either being charged or discharged from the BESS, Equation (12) is defined. Energy stored in the BESS at every instance of time () is a combination the energy stored from the previous time considering the self-discharge of the BESS, and the charging and discharging powers of the BESS. It is computed as shown in Equation (13) and is subject to the constraints defined in Equations (14)–(16), where is the initial energy stored in kWh and is defined by the linear optimization program. This variable may only take a positive value and is equivalent to the energy stored at the last hour of each season to maintain continuity when the energy stored is multiplied for all days in the season. The energy stored in the BESS at all time is limited to the energy capacity of the BESS (), which is defined by the linear optimization program. Equation (17) represents the investment of the BESS as the summation of the power capacity multiplied by a power cost coefficient, the energy capacity multiplied by an energy cost coefficient, and maintenance costs of the BESS over a period of analysis [8]. The maintenance cost of the BESS in present value was computed as shown in Equation (18).
3.1.6. Electricity Cost
The cost of electricity () is defined as the summation of the energy supplied from the grid, in kWh, multiplied by the electricity rate for all hours and seasons () in $/kWh. The cost of electricity over the period of analysis is brought to present value as shown in Equation (19).
3.2. Stochastic Formulation
A stochastic approach is presented to account for the uncertainties associated to solar PV potential. Formulation for the stochastic model is presented below.
3.2.1. Objective Function
The OF for the stochastic MILP formulation is presented in Equation (20), similar to Equation (1). This OF is subject to the set of constraints shown in Equations (21)–(39).
3.2.2. Load
Similar to Equations (2)–(3), the load power and peak power requirement is calculated as shown in Equations (21)–(22), respectively.
3.2.3. Power Balance
The power balance presented in Equation (23) is similar to Equation (4), but considers , which is an integer set from 1 to 10. This is used to consider the 10 potential scenarios for the solar PV output with varying probabilities. These scenarios are the basis for the stochastic approach to solve the prosumer asset size problem.
3.2.4. PV Generators
Equation (24) represents the solar PV investment, similar to Equation (5). The present value for maintenance cost of the PV system is computed as shown in Equation (25). The power from the solar PV system is calculated for all hours, seasons, and scenarios, while the optimal size of the PV system is determined by the algorithm and given the inputted PV potential data, as shown in Equation (26).
3.2.5. Energy Storage
Formulations for the energy storage are shown in Equations (27)–(37) and are similar to Equations (8)–(18).
3.2.6. Electricity Cost
The expected energy from the grid () is computed in Equation (38) as the summation of the power from the grid multiplied by its respective probability, for each time in each scenario for every season. The cost of electricity is defined as the summation of the expected energy supplied from the grid, in kWh, multiplied by the electricity rate for all hours and seasons in $/kWh. The cost of electricity over the period of analysis is brought to present value, as shown in Equation (39).
With the above formulations, constraints, and limitations, the MILP solution was implemented in AMPL. The program minimized the OF and outputted the optimal size of the PV system, energy capacity of the BESS, power capacity of the BESS, and initial energy stored by the BESS.
4. Test and Results
To prove the efficiency of the proposed algorithms, a prosumer with 2MVA of peak-load and 0.98 of power factor is analyzed. The optimization program was run for a 25-year time period under three cases as shown in Table 1. The parameters associated with the solar PV system and the BESS are outlined in Table 2 and Table 3. The electricity rates and time of use demand periods are shown in Table 4 and Table 5, respectively. The industrial demand curve used in analysis is displayed in Figure 1.

Table 1.
Summary of case studies: Participation of solar photovoltaic (PV) panels, energy storage systems, and the electric grid

Table 2.
Solar PV system costs and details (CAD) [40].

Table 3.
Battery energy storage systems (BESS) CAD [41,42,43].

Table 4.
Present time-of-use electricity rates [44].

Table 5.
Time-of-use periods for each season [44].
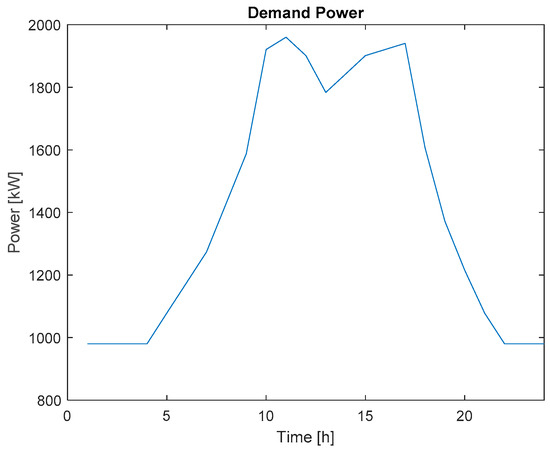
Figure 1.
Load requirements with peak load of 2000 kVA with industrial demand curve [45].
4.1. Deterministic Approach
A summary of the results from the optimization program using a deterministic approach is presented in Table 6. The estimated profiles for seasonal PV power potential in Toronto, Canada are displayed in Figure 2 below, and was calculated as an average of historical solar PV potential data gathered for each day in each season. The results are broken down further in Section 4.1.1, Section 4.1.2 and Section 4.1.3.

Table 6.
Summary of optimal energy storage and PV sizes for case studies, the deterministic approach.
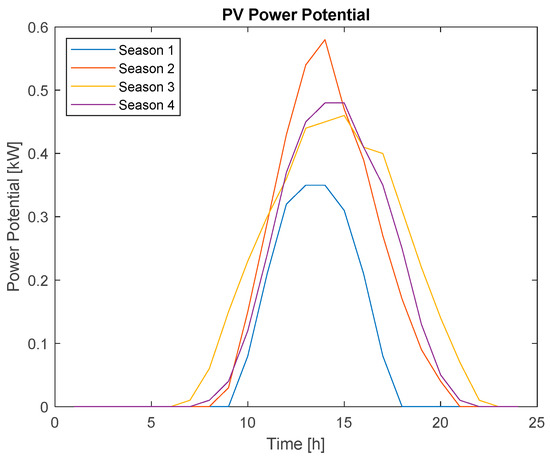
Figure 2.
The estimated PV power potential for Toronto, Canada, shown for one day for each season, determined from data gathered from every individual day in each season [46,47].
4.1.1. Case Study 1: Grid Exclusively
In this case study, the load was operated with only the grid. As a result, the power from the grid in Figure 3 was identical to the load demand in Figure 1. This case was used as the benchmark since it was assumed that the current method to operate the load was solely using power from the grid. The cost for running the plant over 25 years would be approximately 22.9 million CAD when compared to present day value, as seen in Table 6.
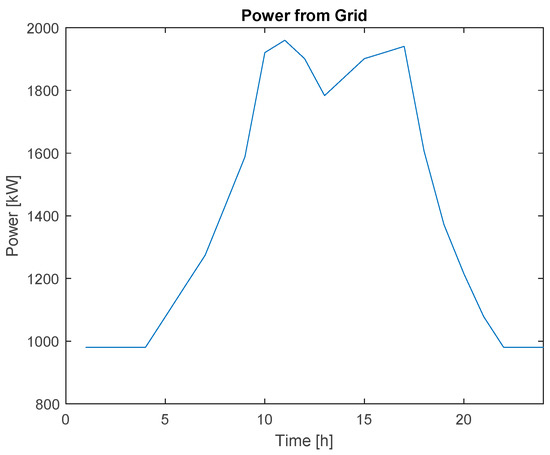
Figure 3.
Power from grid for grid only case.
4.1.2. Case Study 2: Solar PV and Grid
Case study 2 presents the optimal prosumer asset sizes for a scenario where the load is met by power from the solar PV system and the grid. The optimal PV system size was found to be 4888.98 kW and the power generated by the PV system is shown in Figure 4. Since energy storage was not considered for this test case, power produced from the PV system was instantaneously consumed. The remainder of the load that could not be met by the PV power was provided by the grid, as seen in Figure 4. The total cost of running this system for a 25-year period was approximately 18.1 million CAD. In comparison to the benchmark case, this yielded a savings of about 4.87 million CAD.
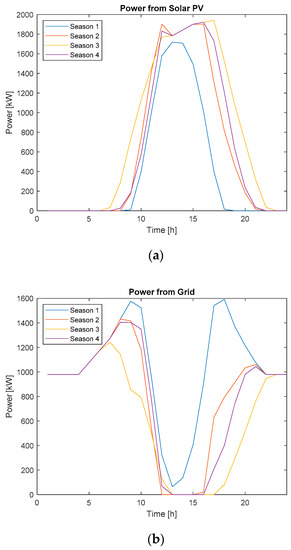
Figure 4.
(a) Solar PV power from a 4888.98 kW system; (b) power from the grid for solar PV and grid power case.
4.1.3. Case Study 3: Solar PV, Energy Storage, and Grid
The optimal PV system size in case study 3 was 4903.28 kW; the potential savings over 25 years suggested that it would be the most economically feasible size. The output power for this PV system size is shown in Figure 5. The option of a BESS with 231.04 kW power capacity and 716.49 kWh energy capacity was also determined for the prosumer, as displayed in Table 6. In Figure 5, the effect of the power capacity constraint can be seen as the BESS charged and discharged at the max capacity for hours at a time as opposed to charging at higher power rates over shorter periods of time. The energy capacity constraint restricted the maximum energy stored in the BESS for each season, as seen in Figure 5. The power that was taken from the grid was restricted by the time of use rates and Figure 5 shows how power from the grid was limited during on-peak hours. The BESS was charged by the grid during off-peak hours and discharged during peak-hours in order for this to happen. As a result of these constraints, the total cost to power the load in the optimal case was approximately 18.0 million CAD, resulting in savings of 4.92 million CAD in comparison to the benchmark case.
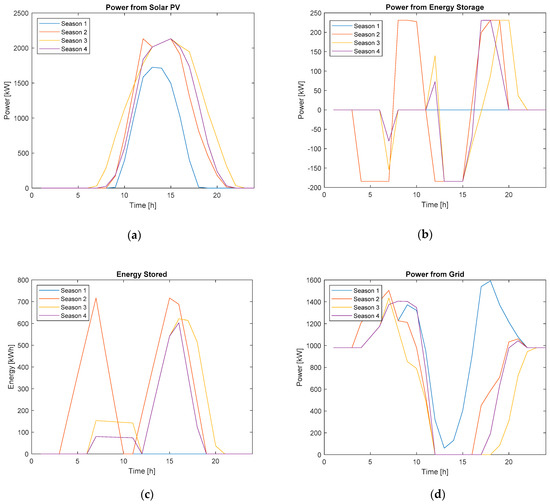
Figure 5.
(a) Solar PV power from a 4903.28 kW system; (b) power from energy storage for solar PV, energy storage, and grid power case; (c) energy stored for solar PV, energy storage, and grid power case; (d) power from the grid for solar PV, energy storage, and grid power case.
4.2. Stochastic Approach
Solar PV potential data was collected over several years for Toronto, Canada and reduced to the 10 most probable scenarios using the scenario reduction technique [48]. Using the 10 scenarios and their respective probabilities, the optimization program was run for the three test cases. A summary of the results from the optimization program using a stochastic approach is presented in Table 7. The stochastic approach did not affect case study 1 as it did not include the use of PV power. Case study 1 is used as a benchmark. The results are analyzed further in Section 4.2.1 and Section 4.2.2.

Table 7.
Summary of optimal energy storage and PV sizes for case studies, a stochastic approach.
4.2.1. Case Study 2: Solar PV and Grid
Case study 2 considers only power from the PV system and grid power to meet the demand. The optimal PV system size was found to be 3671.53 kW. The power produced by the PV system was determined for each scenario, given the 10 scenarios for solar PV potential. One of the 10 scenarios for PV power production is displayed in Figure 6. For each scenario, power from the grid was determined. Given the power from the grid and the probability for each scenario, the expected power from the grid was determined, as seen in Figure 6. The total cost of running the system over a 25-year period was nearly 19.2 million CAD, resulting in a savings of over 3.76 million CAD.
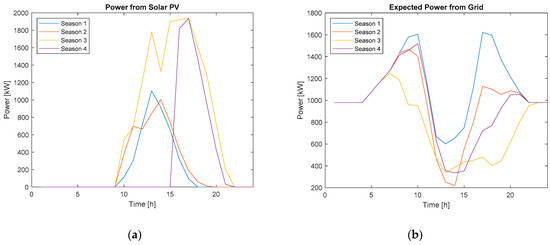
Figure 6.
(a) Solar PV power from a 3671.53 kW System for one scenario; (b) expected power from the grid for solar PV and grid power case.
4.2.2. Case Study 3: Solar PV, Energy Storage, and Grid
Case study 3 considered the use of a PV system with a BESS, while connected to the grid. The optimal PV system size in case study 3 was 4124.57 kW. The output power for this PV system for one of the ten scenarios is shown in Figure 7. The optimal values for the power capacity and energy capacity of the BESS were 1650.70 kW and 12,788.68 kWh, respectively. The power provided by the BESS to the load for one scenario is shown in Figure 7. The optimal value for initial energy stored in the BESS was 4656.70 kWh. For all scenarios, the optimal charging and discharging schedule of the BESS was determined. The cost of electricity was able to be reduced by charging the BESS during off-peak hours and discharged during on-peak hours, as seen in Figure 7. Expected power from the grid was reduced during on-peak hours, as shown in Figure 7. The total cost to run the system was approximately 16.9 million CAD, resulting in a savings of over 6.03 million CAD. This case was proven to be the optimal case.
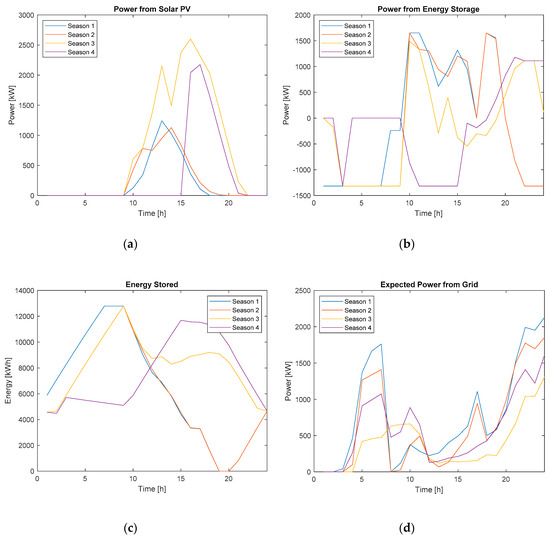
Figure 7.
(a) Solar PV power from a 4124.57 kW system for one scenario; (b) power from energy storage for solar PV, energy storage, and grid power case for one scenario; (c) energy stored for solar PV, energy storage, and grid power case for one scenario; (d) expected power from the grid for solar PV, energy storage, and grid power case.
The analysis performed in this paper assumes current electricity rates specific to Toronto, Canada. While the algorithm accounts for expected increases in the electricity rates over the period of analysis, a sensitivity analysis was conducted to better understand how this assumption will impact the results of the proposed model. For this sensitivity analysis, the electricity rates were varied from ±5% to ±20% and all remaining factors are kept the same. Case 3 that integrates the use of a PV system, BESS, and electricity supplied by the grid was conducted using the stochastic approach presented in this paper. As seen in Table 8, as the electricity rates were decreased, the total cost of the system decreased. This is expected as the electricity rates is directly proportional to the cost of electricity supplied by the grid and the total cost of the system, as seen in Equations (20) and (39), respectively. The optimal sizes of the PV system and BESS is presented in Table 8. As the electricity rates were decreased, the size of the PV system decreased at a greater rate than the size of the BESS. The results suggest that it is not justified to purchase large asset sizes when electricity rates are low. This sensitivity analysis demonstrated that the results of the proposed model were not dependent on the assumption that the electricity rates are specific to Toronto, Canada.

Table 8.
Optimal PV system sizing and BESS capacities for varying electricity rates.
5. Discussion
In this work, deterministic and stochastic formulations are presented to solve for the optimal sizing of a grid-connected prosumer considering the use of a PV system and BESS by minimizing the total cost of the system over a 25-year period. Due to the intermittency of solar irradiation, a stochastic approach was presented to account for the uncertainties of forecasting solar PV potential. For each of the three test cases studied in this paper, the optimal sizes of the PV system and BESS using a deterministic and stochastic approach were discussed and presented in Table 6 and Table 7, respectively. A comparison of the total cost of the system using the deterministic and stochastic approaches is displayed in Figure 8.
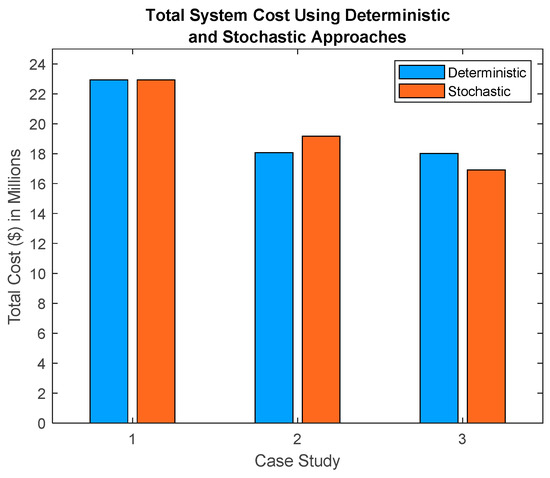
Figure 8.
Comparison of the total cost of the system using deterministic and stochastic approaches for each case study outlined in Table 1.
Case study 1 was unaffected by the stochastic formulations since it did not include the use of a PV system. Case study 2 presents a scenario that includes a PV system and grid connection. Using a stochastic approach yielded an increase in the total cost of the system in comparison to the deterministic approach. This is justified since the stochastic approach considers a variety of PV power potential profiles, where the probabilities of worst-case scenarios are weighted and better represented. When a BESS is incorporated in case study 3, the overall system cost decreases. Furthermore, utilizing a stochastic approach yields a greater savings in comparison to a deterministic approach. This may be attributed to the BESS being better utilized to satisfy the demand of the load during the worst-case PV power potential scenarios. The results suggest that the optimization of prosumer assets such as a PV system and BESS is significant to minimizing the costs of the system.
This paper provides a framework to solve a prosumer asset planning problem. In this work, the costs of the prosumer assets are evaluated for one weekday from each season. The cost of electricity supplied by the grid was defined by the time-of-use electricity rates for each season. Future works could include the weekend and holiday electricity rates. Besides, consumers in deregulated markets with mid and large-sized loads are often subjected to uplift charges. This additional demand charge was neglected in this work, future works may include this.
Following a typical industrial demand curve and given peak-load requirements, the demand power curve is constructed for a typical day. A typical day is defined as a normal weekday, not including weekends and statutory holidays. The demand curve was assembled by averaging out industrial demands curve for said typical day and expanded throughout the analysis. While residential power demand can vary greatly by season, industrial demand shows less variation. For this reason, the demand power is assumed to be identical for every season in the test cases.
Further, the formulations used for determining the total cost of the PV system and BESS were simplified and do not consider the depreciation of asset performance. More formulations that consider the optimal lifetime of the assets and factor replacement costs may be used for improvement. Moreover, a simplistic formulation for the PV cost function was adopted, similar to those seen in [49,50]. The cost of installation for the PV system is considered in the PV capital cost of the proposed algorithm. Future works can adopt a more complex cost calculation for installation depending on the type of installation, such as building integrated or on ground. In addition, this paper considers the capital costs required for the initial investments to be paid for up front. Future work can incorporate the inclusion of loan options for the initial investment and the impact of accumulating interest.
In this work, excess power was not injected back into the grid. Following this assumption, the PV system was constrained such that in the case that PV generation exceeds load consumption when the BESS is fully charged or unavailable, the PV system can curtail undesired excess of power, shown in Equations (7) and (26). Due to policy and market reasons, energy was not sold to the grid in the proposed algorithm, however it can be considered within the cost function. Power injection into the grid can be utilized to maintain the power balance of the microgrid.
6. Conclusions
In this study, we investigated the economic feasibility for a prosumer to utilize a BESS and solar PV system along with grid power to run an industrial sized load. This paper proposed a deterministic and a stochastic mixed-integer linear programming solution to minimize the costs to run a load by considering asset investments and electricity time of use rates.
Both algorithms were successfully able to identify the total costs and optimal asset sizes for the three cases proposed for testing with the industrial load. Case study 1, which solely operated with the grid, proved to be the least economical. Case study 3 was the most economically feasible case test scenario with both the formulations. This is because the scheduling of the BESS, the PV power generation, and the ideal sizing for both assets work concurrently to maximize the contribution of the assets whilst minimizing contributions from the grid. However, the results indicate that it would also be economically feasible to operate with solely a solar PV system if lower capital costs are desired. This option is still considerably better as opposed to case study 1 because of the PV system contribution. Nonetheless, it still falls short to case study 3 because a lack of a BESS imposes energy scheduling limitations and PV power generation is inconsistent. In addition, PV power generation may not be sufficient to solely supple the demand.
Due to the intermittency of solar power generation, it is challenging to accurately measure the solar power generated from the PV system. A stochastic approach was proposed to plan for the uncertainty of forecasting solar power generation. This approach showed that there was a significant economic benefit over 25 years between case studies 2 and 3, but the deterministic approach yielded similar costs.
The deterministic approach provides input as to whether savings for a prosumer are possible but does not provide a realistic output of power from the solar PV system. The stochastic approach determined costs for the prosumer based off a potential worst-case scenario, which better prepares prosumers for costs they may incur. As a result, the stochastic approach is the preferred solution to the prosumer asset planning problem.
As technology advances, the costs of prosumer assets are expected to decrease and the performance of assets are expected to increase. This in turn is expected to increase the number of prosumers, so that the proposed stochastic formulation can be used as framework to determine optimal prosumer asset sizes.
Author Contributions
Conceptualization, C.S. and B.V.; methodology, E.A., K.K. and A.S.; software, E.A., K.K. and A.S.; validation, C.S. and B.V.; investigation, E.A., K.K. and A.S.; resources, E.A. and A.S.; data curation, K.K.; writing—original draft preparation, E.A., K.K. and A.S.; writing—review and editing, C.S. and B.V.; supervision, C.S. and B.V. All authors have read and agreed to the published version of the manuscript.
Funding
This research received funding from IESO.
Conflicts of Interest
The authors declare no conflict of interest.
Nomenclature
| , | Charging coefficient. |
| Discharging coefficient. | |
| Self-discharging of BESS, in %. | |
| Electricity rates, in $/kWh. | |
| Cost per panel, including cost of installation, in CAD. | |
| Cost of electricity supplied by the grid over a period of analysis. | |
| Cost of BESS over a period of analysis. | |
| Cost of solar PV system over a period of analysis. | |
| Total cost of the prosumer model. | |
| Hourly demand, in %. | |
| Initial energy stored, in kWh. | |
| Energy capacity of the BESS, in kWh. | |
| Expected energy from the grid, in kWh. | |
| , | Energy stored in the BESS, in kWh. |
| Present value maintenance costs of the BESS, in $, over a period of analysis. | |
| Annual maintenance costs of the BESS, in $. | |
| Rate of inflation. | |
| Energy cost coefficient, in $/kWh. | |
| Power cost coefficient, in $/kW. | |
| Charging efficiency, in %. | |
| Discharging efficiency, in %. | |
| , | Charging power, in kW. |
| , | Discharging power, in kW. |
| Power capacity of the BESS, in kW. | |
| , | Power supplied by the BESS, in kW. |
| Power factor. | |
| Load power, in kW. | |
| Power supplied by the grid, in kW. | |
| Peak-load requirement, in kW. | |
| , | PV power potential, in kW. |
| , | Power supplied by the PV units, in kW. |
| Probability of each scenario, in %. | |
| Present value maintenance costs of the solar PV system, in $, over a period of analysis. | |
| Annual maintenance costs of the solar PV system, in $. | |
| Index for seasons. | |
| Peak-load requirement, in kVA. | |
| Size of the solar panel, in kW. | |
| PV size, in kW. | |
| Index for time zones. | |
| Index for scenarios. | |
| Period of analysis, in years. |
References
- Zafar, R.; Mahmood, A.; Razzaq, S.; Ali, W.; Naeem, U.; Shehzad, K. Prosumer based energy management and sharing in smart grid. Renew. Sustain. Energy Rev. 2018, 82, 1675–1684. [Google Scholar] [CrossRef]
- Berglund, F.; Zaferanlouei, S.; Korpås, M.; Uhlen, K. Optimal operation of battery storage for a subscribed capacity-based power tariff Prosumer—A norwegian case study. Energies 2019, 12, 4450. [Google Scholar] [CrossRef]
- Nian, V.; Jindal, G.; Li, H. A feasibility study on integrating large-scale battery energy storage systems with combined cycle power generation—Setting the bottom line. Energy 2019, 185, 396–408. [Google Scholar] [CrossRef]
- Koskela, J.; Rautiainen, A.; Järventausta, P. Using electrical energy storage in residential buildings – sizing of battery and photovoltaic panels based on electricity cost optimization. Appl. Energy 2019, 239, 1175–1189. [Google Scholar] [CrossRef]
- Luna, A.C.; Diaz, N.L.; Graells, M.; Vasquez, J.C.; Guerrero, J.M. Mixed-integer-linear-programming-based energy management system for hybrid PV-wind-battery microgrids: Modeling, design, and experimental verification. IEEE Trans. Power Electron. 2017, 32, 2769–2783. [Google Scholar] [CrossRef]
- REopt Lite. Available online: https://reopt.nrel.gov/tool (accessed on 11 March 2020).
- Distributed Energy Resources—Customer Adoption Model (DER-CAM). Available online: https://building-microgrid.lbl.gov/projects/der-cam (accessed on 11 March 2020).
- Diaz, N.L.; Dragicevic, T.; Vasquez, J.C.; Guerrero, J.M. Intelligent distributed generation and storage units for DC microgrids-A new concept on cooperative control without communications beyond droop control. IEEE Trans. Smart Grid 2014, 5, 2476–2485. [Google Scholar] [CrossRef]
- Manditereza, P.T.; Bansal, R. Renewable distributed generation: The hidden challenges – A review from the protection perspective. Renew. Sustain. Energy Rev. 2016, 58, 1457–1465. [Google Scholar] [CrossRef]
- Ruiz-Cortes, M.; Gonzalez-Romera, E.; Amaral-Lopes, R.; Romero-Cadaval, E.; Martins, J.; Milanes-Montero, M.I.; Barrero-Gonzalez, F. Optimal Charge/Discharge Scheduling of Batteries in Microgrids of Prosumers. IEEE Trans. Energy Convers. 2019, 34, 468–477. [Google Scholar] [CrossRef]
- Sommerfeldt, N.; Madani, H. Tillämpad termodynamik och kylteknik, Skolan för industriell teknik och management (ITM), KTH; Energiteknik. Revisiting the techno-economic analysis process for building-mounted, grid-connected solar photovoltaic systems: Part one – review. Renew. Sustain. Energy Rev. 2017, 74, 1379–1393. [Google Scholar] [CrossRef]
- Chalk, S.G.; Miller, J.F. Key challenges and recent progress in batteries, fuel cells, and hydrogen storage for clean energy systems. J. Power Sources 2006, 159, 73–80. [Google Scholar] [CrossRef]
- Venkatasetty, H.V.; Jeong, Y.U. Recent advances in lithium-ion and lithium-polymer batteries. In Proceedings of the Seventeenth Annual Battery Conference on Applications and Advances, Long Beach, CA, USA, 18 January 2002. [Google Scholar]
- Tahir, M.F.; Haoyong, C.; Khan, A.; Javed, M.S.; Laraik, N.A.; Mehmood, K. Optimizing Size of Variable Renewable Energy Sources by Incorporating Energy Storage and Demand Response. IEEE Access 2019, 7, 103115–103126. [Google Scholar] [CrossRef]
- Sikorski, T.; Jasiński, M.; Ropuszyńska-Surma, E.; Węglarz, M.; Kaczorowska, D.; Kostyła, P.; Leonowicz, Z.; Lis, R.; Rezmer, J.; Rojewski, W.; et al. A case study on distributed energy resources and energy-storage systems in a virtual power plant concept: Economic aspects. Energies 2019, 12, 4447. [Google Scholar] [CrossRef]
- Kappner, K.; Letmathe, P.; Weidinger, P. Optimisation of photovoltaic and battery systems from the prosumer-oriented total cost of ownership perspective. EnergySustain. Soc. 2019, 9, 1–24. [Google Scholar] [CrossRef]
- Iqbal, Z.; Javaid, N.; Iqbal, S.; Aslam, S.; Khan, Z.; Abdul, W.; Almogren, A.; Alamri, A. A domestic microgrid with optimized home energy management system. Energies 2018, 11, 1002. [Google Scholar] [CrossRef]
- Fang, X.; Wang, J.; Song, G.; Han, Y.; Zhao, Q.; Cao, Z. Multi-agent reinforcement learning approach for residential microgrid energy scheduling. Energies 2019, 13, 123. [Google Scholar] [CrossRef]
- Bhamidi, L.; Sivasubramani, S. Optimal sizing of smart home renewable energy resources and battery under prosumer-based energy management. IEEE Syst. J. 2020, 1–9. [Google Scholar] [CrossRef]
- Hu, D.; Ryan, S.M. Stochastic vs. deterministic scheduling of a combined natural gas and power system with uncertain wind energy. Int. J. Electr. Power Energy Syst. 2019, 108, 303–313. [Google Scholar] [CrossRef]
- Kerdphol, T.; Fuji, K.; Mitani, Y.; Watanabe, M.; Qudaih, Y. Optimization of a battery energy storage system using particle swarm optimization for stand-alone microgrids. Int. J. Electr. Power Energy Syst. 2016, 81, 32–39. [Google Scholar] [CrossRef]
- Hong, Y.; Lai, Y.; Chang, Y.; Lee, Y.; Lin, C. Optimizing energy storage capacity in islanded microgrids using immunity-based multiobjective planning. Energies 2018, 11, 585. [Google Scholar] [CrossRef]
- Tenfen, D.; Finardi, E.C.; Delinchant, B.; Wurtz, F. Lithium-ion battery modelling for the energy management problem of microgrids. IET Gener. Transm. Distrib. 2016, 10, 576–584. [Google Scholar] [CrossRef]
- Qiu, X.; Nguyen, T.A.; Crow, M.L. Heterogeneous energy storage optimization for microgrids. IEEE Trans. Smart Grid 2016, 7, 1453–1461. [Google Scholar] [CrossRef]
- Moradi, H.; Esfahanian, M.; Abtahi, A.; Zilouchian, A. Modeling a hybrid microgrid using probabilistic reconfiguration under system uncertainties. Energies 2017, 10, 1430. [Google Scholar] [CrossRef]
- Kim, H.; Kim, M.; Kim, S. Multi-objective scheduling optimization based on a modified non-dominated sorting genetic algorithm-II in voltage source Converter−Multi-terminal high voltage DC grid-connected offshore wind farms with battery energy storage systems. Energies 2017, 10, 986. [Google Scholar] [CrossRef]
- Hussain, A.; Bui, V.; Kim, H. Fuzzy logic-based operation of battery energy storage systems (BESSs) for enhancing the resiliency of hybrid microgrids. Energies 2017, 10, 271. [Google Scholar] [CrossRef]
- Rana, M.J.; Abido, M.A. Energy management in DC microgrid with energy storage and model predictive controlled AC–DC converter. IET Gener. Transm. Distrib. 2017, 11, 3694–3702. [Google Scholar] [CrossRef]
- Alsaidan, I.; Khodaei, A.; Gao, W. A comprehensive battery energy storage optimal sizing model for microgrid applications. IEEE Trans. Power Syst. 2018, 33, 3968–3980. [Google Scholar] [CrossRef]
- Yun, P.; Ren, Y.; Xue, Y. Energy-storage optimization strategy for reducing wind power fluctuation via markov prediction and PSO method. Energies 2018, 11, 3393. [Google Scholar] [CrossRef]
- De Quevedo, P.M.; Munoz-Delgado, G.; Contreras, J. Impact of electric vehicles on the expansion planning of distribution systems considering renewable energy, storage, and charging stations. IEEE Trans. Smart Grid 2019, 10, 794–804. [Google Scholar] [CrossRef]
- Home-Ortiz, J.M.; Melgar-Dominguez, O.D.; Pourakbari-Kasmaei, M.; Mantovani, J.R.S. A stochastic mixed-integer convex programming model for long-term distribution system expansion planning considering greenhouse gas emission mitigation. Int. J. Electr. Power Energy Syst. 2019, 108, 86–95. [Google Scholar] [CrossRef]
- Perez, E.; Beltran, H.; Aparicio, N.; Rodriguez, P. Predictive Power Control for PV Plants with Energy Storage. IEEE Trans. Sustain. Energy 2013, 4, 482–490. [Google Scholar] [CrossRef]
- Sabillon, C.; Franco, J.F.; Rider, M.J.; Romero, R. Joint optimal operation of photovoltaic units and electric vehicles in residential networks with storage systems: A dynamic scheduling method. Int. J. Electr. Power Energy Syst. 2018, 103, 136–145. [Google Scholar] [CrossRef]
- McKenna, E.; Thomson, M. High-resolution stochastic integrated thermal–electrical domestic demand model. Appl. Energy 2016, 165, 445–461. [Google Scholar] [CrossRef]
- Renard, P.; Alcolea, A.; Ginsbourger, D. Stochastic versus Deterministic Approaches. In Environmental Modelling: Finding Simplicity in Complexity; Wiley: Hoboken, NJ, USA, 2013; pp. 133–149. [Google Scholar]
- Opathella, C.; Elkasrawy, A.; Mohamed, A.A.; Venkatesh, B. MILP formulation for generation and storage asset sizing and sitting for reliability constrained system planning. Int. J. Electr. Power Energy Syst. 2020, 116, 105529. [Google Scholar] [CrossRef]
- Marchi, B.; Zanoni, S.; Pasetti, M. A techno-economic analysis of Li-ion battery energy storage systems in support of PV distributed generation. In Proceedings of the 21st Summer School F. Turco of Industrial Systems Engineering, Naples, Italy, 13–15 September 2016; pp. 145–149. [Google Scholar]
- Marchi, B.; Pasetti, M.; Zanoni, S.; Zavanella, L.E. The Italian reform of electricity tariffs for non household customers: The impact on distributed generation and energy storage. In Proceedings of the 22nd Summer School F. Turco of Industrial Systems Engineering, Palermo, Italy, 13–15 September 2017; pp. 103–109. [Google Scholar]
- Canadian Solar CS6U-325P Poly Silver Solar Panel. Available online: https://www.wholesalesolar.com/1930006/canadian-solar/solar-panels/canadian-solar-cs6u-325p-poly-silver-solar-panel (accessed on 14 March 2019).
- Rinaldi, S.; Pasetti, M.; Flammini, A.; Ferrari, P.; Sisinni, E.; Simoncini, F. A Testing Framework for the Monitoring and Performance Analysis of Distributed Energy Systems. IEEE Trans. Instrum. Meas. 2019, 68, 3831–3840. [Google Scholar] [CrossRef]
- Masteri, K.; Venkatesh, B.; Freitas, W. A Fuzzy Optimization Model for Distribution System Asset Planning With Energy Storage. IEEE Trans. Power Syst. 2018, 33, 5114–5123. [Google Scholar] [CrossRef]
- Rahmann, C.; Mac-Clure, B.; Vittal, V.; Valencia, F. Break-Even Points of Battery Energy Storage Systems for Peak Shaving Applications. Energies 2017, 10, 833. [Google Scholar] [CrossRef]
- Time-of-Use (TOU) Pricing and Schedules. Available online: https://www.powerstream.ca/customers/rates-support-programs/time-of-use-pricing.html (accessed on 10 February 2019).
- Assessment of Industrial Load for Demand Response across U.S. Regions of the Western Interconnect. Available online: https://info.ornl.gov/sites/publications/Files/Pub45942.pdf (accessed on 27 March 2020).
- Solar Energy Maps Canada (Every Province). (10 February 2019). Available online: https://energyhub.org/solar-energy-maps-canada/ (accessed on 4 March 2019).
- Solar Radiation—Hourly data for Ottawa (Kanata—Orléans). (2019, January 02). Available online: https://ottawa.weatherstats.ca/charts/solar_radiation-hourly.html (accessed on 10 February 2019).
- Growe-Kuska, N.; Heitsch, H.; Romisch, W. Scenario reduction and scenario tree construction for power management problems. In Proceedings of the 2003 IEEE Bologna Power Tech Conference, Bologna, Italy, 23–26 June 2003. [Google Scholar]
- Li, J.; Wei, W.; Xiang, J. A simple sizing algorithm for stand-alone PV/Wind/Battery hybrid microgrids. Energies 2012, 5, 5307–5323. [Google Scholar] [CrossRef]
- Vazquez, M.J.V.; Marquez, J.M.A.; Manzano, F.S. A methodology for optimizing stand-alone PV-system size using parallel-connected DC/DC converters. IEEE Trans. Ind. Electron. 2008, 55, 2664–2673. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).