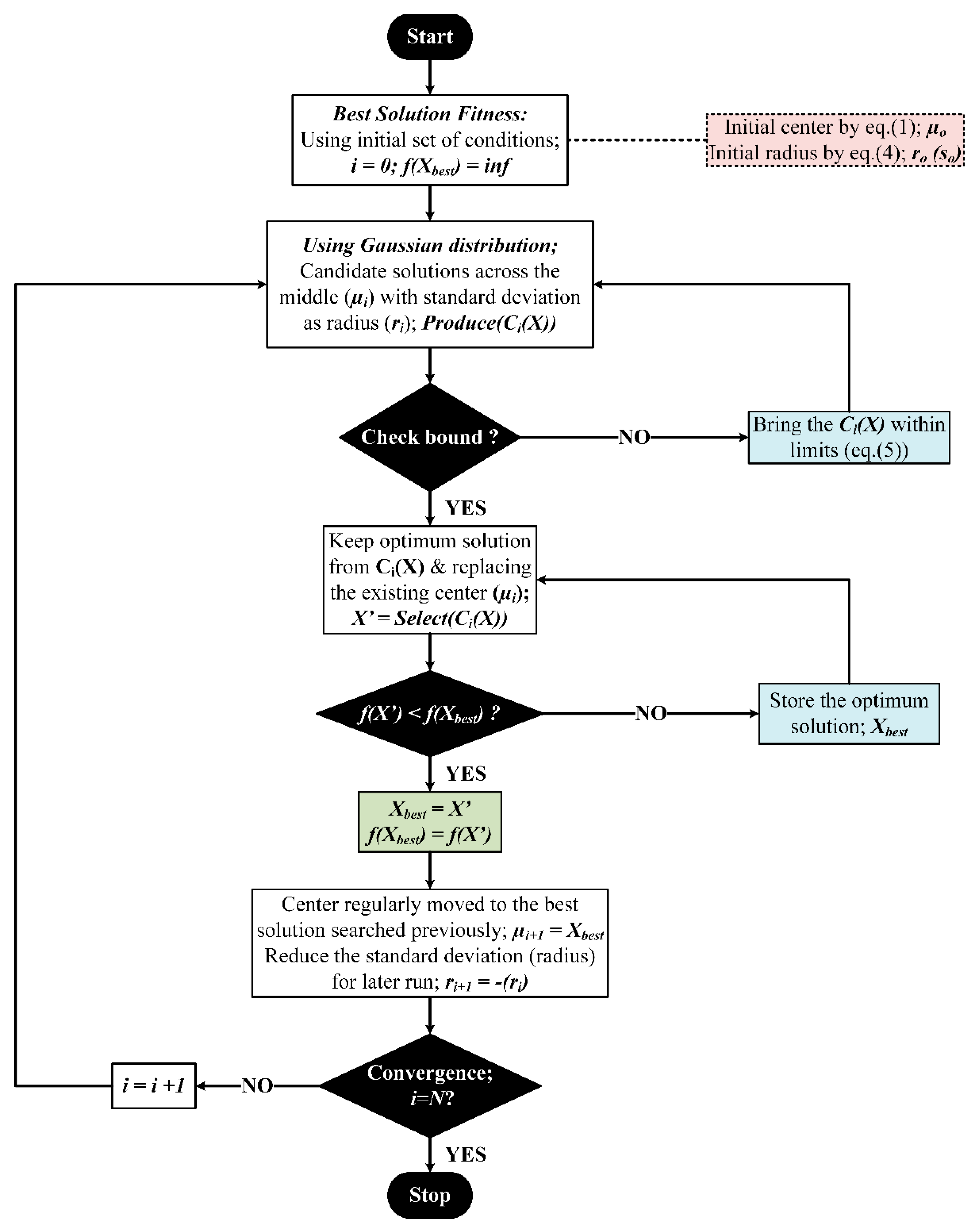
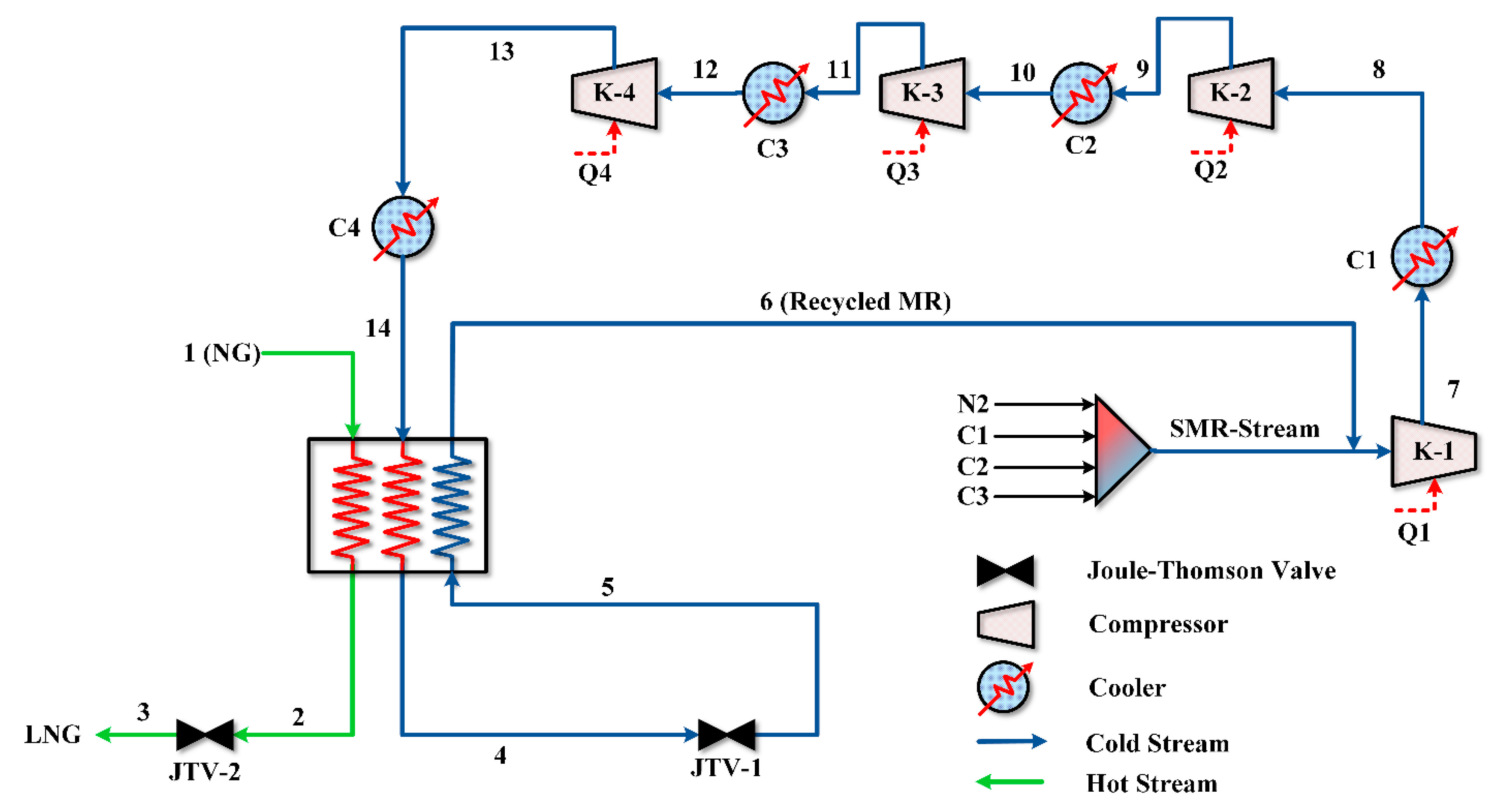
1. Introduction
The continuous growth of human society will adversely affect the world energy requirements in the near future [
1]. The estimates indicate an increase in the worldwide energy of up to 56% from 2010 to 2040 where India and China are the main contributors with increments of 112% in the same era [
1]. Despite the intense research on renewable resources, it is projected that 76% of energy needs will be met by fossil fuels until 2040 [
2]. Among conventional energy resources (i.e., gas, oil, and coal), Natural Gas (NG) has become essential because of its low Greenhouse Gas (GHG) emissions and increased thermal efficiency [
3]. NG is the cleanest fuel with least contribution to climate change and air pollution [
4,
5]. As a result, a significant shift from coal to NG has been witnessed worldwide [
6,
7].
Most of the NG reservoirs are located in the remote areas, thus NG is transported to markets in gaseous or liquid (LNG) forms. The economical and easy transportation of NG over long distances (>2000 km) is a critical factor, which is solved through liquefaction approach. The transportation of NG as LNG is preferred because of its lower cost and high safety compared with a pipeline (gaseous) transportation over long distances [
8]. Due to this, the pipeline gas trade has been reduced by seven times than the LNG trade [
9]. However, a primary issue with LNG processes is operating expenditure in terms of energy required to liquefy NG. It exhibits low energy efficiency, and the energy required is related to the compression power (shaft work) for refrigeration to liquefy NG. The shaft work for refrigeration cycles is dependent on the flow rates of the ingredients of mixed refrigerant (MR) and cycle operating conditions (e.g., refrigerant evaporation and condensation pressure) [
10]. The optimal execution (i.e., via determining the optimal operating pressures and composition of the mixed refrigerant) of the liquefaction processes is minimized by the overall compression power [
11,
12]. This eventually enhances process efficiency by exploiting economic advantages with low energy requirements. Hence, several studies have improved liquefaction processes via sole optimization. For example, Lee et al. [
13] determined the optimal design of the SMR case with minimum shaft work. Shah et al. [
14] were the first to study multi-objective optimization of the C3MR process. They optimized the C3MR process by considering the total shaft work requirement, capital cost, total annual cost, and total hydrocarbon inventory as objective functions.
The process optimization is developed through adaptation of commercial process simulators, and this exhibits comprehensive thermodynamic libraries. The LNG processes are simulated in commercial simulators and optimized by developing a connection between both software environments. For instance, Aspelund et al. [
15] built a simulation environment linked with the optimization algorithm. They used Aspen Hysys
® to model SMR process and subsequently optimized it using a hybrid strategy by combining Nelder–Mead Downhill Simplex and Tabu search algorithms. Khan et al. [
16] decreased the overall compression energy requirement of the SMR process using Non-Linear Programming (NLP) and particle swarm paradigm. Wang et al. [
17] designed the C3MR process in Aspen Plus
® and presented an optimal design through Sequential Quadratic Programming (SQP). Hatcher et al. [
18], Lee et al. [
19], and Mortazavi et al. [
20] also modeled the C3MR process and subsequently optimized it via the Box method, Successive Reduced Quadratic Programming (SRQP), and hybrid optimization (i.e., Genetic Algorithm (GA) and SQP). Lee et al. [
21] applied multi-objective optimization (using SQP) via gProms process simulator to find an optimal design of SMR process. Furthermore, Lee and Moon [
22] have also used the SRQP to find optimal designs of SMR and C3MR liquefaction processes. They applied a mathematical optimization model that includes the cost model, as well as thermodynamic model. However, Tsay and Baldea [
23] reported that modeling, simulation, and optimization become more complicated when phase transition and recycle streams are incorporated into refrigeration cycles. Therefore, they used equation-oriented modeling and optimization strategies [
24,
25] to find the optimal design of SMR liquefaction processes. Moreover, Vikse et al. [
26] presented a versatile simulation method to find an optimal design of complex SMR process. They investigated the capability of nonsmooth framework (i.e., equation-oriented modeling) for the optimal design of SMR process. Ali et al. [
27] employed Generalized Polynomial Chaos (gPC) based surrogate modeling approach to study the operational reliability of the SMR process. Most recently, Zhu et al. [
28] performed experimental investigation to analyze the flow distribution in plate-fin heat exchanger that is mostly used in the SMR process. Khan et al. [
11] proposed a mixed refrigerant composition selection method based on the boiling point difference and specific refrigeration effect of individual components in mixed refrigerant. The proposed selection criteria were applied to the MR used in SMR and C3MR system; and a decrease in energy consumption for compression was observed. In another similar study, Xu et al. [
29] developed a correlation between the ambient temperature and mixed refrigerant composition to evaluate energy utilization for PRICO LNG process. Qadeer et al. [
30] adopted krill-herd optimization strategy for optimal solution of process conditions and MR composition of the SMR process.
Recently, a single-solution based Vortex Search (VS) [
31] algorithm has been evaluated for the design optimization of complex processes such as modified SMR [
32] and self-recuperative high temperature co-electrolysis-based methanol production [
33]. Authors have found best optimal designs through the VS approach. Previously [
32], the VS algorithm was used for the design optimization of modifed SMR process (MR consists of five components; nitrogen, methane, ethane, propane, and i-pentane) instead of conventional and well known SMR process that uses four components, i.e., nitrogen, methane, ethane, and propane. Since the optimization of LNG processes exhibited a significant reduction in exergy destruction and an enhanced the energy efficiency. The process engineers always focus on optimizing the plant design and operation to increase the profits of the chemical processes by improving the energy efficiency (reducing the operating costs). However, the energy efficiency enhancement for the LNG plants through exclusive optimization is a challenging task by virtue of highly complex and nonlinear thermodynamic interactions between the constrained design variables and energy efficiency. Therefore, efficient and rigorous optimization of the LNG processes continues to be an ongoing issue.
The major contribution of this study is the implementation and evaluation of the single-solution based Vortex Search (VS) [
31] methodology to find the optimal design variables (corresponding to minimal energy consumption) of the SMR (for offshore applications) and C3MR (for onshore applications) processes. The SMR and C3MR processes are simulated in Aspen Hysys
® v9. The VS algorithm is coded and modified in MATLAB version 2018b. The simulated LNG processes are linked with VS through ActiveX functionality. Optimal findings are analyzed and compared with the well-known algorithms including the GA and Particle Swarm Optimization (PSO). The VS algorithm can be applied to find the optimal design of any complex chemical process by simulating in Aspen Hysys.
3. Onshore and Offshore LNG Processes
Many liquefaction technologies have been developed for onshore and offshore LNG production. The C3MR, DMR, and cascade processes are considered suitable candidates for onshore LNG production. Whereas, for offshore applications, the SMR, nitrogen-expander-based, and DMR processes are the promising options. The DMR process is considered for both onshore, as well as offshore applications [
36]. Generally, the liquefaction process is selected based on NG reserve’s location (onshore or offshore), production capacity, degree of complexity, and environmental conditions. However, considering the energy efficiency (operating costs), the SMR (PRICO
®) process is the most suitable candidate for small-scale and offshore applications compared with the expander-based LNG processes [
37]. Although, for offshore applications, the nitrogen-expander-based liquefaction process have several dominant features such as safety and simplicity in operation but thermodynamically it is less attractive than the SMR process, due to high exergy destruction. Whereas, the C3MR process is considered as a promising candidate for onshore applications due to its relative high energy efficiency. Furthermore, this process is capable of producing 81% of the base-load LNG [
38]. It is reported [
39] that about 77% of the world’s LNG plants are using the C3MR technology. Nevertheless, the process exhibits a high degree of complexity. Detailed process descriptions of the SMR and C3MR liquefaction processes are described in the forthcoming sections.
3.1. SMR LNG Process Description
A conventional SMR, alternatively known as the PRICO (poly refrigerant integrated cycle operations) process, was first introduced by Black and Veatch in 1970 [
40].
Figure 4 shows that the SMR process consists of compressors to compress the MR in steps with intermediate coolers (air/water), i.e., a cryogenic multistream exchanger for exchanging heat between MR and feed natural gas and expansion valves (Joule–Thomson (JT)). In the SMR LNG cycle, a mixed refrigerant stream comprised of a range of mixture of methane, ethane, propane, and nitrogen is employed to produce a significant refrigeration effect to liquefy natural gas up to a temperature of approximately −159 °C and a pressure of 1.3–2.0 bar. First, the SMR stream is introduced into a refrigeration cycle loop equipped with compression units, including after-coolers/inter-stage coolers. The MR gains heat during the compression process and is removed by air/water-cooled inter-stage coolers. Subsequently, the MR stream enters the cryogenic multistream exchanger and gets condensed. Then, the pressurized liquid MR passes through a JT valve where its pressure is lowered. At the outlet of this JT valve, the MR is obtained with liquid fraction >0.85. This MR (stream-5) exchanges the latent heat with incoming high-pressure MR (stream-14), as well as feed NG (stream-1) and is evaporated. Finally, it is exited as a superheated vapor (stream-6) from the LNG heat exchanger and is subsequently introduced into the compressor (K-1), thereby completing the refrigeration loop.
3.2. C3MR LNG Process Description
Although the SMR and C3MR exhibit resemblance in terms of the MR cycle, the degree of complexity of C3MR exceeds that of SMR. They utilize the same cryogenic heat exchanger (i.e., a plate and fin brazed with aluminum core) [
11]. The C3MR process is less inviting for offshore applications due to its complex structure and large space requirements. Given its ability to match hot (natural gas) and cold (MR boiling) composite curves, the C3MR process performance is lower than that of other available LNG processes. The C3MR process uses the two refrigeration cycles; pure propane (C3) and MR-based refrigeration cycles as shown in
Figure 5. The propane-based refrigeration loop is employed to precool the feed natural gas, as well as the mixed refrigerants. Subsequently, the process of liquefaction and subcooling of the feed natural gas stream is performed through the MR cycle.
3.3. Simulation Basis for LNG Process Modeling
In the study, Aspen Hysys is used to model the SMR and C3MR processes. Optimal conditions for the processes as determined by Khan et al. [
32] are selected to create the base case study. Natural gas feed quality, other process conditions, and assumptions used in the simulation are highlighted in
Table 2. Binary interactions parameters are predicted using the popular Peng–Robinson model, whereas the entropies and enthalpies are evaluated via the Lee–Kesler thermodynamic model. A Minimum Internal Temperature Approach (MITA) value is specified as 3 °C to obtain a more efficient design for the LNG multistream exchangers.
4. Optimization Problem Formulation for SMR and C3MR Processes
The effectiveness of any optimization problem is examined by the mathematical problem formulation. The effectiveness significantly affects the type of optimal candidate set results and optimization elapse time. The following constitute the major components for any general optimization problem:
Target function(s).
Constraint function(s) and their limits(s).
Optimization variables.
Optimizing variable bounds (search area).
Other design parameters, if any.
Total energy requirement in terms of compression power for LNG processes is considered as a target/objective in several different design optimization studies. Therefore, the compression power required as an operating cost is considered as the objective function to liquefy unit mass flow of NG in both LNG processes. Hence, the mathematical optimization problem is expressed as follows:
subject to the MITA values (inside all LNG heat exchangers) as constraints:
where
Y denotes the set of optimizing decision variables and
i denotes the number of compressors.
Parameters including the MR flow rate, condensation pressure, and evaporation pressure were selected as the design variables for SMR process. Whereas, for the C3MR process, the temperatures of the cooling stages in the propane cycle were also considered as the design variables in addition to the MR components flowrates, MR condensation, and evaporation pressures.
Table 3 lists all decision variables (with their bounds) of the SMR and C3MR processes.
Since the optimization of LNG processes is constrained by the MITA inside the LNG heat exchangers. Therefore, the overall compression power (i.e., objective function) was constrained by the MITA value of 3 °C. The MITA value can be 1~3 °C. However, the MITA value of 3 °C is more flexible to ensure the feasibility of the liquefaction with affordable economics.
4.1. Constraint Handling Approach
An exterior penalty function was used to handle the constraints (i.e., MITA value of 3.0 °C), and to further fold the constraints into overall compression power. It has been carried out by several LNG design optimization studies [
12,
30,
32,
41].
Since the overall objective function is formed by combining the required power and constraint as specified in Equations (6) and (7) as follows:
Finally, the objective function is reformulated in Equation (8) as follows:
where
w denotes a positive penalty parameter, whose values correspond to 1.
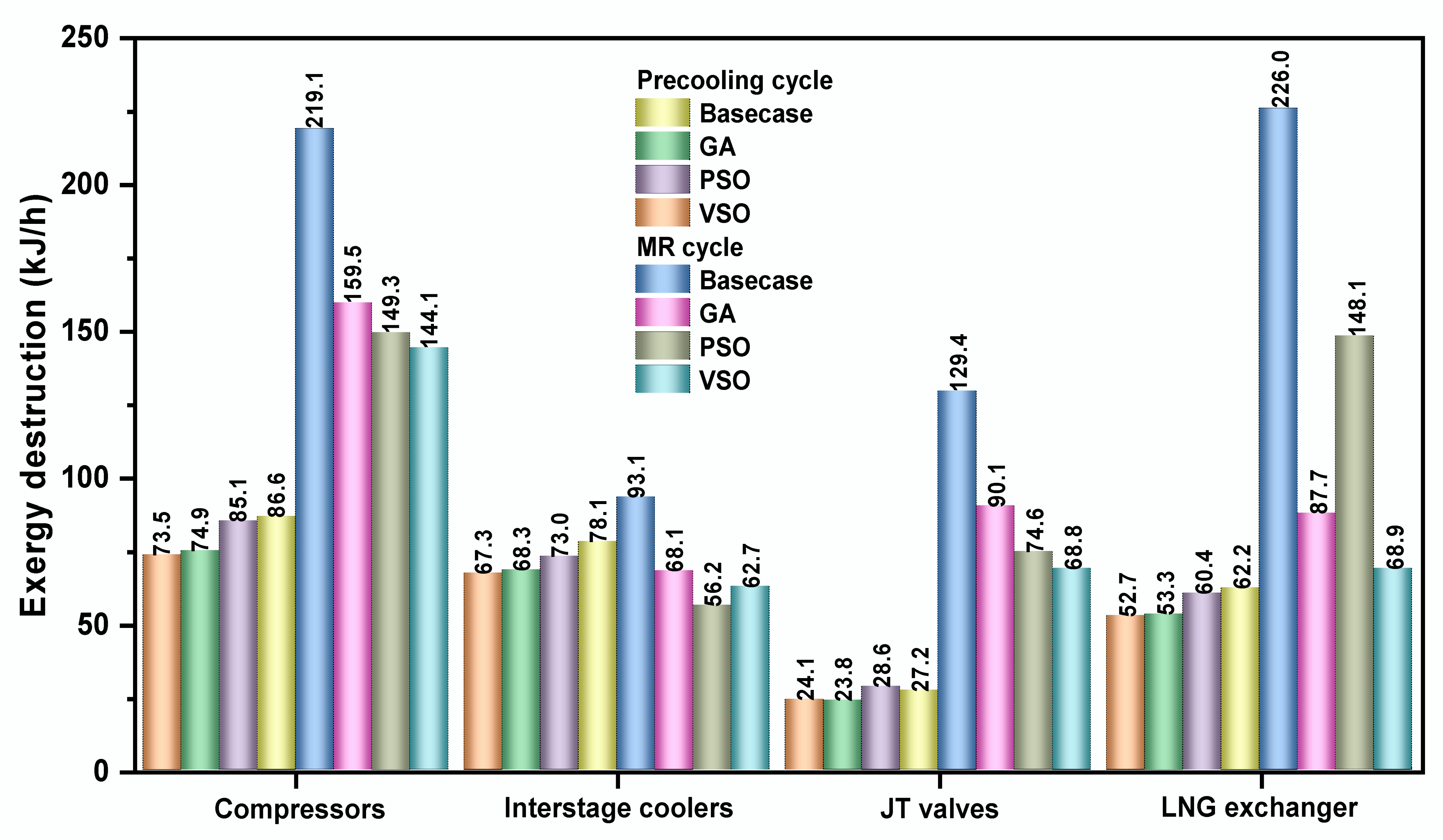
4.2. Exergy Destruction Analysis
Exergy for a refrigeration cycle is the minimum theoretical work required from the environment as the system comes from the dead state to the desired state. Exergy analysis identifies the energy flaws mainly due to the thermodynamic irreversibilities associated with each equipment, as well as the whole process. Thus, exergy analysis provides rigorous directions and attention for further improvement in order to reduce the exergy destruction as much as possible, which ultimately leads to enhance the overall process performance. The exergy destruction associated with SMR and C3MR processes for all cases (i.e., base case, GA-optimized, PSO-optimized, and VS-optimized) were performed using the expressions listed in
Table 4 [
42].
5. Results and Discussion
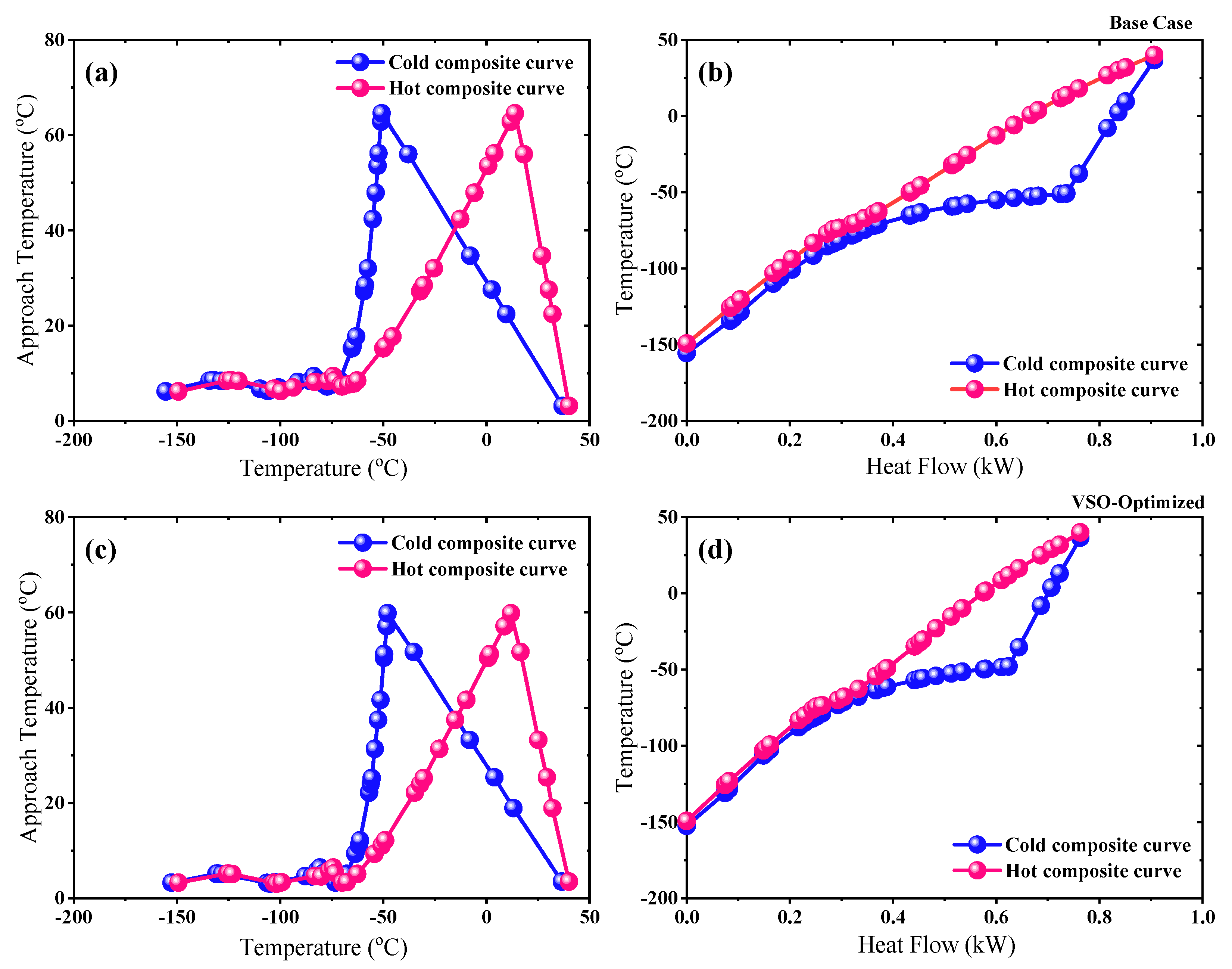
The approach temperature (temperature difference) curve also known as TDCC provides information about the behavior of MITA value along the length of the LNG heat exchangers. Accordingly, the efficient heat transfer can be achieved when the height of the TDCC is close to the specified MITA value of 3 °C. The performance of the LNG processes can also be observed through temperature-heat flow composite curves (THCC). The gap between THCC presents the exergy destruction associated with the LNG heat exchanger.
Figure 6 shows the TDCC and THCC comparison of the VSO-optimized SMR process and the published base case. It can be observed that there is a larger gap between the THCC of base case and the VSO-optimized SMR; especially in a temperature range of −70 to 40 °C. This large gap indicates the exergy destruction inside the cryogenic LNG heat exchanger, which ultimately leads to low energy efficiency. It is necessary to reduce the space/gap between THCC to decrease exergy destruction. Thus, the MR flow should be at the optimal values to cope with the inefficiency present in the system and minimize the compression power required to liquefy the natural gas. Given the application of VS optimization approach, as clearly seen in
Figure 6d, the triangular space is smaller than that of triangular area in
Figure 6b. This reduction in the gap between THCC provides a significant energy savings compared with the base case of the SMR process. It is noted that high MITA value inside multistream heat exchanger continues to exist in the temperature range of −50 and 40 °C (
Figure 6d).
The high MITA value is principally due to the existence of the more volatile component, i.e., propane. The MITA value is reduced via precooling the feed gas and MR prior to entering the LNG cryogenic heat exchanger. This type of precooling conclusively enhances the operation of the C3MR plant by decreasing the temperature gradient in the LNG cryogenic exchanger through propane precooling.
Figure 7 shows the graphical results of the C3MR process for the VS-optimized and base case study. The VS-optimized C3MR process significantly reduces the enclosed space between the THCC as shown in
Figure 7d, whereas the composite curves in the base case exhibit a relatively larger gap.
With respect to a feasible and reliable operation of any cryogenic plant, the composite curve matching approach is widely used as a thermodynamic graphical approach to determine the optimal performance of any heat exchange processes. To obtain high energy efficiency of a LNG process with low required compression power, the hot and cold steam temperature profile (i.e., composite curves) must be close to each other provided it follows the feasible approach temperature of 3 °C.
Table 5 also lists the temperature and pressure for all streams of VS-optimized SMR and C3MR processes.
The optimization of both SMR and C3MR processes was performed by employing well-matured GA and PSO algorithms. The GA and PSO both are categorized as population-based algorithms. The performance of these algorithms strongly depends on the tuning parameters, as well as initial point generation.
Table 6 lists the tuning parameters of PSO and GA, which were fixed during the optimization of SMR and C3MR. These parameters for GA and PSO were adopted from the recent LNG optimization studies [
12,
41,
43].
Furthermore,
Table 7 and
Table 8 list a comparison of the VS-optimized results of SMR and C3MR processes, respectively, with their previously published study results using other well-known optimization algorithms. The base cases for SMR and C3MR were taken from [
44]. The SMR and C3MR processes consume 0.44 and 0.3602 kW compression power to liquefy 1 kg NG with 92% liquefaction rate, respectively.
In case of the SMR process optimization, the operational energy improvements in the compression power correspond to 0.4034 and 0.3862 kW via GA and PSO approaches, respectively. The GA optimized SMR process consumes 8.32% less energy when compared to that of the SMR base case, whereas the PSO-optimized SMR process exhibits 12.23% energy savings when compared with that of the SMR base case. Finally, the VS algorithm is used to optimize the SMR process, and this ensures top-rated optimal conditions over the present approaches. The total compression power decreases by up to 0.3691 kW, and this corresponds to energy savings of 16.1% when compared to that of the base process. In the case of GA and PSO optimization of C3MR, the compression power decreases from 0.3602 to 0.2778 kW and 0.2754 kWh with energy savings equivalent to 22.9% and 23.5%, respectively, when compared to those of the base case. Finally, the VS algorithm results in a power saving of 0.26 kWh in the compression mode having power savings of approximately 27.8% when compared to that of the base case.