Toward Zero-Emission Hybrid AC/DC Power Systems with Renewable Energy Sources and Storages: A Case Study from Lake Baikal Region
Abstract
1. Introduction
1.1. Related Works
1.2. Paper Contribution
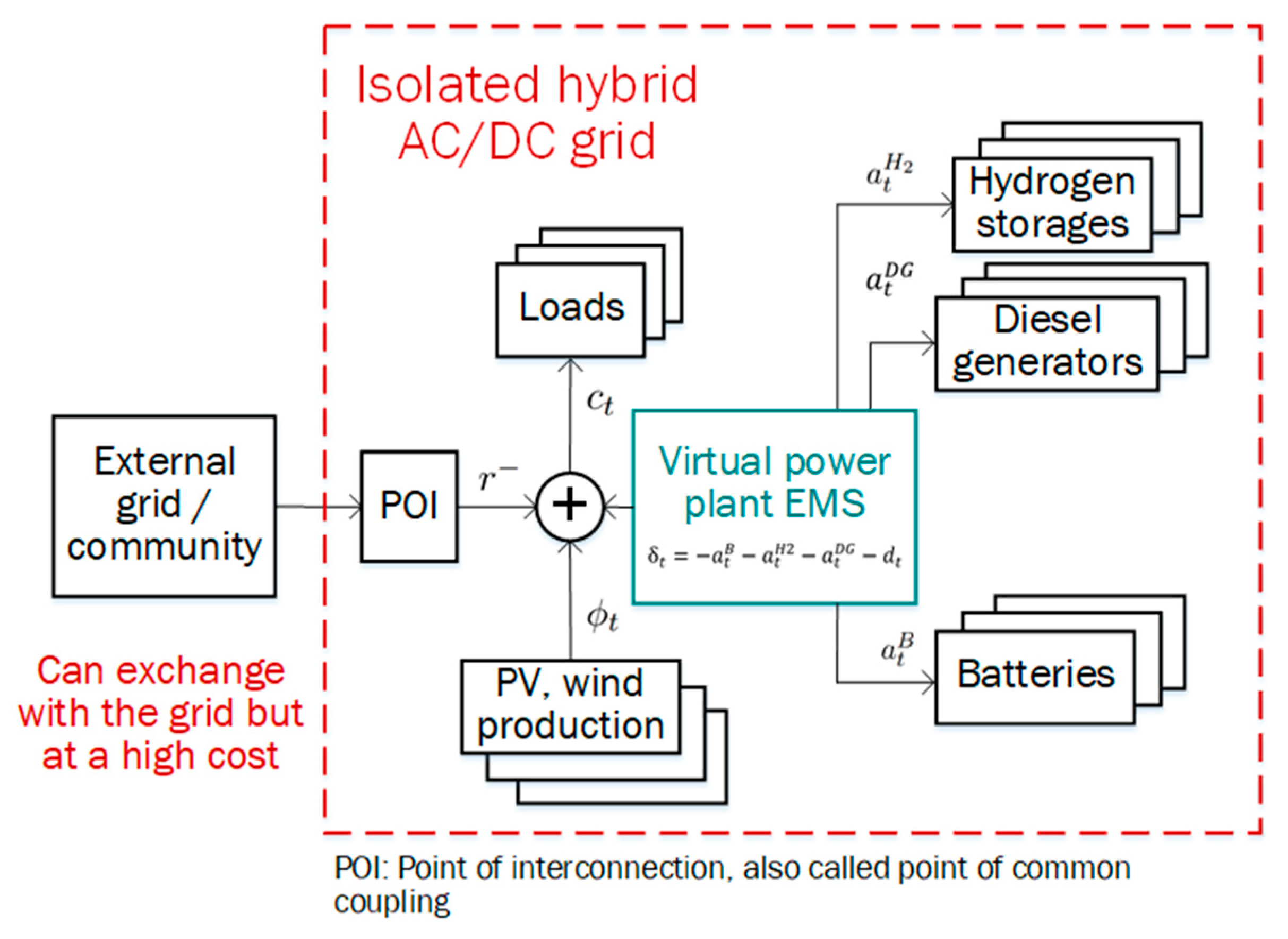
- Isolated work. At this stage the grids are isolated. Each subsystem includes the following elements: load; RES + storage and diesel generation. The control objective for every subsystem is to minimize the power supply cost by means of optimal storage management, which corresponds to minimizing the operating time of the diesel generator. The power supply cost, as well as CO2 emissions are the highest for the isolated work.
- Community forming. Integrating subsystems into a single community is possible only if there is a technical and economic feasibility. For example, the proximity of the transmission network, the reduction in the cost of electricity compared to diesel generation, etc. In this case, after MGs smart connection, the cost of power supply, as well as CO2 emissions will decrease.
- AC/DC system planning. This task is relatively new and poorly studied. Given the high degree of uncertainty due to the complexity of the structure, the presence of RES and storages, as well as a large number of owners, the selection of specific criteria for optimal planning is quite complicated. The most successful, in our opinion, attempt was made in [18].
- AC/DC operational and emergency control-optimal control of normal and emergency conditions for the given network structure.
2. Methodology
2.1. Hybrid Network Operational Control Algorithm
- the more efficient allocation of resources, allowing energy trading at more favorable prices;
- the provision of aggregated reserve,
- decrease in peak power cost.
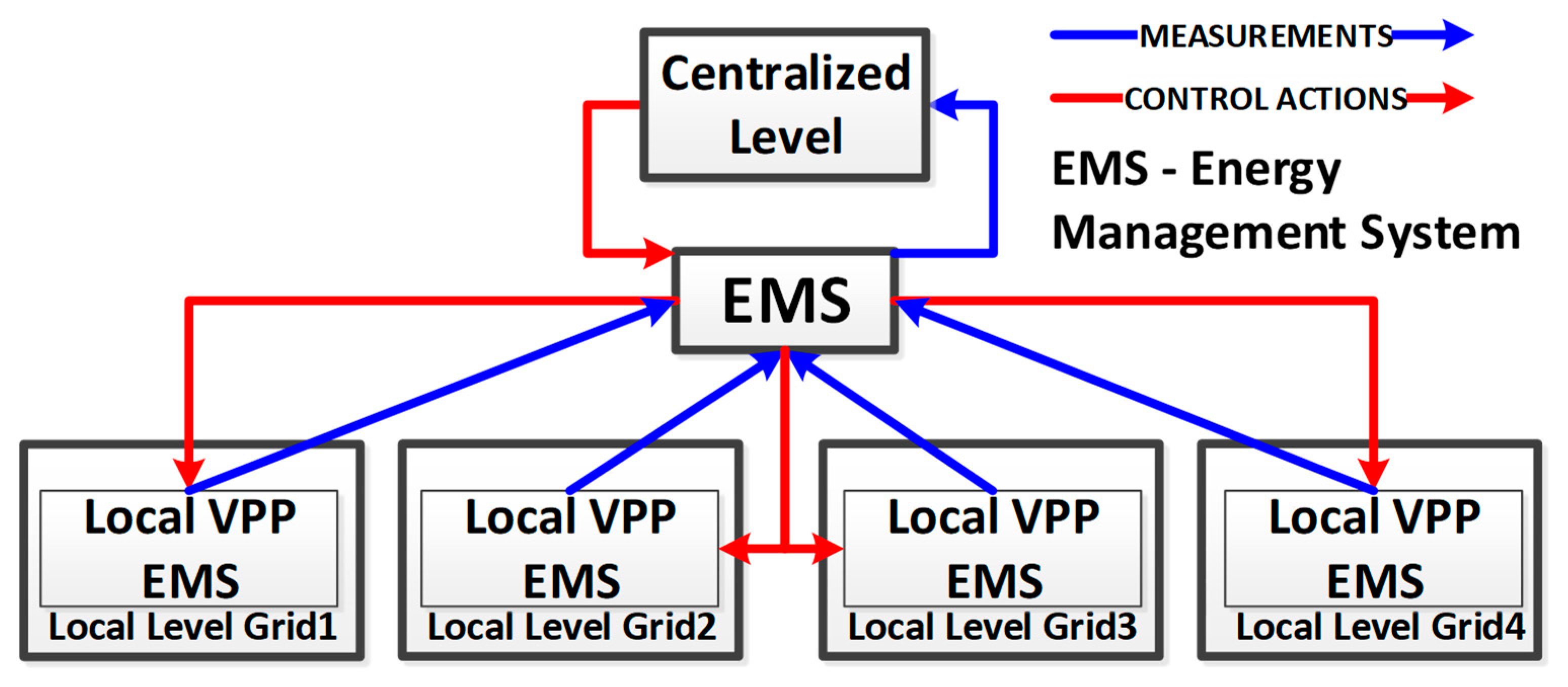
2.1.1. Local Level
2.1.2. Centralized Level
2.1.3. The Relationship between Local and Centralized Levels
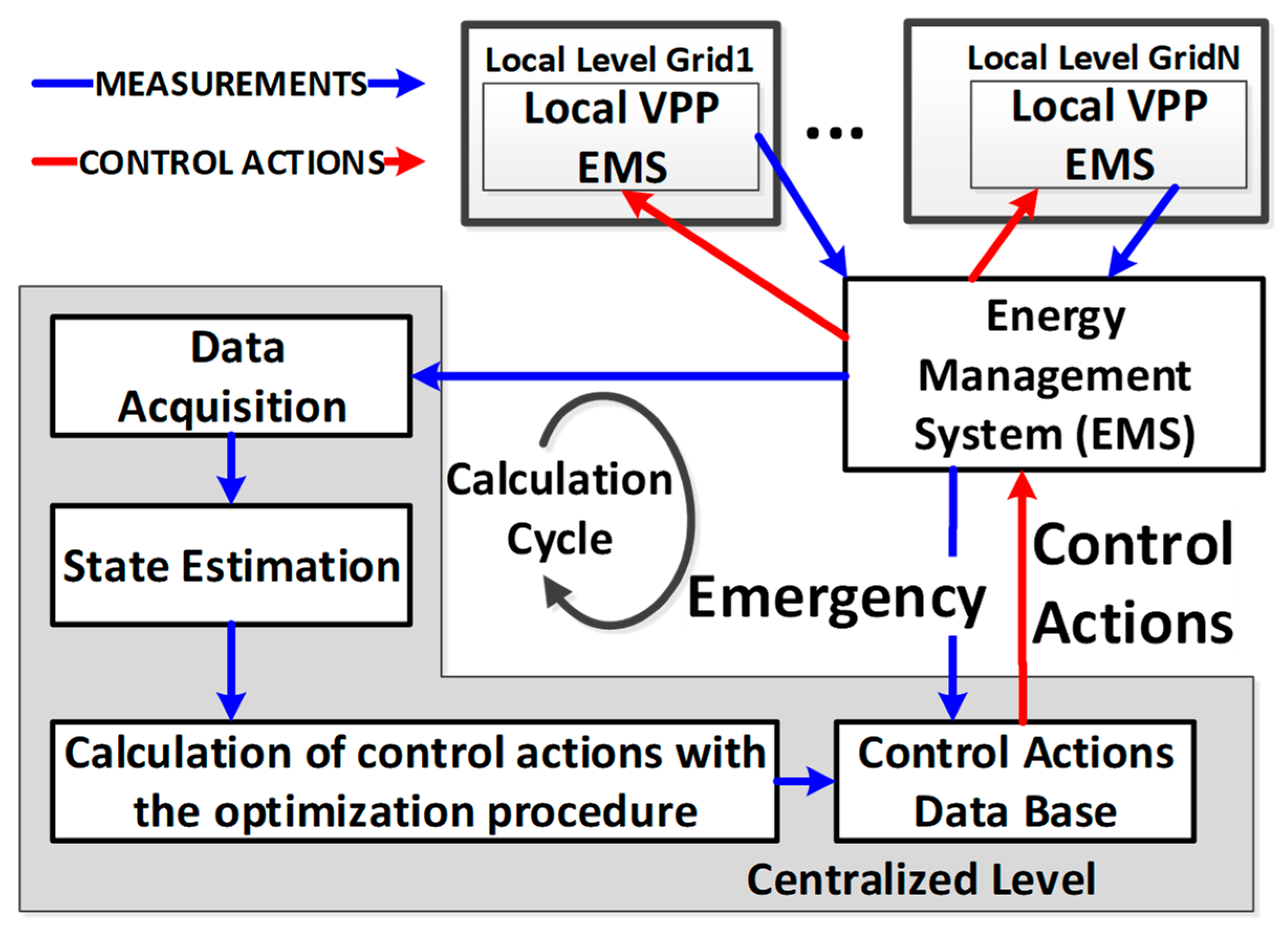
2.2. Hybrid Network Emergency Control Algorithm
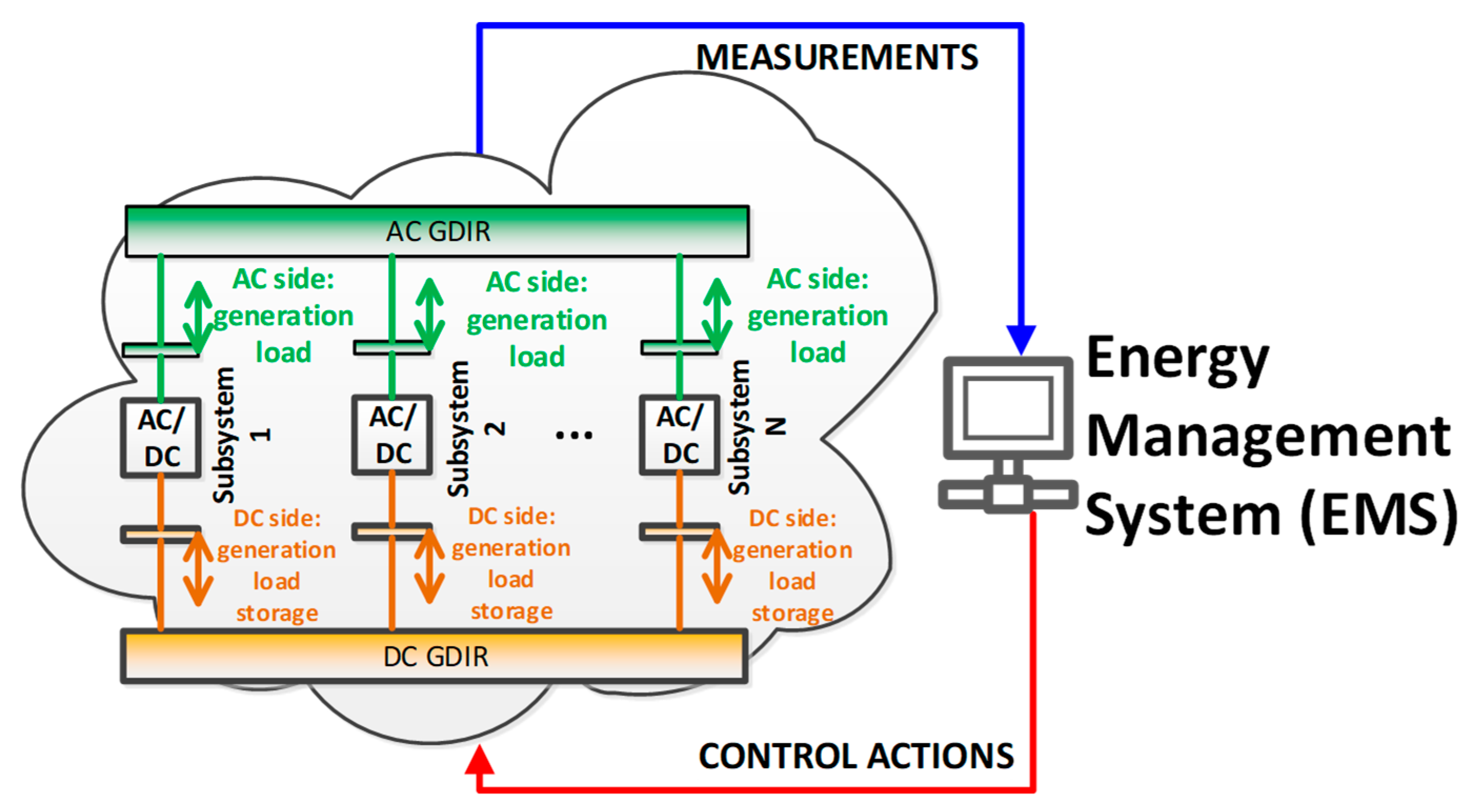
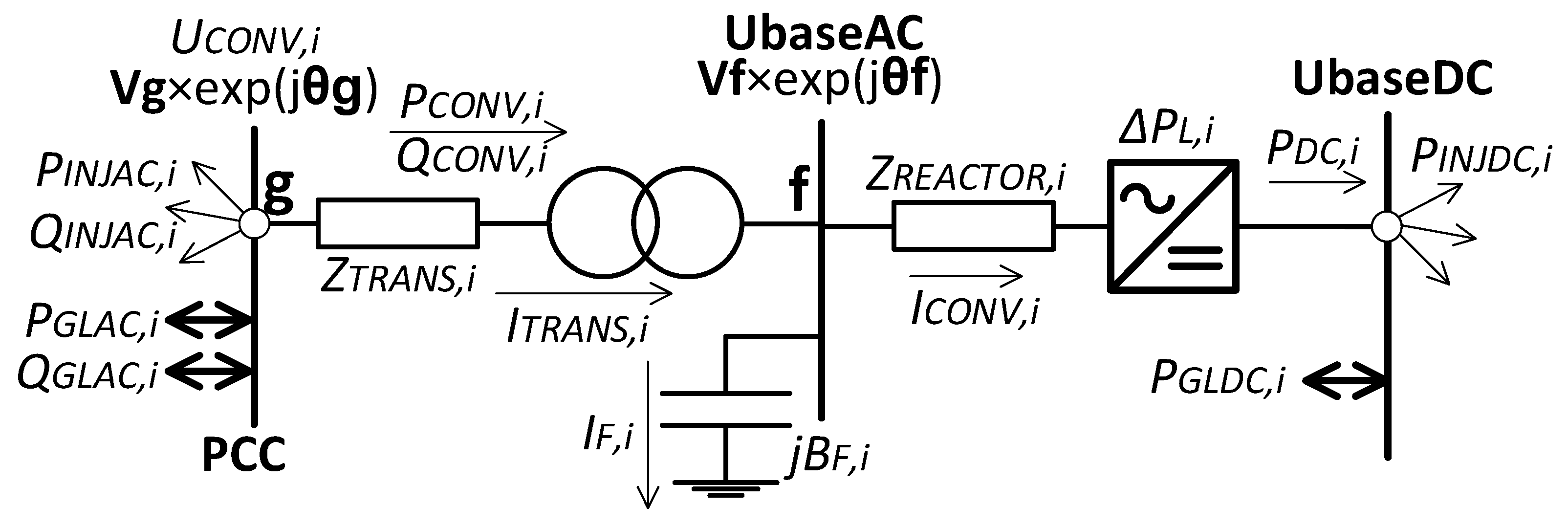
2.3. Power Flow Equations of Hybrid Systems
2.3.1. AC Side Equations
2.3.2. DC Side Equations
3. Case Study and Performance Assessment
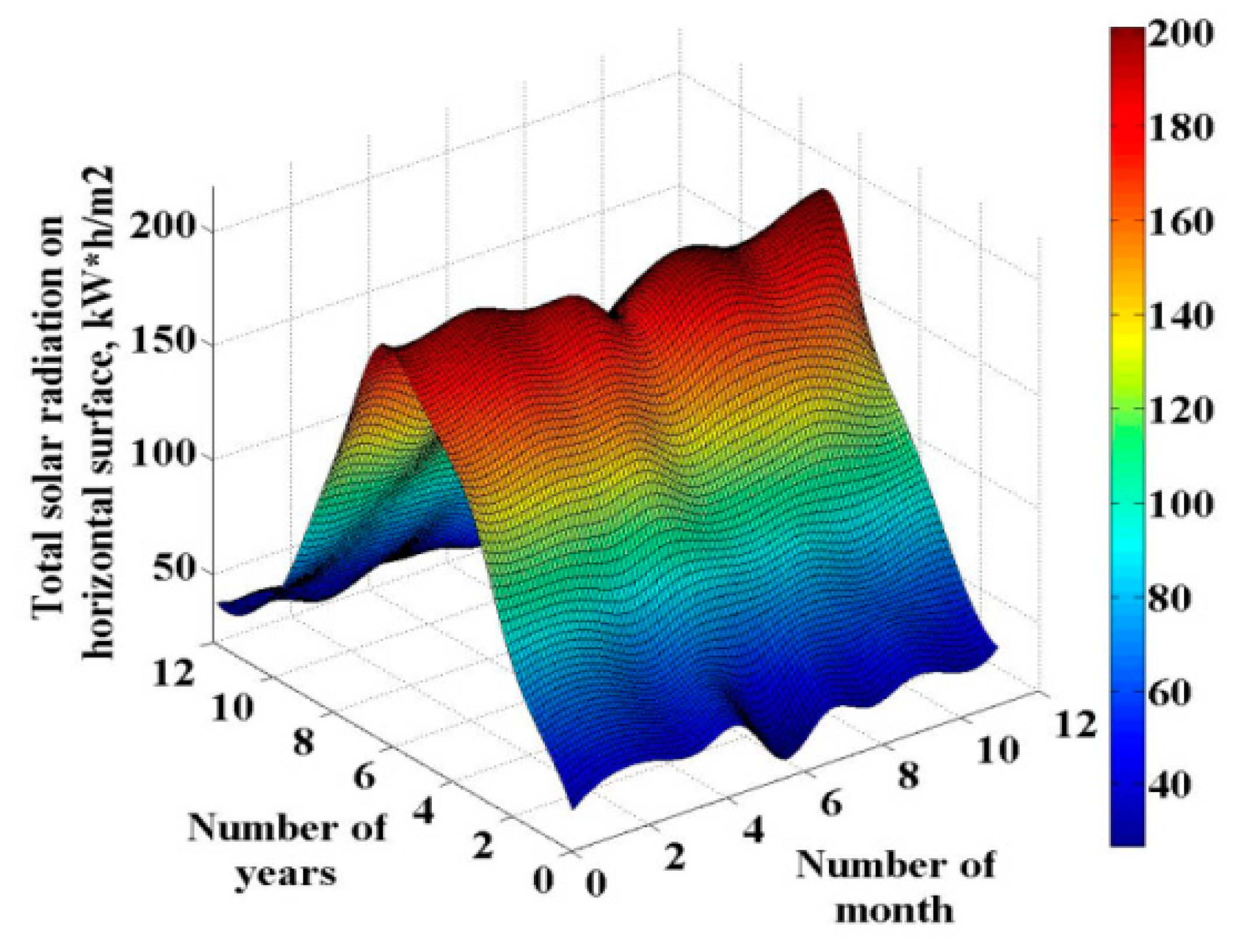
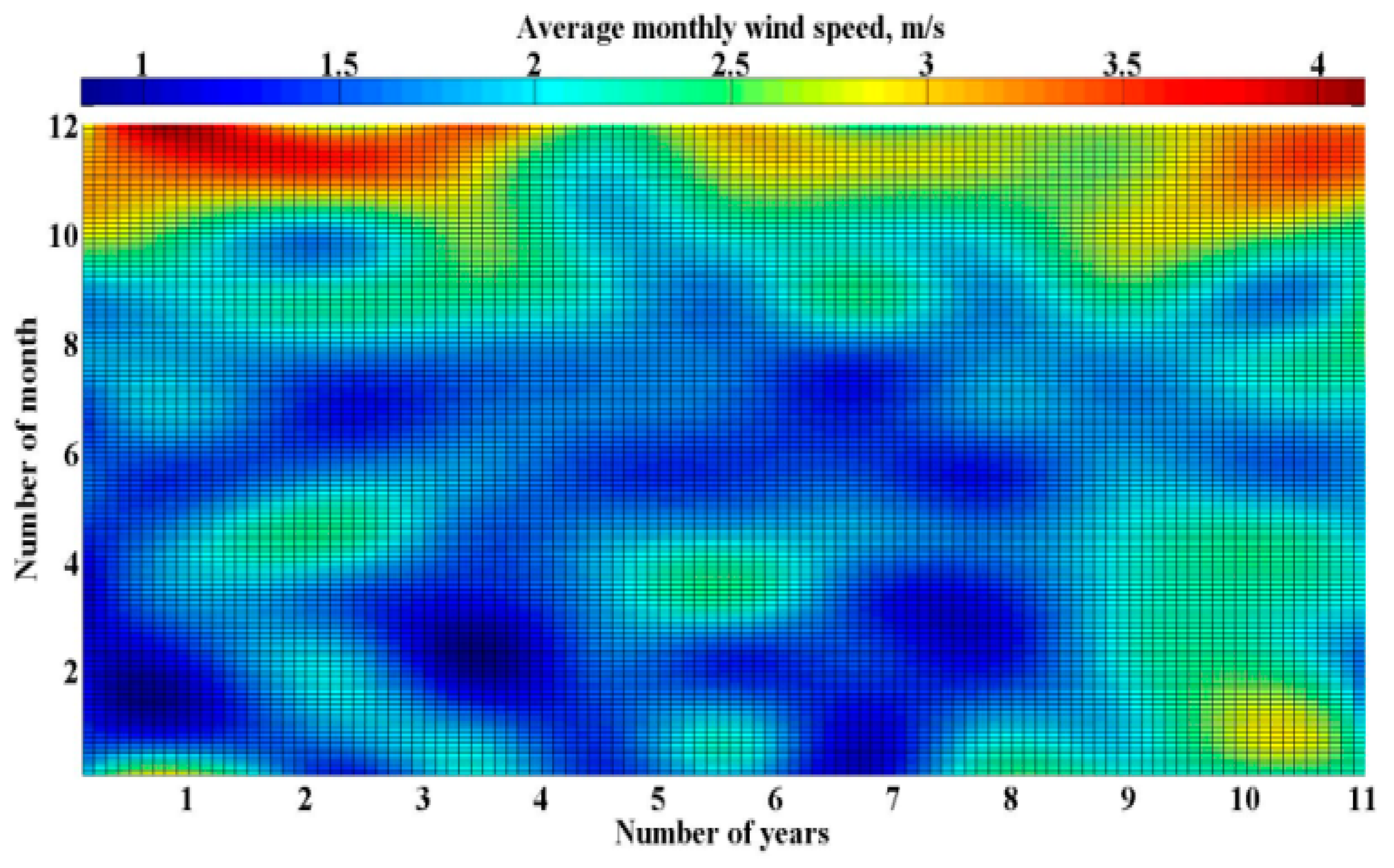
3.1. Data Sets
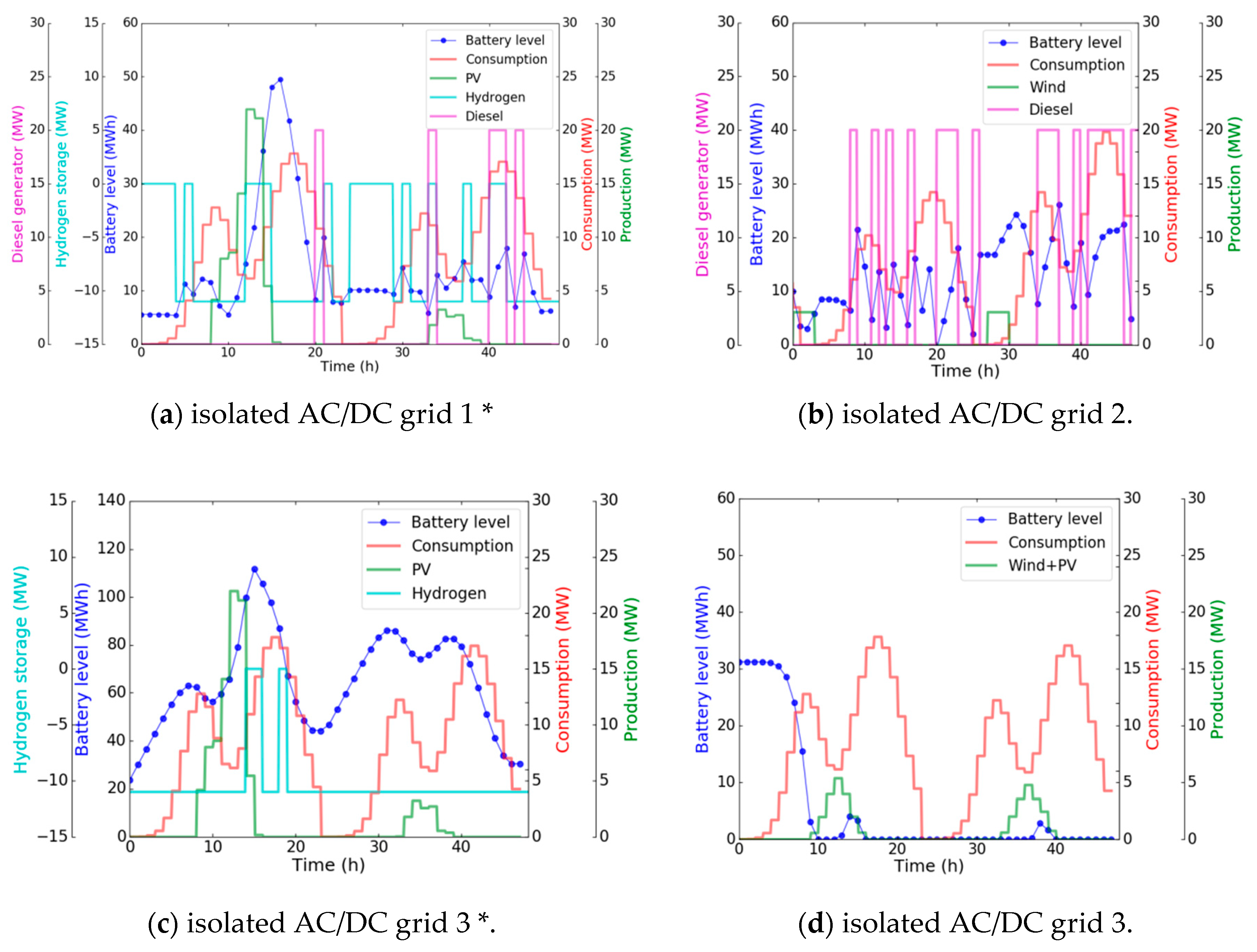
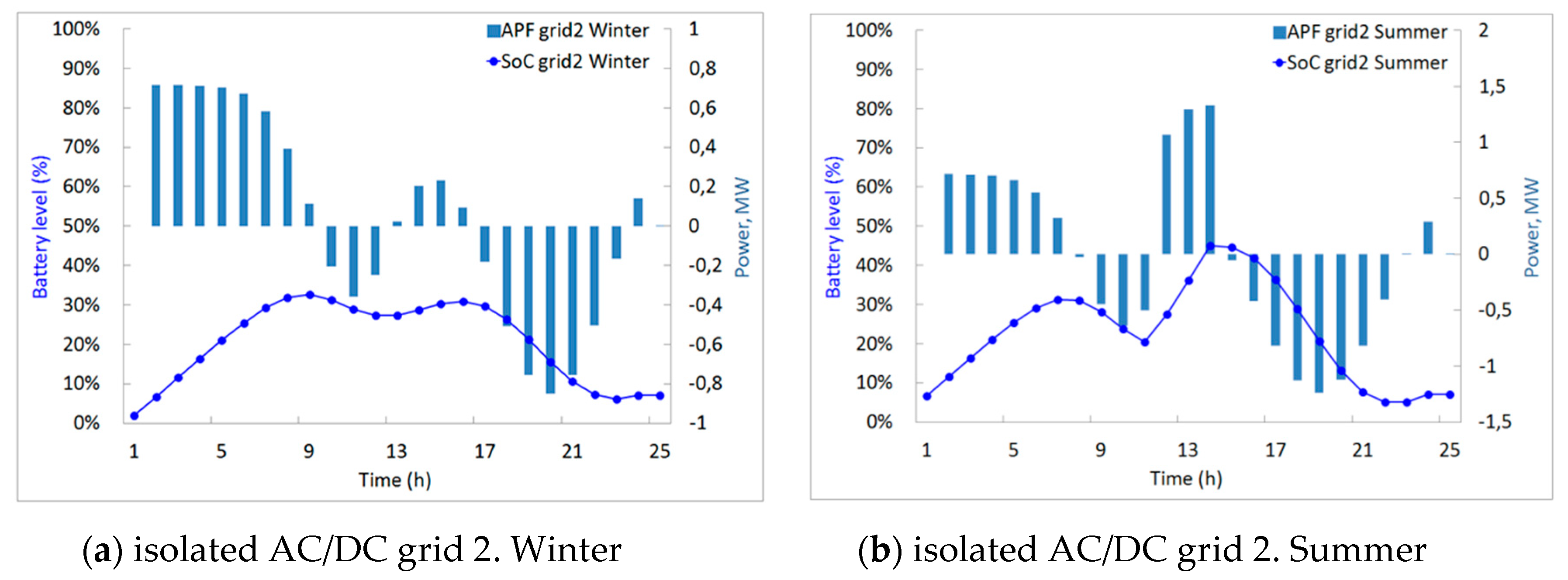
3.2. Local Level of Energy Grid Management
3.3. Load Leveling in MGs Using System of Volterra Equations
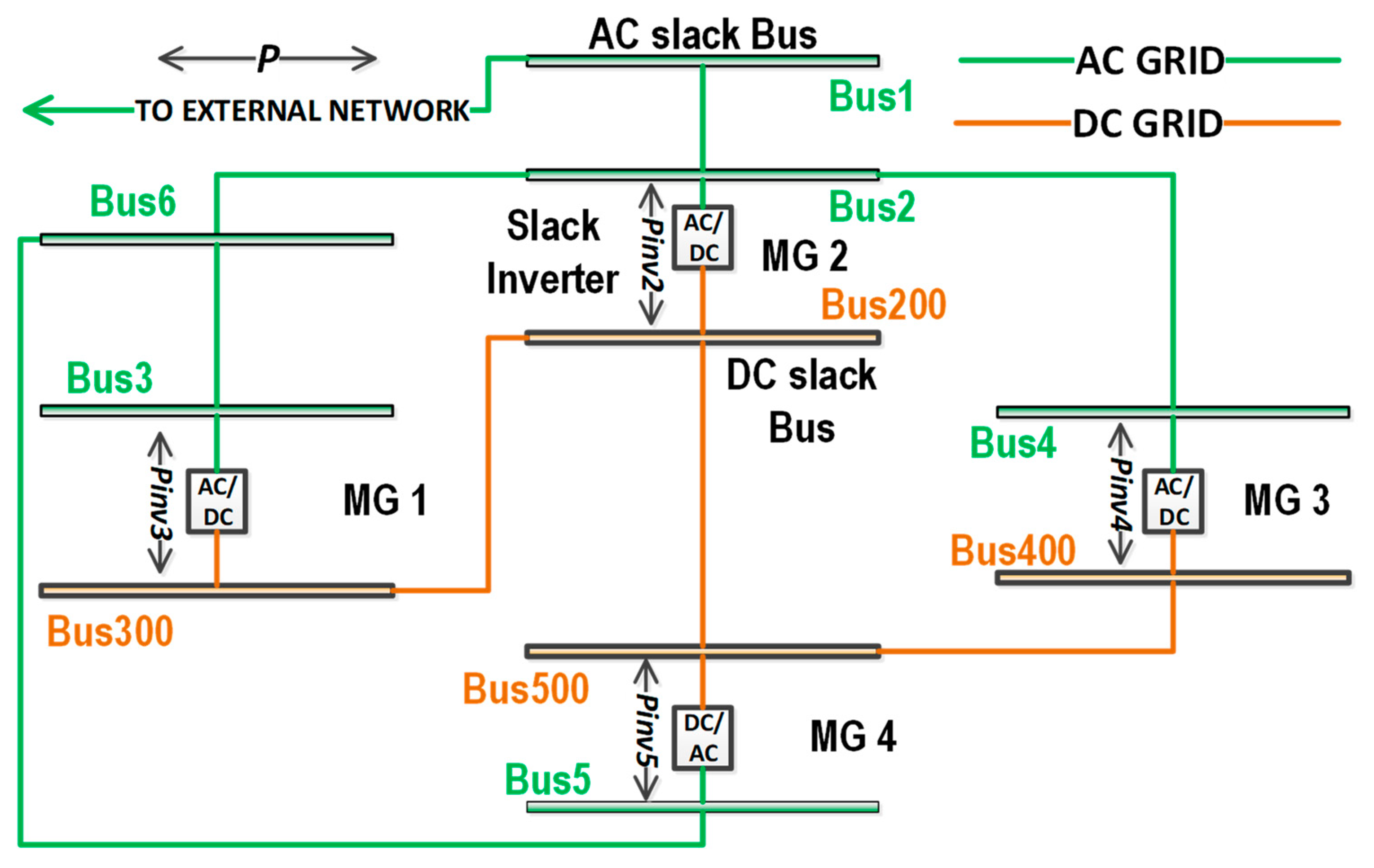
3.4. Hybrid AC/DC Test System
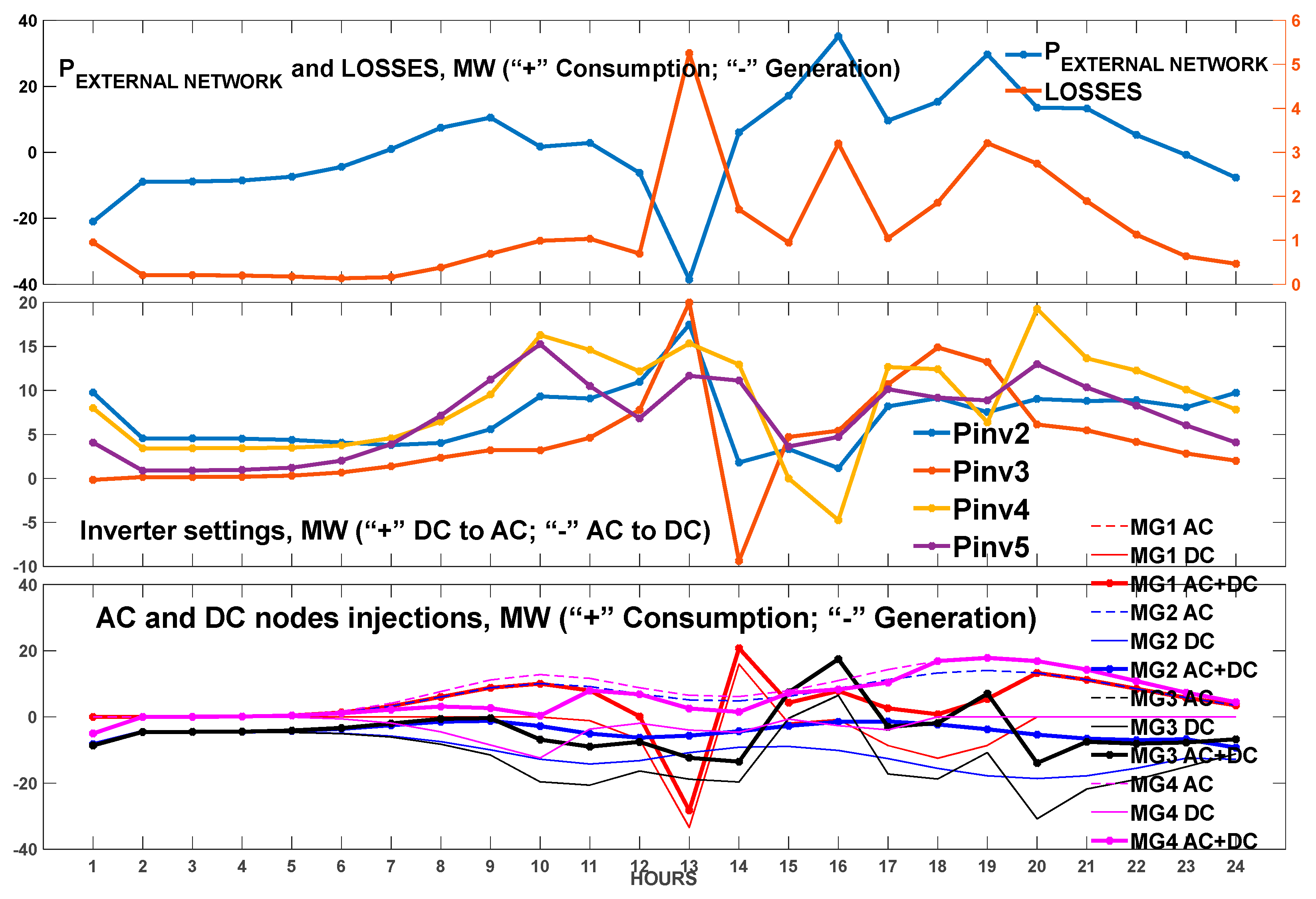
3.5. Centralized Level Operational Control of the Test System
4. Conclusions, Discussion and Further Work
Author Contributions
Funding
Conflicts of Interest
References
- Renewable Capacity Statistics 2019; International Renewable Energy Agency (IRENA): Abu Dhabi, UAE, 2019; p. 60.
- International Renewable Energy Agency (IRENA). Remap 2030. A Renewable Energy Roadmap. Available online: http://www.ourenergypolicy.org/wp-content/uploads/2014/06/REmap.pdf (accessed on 31 January 2020).
- Climate Change 2013. The Physical Science Basis. Working Group I Contribution to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change. Available online: http://www.climatechange2013.org/images/report/WG1AR5_ALL_FINAL.pdf (accessed on 31 January 2020).
- Kyoto Protocol to the United Nations Framework Convention on Climate Change. Available online: https://unfccc.int/resource/docs/convkp/kpeng.pdf (accessed on 31 January 2020).
- The Paris Agreement. A New Framework for Global Climate Action. Available online: http://www.europarl.europa.eu/RegData/etudes/BRIE/2016/573910/EPRS_BRI(2016)573910_EN.pdf (accessed on 31 January 2020).
- Pineda, S.; Bock, A. Renewable-Based generation expansion under a green certificate market. Renew. Energy 2016, 91, 53–63. [Google Scholar] [CrossRef]
- Zamfir, A.; Colesca, S.E.; Corbos, R.-A. Public policies to support the development of renewable energy in Romania: A review. Renew. Sustain. Energy Rev. 2016, 58, 87–106. [Google Scholar] [CrossRef]
- Govinda, R.; Timilsina, B.; Kalim, U.S. Filling the gaps: Policy supports and interventions for scaling up renewable energy development in Small Island Developing States. Energy Policy 2016, 98, 653–662. [Google Scholar]
- Tremblay, O.; Dessaint, L.A.; Dekkiche, A.I. A Generic Battery Model for the Dynamic Simulation of Hybrid Electric Vehicles. In Proceedings of the Vehicle Power and Propulsion Conference, Arlington, TX, USA, 11–14 December 2007; pp. 284–289. [Google Scholar]
- Hampton, S.E.; Izmest’eva, L.R.; Moore, M.V.; Katz, S.L.; Dennis, B.; Silow, E.A. Sixty years of environmental change in the world’s largest freshwater lake–Lake Baikal, Siberia. Glob. Chang. Biol. 2008, 14, 1947–1958. [Google Scholar] [CrossRef]
- Community-Scale Isolated Power Systems. Powering the Blue Economy: Exploring Opportunities for Marine Renewable Energy in Maritime Markets. April 2019. Available online: https://www.energy.gov/sites/prod/files/2019/09/f66/73355-9.pdf (accessed on 31 January 2020).
- Chaudhary, S.K.; Guerrero, J.M.; Teodorescu, R. Enhancing the capacity of the AC distribution system using DC interlinks–A step toward future DC grid. IEEE Trans. Smart Grid 2015, 6, 1722–1729. [Google Scholar] [CrossRef]
- Kurohane, K.; Senjyu, T.; Yona, A.; Urasaki, N.; Goya, T.; Funabashi, T. A hybrid smart AC/DC power system. IEEE Trans. Smart Grid 2010, 1, 199–204. [Google Scholar] [CrossRef]
- El Nozahy, M.S.; Salama, M.M.A. Uncertainty-Based design of a bilayer distribution system for improved integration of PHEVs and PV arrays. IEEE Trans. Sustain. Energy 2015, 6, 659–674. [Google Scholar] [CrossRef]
- Kaipia, T.; Salonen, P.; Lassila, J.; Partanen, J. Application of low voltage DC distribution system, a techno-Economical study. In Proceedings of the 19th International Conference on Electricity Distribution, Vienna, Austria, 21–24 May 2007. [Google Scholar]
- Lotfjou, A.; Fu, Y.; Shahidehpour, M. Hybrid AC/DC transmission expansion planning. IEEE Trans. Power Del. 2012, 27, 1620–1628. [Google Scholar] [CrossRef]
- Doagou-Mojarrad, H.; Rastegar, H.; Gharehpetian, G.B. Probabilistic multi-Objective HVDC/AC transmission expansion planning considering distant wind/solar farms. IET Sci. Meas. Technol. 2016, 10, 140–149. [Google Scholar] [CrossRef]
- Ahmed, H.M.A.; Eltantawy, A.B.; Salama, M.M.A. A Planning Approach for the Network Configuration of AC-DC Hybrid Distribution Systems. IEEE Trans. Smart Grid 2018, 9, 2203–2213. [Google Scholar] [CrossRef]
- Asimakopoulou, G.E.; Dimeas, A.L.; Hatziargyriou, N.D. Leader follower strategies for energy management of multi-Microgrids. IEEE Trans. Smart Grid 2013, 4, 1909–1916. [Google Scholar] [CrossRef]
- Nguyen, T.A.; Crow, M. Stochastic optimization of renewable based microgrid operation incorporating battery operating cost. IEEE Trans. Power Syst. 2016, 31, 2289–2296. [Google Scholar] [CrossRef]
- Francois-Lavet, V.; Tarella, D.; Ernst, D.; Forteneau, R. Deep Reinforcement Learning Solutions for Energy Microgrids Management. European Workshop on Reinforcement Learning. 2016. Available online: http://hdl.handle.net/2268/203831 (accessed on 31 January 2020).
- Tomin, N.; Zhukov, A.; Domyshev, A. Deep Reinforcement Learning for Energy Microgrids Management Considering Flexible Energy Sources. In Proceedings of the EPJ Web Conference 217-2019 International Workshop on Flexibility and Resiliency Problems of Electric Power Systems, Irkutsk, Russia, 26–31 August 2019; Available online: https://doi.org/10.1051/epjconf/201921701016 (accessed on 31 January 2020).
- Duan, J.; Yi, Z.; Shi, D.; Lin, C.; Lu, X.; Wang, Z. Reinforcement-Learning-Based Optimal Control for Hybrid Energy Storage Systems in Hybrid AC/DC Microgrids. IEEE Trans. Ind. Inform. 2019. [Google Scholar] [CrossRef]
- Ji, Y.; Wang, J.; Xu, J.; Fang, X.; Zhang, H. Real-Time Energy Management of a Microgrid Using Deep Reinforcement Learning. Energies 2019, 12, 2291. [Google Scholar] [CrossRef]
- Marvasti, A.K.; Fu, Y.; DorMohammadi, S.; Rais-Rohani, M. Optimal operation of active distribution grids: A system of systems framework. IEEE Trans. Smart Grid 2014, 5, 1228–1237. [Google Scholar] [CrossRef]
- Lv, T.; Ai, Q.; Zhao, Y. A bi-Level multi-Objective optimal operation of grid-Connected microgrids. Electr. Power Syst. Res. 2016, 131, 60–70. [Google Scholar] [CrossRef]
- Erol-Kantarci, M.; Kantarci, B.; Mouftah, H.T. Reliable overlay topology design for the smart microgrid network. IEEE Netw. 2011, 25, 38–43. [Google Scholar] [CrossRef]
- Wang, Z.; Chen, B.; Wang, J.; Begovic, M.M.; Chen, C. Coordinated energy management of networked microgrids in distribution systems. IEEE Trans. Smart Grid 2015, 6, 45–53. [Google Scholar] [CrossRef]
- Wu, J.; Guan, X. Coordinated multi-Microgrids optimal control algorithm for smart distribution management system. IEEE Trans. Smart Grid 2013, 4, 2174–2181. [Google Scholar] [CrossRef]
- Li, Y.; Zhao, T.; Wang, P.; Gooi, H.B.; Wu, L.; Liu, Y.; Ye, J. Optimal operation of multi-Microgrids via cooperative energy and reserve scheduling. IEEE Trans. Ind. Inform. 2018, 14, 3459–3468. [Google Scholar] [CrossRef]
- Cornélusse, B.; Savelli, I.; Paoletti, S.; Giannitrapani, A.; Vicino, A. A community microgrid architecture with an internal local market. Appl. Energy 2019, 242, 547–560. [Google Scholar] [CrossRef]
- lavic, M.; Fonteneau, R.; Ernst, D. Reinforcement Learning for Electric Power System Decision and Control: Past Considerations and Perspectives. IFAC-PapersOnLine 2017, 50, 6918–6927. [Google Scholar]
- Mnih, V.; Kavukcuoglu, K.; Silver, D.; Rusu, A.A.; Veness, J.; Bellemare, G.M.; Graves, A.; Riedmiller, M.; Fidjeland, A.K.; Ostrovski, G.; et al. Human-Level control through deep reinforcement learning. Nature 2015, 518, 529–533. [Google Scholar] [CrossRef] [PubMed]
- Sidorov, D.; Muftahov, I.; Tomin, N.; Karamov, D.; Panasetsky, D.; Dreglea, A.; Liu, F.; Foley, A. A Dynamic Analysis of Energy Storage with Renewable and Diesel Generation using Volterra Equations. IEEE Trans. Ind. Inform. 2019, 16, 3451–3459. [Google Scholar] [CrossRef]
- Sidorov, D.; Tao, Q.; Muftahov, I.; Zhukov, A.; Karamov, D.; Dreglea, A.; Liu, F. Energy balancing using charge/discharge storages control and load forecasts in a renewable-Energy-Based grids. In Proceedings of the 2019 Chinese Control Conference (CCC), Guangzhou, China, 27–30 July 2019; pp. 6865–6870. [Google Scholar] [CrossRef]
- Muftahov, I.R.; Sidorov, D.N. Solvability and numerical solutions of systems of nonlinear volterra integral equations of the first kind with piecewise continuous kernels. Bull. South Ural State Univ. Ser. Math. Model. Program. Comput. Softw. 2016, 9, 130–136. [Google Scholar] [CrossRef]
- Muftahov, I.; Tynda, A.; Sidorov, D. Numeric solution of Volterra integral equations of the first kind with discontinuous kernels. J. Comput. Appl. Math. 2017, 313, 119–128. [Google Scholar] [CrossRef]
- Baradar, M.; Ghandhari, M.A. Multi-Option Unified Power Flow Approach for Hybrid AC/DC Grids Incorporating Multi-Terminal VSC-HVDC. IEEE Trans. Power Syst. 2013, 28, 2376–2383. [Google Scholar] [CrossRef]
- Beerten, J.; Belmans, R. Development of an open source power flow software for high voltage direct current grids and hybrid AC/DC systems: MATACDC. IET Gener. Transm. Distrib. 2015, 9, 966–974. [Google Scholar] [CrossRef]
- Liu, C.; Zhang, B.; Hou, Y.; Wu, F.F.; Liu, Y. An Improved Approach for AC-DC Power Flow Calculation With Multi-Infeed DC Systems. IEEE Trans. Power Syst. 2011, 26, 862–869. [Google Scholar] [CrossRef]
- Tzeng, Y.S.; Chen, N.; Wu, R.N. A detailed R-L fed bridge converter model for power flow studies in industrial AC/DC power systems. IEEE Trans. Ind. Electron. 1995, 42, 531–538. [Google Scholar] [CrossRef]
| Isolated AC/DC Power Grid | Aggregated Power Capacity of DERs | |||||
|---|---|---|---|---|---|---|
| PV, MWp | Wind, MW | PV + Wind, MW | Batteries, MWh | Hydrogen Storages, MW | Diesel Generator, MW | |
| 1 | 120 | - | - | 150 | 11 | 20 |
| 1 | - | 220 | - | 300 | - | 20 |
| 1 | 120 | - | - | 150 | 11 | - |
| 1 | - | - | 33 + 186 | 180 | - | - |
| AC Network | DC Network | ||||||
|---|---|---|---|---|---|---|---|
| From | To | Circuit Number | R,p.u. | X,p.u. | From | To | R,p.u. |
| 1 | 2 | 1 | 0.0017 | 0.0016 | 200 | 300 | 0.00685 |
| 1 | 2 | 2 | 0.0017 | 0.0016 | 200 | 500 | 0.01371 |
| 2 | 6 | 1 | 0.0068 | 0.0065 | 500 | 400 | 0.00685 |
| 2 | 6 | 2 | 0.0068 | 0.0065 | AC side: Ubase = 35 kV, Sbase = 1 MVA; DC side: Ubase = 35 kV, Sbase= 1 MVA; Inverter 2–Udc = const Inverter 3,4,5–Pinv = const PinvMAX = +/− 20 MW | ||
| 6 | 3 | 1 | 3.42 × 106 | 3.42 × 106 | |||
| 6 | 3 | 2 | 3.42 × 106 | 3.42 × 106 | |||
| 6 | 5 | 1 | 0.0068 | 0.0065 | |||
| 6 | 5 | 2 | 0.0068 | 0.0065 | |||
| 2 | 4 | 1 | 0.0068 | 0.0065 | |||
| 2 | 4 | 2 | 0.0068 | 0.0065 | |||
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sidorov, D.; Panasetsky, D.; Tomin, N.; Karamov, D.; Zhukov, A.; Muftahov, I.; Dreglea, A.; Liu, F.; Li, Y. Toward Zero-Emission Hybrid AC/DC Power Systems with Renewable Energy Sources and Storages: A Case Study from Lake Baikal Region. Energies 2020, 13, 1226. https://doi.org/10.3390/en13051226
Sidorov D, Panasetsky D, Tomin N, Karamov D, Zhukov A, Muftahov I, Dreglea A, Liu F, Li Y. Toward Zero-Emission Hybrid AC/DC Power Systems with Renewable Energy Sources and Storages: A Case Study from Lake Baikal Region. Energies. 2020; 13(5):1226. https://doi.org/10.3390/en13051226
Chicago/Turabian StyleSidorov, Denis, Daniil Panasetsky, Nikita Tomin, Dmitriy Karamov, Aleksei Zhukov, Ildar Muftahov, Aliona Dreglea, Fang Liu, and Yong Li. 2020. "Toward Zero-Emission Hybrid AC/DC Power Systems with Renewable Energy Sources and Storages: A Case Study from Lake Baikal Region" Energies 13, no. 5: 1226. https://doi.org/10.3390/en13051226
APA StyleSidorov, D., Panasetsky, D., Tomin, N., Karamov, D., Zhukov, A., Muftahov, I., Dreglea, A., Liu, F., & Li, Y. (2020). Toward Zero-Emission Hybrid AC/DC Power Systems with Renewable Energy Sources and Storages: A Case Study from Lake Baikal Region. Energies, 13(5), 1226. https://doi.org/10.3390/en13051226









