Decentralized Control Method of ISOP Converter for Input Voltage Sharing and Output Current Sharing in Current Control Loop
Abstract
:1. Introduction
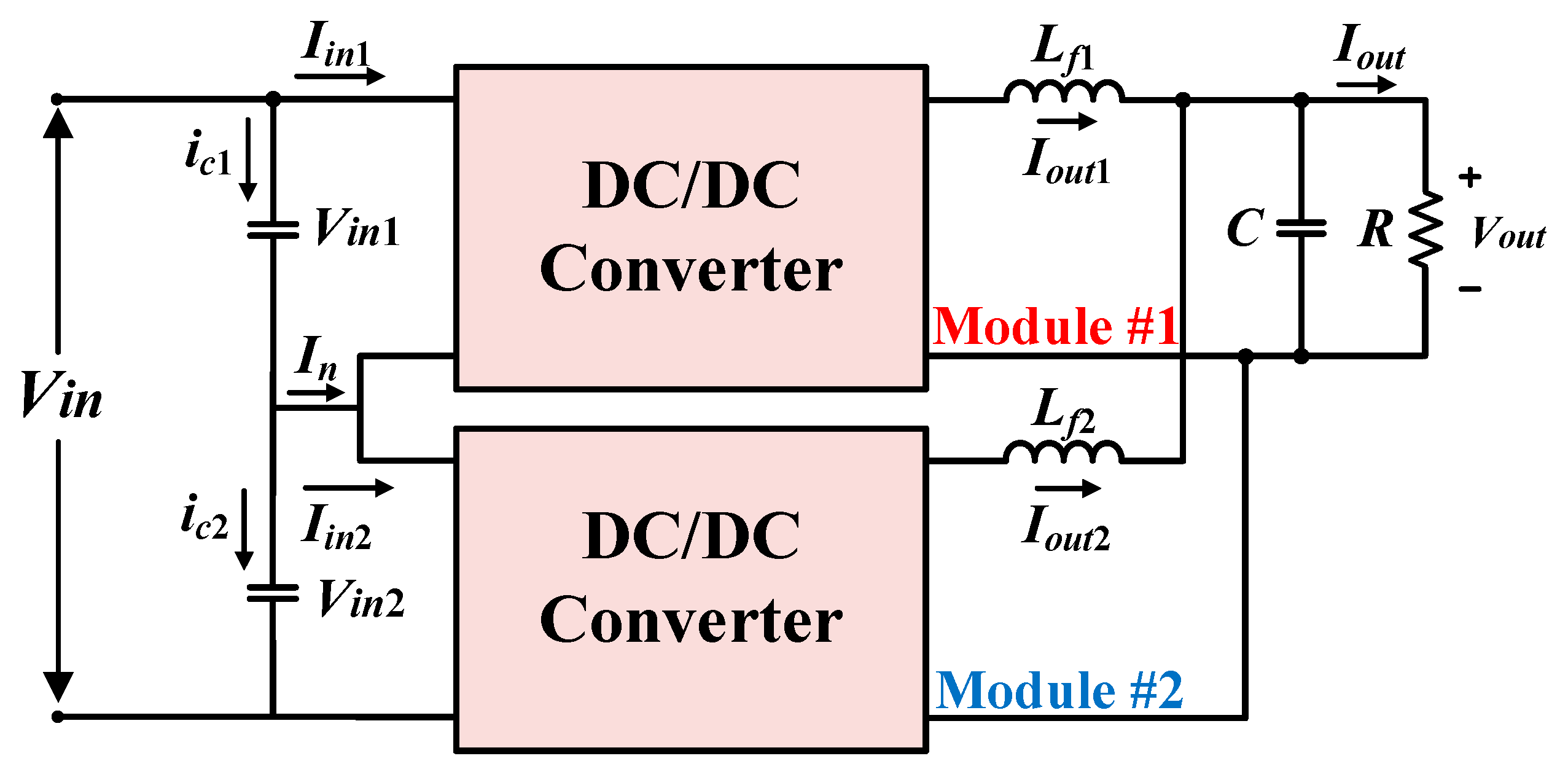
2. Decentralized Control Method
2.1. Operation Principle of Decentralized Control Method
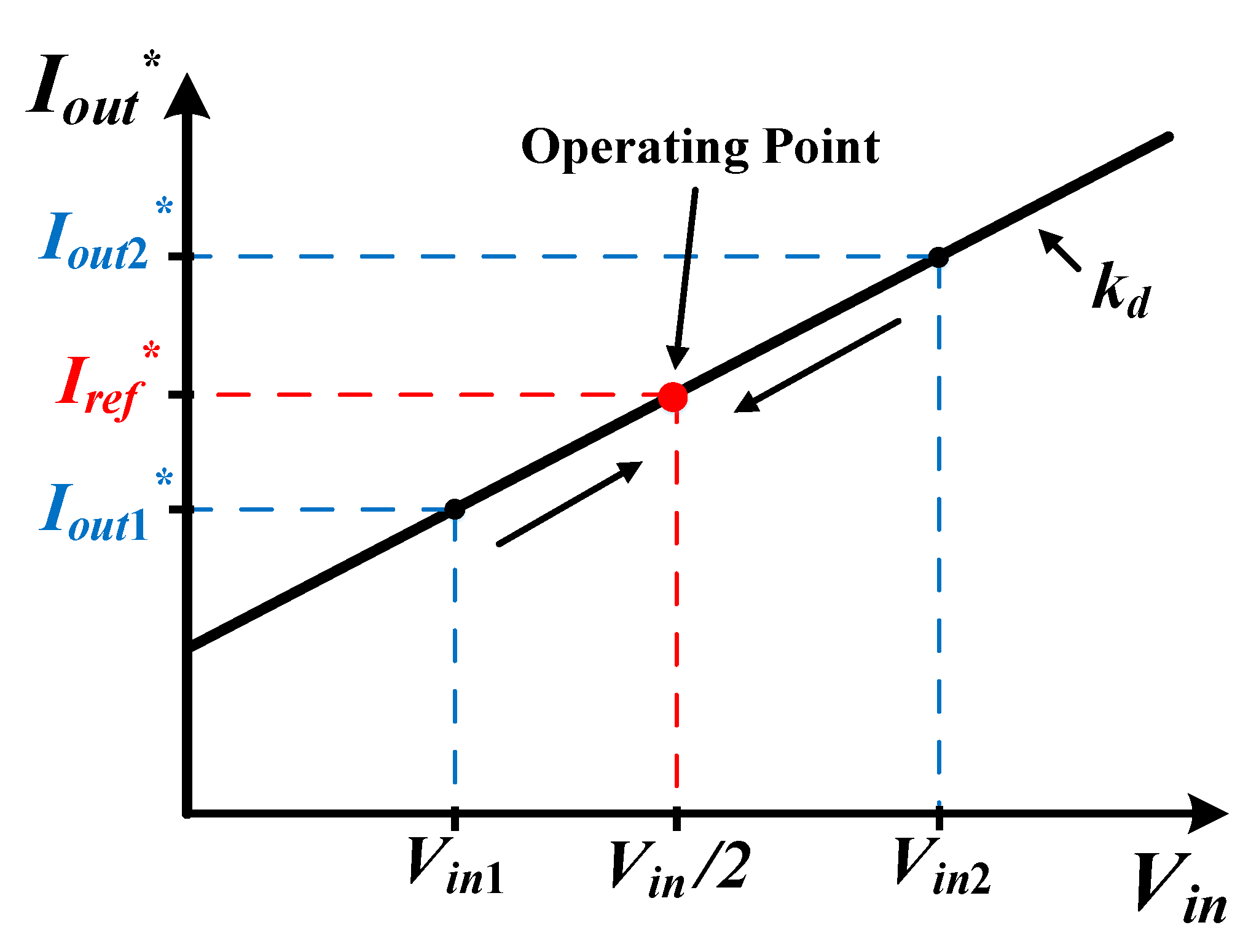
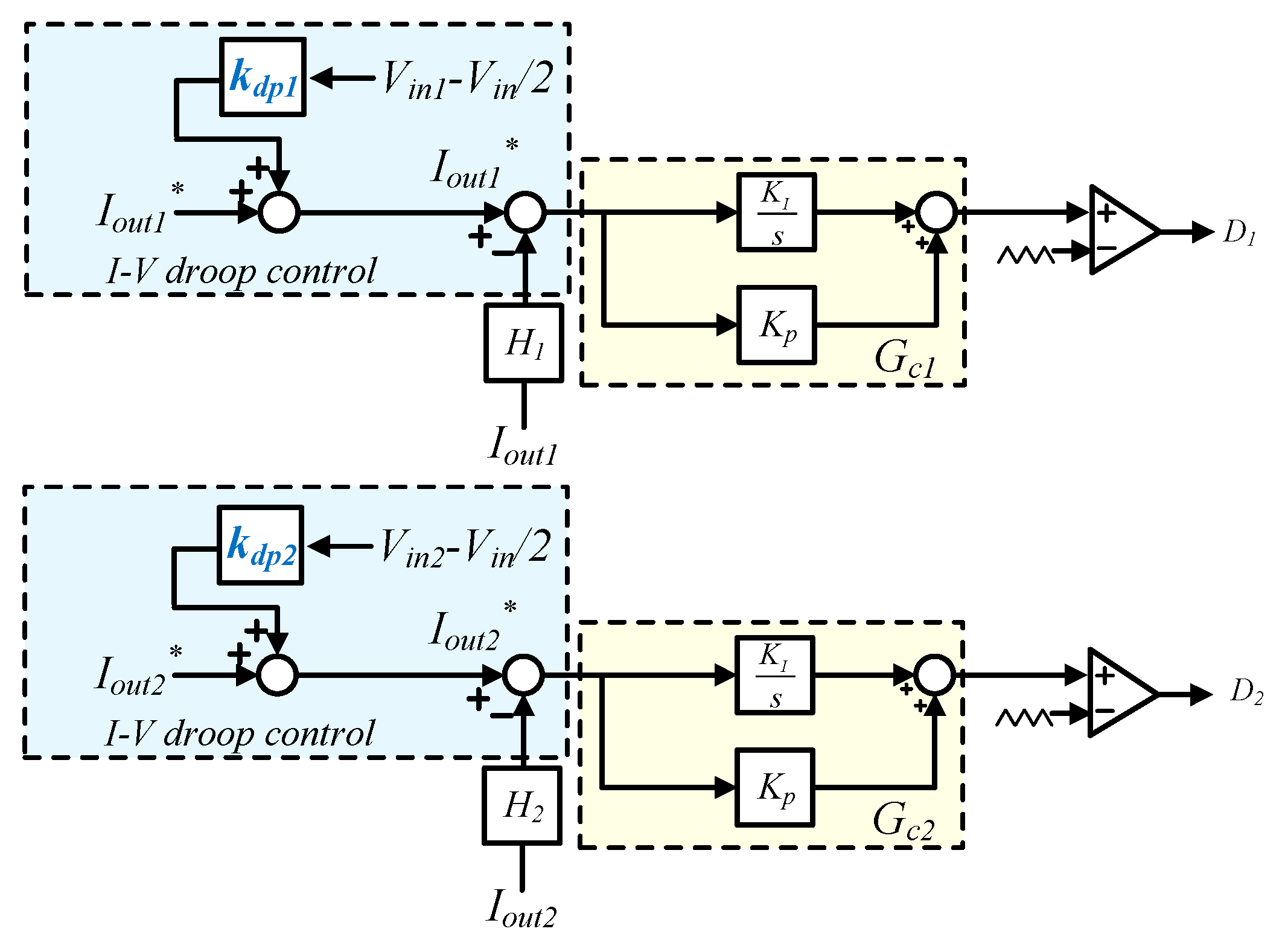
2.2. Proposed Decentralized Control Method
3. Stability Analysis of ISOP Converter with Proposed Control Method
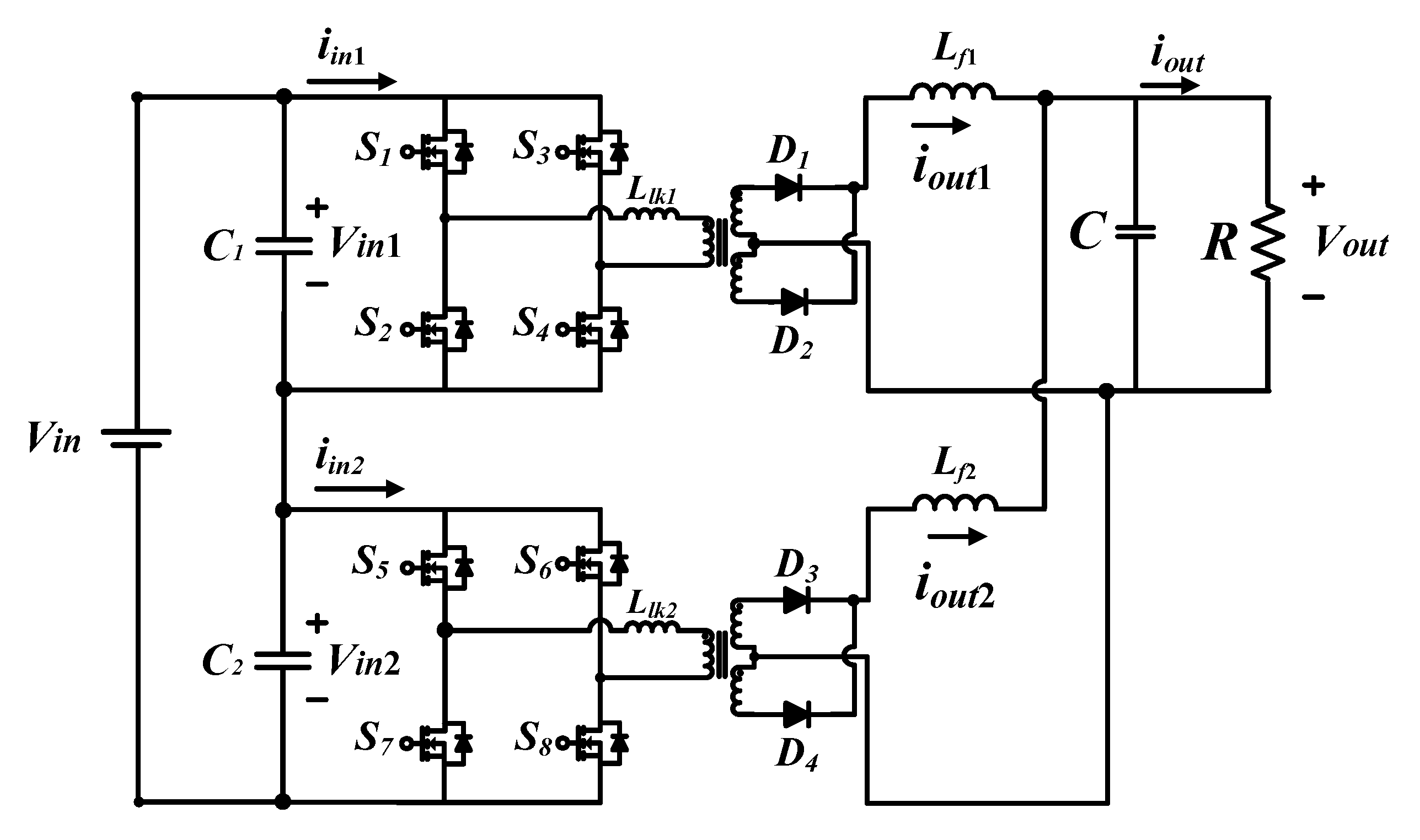
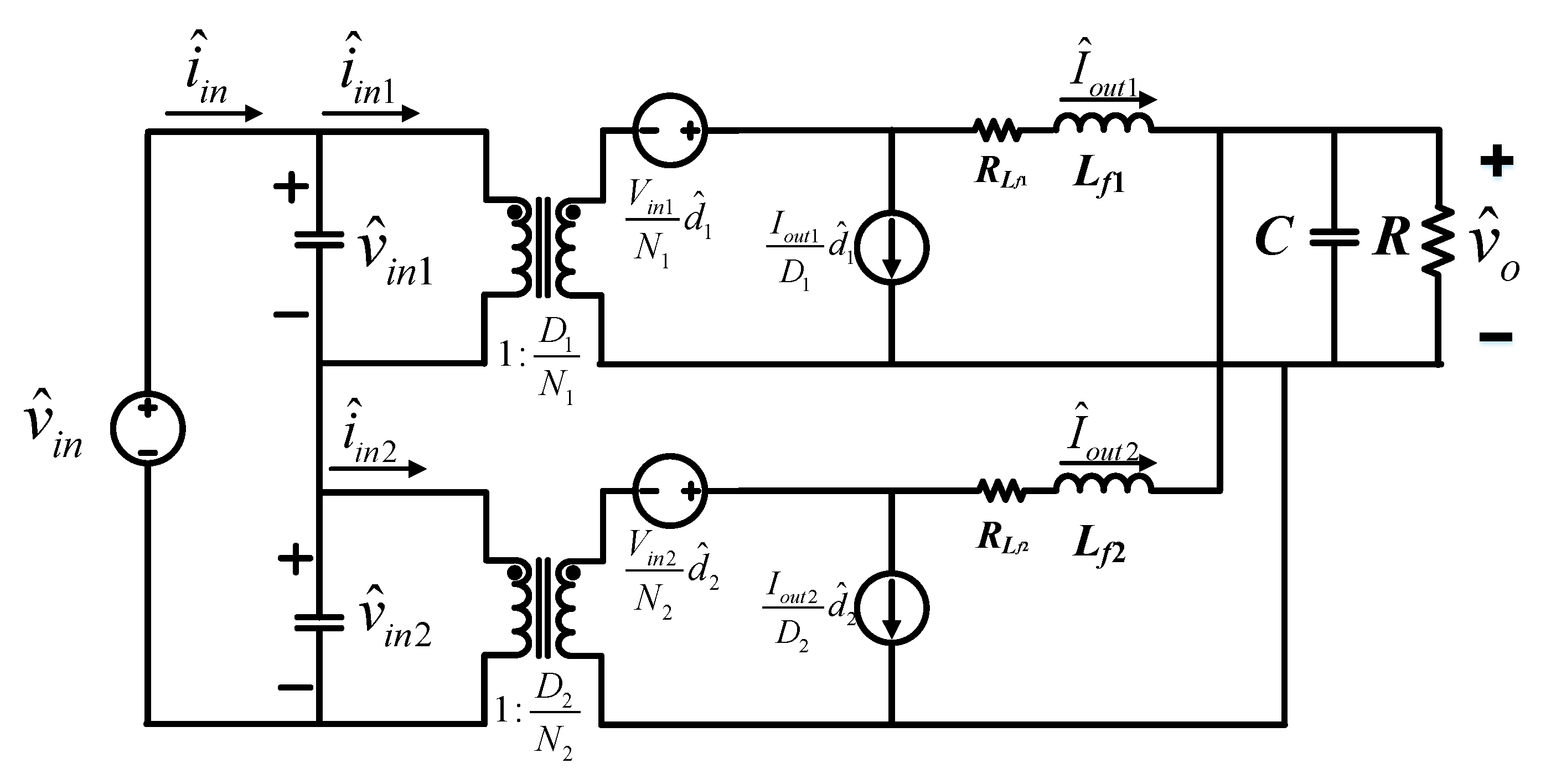
3.1. Small Signal Modeling of ISOP Converter
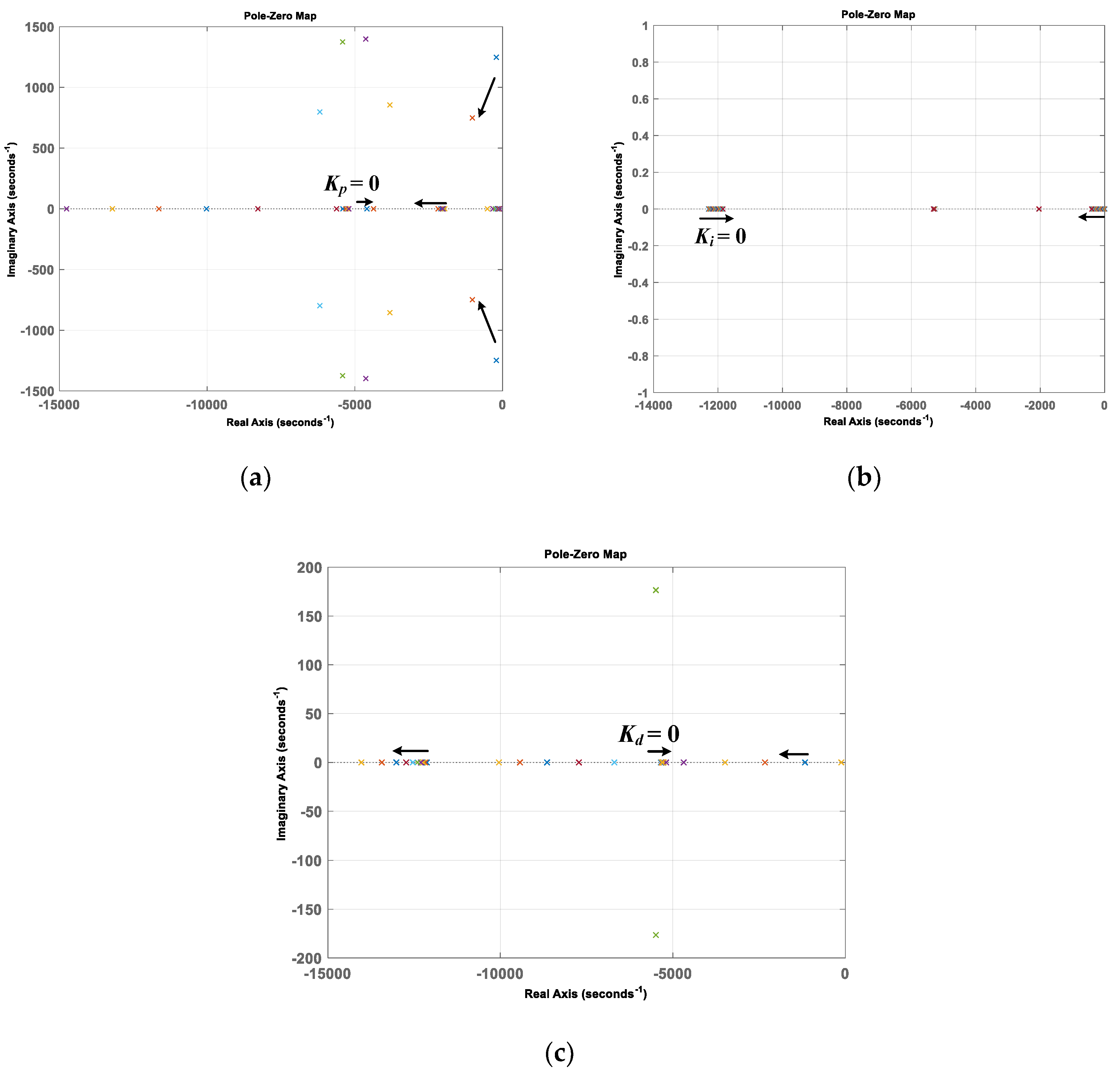
3.2. Stability Analysis of Proposed Control Method
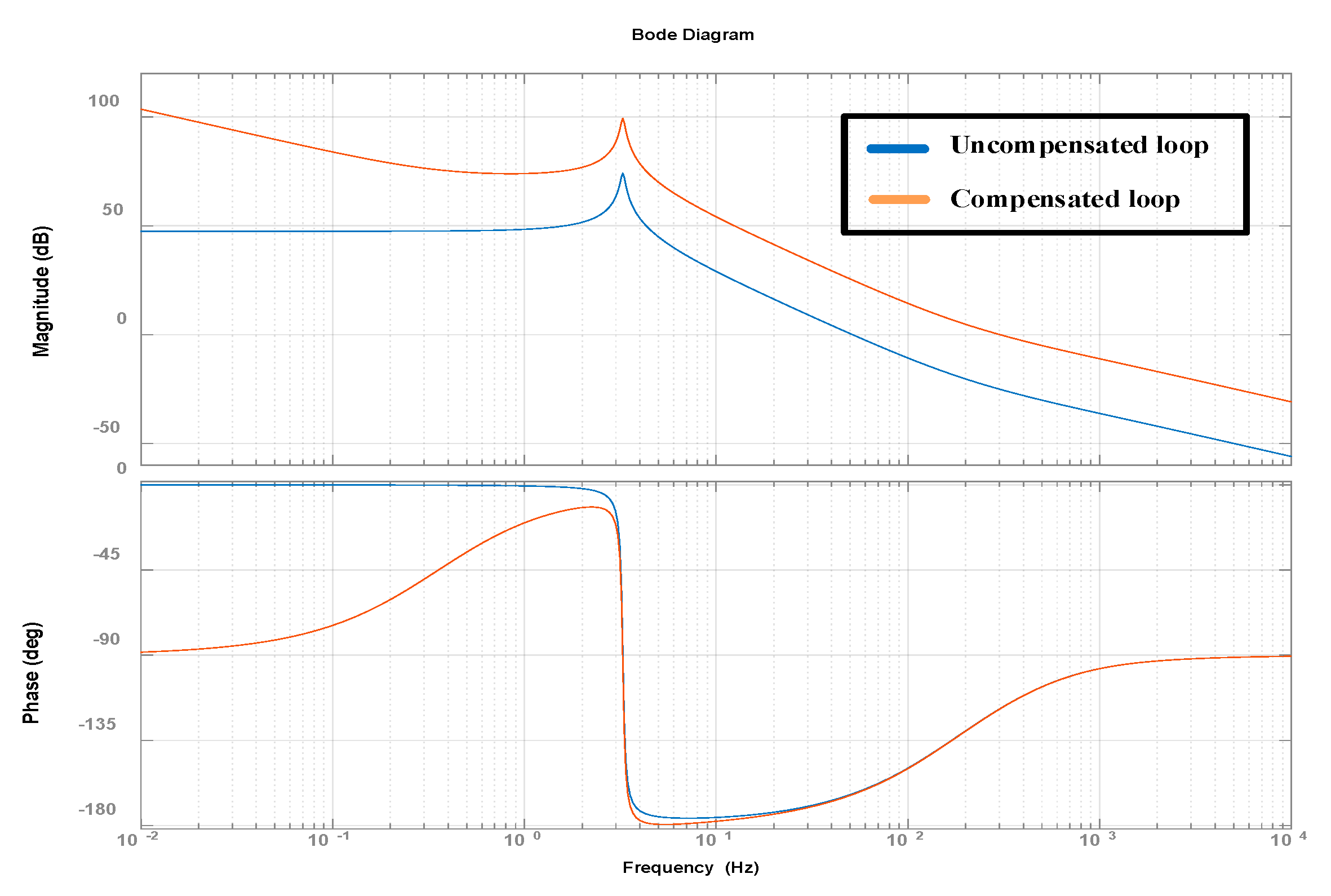
4. Design of Current Control Loop
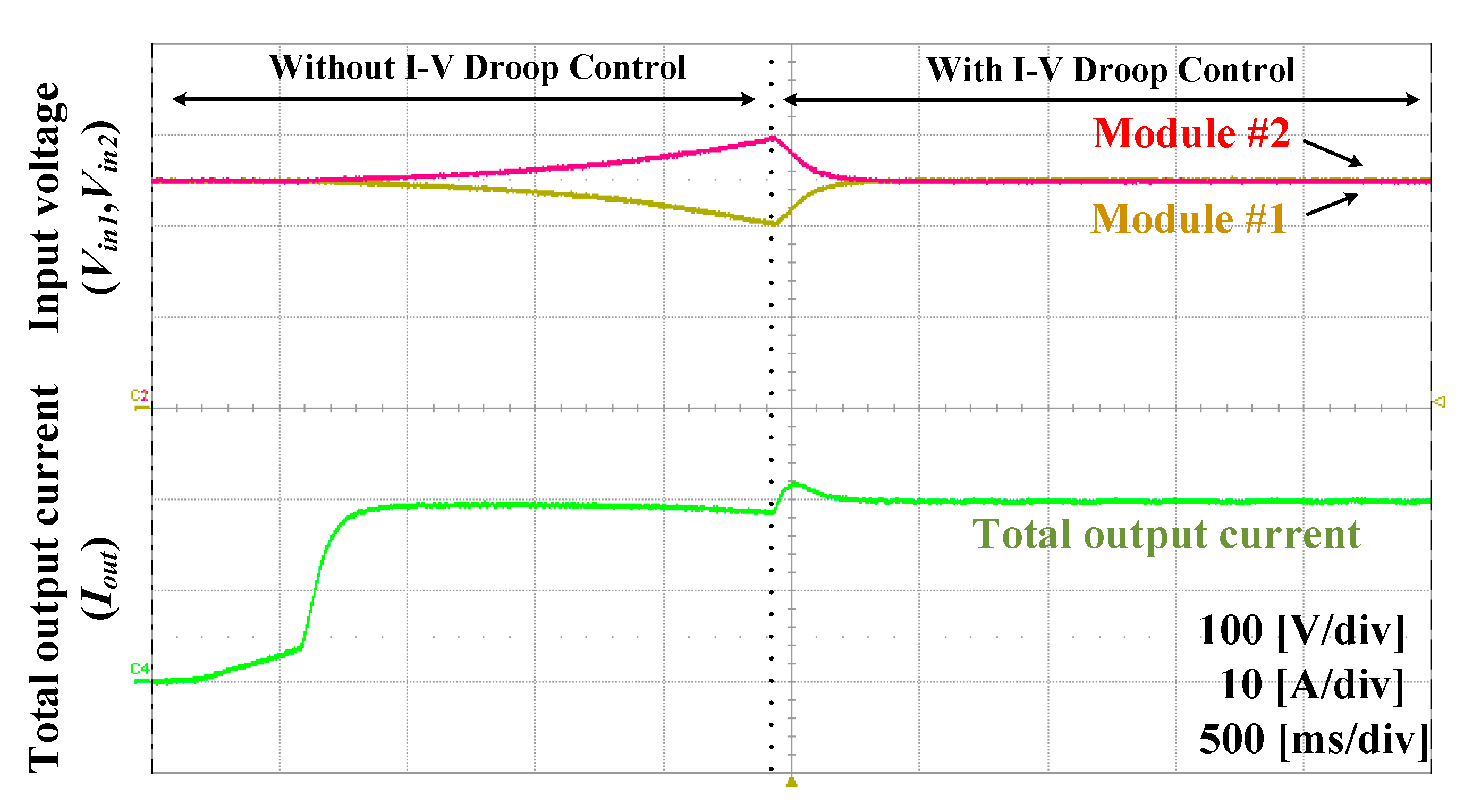
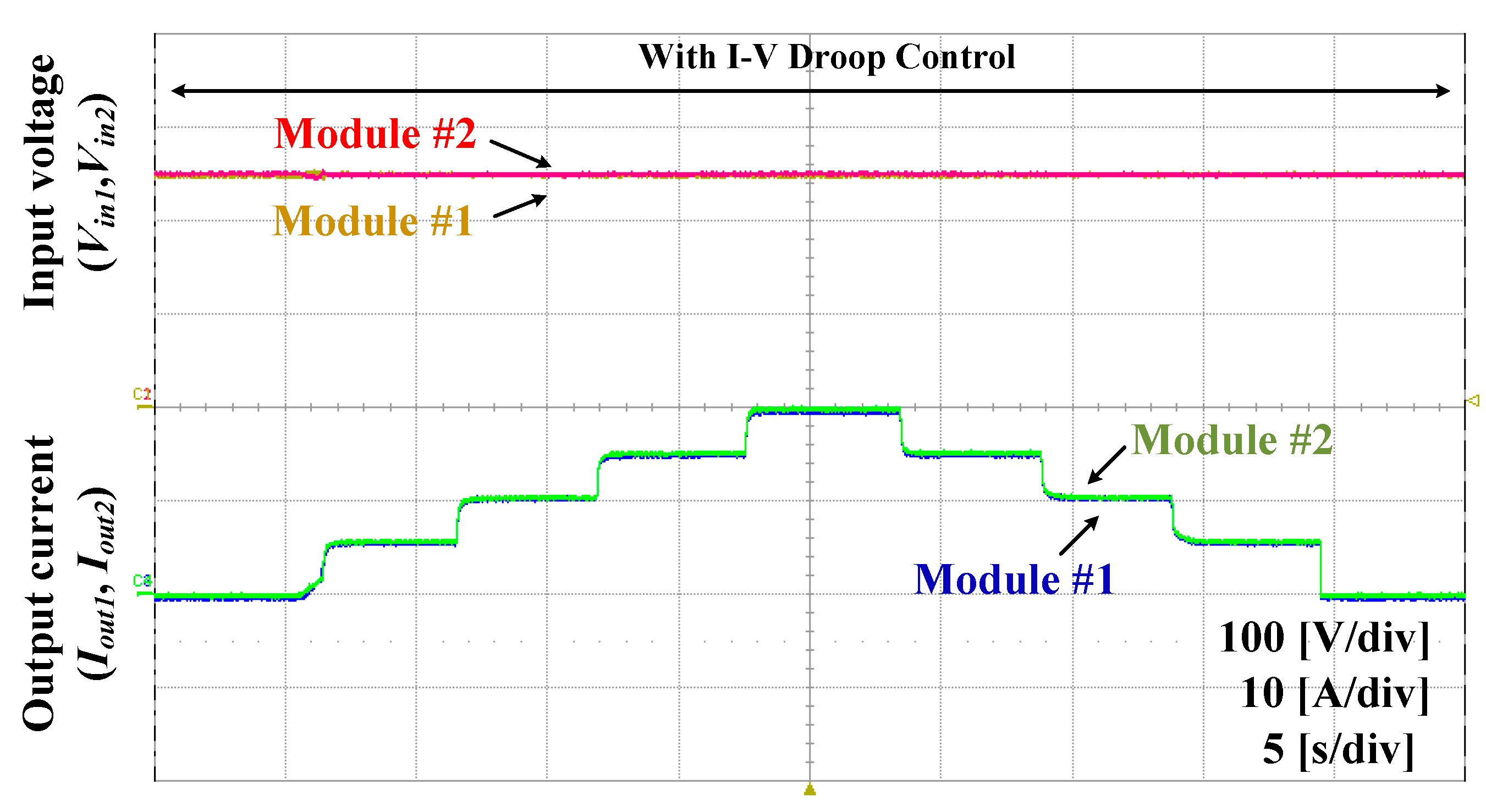
5. Experimental Result
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Lopez, M.; de Vicuna, L.G.; Castilla, M.; Gaya, P.; Lopez, O. Current distribution control design for paralleled DC/DC converters using sliding-mode control. IEEE Trans. Ind. Electron. 2004, 51, 419–428. [Google Scholar] [CrossRef]
- Perreault, D.J.; Selders, R.L.; Kassakian, J.G. Frequency-based current-sharing techniques for paralleled power converters. IEEE Trans. Power Electron. 1998, 13, 626–634. [Google Scholar] [CrossRef]
- Manias, S.N.; Kostakis, G. Modular DC–DC converter for high output voltage applications. Proc. Inst. Electr. Eng. 1993, 140, 97–102. [Google Scholar]
- Luo, S. A review of distributed power systems part I: DC distributed power system. IEEE Aerosp. Electron. Syst. Mag. 2005, 20, 5–16. [Google Scholar] [CrossRef]
- Chen, S.; Yang, S.; Cho, M. Analysis and implementation of an interleaved series input parallel output active clamp forward converter. IET Power Electron. 2013, 6, 774–782. [Google Scholar] [CrossRef]
- Chen, W.; Ruan, X.; Yan, H.; Tse, C.K. DC/DC Conversion Systems Consisting of Multiple Converter Modules: Stability, Control, and Experimental Verifications. IEEE Trans. Power Electron. 2009, 24, 1463–1474. [Google Scholar] [CrossRef]
- Huang, Y.; Tse, C.K.; Ruan, X. General Control Considerations for Input-Series Connected DC/DC Converters. IEEE Trans. Circuits Syst. I Regul. Pap. 2009, 56, 1286–1296. [Google Scholar] [CrossRef]
- Giri, R.; Choudhary, V.; Ayyanar, R.; Mohan, N. Common-duty-ratio control of input-series connected modular DC-DC converters with active input voltage and load-current sharing. IEEE Trans. Ind. Appl. 2006, 42, 1101–1111. [Google Scholar] [CrossRef]
- Shi, J.; Luo, J.; He, X. Common-Duty-Ratio Control of Input-Series Output-Parallel Connected Phase-shift Full-Bridge DC–DC Converter Modules. IEEE Trans. Power Electron. 2011, 26, 3318–3329. [Google Scholar] [CrossRef]
- Kimball, J.W.; Mossoba, J.T.; Krein, P.T. A Stabilizing, High-Performance Controller for Input Series-Output Parallel Converters. IEEE Trans. Power Electron. 2008, 23, 1416–1427. [Google Scholar] [CrossRef]
- Abrehdari, M.; Sarvi, M. Comprehensive sharing control strategy for input-series output-parallel connected modular DC–DC converters. IET Power Electron. 2019, 12, 3105–3117. [Google Scholar] [CrossRef]
- Ruan, X.; Chen, W.; Cheng, L.; Tse, C.K.; Yan, H.; Zhang, T. Control Strategy for Input-Series–Output-Parallel Converters. IEEE Trans. Ind. Electron. 2009, 56, 1174–1185. [Google Scholar] [CrossRef]
- Ayyanar, R.; Giri, R.; Mohan, N. Active input-voltage and load-current sharing in input-series and output-parallel connected modular DC-DC converters using dynamic input-voltage reference scheme. IEEE Trans. Power Electron. 2004, 19, 1462–1473. [Google Scholar] [CrossRef]
- Kim, J.-W.; Yon, J.-S.; Cho, B.H. Modeling, control, and design of input-series-output-parallel-connected converter for high-speed-train power system. IEEE Trans. Ind. Electron. 2001, 48, 536–544. [Google Scholar]
- Grbovic, P.J. Master/Slave Control of Input-Series- and Output-Parallel-Connected Converters: Concept for Low-Cost High-Voltage Auxiliary Power Supplies. IEEE Trans. Power Electron. 2009, 24, 316–328. [Google Scholar] [CrossRef]
- Chen, W.; Fu, X.; Xue, C.; Ye, H.; Syed, W.A.; Shu, L.; Ning, G. Indirect Input-Series Output-Parallel DC–DC Full Bridge Converter System Based on Asymmetric Pulsewidth Modulation Control Strategy. IEEE Trans. Power Electron. 2019, 34, 3164–3177. [Google Scholar] [CrossRef]
- Sha, D.; Guo, Z.; Liao, X. Cross-Feedback Output-Current-Sharing Control for Input-Series-Output-Parallel Modular DC–DC Converters. IEEE Trans. Power Electron. 2010, 25, 2762–2771. [Google Scholar] [CrossRef]
- Sha, D.; Deng, K.; Liao, X. Duty Cycle Exchanging Control for Input-Series-Output-Series Connected Two PS-FB DC-DC Converters. IEEE Trans. Power Electron. 2012, 27, 1490–1501. [Google Scholar] [CrossRef]
- Zumel, P.; Ortega, L.; Lázaro, A.; Fernández, C.; Barrado, A.; Rodrígue, A.; Hernando, M.M. Modular Dual-Active Bridge Converter Architecture. IEEE Trans. Ind. Appl. 2016, 52, 2444–2455. [Google Scholar] [CrossRef]
- Qu, L.; Zhang, D.; Zhang, B. Input Voltage Sharing Control Scheme for Input Series and Output Parallel Connected DC–DC Converters Based on Peak Current Control. IEEE Trans. Ind. Electron. 2019, 66, 429–439. [Google Scholar] [CrossRef]
- Qu, L.; Zhang, D.; Bao, Z. Output Current-Differential Control Scheme for Input-Series–Output-Parallel-Connected Modular DC–DC Converters. IEEE Trans. Power Electron. 2017, 32, 5699–5711. [Google Scholar] [CrossRef]
- Chen, W.; Wang, G.; Ruan, X.; Jiang, W.; Gu, W. Wireless Input-Voltage-Sharing Control Strategy for Input-Series Output-Parallel (ISOP) System Based on Positive Output-Voltage Gradient Method. IEEE Trans. Ind. Electron. 2014, 61, 6022–6030. [Google Scholar] [CrossRef]
- Xu, G.; Sha, D.; Liao, X. Decentralized Inverse-Droop Control for Input-Series–Output-Parallel DC–DC Converters. IEEE Trans. Power Electron. 2015, 30, 4621–4625. [Google Scholar] [CrossRef]






| Parameter | Value |
|---|---|
| Input voltage [V] | 500 [V] |
| Maximum output current #1 [A] | 30 [A] |
| Maximum output current #2 [A] | 30 [A] |
| Total output current [A] | 60 [A] |
| Output voltage [V] | 12 [V] |
| Input capacitor #1 [μF] | 500 [μF] |
| Input capacitor #2 [μF] | 500 [μF] |
| Output capacitor [μF] | 1000 [μF] |
| Turn ratio | 10:1 |
| Switching frequency [kHz] | 20 [kHz] |
| Parameter | Value |
|---|---|
| Leakage inductance of transformer #1 [μH] | 22 [μH] |
| Leakage inductance of transformer #2 [μH] | 17 [μH] |
| Output filter inductance #1 [μH] | 523 [μH] |
| Output filter inductance #2 [μH] | 505 [μH] |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kim, S.-H.; Kim, B.-J.; Park, J.-M.; Won, C.-Y. Decentralized Control Method of ISOP Converter for Input Voltage Sharing and Output Current Sharing in Current Control Loop. Energies 2020, 13, 1114. https://doi.org/10.3390/en13051114
Kim S-H, Kim B-J, Park J-M, Won C-Y. Decentralized Control Method of ISOP Converter for Input Voltage Sharing and Output Current Sharing in Current Control Loop. Energies. 2020; 13(5):1114. https://doi.org/10.3390/en13051114
Chicago/Turabian StyleKim, Sung-Hun, Bum-Jun Kim, Jung-Min Park, and Chung-Yuen Won. 2020. "Decentralized Control Method of ISOP Converter for Input Voltage Sharing and Output Current Sharing in Current Control Loop" Energies 13, no. 5: 1114. https://doi.org/10.3390/en13051114
APA StyleKim, S.-H., Kim, B.-J., Park, J.-M., & Won, C.-Y. (2020). Decentralized Control Method of ISOP Converter for Input Voltage Sharing and Output Current Sharing in Current Control Loop. Energies, 13(5), 1114. https://doi.org/10.3390/en13051114




