A Lifetime-Enhancing Method for Directional Sensor Networks with a New Hybrid Energy-Consumption Pattern in Q-coverage Scenarios
Abstract
1. Introduction
2. Preliminaries
2.1. Network Model
- (1)
- Each sensor node is stationary and can rotate the sensing direction.
- (2)
- Each sensor node has two work modes: active mode and inactive mode.
- (3)
- Each sensor node can become the cluster head or member node.
- (4)
- Each sensor node can reduce data redundancy by data fusion.
- (5)
- All sensor nodes can guarantee the network connectivity.
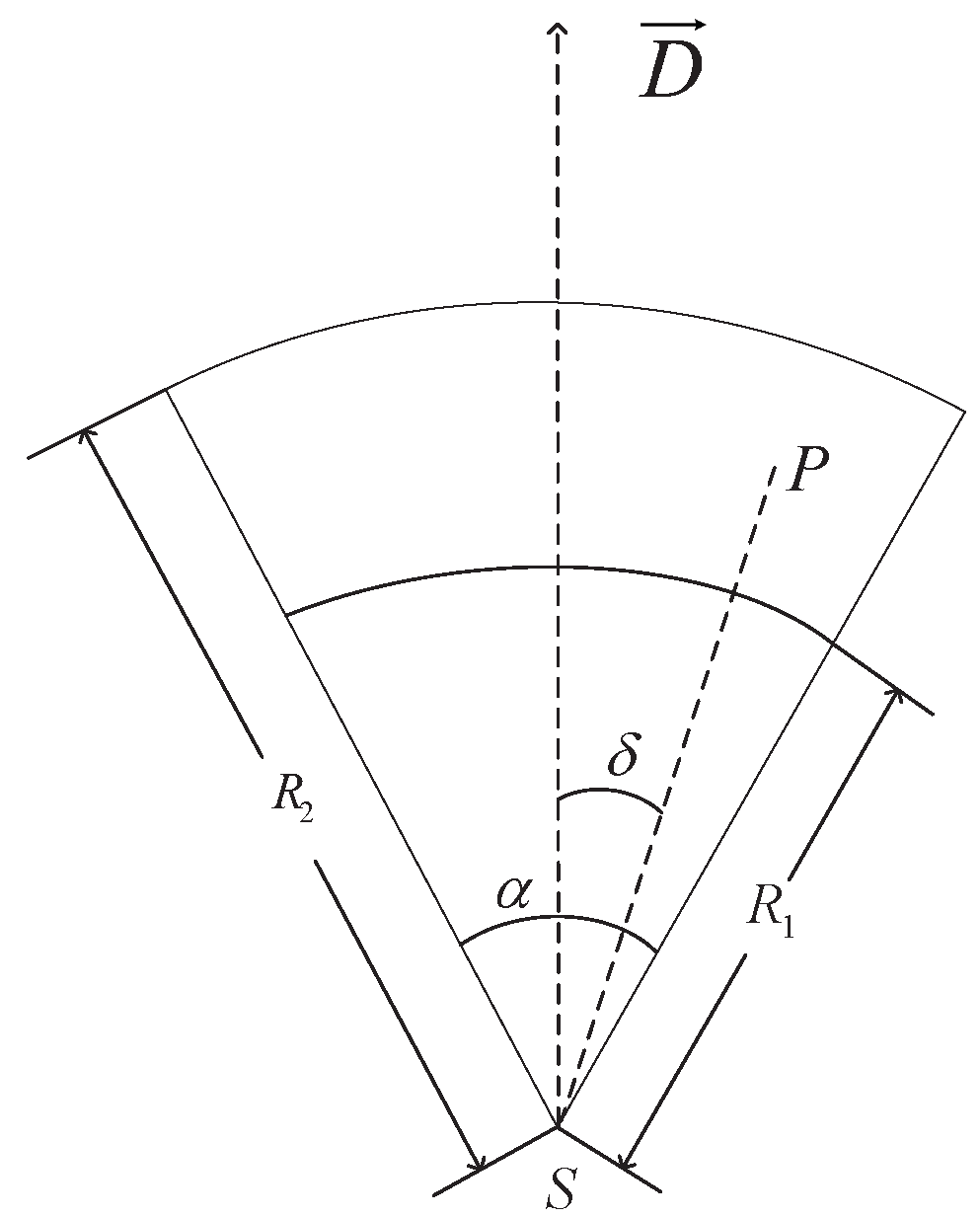
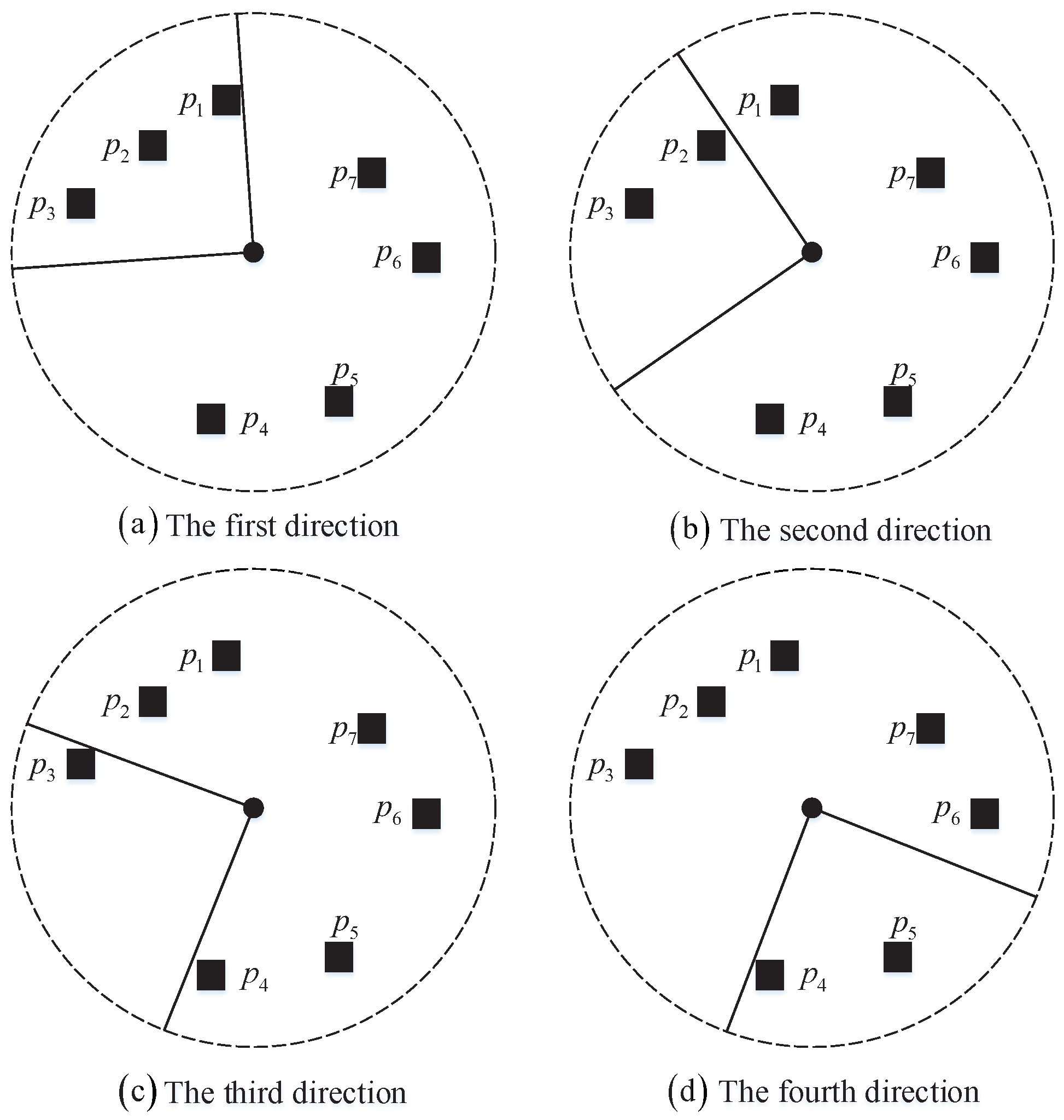
2.2. Directional Probability Sensing Model
2.3. Energy Consumption Model
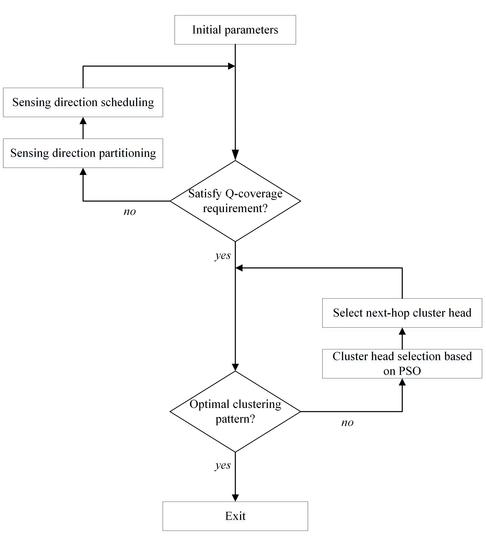
3. Network Lifetime Maximization Problem Statement
3.1. Process of Scheduling Sensing Direction
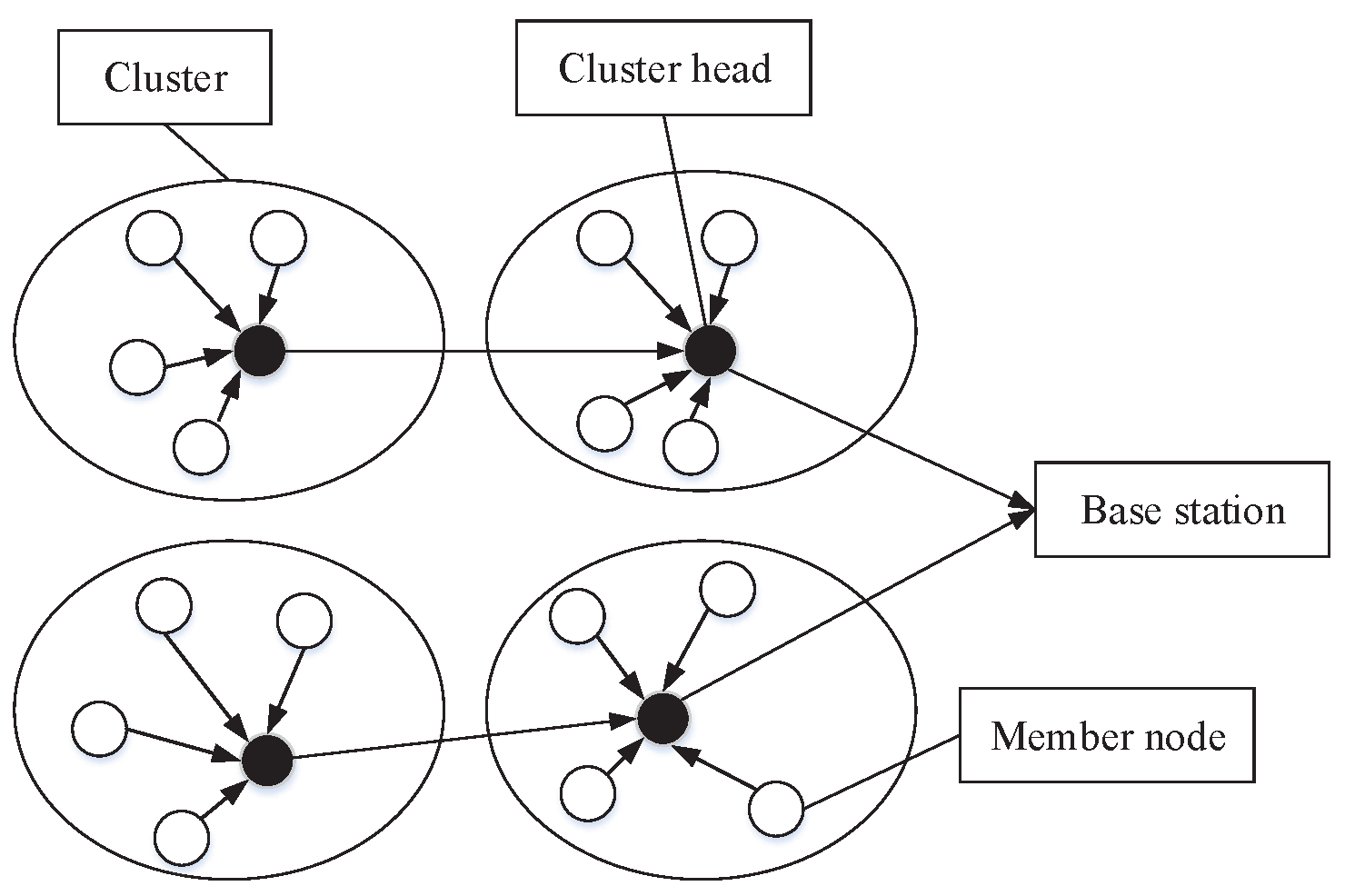
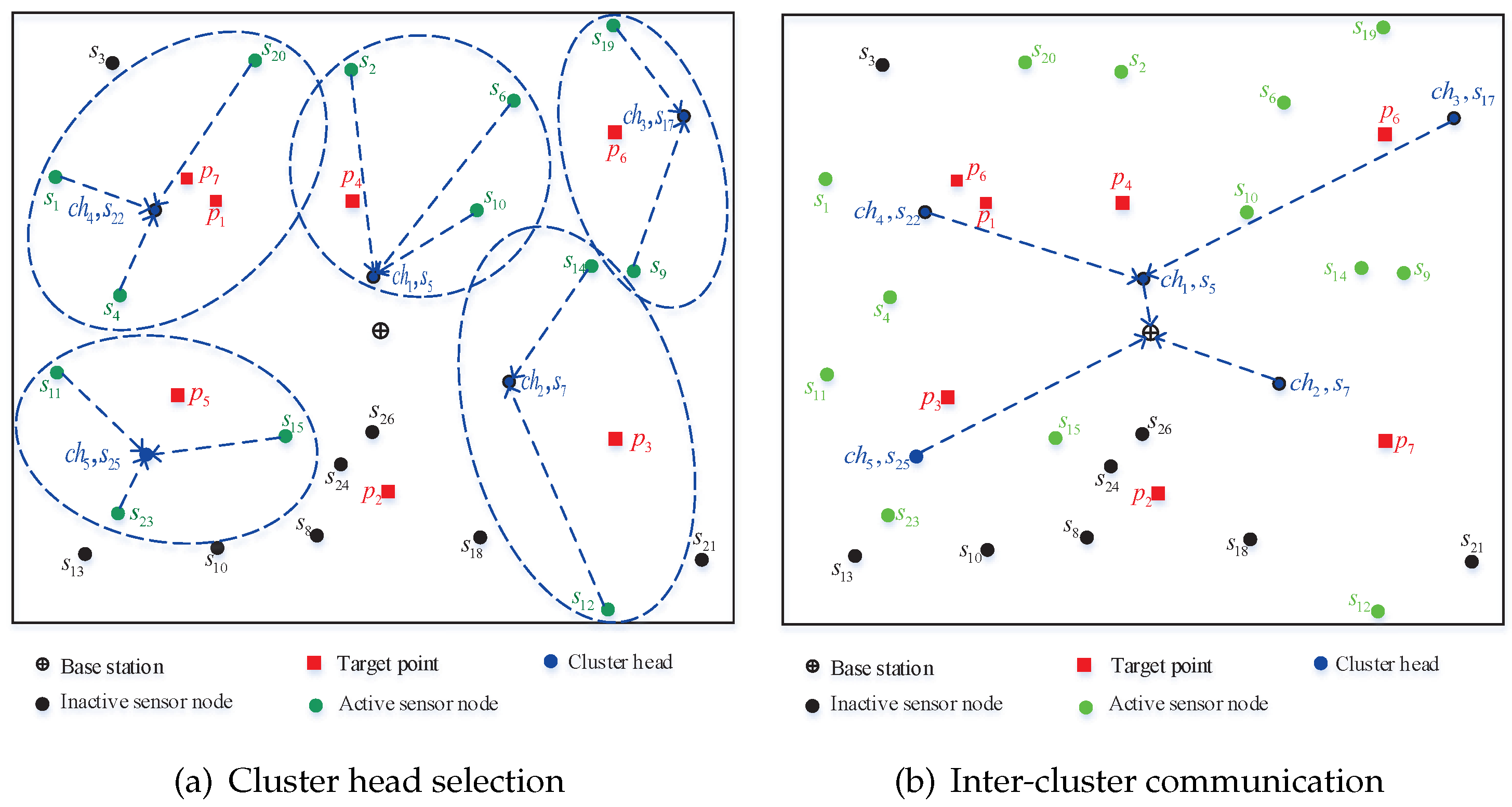
3.2. Process of the Clustering Network
3.3. Problem Formulation
3.3.1. Terminology
- S: sensor node set, i.e., .
- P: target point set, i.e., .
- Q: coverage requirement of target points, i.e., .
- : possible number of sensing directions of sensor node , .
- 5: sensing direction of sensor node .
- : coverage probability that the sensing direction of sensor node can provide to target point , .
- : status of the sensor node, i.e., . If sensor node is active, . Otherwise,.
- : residual energy of the sensor node, i.e., .
- : status of each sensor direction, i.e., . If sensing directionis chosen to accomplish the coverage task, . Otherwise, .
- : cluster head set, i.e., .
- : residual energy of the cluster head, i.e., .
- : The number of sensor nodes in cluster j.
- : The distance between directional sensor node and target point .
3.3.2. Integer Programming Formulation for the Network Lifetime Maximization Problem in Q-Coverage Scenarios
- Sensing direction scheduling optimization model: For a given target point set and directional sensor node set, it is necessary to schedule different sensing direction sets to meet the Q-coverage requirement alternately. According to the different coverage requirements of each target point, we activate partial directional sensor nodes and choose one sensing direction to accomplish the coverage task. When choosing the active nodes, it is important to guarantee sufficient residual energy and activate the minimal number of nodes. Therefore, the sensing direction scheduling problem is described as follows.Minimize:subject to:where is the total number of active nodes and is the total residual energy. Equation (6) shows that the coverage requirement of each target point should be met.
- Cluster head selection optimization model: To select an optimal cluster head set from inactive sensor nodes, it is important to consider energy and distance parameters in order to control the communication energy consumption. For the cluster head selection, we mainly consider following two energy efficiency parameters.
- (1)
- Total residual energy ratio of cluster head candidates:During the process of data transmission, cluster heads consume much more energy than member nodes. It is important to guarantee sufficient residual energy of cluster heads. The first objective function is defined as the total residual energy ratio of cluster head candidates.where is the total residual energy of active sensor nodes and is the total residual energy of cluster head candidates in the current round.
- (2)
- Average intra-cluster distance:In a clustered network, member nodes consume energy to communicate with cluster heads. It is necessary to reduce the distance between member nodes and cluster heads. The second objective function is defined as the average intra-cluster distance.where is the distance between sensor node and cluster head .The above objective functions are not strongly conflicting with each other, so it is wise to give the cluster head selection optimization function as a linear combination. The cluster head selection optimization problem is summarized by the following.Minimize:subject to:where the is a constant given by the importance of the two objective functions.
- Inter-cluster communication optimization model: Inter-cluster communication mainly includes two modes. If the distance between the cluster head and BS d is no more than the threshold distance , the cluster head directly communicates with the BS. If d is over , the cluster head establishes inter-cluster multi-hop routing to communicate with the BS, and the next-hop cluster head is determined by an inter-cluster weight function. The weigh function depends on the following three factors.
- (1)
- Inter-cluster distance:A cluster head should select its next-hop cluster head that is not far away from it. Therefore, the first factor is defined as the inter-cluster distance, i.e., .
- (2)
- Residual energy of the next-hop cluster head:To control the overall communication energy consumption during the process of data transmission, a cluster head should consider the next-hop cluster head with more sufficient residual energy, i.e., .
- (3)
- Number of member nodes in the next-hop cluster:To reduce the load of the next-hop cluster head, a cluster head needs to select its next-hop cluster head with fewer relative member nodes. The third factor is the number of member nodes in the next-hop cluster, i.e., .Taking the three factors into consideration, the inter-cluster communication problem is described as follows.Minimize:subject to:where is a linear combination of the three relative inter-cluster communication factors. When is minimized, the optimal inter-cluster communication is achieved.
4. Proposed Lifetime-Enhancing Method
4.1. Q-coverage Sensing Direction Scheduling Optimization Method
4.1.1. Sensing Direction Partition Algorithm
| Algorithm 1: Sensing direction partition algorithm. |
| Input: Sensor node set: |
| Target point set: |
| Output: Coverage quality that each sensing direction of all sensor nodes can |
| provide to each target point: |
| 1: for n do |
| 2: for do |
| 3: for to m do |
| 4: if then |
| 5: Calculate according to Equation (1); |
| 6: end if |
| 7: end for |
| 8: end for |
| 9: end for |
4.1.2. Q-coverage Sensing Direction Scheduling
4.2. Multi-hop Communication-Based Clustering Optimization Method
| Algorithm 2: Q-coverage sensing direction scheduling algorithm. |
| Input: Sensor node set: |
| Target point set: |
| Output: Status of each sensor node: |
| 1: Get coverage quality that each sensing direction can provide to the target point |
| 2: according to Algorithm 1. |
| 3: while is not met. do |
| 4: for m do |
| 5: if then |
| 6: for n do |
| 7: if then |
| 8: for do |
| 9: if then |
| 10: ; %Select sensor node. |
| 11: ; %Select sensing direction. |
| 12: else if then |
| 13: if then |
| 14: ; |
| 15: ; |
| 16: else if then |
| 17: if then |
| 18: ; |
| 19: ; |
| 20: end if |
| 21: end if |
| 22: end if |
| 23: end for |
| 24: end if |
| 25: end for |
| 26: end if |
| 27: end for |
| 28: end while |
4.2.1. Cluster Head Selection Algorithm Based on PSO
| Algorithm 3: Cluster head selection algorithm based on PSO |
| Input: Sensor nodes set: |
| Status of sensor nodes: |
| Size of swarm: |
| Dimensions of particles: |
| Maximal number of iterations: |
| Output: Optimal cluster head set: |
| 1: Initialize particle |
| 2: %The possible positions of the cluster heads |
| 3: for n do |
| 4: (1) Calculate %According to Equation (9) |
| 5: (2) |
| 6: end for |
| 7: |
| 8: for do |
| 9: for do |
| 10: (1) Update velocity and position of |
| 11: (2) Calculate , and update and |
| 12: (3) Output the optimal cluster head set |
| 13: end for |
| 14: end for |
4.2.2. Inter-Cluster Communication Algorithm
| Algorithm 4: Inter-cluster communication based on the weight function. |
| Input: Sensor node set: |
| Cluster head set: |
| The residual energy of cluster heads: |
| Output: Next-hop cluster head id: |
| 2: if then |
| 3: |
| 4: for to n do |
| 5: if then |
| 6: Calculate |
| 7: ; select j as the next-hop cluster head |
| 8: end if |
| 9: end for |
| 10: end if |
| 11:end for |
5. Simulation Experiment
5.1. Simulation Parameters
5.2. Performance Evaluation
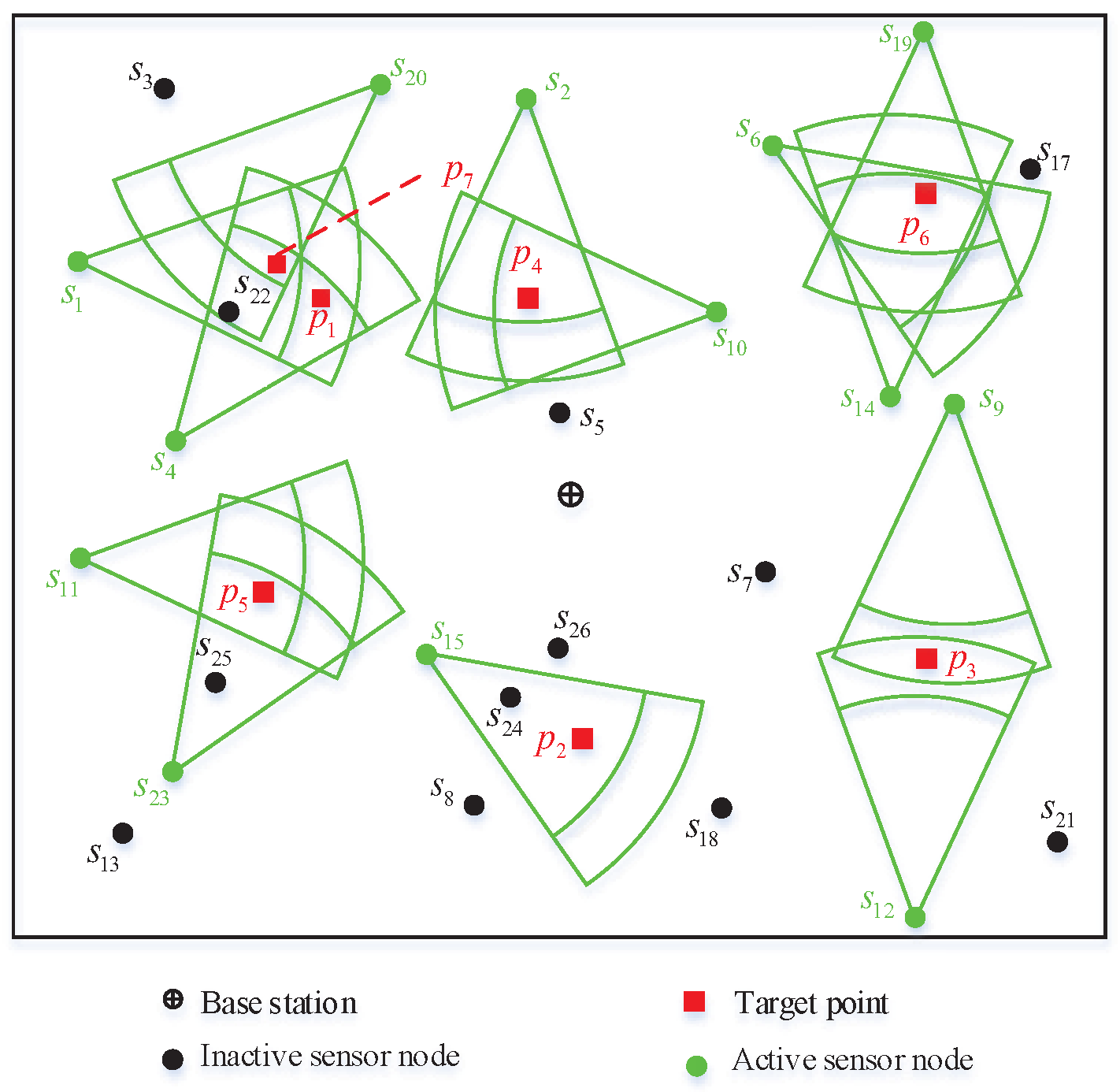
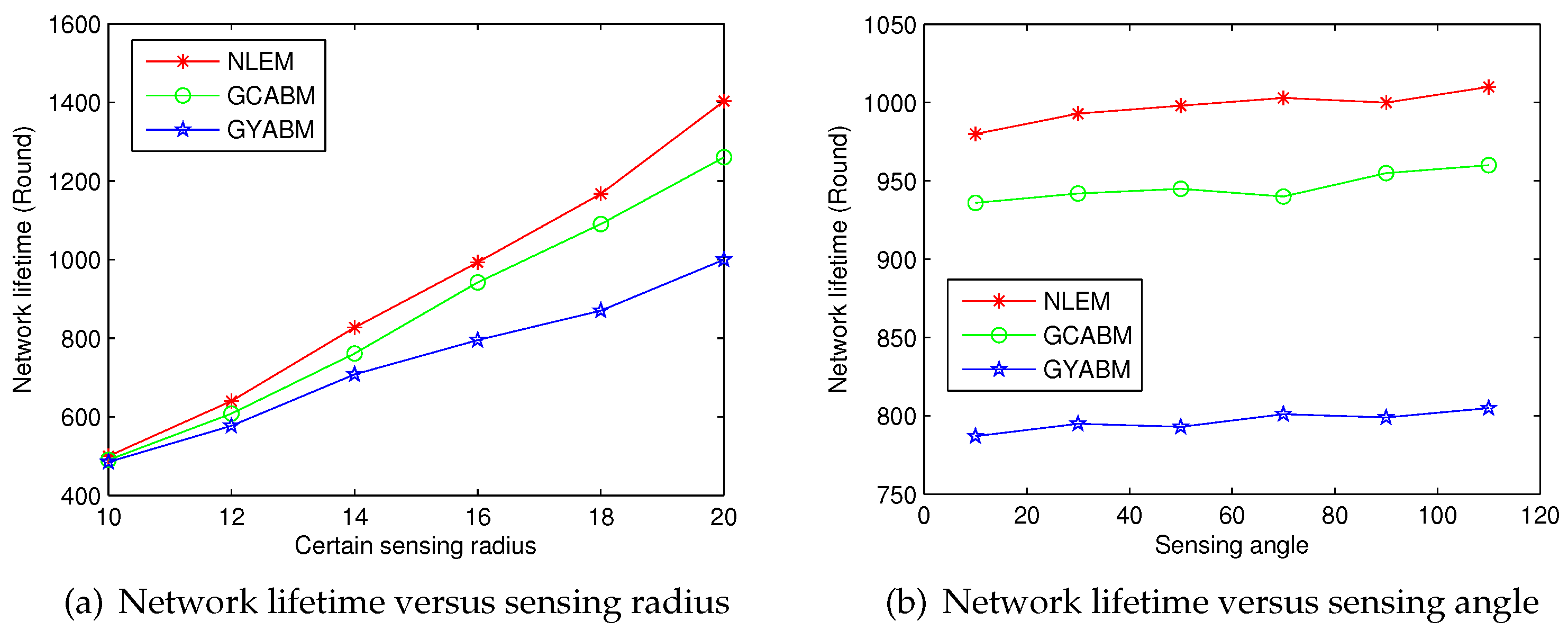
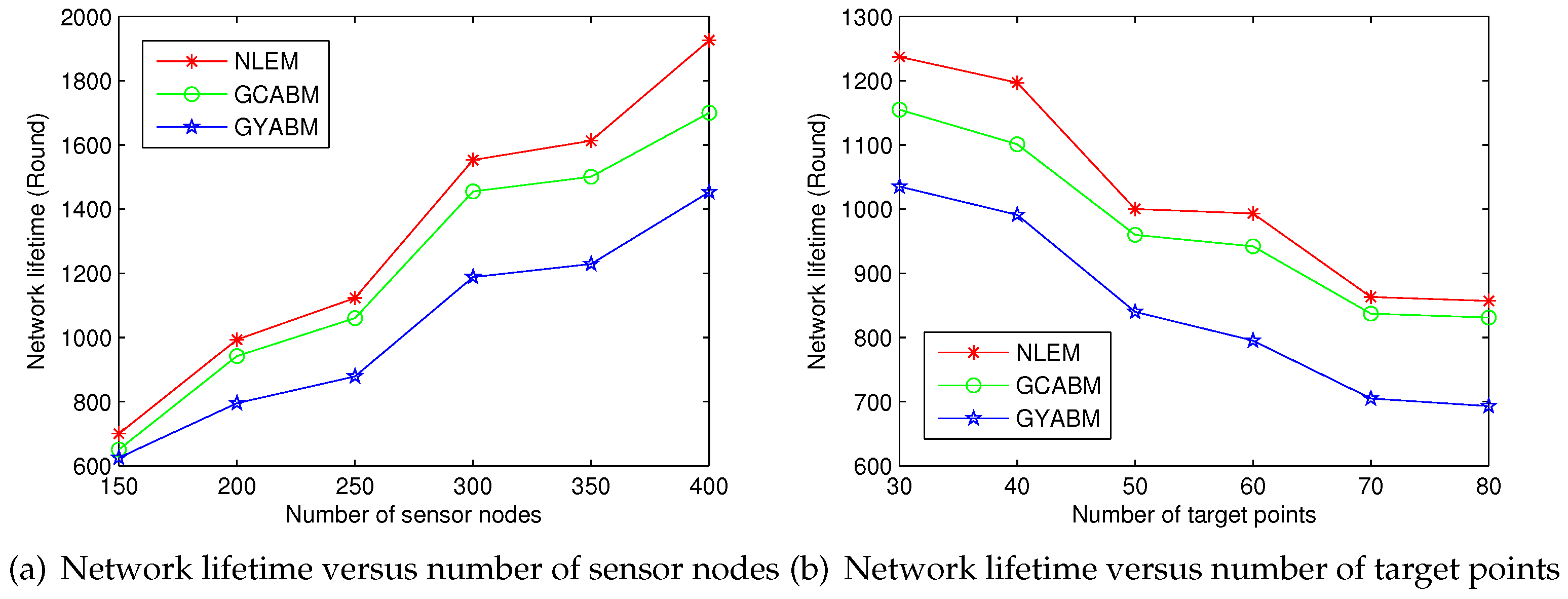
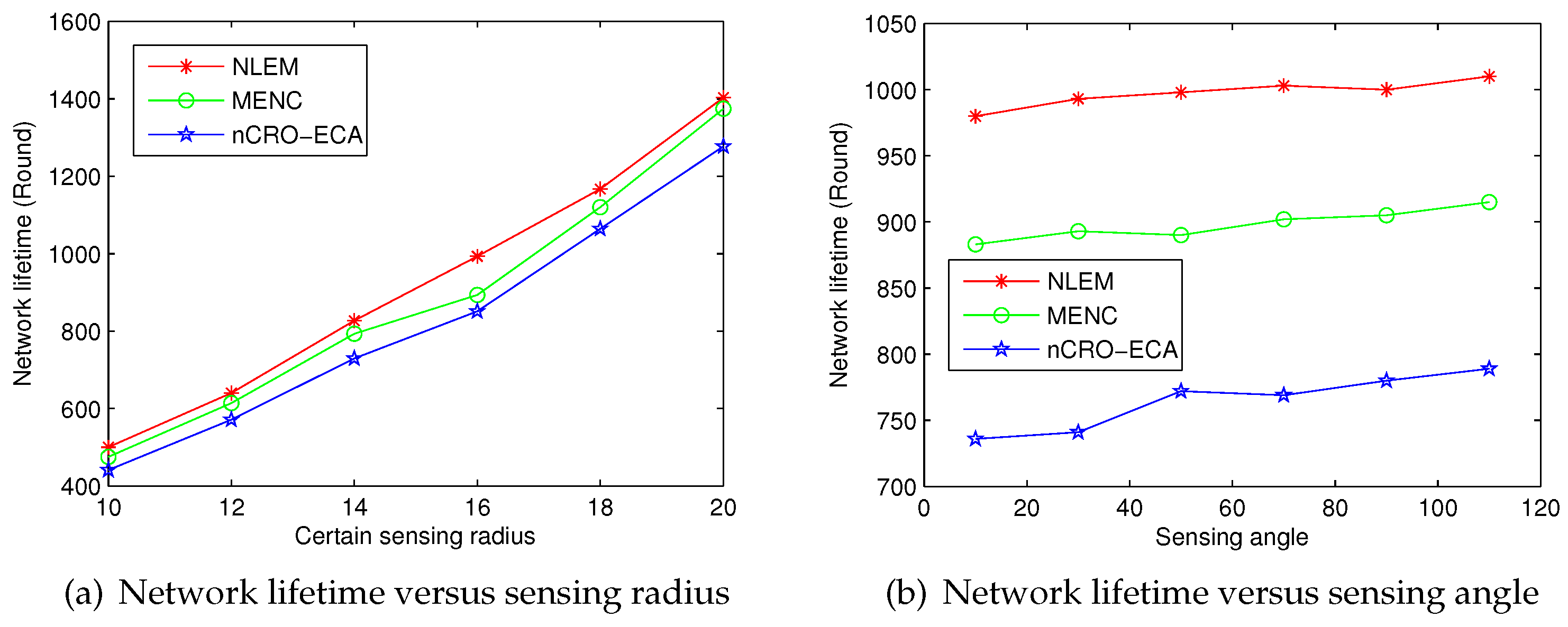
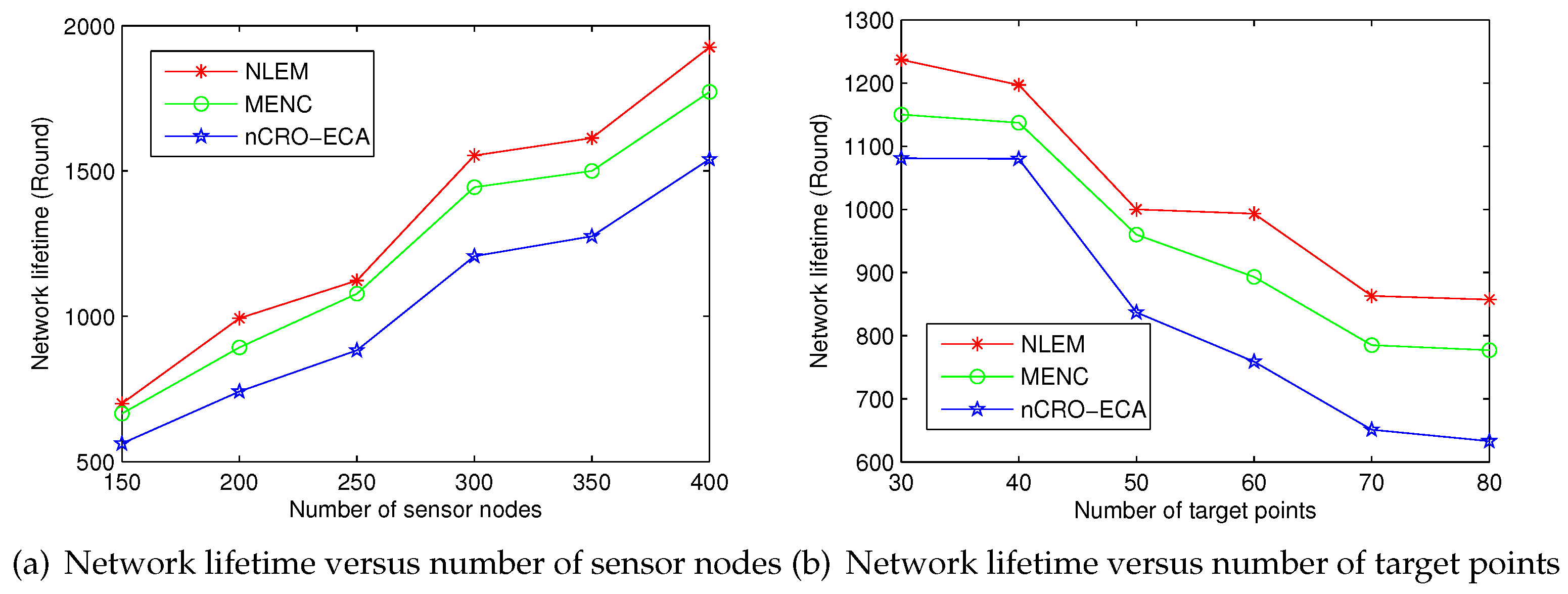
5.2.1. Comparison with Scheduling Optimization Methods
5.2.2. Comparison with the Clustering Optimization Method
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Chen, J.Y.; Wang, B.; Liu, W.Y.; Yang, L.T.; Deng, X.J. Rotating directional sensors to mend barrier gaps in a line-based deployed directional sensor network. IEEE Syst. J. 2017, 11, 1027–1038. [Google Scholar] [CrossRef]
- Xiong, Y.H.; Chen, G.; Lu, M.J.; Wan, X.B.; Wu, M.; She, J.H. A two-phase lifetime-enhancing method for hybrid energy-harvesting wireless sensor network. IEEE Sens. J. 2019. [Google Scholar] [CrossRef]
- Mini, S.; Udgata, S.K.; Sabat, S.L. Sensor deployment and scheduling for target coverage problem in wireless sensor networks. IEEE Sens. J. 2014, 14, 636–644. [Google Scholar] [CrossRef]
- Arivudainambi, D.; Balaji, S.; Pavithra, R.; Shakthivel, R.N. Energy efficient sensor scheduling for Q-coverage problem. In Proceedings of the IEEE International Workshop on Computer Aided Modeling & Design of Communication Links & Networks 2017, Lund, Sweden, 19–21 June 2017. [Google Scholar]
- Rossi, A.; Sevaux, M. Matheuristic approaches for Q-coverage problem versions in wireless sensor networks. Eng. Optim. 2013, 45, 1–16. [Google Scholar]
- Akyildiz, I.F.; Su, W.; Sankarasubramaniam, Y.; Cayirci, E. Wireless sensor networks: A survey. Comput. Netw. 2002, 38, 393–422. [Google Scholar] [CrossRef]
- Tan, R.; Xing, G.L.; Wang, J.P.; So, H.C. Exploiting reactive mobility for collaborative target detection in wireless sensor networks. IEEE Trans. Mobile Comput. 2010, 9, 317–332. [Google Scholar] [CrossRef]
- Pyun, S.Y.; Cho, D.H. Power-saving scheduling for multiple-target coverage in wireless sensor networks. IEEE Commun. Lett. 2009, 13, 130–132. [Google Scholar] [CrossRef]
- Lu, Z.X.; Li, W.W.; Pan, M. Maximum lifetime scheduling for target coverage and data collection in wireless sensor networks. IEEE Trans. Veh. Technol. 2015, 64, 714–727. [Google Scholar] [CrossRef]
- Mohamadi, H.; Salleh, S.; Razali, M.N.; Marouf, S. A new learning automata-based approach for maximizing network lifetime in wireless sensor networks with adjustable sensing ranges. Neurocomputing 2015, 153, 11–19. [Google Scholar] [CrossRef]
- Man, J.; Satish, C.; Bijender, K. Target coverage heuristic based on learning automata in wireless sensor networks. IET Wirel. Sens. Syst. 2018, 8, 109–115. [Google Scholar]
- Yang, C.L.; Chin, K.W. On complete target coverage in wireless sensor networks with random recharging rates. IEEE Wirel. Commun. Lett. 2015, 4, 50–53. [Google Scholar] [CrossRef]
- Cai, Y.L.; Lou, W.; Li, M.L.; Li, X.Y. Energy efficient target-oriented scheduling in directional sensor networks. IEEE Trans. Comput. 2009, 58, 1259–1274. [Google Scholar]
- Wang, L.L.; Wu, X.B.; Huang, C.; Ding, X.; Wang, H.Y. Node scheduling strategy based on target coverage for heterogeneous directional sensor networks. Control Decis. 2016, 31, 2140–2146. [Google Scholar]
- Sharmin, S.; Nur, F.N.; Razzaque, M.A.; Rahman, M.M. Network lifetime aware coverage quality maximization for heterogeneous targets in DSNs. In Proceedings of the Region 10 Conference, Singapore, 22–25 November 2016. [Google Scholar]
- Gil, J.M.; Han, Y.H. A target coverage scheduling scheme based on genetic algorithms in directional sensor networks. Sensors 2011, 11, 1888–1905. [Google Scholar] [CrossRef]
- Zhu, X.J.; Li, J.; Zhou, M.C. Optimal deployment of energy-harvesting directional sensor networks for target coverage. IEEE Syst. J. 2019, 13, 377–387. [Google Scholar] [CrossRef]
- Sadik, M.M.; Malek, S.M.B.; Rahman, A. On balanced K-Cover. Vis. Sens. Network. J. Netw. Comput. Appl. 2016, 72, 72–86. [Google Scholar]
- Wu, Y.G.; Yin, J.P.; Li, M.; En, Z. Efficient algorithms for probabilistic k-coverage in directional sensor networks. In Proceedings of the IEEE International Conference on Intelligent Sensors, Sensor Networks and Information Processing, Sydney, Australia, 15–18 December 2008. [Google Scholar]
- Heinzelman, W.R.; Chandrakasan, A.; Balakrishnan, H. Energy-efficient communication protocol for wireless microsensor networks. In Proceedings of the IEEE Hawaii International Conference on System Sciences, Maui, HI, USA, 7 January 2002. [Google Scholar]
- Lindsey, S. PEGASIS: Power efficient gathering in sensor information systems. In Proceedings of the IEEE Aerospace Conference, Big Sky, MT, USA, 9–16 March 2002. [Google Scholar]
- Younis, O.; Fahmy, S. HEED: A hybrid, energy-efficient, distributed clustering approach for ad hoc sensor networks. IEEE Trans. Mobile Comput. 2004, 3, 366–379. [Google Scholar] [CrossRef]
- Loscri, V.; Morabito, G.; Marano, S. A two-levels hierarchy for low-energy adaptive clustering hierarchy (TL-LEACH). In Proceedings of the IEEE Vehicular Technology Conference, Montreal, QC, Canada, 25–28 September 2006. [Google Scholar]
- Ding, Y.S.; Chen, R.; Hao, K.R. A rule-driven multi-path routing algorithm with dynamic immune clustering for event-driven wireless sensor network. Neurocomputing 2016, 203, 139–149. [Google Scholar] [CrossRef]
- Su, T.S.; Huang, M.W.; Li, W.S.; Hsieh, W.S. Aggregation scheme with secure hierarchical clustering for wireless sensor networks. Int. J. Distrib. Sens. Netw. 2012, 162347, 1–11. [Google Scholar] [CrossRef][Green Version]
- Neogi, S.G.; Bhaskar, A.A.; Chakrabarti, P. Energy efficient hierarchy-based clustering routing protocol for wireless sensor networks. Int. J. Comput. Appl. 2014, 95, 1–8. [Google Scholar]
- Wang, D. An energy-efficient clusterhead assignment scheme for hierarchical wireless sensor networks. Int. J. Wirel. Inf. Netw. 2008, 15, 61–71. [Google Scholar] [CrossRef]
- Boselin, S.R.; Sophia, S. Hierachial distributed clustering algorithm for energy efficient wireless sensor networks. Int. J. Res. Inf. Technol. 2013, 1, 45–55. [Google Scholar]
- Heinzelman, W.B.; Chandrakasan, A.P.; Balakrishnan, H. An application-specific protocol architecture for wireless microsensor networks. IEEE Trans. Wirel. Commun. 2002, 1, 660–670. [Google Scholar] [CrossRef]
- Ran, G.; Zhang, H.Z.; Gong, S.L. Improving on LEACH protocol of wireless sensor networks using fuzzy logic. J. Inf. Comput. Sci. 2010, 7, 767–775. [Google Scholar]
- Tillett, J.; Rao, R.; Sahin, F. Improving on LEACH protocol of wireless sensor networks using fuzzy logic. In Proceedings of the IEEE International Conference on Personal Wireless Communications, Beijing, China, 7–10 September 2003. [Google Scholar]
- Guru, S.M.; Halgamuge, S.K.; Fernando, S. Particle swarm optimisers for cluster formation in wireless sensor networks. In Proceedings of the IEEE International Conference on Intelligent Sensors, Las Vegas, NV, USA, 27–31 October 2003. [Google Scholar]
- Latiff, N.M.A.; Tsimenidis, C.C.; Sharif, B.S. Energy-aware clustering for wireless sensor networks using particle swarm optimization. In Proceedings of the IEEE 18th International Symposium on Personal, Indoor and Mobile Radio Communications, Athens, Greece, 3–7 September 2007. [Google Scholar]
- Singh, B.; Lobiyal, D. A novel energy-aware cluster head selection based on particle swarm optimization for wireless sensor networks. Hum.-Centric Comput. Inf. Sci. 2012, 2, 1–18. [Google Scholar] [CrossRef]
- Rao, P.C.S.; Banka, H. Energy efficient clustering algorithms for wireless sensor networks: Novel chemical reaction optimization approach. Wirel. Netw. 2017, 23, 433–452. [Google Scholar] [CrossRef]
- Rao, P.C.S. PSO-based multiple-sink placement algorithm for protracting the lifetime of wirelss sensor network. In Proceedings of the Second International Conference on Neural Networks; Springer: New Delhi, India, 2016. [Google Scholar]
- Yang, L.; Lu, Y.Z.; Zhong, Y.C.; Wu, X.G.; Yang, S.X. A multi-hop energy neutral clustering algorithm for maximizing network information gathering in energy harvesting wireless sensor networks. Sensors 2016, 16, 26. [Google Scholar] [CrossRef]
- Nayak, P.; Vathasavai, B. Energy efficient clustering algorithm for multi-hop wireless sensor network using type-2 fuzzy logic. IEEE Sens. J. 2017, 17, 4492–4499. [Google Scholar] [CrossRef]
- Mallareddy, A.; Swetha, M.; Rao, R.Y. HWSN: Intra-cluster scheduling and inter cluster multi-hop routing schemes to maximize the network lifetime. Int. J. Res. 2014, 1, 1058–1066. [Google Scholar]
- Kennedy, J. Particle swarm optimization. In Proceedings of the Icnn95-international Conference on Neural Networks, Perth, Australia, 27 November–1 December 1995. [Google Scholar]
| Parameter | Default Value |
|---|---|
| Monitoring area | 50 × 50 m |
| BS position | |
| N | 200 |
| M | 60 |
| 16 m | |
| 21 m | |
| A | |
| 87 m | |
| 30 m | |
| 1 J | |
| 50 nJ/bit | |
| 10 pJ/bit/m | |
| pJ/bit/m | |
| Packet length | 4000 bits |
| Message size | 500 bits |
| Parameter | Value | |
|---|---|---|
| Number of particles | 30 | |
| 2 | ||
| 2 | ||
| [0, 1] | ||
| D | [0, 200] | |
| Number of iteration | 500 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Peng, S.; Xiong, Y. A Lifetime-Enhancing Method for Directional Sensor Networks with a New Hybrid Energy-Consumption Pattern in Q-coverage Scenarios. Energies 2020, 13, 824. https://doi.org/10.3390/en13040824
Peng S, Xiong Y. A Lifetime-Enhancing Method for Directional Sensor Networks with a New Hybrid Energy-Consumption Pattern in Q-coverage Scenarios. Energies. 2020; 13(4):824. https://doi.org/10.3390/en13040824
Chicago/Turabian StylePeng, Song, and Yonghua Xiong. 2020. "A Lifetime-Enhancing Method for Directional Sensor Networks with a New Hybrid Energy-Consumption Pattern in Q-coverage Scenarios" Energies 13, no. 4: 824. https://doi.org/10.3390/en13040824
APA StylePeng, S., & Xiong, Y. (2020). A Lifetime-Enhancing Method for Directional Sensor Networks with a New Hybrid Energy-Consumption Pattern in Q-coverage Scenarios. Energies, 13(4), 824. https://doi.org/10.3390/en13040824