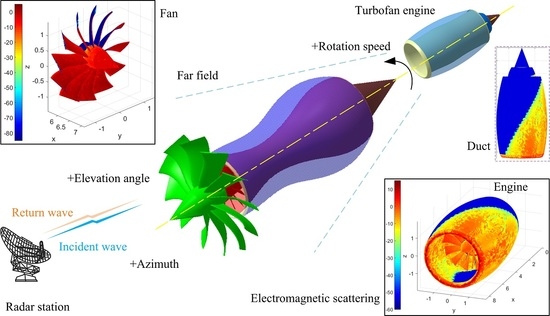
Study of the Radar Cross-Section of Turbofan Engine with Biaxial Multirotor Based on Dynamic Scattering Method
Abstract
1. Introduction
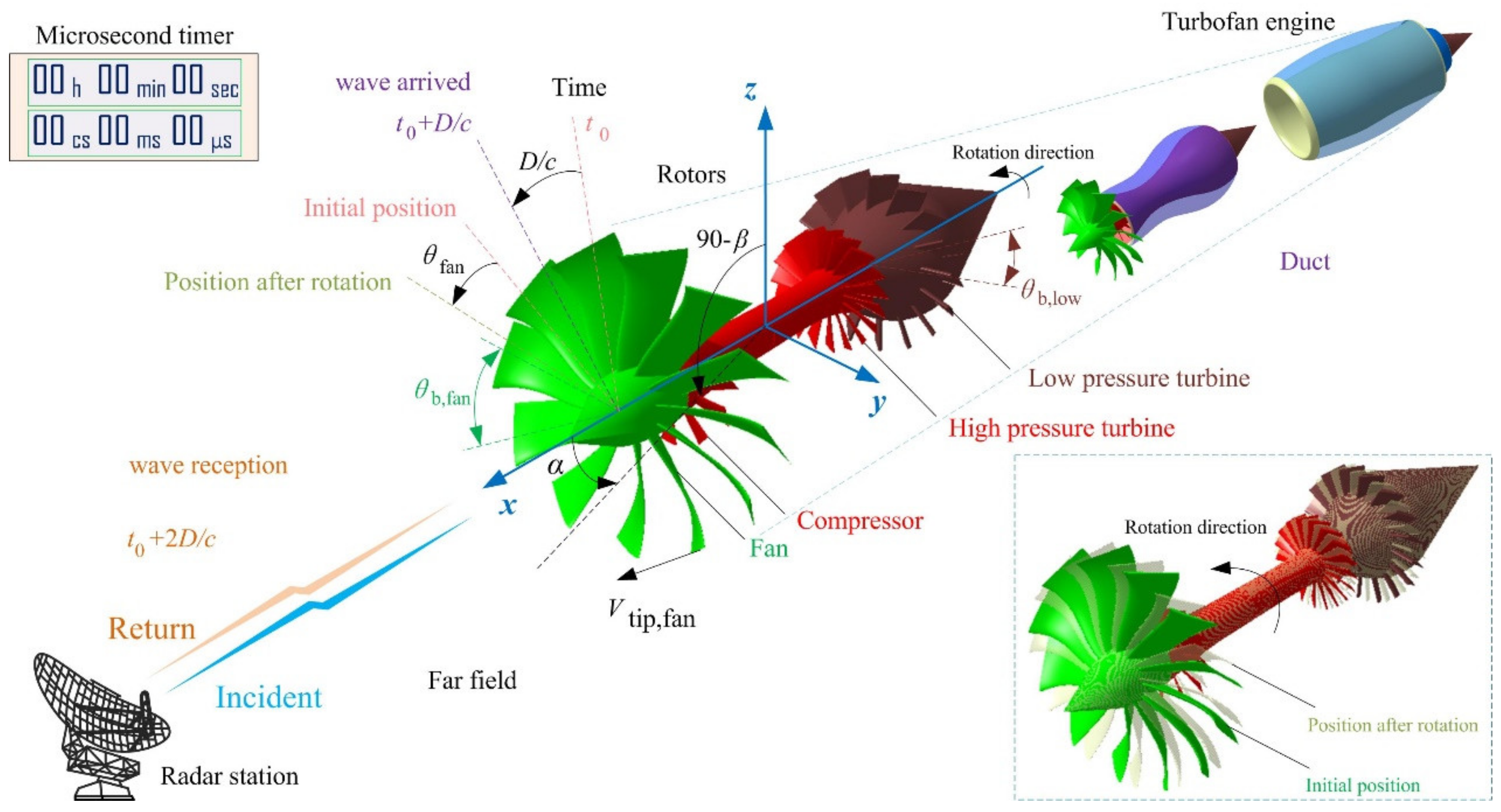
2. Dynamic Scattering Method
2.1. Electromagnetic Scattering Calculation
2.2. Dynamic Simulation Method
2.3. Grid Transformation Method
3. Model
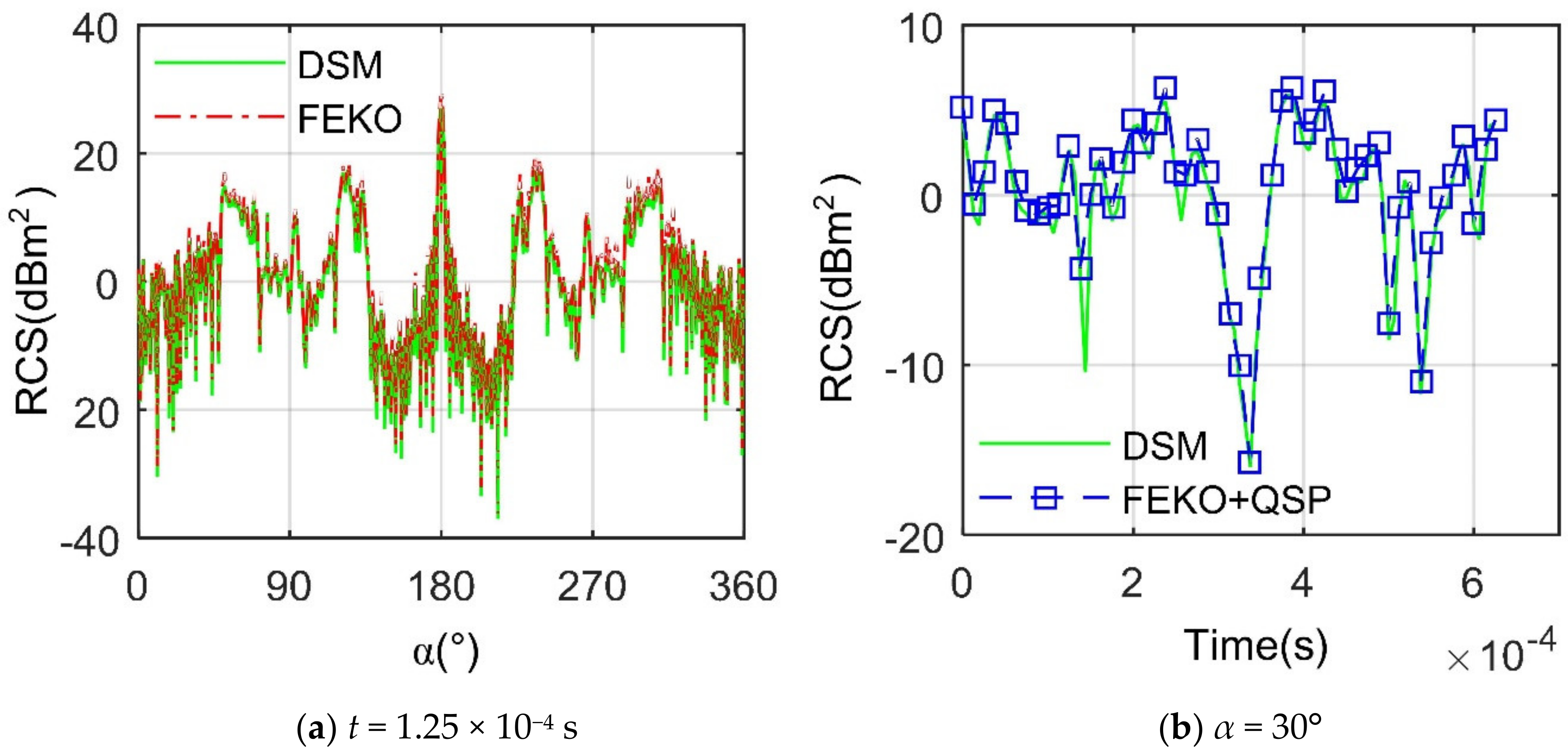
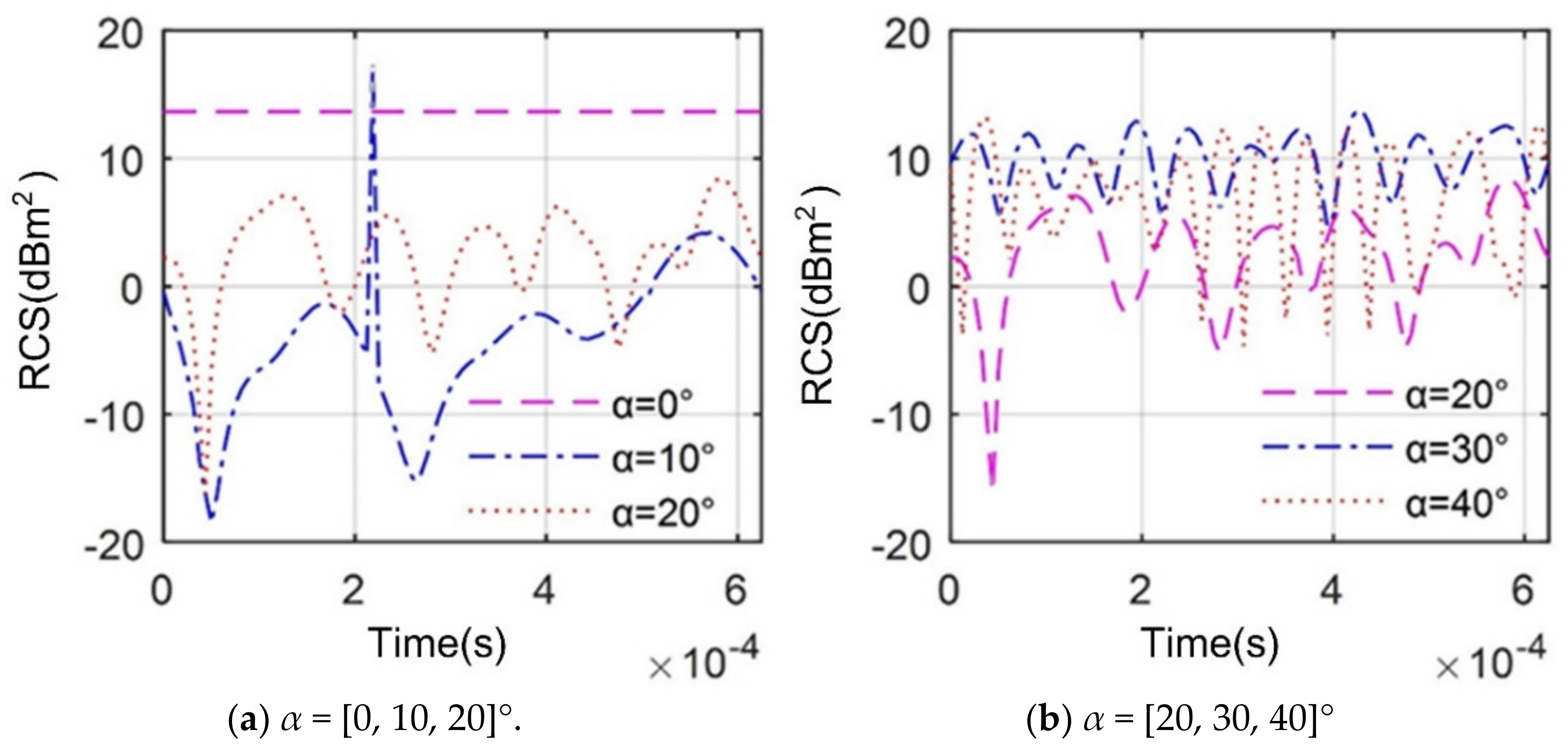
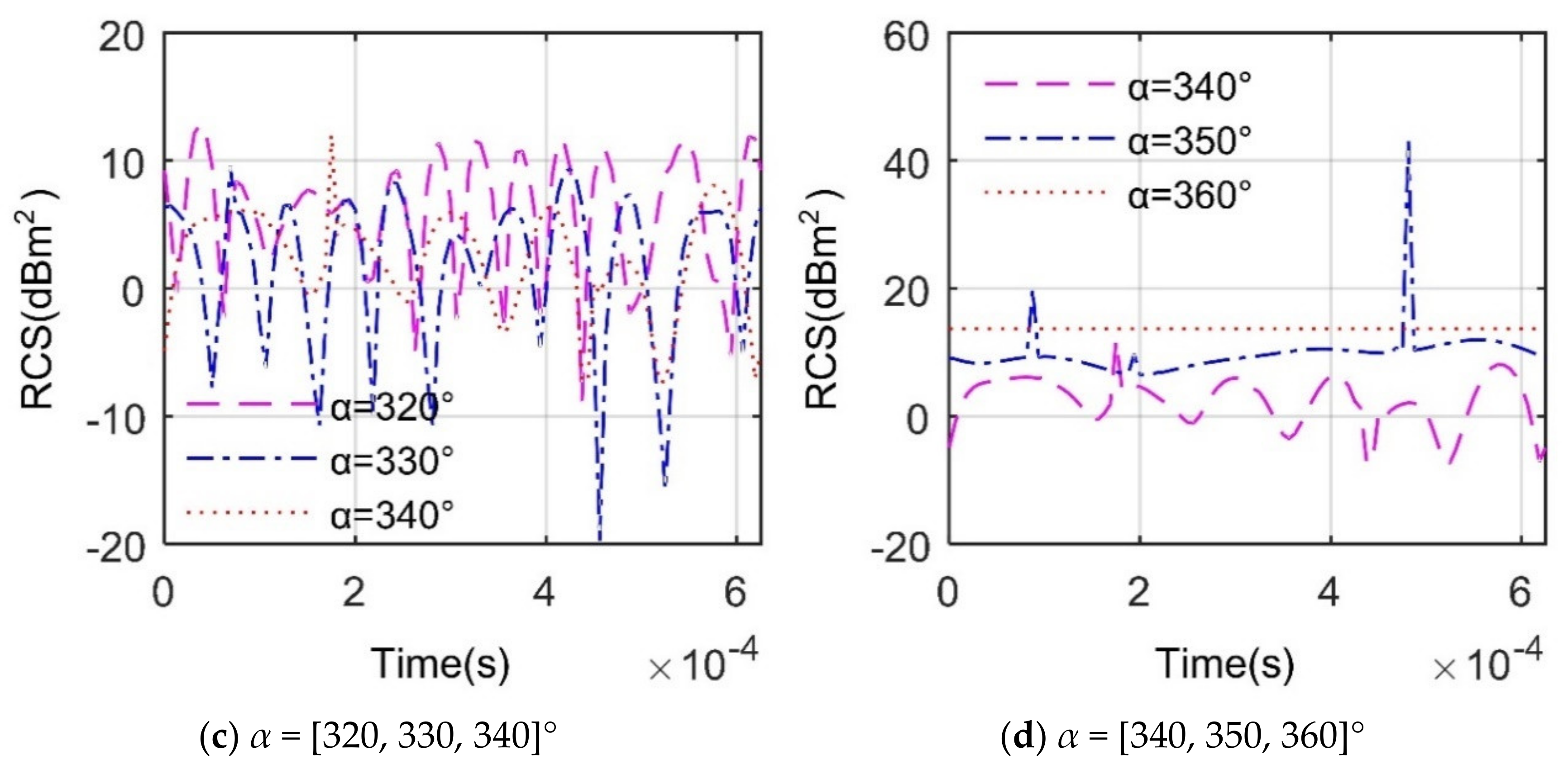
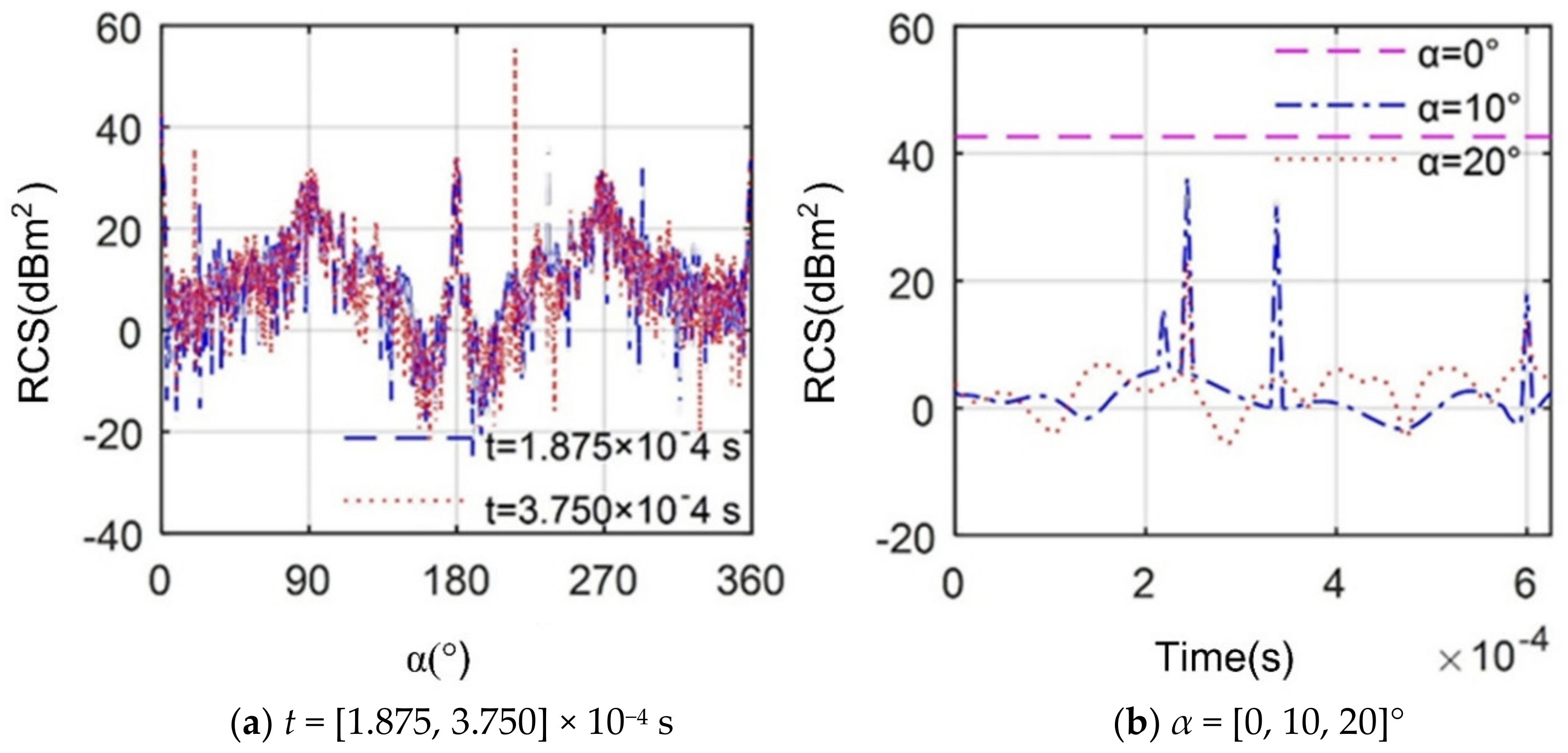
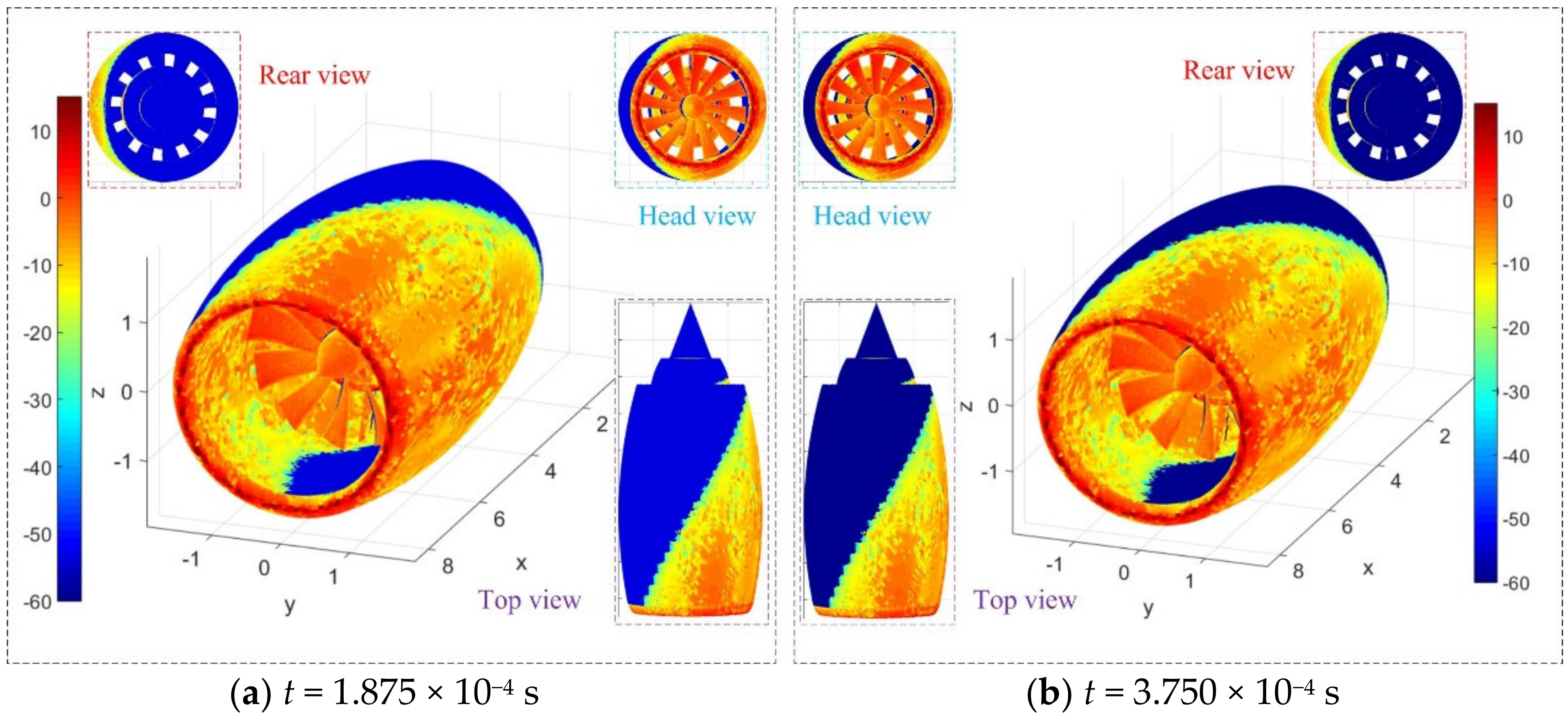
4. Results and Discussion
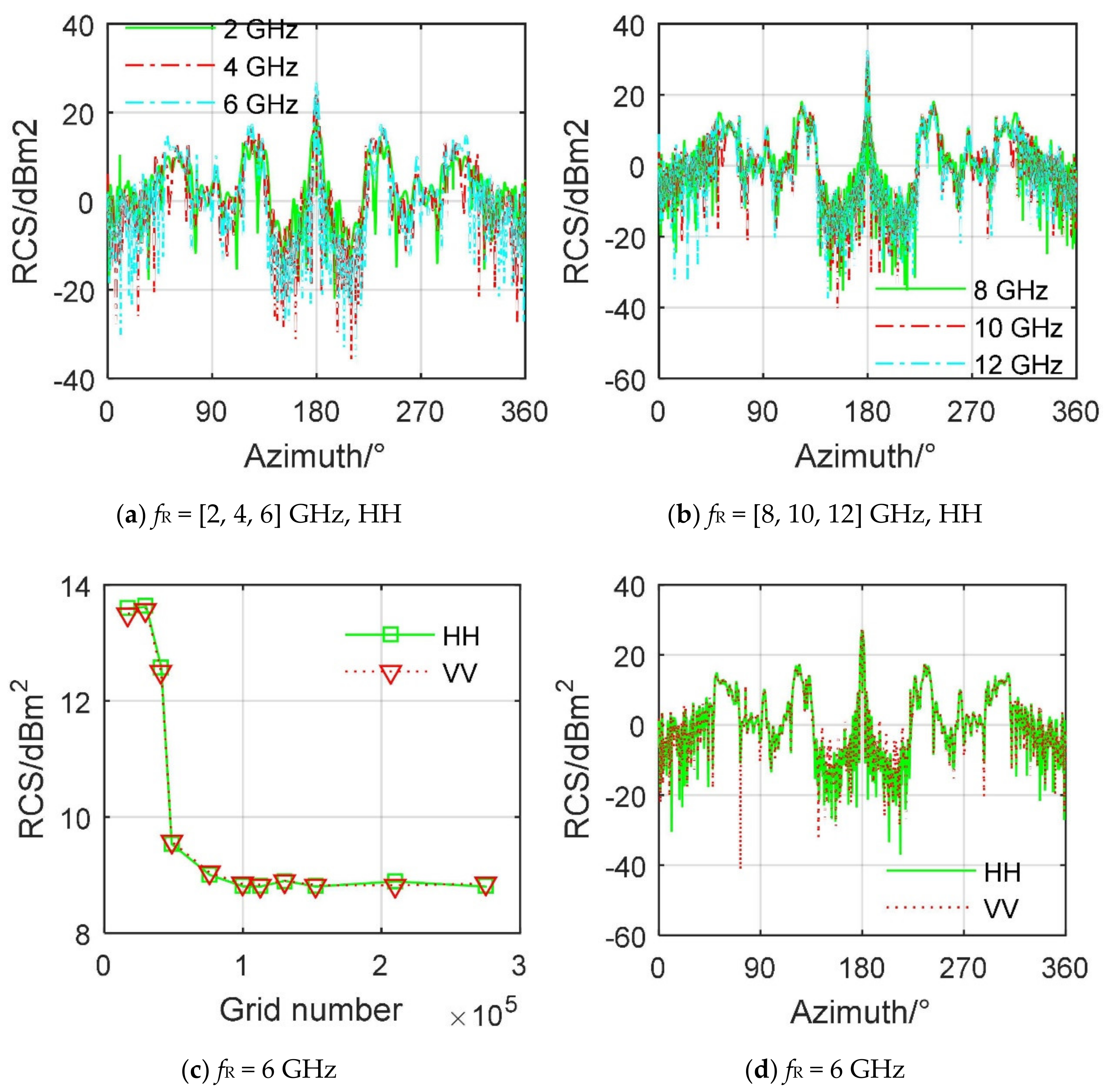
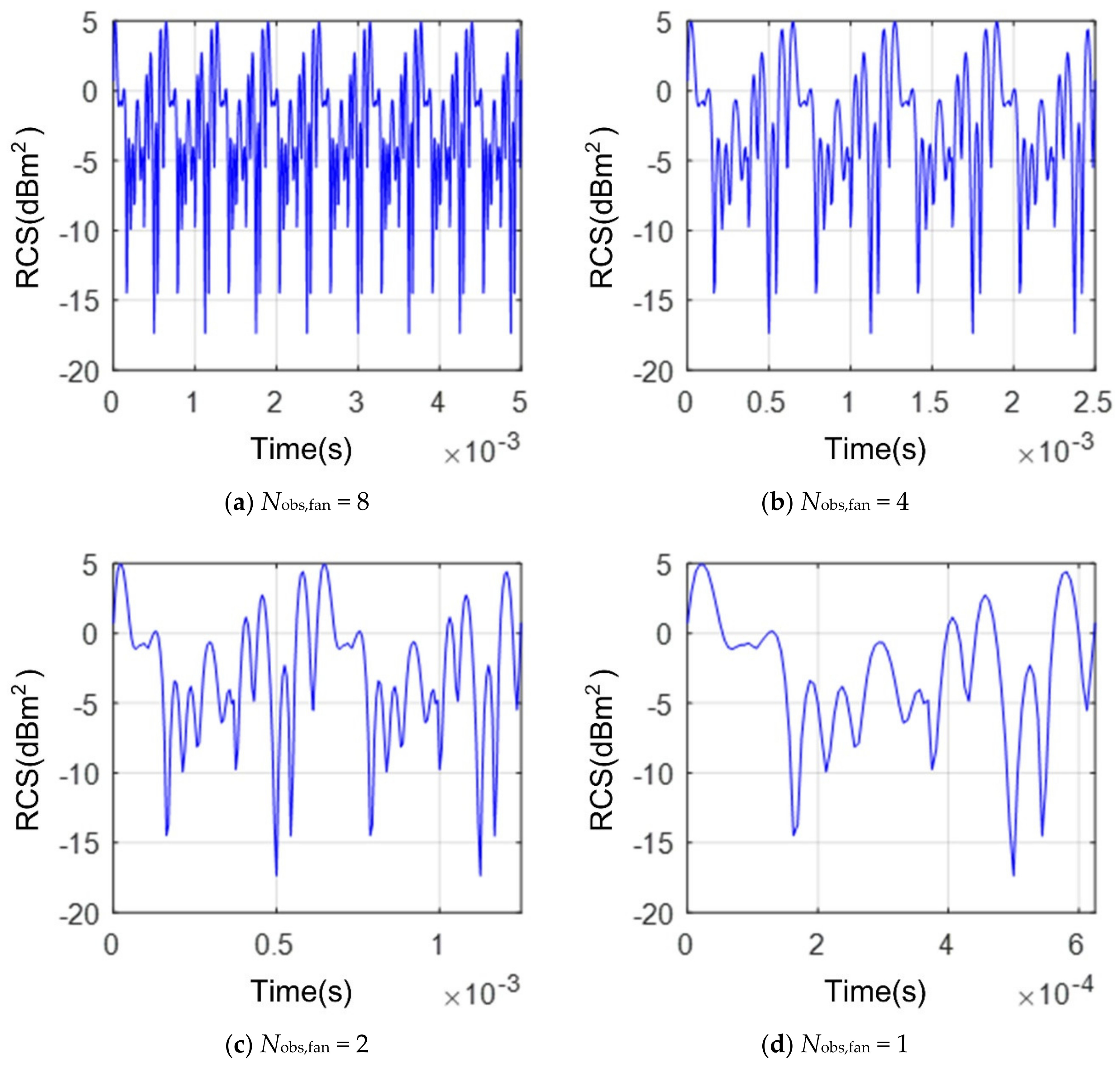
4.1. Effect of Individual Rotor
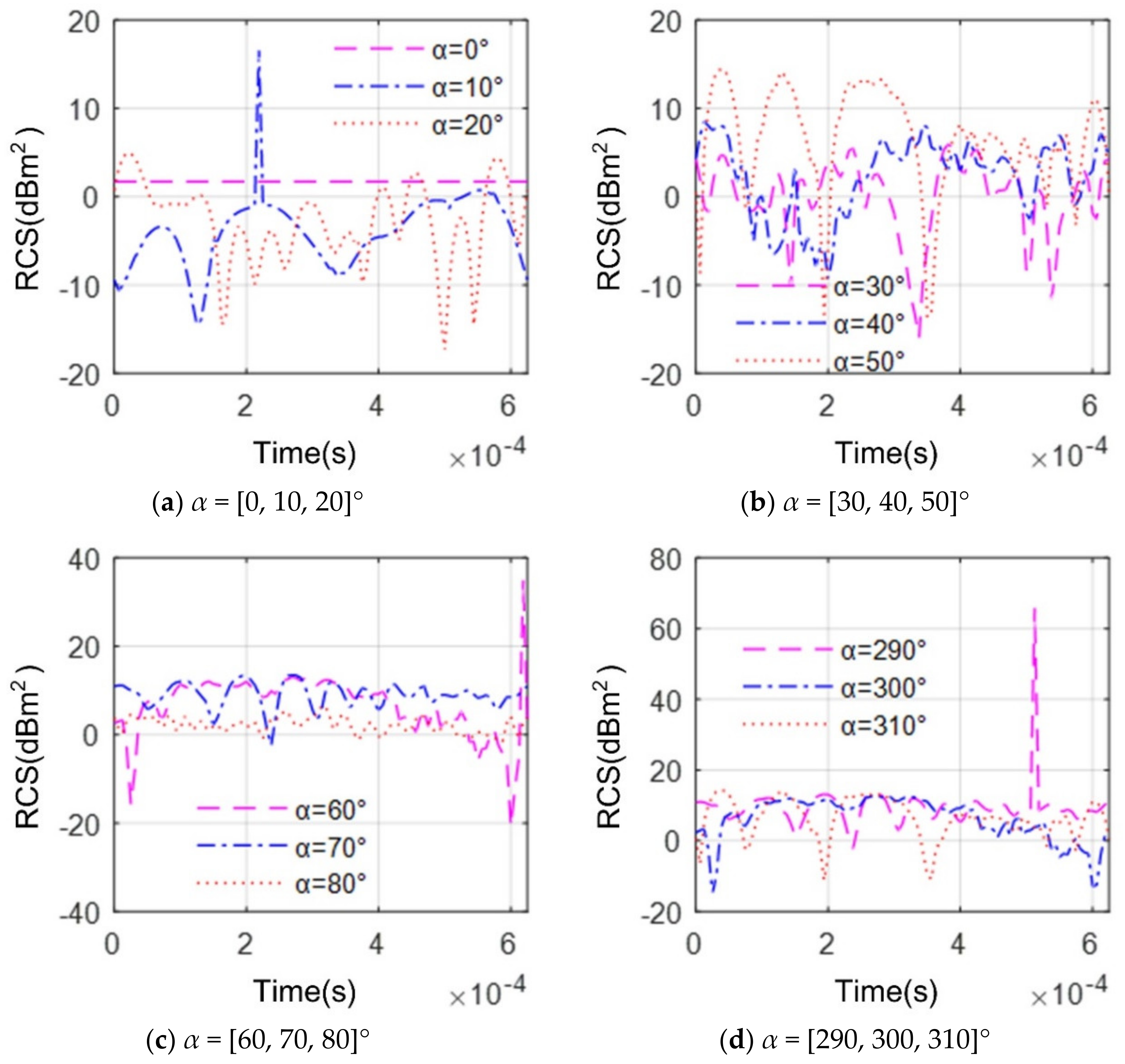
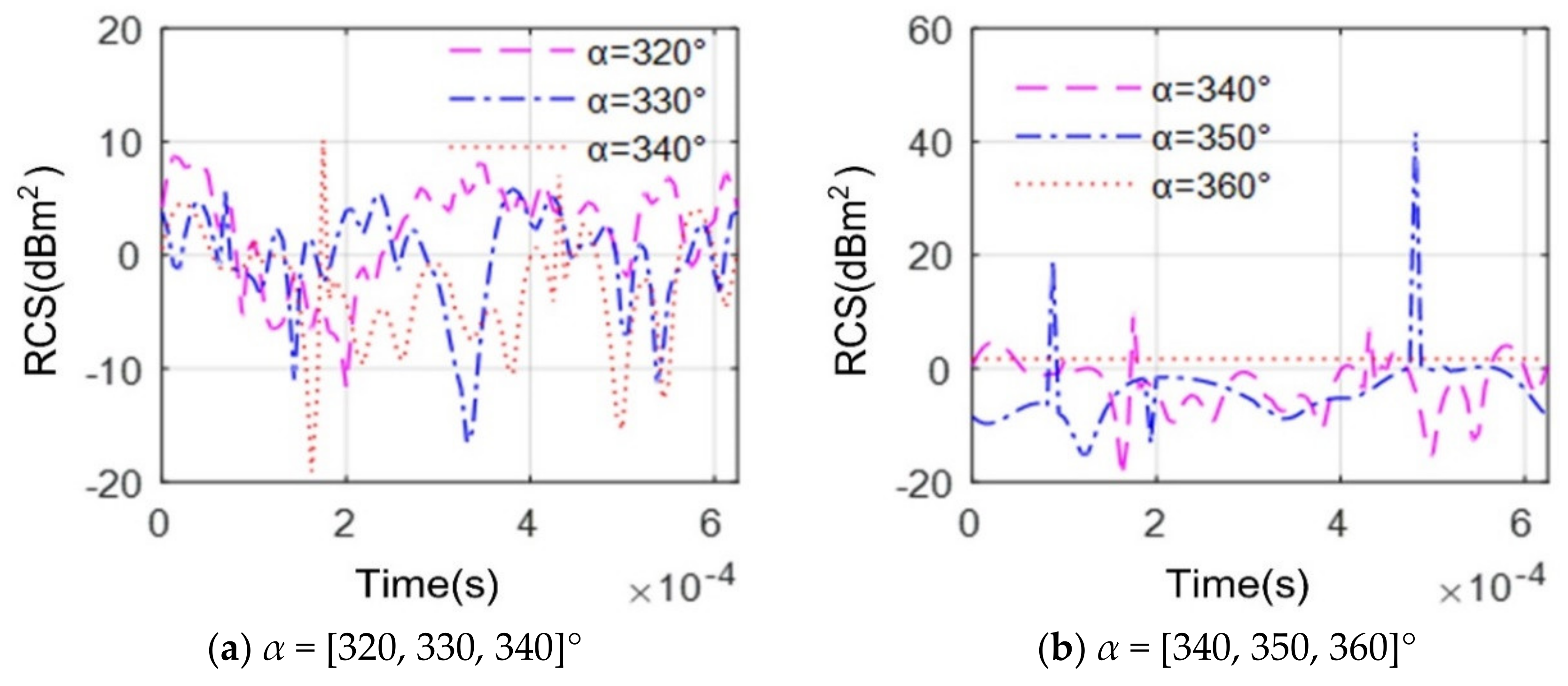
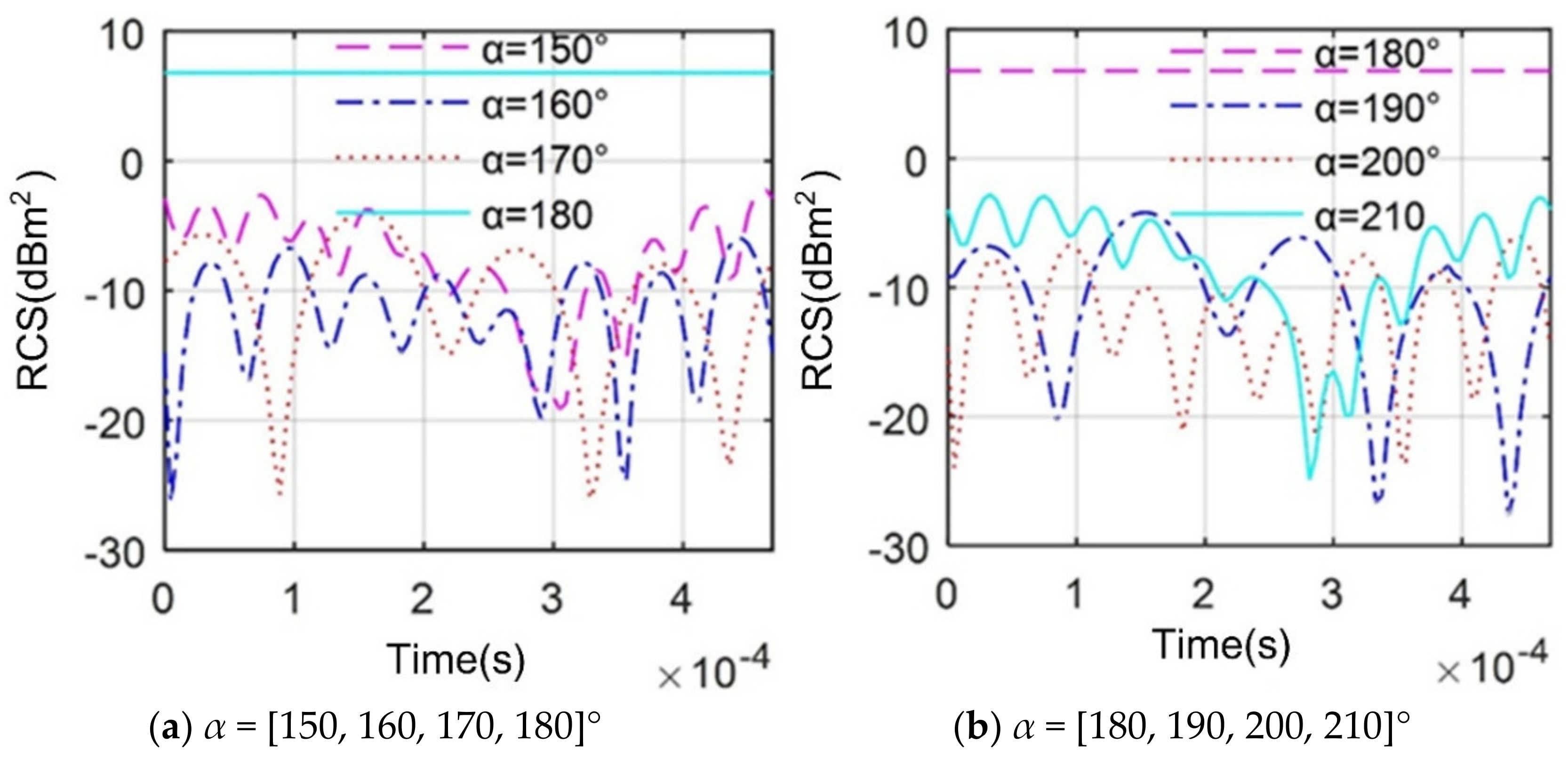
4.2. Effect of Azimuth Angle
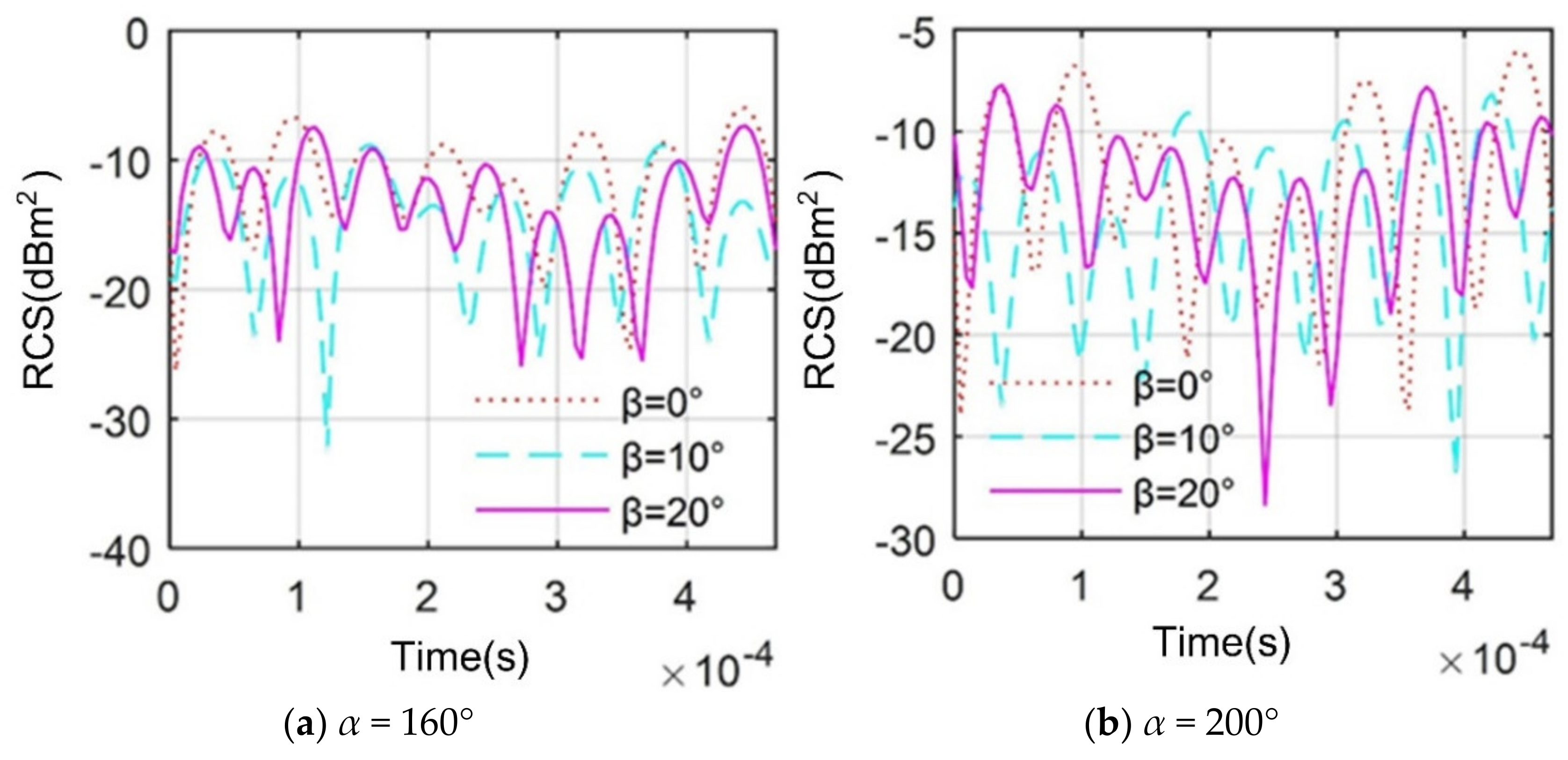
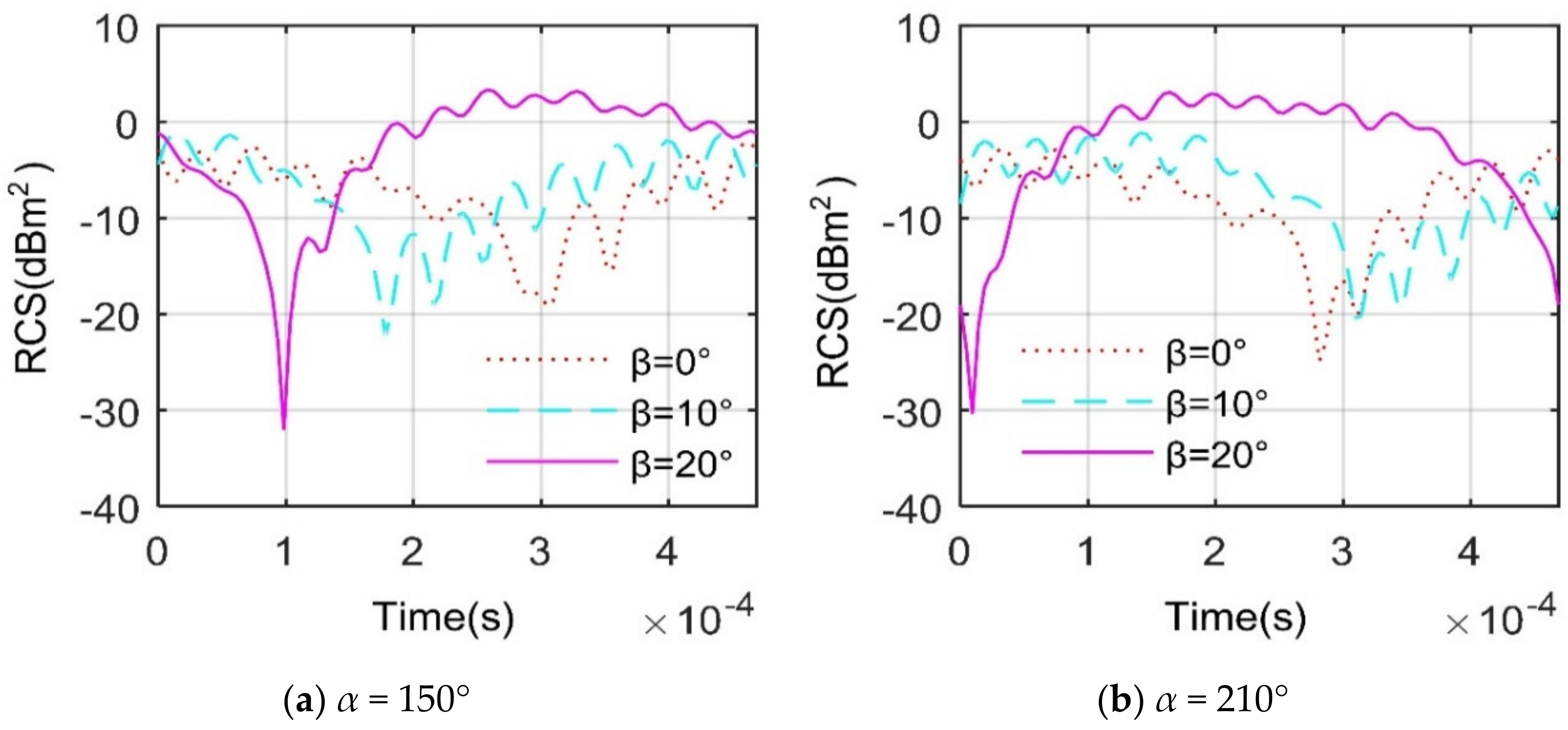
4.3. Effect of Elevation Angle
4.4. Effect of Engine Duct
5. Conclusions
- The electromagnetic scattering characteristics of each rotor during steady engine operation are periodic, and the period is equal to the base pass time of the rotor at the current rotating speed;
- The azimuth and elevation angles have a large impact on the dynamic RCS of the engine. The fan has a great influence on the change of the engine head to the RCS, while the low-pressure turbine has a greater influence on the engine tail RCS;
- The engine duct will greatly increase the RCS level of the entire engine, but will also block the scattering of its internal components. Front and rear rotors are the main influencing factors of engine dynamic RCS.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Nomenclature
| α | the horizontal angle between radar station-engine connection and the positive x-axis |
| β | the elevation angle between the radar station and the engine |
| θ | rotation angle |
| θb | angle between adjacent blades |
| D | distance between the radar and the target |
| c | electromagnetic wave propagation speed |
| Vtip | line speed of the blade tip |
| σ | radar cross-section |
| ωl | angular velocity of the low-speed shaft |
| ωh | angular velocity of the high-speed shaft |
| mengine | the model of the engine |
| Mengine | the grid coordinate matrix of the engine model |
| tbase | base pass time |
| Nfan | number of fan blades |
| ε | a custom difference |
| Tobs | total observation time |
| t | observation time |
| Subscript | |
| fan | fan |
| comp | compressor |
| high | high-pressure turbine |
| low | low-pressure turbine |
Appendix A
References
- Fedele, L.; Di Vito, L.; Ramundo, F.E. Increasing Efficiency in an Aeronautical Engine through Maintenance Evaluation and Upgrades: Analysis of the Reliability and Performance Improvements under Financial Issues. Energies 2020, 13, 3059. [Google Scholar] [CrossRef]
- Gao, X. Numerical Study of Infrared Radiation and Electromagnetic Scattering Characteristics of Aircraft/Exhaust System. Ph.D. Thesis, Northwestern Polytechnical University, Xi’an, China, 2016. [Google Scholar]
- Yang, S.N.; Zhang, Z.X.; Shao, W.R.; Deng, H.W. Numerical Investigation on Electromagnetic Scattering Characteristics for Engine Cavity with Centrocone. Aeroengine 2014, 40, 48–53. [Google Scholar]
- York, M.A.; Hoburg, W.W.; Drela, M. Turbofan engine sizing and tradeoff analysis via signomial programming. J. Aircr. 2017, 55, 988–1003. [Google Scholar] [CrossRef]
- Lu, W.; Huang, G.; Xiang, X.; Wang, J.; Yang, Y. Thermodynamic and Aerodynamic Analysis of an Air-Driven Fan System in Low-Cost High-Bypass-Ratio Turbofan Engine. Energies 2019, 12, 1917. [Google Scholar] [CrossRef]
- Li, Y.F.; Yang, Q.Z.; Gao, X.; Wu, Z.K. Investigation on Radar Cross-Section of S-Shaped Inlets Using IPO and EEC Method. J. Propuls. Technol. 2013, 34, 577–582. [Google Scholar]
- Noh, Y.H.; Park, C.S.; Yook, J.G.; Choi, W.Y.; Jang, Y.H. Analysis for Contribution of Engine Inlet Structure to Monostatic RCS of Aircraft in the VHF Band. In Proceedings of the IEEE International Symposium on Antennas and Propagation & USNC/URSI National Radio Science Meeting, Boston, MA, USA, 8–13 July 2018; pp. 2335–2336. [Google Scholar]
- Zhou, Z.Y.; Huang, J.; Wu, N.N. Acoustic and radar integrated stealth design for ducted tail rotor based on comprehensive optimization method. Aerosp. Sci. Technol. 2019, 92, 244–257. [Google Scholar] [CrossRef]
- Chen, J.J.; Huang, J.W.; Xu, J.D.; Pang, C.S.; Li, J.K. Calculation of attitude angle in dynamic radar targets electromagnetic scattering. J. Proj. Rocket. Missiles Guid. 2010, 30, 183–185. [Google Scholar]
- Tasic, M.; Kolundzija, B.; Milosevic, T. Domain decomposition method for scattering from an aircraft with jet engine inlet cavity. In Proceedings of the International Applied Computational Electromagnetics Society Symposium (ACES), Denver, CO, USA, 25–29 March 2018; pp. 1–2. [Google Scholar]
- Aiello, G.; Alfonzetti, S.; Rizzo, S.A.; Salerno, N. Multi-Objective Optimization of Thin-Film Silicon Solar Cells with Metallic and Dielectric Nanoparticles. Energies 2017, 10, 53. [Google Scholar] [CrossRef]
- Yang, S.N.; Shao, W.R.; Shang, S.T.; Deng, H.W. Study on Radar Stealth Shaping for Single Expansion Ramp with Spherical 2-D Nozzle. Aeroengine 2016, 42, 55–62. [Google Scholar]
- Schapker, R.L. Frequency effects of electromagnetic scattering from underdense turbulent plasmas. AIAA J. 1970, 8, 1582–1590. [Google Scholar] [CrossRef]
- Wang, R.G.; Cheng, Y.; Chen, W. Calculation of RCS of Intake by Means of Mode Superposition. J. Air Force Eng. Univ. (Nat. Sci. Ed. ) 2004, 5, 21–25. [Google Scholar]
- Ling, R.T.; Smith, T.D. Scattering of acoustic and electromagnetic waves by an airfoil. AIAA J. 1989, 27, 268–273. [Google Scholar] [CrossRef]
- Xiao, B.; Zhang, J. Application of SBR-Calculation the RCS of an Arbitrary Shaped Open-Ended Cavity. J. Appl. Sci. 1993, 11, 328–332. [Google Scholar]
- Chen, Q.; Huang, J.; Pan, M.; Lu, F. A Novel Real-Time Mechanism Modeling Approach for Turbofan Engine. Energies 2019, 12, 3791. [Google Scholar] [CrossRef]
- Zhou, Z.Y.; Huang, J.; Yi, M.X. Comprehensive optimization of aerodynamic noise and radar stealth for helicopter rotor based on Pareto solution. Aerosp. Sci. Technol. 2018, 82, 607–619. [Google Scholar] [CrossRef]
- Qin, J.; Pan, M.; Xu, W.; Huang, J. An Output-Based Limit Protection Strategy for Turbofan Engine Propulsion Control with Output Constraints. Energies 2019, 12, 4043. [Google Scholar] [CrossRef]
- Zhou, C.H.; Qian, W.P.; Guo, Y.Q. EM Scattering Model of Dynamic Rigid Target. J. Sichuan Armed Forces 2015, 36, 138–140. [Google Scholar]
- Sobczak, K.; Obidowski, D.; Reorowicz, P.; Marchewka, E. Numerical Investigations of the Savonius Turbine with Deformable Blades. Energies 2020, 13, 3717. [Google Scholar] [CrossRef]
- Jiang, X.W.; Zhao, Q.J. Analysis and evaluation about radar target scattering characteristics of helicopter wing components. J. Aerosp. Power 2016, 31, 2691–2700. [Google Scholar]
- Vijayaraghavan, D.; Keith, T.G. Grid transformation and adaption techniques applied in the analysis of cavitated journal bearings. J. Tribol. 1990, 112, 52–59. [Google Scholar] [CrossRef]
- Song, H.Y.; Liang, L.F.; Zhou, Z.G. The complementary energy principle and generalized variational principles of quasi-static electro-magneto-thermo-elasticity. J. Harbin Eng. Univ. 2011, 32, 33–37. [Google Scholar]
- Eby, M.; Holloway, G. Grid transformation for incorporating the Arctic in a global ocean model. Clim. Dyn. 1994, 10, 241–247. [Google Scholar] [CrossRef]
- Song, H.Y.; Li, H.B.; Liang, L.F.; Zhou, Z.G. The second H-R generalized variational principles of quasi-static electro-magneto-thermo-elasticity. Struct. Environ. Eng. 2010, 37, 8–16. [Google Scholar]
- Zhou, Z.Y.; Huang, J. Target head direction far field radar cross section reduction based on narrow surface element method. Optik 2020, 200, 163230. [Google Scholar] [CrossRef]
- Chen, H.; Wang, Z.L.; Li, J.; Zhang, M.H. Launch vehicle RCS simulation and computing method based on component decomposition. J. Spacecr. TT C Technol. 2014, 33, 198–201. [Google Scholar]
- Tomita, H. A stretched icosahedral grid by a new grid transformation. J. Meteorol. Soc. Jpn. Ser. II 2008, 86, 107–119. [Google Scholar] [CrossRef]
- Singh, S.K.; Khanna, K.; Bose, R.; Panigrahi, B.K.; Joshi, A. Joint-transformation-based detection of false data injection attacks in smart grid. IEEE Trans. Ind. Inform. 2017, 14, 89–97. [Google Scholar] [CrossRef]
- Chen, B.; Tong, C.M.; Li, X.M.; Liu, K.Y. Aircraft Target Recognition Based on HRRP. J. Microw. 2017, 33, 72–77. [Google Scholar]
- Qi, Y.T.; Zhang, X.Y.; Lin, G.; Li, J.Z. A simulation method of aircraft dynamic RCS. Chin. J. Radio Sci. 2018, 34, 97–103. [Google Scholar]
- Daroukh, M.; Moreau, S.; Gourdain, N.; Boussuge, J.F.; Sensiau, C. Tonal Noise Prediction of a Modern Turbofan Engine With Large Upstream and Downstream Distortion. J. Turbomach. 2019, 141, 021010. [Google Scholar] [CrossRef]
- Lv, Z.Y.; Wei, P. Application of small scale grid tomography velocity modeling method in timedepth conversion of low-amplitude structural region. Prog. Geophys. 2020, 1, 1–9. [Google Scholar]
- Pan, R.; Song, Z.; Liu, B. Optimization Design and Analysis of Supersonic Tandem Rotor Blades. Energies 2020, 13, 3228. [Google Scholar] [CrossRef]
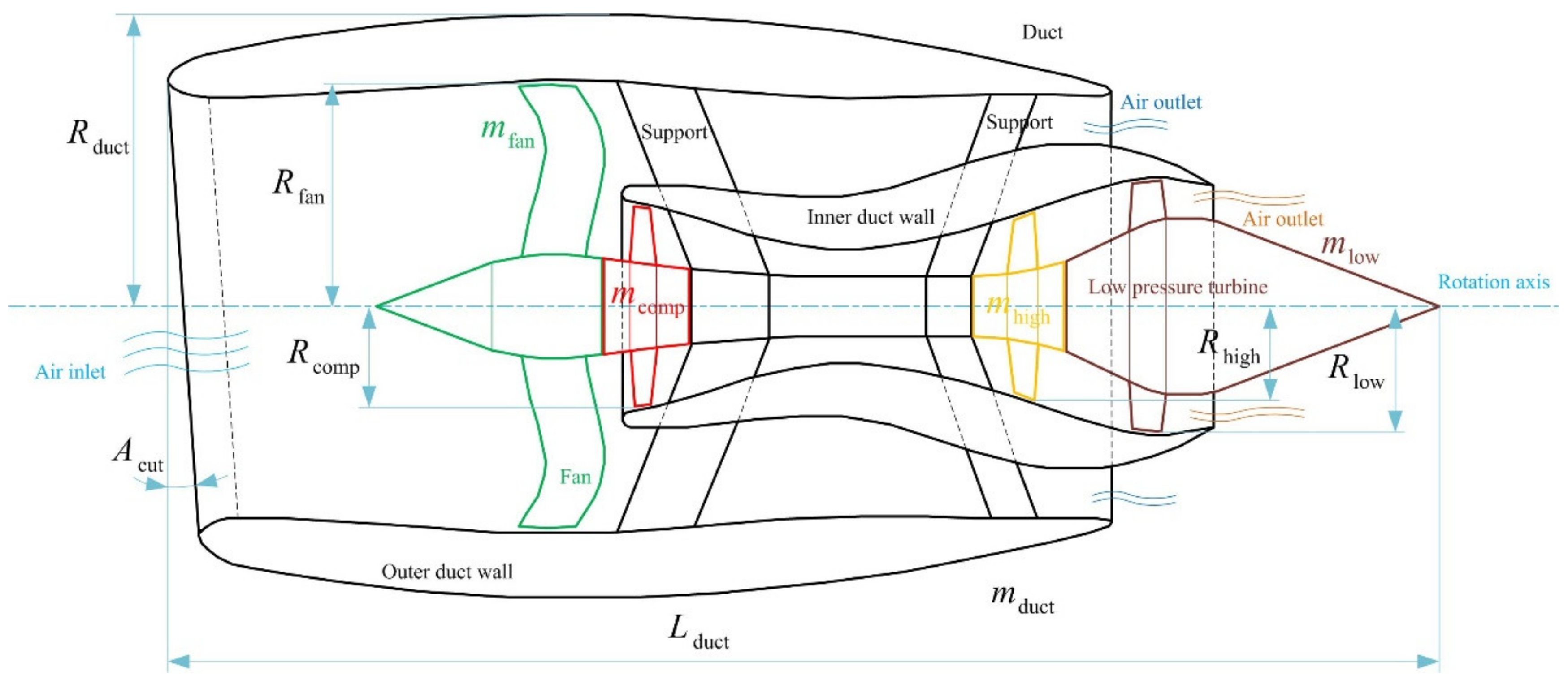

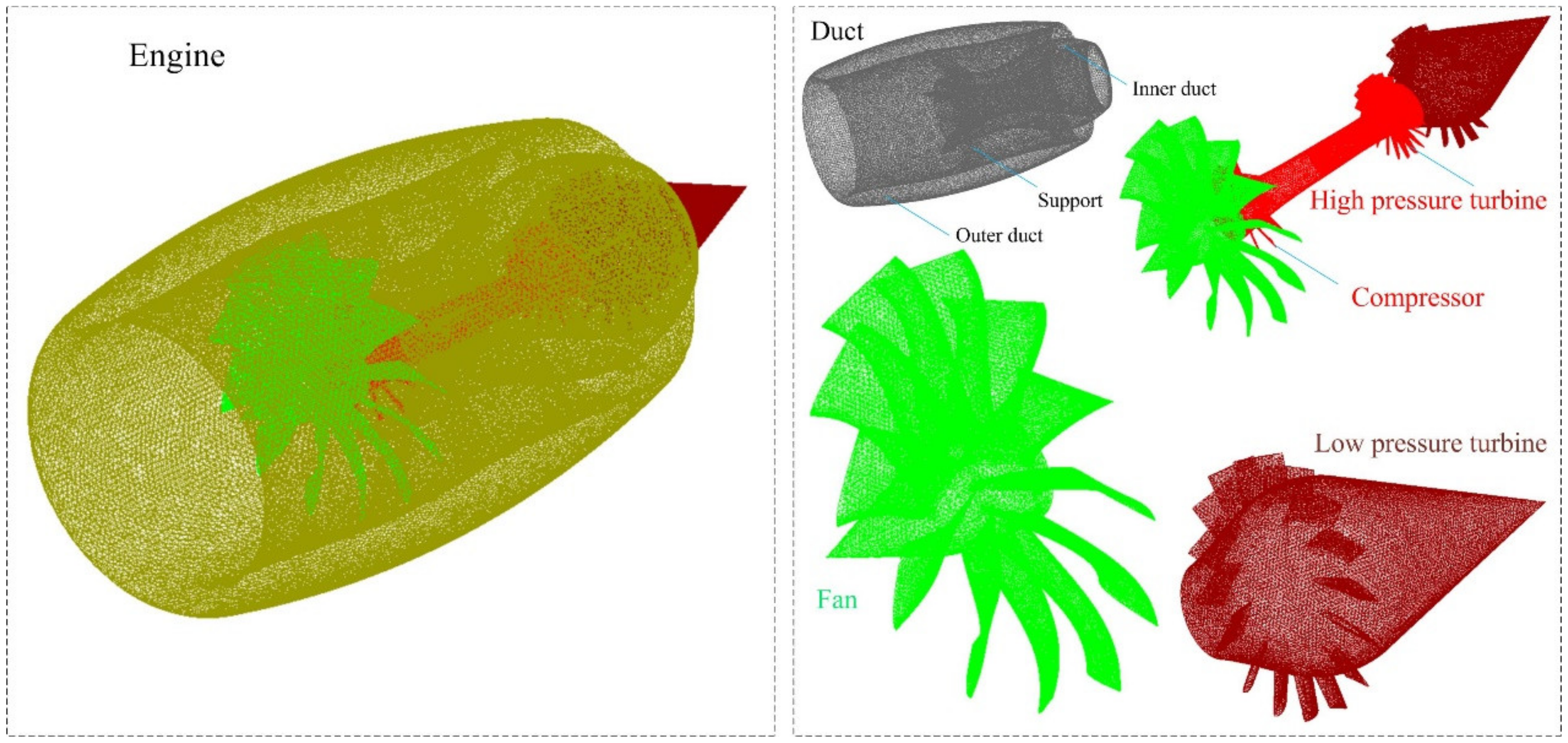


| Model | mfan | mcomp | mhigh | mlow | mduct |
|---|---|---|---|---|---|
| Airfoil | AG 08 | AG 25 | AH 21 | ARA-D 10% | — |
| Outer radius/m | 1.485 | 0.630 | 0.563 | 0.806 | 1.946 |
| Number of blades | 12 | 10 | 18 | 16 | — |
| Model | mfan | mcomp | mhigh | mlow |
|---|---|---|---|---|
| Rotating speed/r/min | 8000 | 10,000 | 10,000 | 8000 |
| Area | Maximum Value/mm | Area | Maximum Value/mm |
|---|---|---|---|
| Global minimum size | 2 | Fan blade trailing edge | 5 |
| Fan blade leading edge | 8 | Fan blade | 25 |
| Fan hub | 35 | Blade trailing edge of mcomp | 4 |
| Blade leading edge of mcomp | 10 | Blade of mcomp | 25 |
| Hub of mcomp | 25 | Blade trailing edge of mhigh | 5 |
| Blade leading edge of mhigh | 10 | Blade of mhigh | 25 |
| Hub of mhigh | 25 | Blade trailing edge of mlow | 6 |
| Blade leading edge of mlow | 10 | Blade of mlow | 25 |
| Hub of mlow | 30 | Support | 50 |
| Inner duct | 120 | Outer duct | 150 |
| α/° | −10 | 0 | 10 | 20 | 30 |
|---|---|---|---|---|---|
| RCS mean/dBm2 | 23.181 | 1.709 | −0.039 | −0.934 | 1.427 |
| α/° | 40 | 50 | 60 | 70 | 80 |
| RCS mean/dBm2 | 3.883 | 9.056 | 16.284 | 9.748 | 2.518 |
| α/° | 150 | 160 | 200 | 210 |
|---|---|---|---|---|
| β = 0° | −6.316 | −10.437 | −10.862 | −6.649 |
| β = 10° | −5.450 | −13.122 | −12.813 | −5.474 |
| β = 20° | −0.460 | −12.180 | −11.966 | −0.496 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, Z.; Huang, J. Study of the Radar Cross-Section of Turbofan Engine with Biaxial Multirotor Based on Dynamic Scattering Method. Energies 2020, 13, 5802. https://doi.org/10.3390/en13215802
Zhou Z, Huang J. Study of the Radar Cross-Section of Turbofan Engine with Biaxial Multirotor Based on Dynamic Scattering Method. Energies. 2020; 13(21):5802. https://doi.org/10.3390/en13215802
Chicago/Turabian StyleZhou, Zeyang, and Jun Huang. 2020. "Study of the Radar Cross-Section of Turbofan Engine with Biaxial Multirotor Based on Dynamic Scattering Method" Energies 13, no. 21: 5802. https://doi.org/10.3390/en13215802
APA StyleZhou, Z., & Huang, J. (2020). Study of the Radar Cross-Section of Turbofan Engine with Biaxial Multirotor Based on Dynamic Scattering Method. Energies, 13(21), 5802. https://doi.org/10.3390/en13215802