A Combined Deep Learning and Ensemble Learning Methodology to Avoid Electricity Theft in Smart Grids

Abstract

Electricity is widely used around 80% of the world. Electricity theft has dangerous effects on utilities in terms of power efficiency and costs billions of dollars per annum. The enhancement of the traditional grids gave rise to smart grids that enable one to resolve the dilemma of electricity theft detection (ETD) using an extensive amount of data formulated by smart meters. This data are used by power utilities to examine the consumption behaviors of consumers and to decide whether the consumer is an electricity thief or benign. However, the traditional data-driven methods for ETD have poor detection performances due to the high-dimensional imbalanced data and their limited ETD capability. In this paper, we present a new class balancing mechanism based on the interquartile minority oversampling technique and a combined ETD model to overcome the shortcomings of conventional approaches. The combined ETD model is composed of long short-term memory (LSTM), UNet and adaptive boosting (Adaboost), and termed LSTM–UNet–Adaboost. In this regard, LSTM–UNet–Adaboost combines the advantages of deep learning (LSTM-UNet) along with ensemble learning (Adaboost) for ETD. Moreover, the performance of the proposed LSTM–UNet–Adaboost scheme was simulated and evaluated over the real-time smart meter dataset given by the State Grid Corporation of China. The simulations were conducted using the most appropriate performance indicators, such as area under the curve, precision, recall and F1 measure. The proposed solution obtained the highest results as compared to the existing benchmark schemes in terms of selected performance measures. More specifically, it achieved the detection rate of 0.92, which was the highest among existing benchmark schemes, such as logistic regression, support vector machine and random under-sampling boosting technique. Therefore, the simulation outcomes validate that the proposed LSTM–UNet–Adaboost model surpasses other traditional methods in terms of ETD and is more acceptable for real-time practices.

1. Introduction

The secure and efficient use of electricity represents a major aspect of the social and economic development of a country. Electricity losses happen during power generation, transmission and delivery to consumers. Essentially, power transmission and delivery have a couple of losses, namely, technical losses (TL) and nontechnical losses (NTL) [1]. TL occur due to the line losses, transformer losses and other power system elements. NTL occur due to the electricity stealing, defective meters, overdue bills and billing mistakes [1]. More generally, NTL are the difference between total losses and TL. Besides, NTL raise electricity prices, increase load-shedding, decrease revenue and decrease energy efficiency. Thus, NTL badly affect both the utilities and a country’s financial state [2,3].

Electricity fraud is one of the chief reasons for the NTL, which accounts for 10–40% of cumulative electricity losses worldwide [4]. Electricity theft comprises of bypassing electricity meters, tampering with meter readings, tampering with meters themselves and cyber-attacks [5,6]. Therefore, the reduction of electricity fraud is a principal concern of the power distribution companies to secure significant amounts of the total electricity losses and revenue [7].

Electricity theft is spreading widely in many developing countries—e.g., India loses 20% of its total electricity due to electricity theft [8], and developed countries. For instance, in the U.S., the revenue loss as a result of electricity fraud is about $6 billion, while in the UK, it costs up to £175 million per annum [9,10]. Moreover, it is stated in [11] that electricity theft accounts for approximately a hundred million Canadian dollars annually. Globally, the utilities lose more than $20 billion per annum through electricity fraud [12].

The introduction of advanced metering infrastructure (AMI) in the smart grid environment provides a massive amount of power consumption users’ records, which makes it easier for utilities to monitor the electricity theft [13,14]. AMI enables price and load forecasting [15,16], energy management [17,18] and consumer behavior characterization [19]. As electricity theft continues to increase, smart meters enable utilities to provide new and innovative solutions to perform electricity theft detection (ETD). Generally, electricity thieves can alter the smart meters’ information physically or through cyber-attacks. Consequently, the primary way of ETD is manually examining the consumers’ electricity meters and comparing the abnormal consumption readings with the previous normal ones, known as the audit and on-site inspection process. However, these methods are costly, inefficient and time-consuming.

In contrast to the manual methods, supervised machine learning solutions have gained the interest of utilities and academia for performing ETD. Studies based on the supervised learning techniques [20,21,22,23,24,25] focus on ETD using the large and imbalanced datasets obtained through the smart meters. However, the performances of these techniques are still not sufficient for the practical applications in utilities. that implies that the techniques raise misclassification scores that lead to the costly procedure of on-site inspections for the final verifications. Therefore, that exhibits the need for a new solution to solve the ETD problem using a large imbalanced dataset to determine the real assessment of the model’s performance.

In ETD literature, the proposed methods are categorized into two major groups: ETD through technical methods and ETD through nontechnical methods. Nontechnical methods cover: the auditing and inspection of illegal electricity consumers, giving awareness to the electricity consumers about electricity theft as a crime and punishment, installing the smart meters that can not be easily tampered with by consumers and reducing electricity theft through the psychosocial methods, such as social support [26]. Technical methods are also broadly classified into three types: state-based solutions (also known as hardware-based solutions), game-theory-based solutions and data-driven solutions (also known as machine learning-based solutions) [12].

In hardware-based solutions, the major focus is on designing specific hardware devices and infrastructures to detect electricity theft. Hardware-based solutions consist of: smart meters with radio-frequency identification tags (RFID), anti-tampering sensors, wireless sensors and distribution transformers [5,27,28,29]. These solutions get high detection efficiency through specific devices, for instance, RFID. The major limitations of the state-based solutions are the high cost of design, the high operational and maintenance costs and the vulnerability to weather conditions. Particularly, due to the inefficiency and high cost of hardware-based solutions, data-driven solutions have gained the interest of researchers. In game-theory-based solutions [30,31], ETD is considered as a contest between the power distribution company and electricity fraudsters, known as the players. Both players want to maximize their utility functions. These solutions are low cost and provide reasonable ways to find the electricity theft. Hence, one of the complicated issues in the game-theory-based procedures is how to form the utility function for each player, which is a challenging and time-consuming problem.

Recently, machine learning approaches have achieved significant importance in ETD. The main purpose of these solutions is to analyze the electricity usage behavior of the consumers based on smart meters’ data. These methods require no additional information about the network topology or hardware devices. Thus, machine learning solutions are further categorized into the supervised and unsupervised learning methods. Unsupervised learning methods have proposed clustering-based solutions to group the similar instances into one cluster [32,33], members of which each have a high false positive rate (FPR). In this paper, a unique supervised learning-based solution, namely, the LSTM–UNet–Adaboost, is proposed to perform the binary classification using the data from on-site inspections. Thus, we describe some recent advances made in this area.

Buzau et al. [34] presented a solution that is based on an extreme gradient boosted tree (XGBoost) for the detection of NTL in smart grids. Their main objective was to rank the list of consumers applying the smart meters’ data and extract features from auxiliary databases. Punmiya et al. [35] introduced a gradient boosting theft detector (GBTD) model, which is composed of three variants of a gradient boosting classifier to perform the ETD. A theft detector is also used for feature engineering-based preprocessing through the GBTD’s feature importance function. Another solution based on the ensemble bagged tree is presented in [21] for the NTL detection, in which an ensemble of individual decision trees is applied to improve the theft detection by aggregating their performances. Buzau et al. [23] submit a hybrid of LSTM and multilayer perceptron (MLP), termed LSTM-MLP, for the NTL detection in the smart grid. LSTM is employed to automate the feature extraction from sequential information, while MLP is used to deal with non-sequential information. Likewise, the authors [36] used a deep neural network for the feature extraction and meta-heuristic technique enabled XGBoost for ETD.

Nelson et al. [24] combined the maximal overlap discrete wavelet packet transform (MODWPT) with the random under-sampling boosting (RUSBoost) technique to obtain the most suitable features for the identification of NTL. Li et al. [37] used a semi-supervised technique to perform the detection of NTL. Tianyu et al. [38] made a semi-supervised deep learning model, known as the multitask feature extracting fraud detector (MFEFD), for ETD: both the supervised and unsupervised learning procedures are combined to capture important features from the labeled and unlabeled data. Maamar et al. [32] offered a hybrid model that utilizes the k-means clustering procedure and deep neural networks (DNN) for ETD in the AMI system, where k-means is utilized to gather consumers having the same electricity consumption behaviors, and DNN is used to detect anomalies in the electricity consumption behaviors of the consumers. Ghasemi et al. [26] proposed a solution comprising of a probabilistic neural network and mathematical model, named the PNN–Levenberg–Marquardt, for the identification of two types of illegal consumers using the observer’s meters. PNN is applied to detect the suspicious consumers, and the Levenberg–Marquardt is practiced for classifying the fraud consumers. In [9], a theft detector is presented, which implements the support vector machine (SVM) for the detection of normal and abnormal consumers using their consumption patterns. Another work [39] proposed a combined data sampling mechanism and performs ETD through the bi-directional gated recurrent unit (GRU).

In recent years, the convolutional neural network (CNN) has achieved success in ETD because it is a deep learning technique that catches high-level features from the electricity consumption dataset. Authors in [20] presented a hybrid wide and deep convolutional neural network (WD-CNN) for ETD. The wide part is used to extract the global features from 1-D data, while the deep component is applied to derive periodicity and non-periodicity from 2-D data. Li et al. [40] introduce a hybrid of CNN and random forest (RF), known as the CNN-RF model, for ETD in smart grids, where the RF is used as the final layer to perform ETD on the extracted features. Hasan et al. [22] made a solution consisting of the hybrid of CNN and LSTM for ETD. LSTM is used to solve the binary classification problem using CNN’s output. In another study [41], the authors introduced a hybrid of CNN and GRU for the detection of abnormal consumers. However, CNN only looks for “what” information is available in the data through down-sampling while ignoring “where” this information is present, which degrades the ETD’s performance. Moreover, in the traditional CNN, final classification is performed through either softmax classifier or sigmoid function that leads to the degradation of generalization ability plus subjecting the model to the local optima.

The aforementioned techniques for ETD are innovative and efficient; however, their performances are inadequate for real practices. Generally, these techniques have several limitations that must be addressed as follows: a model’s bias towards the majority class due to the class imbalance; a model’s performance evaluated on synthetic data does not provide a realistic assessment of the theft detection; models require artificial feature extraction and have poor detection performances, such as low detection scores and high misclassification scores. Hence, this detection score is costly for the utilities, e.g., on-site inspections needed for the confirmation. Thus, the problem of ETD is not fixed completely, which implies a new solution that provides a more accurate theft detection score.

To overcome the limitations of previous studies, we propose a new combined LSTM–UNet–Adaboost solution for ETD in this paper. The prime intention behind the proposed solution is to perform the binary classification over the electricity consumption data to characterize the consumers as either benign or thieves. As compared to the above-mentioned studies, our proposed scheme distinguishes itself: by presenting a new class balancing technique IQMOT to overcome the limitations of class imbalance by implementing a UNet technique to automate the feature extraction that captures both “what” and “where” from the 2-D data rather than only “what”, and by performing the joint training and classification through Adaboost using the features extracted from UNet and LSTM. In this regard, the proposed model gets the advantages of two powerful approaches known as deep learning and ensemble learning. Deep learning is applied to automate the feature extraction, while ensemble learning is used to perform the joint training and classification.

To address the above-mentioned problems, this paper proposes a new and practical solution for ETD utilizing long short-term memory (LSTM), UNet and adaptive boosting (Adaboost), named LSTM–UNet–Adaboost. Moreover, a novel class balancing technique, namely, the interquartile minority oversampling technique (IQMOT), is introduced to address the class imbalance issues. In the proposed methodology, real-world electricity theft cases are initially generated using the IQMOT. Then, it solves the ETD problem using the LSTM–UNet–Adaboost model. Essentially, LSTM is used to capture the daily temporal correlations, while a UNet model is applied to capture the abstract features from 2-D electricity consumption data. Finally, the Adaboost model is used to perform the joint training and classification over the extracted features through LSTM and UNet modules. The proposed methodology automates the concept of feature engineering, known as self-learning. Hence, the underlying intuition of this paper is to generate real-world theft cases through a novel sampling technique and to combine a deep learning technique with ensemble learning to improve the theft detection performance. Therefore, the proposed solution is more efficient and reliable as compared to the conventional approaches.

Thus, the chief contributions of this work are described as follows.

• IQMOT: A novel class balancing technique, named IQMOT, is presented in this paper to overcome the problems of imbalanced data. It generates more practical theft cases as compared to the traditional class balancing techniques.
• LSTM–UNet–Adaboost: We propose a new combined LSTM–UNet–Adaboost model for ETD. The proposed model leverages the advantages of the most recent deep learning technique, i.e., UNet, which is applied for very first time in ETD along with the ensemble learning technique, i.e., Adaboost.
• Comprehensive simulations: We conducted extensive simulations on the real electricity consumption dataset and analyzed our proposed solution with standard techniques. Simulation results demonstrated the superiority and effectiveness of our proposed model over existing benchmarks previously used for ETD.

The remainder of this paper is arranged as follows. Section 2 presents our proposed approach comprising of IQMOT and LSTM–UNet–Adaboost for ETD. Section 3 illustrates and examines the simulation results before concluding the paper in Section 4. Lastly, the future directions are described in Section 5.

2. Proposed Methodology

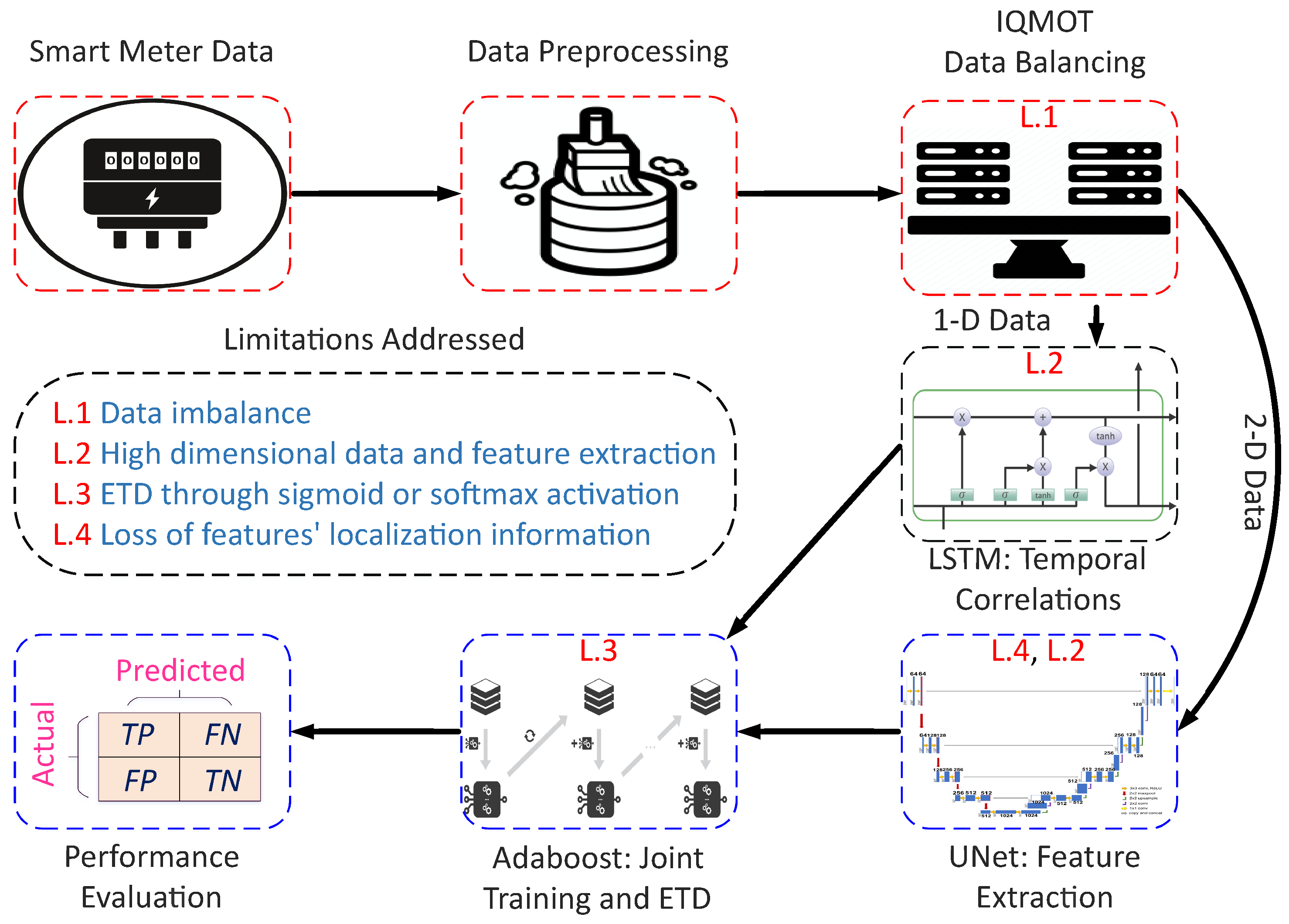
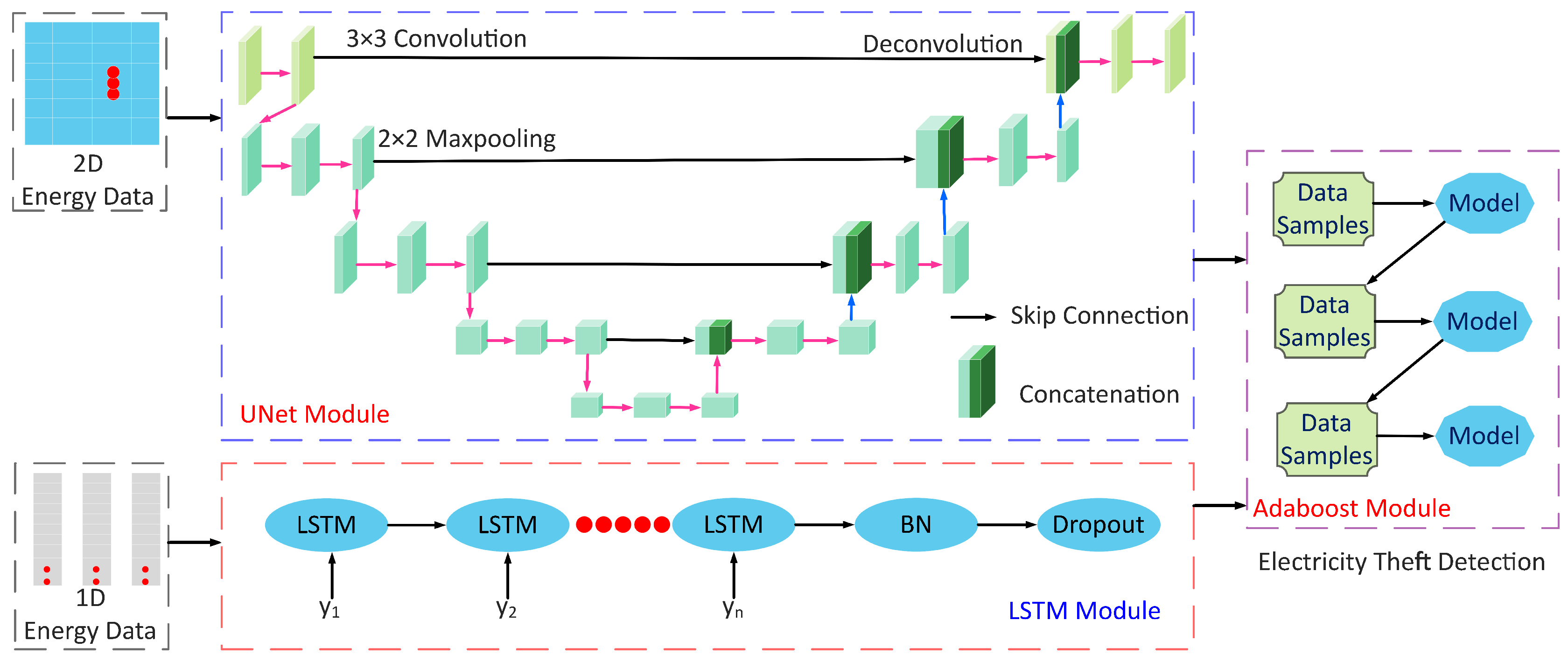
The proposed system model is shown in Figure 1; it has three major stages: (1) data preprocessing, (2) data balancing through IQMOT and (3) data analysis using the UNet-LSTM-Adaboost. The proposed hybrid model practices LSTM, UNet and Adaboost, which solves the limitations of the state-of-the-art techniques for ETD, as mentioned in Section 1. Moreover, we designed a new class balancing mechanism to handle the data imbalance issues faced by the conventional supervised learning techniques. The proposed methodology has the potential to integrate both 1-D and 2-D information obtained from the electricity consumption data. More generally, the LSTM module is used to derive the long-term dependencies from 1-D data, known as the sequential information. The UNet module acquires global features from 2-D electricity consumption data, i.e., non-sequential information. Furthermore, the Adaboost module performs the final joint training and binary classification over the outputs of LSTM and UNet modules, as shown in Figure 1. We validated the proposed model using the real electricity theft data in terms of selected performance indicators for ETD. The proposed LSTM–UNet–Adaboost model is efficient because it performs joint training on both types of inputs, known as the sequential and non-sequential information, provided by LSTM and UNet. In the following sub-sections, a detailed description of each module is given.

2.1. Data

In this paper, a real-time power consumption dataset of users is employed, which was given to us by the State Grid Corporation of China (SGCC) [42]. The metadata information of the SGCC dataset is presented in

Table 1. SGCC dataset information.

Description	Numeric
Total time duration	January-2014–October-2016
Total electricity consumers	42,372
Total electricity thieves	3615
Total electricity normal consumers	38,757

. The dataset contains the daily electricity consumption histories of residential consumers. The SGCC conducts real in-the-field inspections to verify the normal and abnormal consumers. Therefore, SGCC explicitly declares that the given dataset holds 3615 instances of electricity theft, which shows the importance of ETD in China. Additionally, it also contains the missing and erroneous values that require preprocessing, as explained in Section 2.2.

2.2. Data Preprocessing

The real dataset often contains the missing and erroneous values demanded to be resolved by employing the data preprocessing techniques [43]. Thus, the electricity consumption dataset of SGCC contains the missing and erroneous values due to several reasons, such as failure of any smart meter equipment, storage issue and measurement error or unreliable transmission. Moreover, analyzing and cleansing the dataset assists one in finding and eliminating these erroneous and missing values. In this study, the concept of linear interpolation was employed to find and retrieve the missing values found in the dataset [20]. Hence, the missing values were recovered as using the Equation (1):

$$f\left(x_i\right)=\left\{\begin{array}{cc}\hfill & {\displaystyle \frac{z}{2}},x_i\in NaN,x_{i(t-1)},x_{i(t+1)}\notin NaN,\hfill \\ \hfill & 0,x_i\in NaN,x_{i(t-1)}\mathrm{or}{x}_{i(t+1)}\in NaN,\hfill \\ \hfill & x_i{x}_i\notin NaN,\hfill \end{array}\right.$$

(1)

where $z=x_{i(t-1)}+x_{i(t+1)}$. $x_i$ is the current electricity consumption at a certain time t of an $i^{th}$ day. Likewise, $x_{i(t-1)}$ and $x_{i(t+1)}$ are the previous and next values of the current electricity consumption, respectively. Likewise, in the SGCC dataset, we have identified outliers, which skew the data, making the training process complex and have a negative impact on the final ETD performance because of overfitting. In this paper, the “three-sigma rule of thumb” [44] is practiced for detecting and recovering the outliers according to the following equation:

$$O\left(x_{i,t}\right)=\left\{\begin{array}{cc}\hfill & \mathrm{w},if{x}_{i\left(t\right)}>\mathrm{w},\hfill \\ \hfill & x_{i\left(t\right)},otherwise,\hfill \end{array}\right.$$

(2)

where $\mathrm{w}=avg\left(x_{i\left(t\right)}\right)+2\sigma \left(x_{i\left(t\right)}\right)$. After the detection and removal of the missing and outlier values, the dataset needs to be normalized, as the deep neural networks are sensitive to the diverse data that increases the training time. Hence, the data normalization improves the training process of deep learning models by assigning the same scale to all values present in the dataset and bringing them in the range of 0 and 1. Therefore, a min-max normalization concept was applied to scale the dataset as per the following equation [40]:

$$\mathrm{N}\left(x_{i\left(t\right)}\right)=\frac{x_{i\left(t\right)}-min\left(x\right)}{max\left(x\right)-min\left(x\right)},$$

(3)

where $x_{i\left(t\right)}$ is the electricity consumption at a current time t, $min\left(x\right)$ is the least electricity consumption and $max\left(x\right)$ is the highest electricity consumption.

2.3. Data Balancing

In this paper, a new data balancing technique, named IQMOT, is introduced to balance the majority and minority classes. In a real-life scenario, the number of benign consumers is always extensive as compared to the electricity thieves. Similarly, in the SGCC dataset, the benign electricity consumers are higher in number than the electricity thieves, as shown in Table 1. This imbalanced nature of the dataset adversely affects the performances of the supervised learning techniques because of the biasn towards the majority class. Hence, to reduce the class inequality problem, there are two major types of techniques, known as the cost function-based and sampling-based techniques [22].

In the sampling-based techniques, there are three major approaches, including random under-sampling (RUS), random over-sampling (ROS) and oversampling based on synthetic theft instance generation, such as the synthetic minority over-sampling technique (SMOTE). In RUS, it unintelligently discards the samples from the majority class, which contains normal consumers. This method decreases the computationally beneficial dataset size. The unintelligent removal of samples from the majority class creates a loss of potentially important information, while the remainder does not provide a realistic assessment. ROS replicates the minority class instances to balance the majority and minority classes. There is no loss of potentially useful data; however, due to the unintelligent replication of minority instances, the model leads to an overfitting problem. In this regard, SMOTE is an effective synthetic instance generation technique that generates the new minority instances based on the nearest neighbors [45].

Synthetic generation of minority instances avoids the overfitting problem, which occurs due to the ROS technique, although the synthetic forms of theft instances do not reflect the real-world electricity theft cases. Moreover, a synthetic formulation replicates the minority class instances based on the nearest neighbors, which further leads to the overfitting problem. In the light of the above-mentioned limitations, we propose a novel class balancing technique in ETD, named IQMOT, to balance the majority and minority class instances. Moreover, IQMOT-based generated instances reflect the real-word theft cases and improve the model’s performance. Besides, simulation results indicate that the proposed IQMOT is superior over the existing SMOTE technique. The pseudo-code of the proposed IQMOT is described in Algorithm 1.

Algorithm 1 IQMOT algorithm.

1: Given: An imbalanced dataset X with majority class $y_i=0$ and          minority class $z_i=1$,   2: $X=\{(x_{1\left(t\right)},y_1),(x_{2\left(t\right)},y_2),(x_{3\left(t\right)},z_1),(x_{4\left(t\right)},y_2),...,(x_{n\left(t\right)},y_n),$          $(x_{n\left(t\right)},z_n)\}$           where $x_{i\left(t\right)}\in \Re ,$ $y_i\in \left\{0\right\}$ and $z_i\in \left\{1\right\},$   3: Output: Balanced dataset $X^{\prime },$   4: Initialize: Theft consumers $x^{\prime },$ normal consumers x, difference          between thieves and normal consumers D, 25th percentile $p_1$,          50th percentile $p_2$ and 75th percentile $p_3$, 5: Get the total number of thieves and normal consumers,   6: Calculate $p_1$, $p_2$, $p_3$ of theft consumers,   7: Calculate percentage of values falling in each percentile,   8: Get numbers: a, b, c to represent the values fall in each group,   9: For n = 1,2,…,D do   10:     Create $x^{\prime }$ by selecting values from each group with respect          to a, b, c          where $x^{\prime }\in X^{\prime },$   11: End for

In the real dataset comprising of electricity theft consumers, not all theft cases fall in the median of the Gaussian distribution. The electricity theft cases exhibit irregular electricity consumption behaviors, whose consumption values fall outside the median of a normal distribution; they are usually treated as outliers. Therefore, interquartile range is a good statistical tool to indicate such non-normal instances. In this paper, we got inspiration from the outlier detection method, named interquartile range (IQR) [46], to devise the new class balancing technique that generates the NTL instances closer to the realistic theft cases. We refer to the percentiles where the theft cases are distributed into 25th, 50th and 75th percentiles. In the proposed IQMOT technique, we first get these percentiles that tell us the range and type of theft values falling into each of the percentile groups. Likewise, the median or 50th percentile contains the middle or average energy consumption values of electricity thieves.

In the proposed IQMOT, percentiles are used to define the limit over the theft values and gives us the representation of electricity theft cases. After getting the percentiles, the percentage of values coming in each percentile is obtained. Based on the computed percentage, we get a number showing the values of theft consumers lying in each group of percentiles. Similarly, values from each of the percentiles are obtained and a new theft case is produced, which is quite similar to the real theft cases. This process iterates until the minority class (electricity thefts) becomes equal to the majority class (normal consumers). Hence, the newly created minority instances reflect electricity consumption that is similar to the available theft instances in the dataset. 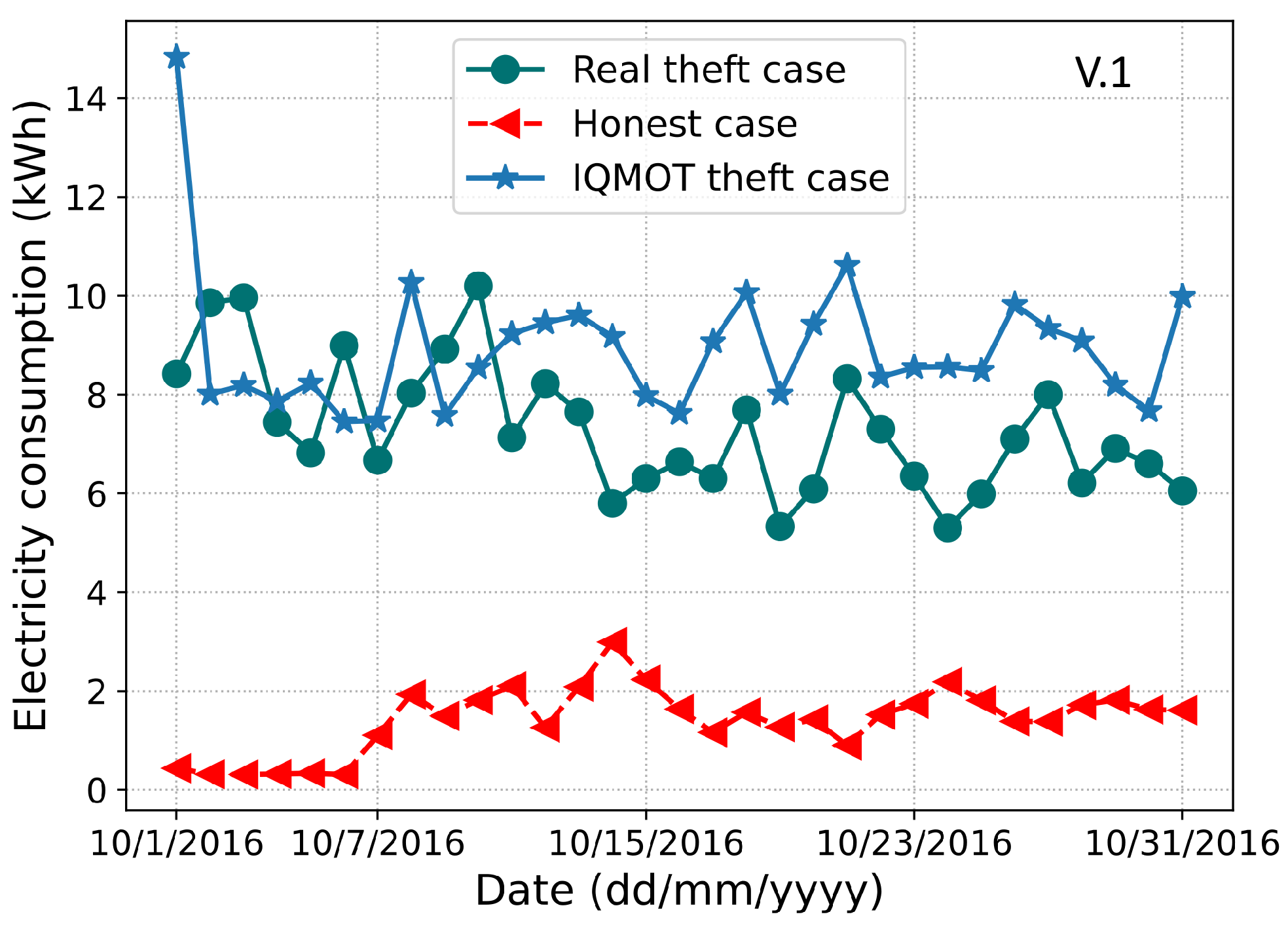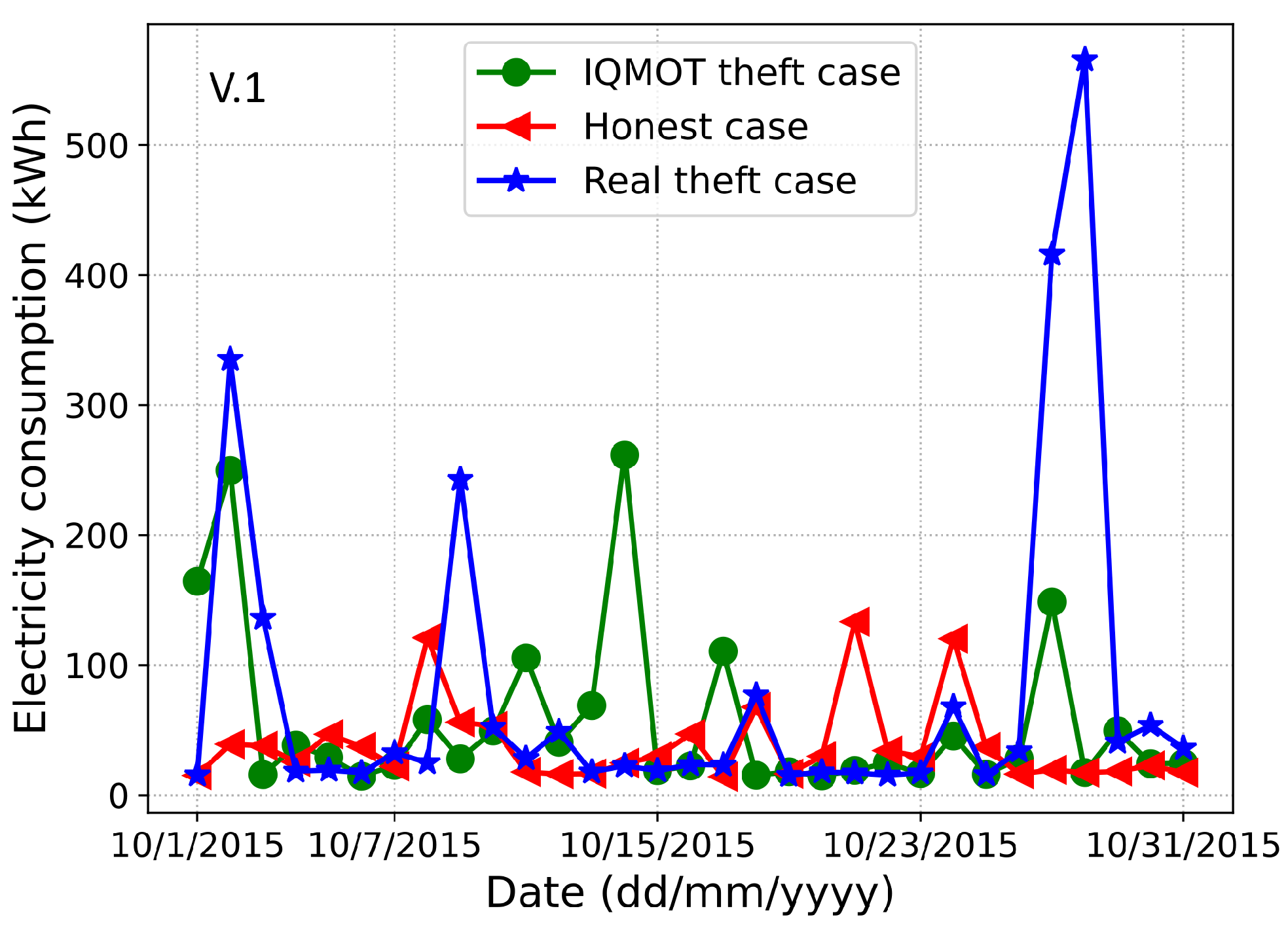In Figure 2 and Figure 3, we observe the resemblance between original theft cases in the dataset and IQMOT-generated theft cases in a month. Moreover, it is evident that the IQMOT-generated theft cases are more realistic regarding the real theft cases. In this way, the proposed IQMOT overcomes the limitations of the above-mentioned traditional class balancing techniques and generates more realistic theft cases.

2.4. Data Analysis

In the data analysis stage, we extract features from the preprocessed dataset and perform ETD. In particular, LSTM and UNet are applied to extract features from the preprocessed dataset and perform joint training through the Adaboost classifier for final classification. The following sub-sections explain the comprehensive description of each module of the LSTM–UNet–Adaboost.

2.4.1. LSTM Module

In this paper, LSTM is applied to capture the long-term associations from electricity consumption data, i.e., temporal correlations from electricity consumption time series at each time step. Therefore, 1-D daily data of electricity consumption is used as input to the LSTM. The electricity consumption data recorded by the smart meters are increasing day by day, which creates a large dataset history of a single user. A simple neural network or recurrent neural network (RNN) is not sufficient to obtain and maintain the long-term dependencies in their memory to forecast the future information. These models are difficult to train over a large historical dataset while trying to extract the long-term temporal correlations, which leads to the gradient vanishing and exploding problem [47]. For this reason, in this paper, the LSTM model is employed to memorize the long-term temporal associations from the extensive historical data.

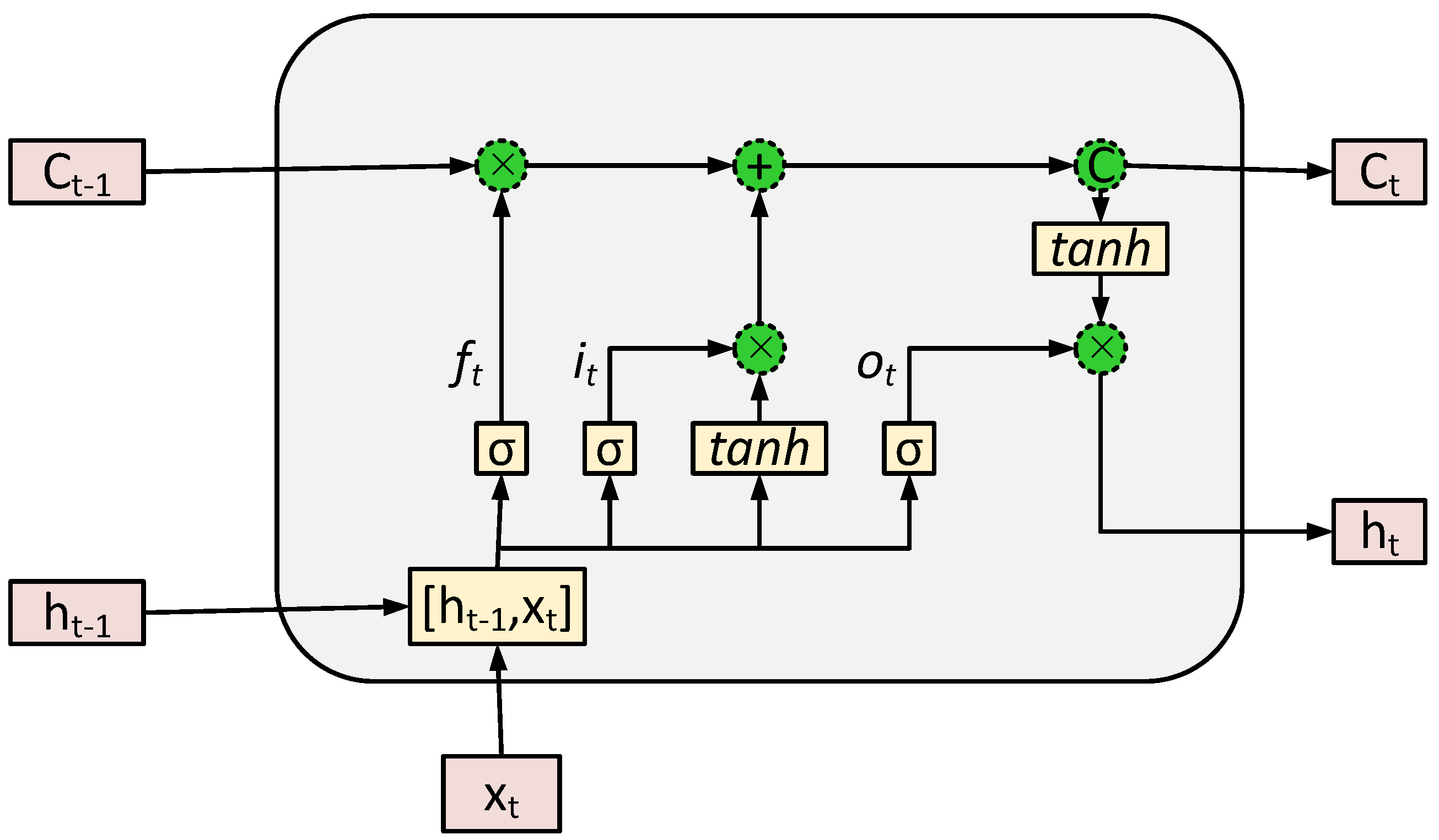
LSTM is a special class of RNN, which has the capability to retain and propagate information from the initial stage towards the final stage of the model [48]. Figure 4 displays the general structure of the LSTM model. It has three important gates, known as input gate $i_t$, output gate $o_t$ and forget gate $f_t$. Its main component is the cell state, which maintains the long-term dependencies along the chain. Thus, the dependencies in the cell state are managed by the aforementioned gates. In Figure 4, $C_t$ and $C_{t-1}$ show the current and previous cell state, respectively. $h_t$ and $h_{t-1}$ show the outputs of the current and previous LSTM units, respectively. Furthermore, $\sigma \left(x\right)=1/1+e^{-\left(x\right)}$ and $tanh\left(x\right)=e^{\left(2x\right)}+1/e^{\left(2x\right)}-1$ represent the sigmoid and hyperbolic tangent functions, respectively. Both functions are non-linear activations in the LSTM model. $W_f,W_i,W_C,W_o$ and $b_f,b_i,b_C,b_o$ are the weights and biases of the LSTM model, respectively. LSTM is based on daily electricity consumption data to produce a single output, known as $h_t$, which is also recognized as the hidden state at the last time step. Hence, LSTM achieves its purpose by processing the following Equations (4)–(9) [48]:

$$f_t=\sigma (W_f[C_{t-1},h_{t-1},x_t]+b_f),$$

(4)

$$i_t=\sigma (W_i[C_{t-1},h_{t-1},x_t]+b_i),$$

(5)

$$\widetilde{C_t}=tanh(W_c[h_{t-1},x_t]+b_c),$$

(6)

$$C_t=f_t.C_{t-1}+i_t.\widetilde{C_t},$$

(7)

$$o_t=\sigma (W_o[C_{t-1},h_{t-1},x_t]+b_o),$$

(8)

$$h_t=o_t.tanh\left(C_t\right).$$

(9)

In this paper, the deep LSTM model is used with a stack of recurrent LSTM layers, since a single layer LSTM model often fails to capture the complete dependencies. 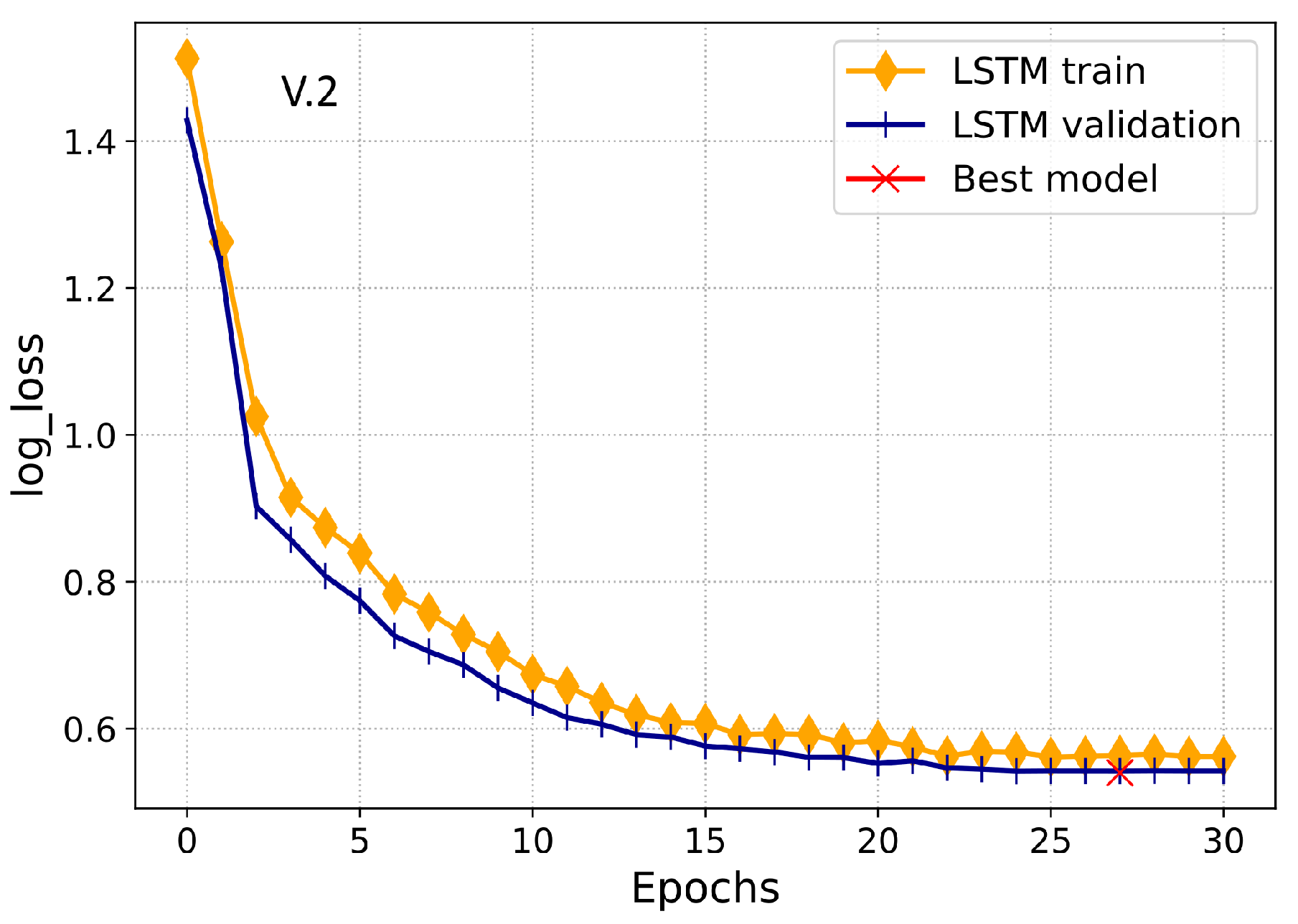The output from each LSTM unit serves as an input to the batch normalization layer, which normalizes the previous layer output at runtime and forwards it to the next layers, where the batch normalization enhances the model convergence, extends the model stability and reduces both the overfitting and training time [49]. After that, the dropout layer is employed with a 0.5% probability that drops 50% of neurons randomly to inhibit the model from overfitting. Moreover, it improves the model’s convergence by preventing the model from being over-dependent on a few neurons, which allows each neuron to work individually. In particular, the LSTM model comprises of three layers with batch normalization and dropout layers. It utilizes 1-D electricity consumption data using the Adam optimizer with the batch-size of 32 and binary cross-entropy as the cost function. Furthermore, a Keras callbacks concept is used during the model’s training to practice the learning rate decay over five epochs and early stopping procedure over 10 epochs. Consequently, these procedures will improve the model’s convergence and effectively mitigate the overfitting problem.

2.4.2. UNet Module

UNet is used in this paper to learn and derive potentially important information from 2-D electricity consumption data. As in [20], the authors explain the effect of the periodicity to illustrate how weekly data can better obtain the periodicity from consumption patterns. For this reason, the energy consumption data are transformed into 2-D weekly data and serve as an input to the UNet model. Furthermore, the authors in [20,22,40] have used a traditional CNN technique to derive high-level features from electricity consumption data. However, if we use the regular convolution network with the pooling and dense operations, the model will only extract high-level features of "what," but not their localization information, "where." As a result, in this paper, UNet is used, which derives both the high-level features and their localization information through the down-sampling and up-sampling strategies, respectively.

The UNet model was originally proposed for biomedical image segmentation [50]. The chief concept behind the semantic image segmentation is to attach the corresponding label of each pixel of the image [51]. In this way, the model predicts each pixel within the image, also known as the dense prediction. Therefore, semantic segmentation problems are considered as classification problems where each feature of a time-series is labeled with its corresponding class. In this paper, we get inspiration from such a semantic segmentation approach where the UNet model extracts the high-level features from the 2-D electricity consumption data and then labels them to their corresponding classes.

The name UNet is used because of its symmetric U-shape architecture, as shown in Figure 5. Its architecture mainly consists of two paths: the contraction path (also called down-sampling or encoder) and the expansion path (also called up-sampling or decoder) [50]. The contraction path performs down-sampling by the convolution and pooling operations, which are used to extract global features from 2-D data. On the other hand, the expansion path does up-sampling over these extracted features through the inverse or transpose convolution operation. Since transposed convolution is the inverse of convolution operation used to perform up-sampling. It tells us the whereabouts of information. We refer to down-sampling because both convolution and pooling operations reduce the size of input features or parameters. Consequently, the model determines parameters through the backpropagation procedure.

UNet has both the long and short skipping connections. The short skipping connections are present in each of the major down or up-sampling blocks, while the long skipping connections are available within the contraction and expansion paths to concatenate the extracted features with their corresponding labels. In this work, the contraction path involves four major blocks where each block contains:

• Two $3\times 3$ convolution layers plus $LeakyReLU$ with batch normalization;
• $2\times 2$ max pooling.

The feature maps are multiplied at each pooling layer, i.e., beginning from 16 feature maps in the first major block, 32 feature maps in the second block and so on. This procedure is also termed as increasing the size of depth and reducing the size of the input. Moreover, the expansion path consists of four major blocks where each block contains:

• Transpose-convolution with a stride of 2;
• Linking with regular convolution features;
• Two $3\times 3$ convolution layers plus $LeakyReLU$ with batch normalization.

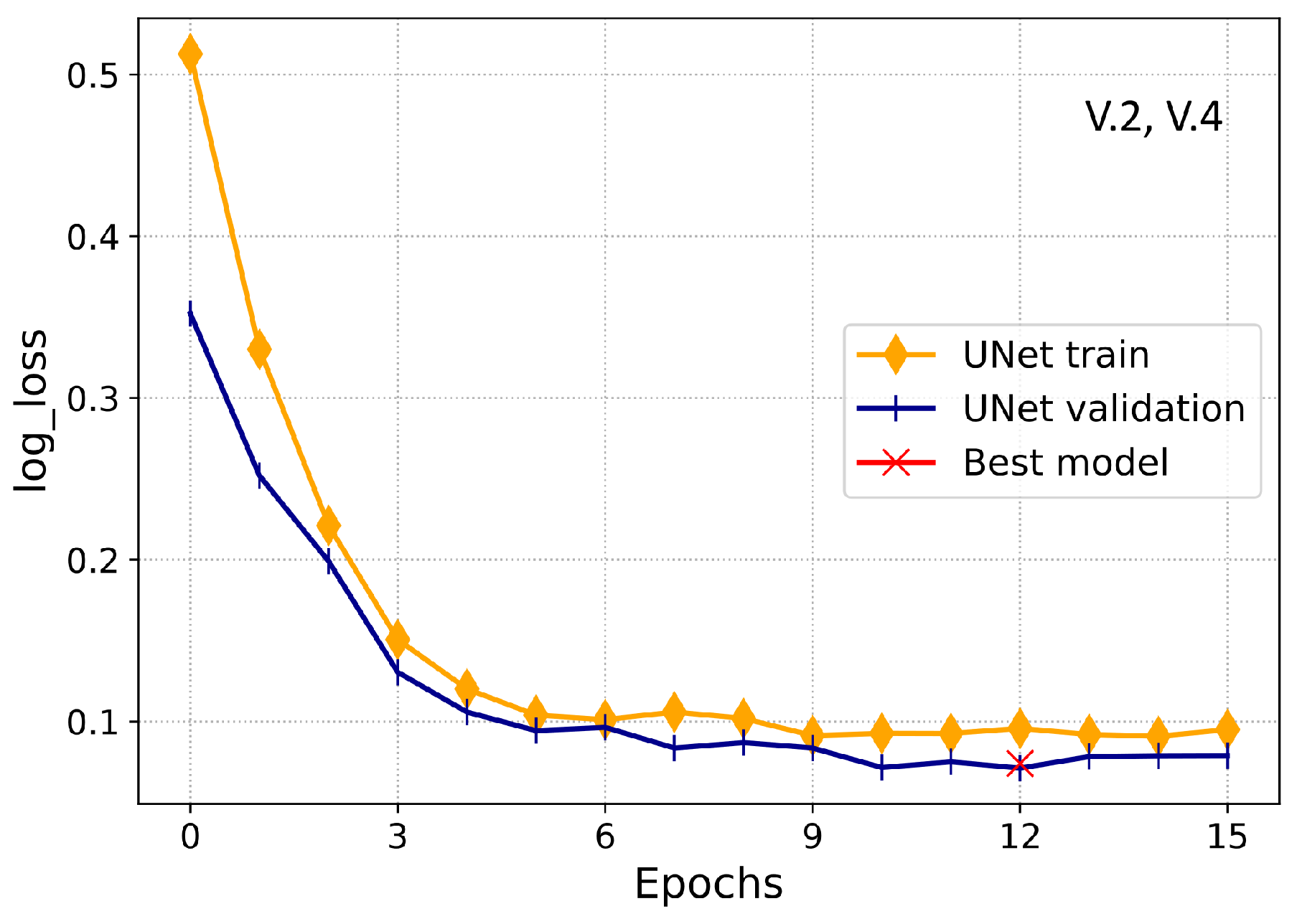
The center of the contraction and expansion path is determined as the bottleneck; it employs a single convolution layer with batch normalization and dropout. In this paper, the UNet model is trained using an Adam optimizer with batch-size of 32 and binary cross-entropy as the cost function. Furthermore, Keras callbacks are used during the UNet training, as already described in Section 2.4.1. Simulation results validate that UNet appears to be very effective and efficient for ETD based on electricity consumption patterns.

2.4.3. Joint Training and Classification Module

For the joint training and classification mechanism, the ensemble learning boosting technique is applied where different weak classifiers are combined to build a powerful classifier, as shown in Figure 5. This is more accurate than the final joint training and classification through a single hidden layer based feed-forward neural network (FFNN)—for instance, a fully connected layer with either sigmoid activation or softmax classifier. To improve the ETD performance, we use Adaboost as a final classifier, which acts as a final layer of the LSTM-UNet to replace the single hidden layer based FFNN used in traditional models [20,22,23]. Therefore, Adaboost simply takes the outputs of LSTM-UNet modules and concatenates them to make a new input for the Adaboost model. Now, the long-term dependencies and high-level features are the inputs of the Adaboost model for the final theft detection. In this context, the proposed model derives the benefits of two powerful procedures of machine learning, known as deep learning and ensemble learning.

Adaboost is formerly designed to solve highly non-linear tasks [24]. The main focus of Adaboost is to learn from the mistakes of previous models and boost the performance of the next model. Thus, the most accurate classifier will be selected to perform the classification task. This process iterates until the training data becomes error-free or the model reaches the specified number of learners. Adaboost has several important hyperparameters, which influentially affect the model’s theft detection performance. Therefore, the grid-search mechanism is applied in this paper to find the most appropriate hyperparameters of Adaboost, as described in Section 2.5.

2.5. Simulation Setting

The proposed model for ETD was implemented in python using the open-source deep learning libraries, known as Keras and Tensorflow. The proposed model was developed and simulated using the SGCC dataset, which contains a total of 42,372 consumers with 1035 days of electricity consumption history, as given in Table 1. For simulations, the dataset was first preprocessed through linear interpolation, three-sigma rule and min-max normalization. After that, the dataset was balanced through the proposed IQMOT technique. In the training procedure, the dataset was partitioned into training, validation and testing sets with a training proportion of 80%, and validation and testing proportions of 10% for each, respectively. LSTM model’s configuration consisted of three layers with batch normalization and dropout layers; each LSTM layer had 60 neurons. Besides, the UNet model’s configuration was the same as already defined in Section 2.4.2. For the training of LSTM, 30 iterations were run initially with a batch-size of 32 using Adam optimizer, while the training of UNet was initially performed by running 15 training iterations with the batch-size of 32. Finally, the Adaboost was executed by utilizing the outputs of LSTM and UNet modules as an input. Furthermore, to select the optimal hyperparameters of the Adaboost and other models, a grid-search algorithm was implemented.

Table 2. Adaboost hyperparameter selected through grid-search.

Hyperparameter	Range of Values	Selected Value
Estimators	100, 200, 300, 400	400
Learning rate	0.1, 0.01, 0.001	0.001

shows the important hyperparameters selected for the Adaboost model using grid-search.

2.6. Loss Function

The most widely used loss function for the classification problem is cross-entropy, to classify only two classes. In this paper, the binary cross-entropy loss function, also known as the logarithmic loss, is used to deal with the binary classification task. The predictions become more accurate as the loss function converges to zero. The binary cross-entropy loss function is calculated using the following formula [23]:

$$log\_loss=\frac{1}{N}\sum _{i=1}^M-(y_{i}log\left(p\left(y_i\right)\right)+(1-y_i)log(1-p\left(y_i\right)),$$

(10)

where N shows the accumulative consumer instances. $y_i$ represents the actual label and $p\left(y_i\right)$ is the likelihood of the electricity theft measured by the proposed model for the $i^{th}$ consumer.

2.7. Performance Evaluation Metrics

In this paper, seven class imbalance metrics are employed to evaluate the performance of the proposed model, which includes area under the curve (AUC), precision, recall, Mathews correlation coefficient (MCC), F1-score, area under the precision-recall curve (PR-AUC) and accuracy. These performance evaluation metrics are determined from the confusion matrix, i.e., a matrix that describes different results in classification problems. Specifically, for the binary classification problem, the confusion matrix returns two rows and two columns, i.e., four possible outcomes. These four possible outcomes are described as follows:

• The true positive (TP) score demonstrates the number of dishonest consumers accurately predicted by the classifier;
• The true negative (TN) score shows the number of honest consumers accurately predicted by the classifier;
• The false positive (FP) score describes the number of honest consumers predicted by the model as thieves;
• The false negative (FN) score highlights the number of dishonest consumers predicted by the model as honest consumers.

The following are the performance metrics given in Equations (11)–(16), as defined in [20,21,24]:

$$Accuracy={\displaystyle \frac{TP+TN}{TP+TN+FP+FN}},$$

(11)

$$Recall={\displaystyle \frac{TP}{TP+FN}},$$

(12)

$$Precision={\displaystyle \frac{TP}{TP+FP}},$$

(13)

$$F1=2\times \frac{Precison\times Recall}{Precison+Recall},$$

(14)

$$AUC=\frac{{\sum }_{i\in positiveclass}RAN{K}_i-\frac{P(1+P)}{2}}{P\times N},$$

(15)

$$MCC=\frac{(TP\times TN-FP\times FN)}{\sqrt{(TP+FP)(TP+FN)(TN+FP)(TN+FN)}}.$$

(16)

where P represents the number of positive samples, N represents the number of negative samples and $RAN{K}_i$ shows the rank value of sample i.

The accuracy of a classifier is a metric used to indicate the percentage of correct predictions. Besides, a recall is another class imbalance metric, which is also termed the detection rate (DR), sensitivity or the true positive rate (TPR) in the literature. It shows the capability of a scheme to detect electricity theft consumers. Likewise, precision is the ability of the classifier to accurately classify normal consumers. However, accuracy, precision and recall metrics using the imbalanced dataset cannot provide a realistic assessment of the model’s ETD performance [7]. Hence, F1-score is another useful class imbalance measure as compared to the metrics described above for ETD’s performance examination. In F1-score, we get the balance of both precision and recall, which shows its usefulness as compared to the other metrics.

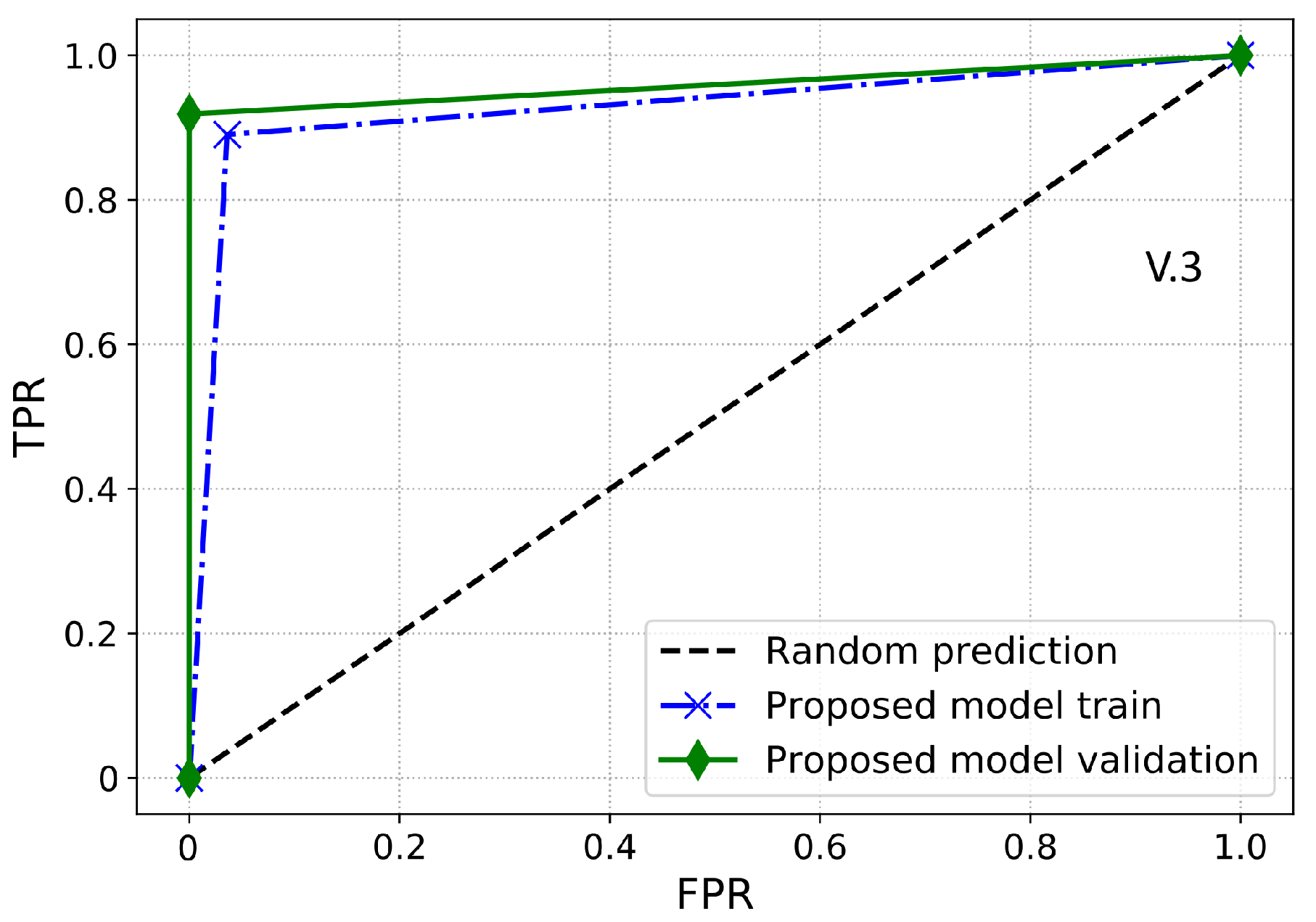
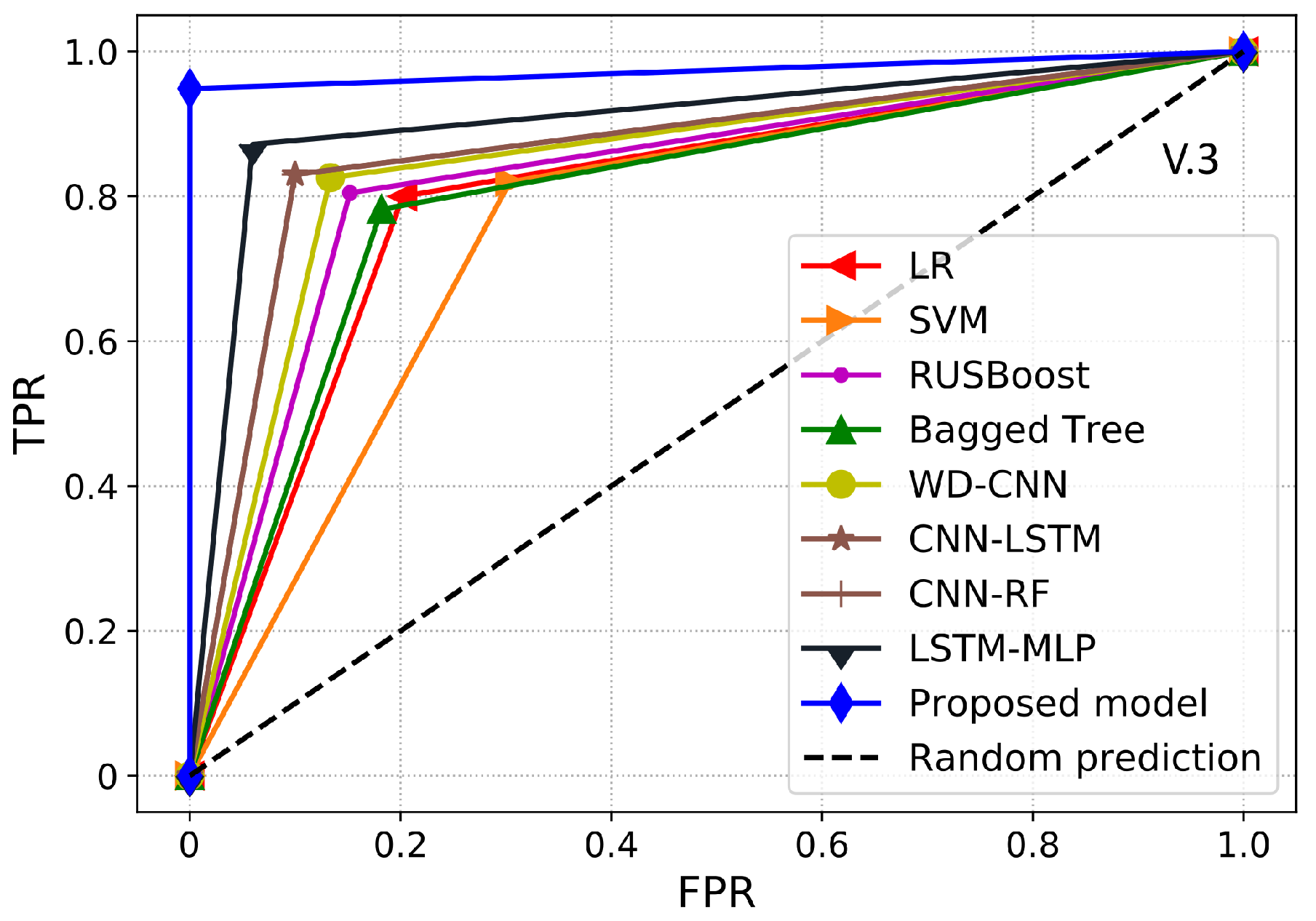
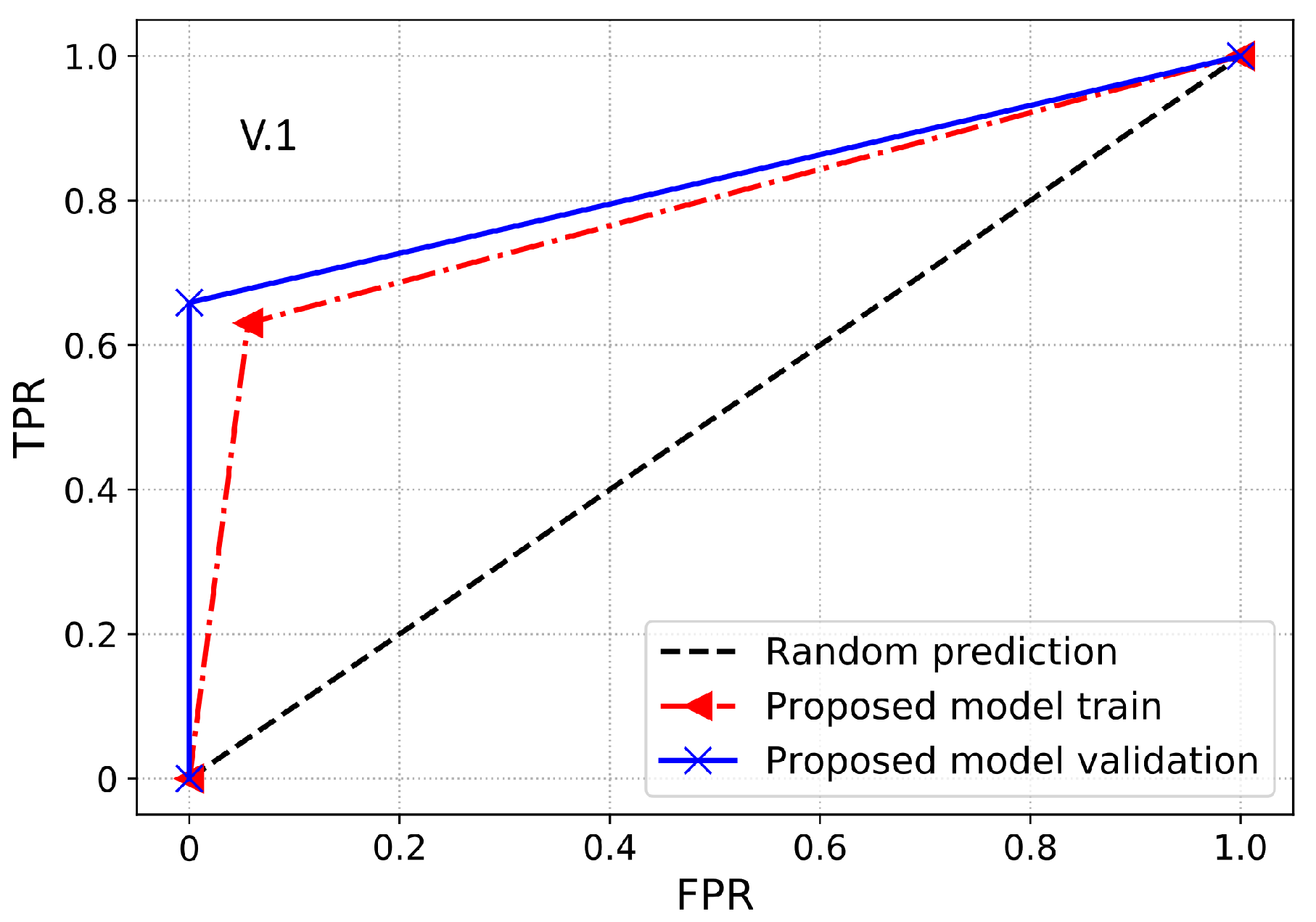
Furthermore, a performance index that is more reliable and accurate for an imbalanced dataset is the AUC. It provides a more realistic assessment of the model’s detection performance in terms of ETD over the imbalanced dataset. Essentially, it is the likelihood that the model ranks a positive sample higher than the negative sample. AUC is also identified as the area under the receiver operating characteristic curve (ROC-AUC). ROC-AUC is used to evaluate the model’s capability to make the separation between the classes. Thus, it is a graphical representation to evaluate the ETD performance of a model by plotting the TPR against the FPR. Moreover, the area under the ROC curve is estimated between the threshold of 0 and 1. If the classifier has a ROC-AUC score higher than 0.5, then it produces a better DR against any random predictions. If the classifier has less than 0.5 ROC-AUC, then it implies that the classifier has limited classification capability.

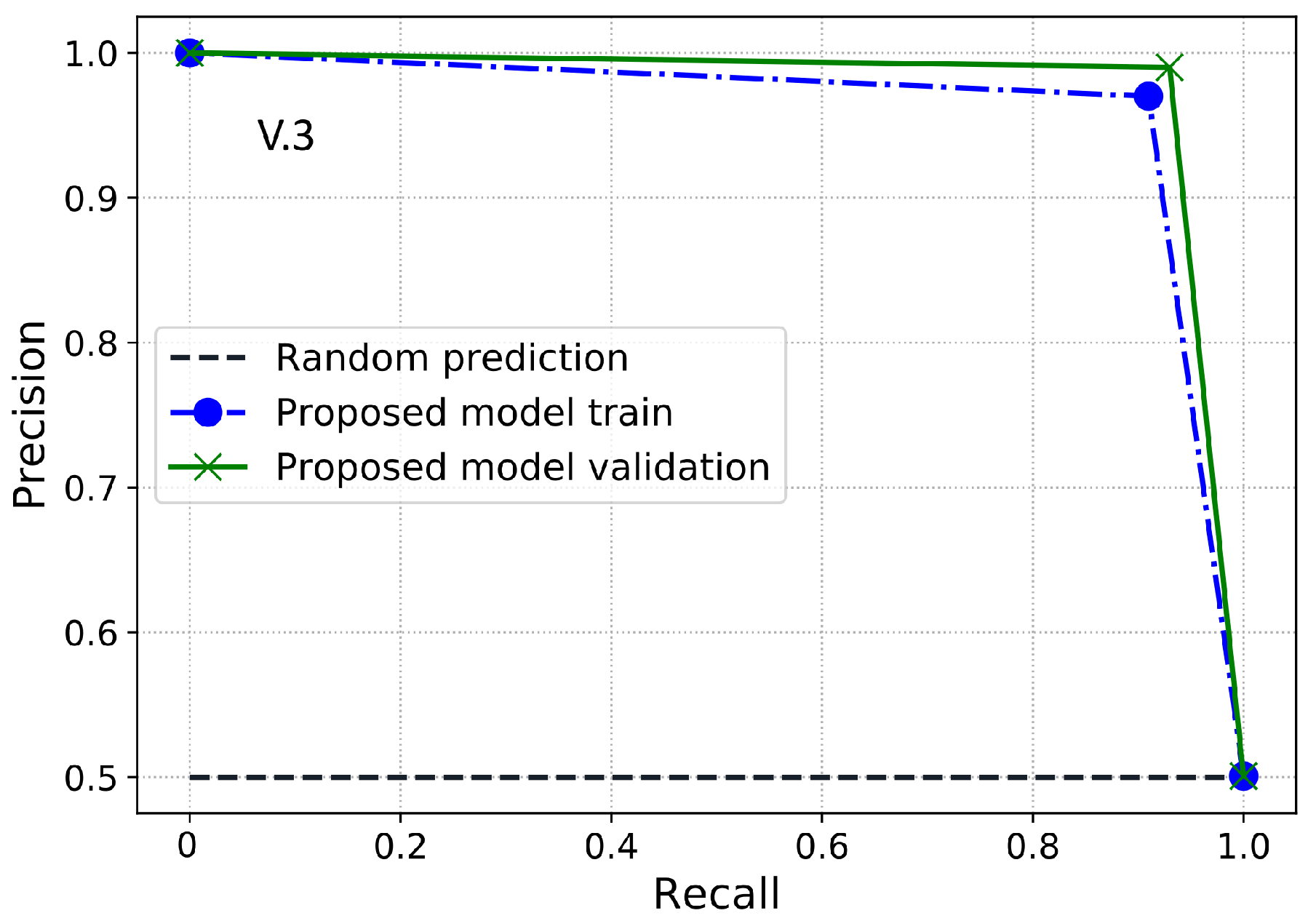
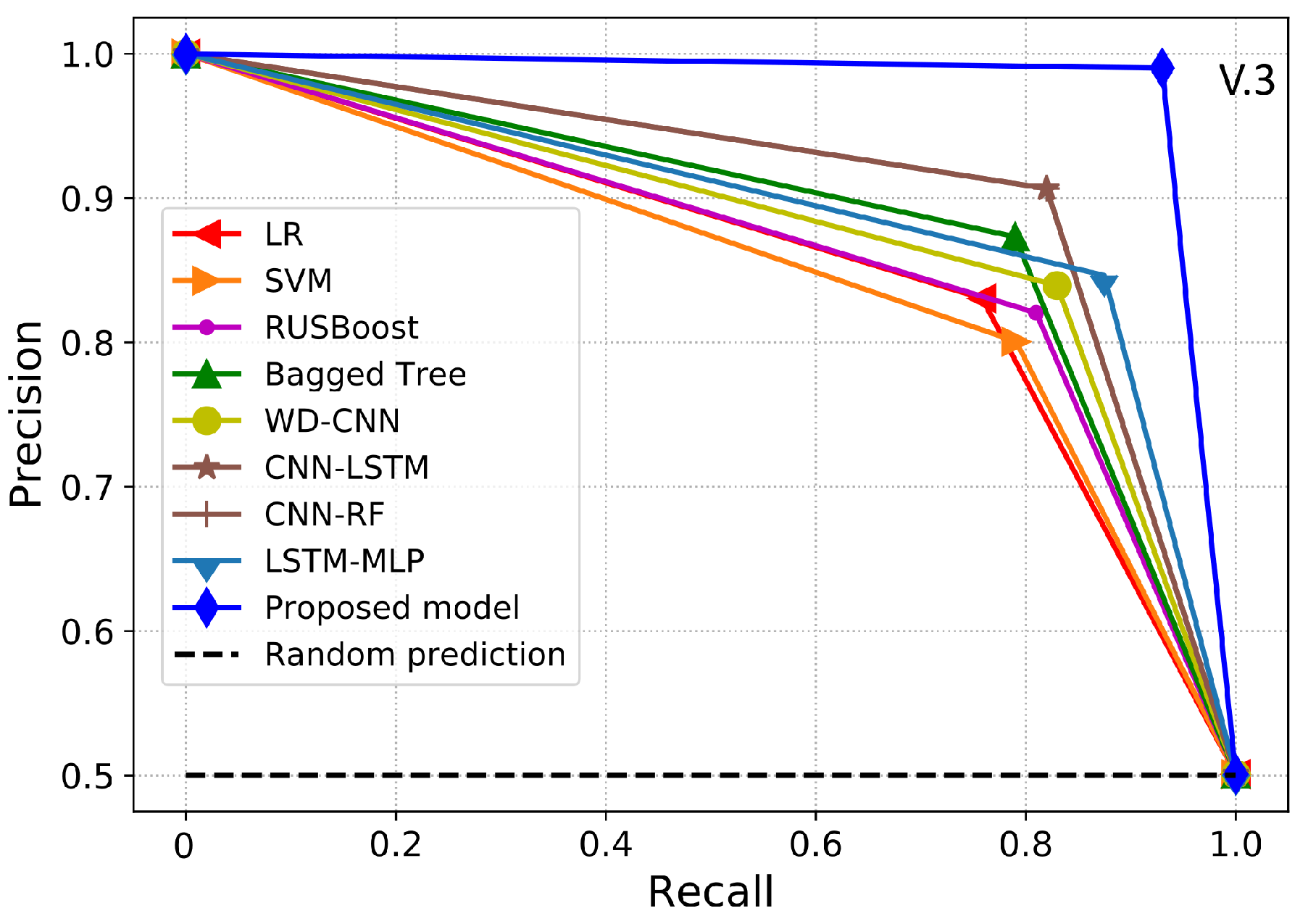
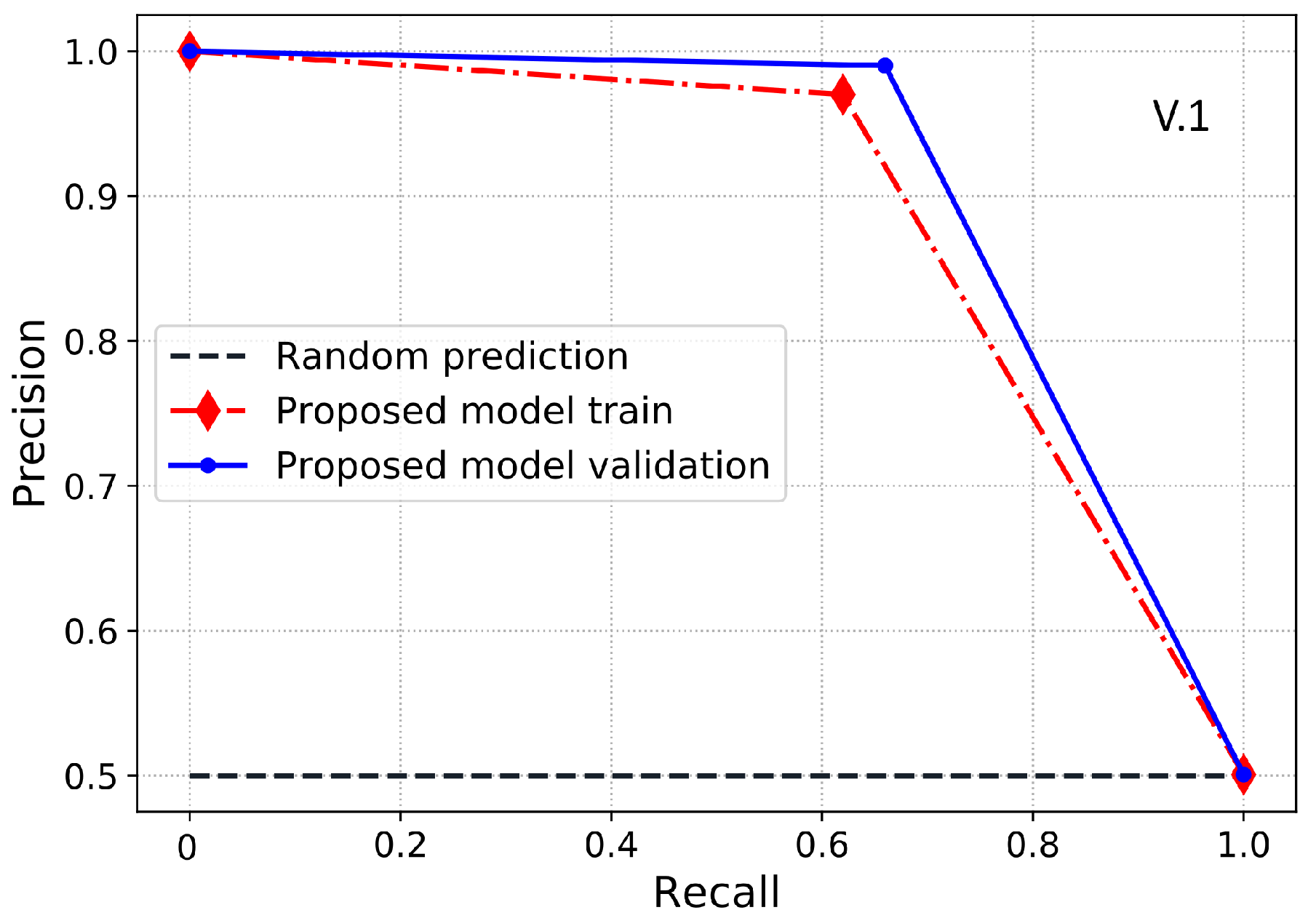
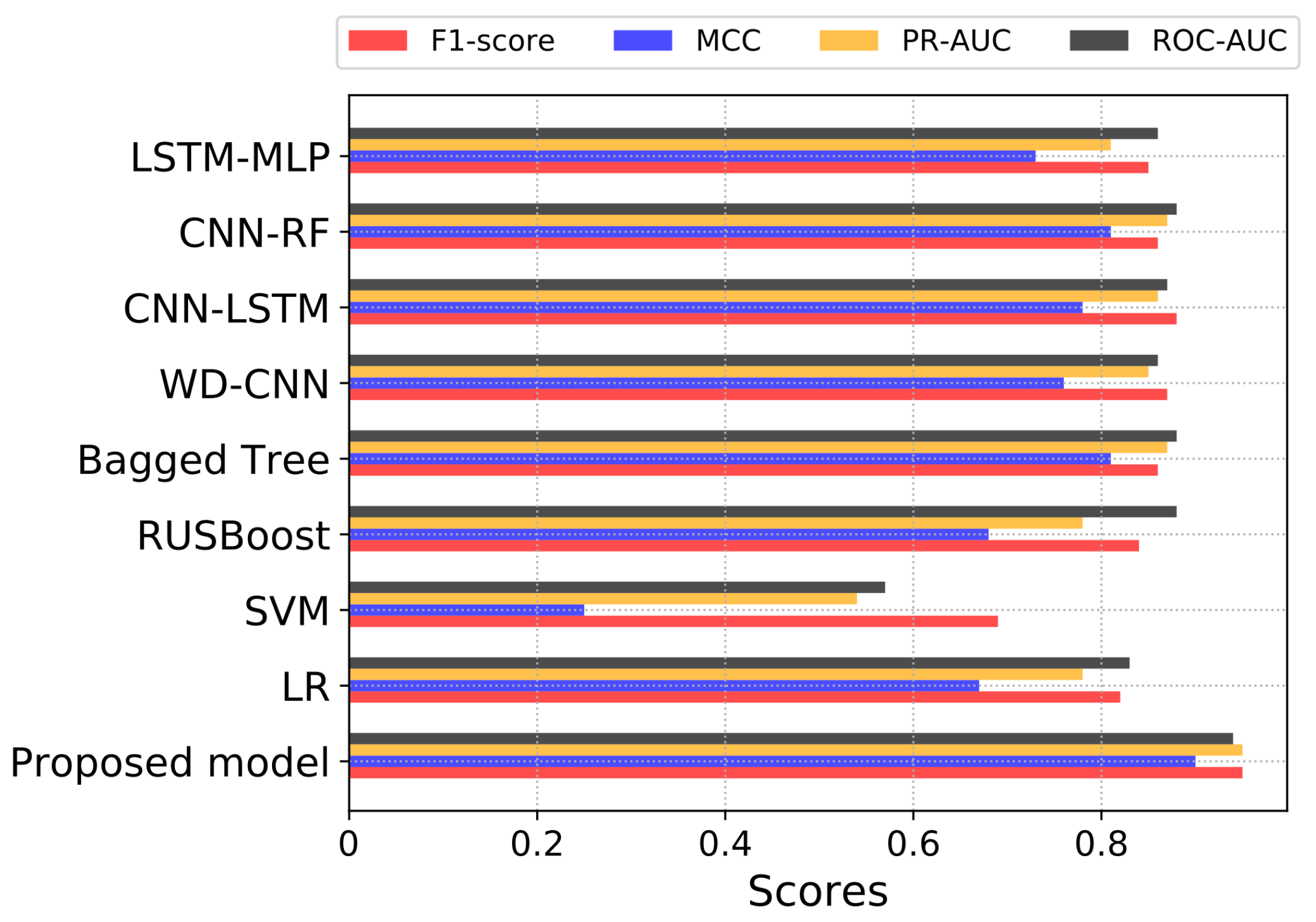
PR-AUC is another useful class imbalance measure employed to assess the model’s performance. Therefore, in this paper, we use PR-AUC, which considers the precision of the classifier and highlights the cost of on-site inspections for the utilities. PR-AUC is examined only when positive samples are on the top rather than the negative samples where the score is improved only when positive samples are on the top and negatives samples are on the bottom. Likewise, MCC is a binary classification metric used to evaluate the model’s performance using the imbalanced data. Moreover, MCC is a more accurate class imbalance metric than the AUC and F1-score because MCC captures the correlation between all four possible outcomes of the confusion matrix and suggests essential evaluation metrics. The MCC score ranges from −1 to 1, where a value near to 1 shows an accurate classification. Likewise, 0 shows the result of random predictions where the model has no class separation capability and −1 dictates incorrect classification. Accordingly, a classifier is good if it achieves ETD objective effectively, i.e., a classifier with a high DR performance and low FPR. The cost of FN is pretty high and important because it shows the cost of energy stolen and not given by the theft consumers. The cost of FP is much lower than FN because it shows the cost of inspection rather than the cost of stolen energy. Hence, in ETD, more importance is given to recall than precision.

2.8. Benchmark Models

In this section, we illustrate the state-of-the-art benchmark models and basic classification techniques used for comparison with our proposed model. For a fair comparison, we implemented a grid-search algorithm to determine the most suitable hyperparameters of the benchmark models.

2.8.1. Logistic Regression (LR)

LR is the primary model for the binary classification task in ETD, which applies the notion of probability and uses the principle of neural networks. For instance, LR for binary classification is similar to the single hidden layer based neural network using the sigmoid activation function. Thus, the sigmoid score ranges between 0 and 1, where a value near to 1 is labeled as theft and near to 0 is classified as honest.

Table 3. LR hyperparameters selected through grid-search.

Hyperparameter	Range of Values	Selected Value
C	0.1, 0.01, 0.001	0.001
R	l1 norm, l2 norm	l2 norm

shows the hyperparameters selected for LR through grid-search.

2.8.2. SVM

SVM is a famous technique used to solve the ETD problem. Many previous studies, such as [52,53], have used SVM to detect the presence of electricity thieves. Moreover, SVM has important hyperparameters obtained by employing the grid-search algorithm, as shown in

Table 4. SVM hyperparameters selected through grid-search.

Hyperparameter	Range of Values	Selected Value
C	0.1, 0.01, 0.001	0.1
$\gamma$	1, 1.5, 6, 10	10

.

2.8.3. RUSBoost

The RUSBoost technique is the combination of RUS and Adaboost. In [24,25], the authors used RUSBoost to perform ETD.

Table 5. RUSBoost hyperparameters selected through grid-search.

Hyperparameter	Range of Values	Selected Value
Learning rate	1.0, 0.1, 0.01	0.1
Estimators	20, 30, 100	30

demonstrates the selection of the RUSBoost’s hyperparameters using the grid-search technique.

2.8.4. Bagged Tree

The authors in [21] use a bagged tree for NTL detection. A bagged tree is an ensemble learning technique, in which a number of training subsets are generated with replacements and different classifiers are trained on these subsets. Finally, a single model is selected based on the majority of votes from each model.

Table 6. Bagged tree hyperparameters selected through grid-search.

Hyperparameter	Range of Values	Selected Value
Estimators	20, 30, 100	30

shows the optimal hyperparameter selection for bagged tree using grid-search.

2.8.5. WD-CNN

The authors in [20] proposed WD-CNN to detect electricity thieves. The authors trained a wide component using 1-D data and the deep component on 2-D data. Therefore, in this paper, we practice the same WD-CNN setting as formerly proposed by the authors [20].

2.8.6. CNN-LSTM

CNN-LSTM is a hybrid deep learning model for NTL detection [22]. It consists of CNN for feature extraction and the derived features further serve as inputs to the LSTM model for classification. Hence, a similar arrangement of CNN-LSTM is used in this paper for comparison.

2.8.7. CNN-RF

CNN-RF is a composite of CNN and RF used for ETD [40]. CNN is applied to derive global features from data. After that, the derived features are delivered to RF for ETD where RF acts as a final layer of CNN. Therefore, the same model arrangement is considered in this paper as a benchmark scheme.

2.8.8. LSTM-MLP

The authors proposed a hybrid LSTM-MLP model using sequential and non-sequential data for NTL detection [23]. For a fair comparison, the same model configuration is used in this paper as that already proposed by the authors [23].

3. Simulation Results and Discussion

In this section, we describe the simulation results of our proposed model together with the performance comparison with state-of-the-art models. Moreover, to validate the LSTM–UNet–Adaboost model’s performance and robustness, seven performance evaluation metrics are used to show the superiority of our proposed model over benchmark schemes for theft detection.

3.1. Performance Comparison with Benchmark Models

This section assesses the performance of our proposed LSTM–UNet–Adaboost model for ETD in the context of smart grids. To estimate the effectiveness of the proposed model, its results were analyzed against other models using the previously mentioned seven performance metrics.

Table 7. Proposed model’s performance comparison with conventional schemes for ETD.

Model	AUC	MCC	F1-Score	Precision	Recall	PR-AUC	Accuracy
LR	0.835	0.670	0.835	0.836	0.834	0.785	0.835
SVM	0.575	0.256	0.698	0.542	0.878	0.548	0.576
CNN-RF	0.889	0.815	0.869	0.965	0.803	0.883	0.900
Bagged Tree	0.883	0.812	0.862	0.956	0.821	0.876	0.882
RUSBoost	0.881	0.689	0.848	0.825	0.824	0.787	0.844
WD-CNN	0.884	0.773	0.878	0.927	0.834	0.864	0.884
LSTM-MLP	0.866	0.732	0.869	0.849	0.889	0.818	0.866
CNN-LSTM	0.889	0.785	0.882	0.946	0.826	0.879	0.889
Proposed model	0.948	0.902	0.954	0.998	0.929	0.958	0.972

presents the results of our proposed model and other existing benchmark models. It is seen that our proposed model achieved 0.94, 0.90, 0.95, 0.99, 0.92, 0.95 and 0.97 for AUC, MCC, F1-score, precision, recall, PR-AUC and accuracy, respectively. Thus, the proposed model outperformed all existing benchmark models in terms of these evaluation metrics. Likewise, CNN-RF was the second-best classifier; however, it had a low DR, i.e., 0.803, in comparison to other models. LSTM-MLP had the second-best DR, i.e., 0.889.

The principal objective of ETD is to improve theft DR and reduce FPR. Particularly, the proposed model presents the best results for each of the class imbalance metrics, as it achieved a DR of 0.92, which is the highest value among all existing benchmark models. Moreover, Table 7 also demonstrates the importance of our proposed IQMOT technique. Despite the performances of other models, such as LR, SVM, CNN-RF, WD-CNN, RUSBoost, bagged tree, LSTM-MLP and CNN-LSTM on the IQMOT-based processed data, our proposed model still outperformed existing models.

Figure 6 shows the ROC-AUC of our proposed LSTM–UNet–Adaboost model; the proposed model has achieved better ROC-AUC than other random predictions in terms of training and validation sets. Similarly to the ROC-AUC, our proposed model has also covered more PR-AUC than any random predictions using IQMOT, as shown in Figure 7. It is worth noting that our proposed scheme has covered more areas over the training and validation sets in terms of ROC-AUC and PR-AUC, which shows the superiority of our proposed scheme. Furthermore, Figure 8 shows the ROC-AUC comparison with existing benchmark models. It is evident that the proposed model has the highest ROC-AUC score and covers more area under the ROC curve. As mentioned earlier, the main goal is to maximize the DR and minimize the FPR in ETD, which has been achieved by our model as compared to the existing models.

Similarly to ROC-AUC, the proposed model has also reported better results in terms of PR-AUC in comparison to other models, as shown in Figure 9. As we have already highlighted in Table 7, our proposed model achieved the highest PR-AUC score, higher than those of other benchmark models.

3.2. Comparison Based on Proposed IQMOT

This section investigates the effects of imbalanced data on supervised learning techniques and the effectiveness of the novel IQMOT technique.

Table 8. IQMOT-based performance comparison.

Metrics	IQMOT	No Balancing	SMOTE
AUC	0.948	0.602	0.906
MCC	0.902	0.753	0.817
F1-score	0.954	0.753	0.901
Precision	0.998	1.00	0.870
Recall	0.929	0.604	0.905
PR-AUC	0.95	0.63	0.85
Accuracy	0.972	0.745	0.906

presents the results of the proposed model with IQMOT, SMOTE and without any class balancing technique to explain the importance of using the proposed IQMOT over the existing benchmark SMOTE technique. It is clear that the proposed IQMOT is more effective as compared to the existing SMOTE. Essentially, based on IQMOT, the proposed model achieved 0.94, 0.90, 0.95, 0.99, 0.92, 0.95 and 0.97 for the AUC, MCC, F1-score, precision, recall, PR-AUC and accuracy, respectively. Based on SMOTE, the proposed model achieved 0.90, 0.81, 0.90, 0.87, 0.90, 0.85 and 0.90 for AUC, MCC, F1, precision, recall, PR-AUC and accuracy, respectively. Consequently, this confirms the advantage of novel IQMOT over existing class balancing techniques.

Moreover, we have examined the effects of highly imbalanced data on the performance of supervised learning methods. In the third column (No Balancing) of Table 8, we express that the performance of the supervised learning model without applying any class balancing technique is worst, where the precision value of 1.00 indicates that the model misclassifies electricity theft consumers as honest consumers. In particular, this shows the significance of the class balancing mechanism and the adverse effect on the performance of supervised learning methods. Moreover, Figure 10 and Figure 11 show that the proposed model covers less area under the PR and ROC curve as no class balancing mechanism is applied. It can be seen that without applying any class balancing technique, the model only achieves 0.63 PR-AUC and 0.60 ROC-AUC over the training and validation sets. This shows the need for a more accurate and useful class balancing technique. Furthermore, Figure 12 shows the performance analysis of the proposed model with benchmark schemes based on four important and useful class imbalance metrics, known as F1-score, MCC, PR-AUC score and ROC-AUC. It is visible that the proposed model shows excellent results compared to existing benchmark models, including LR, SVM, RUSBoost, bagged tree, WD-CNN, CNN-LSTM, CNN-RF and LSTM-MLP. This shows the superiority of the proposed methodology in terms of highly imbalanced ETD problem, which makes it acceptable of real use. Bagged tree and CNN-RF performances are quite similar to each other. Particularly, this paper focuses on raising the ETD performance without taking into account the computational cost of the proposed mechanism.

3.3. Convergence Analysis

The simulations were done on the preprocessed data with a batch-size of 32. Epoch is a parameter that controls the model training. Figure 13 and Figure 14 illustrate the learning process of LSTM and UNet based on the training and validation loss to select the best configuration of a particular model. Figure 13 highlights the learning curve of LSTM in terms of logarithmic loss. In the first attempt, thirty training iterations were passed to the LSTM model; it shows the smooth learning process of the LSTM model and no overfitting happened until the 28th epoch. As we can see that at 28th iteration, the LSTM model performed best and reduced the training and validation loss to 0.67. It shows the gradual convergence of training and validation loss. Finally, the best model was selected at the 28th iteration, as shown in Figure 13, to train the LSTM model.

This process explains that when we pick a small number of epochs, then the LSTM model is not well trained to capture all the temporal correlations from the electricity consumption data. On the other hand, if we choose a considerable amount of training epochs, then the model leads to the overfitting problem. Therefore, it is necessary to select the optimal number of epochs to avoid underfitting and overfitting problems. Figure 14 expresses the learning process of the UNet model based on logarithmic loss; a stable learning process of UNet is presented. For UNet training, 15 epochs were used to get the best fit model. The learning process of the UNet was also very smooth, as both the training and validation losses increasingly converged, which shows that the model gave the best fitting value at the 14th epoch. Finally, the best fit model was selected at the 14th iteration with a validation loss of 0.03 to train the UNet. Consequently, we can see the effects of smooth learning in Table 7; our proposed model outperformed all other benchmark models.

Table 9. Mapping between the identified problems, proposed solution and validation.

Problem Identified	Proposed Solution	Validation
L.1 Model’s biasness due to imbalanced data	S.1 IQMOT	V.1 The proposed IQMOT generates more realistic samples, as shown in Figure 2, Figure 3, Figure 10 and Figure 11
L.2 High-dimensional data and artificial feature extraction	S.2 Deep LSTM and UNet	V.2 The deep LSTM and UNet efficiently extracts the potential features, as given in Figure 13 and Figure 14
L.3 Final ETD through sigmoid or softmax activation based hidden layer	S.3 Adaboost based LSTM-UNet	V.3 Adaboost acts as final layer of LSTM and UNet that gives better results, as depicted in Figure 6, Figure 7, Figure 8 and Figure 9
L.4 Poor ETD performance due to loss of features’ localization information	S.4 UNet captures both what and whereabout of data	V.4 UNet brings significant improvement in ETD results, as shown in Figure 14

presents the mapping between limitations addressed, proposed solution and validation. The proposed solution addresses the limitations of traditional ETD models. It solves the problem of data imbalance through the novel IQMOT technique that generates more efficient theft samples, as depicted in Figure 2 and Figure 3. Moreover, Figure 10 and Figure 11 validate the significance of the proposed IQMOT in terms of no class balancing technique. Afterwards, the proposed solution utilizes the UNet and LSTM to efficiently derive the long-term dependencies and high-level features from high-dimensional data. Figure 13 and Figure 14 show that the LSTM and UNet efficiently capture important information from high-dimensional imbalanced data. Moreover, UNet also catches features’ localizations that are lost by the conventional CNN based approaches, which significantly improves the ETD results, as depicted in Figure 14. Furthermore, to make better predictions, we utilize Adaboost as a classification mechanism that utilizes the features derived by LSTM and UNet. This mechanism avoids the limitation of traditional models, which face the overfitting problem, as validated in Figure 6, Figure 7, Figure 8 and Figure 9. Hence, the proposed methodology performs more better than the conventional schemes for the identification of electricity frauds.

4. Conclusions

• In this work, a combined LSTM–UNet–Adaboost model and a novel class balancing mechanism IQMOT are proposed for ETD in the smart grid environment. IQMOT is introduced to solve the data imbalance concerns faced by the traditional models.
• To increase the model’s theft detection performance and stability, deep learning LSTM and UNet are combined with an ensemble learning Adaboost. Deep learning automates feature extraction from 1-D and 2-D electricity consumption data, whereas ensemble learning is used for joint training and classification. In this way, the LSTM–UNet–Adaboost model gains the benefits of most recent and powerful techniques of deep learning and ensemble learning.
• Extensive simulations were conducted using realistic electricity consumption data of SGCC. During performance evaluation, we employed the grid-search algorithm to obtain the most appropriate values for the hyperparameters of different models for a fair comparison. The proposed model, LSTM–UNet–Adaboost, achieved 0.94, 0.90, 0.95, 0.99, 0.92, 0.95 and 0.97 for AUC, MCC, F1-score, precision, recall, PR-AUC and accuracy on the test dataset, respectively. Thus, the simulation results show the superiority of the combined LSTM–UNet–Adaboost model over existing state-of-the-art methods, including LR, SVM, CNN-RF, WD-CNN, RUSBoost, bagged tree, LSTM-MLP and CNN-LSTM. Moreover, the newly proposed IQMOT was far better than the existing SMOTE by generating more real electricity theft cases. Consequently, the proposed model shows brilliance for practical terms in the smart grid and can be used in many other scenarios, for instance, anomaly detection applications.

5. Future Work

This work solely focused on enhancing the ETD performance against conventional schemes without considering the computational cost. Therefore, we did not take into account the computational time comparison, which is part of our future work. Moreover, in future, we intend to incorporate other features, such as number of appliances, geographical location and temperature, along with the electricity consumption, to improve the ETD performance.