Proportional–Integral–Derivative Controller Design Using an Advanced Lévy-Flight Salp Swarm Algorithm for Hydraulic Systems
Abstract
1. Introduction
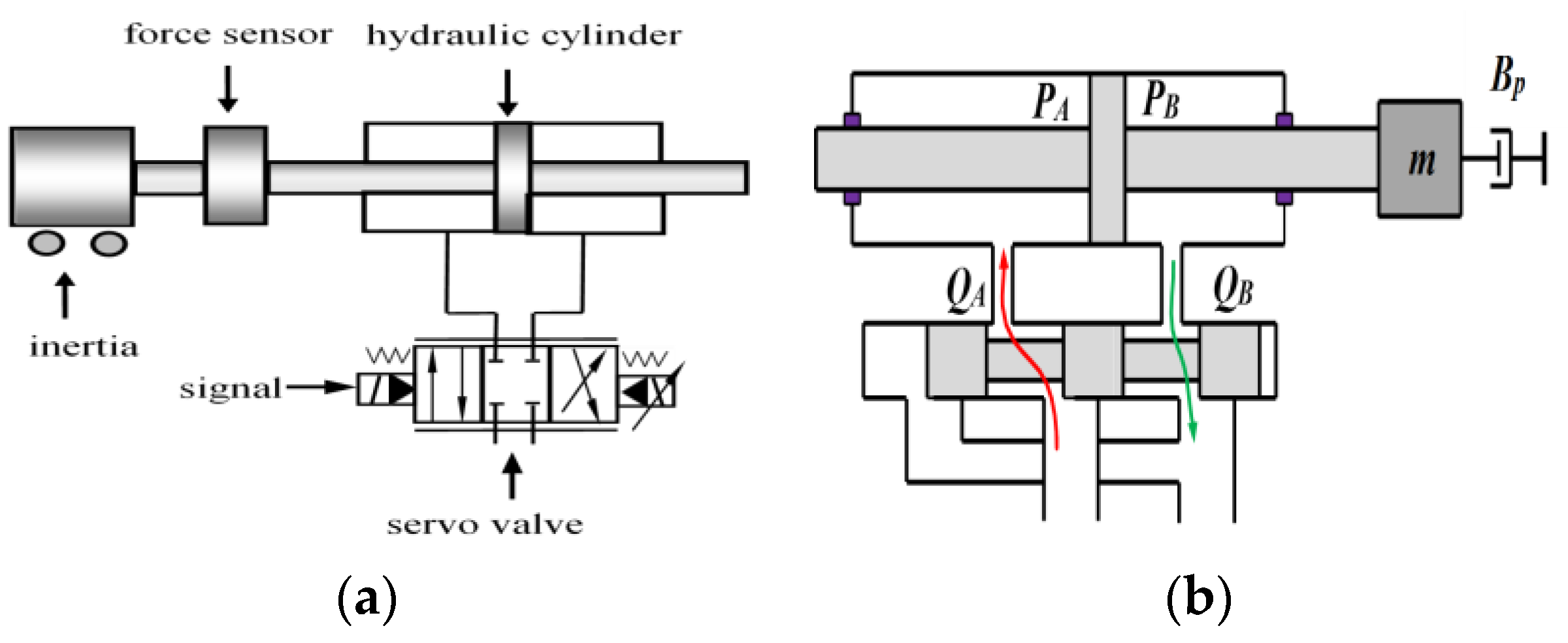
2. Basic System Model
3. The Proposed Meta-Heuristic Approach
3.1. Salp Swarm Algorithm
- Step 1.
- Randomly generate positions in the D-dimensional searching space and then iteratively searches for the best fitness. Initialize N salp positions xi,j (i = 1, 2,…, N), (j = 1, 2,…, D);
- Step 2.
- Update the leader position. the position of the leader in the salp chain can be expressed in Equation (7):where j is the dimension of the searching space, x1,j means the position of leader salp. Fj indicates the food position, in other words, Fj is the current optimal solution. lbj and ubj, respectively, indicate the lower searching bound and the upper searching bound in j-th dimension. P is a probability coefficient in the interval of [0, 1]. The parameter c2 and c3 are random numbers given in the range of [0, 1]. The expression coefficient c1 can be updated in Equation (8):where l and L, respectively, indicate the current iteration and the maximum number of iterations.
- Step 3.
- In each searching process, other salps update their positions by tracking the leader position and other followers’ positions. The position of each follower can be updated as followswhere i ≥ 2 and xi,j show the position of i-th follower salp in j-th dimension.
- Step 4.
- Each fitness value is calculated and compared with other fitness values. Replace the optimal solution and the best fitness value if there is a better fitness value. Record the global optimum solution and fitness value.
- Step 5.
- Judge whether the optimization circumstances meet the end condition. If no, return to step 2 and go on. Otherwise, stop iterative loops.
3.2. Lévy-Flight Salp Swarm Algorithm
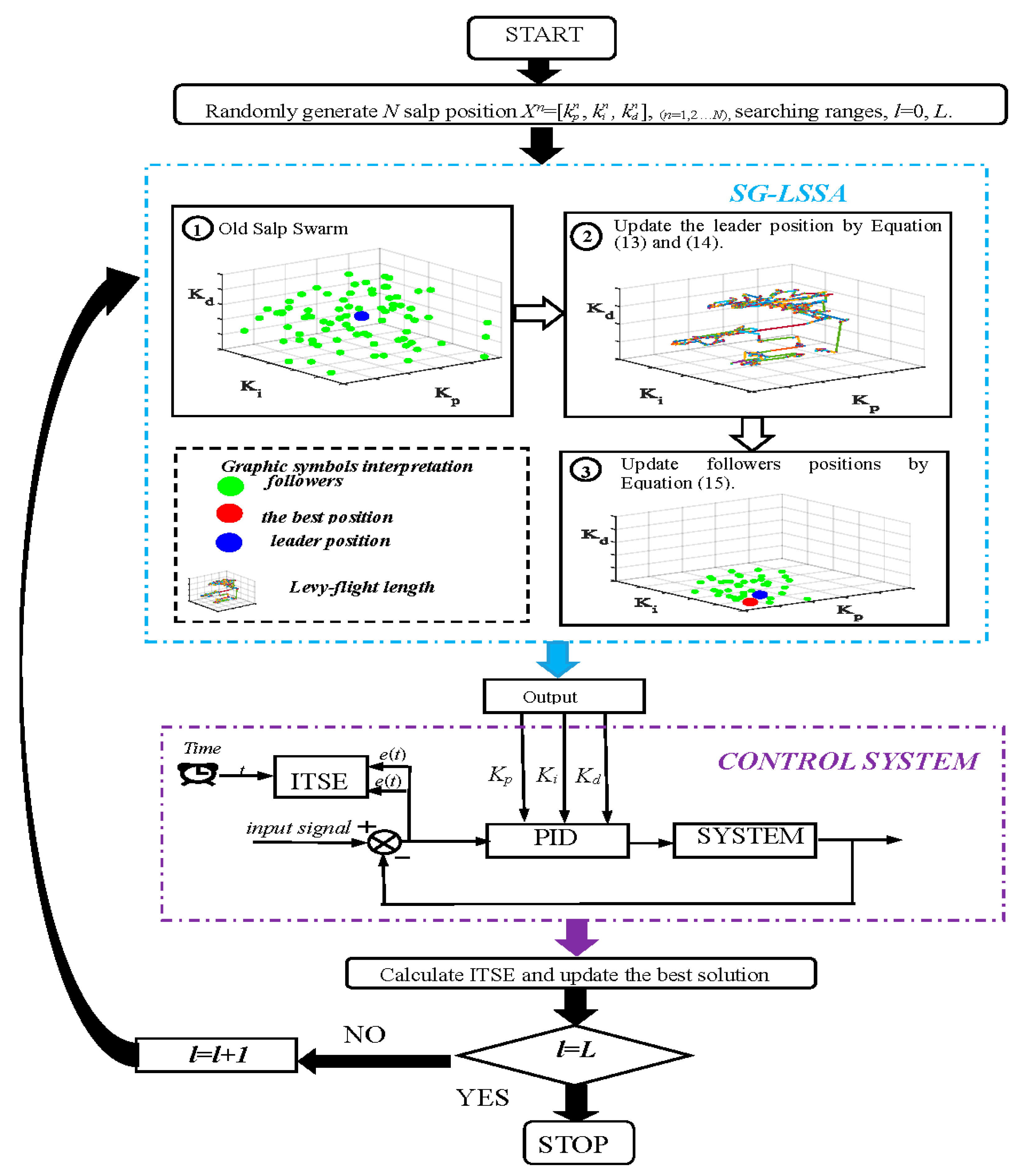
3.3. The Advanced Lévy-Flight Salp Swarm Algorithm
- Step 1.
- Initialize parameters by randomly generating the population size N, the searching dimension, and the maximum number of iterations L. Set reasonable probability coefficient P in the interval of [0, 1]. Determine the lower searching bound lbj and the upper searching bound ubj of the i-th salp in j-th dimension. The i-th salp position in j-th dimensional search space can be represented as xi,j (i = 1, 2,…, N), (j = 1, 2,…, D).
- Step 2.
- Update the leader salp position by judging whether i-th is equal to 1. If i-th is equal to 1, execute Step 2. If i-th is not equal to 1, execute Step 3. Update the new expression coefficient in Equation (14). Randomly select c3 in the interval of [0, 1]. Calculate the current optimal solution Fj in j-th dimension. Update the levy flight trajectory using Equations (11) and (12). Contrast c3 with the probability coefficient P, if c3 is greater than or equal to P, update the first salp position in the j-th dimension using equation in Equation (13): x1,j = Fj + ·Levy. If c3 is less than P, update the first salp position in the j-th dimension using equation in Equation (13): x1,j = Fj − ·Levy.
- Step 3.
- Update other salp positions by randomly selecting rand in [0, 1]. Update the position of the followers using Equation (15).
- Step 4.
- Judgment operation. Calculate and compare all fitness values. If there is a better solution, replace Fj. Calculate l = l + 1. Judge whether l = L. If l is equal to L, Fj is the optimal solution, otherwise return to Step 2.
| Algorithm 1 SG-LSSA |
| Input: Fitness function F(.). dot means the solution. Maximum number of iterations L. Searching dimension j. N positions of salps xi,j (i = 1, 2,…, N), Initial optimum solution Fj. Initial optimum value Fbest. Searching range [lbj, ubj]. l = 0. Power-law exponent β. |
| Output:Fj, Fbest. |
| while (l < L) |
| Calculate the parameter c1 by Equation (14): = (ubj − lbj)·(1−l/(L + 1)) |
| Randomly select the parameter c3 in the range of [0, 1] |
| fori = 1:N |
| if 1 (i = 1) |
| if 2 (c3 >= P) |
| Update x1,j by the equation in Equation (13): x1,j= Fj + ·Levy |
| else |
| Update x1,j by the equation in Equation (13): x1,j = Fj − ·Levy |
| end if 2 |
| else |
| Update xi,j by Equation (15): xi,j = (xi,j + Levy·(xi,j − Fj))·rand |
| end if 1 |
| Calculate the function value F(xi,j) |
| if 3 F(xi,j) is better than Fbest |
| Fj = xi,j |
| Fbest = F(xi,j) |
| end if 3 |
| end for |
| l = l + 1 |
| end while |
4. The Proposed PID Controller Design
4.1. Basic PID Controller Model
4.2. Control Strategy Design
5. Benchmark Function Experiments
5.1. Experimental Parameters
5.2. Comparison Algorithms and Parameters
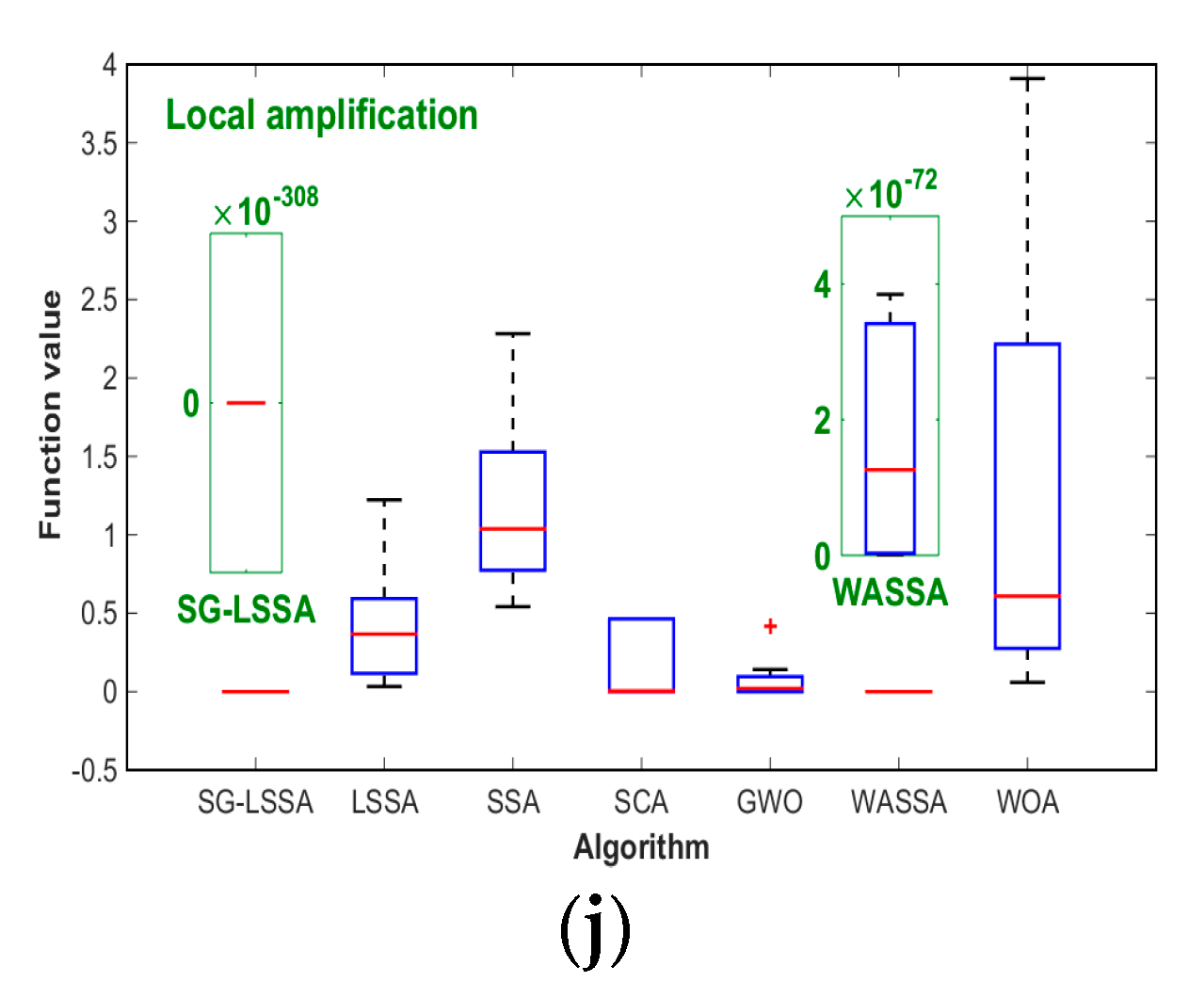
5.3. Testing Results
6. Results and Discussions
6.1. System Parameters and Working Principle
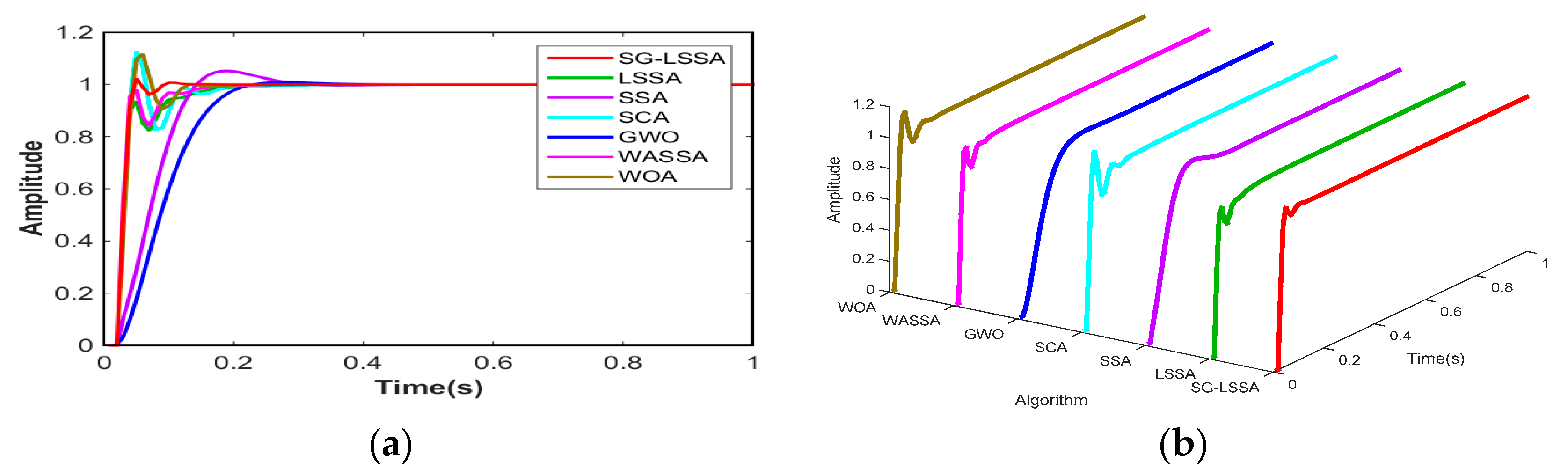
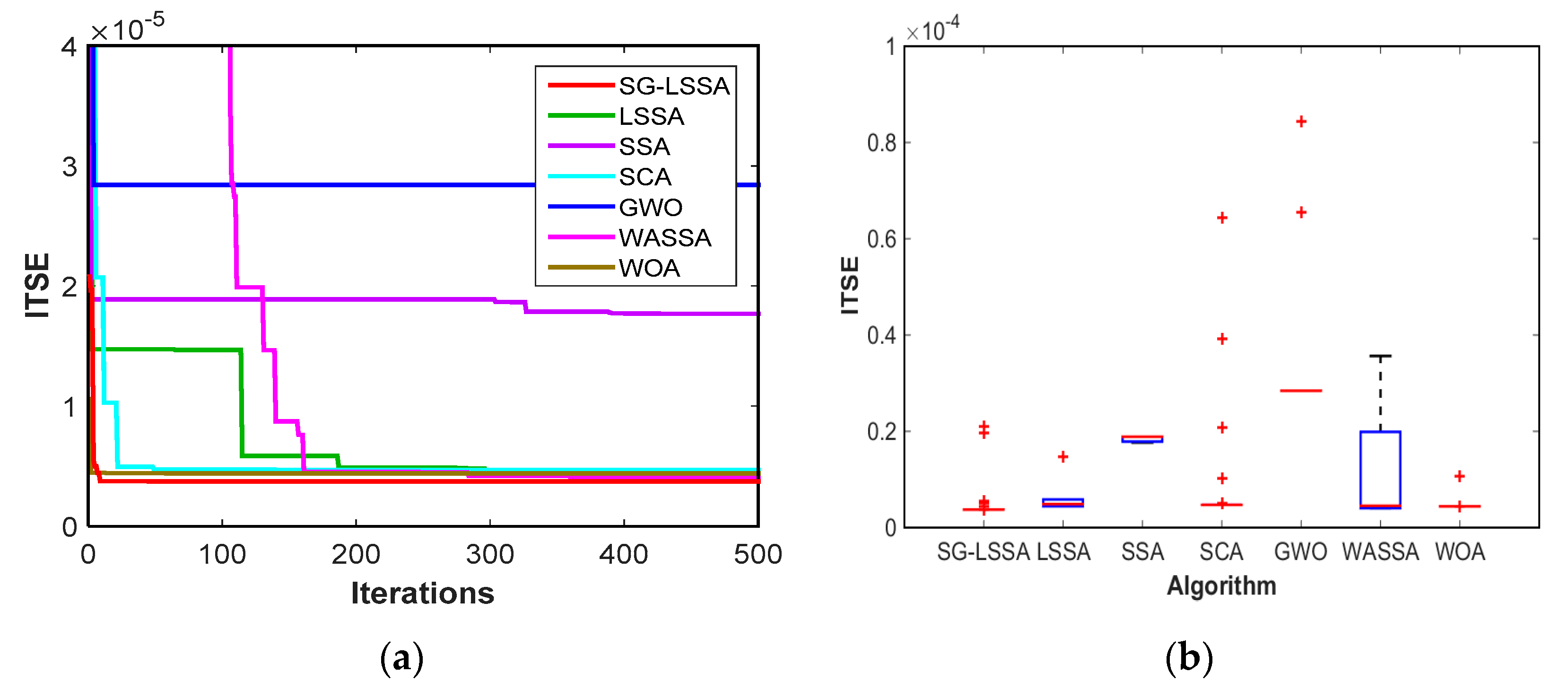
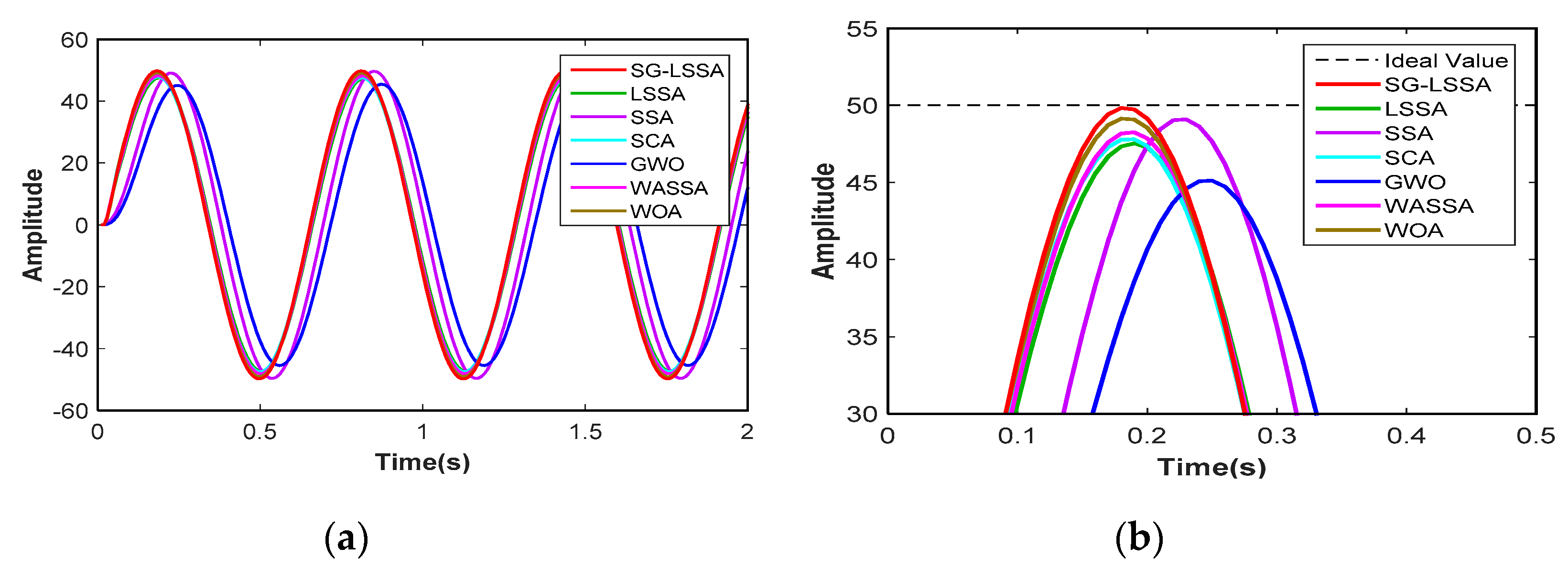
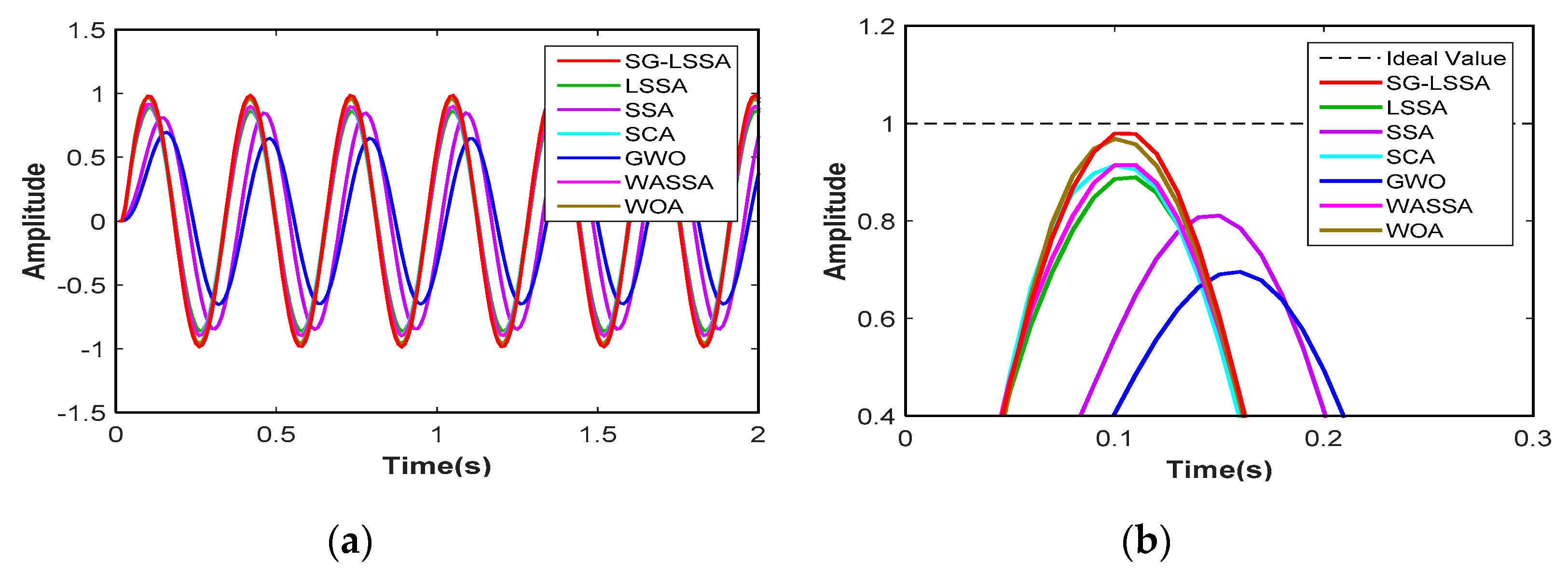
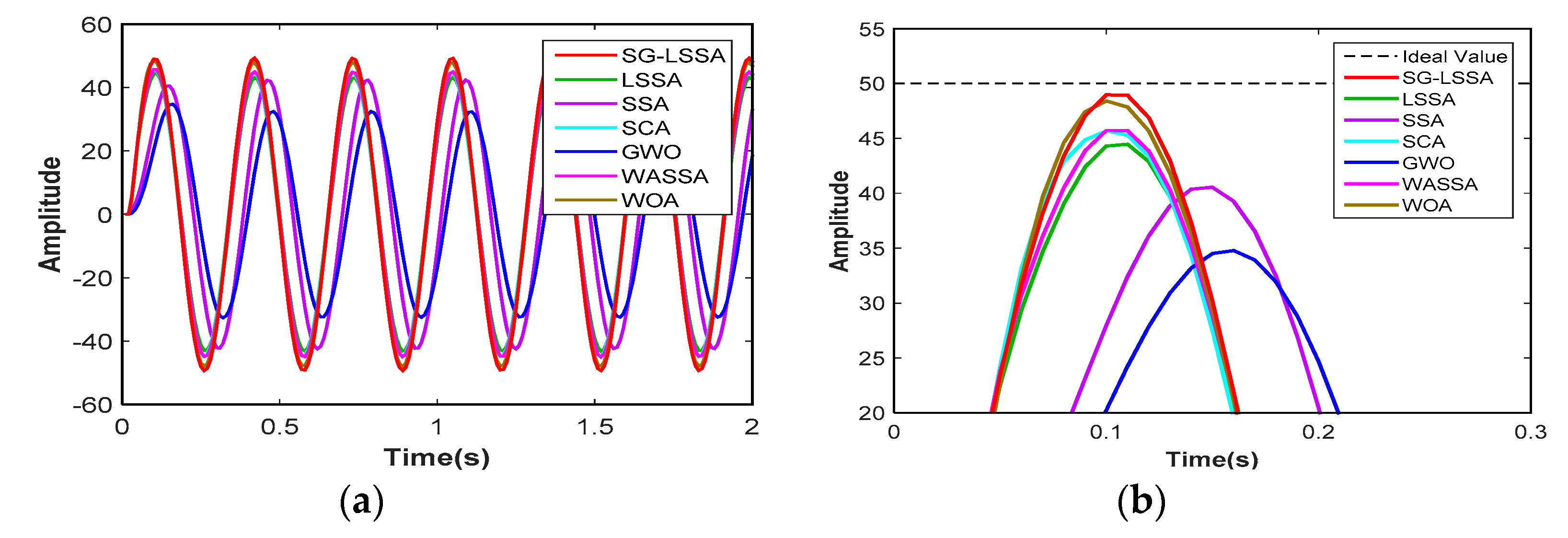
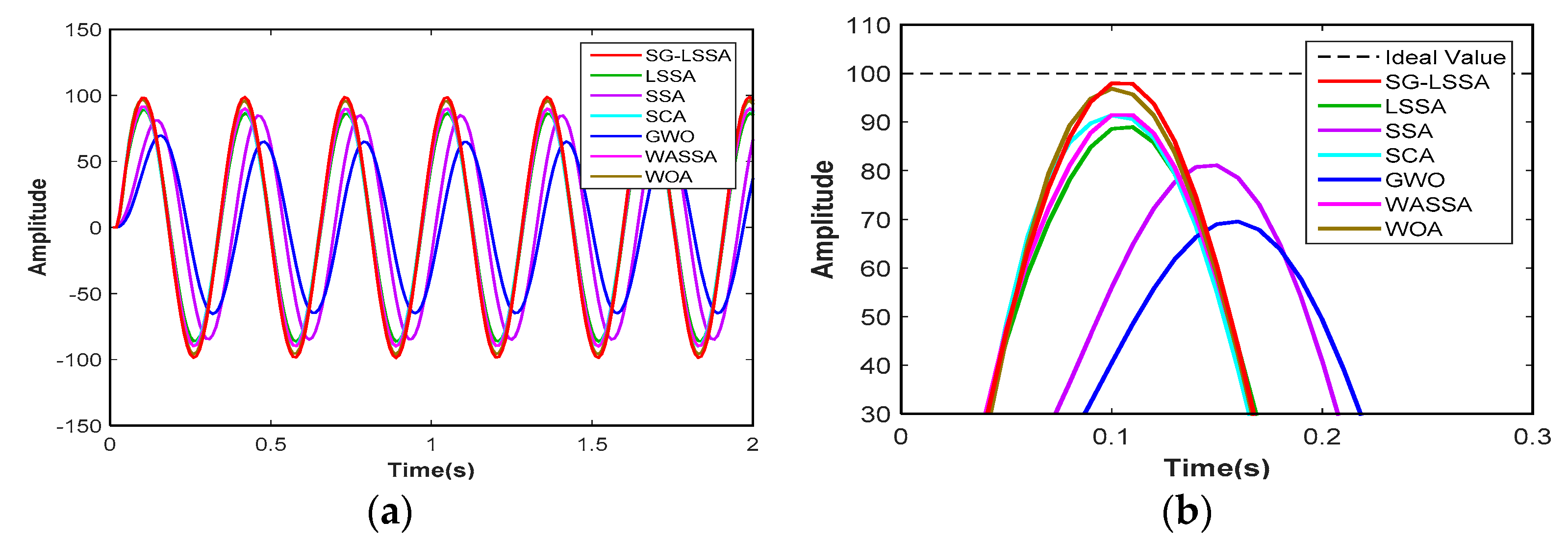
6.2. Temporal Response Characteristic
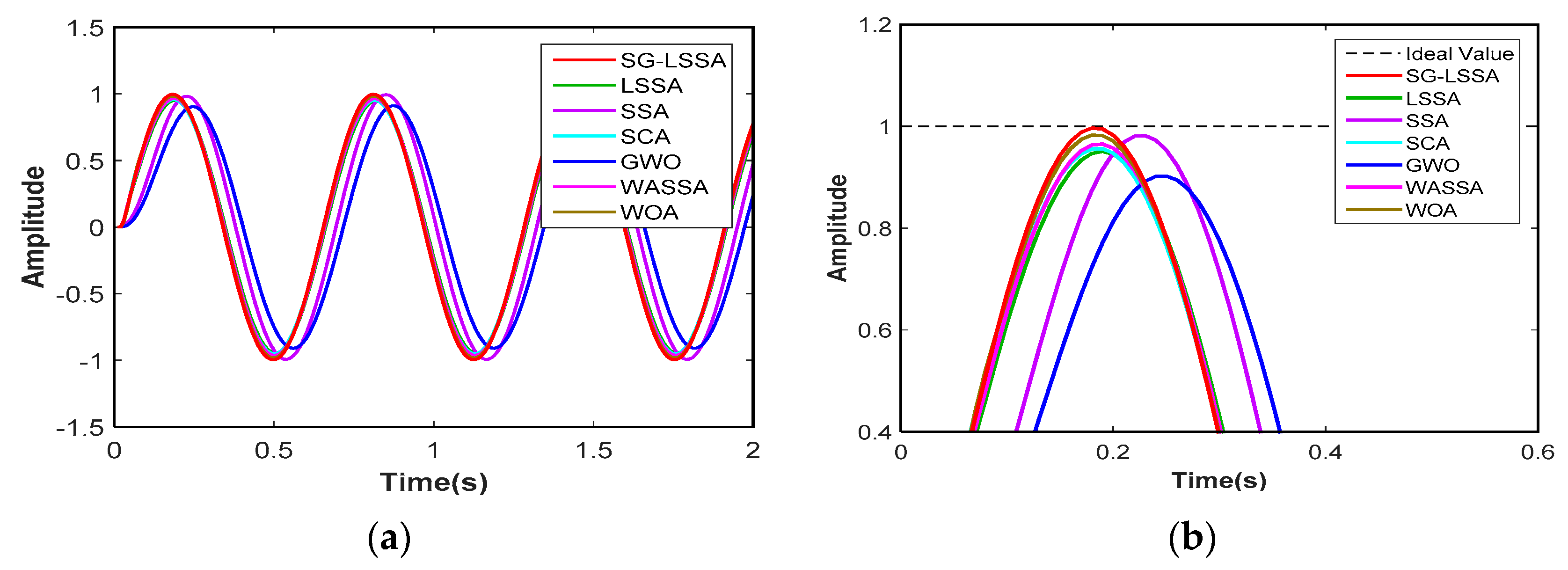
6.3. The Frequency Response Characteristic
7. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Kilic, E.; Dolen, M.; Koku, A.B.; Caliskan, H.; Balkan, T. Accurate pressure prediction of a servo-valve controlled hydraulic system. Mechatronics 2012, 22, 997–1014. [Google Scholar] [CrossRef]
- Lin, A.; Sun, Y.; Zhang, H.; Lin, X.; Yang, L.; Zheng, Q. Fluctuating characteristics of air-mist mixture flow with conjugate wall-film motion in a compressor of gas turbine. Appl. Therm. Eng. 2018, 142, 779–792. [Google Scholar] [CrossRef]
- Xu, B.; Chen, D.; Tolo, S.; Patelli, E.; Jiang, Y. Model validation and stochastic stability of a hydro-turbine governing system under hydraulic excitations. Int. J. Electr. Power Energy Syst. 2018, 95, 156–165. [Google Scholar] [CrossRef]
- Lin, A.; Zheng, Q.; Jiang, Y.; Lin, X.; Zhang, H. Sensitivity of air/mist non-equilibrium phase transition cooling to transient characteristics in a compressor of gas turbine. Int. J. Heat Mass Transf. 2019, 137, 882–894. [Google Scholar] [CrossRef]
- Nguyen, M.T.; Dang, T.D.; Ahn, K.K. Application of Electro-Hydraulic Actuator System to Control Continuously Variable Transmission in Wind Energy Converter. Energies 2019, 12, 2499. [Google Scholar] [CrossRef]
- Xia, L.; Quan, L.; Ge, L.; Hao, Y. Energy efficiency analysis of integrated drive and energy recuperation system for hydraulic excavator boom. Energy Conv. Manag. 2018, 156, 680–687. [Google Scholar] [CrossRef]
- Jia, X.; Zhang, H.; Zheng, Q. Numerical investigation on the effect of hot running rim seal clearance on hot gas ingestion into rotor-stator system. Appl. Therm. Eng. 2019, 152, 79–91. [Google Scholar] [CrossRef]
- Gao, B.; Shao, J.; Yang, X. A compound control strategy combining velocity compensation with ADRC of electro-hydraulic position servo control system. ISA Trans. 2014, 53, 1910–1918. [Google Scholar] [CrossRef] [PubMed]
- Guo, Q.; Zhang, Y.; Celler, B.G.; Su, S.W. State-Constrained Control of Single-Rod Electrohydraulic Actuator with Parametric Uncertainty and Load Disturbance. IEEE Trans. Control Syst. Technol. 2018, 26, 2242–2249. [Google Scholar] [CrossRef]
- Sun, C.; Fang, J.; Wei, J.; Hu, B. Nonlinear Motion Control of a Hydraulic Press Based on an Extended Disturbance Observer. IEEE Access 2018, 6, 18502–18510. [Google Scholar] [CrossRef]
- Yang, Y.; Li, G.; Zhang, Q. A Pressure-Coordinated Control for Vehicle Electro-Hydraulic Braking Systems. Energies 2018, 11, 2336. [Google Scholar] [CrossRef]
- Shen, G.; Zhu, Z.-C.; Li, X.; Tang, Y.; Hou, D.-D.; Teng, W.-X. Real-time electro-hydraulic hybrid system for structural testing subjected to vibration and force loading. Mechatronics 2016, 33, 49–70. [Google Scholar] [CrossRef]
- Kallu, K.; Wang, J.; Abbasi, S.; Lee, M. Estimated Reaction Force-Based Bilateral Control between 3DOF Master and Hydraulic Slave Manipulators for Dismantlement. Electronics 2018, 7, 256. [Google Scholar] [CrossRef]
- Guo, Q.; Wang, Q.; Li, X. Finite-Time Convergent Control of Electrohydraulic Velocity Servo System Under Uncertain Parameter and External Load. IEEE Trans. Ind. Electron. 2019, 66, 4513–4523. [Google Scholar] [CrossRef]
- Jiangbo, Z.; Junzheng, W. The fractional order PI control for an energy saving electro-hydraulic system. Trans. Inst. Meas. Control 2015, 39, 505–519. [Google Scholar] [CrossRef]
- Han, J. From PID to Active Disturbance Rejection Control. IEEE Trans. Ind. Electron. 2009, 56, 900–906. [Google Scholar] [CrossRef]
- Valério, D.; da Costa, J.S. Tuning of fractional PID controllers with Ziegler–Nichols-type rules. Signal Process. 2006, 86, 2771–2784. [Google Scholar] [CrossRef]
- Das, J.; Mishra, S.K.; Saha, R.; Mookherjee, S.; Sanyal, D. Nonlinear modeling and PID control through experimental characterization for an electrohydraulic actuation system: system characterization with validation. J. Braz. Soc. Mech. Sci. Eng. 2016, 39, 1177–1187. [Google Scholar] [CrossRef]
- Padula, F.; Visioli, A. Tuning rules for optimal PID and fractional-order PID controllers. J. Process Control 2011, 21, 69–81. [Google Scholar] [CrossRef]
- Nedic, N.; Prsic, D.; Dubonjic, L.; Stojanovic, V.; Djordjevic, V. Optimal cascade hydraulic control for a parallel robot platform by PSO. Int. J. Adv. Manuf. Technol. 2014, 72, 1085–1098. [Google Scholar] [CrossRef]
- Essa, M.E.-S.M.; Aboelela, M.A.S.; Hassan, M.A.M. Position control of hydraulic servo system using proportional-integral-derivative controller tuned by some evolutionary techniques. J. Vib. Control 2014, 22, 2946–2957. [Google Scholar] [CrossRef]
- Wang, R.; Tan, C.; Xu, J.; Wang, Z.; Jin, J.; Man, Y. Pressure Control for a Hydraulic Cylinder Based on a Self-Tuning PID Controller Optimized by a Hybrid Optimization Algorithm. Algorithms 2017, 10, 19. [Google Scholar] [CrossRef]
- Fan, Y.; Shao, J.; Sun, G. Optimized PID Controller Based on Beetle Antennae Search Algorithm for Electro-Hydraulic Position Servo Control System. Sensors 2019, 19, 2727. [Google Scholar] [CrossRef]
- Li, C.; Mao, Y.; Zhou, J.; Zhang, N.; An, X. Design of a fuzzy-PID controller for a nonlinear hydraulic turbine governing system by using a novel gravitational search algorithm based on Cauchy mutation and mass weighting. Appl. Soft. Comput. 2017, 52, 290–305. [Google Scholar] [CrossRef]
- Mirjalili, S.; Gandomi, A.H.; Mirjalili, S.Z.; Saremi, S.; Faris, H.; Mirjalili, S.M. Salp Swarm Algorithm: A bio-inspired optimizer for engineering design problems. Adv. Eng. Softw. 2017, 114, 163–191. [Google Scholar] [CrossRef]
- Gao, H.; Hou, Y.; Zhang, S.; Diao, M. An Efficient Approximation for Nakagami-m Quantile Function Based on Generalized Opposition-Based Quantum Salp Swarm Algorithm. Math. Probl. Eng. 2019, 2019, 1–13. [Google Scholar]
- Hasanien, H.M.; El-Fergany, A.A. Salp swarm algorithm-based optimal load frequency control of hybrid renewable power systems with communication delay and excitation cross-coupling effect. Electr. Power Syst. Res. 2019, 176, 105938. [Google Scholar] [CrossRef]
- Ali, T.A.A.; Xiao, Z.; Sun, J.; Mirjalili, S.; Havyarimana, V.; Jiang, H. Optimal design of IIR wideband digital differentiators and integrators using salp swarm algorithm. Knowl.-Based Syst. 2019, 182, 104834. [Google Scholar] [CrossRef]
- Zhang, J.; Wang, Z.; Luo, X. Parameter Estimation for Soil Water Retention Curve Using the Salp Swarm Algorithm. Water 2018, 10, 815. [Google Scholar] [CrossRef]
- Wang, J.; Gao, Y.; Chen, X. A Novel Hybrid Interval Prediction Approach Based on Modified Lower Upper Bound Estimation in Combination with Multi-Objective Salp Swarm Algorithm for Short-Term Load Forecasting. Energies 2018, 11, 1561. [Google Scholar] [CrossRef]
- Jumani, T.A.; Mustafa, M.; Anjum, W.; Ayub, S. Salp Swarm Optimization Algorithm-Based Controller for Dynamic Response and Power Quality Enhancement of an Islanded Microgrid. Processes 2019, 7, 840. [Google Scholar] [CrossRef]
- Xing, Z.; Jia, H. Multilevel Color Image Segmentation Based on GLCM and Improved Salp Swarm Algorithm. IEEE Access 2019, 7, 37672–37690. [Google Scholar] [CrossRef]
- Jamil, M.; Yang, X. A literature survey of benchmark functions for global optimisation problems. Int. J. Math. Model. Numer. Optim. 2013, 4, 150–194. [Google Scholar] [CrossRef]
- Yang, X. Test problems in optimization. arXiv 2010, arXiv:1008.0549. Available online: https://arxiv.org/pdf/1008.0549.pdf (accessed on 16 January 2020).
- Mirjalili, S. SCA: A Sine Cosine Algorithm for solving optimization problems. Knowl.-Based Syst. 2016, 96, 120–133. [Google Scholar] [CrossRef]
- Mirjalili, S.; Mirjalili, S.M.; Lewis, A. Grey Wolf Optimizer. Adv. Eng. Softw. 2014, 69, 46–61. [Google Scholar] [CrossRef]
- Wu, J.; Nan, R.; Chen, L. Improved salp swarm algorithm based on weight factor and adaptive mutation. J. Exp. Theor. Artif. Intell. 2019, 31, 493–515. [Google Scholar] [CrossRef]
- Mirjalili, S.; Lewis, A. The Whale Optimization Algorithm. Adv. Eng. Softw. 2016, 95, 51–67. [Google Scholar] [CrossRef]
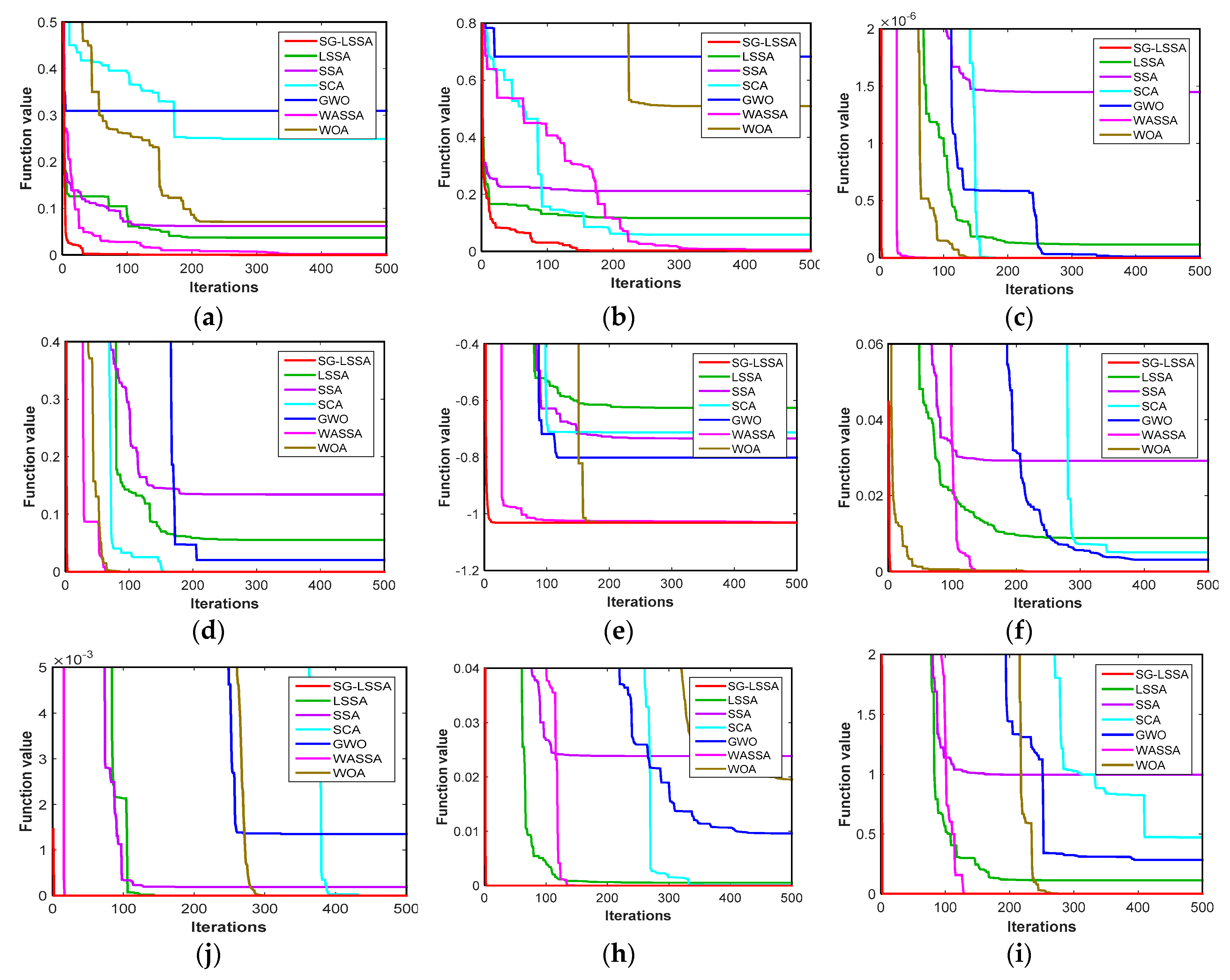

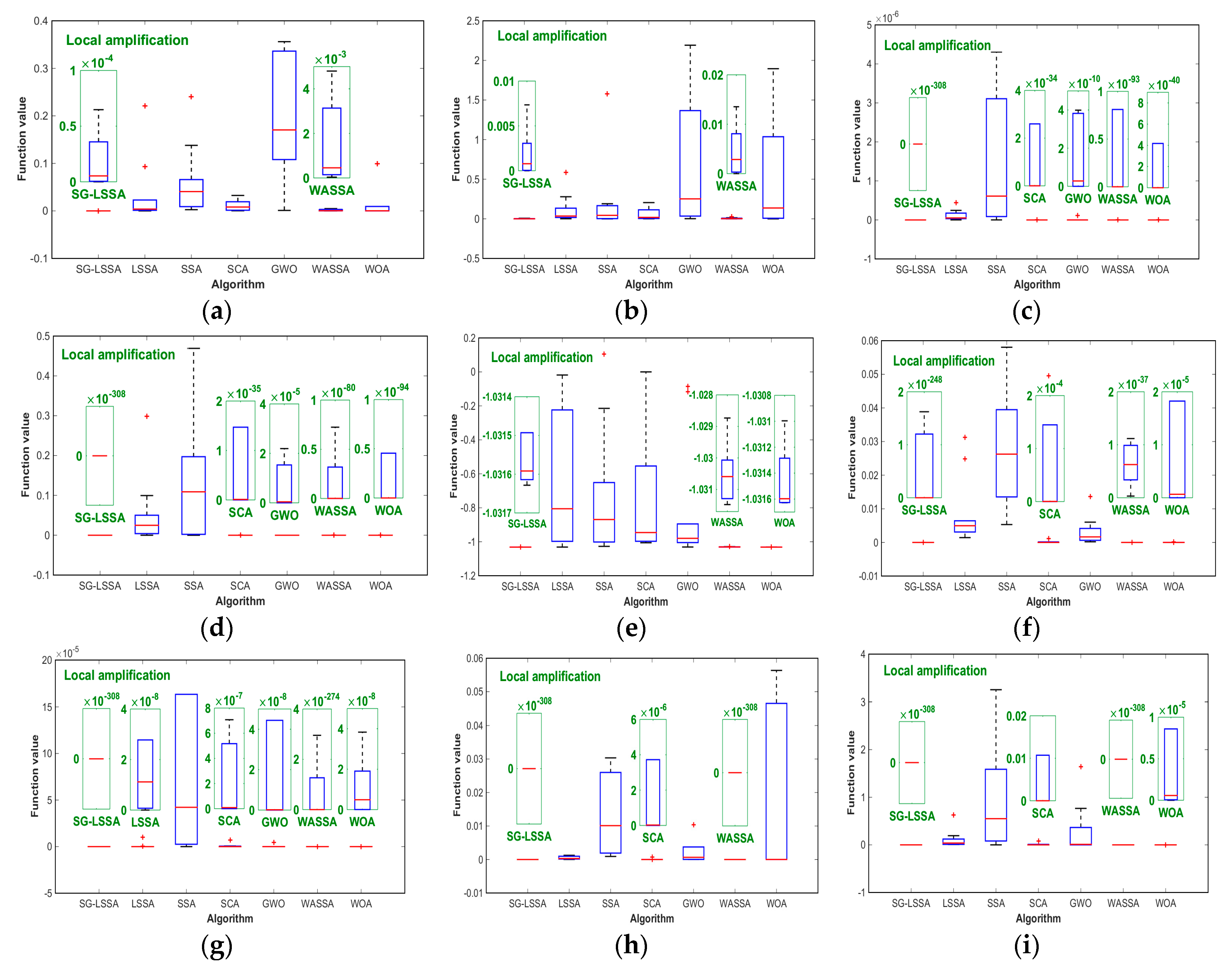


| Function | Formulation | Dim | Range | Optimum |
|---|---|---|---|---|
| Beale | 2 | [−10, 10] | 0 | |
| Booth | 2 | [−10, 10] | 0 | |
| Matyas | 2 | [−10, 10] | 0 | |
| Three-hump Camel | 2 | [−500, 500] | 0 | |
| Six-hump Camel | 2 | [−500, 500] | −1.0316 | |
| Alphine01 | 30 | [−10, 10] | 0 | |
| Csendes | 30 | [−50, 50] | 0 | |
| Griewank | 30 | [−50, 50] | 0 | |
| Rastrigin | 30 | [−5, 5] | 0 | |
| Zakharov | 30 | [−10, 10] | 0 |
| Function | Index | Algorithm | ||||||
|---|---|---|---|---|---|---|---|---|
| SG-LSSA | LSSA | SSA | SCA | GWO | WASSA | WOA | ||
| F1 | Best | 1.7149 × 10−8 | 9.4190 × 10−6 | 0.0026 | 2.7607 × 10−4 | 9.7780 × 10−4 | 3.4501 × 10−5 | 3.4089 × 10−7 |
| Worst | 2.9148 × 10−4 | 0.2208 | 0.2405 | 2.4052 | 1.5090 | 0.0048 | 0.5988 | |
| Average | 4.2382 × 10−5 | 0.0371 | 0.0622 | 0.2489 | 0.3093 | 0.0015 | 0.0709 | |
| F2 | Best | 5.0676 × 10−7 | 0.0016 | 1.1209 × 10−6 | 6.2883 × 10−4 | 0.0021 | 3.8017 × 10−6 | 5.5204 × 10−6 |
| Worst | 0.0073 | 0.5839 | 1.5768 | 0.2049 | 2.1918 | 0.0284 | 1.8955 | |
| Average | 0.0019 | 0.1171 | 0.2117 | 0.0582 | 0.6822 | 0.0062 | 0.5095 | |
| F3 | Best | 0 | 1.1029 × 10−9 | 1.1055 × 10−9 | 4.8778 × 10−51 | 9.7680 × 10−19 | 9.6296 × 10−105 | 2.2145 × 10−62 |
| Worst | 0 | 4.4637 × 10−7 | 4.3044 × 10−6 | 2.7927 × 10−25 | 1.0946 × 10−7 | 1.7998 × 10−92 | 1.2016 × 10−32 | |
| Average | 0 | 1.1609 × 10−7 | 1.4486 × 10−6 | 2.8048 × 10−26 | 1.1041 × 10−8 | 2.2897 × 10−93 | 1.2017 × 10−33 | |
| F4 | Best | 0 | 6.1674 × 10−6 | 5.1275 × 10−6 | 5.1451 × 10−65 | 7.7726 × 10−17 | 2.0094 × 10−97 | 7.1086 × 10−140 |
| Worst | 0 | 0.2989 | 0.4692 | 7.2172 × 10−33 | 0.2050 | 5.2778 × 10−78 | 4.5871 × 10−80 | |
| Average | 0 | 0.0553 | 0.1343 | 7.8696 × 10−34 | 0.0205 | 5.2913 × 10−79 | 4.5871 × 10−81 | |
| F5 | Best | −1.0316 | −1.0314 | −1.0273 | −1.0059 | −1.0312 | −1.0315 | −1.0316 |
| Worst | −1.0303 | −0.0184 | 0.1054 | 5.6927 × 10−60 | −0.0853 | −1.0271 | −1.0307 | |
| Average | −1.0313 | −0.6261 | −0.7338 | −0.7126 | −0.8019 | −1.0303 | −1.0314 | |
| F6 | Best | 1.1249 × 10−258 | 0.0014 | 0.0053 | 6.9374 × 10−12 | 1.9604 × 10−4 | 3.1461 × 10−39 | 1.1122 × 10−58 |
| Worst | 2.0329 × 10−247 | 0.0313 | 0.0581 | 0.0496 | 0.0136 | 2.9003 × 10−37 | 9.1087 × 10−5 | |
| Average | 2.3432 × 10−248 | 0.0089 | 0.0292 | 0.0051 | 0.0031 | 8.0385 × 10−38 | 1.7999 × 10−5 | |
| F7 | Best | 0 | 4.0577 × 10−12 | 2.9637 × 10−8 | 4.3226 × 10−21 | 3.4116 × 10−20 | 9.7588 × 10−319 | 2.1357 × 10−11 |
| Worst | 0 | 1.0193 × 10−5 | 8.9379 × 10−4 | 6.9044 × 10−6 | 0.0134 | 1.3363 × 10−261 | 6.2085 × 10−8 | |
| Average | 0 | 1.0563 × 10−6 | 1.8866 × 10−4 | 8.3207 × 10−7 | 0.0013 | 1.3363 × 10−262 | 1.4029 × 10−8 | |
| F8 | Best | 0 | 5.1896 × 10−6 | 9.1927 × 10−4 | 4.0282 × 10−12 | 3.2142 × 10−6 | 0 | 1.8578 × 10−7 |
| Worst | 0 | 0.0013 | 0.1304 | 7.2423 × 10−4 | 0.0797 | 0 | 0.0564 | |
| Average | 0 | 5.3009 × 10−4 | 0.0239 | 7.7976 × 10−5 | 0.0096 | 0 | 0.0195 | |
| F9 | Best | 0 | 0.0074 | 8.3364 × 10−4 | 5.1159 × 10−12 | 8.0696 × 10−5 | 0 | 7.9581 × 10−13 |
| Worst | 0 | 0.6243 | 3.2526 | 4.6240 | 1.6450 | 0 | 1.3084 × 10−4 | |
| Average | 0 | 0.1128 | 0.9956 | 0.4719 | 0.2836 | 0 | 1.8209 × 10−5 | |
| F10 | Best | 0 | 0.0323 | 0.5413 | 6.5160 × 10−36 | 3.3546 × 10−5 | 6.8725 × 10−75 | 0.0588 |
| Worst | 0 | 1.2227 | 2.2829 | 40.5392 | 0.4203 | 3.8488 × 10−72 | 3.9102 | |
| Average | 0 | 0.4108 | 1.2020 | 4.8680 | 0.0739 | 1.5327 × 10−72 | 1.1359 | |
| Parameters | Algorithm | ||||||
|---|---|---|---|---|---|---|---|
| SG-LSSA | LSSA | SSA | SCA | GWO | WASSA | WOA | |
| KP | 2.2980 | 2.6097 | 0.1011 | 3.1793 | 0 | 2.6767 | 2.6391 |
| Ki | 100 | 72.9233 | 41.4366 | 80.5416 | 29.3905 | 81.9920 | 92.2762 |
| Kd | 0.0111 | 0.0117 | 0.0038 | 0 | 0 | 0.0128 | 0 |
| ITSE | 3.7329 × 10−6 | 4.4337 × 10−6 | 1.7682 × 10−5 | 4.7062 × 10−6 | 2.8424 × 10−5 | 4.0253 × 10−6 | 4.4170 × 10−6 |
| Mp | 0.0236 | 0 | 0.0521 | 0.1276 | 0.0091 | 0 | 0.1182 |
| ts | 0.08 | 0.16 | 0.25 | 0.17 | 0.20 | 0.13 | 0.11 |
| tp | 0.05 | 1 | 0.19 | 0.05 | 0.28 | 1 | 0.06 |
| td | 0.03 | 0.03 | 0.07 | 0.04 | 0.09 | 0.03 | 0.04 |
| er | 3.9733 × 10−12 | 1.6479 × 10−9 | 1.901 6× 10−8 | 1.5339 × 10−8 | 1.4850 × 10−9 | 4.9603 × 10−11 | 1.2672 × 10−11 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fan, Y.; Shao, J.; Sun, G.; Shao, X. Proportional–Integral–Derivative Controller Design Using an Advanced Lévy-Flight Salp Swarm Algorithm for Hydraulic Systems. Energies 2020, 13, 459. https://doi.org/10.3390/en13020459
Fan Y, Shao J, Sun G, Shao X. Proportional–Integral–Derivative Controller Design Using an Advanced Lévy-Flight Salp Swarm Algorithm for Hydraulic Systems. Energies. 2020; 13(2):459. https://doi.org/10.3390/en13020459
Chicago/Turabian StyleFan, Yuqi, Junpeng Shao, Guitao Sun, and Xuan Shao. 2020. "Proportional–Integral–Derivative Controller Design Using an Advanced Lévy-Flight Salp Swarm Algorithm for Hydraulic Systems" Energies 13, no. 2: 459. https://doi.org/10.3390/en13020459
APA StyleFan, Y., Shao, J., Sun, G., & Shao, X. (2020). Proportional–Integral–Derivative Controller Design Using an Advanced Lévy-Flight Salp Swarm Algorithm for Hydraulic Systems. Energies, 13(2), 459. https://doi.org/10.3390/en13020459





