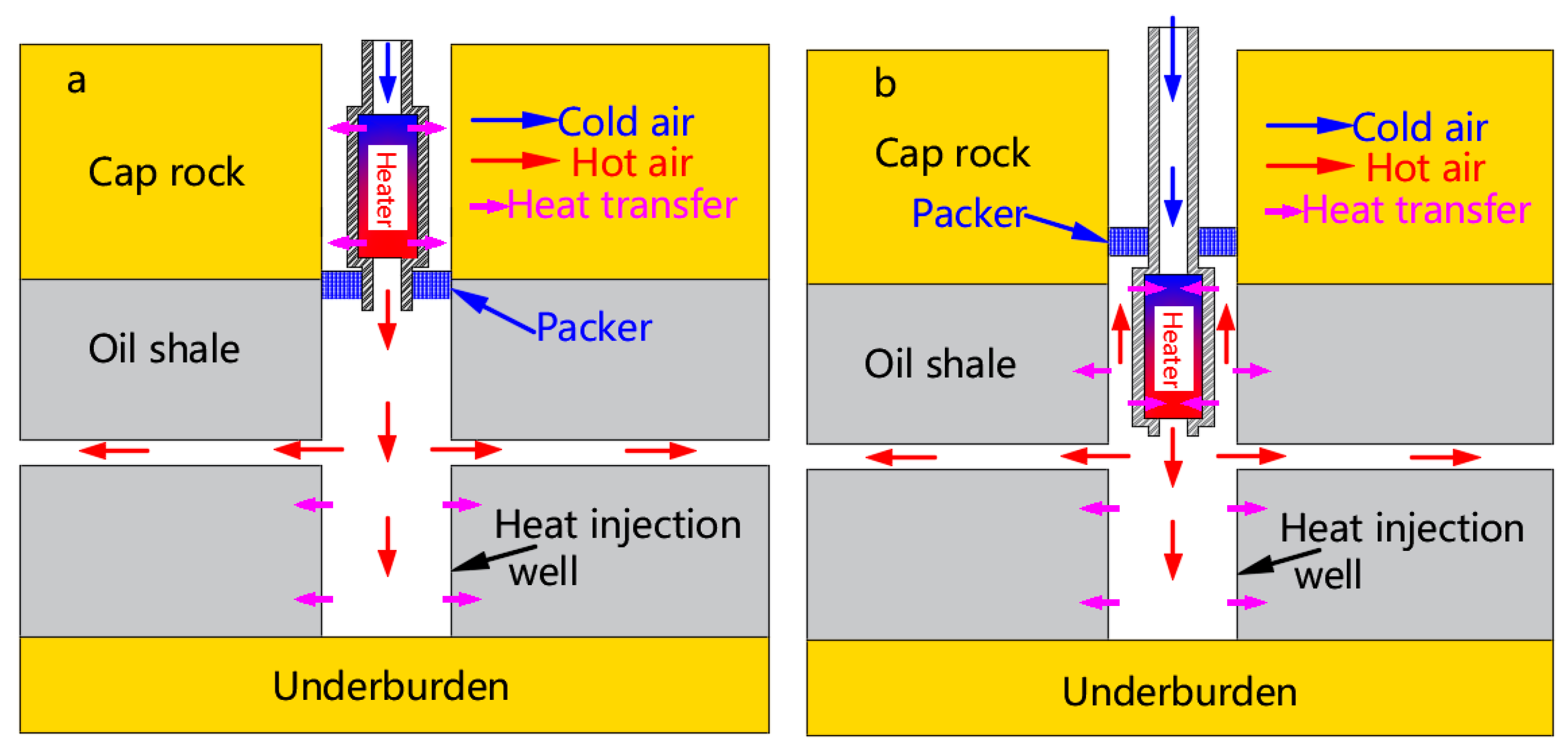
Effects of Packer Locations on Downhole Electric Heater Performance: Experimental Test and Economic Analysis
Abstract
1. Introduction
2. Experimental Setup
2.1. Experimental Apparatus
2.2. Experiment System
2.3. Test Scheme
2.4. Data Processing
2.4.1. Heat Transfer Equations
2.4.2. Economic Analysis
2.4.3. Second-Law Analysis Equations
2.5. Experimental Uncertainty
3. Results and Discussion
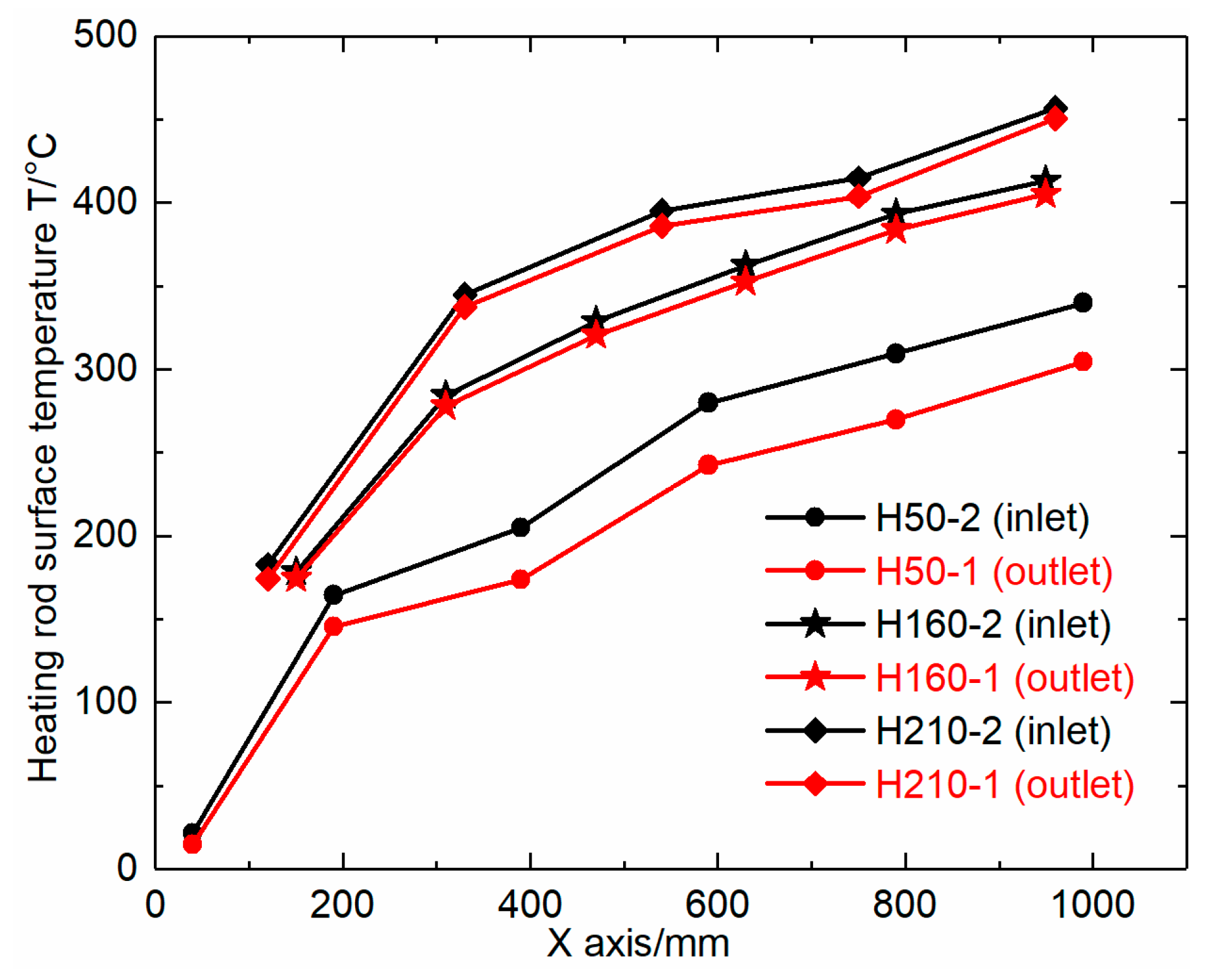
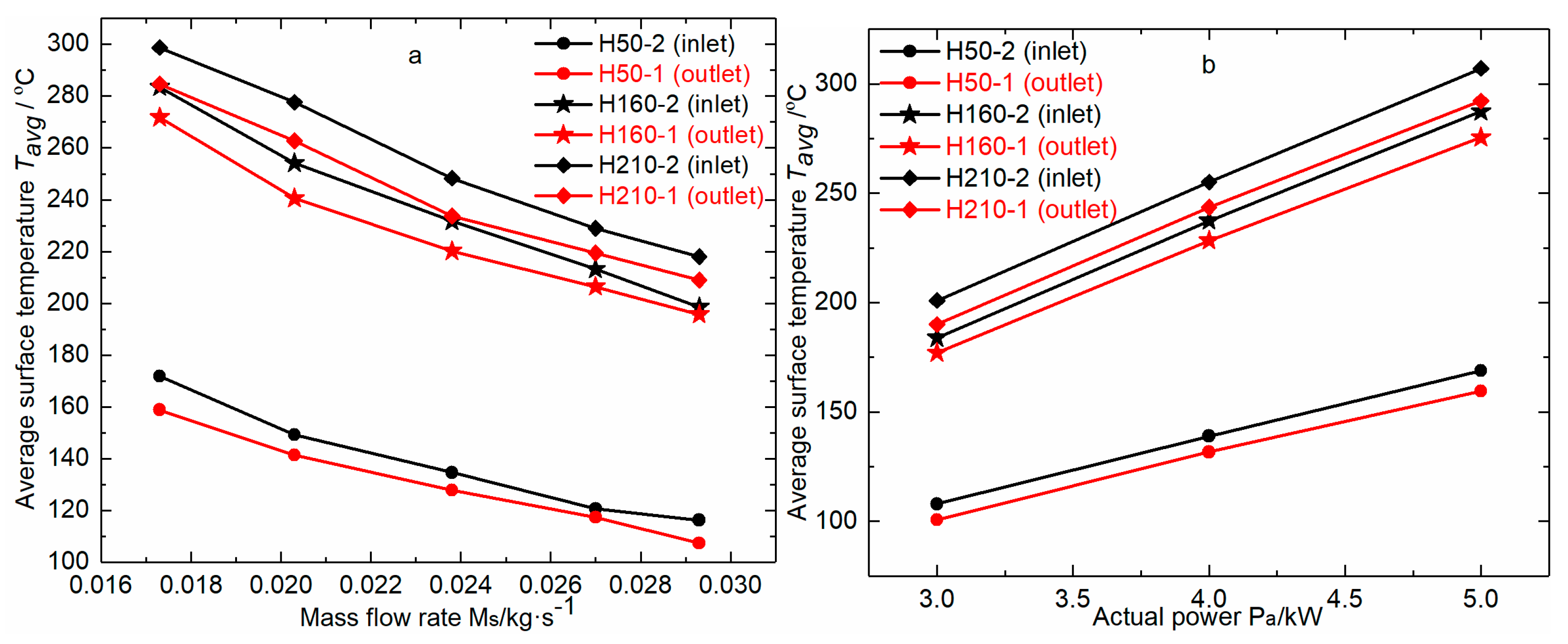
3.1. Heating rod Surface Temperature
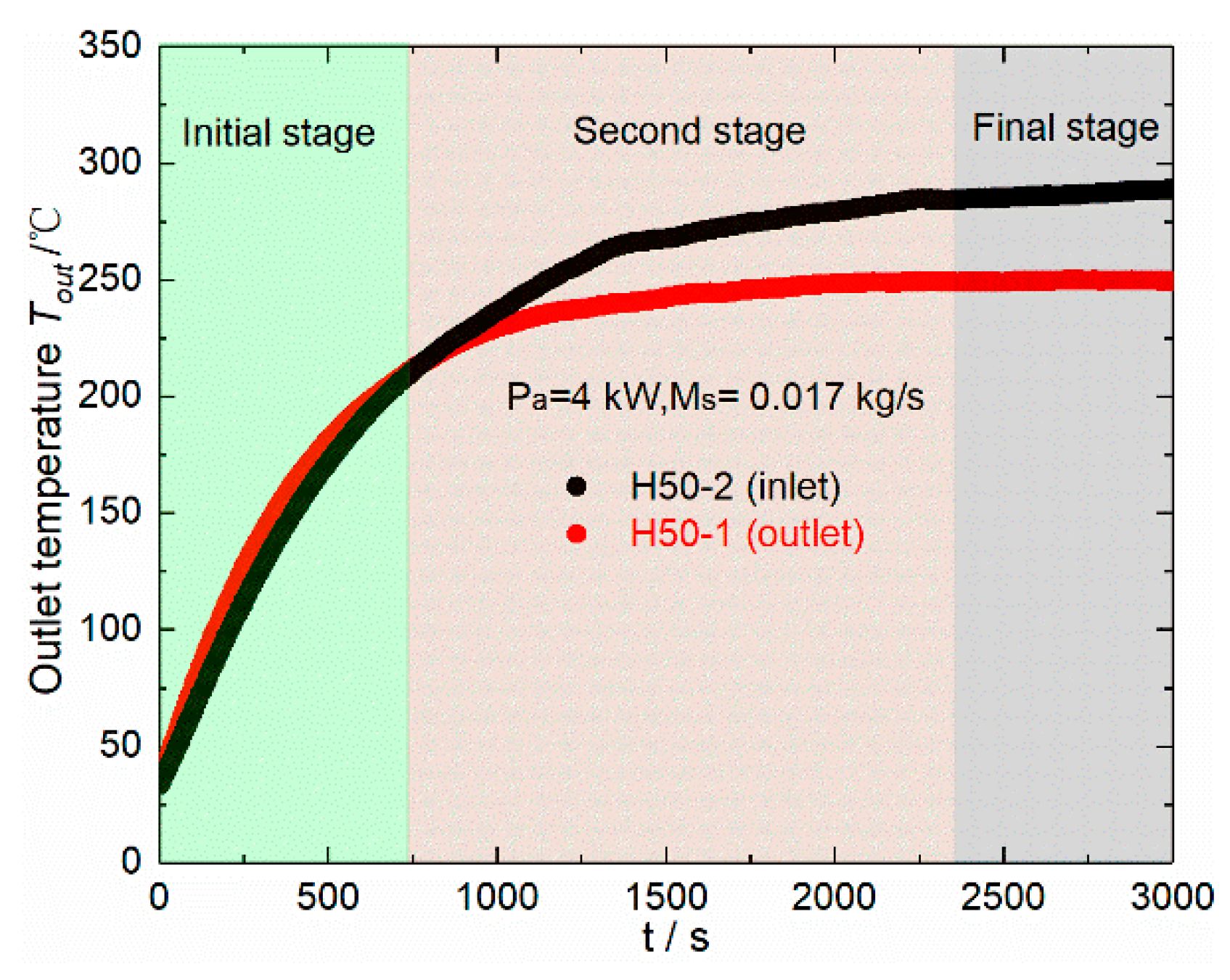
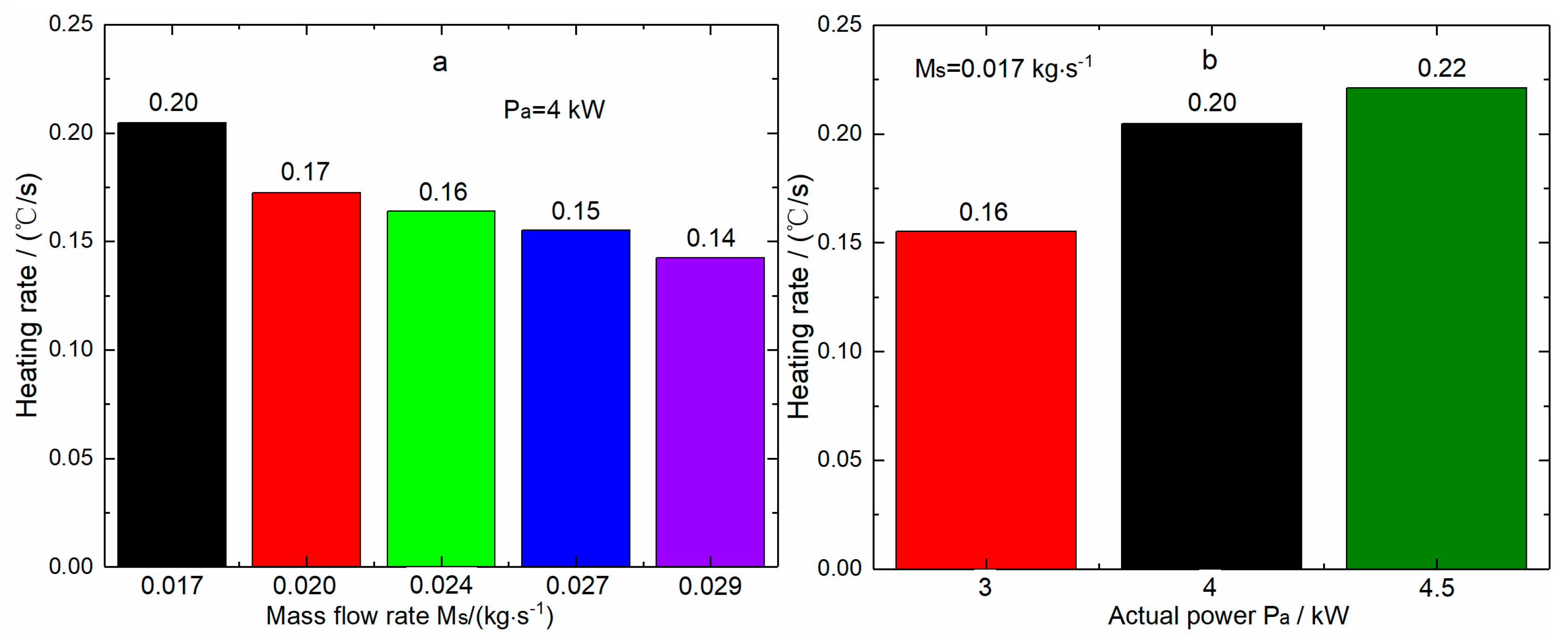
3.2. Outlet Temperature Response Characteristics
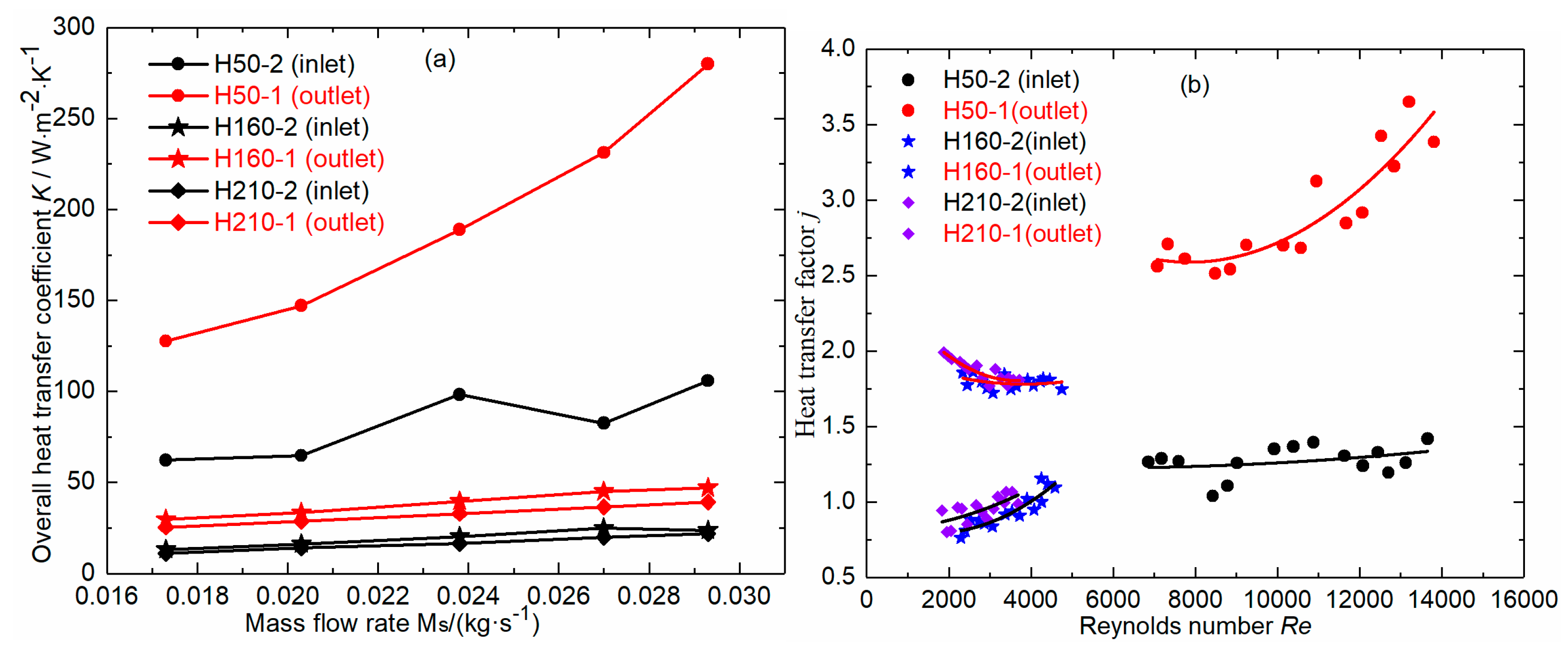
3.3. Heat Transfer Performance
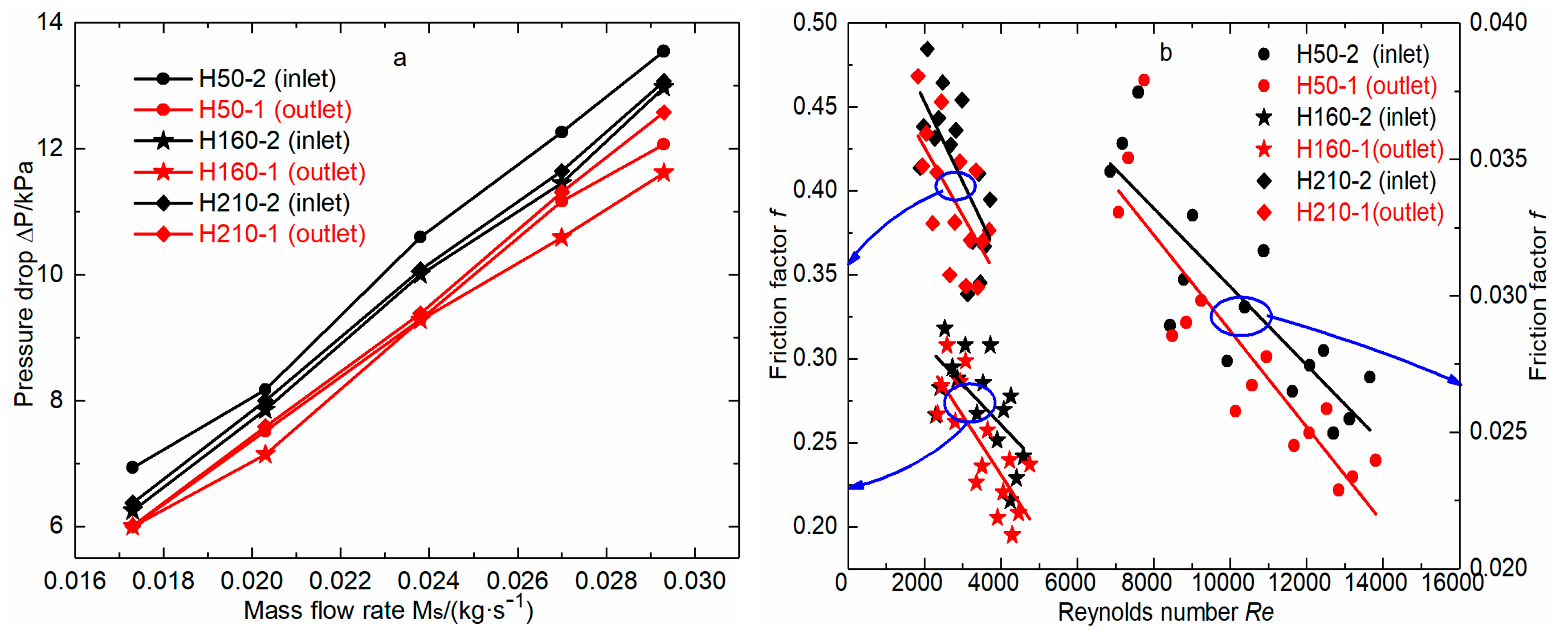
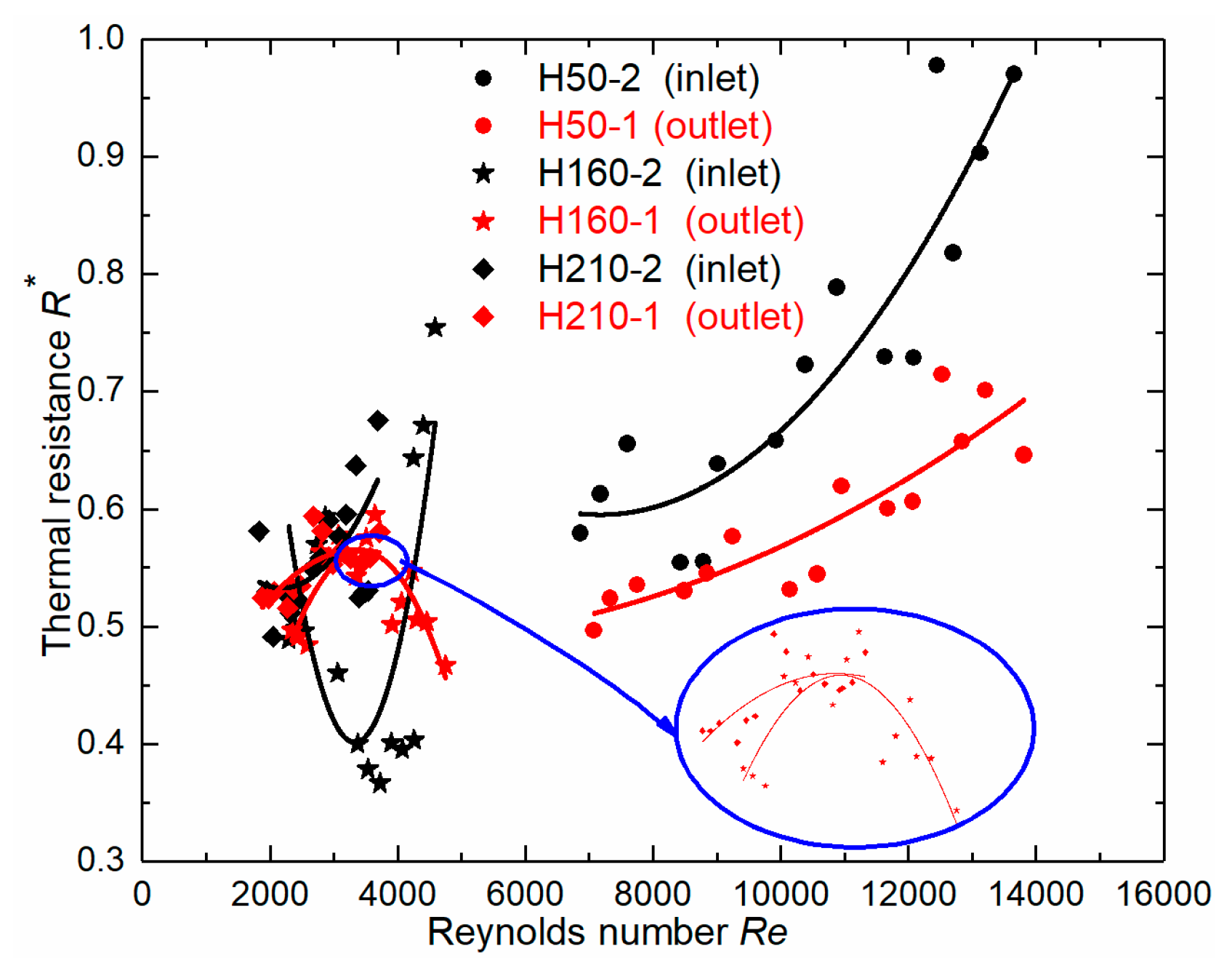
3.4. Resistance Performance
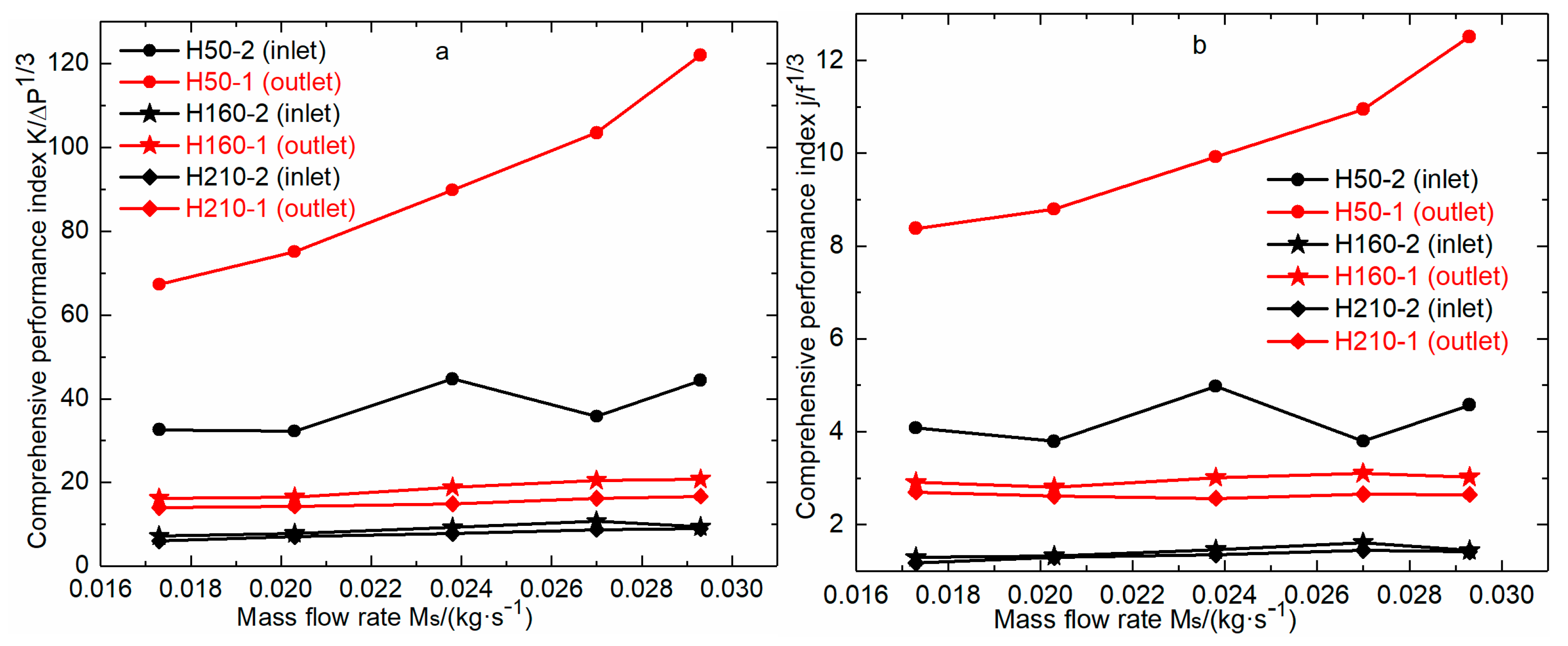
3.5. Comprehensive Performance
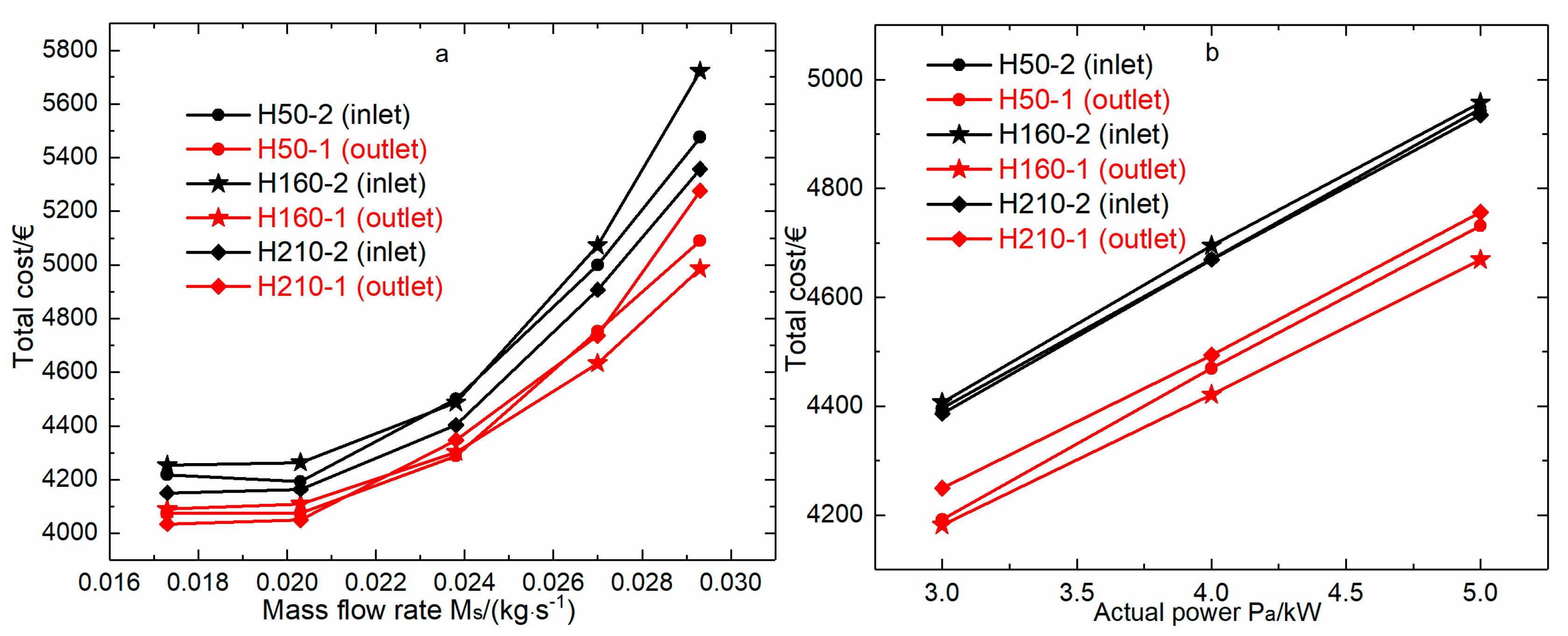
3.6. Economic Analysis
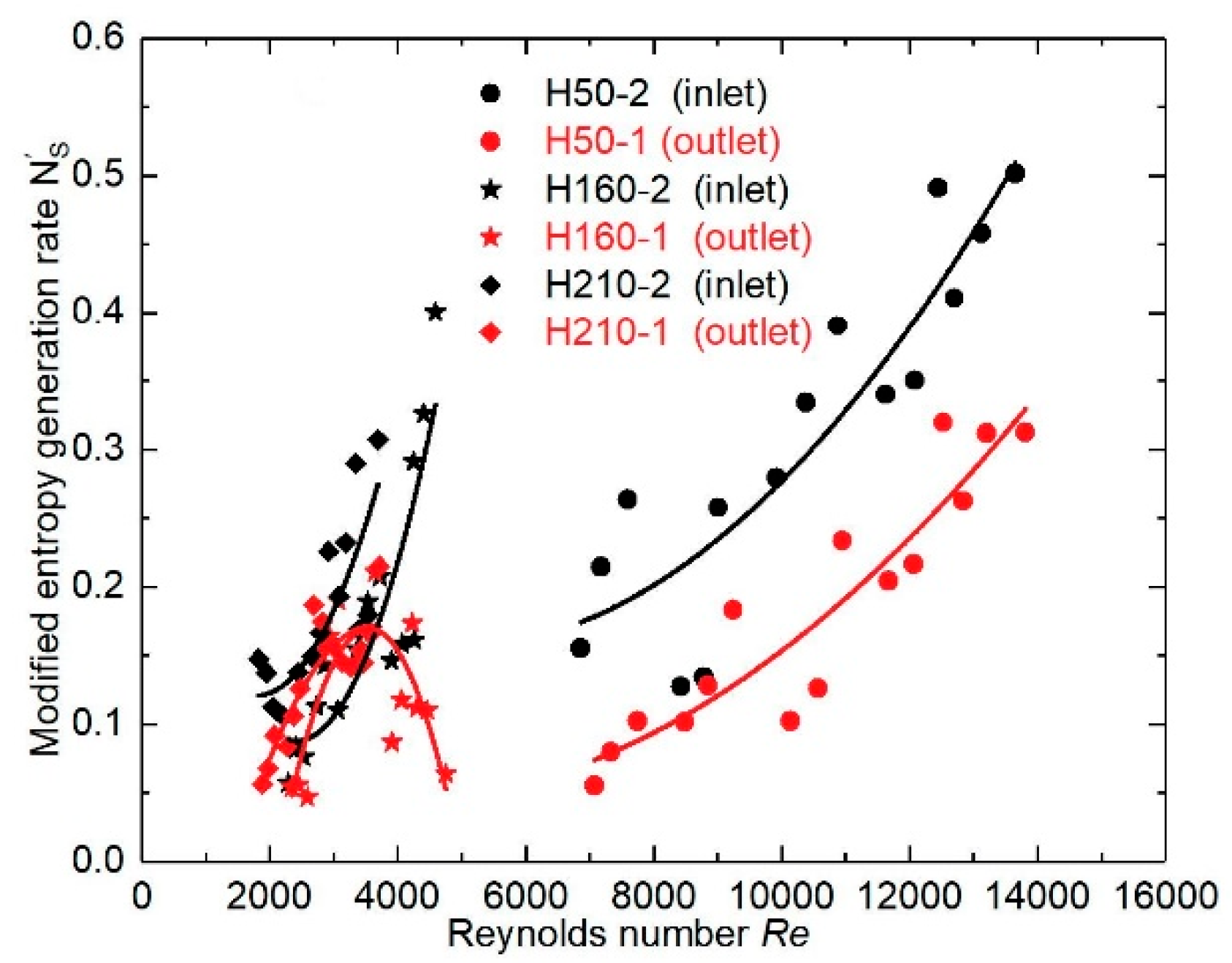
3.7. Performance Evaluation Based on the Second Law of Thermodynamics
4. Conclusions
- (1)
- The surface temperature of the heater with the packer at its outlet was 11.59–26.96% lower than that of the heater in Figure 2. In addition, the heater with the packer at its outlet had an accelerated heating rate in the initial stage, and decreased temperature in the final stage.
- (2)
- Depending on the two comprehensive performance indices, the performance of the heater with the packer at its outlet was 1.87–2.75 times that of the heater in Figure 2.
- (3)
- (4)
- Regarding the comprehensive performance, total cost, and irreversible loss, H50 with the packer at its outlet is the best scheme to exploit deep oil shale resources for energy-efficient oil production.
Author Contributions
Funding
Conflicts of Interest
Nomenclature
| A | Heat transfer area: m2 |
| Hydraulic diameter, m | |
| Entransy dissipation rate, W/K | |
| Convective heat transfer coefficient, W·m−2·K−1 | |
| Overall heat transfer coefficient, W·m−2·K−1 | |
| Mass flow rate, kg/s | |
| Modified entropy generation number | |
| Nusselt number | |
| Actual power, W | |
| Effective power, W | |
| Prandlt number | |
| Reynolds number | |
| Equivalent thermal resistance, K/W | |
| Friction factor | |
| Heat transfer factor | |
| Entropy generation rate, W/K | |
| Heating rod temperature, K | |
| Average heating rod surface temperature, K | |
| The inlet air temperature, K | |
| Greek symbols | |
| Thermal conductivity, W/(m k) | |
| Pressure drop, Pa | |
| Density, kg/m3 | |
| Dynamic viscosity, kg·m−1s−1 | |
| Logarithmic heat transfer temperature difference, K | |
| Maximum temperature difference, K | |
| Minimum temperature difference, K | |
| Subscripts | |
| inlet or inner | |
| outlet or outer | |
| shell-side | |
References
- Shen, F.; Cheng, L.; Sun, Q.; Huang, S. Evaluation of the Vertical Producing Degree of Commingled Production via Waterflooding for Multilayer Offshore Heavy Oil Reservoirs. Energies 2018, 11, 2428. [Google Scholar] [CrossRef]
- Lu, T.; Li, Z.; Zhou, Y. Flow Behavior and Displacement Mechanisms of Nanoparticle Stabilized Foam Flooding for Enhanced Heavy Oil Recovery. Energies 2017, 10, 560. [Google Scholar]
- Wang, L.; Yang, D.; Li, X.; Zhao, J.; Wang, G.; Zhao, Y. Macro and Meso Characteristics of In-Situ Oil Shale Pyrolysis Using Superheated Steam. Energies 2018, 11, 2297. [Google Scholar] [CrossRef]
- Zhou, X.; Yuan, Q.; Zhang, Y.; Wang, H.; Zeng, F.; Zhang, L. Performance evaluation of CO2 flooding process in tight oil reservoir via experimental and numerical simulation studies. Fuel 2019, 236, 730–746. [Google Scholar] [CrossRef]
- Sun, Y.; Liu, Z.; Li, Q.; Deng, S.; Guo, W. Controlling groundwater infiltration by gas flooding for oil shale in situ pyrolysis exploitation. J. Pet. Sci. Eng. 2019, 179, 444–454. [Google Scholar] [CrossRef]
- Saif, T.; Lin, Q.; Gao, Y.; Al-Khulaifi, Y.; Marone, F.; Hollis, D.; Blunt, M.J.; Bijeljic, B. 4D in situ synchrotron X-ray tomographic microscopy and laser-based heating study of oil shale pyrolysis. Appl. Energy 2019, 235, 1468–1475. [Google Scholar] [CrossRef]
- Guo, W.; Wang, Z.; Sun, Z.; Sun, Y.; Lü, X.; Deng, S.; Qu, L.; Yuan, W.; Li, Q. Experimental investigation on performance of downhole electric heaters with continuous helical baffles used in oil shale in-situ pyrolysis. Appl. Therm. Eng. 2019, 147, 1024–1035. [Google Scholar] [CrossRef]
- Wu, Z.; Liu, H. Investigation of hot-water flooding after steam injection to improve oil recovery in thin heavy-oil reservoir. J. Pet. Explor. Prod. Technol. 2019, 9, 1547–1554. [Google Scholar] [CrossRef]
- Huang, S.; Chen, X.; Liu, H.; Xia, Y.; Jiang, J.; Cao, M.; Li, A.; Yang, M. Experimental and numerical study of steam-chamber evolution during solvent-enhanced steam flooding in thin heavy-oil reservoirs. J. Pet. Sci. Eng. 2019, 172, 776–786. [Google Scholar] [CrossRef]
- Du, T.; Chen, Q.; Du, W.; Cheng, L. Performance of continuous helical baffled heat exchanger with varying elliptical tube layouts. Int. J. Heat Mass Transf. 2019, 133, 1165–1175. [Google Scholar] [CrossRef]
- Yadav, S.; Sahu, S.K. Effect of Helical Surface Disc Turbulators on Heat Transfer and Friction Factor Characteristics in the Annuli of a Double-Pipe Heat Exchanger. Chem. Eng. Technol. 2019, 42, 1205–1213. [Google Scholar] [CrossRef]
- Gu, X.; Luo, Y.; Xiong, X.; Wang, K.; Wang, Y. Numerical and experimental investigation of the heat exchanger with trapezoidal baffle. Int. J. Heat Mass Transf. 2018, 127, 598–606. [Google Scholar] [CrossRef]
- Wang, X.; Zheng, N.; Liu, P.; Liu, Z.; Liu, W. Numerical investigation of shell side performance of a double shell side rod baffle heat exchanger. Int. J. Heat Mass Transf. 2017, 108, 2029–2039. [Google Scholar] [CrossRef]
- Gao, B.; Bi, Q.; Nie, Z.; Wu, J. Experimental study of effects of baffle helix angle on shell-side performance of shell-and-tube heat exchangers with discontinuous helical baffles. Exp. Therm. Fluid Sci. 2015, 68, 48–57. [Google Scholar] [CrossRef]
- Stehlik, P.; Němčanský, J.; Kral, D.; Swanson, L.W. Comparison of Correction Factors for Shell-and-Tube Heat Exchangers with Segmental or Helical Baffles. Heat Transf. Eng. 1994, 15, 55–65. [Google Scholar] [CrossRef]
- Boukhadia, K.; Ameur, H.; Sahel, D.; Bozit, M. Effect of the perforation design on the fluid flow and heat transfer characteristics of a plate fin heat exchanger. Int. J. Therm. Sci. 2018, 126, 172–180. [Google Scholar] [CrossRef]
- Churchill, S.W.; Bernstein, M. A correlating equation for forced convection from gases and liquids to a circular cylinder in crossflow. J. Heat Transf. 1977, 99, 300–306. [Google Scholar] [CrossRef]
- Wu, J.; Zhou, J.; Chen, Y.; Wang, M.; Dong, C.; Guo, Y. Experimental investigation on enhanced heat transfer of vertical condensers with trisection helical baffles. Energy Convers. Manag. 2016, 109, 51–62. [Google Scholar] [CrossRef]
- Shah, R.K.; Sekulić, D.P. Fundamentals of Heat Exchanger Design; John Wiley & Sons: New York, NY, USA, 2003. [Google Scholar]
- Taal, M.; Bulatov, I.; Klemeš, J.; Stehlík, P. Cost estimation and energy price forecasts for economic evaluation of retrofit projects. Appl. Therm. Eng. 2003, 23, 1819–1835. [Google Scholar] [CrossRef]
- Wang, K.; Cheng, L. Numerical modeling and multi-objective optimization of a novel cross-flow heat exchanger with rotated aligned tube bank. Sci. China Technol. Sci. 2018, 61, 982–993. [Google Scholar] [CrossRef]
- Li, J.; Wang, K.; Cheng, L. Experiment and optimization of a new kind once-through heat recovery steam generator (HRSG) based on analysis of exergy and economy. Appl. Therm. Eng. 2017, 120, 402–415. [Google Scholar] [CrossRef]
- Mu, M.; Han, X.; Jiang, X. Combined fluidized bed retorting and circulating fluidized bed combustion system of oil shale: 3. Exergy analysis. Energy 2018, 151, 930–939. [Google Scholar] [CrossRef]
- Han, X.; Niu, M.; Jiang, X. Combined fluidized bed retorting and circulating fluidized bed combustion system of oil shale: 2. Energy and economic analysis. Energy 2014, 74, 788–794. [Google Scholar] [CrossRef]
- Chen, X.; Zhao, T.; Zhang, M.; Chen, Q. Entropy and entransy in convective heat transfer optimization: A review and perspective. Int. J. Heat Mass Transf. 2019, 137, 1191–1220. [Google Scholar] [CrossRef]
- Liu, J.; Jiang, Y.; Wang, B.; He, S. Assessment and optimization assistance of entropy generation to air-side comprehensive performance of fin-and-flat tube heat exchanger. Int. J. Therm. Sci. 2019, 138, 61–74. [Google Scholar] [CrossRef]
- Qian, S.; Huang, L.; Aute, V.; Hwang, Y.; Radermacher, R. Applicability of entransy dissipation based thermal resistance for design optimization of two-phase heat exchangers. Appl. Therm. Eng. 2013, 55, 140–148. [Google Scholar] [CrossRef]
- Guo, Z.Y.; Liu, X.B.; Tao, W.Q.; Shah, R.K. Effectiveness–thermal resistance method for heat exchanger design and analysis. Int. J. Heat Mass Transf. 2010, 53, 2877–2884. [Google Scholar] [CrossRef]
- Moffat, R.J. Describing the uncertainties in experimental results. Exp. Therm. Fluid Sci. 1988, 1, 3–17. [Google Scholar] [CrossRef]
- Kline, S.J. Describing Uncertainties in Single-Sample Experiments. Mech. Eng. 1953, 75, 3–8. [Google Scholar]
- Wang, S.; Jiang, X.; Han, X.; Tong, J. Investigation of Chinese oil shale resources comprehensive utilization performance. Energy 2012, 42, 224–232. [Google Scholar] [CrossRef]
- Yan, J.W.; Jiang, X.M.; Han, X.X. Study on the Characteristics of the Oil Shale and Shale Char Mixture Pyrolysis. Energy Fuels 2009, 23, 5792–5797. [Google Scholar] [CrossRef]
- Pan, L.; Dai, F.; Li, G.; Liu, S. A TGA/DTA-MS investigation to the influence of process conditions on the pyrolysis of Jimsar oil shale. Energy 2015, 86, 749–757. [Google Scholar] [CrossRef]
- Cheikh Moine, E.; Groune, K.; El Hamidi, A.; Khachani, M.; Halim, M.; Arsalane, S. Multistep process kinetics of the non-isothermal pyrolysis of Moroccan Rif oil shale. Energy 2016, 115, 931–941. [Google Scholar] [CrossRef]
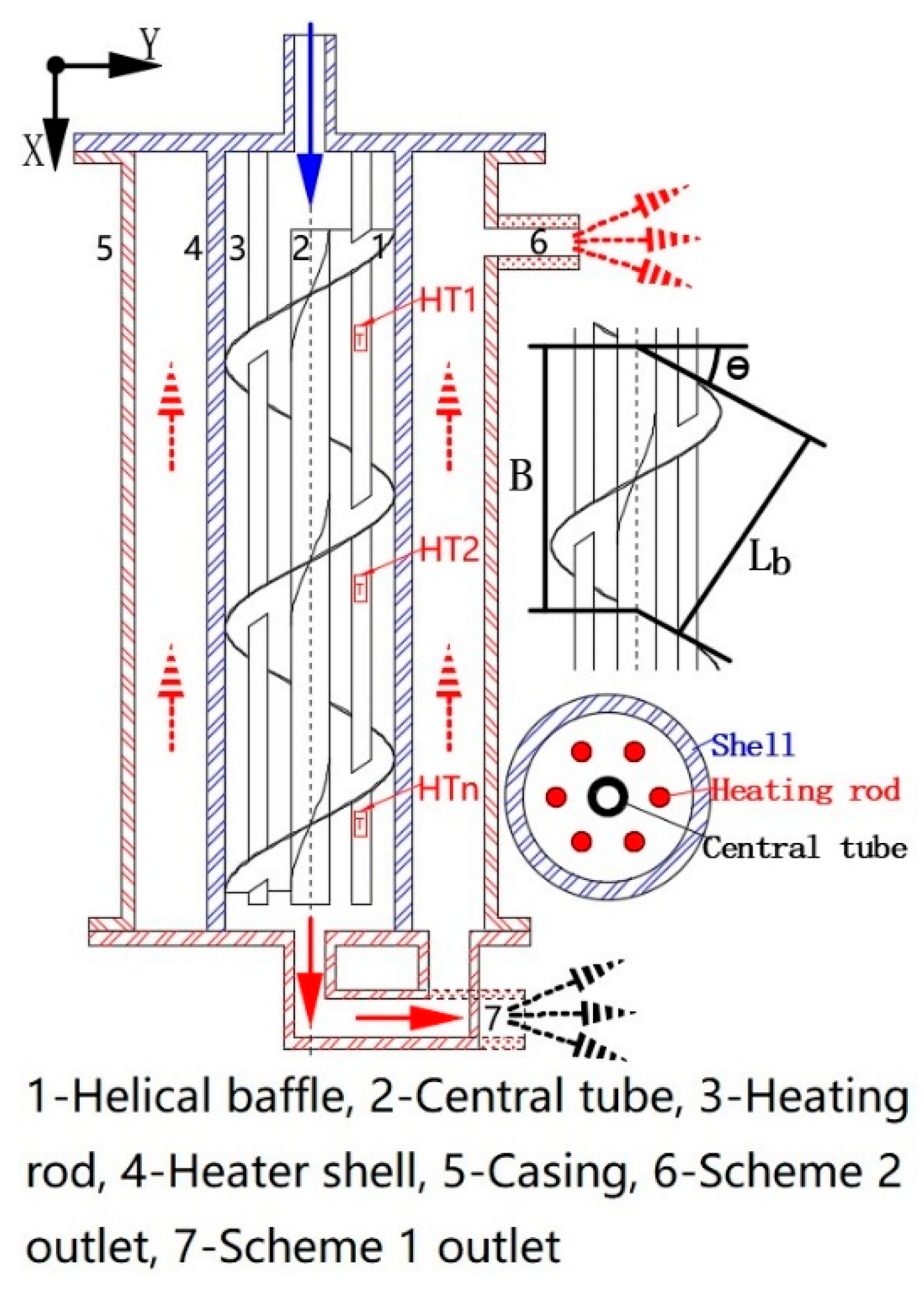

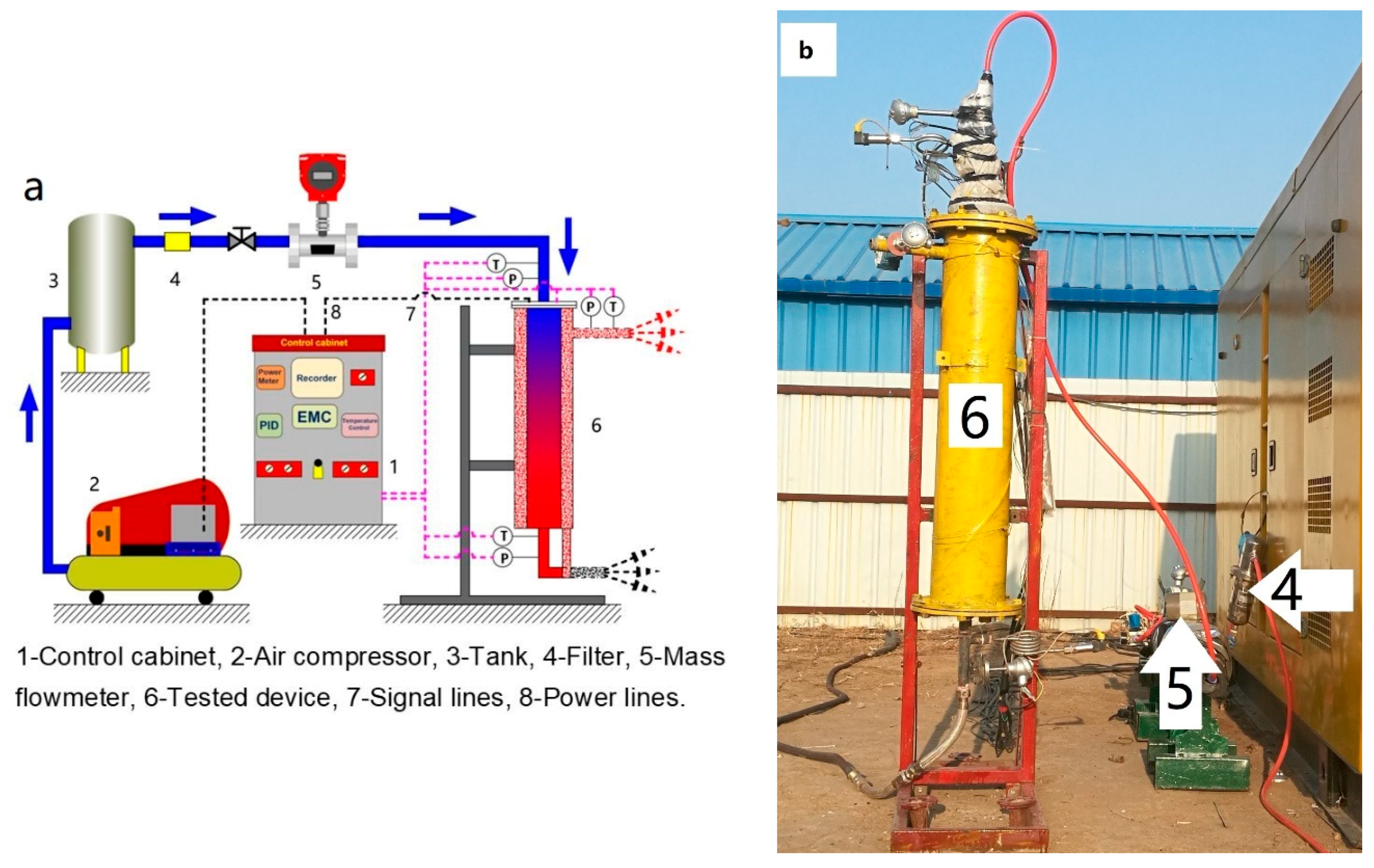
| Heater | Pitch (mm) | Locations on Heating Rod Along X Axis (mm) |
|---|---|---|
| H50 | 50 | 50, 190, 390, 590, 790, 990 |
| H160 | 160 | 150, 310, 470, 630, 790, 950 |
| H210 | 210 | 120, 330, 540, 750, 960 |
| Design Pressure Value (Pa) | Design Temperature Value (°C) | ||
|---|---|---|---|
| 1000 | 2.00 | 0–100 | 1.00 |
| 10,000 | 1.30 | 300 | 1.60 |
| 50,000–700,000 | 1.00 | 500 | 2.10 |
| Uncertainty Item | Symbol | Unit | Value |
|---|---|---|---|
| Actual power | % | ±(1.00–1.25) | |
| Mass flow rate | % | ±(0.16–0.24) | |
| Surface temperature | % | ±(0.23–0.26) | |
| Inlet temperature | % | ±(0.16–0.21) | |
| Outlet temperature | % | ±(0.15–0.18) | |
| Heat transfer coefficient | % | ±(3.68–5.71) | |
| Heat transfer factor | % | ±(2.05–2.63) | |
| Pressure drop | % | ±(0.15–0.19) | |
| Friction factor | % | ±(2.17–2.59) |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guo, W.; Wang, Z.; Sun, Y.; Lü, X.; Wang, Y.; Deng, S.; Li, Q. Effects of Packer Locations on Downhole Electric Heater Performance: Experimental Test and Economic Analysis. Energies 2020, 13, 377. https://doi.org/10.3390/en13020377
Guo W, Wang Z, Sun Y, Lü X, Wang Y, Deng S, Li Q. Effects of Packer Locations on Downhole Electric Heater Performance: Experimental Test and Economic Analysis. Energies. 2020; 13(2):377. https://doi.org/10.3390/en13020377
Chicago/Turabian StyleGuo, Wei, Zhendong Wang, Youhong Sun, Xiaoshu Lü, Yuan Wang, Sunhua Deng, and Qiang Li. 2020. "Effects of Packer Locations on Downhole Electric Heater Performance: Experimental Test and Economic Analysis" Energies 13, no. 2: 377. https://doi.org/10.3390/en13020377
APA StyleGuo, W., Wang, Z., Sun, Y., Lü, X., Wang, Y., Deng, S., & Li, Q. (2020). Effects of Packer Locations on Downhole Electric Heater Performance: Experimental Test and Economic Analysis. Energies, 13(2), 377. https://doi.org/10.3390/en13020377