Development of a Tool for Optimizing Solar and Battery Storage for Container Farming in a Remote Arctic Microgrid
Abstract
1. Introduction
2. Container Farming
3. Methods
3.1. Container Farm Load Data
3.2. Model Summary
3.3. List of Model Simulation Cases
4. Results and Discussion
4.1. Base Case Simulations
4.1.1. Baseline Simulation
4.1.2. Solar and Storage Simulations
4.1.3. Lighting Simulations
4.1.4. Sensitivity Analysis for FEWMORE Solar Simulation
4.2. Dispatchability Case
4.2.1. Baseline Simulation
4.2.2. Solar and Storage Simulations
4.2.3. Demand-Side Management (DSM)
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A. Model Inputs and Outputs
Appendix A.1. Time Series Inputs
- Electric Load profile (lt) [kW]
- ○
- Base Case: Collected profile from CropBox operation for one year in Whitehorse, Yukon
- ○
- Dispatchability Case: Synthetic profile disaggregated by load
- Ambient Temperature profile (Tamb,t) [°C]
- Ambient humidity ratio (RHt) [kgH2O / kgdryair]
- Solar Yield profile (st) [kWAC / kWpDC installed]
Appendix A.2. Economic Inputs
- Grid Price (unsubsidized): CG = $0.67/kWh
- Project Lifetime: y = 20 years (for all equipment, except battery storage, which has a 10-year lifetime)
- Real Discount Rate: 3%
- Real Grid Escalation Rate: 3%
- Solar Capacity Cost (installed): CS = $4500/kW
- Solar Operation & Maintenance (O&M) Cost: OS = $50/kW/yr
- Capacity cost of battery inverter (installed): CI =$1000/kW
- Capacity cost of battery storage (installed): CE =$1000/kWh
- Battery O&M Cost: $0.005/kWhthroughput
Appendix A.3. Technology Inputs
- Battery Round-Trip Efficiency: 90%
- Battery Depth-of-Discharge: DOD = 80%
- Battery Self-Discharge Rate: SD = 0.03%/hr
- Container Farm Size: 2.4m × 2.4m × 12.2m (8ft × 8 ft × 40ft)
- Container Insulation: R = 96.5 W/m2-K (17 [1/(Btu/hr-ft2-oF)])
- Heating Efficiency: η = 0.8
- Cooling Energy-Efficiency Ratio (EER) = 3.22 (Wtherm/WAC) (11 [Btu/hr/WAC])
Appendix A.4. Model Outputs
- Capacity Planning
- ○
- Capacity of solar array [kW]
- ○
- Capacity of battery storage [kWh]
- ○
- Capacity of battery inverter [kW]
- Dispatch Scheduling
- ○
- Time series of solar output [kW]
- ○
- Time series of solar curtailment [kW]
- ○
- Time series of grid purchases [kW]
- ○
- Time series of battery charging/discharging [kW]
- ○
- Time series of demand-side management strategies of specific load [kW]
- Total Energy Output
- ○
- Amount of grid electricity consumed [MWh/yr]
- ○
- Amount of solar electricity generated and curtailed [MWh/yr]
- Total Project Cost Objective
- ○
- Total costs of installing and maintaining solar and storage system
- ○
- Cost of replacing battery storage system in Year 10
- ○
- Total cost of grid electricity purchased
Appendix B. Model Condensed Mathematical Form
Appendix B.1. Decision Variables
- Amount of solar capacity to install (S) [kW]
- Amount of battery storage capacity to install (E) [kWh]
- Amount of battery inverter capacity to install (I) [kW]
- Dispatch time series of battery storage (charge and discharge) (E in/out,t) [kWh]
- Dispatch time series of solar electricity curtailment (Rt) [kWh]
- Dispatch time series of grid electricity purchases (Gt) [kWh]
- Dispatch time series of heating/cooling system (for Dispatchability Case) (Qheat/cool,t) [kWh]
- Dispatch time series of ventilation system (for Dispatchability Case) (Vt) [air changes per hour]
- Dispatch time series of dehumidification (for Dispatchability Case) (Wt) [binary]
Appendix B.2. Objective
- Minimize total project costs of container farm energy operations over lifetime:where the summation is over all hourly time steps, t, of a year, y, which are summed over the 20-year lifetime as part of a discounted cash flow.
Appendix B.3. Defined Variables
- Current amount of energy stored in battery storage:where c and d are the charging and discharging efficiencies, respectively, and the product of which results in a round-trip efficiency of 90%.SEt+1 = SD*[c*Ein,t – (1/d)*+Eout,t]
Appendix B.4. Constraints
- Overall electricity flows must be balanced in each time step:Gt + St + Eout,t = lt + Ein,t + Rt
- Storage state of charge must lie within limits [kWh], given an initial state of charge of 0%:0 < SEt < DOD*E
- Battery charging/discharging cannot exceed power requirements of inverter [kW]:0 < Ein/out,t < I
- Sensible thermal energy must be balanced at all times:where Qmech,t is the heat gain of all equipment in time step t; Qcond,t is the heat loss due to conduction through the container envelope; Qvent/inf,t is the heat loss due to ventilation and infiltration; and QET,t is the heat loss due to evaporative cooling from plant evapotranspiration (See Appendix C).η*Qheat,t + Qmech,t = EER*Qcool,t + Qvent/inf,t + Qcond,t + QET,t
- Latent thermal energy must be balanced at all times by balancing moisture flows in the container:where LET,t is the moisture, in liters of water, emitted by plants; Ldehum,t is the moisture removed by the dehumidifier; and Lvent/inf,t is the moisture added or removed via air exchanges with the ambient environment.LET,t = Ldehum,t + Lvent/inf,t
Appendix C. Container Farm Energy Modeling
Appendix C.1. Conduction
Appendix C.2. Ventilation/Infiltration
Appendix C.3. Evapotranspiration
References
- Holdmann, G.P.; Wies, R.W.; Vandermeer, J.B. Renewable energy integration in Alaska’s remote islanded microgrids: Economic drivers, technical strategies, technological niche development, and policy implications. Proc. IEEE 2019, 107, 1820–1837. [Google Scholar] [CrossRef]
- Tracking SDG7: The Energy Progress Report (2019); The World Bank Group: Washington, DC, USA, 2019.
- Ma, T.; Yang, H.; Lu, L. Performance evaluation of a stand-alone photovoltaic system on an isolated island in Hong Kong. Appl. Energy 2013, 112, 663–672. [Google Scholar] [CrossRef]
- Jacobson, M.Z.; Delucchi, M.A.; Cameron, M.A.; Coughlin, S.J.; Hay, C.A.; Manogaran, I.P.; Shu, Y.; von Krauland, A.-K. Impacts of green new deal energy plans on grid stability, costs, jobs, health, and climate in 143 countries. One Earth 2019, 1, 449–463. [Google Scholar] [CrossRef]
- Harish, V.S.K.V.; Kumar, A. Demand side management in India: Action plan, policies and regulations. Renew. Sustain. Energy Rev. 2014, 33, 613–624. [Google Scholar] [CrossRef]
- Pina, A.; Silva, C.; Ferrão, P. The impact of demand side management strategies in the penetration of renewable electricity. Energy 2012, 41, 128–137. [Google Scholar] [CrossRef]
- Lovins, A.B. Reliably integrating variable renewables: Moving grid flexibility resources from models to results. Electr. J. 2017, 30, 58–63. [Google Scholar] [CrossRef]
- Snyder, E.H.; Meter, K. Food in the last frontier: Inside alaska’s food security challenges and opportunities. Environment 2015, 57, 19–33. [Google Scholar] [CrossRef]
- Bergen, M. Personal Communication; Kotzebue Electric Association: Kotzebue, AK, USA, 2020. [Google Scholar]
- CropBox: A Farm in a Shipping Container. Available online: https://cropbox.co/ (accessed on 27 July 2020).
- The Impact of “Plant Factories” on the Electric Grid | Greentech Media. Available online: https://www.greentechmedia.com/articles/read/the-impact-of-plant-factories-on-the-electric-grid (accessed on 11 June 2020).
- Houtman, J.A. Purdue E-Pubs Design and Plan of a Modified Hydroponic Shipping Container for Research Part of the Agriculture Commons, Art and Design Commons, and the Bioresource and Agricultural Engineering Commons Recommended Citation. Master’s Thesis, Purdue University, West Lafayette, IN, USA, 2016. [Google Scholar]
- Sparks, R. Mapping and Analyzing Energy Use and Efficiency in a Modified Hydroponic Shipping Container. Master’s Thesis, Purdue University, West Lafayette, IN, USA, 2016. [Google Scholar]
- Zia, M.F.; Elbouchikhi, E.; Benbouzid, M. Microgrids energy management systems: A critical review on methods, solutions, and prospects. Appl. Energy 2018, 222, 1033–1055. [Google Scholar] [CrossRef]
- Olatomiwa, L.; Mekhilef, S.; Ismail, M.S.; Moghavvemi, M. Energy management strategies in hybrid renewable energy systems: A review. Renew. Sustain. Energy Rev. 2016, 62, 821–835. [Google Scholar] [CrossRef]
- Teichgraeber, H.; Brandt, A.R. Clustering methods to find representative periods for the optimization of energy systems: An initial framework and comparison. Appl. Energy 2019, 239, 1283–1293. [Google Scholar] [CrossRef]
- Hafez, O.; Bhattacharya, K. Optimal planning and design of a renewable energy based supply system for microgrids. Renew. Energy 2012, 45, 7–15. [Google Scholar] [CrossRef]
- Singh, S.; Singh, M.; Kaushik, S.C. Feasibility study of an islanded microgrid in rural area consisting of pv, wind, biomass and battery energy storage system. Energy Convers. Manag. 2016, 128, 178–190. [Google Scholar] [CrossRef]
- Shoeb, M.; Shafiullah, G. Renewable energy integrated islanded microgrid for sustainable irrigation—A bangladesh perspective. Energies 2018, 11, 1283. [Google Scholar] [CrossRef]
- García Tapia, V. Hybrid Renewable Energy System for Controlled Environment Agriculture. Master’s Thesis, KTH School of Industrial Engineering and Management, Stockholm, Sweden, 2018. [Google Scholar]
- Anderson, K.; Elgqvist, E. Evaluate Distributed Energy Technologies for Cost Savings and Resilience With REopt Lite Economic Sizing and Dispatch Resilience Evaluation When To Use REopt Lite; NREL: Golden, CO, USA, 2020. [Google Scholar]
- Hale, E.; Stoll, B.; Mai, T. Capturing the Impact of Storage and Other Flexible Technologies on Electric System Planning; NREL: Golden, CO, USA, 2016. [Google Scholar]
- Neves, D.; Pina, A.; Silva, C.A. Demand response modeling: A comparison between Tools. Appl. Energy 2015, 146, 288–297. [Google Scholar] [CrossRef]
- Neves, D.; Silva, C.A. Optimal electricity dispatch on isolated mini-grids using a demand response strategy for thermal storage backup with genetic algorithms. Energy 2015, 82, 436–445. [Google Scholar] [CrossRef]
- Zhang, S.; Schulman, B. A numerical model for simulating the indoor climate inside the growing chambers of vertical farms with case studies. Int. J. Environ. Sci. Dev. 2017, 8, 728–735. [Google Scholar] [CrossRef]
- Karan, E.; Asadi, S.; Mohtar, R.; Baawain, M. Towards the optimization of sustainable food-energy-water systems: A stochastic approach. J. Clean. Prod. 2018, 171, 662–674. [Google Scholar] [CrossRef]
- Arctic Town Grows Fresh Produce in Shipping Container Vertical Garden. Available online: https://inhabitat.com/agtech-start-up-plenty-plans-to-grow-hydroponic-peaches/ (accessed on 11 June 2020).
- Sæterbø, M. Arctic Agriculture by Using Fish Farming Waste in Northern Norway; UiT Norges arktiske universitet: Tromso, Norway, 2019. [Google Scholar]
- Bos-Jabbar, T. Personal Communication; ColdAcre Food Systems: Yukon, BC, Canada, 2020. [Google Scholar]
- Trane Technologies Inc. Engineers Newsletter Providing Insights for Today’s Hvac System Designer Volume 48-3 Indoor Agriculture: HVAC System Design Considerations. Available online: https://www.trane.tm/content/dam/Trane/Commercial/global/products-systems/education-training/engineers-newsletters/airside-design/admapn071en-082019.pdf (accessed on 20 June 2020).
- Commercial Dehumidifiers | Industrial Dehumidifiers | Quest. Available online: https://www.questclimate.com/ (accessed on 28 June 2020).
- Carbon Dioxide in Greenhouses. Available online: http://www.omafra.gov.on.ca/english/crops/facts/00-077.htm (accessed on 25 June 2020).
- Hachem-vermette, C.; Dara, C.; Kane, R. Towards net zero energy modular housing: A case study. Modul. Offsite Constr. Summit Proc. 2018. [Google Scholar] [CrossRef]
- Alaska Energy Authority. Personal Communication; Alaska Energy Authority: Anchorage, AK, USA, 2020. [Google Scholar]
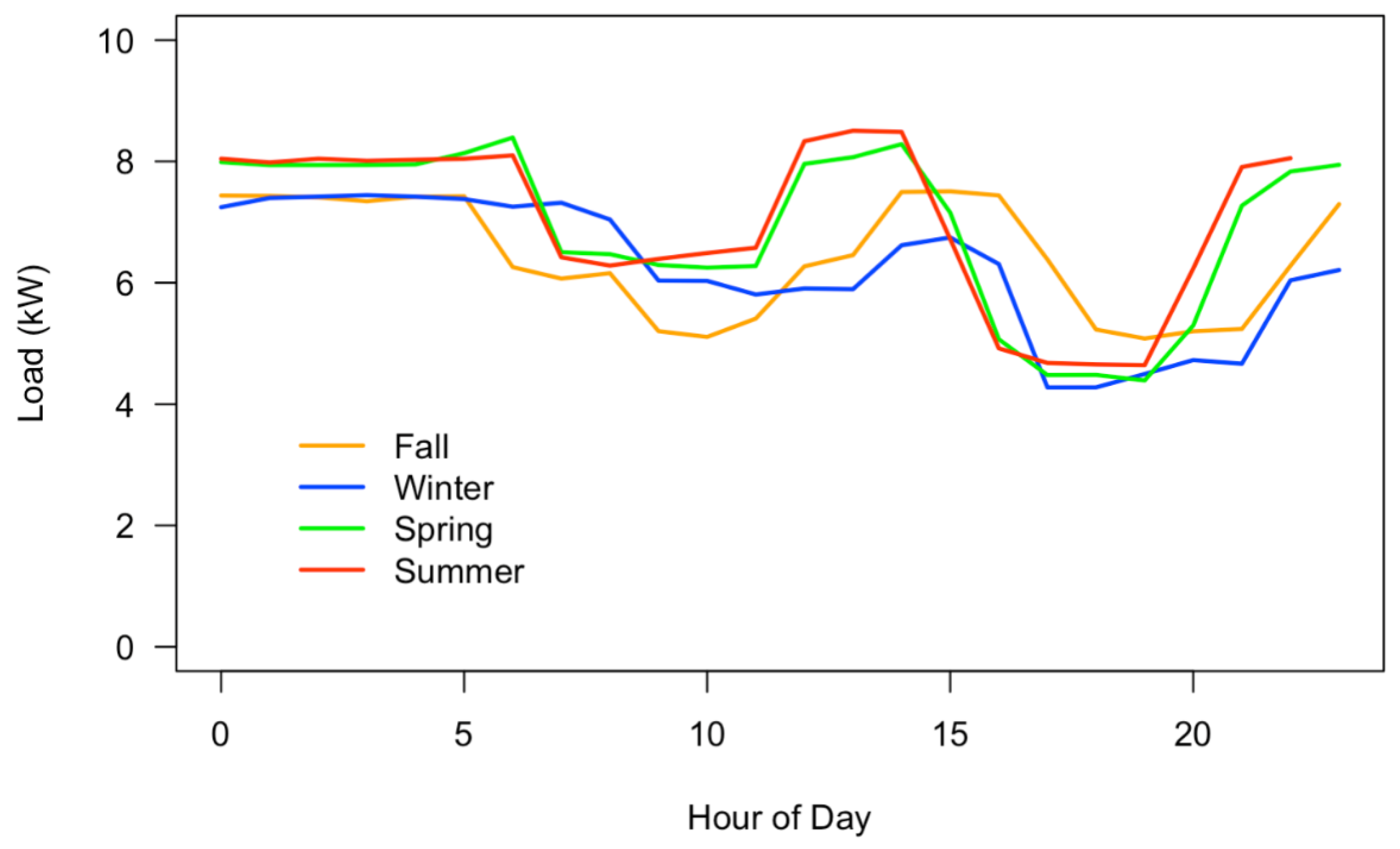
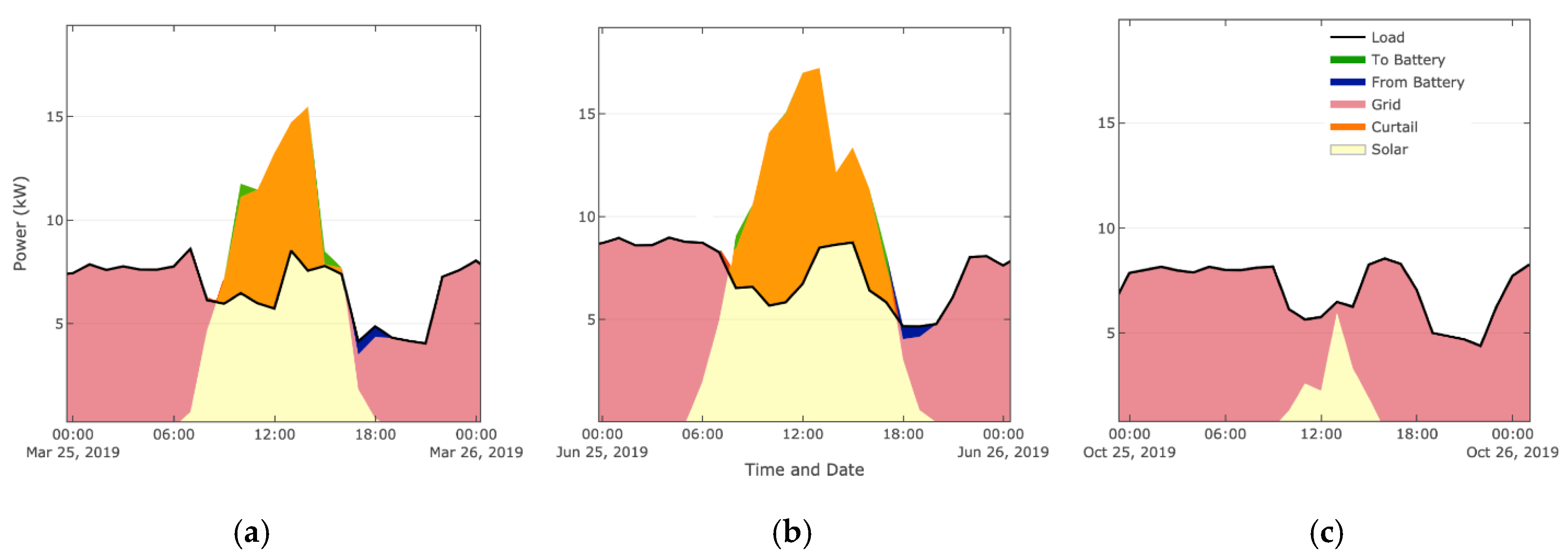
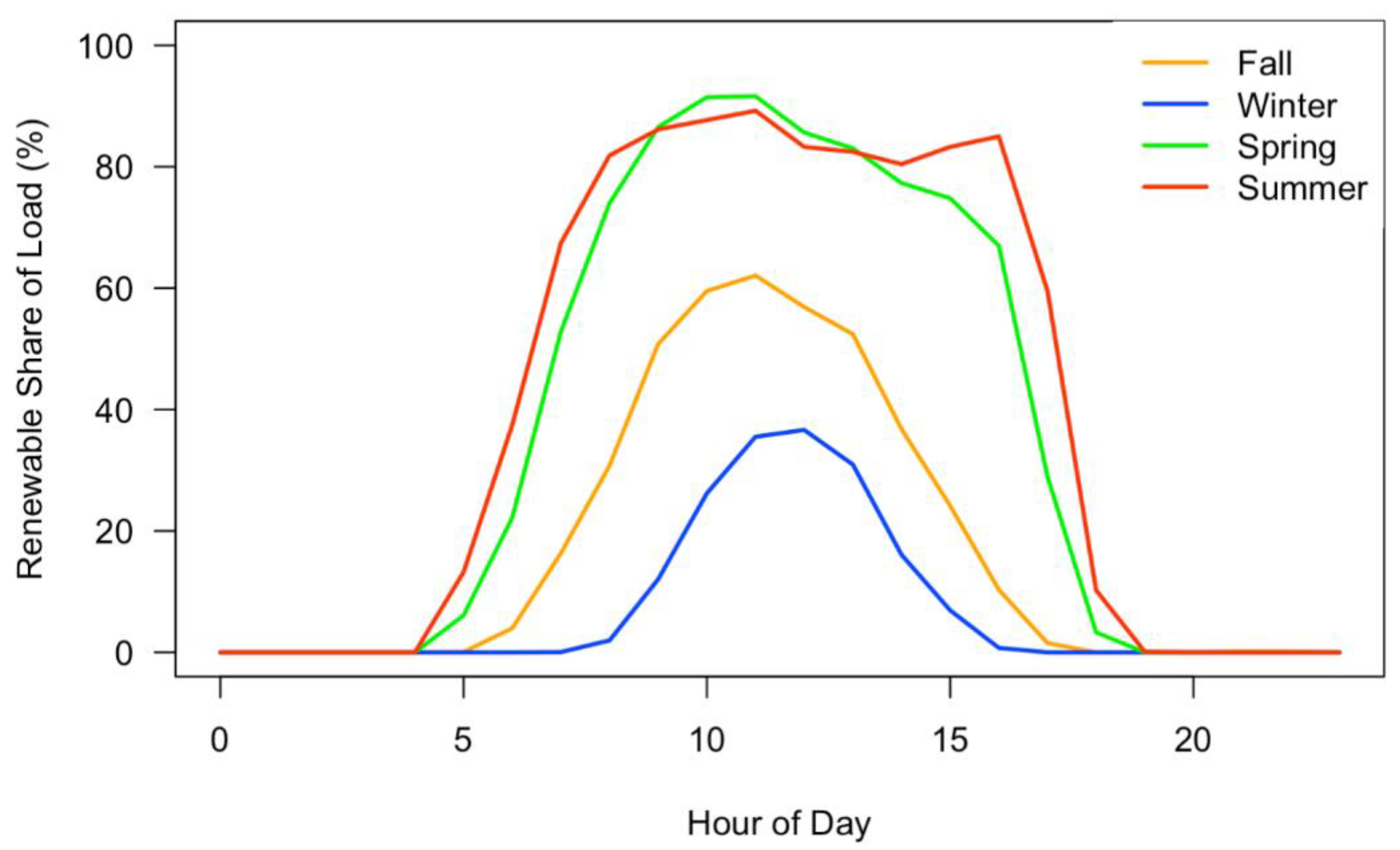
| Load | Power (W) | Duration |
|---|---|---|
| Air Circulation Fans | 220 | Always On |
| Water Pumps | 720 | Always On |
| Lighting | 4500 | 18 h/day |
| Heating/Cooling | 2000 | As needed to maintain 20 °C |
| Ventilation/Exhaust Fan | 110 | As needed |
| Dehumidification | 1500 | As needed to maintain 65–75% relative humidity |
| Base Case: | Dispatchability Case: | Model Notes |
|---|---|---|
| Collected | Synthetic Load Profile | |
| Load Profile | ||
| Baseline | Baseline | Only grid electricity is used (no optimization is performed) |
| Solar | Solar | Amount of solar capacity optimized |
| Solar & Storage | Solar & Storage | Amount of solar and battery/inverter capacity optimized |
| Lighting with Solar | - | Lighting is shifted to be symmetric around solar noon for Collected Load Profile and only solar is optimized |
| Lighting with Solar & Storage | - | Same as above, except both solar and storage are optimized |
| - | Ventilation | The number of air changes per hour (ACH) ventilated to provide cooling/dehumidification is optimized, and the amount of solar and storage is optimized |
| - | Dehumidification | Same as Ventilation simulation, except the operation of the dehumidifier (on/off) is also optimized |
| Model | FEWMORE | HOMER | ||||||
|---|---|---|---|---|---|---|---|---|
| Simulation Name | Baseline | Solar | Storage | Lighting | Baseline | Solar | Storage | Lighting |
| Total Cost (k$) | 783.3 | 675.1 | 675 | 674.9 | 783.4 | 725 | 725.7 | 710.4 |
| Produce Cost ($/kg) | $7.17 | $6.20 | $6.20 | $6.18 | $7.17 | $6.64 | $6.64 | $6.51 |
| Grid Energy (MWh/yr) | 58.4 | 44.3 | 44 | 44.2 | 58.4 | 47.7 | 47.6 | 46.5 |
| Solar (kW) | - | 17.1 | 17.5 | 17.3 | - | 15.6 | 15.6 | 15.8 |
| Storage (kWh) | - | - | 1.2 | - | - | - | 1 | - |
| Inverter (kW) | - | - | 0.5 | - | - | - | 0.66 | - |
| Simulation Name | ||||
|---|---|---|---|---|
| Output | Base | Solar | Ventilation | Dehumidification |
| Total Cost (k$) | 824 | 706 | 674 | 678 |
| Produce Cost ($/kg) | $7.55 | $6.47 | $6.18 | $6.23 |
| Grid Energy (MWh/yr) | 62.4 | 44.8 | 42.5 | 42.8 |
| Cooling Energy (MWh/yr) | 11.4 | 11.4 | 9 | 9.2 |
| Heating Energy (MWh/yr) | 0 | 0 | 0 | 0.5 |
| Solar (kW) | - | 21.5 | 21.3 | 21.4 |
| Storage (kWh) | - | - | 0 | 0 |
| Inverter (kW) | - | - | 0 | 0 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sambor, D.J.; Wilber, M.; Whitney, E.; Jacobson, M.Z. Development of a Tool for Optimizing Solar and Battery Storage for Container Farming in a Remote Arctic Microgrid. Energies 2020, 13, 5143. https://doi.org/10.3390/en13195143
Sambor DJ, Wilber M, Whitney E, Jacobson MZ. Development of a Tool for Optimizing Solar and Battery Storage for Container Farming in a Remote Arctic Microgrid. Energies. 2020; 13(19):5143. https://doi.org/10.3390/en13195143
Chicago/Turabian StyleSambor, Daniel J., Michelle Wilber, Erin Whitney, and Mark Z. Jacobson. 2020. "Development of a Tool for Optimizing Solar and Battery Storage for Container Farming in a Remote Arctic Microgrid" Energies 13, no. 19: 5143. https://doi.org/10.3390/en13195143
APA StyleSambor, D. J., Wilber, M., Whitney, E., & Jacobson, M. Z. (2020). Development of a Tool for Optimizing Solar and Battery Storage for Container Farming in a Remote Arctic Microgrid. Energies, 13(19), 5143. https://doi.org/10.3390/en13195143





