Energy Modeling of a Refiner in Thermo-Mechanical Pulping Process Using ANFIS Method
Abstract
1. Introduction
2. Thermo-Mechanical Pulping Process
3. Intelligent Method
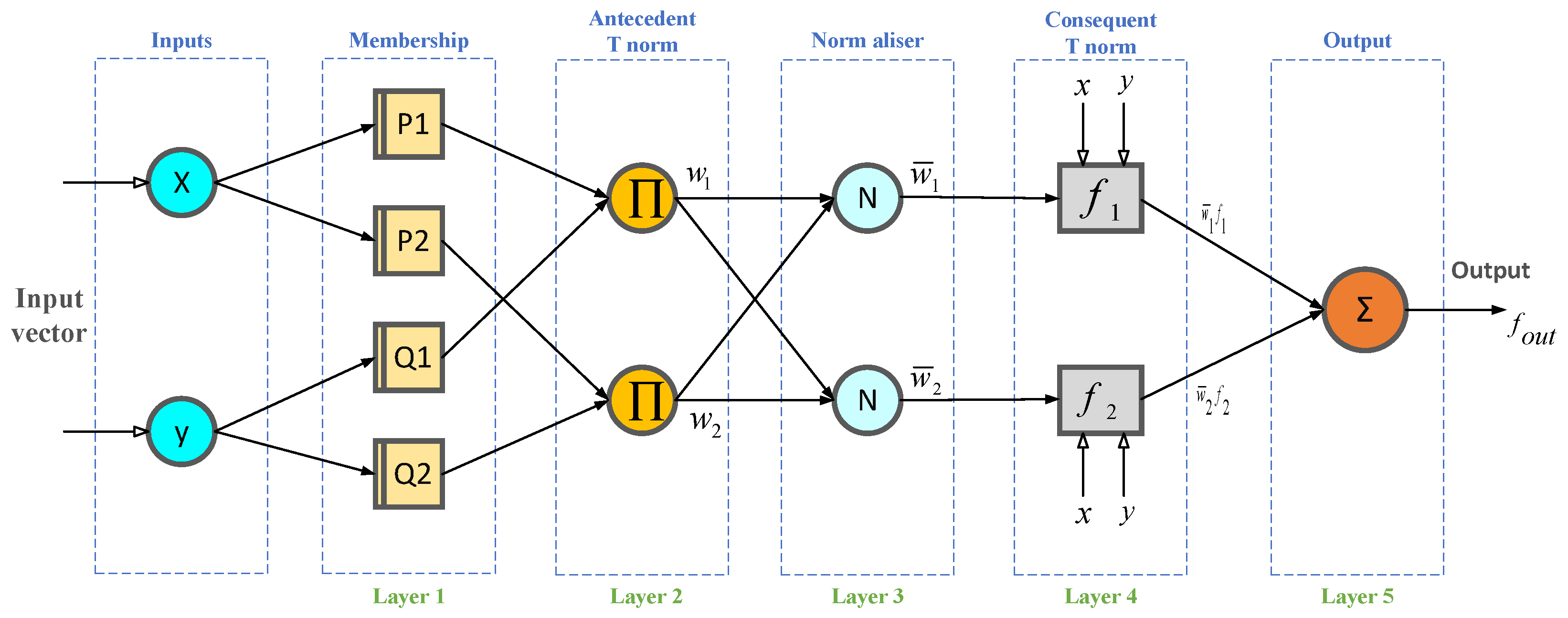
3.1. Adaptive Neuro-Fuzzy Inference System (ANFIS)
3.2. Biogeography-Based Optimization Algorithm (BBO)
3.3. Teaching Learning-Based Optimization Algorithm (TLBO)
3.4. Particle Swarm Optimization (PSO)
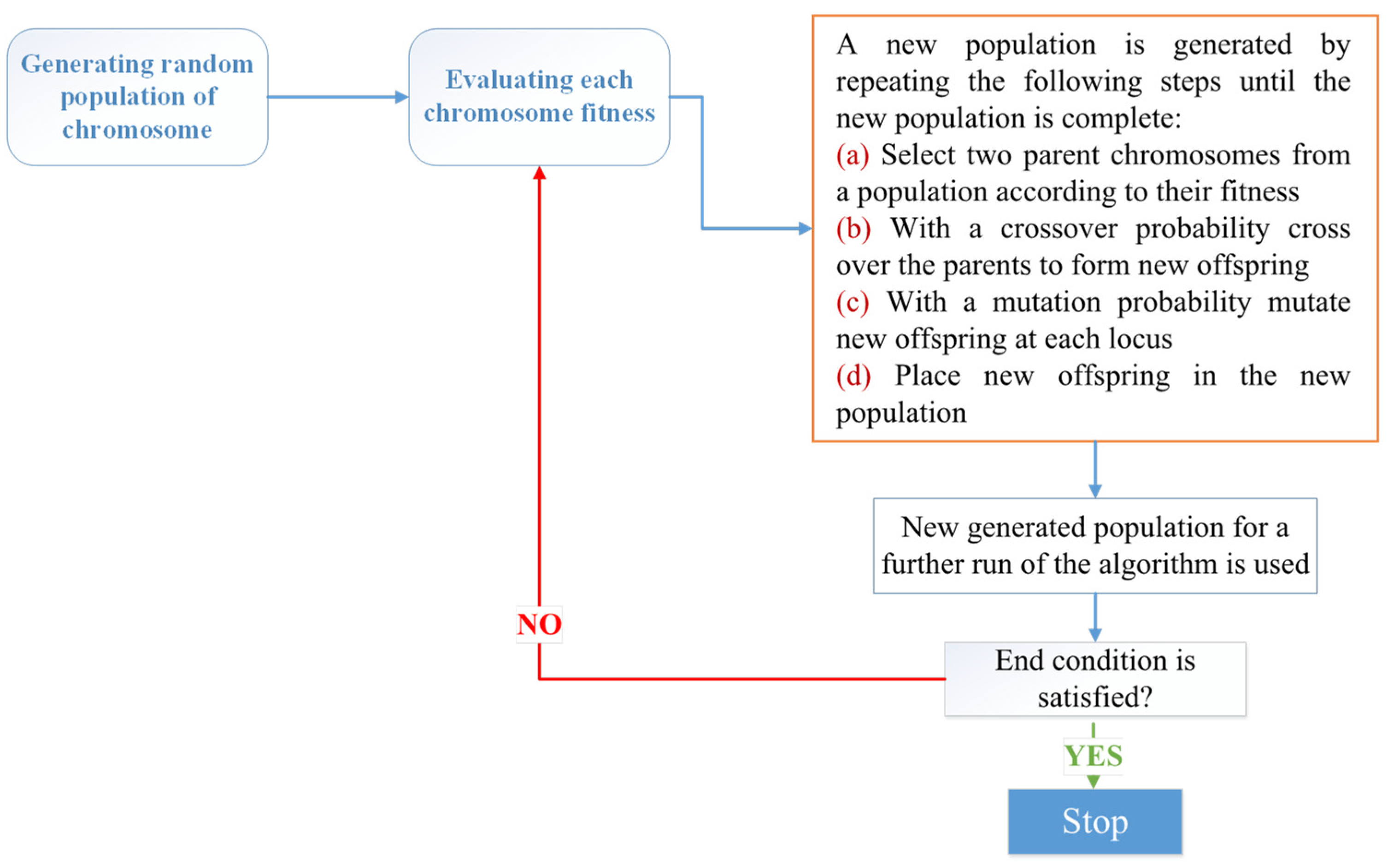
3.5. Genetic Algorithm (GA)
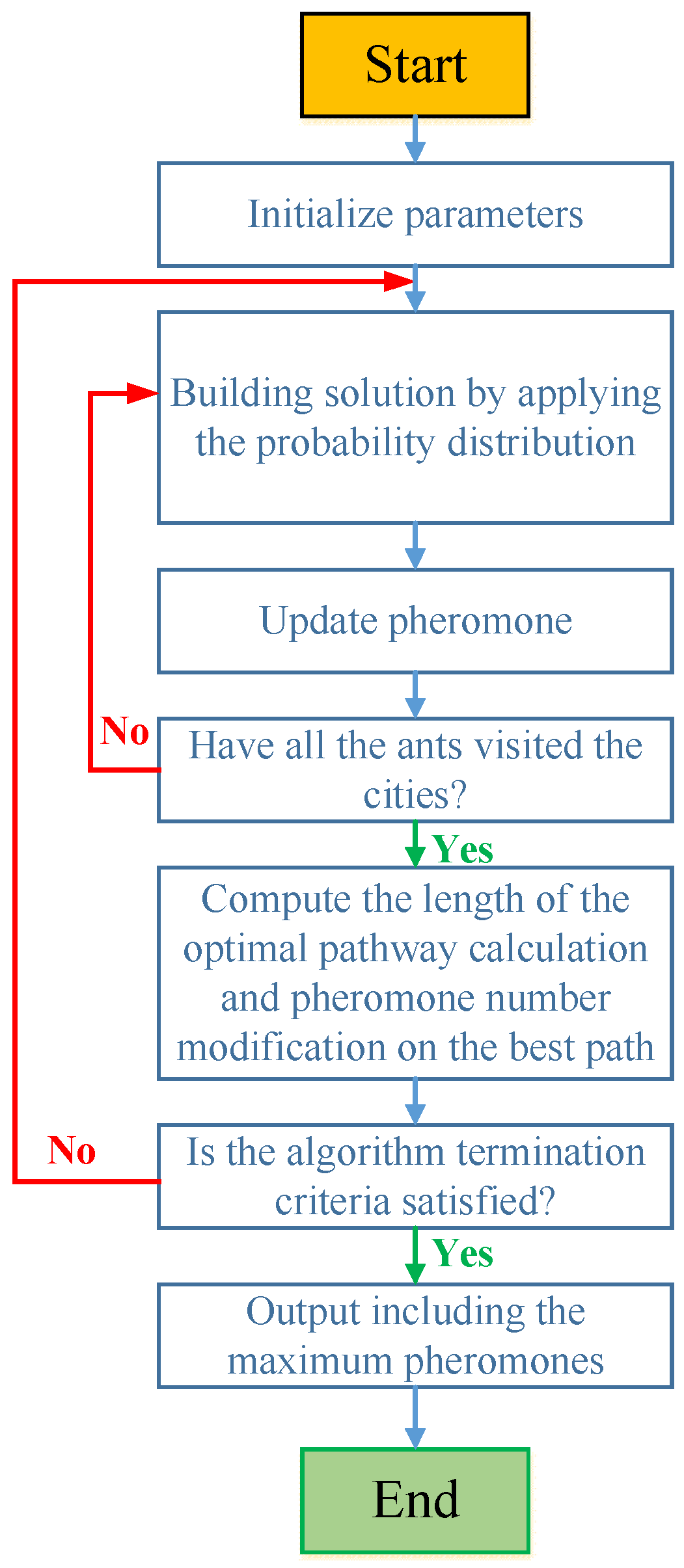
3.6. Ant Colony Optimization Algorithm (ACO)
3.7. Differential Evolution (DE)
3.8. The Proposed Hybrid Methods for the Refiner Simulation
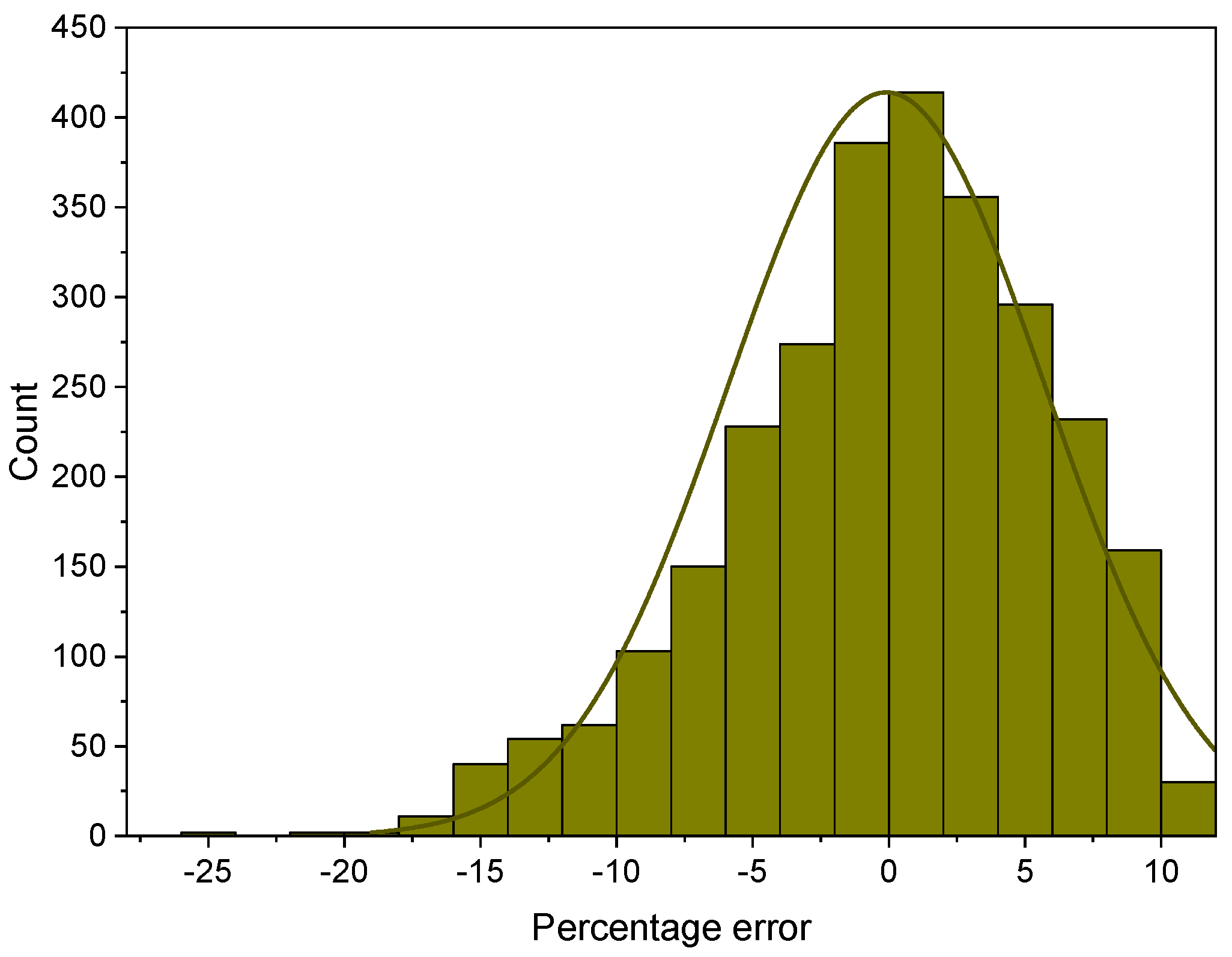
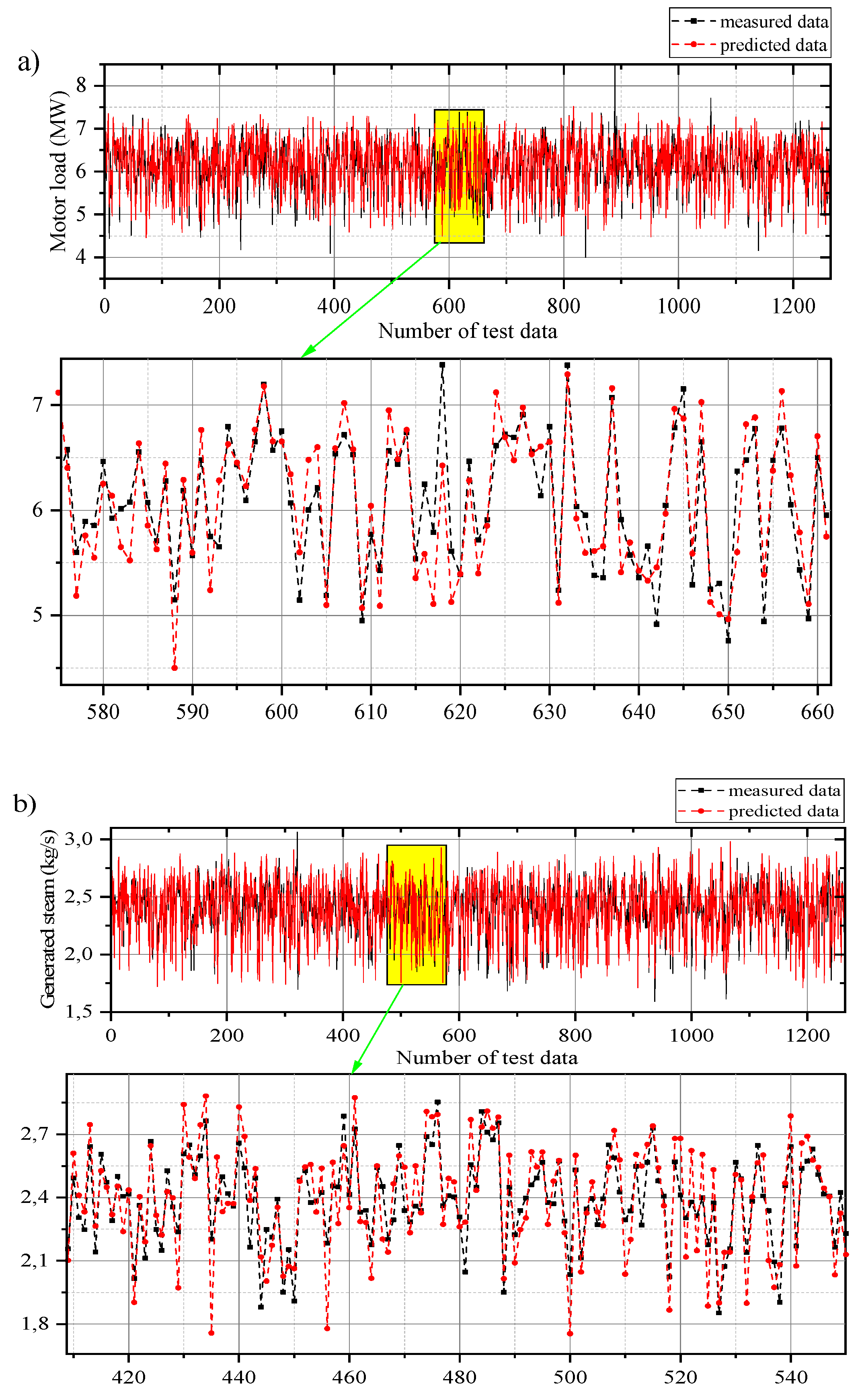
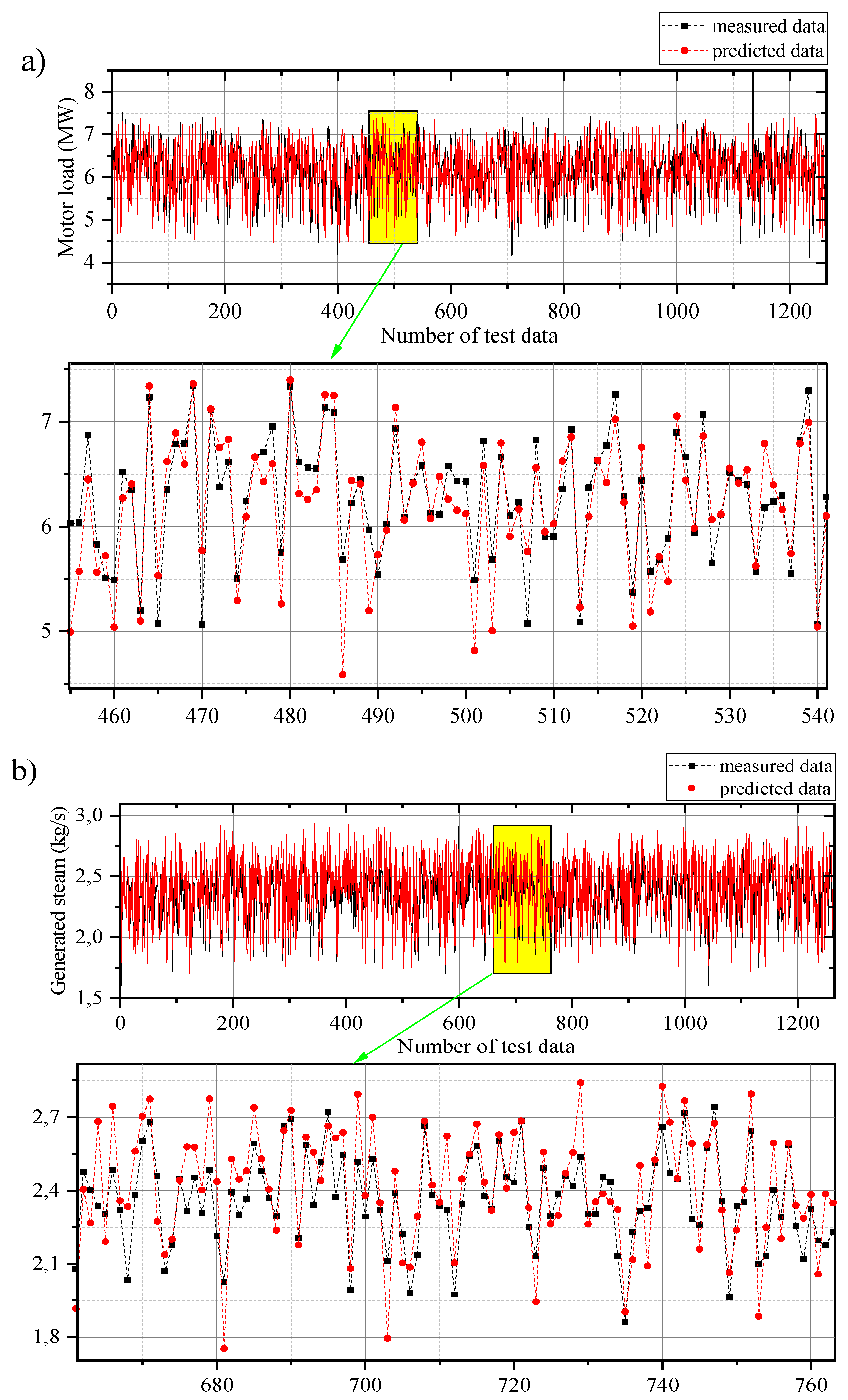
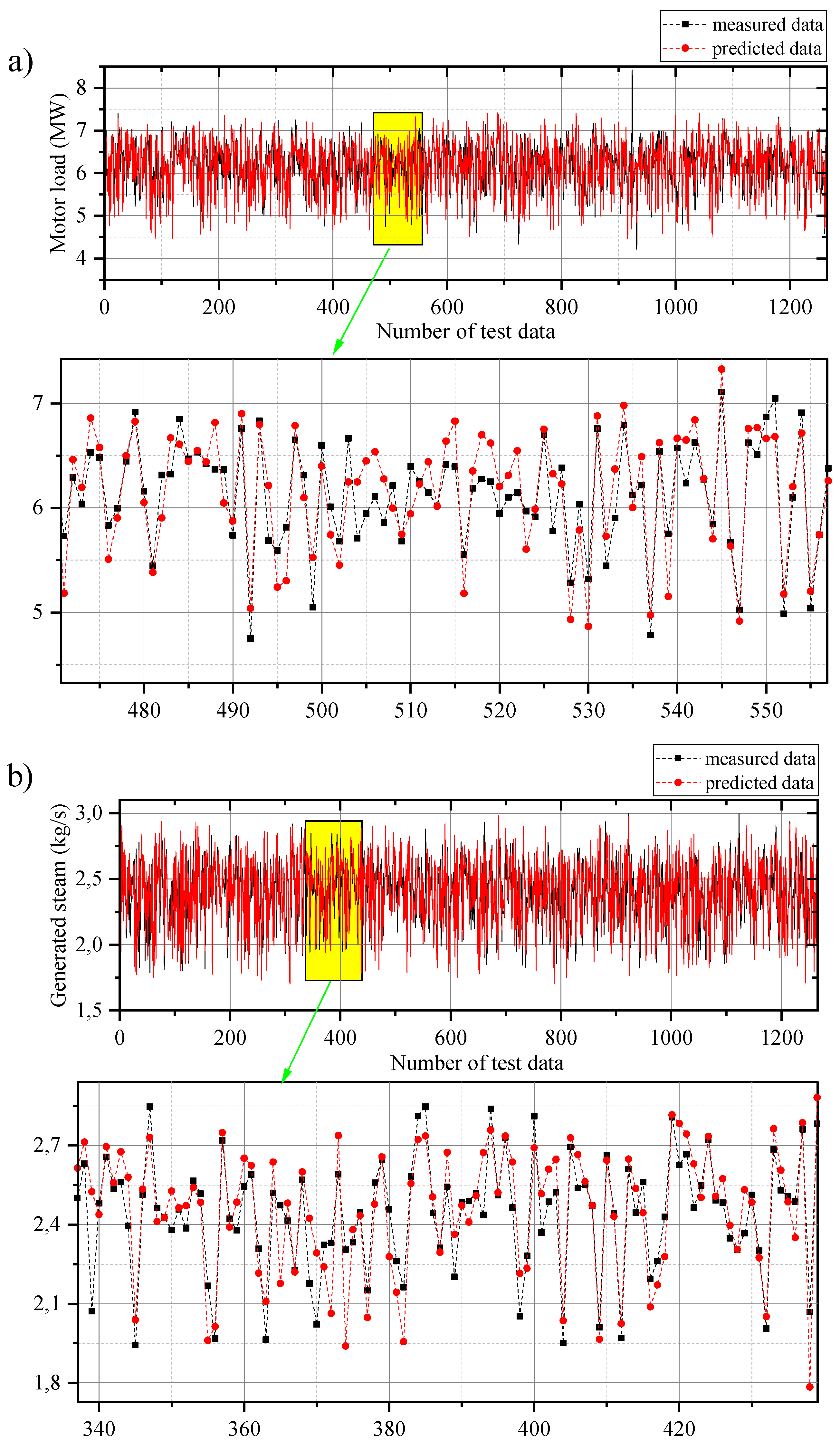
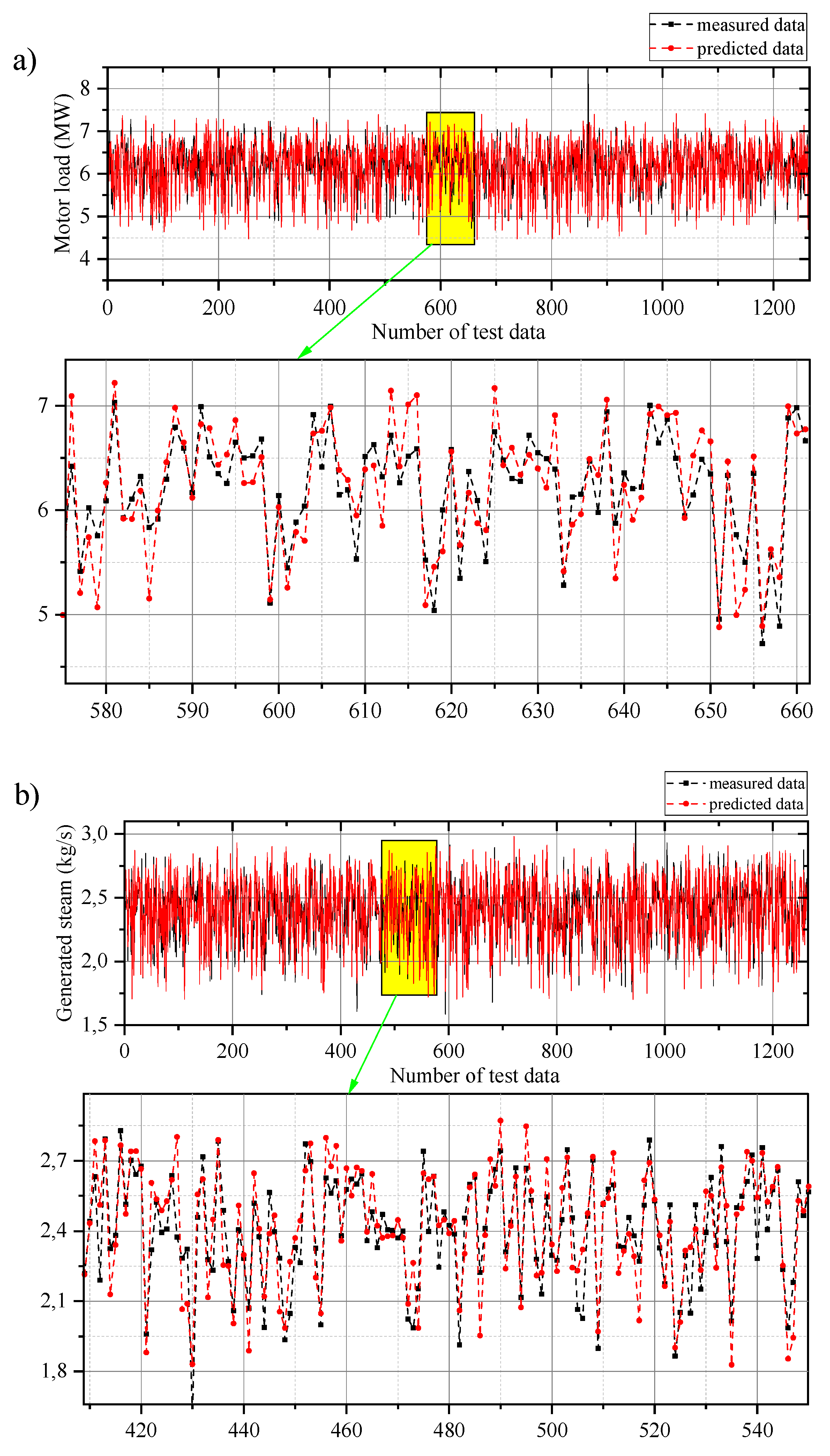
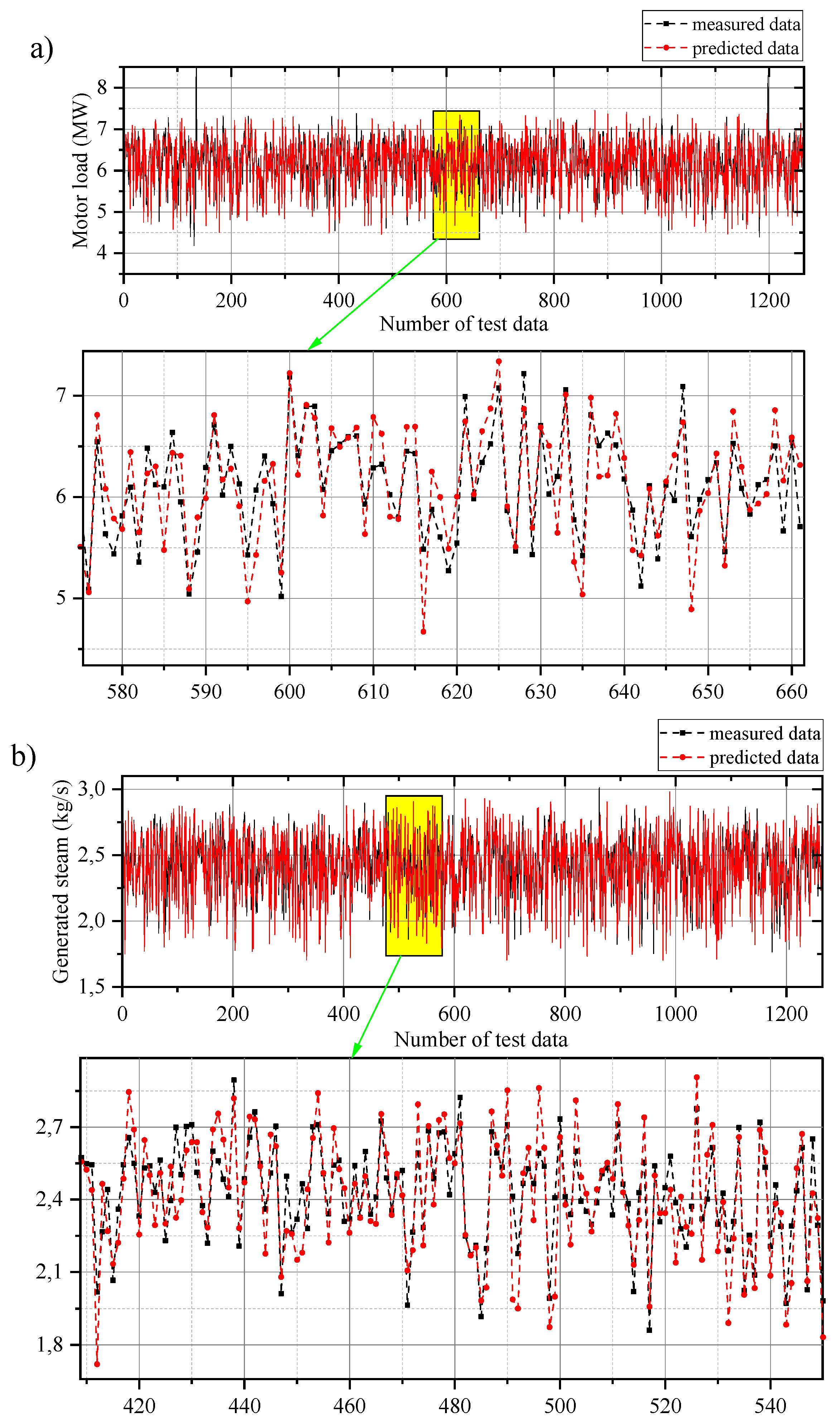
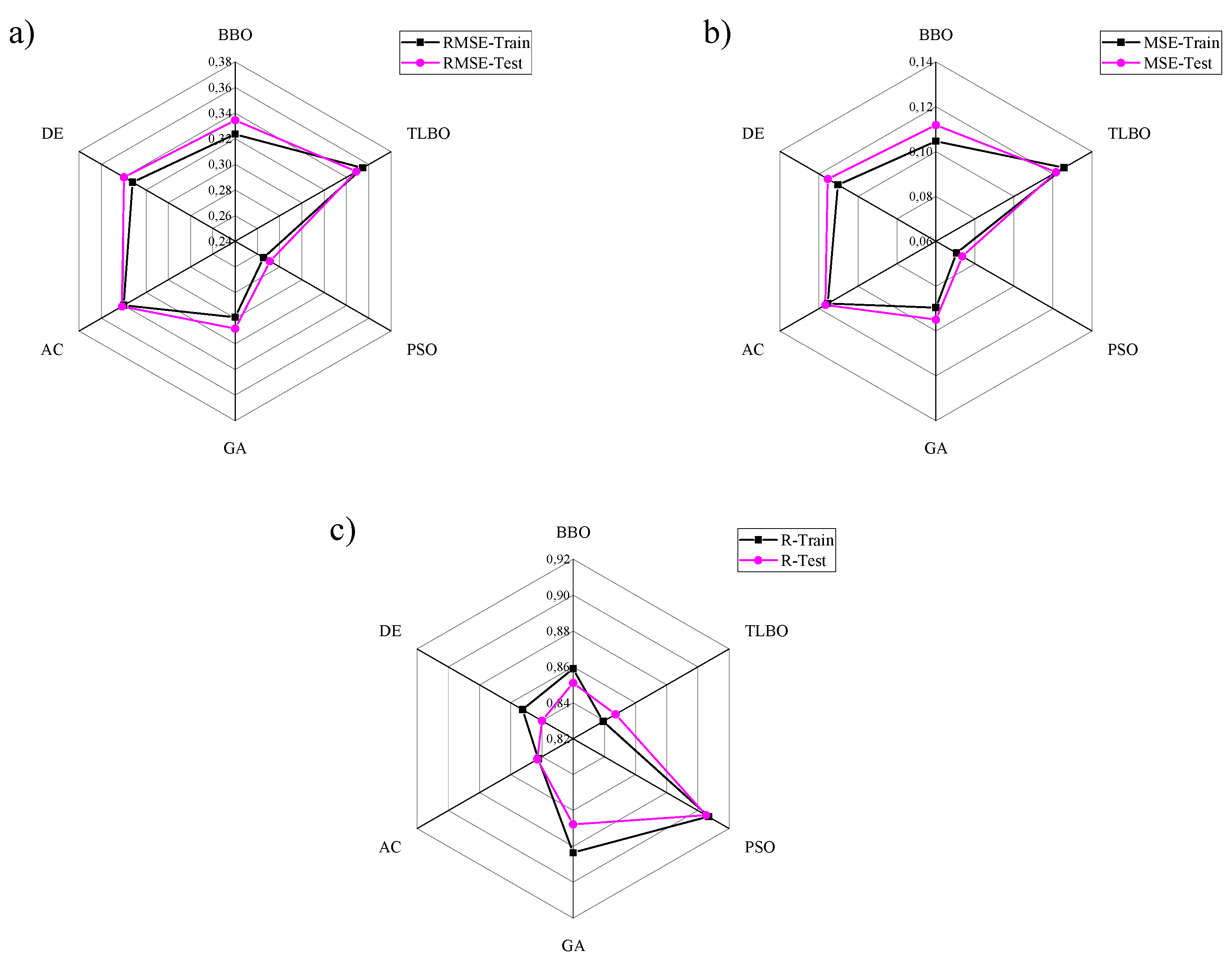
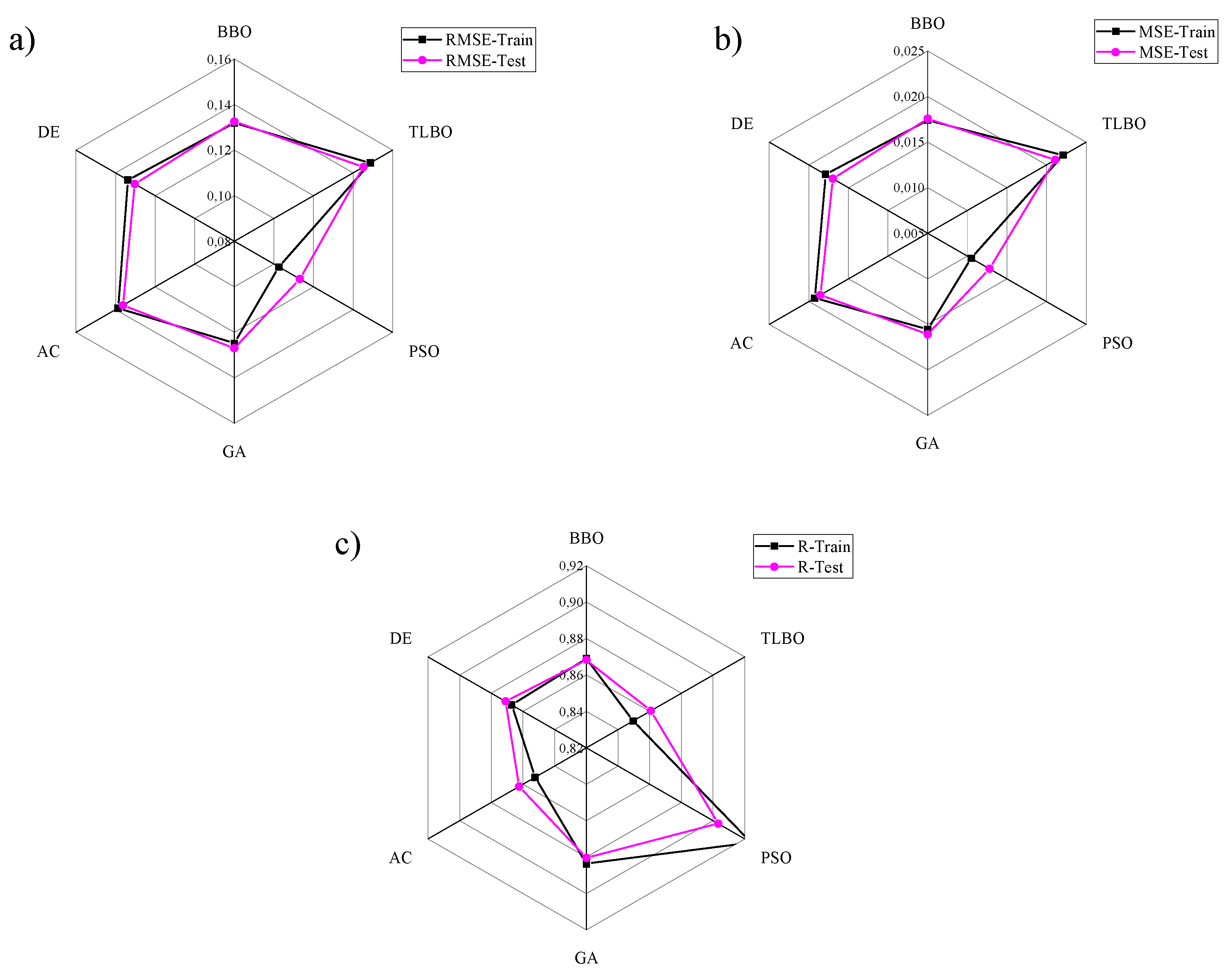
4. Results and Discussion
4.1. Data Validation
4.2. Models Comparison
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Nomenclature
| TMP | Thermo-mechanical pulping | Variables | |
| BBO | Biogeography-based optimization algorithm | MSE | Mean-square-error |
| GA | Genetic algorithm | RMSE | Root-mean-square error |
| PSO | Particle swarm optimization algorithm | MAPE | Mean-absolute percentage error |
| DE | Differential evolution | Correlation coefficient | |
| ACO | Ant colony optimization algorithm | Determination coefficient | |
| TLBO | Teaching learning-based optimization algorithm | Refining motor load | |
| ANFIS | Adaptive neuro-fuzzy inference system | Refining dilution water flow rate | |
| RBF | Radial basis function | Refining plate gap | |
| LC | Low consistency | Refining production rate |
References
- Talebjedi, B.; Behbahaninia, A. Availability analysis of an Energy Hub with CCHP system for economical design in terms of Energy Hub operator. J. Build. Eng. 2021, 33, 101564. [Google Scholar] [CrossRef]
- Bajpai, P. Pulp and Paper Industry. In Energy Conserv, 1st ed.; Elsevier: Amsterdam, The Netherlands, 2016. [Google Scholar]
- Akhtar, M.; Scott, G.M.; E Swaney, R.; Shipley, D.F. Biomechanical pulping: A mill-scale evaluation. Resour. Conserv. Recycl. 2000, 28, 241–252. [Google Scholar] [CrossRef]
- Corcelli, F.; Ripa, M.; Ulgiati, S. Efficiency and sustainability indicators for papermaking from virgin pulp—An emergy-based case study. Resour. Conserv. Recycl. 2018, 131, 313–328. [Google Scholar] [CrossRef]
- Gullichsen, J.; Paulapuro, H.; Sundholm, J. Thermomechanical pulping. In Papermaking Science and Technology, Book 5: Mechanical Pulping; Fapet Oy: Jyväskylä, Finland, 1999; pp. 159–218. [Google Scholar]
- Ottestam, C.; Salmén, L. Fracture energy of wood; relation to mechanical pulping. Nord. Pulp Pap. Res. J. 2001, 16, 140–142. [Google Scholar] [CrossRef]
- Holmberg, J.M.; Gustavsson, L. Biomass use in chemical and mechanical pulping with biomass-based energy supply. Resour. Conserv. Recycl. 2007, 52, 331–350. [Google Scholar] [CrossRef]
- Fracaro, G.; Vakkilainen, E.; Hamaguchi, M.; Souza, S.N.M. Energy Efficiency in the Brazilian Pulp and Paper Industry. Energies 2012, 5, 3550–3572. [Google Scholar] [CrossRef]
- Johansson, O.; Jackson, M.; Wild, N.W. Three steps to improved TMP operating efficiency. In International Mechanical Pulping Conference; TAPPI: Peachtree Corners, GA, USA, 2007; pp. 356–369. [Google Scholar]
- Machani, M.; Nourelfath, M.; D’Amours, S. A mathematically-based framework for evaluating the technical and economic potential of integrating bioenergy production within pulp and paper mills. Biomass Bioenergy 2014, 63, 126–139. [Google Scholar] [CrossRef]
- Baruah, D.; Baruah, D.; Hazarika, M.K. Artificial neural network based modeling of biomass gasification in fixed bed downdraft gasifiers. Biomass Bioenergy 2017, 98, 264–271. [Google Scholar] [CrossRef]
- Strand, B.C.; Fralic, G. May. Economic benefits from advanced quality control of TMP mills. In Control Systems, Preprints, Conference; Control Systems Conference 2000, 2000; pp. 11–15. [Google Scholar]
- Rudie, A.; Sabourin, M. Wood influence on thermomechanical pulp quality: Fibre separation and fibre breakage. J. Pulp Pap. Sci. 2002, 28, 359–363. [Google Scholar]
- Illikainen, M. Mechanisms of Thermo-Mechanical Pulp Refining. Ph.D Thesis, University of Oulu, Oulu, Finland, 2008. [Google Scholar]
- Tian, H.; Lu, Q.; Gopaluni, B.; Zavala, V.M.; Olson, J.A. An economic model predictive control framework for mechanical pulping processes. Control Eng. Pract. 2019, 85, 100–109. [Google Scholar] [CrossRef]
- Zhang, W.; He, J.; Engstrand, P.; Björkqvist, O. Economic Evaluation on Bio-Synthetic Natural Gas Production Integrated in a Thermomechanical Pulp Mill. Energies 2015, 8, 12795–12809. [Google Scholar] [CrossRef]
- Khokhar, G.M. Numerical Simulation of the Flow in a Disc Refiner. Master’s Thesis, KTH Royal Institute of Technology, Stockholm, Sweden, 2011. [Google Scholar]
- Wang, P.; Yang, J.; Wang, J. Computer simulation of refining process of a high consistency disc refiner based on CFD. AIP Conf. Proc. 2017, 1864, 020079. [Google Scholar]
- Huhtanen, J.P.T.; Karvinen, R.J. Interaction of non-Newtonian fluid dynamics and turbulence on the behavior of pulp suspension flows. Annu. Trans. Nord. Rheol. Soc. 2005, 13, 177–186. [Google Scholar]
- Elahimehr, A.; Olson, J.A.; Martinez, D.M. Understanding LC refining: The effect of plate pattern and refiner operation. Nord. Pulp Pap. Res. J. 2013, 28, 386–391. [Google Scholar] [CrossRef]
- Mithrush, T.L. An Experimental Study of Fluid Flow in a Low Consistency Refiner. Doctoral Dissertation, University of British Columbia, Vancouver, BC, Canada, 2013. [Google Scholar]
- Khan, P.W.; Byun, Y.-C.; Lee, S.-J.; Kang, D.-H.; Kang, J.-Y.; Park, H.-S. Machine Learning-Based Approach to Predict Energy Consumption of Renewable and Nonrenewable Power Sources. Energies 2020, 13, 4870. [Google Scholar] [CrossRef]
- De Grève, Z.; Bottieau, J.; Vangulick, D.; Wautier, A.; Dapoz, P.-D.; Arrigo, A.; Toubeau, J.-F.; Vallée, F. Machine Learning Techniques for Improving Self-Consumption in Renewable Energy Communities. Energies 2020, 13, 4892. [Google Scholar] [CrossRef]
- Bishop, C. Pattern Recognition and Machine Learning; Springer: Berlin/Heidelberg, Germany, 2006. [Google Scholar]
- Marcjasz, G. Forecasting Electricity Prices Using Deep Neural Networks: A Robust Hyper-Parameter Selection Scheme. Energies 2020, 13, 4605. [Google Scholar] [CrossRef]
- Simula, O.; Alhoniemi, E.; Science, I. SOM Based Analysis of Pulping Process Data. Available online: https://link.springer.com/chapter/10.1007/BFb0100524 (accessed on 30 September 2020).
- Ciesielski, K.; Olejnik, K. Application of Neural Networks for Estimation of Paper Properties Based on Refined Pulp Properties. FIBRES Text. East. Eur. 2014, 5, 126–132. [Google Scholar]
- Du, H. Multivariable Predictive Control of a TMP Plant. Ph.D. Thesis, University of British Columbia, Vancouver, BC, Canada, 1998. [Google Scholar]
- Lama, I.P.M.; Stuart, P. Controllability analysis of a TMP-newsprint refining process. Pulp Pap. Can. 2006, 107, 44–48. [Google Scholar]
- Musavi, M.T.; Coughlin, D.R.; Qiao, M. Prediction of wood pulp K with radial basis function neural network. In Proceedings of the ISCAS’95—International Symposium on Circuits and Systems, Seattle, WA, USA, 30 April–3 May 1995; pp. 1716–1719. [Google Scholar]
- Molga, E.; Cherbański, R. Hybrid first-principle–neural-network approach to modelling of the liquid–liquid reacting system. Chem. Eng. Sci. 1999, 54, 2467–2473. [Google Scholar] [CrossRef]
- Dufour, P.; Bhartiya, S.; Dhurjati, P.S.; Iii, F.J.D. Neural network-based software sensor: Training set design and application to a continuous pulp digester. Control Eng. Pract. 2005, 13, 135–143. [Google Scholar] [CrossRef][Green Version]
- Huhtanen, J.P. Numerical study on refiner flows: Determination of refining efficiency and pulp quality by mixing analogy. In International Mechanical Pulping Conference IMPC; Tippa Press: Minneapolis, MN, USA, 2007. [Google Scholar]
- Smook, G.A. Handbook for Pulp and Paper Technologists; Joint Textbook Com mittee of the Paper Industry, Angus Wilde Publications: Vancouver, BC, Canada, 1992; ISBN 0969462816. [Google Scholar]
- Stationwala, M.I.; Atack, D.; Wood, J.R.; Wild, D.J.; Karnis, A. The effect of control variables on refining zone conditions and pulp properties. In Proceedings of the 1979 International Mechanical Pulping Conference, Toronto, ON, Canada, 11–14 June 1979. [Google Scholar]
- Buragohain, M.; Mahanta, C. A novel approach for ANFIS modelling based on full factorial design. Appl. Soft Comput. 2008, 8, 609–625. [Google Scholar] [CrossRef]
- Khosravi, A.; Machado, L.; Nunes, R. Estimation of density and compressibility factor of natural gas using artificial intelligence approach. J. Pet. Sci. Eng. 2018, 168, 201–216. [Google Scholar] [CrossRef]
- MacArthur, R.; Wilson, E. The Theory of Biogeography; Princeton University Press: Princeton, NJ, USA, 1967. [Google Scholar]
- Simon, D. Biogeography-based optimization. IEEE Trans. Evol. Comput. 2008, 12, 702–713. [Google Scholar] [CrossRef]
- Rao, R.V.; Savsani, V.J.; Vakharia, D. Teaching–learning-based optimization: A novel method for constrained mechanical design optimization problems. Comput. Des. 2011, 43, 303–315. [Google Scholar] [CrossRef]
- Rao, R.V.; Savsani, V.J.; Vakharia, D. Teaching–Learning-Based Optimization: An optimization method for continuous non-linear large scale problems. Inf. Sci. 2012, 183, 1–15. [Google Scholar] [CrossRef]
- Eberhart, R.; Kennedy, J. A new optimizer using particle swarm theory. In Proceedings of the 6th International Symposium on Micro Machine and Human Science, Nagoya, Japan, 3–6 December 2017; pp. 39–43. [Google Scholar]
- Khosravi, A.; Koury, R.; Machado, L.; Pabon, J.J. Prediction of wind speed and wind direction using artificial neural network, support vector regression and adaptive neuro-fuzzy inference system. Sustain. Energy Technol. Assess. 2018, 25, 146–160. [Google Scholar] [CrossRef]
- Khosravi, A.; Machado, L.; Nunes, R. Time-series prediction of wind speed using machine learning algorithms: A case study Osorio wind farm, Brazil. Appl. Energy 2018, 224, 550–566. [Google Scholar] [CrossRef]
- Haider, M.A.; Pakshirajan, K.; Singh, A.; Chaudhry, S. Artificial neural network-genetic algorithm approach to optimize media constituents for enhancing lipase production by a soil microorganism. Appl. Biochem. Biotechnol. 2008, 144, 225–235. [Google Scholar] [CrossRef]
- Akhoondzadeh, M. Ant Colony Optimization detects anomalous aerosol variations associated with the Chile earthquake of 27 February 2010. Adv. Space Res. 2015, 55, 1754–1763. [Google Scholar] [CrossRef]
- Storn, R.; Price, K. Differential Evolution—A Simple and Efficient Heuristic for global Optimization over Continuous Spaces. J. Glob. Optim. 1997, 11, 341–359. [Google Scholar] [CrossRef]
- Abbass, H.; Sarker, R.; Newton, C. PDE: A Pareto-frontier differential evolution approach for multi-objective optimization problems. In Proceedings of the 2001 Congress on Evolutionary Computation (IEEE Cat No 01TH8546), Seoul, Korea, 27–30 May 2001. [Google Scholar]
- Karaboğa, D.; Ökdem, S. A simple and global optimization algorithm for engineering problems: Differential evolution algorithm. Turk. J. Electr. Eng. Comput. Sci. 2004, 12, 53–60. [Google Scholar]
- Chatterjee, I. Multi-Population-Based Differential Evolution Algorithm for Optimization Problems. Master’s Thesis, New Jersey Institute of Technology, Newark, NJ, USA, 2017. [Google Scholar]
- Li, B.; Li, H.; Zha, Q.; Bandekar, R.; Alsaggaf, A.; Ni, Y. Effects of wood quality and refining process on TMP pulp and paper quality. BioResources 2011, 6, 3569–3584. [Google Scholar]
- Qian, X.; Tessier, P. A mechanistic model for predicting pulp properties from refiner operating conditions. Tappi J. 1996, 78, 215–222. [Google Scholar]
- Khosravi, A.; Koury, R.; Machado, L.; Pabon, J. Prediction of hourly solar radiation in Abu Musa Island using machine learning algorithms. J. Clean. Prod. 2018, 176, 63–75. [Google Scholar] [CrossRef]
- Schwartz, H.M.; Chang, G.-K.; Liu, Y.; Phung, T. A method of modeling, predicting and controlling TMP pulp properties. In Proceedings of the 1996 IEEE International Conference on Control Applications IEEE International Conference on Control Applications held together with IEEE International Symposium on Intelligent Contro, Dearborn, MI, USA, 15 September–18 November 1996. [Google Scholar]
- Harinath, E.; Biegler, L.; Dumont, G.A. Predictive optimal control for thermo-mechanical pulping processes with multi-stage low consistency refining. J. Process. Control 2013, 23, 1001–1011. [Google Scholar] [CrossRef]
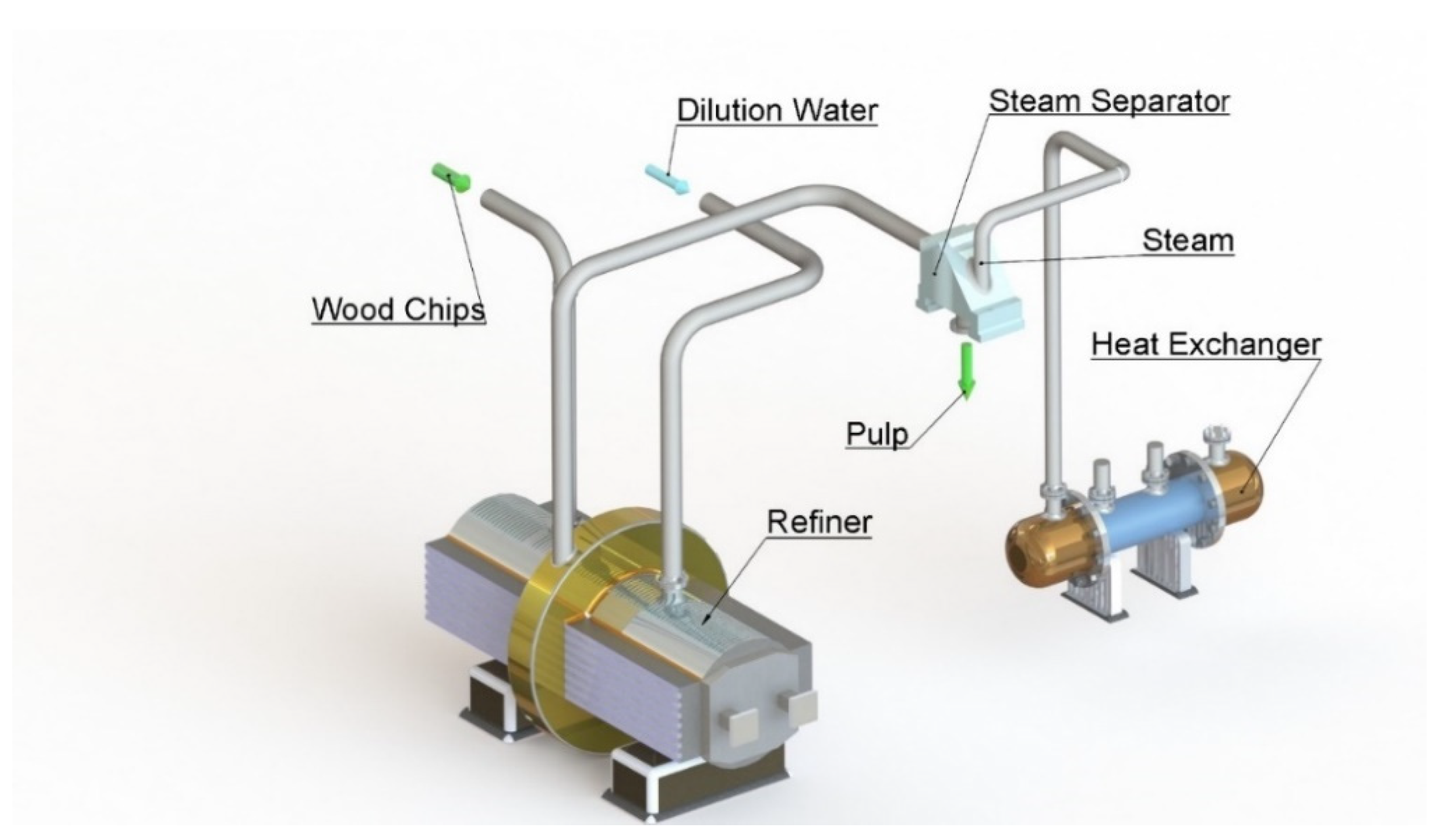







| Refining Plate Gap | Refining Dilution Water | Site Ambient Temperature | Feeder Screw Speed | Refining Motor Load | Refining Generated Steam | |
|---|---|---|---|---|---|---|
| predictor variables | ✓ | ✓ | ✓ | ✓ | ||
| Target variable | ✓ | ✓ |
| Parameter | Measure |
|---|---|
| 0.84 | |
| Optimization Algorithm | MSE-Train | MSE-Test | RMSE-Train | RMSE-Test | R-Train | R-Test |
|---|---|---|---|---|---|---|
| TLBO | 0.1256 | 0.1216 | 0.3544 | 0.3488 | 0.8392 | 0.8472 |
| BBO | 0.1046 | 0.1118 | 0.3235 | 0.3344 | 0.859 | 0.8511 |
| DE | 0.1103 | 0.1155 | 0.3321 | 0.3398 | 0.8524 | 0.840 |
| AC | 0.1155 | 0.1167 | 0.3399 | 0.3416 | 0.8424 | 0.843 |
| GA | 0.08954 | 0.09494 | 0.29924 | 0.30813 | 0.8835 | 0.8677 |
| PSO | 0.0705 | 0.0735 | 0.2655 | 0.2712 | 0.9068 | 0.9052 |
| Optimization Algorithm | MSE-Train | MSE-Test | RMSE-Train | RMSE-Test | R-Train | R-Test |
|---|---|---|---|---|---|---|
| TLBO | 0.0221 | 0.0211 | 0.1487 | 0.1452 | 0.8496 | 0.8607 |
| BBO | 0.0174 | 0.01757 | 0.13194 | 0.13256 | 0.8689 | 0.8682 |
| DE | 0.01789 | 0.01697 | 0.1337 | 0.1303 | 0.8672 | 0.871 |
| AC | 0.01925 | 0.01856 | 0.1387 | 0.1362 | 0.8524 | 0.8624 |
| GA | 0.01556 | 0.01611 | 0.12476 | 0.12694 | 0.8836 | 0.8804 |
| PSO | 0.0105 | 0.0128 | 0.1025 | 0.1131 | 0.924 | 0.9032 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Talebjedi, B.; Khosravi, A.; Laukkanen, T.; Holmberg, H.; Vakkilainen, E.; Syri, S. Energy Modeling of a Refiner in Thermo-Mechanical Pulping Process Using ANFIS Method. Energies 2020, 13, 5113. https://doi.org/10.3390/en13195113
Talebjedi B, Khosravi A, Laukkanen T, Holmberg H, Vakkilainen E, Syri S. Energy Modeling of a Refiner in Thermo-Mechanical Pulping Process Using ANFIS Method. Energies. 2020; 13(19):5113. https://doi.org/10.3390/en13195113
Chicago/Turabian StyleTalebjedi, Behnam, Ali Khosravi, Timo Laukkanen, Henrik Holmberg, Esa Vakkilainen, and Sanna Syri. 2020. "Energy Modeling of a Refiner in Thermo-Mechanical Pulping Process Using ANFIS Method" Energies 13, no. 19: 5113. https://doi.org/10.3390/en13195113
APA StyleTalebjedi, B., Khosravi, A., Laukkanen, T., Holmberg, H., Vakkilainen, E., & Syri, S. (2020). Energy Modeling of a Refiner in Thermo-Mechanical Pulping Process Using ANFIS Method. Energies, 13(19), 5113. https://doi.org/10.3390/en13195113










