Chattering-Free Single-Phase Robustness Sliding Mode Controller for Mismatched Uncertain Interconnected Systems with Unknown Time-Varying Delays
Abstract
1. Introduction
- (1)
- Propose an IVSC that eliminates the reaching phase by establishing a new sliding function. It enables the plant’s trajectories always start from the initial time instance.
- (2)
- A DSPRSMC is constructed based on an output signal and the estimated state variables from a reduced-order sliding mode estimator (ROSME). As a result, the robust property of the system is guaranteed and the overall stability of the system is assured.
- (3)
- (4)
- The chattering in control input is alleviated by combining the well-known Barbalat’s lemma and Lyapunov stability theory. Also, computer simulation results are provided to show the feasibility of the proposed scheme as well as to demonstrate the effectiveness of the analytical results.
2. System Descriptions and Problem Formulation
- A1:
- The matrices and have full rank and
- A2:
- The matched disturbance input satisfies the conditions that there exist nonnegative, but unknown, constants and such thatfor:
- A3:
- The matrices and denote the mismatched parameter uncertainties in the state of each isolated subsystem and interconnection elements. We assume that for all and
- Property 1:
- is non-singular.
- Property 2:
- When the reaching phase is eliminated, the states of the plant move into switching surface from the initial time instance. As a result, the reduced-order sliding mode dynamics is asymptotically stable.
- Property 3:
- Owing to assumption 2 and 3, the sliding mode dynamics must guarantee the invariant property for any uncertainties and external disturbances.
3. Main Results
3.1. Design a Novel ROSME for the Interconnected Systems with Time-Varying Delay
3.2. Construct a DSPRSMC for Reducing the Chattering Phenomenon
4. Asymptotically Stable Conditions by LMI Theory
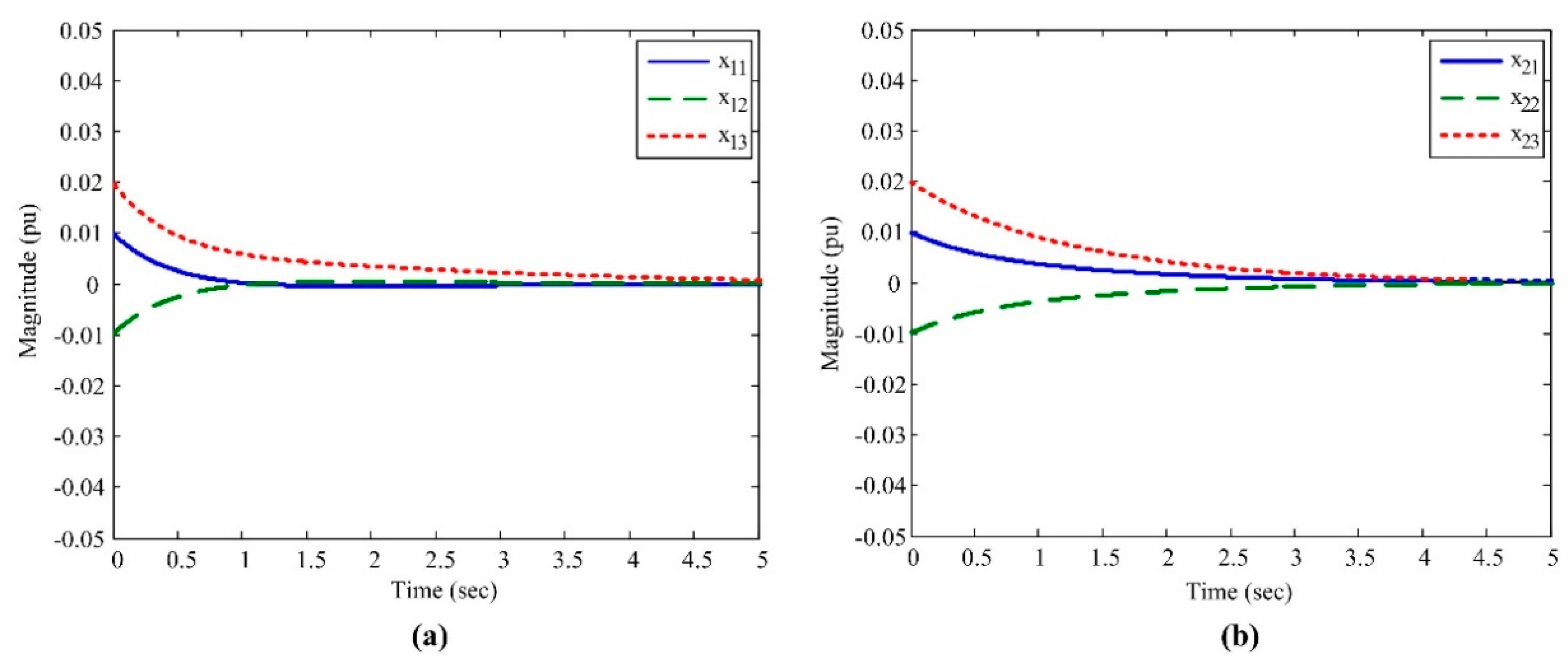
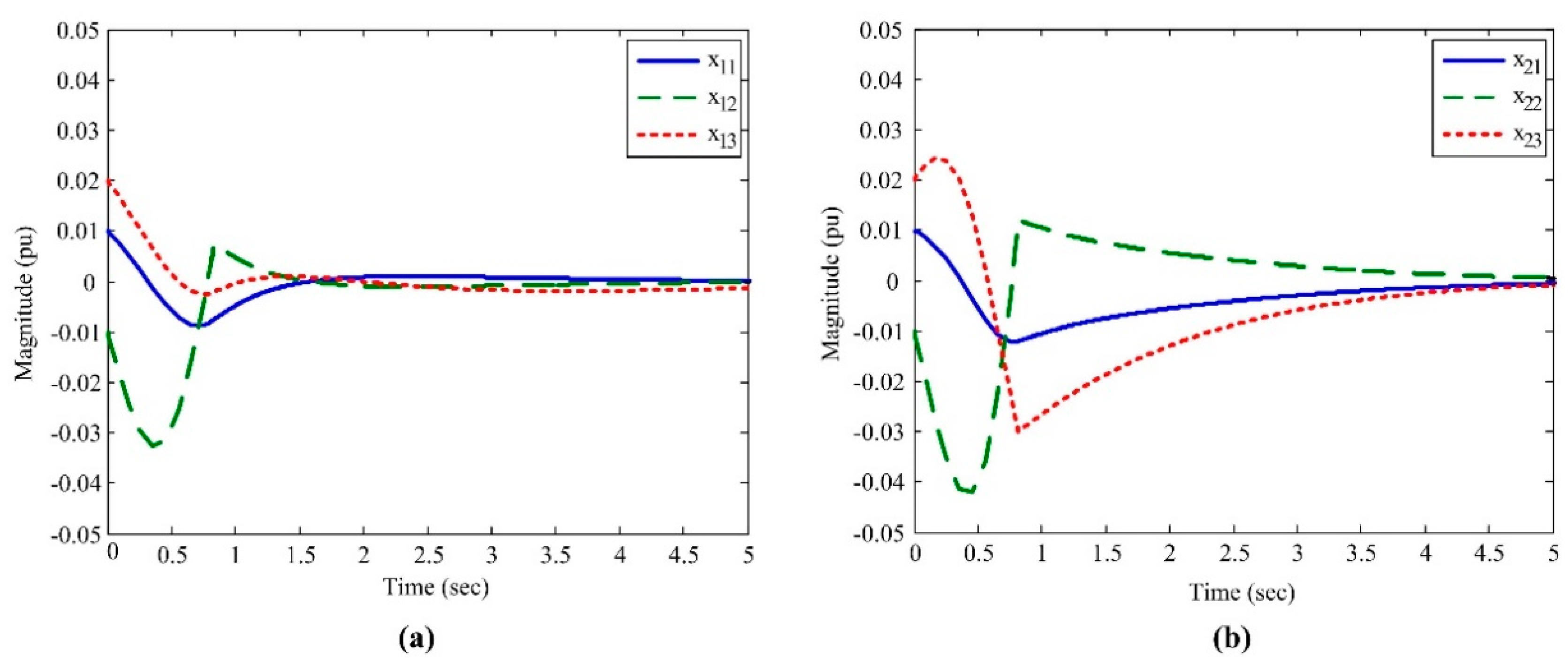
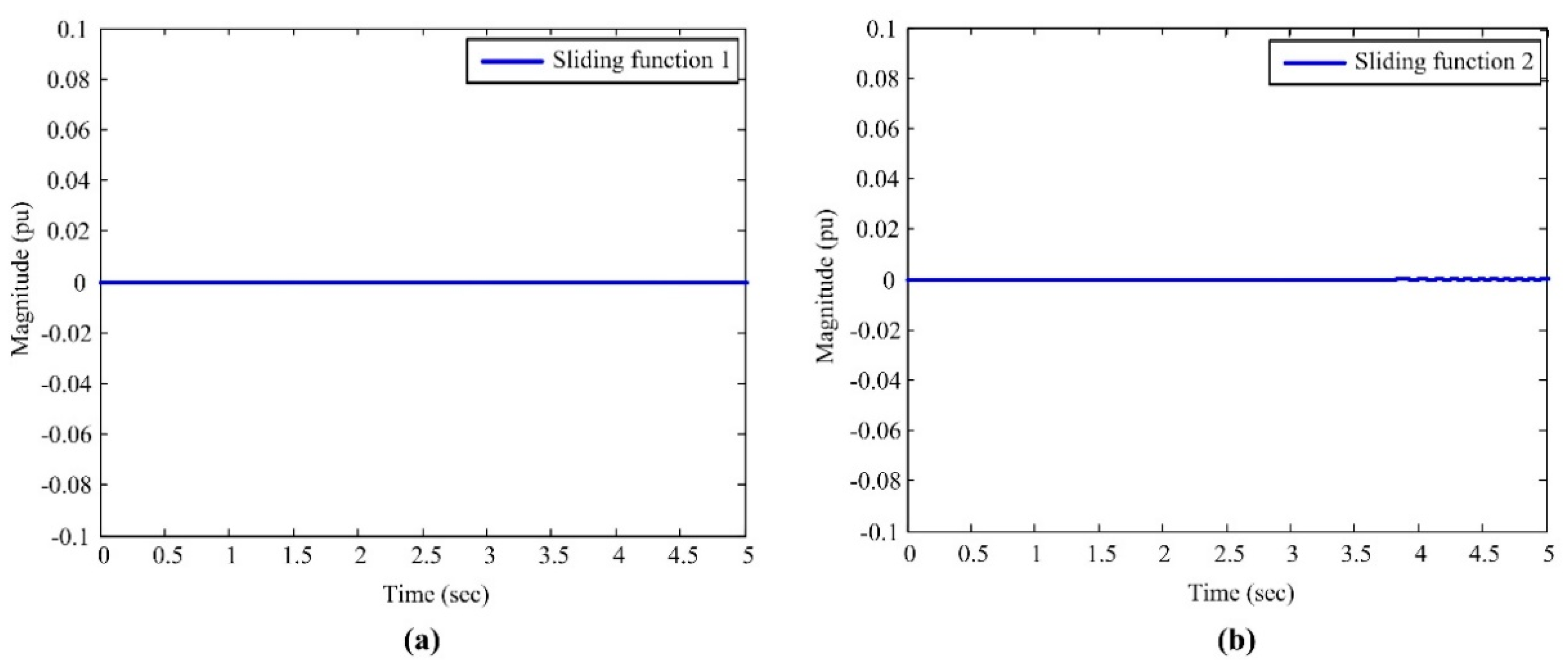
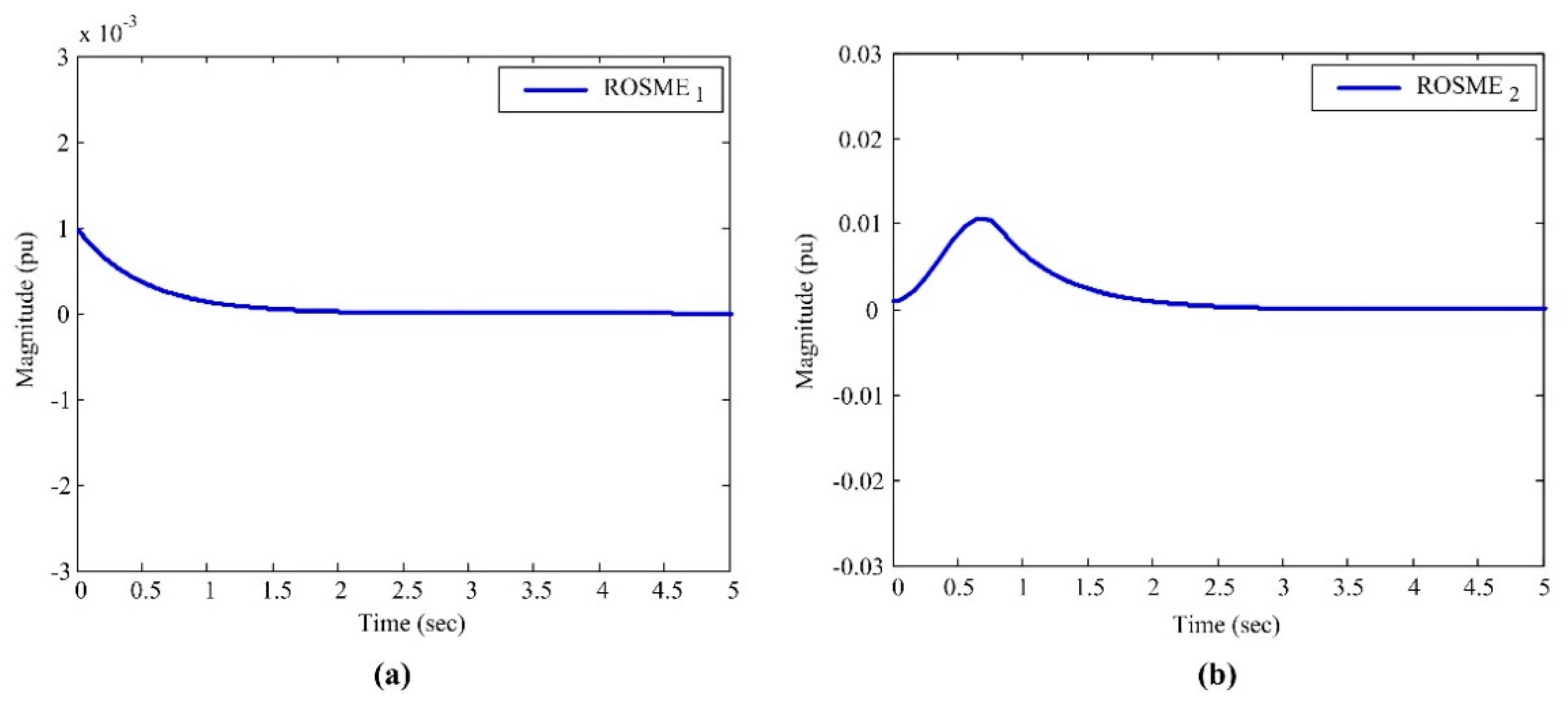
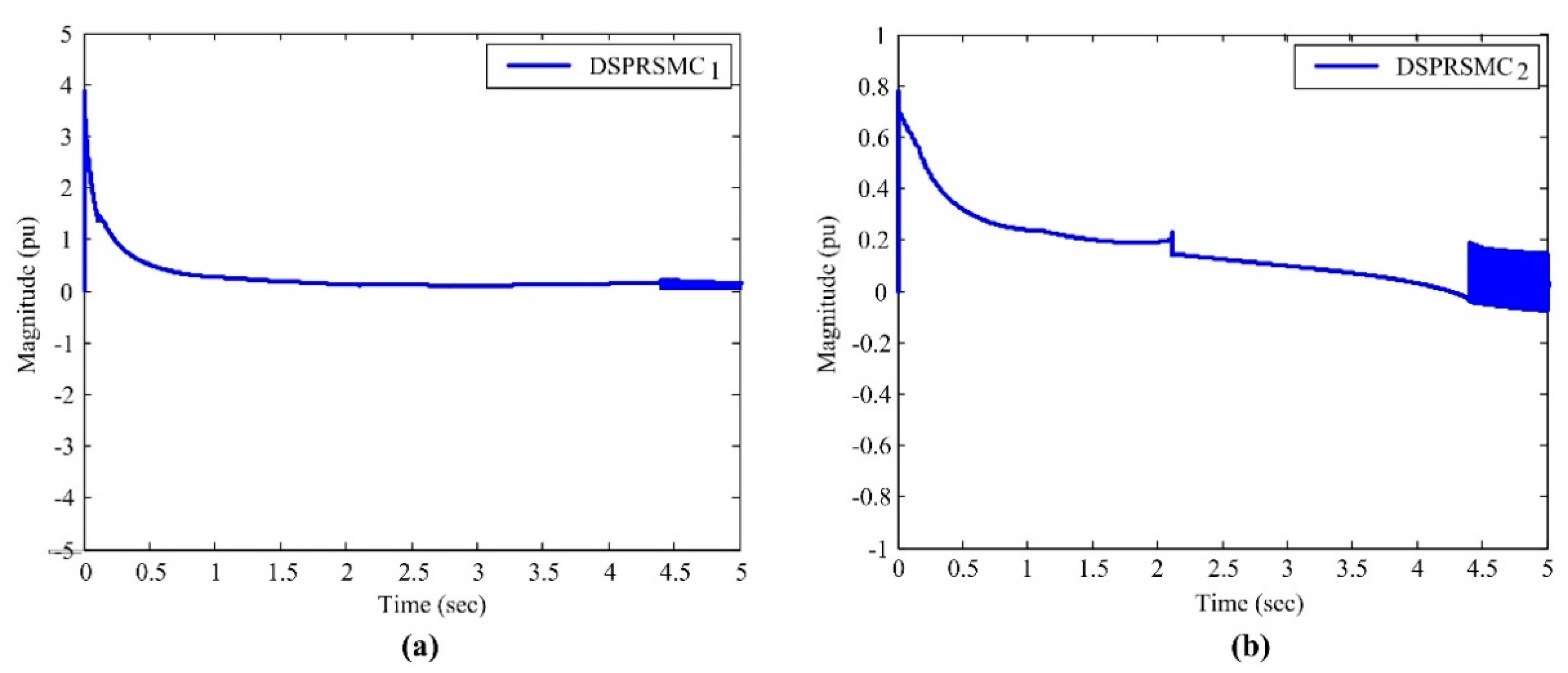
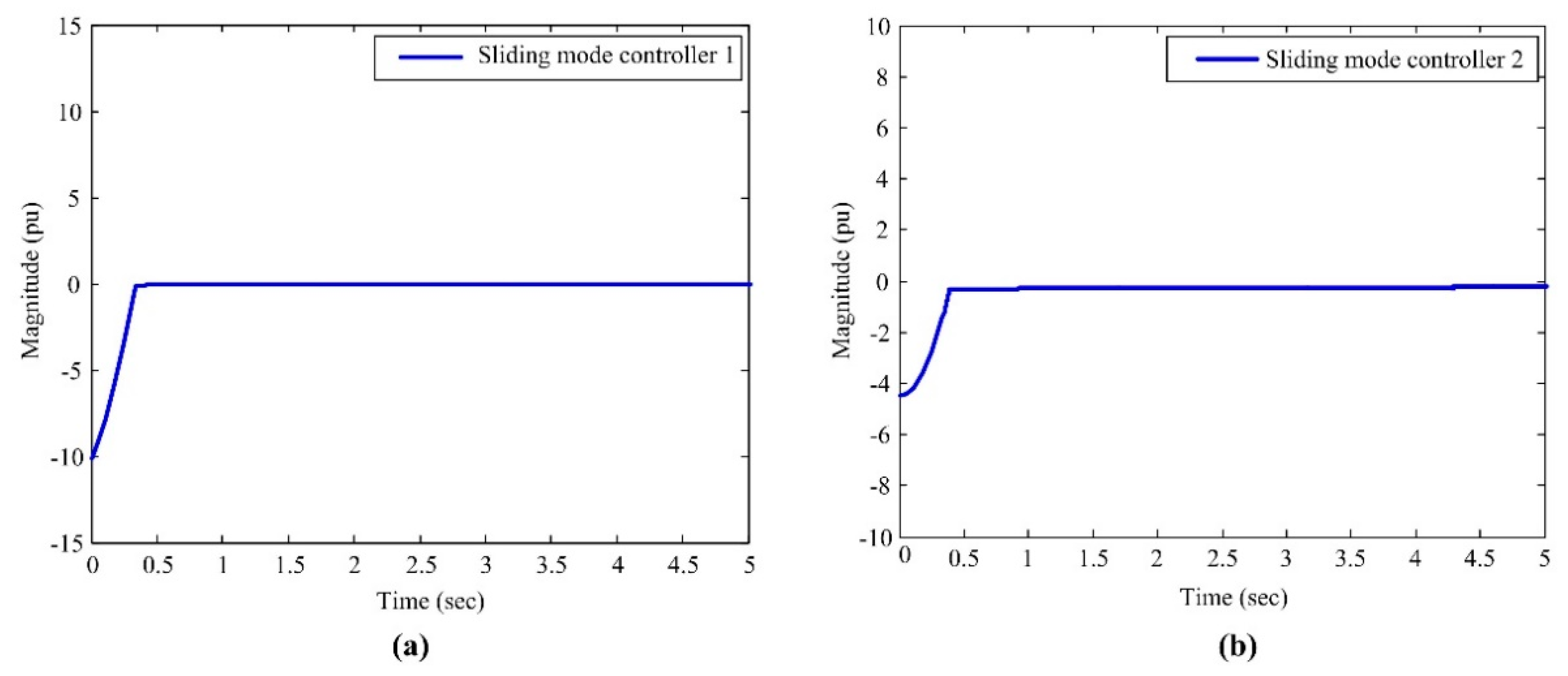
5. Numerical Simulation
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| TVSC | traditional variable structure control |
| IVSC | improved variable structure control |
| FOSME | full order sliding mode estimator |
| ROSME | reduced-order sliding mode estimator |
| LMI | linear matrix inequality |
| DSMC | decentralized sliding mode controller |
| DSPRSMC | decentralized single-phase robustness sliding mode controller |
Appendix A
Appendix B
Appendix C
Appendix D
References
- Wang, Y.; Luo, G.; Gu, L.; Li, X. Fractional-order nonsingular terminal sliding mode control of hydraulic manipulators using time delay estimation. J. Vibrat. Control 2016, 22, 3998–4011. [Google Scholar] [CrossRef]
- Van, M.; Ge, S.S.; Ren, H. Finite-Time Fault Tolerant Control for Robot Manipulators Using Time Delay Estimation and Continuous Nonsingular Fast Terminal Sliding Mode Control. IEEE Trans. Cybern. 2017, 47, 1681–1693. [Google Scholar] [CrossRef] [PubMed]
- Ansarifar, G.R.; Akhavan, H.R. Sliding mode control design for a PWR nuclear reactor using sliding mode observer during load following operation. Ann. Nucl. Energy 2015, 75, 611–619. [Google Scholar] [CrossRef]
- Moreau, R.; Pham, M.T.; Tavakoli, M.; Le, M.Q.; Redarce, T. Sliding mode bilateral teleoperation control design for master–slave pneumatic servo systems. Control Eng. Pract. 2012, 20, 584–597. [Google Scholar] [CrossRef]
- Yang, B.; Yu, T.; Shu, H.; Zhu, D.; An, N.; Sang, Y.; Jiang, L. Perturbation observer based fractional-order sliding-mode controller for MPPT of grid-connected PV inverters: Design and real-time implementation. Control Eng. Pract. 2018, 79, 105–125. [Google Scholar] [CrossRef]
- Nguyen, M.T.; Dang, T.D.; Kyoung, K.A. Application of electro-hydraulic actuator system to control continuously variable transmission in wind energy converter. Energies 2019, 12, 2499. [Google Scholar] [CrossRef]
- Derbeli, M.; Barambones, O.; Ramos-Hernanz, J.A.; Sbita, L. Real-time implementation of a super twisting algorithm for PEM fuel cell power system. Energies 2019, 12, 1594. [Google Scholar] [CrossRef]
- Shen, Y.; Qiu, Y.-y. On multiple limit cycles in sliding-mode control systems via a generalized describing function approach. Nonlinear Dyn. 2015, 82, 819–834. [Google Scholar] [CrossRef]
- Yan, X.G.; Spurgeon, S.K.; Edwards, C. Static output feedback sliding mode control for time-varying delay systems with time-delayed nonlinear disturbances. Inter. J. Robust Nonlinear Control 2010, 20, 777–788. [Google Scholar] [CrossRef]
- Yan, X.G.; Spurgeon, S.K.; Edward, C. Memoryless static output feedback sliding mode control for nonlinear systems with delayed disturbances. IEEE Trans. Autom. Control 2014, 59, 1906–1912. [Google Scholar] [CrossRef]
- Hung, J.Y.; Gao, W.; Hung, J.C. Variable structure control: A survey. IEEE Trans. Ind. Electron. 1993, 40, 2–22. [Google Scholar] [CrossRef]
- Zak, S.H. Systems and Control; Oxford University Press: New York, NY, USA, 2003. [Google Scholar]
- Edwards, C.; Spurgeon, S. Sliding Mode Control: Theory and Applications; Taylor & Francis: London, UK, 1998. [Google Scholar]
- Hu, H.; Zhao, D.; Zhang, Q. Observer-based decentralized control for uncertain interconnected systems of neutral type. Math. Prob. Eng. 2013, 2013, 12. [Google Scholar] [CrossRef]
- Yan, X.G.; Spurgeon, S.K.; Edwards, C. Global decentralised static output feedback sliding-mode control for interconnected time-delay systems. IET Control Theory Appl. 2012, 6, 192–202. [Google Scholar] [CrossRef]
- Ma, Y.; Jin, S.; Gu, N. Decentralised memory static output feedback control for the nonlinear time-delay similar interconnected systems. Int. J. Syst. Sci. 2015, 47, 2–13. [Google Scholar] [CrossRef]
- Yan, J.; Chang, W.; Lin, J.; Shyu, K. Adaptive chattering free variable structure control for a class of chaotic systems with unknown bounded uncertainties. Phys. Lett. A 2005, 335, 274–281. [Google Scholar] [CrossRef]
- Xin, L.; Wang, Q.; Li, Y. A new fast nonsingular terminal sliding mode control for a class of second-order uncertain systems. Math. Prob. Eng. 2016, 2016, 1–12. [Google Scholar] [CrossRef]
- Nguyen, C.T.; Tsai, Y.-W. Finite-Time Output Feedback Controller based on Observer for the Time-Varying Delayed Systems: A Moore-Penrose Inverse Approach. Math. Prob. Eng. 2017, 2017, 1–13. [Google Scholar] [CrossRef]
- Chung, C.W.; Chang, Y. Design of a sliding mode controller for decentralised multi-input systems. IET Control Theory Appl. 2011, 5, 221–230. [Google Scholar] [CrossRef]
- Hsu, K.C. Decentralized variable-structure control design for uncertain large-scale systems with series nonlinearities. Int. J. Control 1997, 68, 1231–1240. [Google Scholar] [CrossRef]
- Tsai, Y.-W.; Shyu, K.K.; Chang, K.C. Decentralized variable structure control for mismatched uncertain large-scale systems: A new approach. Syst. Contr. Lett. 2001, 43, 117–125. [Google Scholar] [CrossRef]
- Wang, H.; Zhou, Q.; Yang, X.; Karimi, H. Robust decentralized adaptive neural control for a class of nonaffine nonlinear large-scale systems with unknown dead zones. Math. Prob. Eng. 2014, 2014, 841306. [Google Scholar] [CrossRef]
- Hua, C.C.; Guan, X.P. Output feedback stabilization for time-delay nonlinear interconnected systems using neural networks. IEEE Trans. Neural Netw. 2008, 19, 673–688. [Google Scholar] [PubMed]
- Tong, S.C.; Li, Y.M.; Zhang, H.G. Adaptive neural network decentralized backstepping output-feedback control for nonlinear large-scale systems with time delays. IEEE Trans. Neural Netw. 2011, 22, 1073–1086. [Google Scholar] [CrossRef] [PubMed]
- Ye, X. Decentralized adaptive stabilization of large-scale nonlinear time-delay systems with unknown high-frequency-gain signs. IEEE Trans. Autom. Control 2011, 56, 1473–1478. [Google Scholar] [CrossRef]
- Tong, S.C.; Liu, C.L.; Li, Y.M.; Zhang, H.G. Adaptive fuzzy decentralized control for large-scale nonlinear systems with time-varying delays and unknown high-frequency gain sign. IEEE Trans. Syst. Man Cybern. B Cybern. 2011, 42, 474–485. [Google Scholar] [CrossRef]
- Yang, Y.; Yue, D.; Xue, Y.S. Decentralized adaptive neural output feedback control of a class of large-scale time-delay systems with input saturation. J. Frankl. Inst. 2015, 352, 2129–2151. [Google Scholar] [CrossRef]
- Shao, S.; Yang, H.; Jiang, B.; Cheng, S. Decentralized fault tolerant control for a class of interconnected nonlinear systems. IEEE Trans. Cybern. 2018, 48, 178–186. [Google Scholar] [CrossRef]
- Yan, X.G.; Spurgeon, S.K. Delay-independent decentralized output feedback control for large-scale systems with nonlinear interconnections. Int. J. Control 2014, 87, 473–482. [Google Scholar] [CrossRef]
- Kalsi, K.; Lian, J.; Zak, S.H. Decentralized dynamic output feedback control of nonlinear interconnected systems. IEEE Trans. Autom. Control 2010, 55, 1964–1970. [Google Scholar] [CrossRef]
- Aghababa, M.P.; Akbari, M.E. A chattering-free robust adaptive sliding mode controller for synchronization of two different chaotic systems with unknown uncertainties and external disturbances. Appl. Math. Comput. 2012, 218, 5757–5768. [Google Scholar] [CrossRef]
- Falahpoor, M.; Ataei, M.; Kiyoumarsi, A. A chattering-free sliding mode control design for uncertain chaotic systems. Chaos Solitons Fractals 2009, 42, 1755–1765. [Google Scholar] [CrossRef]
- Tseng, M.L.; Chen, M.S. Chattering reduction of sliding mode control by low-pass filtering the control signal. Asian J. Control 2010, 12, 392–398. [Google Scholar] [CrossRef]
- Defoort, M.; Floquet, T.; Kokosy, A.; Perruquetti, W. A novel higher-order sliding mode control scheme. Syst. Contr. Lett 2009, 58, 102–108. [Google Scholar] [CrossRef]
- Chang, J.L. On chattering-free dynamic sliding mode controller design. J. Control Sci. Eng. 2012, 2012, 1–7. [Google Scholar] [CrossRef]
- Li, P.; Zheng, Z.Q. Robust adaptive second-order sliding-mode control with fast transient performance. IET Control Theory Appl. 2012, 6, 305–312. [Google Scholar] [CrossRef]
- Chang, J.L. Dynamic sliding mode controller design for reducing chattering. J. Chin. Inst. Eng. 2014, 37, 71–78. [Google Scholar] [CrossRef]
- Mondal, S.; Mahanta, C. Chattering free adaptive multivariable sliding mode controller for systems with matched and mismatched uncertainty. ISA Trans. 2013, 52, 335–341. [Google Scholar] [CrossRef] [PubMed]
- Cheng, C.C.; Wen, C.C.; Lee, W.T. Design of decentralized sliding surfaces for a class of large-scale systems with mismatched perturbations. Int. J. Control 2009, 82, 2013–2025. [Google Scholar] [CrossRef]
- Zhang, J.H.; Xia, Y.Q. Design of static output feedback sliding mode control for uncertain linear systems. IEEE Trans. Ind. Electron. 2010, 57, 2161–2170. [Google Scholar] [CrossRef]
- Choi, H.H. An LMI-based switching surface design method for a class of mismatched uncertain systems. IEEE Trans. Autom. Control 2003, 48, 1634–1638. [Google Scholar] [CrossRef]
- Choi, H.H. Frequency domain interpretations of the invariance condition of sliding mode control theory. IET Control Theory Appl. 2007, 1, 869–874. [Google Scholar] [CrossRef]
- Haskara, I.; Ozguner, U.; Utkin, V. On variable structure observers. In Proceedings of the 1996 IEEE International Workshop on Variable Structure Systems, Tokyo, Japan, 5–6 December 1996. [Google Scholar]
- Luenberger, D.G. An introduction to observers. IEEE Trans. Autom. Contr. 1971, AC–16, 596–602. [Google Scholar] [CrossRef]
- Ghanaatian, M.; Lotfifard, S. Control of flywheel energy storage systems in presence of uncertainties. IEEE Trans. Sustain. Energy 2018, 10, 36–45. [Google Scholar] [CrossRef]
- Shabestari, P.M.; Ziaeinejad, S.; Mehrizi-Sani, A. Reachability analysis for a grid-connected voltage-sourced converter (VSC). In Proceedings of the 2018 IEEE Applied Power Conference and Exposition (APEC), San Antonio, TX, USA, 4 March 2015; pp. 2349–2354. [Google Scholar]
- Nikola, L.; Neven, B.; Niksa, V. Sliding Mode Observer-Based Load Angle Estimation for Salient-Pole Wound Rotor Synchronous Generators. Energies 2019, 12, 1609. [Google Scholar] [CrossRef]
- Elavarasan, R.M.; Ghosh, A.; K, T.M.; Krishnamurthy, A.; Saravanan, M. Investigations on performance enhancement measures of the bidirectional converter in PV–wind interconnected microgrid system. Energies 2019, 12, 2672. [Google Scholar] [CrossRef]
- Duong, M.Q.; Nguyen, V.T.; Sava, G.N.; Scripcariu, M.; Mussetta, M. Design and simulation of PI-type control for the Buck Boost converter. In Proceedings of the 2017 International Conference on Energy and Environment, Suzhou, China, 22–24 March 2017; pp. 79–82. [Google Scholar]
- Boyd, S.; El Ghaoui, L.; Feron, E.; Balakrishnan, V. Linear Matrix Inequalities in System and Control Theory; SIAM Studies in Applied Mathematics; SIAM: Philadelphia, PA, USA, 1994.
- Gahinet, P.; Nemirovski, A.; Laub, A.; Chilali, M. LMI Control Toolbox; Math. Works Inc.: Natick, MA, USA, 1994. [Google Scholar]
- Lian, J.; Zhao, J. Output feedback variable structure control for a class of uncertain switched systems. Asian J. Control 2009, 11, 31–39. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nguyen, C.-T.; Duong, T.L.; Duong, M.Q.; Le, D.T. Chattering-Free Single-Phase Robustness Sliding Mode Controller for Mismatched Uncertain Interconnected Systems with Unknown Time-Varying Delays. Energies 2020, 13, 282. https://doi.org/10.3390/en13010282
Nguyen C-T, Duong TL, Duong MQ, Le DT. Chattering-Free Single-Phase Robustness Sliding Mode Controller for Mismatched Uncertain Interconnected Systems with Unknown Time-Varying Delays. Energies. 2020; 13(1):282. https://doi.org/10.3390/en13010282
Chicago/Turabian StyleNguyen, Cong-Trang, Thanh Long Duong, Minh Quan Duong, and Duc Tung Le. 2020. "Chattering-Free Single-Phase Robustness Sliding Mode Controller for Mismatched Uncertain Interconnected Systems with Unknown Time-Varying Delays" Energies 13, no. 1: 282. https://doi.org/10.3390/en13010282
APA StyleNguyen, C.-T., Duong, T. L., Duong, M. Q., & Le, D. T. (2020). Chattering-Free Single-Phase Robustness Sliding Mode Controller for Mismatched Uncertain Interconnected Systems with Unknown Time-Varying Delays. Energies, 13(1), 282. https://doi.org/10.3390/en13010282






