Abstract
As the integration of High Voltage Direct Current (HVDC) systems on modern power networks continues to expand, challenges have appeared in different fields of the network architecture. In the Supervisory, Control and Data Acquisition (SCADA) field, software and toolboxes are expected to be modified to meet the new network characteristics. Therefore, this paper presents a unified Weighted Least Squares (WLS) state estimation algorithm suitable for hybrid HVDC/AC transmission systems, based on Voltage Source Converter (VSC). The mathematical formulas of the unified approach are derived for modelling the AC, DC and converter coupling components. The method couples the AC and DC sides of the converter through power and voltage constraints and measurement functions. Two hybrid power system test cases have been studied to validate this work, a 4-AC/4-DC/4-AC network and Cigre B4 DC test case network. Furthermore, comparison between the fully decentralized state estimation and the unified method is provided, which indicated an accuracy improvement and error reduction.
Keywords:
state estimation; WLS; unified; HVDC/AC; AC/DC; transmission; hybrid; distributed; decentralized; VSC; HVDC 1. Introduction
The modern power network has changed in many aspects; the power reliability, stability and control has improved dramatically. However, the supervision and energy management systems have became more demanding and complicated [1]. The power grid is continuously expanding with the deployment of large-scale low-carbon technologies, super-grids and continental transmission networks [1,2,3,4,5]. As a result, a definition of hybrid Alternating Current (AC)/Direct Current (DC) networks has become realistic with cost-effective and high power capability advantages. More specifically, the intensive integration of HVDC grids has provided a controllable network with an overall better performance over the conventional high voltage networks [1,3,6]. Besides, it has allowed asynchronous power networks to interconnect, and to achieve higher power transfer capability [2,6,7]. As a result, the demand for an hybrid HVDC/AC network SCADA/Energy Management Systems (EMS) became essential with new and high priority functions for controlling HVDC alongside AC [1,8,9].
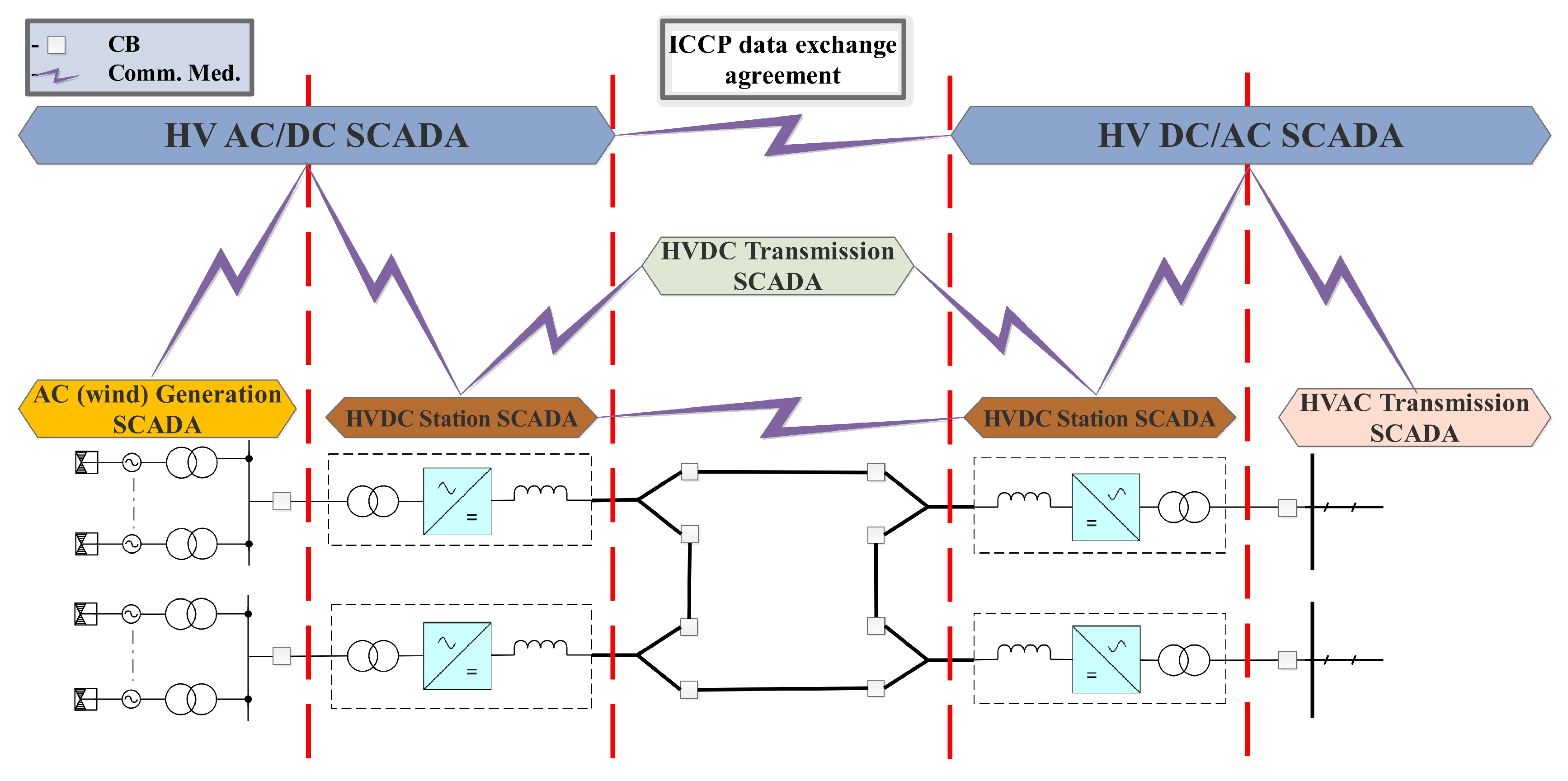
Back in 1970s, a centralized (monolithic) SCADA with remote data equipment started to be used to control the different power network sectors (generation, transmission and distribution) [2,10,11]. However, this has changed when each section became larger, and dedicated but connected SCADAs were provided for each energy level, later called hierarchical control and supervision (stations and sub-stations) [2,12]. The same architecture is used with the HVDC stations and transmission grids, they are operated by separate SCADA systems as shown in Figure 1 [1,2,3,13,14,15]. As a result, the research on SCADA for hybrid HVDC/AC transmission (mainly VSC based) is divided into two main approaches, a distributed or decentralized approach such as in [16,17,18,19], and centralized or hierarchical structure such as in [1,2,20,21,22]. In the centralized approach, both AC and DC sides are controlled by one unified SCADA, leading to several challenges and modifications have to be addressed such as:
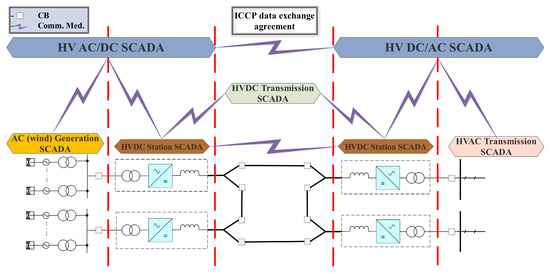
Figure 1.
Modern SCADA Interface of multi-system hybrid HVDC/AC transmission networks.
- New timescales requirements in data transmission [23];
- Advanced Remote Terminal Unit (RTU) and Intelligent Electronic Devices (IED) characteristics (e.g., hybrid HVDC/AC sensors/transducers) [23];
- Unified Human Machine Interface (HMI) and power system applications for AC and DC network (i.e., modified toolboxes such as the state estimator and fault detection blocks) [1];
- Cyber-security and communication overload traffic [1].
A state estimator toolbox is part of the power system applications available in SCADA/EMS; it is used for better observation of the network states by processing noisy and redundant measurements [24,25,26]. The tool requires accurate modeling of the network, including the network circuit breakers states and settings [9].
A hybrid HVDC/AC system state estimator requires modification over the traditional AC method. First, the DC side components and measurements have to be included. Second, the coupling between the AC and DC sides has to be modeled (hence, the converter impact). Third, a robust estimation has to be guaranteed using an AC and DC bad data detection block [19,27,28] or using an estimation algorithm claimed to be robust (e.g., Least Absolute Value (LAV) [29,30]).
In this paper, formulation and implementation of a state estimator are provided based on WLS for hybrid VSC-HVDC/AC transmission networks. The additional modifications on the AC and DC sides coupling are derived and explained. The converters at the Point of Common Coupling (PCC) are modeled as VSC based. The algorithm estimates the AC and DC system states and the converter’s sides coupling in a unified form.
The structure of the paper is as follows: Section 2 goes through a literature review on VSC converters and the state estimation toolbox. Section 3 reviews the WLS state estimator and the mathematical formulations. Section 4 introduces the unified multi-system hybrid VSC-HVDC/AC state estimator. Section 5 presents the results and the validation of the modified method. Section 6 concludes the work of this paper.
2. VSC and SE Toolbox: Literature Review
2.1. Voltage Source Converter (VSC): Modes of Operation
The deployment of the HVDC technologies continues to increase due to the ability to interconnect long distance networks that can be weak/strong or operated in two different AC frequencies [3,6,7,31]. Recent research interests and development are focusing on the VSC type converters due to the ability to provide (support) bidirectional active power and direct reactive power to the AC side [3]. In addition to the ability to regulate the voltage magnitude at both sides of the converter. Furthermore, VSC made connecting multi-terminal network (more than 3) possible with routable power flow. Moreover, VSCs are suitable for connecting off-shore wind farms and weak AC grids [1,3,6,7,9,31].
A VSC-HVDC network can be presented as two VSC connected back-to-back (or through a DC link) as shown in Figure 2. One of the converter is operated as a rectifier (regulate the DC voltage level), the other is operated as an inverter (regulate the active and reactive power) [6,31].

Figure 2.
Back-2-Back VSC HVDC network.
The VSC can exhibit different control modes which provide the advantage of the independently control of the active and reactive power. These AC and DC sides control modes can be briefly described as follow [9,32,33]:
- On the DC side:
- Constant active P: The converter is injecting constant active power to the AC side.
- Constant DC voltage V: The converter aims to maintain the DC bus voltage regulated by keeping the active power flow float (not constant), also referred to as DC Slack bus.
- Droop control of P and : The converter works on a relation between the real power injected to the DC grid and the voltage level of the same bus.
- On AC side:
- PV: The voltage level is fixed (regulated) while the reactive power is float and adapts the regulator to ensure constant AC bus voltage magnitude.
- PQ: The reactive power is fixed and injected to the AC grid regardless of the AC bus voltage magnitude state.
2.2. The State Estimation Toolbox
The state estimator toolbox is run separately on different power system levels (from generation to distribution/demand), due to the different operators of the networks. As a result a form of quasi-centralized or multi-level form of SCADA is existed [10,13,34]. However, after the deployment of the HVDC grids, the AC and DC systems operators—in most of the cases—are not the same, resulting on a fully distributed/decentralized control of the hybrid VSC-HVDC/AC network [3,28,35].
Despite, the advantages that the distributed supervisions offers [15,16,17,19,36,37], the current SCADA architecture is still structured for unified/centralized approaches, especially at high voltage levels [38]. Therefore, a single system operator of an hybrid VSC-HVDC/AC transmission network can be interested in a unified state estimator tool [1].
The state estimation on AC systems has been implemented and researched in several publications such as [26,34,39,40,41,42]. However, further challenges and research issues have been revealed with the integration of the VSC-DC grids. The state estimation toolbox has new requirements in performance, efficiency and reliability [43], leading to an ongoing research in state estimation algorithms for VSC-HVDC/AC networks [27,30,44].
The DC static state estimation used to be discussed and explained to simplify the definition of state estimation due to the possibility of linearisation [24]. However, researchers further explore robust DC side SE algorithms. An artificial intelligence state estimation algorithm based on Belief Propagation is proposed in [45]. Similar machine learning based algorithms are used in [26,46]. In addition, since the trend focuses on VSC-HVDC/AC state estimator, traditional methods such as LAV state estimators are being explored. A robust AC/HVDC state estimation based on LAV for VSC-DC is presented in [30]. An improved sequential weighted state estimator method for multi-terminal VSC-DC is proposed by [47,48]. Furthermore, Phasor Measurements Unit (PMU) based state estimators for transmission links are proposed in [49,50]. A fast decoupled state estimator for hybrid AC/DC networks with VSC is provided in [51]. Researchers in [38] has proposed a unified approach for VSC-HVDC/AC state estimator based on Hachtel’s augmented matrix method and integrated a bad data analyser. They argue that the unified approach increase the bad data recognition accuracy and improve the system states presentation. On the other hand, distributed approach AC/DC state estimator is presented in [28], it decomposes the network and uses Lagrangian relaxation based approach and block wise Gauss-Seidel algorithms to solve the SE problem. A comparison between centralized and distributed SE for hybrid AC/DC networks is available in [36].
Despite the wide and variant literature, WLS algorithm is still commonly deployed method in SCADA/EMS power system applications [9]. Therefore, this paper focuses on the extension of the WLS algorithm to deal with hybrid VSC-HVDC/AC unified state estimation through power and voltage coupling at the converter PCC.
3. State Estimation and Power Flow: Mathematical Background
3.1. Weighted Least Squares (WLS) Algorithm
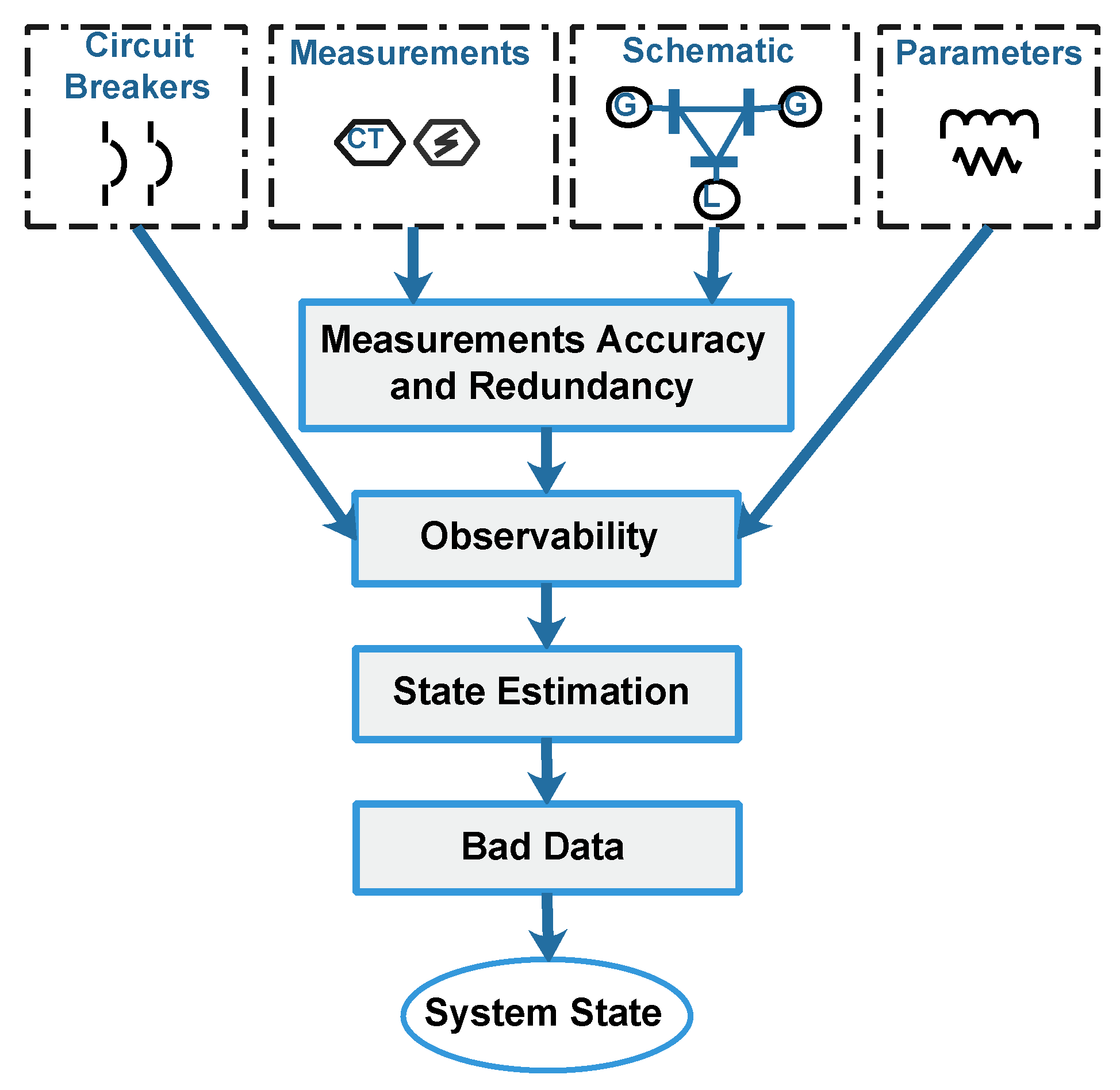
The state estimation toolbox focuses on determining the system states using the maximum available measurements from the grid. However, it requires some pre and post-processing stages, as shown in Figure 3. The pre-processing stages include observability analysis (measurements, network model and circuit breakers states), while the post-processing includes bad data detection and elimination processes [24,52,53].
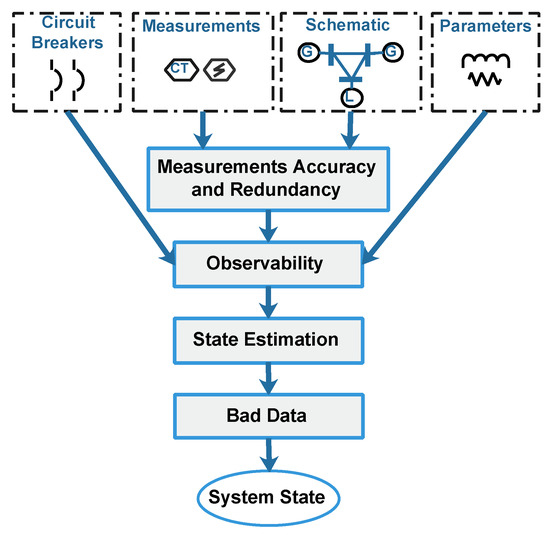
Figure 3.
State estimation stages.
The state estimator aims to reduce or eliminate the errors in the collected measurements from the network to achieve the closest possible estimates of the system states. It assumes that the system measurements are corrupted (noisy) with error e as shown in the equation below:
The WLS state estimation algorithm is commonly used in SCADA and EMS. It aims to minimize the square error (residual r) of the measurements by solving the following minimizing objective function:
where, is the measurements vector with n measurements, x is the state variable vector, is a vector of non-linear equations evaluated at the state variable x, e is the error (assumed to be Gaussian noise), and is a diagonal matrix that contains all measurements variances, for independent measurements.
Equation (2) can be reformulated in matrix minimization form as follow:
The state variables x of an AC system with n buses are ; the voltage angle of the slack (reference) bus is set to zero, and and are the bus phase angle and voltage magnitude respectively [24].
This minimization problem can be reformulated and solved using Taylor series and Newton-Raphson as explained in [9], which results with the following formulas:
where is the change/update on the system states, and calculated as follow:
where is the Gain matrix and is the Jacobian matrix.
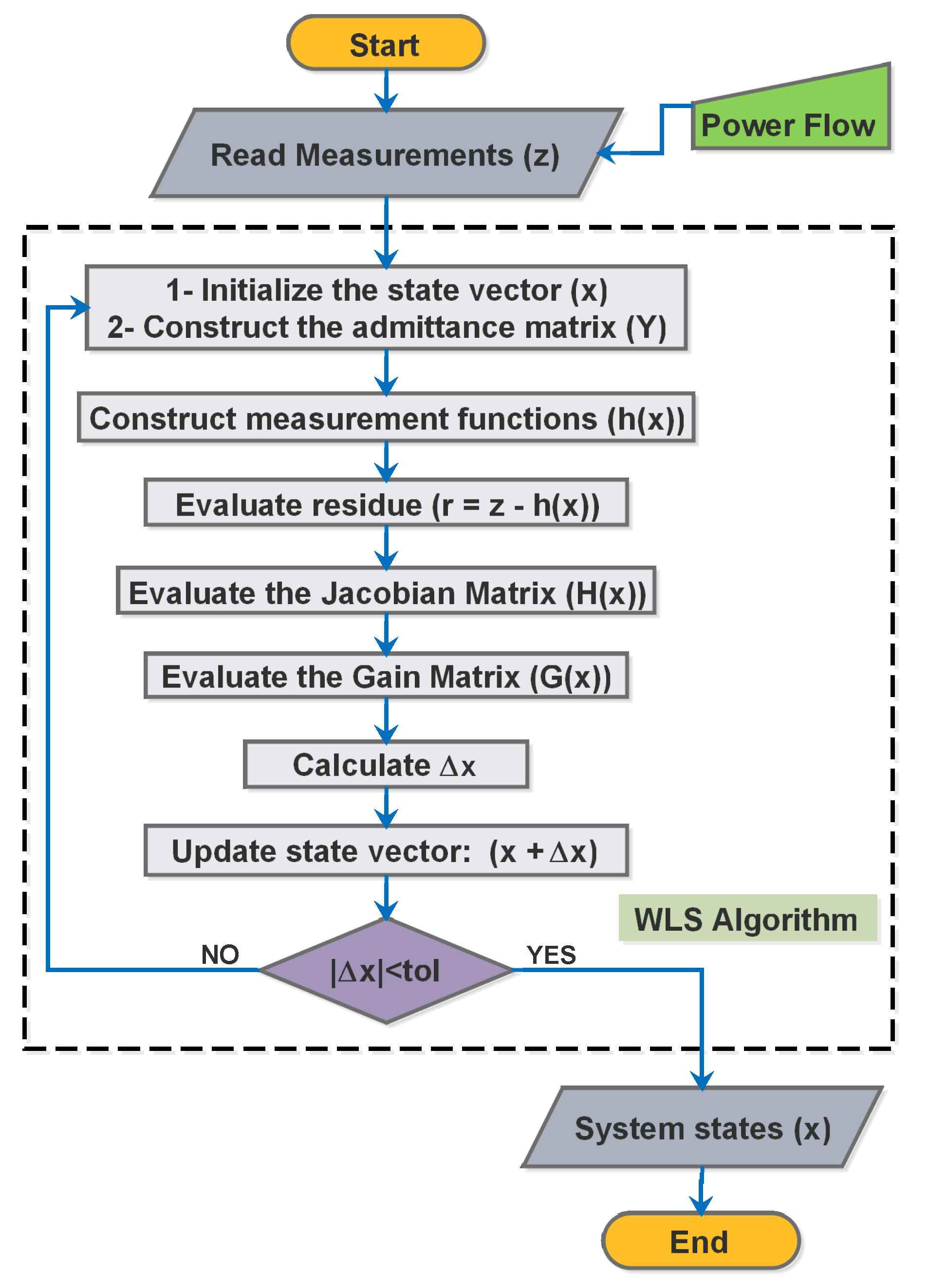
Equation (8) shows the complete formula for the system states updates (). The WLS estimation algorithm steps are shown in Figure 4 flowchart.
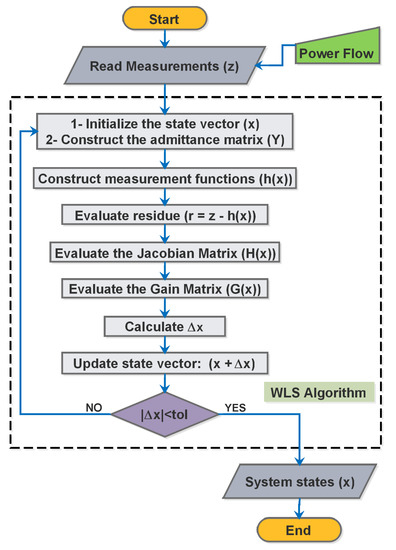
Figure 4.
State estimation algorithm.
3.2. AC Power Flow Calculations
The AC non-linear measurement functions are expressed as equations related to the current flow between buses, the power flow in the lines and the power injected into/from a bus [24]. These formulas can be categorized as follow:
- and for active and reactive power injection at bus i respectively:
- and for active and reactive power flow from bus i to j respectively:
- for current flow from bus i to j:
If shunt admittance is ignored, then:
where i and j are ‘from’ and ‘to’ buses respectively, is voltage magnitude and is phase angle where , is the element of the complex admittance matrix, is the shunt admittance, represents all the buses connected to bus i [24].
3.3. DC Power Flow Calculations
On the DC side, the measurement functions are expressed as real power injection, power flow and current flow expressions as defined below:
- for real power injection at bus i:if droop control is used, the the real power injection at bus i becomes:where,
- for real power flow from bus i to j:
- for current flow from bus i to j:
3.4. Converter Power Coupling
The power relation between the AC and DC sides through the converter can be presented as follows [54]:
where is the converter loss itself and can be calculated through experimental statistical approach based on Equation (21) and the current through the converter () [7,26]:
a, b and c are factors that depend on the converter type, operating condition and components (number of diodes, switches etc.…). These values are represented as follow [7,54]:
- a has a typical value of pu and it represents the no load losses of transformers and averaged axillary equipment losses, such as heating and cooling losses;
- b has a typical value of pu and it represents the switching losses of valves and freewheeling diodes;
- c represents the conduction losses of the valves and depends on the operating condition of the converter (rectifier or inverter). it is typical values are:
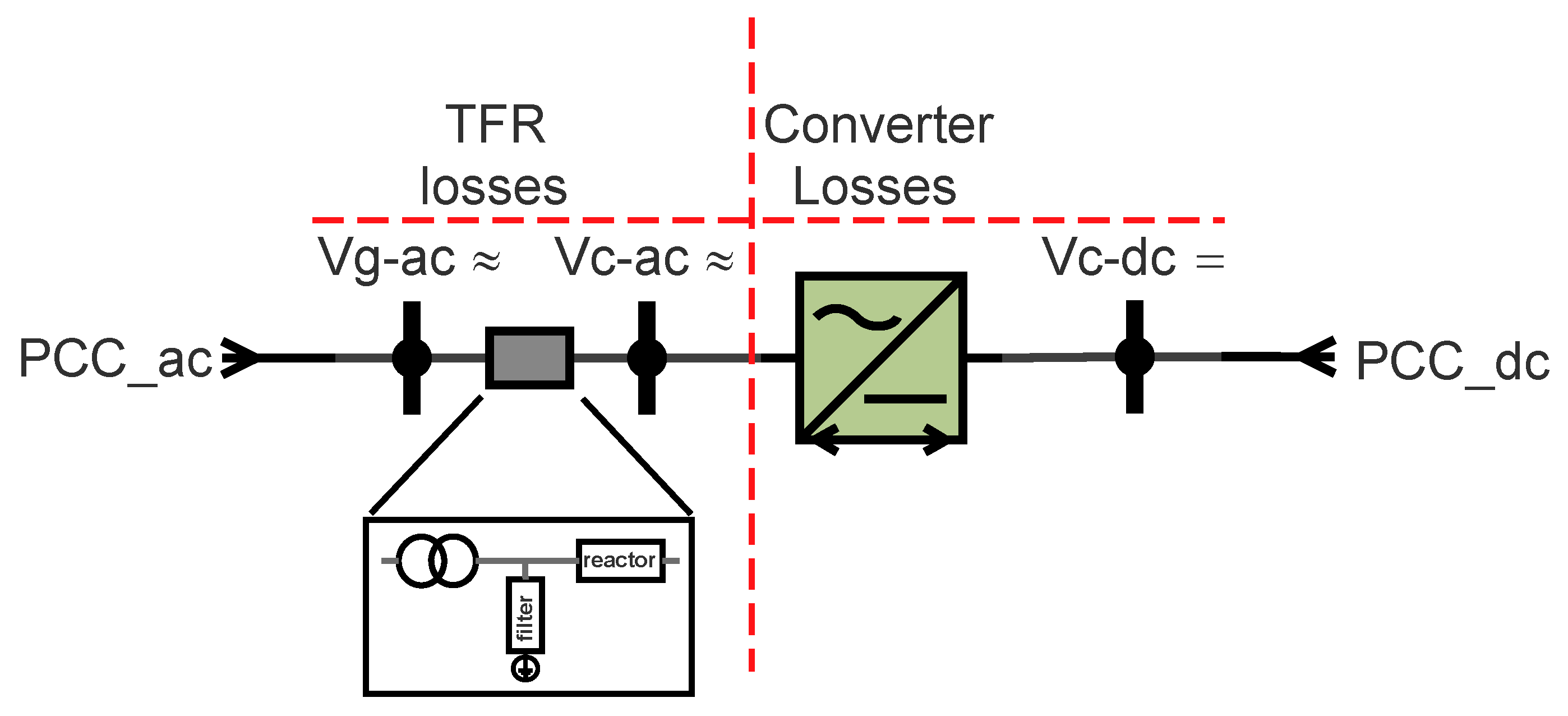
In addition to the converter losses themselves (), there are the AC side transformer, filter and reactor (Transformer, Filter and Reactor (TFR)) losses as shown in Figure 5. In this work, the TFR term is used to refer to these losses as part of the AC grid.
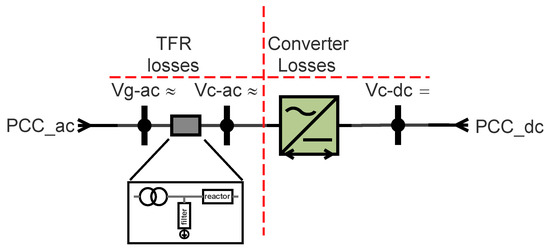
Figure 5.
Converter power loss schematic.
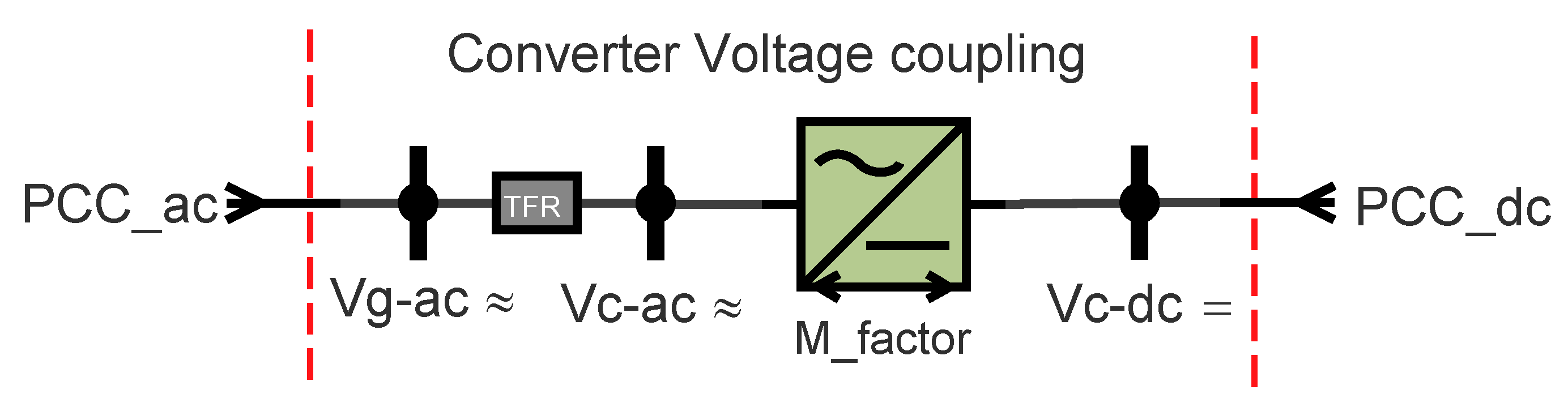
3.5. Converter Voltage Coupling
The converter can be dealt with as a transformer where the voltage levels on both sides are maintained by ratio (modulation index) as shown in Figure 6 [9,30]. Considering that, if the converter can provide a ratio between the AC and DC sides voltages, then this extra information can be used as a redundant measurement in the state estimator.
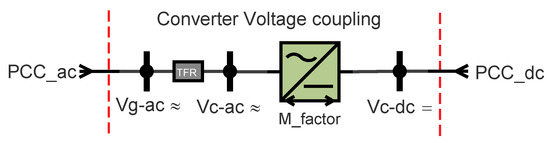
Figure 6.
Converter voltage coupling.
Let be a redundant measurement provided from the converter at the moment of measuring. Then the voltage relation between both sides of the converter is:
is calculated based on the converter current direction as shown in (24), where is the TFR voltage drop.
Equation (23) can be reformulated as an equality constraint in the WLS algorithm.
where K is the voltage conversion factor, it can have different values based on the AC side network topology and converter type as shown below, see [9,30]:
4. The Unified WLS for HV-(AC/VSC-DC/AC) Transmission Network
Considering the presented AC and DC side coupling approaches, a unified state estimator can be constructed. It is a single state estimator that solves one algorithm for the whole VSC-HVDC/AC system together, using a single unified Jacobian matrix. The modified measurements input for the WLS is formulated below:
where
- are the AC side measurements and can be in the form of ;
- are the DC side measurements and can be in the form of ;
- are zero measurements and represent the right side of converter power coupling constraints;
- are the to ratios (measurements), calculated and transmitted by the converter;
- n, m and k are the number of AC systems, DC systems and converters respectively.
The measurement functions in the unified WLS have the same format of the z vector.
The new Jacobian matrix is formatted in the following manner:
Which can be reformatted differently to simplify the structure as shown below:
The expanded unified Jacobian matrix in (29) represents all hybrid VSC-HVDC/AC system components in one matrix. It includes the AC, DC and converter power and voltage coupling elements, and it is structured for AC systems, DC systems and Converters.
where
- is the partial derivative of to and
- is the partial derivative of to and ↔ 0-matrix
- is the partial derivative of to ↔ 0-matrix
- is the partial derivative of to
- is the partial derivative of the power coupling constraint to and
- is the partial derivative of the power coupling constraint to
- is the partial derivative of to and
- is the partial derivative of to
The following subsection presents the partial derivatives of the additional components to the unified Jacobian matrix . The traditional AC and DC derivative components are available in Appendix A.1 and Appendix A.2 respectively.
4.1. Converter Components: Power Coupling
presents the partial derivative of the power coupling constraint at both sides of the converter. For the DC side: Taking the partial derivatives to the DC voltage magnitude as shown in Equation (30).
For the AC side:
4.2. Converter Components: Voltage Coupling
presents the partial derivative of the voltage coupling at both sides of the converter. For the DC side: Taking the partial derivatives to the DC voltage magnitude as shown in Equation (36).
For the AC side:
Taking the partial derivatives to the AC voltage magnitude, it can be expressed as shown in Equation (38).
Since the constraint is angle free, then taking the partial derivatives to the phase angles is zero as shown in Equation (39).
It is worthy to note the can be included in the system states instead of system measurements, which makes the system states vector contains: AC phase angles and voltages, DC voltages and .
5. Decentralized vs. Power Coupling vs. Unified: State Estimation Simulations
In this section, a validation of the unified WLS is provided along with a comparison with the decentralized approach. The unified WLS uses the power and voltage coupling of the converter to connect the decentralized AC and DC grids.
The unified approach of the WLS state estimator was implemented on Julia optimization programming language [55]. It was structured in a flexible way that allows easy switching between the different test cases and scenarios (Decentralized, converter power/voltage coupling and unified). The WLS algorithm was implemented in recursion loops with dictionaries and data structures for better memory optimization and arithmetical processing. The true measurements of the hybrid VSC-HVDC/AC systems were obtained by the power-flow solver from PowerModelsACDC.jl (Julia library) [54]. The noisy measurements are calculated by adding Gaussian noise to the true measurements based on Equation (40).
The Gaussian noise is generated with equals to the true measurement and is calculated from Equation (41) [56]. Further details on the equation derivation are available in [25].
where is assumed to cover of the Gaussian distribution curve (), and is the additional error percentage. In this work, all noisy measurements were corrupted with 3% percentage error, except measurements with 1%.
The simulation study compares between the different state estimation scenarios as follow:
- Decentralized: The systems are assumed to be separated with no data/measurements exchange (no coupling). The Jacobian matrix is reduced to contain only AC and DC components, and multi-thread WLSs are run for each AC and DC system.
- Converter P-Coupling: A single WLS is run centralized with the converter power coupling constraints added to the Jacobian matrix.
- Converter PV-Coupling (unified): The power constraints and voltage coupling measurements are taken into the centralized WLS estimation, forming the unified estimation approach.
The WLS algorithm is configured to have a maximum number of iteration equal to 20 and the tolerance stop condition, related to the change of correction (), equal to . The weights of the measurements are are shown in Table 1.

Table 1.
Measurements weights (variances ).
5.1. Hybrid VSC-HVDC/AC Networks Test Cases
Two hybrid VSC-HVDC/AC networks were modeled to test the algorithm (Section 5.1.1 and Section 5.1.2). Both networks are assumed to have bipolar DC links (hence ). The following subsections present each network WLS simulation results for three scenarios: Decentralized AC and DC systems, AC/DC power coupling and unified.
5.1.1. Four(4)-AC/Four(4)-DC/Four(4)-AC Network
The first network is comprised of two 4-bus AC systems, numbered from 1 to 4 and 5 to 8, respectively, connected by a DC grid, as shown in Figure 7. The AC systems have two AC generators at bus 1 and 6; both considered slack buses (references). The AC load is presented only at bus 8. The DC grid has 4 buses, with bus 1 as a slack bus. Bus 3 has a virtual converter is used to force the power flow direction.

Figure 7.
4AC-4DC-4AC network.
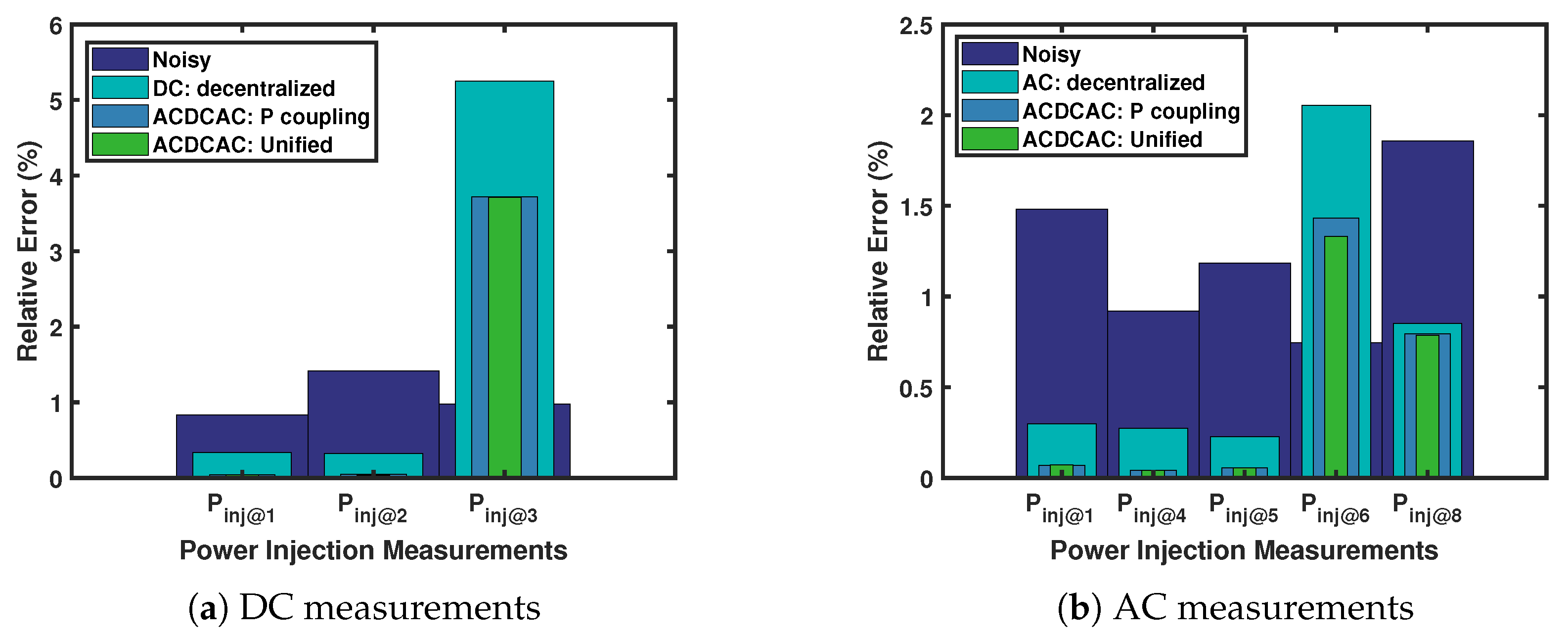
In Table 2 and Table 3, the true, noisy and estimated measurements of the DC and AC systems are presented respectively, where T1 is: Decentralized, T2: With converter P-coupling, and T3: Unified. Figure 8 visualizes the accuracy performance for the three scenarios in some of the AC and DC power injection measurements. It shows the error between the true measurements against the noisy and estimated measurements. The bars represent the relative error in percentages, lower means closer to the true measurement. In Figure 8a, the estimation of the DC power injection at bus 3 has shown high relative error in the three estimation approaches because this measurement represents a virtual converter.

Table 2.
DC systems measurements .

Table 3.
AC systems measurements .
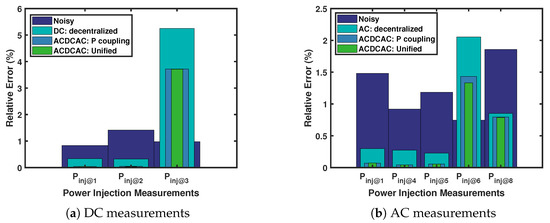
Figure 8.
The relative error in power injection measurements.
The converter power coupling measurement is presented as a power constraint equal to zero (Equation (20)), and it aims to correct the power measurements related to the converter. While the voltage coupling measurement is defined as a ratio () that relates the voltage magnitudes of both sides of the converter. The unified WLS was able to accurately estimates the measurements and the power coupling constraints as shown in Table 4.

Table 4.
The converter coupling measurements.
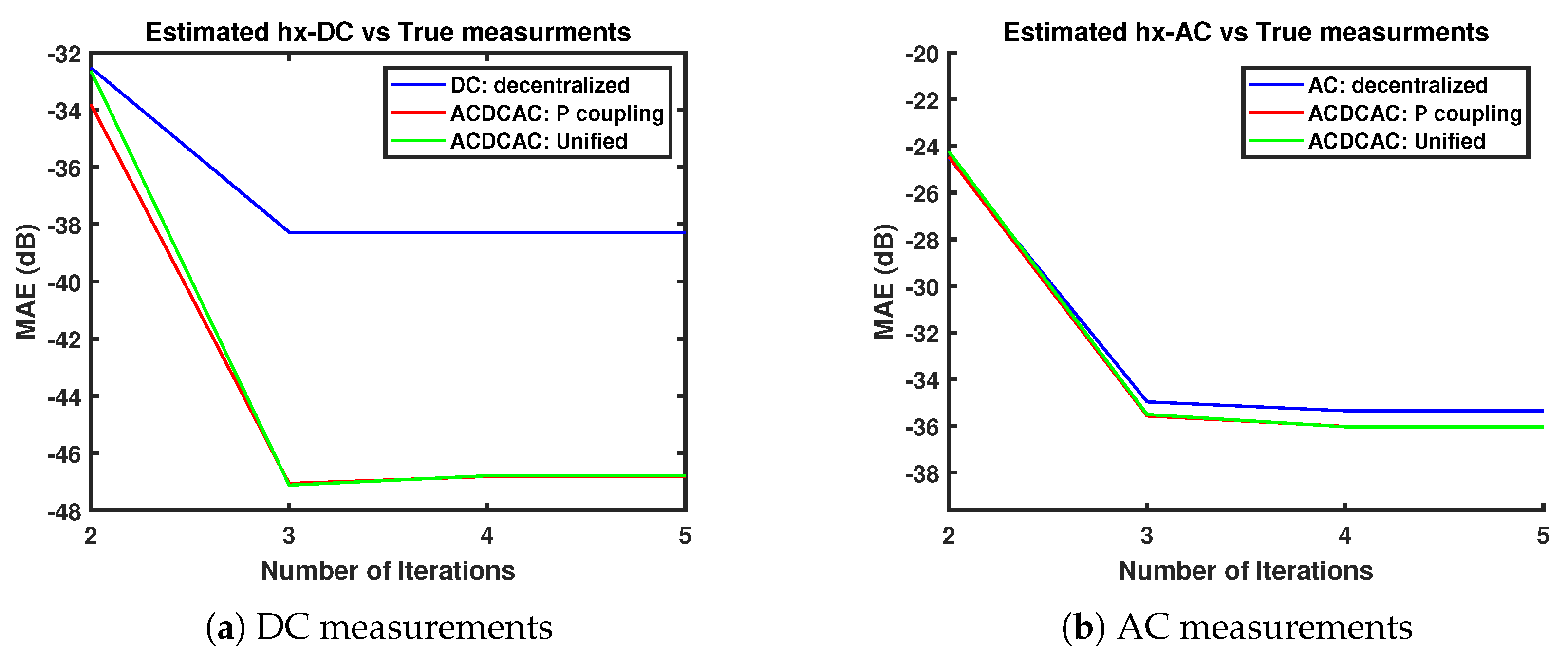
Figure 9 shows the Mean Absolute Error (MAE) of the converter measurements. In (a) the converter power coupling has minimized the error in the DC grid measurements compared to the decentralized method, it has reduced from −38.2754 dB to −46.7865 dB (14.09% less in linear form). This case concludes that on the DC side a dramatical improvement can be achieved whenever the noisy measurements are close to the converter. In (b) it shows a slightly similar impact on the AC side, the MAE has decreased by −0.6857 dB.
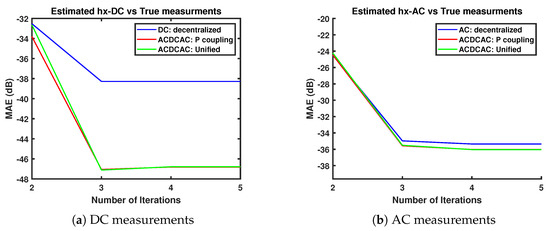
Figure 9.
MAE of the AC and DC measurements in the 4AC-4DC-4AC network.
The DC system states estimation are shown in Table 5. For the three different scenarios, the estimations are almost identical, and the error is lower than 5 digits (). That is due to the low number of the DC buses and the linear feature of the DC components.

Table 5.
DC systems SE: Decentralized/Power coupling/Unified.
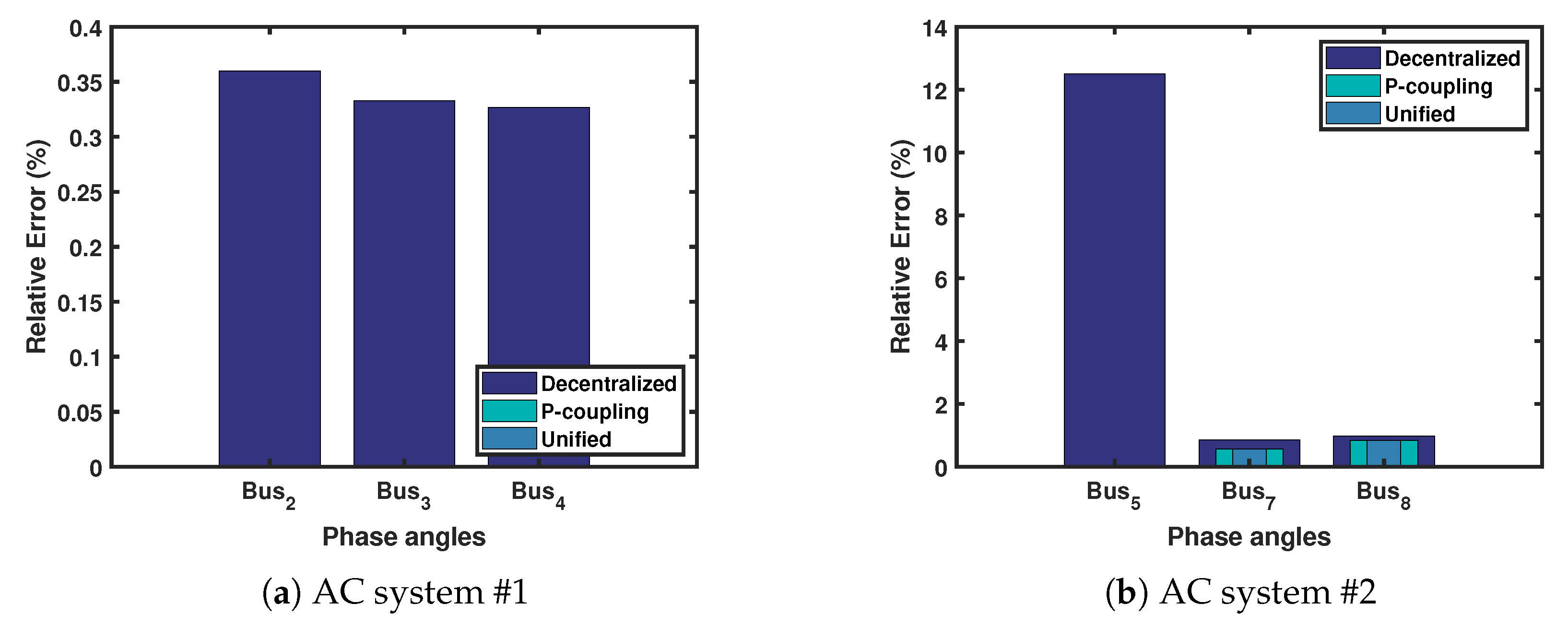
The AC side voltages and phase angles (in radian) estimations are available in Appendix B.1 for the three scenarios. The unified approach has shown better estimates at bus 7 and 8 compared to the other scenarios. However, the overall error is expected to be low since the AC systems do not have many buses and branches. Figure 10 shows the relative error in the phase angles for each scenario. In (a), the P-coupling and unified approaches were able to provide 5-digits accuracy in the phase angles compared to the decentralized approach. The unified approach was able to preserve the power coupling corrections on the measurements level while improving the estimates of the voltage states using the voltage coupling (e.g., Bus 7 in Table A3).
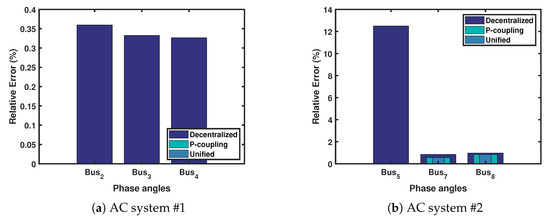
Figure 10.
Relative error of the phase angles states in AC systems 1 and 2.
5.1.2. Cigre B4 AC/DC/AC Network
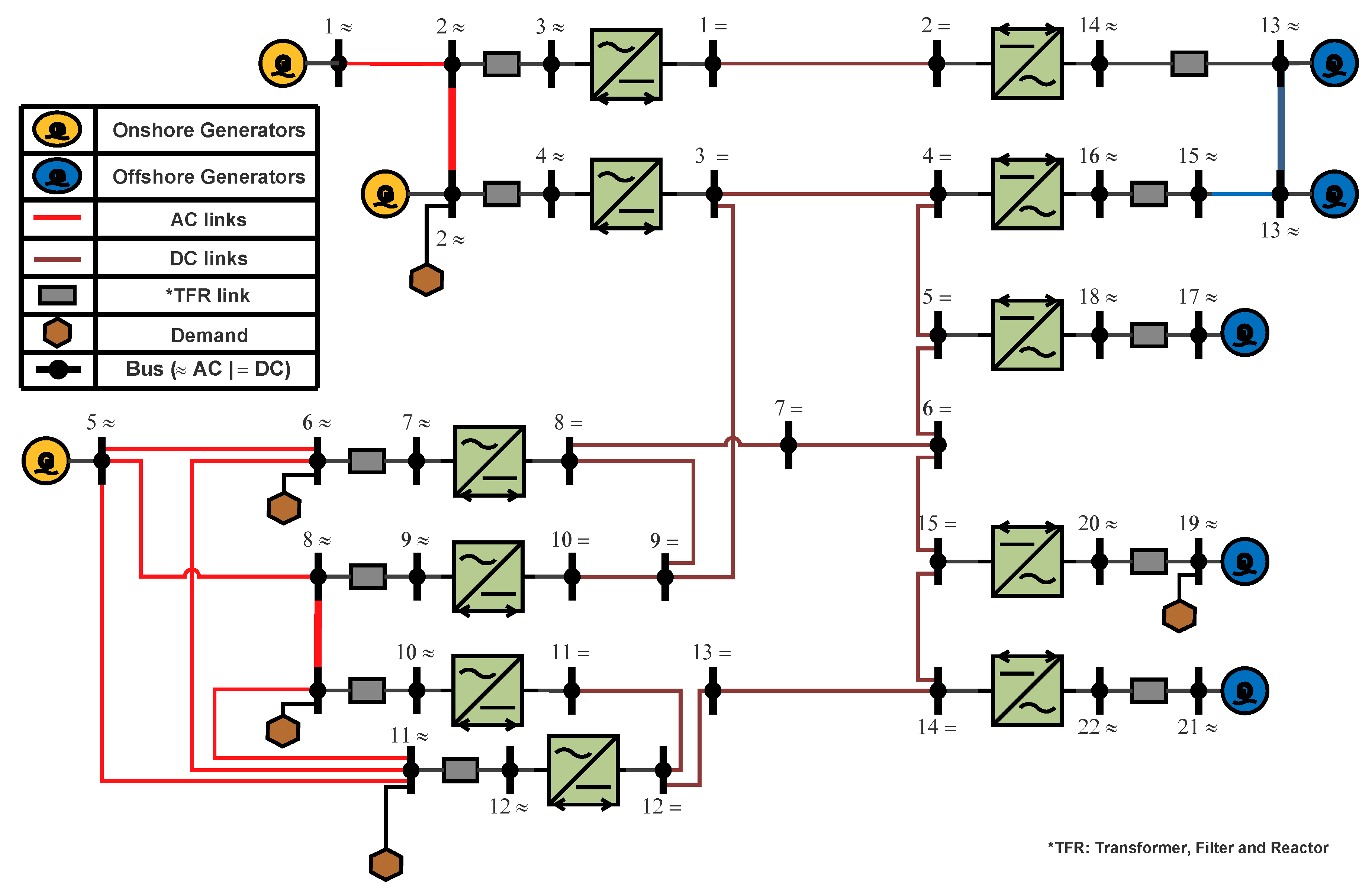
The second network case is a modified version of the Cigre B4 DC grids test system [57]. It has 6 AC systems—22 buses-, 2 DC systems—15 buses-, 8 AC generators (onshore and offshore), 11 converters (rectifiers and inverters) and 5 demand nodes/buses as shown in Figure 11. A total of 109 measurements (z) were used in the unified WLS, divided into 66 AC, 21 DC and 22 converter measurements. Note that the decentralized approach used AC and DC measurements only. Gaussian noise was added to all measurements except the slack buses voltages. Measurements types and counts are shown in Table 6.
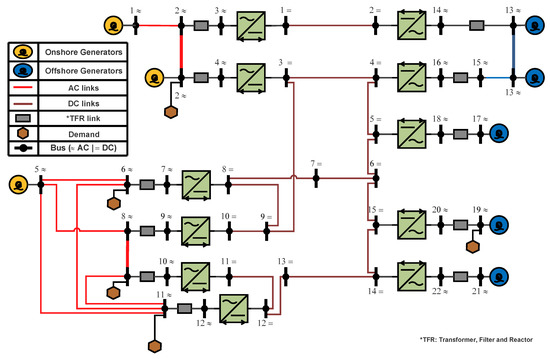
Figure 11.
Multi-HVDC/AC transmission systems based on Cigre B4 network test case.

Table 6.
Cigre B4 SE measurements.
Table 7 shows the estimates of the converter measurements and constraints. A similar conclusion to the previous test case can be found, the power coupling minimizes the error in the power measurements near the converter (injected and ). However, in some cases that correction can lead to errors in the voltage magnitude at both sides of the converter, which the voltage coupling can correct.

Table 7.
The converter coupling measurements.
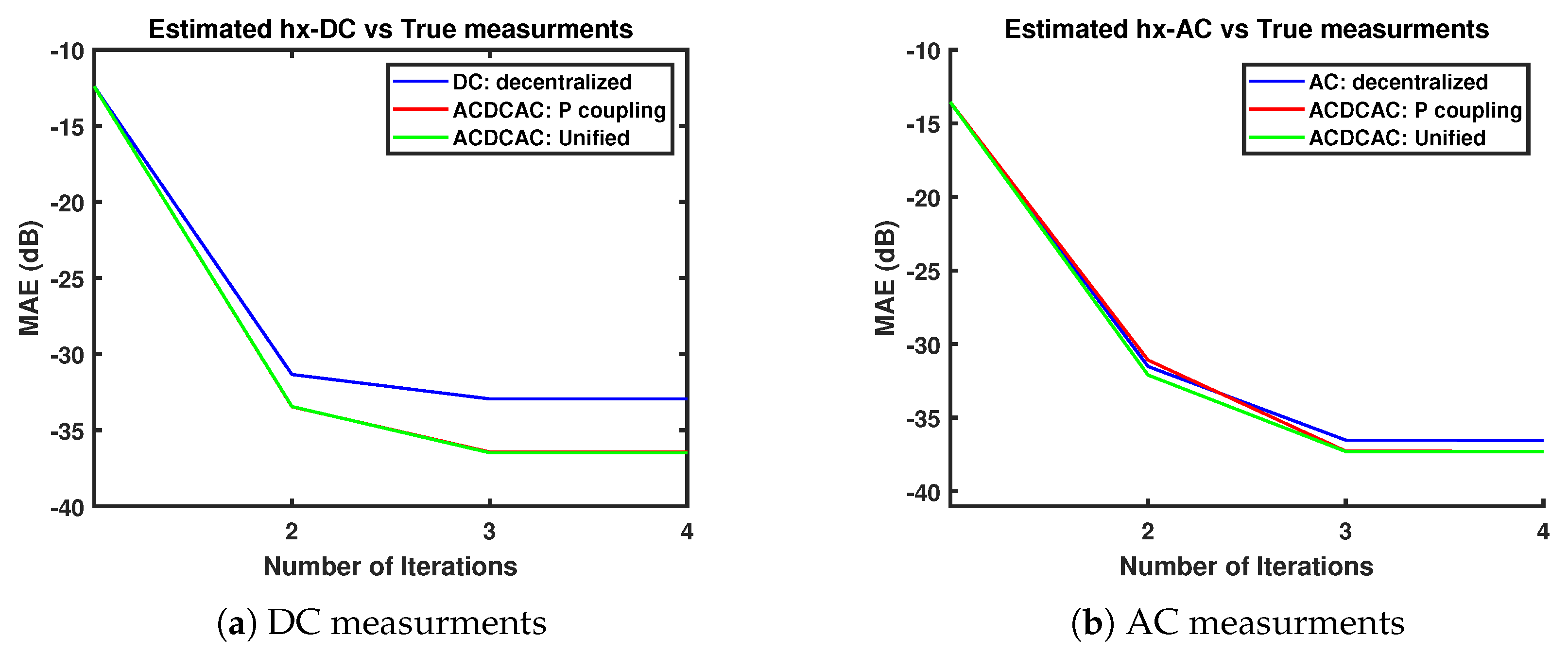
In Figure 12, the unified WLS has estimated the AC and DC measurements better than the decentralized approach, the MAE has reduced by −0.7577 dB and −3.5393 dB respectively. This pattern of accuracy performance in the Cigre B4 model is similar to the previous test case in Figure 9.
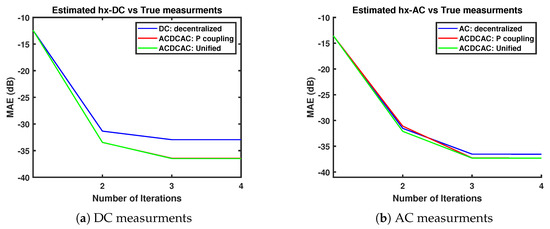
Figure 12.
MAE of the AC and DC measurements in the Cigre B4 network.
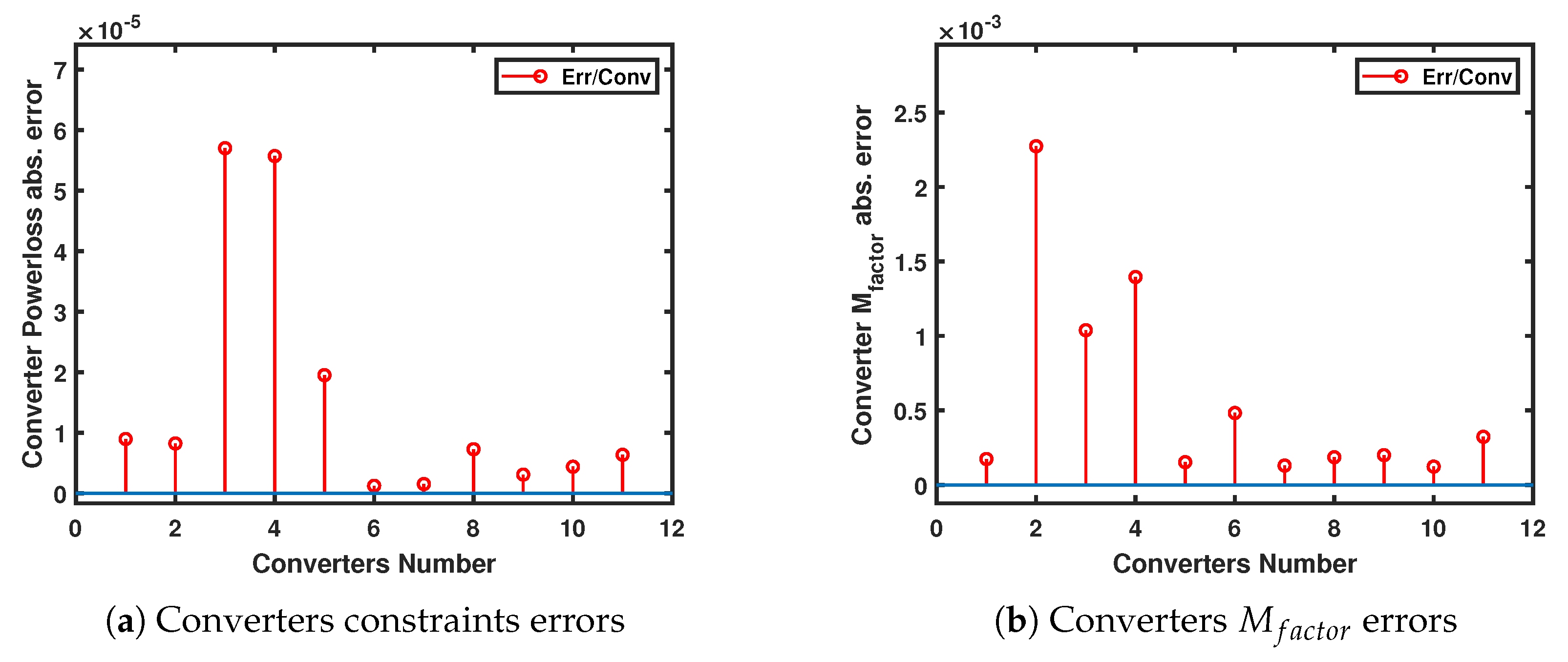
In addition, the unified WLS has shown relatively low errors in the estimates of the power couplings constraints and the voltage coupling measurements as shown in Figure 13a,b respectively. In (a), the estimated constraint values are compared with zero, while in (b) the estimated are compared with the true measurements.
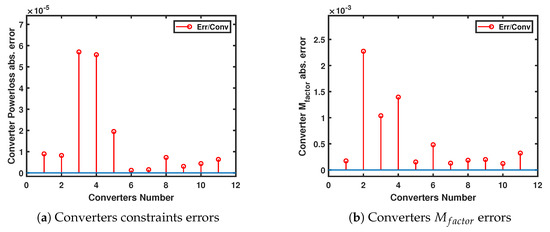
Figure 13.
Absolute error of the power and voltage coupling measurements of the Cigre B4 network.
Table 8 shows the DC systems states estimation results for the three scenarios respectively, where T1 is: Decentralized, T2: With converter P-coupling, and T3: Unified. It can be noticed that the error in the decentralized method is higher than the other two scenarios (e.g., bus 6, 11, 12 and 13). In addition, whenever the system has many buses but less trusted redundant measurements, the possibility of having errors is more elevated.

Table 8.
DC systems SE: Decentralized/Power coupling/Unified.
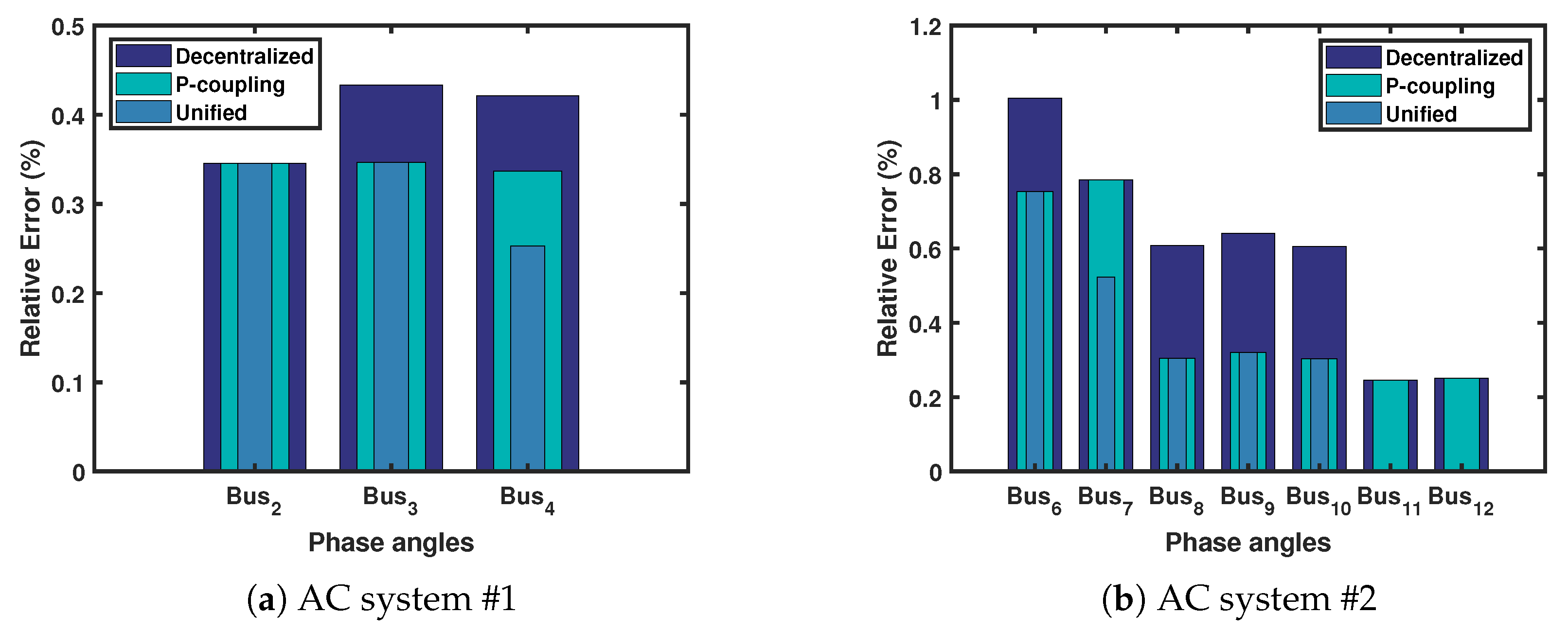
Appendix B.2 contains the numerical values of the AC side estimations for the three scenarios in tables. In this test case, the 2nd AC system has the largest errors, mainly on the phase angle states. That is because the only trusted measurement is the voltage magnitude of the slack bus (#5), while the rest of the measurements are noisy. However, the unified state estimation was able to reduce that error compared to the other two scenarios, due to the converter coupling -redundant- measurements and constraints. Figure 14 shows the relative error for each scenario in two AC systems with the largest errors in phase angles (radian) up to 5 digits.
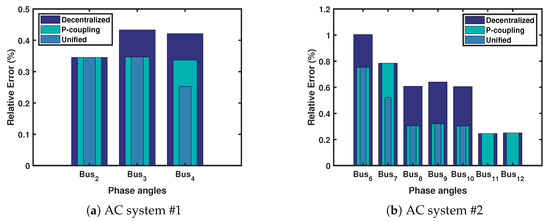
Figure 14.
Relative error of the phase angles states in AC systems 1 and 2.
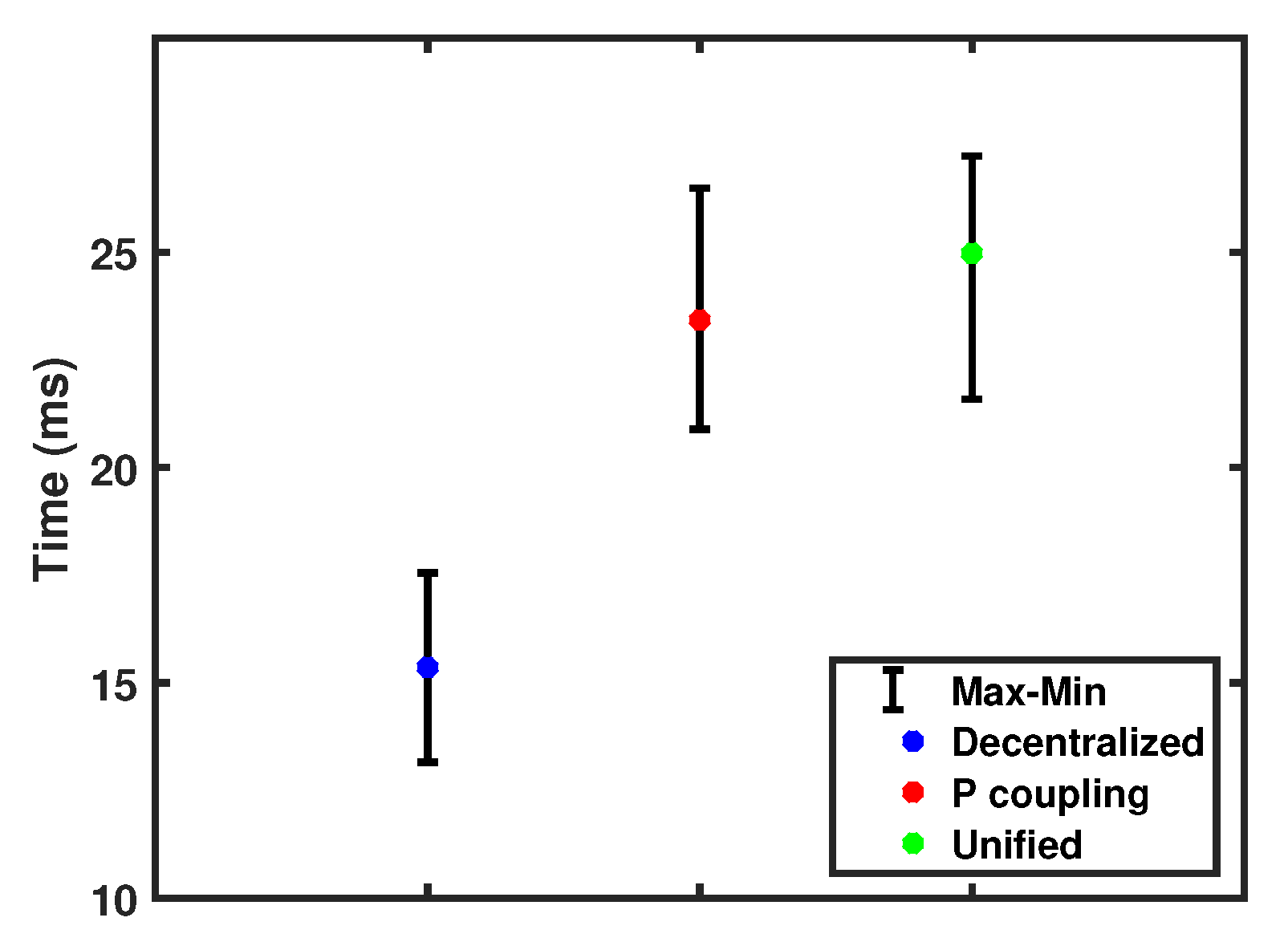
The time performance of the three scenarios was calculated for 100 simulations on Cigre B4 test case. It was concluded that the unified WLS time performance was a downside for this approach. Figure 15 shows that the decentralized approach was 62% faster than the unified method. In addition, the decentralized approach showed fewer memory allocations and storage consumption, as shown in Table 9. These outcomes were expected since the unified approach has 65.1% more measurements to be processed. However, a pre-processing algorithm can build a trade-off between the estimation accuracy and the computational performance by selectively pick the most dominant measurements. In other words, the unified WLS computational drawback can be minimized by having sufficient and the most effective measurements.
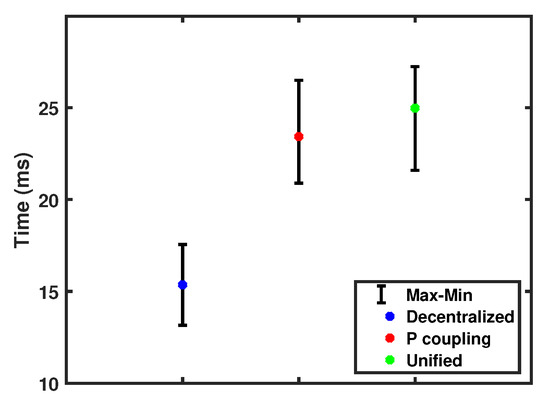
Figure 15.
The time performance of the decentralized vs. P-coupling vs. unified approaches.

Table 9.
Memory performance and storage.
6. Main Conclusions
The work in this paper presents a unified state estimator toolbox based on WLS algorithm that is suitable for hybrid VSC based HVDC/AC transmission networks. The estimator solves a centralized Newton-Raphson that uses AC, DC and converter measurements to provide better system states estimates for the system operators. The modified method has extended the WLS measurements function and the Jacobian matrix to include VSC-HVDC/AC coupling components, such as power constraints and voltage ratios. The algorithm demands that the AC, DC and converter measurements to be available in synchronized time. The approach was simulated in two different network cases with multiple AC and DC systems. A comparison between the unified WLS and the decentralized method was investigated. It was shown that the accuracy of the system states estimations has been improved and benefited from the converter coupling -redundant- measurements. Moreover, the overall errors in the measurements have been reduced compared to the decentralized WLS. However, higher computational power was required for the unified WLS and the power coupling method. Besides, it is worthy to note that the current stage of the algorithm is still missing the robustness feature against bad data.
Author Contributions
Formal analysis, M.A.; Methodology, M.A.; Software, M.A.; Supervision, H.L. and H.M.; Validation, M.A.; Writing–original draft, M.A.; Writing–review & editing, H.L. and H.M. All authors have read and agreed to the published version of the manuscript.
Funding
This project has received funding from the European Union’s Horizon 2020 research and innovation programme under the Marie Skłodowska-Curie grant agreement InnoDC No 765585. This document reflects only the author’s views; the European Commission is not responsible for any use that may be made of the information it contains.
Acknowledgments
The authors gratefully acknowledge the contributions of Konstantinos Kotsalos for his supports in paper proofreading.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
| AC | Alternating Current |
| DC | Direct Current |
| EMS | Energy Management Systems |
| HVDC | High Voltage Direct Current |
| IED | Intelligent Electronic Devices |
| LAV | Least Absolute Value |
| MAE | Mean Absolute Error |
| PCC | Point of Common Coupling |
| PMU | Phasor Measurements Unit |
| RTU | Remote Terminal Unit |
| SCADA | Supervisory, Control and Data Acquisition |
| TFR | Transformer, Filter and Reactor |
| VSC | Voltage Source Converter |
| WLS | Weighted Least Squares |
Appendix A
The traditional partial derivative of the AC and DC components in the Jacobian Matrix:
Appendix A.1. AC Components
presents the partial derivative of the voltage magnitude at bus i ()
presents the partial derivative of the active power injections at bus i ()
presents the partial derivative of the reactive power injections at bus i ()
presents the partial derivative of the active power flow from bus i to bus j ()
presents the partial derivative of the reactive power flow from bus i to bus j ()
presents the partial derivative of the current flow from bus i to bus j ()-shunt admittance is ignored
Appendix A.2. DC Components
presents the partial derivative of the voltage magnitude at bus i ()
presents the partial derivative of the real power injections at bus i ()
presents the partial derivative of the real power flow from bus i to bus j ()
presents the partial derivative of the current flow from bus i to bus j ()
Appendix B
The AC system states estimation of the WLS simulations.
Appendix B.1. AC SE of Case 1
The estimations of the AC systems states (in Vpu and radian) are shown in Table A1, Table A2 and Table A3 for the three scenarios respectively.

Table A1.
AC systems SE: Decentralized.
Table A1.
AC systems SE: Decentralized.
| Sys. # | Bus # | ||||||
|---|---|---|---|---|---|---|---|
| 1 | 1.0 | 1.0600 | 1.0600 | −0.0000 | 0.0000 | 0.0000 | 0.0000 |
| 2.0 | 1.0569 | 1.0569 | −0.0000 | −0.0278 | −0.0277 | 0.0001 | |
| 3.0 | 1.0551 | 1.0551 | −0.0000 | −0.0601 | −0.0599 | 0.0002 | |
| 4.0 | 1.0540 | 1.0540 | −0.0000 | −0.0612 | −0.0610 | 0.0002 | |
| 2 | 5.0 | 1.0615 | 1.0615 | 0.0000 | 0.0004 | 0.0003 | 0.0001 |
| 6.0 | 1.0600 | 1.0600 | 0.0000 | 0.0000 | −0.0000 | 0.0000 | |
| 7.0 | 1.0433 | 1.0432 | 0.0001 | −0.0353 | −0.0350 | −0.0003 | |
| 8.0 | 1.0289 | 1.0287 | 0.0002 | −0.0721 | −0.0714 | −0.0007 |

Table A2.
AC systems SE: With converter power coupling.
Table A2.
AC systems SE: With converter power coupling.
| Sys. # | Bus # | ||||||
|---|---|---|---|---|---|---|---|
| 1 | 1.0 | 1.0600 | 1.0600 | −0.0000 | 0.0000 | 0.0000 | 0.0000 |
| 2.0 | 1.0569 | 1.0569 | 0.0000 | −0.0278 | −0.0278 | −0.0000 | |
| 3.0 | 1.0551 | 1.0551 | 0.0000 | −0.0601 | −0.0601 | −0.0000 | |
| 4.0 | 1.0540 | 1.0540 | 0.0000 | −0.0612 | −0.0612 | −0.0000 | |
| 2 | 5.0 | 1.0615 | 1.0615 | 0.0000 | 0.0004 | 0.0004 | 0.0000 |
| 6.0 | 1.0600 | 1.0600 | 0.0000 | 0.0000 | −0.0000 | 0.0000 | |
| 7.0 | 1.0433 | 1.0432 | 0.0001 | −0.0353 | −0.0351 | −0.0002 | |
| 8.0 | 1.0289 | 1.0287 | 0.0002 | −0.0721 | −0.0715 | −0.0006 |

Table A3.
AC systems SE: Unified.
Table A3.
AC systems SE: Unified.
| Sys. # | Bus # | ||||||
|---|---|---|---|---|---|---|---|
| 1 | 1.0 | 1.0600 | 1.0600 | −0.0000 | 0.0000 | 0.0000 | 0.0000 |
| 2.0 | 1.0569 | 1.0569 | 0.0000 | −0.0278 | −0.0278 | −0.0000 | |
| 3.0 | 1.0551 | 1.0551 | 0.0000 | −0.0601 | −0.0601 | −0.0000 | |
| 4.0 | 1.0540 | 1.0540 | 0.0000 | −0.0612 | −0.0612 | −0.0000 | |
| 2 | 5.0 | 1.0615 | 1.0615 | 0.0000 | 0.0004 | 0.0004 | 0.0000 |
| 6.0 | 1.0600 | 1.0600 | 0.0000 | 0.0000 | −0.0000 | 0.0000 | |
| 7.0 | 1.0433 | 1.0433 | 0.0000 | −0.0353 | −0.0351 | −0.0002 | |
| 8.0 | 1.0289 | 1.0287 | 0.0002 | −0.0721 | −0.0715 | −0.0006 |
Appendix B.2. AC SE of Case 2
The three scenarios AC systems state estimations are shown in Table A4, Table A5 and Table A6 respectively.

Table A4.
AC systems SE: Decentralized.
Table A4.
AC systems SE: Decentralized.
| Sys. # | Bus # | ||||||
|---|---|---|---|---|---|---|---|
| 1 | 1.0 | 1.0000 | 1.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 |
| 2.0 | 1.0000 | 1.0000 | 0.0000 | −0.1157 | −0.1161 | 0.0004 | |
| 3.0 | 1.0003 | 1.0003 | 0.0000 | −0.1154 | −0.1159 | 0.0005 | |
| 4.0 | 0.9970 | 1.9970 | 0.0000 | −0.1187 | −0.1192 | 0.0005 | |
| 2 | 5.0 | 1.0000 | 1.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 |
| 6.0 | 0.9969 | 0.9969 | 0.0000 | −0.0398 | −0.0394 | −0.0004 | |
| 7.0 | 0.9984 | 0.9984 | 0.0000 | −0.0382 | −0.0379 | −0.0003 | |
| 8.0 | 0.9968 | 0.9968 | 0.0000 | −0.0329 | −0.0327 | −0.0002 | |
| 9.0 | 0.9985 | 0.9986 | −0.0000 | −0.0312 | −0.0310 | −0.0002 | |
| 10.0 | 0.9967 | 0.9967 | −0.0000 | −0.0330 | −0.0328 | −0.0002 | |
| 11.0 | 0.9965 | 0.9965 | −0.0000 | −0.0407 | −0.0406 | −0.0001 | |
| 12.0 | 0.9973 | 0.9973 | −0.0000 | −0.0399 | −0.0398 | −0.0001 | |
| 3 | 13.0 | 1.0000 | 1.0000 | −0.0000 | 0.0000 | 0.0000 | 0.0000 |
| 14.0 | 0.9995 | 0.9995 | −0.0000 | −0.0005 | −0.0005 | 0.0000 | |
| 15.0 | 1.0000 | 1.0000 | −0.0000 | 0.0000 | −0.0000 | 0.0000 | |
| 16.0 | 0.9995 | 0.9995 | −0.0000 | −0.0005 | −0.0005 | 0.0000 | |
| 4 | 17.0 | 1.0000 | 1.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 |
| 18.0 | 0.9990 | 0.9990 | 0.0000 | −0.0010 | −0.0010 | 0.0000 | |
| 5 | 19.0 | 1.0000 | 1.0000 | −0.0000 | 0.0000 | 0.0000 | 0.0000 |
| 20.0 | 1.0001 | 1.0001 | 0.0000 | 0.0001 | 0.0001 | 0.0000 | |
| 6 | 21.0 | 1.0000 | 1.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 |
| 22.0 | 0.9995 | 0.9995 | 0.0000 | −0.0005 | −0.0005 | 0.0000 |

Table A5.
AC systems SE: With converter power coupling.
Table A5.
AC systems SE: With converter power coupling.
| Sys. # | Bus # | ||||||
|---|---|---|---|---|---|---|---|
| 1 | 1.0 | 1.0000 | 1.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 |
| 2.0 | 1.0000 | 1.0000 | 0.0000 | −0.1157 | −0.1161 | 0.0004 | |
| 3.0 | 1.0003 | 1.0003 | 0.0000 | −0.1154 | −0.1158 | 0.0004 | |
| 4.0 | 0.9970 | 1.9970 | 0.0000 | −0.1187 | −0.1191 | 0.0004 | |
| 2 | 5.0 | 1.0000 | 1.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 |
| 6.0 | 0.9969 | 0.9969 | 0.0000 | −0.0398 | −0.0395 | −0.0003 | |
| 7.0 | 0.9984 | 0.9984 | 0.0000 | −0.0382 | −0.0380 | −0.0002 | |
| 8.0 | 0.9968 | 0.9968 | 0.0000 | −0.0329 | −0.0328 | −0.0001 | |
| 9.0 | 0.9985 | 0.9986 | −0.0000 | −0.0312 | −0.0311 | −0.0001 | |
| 10.0 | 0.9967 | 0.9967 | −0.0000 | −0.0330 | −0.0329 | −0.0001 | |
| 11.0 | 0.9965 | 0.9965 | −0.0000 | −0.0407 | −0.0406 | −0.0001 | |
| 12.0 | 0.9973 | 0.9973 | −0.0000 | −0.0399 | −0.0398 | −0.0001 | |
| 3 | 13.0 | 1.0000 | 1.0000 | −0.0000 | 0.0000 | 0.0000 | 0.0000 |
| 14.0 | 0.9995 | 0.9995 | −0.0000 | −0.0005 | −0.0005 | 0.0000 | |
| 15.0 | 1.0000 | 1.0000 | −0.0000 | 0.0000 | −0.0000 | 0.0000 | |
| 16.0 | 0.9995 | 0.9995 | −0.0000 | −0.0005 | −0.0005 | 0.0000 | |
| 4 | 17.0 | 1.0000 | 1.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 |
| 18.0 | 0.9990 | 0.9990 | 0.0000 | −0.0010 | −0.0010 | 0.0000 | |
| 5 | 19.0 | 1.0000 | 1.0000 | −0.0000 | 0.0000 | 0.0000 | 0.0000 |
| 20.0 | 1.0001 | 1.0001 | 0.0000 | 0.0001 | 0.0001 | 0.0000 | |
| 6 | 21.0 | 1.0000 | 1.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 |
| 22.0 | 0.9995 | 0.9995 | 0.0000 | −0.0005 | −0.0005 | 0.0000 |

Table A6.
AC systems SE: Unified.
Table A6.
AC systems SE: Unified.
| Sys. # | Bus # | ||||||
|---|---|---|---|---|---|---|---|
| 1 | 1.0 | 1.0000 | 1.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 |
| 2.0 | 1.0000 | 1.0000 | 0.0000 | −0.1157 | −0.1161 | 0.0004 | |
| 3.0 | 1.0003 | 1.0003 | 0.0000 | −0.1154 | −0.1158 | 0.0004 | |
| 4.0 | 0.9970 | 1.9970 | 0.0000 | −0.1187 | −0.1190 | 0.0003 | |
| 2 | 5.0 | 1.0000 | 1.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 |
| 6.0 | 0.9969 | 0.9969 | 0.0000 | −0.0398 | −0.0395 | −0.0003 | |
| 7.0 | 0.9984 | 0.9984 | 0.0000 | −0.0382 | −0.0380 | −0.0002 | |
| 8.0 | 0.9968 | 0.9968 | 0.0000 | −0.0329 | −0.0328 | −0.0001 | |
| 9.0 | 0.9985 | 0.9986 | −0.0000 | −0.0312 | −0.0311 | −0.0001 | |
| 10.0 | 0.9967 | 0.9967 | −0.0000 | −0.0330 | −0.0329 | −0.0001 | |
| 11.0 | 0.9965 | 0.9965 | −0.0000 | −0.0407 | −0.0407 | −0.0000 | |
| 12.0 | 0.9973 | 0.9973 | −0.0000 | −0.0399 | −0.0399 | −0.0000 | |
| 3 | 13.0 | 1.0000 | 1.0000 | −0.0000 | 0.0000 | 0.0000 | 0.0000 |
| 14.0 | 0.9995 | 0.9995 | −0.0000 | −0.0005 | −0.0005 | 0.0000 | |
| 15.0 | 1.0000 | 1.0000 | −0.0000 | 0.0000 | −0.0000 | 0.0000 | |
| 16.0 | 0.9995 | 0.9995 | −0.0000 | −0.0005 | −0.0005 | 0.0000 | |
| 4 | 17.0 | 1.0000 | 1.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 |
| 18.0 | 0.9990 | 0.9990 | 0.0000 | −0.0010 | −0.0010 | 0.0000 | |
| 5 | 19.0 | 1.0000 | 1.0000 | −0.0000 | 0.0000 | 0.0000 | 0.0000 |
| 20.0 | 1.0001 | 1.0001 | 0.0000 | 0.0001 | 0.0001 | 0.0000 | |
| 6 | 21.0 | 1.0000 | 1.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 |
| 22.0 | 0.9995 | 0.9995 | 0.0000 | −0.0005 | −0.0005 | 0.0000 |
References
- Roberson, D.; Kim, H.C.; Chen, B.; Page, C.; Nuqui, R.; Valdes, A.; Macwan, R.; Johnson, B.K. Improving Grid Resilience Using High-Voltage dc: Strengthening the Security of Power System Stability. IEEE Power Energy Mag. 2019, 17, 38–47. [Google Scholar] [CrossRef]
- Lambrechts, J.W.; Sinha, S. Microsensing Networks for Sustainable Cities; Springer: Cham, Switzerland, 2016. [Google Scholar]
- Li, Z.; Zhan, R.; Li, Y.; He, Y.; Hou, J.; Zhao, X.; Zhang, X.P. Recent developments in HVDC transmission systems to support renewable energy integration. Glob. Energy Interconnect. 2018, 1, 595–607. [Google Scholar] [CrossRef]
- Ayiad, M.; Martins, H.; Nduka, O.; Pal, B. State Estimation of Low Voltage Distribution Network with Integrated Customer-Owned PV and Storage Unit. In Proceedings of the 2019 IEEE Milan PowerTech, Milan, Italy, 23–27 June 2019; pp. 1–6. [Google Scholar]
- Ardelean, M.; Minnebo, P.; Gerbelová, H. Optimal Paths for Electricity Interconnections between Central Asia and Europe; Technical Report; Publications Office of the European Union: Luxembourg, 2020. [Google Scholar] [CrossRef]
- Arrillaga, J.; Liu, Y.; Watson, N. Flexible Power Transmission: The HVDC Options. In Flexible Power Transmission: The HVDC Options; Wiley: Hoboken, NJ, USA, 2007; pp. 1–362. [Google Scholar] [CrossRef]
- Liang, J.; Bellmunt, O.; Van Hertem, D. HVDC Grid Layouts: For Offshore and Supergrid of the Future; Wiley: Hoboken, NJ, USA, 2016; pp. 171–191. [Google Scholar] [CrossRef]
- Vincenzo, G.; Flavia, G.; Gianluca, F.; Manuel, S.J.; Ioulia, P.; Alexandru, C.; Ijeoma, O.; Maria, M.A.; Tauno, O.; Isabella, M.; et al. Smart Grid Projects in Europe—Lessons Learned and Current Developments; Publications Office of the European Union: Luxembourg, 2011. [Google Scholar]
- Acha, E.; Roncero-Sánchez, P.; Villa-Jaen, A.; Castro, L.; Kazemtabrizi, B. VSC-FACTS-HVDC: Analysis, Modelling and Simulation in Power Grids; Wiley: Hoboken, NJ, USA, 2019. [Google Scholar]
- Wood, A.J.; Wollenberg, B.F. Power Generation, Operation, and Control, 3rd ed.; Wiley: Hoboken, NJ, USA, 2013; p. 656. [Google Scholar]
- Northcote-Green, J.; Wilson, R. Control and Automation of Electrical Power Distribution Systems; CRC Press: Boca Raton, FL, USA, 2017; pp. 1–464. [Google Scholar] [CrossRef]
- Miceli, R. Energy Management and Smart Grids. Energies 2013, 6, 2262–2290. [Google Scholar] [CrossRef]
- Agelidis, V.; Demetriades, G.; Flourentzou, N. Recent Advances in High-Voltage Direct-Current Power Transmission Systems. In Proceedings of the 2006 IEEE International Conference on Industrial Technology, Mumbai, India, 15–17 December 2007; pp. 206–213. [Google Scholar] [CrossRef]
- Pirooz Azad, S.; Taylor, J.A.; Iravani, R. Decentralized Supplementary Control of Multiple LCC-HVDC Links. IEEE Trans. Power Syst. 2016, 31, 572–580. [Google Scholar] [CrossRef]
- Yang, S.; Tang, Y.; Wang, P. Distributed Control for a Modular Multilevel Converter. IEEE Trans. Power Electron. 2018, 33, 5578–5591. [Google Scholar] [CrossRef]
- Andreasson, M.; Dimarogonas, D.V.; Sandberg, H.; Johansson, K.H. Distributed Controllers for Multiterminal HVDC Transmission Systems. IEEE Trans. Control. Netw. Syst. 2017, 4, 564–574. [Google Scholar] [CrossRef]
- Gavriluta, C.; Caire, R.; Gomez-Exposito, A.; Hadjsaid, N. A Distributed Approach for OPF-Based Secondary Control of MTDC Systems. IEEE Trans. Smart Grid 2018, 9, 2843–2851. [Google Scholar] [CrossRef]
- Li, Y.; Wu, S. Controlled Islanding for a Hybrid AC/DC Grid with VSC-HVDC Using Semi-Supervised Spectral Clustering. IEEE Access 2019, 7, 10478–10490. [Google Scholar] [CrossRef]
- Meyer-Huebner, N.; Suriyah, M.; Leibfried, T. Distributed Optimal Power Flow in Hybrid AC-DC Grids. IEEE Trans. Power Syst. 2019, 34, 2937–2946. [Google Scholar] [CrossRef]
- Radwan, A.A.A.; Mohamed, Y.A.I. Networked Control and Power Management of AC/DC Hybrid Microgrids. IEEE Syst. J. 2017, 11, 1662–1673. [Google Scholar] [CrossRef]
- Sahoo, S.K.; Sinha, A.K.; Kishore, N.K. Control Techniques in AC, DC, and Hybrid AC-DC Microgrid: A Review. IEEE J. Emerg. Sel. Top. Power Electron. 2018, 6, 738–759. [Google Scholar] [CrossRef]
- García-López, F.D.P.; Barragán-Villarejo, M.; Marano-Marcolini, A.; Maza-Ortega, J.; Martinez-Ramos, J. Experimental Assessment of a Centralised Controller for High-RES Active Distribution Networks. Energies 2018, 11, 3364. [Google Scholar] [CrossRef]
- Wang, M.; Abedrabbo, M.; Leterme, W.; Van Hertem, D.; Spallarossa, C.; Oukaili, S.; Grammatikos, I.; Kuroda, K. A Review on AC and DC Protection Equipment and Technologies: Towards Multivendor Solution. In Proceedings of the CIGRE Winnipeg 2017 Colloquium, Winnipeg, MB, Canada, 30 September–6 October 2017. [Google Scholar]
- Abur, A.; Gomez-Exposito, A. Power System State Estimation: Theory and Implementation; Marcel Dekker: New York, NY, USA, 2004; Volume 24. [Google Scholar]
- Singh, R. State Estimation in Power Distribution Network Operation. Ph.D. Thesis, Imperial College London, London, UK, 2009. [Google Scholar]
- Zhao, J.; Gomez-Exposito, A.; Netto, M.; Mili, L.; Abur, A.; Terzija, V.; Kamwa, I.; Pal, B.C.; Singh, A.K.; Qi, J.; et al. Power System Dynamic State Estimation: Motivations, Definitions, Methodologies and Future Work. IEEE Trans. Power Syst. 2019, 34, 3188–3198. [Google Scholar] [CrossRef]
- de la Villa Jaen, A.; Acha, E.; Exposito, A.G. Voltage Source Converter Modeling for Power System State Estimation: STATCOM and VSC-HVDC. IEEE Trans. Power Syst. 2008, 23, 1552–1559. [Google Scholar] [CrossRef]
- Donde, V.; Feng, X.; Segerqvist, I.; Callavik, M. Distributed State Estimation of Hybrid AC/HVDC Grids by Network Decomposition. IEEE Trans. Smart Grid 2016, 7, 974–981. [Google Scholar] [CrossRef]
- Göl, M.; Abur, A. LAV Based Robust State Estimation for Systems Measured by PMUs. IEEE Trans. Smart Grid 2014, 5, 1808–1814. [Google Scholar] [CrossRef]
- Mouco, A.; Abur, A. A robust state estimator for power systems with HVDC components. In Proceedings of the 2017 North American Power Symposium (NAPS), Morgantown, WV, USA, 17–19 September 2017; pp. 1–5. [Google Scholar]
- Flourentzou, N.; Agelidis, V.; Demetriades, G. VSC-based HVDC power transmission systems: An overview. IEEE Trans. Power Electron. 2009, 24, 592–602. [Google Scholar] [CrossRef]
- Maza-Ortega, J.M.; Gómez-Expósito, A.; Barragán-Villarejo, M.; Romero-Ramos, E.; Marano-Marcolini, A. Voltage source converter-based topologies to further integrate renewable energy sources in distribution systems. IET Renew. Power Gener. 2012, 6, 435–445. [Google Scholar] [CrossRef]
- Beerten, J.; Belmans, R. Development of an open source power flow software for high voltage direct current grids and hybrid AC/DC systems: MATACDC. IET Gener. Transm. Distrib. 2015, 9, 966–974. [Google Scholar] [CrossRef]
- Jiang, W.; Vittal, V.; Heydt, G.T. A Distributed State Estimator Utilizing Synchronized Phasor Measurements. IEEE Trans. Power Syst. 2007, 22, 563–571. [Google Scholar] [CrossRef]
- Kong, X.; Yan, Z.; Guo, R.; Xu, X.; Fang, C. Three-Stage Distributed State Estimation for AC-DC Hybrid Distribution Network Under Mixed Measurement Environment. IEEE Access 2018, 6, 39027–39036. [Google Scholar] [CrossRef]
- Grahn, P.; Briggner, V.; Johansson, L.; Babazadeh, D.; Nordstrom, L.; Babazadeh, D. Centralized versus distributed state estimation for hybrid AC/HVDC grid. In Proceedings of the 2017 IEEE PES Innovative Smart Grid Technologies Conference Europe (ISGT-Europe), Torino, Italy, 26–29 September 2017; pp. 1–6. [Google Scholar] [CrossRef]
- Xia, N.; Gooi, H.B.; Chen, S.; Hu, W. Decentralized State Estimation for Hybrid AC/DC Microgrids. IEEE Syst. J. 2018, 12, 434–443. [Google Scholar] [CrossRef]
- Martinez, R.; Fuerte Esquivel, C. A new unified approach for the state estimation and bad data analysis of electric power transmission systems with multi-terminal VSC-based HVDC networks. Electr. Power Syst. Res. 2018, 160, 251–260. [Google Scholar] [CrossRef]
- Xu, B.; Abur, A. State estimation of systems with embedded FACTS devices. In Proceedings of the 2003 IEEE Bologna Power Tech Conference Proceedings, Bologna, Italy, 23–26 June 2003; Volume 1, p. 5. [Google Scholar] [CrossRef]
- Rakpenthai, C.; Premrudeepreechacharn, S.; Uatrongjit, S.; Watson, N.R. State Estimation of Power System with UPFC Using Interior Point WLAV Method. In Proceedings of the 2006 38th North American Power Symposium, Ann Arbor, MI, USA, 24–27 September 2006; pp. 411–415. [Google Scholar] [CrossRef]
- Korres, G.N. A Distributed Multiarea State Estimation. IEEE Trans. Power Syst. 2011, 26, 73–84. [Google Scholar] [CrossRef]
- Carquex, C.; Rosenberg, C.; Bhattacharya, K. State Estimation in Power Distribution Systems Based on Ensemble Kalman Filtering. IEEE Trans. Power Syst. 2018, 33, 6600–6610. [Google Scholar] [CrossRef]
- Podmore, R.; Robinson, M.R. The Role of Simulators for Smart Grid Development. IEEE Trans. Smart Grid 2010, 1, 205–212. [Google Scholar] [CrossRef]
- Unamuno, E.; Barrena, J.A. Hybrid ac/dc microgrids Part I: Review and classification of topologies. Renew. Sustain. Energy Rev. 2015, 52, 1251–1259. [Google Scholar] [CrossRef]
- Cosovic, M.; Vukobratovic, D. Fast real-time DC state estimation in electric power systems using belief propagation. In Proceedings of the 2017 IEEE International Conference on Smart Grid Communications (SmartGridComm), Dresden, Germany, 23–27 October 2017; pp. 207–212. [Google Scholar] [CrossRef]
- Zhang, L.; Wang, G.; Giannakis, G.B. Real-Time Power System State Estimation and Forecasting via Deep Unrolled Neural Networks. IEEE Trans. Signal Process. 2019, 67, 4069–4077. [Google Scholar] [CrossRef]
- Yang, X.; Zhang, H.; Li, Q.; Guo, Z.; Zhao, K.; Li, X.; Han, F. A weight modification sequential method for VSC-MTDC power system state estimation. IOP Conf. Ser. Mater. Sci. Eng. 2017, 207, 012071. [Google Scholar] [CrossRef]
- Ding, Q.; Chung, T.S.; Zhang, B. An improved sequential method for AC/MTDC power system state estimation. IEEE Trans. Power Syst. 2001, 16, 506–512. [Google Scholar] [CrossRef]
- Zamora, E.; Fuerte Esquivel, C.; Pizano-Martínez, A.; Estrada-Garcia, H. Hybrid state estimator considering SCADA and synchronized phasor measurements in VSC-HVDC transmission links. Electr. Power Syst. Res. 2016, 133, 42–50. [Google Scholar] [CrossRef]
- Li, W. PMU-based State Estimation for Hybrid AC and DC Grids. Ph.D. Thesis, KTH, Electric Power and Energy Systems, Stockholm, Sweden, 2018. [Google Scholar]
- Zhang, T.; Wang, Y.; Zhai, M.; Huang, Y.; Zhao, L. Fast Decoupling Algorithm of State Estimation for Hybrid AC/DC Power Systems with Voltage Source Converter. Dianli Xitong Zidonghua/Autom. Electr. Power Syst. 2018, 42, 70–76. [Google Scholar] [CrossRef]
- Filho, M.B.D.C.; Silva, A.M.L.; Falcao, D.M. Bibliography on power system state estimation (1968–1989). IEEE Trans. Power Syst. 1990, 5, 950–961. [Google Scholar] [CrossRef]
- Monticelli, A. State Estimation in Electric Power Systems: A Generalized Approach; Kluwer Academic Publishers: Boston, MA, USA, 1999. [Google Scholar]
- Ergun, H.; Dave, J.; Van Hertem, D.; Geth, F. Optimal Power Flow for AC/DC Grids: Formulation, Convex Relaxation, Linear Approximation, and Implementation. IEEE Trans. Power Syst. 2019, 34, 2980–2990. [Google Scholar] [CrossRef]
- Bezanson, J.; Edelman, A.; Karpinski, S.; Shah, V.B. Julia: A fresh approach to numerical computing. SIAM Rev. 2017, 59, 65–98. [Google Scholar] [CrossRef]
- Singh, R.; Pal, B.C.; Jabr, R.A. Statistical Representation of Distribution System Loads Using Gaussian Mixture Model. IEEE Trans. Power Syst. 2010, 25, 29–37. [Google Scholar] [CrossRef]
- Vrana, T.; Dennetiere, S.; Yang, Y.; Jardini, J.; Jovcic, D.; Saad, H. The Cigré B4 DC grid test system. CIGRE Electra 2013, 270, 9. [Google Scholar]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).