Modelling of the Long-Term Acid Gas Sequestration and Its Prediction: A Unique Case Study
Abstract
1. Introduction
2. Geological Setting and Model Construction
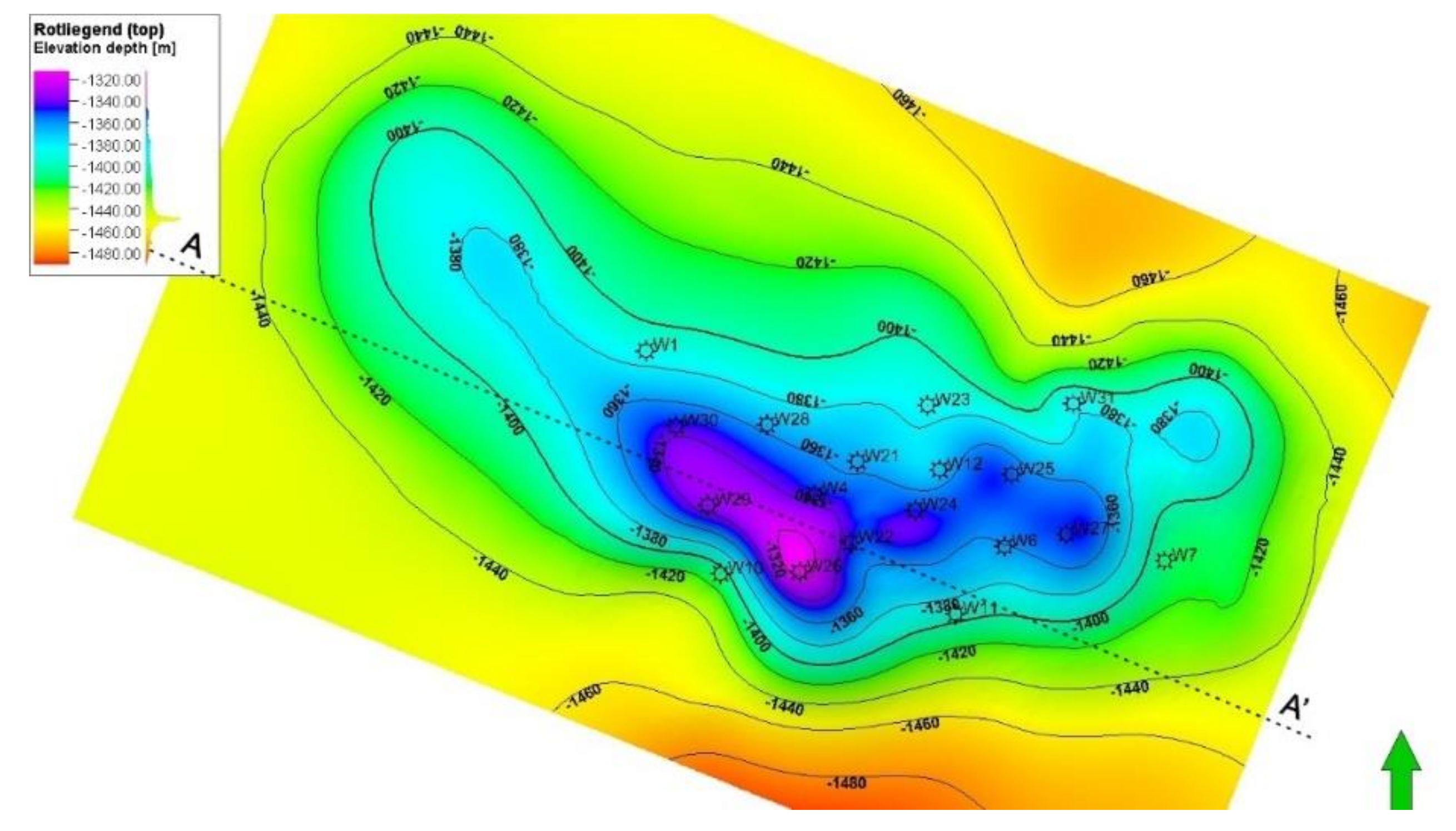
2.1. Geological Setting
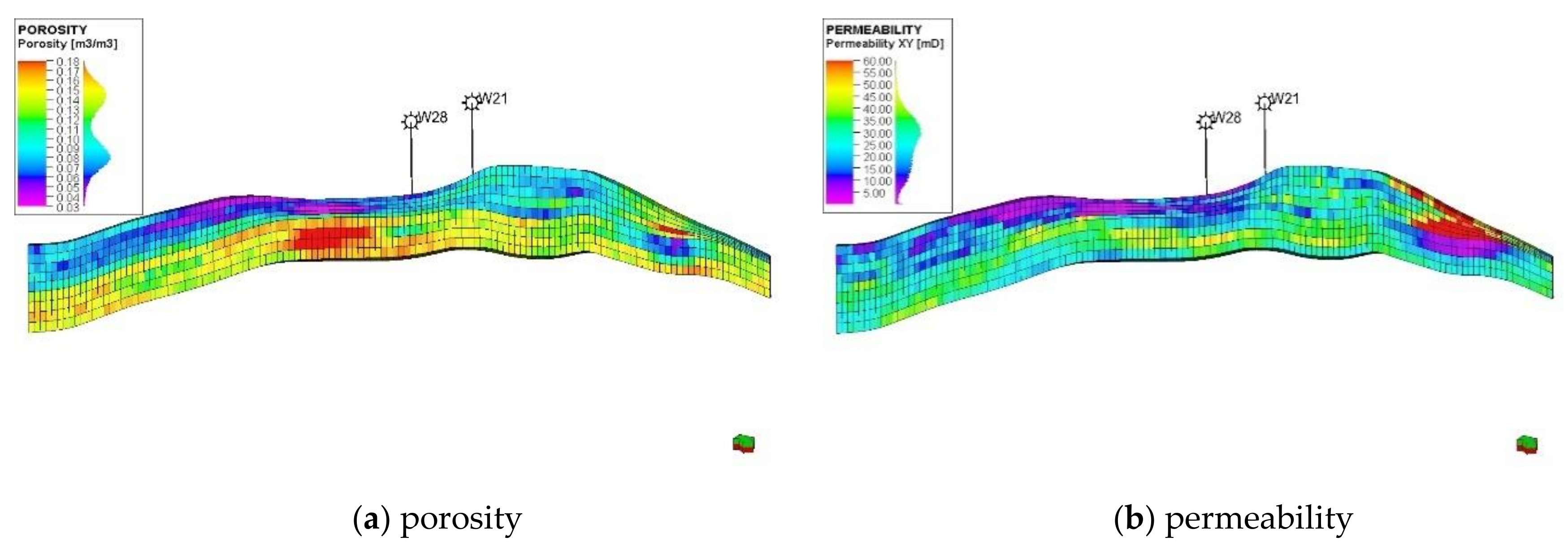
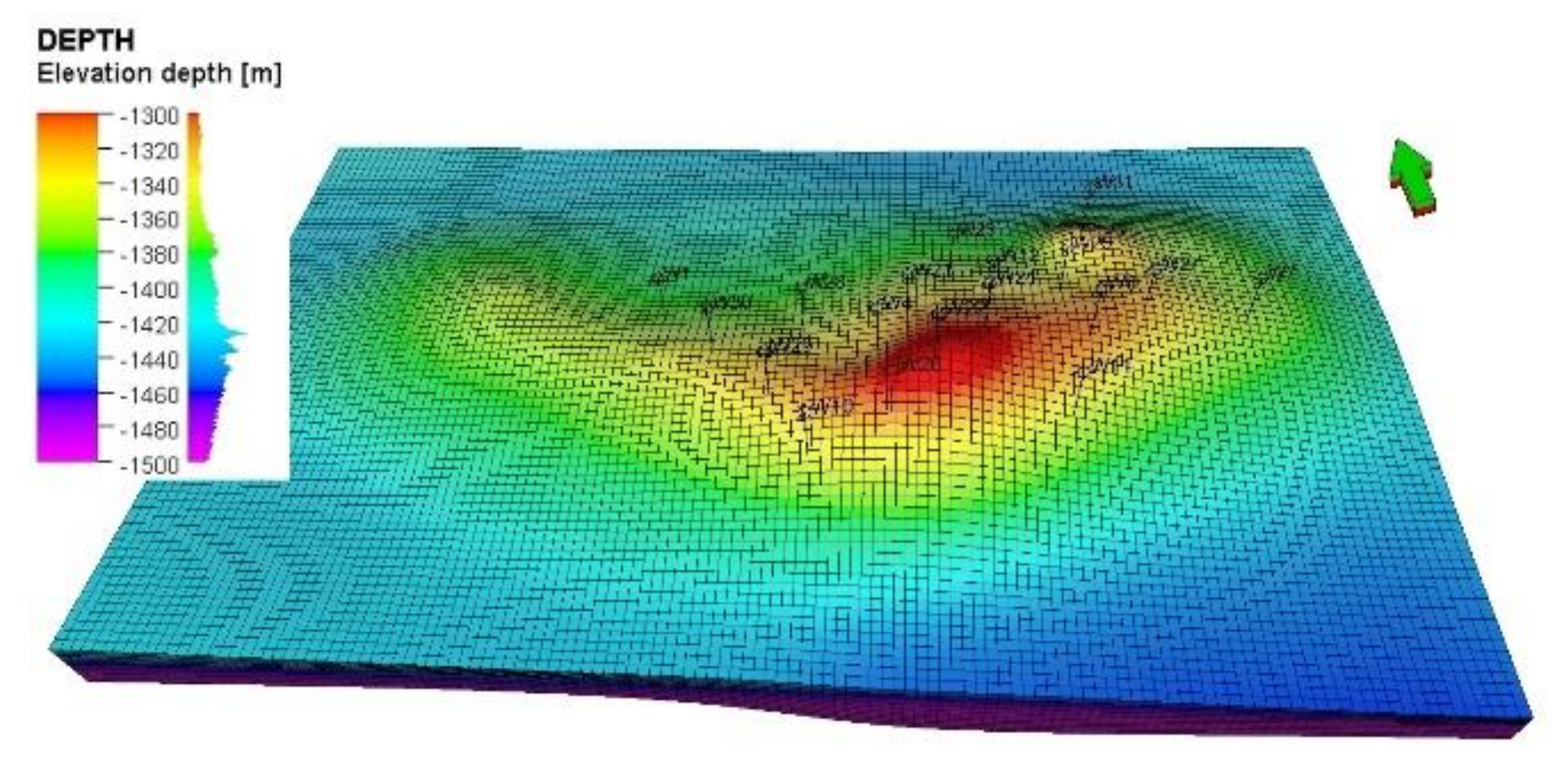
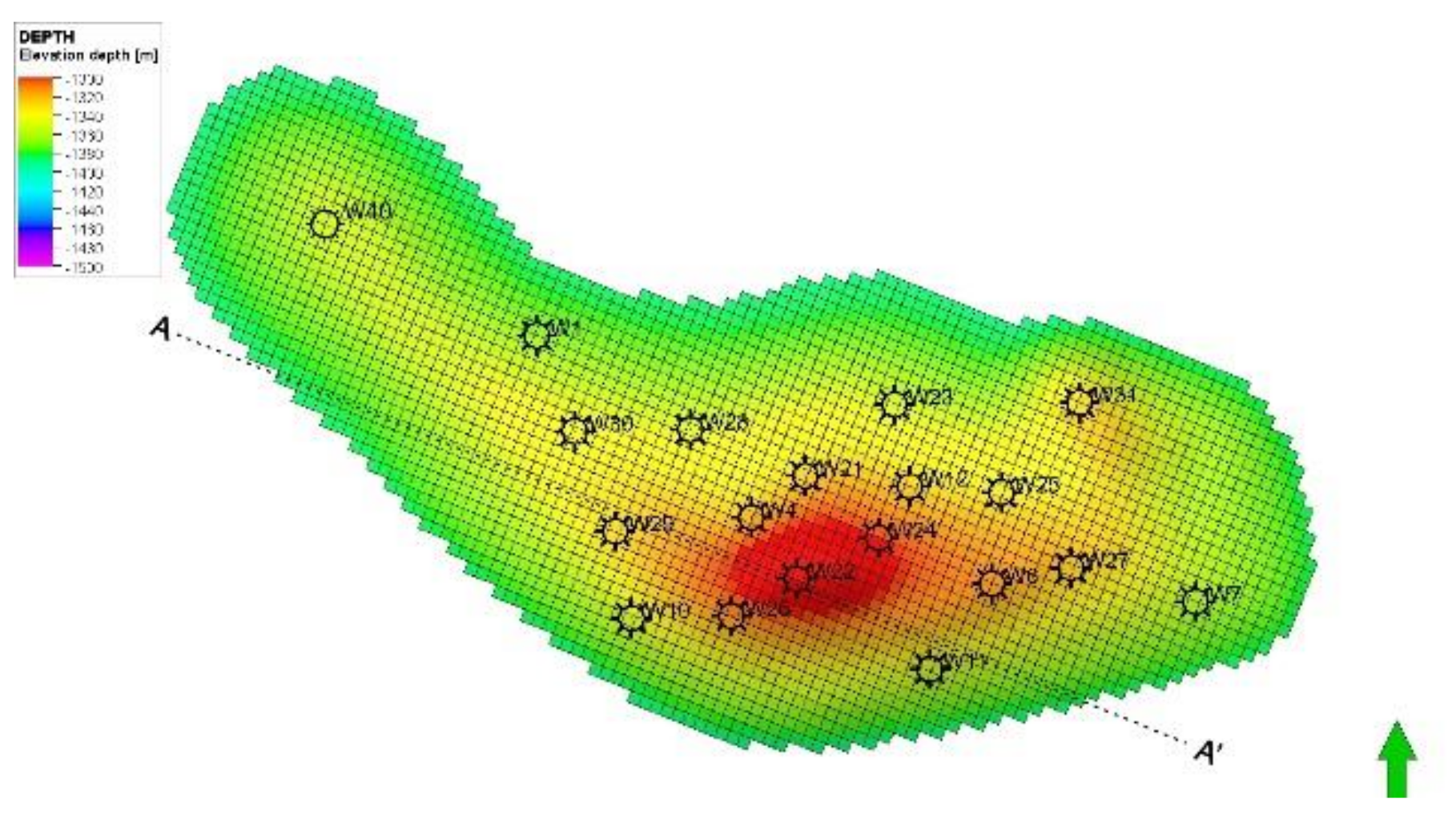
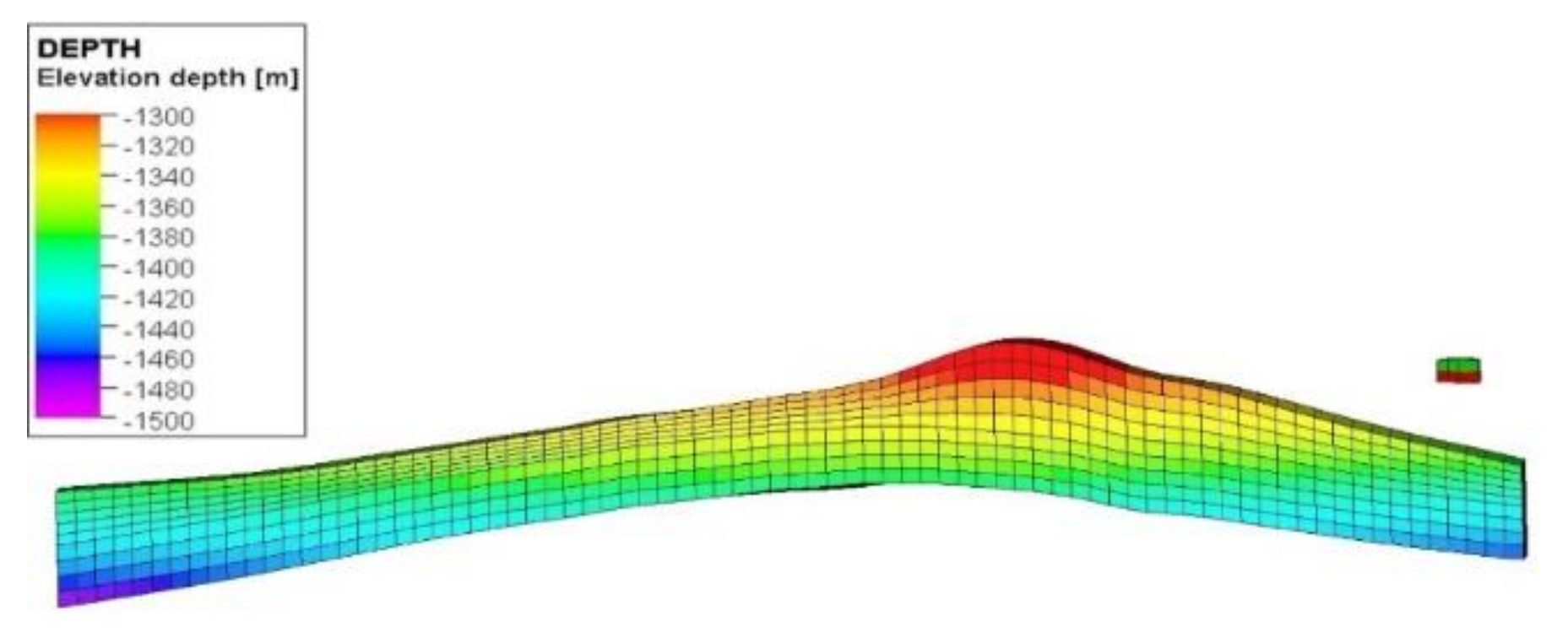
2.2. Geological Modelling
3. Dynamic Simulation Model
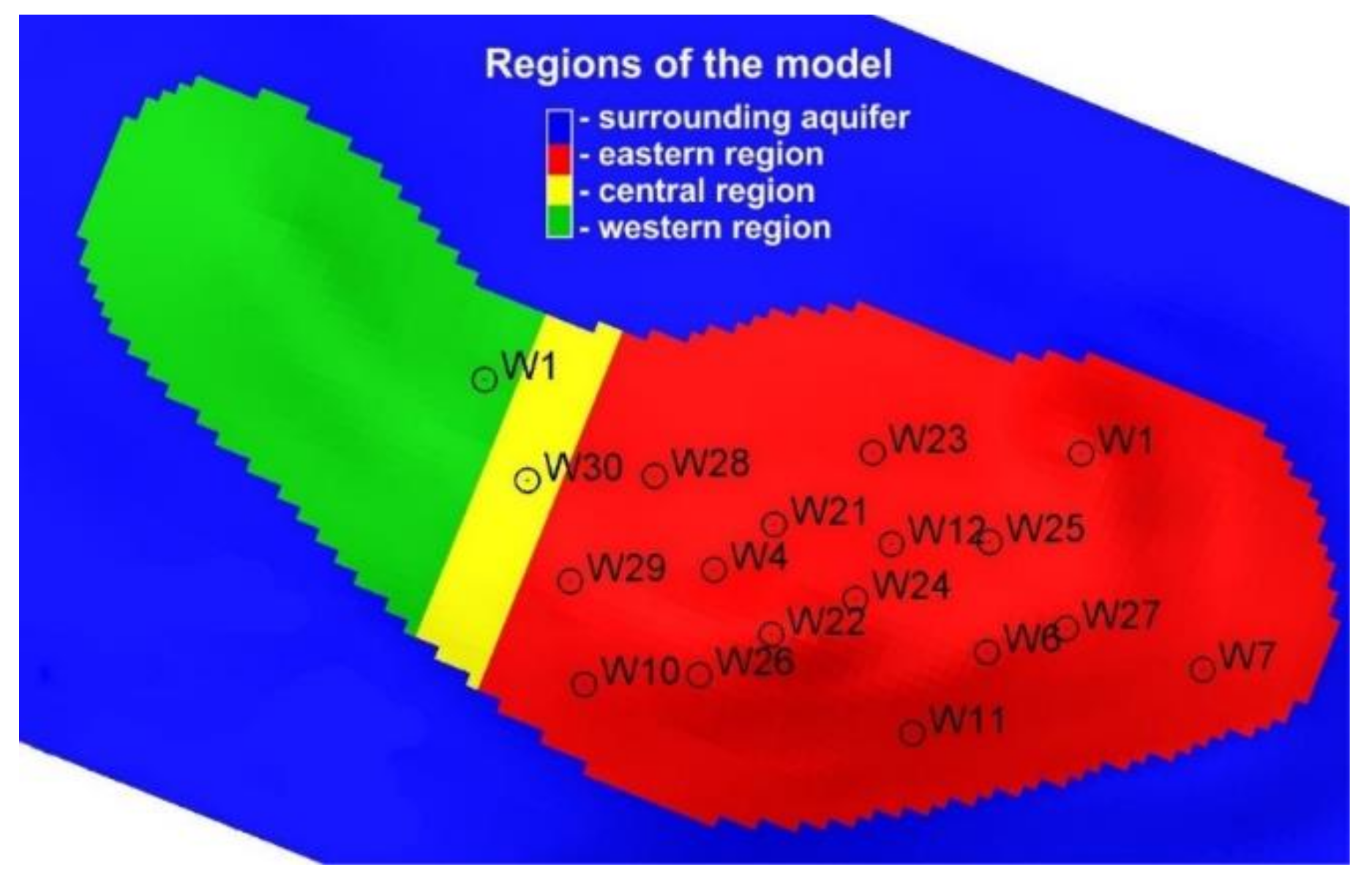
3.1. Model Construction
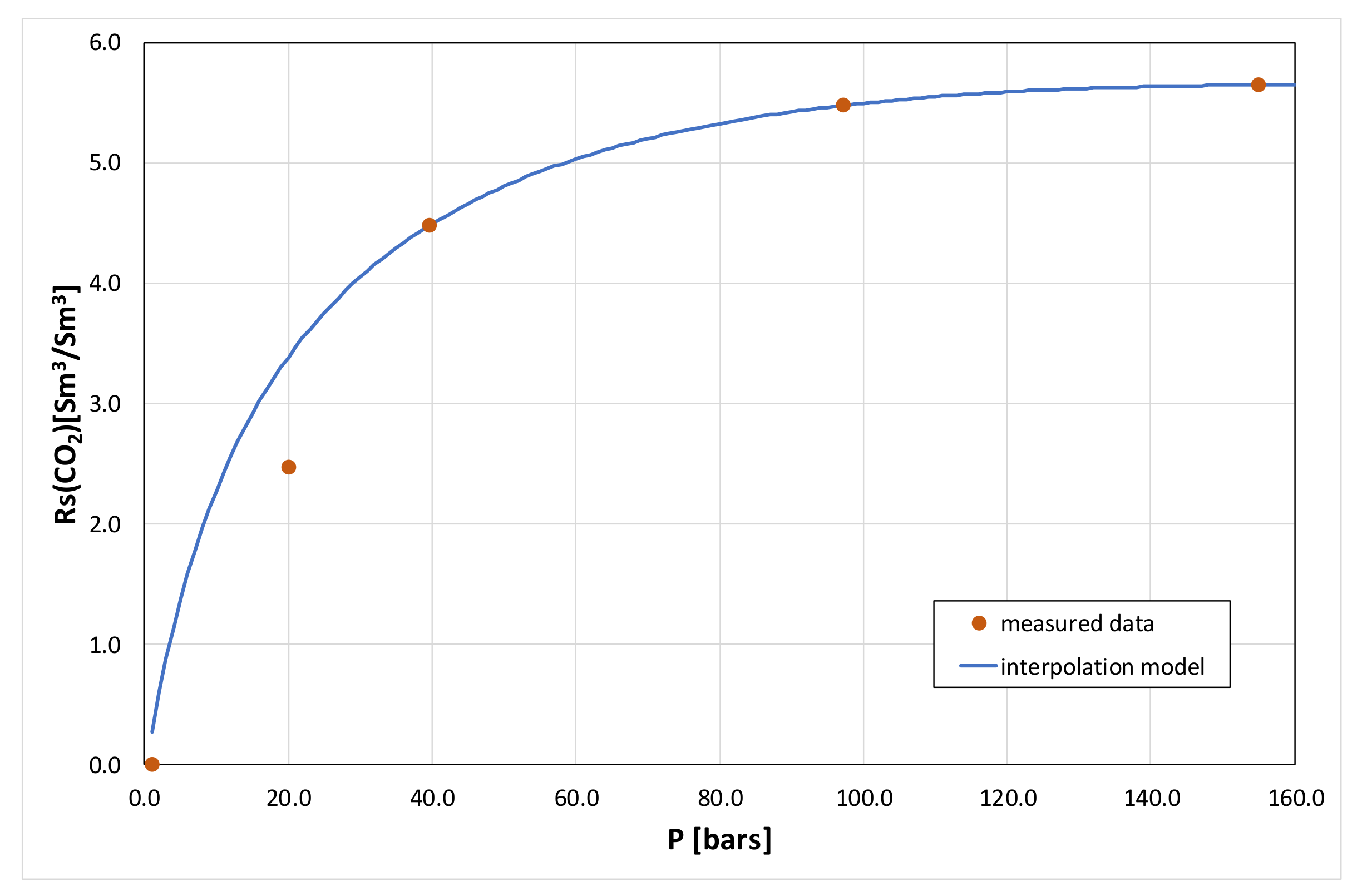
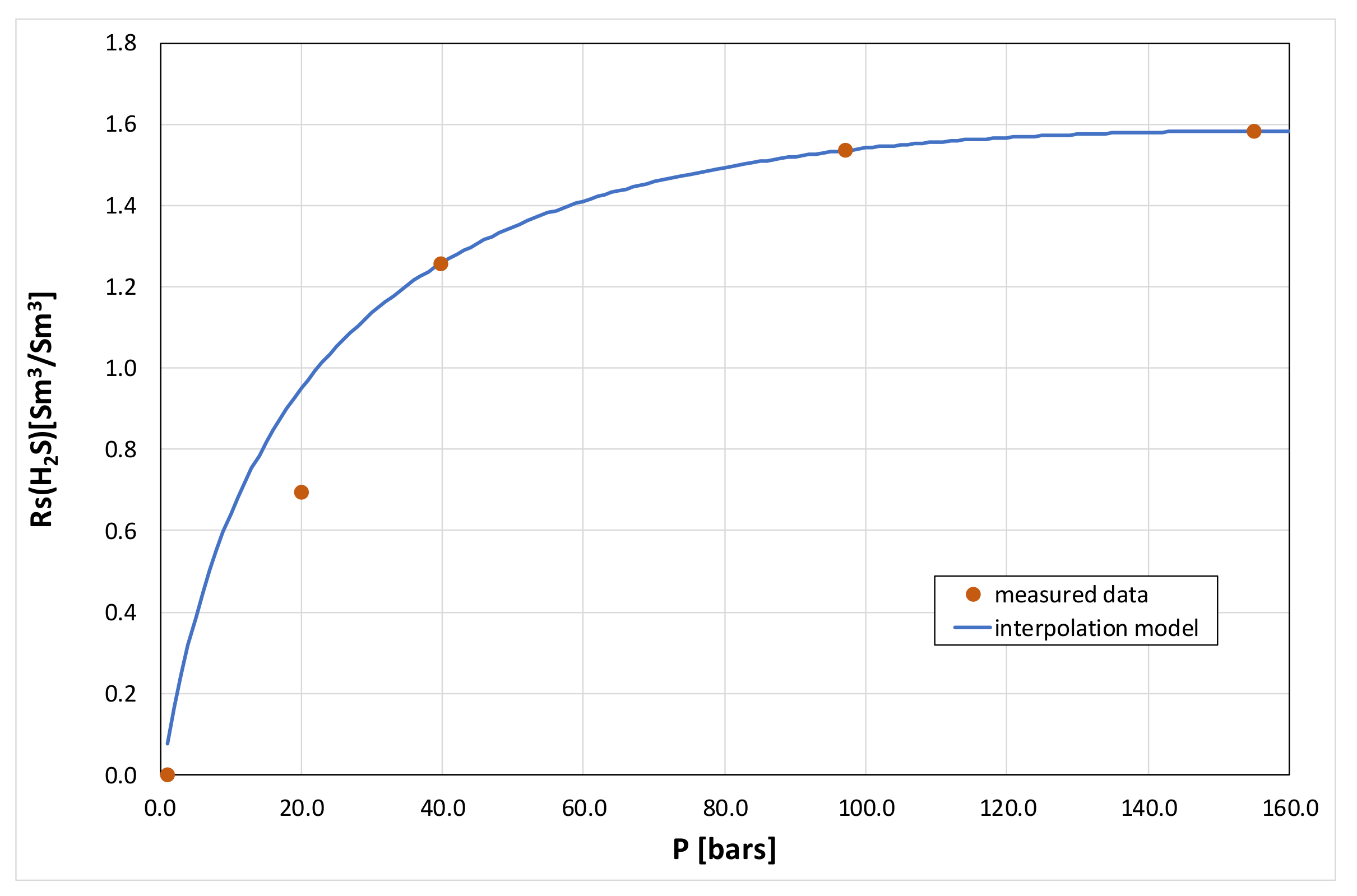
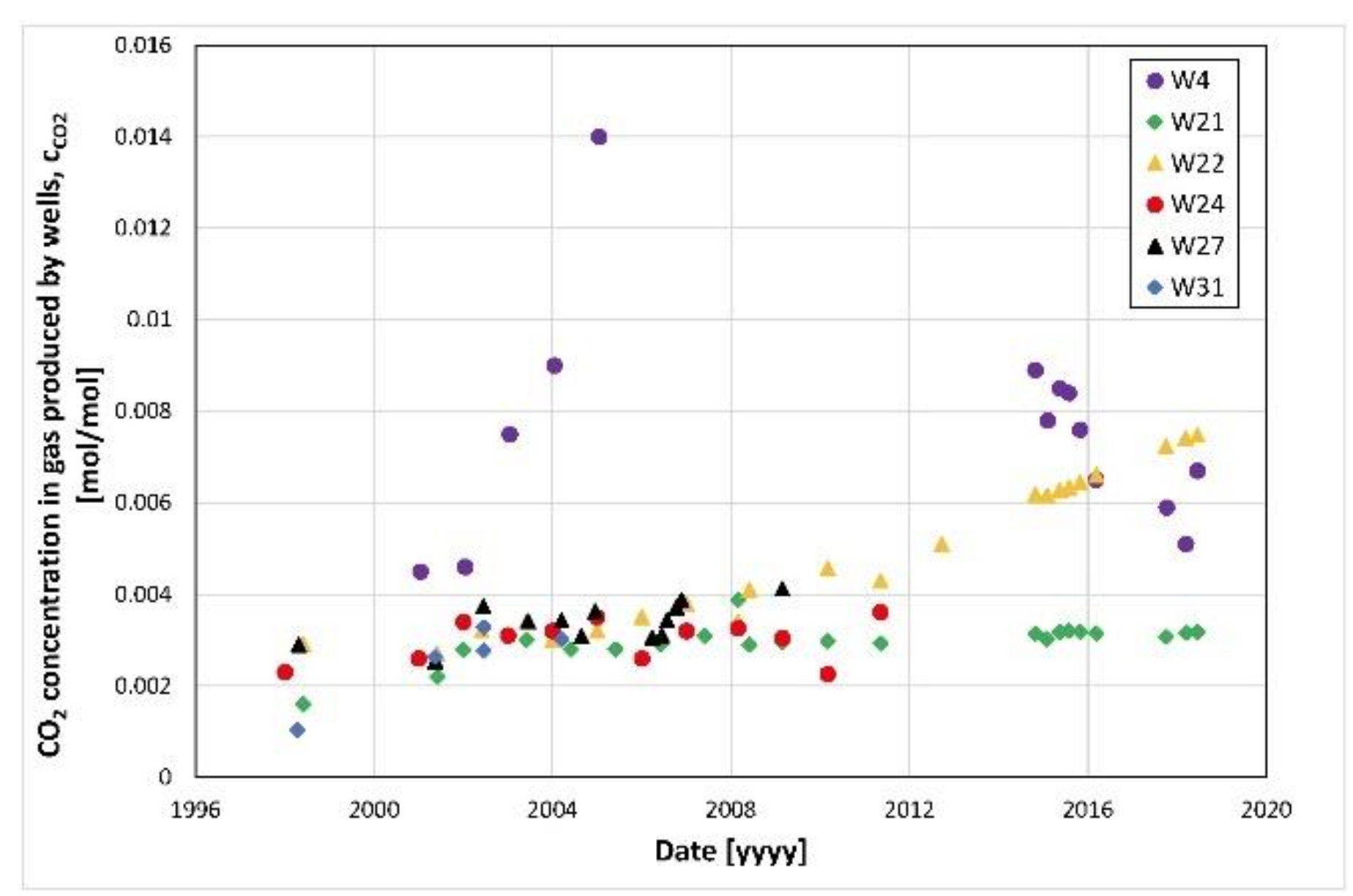
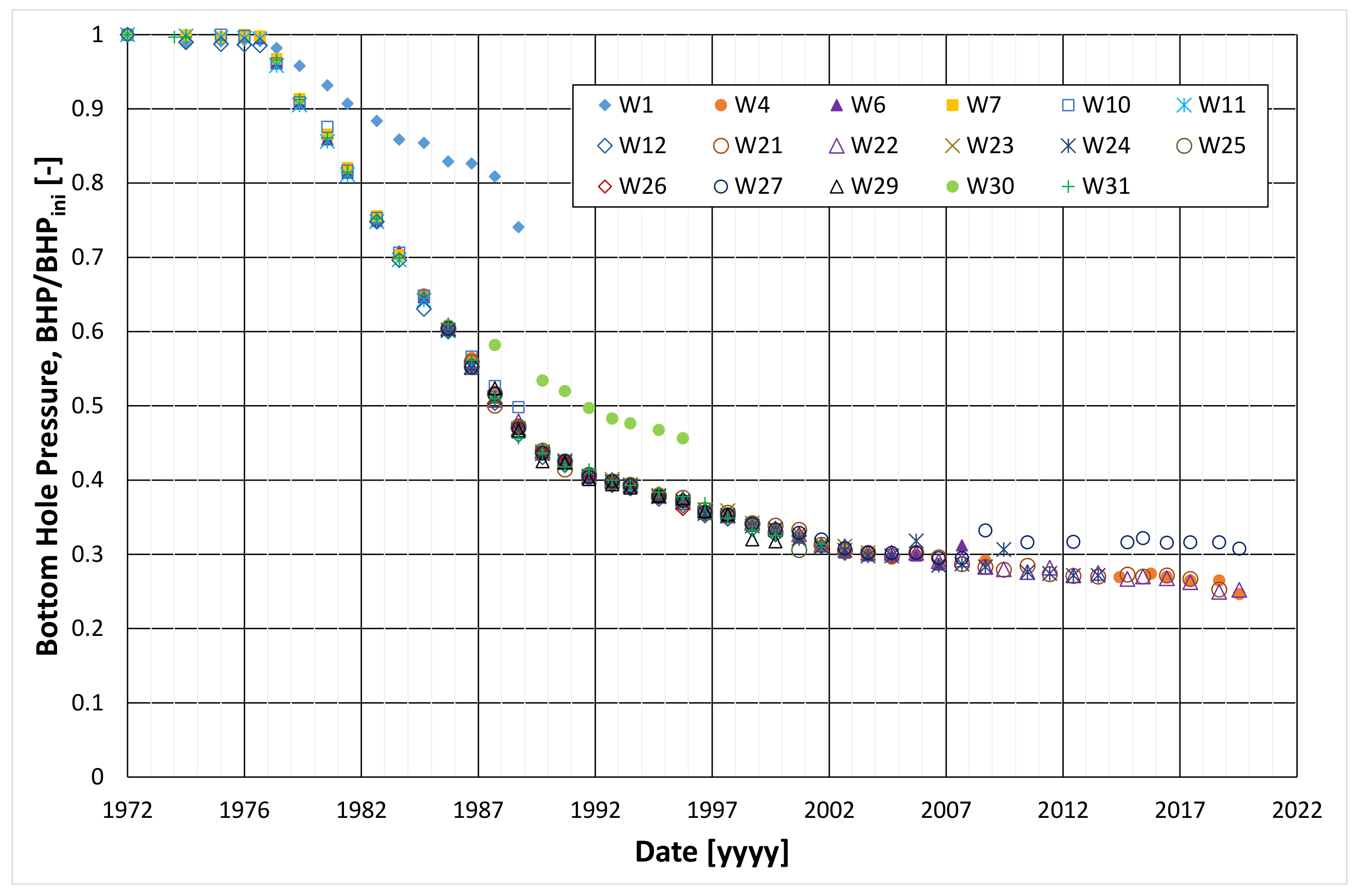
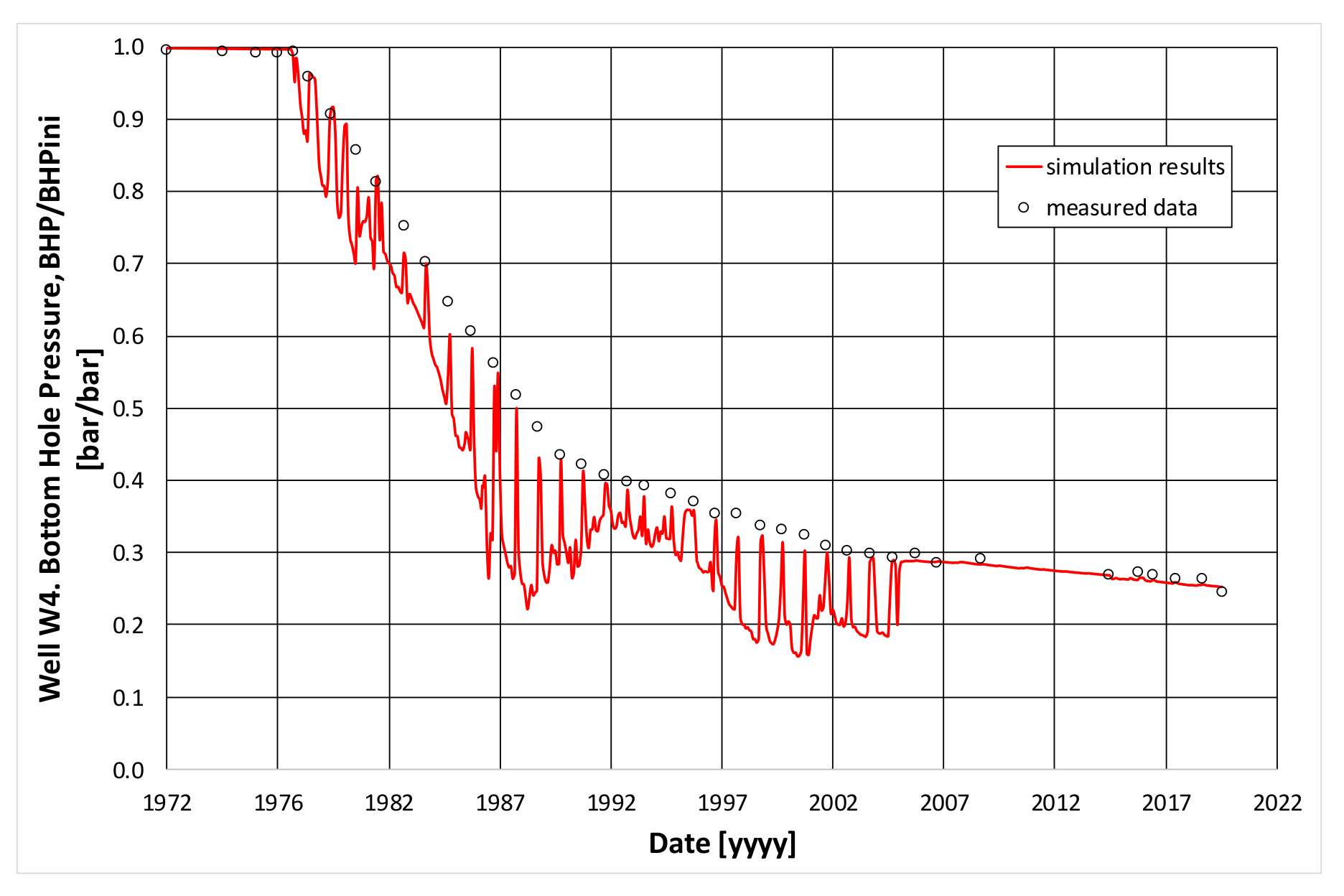
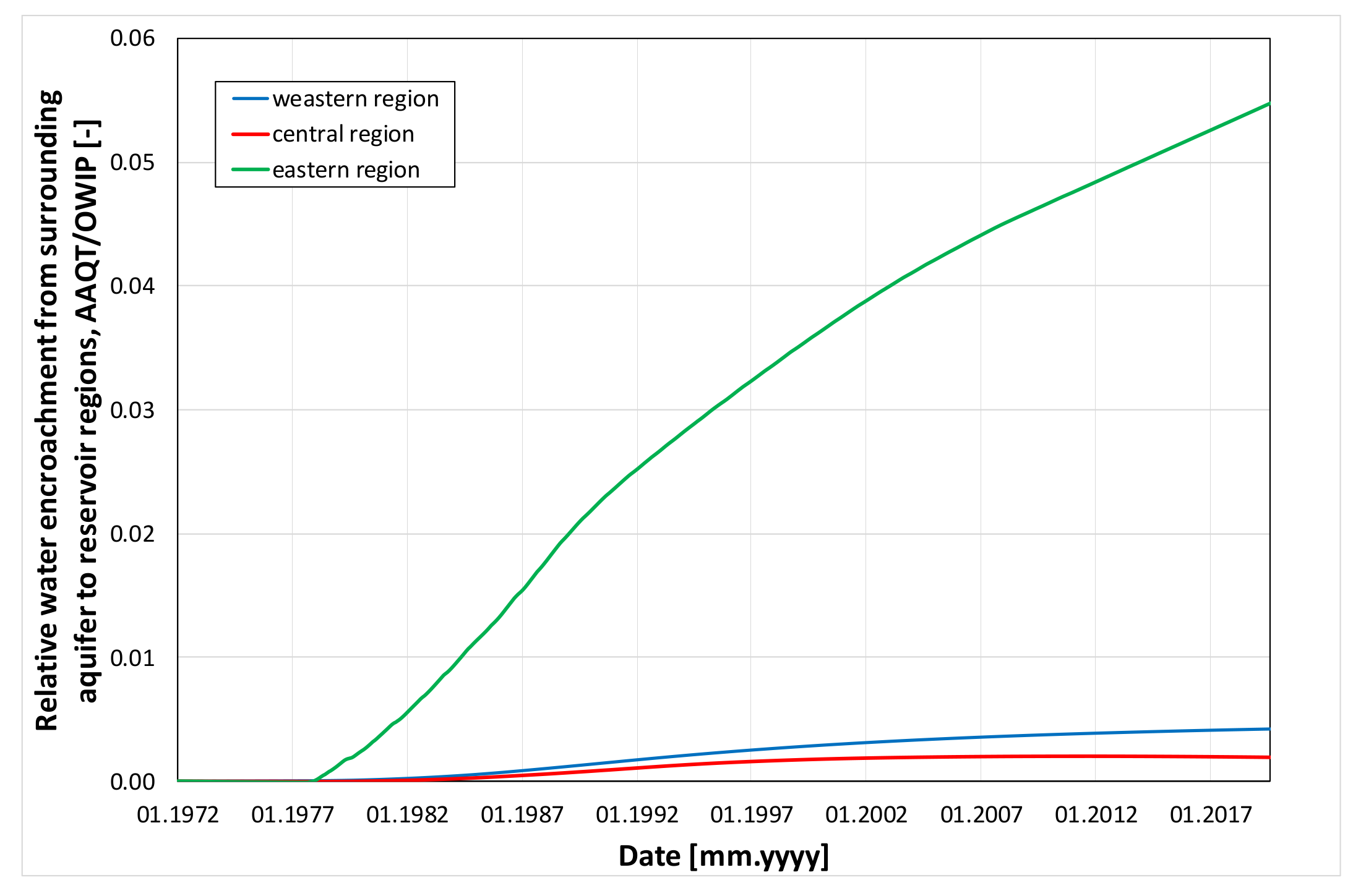
3.2. Model Calibration
- production phase (1972–1995): production of the original natural gas,
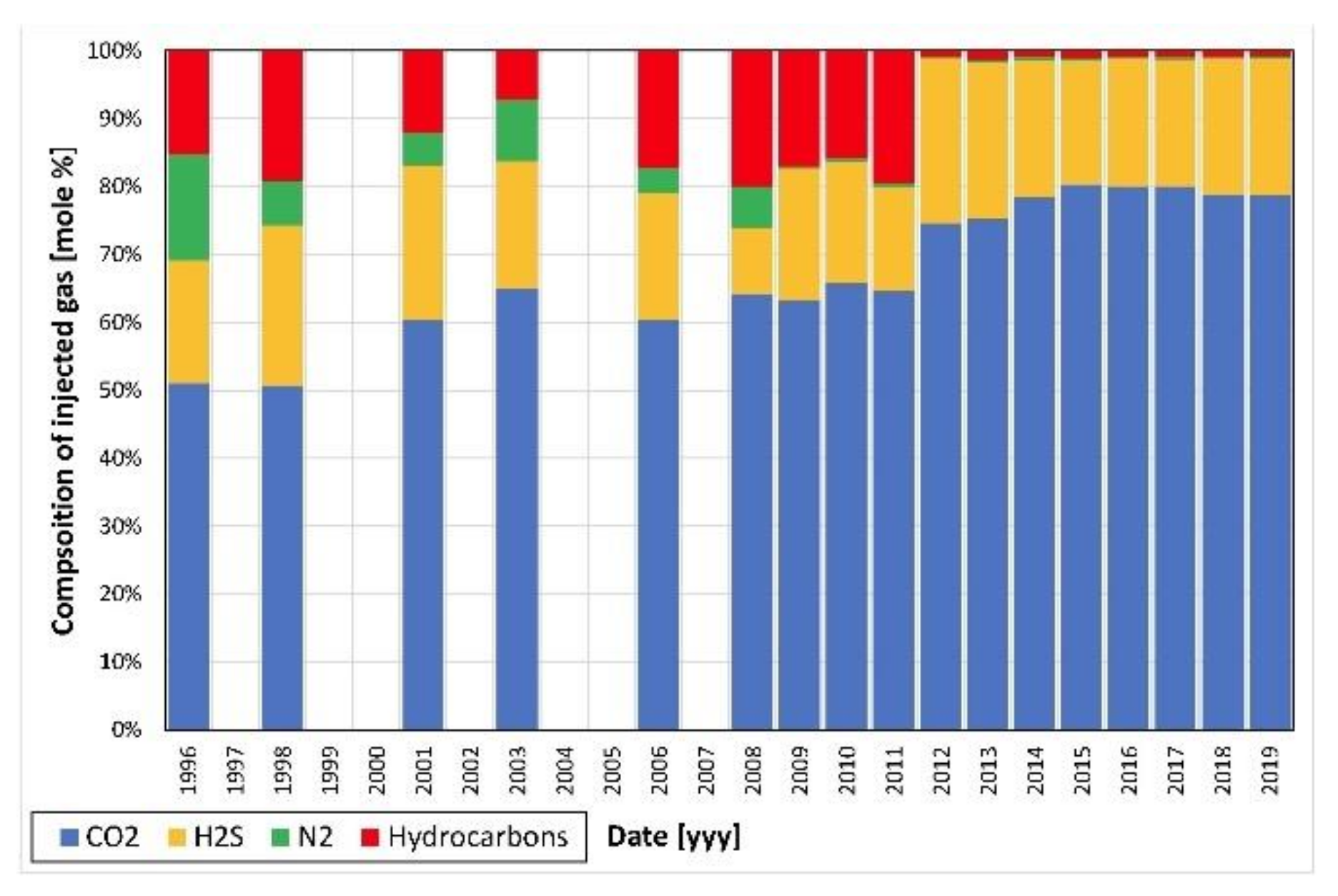
- injection phase (1996–present): continuation of the gas production concomitant with acid gas reinjection.
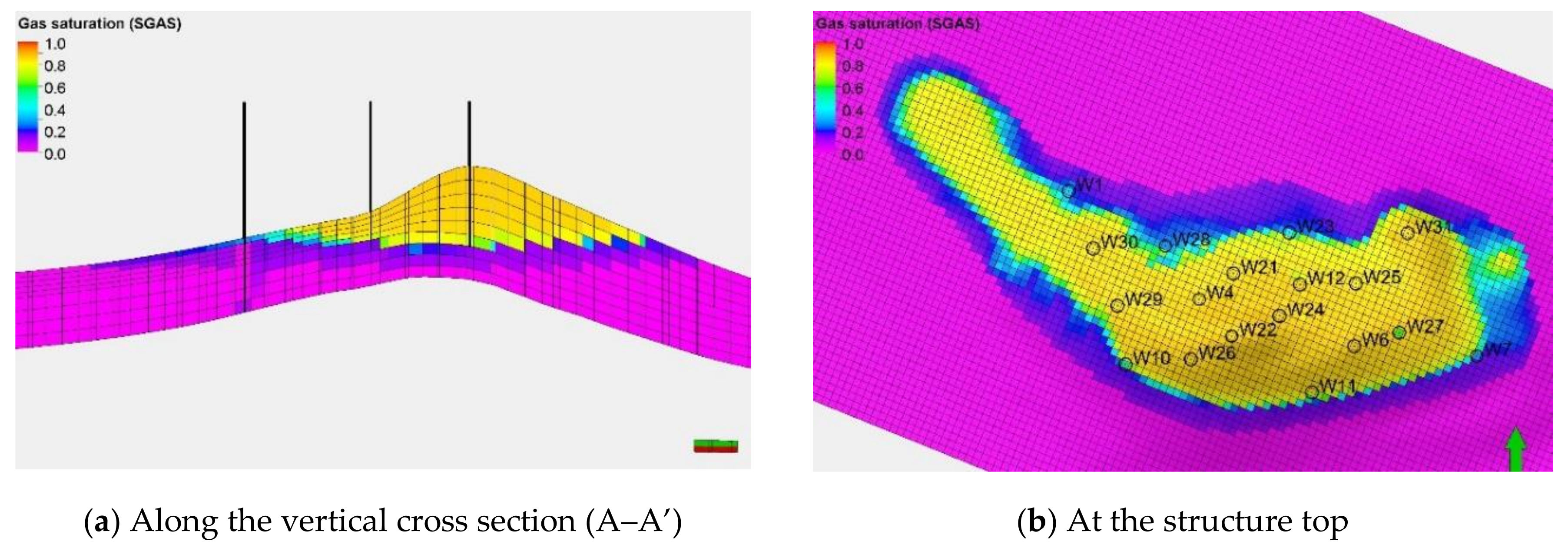
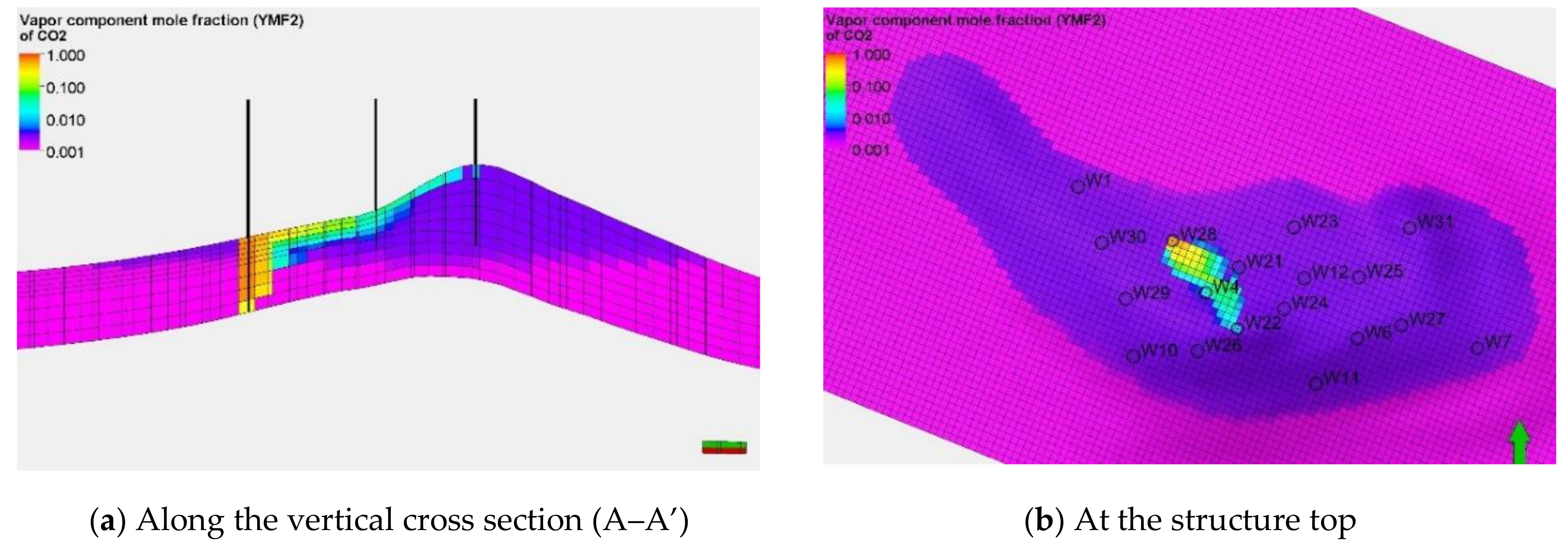
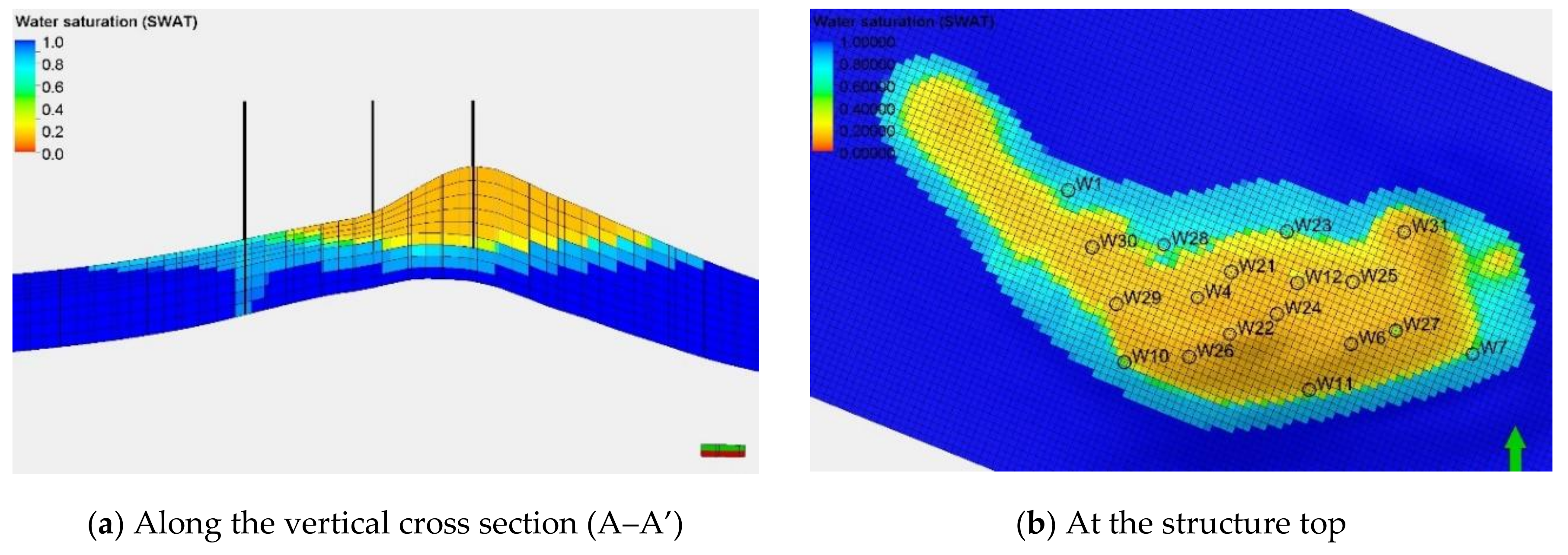
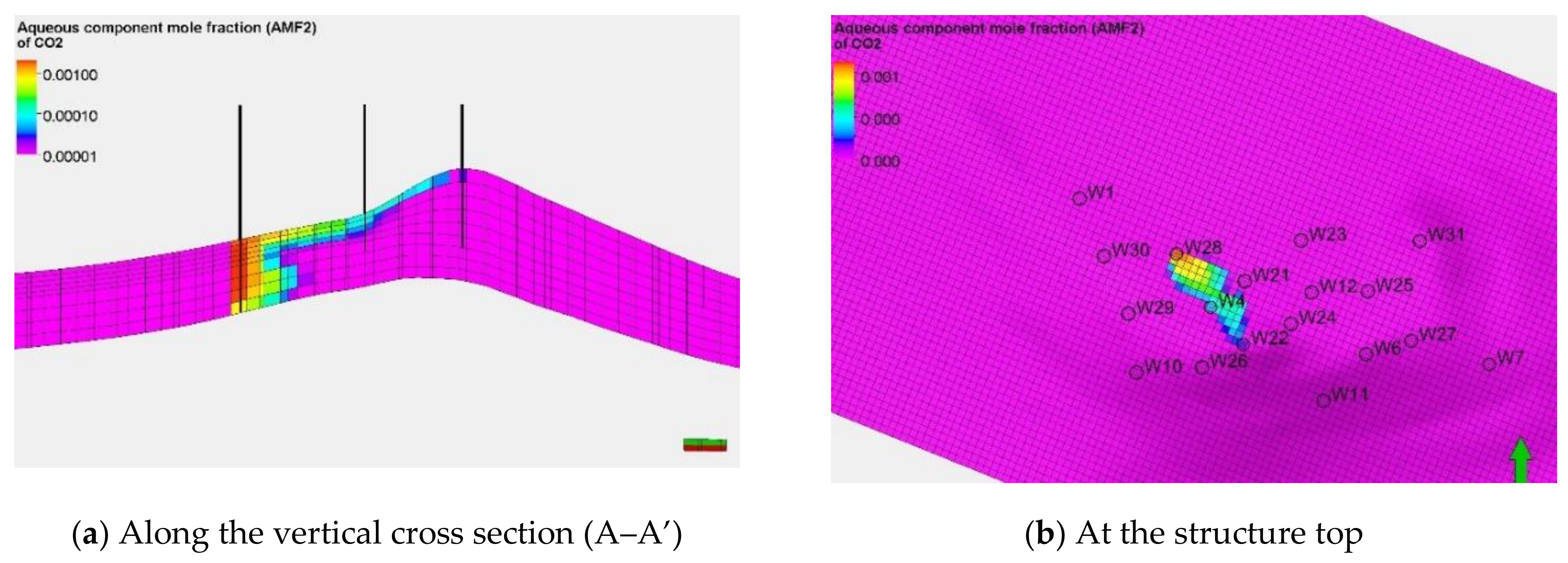
4. Analysis of Simulation Results—Detailed Description of the On-Going Sequestration Process
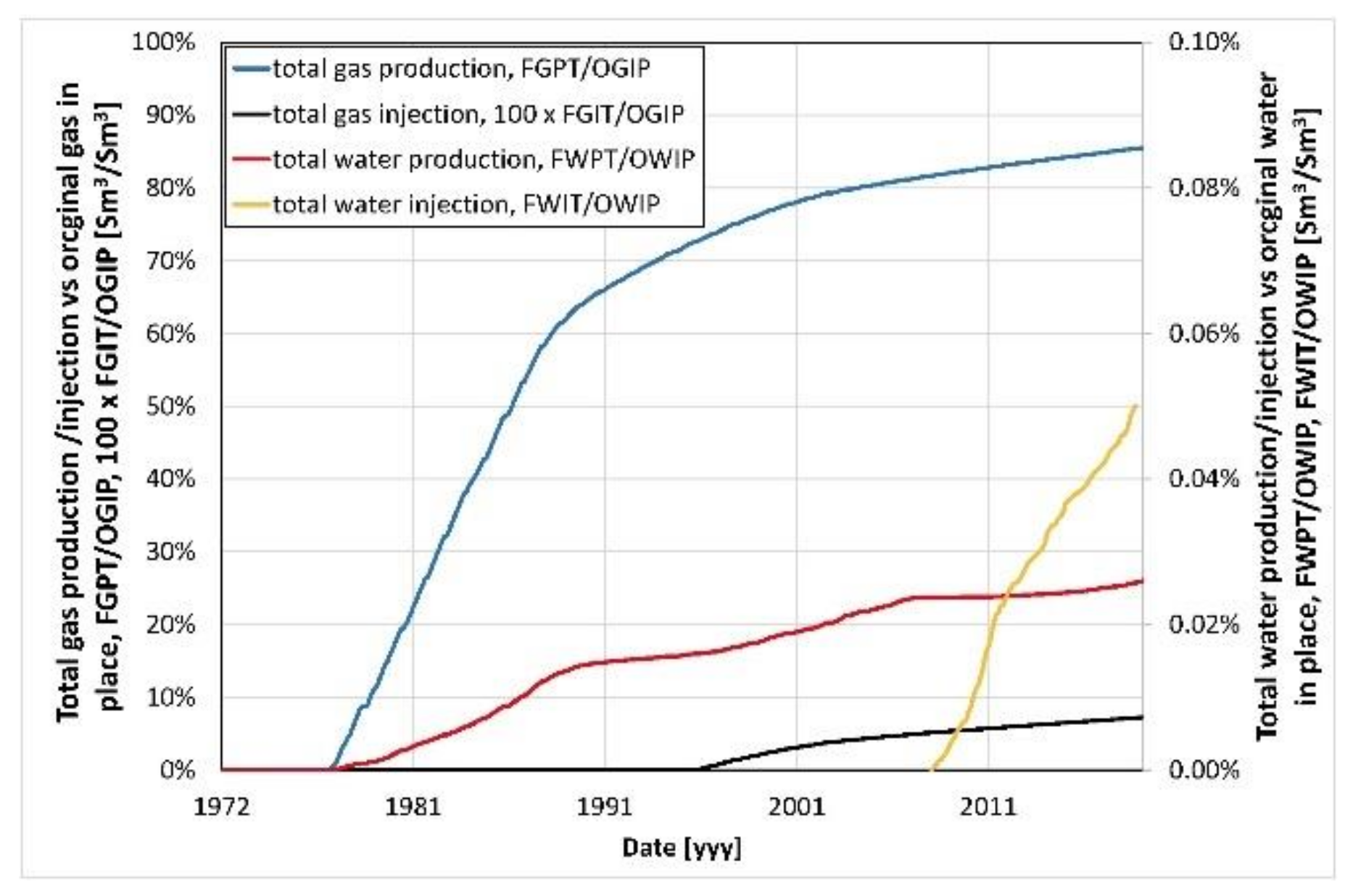
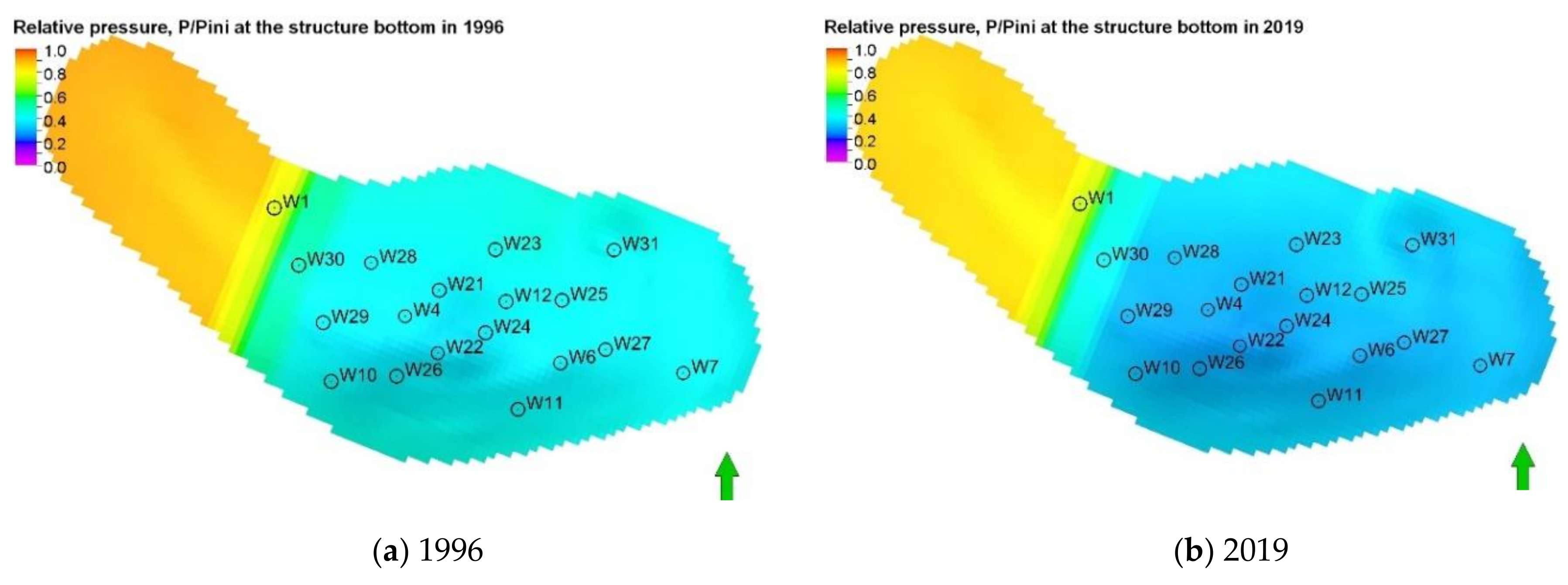
4.1. Process Basic Parameters
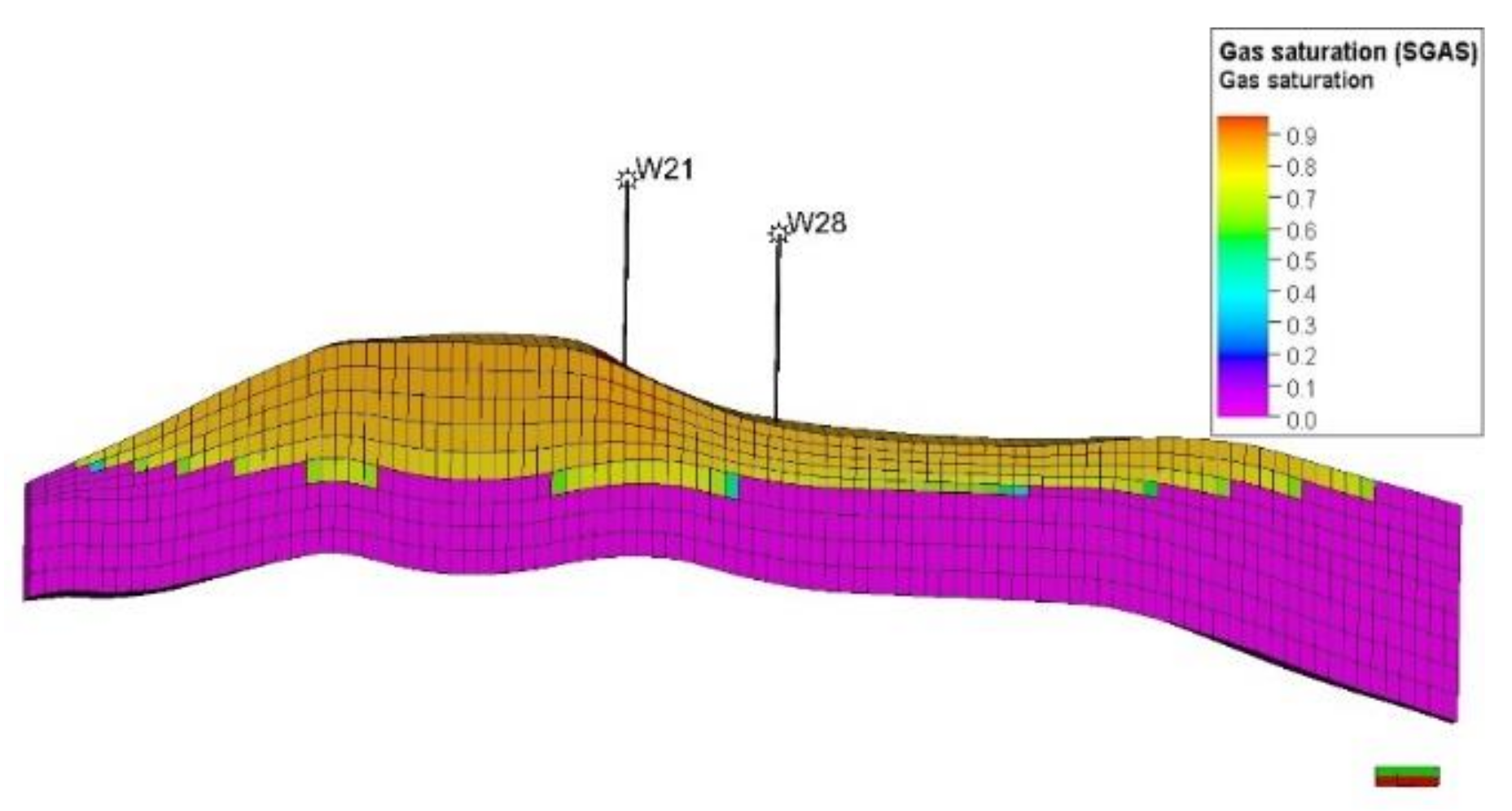
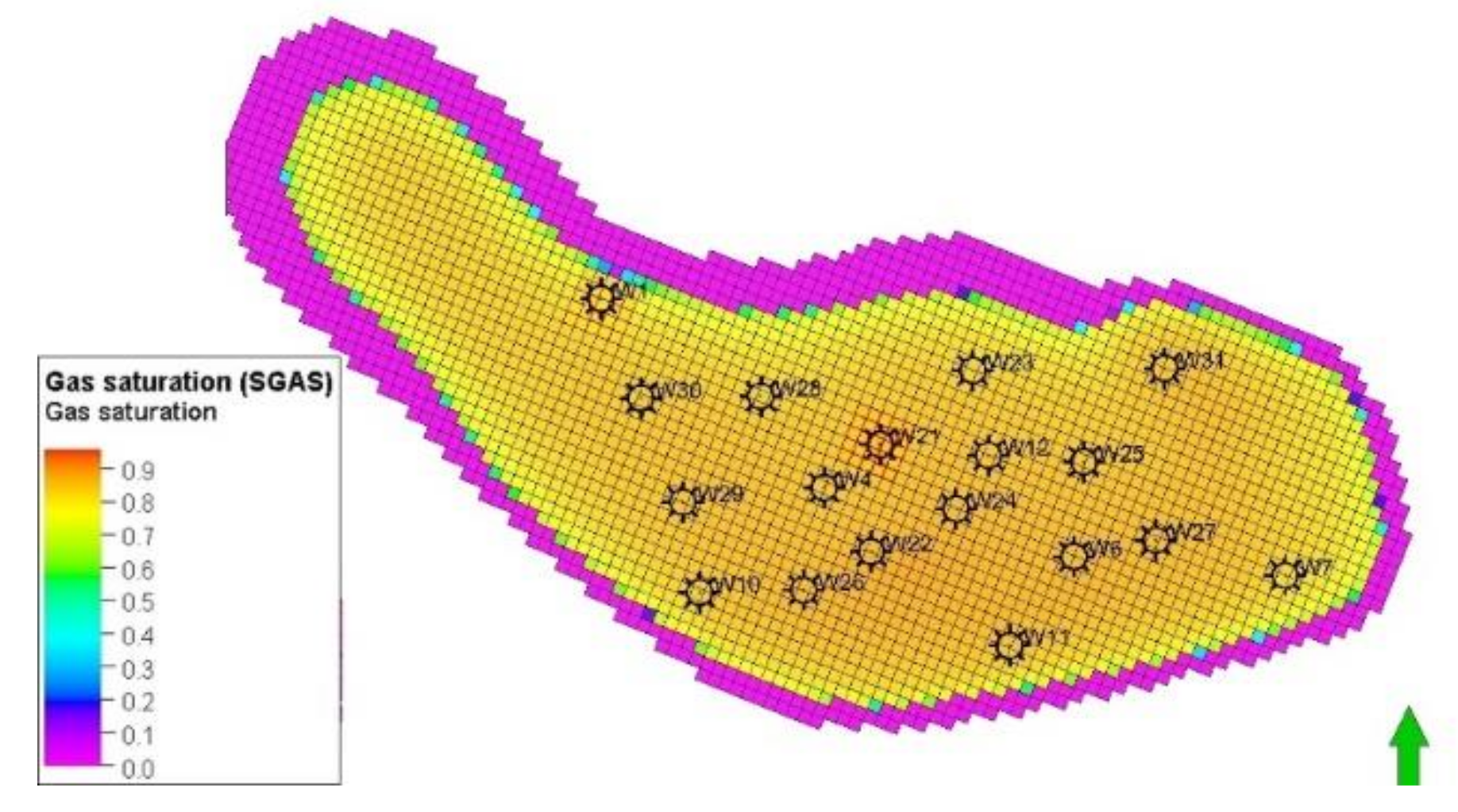
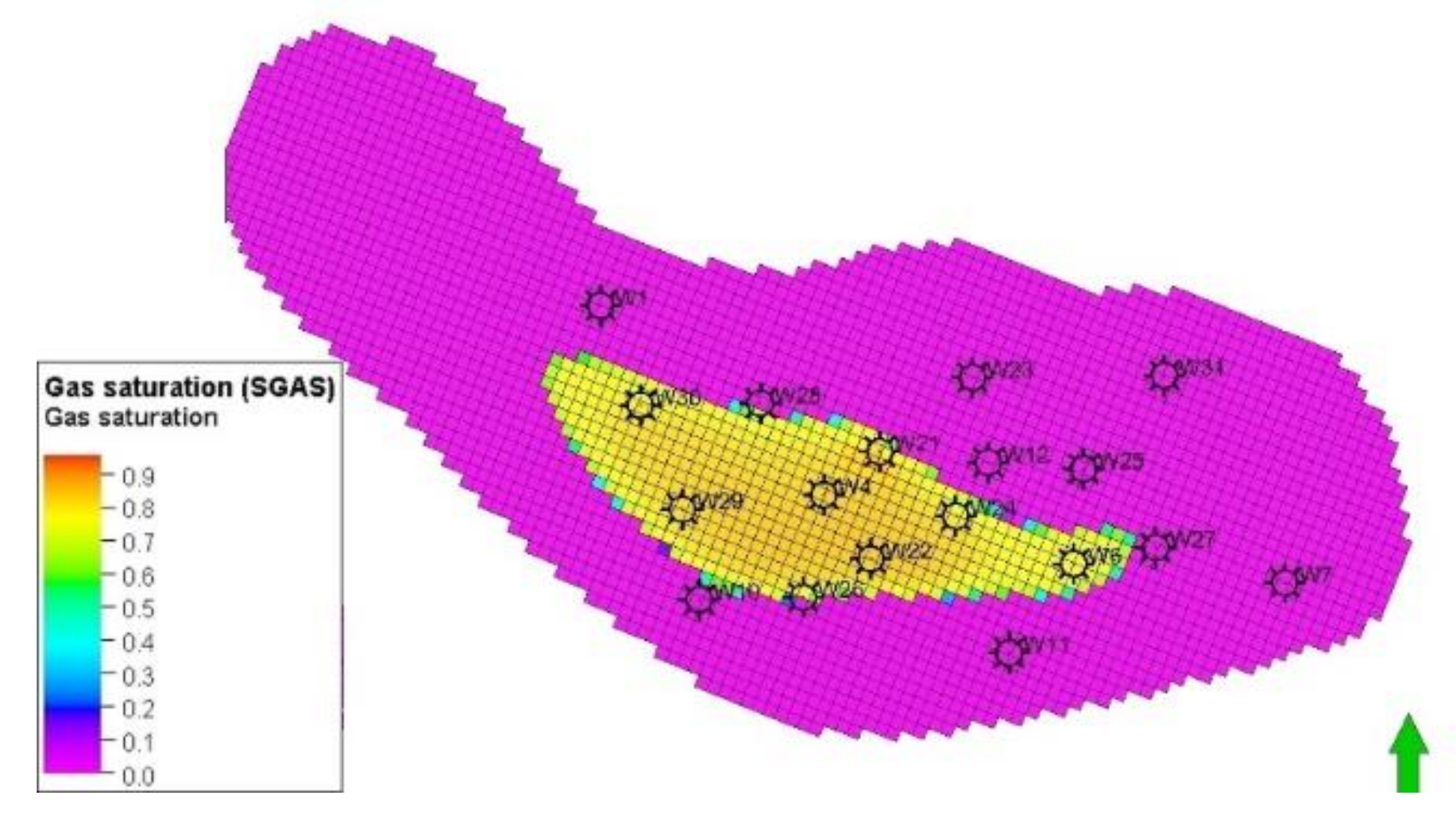
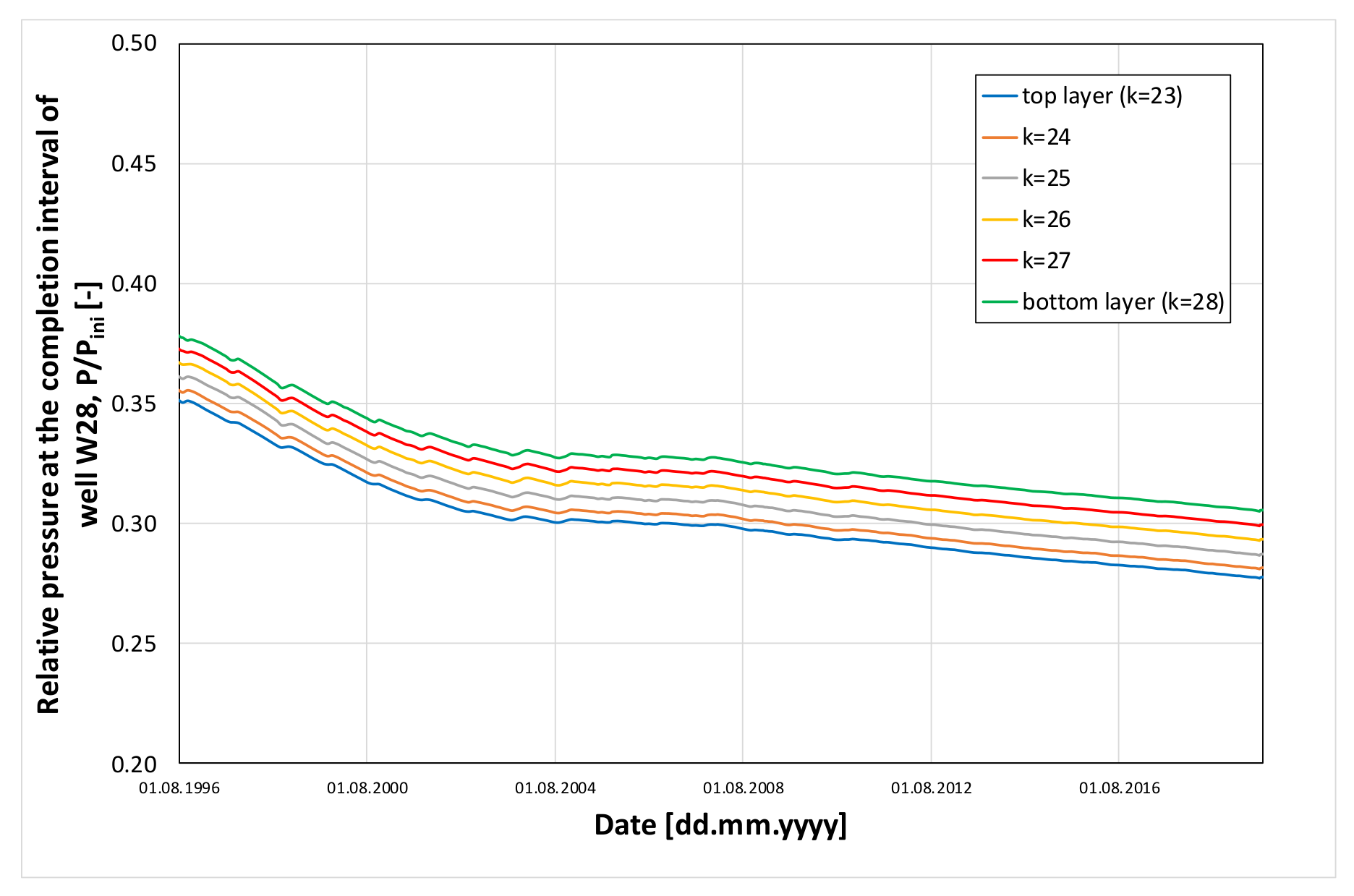
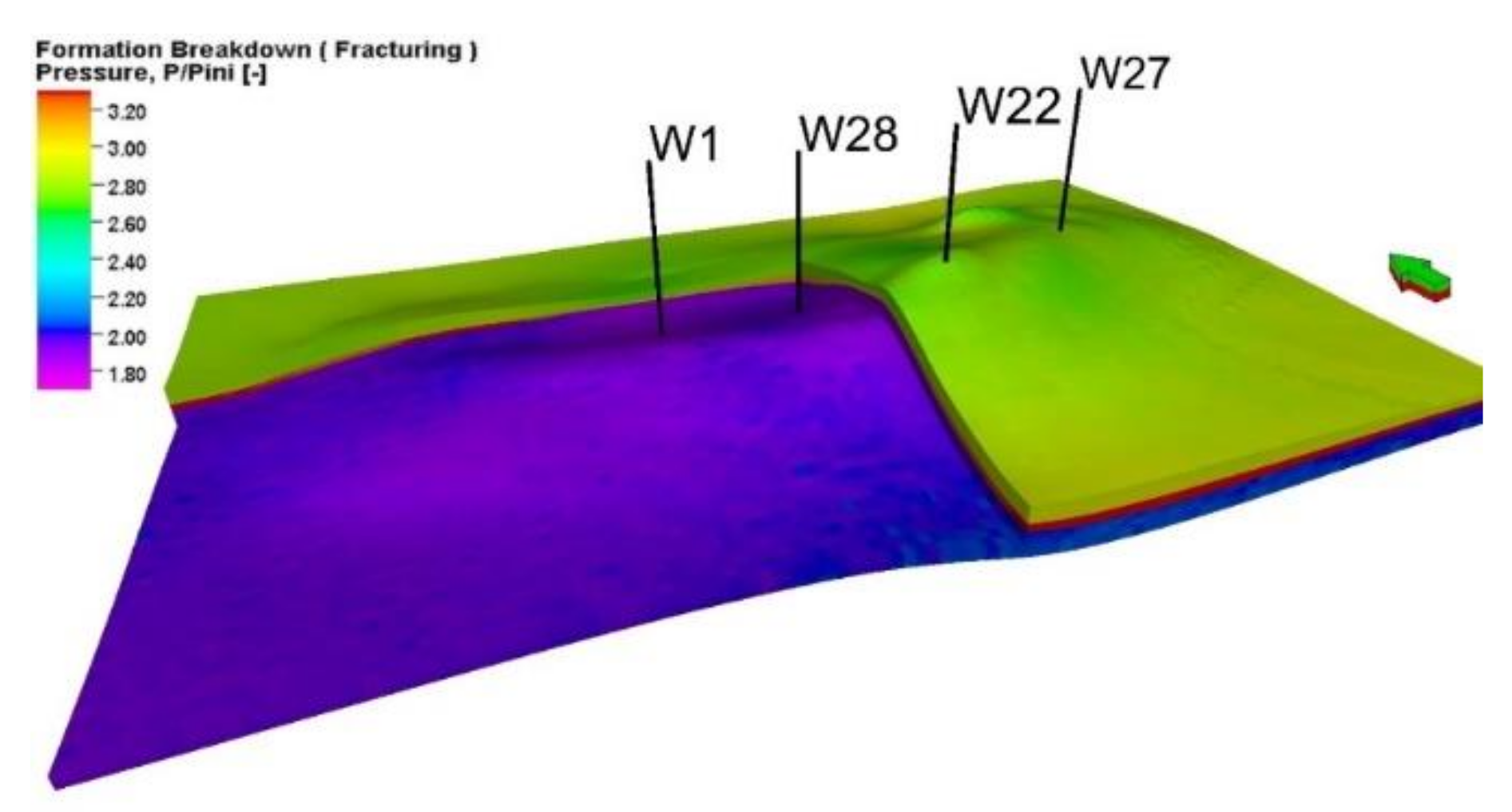
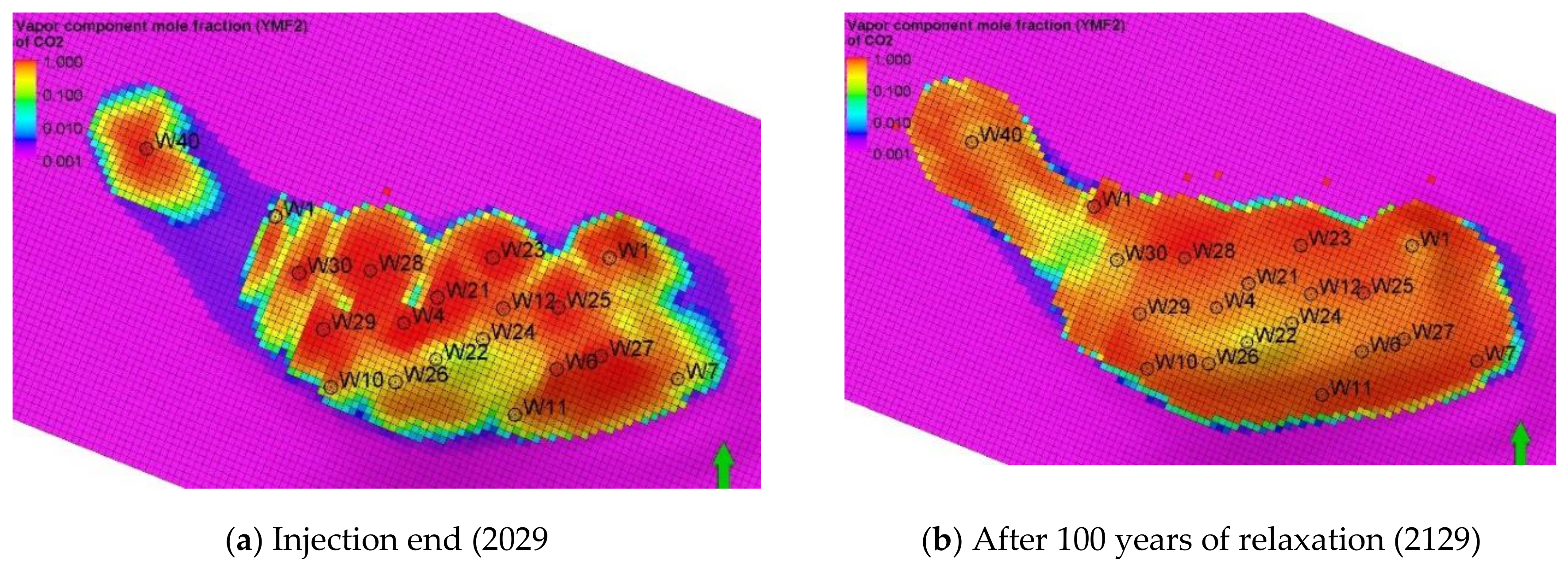
4.2. Leakage Risk Factor Analysis
5. Storage Capacity Analysis for a Full-Scale CO2 Sequestration Scenario at Borzęcin
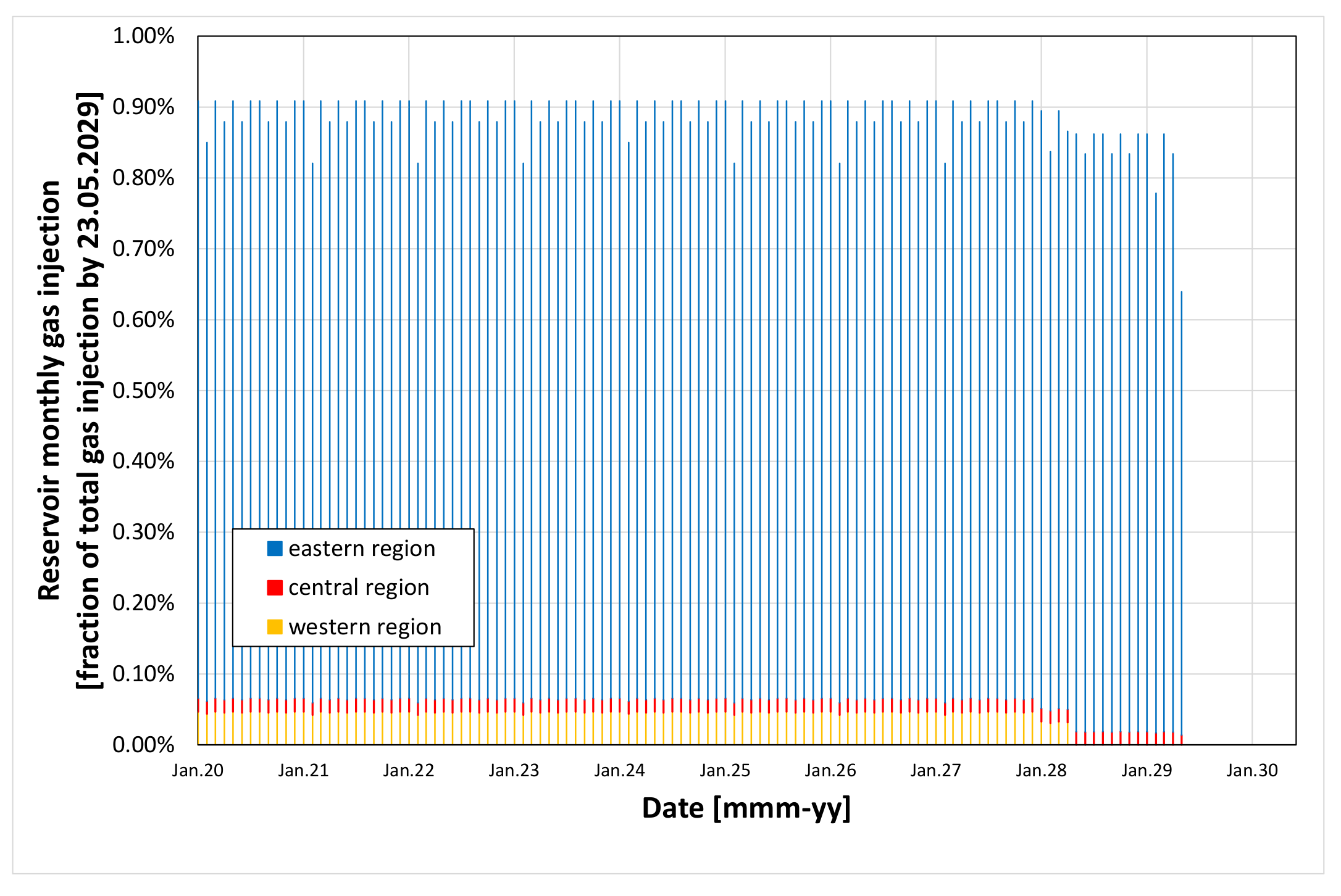
5.1. Simulation Forecast Assumptions
- –
- the amount of gas in place is reduced to 85% of the original gas in place (Figure 15),
- –
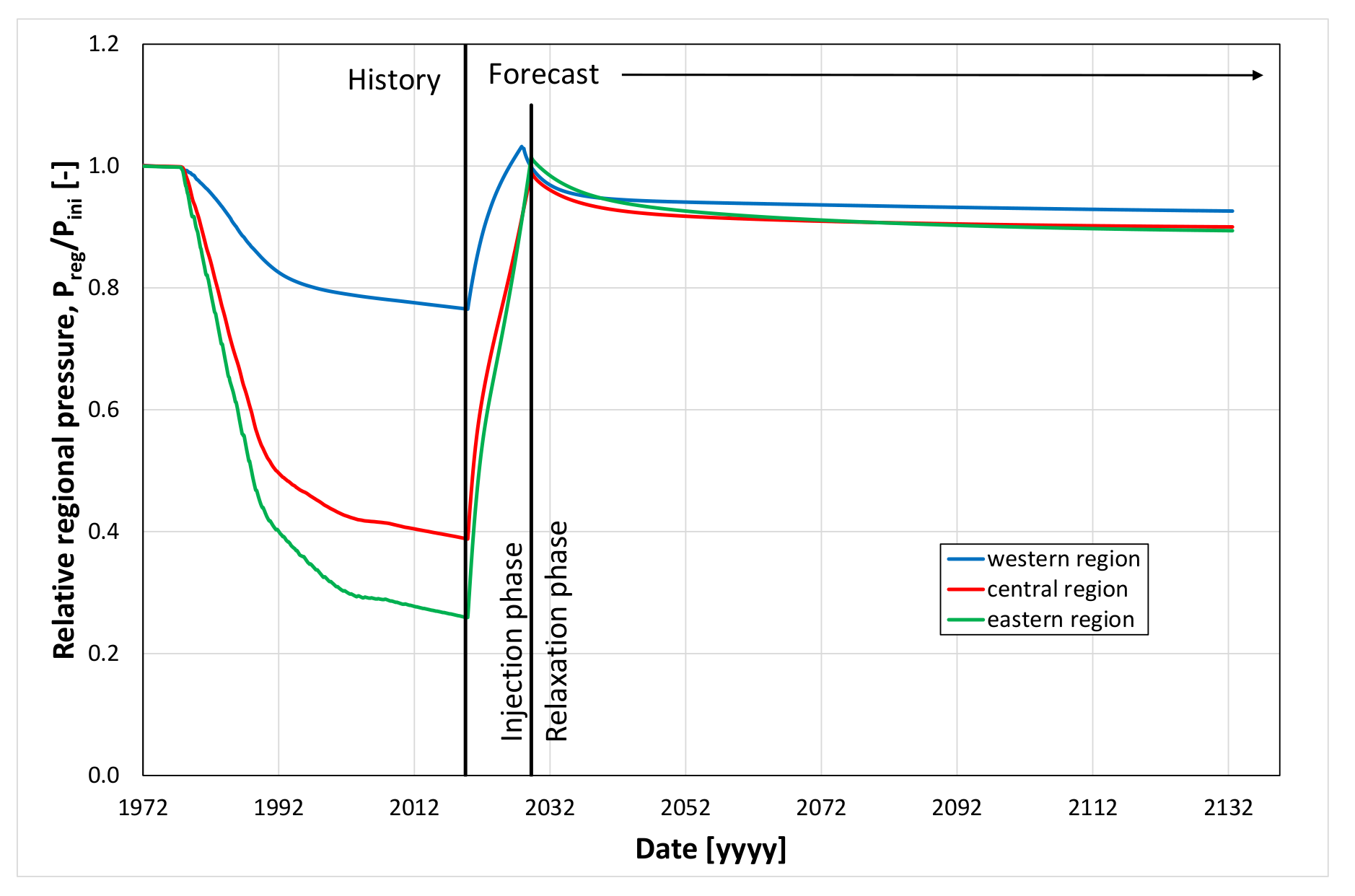
- the average reservoir pressure is also significantly reduced, in particular, it reaches less than 30% of the initial pressure in the dominant eastern region of the structure (Figure 20),
- –
- most of the producing wells can be converted to injection wells at relatively low cost,
- –
- in addition, other elements of the existing surface installation can be converted for the purposes of an alternative sequestration project.
- –
- no spill-out of the injected CO2 beyond the structural trap,
- –
- maximum pressure in the structure volume below the fracturing pressure,
- –
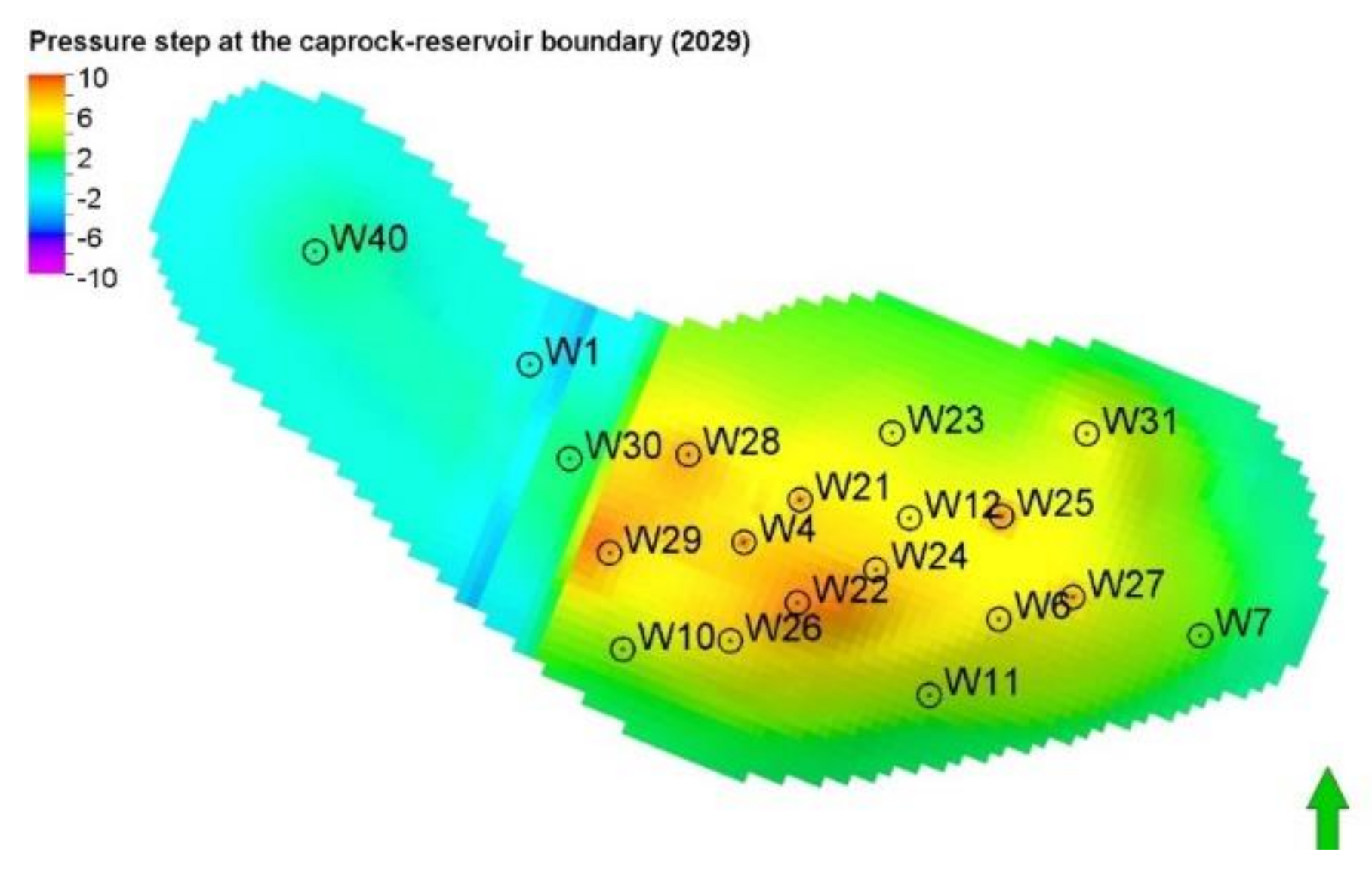
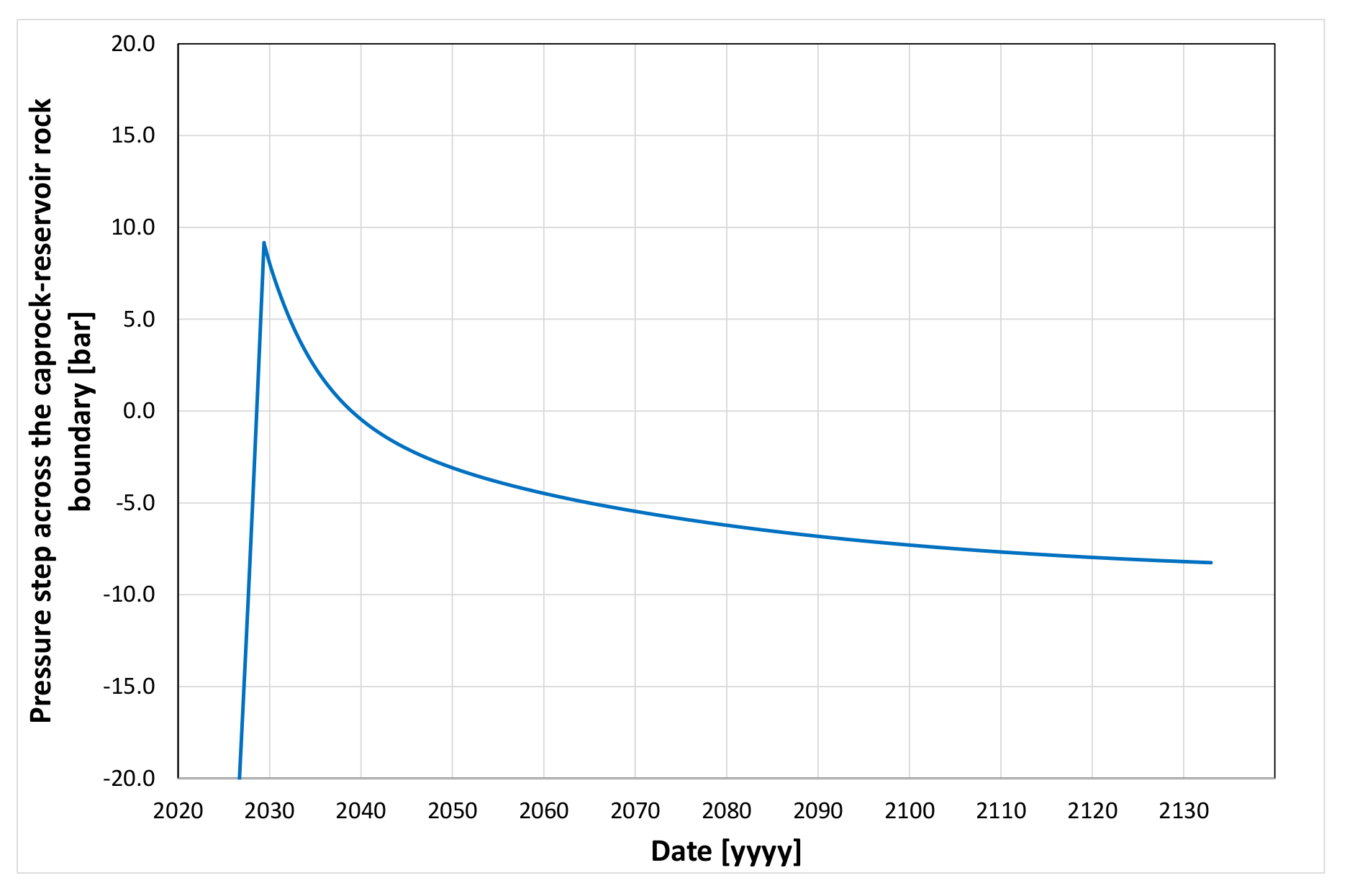
- maximum pressure step across the caprock–reservoir rock boundary below the threshold displacement pressure.
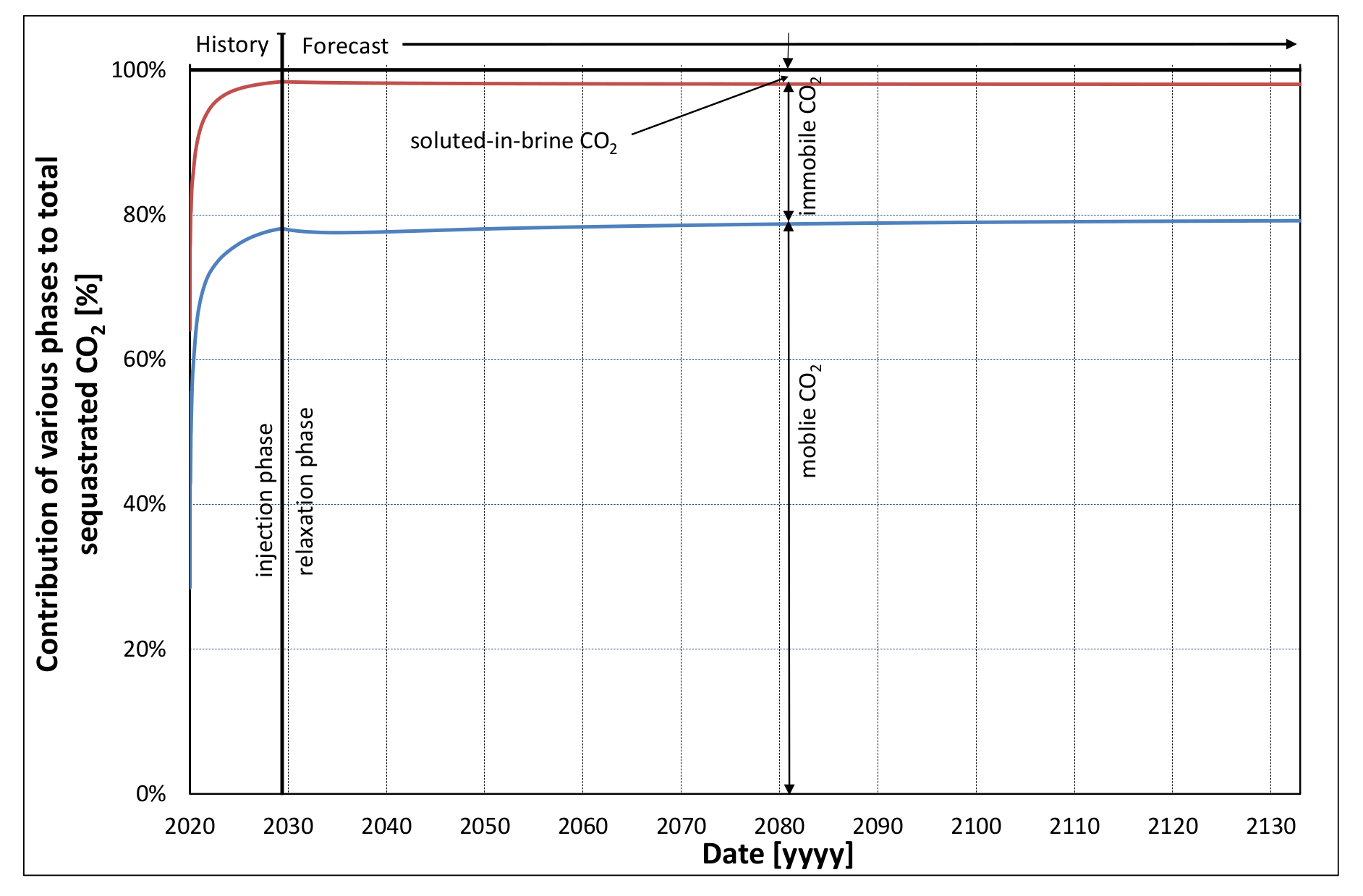
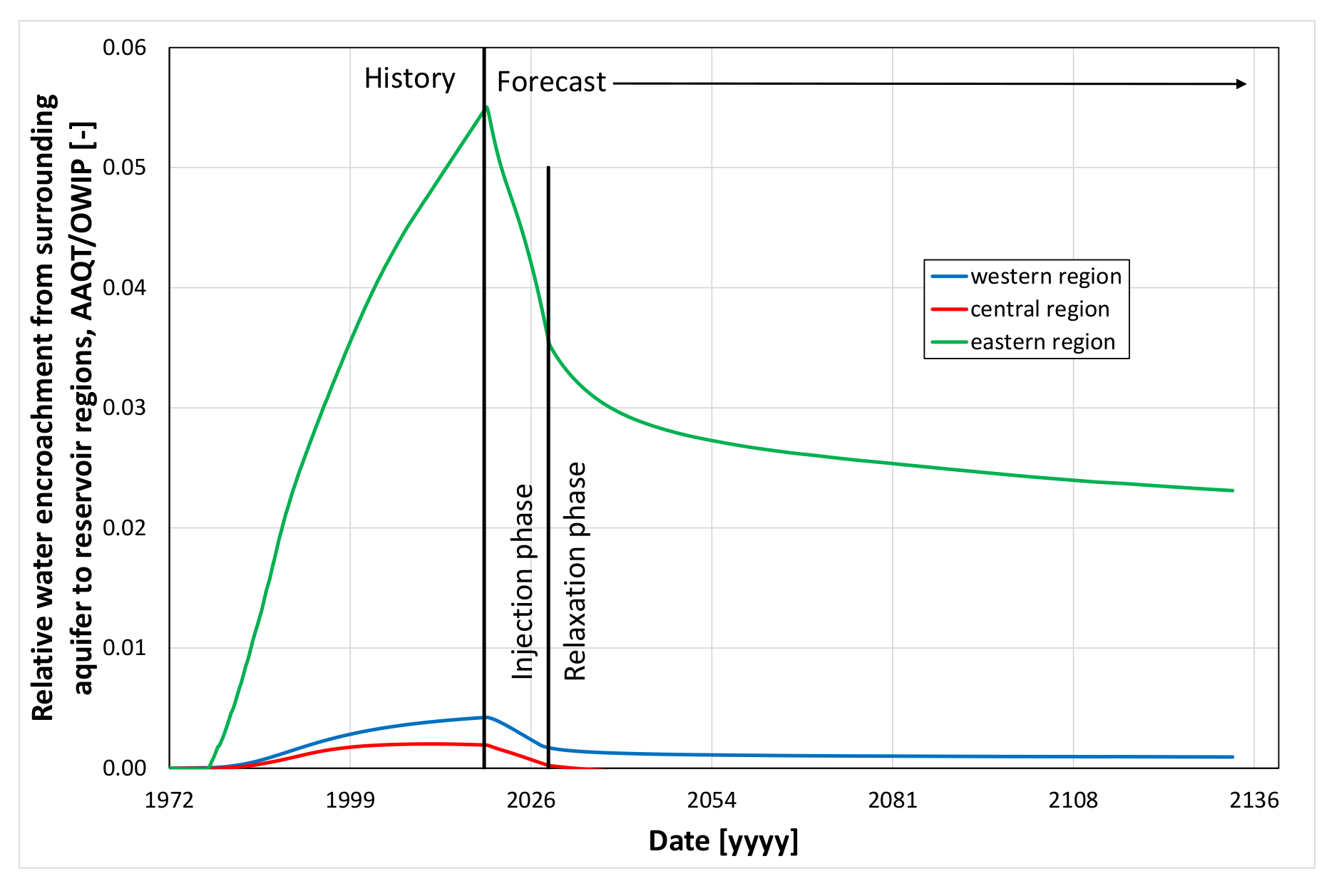
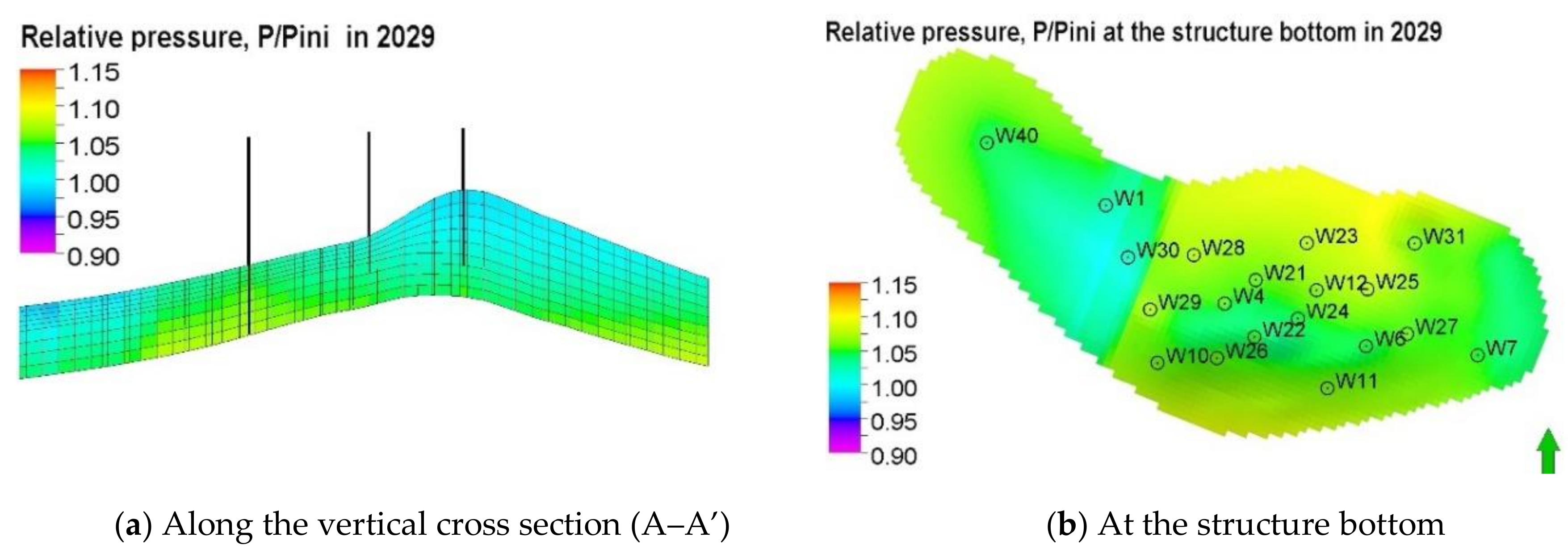
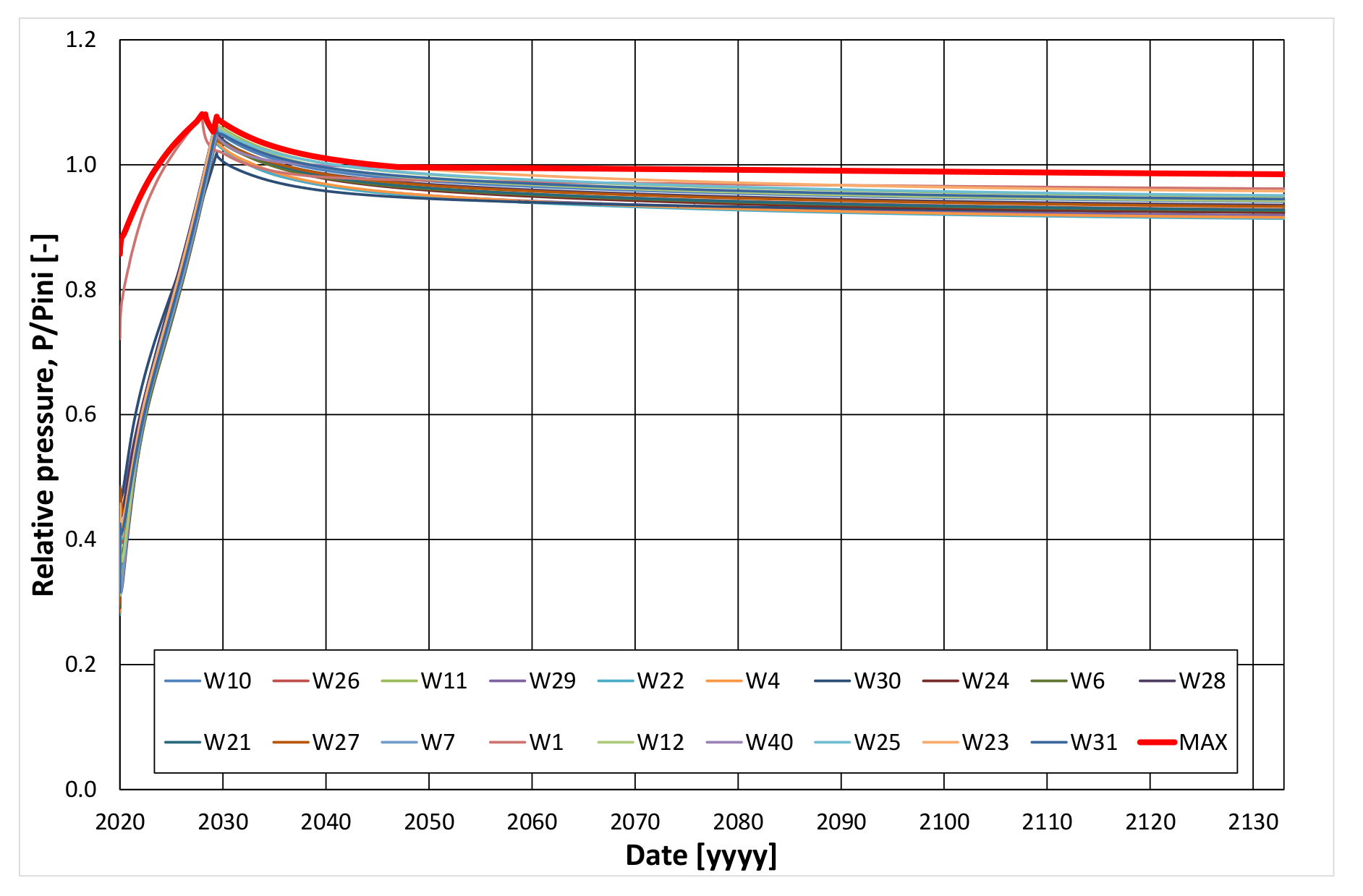
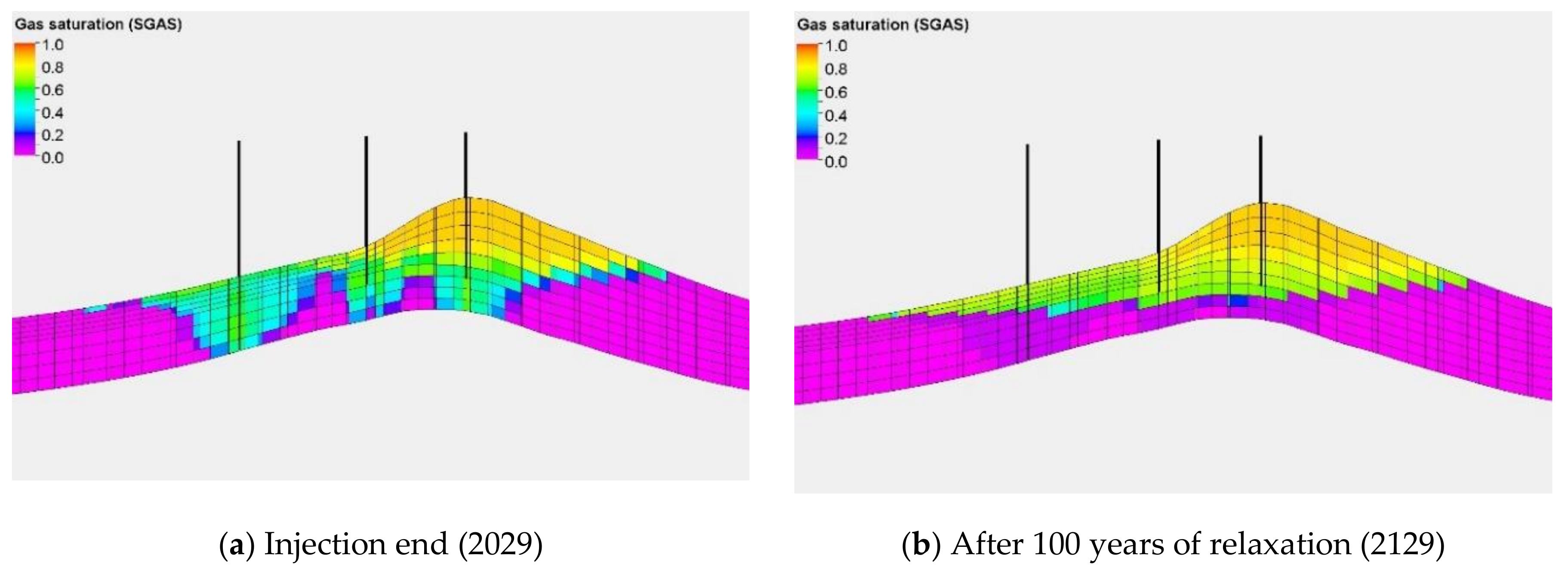
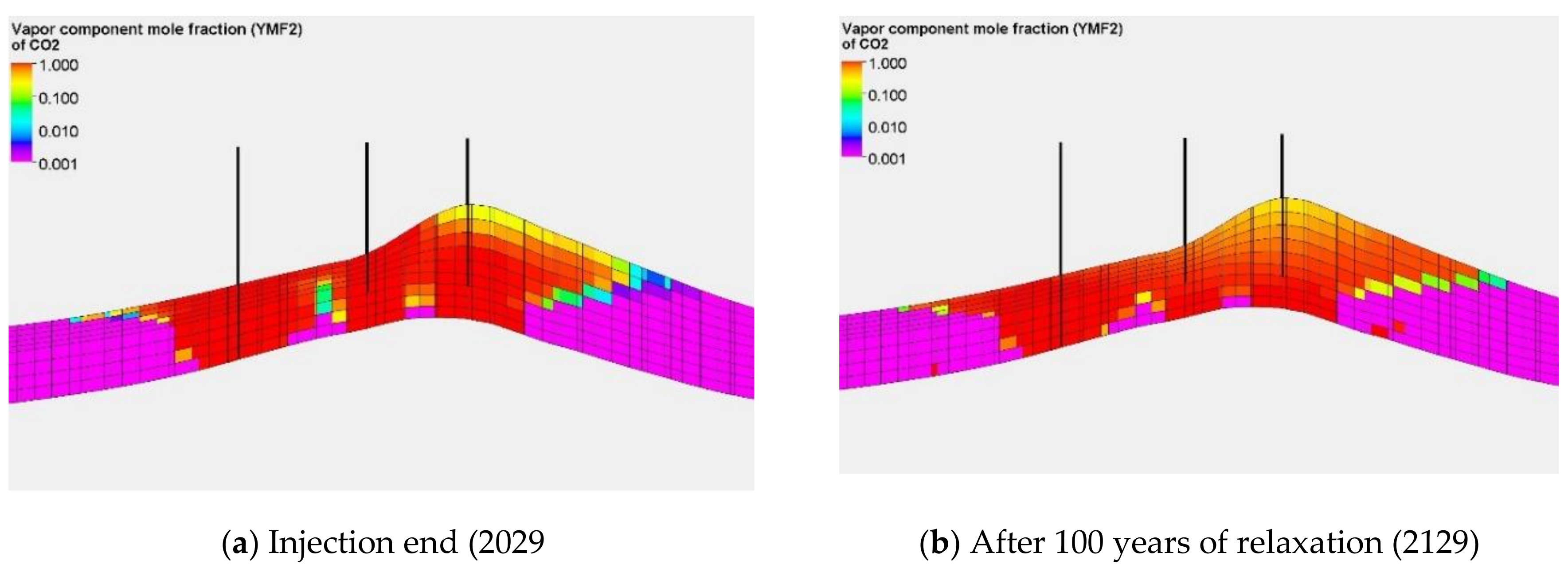
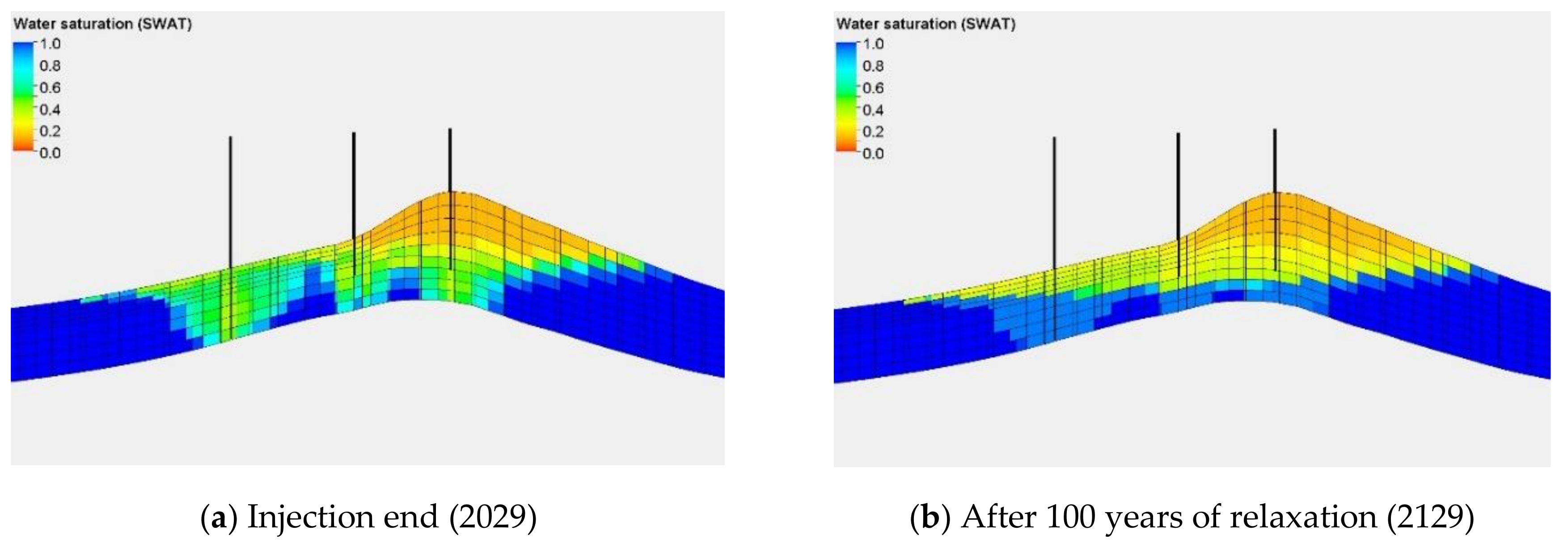
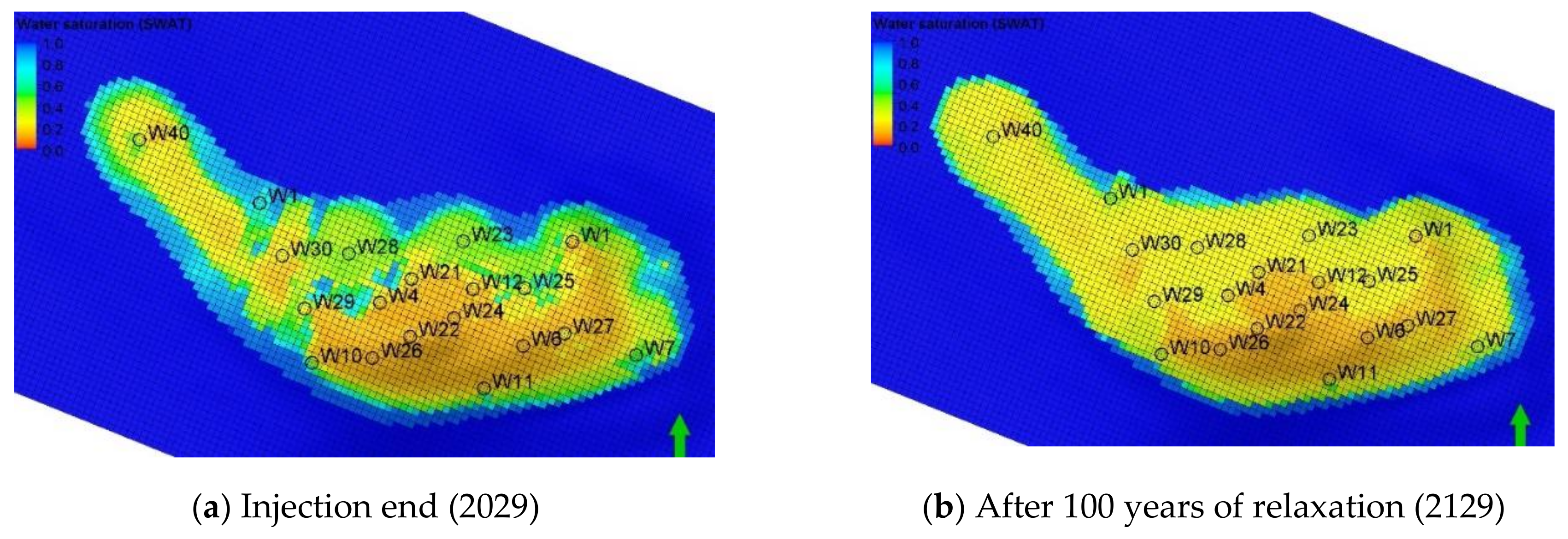
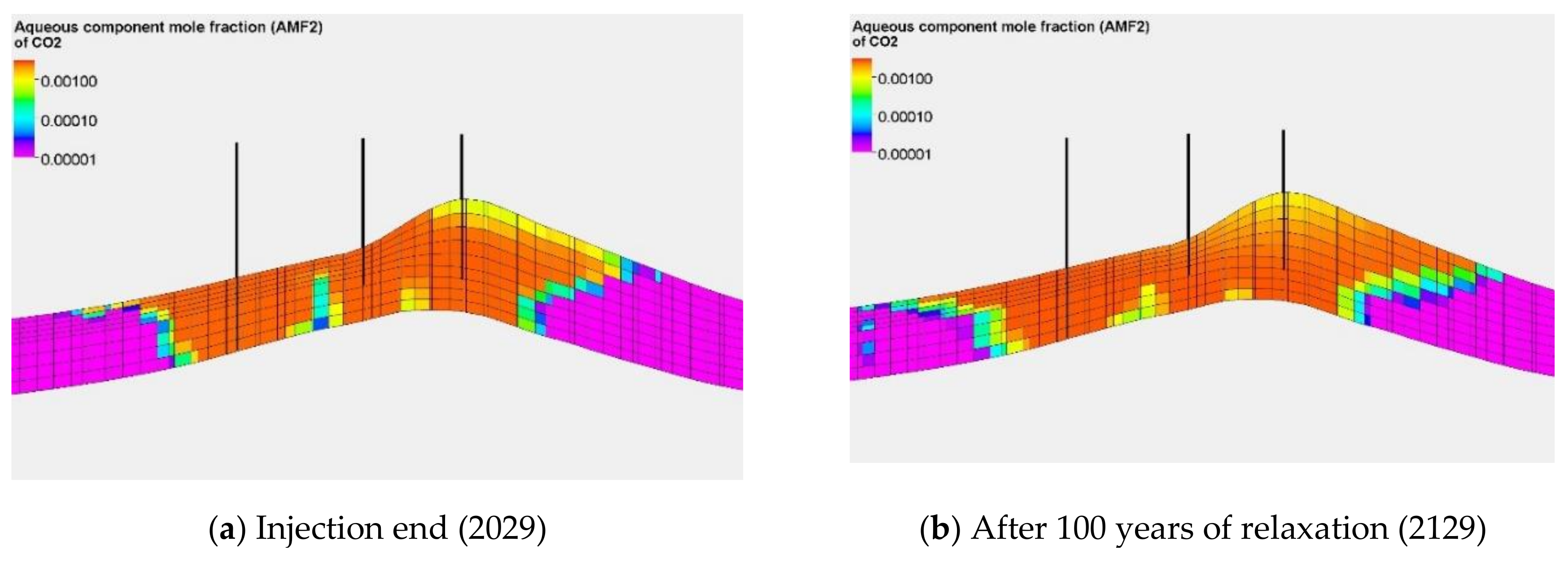
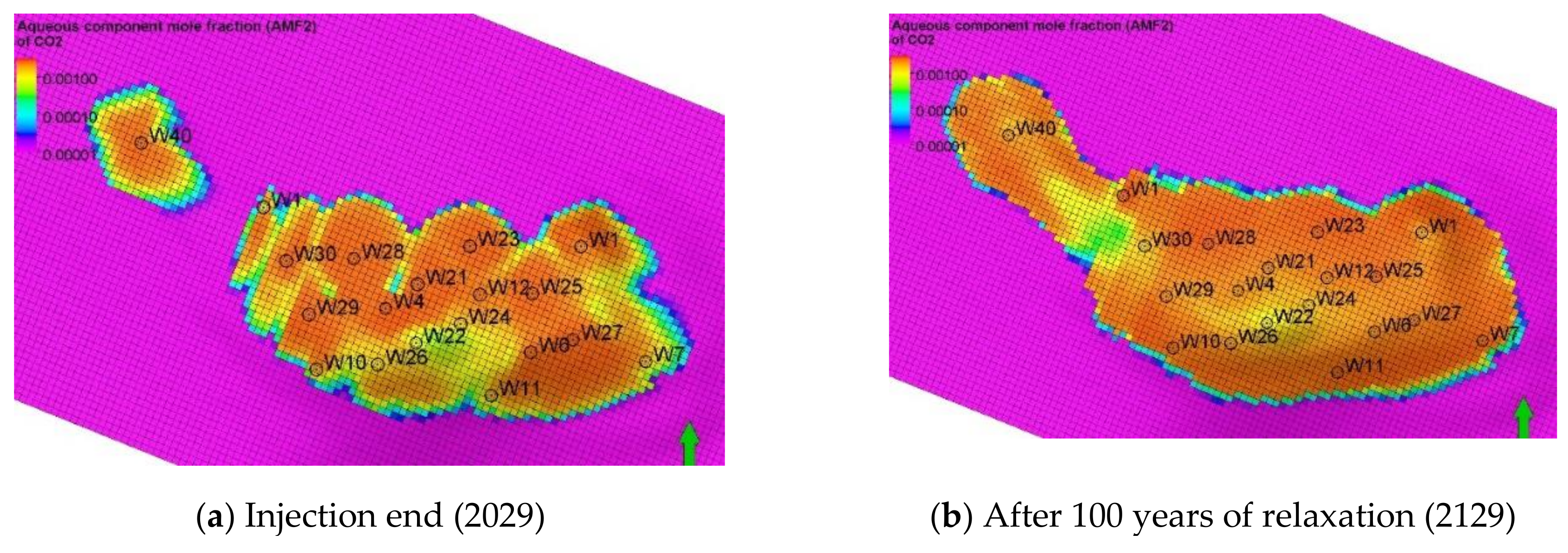
5.2. Simulation Forecast Results and Analysis
- –
- –
- –
- –
6. Summary and Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Lubaś, J.; Szott, W. 15-year experience of acid gas storage in the natural gas structure of Borzęcin—Poland. Nafta-Gaz 2010, 66, 333–338. [Google Scholar]
- In Salah Fact Sheet: Carbon Dioxide Capture and Storage Project. Available online: https://sequestration.mit.edu/tools/projects/in_salah.html (accessed on 14 March 2020).
- GDF K12-B Offshore CO2 Injection Project. Available online: https://www.co2-cato.org/cato/locations/regions/western-netherlands/gdf-k12-b-offshore-co2-injection-project (accessed on 14 March 2020).
- Akervoll, I.; Lindeberg, E.; Lackner, A. Feasibility of Reproduction of Stored CO2 from the Utsira Formation at the Sleipner Gas Field. Energy Procedia 2009, 1, 2557–2564. [Google Scholar] [CrossRef]
- Weyburn-Midale. The IEAGHG Weyburn-Midale CO2 Monitoring and Storage Project. Available online: https://ptrc.ca/projects/past-projects/weyburn-midale (accessed on 14 March 2020).
- Read, A.; Onno, T.; Menno, R.; Jonker, T.; Hylkema, H. Update on the ROAD Project and Lessons Learnt. Energy Procedia 2014, 63, 6079–6095. [Google Scholar] [CrossRef]
- Estubliera, A.; Lacknerb, A.S. Long-term simulation of the Snøhvit CO2 storage. Energy Procedia 2009, 1, 3221–3228. [Google Scholar] [CrossRef]
- Lubaś, J.; Szott, W.; Jakubowicz, P. Effects of Acid Gas Reinjection on CO2 Concentration in Natural Gas Produced from Borzęcin Reservoir. Nafta-Gaz 2012, 68, 405–410. [Google Scholar]
- Van der Meer, L.G.H. Computer modelling of underground CO storage. Energy Convers. Manag. 1996, 37, 1155–1160. [Google Scholar] [CrossRef]
- Jiang, X.; Akber Hassan, W.A.; Gluyas, J. Modelling and monitoring of geological carbon storage: A perspective on cross-validation. Appl. Energy 2013, 112, 784–792. [Google Scholar] [CrossRef]
- Agarwal, R.K. Modeling, Simulation, and Optimization of Geological Sequestration of CO2. ASME J. Fluids Eng. 2019, 141, 100801. [Google Scholar] [CrossRef]
- Soltanian, M.R. Multicomponent reactive transport of carbon dioxide in fluvial heterogeneous aquifers. J. Nat. Gas Sci. Eng. 2019, 65, 212–223. [Google Scholar] [CrossRef]
- Gershenzon, N.I. Influence of small-scale fluvial architecture on CO2 trapping processes in deep brine reservoirs. Water Resour. Res. 2015, 51, 8240–8256. [Google Scholar] [CrossRef]
- Polish Oil and Gas Company. Geological Documentation of the Borzęcin Natural Gas Reservoir, 1999. Personal communication, 2019. [Google Scholar]
- Szott, W.; Gołąbek, A.; Miłek, K. Symulacyjne badanie procesów sekwestracji gazów kwaśnych w wodach podścielających złoża naftowe (Simulation studies of acid gas sequestration in aquifers underlying gas reservoirs). Pr. Inst. Naft. I Gazu 2009, 165, 1–89. [Google Scholar]
- Szott, W.; Łętkowski, P.; Gołąbek, A.; Miłek, K. Ocena efektów wspomaganego wydobycia ropy naftowej i gazu ziemnego z wybranych złóż krajowych z zastosowaniem zatłaczania CO2 (Assessment of EOR/EGR processes by CO2 injection for selected Polish oil and gas reservoirs). Pr. Nauk. Inst. Naft. I Gazu 2012, 184, 1–161. [Google Scholar]
- Warnecki, M.; Wojnicki, M. Monitoring of acid gas migration in the Borzęcin structure. Unpublished Work.
- Polish Oil and Gas Company. Historical production data of the Borzęcin reservoir—reported by Polish Oil and Gas Company (POGC)—various reports in free format 1972–2019. Personal communication, 2019. [Google Scholar]
- Mortezaei, K.; Amirlatifi, A.; Ghazanfari, E.; Vahedifard, F. Potential CO2 Leakage from Geological Storage Sites: Advances and Challenges. J. Environ. Geotech. 2018. [Google Scholar] [CrossRef]
- Jin, X.; Shah, S.N.; Roegiers, J.-C.; Hou, B. Breakdown Pressure Determination—A Fracture Mechanics Approach. In Proceedings of the SPE Annual Technical Conference and Exhibition, New Orleans, LA, USA, 30 September–2 October 2013. SPE 166434. [Google Scholar]
- Szott, W.; Słota-Valim, M.; Gołąbek, A.; Łętkowski, P. Geomechanical modelling of the Borzęcin structure. Unpublished Work.
- Thomas, L.K.; Katz, D.L.; Tek, M.R. Threshold Pressure Phenomena in Porous Media. Soc. Pet. Eng. J. 2013, 8, 174–184. [Google Scholar] [CrossRef]
- Farokhpoora, R.; Akervolb, I.; Torsætera, O.; Bjørkvikb, B.J.A. CO2 capillary entry pressure into flow barrier and caprock. In Proceedings of the International Symposium of the Society of Core Analysts, Napa Valley, CA, USA, 2013, 16–19 September; pp. 1–8.
- Bhowmik, S.; Srinivasan, S.; Bryant, S.L. Predicting the Migration of CO2 Plume Using Injection Data and a Distance-Metric Approach to Reservoir-Model Selection. Soc. Pet. Eng. 2010. [Google Scholar] [CrossRef]
- Bachu, S.; Bonijoly, D.; Bradshaw, J.; Burruss, R.; Holloway, S.; Christensen, N.P.; Mathiassen, O.M. CO2 storage capacity estimation: Methodology and gaps. Int. J. Greenh. Gas. Control. 2007, 1, 430–443. [Google Scholar] [CrossRef]
- Kopp, A.; Probst, P.; Class, H.; Hurter, S.; Helmig, R. Estimation of CO2 Storage Capacity Coefficients in Geologic Formations. Energy Procedia 2009, 1, 2863–2870. [Google Scholar] [CrossRef]
- Suekane, T.; Nobuso, T.; Hirai, S.; Kiyota, M. Geological storage of carbon dioxide by residual gas and solubility trapping. Int. J. Greenh. Gas. Control. 2008, 2, 58–64. [Google Scholar] [CrossRef]

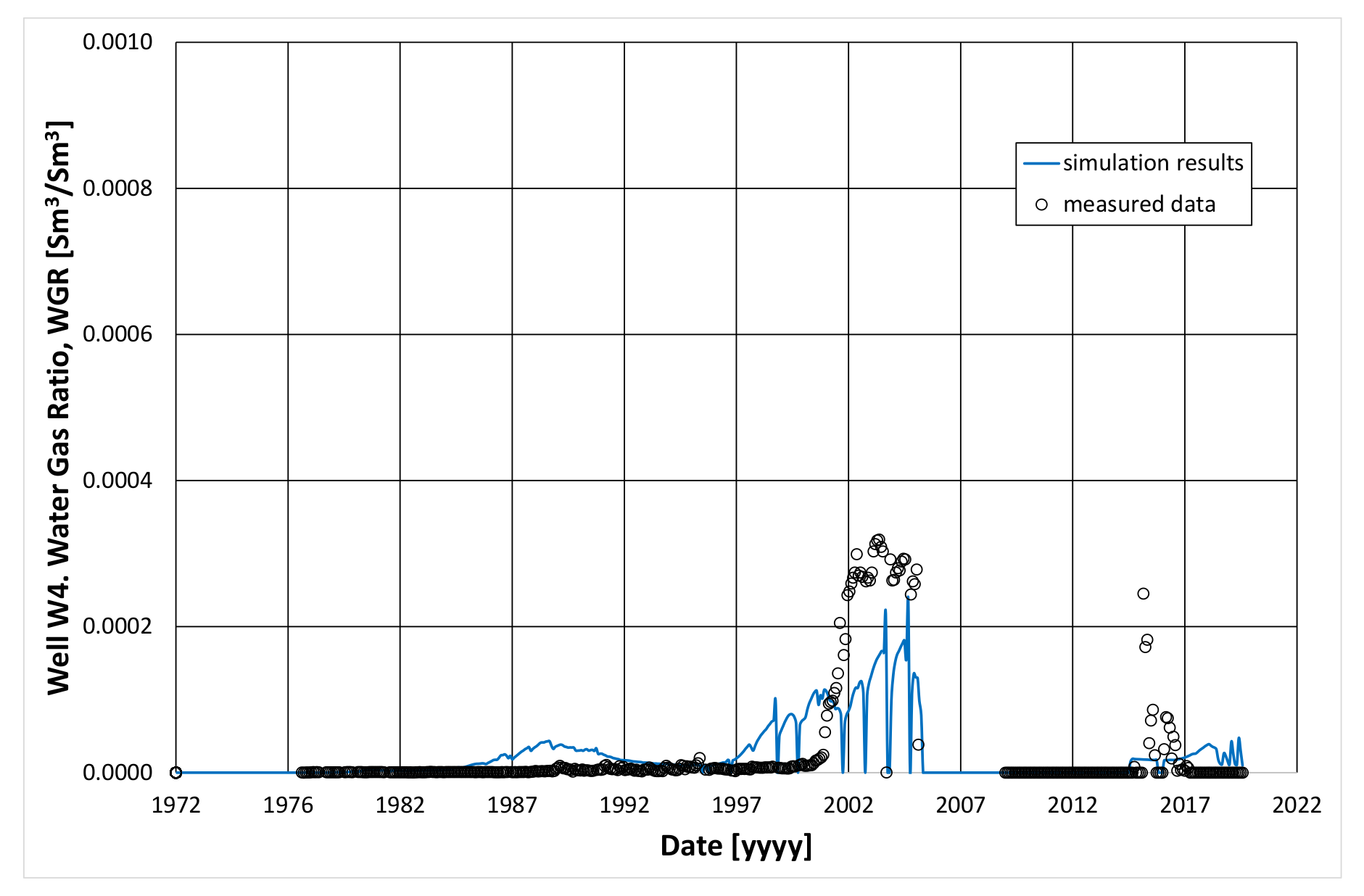
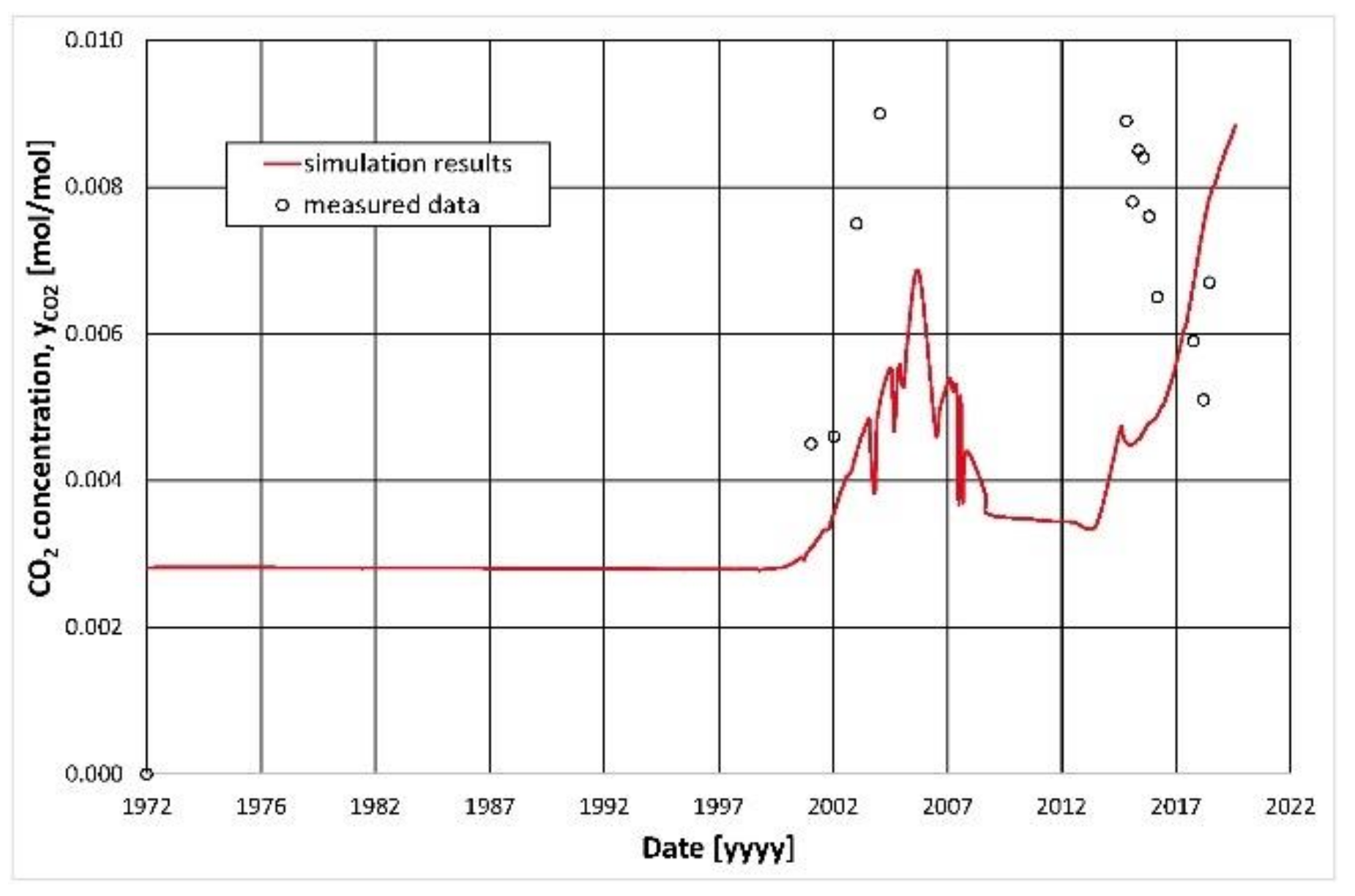
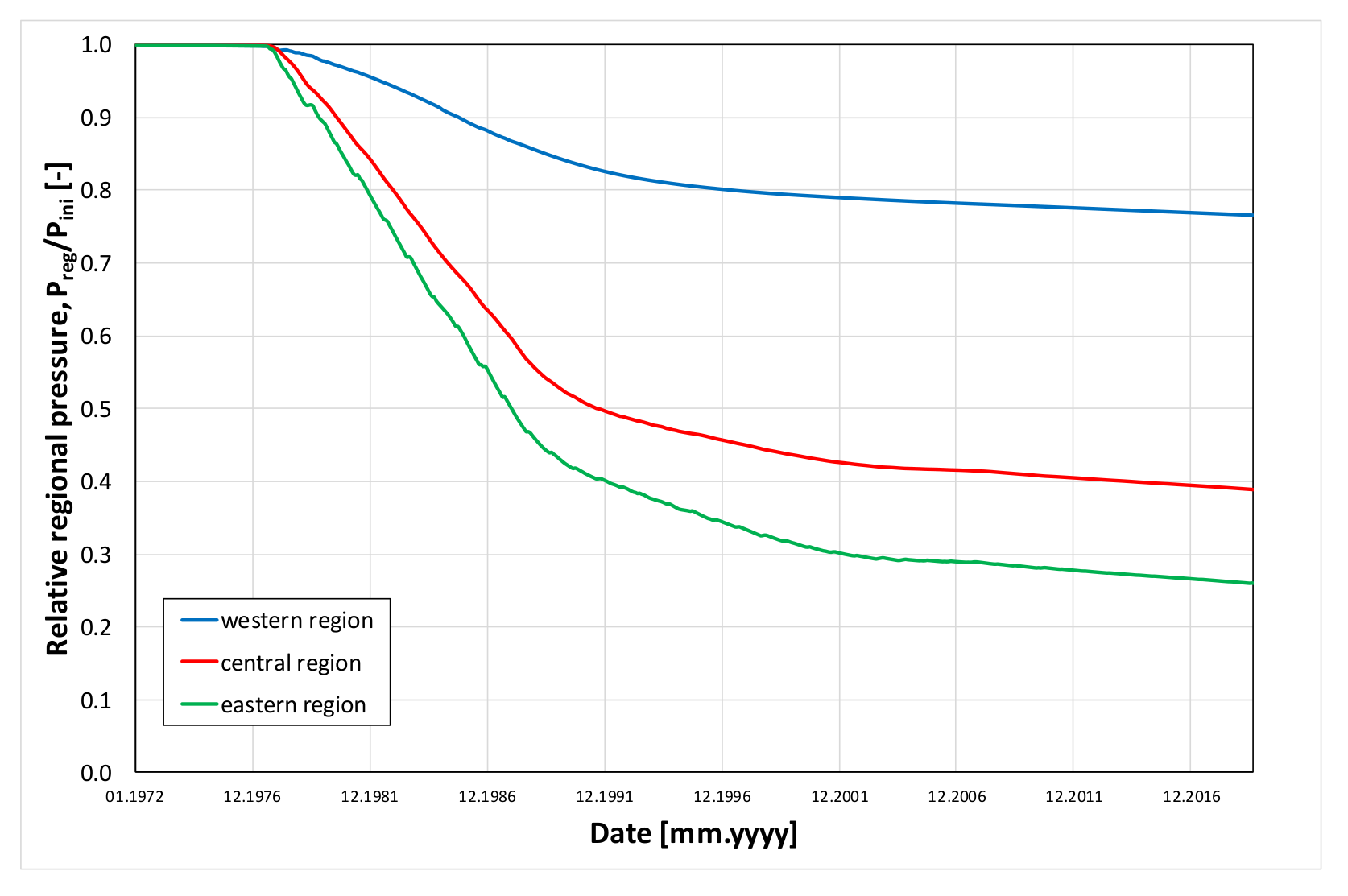
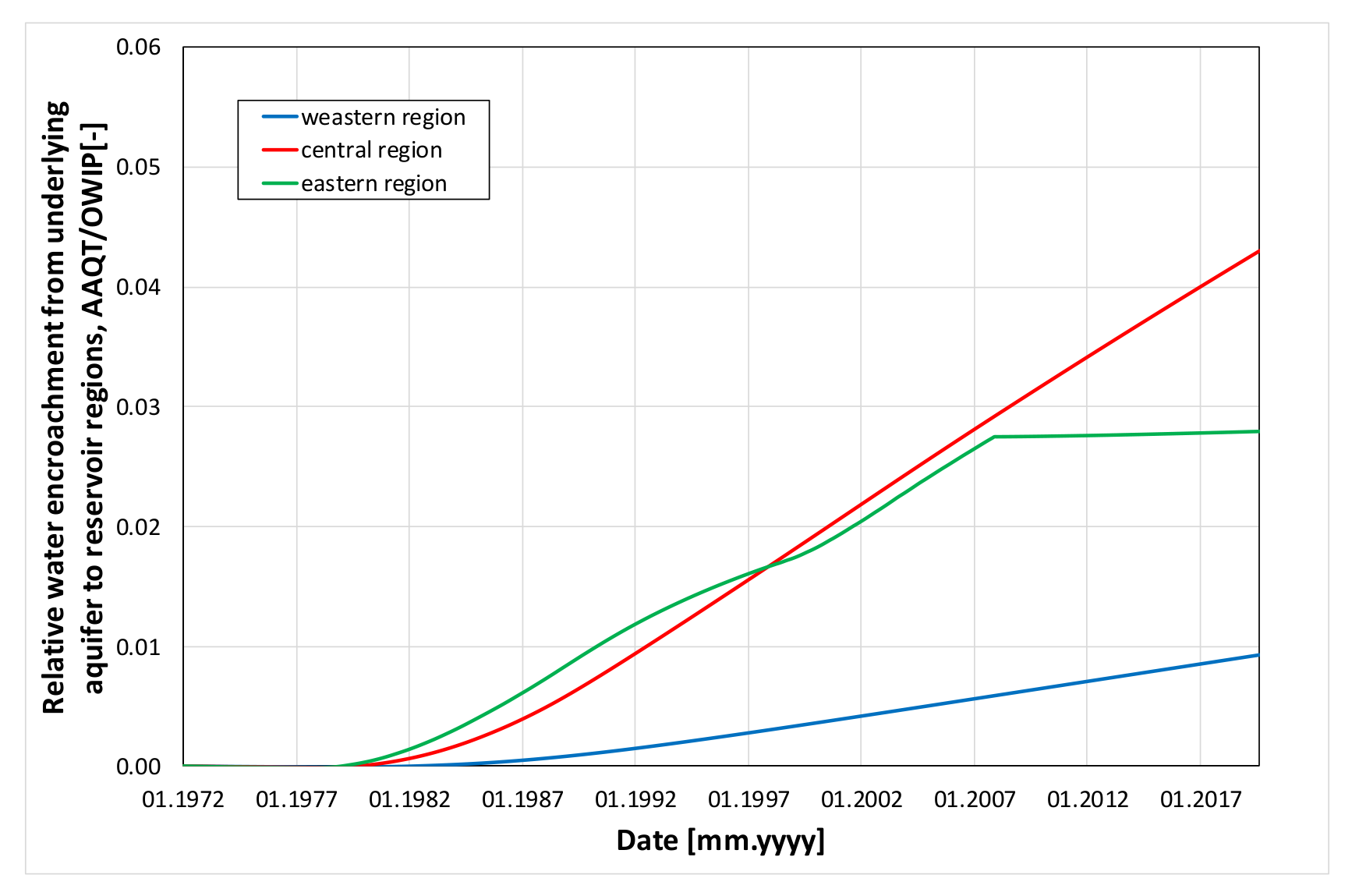






| Component | Mole Fraction |
|---|---|
| N2 | 0.36300 |
| CO2 | 0.00284 |
| H2S | 0.00129 |
| C1 | 0.61100 |
| C2 | 0.01970 |
| C3+ | 0.00461 |
| Region | Time Constant, Tc | Influx Constant, β |
|---|---|---|
| [d] | [m3/bar] | |
| Western | 0.65 | 1.89 |
| Central | 0.41 | 1.89 |
| Eastern | 0.03 | 0.25 |
| Drainage Zone of Well | Depth Interval | Modified Parameter | Multiplicative Factor |
|---|---|---|---|
| W1 | total reservoir thickness | horizontal permeability, kx | 0.10 |
| W4 | top layers | horizontal permeabilities, kx, ky | 0.25 |
| W4 | total reservoir thickness | vertical permeability, kz | 0.50 |
| W11 | total reservoir thickness | Swcr | 2.00 |
| W21 | top layers | horizontal permeabilities, kx, ky | 0.10 |
| W21 | total reservoir thickness | vertical permeability, kz | 1.50 |
| W22 | total reservoir thickness | horizontal permeability, ky | 0.10 |
| W24 | top layers | horizontal permeabilities, kx, ky | 0.10 |
| W25 | top layers | horizontal permeabilities, kx, ky | 0.03 |
| W25 | total reservoir thickness | vertical permeability, kz | 1.50 |
| W27 | top layers | horizontal permeabilities, kx, ky | 0.10 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Szott, W.; Łętkowski, P.; Gołąbek, A.; Miłek, K. Modelling of the Long-Term Acid Gas Sequestration and Its Prediction: A Unique Case Study. Energies 2020, 13, 4701. https://doi.org/10.3390/en13184701
Szott W, Łętkowski P, Gołąbek A, Miłek K. Modelling of the Long-Term Acid Gas Sequestration and Its Prediction: A Unique Case Study. Energies. 2020; 13(18):4701. https://doi.org/10.3390/en13184701
Chicago/Turabian StyleSzott, Wiesław, Piotr Łętkowski, Andrzej Gołąbek, and Krzysztof Miłek. 2020. "Modelling of the Long-Term Acid Gas Sequestration and Its Prediction: A Unique Case Study" Energies 13, no. 18: 4701. https://doi.org/10.3390/en13184701
APA StyleSzott, W., Łętkowski, P., Gołąbek, A., & Miłek, K. (2020). Modelling of the Long-Term Acid Gas Sequestration and Its Prediction: A Unique Case Study. Energies, 13(18), 4701. https://doi.org/10.3390/en13184701





