En-Route Battery Management and a Mixed Network Equilibrium Problem Based on Electric Vehicle Drivers’ En-Route Recharging Behaviors
Abstract
1. Introduction
2. Base Model
2.1. The Characterization of a Traffic Network
2.2. Definition and Formulation of a Mixed User Equilibrium
2.3. Solution Procedure
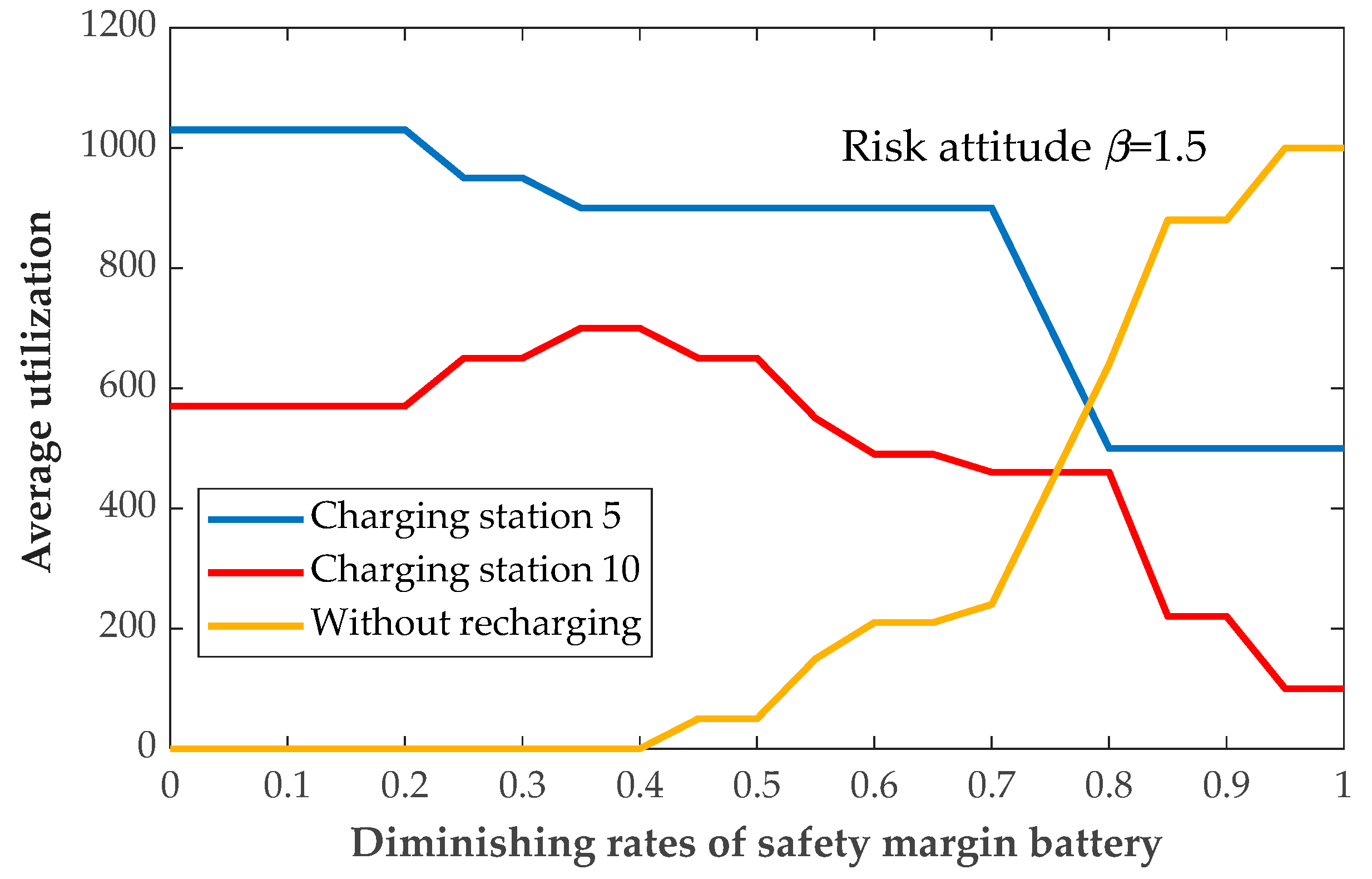
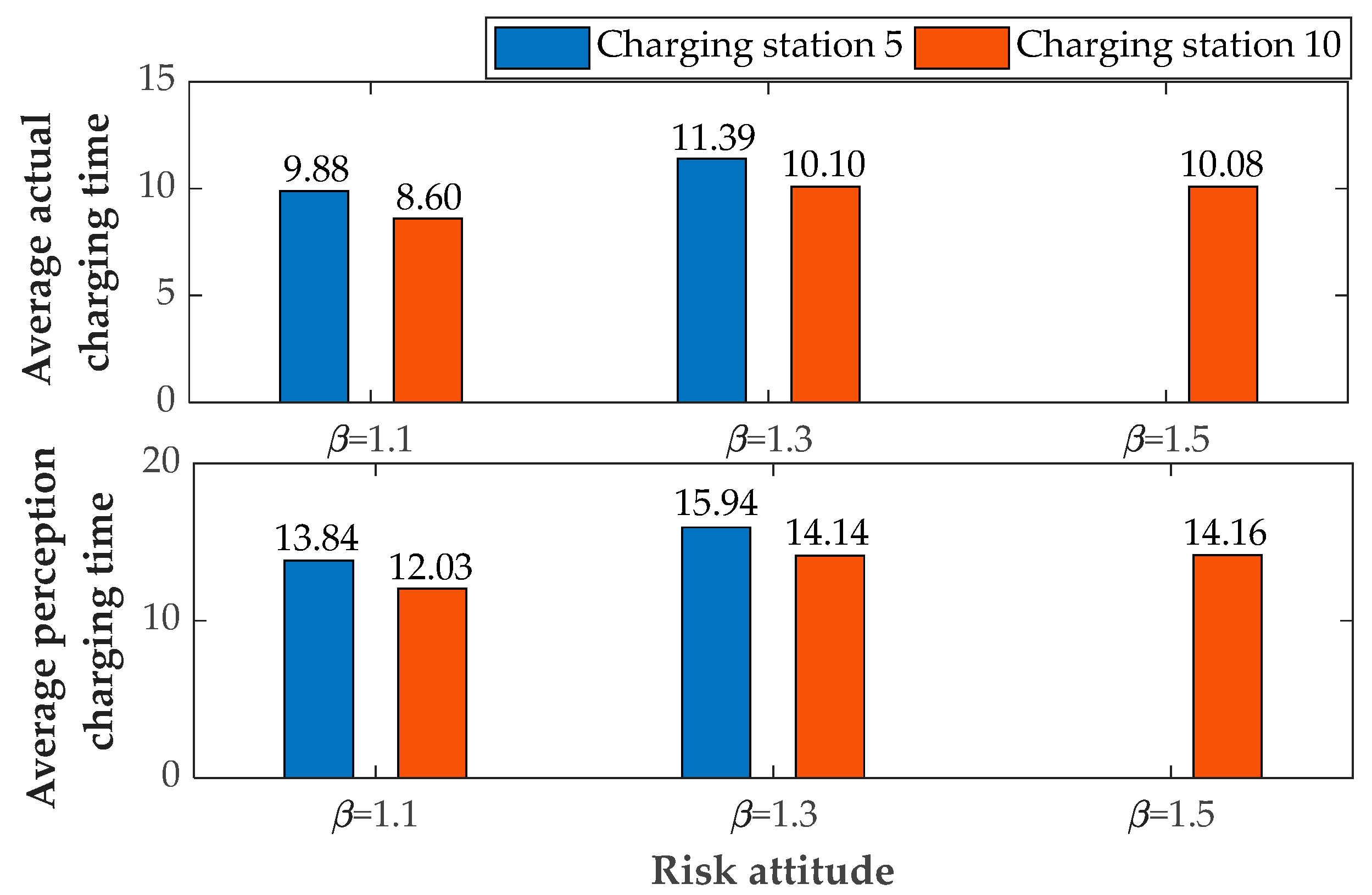
3. Numerical Example
4. Conclusions and Future Work
Author Contributions
Funding
Conflicts of Interest
Nomenclature
| the traffic network | |
| the set of nodes in the traffic network | |
| the set of links in the traffic network, and denote a link | |
| the set of origin-destination pairs, is the origin-destination pair index | |
| the set of paths between origin-destination pair , and is the path index | |
| the set of travel demand between origin-destination pair | |
| the traffic flow on link | |
| the travel distance of link | |
| the path-link incidence, if path traverses link , then , otherwise | |
| the link ’s free-flow travel time | |
| the link ’s capacity | |
| the set of types of vehicles drivers in the network, denote a type of drivers | |
| the set of all usable paths between OD pair | |
| the minimal actual time (minutes) that drivers need to spend on recharging activity when he/she choose route | |
| the coefficient and relate to the drivers’ risk attitudes | |
| the coefficient and relates to BEV drivers’ perception errors of the values of recharging time | |
| the coefficient and relate to the drivers’ risk attitudes | |
| the type ’s travel demand | |
| the traffic flow of type on path between OD pair | |
| the travel time (minutes) of path between OD pair | |
| the recharging amount of electricity on theory at charging stations for type drivers | |
| the actually recharging amount of electricity for type drivers | |
| the recharging time function for drivers to recharge some amount of electricity at node | |
| the fixed recharging time | |
| the variable recharging time | |
| the battery charge after recharging | |
| the battery size | |
| the initial state of battery | |
| the node-link incidence matrix associated with the network | |
| the vector with a length of | |
| the binary variable, if link is used, then , otherwise | |
| the binary variable, if charging stations is selected, then , otherwise | |
| the variable, if link is used by driver , then , otherwise unrestricted |
References
- He, F.; Yin, Y.; Wang, J.; Yang, Y. Sustainability SI: Optimal Prices of Electricity at Public Charging Stations for Plug-in Electric Vehicles. Netw. Spat. Econ. 2013, 16, 131–154. [Google Scholar] [CrossRef]
- Gardner, L.M.; Duell, M.; Waller, S.T. A framework for evaluating the role of electric vehicles in transportation network infrastructure under travel demand variability. Transp. Res. Part A 2013, 49, 76–90. [Google Scholar] [CrossRef]
- Efthymiou, D.; Chrysostomou, K.; Morfoulaki, M.; Aifantopoulou, G. Electric vehicles charging infrastructure location: A genetic algorithm approach. Eur. Transp. Res. Rev. 2017, 9, 27. [Google Scholar] [CrossRef]
- Liu, Z.; Song, Z. Network user equilibrium of battery electric vehicles considering flow-dependent electricity consumption. Transp. Res. Part C Emerg. Technol. 2018, 95, 516–544. [Google Scholar] [CrossRef]
- Pearre, N.S.; Kempton, W.; Guensler, R.L.; Elango, V.V. Electric vehicles: How much range is required for a day’s driving? Transp. Res. Part C Emerg. Technol. 2011, 19, 1171–1184. [Google Scholar] [CrossRef]
- Guo, F.; Yang, J.; Lu, J. The battery charging station location problem: Impact of users’ range anxiety and distance convenience. Transp. Res. Part E Logist. Transp. Rev. 2018, 114, 1–18. [Google Scholar] [CrossRef]
- Bi, J.; Wang, Y.; Sun, S.; Guan, W. Predicting Charging Time of Battery Electric Vehicles Based on Regression and Time-Series Methods: A Case Study of Beijing. Energies 2018, 11, 1040. [Google Scholar] [CrossRef]
- Kuby, M.; Lim, S. The flow-refueling location problem for alternative-fuel vehicles. Socio-Econ. Plan. Sci. 2005, 39, 125–145. [Google Scholar] [CrossRef]
- Wang, Y.-W.; Lin, C.-C. Locating road-vehicle refueling stations. Transp. Res. Part E Logist. Transp. Rev. 2009, 45, 821–829. [Google Scholar] [CrossRef]
- Franke, T.; Neumann, I.; Bühler, F.; Cocron, P.; Krems, J.F. Experiencing Range in an Electric Vehicle: Understanding Psychological Barriers. Appl. Psychol. 2011, 61, 368–391. [Google Scholar] [CrossRef]
- Franke, T.; Krems, J.F. Understanding charging behaviour of electric vehicle users. Transp. Res. Part F Traffic Psychol. Behav. 2013, 21, 75–89. [Google Scholar] [CrossRef]
- Nadine, R.; Thomas, F.; Josef, F.K. Understanding the impact of electric vehicle driving experience on range anxiety. Hum. Factors 2014, 57, 177–187. [Google Scholar]
- Bagloee, S.A.; Sarvi, M.; Patriksson, M.; Rajabifard, A. A Mixed User-Equilibrium and System-Optimal Traffic Flow for Connected Vehicles Stated as a Complementarity Problem. Comput.-Aided Civ. Infrastruct. Eng. 2017, 2, 213–580. [Google Scholar] [CrossRef]
- Xie, C.; Liu, Z. On the stochastic network equilibrium with heterogeneous choice inertia. Transp. Res. Part B Methodol. 2014, 66, 90–109. [Google Scholar] [CrossRef]
- Lou, Y.; Yin, Y.; Lawphongpanich, S. Robust congestion pricing under boundedly rational user equilibrium. Transp. Res. Part B Methodol. 2010, 44, 15–28. [Google Scholar] [CrossRef]
- Zhao, C.-L.; Huang, H.-J. Experiment of boundedly rational route choice behavior and the model under satisficing rule. Transp. Res. Part C Emerg. Technol. 2016, 68, 22–37. [Google Scholar] [CrossRef]
- Zhang, J.; Yang, H. Modeling route choice inertia in network equilibrium with heterogeneous prevailing choice sets. Transp. Res. Part C Emerg. Technol. 2015, 57, 42–54. [Google Scholar] [CrossRef]
- He, F.; Yin, Y.; Lawphongpanich, S. Network equilibrium models with battery electric vehicles. Transp. Res. Part B Methodol. 2014, 67, 306–319. [Google Scholar] [CrossRef]
- Xie, C.; Wu, X.; Boyles, S. Network equilibrium of electric vehicles with stochastic range anxiety. In Proceedings of the 17th International IEEE Conference on Intelligent Transportation Systems (ITSC), Qingdao, China, 8–11 October 2014; pp. 2505–2510. [Google Scholar]
- Jiang, N.; Xie, C. Computing and Analyzing Mixed Equilibrium Network Flows with Gasoline and Electric Vehicles. Comput.-Aided Civ. Infrastruct. Eng. 2014, 29, 626–641. [Google Scholar] [CrossRef]
- Xu, M.; Meng, Q.; Liu, K. Network user equilibrium problems for the mixed battery electric vehicles and gasoline vehicles subject to battery swapping stations and road grade constraints. Transp. Res. Part B Methodol. 2017, 99, 138–166. [Google Scholar] [CrossRef]
- Becker, G.S. A Theory of the Allocation of Time. Econ. J. 1965, 75, 493–517. [Google Scholar] [CrossRef]
- Jafari, E.; Boyles, S.D. Multicriteria Stochastic Shortest Path Problem for Electric Vehicles. Netw. Spat. Econ. 2017, 17, 1043–1070. [Google Scholar] [CrossRef]
- Agrawal, S.; Zheng, H.; Peeta, S.; Kumar, A. Routing aspects of electric vehicle drivers and their effects on network performance. Transp. Res. Part D Transp. Environ. 2016, 46, 246–266. [Google Scholar] [CrossRef]
- US Department of Energy, 2020. Available online: http://www.fueleconomy.gov/feg/evtech.shtml (accessed on 10 April 2020).
- Nguyen, S.; Dupuis, C. An Efficient Method for Computing Traffic Equilibria in Networks with Asymmetric Transportation Costs. Transp. Sci. 1984, 18, 185–202. [Google Scholar] [CrossRef]
- Nissan, 2020. Available online: https://www.nissanusa.com/vehicles/electric-cars/leaf/features/range-charging-battery.html (accessed on 10 April 2020).
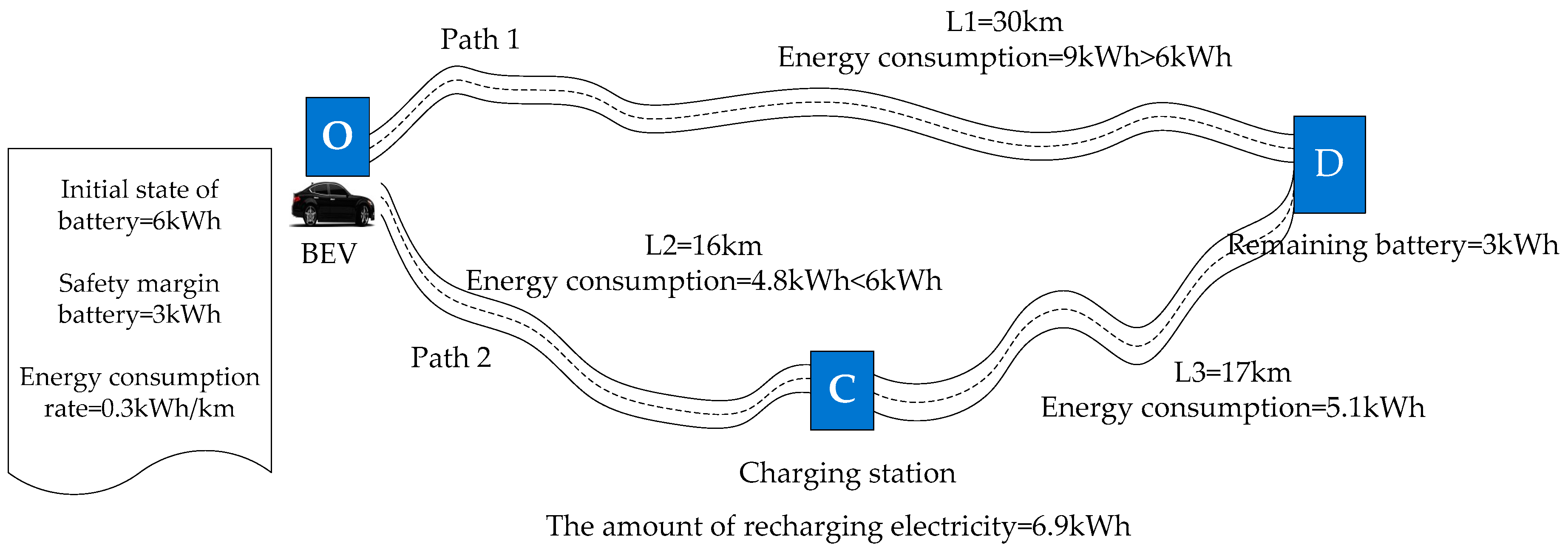
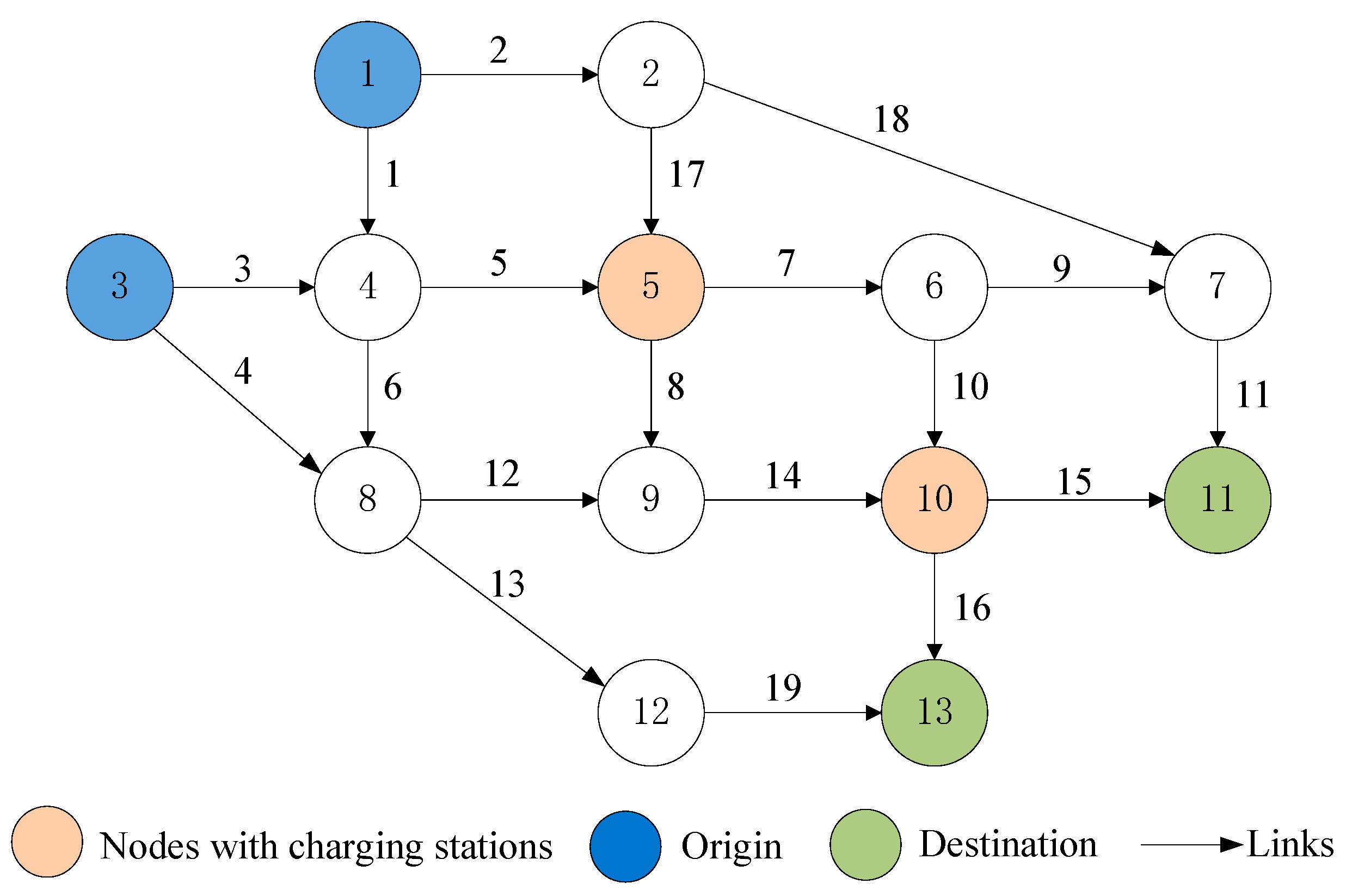

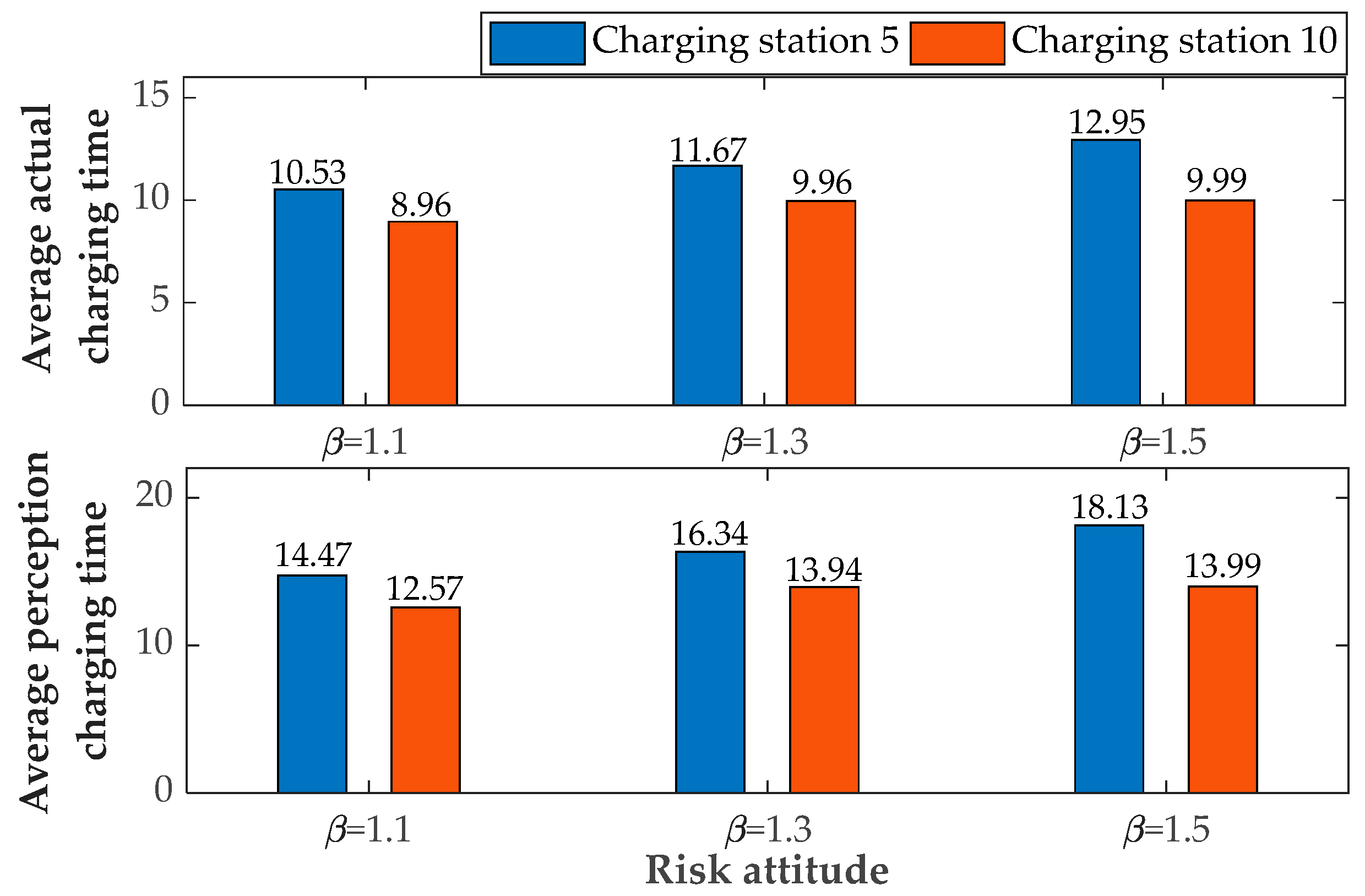

| Link | Distance | Free-Flow Travel Time | Capacity | Link | Distance | Free-Flow Travel Time | Capacity |
|---|---|---|---|---|---|---|---|
| 1 | 14 | 7 | 3000 | 11 | 18 | 9 | 5000 |
| 2 | 18 | 9 | 2000 | 12 | 20 | 10 | 5500 |
| 3 | 18 | 9 | 2000 | 13 | 18 | 9 | 2000 |
| 4 | 24 | 12 | 2000 | 14 | 12 | 6 | 4000 |
| 5 | 6 | 3 | 3500 | 15 | 18 | 9 | 3000 |
| 6 | 18 | 9 | 4000 | 16 | 16 | 8 | 3000 |
| 7 | 10 | 7 | 5000 | 17 | 14 | 7 | 2000 |
| 8 | 26 | 13 | 2500 | 18 | 20 | 10 | 5000 |
| 9 | 10 | 5 | 2500 | 19 | 18 | 9 | 2000 |
| 10 | 18 | 9 | 2000 |
| Origin-Destination (OD) Pair | Total Demands | Driver’s Type | Proportion | ||
|---|---|---|---|---|---|
| (1,11) | 5000 | BEV | 1.1 | (1.2, 50%; 1.5, 40%; 2, 10%) | 10% |
| 1.3 | 10% | ||||
| 1.5 | 10% | ||||
| (1,13) | 3000 | BEV | 1.1 | (1.2, 50%; 1.5, 40%; 2, 10%) | 10% |
| 1.3 | 10% | ||||
| 1.5 | 10% | ||||
| (3,11) | 5000 | BEV | 1.1 | (1.2, 50%; 1.5, 40%; 2, 10%) | 10% |
| 1.3 | 10% | ||||
| 1.5 | 10% | ||||
| (3,13) | 3000 | BEV | 1.1 | (1.2, 50%; 1.5, 40%; 2, 10%) | 10% |
| 1.3 | 10% | ||||
| 1.5 | 10% |
| Battery Safety Margin | ||
|---|---|---|
| (, 60%; , 30%; , 10%) | ||
| (, 60%; , 30%; , 10%) | ||
| (, 60%; , 30%; , 10%) |
| OD | Path ID | Node Sequence | Path Flow (the Number of Vehicles on Each Path) | Path Travel Time (Actual Time) | ||
|---|---|---|---|---|---|---|
| Electric Vehicle (Energy Consumption) | Gasoline Vehicle | Total | ||||
| (1,11) | 1 | 1–2–7–11 | 0 (9.35 kWh) | 3330 | 3330 | 49.63 min |
| 2 | 1–4–5–6–7–11 | 1500 (9.67 kWh) | 0 | 1500 | 51.09 min | |
| 3 | 1–4–8–9–10–11 | 0 (13.69 kWh) | 170 | 170 | 49.63 min | |
| (1,13) | 4 | 1–4–5–6–10–13 | 900 (10.69 kWh) | 900 | 900 | 50.53 min |
| 5 | 1–4–8–9–10–13 | 0 (13.36 kWh) | 1295 | 1295 | 49.07 min | |
| 6 | 1–4–8–12–13 | 0 (11.36 kWh) | 805 | 805 | 49.07 min | |
| (3,11) | 7 | 3–4–5–6–7–11 | 860 (10.35 kWh) | 1286 | 2166 | 63.90 min |
| 8 | 3–4–5–6–10–11 | 640 (11.69 kWh) | 0 | 640 | 63.90 min | |
| 9 | 3–4–5–9–10–11 | 0 (13.36 kWh) | 390 | 390 | 63.80 min | |
| 10 | 3–8–9–10–11 | 0 (12.36 kWh) | 1804 | 1804 | 63.90 min | |
| (3,13) | 11 | 3–4–5–6–10–13 | 960 (11.36 kWh) | 60 | 60 | 63.33 min |
| 12 | 3–8–9–10–13 | 0 (12.02 kWh) | 161 | 161 | 63.33 min | |
| 13 | 3–8–12–13 | 0 (10.02 kWh) | 1879 | 1879 | 63.33 min | |
| OD | Path ID | Node Sequence | Total Flow | Path Travel Time (Actual Time) |
|---|---|---|---|---|
| (1,11) | 1 | 1–2–7–11 | 3388 | 50.26 min |
| 2 | 1–4–5–6–7–11 | 1155 | 50.25 min | |
| 3 | 1–4–8–9–10–11 | 457 | 50.25 min | |
| (1,13) | 4 | 1–4–5–6–10–13 | 722 | 49.35 min |
| 5 | 1–4–8–9–10–13 | 1431 | 49.35 min | |
| 6 | 1–4–8–12–13 | 847 | 49.35 min | |
| (3,11) | 7 | 3–4–5–6–7–11 | 2319 | 63.92 min |
| 8 | 3–4–5–6–10–11 | 538 | 63.92 min | |
| 9 | 3–4–5–9–10–11 | 388 | 63.92 min | |
| 10 | 3–8–9–10–11 | 1755 | 63.92 min | |
| (3,13) | 11 | 3–4–5–6–10–13 | 940 | 63.02 min |
| 12 | 3–8–9–10–13 | 190 | 63.02 min | |
| 13 | 3–8–12–13 | 1870 | 63.02 min |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, K.; Luo, S.; Zhou, J. En-Route Battery Management and a Mixed Network Equilibrium Problem Based on Electric Vehicle Drivers’ En-Route Recharging Behaviors. Energies 2020, 13, 4061. https://doi.org/10.3390/en13164061
Liu K, Luo S, Zhou J. En-Route Battery Management and a Mixed Network Equilibrium Problem Based on Electric Vehicle Drivers’ En-Route Recharging Behaviors. Energies. 2020; 13(16):4061. https://doi.org/10.3390/en13164061
Chicago/Turabian StyleLiu, Kai, Sijia Luo, and Jing Zhou. 2020. "En-Route Battery Management and a Mixed Network Equilibrium Problem Based on Electric Vehicle Drivers’ En-Route Recharging Behaviors" Energies 13, no. 16: 4061. https://doi.org/10.3390/en13164061
APA StyleLiu, K., Luo, S., & Zhou, J. (2020). En-Route Battery Management and a Mixed Network Equilibrium Problem Based on Electric Vehicle Drivers’ En-Route Recharging Behaviors. Energies, 13(16), 4061. https://doi.org/10.3390/en13164061