Multi-Step Solar Irradiance Forecasting and Domain Adaptation of Deep Neural Networks
Abstract
1. Introduction
2. Materials and Methods
2.1. Structure of the Multi-Step Neural Predictors
2.1.1. The Recursive (Rec) Approach
2.1.2. The Multi-Model (MM Approach
2.1.3. The Multi-Output (MO) Approach
2.2. Model Identification Strategies
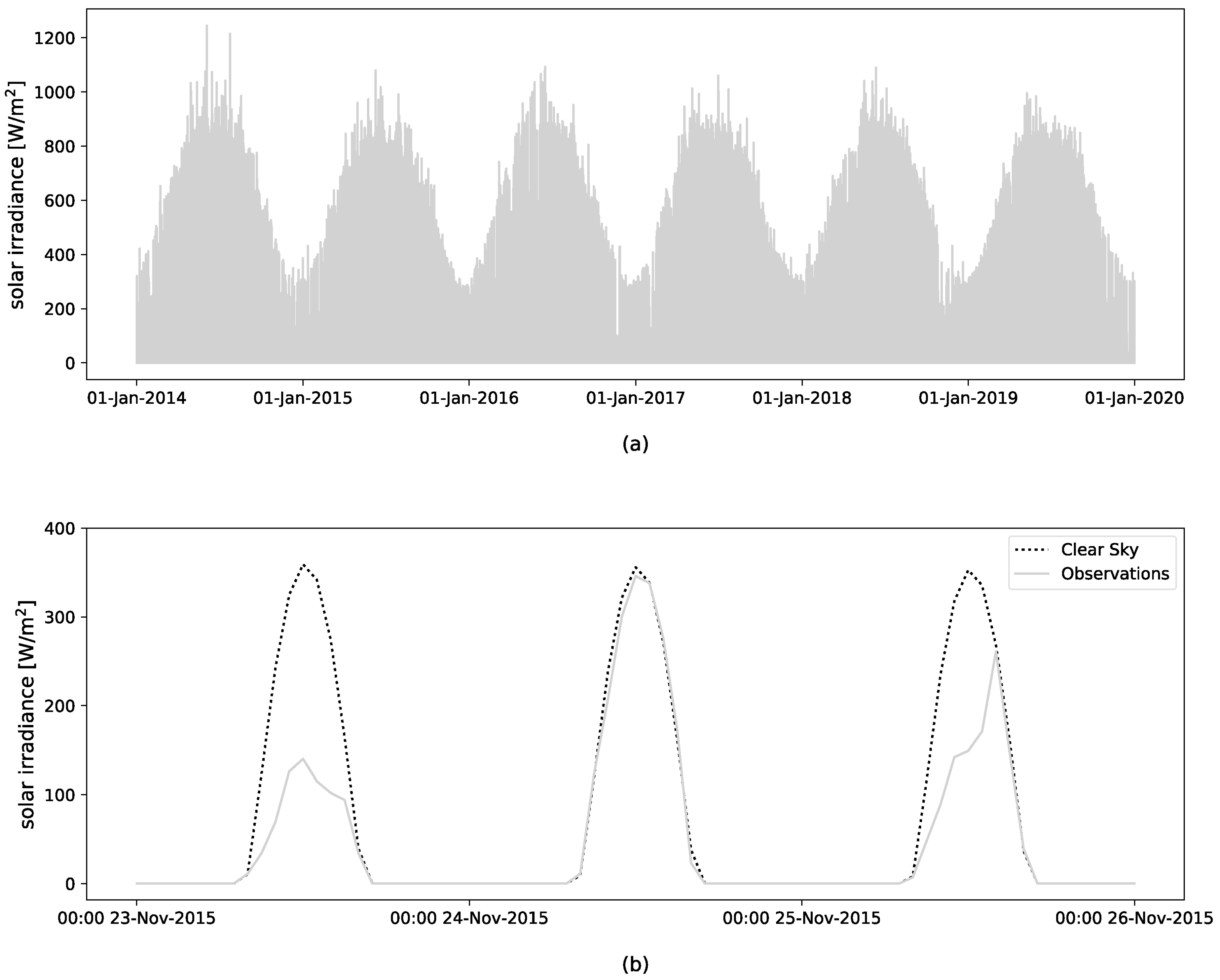
2.3. Preliminary Analysis of Solar Data
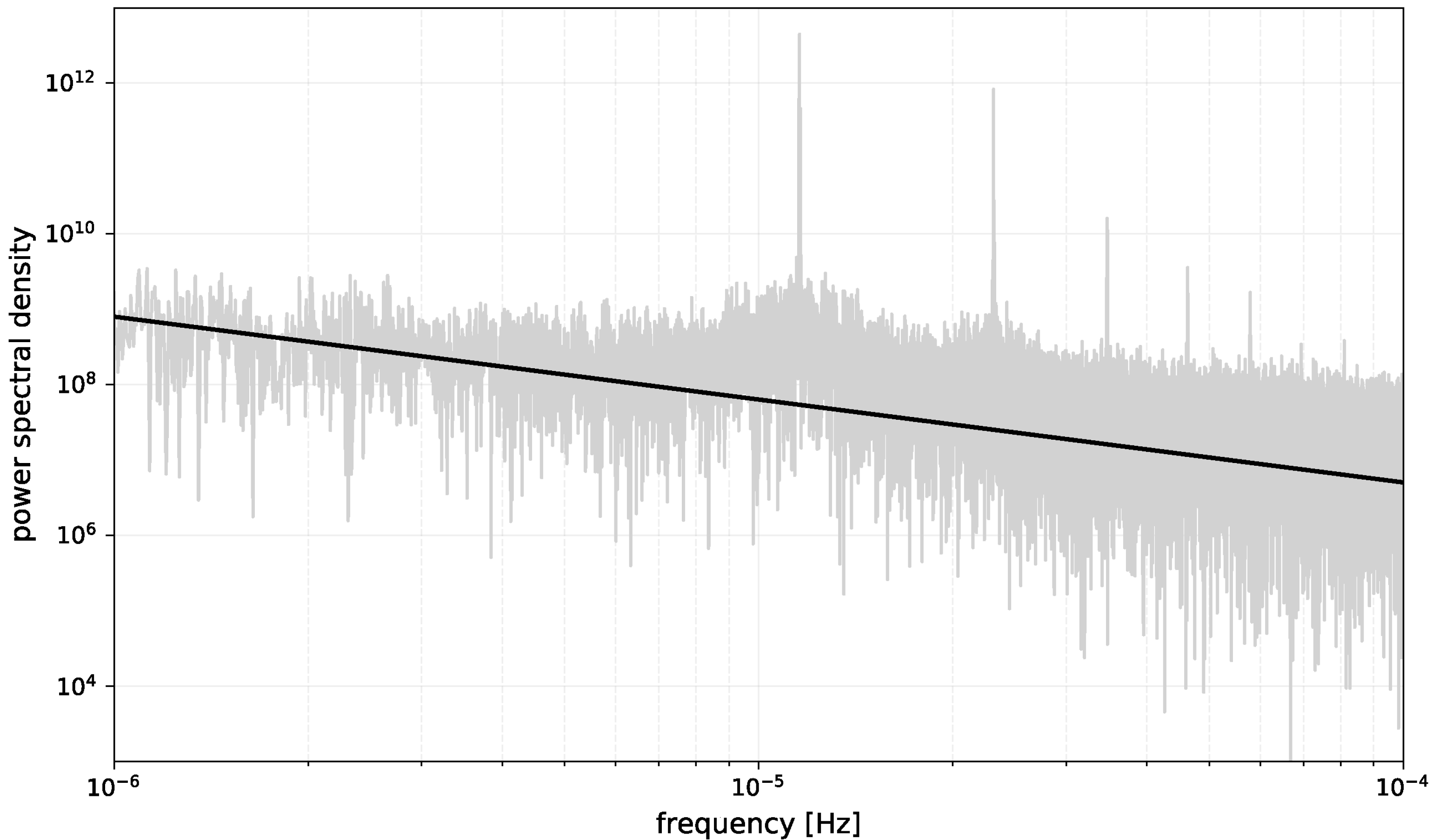
2.3.1. Fluctuation of Solar Radiation
2.3.2. Mutual Information
2.4. Benchmark Predictors of Hourly Solar Irradiance
- The “clear sky” model, Clsky in the following, computed as explained in Section 2.2, which represents the average long-term cycle;
- The so-called Pers24 model expressed as , which represents the memory linked to the daily cycle;
- A classical persistent model, Pers in what follows, where , representing the component due to a very short-term memory.
2.5. Performance Assessment Metrics
3. Results
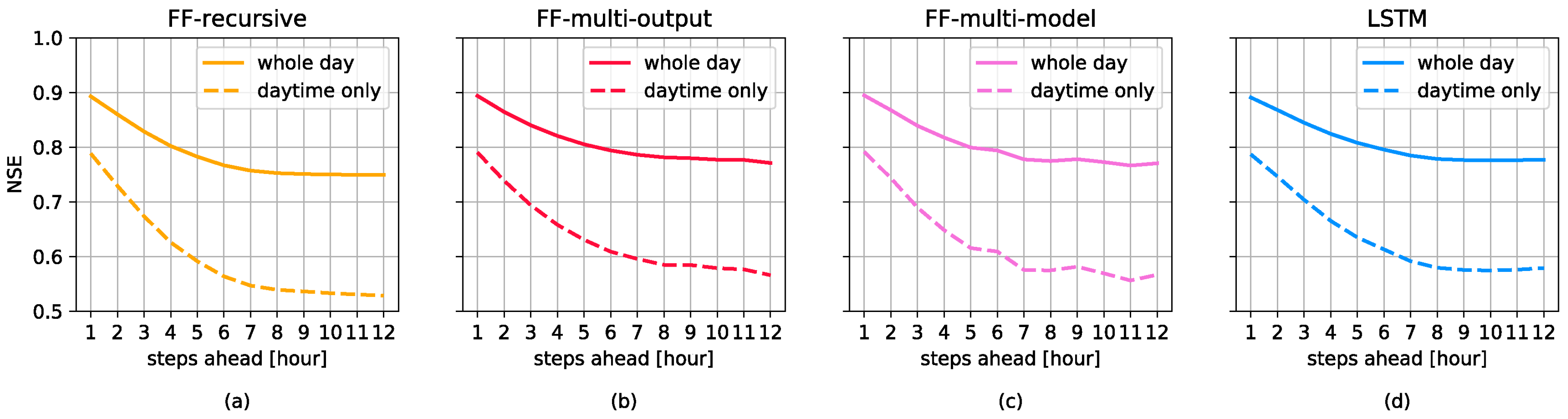
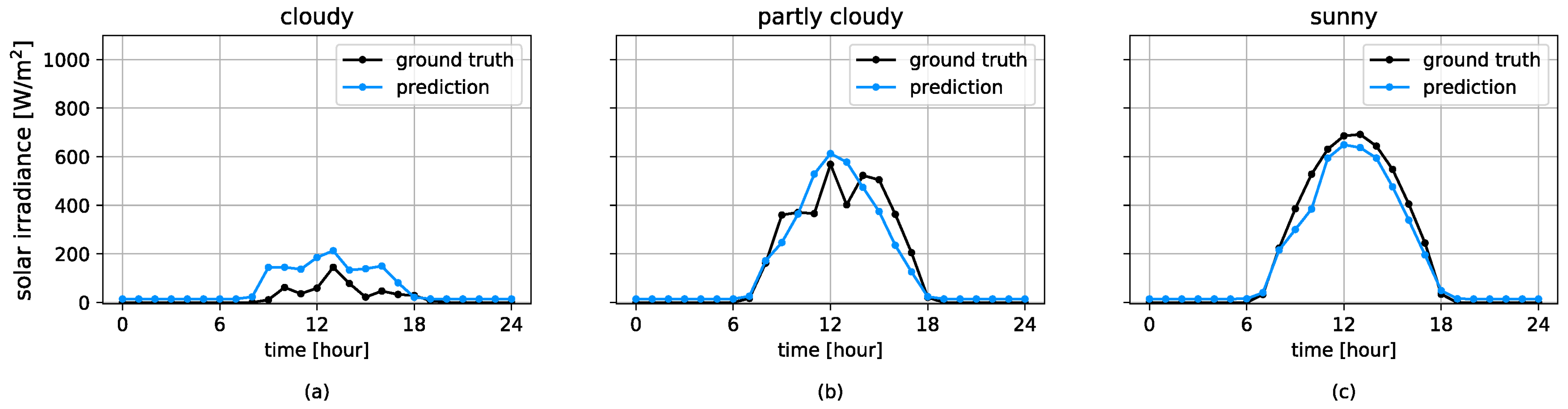
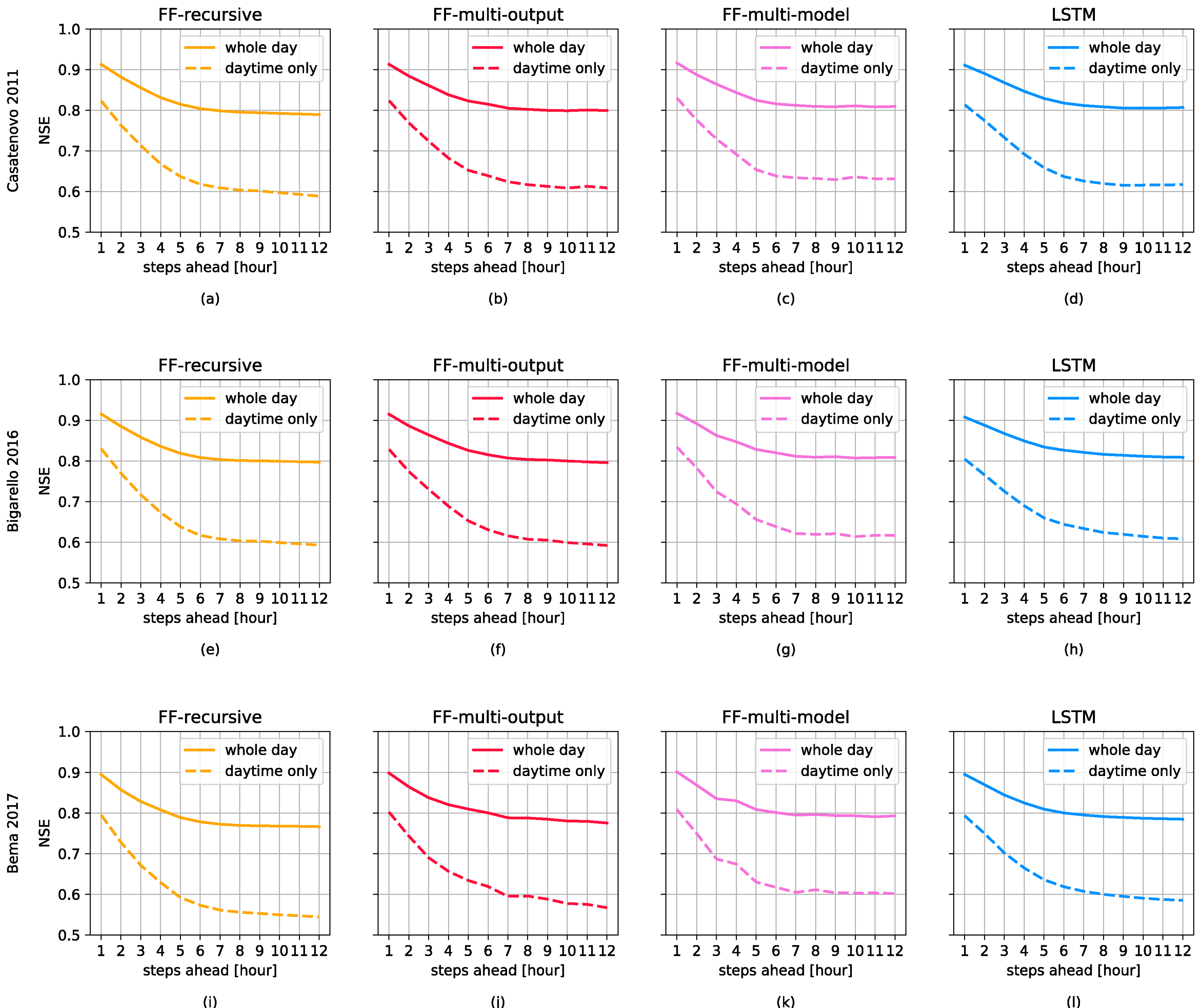
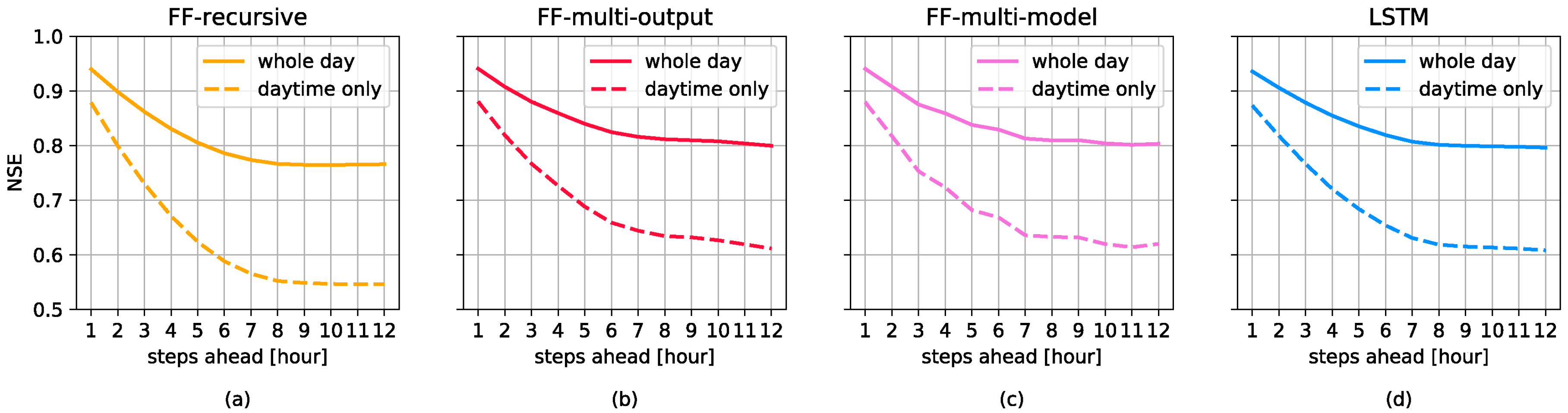
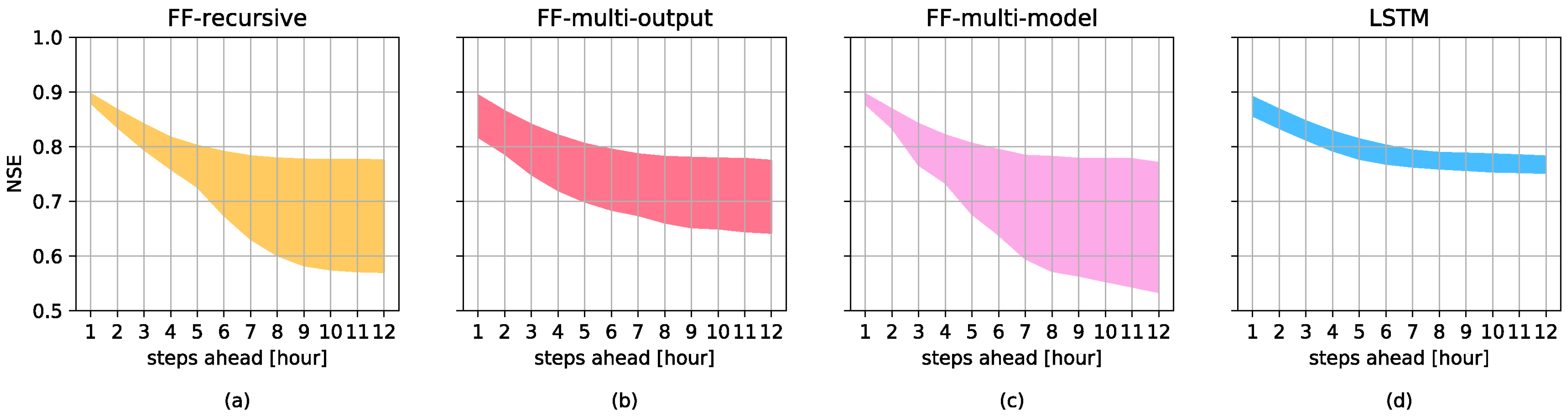
3.1. Forecasting Perfomances
3.2. Domain Adaptation
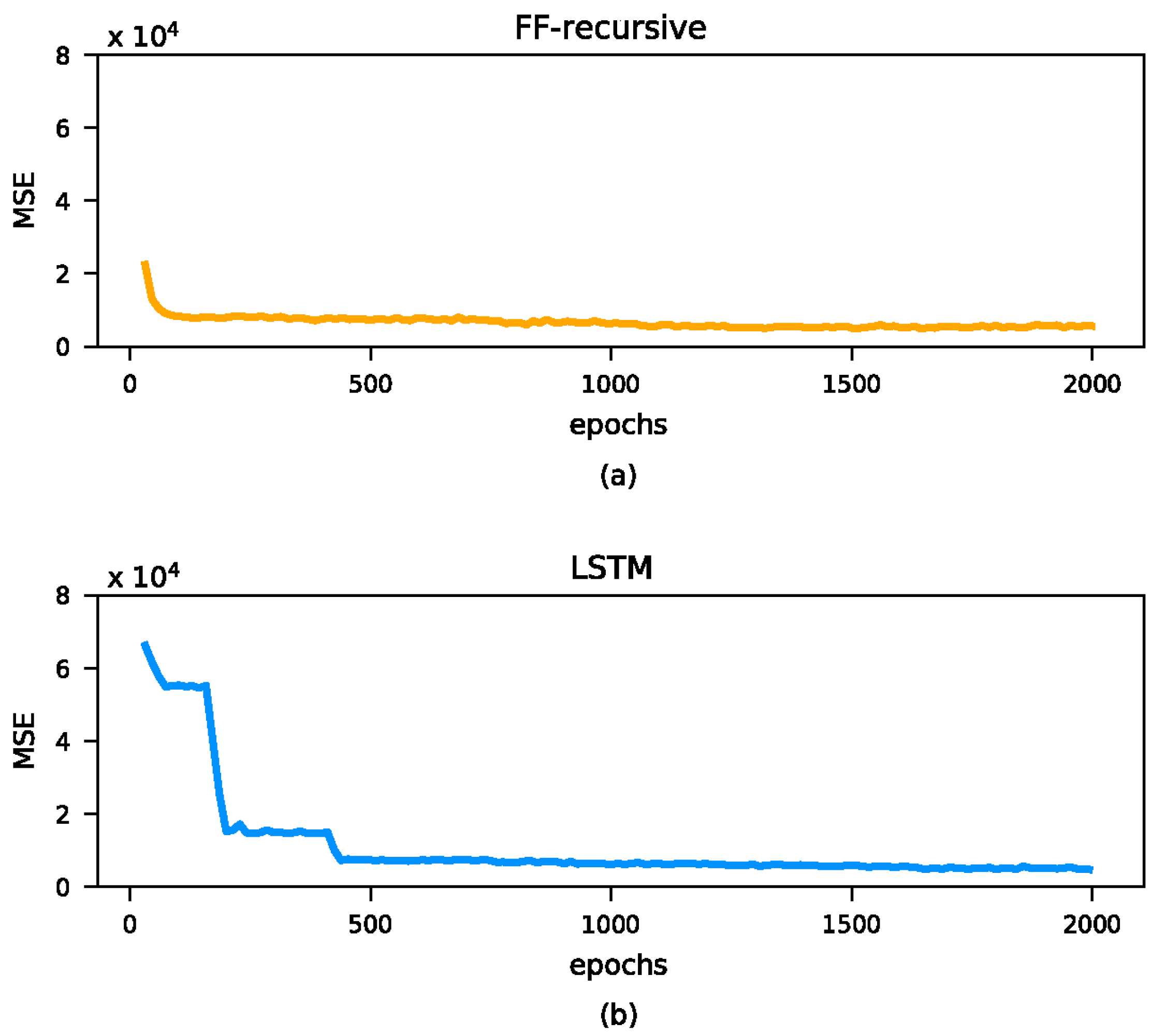
4. Some Remarks on Network Implementations
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Shah, A.S.B.M.; Yokoyama, H.; Kakimoto, N. High-precision forecasting model of solar irradiance based on grid point value data analysis for an efficient photovoltaic system. IEEE Trans. Sustain. Energy 2015, 6, 474–481. [Google Scholar] [CrossRef]
- Urrego-Ortiz, J.; Martínez, J.A.; Arias, P.A.; Jaramillo-Duque, Á. Assessment and Day-Ahead Forecasting of Hourly Solar Radiation in Medellín, Colombia. Energies 2019, 12, 4402. [Google Scholar] [CrossRef]
- Mpfumali, P.; Sigauke, C.; Bere, A.; Mulaudzi, S. Day Ahead Hourly Global Horizontal Irradiance Forecasting—Application to South African Data. Energies 2019, 12, 3569. [Google Scholar] [CrossRef]
- Mohamed, A.; Salehi, V.; Ma, T.; Mohammed, O. Real-time energy management algorithm for plug-in hybrid electric vehicle charging parks involving sustainable energy. IEEE Trans. Sustain. Energy 2014, 5, 577–586. [Google Scholar] [CrossRef]
- Bhatti, A.R.; Salam, Z.; Aziz, M.J.B.A.; Yee, K.P.; Ashique, R.H. Electric vehicles charging using photovoltaic: Status and technological review. Renew. Sustain. Energy Rev. 2016, 54, 34–47. [Google Scholar] [CrossRef]
- Sáez, D.; Ávila, F.; Olivares, D.; Cañizares, C.; Marín, L. Fuzzy prediction interval models for forecasting renewable resources and loads in microgrids. IEEE Trans. Smart Grid 2015, 6, 548–556. [Google Scholar]
- Yadav, A.K.; Chandel, S.S. Solar radiation prediction using Artificial Neural Network techniques: A review. Renew. Sustain. Energy Rev. 2014, 772–781. [Google Scholar] [CrossRef]
- Wan, C.; Zhao, J.; Song, Y.; Xu, Z.; Lin, J.; Hu, Z. Photovoltaic and solar power forecasting for smart grid energy management. CSEE J. Power Energy Syst. 2015, 1, 38–46. [Google Scholar] [CrossRef]
- Voyant, C.; Notton, G.; Kalogirou, S.; Nivet, M.; Paoli, C.; Motte, F.; Fouilloy, A. Machine learning methods for solar radiation forecasting: A review. Renew. Energy 2017, 105, 569–582. [Google Scholar] [CrossRef]
- Sobri, S.; Koohi-Kamali, S.; Rahim, N.A. Solar photovoltaic generation forecasting methods: A review. Energy Convers. Manag. 2018, 156, 459–497. [Google Scholar] [CrossRef]
- Sun, H.; Yan, D.; Zhao, N.; Zhou, J. Empirical investigation on modeling solar radiation series with ARMA–GARCH models. Energy Convers. Manag. 2015, 92, 385–395. [Google Scholar] [CrossRef]
- Lauret, P.; Boland, J.; Ridley, B. Bayesian statistical analysis applied to solar radiation modelling. Renew. Energy 2013, 49, 124–127. [Google Scholar] [CrossRef]
- Kwon, Y.; Kwasinski, A.; Kwasinski, A. Solar Irradiance Forecast Using Naïve Bayes Classifier Based on Publicly Available Weather Forecasting Variables. Energies 2019, 12, 1529. [Google Scholar] [CrossRef]
- Piri, J.; Kisi, O. Modelling solar radiation reached to the earth using ANFIS, NN-ARX, and empirical models (case studies: Zahedan and Bojnurd stations). J. Atmos. Solar Terr. Phys. 2015, 123, 39–47. [Google Scholar] [CrossRef]
- Gholipour, A.; Lucas, C.; Araabi, B.N.; Mirmomeni, M.; Shafiee, M. Extracting the main patterns of natural time series for long-term neurofuzzy prediction. Neural Comput. Appl. 2007, 16, 383–393. [Google Scholar] [CrossRef]
- Dawan, P.; Sriprapha, K.; Kittisontirak, S.; Boonraksa, T.; Junhuathon, N.; Titiroongruang, W.; Niemcharoen, S. Comparison of Power Output Forecasting on the Photovoltaic System Using Adaptive Neuro-Fuzzy Inference Systems and Particle Swarm Optimization-Artificial Neural Network Model. Energies 2020, 13, 351. [Google Scholar] [CrossRef]
- Kisi, O. Modeling solar radiation of Mediterranean region in Turkey by using fuzzy genetic approach. Energy 2014, 64, 429–436. [Google Scholar] [CrossRef]
- Shakya, A.; Michael, S.; Saunders, C.; Armstrong, D.; Pandey, P.; Chalise, S.; Tonkoski, R. Solar irradiance forecasting in remote microgrids using Markov switching model. IEEE Trans. Sustain. Energy 2017, 8, 895–905. [Google Scholar] [CrossRef]
- Sharma, N.; Sharma, P.; Irwin, D.; Shenoy, P. Predicting solar generation from weather forecasts using machine learning. In Proceedings of the IEEE International Conference on Smart Grid Communications (SmartGridComm), Brussels, Belgium, 17–20 October 2011; pp. 528–533. [Google Scholar]
- Hassan, M.Z.; Ali, M.E.K.; Ali, A.S.; Kumar, J. Forecasting Day-Ahead Solar Radiation Using Machine Learning Approach. In Proceedings of the 4th Asia-Pacific World Congress on Computer Science and Engineering (APWC on CSE), Mana Island, Fiji, 11–13 December 2017; pp. 252–258. [Google Scholar]
- Bae, K.Y.; Jang, H.S.; Sung, D.K. Hourly solar irradiance prediction based on support vector machine and its error analysis. IEEE Trans. Power Syst. 2017, 32, 935–945. [Google Scholar] [CrossRef]
- Capizzi, G.; Napoli, C.; Bonanno, F. Innovative second-generation wavelets construction with recurrent neural networks for solar radiation forecasting. IEEE Trans. Neural Netw. Learn. Syst. 2012, 23, 1805–1815. [Google Scholar] [CrossRef]
- Lotfi, M.; Javadi, M.; Osório, G.J.; Monteiro, C.; Catalão, J.P.S. A Novel Ensemble Algorithm for Solar Power Forecasting Based on Kernel Density Estimation. Energies 2020, 13, 216. [Google Scholar] [CrossRef]
- McCandless, T.; Dettling, S.; Haupt, S.E. Comparison of Implicit vs. Explicit Regime Identification in Machine Learning Methods for Solar Irradiance Prediction. Energies 2020, 13, 689. [Google Scholar] [CrossRef]
- Crisosto, C.; Hofmann, M.; Mubarak, R.; Seckmeyer, G. One-Hour Prediction of the Global Solar Irradiance from All-Sky Images Using Artificial Neural Networks. Energies 2018, 11, 2906. [Google Scholar] [CrossRef]
- Ji, W.; Chee, K.C. Prediction of hourly solar radiation using a novel hybrid model of ARMA and TDNN. Solar Energy 2011, 85, 808–817. [Google Scholar] [CrossRef]
- Zhang, N.; Behera, P.K. Solar radiation prediction based on recurrent neural networks trained by Levenberg-Marquardt backpropagation learning algorithm. In Proceedings of the 2012 IEEE PES Innovative Smart Grid Technologies (ISGT), Washington, DC, USA, 16–20 January 2012; pp. 1–7. [Google Scholar]
- Zhang, N.; Behera, P.K.; Williams, C. Solar radiation prediction based on particle swarm optimization and evolutionary algorithm using recurrent neural networks. In Proceedings of the IEEE International Systems Conference (SysCon), Orlando, FL, USA, 15–18 April 2013; pp. 280–286. [Google Scholar]
- Jaihuni, M.; Basak, J.K.; Khan, F.; Okyere, F.G.; Arulmozhi, E.; Bhujel, A.; Park, J.; Hyun, L.D.; Kim, H.T. A Partially Amended Hybrid Bi-GRU—ARIMA Model (PAHM) for Predicting Solar Irradiance in Short and Very-Short Terms. Energies 2020, 13, 435. [Google Scholar] [CrossRef]
- Zang, H.; Cheng, L.; Ding, T.; Cheung, K.W.; Liang, Z.; Wei, Z.; Sun, G. Hybrid method for short-term photovoltaic power forecasting based on deep convolutional neural network. IET Generation Transm. Distrib. 2018, 12, 4557–4567. [Google Scholar] [CrossRef]
- Yona, A.; Senjyu, T.; Funabashi, T.; Kim, C. Determination method of insolation prediction with fuzzy and applying neural network for long-term ahead PV power output correction. IEEE Trans. Sustain. Energy 2013, 4, 527–533. [Google Scholar] [CrossRef]
- Yang, H.; Huang, C.; Huang, Y.; Pai, Y. A weather-based hybrid method for 1-day ahead hourly forecasting of PV power output. IEEE Trans. Sustain. Energy 2014, 5, 917–926. [Google Scholar] [CrossRef]
- Liu, J.; Fang, W.; Zhang, X.; Yang, C. An improved photovoltaic power forecasting model with the assistance of aerosol index data. IEEE Trans. Sustain. Energy 2015, 6, 434–442. [Google Scholar] [CrossRef]
- Ehsan, R.M.; Simon, S.P.; Venkateswaran, P.R. Day-ahead forecasting of solar photovoltaic output power using multilayer perceptron. Neural Comput. Appl. 2017, 28.12, 3981–3992. [Google Scholar] [CrossRef]
- Wojtkiewicz, J.; Hosseini, M.; Gottumukkala, R.; Chambers, T.L. Hour-Ahead Solar Irradiance Forecasting Using Multivariate Gated Recurrent Units. Energies 2019, 12, 4055. [Google Scholar] [CrossRef]
- Abdel-Nasser, M.; Mahmoud, K. Accurate photovoltaic power forecasting models using deep LSTM-RNN. Neural Comput. Appl. 2019, 31, 2727–2740. [Google Scholar] [CrossRef]
- Lai, G.; Chang, W.; Yang, Y.; Liu, H. Modeling long-and short-term temporal patterns with deep neural networks. In Proceedings of the 41st International Conference on Research and Development in Information Retrieval, Ann Arbor, MI, USA, 8–12 July 2018; pp. 95–104. [Google Scholar]
- Maitanova, N.; Telle, J.-S.; Hanke, B.; Grottke, M.; Schmidt, T.; Maydell, K.; Agert, C. A Machine Learning Approach to Low-Cost Photovoltaic Power Prediction Based on Publicly Available Weather Reports. Energies 2020, 13, 735. [Google Scholar] [CrossRef]
- Fouilloy, A.; Voyant, C.; Notton, G.; Motte, F.; Paoli, C.; Nivet, M.L.; Guillot, E.; Duchaud, J.L. Solar irradiation prediction with machine learning: Forecasting models selection method depending on weather variability. Energy 2020, 165, 620–629. [Google Scholar] [CrossRef]
- Notton, G.; Voyant, C.; Fouilloy, A.; Duchaud, J.L.; Nivet, M.L. Some applications of ANN to solar radiation estimation and forecasting for energy applications. Appl. Sci. 2019, 9, 209. [Google Scholar] [CrossRef]
- Husein, M.; Chung, I.-Y. Day-Ahead Solar Irradiance Forecasting for Microgrids Using a Long Short-Term Memory Recurrent Neural Network: A Deep Learning Approach. Energies 2019, 12, 1856. [Google Scholar] [CrossRef]
- Aslam, M.; Lee, J.-M.; Kim, H.-S.; Lee, S.-J.; Hong, S. Deep Learning Models for Long-Term Solar Radiation Forecasting Considering Microgrid Installation: A Comparative Study. Energies 2020, 13, 147. [Google Scholar] [CrossRef]
- Dercole, F.; Sangiorgio, M.; Schmirander, Y. An empirical assessment of the universality of ANNs to predict oscillatory time series. IFAC-PapersOnLine 2020, in press. [Google Scholar]
- Sangiorgio, M.; Dercole, F. Robustness of LSTM Neural Networks for Multi-step Forecasting of Chaotic Time Series. Chaos Solitons Fractals 2020, 139, 110045. [Google Scholar] [CrossRef]
- Hochreiter, S.; Schmidhuber, J. Long short-term memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef]
- Schmidhuber, J. Deep learning in neural networks: An overview. Neural Netw. 2015, 61, 85–117. [Google Scholar] [CrossRef] [PubMed]
- Goodfellow, I.; Bengio, Y.; Courville, A. Deep Learning; MIT Press: Cambridge, MA, USA, 2016. [Google Scholar]
- Chollet, F. Keras: The python deep learning library. Astrophysics Source Code Library. Available online: https://keras.io (accessed on 25 June 2020).
- Paszke, A.; Gross, S.; Massa, F.; Lerer, A.; Bradbury, J.; Chanan, G.; Killeen, T.; Lin, Z.; Gimelshein, N.; Antiga, L.; et al. PyTorch: An imperative style, high-performance deep learning library. Adv. Neural Inf. Process. Syst. 2019, 8024–8035. [Google Scholar]
- Ineichen, P.; Perez, R. A new airmass independent formulation for the Linke turbidity coefficient. Solar Energy 2012, 73, 151–157. [Google Scholar] [CrossRef]
- Perez, R.; Ineichen, P.; Moore, K.; Kmiecik, M.; Chain, C.; George, R.; Vignola, F. A new operational model for satellite-derived irradiances: Description and validation. Solar Energy 2002, 73, 307–317. [Google Scholar] [CrossRef]
- PV Performance Modeling Collaborative. Available online: https://pvpmc.sandia.gov (accessed on 2 May 2020).
- Miramontes, O.; Rohani, P. Estimating 1/fα scaling exponents from short time-series. Phys. D Nonlinear Phenom. 2002, 166, 147–154. [Google Scholar] [CrossRef]
- Fortuna, L.; Nunnari, G.; Nunnari, S. Nonlinear Modeling of Solar Radiation and Wind Speed Time Series; Springer International Publishing: Cham, Switzerland, 2016. [Google Scholar]
- Jiang, A.H.; Huang, X.C.; Zhang, Z.H.; Li, J.; Zhang, Z.Y.; Hua, H.X. Mutual information algorithms. Mech. Syst. Signal Process. 2010, 24, 2947–2960. [Google Scholar] [CrossRef]
- Zhang, J.; Florita, A.; Hodge, B.M.; Lu, S.; Hamann, H.F.; Banunarayanan, V.; Brockway, A.M. A suite of metrics for assessing the performance of solar power forecasting. Solar Energy 2015, 111, 157–175. [Google Scholar] [CrossRef]
- Nash, J.E.; Sutcliffe, J.V. River flow forecasting through conceptual models part I—A discussion of principles. J. Hydrol. 1970, 10, 282–290. [Google Scholar] [CrossRef]
- Glorot, X.; Bordes, A.; Bengio, Y. Domain adaptation for large-scale sentiment classification: A deep learning approach. In Proceedings of the 28th international conference on machine learning (ICML), Bellevue, DC, USA, 28 June–2 July 2011; pp. 513–520. [Google Scholar]
- Yosinski, J.; Clune, J.; Bengio, Y.; Lipson, H. How transferable are features in deep neural networks? Adv. Neural Inf. Process. Syst. 2014, 3320–3328. [Google Scholar]
- Cuéllar, M.P.; Delgado, M.; Pegalajar, M.C. An application of non-linear programming to train recurrent neural networks in time series prediction problems. In Proceedings of the 7th International Conference on Enterprise Information Systems (ICEIS), Miami, FL, USA, 24–28 May 2005; pp. 95–102. [Google Scholar]

| Index | Pers | Pers24 | Clsky |
|---|---|---|---|
| Bias | 0.07 | 0.01 | −46.20 |
| MAE | 87.78 | 59.24 | 74.07 |
| RMSE | 158.40 | 136.63 | 146.39 |
| NSE | 0.51 | 0.63 | 0.58 |
| Index | Pers | Pers24 | Clsky |
|---|---|---|---|
| Bias | 28.82 | 7.08 | −89.91 |
| MAE | 175.89 | 131.71 | 154.35 |
| RMSE | 228.24 | 204.91 | 212.97 |
| NSE | 0.11 | 0.28 | 0.22 |
| Index | FF-Recursive | FF-Multi-Output | FF-Multi-Model | LSTM |
|---|---|---|---|---|
| Bias | −1.49 | −0.28 | 0.17 | −4.19 |
| MAE | 40.26 | 40.39 | 39.26 | 45.91 |
| RMSE | 84.33 | 82.60 | 82.29 | 82.09 |
| NSE | 0.86 | 0.87 | 0.87 | 0.87 |
| S | 0.42 | 0.44 | 0.44 | 0.44 |
| Index | FF-Recursive | FF-Multi-Output | FF-Multi-Model | LSTM |
|---|---|---|---|---|
| Bias | 3.79 | 6.59 | 6.46 | 12.11 |
| MAE | 86.31 | 84.63 | 84.75 | 86.01 |
| RMSE | 125.35 | 122.87 | 122.74 | 121.78 |
| NSE | 0.73 | 0.74 | 0.74 | 0.75 |
| S | 0.41 | 0.42 | 0.42 | 0.43 |
| Index | 1 Hour Ahead | 3 Hours Ahead | 6 Hours Ahead |
|---|---|---|---|
| Cloudy | 0.44 | 0.06 | −0.45 |
| Partly cloudy | 0.65 | 0.59 | 0.59 |
| Sunny | 0.89 | 0.83 | 0.73 |
| Hyperparameter | Search Range | Optimal Values | |||
|---|---|---|---|---|---|
| FF-Recursive | FF-Multi-Output | FF-Multi-Model | LSTM | ||
| Hidden layers | 3–5 | 3 | 5 | 5 | 3 |
| Neurons per layer | 5–10 | 5 | 10 | 10 | 5 |
| Learning rate | 10−2–10−3 | 10−3 | 10−2 | 10−2 | 10−3 |
| Decay rate | 0–10−4 | 0 | 10−4 | 10−4 | 10−4 |
| Batch size | 128–512 | 512 | 128 | 512 | 512 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guariso, G.; Nunnari, G.; Sangiorgio, M. Multi-Step Solar Irradiance Forecasting and Domain Adaptation of Deep Neural Networks. Energies 2020, 13, 3987. https://doi.org/10.3390/en13153987
Guariso G, Nunnari G, Sangiorgio M. Multi-Step Solar Irradiance Forecasting and Domain Adaptation of Deep Neural Networks. Energies. 2020; 13(15):3987. https://doi.org/10.3390/en13153987
Chicago/Turabian StyleGuariso, Giorgio, Giuseppe Nunnari, and Matteo Sangiorgio. 2020. "Multi-Step Solar Irradiance Forecasting and Domain Adaptation of Deep Neural Networks" Energies 13, no. 15: 3987. https://doi.org/10.3390/en13153987
APA StyleGuariso, G., Nunnari, G., & Sangiorgio, M. (2020). Multi-Step Solar Irradiance Forecasting and Domain Adaptation of Deep Neural Networks. Energies, 13(15), 3987. https://doi.org/10.3390/en13153987






