Forecasting Hierarchical Time Series in Power Generation
Abstract
1. Introduction
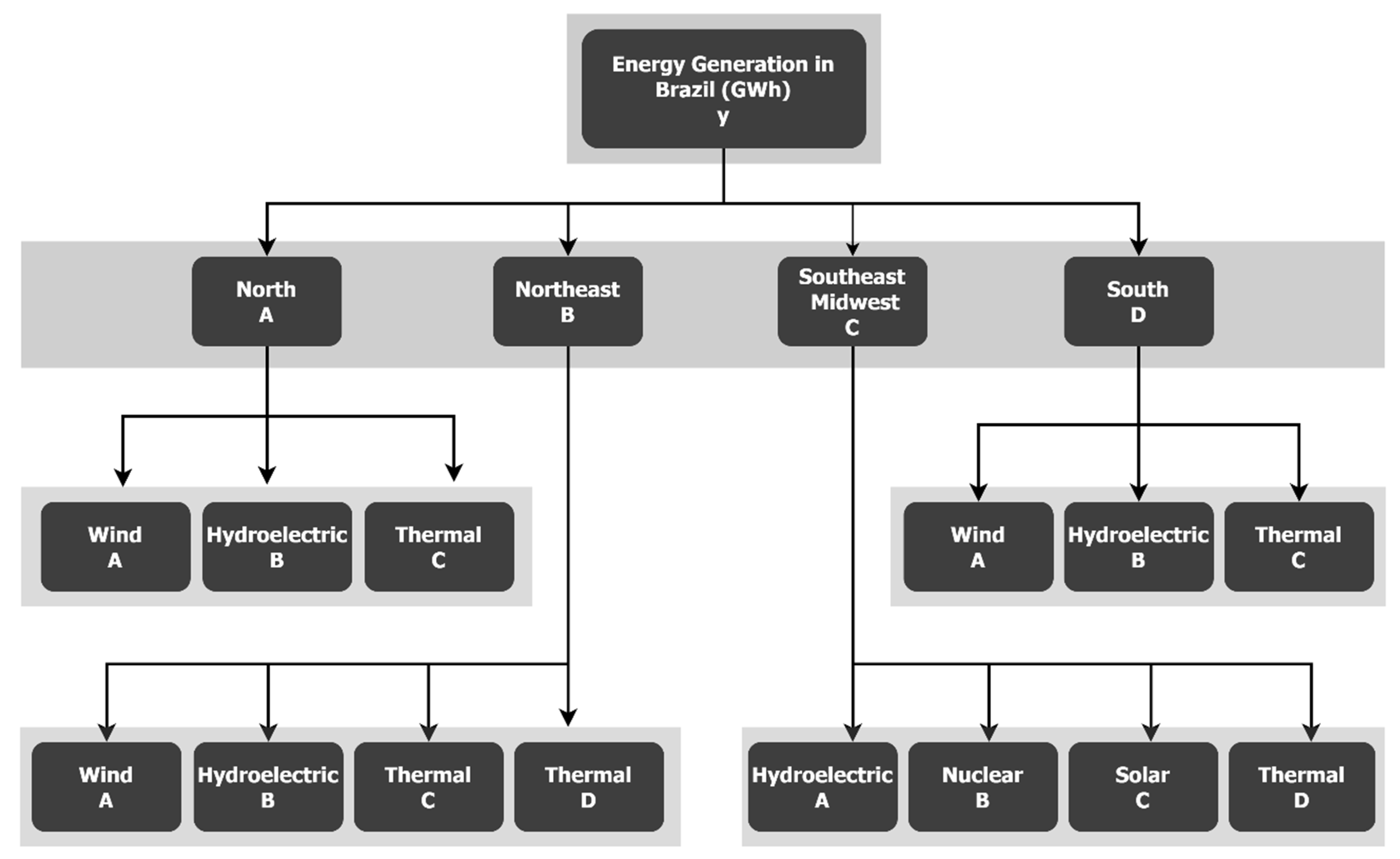
2. Materials and Methods
2.1. The Bottom-Up (BU) Approach
2.2. The Top-Down (TD) Approach
2.3. The Optimal Reconciliation Approaches
2.4. ARIMA and ETS Formulation
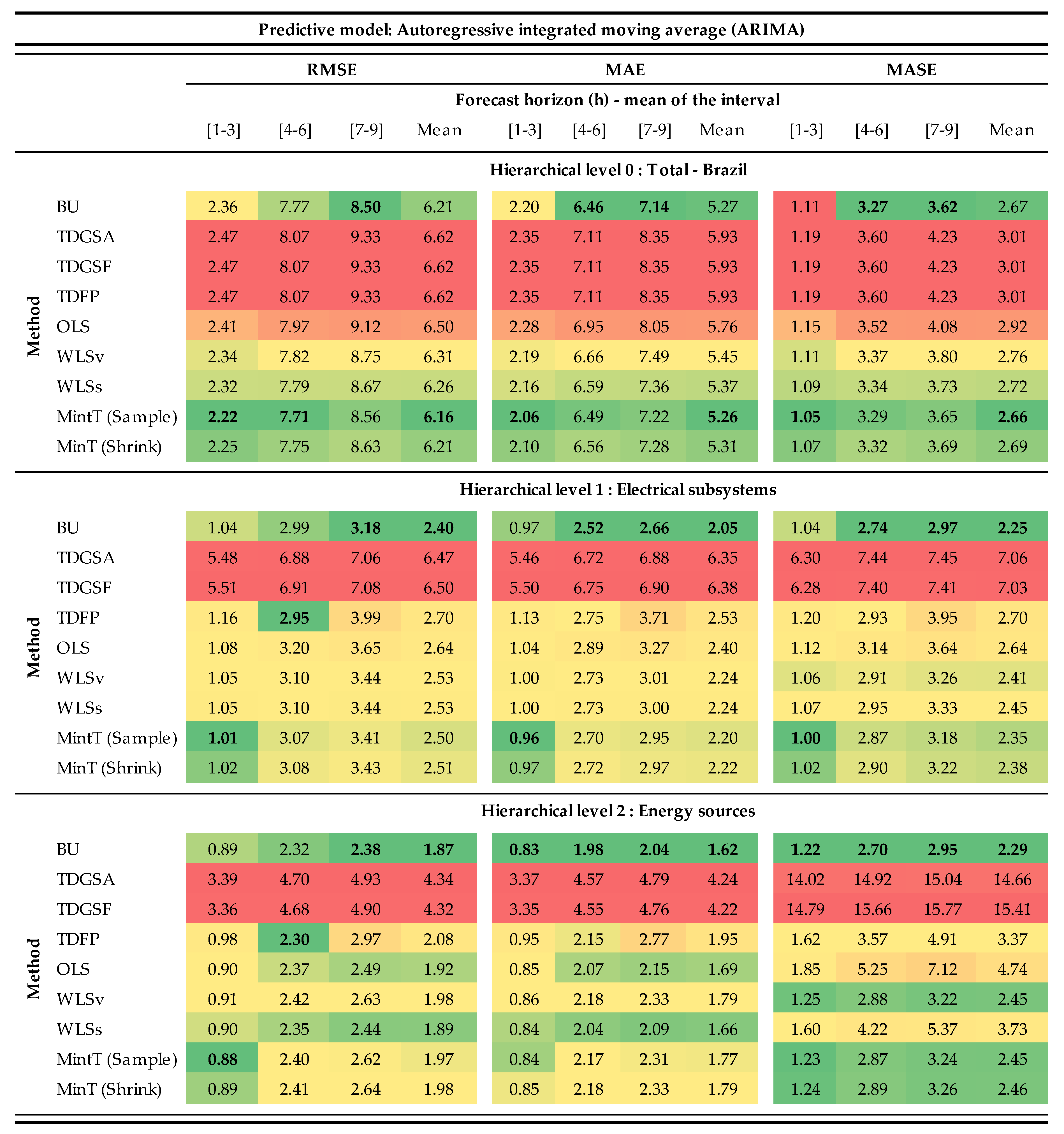
2.5. Evaluating Forecast Accuracy
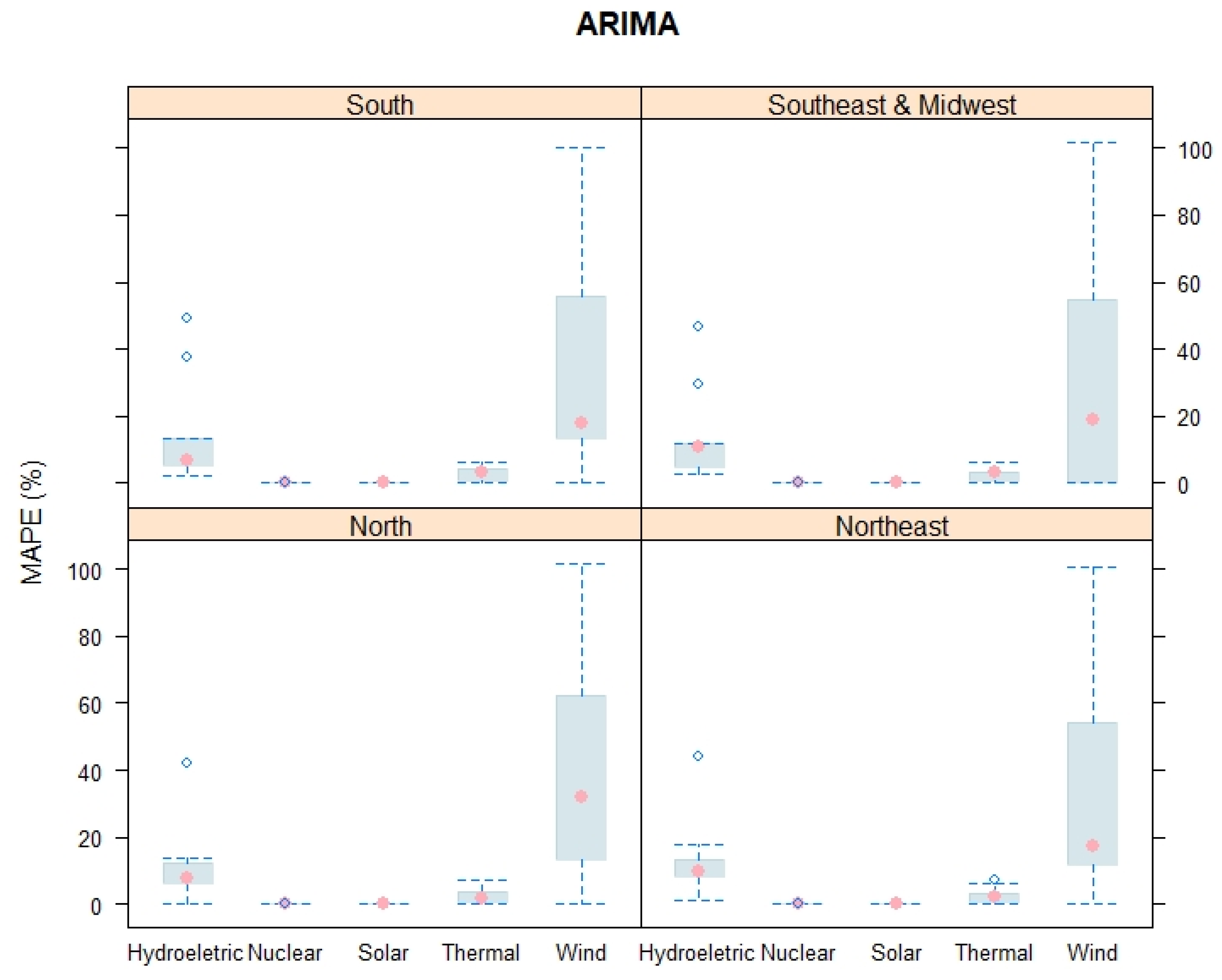
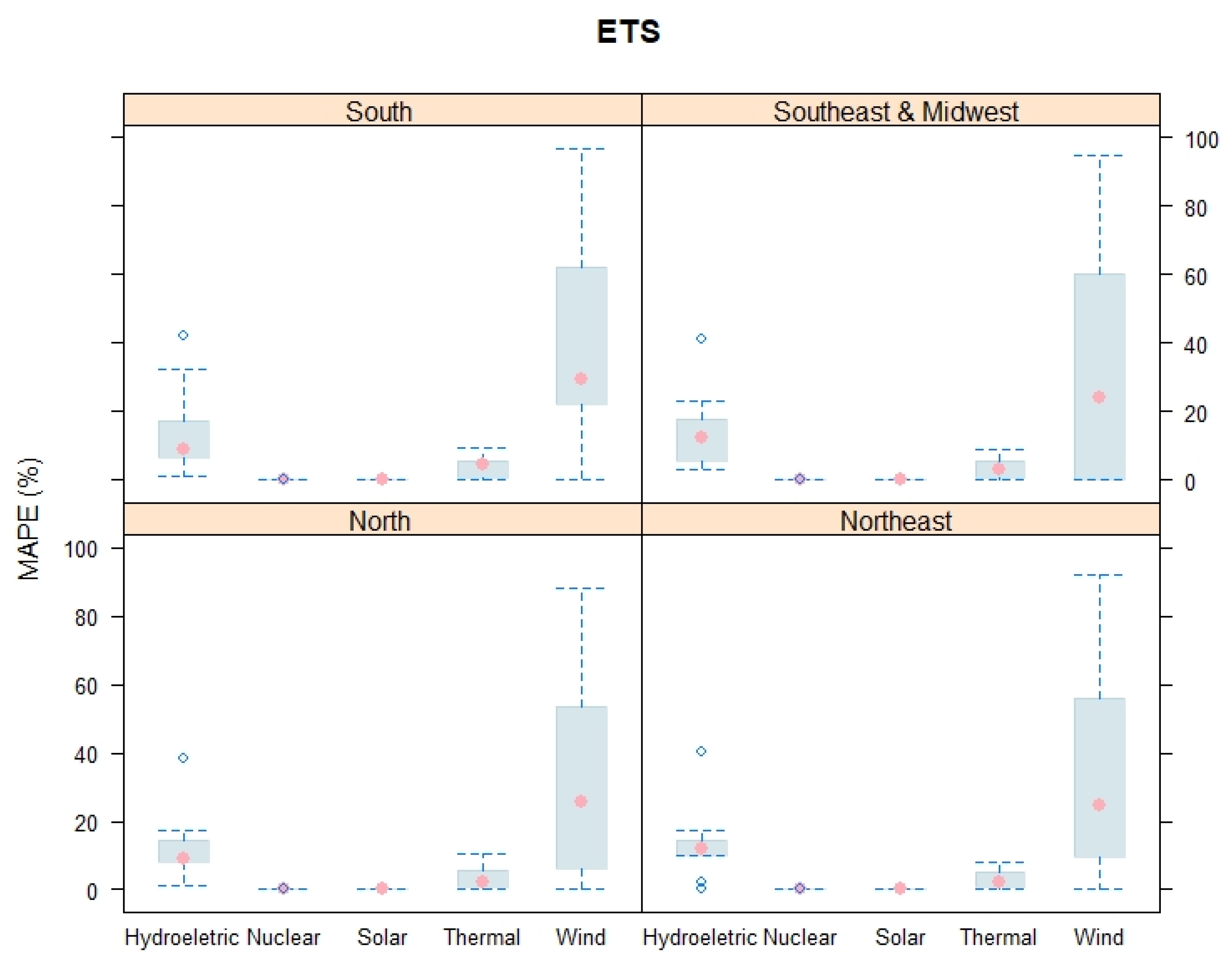
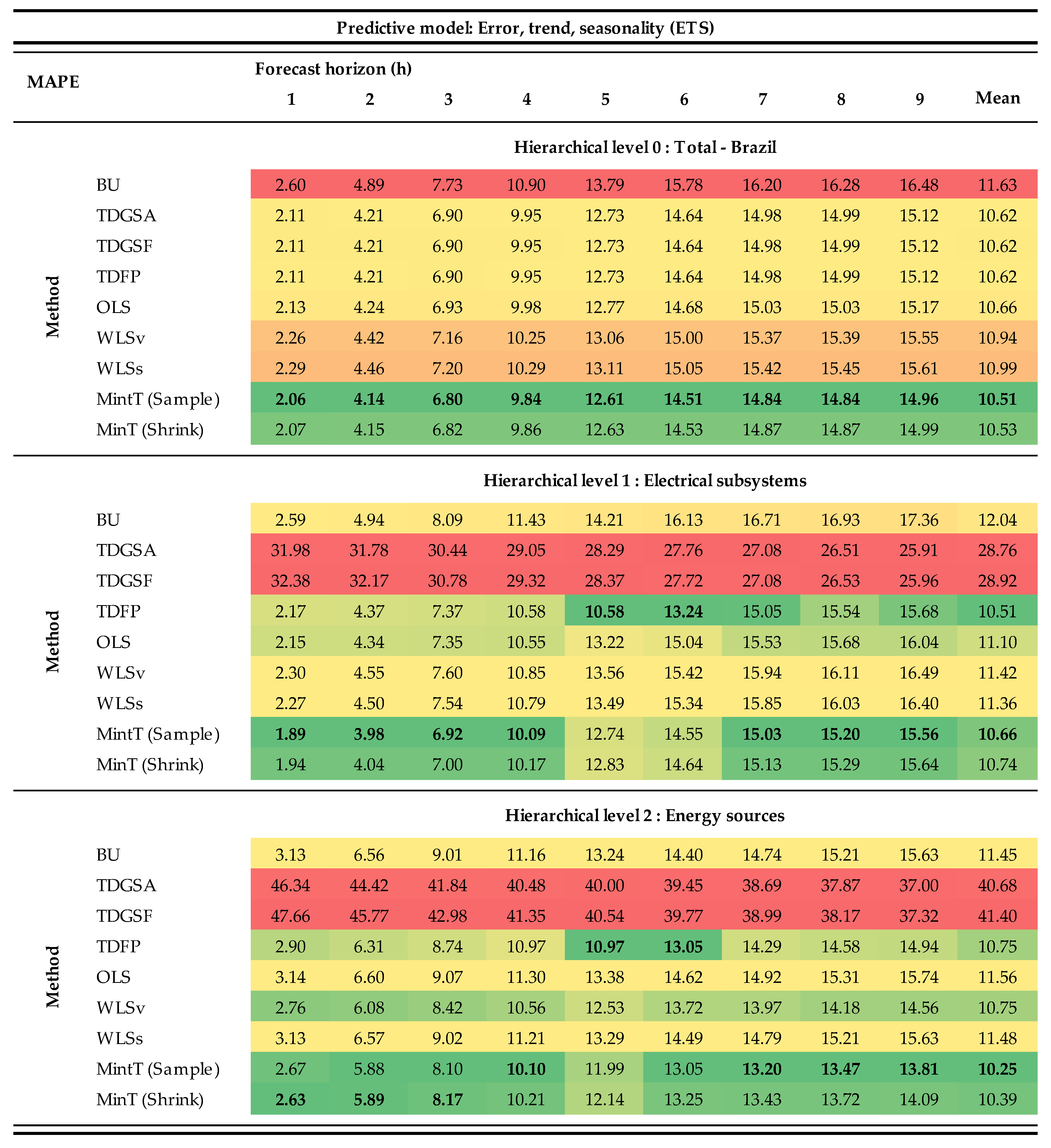
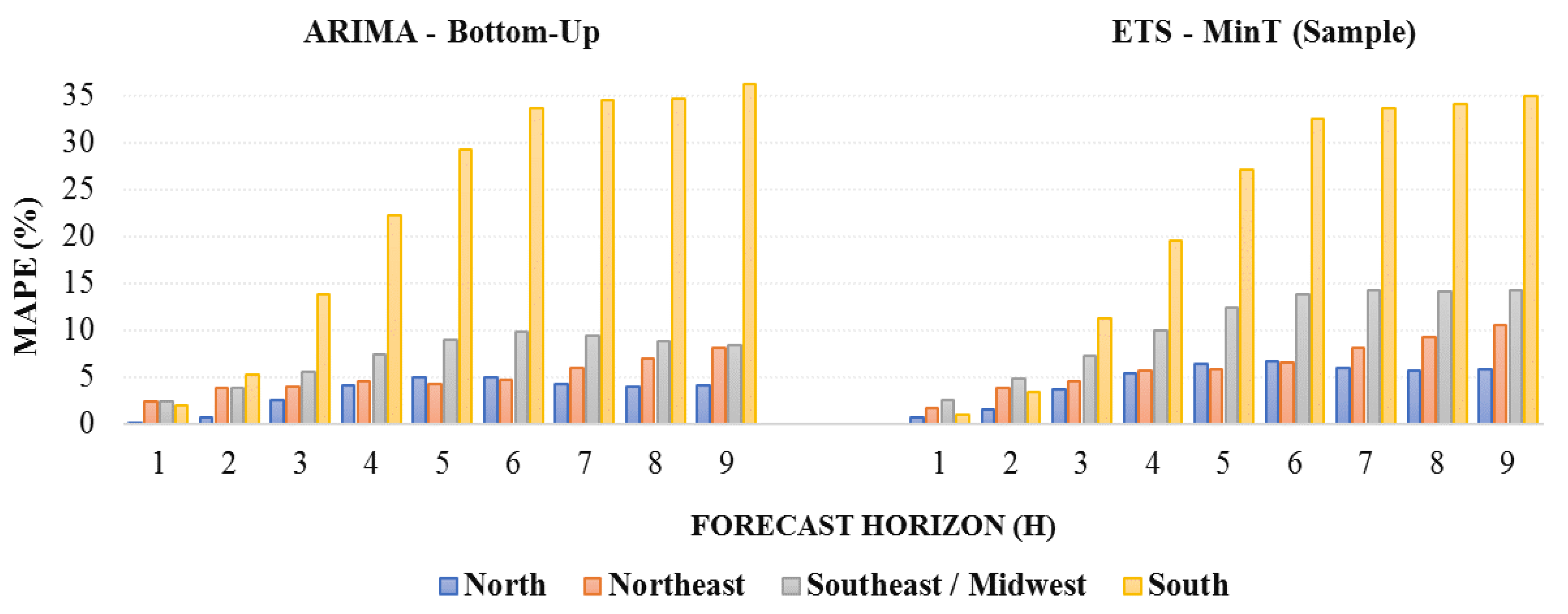
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| ARIMA | Autoregressive integrated moving average model |
| BU | Bottom-up |
| ETS | Error, trend, and seasonality model |
| GWh | Gigawatt hours |
| MAPE | Mean absolute percentage error |
| MinT | Minimum trace reconciliation |
| OLS | Ordinary least squares |
| ONS | Operator of the National System |
| TD | Top-down |
| TDFP | Top-down forecast proportions |
| TDGSA | Top-down Gross-Sohl method A |
| TDGSF | Top-down Gross-Sohl method F |
| WLS | Weighted least squares |
Nomenclature
| Level of disaggregation | |
| Forecast horizon | |
| -dimensional vector of -step-ahead forecasts | |
| Unknown conditional mean of the most disaggregated series | |
| Error for each forecast horizon | |
| Covariance matrix | |
| Set of proportions in an m-dimensional vector | |
| The average of the historical proportions | |
| Summing matrix | |
| The sum of the -step-ahead forecasts for TD | |
| Covariance matrix of the corresponding h-step ahead base forecast errors | |
| Total level of power generation | |
| an -dimensional vector of -step-ahead forecasts | |
| The -step-ahead forecast for TD | |
| Reconciled forecasts | |
| Shrinkage estimator |
Appendix A

References
- Medojevic, M.; Medic, N.; Marjanovic, U.; Lalic, B.; Majstorovic, V. Exploring the impact of industry 4.0 concepts on energy and environmental management systems: Evidence from Serbian manufacturing companies. In Proceedings of the IFIP International Conference on Advances in Production Management Systems, Austin, TX, USA, 1–5 September 2019; pp. 355–362. [Google Scholar]
- Alcácer, V.; Cruz-Machado, V. Scanning the industry 4.0: A literature review on technologies for manufacturing systems. Eng. Sci. Technol. Int. J. 2019, 22, 899–919. [Google Scholar] [CrossRef]
- Bourdeau, M.; Zhai, X.Q.; Nefzaoui, E.; Guo, X.; Chatellier, P. Modeling and forecasting building energy consumption: A review of data-driven techniques. Sustain. Cities Soc. 2019, 48, 101533. [Google Scholar] [CrossRef]
- Hammad, M.A.; Jereb, B.; Rosi, B.; Dragan, D. Methods and models for electric load forecasting: A comprehensive review. Logist. Sustain. Transp. 2020, 11, 51–76. [Google Scholar] [CrossRef]
- Runge, J.; Zmeureanu, R. Forecasting energy use in buildings using artificial neural networks: A review. Energies 2019, 12, 3254. [Google Scholar] [CrossRef]
- Choi, Y.B. Paradigms and Conventions: Uncertainty, Decision Making, and Entrepreneurship; University of Michigan Press: Ann Arbor, MI, USA, 1993. [Google Scholar]
- Jiang, W.; Yan, Z.; Feng, D.H.; Hu, Z. Wind speed forecasting using autoregressive moving average/generalized autoregressive conditional heteroscedasticity model. Eur. Trans. Electr. Power 2012, 22, 662–673. [Google Scholar] [CrossRef]
- Hao, C.H.E.N. A new method of load forecasting based on generalized autoregressive conditional heteroscedasticity model. Autom. Electr. Power Syst. 2007, 15, 012. [Google Scholar]
- Stefenon, S.F.; Ribeiro, M.H.D.M.; Nied, A.; Mariani, V.C.; dos Santos Coelho, L.; da Rocha, D.F.M.; Grebogif, R.B.; de Barros Ruano, A.E. Wavelet group method of data handling for fault prediction in electrical power insulators. Int. J. Electr. Power Energy Syst. 2020, 123, 106269. [Google Scholar] [CrossRef]
- Frizzo Stefenon, S.; Silva, M.C.; Bertol, D.W.; Meyer, L.H.; Nied, A. Fault diagnosis of insulators from ultrasound detection using neural networks. J. Intell. Fuzzy Syst. 2019, 37, 6655–6664. [Google Scholar] [CrossRef]
- Gupta, S.; Srinivasan, D.; Reindl, T. Forecasting solar and wind data using dynamic neural network architectures for a micro-grid ensemble. In Proceedings of the 2013 IEEE Computational Intelligence Applications in Smart Grid (CIASG), Singapore, 16–19 April 2013; IEEE: New York, NY, USA, 2013; pp. 87–92. [Google Scholar]
- Frizzo Stefenon, S.; Zanetti Freire, R.; dos Santos Coelho, L.; Meyer, L.H.; Bartnik Grebogi, R.; Gouvêa Buratto, W.; Nied, A. Electrical insulator fault forecasting based on a wavelet neuro-fuzzy system. Energies 2020, 13, 484. [Google Scholar] [CrossRef]
- Moghaddam, A.A.; Seifi, A.R. Study of forecasting renewable energies in smart grids using linear predictive filters and neural networks. IET Renew. Power Gener. 2011, 5, 470–480. [Google Scholar] [CrossRef]
- Barbounis, T.G.; Theocharis, J.B. A locally recurrent fuzzy neural network with application to the wind speed prediction using spatial correlation. Neurocomputing 2007, 70, 1525–1542. [Google Scholar] [CrossRef]
- Xia, J.; Zhao, P.; Dai, Y. Neuro-fuzzy networks for short-term wind power forecasting. In Proceedings of the 2010 International Conference on Power System Technology, Hangzhou, China, 24–28 October 2010; IEEE: New York, NY, USA, 2010; pp. 1–5. [Google Scholar]
- Dawan, P.; Sriprapha, K.; Kittisontirak, S.; Boonraksa, T.; Junhuathon, N.; Titiroongruang, W.; Niemcharoen, S. Comparison of power output forecasting on the photovoltaic system using adaptive neuro-fuzzy inference systems and particle swarm optimization-artificial neural network model. Energies 2020, 13, 351. [Google Scholar] [CrossRef]
- Hyndman, R.J.; Kandahar, Y. Automatic time series forecasting: The forecast package for R. J. Stat. Softw. 2008, 26, 1–22. [Google Scholar]
- Athanasopoulos, G.; Ahmed, R.A.; Hyndman, R.J. Hierarchical forecasts for Australian domestic tourism. Int. J. Forecast. 2009, 25, 146–166. [Google Scholar] [CrossRef]
- Hyndman, R.J.; Ahmed, R.A.; Athanasopoulos, G.; Shang, H.L. Optimal combination forecasts for hierarchical time series. Comput. Stat. Data Anal. 2011, 55, 2579–2589. [Google Scholar] [CrossRef]
- Almeida, V.; Ribeiro, R.; Gama, J. Hierarchical time series forecast in electrical grids. In Information Science and Applications (ICISA); Springer: Singapore, 2016; pp. 995–1005. [Google Scholar]
- Panamtash, H.; Zhou, Q. Coherent probabilistic solar power forecasting. In Proceedings of the 2018 IEEE International Conference on Probabilistic Methods Applied to Power Systems (PMAPS), Boise, ID, USA, 24–28 June 2018; IEEE: New York, NY, USA, 2018; pp. 1–6. [Google Scholar]
- Abouarghoub, W.; Nomikos, N.K.; Petropoulos, F. On reconciling macro and micro energy transport forecasts for strategic decision making in the tanker industry. Transp. Res. Part E Logist. Transp. Rev. 2018, 113, 225–238. [Google Scholar] [CrossRef]
- Auder, B.; Cugliari, J.; Goude, Y.; Poggi, J.M. Scalable clustering of individual electrical curves for profiling and bottom-up forecasting. Energies 2018, 11, 1893. [Google Scholar] [CrossRef]
- Silva, F.L.; Souza, R.C.; Oliveira, F.L.C.; Lourenco, P.M.; Calili, R.F. A bottom-up methodology for long term electricity consumption forecasting of an industrial sector-Application to pulp and paper sector in Brazil. Energy 2018, 144, 1107–1118. [Google Scholar] [CrossRef]
- Ghedamsi, R.; Settou, N.; Gouareh, A.; Khamouli, A.; Saifi, N.; Recioui, B.; Dokkar, B. Modeling and forecasting energy consumption for residential buildings in Algeria using bottom-up approach. Energy Build. 2016, 121, 309–317. [Google Scholar] [CrossRef]
- Kosiorowski, D.; Mielczarek, D.; Rydlewski, J. Forecasting of a hierarchical functional time series on example of macromodel for day and night air pollution in silesia region: A critical overview. arXiv 2017, arXiv:1712.03797. [Google Scholar]
- Wickramasuriya, S.L.; Athanasopoulos, G.; Hyndman, R.J. Optimal forecast reconciliation for hierarchical and grouped time series through trace minimization. J. Am. Stat. Assoc. 2019, 114, 804–819. [Google Scholar] [CrossRef]
- National System Operator. Operation History (Report of Power Generation). 2020. Available online: http://www.ons.org.br/paginas/resultados-da-operacao/historico-da-operacao (accessed on 15 May 2020).
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2020; Available online: https://www.R-project.org/ (accessed on 15 May 2020).
- Orcutt, G.H.; Watts, H.W.; Edwards, J.B. Data aggregation and information loss. Am. Econ. Rev. 1968, 58, 773–787. [Google Scholar]
- Gross, C.W.; Sohl, J.E. Disaggregation methods to expedite product line forecasting. J. Forecast. 1990, 9, 233–254. [Google Scholar] [CrossRef]
- Oliveira, J.M.; Ramos, P. Assessing the performance of hierarchical forecasting methods on the retail sector. Entropy 2019, 21, 436. [Google Scholar] [CrossRef]
- Yang, D.; Kleissl, J.; Gueymard, C.A.; Pedro, H.T.; Coimbra, C.F. History and trends in solar irradiance and PV power forecasting: A preliminary assessment and review using text mining. Sol. Energy 2018, 168, 60–101. [Google Scholar] [CrossRef]
- Panigrahi, S.; Behera, H.S. A hybrid ETS–ANN model for time series forecasting. Eng. Appl. Artif. Intell. 2017, 66, 49–59. [Google Scholar] [CrossRef]
- Dong, Z.; Yang, D.; Reindl, T.; Walsh, W.M. Short-term solar irradiance forecasting using exponential smoothing state space model. Energy 2013, 55, 1104–1113. [Google Scholar] [CrossRef]
- Box, G.E. Jenkins. In Time Series Analysis: Forecasting and Control; Holden-Day Inc.: New York, NY, USA, 1976. [Google Scholar]
- Pegels, C.C. Exponential forecasting: Some new variations. Manag. Sci. 1969, 311–315. [Google Scholar]
- Gardner, E.S., Jr. Exponential smoothing: The state of the art. J. Forecast. 1985, 4, 1–28. [Google Scholar] [CrossRef]
- Hyndman, R.J.; Koehler, A.B.; Snyder, R.D.; Grose, S. A state space framework for automatic forecasting using exponential smoothing methods. Int. J. Forecast. 2002, 18, 439–454. [Google Scholar] [CrossRef]
- Taylor, J.W. Exponential smoothing with a damped multiplicative trend. Int. J. Forecast. 2003, 19, 715–725. [Google Scholar] [CrossRef]
- Liu, Z.; Yan, Y.; Yang, J.; Hauskrecht, M. Missing value estimation for hierarchical time series: A study of hierarchical Web traffic. In Proceedings of the 2015 IEEE International Conference on Data Mining, Atlantic City, NJ, USA, 14–17 November 2015; IEEE: New York, NY, USA, 2015; pp. 895–900. [Google Scholar]
- Weiss, C. Essays in Hierarchical Time Series Forecasting and Forecast Combination. Ph.D. Thesis, University of Cambridge, Cambridge, UK, 2018. [Google Scholar]
- Hong, T.; Xie, J.; Black, J. Global energy forecasting competition 2017: Hierarchical probabilistic load forecasting. Int. J. Forecast. 2019, 35, 1389–1399. [Google Scholar] [CrossRef]

| Subsystem/Source | Wind | Hydro | Thermal | Solar | Nuclear | Total (GWh—Subsystem) | % | |
|---|---|---|---|---|---|---|---|---|
| North | (A) | 2688 | 125,182 | 31,489 | 0 | 0 | 159,359 | 14.3% |
| Northeast | (B) | 85,377 | 37,705 | 36,699 | 4626 | 0 | 164,407 | 14.7% |
| Southeast/Midwest | (C) | 0 | 518,714 | 73,555 | 2437 | 31,805 | 626,511 | 56.1% |
| South | (D) | 11,326 | 135,914 | 19,472 | 0 | 0 | 166,712 | 14.9% |
| Total (GWh—Source) | 99,391 | 817,516 | 161,215 | 7063 | 31,805 | 1,116,989 | 100% | |
| % | 8.9% | 73.2% | 14.4% | 0.6% | 2.8% | 100% | - | |
| TD Gross-Sohl Method A TDGSA | TD Gross-Sohl Method F TDGSF | TD Forecast Proportions TDFP |
|---|---|---|
| for . Each proportion reflects the average of the historical proportions of the bottom-level series , t over the period relative to the total aggregate . | for . Each proportion takes the average historical value of the bottom-level series related to the average value of the total aggregate . | where , is the -step-ahead forecast and is the sum of the -step-ahead forecasts below the node that is levels above node . |
| Procedure | Description |
|---|---|
| OLS | where . This is the most simplifying premise, and collapses the MinT estimator to the OLS estimator, proposed by Hyndman et al. [19]. This is optimal when the base forecast errors are uncorrelated and equivariant. |
| WLSv | where and: , is the unbiased sample covariance estimator of the in-sample one-step-ahead base forecast errors. In this case, we can describe MinT as a WLS estimator applying variance scaling [27]. |
| WLSs | where and with being a unit column vector of dimension . We assume that each of the bottom-level base forecast errors has a variance and is uncorrelated between nodes. Consequently, every element of the diagonal matrix receives the number of forecast error variances contributing to that aggregation level [27]. This estimator depends only on the grouping structure of the hierarchy. |
| MinT (Sample) | where , the unrestricted sample covariance estimator for [27]. In the results section, we denote this as MinT (Sample). |
| MinT (Shrink) | ; , is a shrinkage estimator with diagonal target, , which is a diagonal matrix comprising the diagonal entries of , and is the shrinkage intensity parameter. Thus, off-diagonal elements of are shrunk toward zero and diagonal elements (variances) remain unchanged [27]. Wickramasuriya, Athanasopoulos and Hyndman [27] suggested a scale and location invariant shrinkage estimator by parameterizing the shrinkage in terms of variances and correlations: , where is the th element of , the -step-ahead sample correlation matrix to shrink it toward an identity matrix. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Silveira Gontijo, T.; Azevedo Costa, M. Forecasting Hierarchical Time Series in Power Generation. Energies 2020, 13, 3722. https://doi.org/10.3390/en13143722
Silveira Gontijo T, Azevedo Costa M. Forecasting Hierarchical Time Series in Power Generation. Energies. 2020; 13(14):3722. https://doi.org/10.3390/en13143722
Chicago/Turabian StyleSilveira Gontijo, Tiago, and Marcelo Azevedo Costa. 2020. "Forecasting Hierarchical Time Series in Power Generation" Energies 13, no. 14: 3722. https://doi.org/10.3390/en13143722
APA StyleSilveira Gontijo, T., & Azevedo Costa, M. (2020). Forecasting Hierarchical Time Series in Power Generation. Energies, 13(14), 3722. https://doi.org/10.3390/en13143722





