Heat Exchanger Sizing for Organic Rankine Cycle
Abstract
1. Introduction
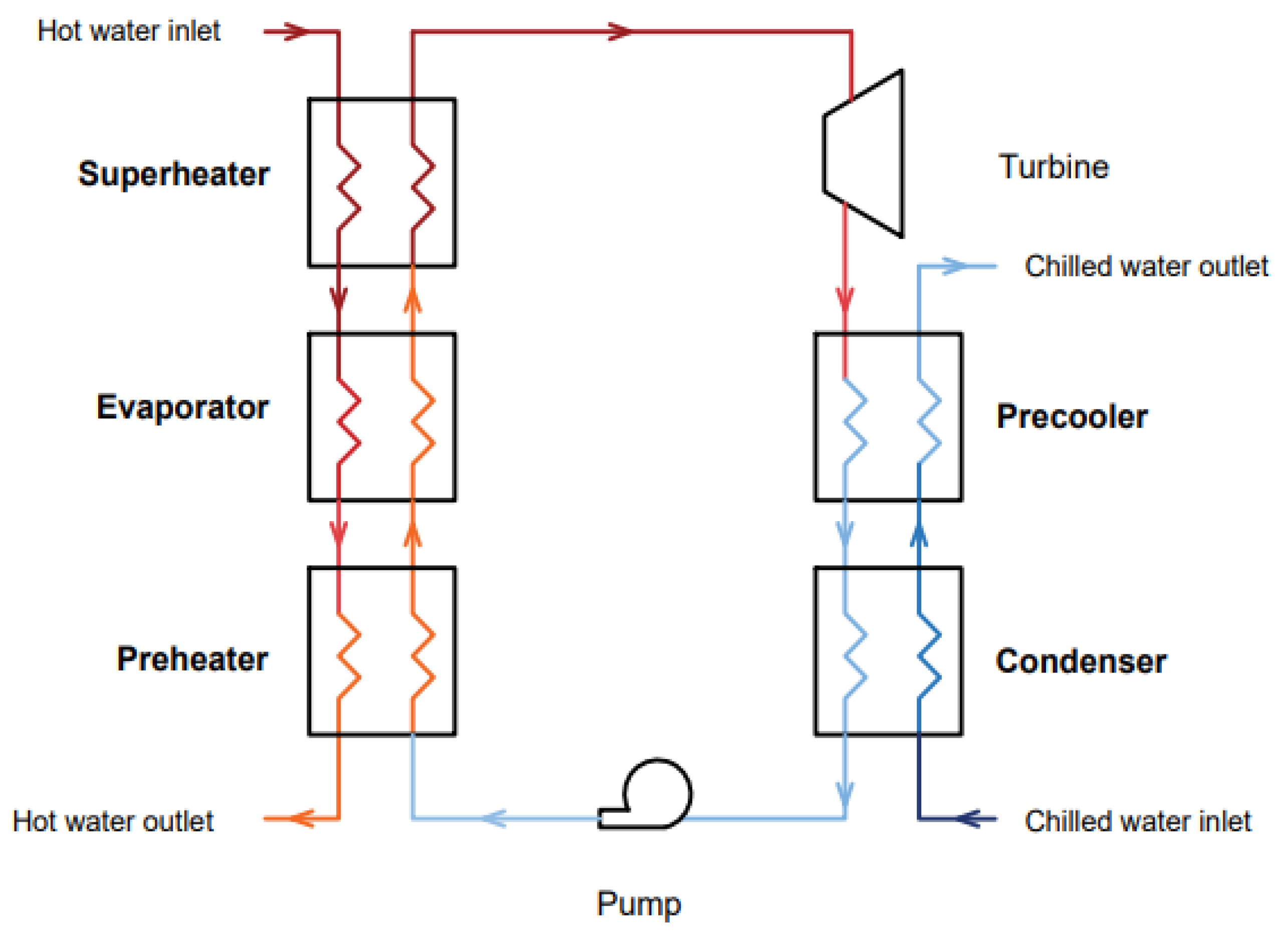
2. Materials and Methods
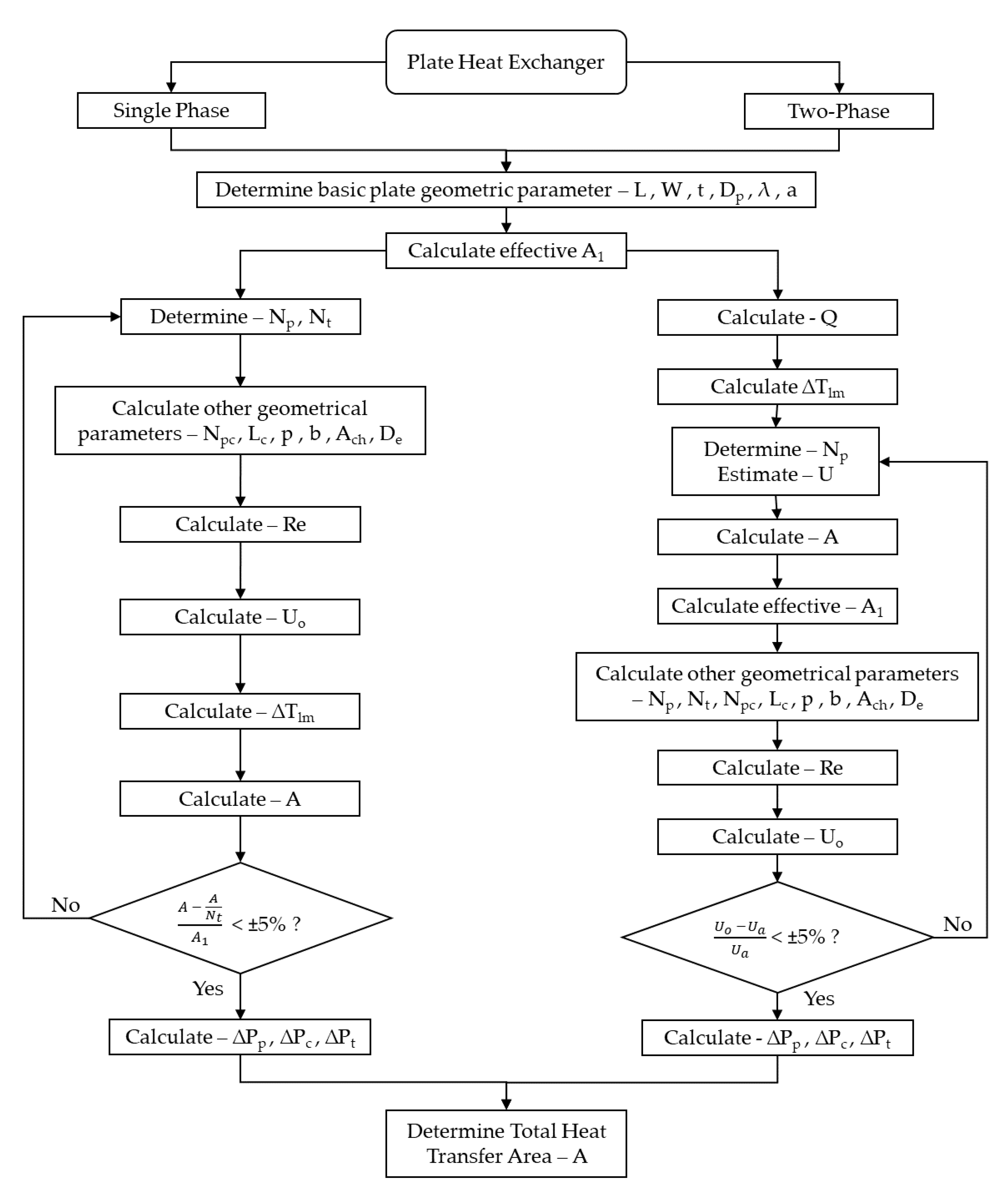
2.1. Plate Heat Exchanger
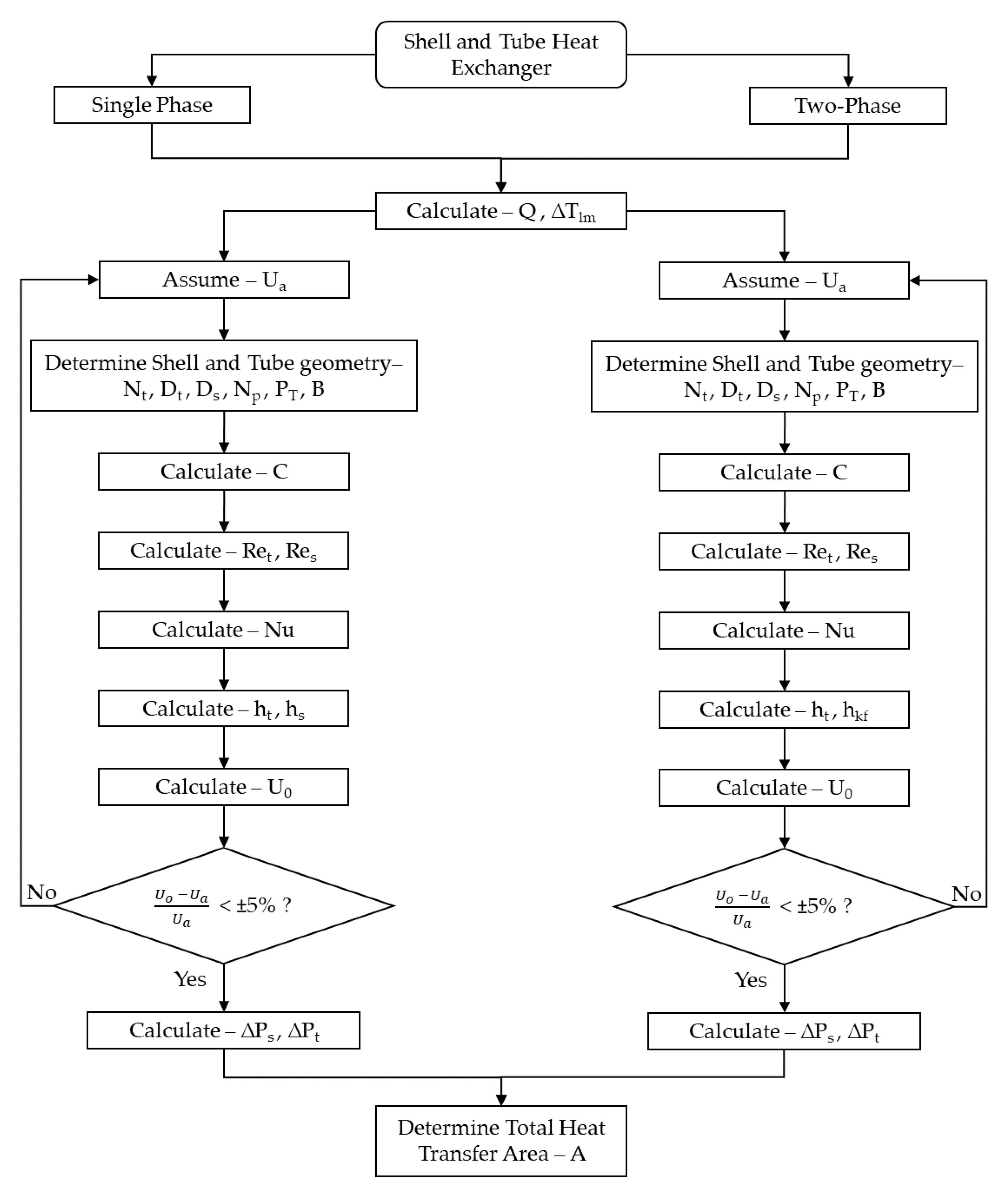
2.2. Shell and Tube Heat Exchanger
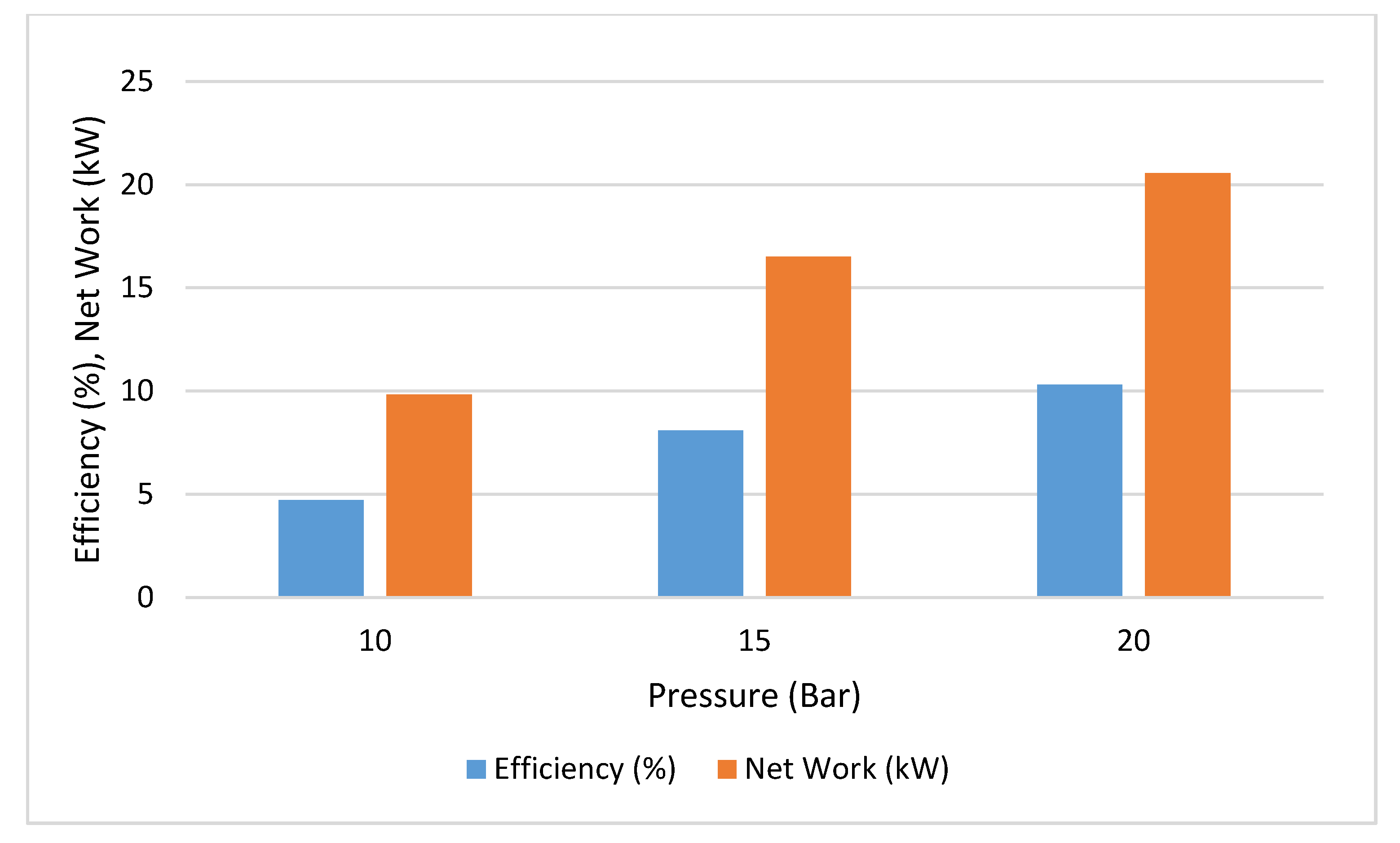
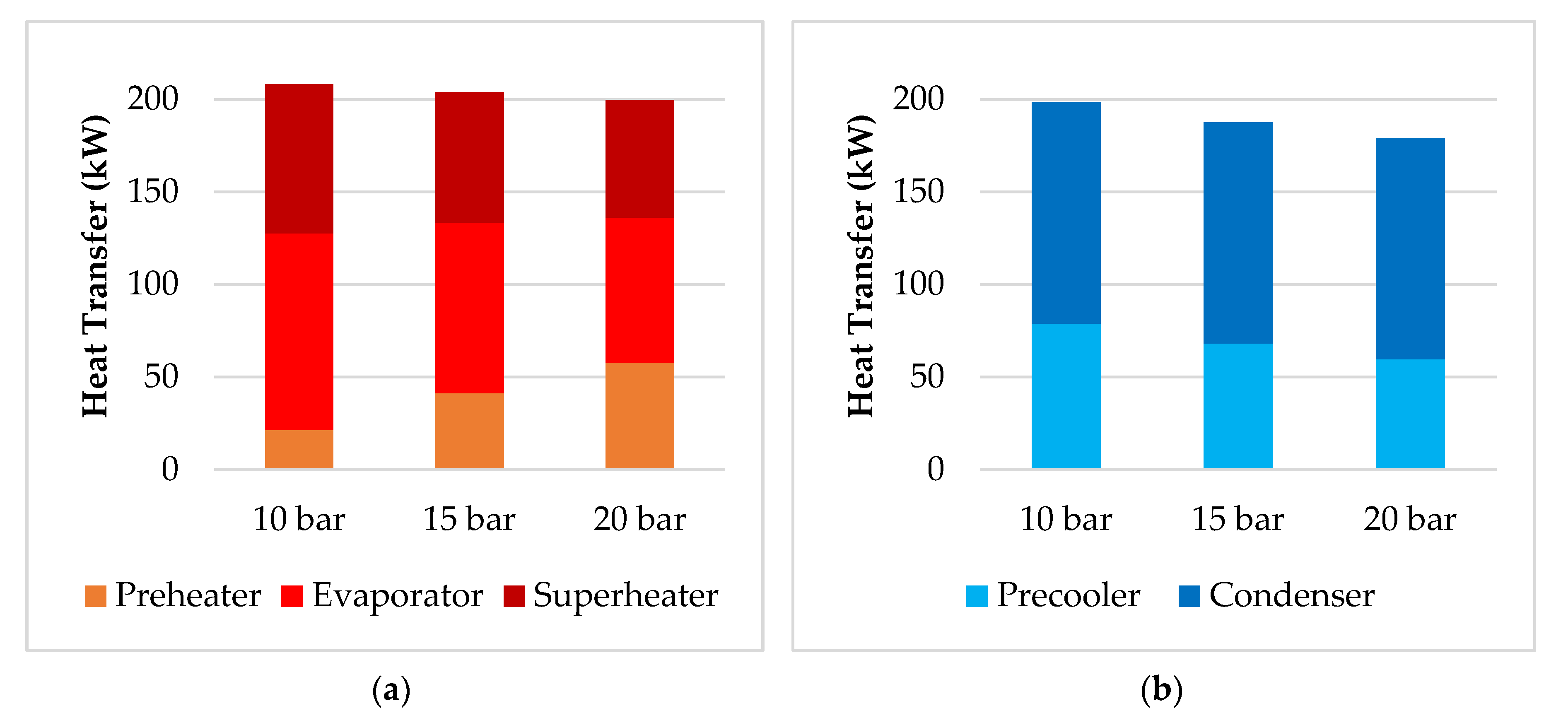
3. Results/Discussion
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
Nomenclature
| A | Area (m2) |
| Ach | Channel flow area (m2) |
| b | Mean Channel Spacing (m) |
| B | Baffle spacing (m) |
| C | Tube clearance (m) |
| De | Equivalent channel diameter (m) |
| Dp | Port Diameter (m) |
| Do | External Tube Diameter (m) |
| Dt | Internal Tube Diameter (m) |
| Ds | Shell Diameter (m) |
| Gc | Mass flow per channel (kg/m2s) |
| Gp | Port mass velocity (kg/m2s) |
| k | Thermal Conductivity (W/mK) |
| L | Effective Length (m) |
| Lc | Compressed Plate Pack Length (m) |
| Lh | Horizontal Port Distance (m) |
| Lv | Vertical Port Distance (m) |
| ṁ | Mass flow rate (kg/s) |
| Ncp | Number of channels per pass (-) |
| Np | Number of passes (-) |
| Nt | Number of tubes (-) |
| p | Plate Pitch (m) |
| Q | Heat transfer rate (kJ/s) |
| t | Plate Thickness (m) |
| upc | Channel velocity (m/s) |
| U | Overall heat transfer coefficient (W/m2K) |
| W | Effective Width (m) |
| Greek letters | |
| β | Corrugation Angle |
| λ | Corrugation Wavelength |
| Φ | Surface Enlargement Factor |
| Subscripts | |
| c | cold side |
| e | equivalent |
| f | frictional |
| h | hot side |
| i | internal |
| o | external |
| r | return |
| s | shell |
| t | tube |
References
- IEA. World Energy Outlook 2019; IEA: Paris, France, 2019.
- U.S. Energy Information Administration. International Energy Outlook 2019; U.S. Department of Energy: Washington, DC, USA, 2019.
- Rogelj, J.; Schaeffer, M.; Meinshausen, M.; Knutti, R.; Alcamo, J.; Riahi, K.; Hare, W. Zero emission targets as long-term global goals for climate protection. Environ. Res. Lett. 2015, 10, 105007. [Google Scholar] [CrossRef]
- Wu, X.; Hu, Y.; Li, Y.; Yang, J.; Duan, L.; Wang, T.; Adcock, T.; Jiang, Z.; Gao, Z.; Lin, Z.; et al. Foundations of offshore wind turbines: A review. Renew. Sustain. Energy Rev. 2019, 104, 379–393. [Google Scholar] [CrossRef]
- Kannan, N.; Vakeesan, D. Solar energy for future world: A review. Renew. Sustain. Energy Rev. 2016, 62, 1092–1105. [Google Scholar] [CrossRef]
- Shi, L.; Shu, G.; Tian, H.; Deng, S. A review of modified Organic Rankine cycles (ORCs) for internal combustion engine waste heat recovery (ICE-WHR). Renew. Sustain. Energy Rev. 2018, 92, 95–110. [Google Scholar] [CrossRef]
- Papapetrou, M.; Kosmadakis, G.; Cipollina, A.; La Commare, U.; Micale, G. Industrial waste heat: Estimation of the technically available resource in the EU per industrial sector, temperature level and country. Appl. Therm. Eng. 2018, 138, 207–216. [Google Scholar] [CrossRef]
- Zhai, H.; An, Q.; Shi, L.; Lemort, V.; Quoilin, S. Categorization and analysis of heat sources for organic Rankine cycle systems. Renew. Sustain. Energy Rev. 2016, 64, 790–805. [Google Scholar] [CrossRef]
- Wang, E.; Zhang, H.; Fan, B.; Ouyang, M.; Zhao, Y.; Mu, Q. Study of working fluid selection of organic Rankine cycle (ORC) for engine waste heat recovery. Energy 2011, 36, 3406–3418. [Google Scholar] [CrossRef]
- Bao, J.; Zhao, L. A review of working fluid and expander selections for organic Rankine cycle. Renew. Sustain. Energy Rev. 2013, 24, 325–342. [Google Scholar] [CrossRef]
- Petr, P.; Raabe, G. Evaluation of R-1234ze(Z) as drop-in replacement for R-245fa in Organic Rankine Cycles—From thermophysical properties to cycle performance. Energy 2015, 93, 266–274. [Google Scholar] [CrossRef]
- Ziviani, D.; Dickes, R.; Quoilin, S.; Lemort, V.; De Paepe, M.; Van Den Broek, M. Organic Rankine cycle modelling and the ORCmKit library: Analysis of R1234ze (Z) as Drop-in Replacement of R245fa for Low-Grade Waste Heat Recovery. In Proceedings of the 29th International Conference on Efficiency, Cost, Optimization, Simulation and Environmental Impact of Energy Systems, Portoroz, Slovenia, 19–23 June 2016; pp. 1–13. [Google Scholar]
- Yang, J.; Ye, Z.; Yu, B.; Ouyang, H.; Chen, J. Simultaneous experimental comparison of low-GWP refrigerants as drop-in replacements to R245fa for Organic Rankine cycle application: R1234ze(Z), R1233zd(E), and R1336mzz(E). Energy 2019, 173, 721–731. [Google Scholar] [CrossRef]
- Darvish, K.; Ehyaei, M.; Atabi, F.; Rosen, M. Selection of optimum working fluid for organic rankine cycles by exergy and exergy-economic analyses. Sustainability 2015, 7, 15362–15383. [Google Scholar] [CrossRef]
- Moles, F.; Navarro-Esbrí, J.; Peris, B.; Mota-Babiloni, A.; Mateu-Royo, C. R1234yf and R1234ze as alternatives to R134a in Organic Rankine Cycles for low temperature heat sources. Energy Procedia 2017, 142, 1192–1198. [Google Scholar] [CrossRef]
- Feru, E.; Willems, F.; Rojer, C.; Jager, B.; Steinbuch, M. Heat exchanger modeling and identification for control of Waste Heat Recovery systems in diesel engines. In Proceedings of the American Control Conference, Washington, DC, USA, 16–19 June 2013; pp. 2860–2865. [Google Scholar]
- Konur, O.; Saatcioglu, O.; Korkmaz, S.; Erdogan, A.; Colpan, C. Heat exchanger network design of an organic Rankine cycle integrated waste heat recovery system of a marine vessel using pinch point analysis. Int. J. Energy Res. 2020. [Google Scholar] [CrossRef]
- Ozkol, I.; Komurgoz, G. Determination of the optimum geometry of the heat exchanger body via a genetic algorithm. Numer. Heat Transf. Part A Appl. 2005, 48, 283–296. [Google Scholar] [CrossRef]
- Zhu, J.; Zhang, W. Optimization design of plate heat exchangers (PHE) for geothermal district heating systems. Geothermics 2004, 33, 337–347. [Google Scholar] [CrossRef]
- Khan, T.; Khan, M.; Chyu, M.; Ayub, Z. Experimental investigation of single phase convective heat transfer coefficient in a corrugated plate heat exchanger for multiple plate configurations. Appl. Therm. Eng. 2010, 30, 1058–1065. [Google Scholar] [CrossRef]
- Nilpueng, K.; Wongwises, S. Experimental study of single-phase heat transfer and pressure drop inside a plate heat exchanger with a rough surface. Exp. Therm. Fluid Sci. 2015, 68, 268–275. [Google Scholar] [CrossRef]
- Edwards, J.E. Design and Rating of Shell and Tube Heat Exchangers; P & I Design Ltd.: Teesside, UK, 2008. [Google Scholar]
- Li, Y.; Jiang, X.; Huang, X.; Jia, J.; Tong, J. Optimization of high-pressure shell-and-tube heat exchanger for syngas cooling in an IGCC. Int. J. Heat Mass Transf. 2010, 53, 4543–4551. [Google Scholar] [CrossRef]
- Nasr, M.; Polley, G. An algorithm for cost comparison of optimized shell-and-tube heat exchangers with tube inserts and plain tubes. Chem. Eng. Technol. Ind. Chem. Plant Equip. Process Eng. Biotechnol. 2000, 23, 267–272. [Google Scholar] [CrossRef]
- Arjun, K.; Gopu, K. Design of shell and tube heat exchanger using computational fluid dynamics tools. Res. J. Eng. Sci. 2014, 3, 8–16. [Google Scholar]
- Selbaş, R.; Kızılkan, O.; Reppich, M. A new design approach for shell-and-tube heat exchangers using genetic algorithms from economic point of view. Chem. Eng. Process. Process Intensif. 2006, 45, 268–275. [Google Scholar] [CrossRef]
- Park, B.; Usman, M.; Imran, M.; Pesyridis, A. Review of Organic Rankine Cycle experimental data trends. Energy Convers. Manag. 2018, 173, 679–691. [Google Scholar] [CrossRef]
- Imran, M.; Usman, M.; Park, B.S.; Kim, H.J.; Lee, D.H. Multi-objective optimization of evaporator of organic Rankine cycle (ORC) for low temperature geothermal heat source. Appl. Therm. Eng. 2015, 80, 1–9. [Google Scholar] [CrossRef]
- Zheng, X.; Luo, X.; Luo, J.; Chen, J.; Liang, Y.; Yang, Z.; Chen, Y.; Wang, H. Experimental investigation of operation behavior of plate heat exchangers and their influences on organic Rankine cycle performance. Energy Convers. Manag. 2020, 207, 112528. [Google Scholar] [CrossRef]
- Walraven, D.; Laenen, B.; D’haeseleer, W. Comparison of shell-and-tube with plate heat exchangers for the use in low-temperature organic Rankine cycles. Energy Convers. Manag. 2014, 87, 227–237. [Google Scholar] [CrossRef]
- Pandya, N.; Shah, H.; Molana, M.; Tiwari, A. Heat transfer enhancement with nanofluids in plate heat exchangers: A comprehensive review. Eur. J. Mech. B Fluids 2020, 81, 173–190. [Google Scholar] [CrossRef]
- Xu, J.; Luo, X.; Chen, Y.; Mo, S. Multi-criteria design optimization and screening of heat exchangers for a subcritical ORC. Energy Procedia 2015, 75, 1639–1645. [Google Scholar] [CrossRef][Green Version]
- Yamada, N.; Mohamad, N.; Kien, T. Study on thermal efficiency of low- to medium-temperature organic Rankine cycles using HFO−1234yf. Renew. Energy 2012, 41, 368–375. [Google Scholar] [CrossRef]
- Zhang, X.; Wu, L.; Wang, X.; Ju, G. Comparative study of waste heat steam SRC, ORC and S-ORC power generation systems in medium-low temperature. Appl. Therm. Eng. 2016, 106, 1427–1439. [Google Scholar] [CrossRef]
- Gebremariam, A. Gasketed Plate Type Heat Exchanger Design Software; Turku University of Applied Sciences: Turku, Finland, 2016. [Google Scholar]
- Soni, N.; Patel, J. Effect of corrugation angle on performance evaluation of plate type heat exchangers. Int. J. Adv. Res. Innov. Ideas Educ. 2017, 3, 1376–1381. [Google Scholar]
- Mota, F.; Carvalho, E.; Ravagnani, M. Modeling and Design of Plate Heat Exchanger. In Heat Transfer Studies and Applications; IntechOpen: Rijeka, Croatia, 2015; ISBN 978-953-51-2146-6. [Google Scholar]
- Rohmah, N.; Pikra, G.; Purwanto, A.; Pramana, R. The effect of plate spacing in plate heat exchanger design as a condenser in organic Rankine cycle for low temperature heat source. Energy Procedia 2015, 68, 87–96. [Google Scholar] [CrossRef][Green Version]
- Kern, D.Q. Process Heat Transfer; Tosho Printing Co., Ltd.: Tokyo, Japan, 1983. [Google Scholar]
- Peters, M.; Timmerhaus, K.; West, R. Plant Design and Economics for Chemical Engineers, 5th ed.; McGraw-Hill Education: New York, NY, USA, 2003. [Google Scholar]


| Geometrical Parameters | Symbol | Value | Unit |
|---|---|---|---|
| Effective Length | L | 0.4 | m |
| Effective Width | W | 0.2 | m |
| Plate Thickness | t | 0.001 | m |
| Port Diameter | Dp | 0.018 | m |
| Vertical and Horizontal Port Distance | Lv/Lh | 0.01/0.02 | m |
| Corrugation Wavelength | λ | 0.009 | m |
| Corrugation Angle | β | 60 | ° |
| Compressed Plate Pack Length | Lc | 0.3 | m |
| Surface Enlargement Factor | Φ | 1.25 | − |
| Stainless Steel Thermal Conductivity | k | 16 | W/mK |
| Geometrical Parameters | Symbol | Value | Unit |
|---|---|---|---|
| Internal Tube Diameter | Dt | 0.019 | m |
| Shell Diameter | Ds | 0.203 | m |
| Number of Tubes | Nt | 24 | |
| Number of Tube Passes | Np | 2 | |
| Square Pitch Length | PT | 0.238 | m |
| Tube Clearance | C | 0.005 | m |
| Baffle Spacing | B | 0.305 | m |
| Pressure (bar) | Surface Area (m2) | |||||
|---|---|---|---|---|---|---|
| Preheater | Evaporator | Superheater | Precooler | Condenser | ||
| PHX | 10 | 2.60 | 4.82 | 5.04 | 8.00 | 13.21 |
| 15 | 3.66 | 4.60 | 4.82 | 7.73 | 13.21 | |
| 20 | 4.30 | 4.17 | 4.53 | 7.28 | 13.21 | |
| STHX | 10 | 2.39 | 7.01 | 7.22 | 9.37 | 25.46 |
| 15 | 3.90 | 7.37 | 6.53 | 8.86 | 25.46 | |
| 20 | 4.88 | 7.26 | 6.01 | 8.59 | 25.46 | |
| Pressure (bar) | Pressure Drop (kPa) | Net Work Change (%) | Efficiency Change (%) | |
|---|---|---|---|---|
| PHX | 10 | 11.00 | 2.08 | 2.12 |
| 15 | 7.29 | 0.49 | 0.51 | |
| 20 | 5.40 | 0.19 | 0.21 | |
| STHX | 10 | 0.41 | 0.08 | 0.08 |
| 15 | 0.38 | 0.03 | 0.03 | |
| 20 | 0.34 | 0.01 | 0.01 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bull, J.; Buick, J.M.; Radulovic, J. Heat Exchanger Sizing for Organic Rankine Cycle. Energies 2020, 13, 3615. https://doi.org/10.3390/en13143615
Bull J, Buick JM, Radulovic J. Heat Exchanger Sizing for Organic Rankine Cycle. Energies. 2020; 13(14):3615. https://doi.org/10.3390/en13143615
Chicago/Turabian StyleBull, James, James M. Buick, and Jovana Radulovic. 2020. "Heat Exchanger Sizing for Organic Rankine Cycle" Energies 13, no. 14: 3615. https://doi.org/10.3390/en13143615
APA StyleBull, J., Buick, J. M., & Radulovic, J. (2020). Heat Exchanger Sizing for Organic Rankine Cycle. Energies, 13(14), 3615. https://doi.org/10.3390/en13143615






