Comparison of Control Strategies to Realize Synthetic Inertia in Converters

Abstract

The increasing amount of renewable energy sources in the electrical energy system leads to an increasing number of converter-based generators connected to the electrical power grid. Other than conventional power plants that are often connected to the grid via synchronous generators, converter-based generators do not provide mechanical inertia intrinsically. Therefore, ensuring frequency stability in the electrical power grid might become even more difficult in the future. With the concept of synthetic inertia, the converter-based generators partially imitate the behavior of conventional generators. By implementing such a concept in converters, they are capable of contributing to frequency stability as well. This paper compares two strategies to realize synthetic inertia by modeling converter-based generators in MATLAB/SIMULINK and simulating their behavior in a small Microgrid. The results prove that any kind of realization of synthetic inertia helps to improve frequency stability. Each of the two investigated strategies may have their scope of application in a future electrical energy system.

1. Introduction

Generators in conventional power plants provide mechanical inertial response due to their rotating masses. The entirety of all rotating masses results in a network inertia constant, which represents a characteristic value of how the electric power grid instantaneously reacts to power disturbances caused by imbalances between load and generation. The globally desired goal of reducing greenhouse gases by integrating renewable energy sources (RES) into the power grid generally leads to a displacement of conventional power plants. In further consequence, the network inertia constant in the electric power system decreases, since a high amount of RES is mainly based on converter-based generators, which do not inherently provide an inertial response. A decreased network inertia constant may lead to critical stability challenges [1]. Results of a reduced inertia in the system are more frequent large frequency deviations which may affect system operation, security and reliability by overloading transmission lines, damaging equipment or triggering system defence plans and protection relays [2]. Such frequency stability issues due to reduced inertia already appear today, especially in smaller interconnected areas such as in the United Kingdom [3] or the Nordic synchronous area [4]. According to [5], the predicted decrease of system inertia in the regional group Central Europe may not lead to an unacceptable frequency behavior in the near future. But particularly in the case of a system split after a disturbance, the resulting imbalance combined with low inertia could result in unstable system behavior. The purpose of the concept of synthetic inertia (SI) is to mimic the behavior of the inertial response of synchronous generators. The aim of its implementation in converter-based generators is to maintain frequency stability in a future electric power system with a high amount of RES integrated in the grid. Several studies have already shown the usefulness of the concept of synthetic inertia to improve resilience in the electric power system [6,7]. A possible challenge for the introduction of synthetic inertia is the lack of harmonized requirements in international grid codes and financial incentives to equip converters with the capability to provide such a service. Possible ways to realize a market for providing synthetic inertia are discussed in [8,9].

There are several strategies to realize synthetic inertia. The paper [10] presents an overview of current state-of-the-art strategies to realize synthetic inertia and compares them. Conventional converter control of grid-connected converters is mainly based on a “grid-following” approach, which means that the converter synchronizes with a stable voltage at its terminals. Some converters are capable of producing an output voltage on their own. A corresponding converter control is usually referred to as “grid-forming” control. The most straightforward approach to realize synthetic inertia is based on a grid-following approach where the local frequency measurement is used in order to provide a power reference that behaves identical to the inertial response of conventional generators according to the swing equation. Such an approach has been studied in several works [11,12,13]. However, the necessary power output for such a grid-following approach to realize synthetic inertia is coupled with a delay of the frequency measurement that may lead to instabilities [14]. Therefore, recent activities concentrate on grid-forming control techniques, which do not necessariliy have such an inherent delay, but are capable of instantly providing a power response in case the frequency changes. The “virtual synchronous machine” is a popular concept that implements such an approach and goes beyond by trying to exactly imitate the behavior of a synchronous machine [15]. Converters implementing such a control approach are also called “synchronverters” [16]. A variety of reasearch activities investigated strategies to emulate synchronous machines in the converter control [17,18,19]. However, according to Milano et al. [1] this approach has its limitations and may also be a wasteful approach, considering that many strengths of a converter-based generator become unused, as for example its very fast control system emulates the comparably slow dynamics of a synchronous machine. An overview of possible grid-forming control strategies such as droop control, synchronverters, machine matching control or virtual oscillator control is given in [20].

Based on the control approach that is used, which is either a grid-following or a grid-forming control approach, the converter control has to be designed accordingly. Basic structures to realize the converter control including the grid synchronization, the voltage and current control, as well as the PWM generation are presented in [21]. Several studies investigated the behavior of grid-following and grid-forming approaches to realize synthetic inertia via simulations by using and expanding these basic control structures. An example of a simulation of the behavior of different grid-forming strategies to realize synthetic inertia is performed in [22]. By using an IEEE nine-bus test system, Ref. [22] proves that the presence of grid-forming converters improves the frequency stability metrics compared to a test system without their integration. The paper also reveals that under large load disturbances it is vital to implement a current limiting scheme. In [23] a qualitative analysis of the characteristics of grid-following and grid-forming control topologies to provide a transient response is carried out. A minimum measuring period of about 20 $\mathrm{m}$$\mathrm{s}$ to detect the grid voltage and to generate a corresponding response in grid-following converters is stated as the major drawback of grid-following converters compared to grid-forming converters in [23], especially since grid-forming converters are theoretically capable of injecting power into the grid instantaneously after a grid event. However, a comparison of the effectiveness of the two approaches to realize synthetic inertia may still be an issue to be investigated in more detail, especially as most existing converters are based on a grid-following control structure, also due to its easier and cheaper implementation. Changing the control approach of existing converters to a grid-forming control approach is not an option, but upgrading a grid-following approach by a corresponding realization of synthetic inertia may be a feasible option. In addition, there are several open questions of how to realize a grid-forming control structure, e.g., an appropriate current limitation. Therefore, this paper investigates the differences between a grid-following and a grid-forming control approach in more detail in order to compare their effectiveness.

This paper is structured as follows. Section 2 presents the basics on realizing synthetic inertia by describing the inertial response of conventional generators. Building on that, Section 3 describes the models in Section 3.2 and Section 3.3 that are used to investigate two strategies to realize synthetic inertia. Section 4.2.1 presents simulation results of a load-step in a Microgrid. Section 4.2.2 presents the results of a sensitivity analysis and Section 5 concludes the paper.

The nomenclature used in this paper is described in the following. Uppercase and lowercase letters are used to distinguish between unit-based and normalized values. Uppercase letters are used for unit-based values, while lowercase letters are used for normalized values. The unit of the normalized values is described with “pu”. To distinguish between phasors and instantaneous values, the index “t” is used for instantaneous values. Symbols in bold indicate a vector. Nominal values are described with the index “n”. A summarized list of all symbols used in this paper can be found below.

2. Strategies to Realize Synthetic Inertia

The majority of generators in power plants are synchronous machines. A change of their electrical load leads to a mechanical torque on the rotor of these synchronous machines. The rotor of these synchronous machines has a certain mass, which manifests itself in the form of inertia in case of a load change. Based on the swing equation, the electromagnetic torque M and the mechanical torque $M_m$ coming from a turbine are set in context by

$$\begin{array}{cc}\hfill M_m-M& =J\dot{\omega }\hfill \end{array}$$

(1)

where $\omega$ is the rotational speed, $\dot{w}$ is its derivative and J is the rotation inertia of the synchronous machine. The relationship between the power difference of mechanical power $P_m$ and electrical power P during a load-step then becomes

$$\begin{array}{cc}\hfill P_m-P& =∆P=J\dot{\omega }\omega \hfill \end{array}$$

(2)

by multiplying the equation above by $\omega$. By introducing the inertia constant $H=\frac{1}{2}\frac{J{\omega }_n^2}{S_n}$ and the starting time constant $T_A=2H$, the equation can be rearranged to

$$\begin{array}{cc}\hfill T_A\dot{\omega }\omega & =\frac{∆P}{S_n}{\omega }_n^2=∆p{\omega }_n^2\hfill \end{array}$$

(3)

where $S_n$ is the nominal apparent power and ${\omega }_n$ is the nominal rotation speed of the synchronous machine. The load-frequency control in a synchronous area in a first step is handled via the so-called “frequency containment reserves” (FCR). The droop control of FCR is realized in the speed governor of a synchronous machine, whose reference power output is proportional to the change of speed. In the equation above, according to Zhong and Weiss [24] the FCR can be taken into account by adding a second term

$$\begin{array}{cc}\hfill T_A\dot{\omega }\omega & =∆p{\omega }_n^2+\frac{1}{\sigma }∆\omega {\omega }_n\hfill \end{array}$$

(4)

where $\sigma =\frac{\frac{∆f}{f_n}}{\frac{∆P}{S_n}}$ is the droop, which is a proportional factor with $\left[\sigma \right]=\frac{\mathrm{Hz}{\mathrm{Hz}}^{-1}}{\mathrm{W}{\mathrm{W}}^{-1}}$. By assuming $\omega \approx {\omega }_n$ the equation can be rearranged to

$$\begin{array}{cc}\hfill T_A\dot{\omega }& =∆p{\omega }_n+\frac{1}{\sigma }∆\omega \hfill \end{array}$$

(5)

Imitating a power output according to Equation (5) in converter-based generators is termed as “synthetic inertia”. This paper considers two approaches to realize such a synthetic inertia:

• “Active synthetic inertia”, realized by using a grid-forming control strategy that relies on determining the grid angle based on Equation (5) and
• “Passive synthetic inertia”, realized by calculating a reference power according to Equation (4) that is used in the control of a grid-following converter.

The first approach is the best way to imitate the behavior of a synchronous machine but its drawback is the complex control structure that has to be implemented in a converter. The quality of the power output of the second approach, on the other hand, relies mainly on the quality of the frequency measurement device that is used, whose design is a trade-off between accuracy and speed. An actual implementation of the two approaches is described in Section 3.

3. Model Description

As already mentioned in Section 2, the realization of an “active synthetic inertia” is based on grid-forming converters. Grid-forming converters actively control their output voltage and therefore are capable of building an island grid. Active synthetic inertia in grid-forming converters can be realized by calculating a reference grid angle $\theta$ based on Equation (5), which is used in the converter control instead of using a fixed value ${\omega }_{n}t$. Section 3.2 describes the realization of active synthetic inertia in more detail. Section 2 also describes the basis for the realization of “passive synthetic inertia”, which is the only way to realize synthetic inertia in grid-following converters. Passive synthetic inertia is based on a calculation of the reference power based on Equation (5). The grid synchronization of grid-following converters measures the grid angle $\theta$ and the grid frequency f. The latter can be used in a feed-forward control to calculate a reference power according to Equation (5). Section 3.3 describes the realization of passive synthetic inertia in more detail. For both approaches of realizing synthetic inertia, a simplified model of a converter is used in this paper. The model of the three-phase voltage source converter (VSC) used in Figure 1 represents a two-level converter consisting of a DC-link and an inverter, followed by an LC-filter. To simplify matters, the DC link is represented by a constant voltage source. The inverter is modeled by a self-commutated three-phase bridge that is controlled by a pulse-width modulation (PWM) signal. The output filter consists of an LC-filter, with the resistance representing the parasitic resistance of the inductance.

3.1. Design Considerations for the Output Filter

Because of the fast switching inverter, an output filter is required to smooth the AC output currents. A series inductor fulfills this task. Its value is determined on the basis of the maximum AC current ripple $∆I_{rip}$ that is permissible at the converter output. According to Teodorescu [21] a corresponding calculation of this value for two-level PWM converters can be carried out by

$$\begin{array}{cc}\hfill L& =\frac{U_{DCL}}{2·∆I_{rip}·f_{sw}}\hfill \end{array}$$

(6)

where $f_{sw}$ is the switching frequency of the PWM generation and $U_{DCL}$ is the DC-link voltage. The capacitors at the converter output are used to filter the switching frequency harmonics. Figure 1 shows that the capacitor voltage is sensed for the converter control. In this way, the power factor at the terminals of the converter is reduced because part of the reactive power of the inductors is compensated for by the capacitors. The desired power factor at the converter output is the basis for calculating the value of the capacitors. According to Beres et al. [25] this calculation can be carried out by

$$\begin{array}{cc}\hfill C& =0.05·\frac{1}{{\omega }_n\frac{U_n^2}{S_n}}\hfill \end{array}$$

(7)

with $S_n$ as the nominal apparent power of the converter.

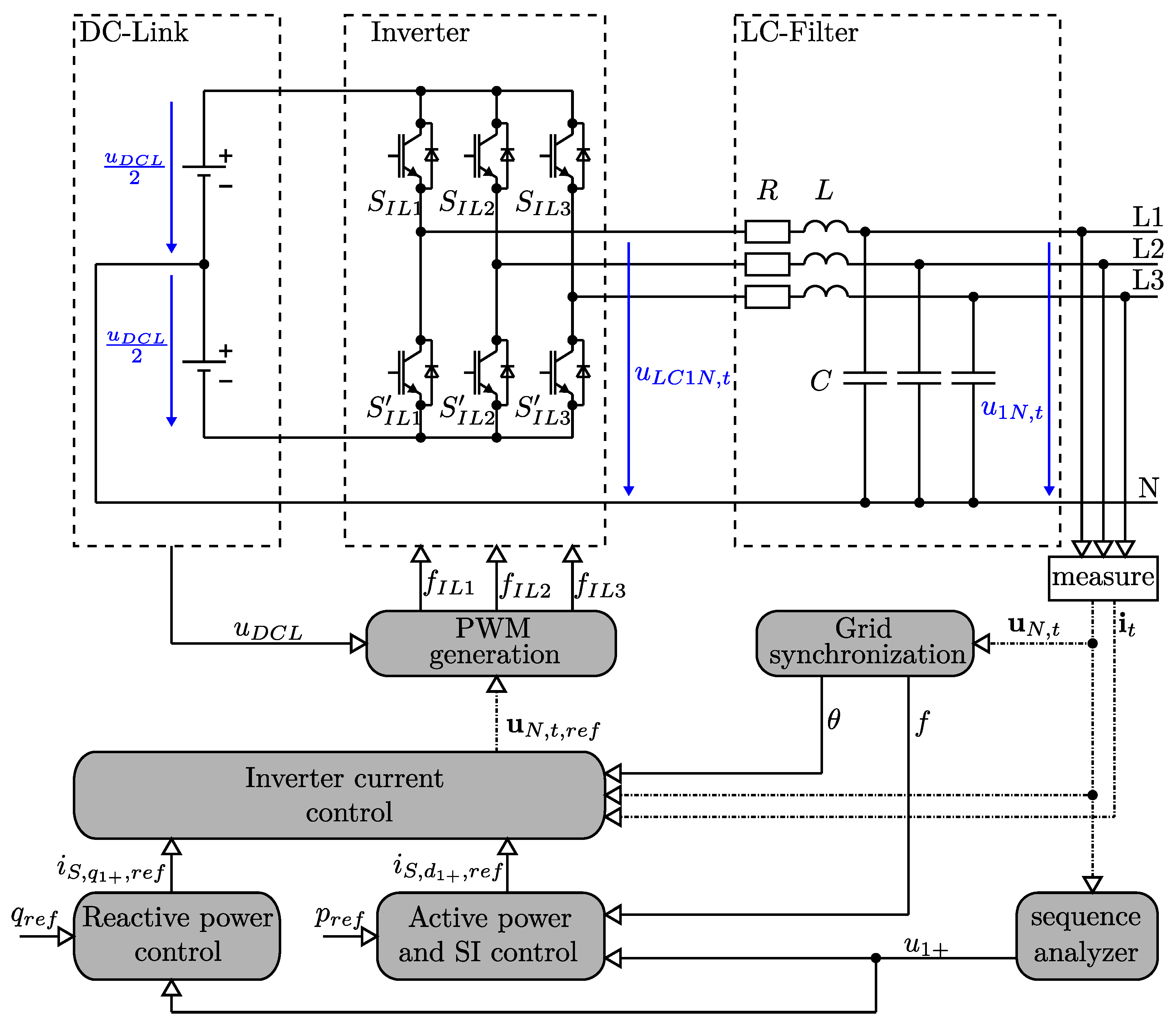
3.2. Model of a Grid-Forming Converter with Active Synthetic Inertia

In order to describe the realization of active synthetic inertia, Figure 1 shows a simplified converter model of a grid-forming converter and its control.

The different components of the control structure are described in the following sections.

3.2.1. Power Calculation

At the output of the converter the instantaneous phase-to-neutral voltages ${\mathbf{u}}_{N,t}$ and the instantaneous phase currents ${\mathbf{i}}_t$ are measured. In the “power calculation” these values are used to calculate the power output by using $p={\mathbf{u}}_{N,t}^{\top }·{\mathbf{i}}_t$. This power is used in the “SI control” to calculate the reference angle $\theta$ as shown in Figure 2.

The droop share is provided with a rate limiter in order to decouple it from the power output related to synthetic inertia.

3.2.2. SI Control

Figure 2 is based on Equation (5), which is transformed into the Laplace domain:

$$\begin{array}{cc}\hfill T_{A}s\omega & =∆p{\omega }_n+\frac{1}{\sigma }∆\omega \hfill \end{array}$$

(8)

and integrated to determine the grid angle $\theta$ as follows

$$\begin{array}{cc}\hfill \theta & =\frac{1}{s}\omega =\frac{1}{s^2}\frac{1}{T_A}\left[(p_{ref}-p){\omega }_n+\frac{1}{\sigma }({\omega }_n-\omega )\right]\hfill \end{array}$$

(9)

3.2.3. Cascaded Voltage- and Current Control

The grid angle $\theta$, combined with two reference voltages $u_{S,d_{1+},ref}$ and $u_{S,q_{1+},ref}$, which represent the direct/active- and quadrature/reactive-, positive-sequence component of the voltage space vector ${\mathbf{u}}_{S,ref}$, are used as input of the “cascaded voltage- and current control”. This cascaded voltage- and current control is shown in Figure 3.

It consists of the voltage control (lower part in the figure) and the current control (upper part in the figure), which both use the synchronous reference frame (SRF) to control the direct/active- and quadrature/reactive- voltage- and current component via PI-controllers. Park-transformations are used to calculate the voltage space vector ${\mathbf{u}}_{S,dq}$ and the current space vector ${\mathbf{i}}_{S,dq}$ based on the measured voltages ${\mathbf{u}}_{N,t}$ and the measured currents ${\mathbf{i}}_t$. To decouple the direct/active- and quadrature/reactive components in the current control the decoupling terms $\frac{\omega }{{\omega }_n}l$ have to be taken into account. Across the LC-filter a voltage drop occurs that can be described by the difference between the voltage ${\mathbf{u}}_{LC,t}$ at the output of the inverter and the voltage ${\mathbf{u}}_{N,t}$ at the converter output. The voltage drop over the LC-filter can be calculated by using the normalized inductance l

$$\begin{array}{cc}\hfill l& =\frac{{\omega }_n·L}{\frac{U_n^2}{S_n}}\hfill \end{array}$$

(10)

with the equation

$$\begin{array}{cc}\hfill {\mathbf{u}}_{LC,S,dq}& ={\mathbf{u}}_{S,dq}+j\frac{\omega }{{\omega }_n}l·{\mathbf{i}}_{S,dq}=\left(\begin{array}{c}{u}_{S,d}+i_{S,d}R-\frac{\omega }{{\omega }_n}l·i_{S,q}\\ u_{S,q}+i_{S,q}R+\frac{\omega }{{\omega }_n}l·i_{S,d}\end{array}\right)\hfill \end{array}$$

(11)

The same applies to the voltage control by using the decoupling terms $\frac{\omega }{{\omega }_n}c$ to take into account the currents through the capacitors in the LC-filter. The value of these currents can be calculated by using the normalized capacitance c

$$\begin{array}{cc}\hfill c& =\frac{{\omega }_{n}C}{\frac{U_n^2}{S_n}}\hfill \end{array}$$

(12)

with the equation

$$\begin{array}{cc}\hfill {\mathbf{i}}_{LC,S,dq}& ={\mathbf{u}}_{S,dq}·j\frac{\omega }{{\omega }_n}c=\left(\begin{array}{c}-u_{S,q}\frac{\omega }{{\omega }_n}c\\ u_{S,d}\frac{\omega }{{\omega }_n}c\end{array}\right)\hfill \end{array}$$

(13)

The voltage control delivers a reference current space vector ${\mathbf{i}}_{S,d{q}_{1+},ref}$ which is used in the current control. The current control delivers an instantaneous reference voltage vector ${\mathbf{u}}_{N,t,ref}$ which is used as input of the “PWM generation”.

3.2.4. Tuning Considerations

The tuning of the cascaded control structure relies on a decoupled consideration of the voltage- and the current control which is achieved by tuning the current control much faster (about ten times) than the voltage control. The tuning then can be performed in a stepwise approach according to Henninger [26]. In a first step the current control is tuned. By using the decoupling network shown in Figure 3 the active- and reactive currents can be controlled separately via PI-controllers. According to Yazdani and Iravani [27] the tuning of these PI-controllers can be carried out as follows. The PI-controllers are represented by $R_I\left(s\right)$ in the Laplace domain

$$\begin{array}{cc}\hfill R_I\left(s\right)& =K_{I,P}+\frac{K_{I,I}}{s}\hfill \end{array}$$

(14)

By neglecting the dynamics of the PWM generation and the inverter, which are considered to act very fast due to high switching frequency, the plant only consists of the LC-filter. Therefore, the transfer function of the LC-filter $G_I\left(s\right)$ can be described by

$$\begin{array}{cc}\hfill G_I\left(s\right)& =\frac{\frac{1}{R}}{1+s\frac{L}{R}}\hfill \end{array}$$

(15)

resulting in a loop gain $L_I\left(s\right)$ of

$$\begin{array}{cc}\hfill L_I\left(s\right)& =R_I\left(s\right)G_I\left(s\right)=\frac{K_{I,P}}{sL}·\frac{s+\frac{K_{I,I}}{K_{I,P}}}{s+\frac{R}{L}}\hfill \end{array}$$

(16)

By choosing $K_{I,P}=\frac{L}{{\tau }_i}$ and $K_{I,I}=\frac{R}{{\tau }_i}$ the closed-loop transfer function $\frac{L_I\left(s\right)}{1+L_I\left(s\right)}$ has a first-order behavior with a freely selectable time constant ${\tau }_i$.

According to Henninger [26] the voltage controller can be tuned in a second step. The PI-controllers of the voltage control are represented by $R_U\left(s\right)$ in the Laplace domain

$$\begin{array}{cc}\hfill R_U\left(s\right)& =K_{U,P}+\frac{K_{U,I}}{s}\hfill \end{array}$$

(17)

From the point of view of the voltage control, the transfer function of the plant also includes the transfer function of the current control. Due to the tuning of the current control it can be taken into account by a simple first-order transfer function. The voltage output of the converter only depends on the current through the capacitance of the LC-filter. As a consequence, the transfer function of the plant can be summarized as

$$\begin{array}{cc}\hfill G_U\left(s\right)& =\frac{1}{1+{\tau }_{i}s}\frac{1}{sC}\hfill \end{array}$$

(18)

This results in a loop gain $L_U\left(s\right)$ of

$$\begin{array}{cc}\hfill L_U\left(s\right)& =R_U\left(s\right)G_U\left(s\right)=\left(K_{U,P}+\frac{K_{U,I}}{s}\right)\frac{1}{1+{\tau }_{i}s}\frac{1}{sC}\hfill \end{array}$$

(19)

whose parameters $K_{U,P}$ and $K_{U,I}$ can be tuned by using the symmetrical optimum according to Yazdani and Iravani [27] with

$$\begin{array}{cc}\hfill K_{U,P}& =\frac{C}{{\tau }_i}\sqrt{\frac{1-sin{\mathsf{\Phi }}_R}{1+sin{\mathsf{\Phi }}_R}}\hfill \end{array}$$

(20)

and

$$\begin{array}{cc}\hfill K_{U,I}& =\frac{K_{U,P}}{{\tau }_i}\frac{1-sin{\mathsf{\Phi }}_R}{1+sin{\mathsf{\Phi }}_R}\hfill \end{array}$$

(21)

where ${\mathsf{\Phi }}_R$ is the desired phase margin.

3.2.5. PWM Generation

The PWM generation generates the PWM-signals $f_{IL1}$, $f_{IL2}$ and $f_{IL3}$ based on the instantaneous reference voltage vector ${\mathbf{u}}_{N,t,ref}$. These PWM-signals control the switches $S_{IL1}$, $S_{IL2}$ and $S_{IL3}$. The complementary switches $S_{IL1}^{\prime }$, $S_{IL2}^{\prime }$ and $S_{IL3}^{\prime }$ are controlled by the PWM-signals $f_{IL1}^{\prime }$, $f_{IL2}^{\prime }$ and $f_{IL3}^{\prime }$. In order to speed up the simulation, this paper uses an average-model based VSC, which is available in MATLAB/SIMULINK [28]. As the reference voltage ${\mathbf{u}}_{N,t,ref}$ can be used directly as an input of the VSC model, an actual representation of the PWM generation is not necessary.

3.3. Model of a Grid-Following Converter with Passive Synthetic Inertia

In order to describe the realization of passive synthetic inertia, Figure 4 shows a simplified converter model and its control of a grid-following converter.

For the PWM generation the same properties as for Section 3.2.5 apply.

3.3.1. Grid Synchronization and Sequence Analyzer

Compared to a grid-forming converter that generates its own angle $\theta$ in order to build a reference signal for the PWM generation, a grid-following converter relies on an angle $\theta$ that is determined from the voltages ${\mathbf{u}}_{N,t}$ measured at the terminals of the converter. The “grid synchronization” accomplishes this task. The most common structure for grid synchronization is based on the synchronous reference phase-locked loop (SRF-PLL) which is shown in Figure 5.

Via a Park-transformation the voltage vector ${\mathbf{u}}_{N,t}$ is transformed into a voltage space vector in the dq-plane, whose reactive/quadrature component $u_{S,q}$ is controlled via PID-controller in order to synchronize the output $\theta$ of an integrator with the measured voltage vector ${\mathbf{u}}_{N,t}$. In the case of an unsymmetrical voltage vector ${\mathbf{u}}_{N,t}$ or in case it contains harmonics the reactive/quadrature component $u_{S,q}$ oscillates. In order to provide a frequency measurement by the SRF-PLL, therefore, a filtering method is necessary. Figure 5 shows a low-pass filter to accomplish this task. The speed and accuracy of active synthetic inertia depends heavily on the tuning of this low-pass filter.

The “sequence analyzer” shown in Figure 4 determines the normalized positive-sequence voltage $u_{1+}$ which is used in the active- and reactive power control to calculate a corresponding current reference.

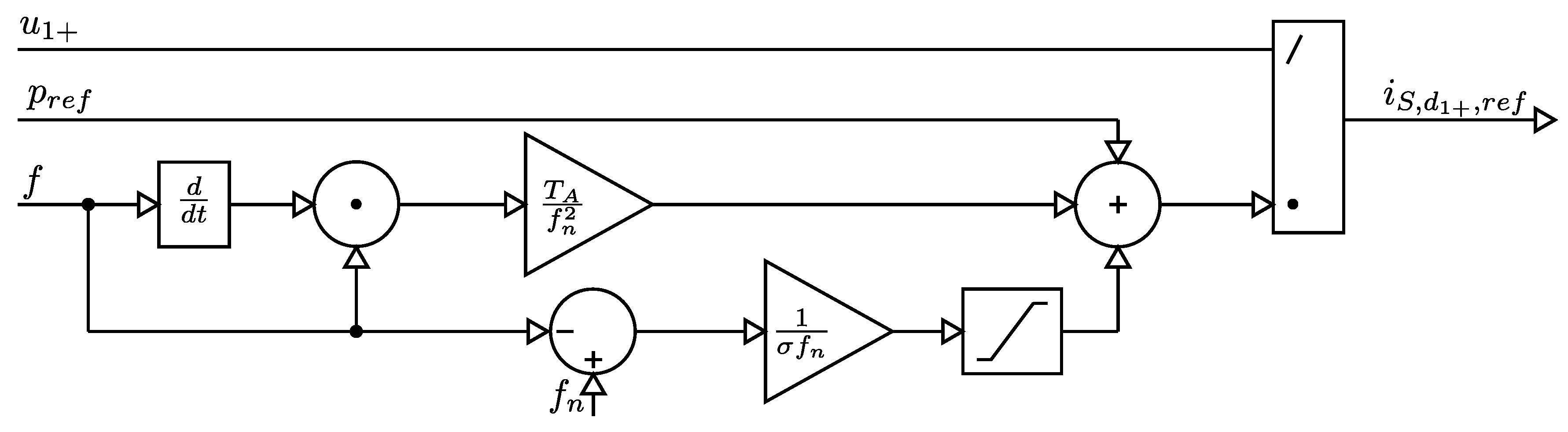
3.3.2. Active Power and SI Control

The “active power- and SI control” calculates an active current reference signal $i_{S,d_{1+},ref}$ in the positive-sequence system. Figure 6 shows the structure of how this task can be accomplished.

The basic structure of the converter model has already been described in Section 3 and consists of a simplified DC-Link and an inverter, followed by an output filter. Based on Equation (4) the passive synthetic inertia is implemented by using the measured frequency of the grid synchronization

$$\begin{array}{cc}\hfill ∆p& =T_A\frac{df}{dt}\frac{f}{f_n^2}+\frac{1}{\sigma f_n}\left(f-f_n\right)\hfill \end{array}$$

(22)

The derivative $\frac{df}{dt}$ in this equation which is also shown in Figure 6 reacts very sensitive to changes of the frequency. Therefore, an appropriate filtering method has to be implemented. A possible way to do so is discussed in more detail in Section 4.1. As shown in Figure 6 the droop share is provided with a rate limiter in order to decouple it from the power output related to synthetic inertia. Besides this power reference signal $∆p$, which is only different to zero when frequency gradients occur, the steady-state power reference signal $p_{ref}$ is added. In order to take into account the voltage $u_{1+}$, this reference power is divided by $u_{1+}$ in order to guarantee a corresponding current reference $i_{S,d_{1+},ref}$ in steady-state.

3.3.3. Reactive Power Control

The “reactive power control” provides a current reference signal $i_{S,q_{1+},ref}$ in the positive-sequence system by calculating

$$\begin{array}{cc}\hfill i_{S,q_{1+},ref}& =\frac{q_{ref}}{u_{1+}}\hfill \end{array}$$

(23)

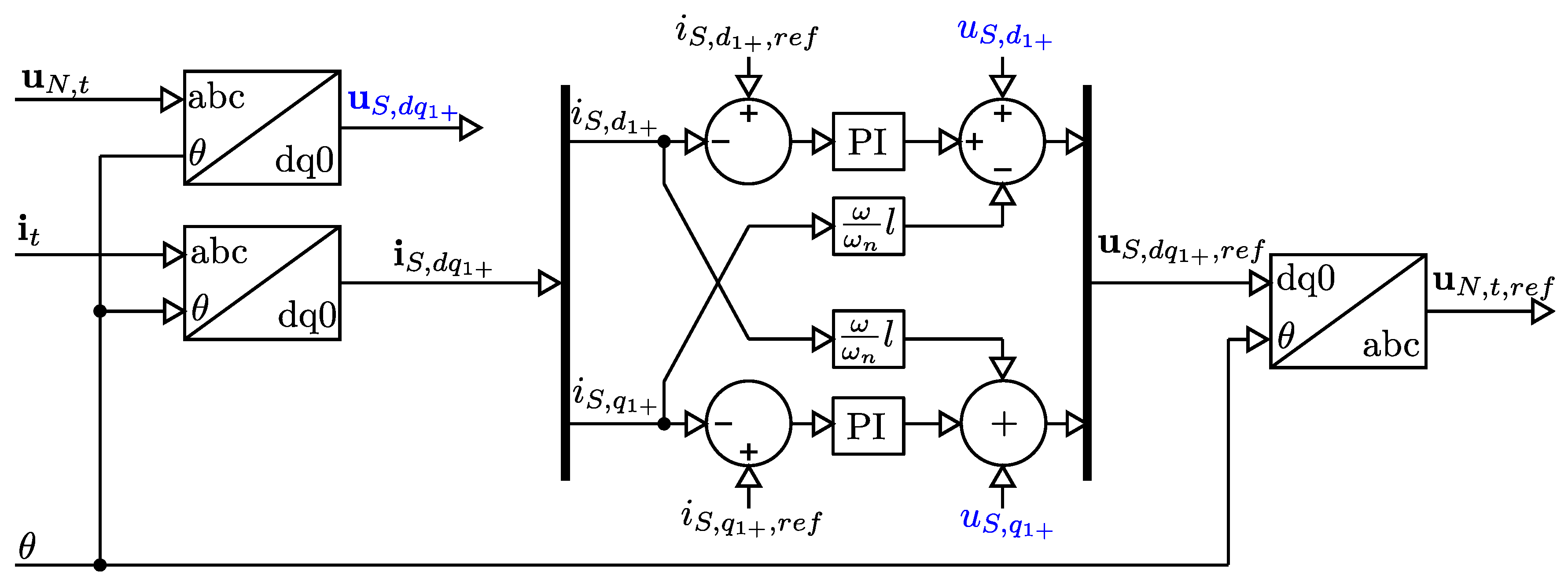
3.3.4. Inverter Current Control

The “inverter current control” uses the current reference signals $i_{S,d_{1+},ref}$ and $i_{S,q_{1+},ref}$, which are components of the current space vector in the dq-plane, the grid angle $\theta$ provided by the grid synchronization, the measured voltage vector ${\mathbf{u}}_{N,t}$ and the current vector ${\mathbf{i}}_t$ in order to determine a voltage reference vector ${\mathbf{u}}_{N,t,ref}$ for the PWM generation. The control structure of the current control is shown in Figure 7 and basically has the same structure as the current control of the cascaded voltage- and current control shown in Figure 3, which is also based on a synchronous reference frame.

It uses the angle $\theta$ for Park-transformations of the voltage vector ${\mathbf{u}}_{N,t}$ and the current vector ${\mathbf{i}}_t$. The current components are controlled via PI-controllers each. By using the decoupling terms $\frac{\omega }{{\omega }_n}l$ each component can be controlled separately. Before generating the reference voltage vector ${\mathbf{u}}_{N,tref}$ by an inverse Park-transformation, the voltage components in the dq-plane are added to the output of the PI-controller.

3.3.5. Tuning Considerations

In order to tune the PI-controllers of Figure 7 the same considerations as already mentioned for the current controller in Section 3.2.3 can be applied. This leads to a choice of parameters of the corresponding PI-controllers of $K_{I,P}=\frac{L}{{\tau }_i}$ and $K_{I,I}=\frac{R}{{\tau }_i}$.

4. Simulation

Basically, all converter-based technologies are capable of providing synthetic inertia by using one of the control strategies presented above. However, technologies based on renewable energy sources may have trouble providing the necessary power response at any given time. For example, there are wind turbines that are already commercially available today, which are capable of providing synthetic inertia [29,30,31]. One approach used in wind turbines to generate an inertial response is to temporarily increase the active power output based on the energy of the rotating masses. In response to a drop in grid frequency they temporarily increase their active power even beyond the available power from the wind by drawing energy from the rotating masses of the generator, the shaft and the blades. But at low wind speeds, the available energy in the rotating masses may be too low to provide a noteworthy amount of synthetic inertia, or the rotor may even stand still, which makes it impossible to provide inertial response. Assuming that synthetic inertia plays a key role regarding frequency stability in a future energy system, a certain percentage of technologies providing such a service may be required to deliver synthetic inertia at any time. Aside from technologies based on renewable energy sources, battery energy storage systems can meet such a requirement. Furthermore, battery energy storage systems are considered to be very well-suited to deliver such kind of highly dynamic system service and are also considered to replace conventional generators, which provide frequency reserves, to some extent in a future energy system [32]. Therefore, the following simulations consider battery converter systems for parametrization of the simulation models.

Section 4.1 describes the simulation set-up, Section 4.2 presents relevant simulation results and Section 4.3 discusses the results.

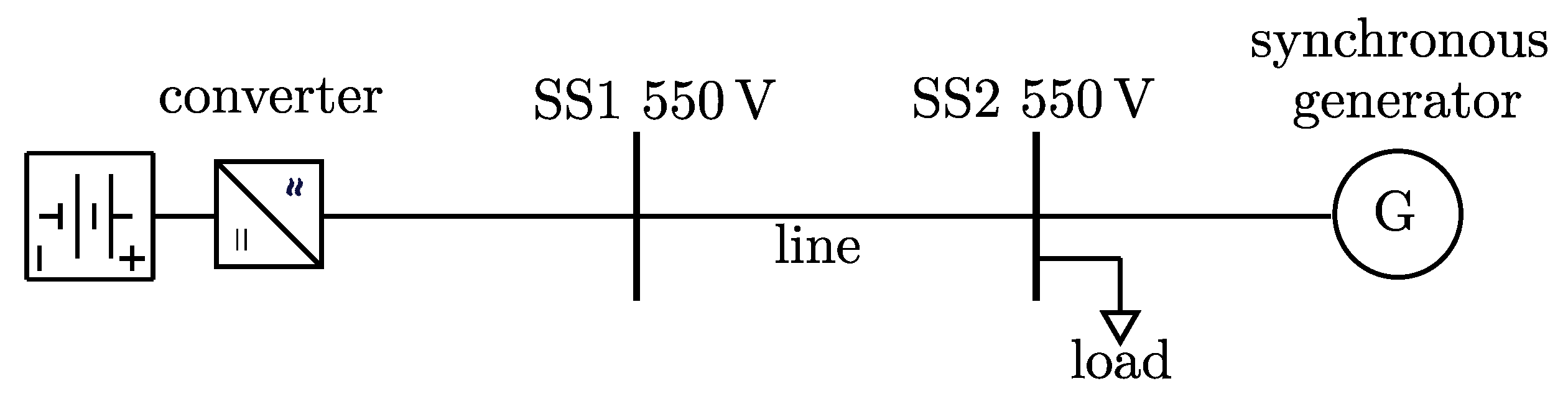
4.1. Simulation Set-Up

Figure 8 shows a small Microgrid by which the behavior of the two converter models presented above is investigated. The Microgrid consists of a converter, a line, a load and a synchronous generator. Via electromagnetic transient (EMT) simulations in MATLAB/SIMULINK, the performance of the active- and passive synthetic inertia approaches in reaction to load-steps is investigated and compared.

The parameters used in the simulation are summarized in

Table 1. Parameters used in the simulation.

Converter		Generator		Line
Parameter	Value	Parameter	Value	Parameter	Value
$U_n$	550$\mathrm{V}$	$U_n$	550$\mathrm{V}$	R	$0.01$$\mathsf{\Omega }$
$S_n$	650 kVA	$S_n$	1 MVA	L	$0.1$$\mathrm{m}$$\mathrm{H}$
$U_{DCL}$	900$\mathrm{V}$
L	260$\mathsf{\mu }$$\mathrm{H}$
R	1$\mathrm{m}$$\mathsf{\Omega }$
C	342$\mathsf{\mu }$$\mathrm{F}$
${\tau }_i$	$0.1$$\mathrm{m}$$\mathrm{s}$	${\tau }_{SM,G}$	5$\mathrm{s}$
$K_{I,P}$	$2.6$ pu
$K_{I,I}$	10 pu
${\mathsf{\Phi }}_R$	60${}^{\circ }$
$K_{U,P}$	$0.916$ pu
$K_{U,I}$	658 pu
$\sigma$	$\frac{1}{100}$  pu	$\sigma$	$\frac{1}{100}$  pu
$T_A$	10$\mathrm{s}$	$T_A$	$0.8$$\mathrm{s}$

. As already mentioned, the converter parameters are based on a converter that is used in a battery energy storage system which is described in more detail in [33]. For the synchronous generator, a MATLAB/SIMULINK-internal pre-set model is used [28]. As governor for the synchronous generator the MATLAB/SIMULINK-internal “SM Governor with Droop” is used, where a time constant ${\tau }_{SM,G}$ and a droop $\sigma$ are used that are listed in Table 1. As automatic voltage regulator of the synchronous generator the MATLAB/SIMULINK-internal model “ST1A Excitation system” with pre-set parameters is used. The constant impedance load is configured as a base load with $465\mathrm{k}\mathrm{W}$ that is distributed between converter and generators with a reference power of the converter of $0.1$ pu and a reference power of the generator of $0.4$ pu.

First-order filter elements with a time constant of 1 $\mathrm{s}$ are used to implement the rate limiter in the control structures shown in Figure 2 and Figure 6. As already mentioned above, the realization of passive synthetic inertia requires several other filter elements. One of such filter elements is needed for the grid synchronization shown in Figure 5. The frequency output of the SRF-PLL shown in Figure 5 requires an output filter in order to filter asymmetry of the input voltage ${\mathbf{u}}_{N,t}$ or harmonics in this input voltage. In the following simulations, this filter is realized as a second-order filter with a cut-off frequency of 10 $\mathrm{Hz}$. Another filter element is necessary in the active power and SI control shown in Figure 6. The use of a numerical derivative without filtering might be very sensitive to the dynamics of the entire model during simulation. But also in case of the implementation in a real converter system such a filtering method may be necessary. The frequency in real converter systems is usually measured in discrete time steps. The corresponding numerical calculation of the derivative might be sensitive to measurement errors. An appropriate filtering method can be applied to smooth the corresponding output of this calculation. For the following simulations, the filter element in Figure 6 is modeled as a first-order filtered-derivative with a time constant of 50 $\mathrm{m}$$\mathrm{s}$.

4.2. Results

An active power load-step in the Microgrid is the simplest way to compare the behavior of the two presented control strategies of synthetic inertia. Therefore, Section 4.2.1 presents the simulation results of a single active power load-step in more detail. Building on that, a sensitivity analysis for different values of this active power load-step is performed. This sensitivity analysis also investigates the influence of the starting time constant $T_A$ for both control strategies. Section 4.2.2 presents the results of this sensitivity analysis.

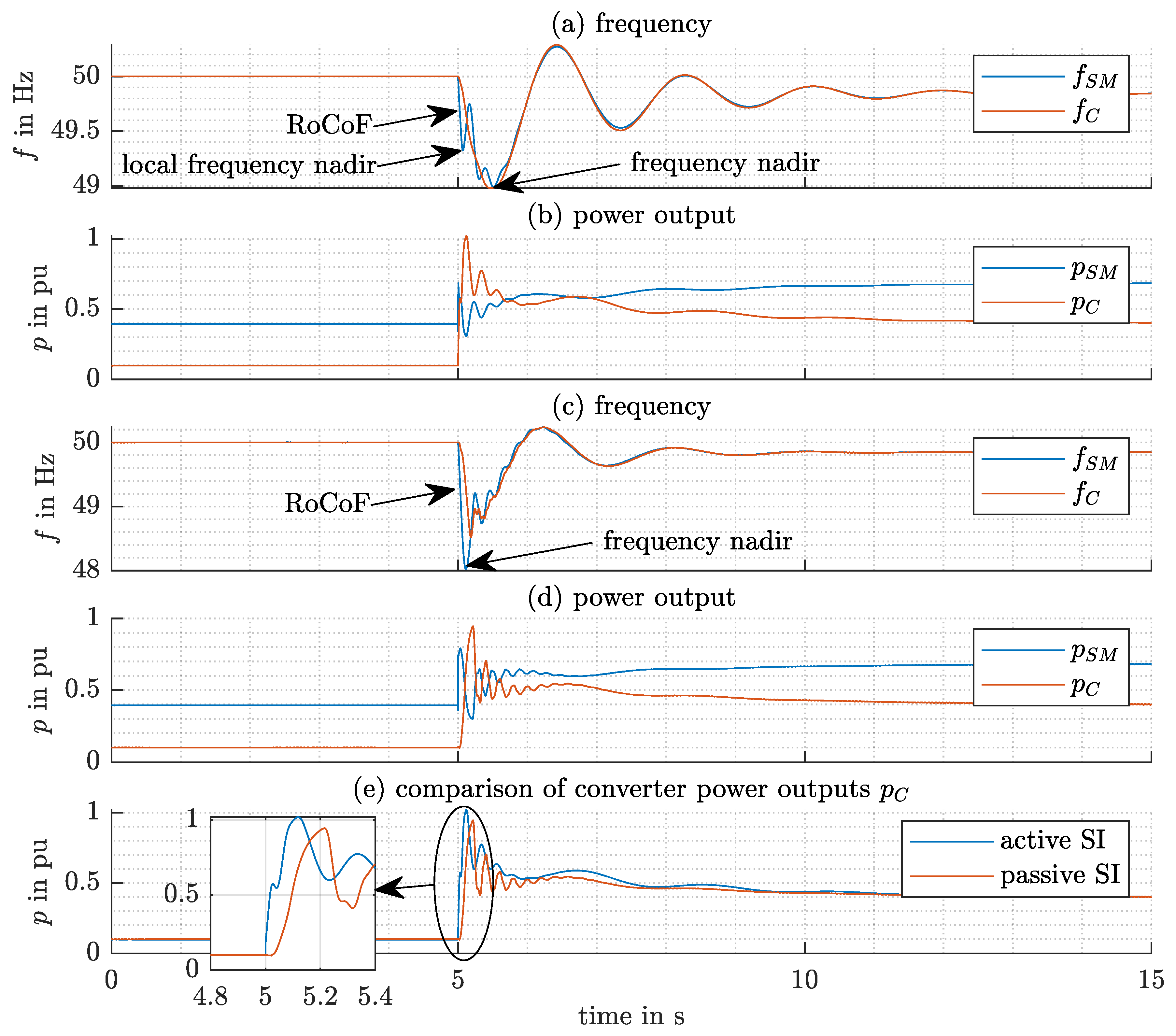
4.2.1. Simulation of a Single Load-Step for Both Models

In order to investigate the reaction to a load-step, the power of the load shown in Figure 8 is increased by 500 $\mathrm{k}$$\mathrm{W}$, which leads to a maximum power output of the converter if the starting time constant of $T_A=10\mathrm{s}$ listed in Table 1 is taken into account.

The simulation results of such a load-step at 5 $\mathrm{s}$ are shown in Figure 9. The figure compares the behavior of the active synthetic inertia ((a) and (b)) and the passive synthetic inertia ((c) and (d)). It shows the frequency of the generator $f_{SM}$ and the converter $f_C$ in (a) and (c), and the normalized power output of the generator $p_{SM}$ and the converter $p_C$ in (b) and (d). Figure 9e shows a comparison of the power outputs $p_C$ of active- and passive synthetic inertia. For both variants identical parameters according to Table 1 are applied.

The comparison of both simulation results shows a significantly improved frequency stability in case of active synthetic inertia leading to a frequency nadir (minimum frequency) of 49 $\mathrm{Hz}$, compared to a frequency nadir of 48 $\mathrm{Hz}$ in case of passive synthetic inertia. A zoomed area of the relevant time range of the power output in Figure 9 shows a noticeable delay of passive synthetic inertia compared to active synthetic inertia. This delay results from the filtering methods used in the SRF-PLL and the derivative of passive synthetic inertia. Both, the second-order low-pass filter, whose influence can be seen in the delayed frequency output shown in Figure 9c, as well as the first-order filtered-derivative contribute to this delay and cause the power output of passive synthetic inertia not to reach the full power output of 1 pu as it is the case with active synthetic inertia. Comparing the time of occurrence of the frequency nadir in Figure 9c with the peak power output of passive synthetic inertia in Figure 9d shows that the peak power occurs after the frequency nadir. For active synthetic inertia on the other hand such a comparison in Figure 9a,b shows that the first local frequency nadir occurs about at the same time as the peak power output of active synthetic inertia.

The frequency nadir is significantly influenced by the Rate of Change of Frequency (RoCoF) at the beginning of the load-step. The faster the reaction of synthetic inertia, the faster this RoCoF at the beginning of the load-step can be limited and the less pronounced the frequency nadir becomes. Therefore, the delayed reaction of passive synthetic inertia leads to a lower frequency nadir than in case of active synthetic inertia. Of course, it is theoretically possible to minimize the delays due to the PLL and the derivative computation, but at the cost of increasing the sensitivity of the system towards noise, faults and other fast transients.

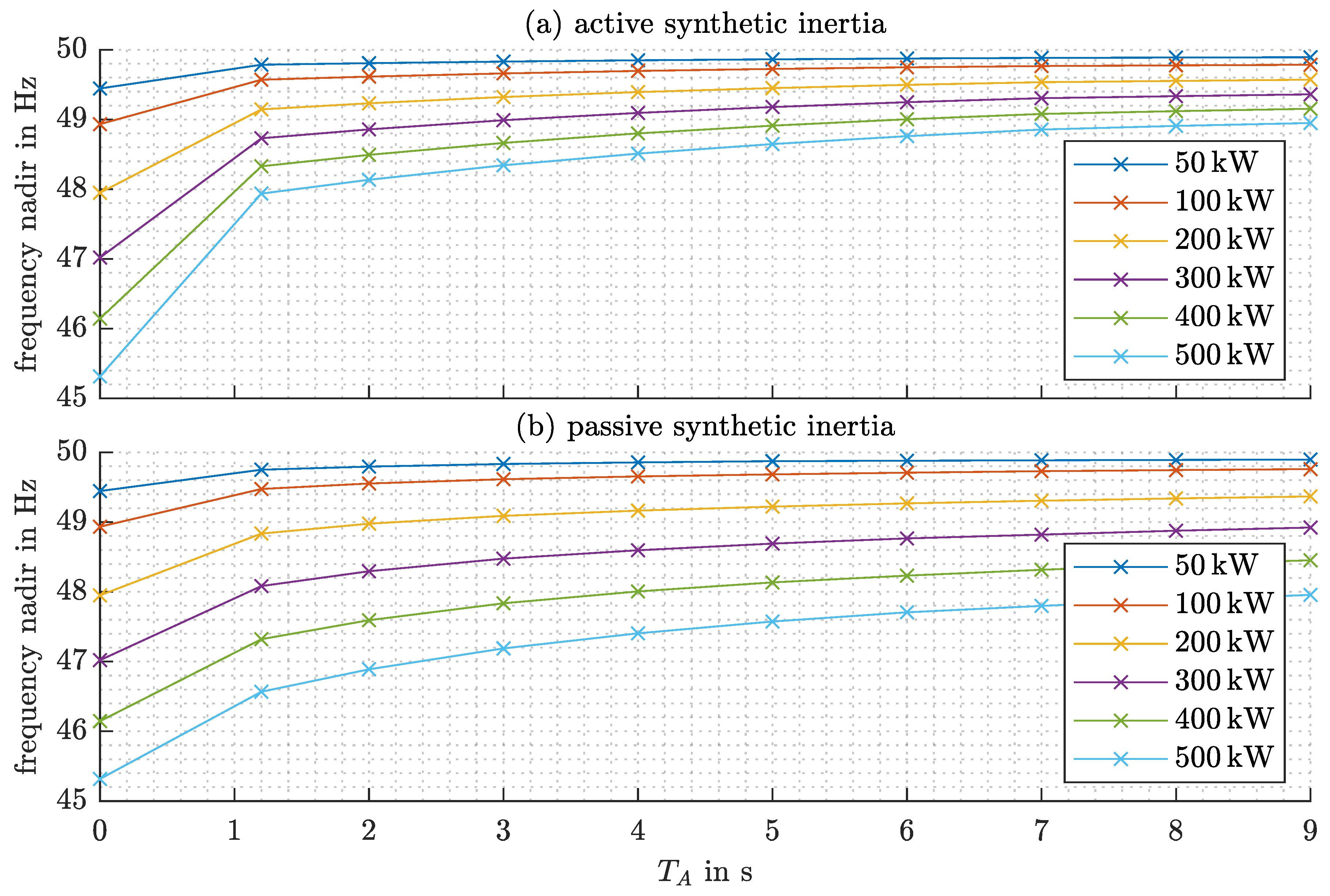
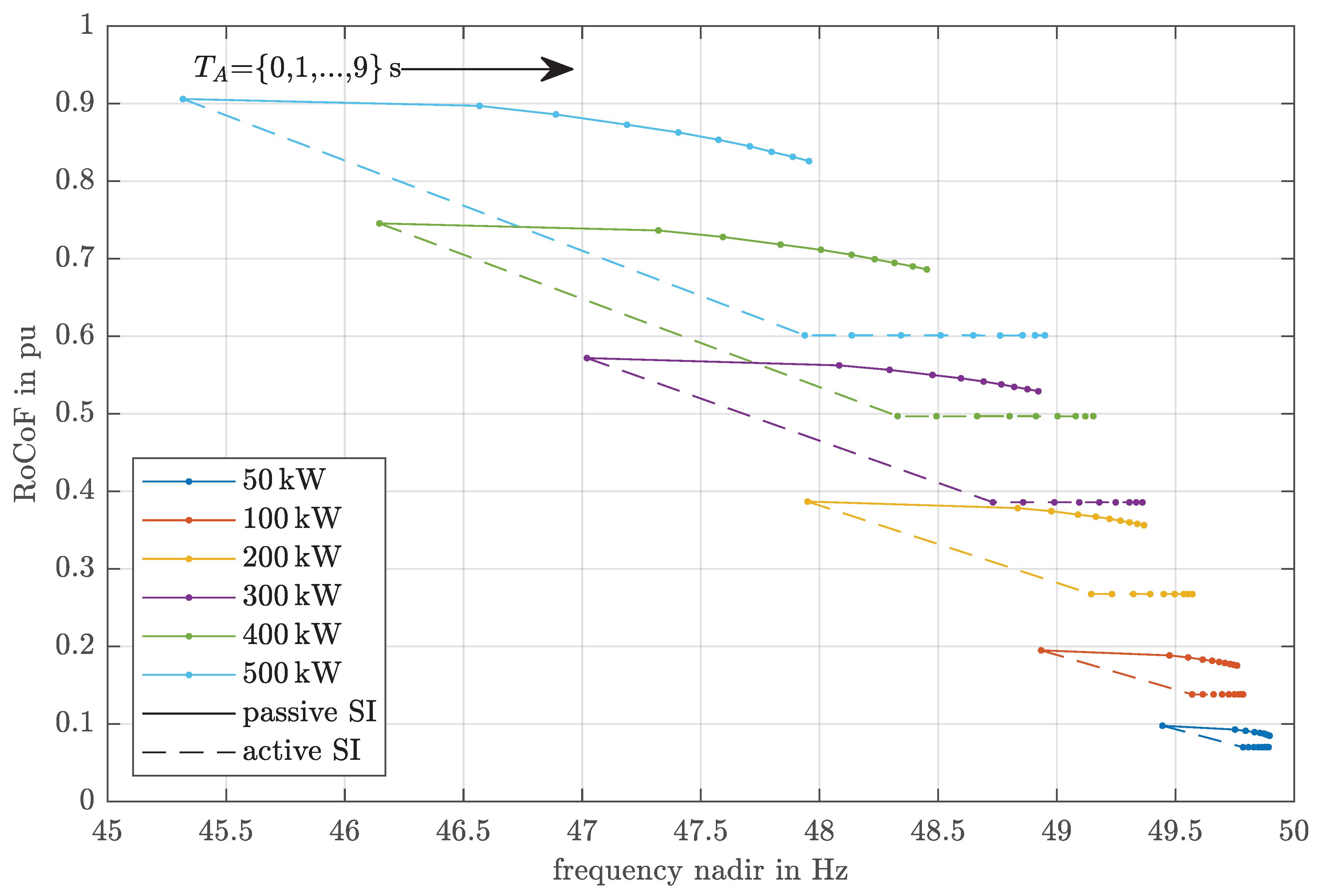
4.2.2. Sensitivity Analysis

In order to investigate the behavior of active- and passive synthetic inertia in dependence of the size of the load-step and the starting time constant of the converter, a sensitivity analysis is performed. The active power value of the load-step is varied with values of the set {50, 100, 200, 300, 400, 500} $\mathrm{k}\mathrm{W}$ and the starting time constant is varied with values of the set {1, 2, 3, 4, 5, 6, 7, 8, 9} $\mathrm{s}$ for both models. Figure 10 shows the outcome of this sensitivity analysis. It displays the frequency nadir of the synchronous generator as a consequence of the corresponding load-step. A starting time constant of $T_A=0 \mathrm{s}$ means that synthetic inertia is inactive and the synchronous generator is the only equipment in the Microgrid that dynamically stabilizes the frequency.

As already shown in Figure 9 and described above, passive synthetic inertia is less effective in improving frequency stability as a consequence of the filtering techniques that are necessary to be implemented in the converter control. This can also be seen in Figure 10, which shows that compared to $T_A=0 \mathrm{s}$, where only the synchronous generator stabilizes the Microgrid, already a small starting time constant of $T_A=1 \mathrm{s}$ massively helps to reduce the frequency drop in case of active synthetic inertia, whereas passive synthetic inertia has much less effect on the frequency nadir. During very small load-steps, the effectiveness between the two strategies is hardly visible, but becomes clearly visible with growing values of the load-step. Especially for small values of the starting time constant $T_A$, the effectiveness of active synthetic inertia is much higher compared to passive synthetic inertia. With increasing value of the starting time constant, a saturation effect becomes visible for both control strategies. This saturation effect can be argued with a limited power gradient of both control strategies. As already described in Section 4.2.1 for passive synthetic inertia, situations may occur when the RoCoF at the beginning of the load-step is so high that the time which is necessary to reach a certain amount of power output inherently leads to a certain frequency nadir, regardless of the value of the starting time constant. This is due to the limited maximum power gradient of the converter and its control.

The impact of the two control strategies on the RoCoF can be seen more clearly in Figure 11.

Figure 11 shows the RoCoF over the frequency nadir for all results of the sensitivity analysis. The starting time constant of $T_A=0 \mathrm{s}$ indicates the inactivity of synthetic inertia and is the starting point for the lines which represent the increasing value of $T_A$, whose course continuously runs from the left to the right. While the RoCoF in case of using active synthetic inertia reaches its lowest value already at the lowest value of the starting time constant $T_A=1 \mathrm{s}$, the RoCoF in case of using passive synthetic inertia continuously decreases with an increasing value of the starting time constant.

4.3. Discussion

Figure 9, Figure 10 and Figure 11 show that both strategies to realize synthetic inertia are capable of improving frequency stability during power deviations. The positive effect of synthetic inertia on frequency stability has already been proven in several other studies [34,35]. The simulations above confirm these findings. In particular, the use of grid-forming converters and their positive effect on frequency stability has been shown already [20]. The simulations performed in this paper allow to compare the effectiveness of the approaches of passive- and active synthetic inertia. With increasing starting time constant, the effect of passive synthetic inertia increases, while the effect of active synthetic inertia is already saturated at small values of the starting time constant. Figure 11 shows that the reason lies in the influence of synthetic inertia on the RoCoF. In case of active synthetic inertia, the minimum of the RoCoF is reached already at very small values of the starting time constant, whereas in case of passive synthetic inertia the RoCoF continuously decreases further with increasing value of the starting time constant. Therefore, the inevitable delay due to filtering methods in case of passive synthetic inertia can be compensated somewhat by choosing a higher starting time constant. A direct comparison of a grid-following and a grid-forming approach has also been carried out in [36]. The results in [36] show a larger variance of the frequency nadir in case of the grid-following approach, which can be confirmed by the simulation results generated in this paper. The finding of a higher necessary starting time constant in case of passive synthetic inertia in order to reach similar frequency metrics compared to active synthetic inertia resembles the statement in [36] of a necessary higher peak power injection of grid-following converters to reach similar frequency metrics compared to grid-forming converters.

In order to ensure a flawless operation of the loads connected to a grid, certain requirements regarding power quality have to be met. One of these requirements are frequency limits within which a grid has to be operated. According to relevant power quality standards [37], even in island operation the frequency has to be kept within certain limits. The lower value for this frequency limits during island operation is 49 $\mathrm{Hz}$ [37]. Keeping in mind this requirement, Figure 10 shows that by using active synthetic inertia, load-steps of up to 500 $\mathrm{k}$$\mathrm{W}$ are possible while still remaining in the allowable frequency range. By using passive synthetic inertia, on the other hand, Figure 10 shows that only a maximum load-step of 300 $\mathrm{k}$$\mathrm{W}$ would be possible.

5. Conclusions

This paper compares two possible strategies to realize synthetic inertia in converters. The first strategy is based on a converter control that provides grid-forming character, while the second strategy relies on the measurement of the frequency in the grid and the determination of a corresponding power reference for a conventional grid-following converter control based on this frequency measurement. According to their implementation the first strategy is called “active synthetic inertia” and the second is called “passive synthetic inertia” in this paper. For both strategies a simplified converter model and converter controls corresponding to each strategy are created in MATLAB/SIMULINK. These models are used in a small Microgrid, consisting of a converter, a line and a synchronous generator with a load to investigate the behavior of the two strategies in case of a load-step in the Microgrid by simulation. A sensitivity analysis is performed where the starting time constant and the power of the load-step are varied in order to compare the influence of the two strategies on the frequency in the Microgrid. The results show that both strategies are useful for improving frequency stability, but active synthetic inertia is much more effective than passive synthetic inertia. As the implementation of active synthetic inertia requires a complex control structure it may not be possible to implement it in existing converter systems. Passive synthetic inertia on the other hand relies on the determination of a reference power, which is much easier to retrofit in existing converter systems. Both realizations of synthetic inertia therefore may be required to guarantee frequency stability in a future power system with reduced conventional system inertia. One future research goal is the implementation of the presented synthetic inertia control strategies in real converter systems. Another research goal is the investigation of a large-scale application of the presented synthetic inertia control strategies in the ENTSO-E regional group Continental Europe [38]. Assuming decreasing system inertia caused by a smaller number of conventional generators, the effects of varying shares of converter systems equipped with synthetic inertia control strategies on the frequency stability will be examined.