Total Cost of Ownership Model and Significant Cost Parameters for the Design of Electric Bus Systems
Abstract
1. Introduction
1.1. Different Types of Electric Buses
1.2. Aim of the Paper
1.3. Limitations
1.4. Structure of the Paper
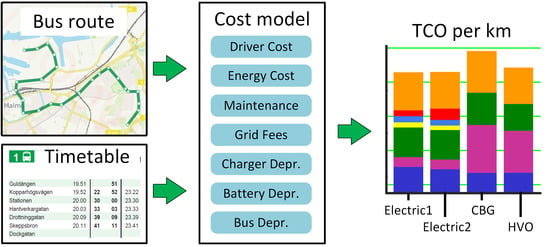
2. Model for Total Cost of Ownership
2.1. Method
2.2. Output of the Total Cost of Ownership Model
2.3. Parameters Used to Determine Total Cost of Ownership
- Driver time per year;
- Energy use per year;
- Total driven distance per year;
- Trip distance per year;
- Number of places with chargers (i.e., number of grid connections);
- Total combined power of all chargers;
- Number of chargers;
- Number of buses;
- Bus battery size.
2.4. Simplifications Aimed to Find General Trends Rather than Route-Specific Results
2.5. Cost of Conventional Combustion Engine Buses
3. Model Input Parameters and Variables
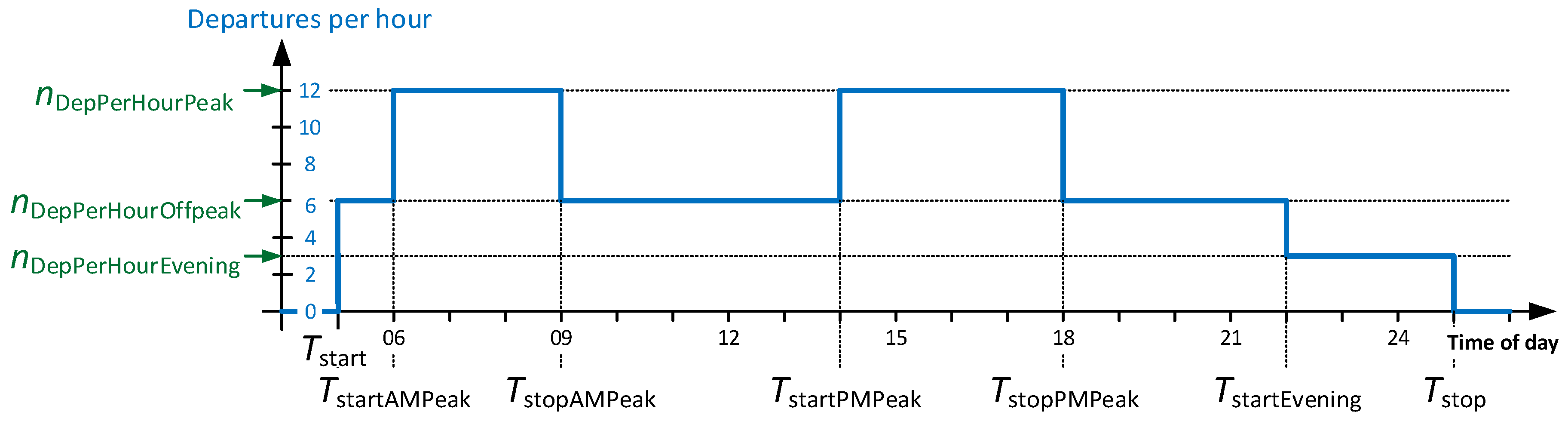
3.1. Route Variables
3.2. Timetable Variables
3.3. Bus, Driver and Battery Parameters
3.4. Electric Grid Parameters
3.5. Charger Parameters
3.6. Other Parameters
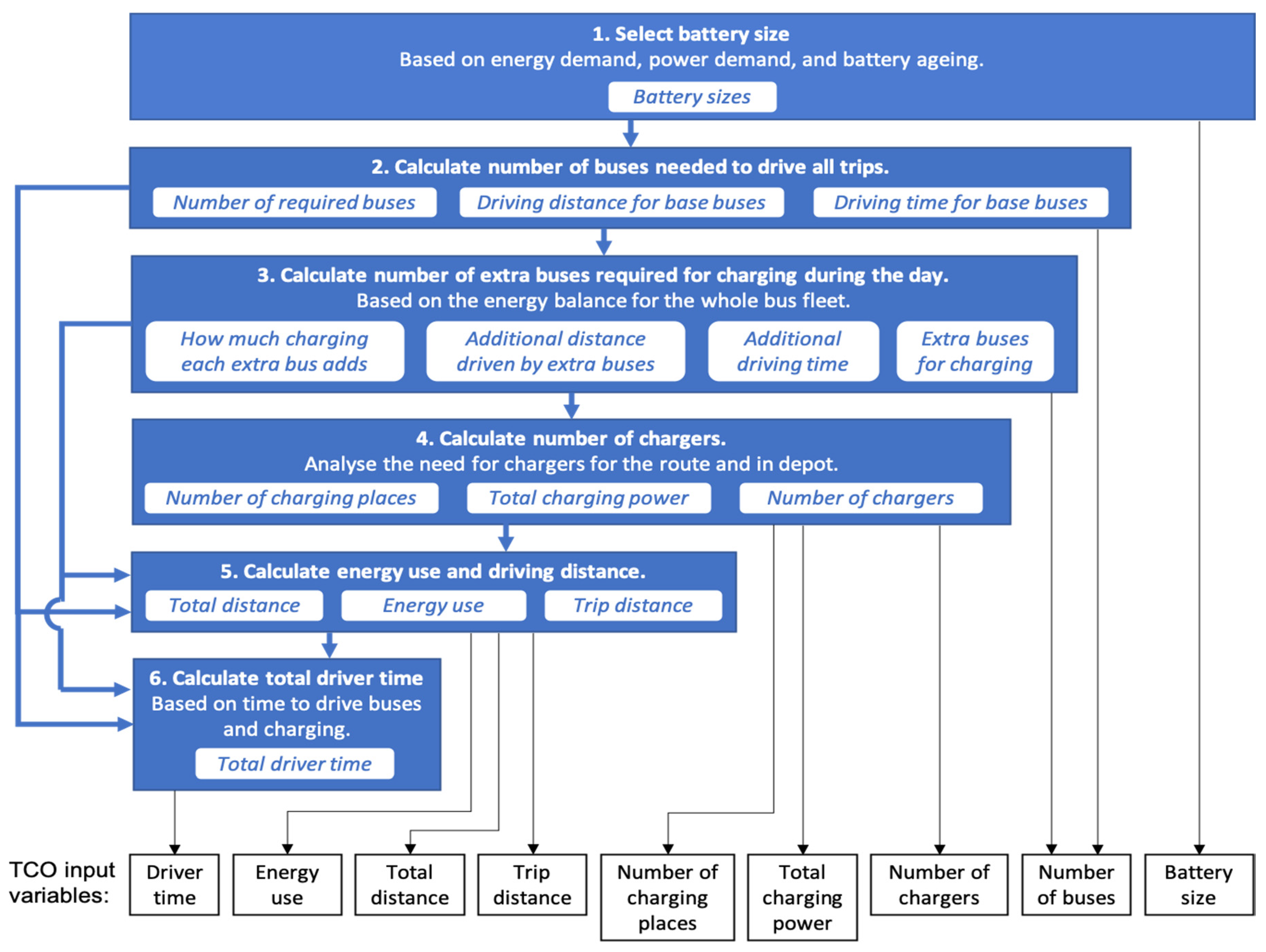
4. Calculating TCO Input Variables from Timetable and Bus Route Parameters
4.1. Battery Size and Need to Charge during the Day
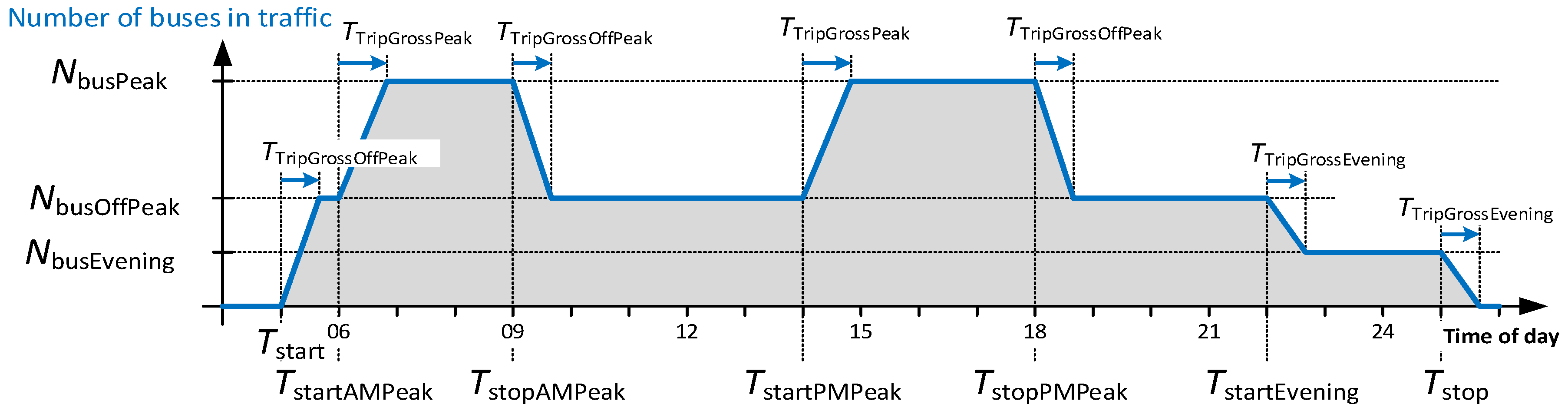
4.2. Determining the Number of Buses Needed to Drive the Trips
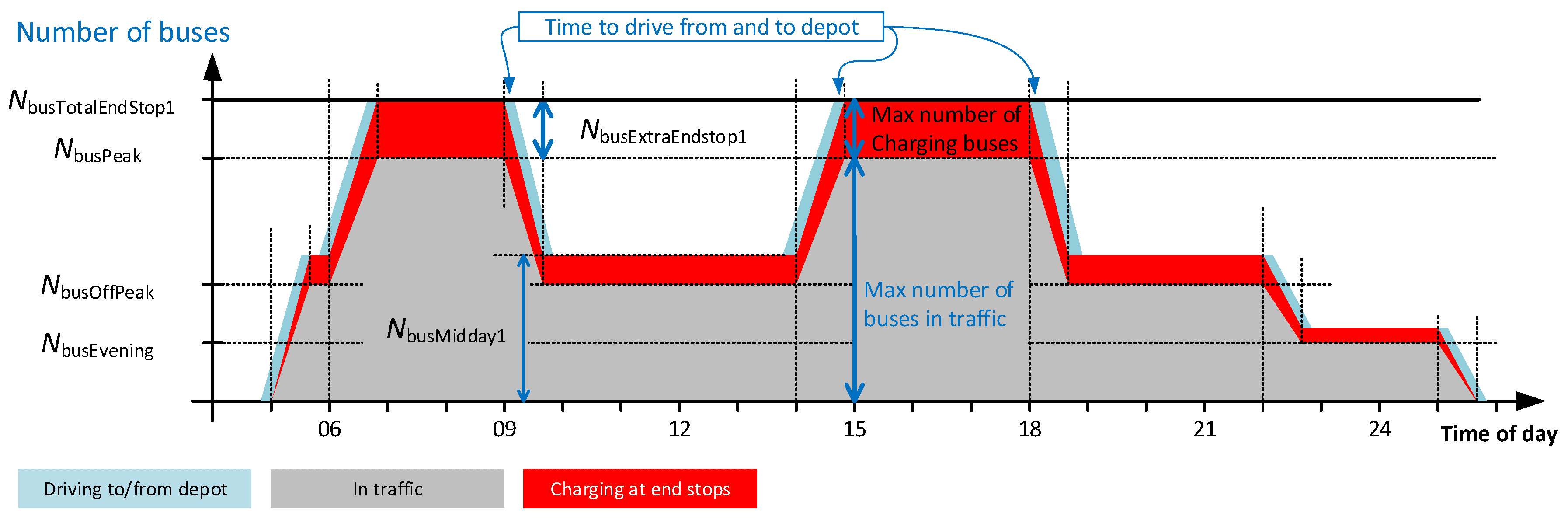
4.3. Determining the Number of Extra Buses to Provide Time to Charge
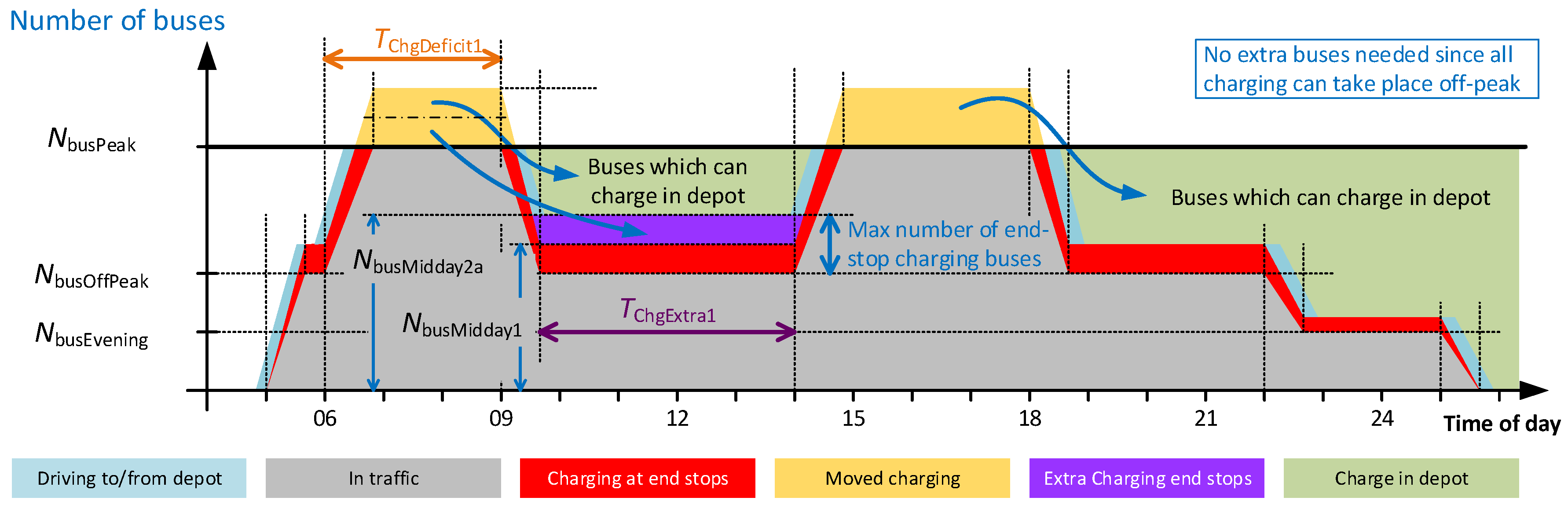
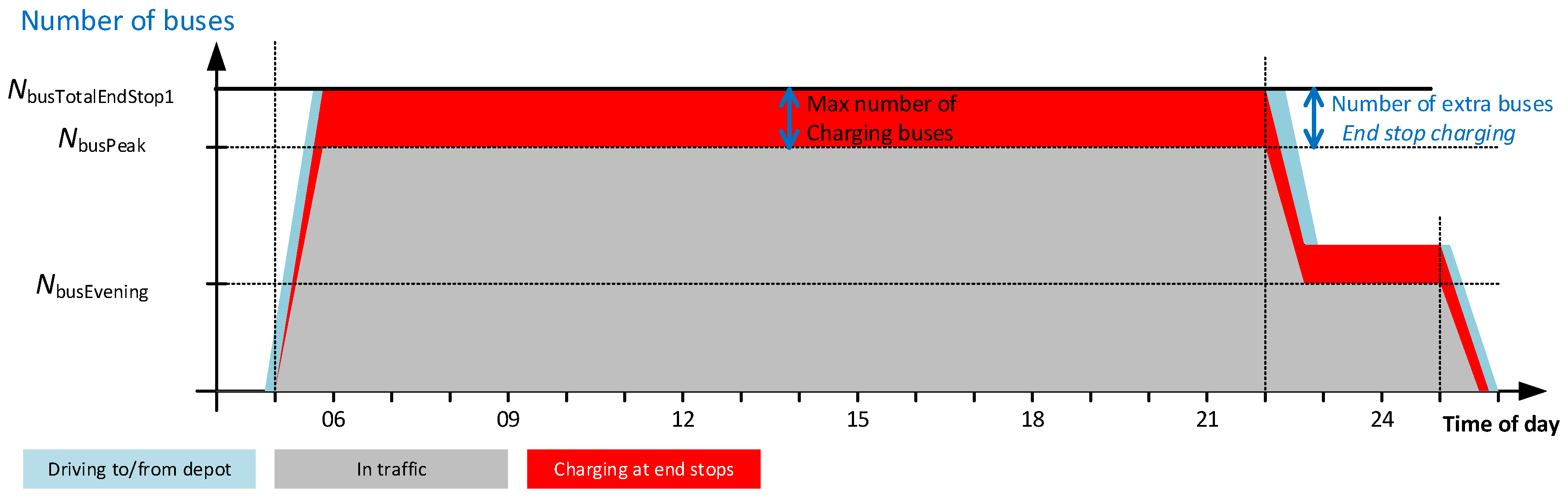
4.3.1. Extra Buses for End-Stop Charging for a Whole Day (EndStop1)
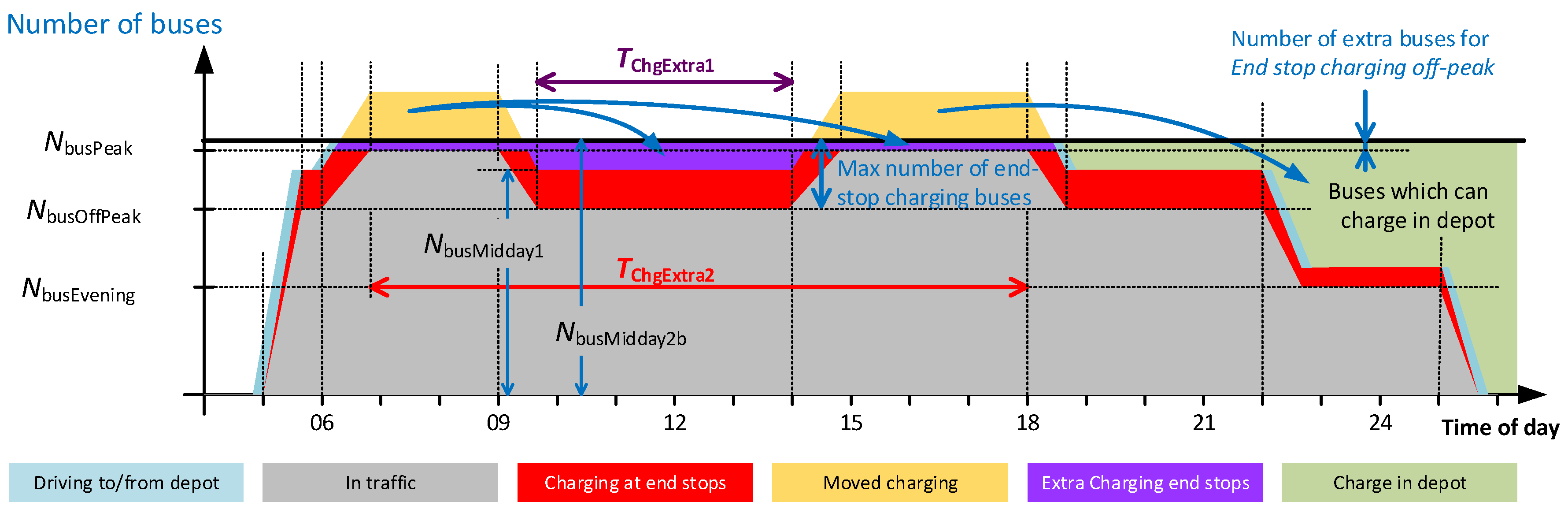
4.3.2. Extra Buses for End-Stop Charging during Off-Peak Time Only (EndStop2)
4.4. Number of Chargers
4.5. Calculating Energy Use and Driving Distance
4.6. Calculating Total Driver Time
4.7. TCO for Combustion Engine Buses
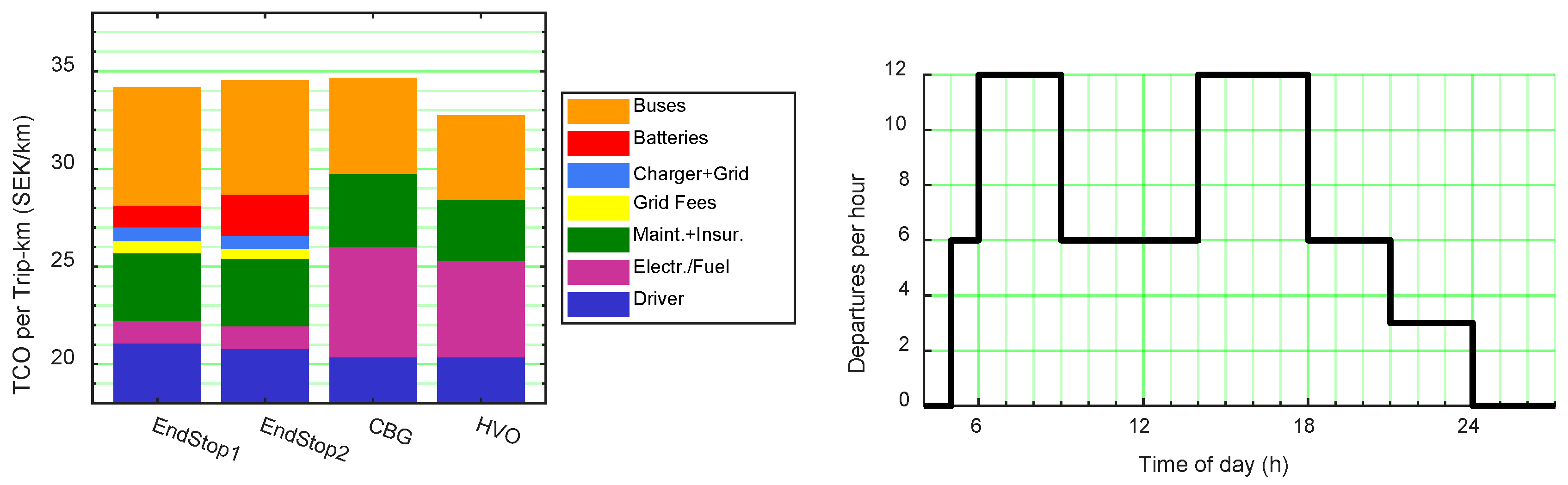
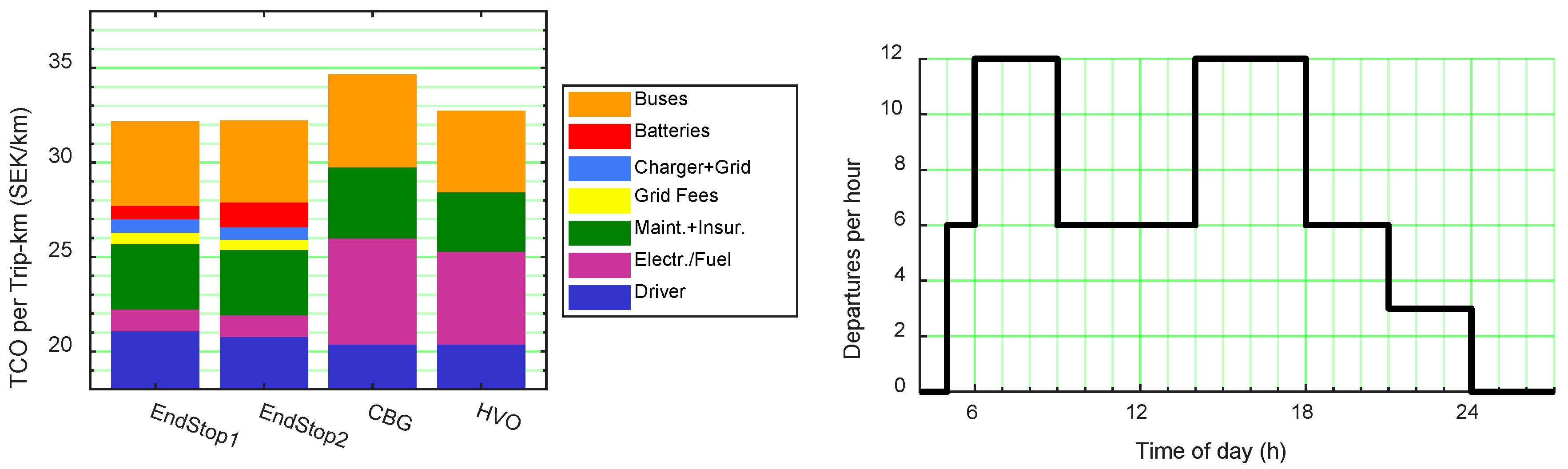
5. TCO Analysis
5.1. Cost Comparison for Different Bus Types
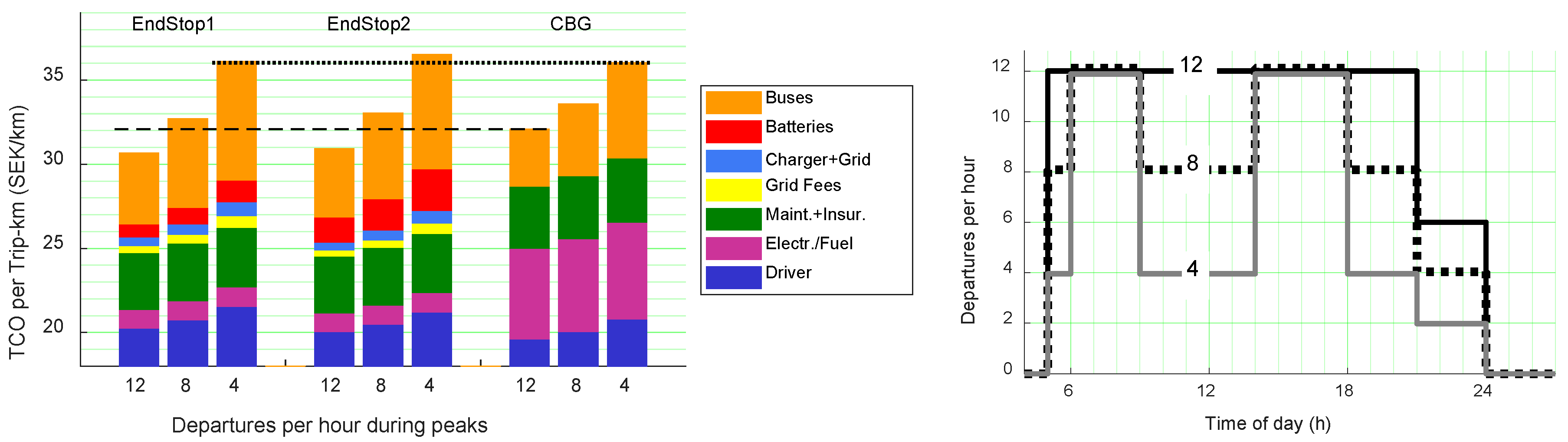
5.2. TCO Variations for Different Timetables
5.3. TCO with Future Cost Levels
6. Concluding Discussions
6.1. Main Findings
- A new model that demonstrates how to calculate the TCO for electric buses that depends on the nine most significant input variables. The calculations result in four operating and three annual depreciation cost parameters that forms the TCO.
- Testing of the method in a Swedish context from 2019 showed that the TCO for electric buses is generally in line with buses powered by biomethane and slightly higher than buses powered by HVO. However, the TCO can be both higher or lower depending on cost variations related to departures per hour, electric grid connections, the distance to the depot, and the length of the route. It is likely that future TCOs will be lower for electric buses when compared to buses powered by biomethane or HVO, mainly due to lower prices for batteries and buses and costs related to maintenance.
6.2. Critical Assessment and Comparisons with Other Studies
6.3. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Borén, S. Electric buses’ sustainability effects, noise, energy use, and costs. Int. J. Sustain. Transp. 2019, 1–16. [Google Scholar] [CrossRef]
- Johansson, T.B.; Kågesson, P.; Johansson, H.; Jonsson, L.; Westin, J.; Hejenstedt, H.; Hådell, O.; Holmgren, K.; Wollin, P. Fossilfrihet på väg; Ministry of Enterprise, SOU: Stockholm, Sweden, 2013.
- UK Department for Transport. The Road to Zero; Department of Transport: London, UK, 2018.
- BloombergNEF Electric Vehicle Outlook 2020—Executive Summary. Available online: https://bnef.turtl.co/story/evo-2020/page/1 (accessed on 2 June 2020).
- IEA. Global EV Outlook 2019; IEA: Paris, France, 2019. [Google Scholar]
- Rask, K. Allt om elbil. 2019. Available online: https://alltomelbil.se/elbilen-blir-lonsam-allt-snabbare-jamfort-med-fossilalternativ/ (accessed on 2 June 2020).
- Borén, S.; Nurhadi, L.; Ny, H. Preferences of Electric Buses in public Transport; Conclusions from Real Life Testing in Eight Swedish Municipalities. Int. J. Environ. Ecol. Eng. 2016, 10, 259–268. [Google Scholar]
- Quarles, N.; Kockelman, K.M.; Mohamed, M. Costs and Benefits of Electrifying and Automating Bus Transit Fleets. Sustainability 2020, 12, 3977. [Google Scholar] [CrossRef]
- Sheth, A.; Sarkar, D. Life cycle cost analysis for electric vs diesel bus transit in an Indian scenario. Int. J. Technol. 2019, 10, 105–115. [Google Scholar] [CrossRef]
- Topal, O.; Nakir, İ. Total Cost of Ownership Based Economic Analysis of Diesel, CNG and Electric Bus Concepts for the Public Transport in Istanbul City. Energies 2018, 11, 2369. [Google Scholar] [CrossRef]
- Moro, A.; Lonza, L. Electricity carbon intensity in European Member States: Impacts on GHG emissions of electric vehicles. Transp. Res. Part D Transp. Environ. 2018, 64, 5–14. [Google Scholar] [CrossRef] [PubMed]
- Nordelöf, A.; Romare, M.; Tivander, J. Life cycle assessment of city buses powered by electricity, hydrogenated vegetable oil or diesel. Transp. Res. Part D Transp. Environ. 2019, 75, 211–222. [Google Scholar] [CrossRef]
- Grauers, A.; Olsson, O.; Carlsson, N.; Ohlin, G.; Rosengren, L.-G. Analys av Energiförsörjning för Elektrifierade Bussystem; Chalmers University of Technology: Gothenburg, Sweden, 2016. [Google Scholar]
- Xylia, M.; Leduc, S.; Patrizio, P.; Kraxner, F.; Silveira, S. Locating charging infrastructure for electric buses in Stockholm. Transp. Res. Part C Emerg. Technol. 2017, 78, 183–200. [Google Scholar] [CrossRef]
- Borén, S.; Grauers, A. Stakeholder collaboration models for public transport procurement of electric bus systems. Int. J. Sustain. Policy Pract. 2019, 15, 19–29. [Google Scholar] [CrossRef]
- GIRO Inc. HASTUS Software. Available online: https://www.giro.ca/en-ca/our-solutions/hastus-software/ (accessed on 1 June 2020).
- Optibus Optibus—The Future of Mass Transit. Today. Available online: https://www.optibus.com (accessed on 1 June 2020).
- Automated Business Solutions PtMS for Windows. Available online: http://ptmsforwindows.com/ (accessed on 1 June 2020).
- MathWorks MATLAB. Available online: https://uk.mathworks.com/products/matlab.html (accessed on 9 June 2020).
- Nurhadi, L.; Borén, S.; Ny, H. Advancing from Efficiency to Sustainability in Swedish Medium-sized Cities: An Approach for Recommending Powertrains and Energy Carriers for Public Bus Transport Systems. Procedia-Soc. Behav. Sci. 2014, 111, 1218–1225. [Google Scholar] [CrossRef]
- Ntemiris, S.; Grauers, A. EAEB Project - Role Playing Workshop; Chalmers University of Technology: Gothenburg, Sweden, 2017. [Google Scholar]
- Mahmoud, M.; Garnett, R.; Ferguson, M.; Kanaroglou, P. Electric buses: A review of alternative powertrains. Renew. Sustain. Energy Rev. 2016, 62, 673–684. [Google Scholar] [CrossRef]
- Tong, F.; Hendrickson, C.; Biehler, A.; Jaramillo, P.; Seki, S. Life cycle ownership cost and environmental externality of alternative fuel options for transit buses. Transp. Res. Part D Transp. Environ. 2017, 57, 287–302. [Google Scholar] [CrossRef]
- Meishner, F.; Uwe Sauer, D. Technical and economic comparison of different electric bus concepts based on actual demonstrations in European cities. IET Electr. Syst. Transp. 2020, 10, 144–153. [Google Scholar] [CrossRef]




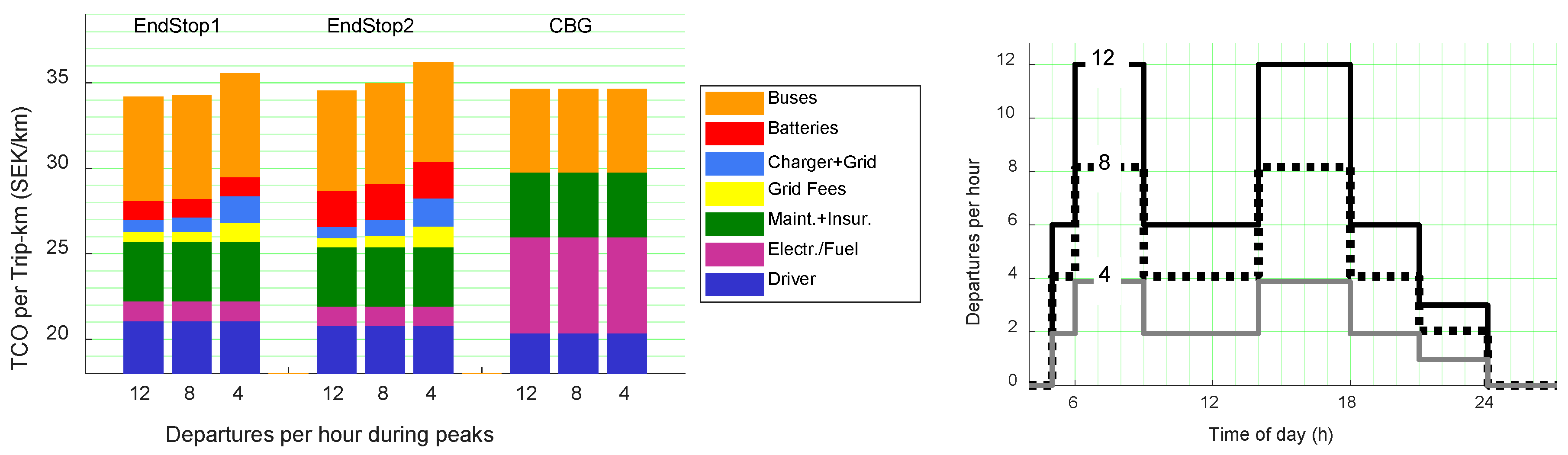
| Cost Parameters | HVO | Biomethane | Electricity | |
|---|---|---|---|---|
| End-Stop | End-Stop Off-Peak | |||
| Price (Million SEK) | 2.2 | 2.5 | 3 (excl. battery) | |
| Battery capacity (kWh) | - | - | 100 | 200 |
| Max energy used between charging (kWh) | - | - | 25 | 75 |
| Maintenance including chargers (SEK/km) | 3 | 3.6 | 3.3 | 3.3 |
| Bus Economic Life (year) | 10 | 10 | 10 | 10 |
| Battery Economic Life (year) | - | - | 7 | 7 |
| Battery Price (SEK/kWh) | - | - | 4000 | 4000 |
| Energy Cost (SEK/kWh) | 3.5 | 4 | 0.82 | 0.82 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Grauers, A.; Borén, S.; Enerbäck, O. Total Cost of Ownership Model and Significant Cost Parameters for the Design of Electric Bus Systems. Energies 2020, 13, 3262. https://doi.org/10.3390/en13123262
Grauers A, Borén S, Enerbäck O. Total Cost of Ownership Model and Significant Cost Parameters for the Design of Electric Bus Systems. Energies. 2020; 13(12):3262. https://doi.org/10.3390/en13123262
Chicago/Turabian StyleGrauers, Anders, Sven Borén, and Oscar Enerbäck. 2020. "Total Cost of Ownership Model and Significant Cost Parameters for the Design of Electric Bus Systems" Energies 13, no. 12: 3262. https://doi.org/10.3390/en13123262
APA StyleGrauers, A., Borén, S., & Enerbäck, O. (2020). Total Cost of Ownership Model and Significant Cost Parameters for the Design of Electric Bus Systems. Energies, 13(12), 3262. https://doi.org/10.3390/en13123262