Review of Dynamic Positioning Control in Maritime Microgrid Systems
Abstract
1. Introduction
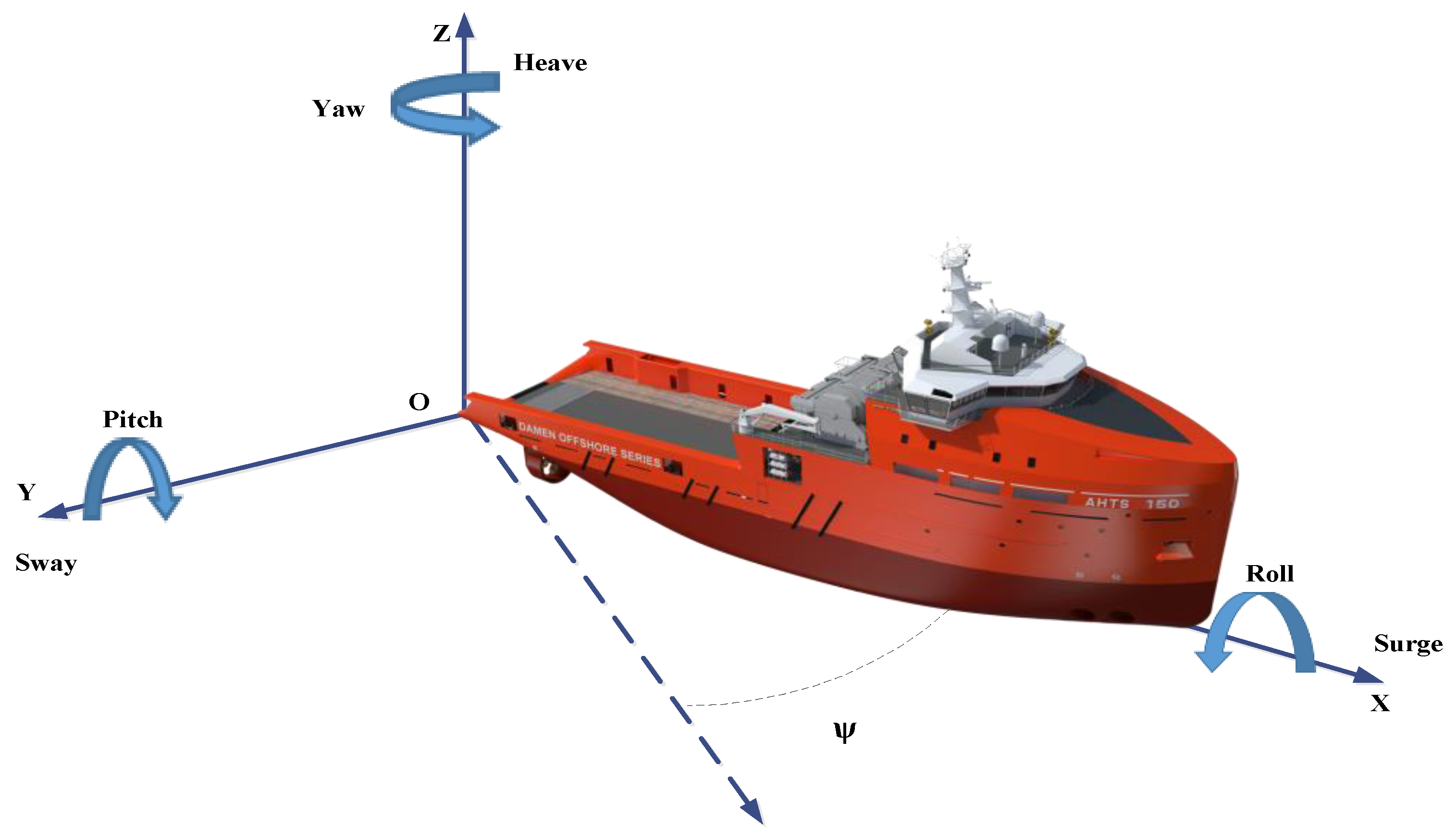
2. Marine Vessel DPS Description
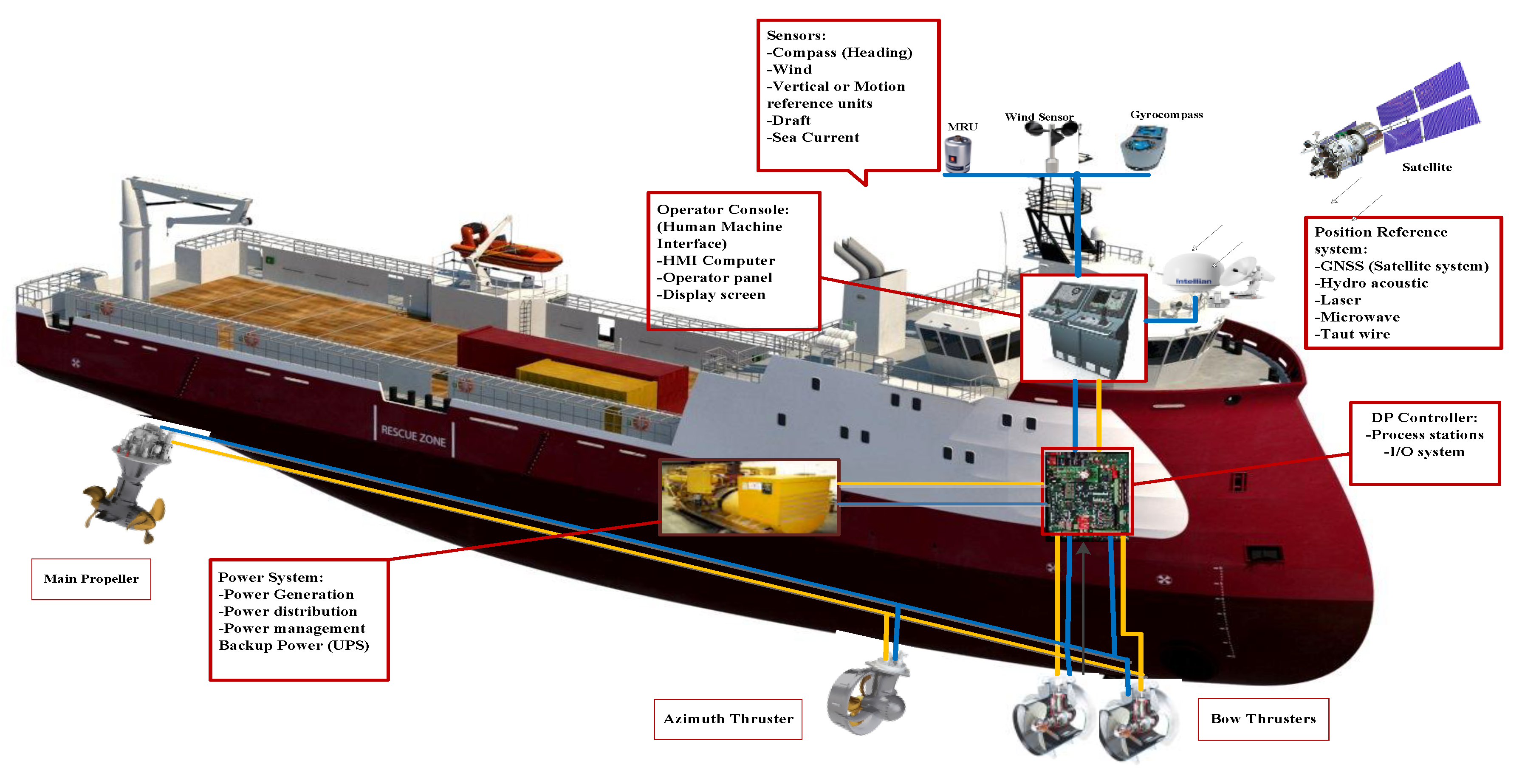
2.1. Overview of DPS Applications
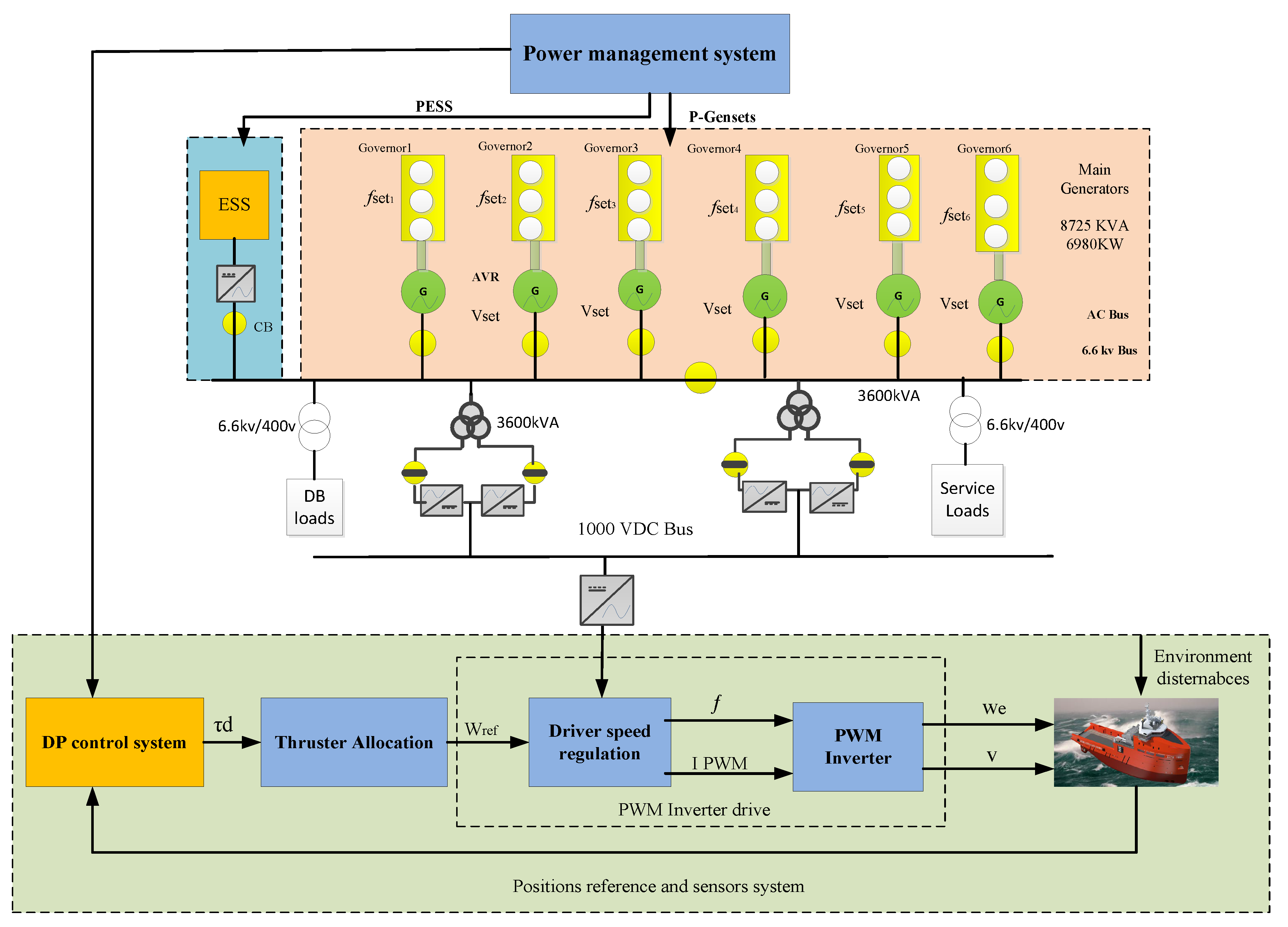
2.1.1. Power Subsystem
2.1.2. Signal Processing Subsystem
2.1.3. Sensors Subsystem
- CPU Processor/joystick systems console
- Instruments sensor units, etc.
- Station reference unit consists of:
- -
- Navigation system
- -
- Acoustic systems
- -
- Microwave and laser systems
- -
- The interface control unit, which is used as an interface to read the thrusters, switchboard feedback signals, as well as outputting command signals from the DP system to external units.
- Observing system and operator control panels.
2.1.4. Thruster Subsystem
2.1.5. Power Management Subsystem
2.2. Dynamic Positioning Vessel Classification
- DP class 1 is not redundant and can be positioned for a particular fault.
- DP class 2 is redundant to facilitate no particular fault in the operational condition lead to system failure. Therefore, loss of vessel position does not occur due to a particular fault on the power generations, distributions, and automatic valves, etc. However, it possibly failure will happen for example in cables, pipes, manual valves as a static system.
- In vessels with DP class 3, flooding or firing occurs must also be removed in a non-system enclosure. A loss of position should not result in a sudden defeat, including the entire distillation section of the fire or the dewatering chamber.
2.3. Dynamic Positioning Mathematical Model
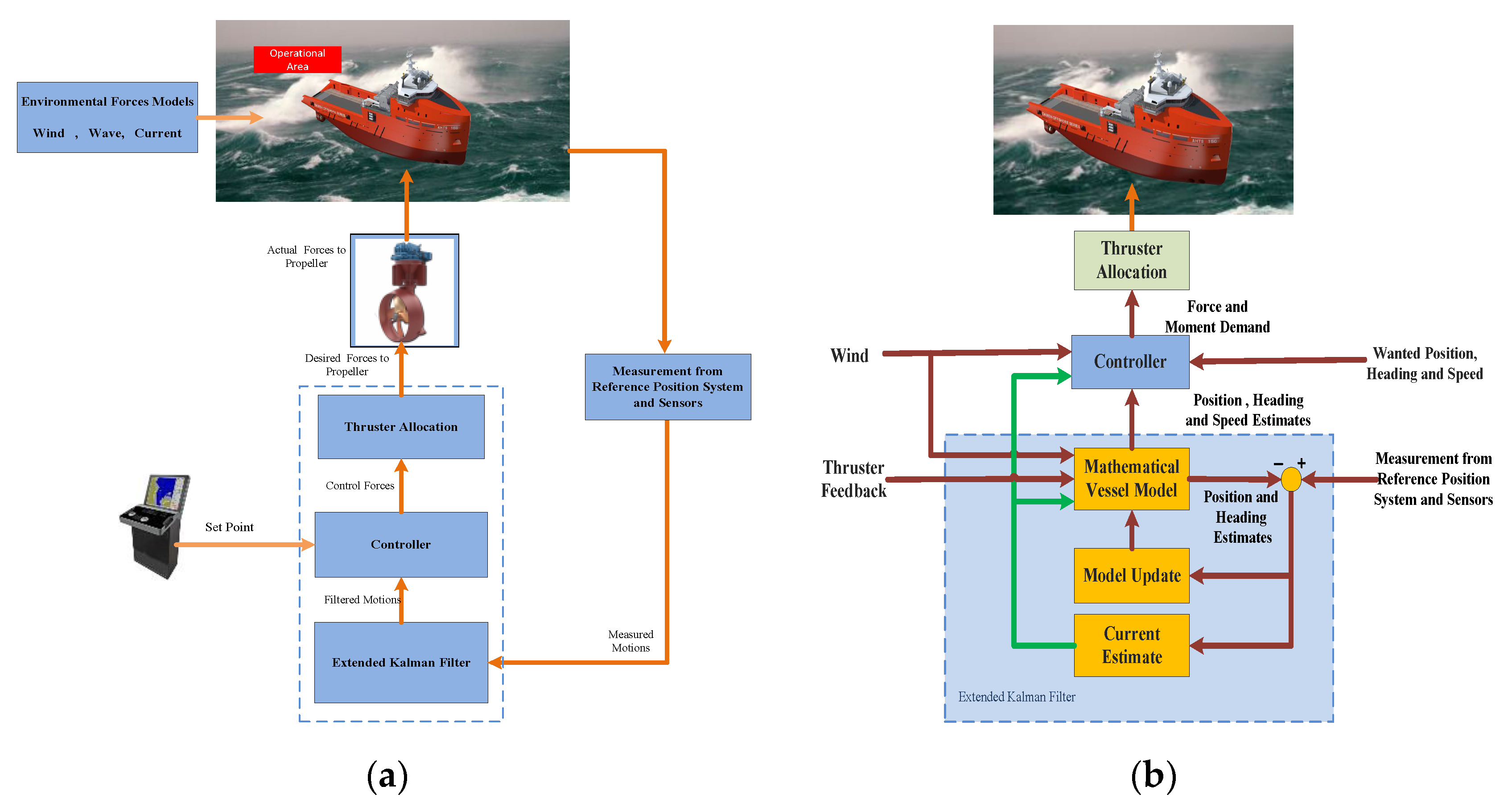
2.4. Dynamic Positioning Control Principles
3. Review of Dynamic Positioning Controls
3.1. Expanded Kalman Filter (EKF)
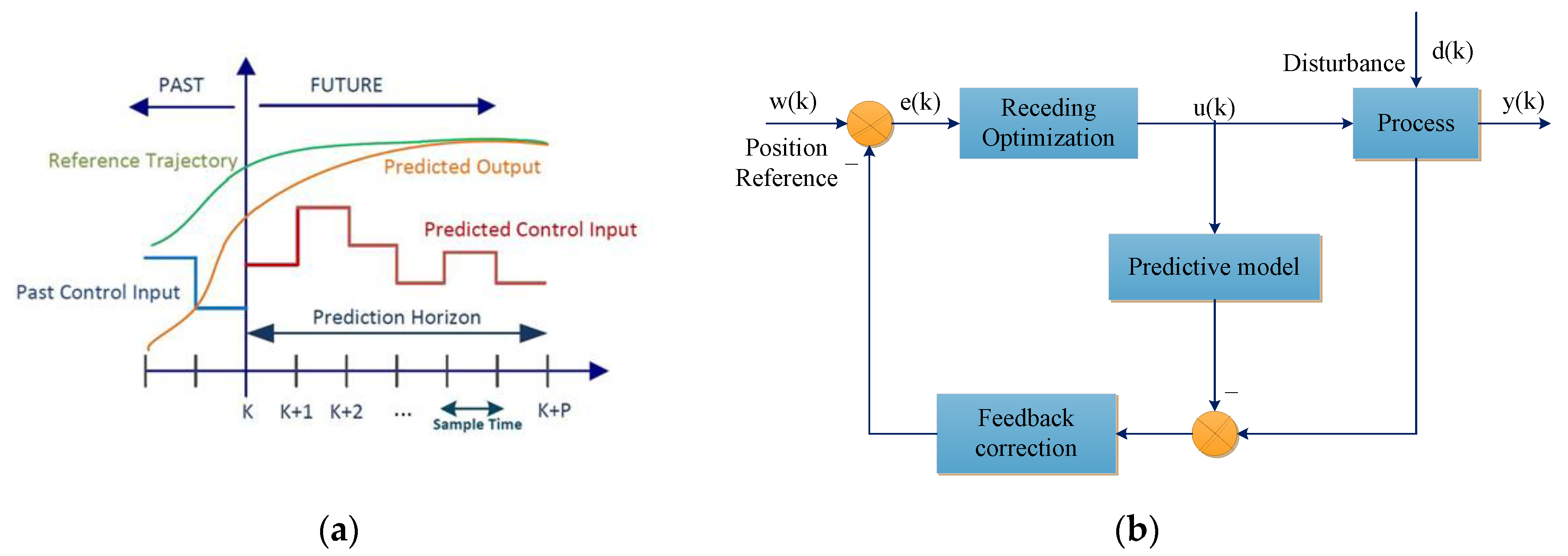
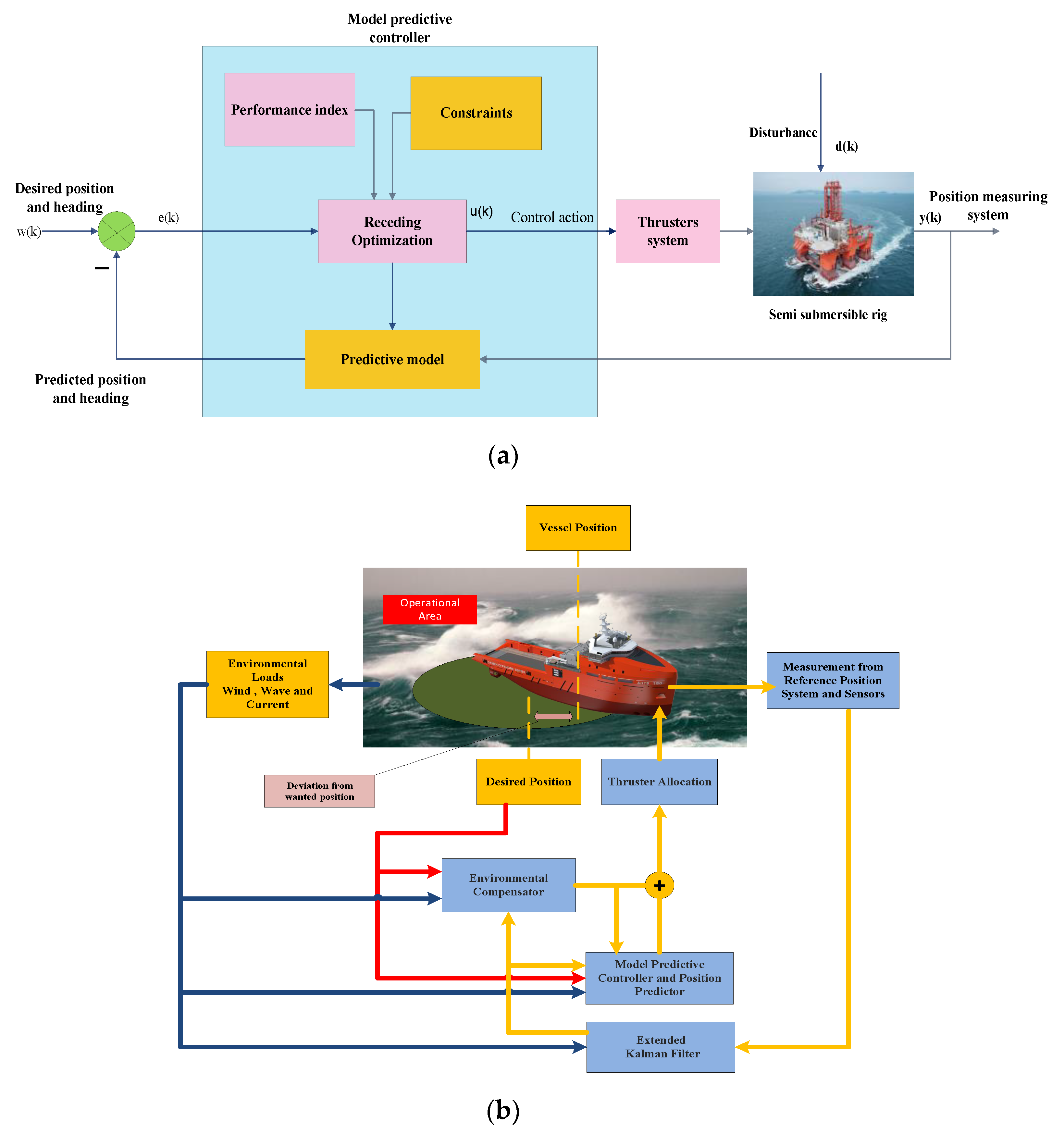
3.2. Model Predictive Control Model
- For measuring the average of environmental forces induced by the sea disturbances, the environment compensator is used to maintain the necessary position under averaged conditions.
- Predicting the current position of the ship movement as input for the MPC control. While the operational restrictions are predicted to be overcome, the controller responds to guarantee that the ship stays within the functional area. For the nonlinear predictor controller, a model is an online optimization feature that finds the best possible mix between the use of thruster and the prediction of passing through operational constraints. The position predictor includes the ship motion mathematical model used in the DP Kalman filter.
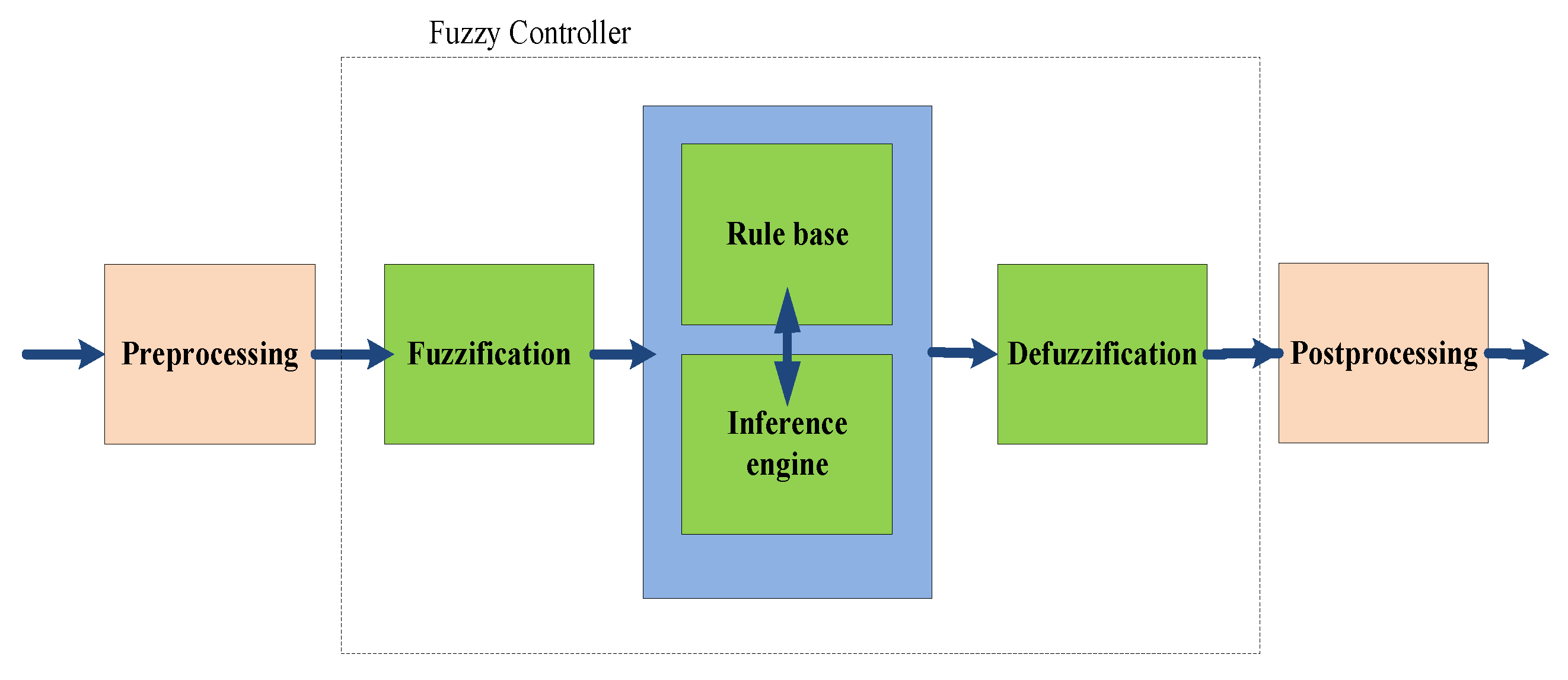
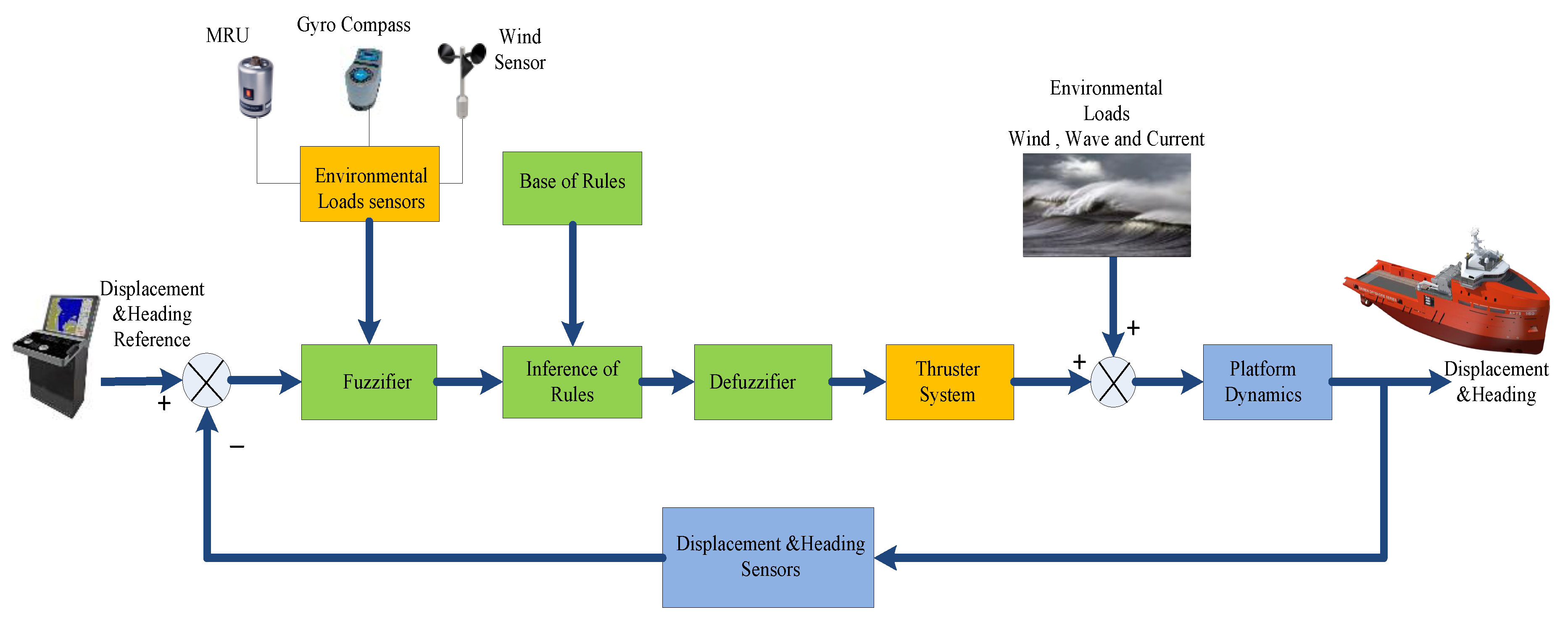
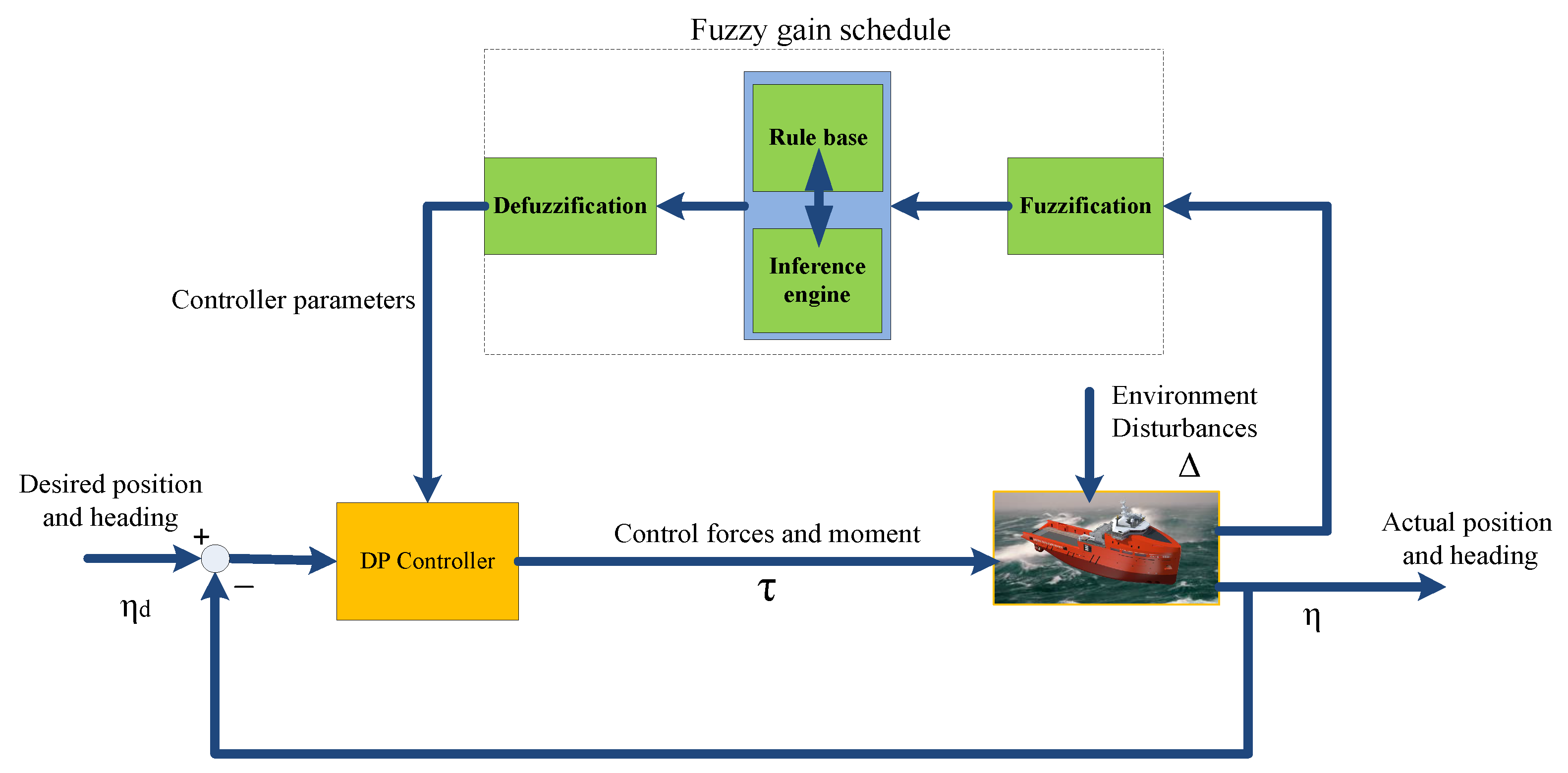
3.3. Fuzzy Logic Control Method
3.3.1. Preprocessing
- Adjusting the gradation error function as integers.
- Normalizing or scrambling to a specific standard collection.
- Clarifying due to the Removal of the noise of environmental sensors.
- Combining several measurements to achieve main indicators, variation, and integration.
3.3.2. Fuzzification and Defuzzification
3.4. Fuzzy Adaptive Control (FAC)
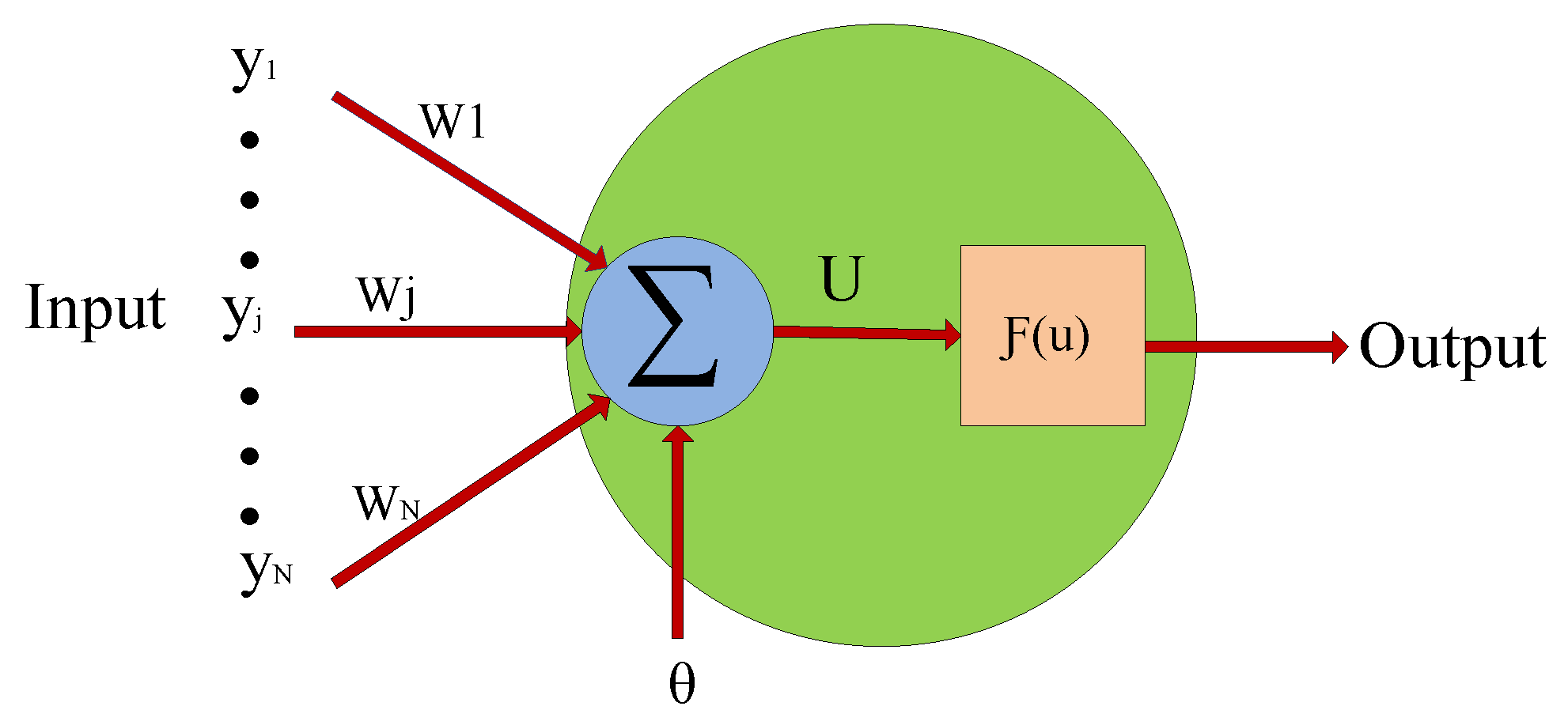
3.5. Neural Network Control Method
3.6. Neuro-Fuzzy Control Method
- To overcome the computational difficulties of the conservative BPAL method, the derivatives of the virtual control signals are found through the dynamic surface control.
- The proposed designed controller could be easily employed in practical applications with no requirement to apply the neural network and state approximations to collect model parameters.
- The prediction errors were combined with position signal errors to organize the neural network updating laws, which improves the neuron weight adjustment and tracking performance.
3.7. Adaptive Sliding Mode
4. Conclusions and Future Research
Author Contributions
Funding
Conflicts of Interest
Appendix A
| Mathematical Models | Formula | Description |
|---|---|---|
| Three degrees of freedom (3DOF), Low frequency (LF) of vessel movements [22,23] | ship velocity vector position and orientation where M is the inertial system matrix with the assumption that my plane includes mass distribution. The linear damping matrix is introduced with matrix D for LF application. The relation between and is given by 3DOF with principle rotation matrix about the z-axis, where is the swaying angle. | |
| Environmental Disturbances | The transfer function is used for simulating the wave forces and moments and passing band limit in a surface vessel in 3DOF. -This Model was introduced by Saelid [6], where he proposed the term as a damping term to develop the performance of the Pierson-Moskowitz spectrum. Beside KI is again for i = 1, 2, 3, expressive X, Y, and N. -Three different coefficients are used For generating forces () and moment () |
| Network Functions | Formula | Comments |
|---|---|---|
| Linear | frequently is used for NN activation function | |
| Higher-order exhibited | x is a weighted as linear terms of the input variable. | |
| Delta | Seldom used |
| Activation Functions | Formula a = f(x) | Derivatives | Comments |
|---|---|---|---|
| Sigmoid | Frequently uses and derivative of x as f(x) can be computed directly. | ||
| Hyperbolic tangent | T = temperature parameter | ||
| Inverse tangent | Less frequently used | ||
| Linear | a | Most commonly used |
| Control Models | Advantages | Disadvantages |
|---|---|---|
| Model predictive control include Extended Kalman filters [30,31,32,33,34,35] |
|
|
| Neuro-PD controller [21] |
|
|
| Adaptive neural networks controller [22,89,90] |
|
|
| Neuro-Fuzzy controller [21,23] |
|
|
| Fuzzy controller [62,63,64,65,66,67,68,69,70,71,72,73,74,75,76,77,78,79] |
|
|
| Adaptive fuzzy controller (AFC) [15,16,17,18,19,20] |
|
|
| PID controller [2,24,25,26,27,28,29] |
|
|
References
- Grimble, M.J.; Patton, R.J.; Wise, D.A. The design of dynamic ship positioning control systems using stochastic optimal control theory. Optim. Control Appl. Methods 1980, 1, 167–202. [Google Scholar] [CrossRef]
- Fossen, T.I. A survey on nonlinear ship control: From theory to practice. IFAC Proc. Vol. 2000, 33, 1–16. [Google Scholar] [CrossRef]
- Grimble, M.; Patton, R.; Wise, D. The design of dynamic ship positioning control systems using extended Lalman filtering techniques. In Proceedings of the OCEANS ’79, San Diego, CA, USA, 17–19 September 1979; pp. 488–497. [Google Scholar]
- Balchen, J.; Jenssen, N.; Mathisen, E.; Saelid, S. Dynamic positioning of floating vessels based on Kalman filtering and optimal control. In Proceedings of the 19th IEEE Conference on Decision and Control including the Symposium on Adaptive Processes, Albuquerque, NM, USA, 10–12 December 1980; pp. 852–864. [Google Scholar]
- Grimble, M.J.; Patton, R.J.; Wise, D.A. Use of Kalman filtering techniques in dynamic ship-positioning systems. IEE Proc. D Control Theory Appl. 1980, 127, 93–102. [Google Scholar] [CrossRef]
- Saelid, S.; Jenssen, N.; Balchen, J. Design and analysis of a dynamic positioning system based on Kalman filtering and optimal control. IEEE Trans. Autom. Control 1983, 28, 331–339. [Google Scholar] [CrossRef]
- Balchen, J.G.; Jenssen, N.A.; Sælid, S. Dynamic positioning using Kalman filtering and optimal control theory. Autom. Offshore Oil Field Oper. 1976, 183, 186. [Google Scholar]
- Fossen, T.I.; Grovlen, A. Nonlinear output feedback control of dynamically positioned ships using vectorial observer backstepping. IEEE Trans. Control Syst. Technol. 1998, 6, 121–128. [Google Scholar] [CrossRef]
- Fossen, T.I.; Strand, J.P. Passive nonlinear observer design for ships using lyapunov methods: Full-scale experiments with a supply vessel. Automatica 1999, 35, 3–16. [Google Scholar] [CrossRef]
- Loria, A.; Fossen, T.I.; Panteley, E. A separation principle for dynamic positioning of ships: Theoretical and experimental results. IEEE Trans. Control Syst. Technol. 2000, 8, 332–343. [Google Scholar] [CrossRef]
- Hu, X.; Du, J.; Li, J.; Sun, Y. Asymptotic regulation of dynamically positioned vessels with unknown dynamics and external disturbances. J. Navig. 2020, 73, 253–266. [Google Scholar] [CrossRef]
- Fossen, T.I.; Paulsen, M.J. Adaptive feedback linearization applied to steering of ships. In Proceedings of the IEEE Conference on Control Applications, Dayton, OH, USA, 13–16 September 1992; pp. 1088–1093. [Google Scholar]
- Candeloro, M.; Sørensen, A.J.; Longhi, S.; Dukan, F. Observers for dynamic positioning of ROVs with experimental results. IFAC 2012, 45, 85–90. [Google Scholar] [CrossRef]
- Yamamoto, M.; Morooka, C.K. Dynamic positioning system of the semi-submersible platform using fuzzy control. J. Braz. Soc. Mech. Sci. Eng. 2005, 27, 449–455. [Google Scholar] [CrossRef]
- Hu, X.; Du, J.; Shi, J. Adaptive fuzzy controller design for dynamic positioning system of vessels. Appl. Ocean Res. 2015, 53, 46–53. [Google Scholar] [CrossRef]
- Tao, W.; Shaocheng, T. Adaptive fuzzy robust control for nonlinear system with dynamic uncertainties based on backstepping. In Proceedings of the International Conference on Innovative Computing Information and Control, Dalian, Liaoning, China, 18–20 June 2008. [Google Scholar]
- Stephens, R.I.; Burnham, K.J.; Reeve, P.J. A practical approach to the design of fuzzy controllers with application to dynamic ship positioning. IFAC Proc. Vol. 1995, 28, 370–377. [Google Scholar] [CrossRef]
- He, H.; Xu, S.; Wang, L.; Li, B. Mitigating surge–pitch coupled motion by a novel adaptive fuzzy damping controller for a semisubmersible platform. J. Mar. Sci. Technol. 2020, 25, 234–248. [Google Scholar] [CrossRef]
- Wang, Y.; Zhang, X.; Fu, Y.; Ding, F.; Fu, M.; Wang, C. Adaptive Fuzzy Sliding Mode Controller for Dynamic Positioning of FPSO Vessels. In Proceedings of the OCEANS 2019-Marseille, Marseille, France, 17–20 June 2019; pp. 1–7. [Google Scholar]
- Fang, M.C.; Lee, Z.Y. Application of neuro-fuzzy algorithm to a portable dynamic positioning control system for ships. Int. J. Nav. Archit. Ocean Eng. 2016, 8, 38–52. [Google Scholar] [CrossRef]
- Jang, J.S.; Sun, C.T. Neuro-fuzzy modeling and control. Proc. IEEE 1995, 83, 378–406. [Google Scholar] [CrossRef]
- Zhang, D.; Ashraf, M.A.; Liu, Z.; Peng, W.X.; Golkar, M.J.; Mosavi, A. Dynamic modeling and adaptive controlling in GPS-intelligent buoy (GIB) systems based on neural-fuzzy networks. Ad Hoc Netw. 2020, 103, 102149. [Google Scholar] [CrossRef]
- Du, J.; Yang, Y.; Wang, D.; Guo, C. A robust adaptive neural networks controller for maritime dynamic positioning system. Neurocomputing 2013, 110, 128–136. [Google Scholar] [CrossRef]
- Sørensen, A.J. A survey of dynamic positioning control systems. Annu. Rev. Control 2011, 35, 123–136. [Google Scholar] [CrossRef]
- Nguyen, T.D.; Sørensen, A.J.; Quek, S.T. Design of hybrid controller for dynamic positioning from calm to extreme sea conditions. Automatica 2007, 43, 768–785. [Google Scholar] [CrossRef]
- Fossen, T.I. Handbook of Marine Craft Hydrodynamics and Motion Control. IEEE Control Syst. 2016, 36, 78–79. [Google Scholar]
- Ambrosovskaya, M.E. Design and control session approach for advanced testing of DP control system. In Proceedings of the MTS DP Conference, Houston, TX, USA, 14–15 October 2014. [Google Scholar]
- Donnarumma, S.; Figari, M.; Martelli, M.; Vignolo, S.; Viviani, M. Design and validation of dynamic positioning for marine systems: A case study. IEEE J. Ocean. Eng. 2018, 43, 677–688. [Google Scholar] [CrossRef]
- Dynamic Positioning System, Dual Redundant-K-Pos DP-21/22-Kongsberg Maritime. Available online: https://www.km.kongsberg.com/ks/web/nokbg0240.nsf/AllWeb/A18DA50D246AC221C1256A46002D6505?OpenDocument (accessed on 25 December 2018).
- Sotnikova, M.V.; Veremey, E.I. Dynamic positioning based on nonlinear MPC. IFAC Proc. Vol. 2013, 46, 37–42. [Google Scholar] [CrossRef]
- Veksler, A.; Johansen, T.A.; Borrelli, F.; Realfsen, B. Dynamic positioning with model predictive control. IEEE Trans. Control Syst. Technol. 2016, 24, 1340–1353. [Google Scholar] [CrossRef]
- Zheng, H.; Negenborn, R.R.; Lodewijks, G. Trajectory tracking of autonomous vessels using model predictive control. IFAC Proc. Vol. 2014, 47, 8812–8818. [Google Scholar] [CrossRef]
- Yan, Z.; Wang, J. Model predictive control for tracking of under actuated vessels based on recurrent neural networks. IEEE J. Ocean. Eng. 2012, 37, 717–726. [Google Scholar] [CrossRef]
- Chen, H.; Wan, L.; Wang, F.; Zhang, G. Model predictive controller design for the dynamic positioning system of a semi-submersible platform. J. Mar. Sci. Appl. 2012, 11, 361–367. [Google Scholar] [CrossRef]
- Zheng, H.; Wu, J.; Wu, W.; Zhang, Y. Robust dynamic positioning of autonomous surface vessels with tube-based model predictive control. Ocean Eng. 2020, 199, 106820. [Google Scholar] [CrossRef]
- Kanellos, F.; Anvari-Moghaddam, A.; Guerrero, J. Smart shipboard power system operation and management. Inventions 2016, 1, 22. [Google Scholar] [CrossRef]
- Zahedi, B.; Norum, L.E.; Ludvigsen, K.B. Optimized efficiency of all-electric ships by dc hybrid power systems. J. Power Sources 2014, 255, 341–354. [Google Scholar] [CrossRef]
- Veksler, A.; Johansen, T.A.; Skjetne, R. Transient power control in dynamic positioning-governor feedforward and dynamic thrust allocation. IFAC Proc. Vol. 2012, 45, 158–163. [Google Scholar] [CrossRef]
- Johansen, T.A.; Bo, T.I.; Mathiesen, E.; Veksler, A.; Sorensen, A.J. Dynamic positioning system as dynamic energy storage on diesel-electric ships. IEEE Trans. Power Syst. 2014, 29, 3086–3091. [Google Scholar] [CrossRef]
- Veksler, A.; Johansen, T.A.; Skjetne, R.; Mathiesen, E. Thrust allocation with dynamic power consumption modulation for diesel-electric ships. IEEE Trans. Control Syst. Technol. 2016, 24, 578–593. [Google Scholar] [CrossRef]
- Veksler, A.; Johansen, T.A.; Skjetne, R.; Mathiesen, E. Reducing power transients in diesel-electric dynamically positioned ships using re-positioning. In Proceedings of the IEEE IECON Conference, Dallas, TX, USA, 29 October–1 November 2014; pp. 268–273. [Google Scholar]
- Veksler, A.; Johansen, T.A.; Skjetne, R. Thrust allocation with power management functionality on dynamically positioned vessels. In Proceedings of the American Control Conference, Montreal, QC, Canada, 27–29 June 2012; pp. 1468–1475. [Google Scholar]
- Sorensen, A.J.; Skjetne, R.; Bo, T.; Miyazaki, M.R.; Johansen, T.A.; Utne, I.B.; Pedersen, E. Toward safer, smarter, and greener ships: Using hybrid marine power plants. IEEE Electrif. Mag. 2017, 5, 68–73. [Google Scholar] [CrossRef]
- Skjong, E.; Johansen, T.A.; Molinas, M.; Sorensen, A.J. Approaches to economic energy management in diesel-electric marine vessels. IEEE Trans. Transp. Electrif. 2017, 3, 22–35. [Google Scholar] [CrossRef]
- Kanellos, F.D. Optimal power management with GHG emissions limitation in all-electric ship power systems comprising energy storage systems. IEEE Trans. Power Syst. 2014, 29, 330–339. [Google Scholar] [CrossRef]
- Geertsma, R.D.; Negenborn, R.R.; Visser, K.; Hopman, J.J. Design and control of hybrid power and propulsion systems for smart ships: A review of developments. Appl. Energy 2017, 194, 30–54. [Google Scholar] [CrossRef]
- Radan, D.; Johansen, T.A.; Sørensen, A.J.; Ådnanes, A.K. Optimization of load-dependent start tables in marine power management systems with blackout prevention. WSEAS Trans. Syst. 2005, 1109–2734, 1861–1867. [Google Scholar]
- Shen, Q.; Ramachandran, B.; Srivastava, S.K.; Andrus, M.; Cartes, D.A. Power and energy management in integrated power system. In Proceedings of the 2011 IEEE Electric Ship Technologies Symposium, Alexandria, VA, USA, 10–13 April 2011; pp. 414–419. [Google Scholar]
- Morishita, H.M.; Tannuri, E.A.; Bravin, T.T. Methodology for dynamic analysis of offloading operations. Proc. IFAC CAMS 2004, 459–464. [Google Scholar] [CrossRef]
- Fossen, T.I. Guidance and Control of Ocean Vehicles; Wiley: Hoboken, NJ, USA, 1994. [Google Scholar]
- MSC/Circular. 645 Guidelines for Vessels with Dynamic Positioning Systems. Available online: https://puc.overheid.nl/nsi/doc/PUC_1730_14/ (accessed on 5 June 2020).
- Giddings, I.C. Quality Assurance Session IMO Guidelines for Vessels with Dynamic Positioning Systems. Available online: https://dynamic-positioning.com/proceedings/dp2013/quality_giddings_pp.pdf (accessed on 16 October 2013).
- DNV GL Rules for Classification: Ships-January 2017-DNV GL. Available online: https://www.dnvgl.com/news/dnv-gl-rules-for-classification-ships-january-2017–84330 (accessed on 1 January 2017).
- DNV-GL Rules. Rules for Classification of Ships-Dynamic Positioning System-Enhanced Reliability; DNV-GL Rules: Oslo, Norway, 2016. [Google Scholar]
- Balchen, J.G.; Jenssen, N.A.; Mathisen, E.; Sælid, S. A dynamic positioning system based on Kalman filtering and optimal control. Modeling Identif. Control 1980, 1, 135–163. [Google Scholar] [CrossRef]
- Reid, R.; Tugcu, A.; Mears, B. The use of wave filter design in Kalman filter state estimation of the automatic steering problem of a tanker in a seaway. IEEE Trans. Autom. Control 1984, 29, 577–584. [Google Scholar] [CrossRef]
- Fossen, T.I.; Perez, T. Kalman filtering for positioning and heading control of ships and offshore rigs. IEEE Control Syst. 2009, 29, 32–46. [Google Scholar]
- Sørensen, A.J.; Sagatun, S.I.; Fossen, T.I. Design of a dynamic positioning system using model-based control. Control Eng. Pract. 1996, 4, 359–368. [Google Scholar] [CrossRef]
- Fung, P.; Grimble, M. Dynamic ship positioning using a self-tuning Kalman filter. IEEE Trans. Autom. Control 1983, 28, 339–350. [Google Scholar] [CrossRef]
- Morari, M.; Lee, J.H. Model predictive control: Past, present and future. Comput. Chem. Eng. 1999, 23, 667–682. [Google Scholar] [CrossRef]
- Mayne, D.Q.; Rawlings, J.B.; Rao, C.V.; Scokaert, P.O.M. Constrained model predictive control: Stability and optimality. Automatica 2000, 36, 789–814. [Google Scholar] [CrossRef]
- Baaklini, N.; Mamdani, E.H. Prescriptive methods for deriving control policy in a fuzzy-logic controller. Electron. Lett. 1975, 11, 625–626. [Google Scholar]
- Golea, N.; Golea, A.; Barra, K.; Bouktir, T. Observer-based adaptive control of robot manipulators: Fuzzy systems approach. Appl. Soft Comput. 2008, 8, 778–787. [Google Scholar] [CrossRef]
- Lee, C.C. Fuzzy logic in control systems: Fuzzy logic controller-Part I. IEEE Trans. Syst. Man Cybern. 1990, 20, 404–418. [Google Scholar] [CrossRef]
- Lee, C.C. Fuzzy logic in control systems: Fuzzy logic controller-Part II. IEEE Trans. Syst. Man Cybern. 1990, 20, 419–435. [Google Scholar] [CrossRef]
- Ross, T.J. Fuzzy Logic with Engineering Applications; John Wiley: Hoboken, NJ, USA, 2004. [Google Scholar]
- Xu, S.; Wang, X.; Yang, J.; Wang, L. A fuzzy rule-based PID controller for dynamic positioning of vessels in variable environmental disturbances. J. Mar. Sci. Technol. 2019. [Google Scholar] [CrossRef]
- Chen, B.S.; Tseng, C.S.; Uang, H.J. Robustness design of nonlinear dynamic systems via fuzzy linear control. IEEE Trans. Fuzzy Syst. 1999, 1, 571–585. [Google Scholar] [CrossRef]
- Ishaque, K.; Abdullah, S.S.; Ayob, S.M.; Salam, Z. A simplified approach to design fuzzy logic controller for an underwater vehicle. Ocean Eng. 2011, 38, 271–284. [Google Scholar] [CrossRef]
- Chang, W.J.; Chen, G.J.; Yeh, Y.L. Fuzzy control of dynamic positioning systems for ships. J. Mar. Sci. Technol. 2002, 10, 47–53. [Google Scholar]
- Do, V.D.; Dang, X.K.; Ho, L.A.H. Enhancing quality of the dynamic positioning system for supply vessel under unexpected impact based on fuzzy Takagi-Sugeno algorithm. J. Mar. Sci. Technol. 2017, 51, 92–95. [Google Scholar]
- Chen, X.T.; Tan, W.W. A type-2 fuzzy logic controller for dynamic positioning systems. In Proceedings of the 8th IEEE International Conference on Control and Automation, Xiamen, China, 9–11 June 2010; pp. 1013–1018. [Google Scholar]
- Ho, W.H.; Chen, S.H.; Chou, J.H. Optimal control of Takagi-Sugeno fuzzy-model-based systems representing dynamic ship positioning systems. Appl. Soft Comput. 2013, 13, 3197–3210. [Google Scholar] [CrossRef]
- Lee, T.H.; Cao, Y.; Lin, Y.M. Dynamic positioning of drilling vessels with a fuzzy logic controller. Int. J. Syst. Sci. 2002, 33, 979–993. [Google Scholar] [CrossRef]
- Amjad, M.; Ishaque, K.; Abdullah, S.S.; Salam, Z. An alternative approach to design a Fuzzy Logic Controller for an autonomous underwater vehicle. In Proceedings of the 2010 IEEE Conference on Cybernetics and Intelligent Systems, Singapore, 28–30 June 2010; pp. 195–200. [Google Scholar]
- Zheng, M.; Zhou, Y.; Yang, S. Robust fuzzy sampled-data control for dynamic positioning ships. J. Shanghai Jiaotong Univ. 2018, 23, 209–217. [Google Scholar] [CrossRef]
- Do, V.D.; Dang, X.K. The fuzzy particle swarm optimization algorithm design for dynamic positioning system under unexpected impacts. J. Mech. Eng. Sci. 2019, 13, 5407–5423. [Google Scholar]
- Do, V.D.; Dang, X.K.; Huynh, L.T.; Ho, V.C. Optimized Multi-cascade Fuzzy Model for Ship Dynamic Positioning System Based on Genetic Algorithm. In International Conference on Industrial Networks and Intelligent Systems; Springer: Ho Chi Minh City, Vietnam, August 2019; Volume 293. [Google Scholar]
- Xie, W.; Han, Z.; Wu, F.; Zhu, S. H∞ observer–controller synthesis approach in low frequency for T–S fuzzy systems. IET Control Theory Appl. 2020, 14, 738–749. [Google Scholar] [CrossRef]
- Hunt, K.J.; Sbarbaro, D.; Żbikowski, R.; Gawthrop, P.J. Neural networks for control systems—A survey. Automatica 1992, 28, 1083–1112. [Google Scholar] [CrossRef]
- Kalogirou, S.A. Artificial neural networks in renewable energy systems applications: A review. Renew. Sustain. Energy Rev. 2001, 5, 373–401. [Google Scholar] [CrossRef]
- Willis, M.J.; Montague, G.A.; di Massimo, C.; Tham, M.T.; Morris, A.J. Artificial neural networks in process estimation and control. Automatica 1992, 28, 1181–1187. [Google Scholar] [CrossRef]
- Jain, A.K.; Mao, J.; Mohiuddin, K.M. Artificial neural networks: A tutorial. Computer 1996, 29, 31–44. [Google Scholar] [CrossRef]
- Nguyen, D.H.; Widrow, B. Neural networks for self-learning control systems. IEEE Control Syst. Mag. 1990, 10, 18–23. [Google Scholar] [CrossRef]
- Fang, M.C.; Yi, L.Z. Portable dynamic positioning control system on a barge in short-crested waves using the neural network algorithm. China Ocean Eng. 2013, 27, 469–480. [Google Scholar] [CrossRef]
- Chen, F.-C. Back-propagation neural networks for nonlinear self-tuning adaptive control. IEEE Control Syst. Mag. 1990, 10, 44–48. [Google Scholar] [CrossRef]
- Goh, A.T.C. Back-propagation neural networks for modeling complex systems. Artif. Intell. Eng. 1995, 9, 143–151. [Google Scholar] [CrossRef]
- Zhao, Z.; He, W.; Ge, S.S. Adaptive neural network control of a fully actuated marine surface vessel with multiple output constraints. IEEE Trans. Control Syst. Technol. 2013, 22, 1536–1543. [Google Scholar]
- Zhang, C.; Wang, C.; Wei, Y.; Wang, J. Neural network adaptive position tracking control of the underactuated autonomous surface vehicle. J. Mech. Sci. Technol. 2020, 34, 855–865. [Google Scholar] [CrossRef]
- Shen, Z.; Bi, Y.; Wang, Y.; Guo, C. MLP neural network-based recursive sliding mode dynamic surface control for trajectory tracking of fully actuated surface vessel subject to unknown dynamics and input saturation. Neurocomputing 2020, 377, 103–112. [Google Scholar] [CrossRef]
- Zhu, X.; Sun, L.; Li, B. Dynamic analysis of vessel/riser/equipment system for deep-sea mining with RBF neural network approximations. Mar. Georesources Geotechnol. 2020, 38, 174–192. [Google Scholar] [CrossRef]
- Liang, K.; Lin, X.; Chen, Y.; Li, J.; Ding, F. Adaptive sliding mode output feedback control for dynamic positioning ships with input saturation. Ocean Eng. 2020, 206, 107245. [Google Scholar] [CrossRef]
- Tannuri, E.A.; Agostinho, A.C.; Morishita, H.M.; Moratelli, L., Jr. Dynamic positioning systems: An experimental analysis of sliding mode control. Control Eng. Pract. 2010, 18, 1121–1132. [Google Scholar] [CrossRef]
- Wang, R.; Chen, Z.; Zhang, W.; Zhu, Q. Sliding-Mode Control of STENA DRILLMAX Drillship with Environmental Disturbances for Dynamic Positioning. In Proceedings of the 11th International Conference on Modelling, Identification, and Control (ICMIC2019), Tianjin, China, 13–15 July 2019. [Google Scholar]
| Classification | IMO | LR | DNV | ABS | |
|---|---|---|---|---|---|
| Description | |||||
| No redundancy exists, the vessel is provided by the manually stationary keeping and automatically heading control under the sea disturbances. | Class 0 | DP(M) | DNV-T | DPS-0 | |
| No redundancy exists, only one computer system for the DPS is equipped to automatically control the deviation of the vessel station and heading displacement. | Class 1 | DP(A) | DNV-AUT DNV-AUTS | DPS-1 | |
| Two redundant computer systems are used to automatically control the station and heading movement under the sea disturbances. Hence, the vessel position will not lose due to the failure of the dynamic system. | Class 2 | DP(2A) | DNV-AUTR | DPS-2 | |
| Three redundant computer systems are employed to control heading and environmental disturbances, during the DPS failure containing the loss of the unit due to overflow or fire situations. | Class 3 | DP(3A) | DNV-AUTRO | DPS-3 | |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mehrzadi, M.; Terriche, Y.; Su, C.-L.; Othman, M.B.; Vasquez, J.C.; Guerrero, J.M. Review of Dynamic Positioning Control in Maritime Microgrid Systems. Energies 2020, 13, 3188. https://doi.org/10.3390/en13123188
Mehrzadi M, Terriche Y, Su C-L, Othman MB, Vasquez JC, Guerrero JM. Review of Dynamic Positioning Control in Maritime Microgrid Systems. Energies. 2020; 13(12):3188. https://doi.org/10.3390/en13123188
Chicago/Turabian StyleMehrzadi, Mojtaba, Yacine Terriche, Chun-Lien Su, Muzaidi Bin Othman, Juan C. Vasquez, and Josep M. Guerrero. 2020. "Review of Dynamic Positioning Control in Maritime Microgrid Systems" Energies 13, no. 12: 3188. https://doi.org/10.3390/en13123188
APA StyleMehrzadi, M., Terriche, Y., Su, C.-L., Othman, M. B., Vasquez, J. C., & Guerrero, J. M. (2020). Review of Dynamic Positioning Control in Maritime Microgrid Systems. Energies, 13(12), 3188. https://doi.org/10.3390/en13123188








