1. Introduction
As wind energy grows as a main energy resource for the whole world, further research is still needed to reduce the cost of wind energy to keep it economically competitive [
1]. Turbine wakes affect both the power production and operation and maintenance costs of wind energy. Wind tunnel experiments at meter-scale or even smaller wind turbines [
2,
3,
4,
5,
6,
7,
8] and field measurements of subscale wind turbines (e.g., the SWiFT facility [
9,
10,
11,
12]) play a vital rule in understanding the dynamics of turbine wakes and provide valuable datasets for validating computational models. However, the sizes of these meter-scale turbines and subscale turbines are often much smaller than a full-scale wind turbine, which calls into question how well these small-scale wind turbines can represent full-scale wind turbines [
13].
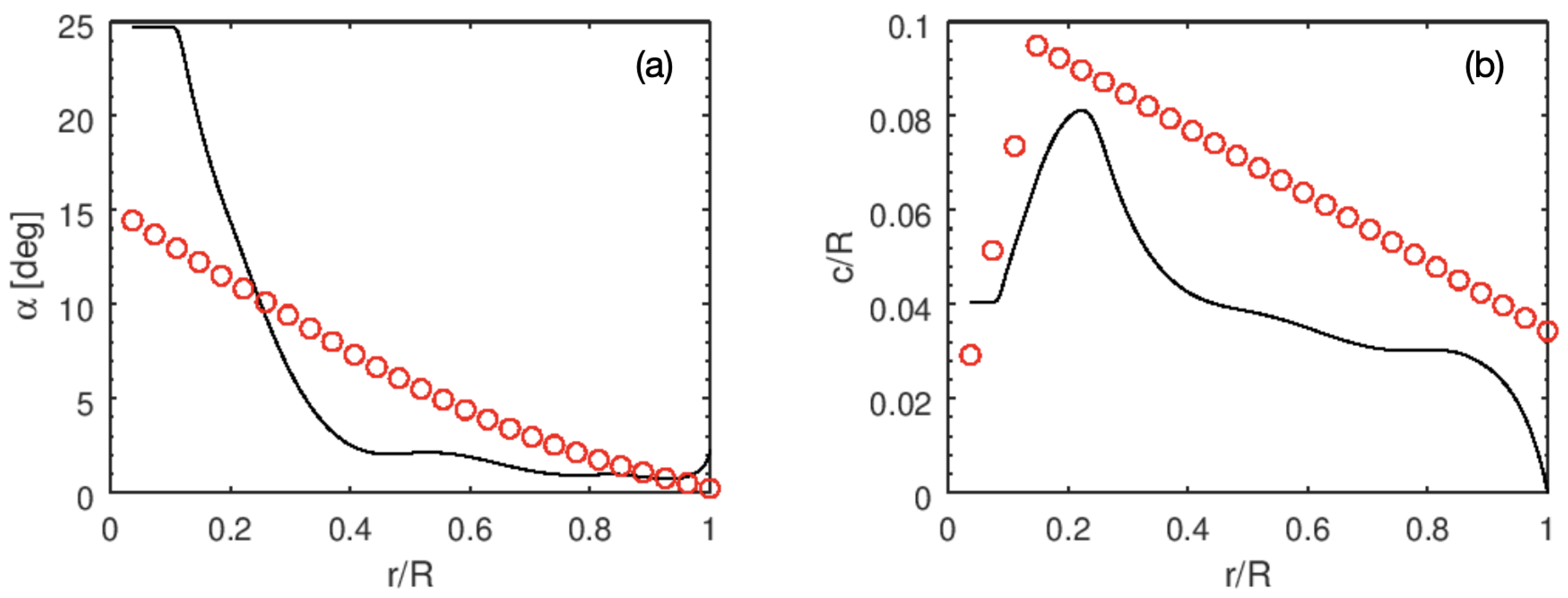
When designing a meter-scale or a subscale wind turbine, geometric, kinematic and dynamic similarities should be maintained to ensure their equivalence to a full-scale wind turbine. For a meter-scale wind turbine, which can be about 1000 times smaller than a full-scale wind turbine, it is even challenging to ensure only geometric similarity (e.g., the rotor diameter and chord length) and the kinematic similarity (e.g., the tip speed ratio
, where Ω is the rotor rotating speed,
R is the rotor radius and
U is the incoming wind speed). As such, researchers often build a meter-scale wind turbine in a way that the power coefficient and thrust coefficient are similar to that of a full-scale wind turbine [
6]. For the scale effects on turbine wakes, Howard and Guala [
14] compared the velocity deficits of a meter-scale turbine with that of the University of Minnesota 2.5 MW EOLOS turbine and observed significant differences at
and
turbine downwind locations but relatively small differences at
turbine downwind location, where
D is the rotor diameter. Heisel, Hong and Guala [
15] further compared the wake meandering from the meter-scale turbine and the EOLOS turbine and observed similar meandering frequencies related to the bluff body shear layer instability.
For a subscale wind turbine, which may be 3 or 4 times smaller than a full-scale wind turbine, the geometric similarity and the kinematic similarity can be ensured relatively easier compared to meter-scale wind turbines. However, because of the difference in Reynolds number, the dynamic similarity, namely the distributions of lift and drag coefficients along the blade for wind turbines, still cannot be guaranteed easily while keeping the geometric and kinematic similarities. Kelley et al. [
16] proposed to loosely maintain the dynamic similarity by keeping the same dimensionless bound circulation along the blade by relaxing the constraints on the geometric similarity. Although the aerodynamics of a subscale wind turbine can be made closer to a full-scale wind turbine, an important difference is that the subscale wind turbine is located closer to the ground where the mean shear stress and the turbulence intensity change significantly with distance from the ground. However, how this difference affects the representation of a subscale wind turbine wake to that of a full-scale wind turbine is not clear yet. To address this issue, in this work we simulate a subscale wind turbine and a full-scale wind turbine, which are geometrically and kinematically equivalent, and are dynamically equivalent by applying the same lift and drag coefficients in turbine parameterizations, and under the same turbulent boundary layer inflow.
It is noted that this work is different from the studies in the literature on investigating the effects of inflow turbulence on turbine wakes. In the literature, the turbine wakes under different turbulent inflows, which are due to different ground roughness lengths, were investigated in [
2,
17] using wind tunnel experiments and large-eddy simulation, respectively. The effects of different inflow turbulence on turbine wakes, which is caused by different thermal stratifications, were studied using wind tunnel experiments and large-eddy simulation in [
18,
19], respectively. In [
20], turbine wakes under different inflow turbulence caused by an upwind hill of different heights were simulated using large-eddy simulation. In [
21], the coherent tip vortices of a utility-scale wind turbine were investigated for inflows of different turbulence intensities. In [
22], the wake meandering of a utility-scale wind turbine was investigated for inflows of different turbulence intensities. All these studies were focused on the wake of one-size wind turbine. To the best of our knowledge, no studies have been carried out on comparing wakes from turbines of different sizes, which is critical as we use the knowledge from a subscale wind turbine to a full-scale wind turbine.
The rest of the paper is organized as follows: in
Section 2 we briefly describe large-eddy simulation with actuator surface models for turbine blades and nacelle; we then compare the results from the two turbines of different sizes in
Section 4; at last we draw conclusions from this work in
Section 5.
2. Numerical Method
The Virtual Flow Simulator (VFS-Wind) code [
23,
24,
25] is employed in this work to simulate wakes from the two turbines, which solves the incompressible Navier–Stokes equations in curvilinear coordinates shown as follows:
where
(
) are the Cartesian coordinates,
(
) are the curvilinear coordinates,
denotes the contravariant volume flux,
are the velocity vector in Cartesian coordinates,
J is the Jacobian of the geometric transformation,
represent the transformation metrics,
represents the contravariant metric tensor,
ρ is the density,
μ is the dynamic viscosity,
p is the pressure,
are the body forces from actuator type turbine models, and
is the subgrid scale stress modeled using the dynamic subgrid scale model [
26]. The governing equations are discretized in space using a second-order central differencing scheme and in time using a second-order accurate fractional step method. The pressure Poisson equation is solved using an algebraic multigrid acceleration along with GMRES solver. The momentum equation is solved using the matrix-free Newton–Krylov method. The VFS-Wind code has been validated extensively using laboratory and field measurements [
21,
24] and applied to utility-scale wind turbines [
22,
27,
28].
The actuator surface models for turbine blades and nacelle developed in [
25] are employed in this work. In the actuator surface model for turbine blades, the blade is represented with the actuator surface defined by chords at different radial locations. Forces computed using the blade element method are distributed on the actuator surface to represent the effect of blades on the incoming flow. Compared with the actuator line parameterization, the actuator surface can represent better the geometrical effect of the blade in the chordwise direction. A model for the nacelle is also necessary for accurately predicting turbine wakes, which affects the hub vortex and meandering in the far wake [
29]. In this work the nacelle is represented using an actuator surface formed by the actual surface of the nacelle. The effects of nacelle on the incoming flow are modeled using distributed forces with the wall-normal component calculated by satisfying the no-flux boundary condition and the wall-tangent component calculated by specifying a friction coefficient.
4. Results
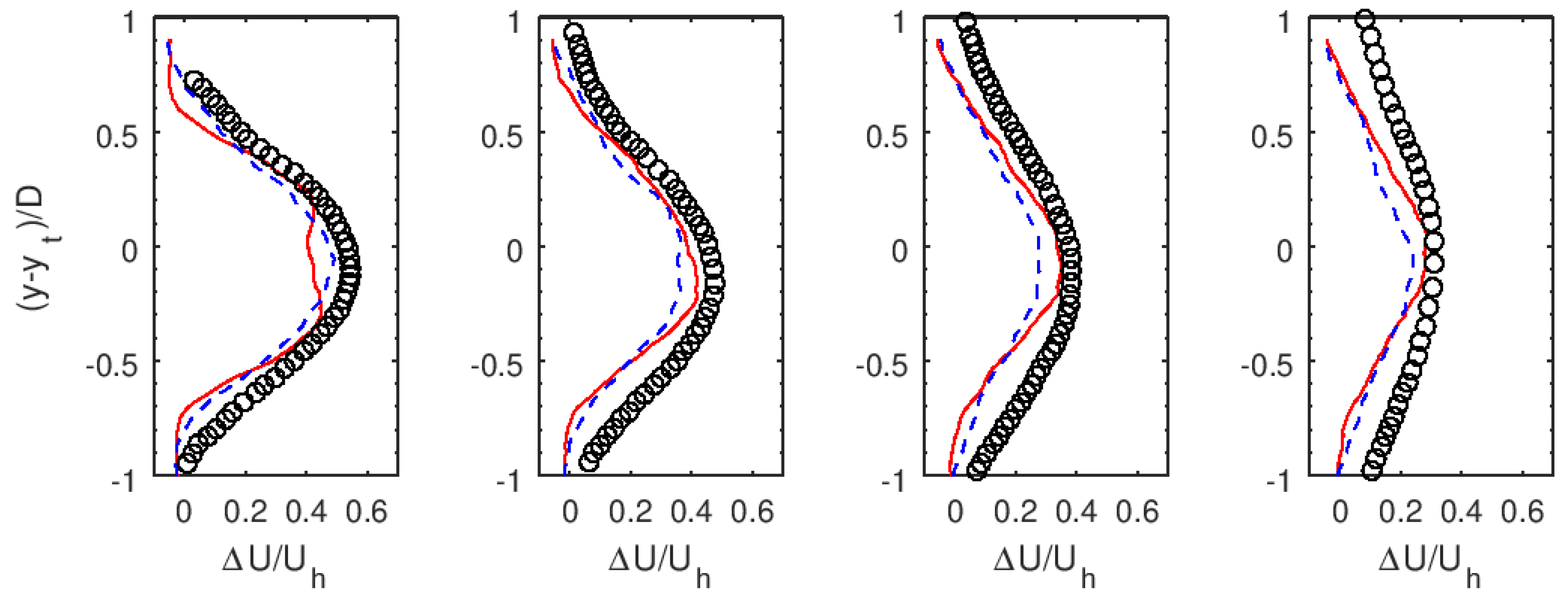
As no measurements are available for the employed turbine designs, we attempt to validate the employed computational setup by comparing the simulated velocity deficit
with the measurements at the SWiFT site considering the T27 turbine and the SWiFT turbine are of the same size and have comparable blade designs, in which the velocity deficit
is defined as
where
U is the time-averaged downwind velocity at different downwind locations,
is the time-averaged incoming downwind velocity (which is taken at
upwind the turbine). As in [
33], a slight offset of
is imposed in the negative
y direction to compensate for the wake deflection observed in the measured data. It is seen in
Figure 4 that the simulation velocity deficit profiles show an overall good agreement with the measurements considering the complex wind and turbine operating conditions in the field and different turbine designs. It is also noticed the lateral velocity deficit profiles from the T80 case and the T27 case are very similar at the considered turbine downwind locations.
We then examine the contours of the instantaneous downwind velocity from the two cases in
Figure 5. It is seen that the wake remains an annular shape until about
downwind of the T80 turbine, while becomes unstable immediately downwind of the T27 turbine. At further downwind locations, the flow structures of the T80 turbine’s wake remain quite coherent with its center biased towards the ground, which, on the other hand, looks chaotic and meanders significantly in the vertical direction with its center shifting above the centerline of the rotor for the T27 turbine.
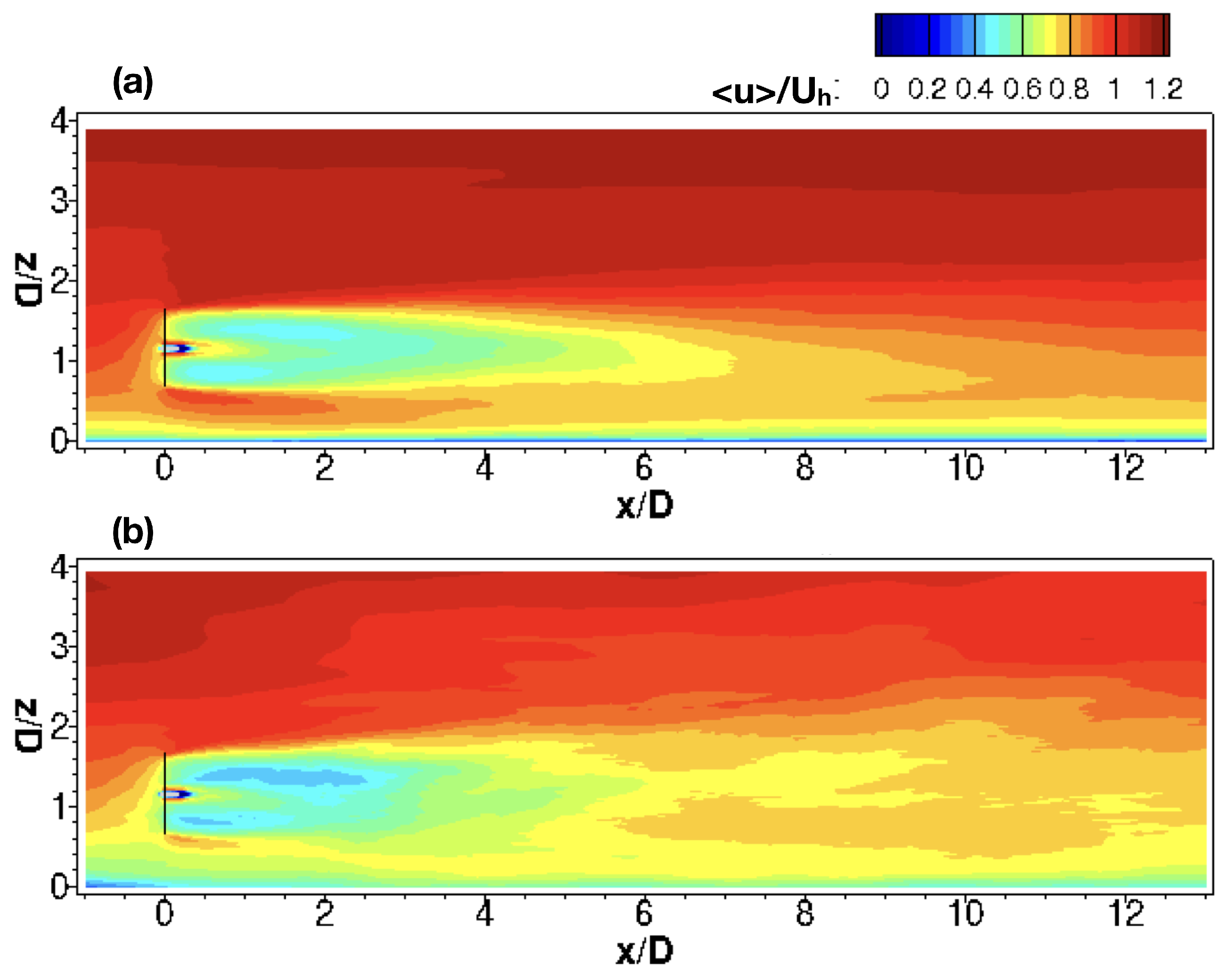
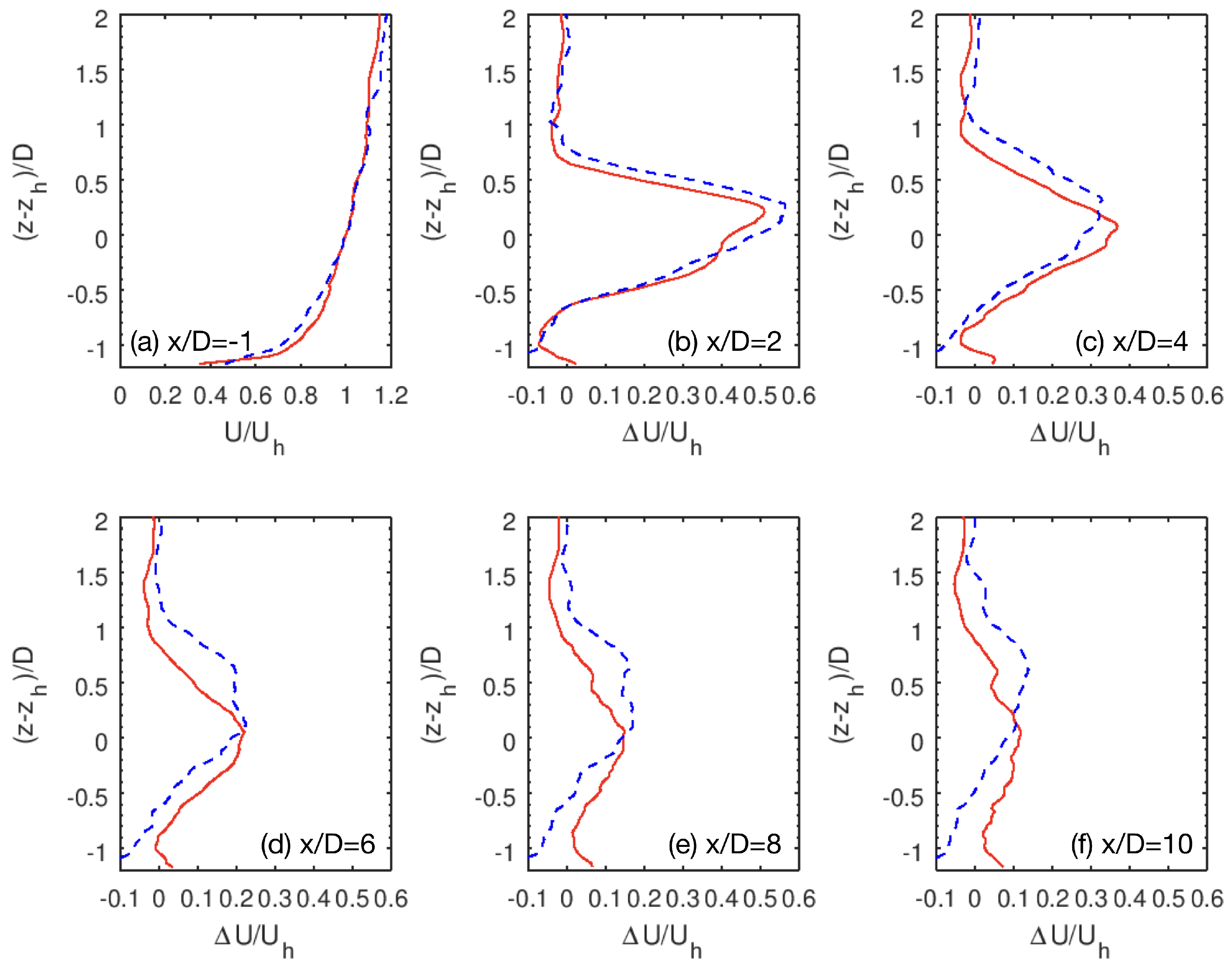
Next, we examine the time-averaged quantities from the two cases. In
Figure 6 we compare the time-averaged downwind velocity from the two cases. It is seen that the velocity deficits from the T27 case are higher for the upper parts of the wake when
, which are similar for the T80 case. At far wake locations, the wake center from the T80 case is below the hub height, while above the hub height for the T27 case.
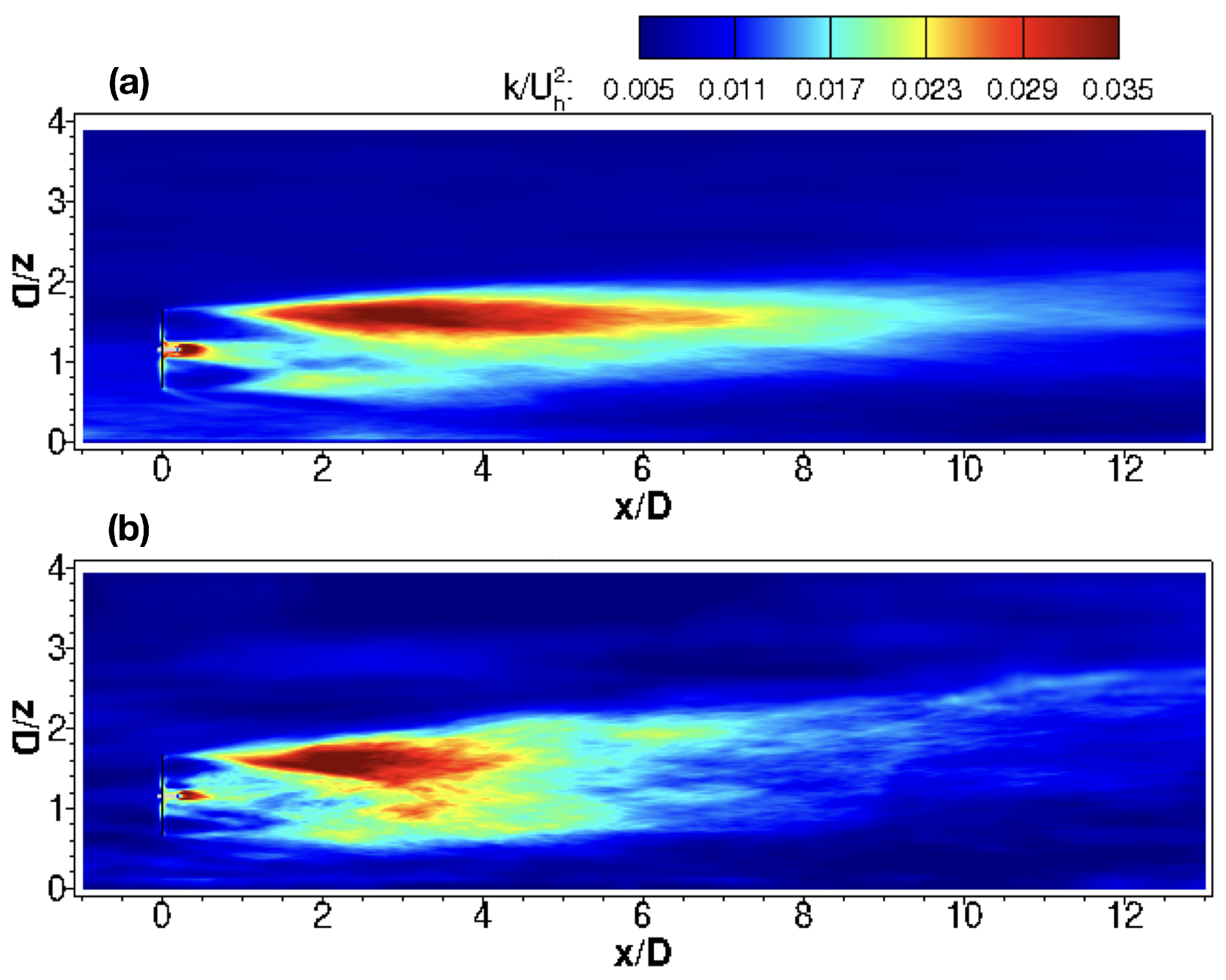
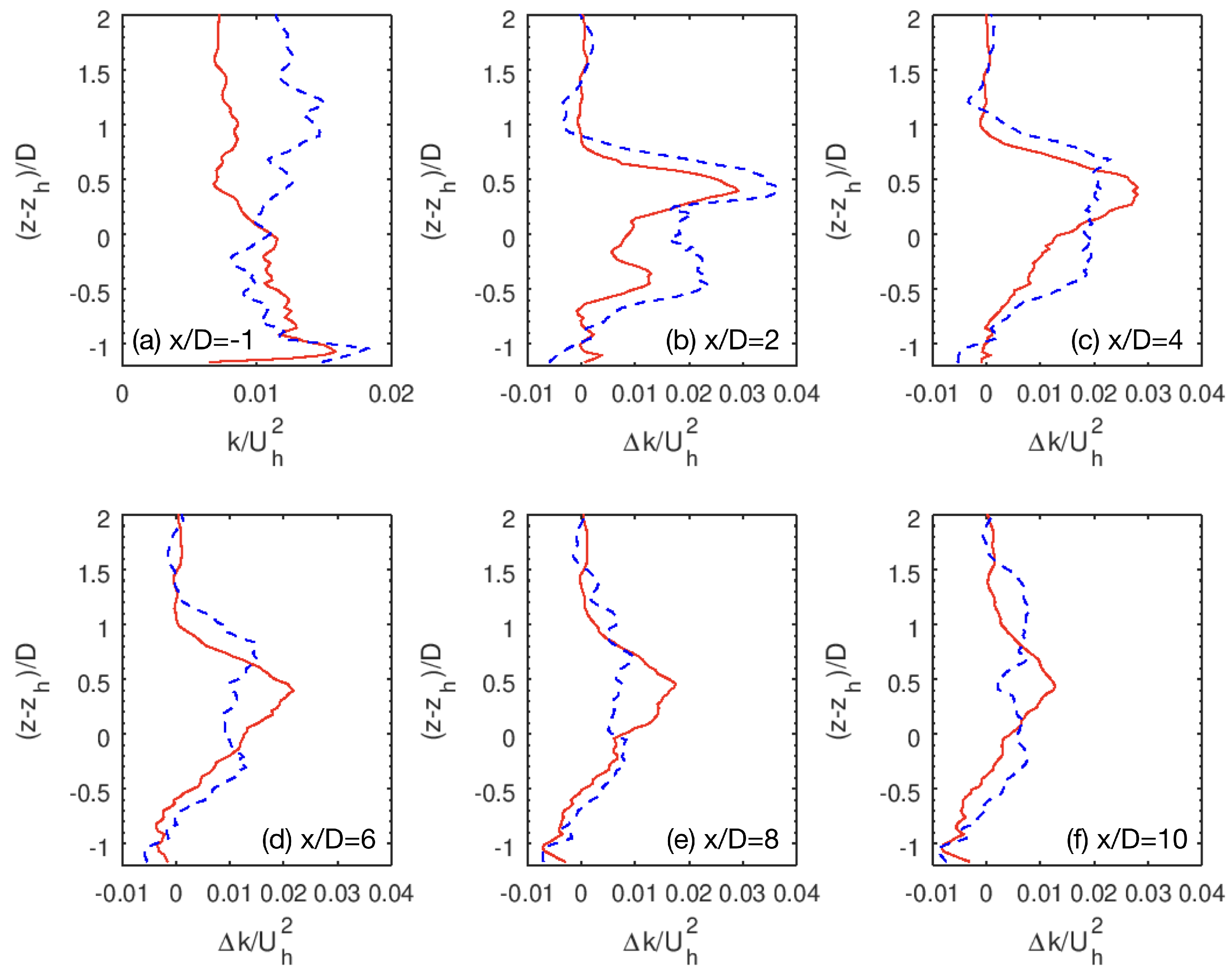
In
Figure 7 we examine the turbulence kinetic energy (TKE) from the two cases. One similar observation from the two cases is that the high TKE region are in the top shear layer for both cases. One significant difference between the two cases is that the high TKE region persists to about
downwind the turbine for the T80 case, which only persists to about
turbine downwind for the T27 case.
To qualitatively show the differences between the two cases, we examine the time-averaged velocity deficit (Equation (
3)) and the turbine-added TKE profiles. The turbine-added TKE (
) is defined as
where
k is the TKE at different downwind locations,
is the TKE of the inflow (which is taken at
upwind of the turbine for the present cases). It is seen in
Figure 8a that incoming time-averaged downwind velocity profiles normalized using the corresponding length and velocity scales are quite similar, with one difference that the incoming velocity is slightly lower for the lower part of the turbine for the T27 case. At
, the velocity deficit profiles are similar between the two cases with slightly higher velocity deficits from the T27 case. Moving to further downwind locations, the center of the wake gradually shifts to the upper part of the wake, which is above the upper tip of the turbine at
.
In
Figure 9 we compare the turbine-added TKE from the two cases. First, we examine the normalized TKE at the
upwind of the turbine in
Figure 9a. Because of different turbine sizes and hub heights, it is seen that the TKE of the inflow in the turbine region are quite different between the two cases, that the inflow TKE for the T27 case is higher than the T80 case for locations above the hub height while slightly lower for locations below the hub height. At
, the vertical distributions from the two cases are similar, in that two peaks exist within the turbine top and bottom shear layers, respectively, with the one on the top about 1.5 times higher. At this location, it is also noticed that the normalized
from the T27 case is higher at almost all
z locations. Starting from
, one observation is that the bottom peak of
disappears for both cases. One major difference is that the top peak of
still exists for the T80 case, which becomes flat and with a much wider high
region for the T27 case. It is also noticed that the maximum
from the T80 case is much higher than that from the T27 case. These observations are consistent with the lower incoming TKE for the upper region of the T80 case allowing the wake to maintain coherent helical wake vorticity structures for longer distance downstream than for the same region of the T27 case, where the higher incoming turbulence likely drives these structures to mix in to more evenly distributed vorticity sooner.
To explore the reason for different distributions of velocity deficits and turbine-added TKE, we examine the mean kinetic energy (MKE) equation integrated over
plane, which is shown as follows:
where
,
,
,
,
,
are the convection of the MKE by the mean flow, transport terms due to mean pressure, turbulence fluctuations, the diffusion term, the negative of turbulence production term (which transfers energy from the mean flow to turbulence), and the dissipation term, respectively. The expressions for the various terms in Equation (
5) are given as follows:
where
is the coordinate of the rotor center in the lateral direction,
R is the rotor radius,
is the strain rate tensor. The turbulence convection term
is further decomposed into three components for the contributions from three directions as follows:
where
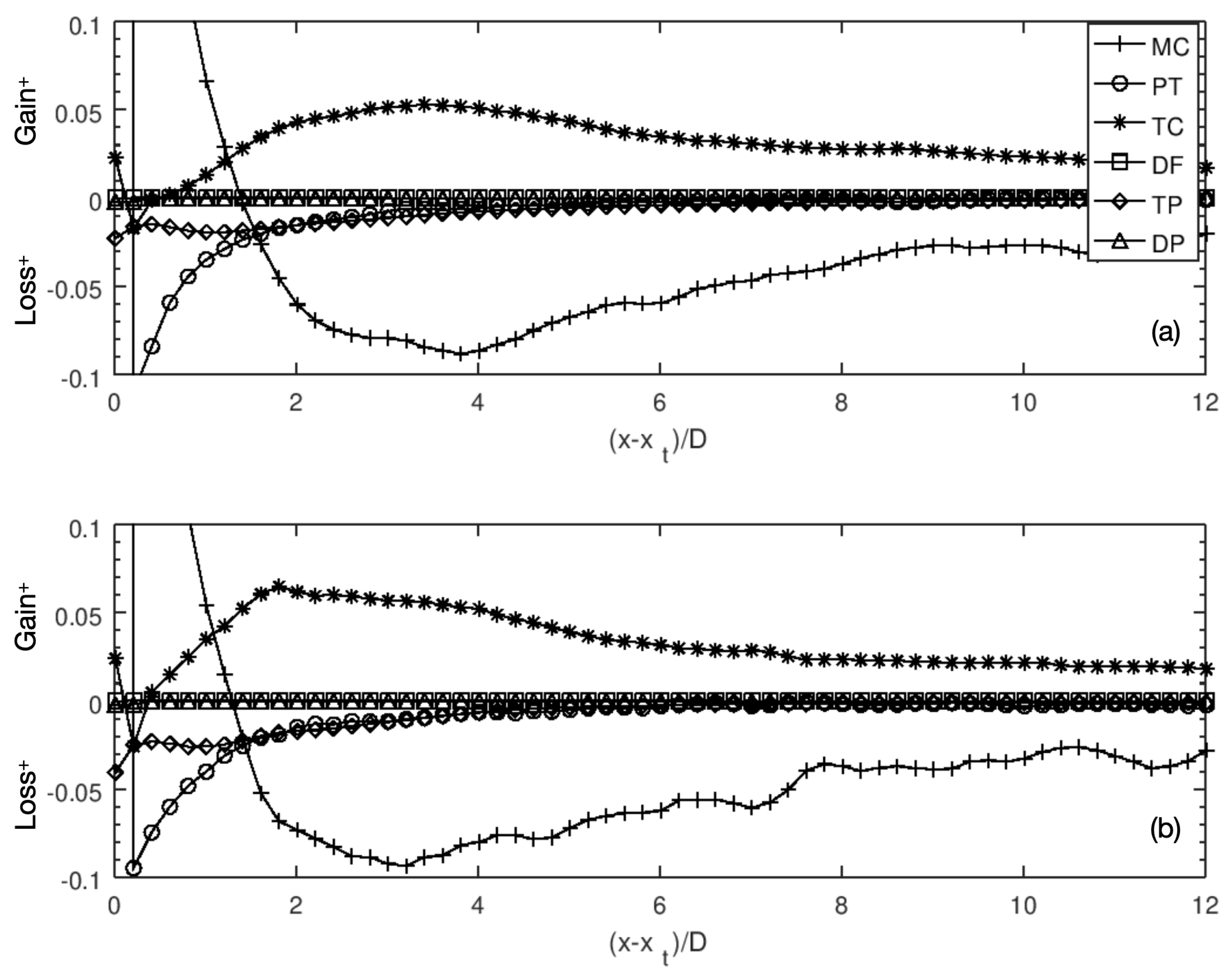
First, we show in
Figure 10 different terms in Equation (
5) for both cases. It is seen that the mean convection (
) term is balanced with the pressure transport term in the near wake region where the pressure recovers to the ambient pressure by extracting mean kinetic energy from the wake. In the far wake region, the
term is mainly balanced with the turbulence convection (
) term. The above observations are similar to the wake of a model wind turbine located downwind of a three-dimensional hill [
20]. The major differences between the T80 and the T27 cases are observed in the
and
terms, of which the magnitudes are higher in the near wake for the T27 case.
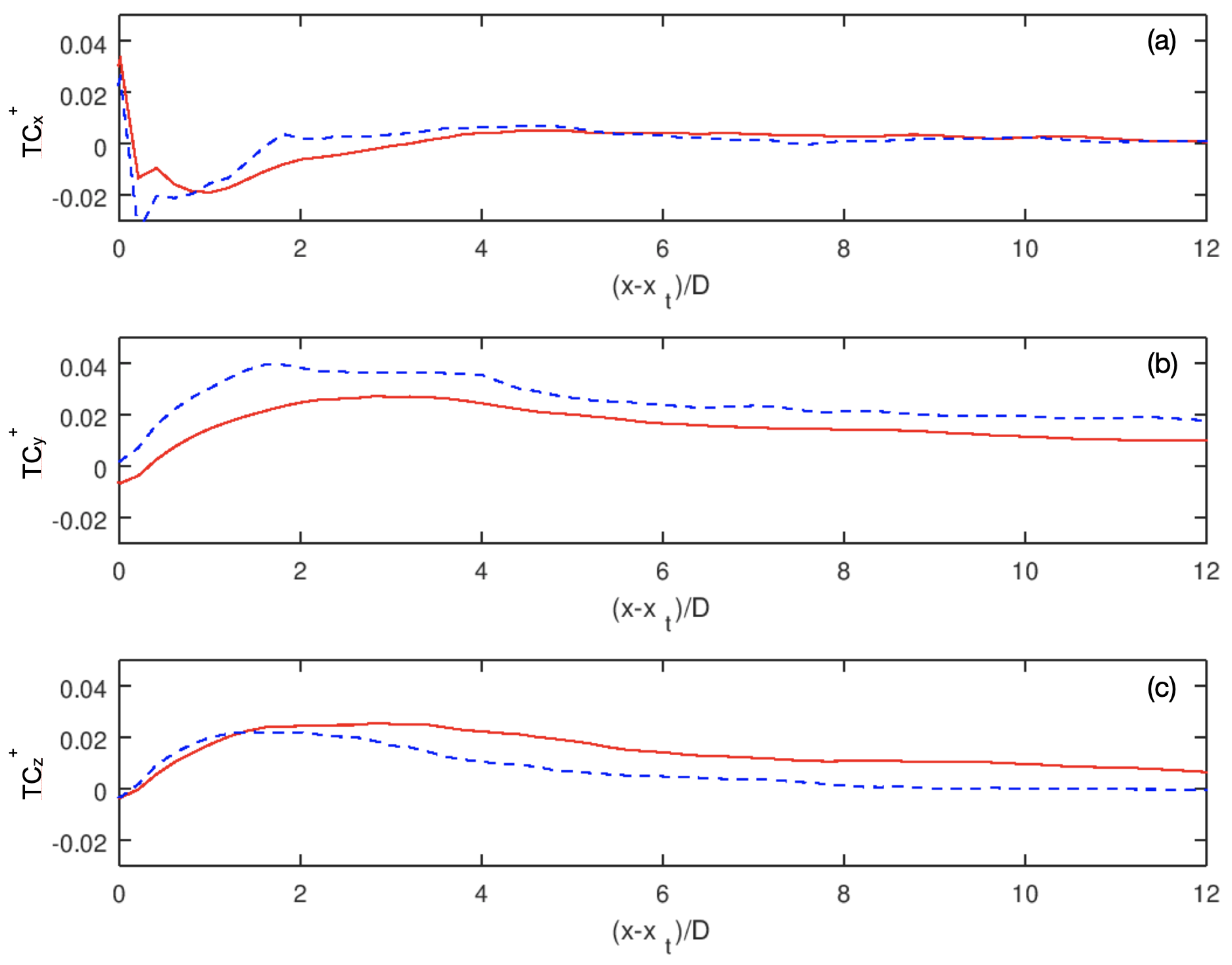
In
Figure 11 we compare the three components of the
term between the T80 and T27 cases. It is seen that the mean kinetic energy losses are due to the downwind component of the turbulence convection term
term when
and
for the T80 and T27 cases, respectively. At further downwind locations the effect of the
term on the MKE budget is negligible. On the other hand, the other two components of the turbulence convection terms
and
contributes positively to the MKE budget at almost all downwind locations except in the region immediately downwind the turbine. The
term from the T27 case is higher than that from the T80 case for all downwind locations. On the other hand, the
term from the T27 case is almost the same as that from the T80 case for
, while lower than that from the T80 case for further downwind locations. That MKE entrainment from the top is lower than that from two sides explains the upward shift of the wake center observed in
Figure 8 for the T27 case.
To better understand the differences in
and
terms between the two cases, we examine the averaged Reynolds stress and downwind velocity on the control surface from the two cases in
Figure 12 and
Figure 13, in which different terms are defined as follows:
As seen in
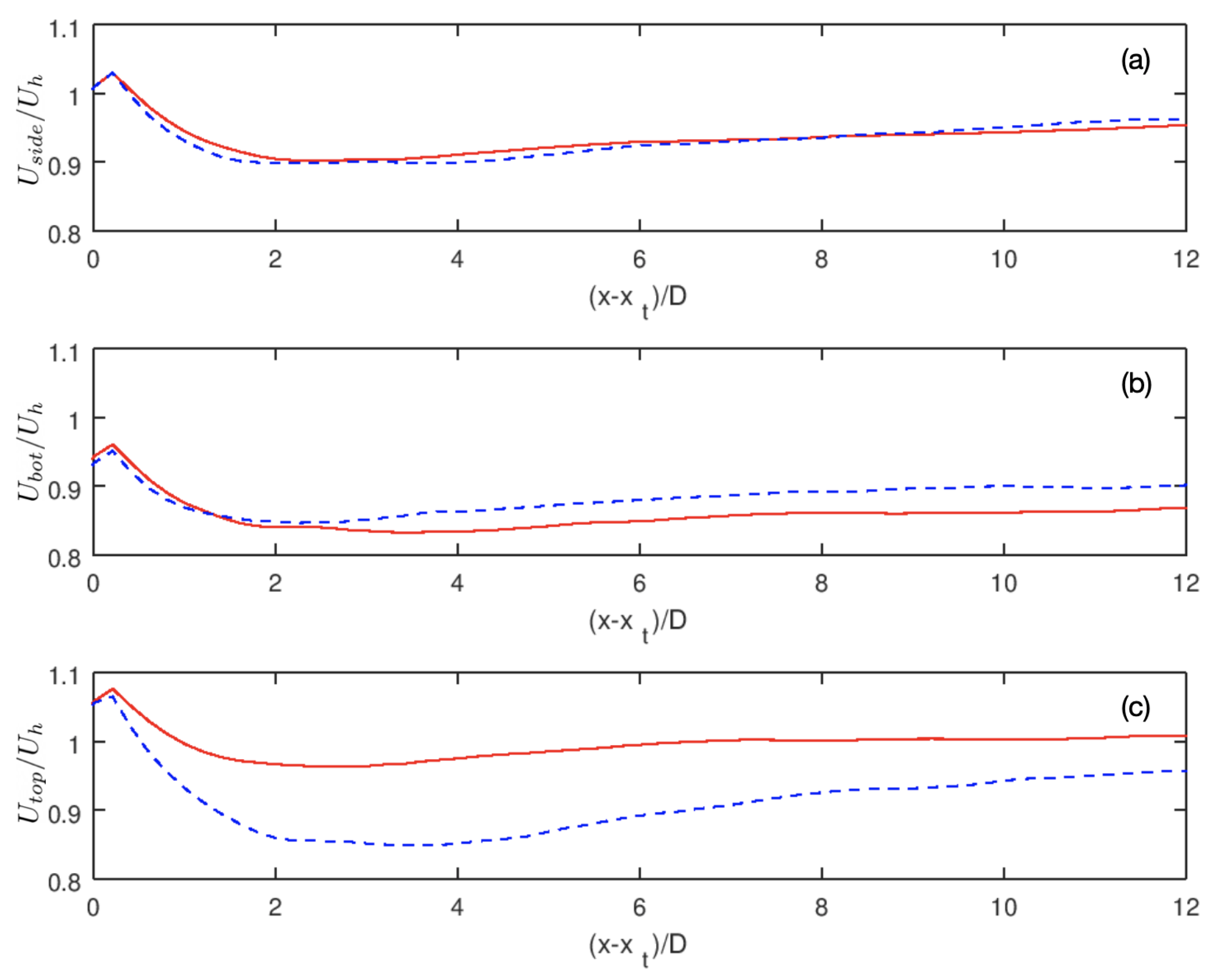
Figure 12a, the averaged downwind velocity on the two sides of the surface are nearly the same for the T80 and T27 cases. The averaged Reynolds stress term
from the T27 case, on the other hand, is larger than that from the T80 case as shown in
Figure 13a, which is the key reason the
term the T27 case is larger than that from the T80 case (shown in
Figure 11b). On the bottom of the control surface, the averaged downwind velocity from the T27 case is larger than that from the T80 case (as shown in
Figure 12b), while the
from the T27 case is smaller than that from the T80 case from
to
rotor downwind and close to zero at further downwind locations, which is the same as the T80 case (shown in
Figure 13b). This makes that the differences in entrainment from the bottom surface are insignificant between the two cases especially at far wake locations. On the other hand, the averaged downwind velocity on the top surface is significantly lower for the T27 case at all downwind locations as shown in
Figure 12c, which is caused by the upward shift of the wake center for the T27 case as shown in
Figure 8. Meanwhile, the
from the T27 case is also significantly lower than that from the T80 case at downwind locations
. Therefore, this explains why the
term from the T27 case is lower than that from the T80 case at downwind locations
(shown in
Figure 11c).
To explore the reason for the different downwind variations of the TKE shown in
Figure 9, we compare the turbulence production term from the two cases in
Figure 14. It is observed that the magnitude of the
term from the T27 case is significantly larger than that from the T80 case when
, while is similar to that from the T80 case at further downwind locations. Higher
term indicates more energy is transferred to TKE from MKE. This is consistent to what we observed in
Figure 9 that the TKE from the T27 case is significantly higher than that from the T80 case in the near wake region.