1. Introduction
Integrated energy system includes four energy forms: cold, heat, electricity and gas, which contains various types of energy supply equipment with non-linear partial load characteristics and various types of loads [
1,
2]. Internet of Things technology and information technology are used to uniformly integrate and schedule all energy supply equipment in the system to achieve optimal energy supply and energy efficiency improvement of the load system [
3]. CCHP (combined cooling heating and power) system, as a typical representative of integrated energy systems [
4,
5,
6], has become an important means to realize the transformation of energy production and consumption, improve the efficiency of comprehensive energy utilization and solve energy and environmental problems, with its high energy utilization efficiency and flexible and reliable energy supply mode.
In terms of the operation and dispatching of the integrated energy system, the two most common dispatching strategies in the integrated energy system are following thermal load strategy and following electrical load strategy [
7,
8,
9,
10]. At present, there are many researches on these two dispatching strategies and the daily energy forecasting worldwide, however, this research focuses on different aspects due to different factors, such as application scenarios and configurations of research objects. A group of scholars from Budapest University of Technology and Economics, such as Olaszi, Balint D., Sores, Peter etc., have a lot of research on daily energy forecasting within the day-ahead market [
11,
12], which are the basis of commercially available, daily energy forecasting software and are useful in the automatic prediction of solar and wind power based systems. In [
13], an adaptive algorithm and an energy market oriented remote-controlled strategy is proposed and daily energy forecasting problems are analyzed by Olaszi, Balint D. In [
14], an interval optimization method to optimally schedule electric vehicles (EV) with consideration of the uncertainty of RES generation and loads is proposed, which provides good reference for grid interacting, considering the uncertainty of RES generation and loads. Li H. et al. [
15] took the combined heat and power system as the research object, analyzed the system operating status under the following thermal load strategy and following electrical load strategy, respectively considering different load heat and power ratios, and suggested that the system should run at the optimal thermoelectric equilibrium point in order to obtain the maximum economic and energy saving benefits. In order to improve the comprehensive operation efficiency of the CCHP system, an optimal control strategy, based on the integrated effect boundary (IEC), based on following thermal load strategy and following electrical load strategy, was proposed in [
16], and a building-type CCHP system case was used to prove the feasibility of the control strategy. The following thermal and electrical load dispatching mode are simple and convenient for real-time load tracking, however, due to the oversimplification of the dispatching model, there is a problem of insufficient energy supply economy [
17,
18,
19].
Another major operating mode of the integrated energy system is economically optimized operation dispatching. A day-ahead energy saving and economic operation dispatching model for integrated energy system was established in [
20], and a two-stage Lagrangian relaxation iterative algorithm was used to solve the model. Compared with the traditional operation mode, the coal consumption rate index of the system is reduced after adopting the strategy by the model. Stadler M. et al. [
21,
22] researched on the commercial building type integrated energy system and established the system’s optimal dispatching model, with the optimization goal of minimum daily operating cost of the system. The model was solved using CPLEX, and the example showed that the strategy proposed could save 11% of annual operating costs of the commercial building system, while reducing annual carbon emissions by 8%. Jayasekara S. et al. [
23] analyzed the economic indicators of the day-ahead scheduling plan for a large-scale park integrated energy system. Compared with the traditional electric and heat separated supply mode, it was concluded that the integrated energy system is more economical and reliable than traditional energy supply mode. The problem with economic optimal dispatching strategy is that the formulated dispatching plan is based on the previously predicted load and renewable energy output, however, there will be load and renewable energy output prediction errors in the real-time operation of the system, which will cause the system to fail to fully operate according to the day-ahead economic optimal dispatching plan [
24].
Regarding how to improve the day-ahead dispatching plan of the integrated energy system to ensure the real-time operation of the system, there have been some studies on model predictive control (MPC), based on the uncertainty of forecasting. In [
25], the integration of storage systems is applied in the Kuramoto-like grid models, to improve the power quality and ensure power supply in the presence of stochastic wind power. McLarty D. et al. [
26] studied the real-time optimization dispatching problem of a campus integrated energy system. First, the day-ahead dispatching plan was formulated based on the day-ahead dispatching model, and then the real-time load prediction results were used to replace the original day-ahead load prediction results, to calculate the real-time power deficit of the system. Afterwards, a feedback correction controller was introduced to apply the electric power of the public network and the heat and cold energy storage device, to balance the power deficit, which achieved the goal of real-time operation of the system. Houwing M. et al. [
27] applied the model predictive control method to the real-time optimization model of the integrated energy system and added a rolling optimization procedure on the basis of the day-ahead optimization model, to make the scheduling strategy more in line with the actual operating conditions. In [
28], Juan Ospina proposes a novel control solution designed to solve the local and grid-connected distributed energy resources (DERs) management problem, using sampling-based model predictive control (SBMPC). In [
29], a novel model predictive control (MPC)-based operation strategy is presented, to minimize distribution system customer interruption cost and improve the distribution system reliability by coordinating multiple power supplies from EES, RER and external grid. In [
30], an MPC-based iterative distributed algorithm is deployed within a framework that allows the integrated energy system to dynamically adapt to changes in the operating environment, which can handle both the variability and unpredictability of renewable energy sources, as well as increasing system complexity. Xu X. et al. [
31] first established the day-ahead economic dispatching model and then revised the day-ahead load forecast data, on the basis of ultra-short-term load forecast. Only the grid connection situation was considered in the revision and the unbalanced electric, heating and cooling load are all satisfied by the energy storage device, that is, the energy storage device is called to meet the real-time load balance in the system. Mehrjoo M. et al. [
32] balanced the instantaneous power by applying the peak shaving device. After the peak shaving device is applied, the exchange power on the contact bus is ideally consistent with the previous day-ahead scheduling plan. A small amount of power deviation occurs when the adjustable capacity of the peak shaving device is zero and the degree of power imbalance is much smaller than when only the day-ahead scheduling plan is adopted.
In summary, for the real-time optimal operation and scheduling of integrated energy systems, research is currently focused on two simplified scheduling methods, namely the following thermal load dispatching strategy and following electrical load dispatching strategy, and how to reduce the errors in the optimal dispatch prediction process. The application of energy storage and peak shaving devices to suppress unbalanced power using model predictive control (MPC) is also one of the research topics. However, due to the structural differences and energy forms diversity of the integrated energy system, how to consider the real-time economic allocation of the unbalanced power to all of the energy supply and storage equipment according to the characteristics of the integrated energy system and the combination of real-time dispatching strategy with the day-ahead dispatching strategy, has research significance. The integrated energy system is a non-linear system with multiple energy sources, complex characteristics of energy supply and storage equipment and the strong randomness of load and renewable power output. When the renewable power output and the load of cold, heat and power deviate from the previous forecast values, the equipment operation mode needs adjustment to ensure the economical and optimal operation of the system.
To solve the above problems, this paper analyzes the real-time optimized operation structure of the integrated energy system and combines the characteristics of the integrated energy system to modify the day-ahead optimization scheduling method. A real-time error correction operation model for the integrated energy system is proposed and the model makes real-time corrections to the day-ahead operation strategy of the integrated energy system, to offset forecast errors from the renewable power generation system and multi-energy load system, which ensures the safety, stability and economy of the real-time operation of the integrated energy system.
2. Real-Time Optimized Operation Structure of the Integrated Energy System
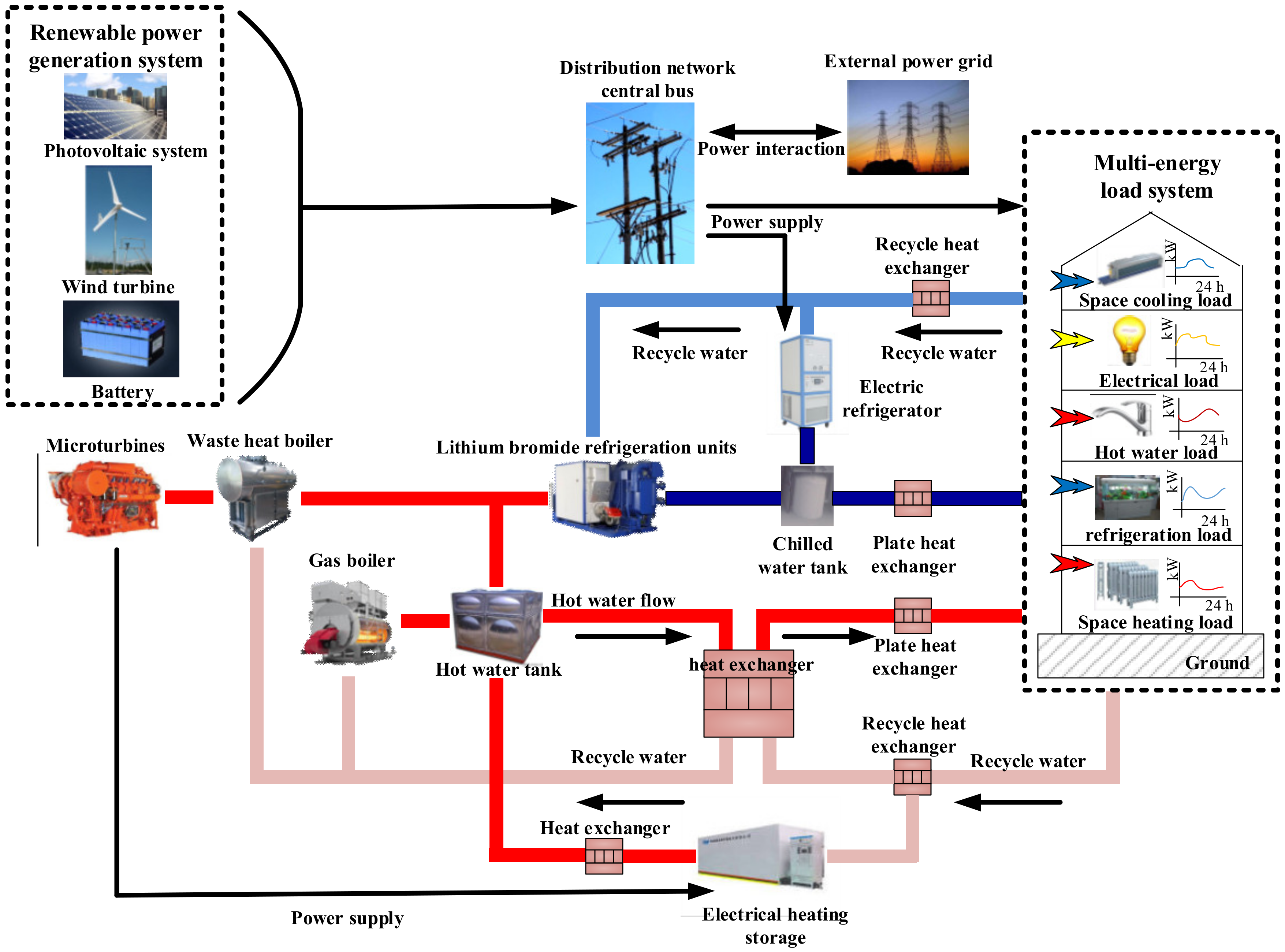
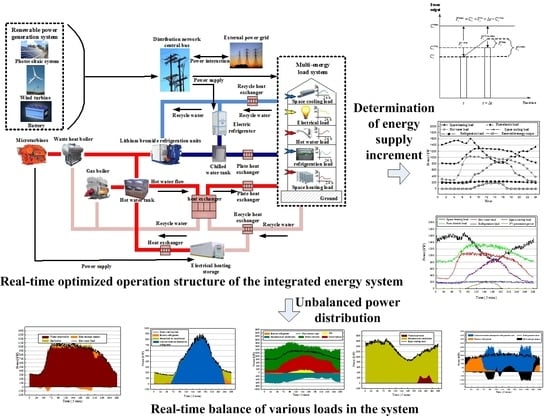
The integrated energy system includes four energy forms: cold, heat, electricity and gas, which contains various types of energy supply equipment and various types of loads. The main equipment in the real-time optimized operation structure of the integrated energy system studied in this paper include micro gas turbine, waste heat boiler, Lithium bromide absorption refrigeration unit, gas boiler, household air conditioning system, electric refrigerator, battery, heat (cold) storage device, wind turbine, Photovoltaic cells. The integrated energy system exchanges power through the centralized power bus, with the distribution network and the real-time operation structure of the system as shown in
Figure 1.
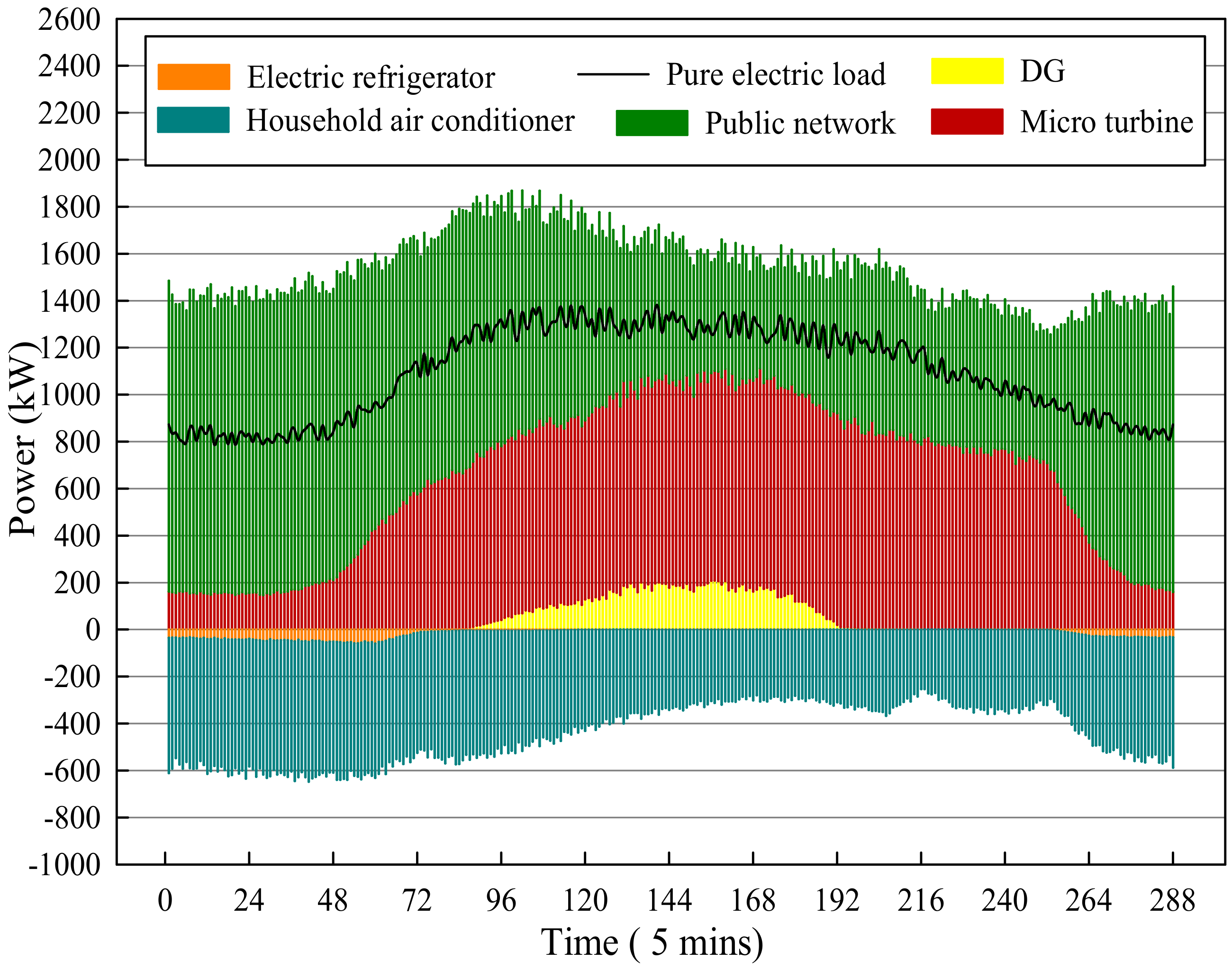
In terms of the electrical energy interconnected part, there is bidirectional power flow between the system and the external power grid. When the power generated by the integrated energy system in real-time operation is greater than the load, it can be sold to the external power grid in real time; otherwise, it can be purchased from the grid. The maximum power exchange value of the integrated energy system with the external power grid is restricted by the state grid for avoiding overload of public power lines and ensures the stability of electricity grids [
33]. In terms of the gas energy interconnected part within the system, there is only a one-way transaction between the integrated energy system and the gas company, and there is no natural gas production inside.
In the combined cooling, heating and power energy supply system, the micro turbine is one of the most important energy supply equipments. The micro turbine generates electricity through natural gas and the high-temperature flue gas enters the waste heat boiler. The waste heat is converted into high-temperature steam and then enters the lithium bromide absorption refrigeration unit to achieve the purpose of cold-water production.
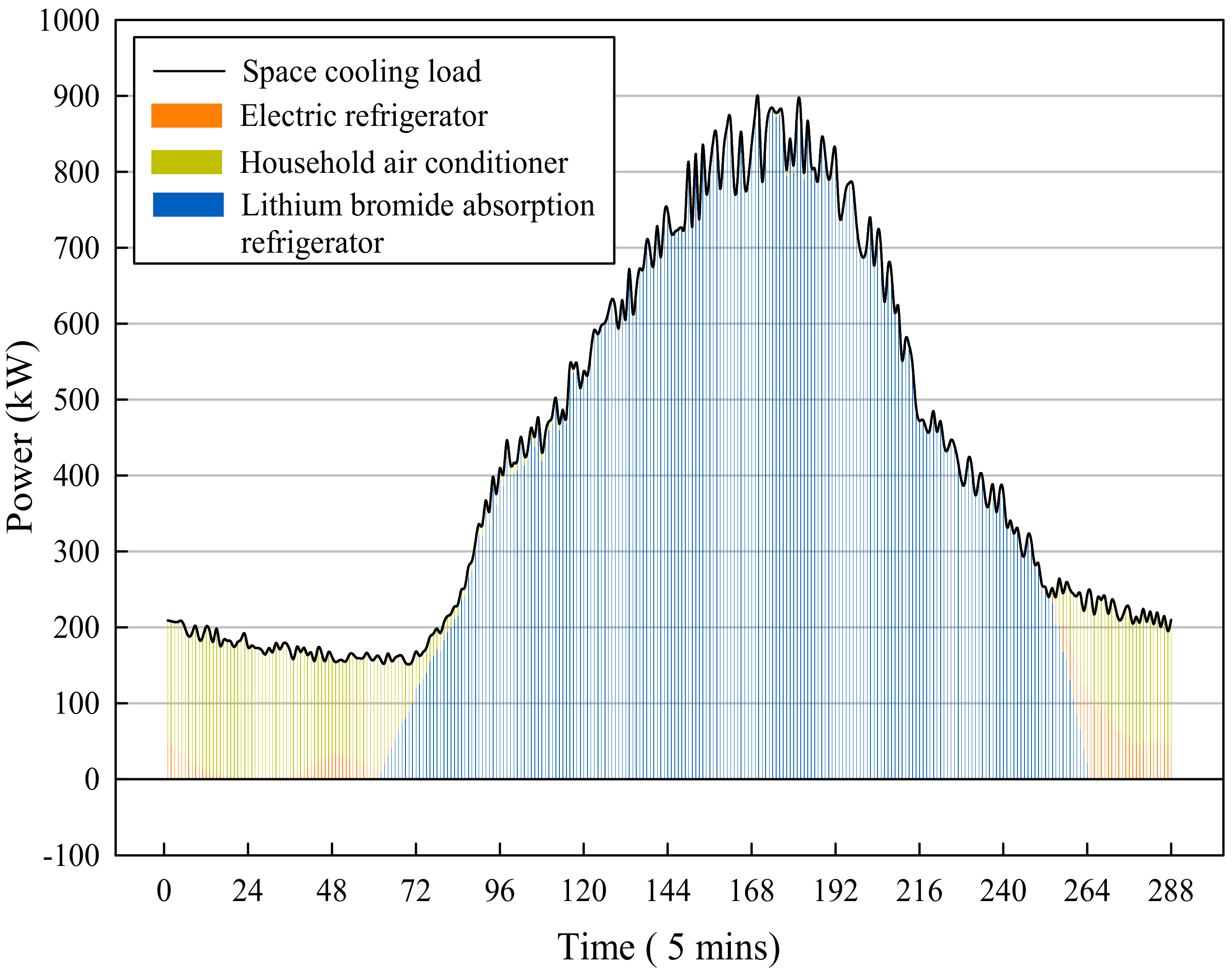
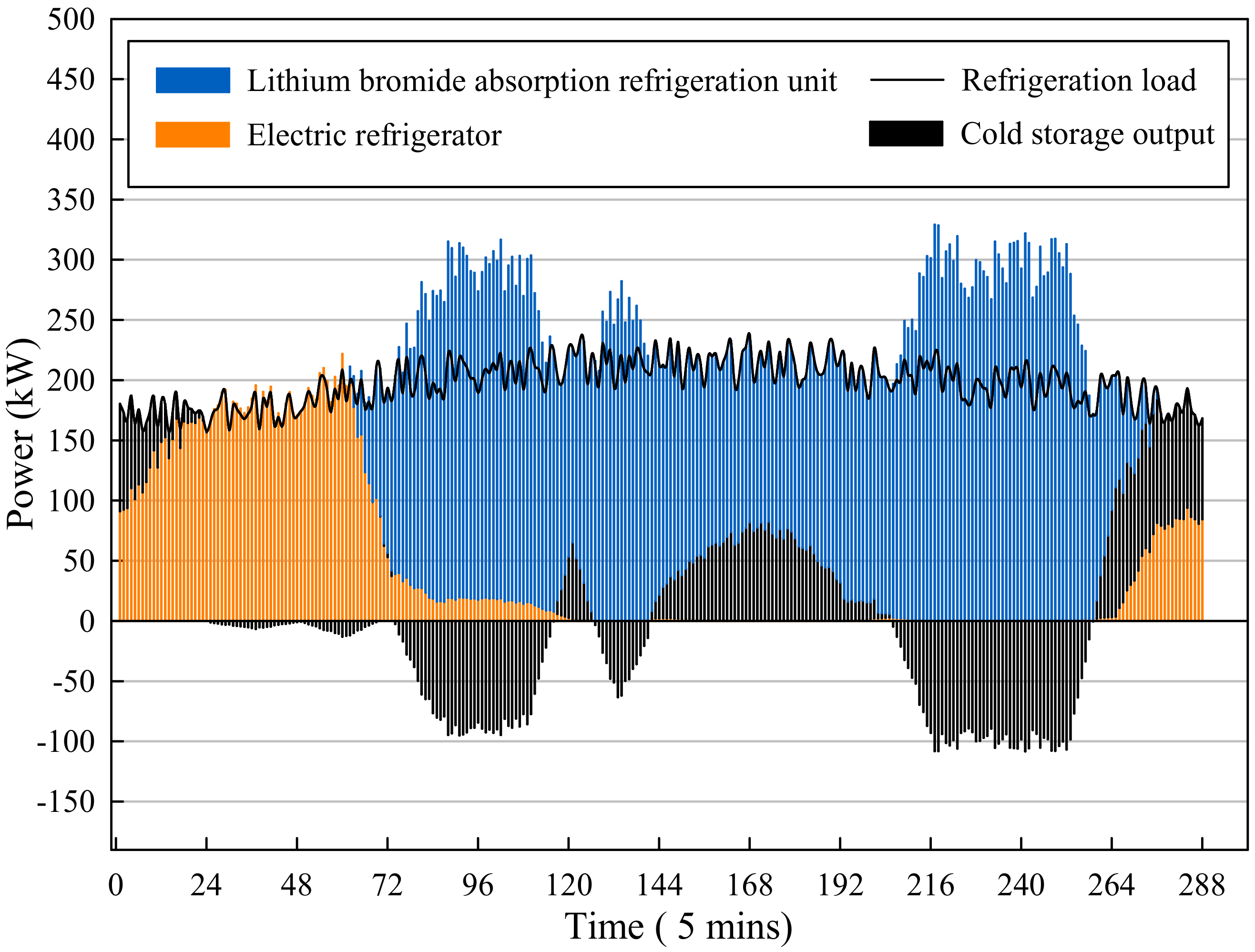
In the cold energy interconnected part, the electric refrigerator connects with the chilled water tank, which performs as a peak-shaving device for the refrigeration load, which provides cold water when the lithium bromide absorption refrigeration unit supplies insufficiently cooling energy and the cold storage device stores cold water when the cooling power output of the lithium bromide absorption refrigerator or the electric refrigerator is sufficient, while releasing the cooling capacity when needed.
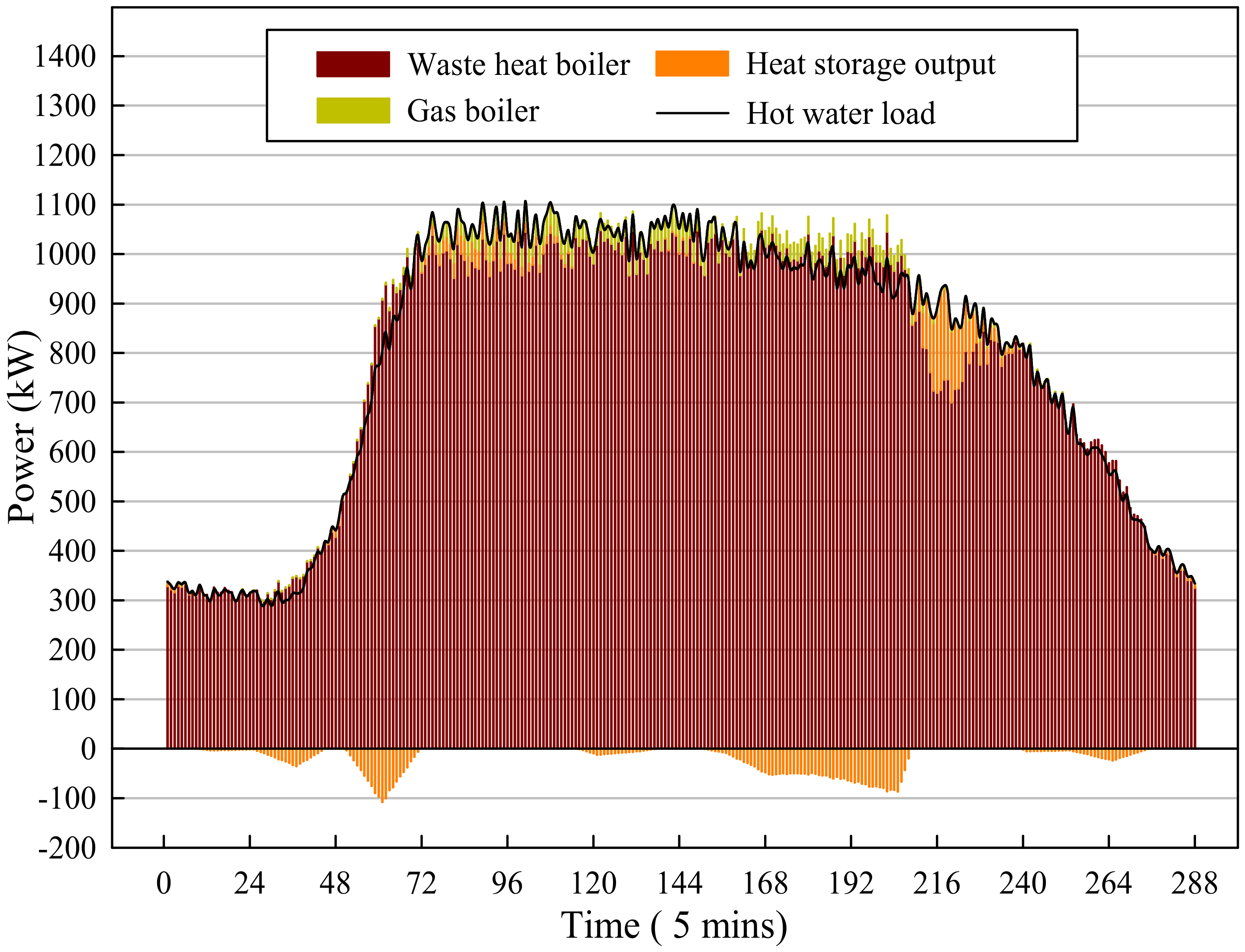
In the heat energy interconnected part, the heat storage device can store the high-temperature hot water generated by the gas boiler or waste heat boiler and release the heat energy when the system has insufficient heating power supply.
The integrated energy system is also equipped with a photovoltaic power generation system and a wind turbine, the output of which can not only supply internal electrical loads, but also exchange power with external power grids. The household air conditioners in the systems can only supply space cooling and heating loads as the peak shaving equipment. The mathematical models and operating constraints of various energy supply equipment and energy storage equipment in the integrated energy system have been given in [
34].
3. Real-Time Error Correction Operation Model for Integrated Energy System
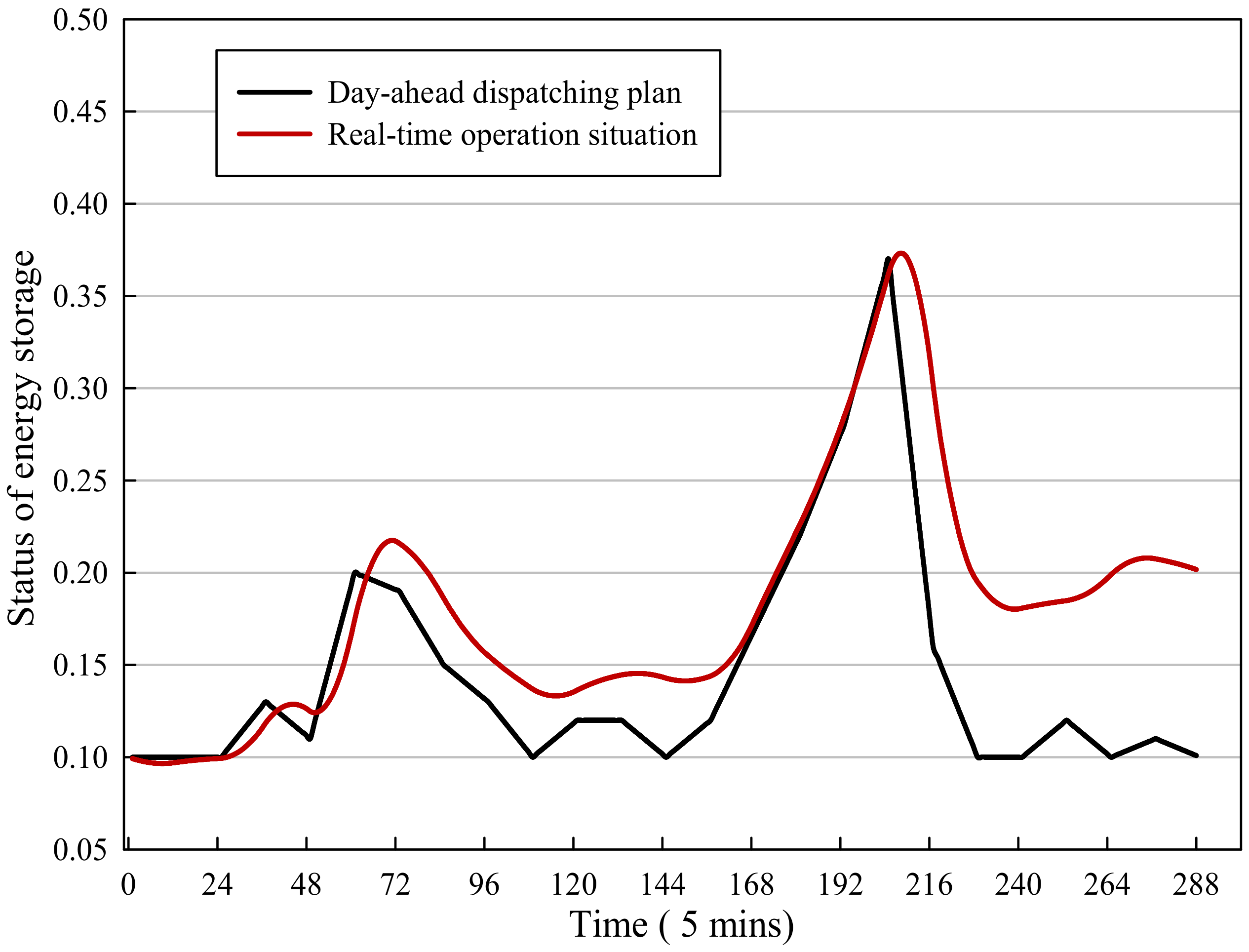
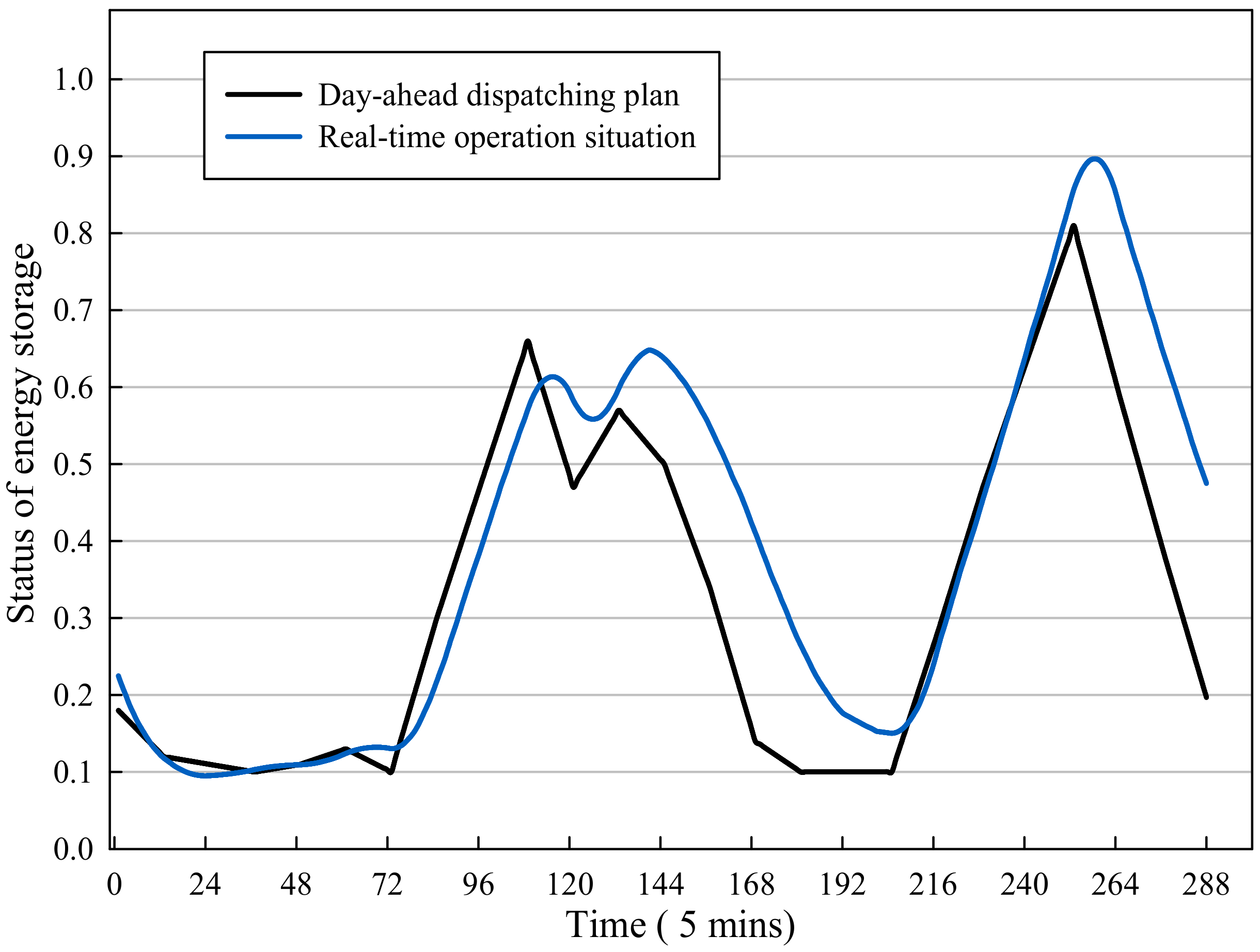
The real-time operation of the integrated energy system is based on the day-ahead optimization scheduling plan, with the time scale of one hour per power output, which has the goal of peak shifting and valley filling to reduce operating costs by the overall scheduling of all the energy supply equipment in the integrated energy system, based on peak and valley electricity prices from the perspective of a day as the optimization cycle. During real-time operation, the real-time values of renewable energy generation equipment output and various types of load deviate from the predicted value and need to be adjusted by various types of energy supply equipment and storage devices in the dispatch system, to ensure the balance of supply and demand within the entire system and ensure that the system could operate safely and stably.
Due to the revision of the previous dispatching plan, the original dispatching strategy became no longer applicable. A real-time error correction operation model of the integrated energy system is proposed to perform real-time operation correction based on the day-ahead dispatching plan.
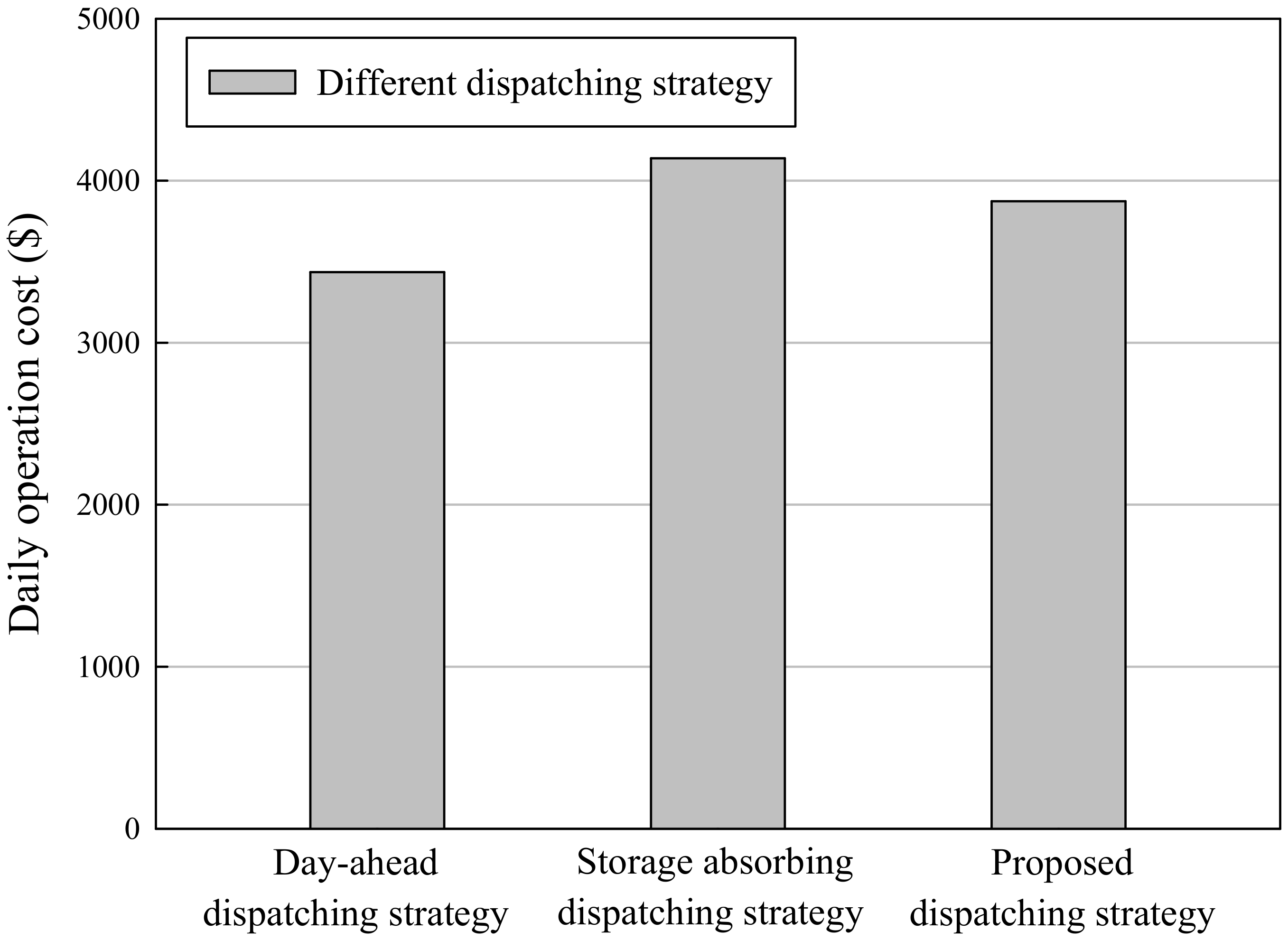
The real-time error correction operation model is a static optimization model which focuses on the single-point operation correction at the next moment and the optimization goal of the model cannot be selected as economically optimal, because in a single moment of operation, the economically optimal scheduling method uses all energy storage to smooth the unbalanced power, which will lead to a large discrepancy with the previously planned operation strategy, resulting in the phenomenon of local optimal operation interfering the global optimal operation.
For example, in a simple integrated energy system containing only a micro gas turbine based CCHP unit and a set of cold and heat energy storage equipment, generally speaking, the unit power adjustment cost of energy storage is the lowest, while the unit power adjustment cost of the micro gas turbine based CCHP unit is higher, along with the fuel cost required to adjust the operating power. In the day-ahead economic dispatch, due to the characteristics of time-of-use electricity prices and load curves, energy storage equipment is generally arranged to charge at low electricity prices at night and to release energy when the electricity price is high during the daytime [
34]. In other words, during the period of low electricity prices, various types of electric-heat (cold) conversion equipment should be used to supply multi-energy loads and the energy storage equipment should be in a charged state from the global perspective to improve system economy. Suppose at one moment
t within the period of low electricity prices at night, the heating or cooling load is greater than expected; then, at this single point of time, the economically optimal dispatching solution for the time interval is to allow the energy storage to undertake the unbalanced power, but as a cost at this time, the energy stored is released and the energy storage capacity is reduced, so there is not much energy to release during the day when the electricity price is high, and the economy of the entire system will be affected. Therefore, from a global perspective, a reasonable approach should be to increase the power output of electric-heat (cold) conversion equipment to compensation the power deficit, rather than the discharge of energy storage equipment with low costs at that time.
In the process of real-time operation correction, the concept of multi equipment energy supply droop control in the integrated energy system is put forward. Considering the total capacity of each energy supply and energy storage equipment, adjustable margin, power climbing speed and adjustment cost, the droop rate of each equipment at the next moment was formulated and the unbalanced power is shared by each energy supply and energy storage equipment, which ensures the power output change trend of the energy supply equipment consistent with the day-ahead dispatching plan at the next time interval and the global economic operation of the integrated energy system.
3.1. Determination of Energy Supply Increment
In the operation of an integrated energy system, two multi-energy loads and renewable energy generation predictions with different time scales are generally required, which are short-term prediction and ultra-short-term prediction. Among them, the short-term prediction generally refers to the day-ahead or a few days ago prediction; the time scale is carried out by days and is generally used for day-ahead dispatching, while the ultra-short-term prediction is generally executed in units of minutes and used for predicting the multi-energy loads and the renewable energy power generation situation at the next moment, which are used for guiding the dispatch system and dispatch personnel to perform related dispatch operations [
35,
36,
37].
The reason why we need ultra-short-term prediction is that the multi-energy loads and renewable energy power generation conditions predicted day-ahead generally deviate from the actual situation, and the results of ultra-short-term forecasting can nearly be regarded as real-time data, although there will still be some tiny deviations between them, but this difference can be resolved by system inertia.
Suppose the day-ahead predicted value of the electrical load in the integrated energy system at time
is
, the day-ahead predicted value of the space heating load and hot water load at time
are
and
respectively, the day-ahead predicted value of the space cooling load and refrigeration load at time
are
and
respectively, the day-ahead predicted generated power value of the renewable power generation system is
; The electrical load value at time
obtained by ultra-short-term load prediction at time
t is
, the space heating load and hot water load at time
obtained by ultra-short-term load prediction at time
t are
and
respectively, the space cooling load and refrigeration load at time
obtained by ultra-short-term load prediction at time
t are
and
respectively, the generated power value of the renewable power generation system at time
obtained by ultra-short-term power generation prediction at time
t is
, then the adjustment increment of the system’s pure electrical load at time
is:
The increment of the system’s space heating load at time
is:
The increment of the system’s hot water load at time
is:
The increment of the system’s space cooling load at time
is:
The increment of the system’s refrigeration load at time
is:
In the above equations, the reason we make the difference is because the forecast is deviated, and the day-ahead dispatching plan is made based on the results of the day-ahead prediction. The day-ahead dispatching plan takes a quite long calculation time and if the results of ultra-short-term load prediction are substituted into the day-ahead dispatching model, the calculation time requirements cannot be met. Therefore, this paper proposes the real-time dispatching model of the integrated energy system. At time , the task that needs to be accomplished is to distribute these load adjustment increments to each energy supply equipment and energy storage device to complete the real-time operation correction. Since the processing methods of various types of load are similar, the space heating load increment distribution is taken as an example for description and the other types of load increment can be distributed with reference to the space heating load.
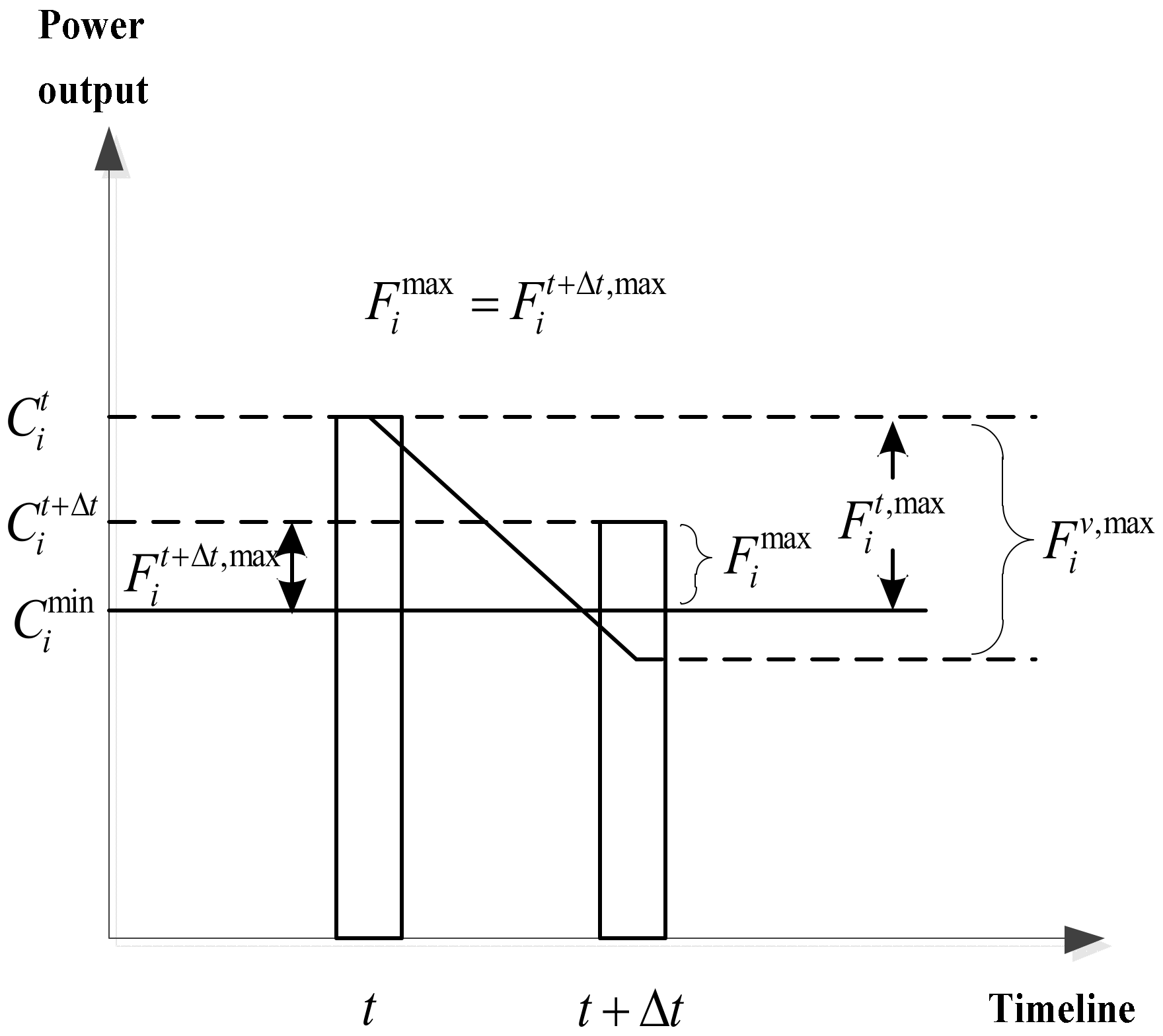
3.2. Real-Time Maximum Adjustable Power Output Constraint
The maximum adjustable power output of the energy supply equipment and energy storage equipment in the integrated energy system is subject to power upper and lower limit and power climbing speed. When
is a positive value, which means additional power supply is required, the power upward adjustment margin of the
ith space heating load energy supply and storage device at time
t is:
The power upward adjustment margin of the
ith space heating load energy supply and storage device at time
is:
where
and
are the maximum upward power adjustment ranges of the
ith space heating load energy supply and storage equipment at time
t and
respectively,
and
are the real-time power output and planned power output of of the
ith space heating load energy supply and storage equipment at time
t and
respectively,
is the upper limit of the power output of the
ith space heating load energy supply and storage equipment.
The power climbing constraints are:
where
is the maximum increasing rate of the
ith space heating load energy supply and storage equipment,
is the maximum power increase in period of
.
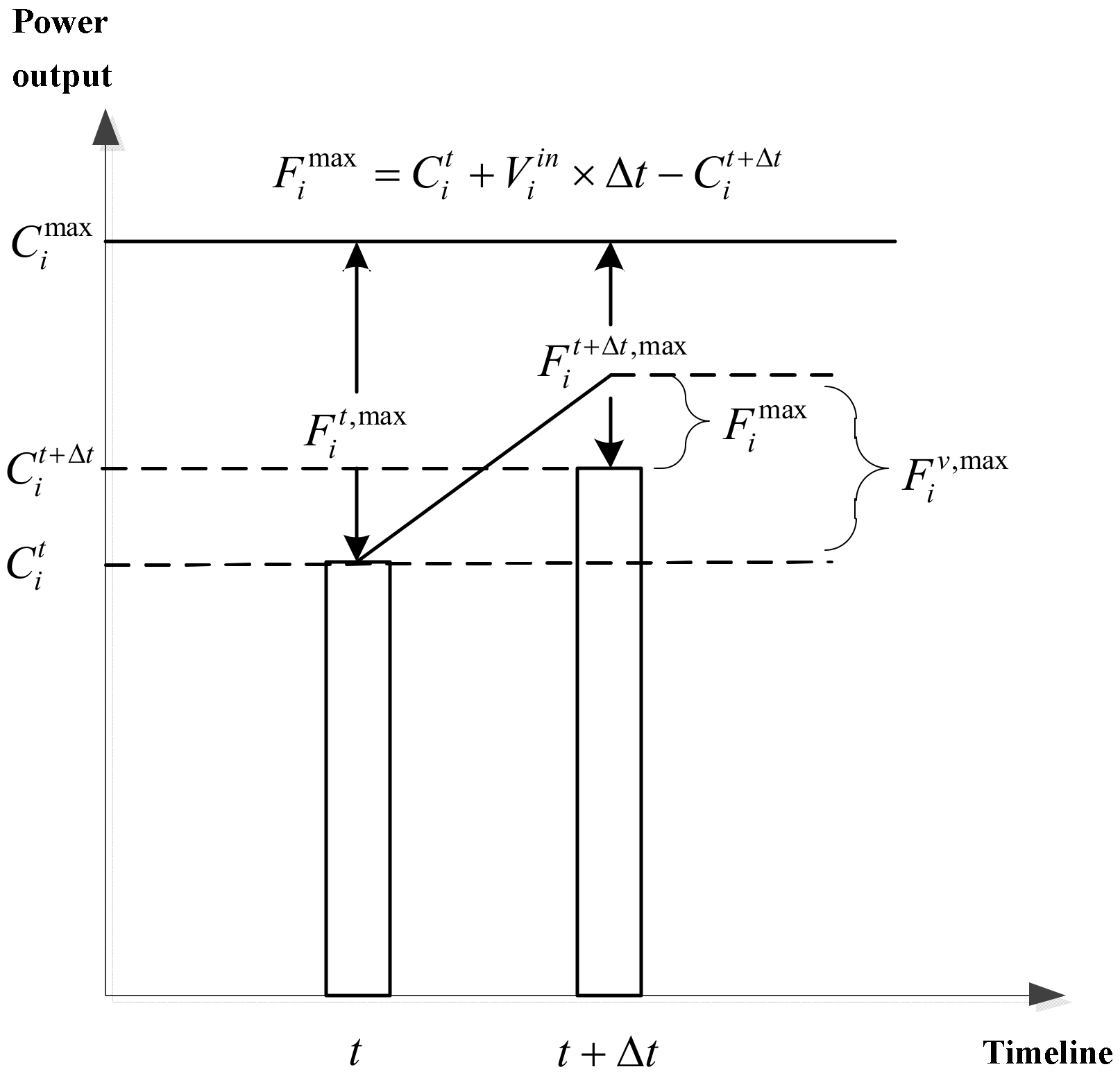
By comparing
and
, the maximum planned power adjustment amount
of the equipment at time
can be obtained. When
is greater than
, which means there is sufficient adjustable capacity; as shown in
Figure 2, the maximum planned power adjustment amount
is as follows:
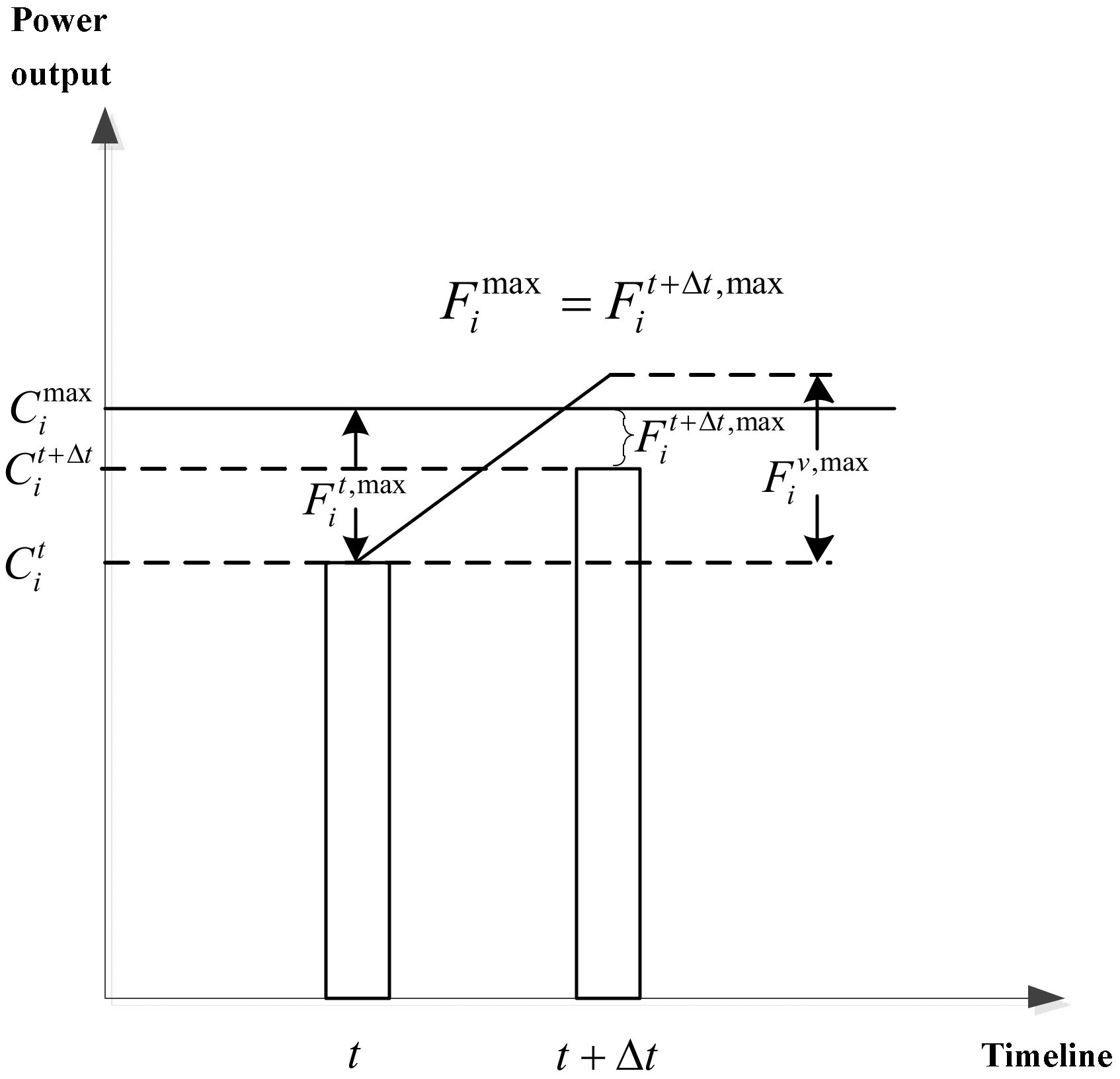
When
is less than
, which means there is not enough adjustable capacity, as shown in
Figure 3, the maximum planned power adjustment amount
is as follows:
When
is a negative value which means reduction of power supply is required, the power downward adjustment margin of the
ith space heating load energy supply and storage device at time
t is:
The power downward adjustment margin of the
ith space heating load energy supply and storage device at time
is:
where
and
are the maximum downward power adjustment ranges of the
ith space heating load energy supply and storage equipment at time
t and
respectively,
and
are the real-time power output and planned power output of the
ith space heating load energy supply and storage equipment at time
t and
respectively,
is the lower limit of the power output of the
ith space heating load energy supply and storage equipment.
The power climbing constraints are:
where
is the maximum decreasing rate of the
ith space heating load energy supply and storage equipment,
is the maximum power decrease in period of
.
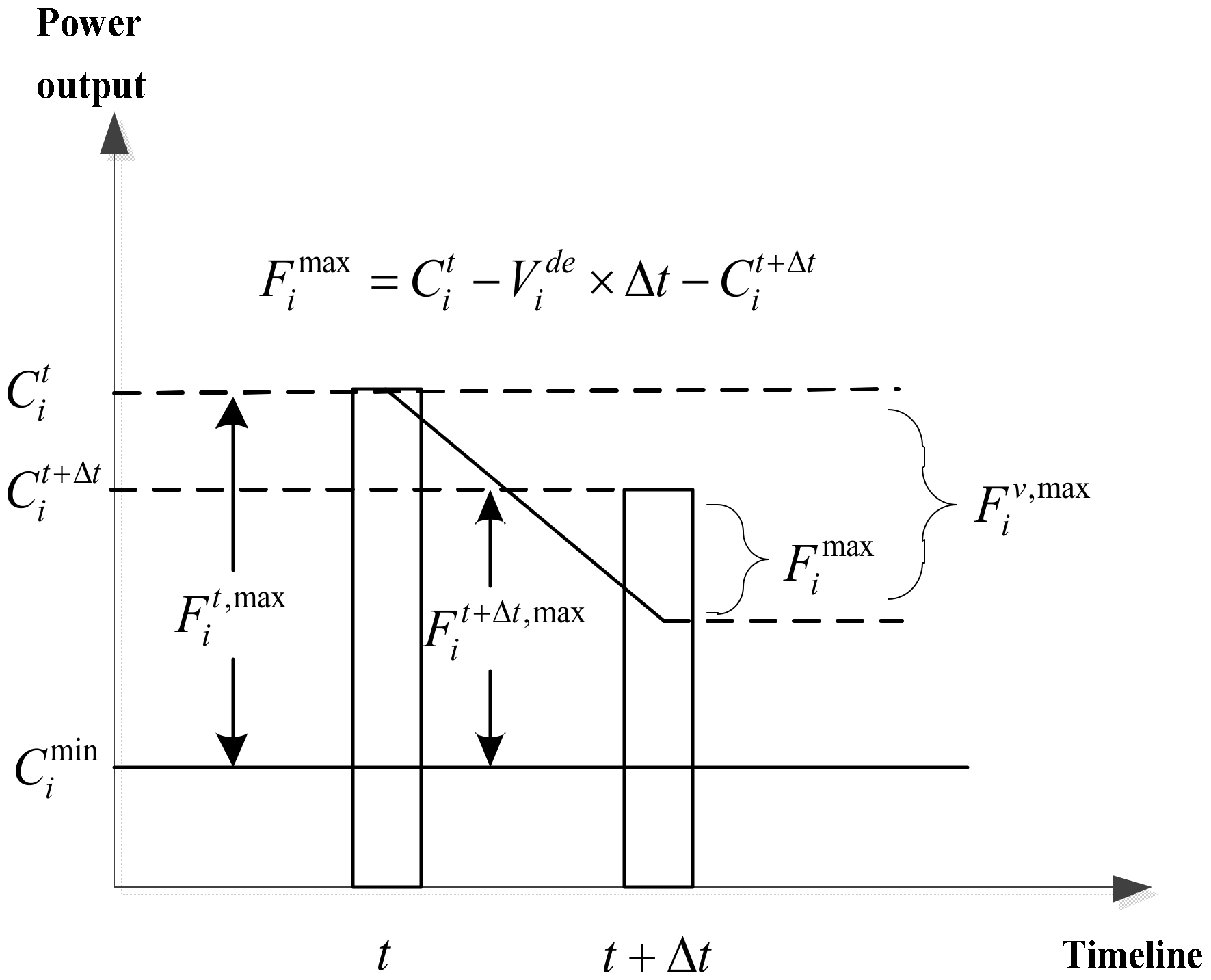
By comparing
and
, the maximum planned power adjustment amount
of the equipment at time
can be obtained. When
is greater than
, which means there is sufficient adjustable capacity, as shown in
Figure 4, the maximum planned power adjustment amount
is as follows:
When
is less than
, which means there is not enough adjustable capacity as shown in
Figure 5, the maximum planned power adjustment amount
is as follows:
3.3. Determination of Real-Time Error Correction Droop Rate of Energy Supply Distribution
Select the space heating load energy supply and storage equipment in the integrated energy system and define the energy supply coefficient of the
ith energy supply and storage equipment as:
The absolute value operation is added, in order to avoid the increase of the charging power if the energy storage device is in the charging state, when the energy supply increment is positive and additional power supply is required, but reduce the charging power to convert it into an equivalent energy supply unit and perform energy supply together with other energy supply equipment.
Count all the adjustable energy supply units and sum the energy supply coefficients of all units:
where
is the energy supply coefficient of the
ith energy supply and storage equipment,
is the total energy supply coefficient,
n is the number of space heating load energy supply and storage units with adjustable capacity.
Therefore, the real-time error correction energy supply distribution droop rate of the
ith energy supply and storage equipment is:
At time
, the energy supply adjustment power undertaken by the
ith energy supply and storage equipment is:
where
is the unbalanced power to be allocated and
is the energy supply adjustment power undertaken by the
ith energy supply and storage equipment.
3.4. Verification and Updating the Real-Time Energy Supply Adjustment Power
When the adjustment power is distributed by the real-time error correction droop rate, it is necessary to verify whether the energy supply adjustment power undertaken by the
ith energy supply and storage equipment exceeds the maximum planned power adjustment amount
. Considering that it is possible that a device cannot undertake the adjustment power determined by the droop rate, due to power output exceeding the limit, it is necessary to allocate the adjustment power multiple times. Therefore, the energy supply adjustment power undertaken by the
ith energy supply and storage equipment can be written as:
At the first adjustment:
where
is the planned power output of the
ith energy supply and storage equipment at time
after the last distribution.
When
, the device cannot undertake the task of drooping power adjustment, the planned power output of the
ith energy supply and storage equipment at time
is set as:
When
, the device could undertake the task of drooping power adjustment, the planned power output of the
ith energy supply and storage equipment at time
is set as:
If there is energy supply equipment that cannot undertake the drooping power adjustment task, there will still be a certain amount of power deficit. At this time, the algorithm returns to
Section 3.3 for the redistribution of the unbalanced power, until all the energy supply equipment is adjusted according to the drooping power and the real-time operation error correction task is completed.
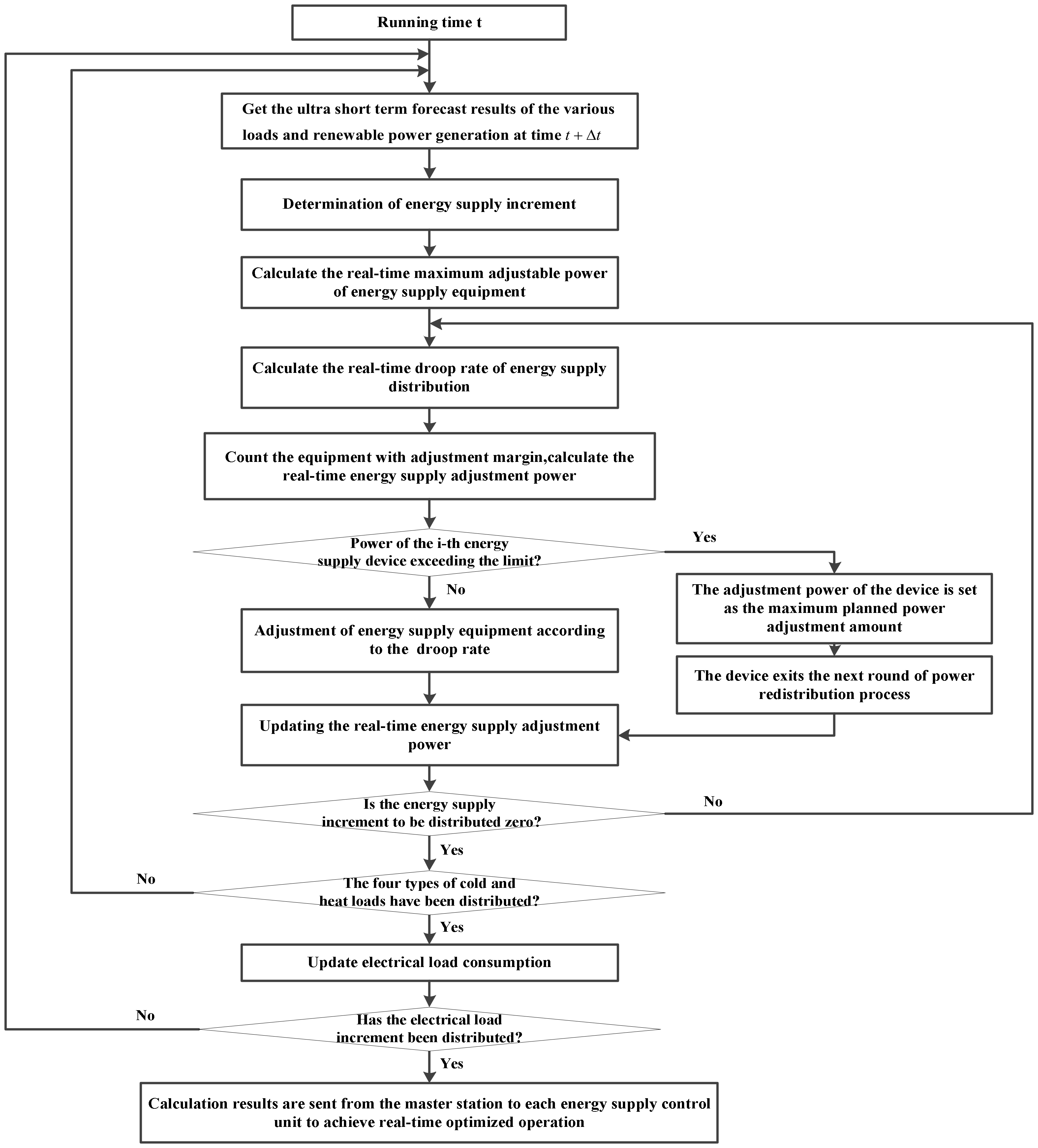
3.5. Real-Time Operation Error Correction Process
The above real-time operation error correction model takes space heating load as an example for illustration. In the actual operation process, four other types of loads must be considered. Among them, the real-time unbalanced power distribution and adjustment of hot water load, space cooling load and refrigeration load can refer to space heating load. When the adjustment of these four types of loads is completed, the power consumption of all energy supply equipment that consumes electricity for cold or heat energy production is updated. Combining the ultra-short-term electrical load forecast and renewable energy power generation forecast at time , the ultra-short-term forecast results of the net electrical load are obtained, and then the real-time unbalanced power distribution of electrical loads is performed, with reference to the above types of loads.
The real-time error correction operation algorithm is written in Matlab (R2012a, MathWorks, Natick, MA, USA) to solve the real-time error correction operation model of the integrated energy system in this paper. The real-time operation error correction process for the integrated energy system can be described by
Figure 6.