An Efficient Analytical Approach for the Solution of Certain Fractional-Order Dynamical Systems
Abstract
1. Introduction
2. Preliminaries
3. Homotopy Perturbation Shehu Transform Method
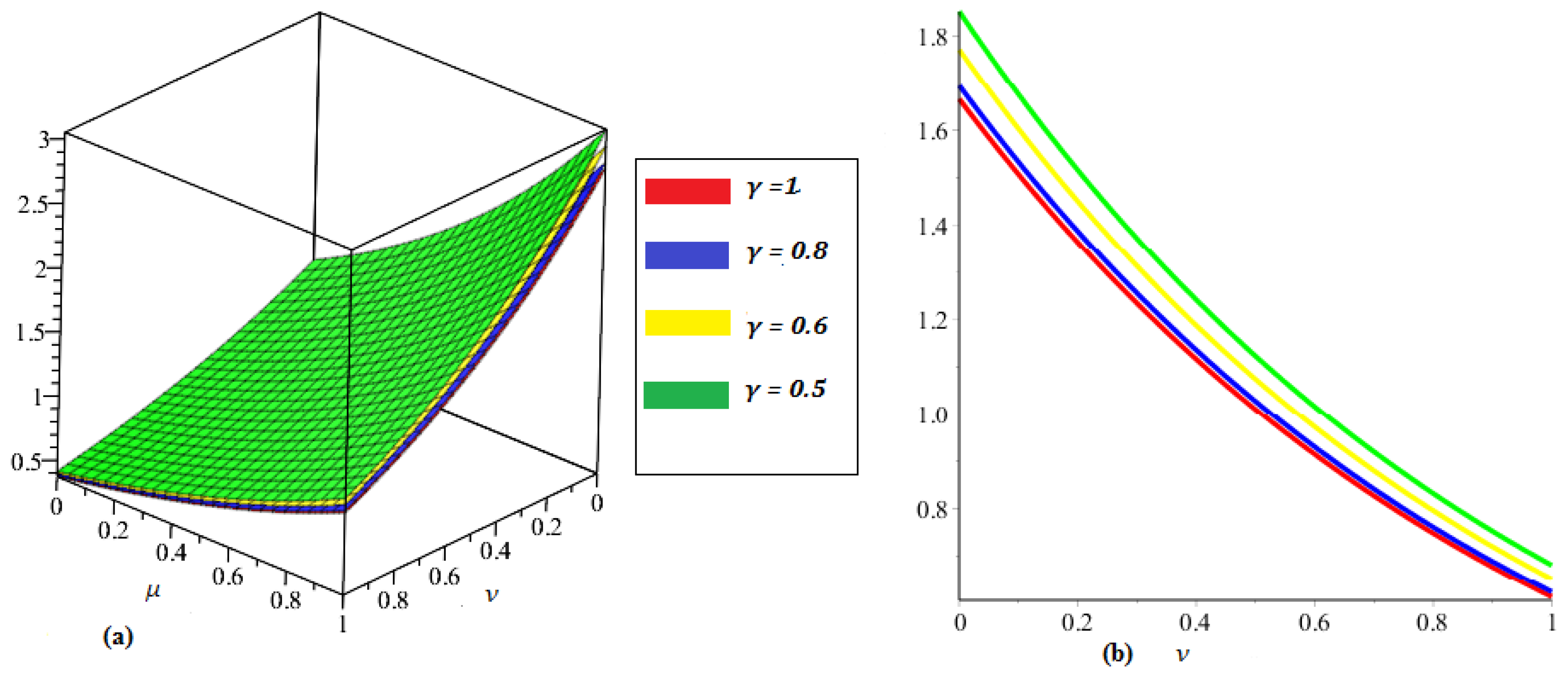
4. Applications
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Data Availability
References
- Linge, S.; Sundnes, J.; Hanslien, M.; Lines, G.T.; Tveito, A. Numerical solution of the bidomain equations. Philos. Trans. R. Soc. Math. Phys. Eng. Sci. 2009, 367, 1931–1950. [Google Scholar] [CrossRef] [PubMed]
- Sundnes, J.; Lines, G.T.; Mardal, K.A.; Tveito, A. Multigrid block preconditioning for a coupled system of partial differential equations modeling the electrical activity in the heart. Comput. Methods Biomech. Biomed. Eng. 2002, 5, 397–409. [Google Scholar] [CrossRef] [PubMed]
- Sundnes, J.; Lines, G.T.; Tveito, A. An operator splitting method for solving the bidomain equations coupled to a volume conductor model for the torso. Math. Biosci. 2005, 194, 233–248. [Google Scholar] [CrossRef] [PubMed]
- Aksikas, I.; Fuxman, A.; Forbes, J.F.; Winkin, J.J. LQ control design of a class of hyperbolic PDE systems: Application to fixed-bed reactor. Automatica 2009, 45, 1542–1548. [Google Scholar] [CrossRef]
- Moghadam, A.A.; Aksikas, I.; Dubljevic, S.; Forbes, J.F. LQ control of coupled hyperbolic PDEs and ODEs: Application to a CSTR-PFR system. IFAC Proc. Vol. 2010, 43, 721–726. [Google Scholar] [CrossRef]
- Fackeldey, K.; Krause, R. Multiscale coupling in function space—Weak coupling between molecular dynamics and continuum mechanics. Int. J. Numer. Methods Eng. 2009, 79, 1517–1535. [Google Scholar] [CrossRef]
- Hedrih, K.R. Fractional order hybrid system dynamics. PAMM 2013, 13, 25–26. [Google Scholar] [CrossRef]
- Lin, L.L.; Li, Z.Y.; Lin, B. Engineering waveguide-cavity resonant side coupling in a dynamically tunable ultracompact photonic crystal filter. Phys. Rev. B 2005, 72, 165330. [Google Scholar] [CrossRef]
- Mahmood, S.; Shah, R.; Arif, M. Laplace Adomian Decomposition Method for Multi Dimensional Time Fractional Model of Navier-Stokes Equation. Symmetry 2019, 11, 149. [Google Scholar] [CrossRef]
- Shah, R.; Khan, H.; Kumam, P.; Arif, M. An analytical technique to solve the system of nonlinear fractional partial differential equations. Mathematics 2019, 7, 505. [Google Scholar] [CrossRef]
- Shah, R.; Khan, H.; Baleanu, D. Fractional Whitham–Broer–Kaup Equations within Modified Analytical Approaches. Axioms 2019, 8, 125. [Google Scholar]
- Srivastava, H.M.; Shah, R.; Khan, H.; Arif, M. Some analytical and numerical investigation of a family of fractional-order Helmholtz equations in two space dimensions. Math. Methods Appl. Sci. 2020, 43, 199–212. [Google Scholar]
- Wald, R.M. Construction of solutions of gravitational, electromagnetic, or other perturbation equations from solutions of decoupled equations. Phys. Rev. Lett. 1978, 41, 203. [Google Scholar]
- Bateman, H. Some recent researches on the motion of fluids. Mon. Weather. Rev. 1915, 43, 163–170. [Google Scholar] [CrossRef]
- Khan, H.; Khan, A.; Al-Qurashi, M.; Shah, R.; Baleanu, D. Modified Modelling for Heat Like Equations within Caputo Operator. Energies 2020, 13, 2002. [Google Scholar] [CrossRef]
- Naghipour, A.; Manafian, J. Application of the Laplace Adomian decomposition and implicit methods for solving Burgers’ equation. TWMS J. Pure Appl. Math. 2015, 6, 68–77. [Google Scholar]
- Rashidi, M.M.; Erfani, E. New analytical method for solving Burgers’ and nonlinear heat transfer equations and comparison with HAM. Comput. Phys. Commun. 2009, 180, 1539–1544. [Google Scholar] [CrossRef]
- Moslem, W.M.; Sabry, R. Zakharov–Kuznetsov–Burger’s equation for dust ion acoustic waves. Chaos Solitons Fractals 2008, 36, 628–634. [Google Scholar] [CrossRef]
- Kannan, R.; Wang, Z.J. A study of viscous flux formulations for a p-multigrid spectral volume Navier stokes solver. J. Sci. Comput. 2009, 41, 165. [Google Scholar]
- Kannan, R.; Wang, Z.J. LDG2: A variant of the LDG flux formulation for the spectral volume method. J. Sci. Comput. 2011, 46, 314–328. [Google Scholar] [CrossRef]
- Kannan, R.; Wang, Z.J. The direct discontinuous Galerkin (DDG) viscous flux scheme for the high order spectral volume method. Comput. Fluids 2010, 39, 2007–2021. [Google Scholar] [CrossRef]
- Kannan, R. A high order spectral volume formulation for solving equations containing higher spatial derivative terms: Formulation and analysis for third derivative spatial terms using the LDG discretization procedure. Commun. Comput. Phys. 2011, 10, 1257–1279. [Google Scholar] [CrossRef]
- Shah, R.; Khan, H.; Baleanu, D.; Kumam, P.; Arif, M. A semi-analytical method to solve family of Kuramoto–Sivashinsky equations. J. Taibah Univ. Sci. 2020, 14, 402–411. [Google Scholar]
- Adomian, G. Solving Frontier Problems of Physics: The Decomposition Method, with a Preface by Yves Cherruault; Fundamental Theories of Physics, Kluwer Academic Publishers Group: Dordrecht, The Netherlands, 1994. [Google Scholar]
- He, J.H. Variational iteration method–a kind of non-linear analytical technique: Some examples. Int. J. Non-Linear Mech. 1999, 34, 699–708. [Google Scholar] [CrossRef]
- Shah, R.; Khan, H.; Baleanu, D.; Kumam, P.; Arif, M. The analytical investigation of time-fractional multi-dimensional Navier–Stokes equation. Alexandria Eng. J. 2020. [Google Scholar] [CrossRef]
- Liao, S.J. Beyond Perturbation: Introduction to the Homotopy Analysis Method; Champan Hall, CRC: Boca Raton, FL, USA, 2003. [Google Scholar]
- Zhou, J.K. Differential Transformation and Its Applications for Electrical Circuits; Huazhong University Press: Wuhan, China, 1986; pp. 1279–1289. [Google Scholar]
- Hilfer, R. Fractional diffusion based on Riemann-Liouville fractional derivatives. J. Phys. Chem. B 2000, 104, 3914–3917. [Google Scholar]
- Ibrahim, R.W. Solutions to systems of arbitrary-order differential equations in complex domains. Electron. J. Differ. Equations 2014, 46, 1–13. [Google Scholar]
- Khan, H.; Shah, R.; Baleanu, D.; Kumam, P.; Arif, M. Analytical Solution of Fractional-Order Hyperbolic Telegraph Equation, Using Natural Transform Decomposition Method. Electronics 2019, 8, 1015. [Google Scholar] [CrossRef]
- Shah, R.; Khan, H.; Mustafa, S.; Kumam, P.; Arif, M. Analytical Solutions of Fractional-Order Diffusion Equations by Natural Transform Decomposition Method. Entropy 2019, 21, 557. [Google Scholar] [CrossRef]
- Oldham, K.B. Fractional differential equations in electrochemistry. Adv. Eng. Softw. 2010, 41, 9–12. [Google Scholar] [CrossRef]
- Scalas, E.; Gorenflo, R.; Mainardi, F. Fractional calculus and continuous-time finance. Phys. Stat. Mech. Appl. 2000, 284, 376–384. [Google Scholar] [CrossRef]
- Liu, F.; Anh, V.; Turner, I. Numerical solution of the space fractional Fokker–Planck equation. J. Comput. Appl. Math. 2004, 166, 209–219. [Google Scholar] [CrossRef]
- Maleknejad, K.; Shahrezaee, M.; Khatami, H. Numerical solution of integral equations system of the second kind by block–pulse functions. Appl. Math. Comput. 2005, 166, 15–24. [Google Scholar]
- Khan, H.; Shah, R.; Arif, M.; Bushnaq, S. The Chebyshev Wavelet Method (CWM) for the Numerical Solution of Fractional HIV Infection of CD4+T Cells Model. Int. J. Appl. Comput. Math. 2020, 6, 1–17. [Google Scholar] [CrossRef]
- Ali, I.; Khan, H.; Shah, R.; Baleanu, D.; Kumam, P.; Arif, M. Fractional View Analysis of Acoustic Wave Equations, Using Fractional-Order Differential Equations. Appl. Sci. 2020, 10, 610. [Google Scholar]
- Jan, R.; Xiao, Y. Effect of partial immunity on transmission dynamics of dengue disease with optimal control. Math. Methods Appl. Sci. 2019, 42, 1967–1983. [Google Scholar] [CrossRef]
- Jan, R.; Xiao, Y. Effect of pulse vaccination on dynamics of dengue with periodic transmission functions. Adv. Differ. Equ. 2019, 1, 368. [Google Scholar] [CrossRef]
- Lazopoulos, K.; Lazopoulos, A. On the mathematical formulation of fractional derivatives. Prog. Fract. Differ. Appl. 2019, 5, 261–267. [Google Scholar]
- He, J.H. Homotopy perturbation technique. Comput. Methods Appl. Mech. Eng. 1999, 178, 257–262. [Google Scholar] [CrossRef]
- He, J.H. A coupling method of a homotopy technique and a perturbation technique for non-linear problems. Int. J. Non-Linear Mech. 2000, 35, 37–43. [Google Scholar] [CrossRef]
- He, J.H. Application of homotopy perturbation method to nonlinear wave equations. Chaos Solitons Fractals 2005, 26, 695–700. [Google Scholar] [CrossRef]
- He, J.H. Homotopy perturbation method for bifurcation of nonlinear problems. Int. J. Nonlinear Sci. Numer. Simul. 2005, 6, 207–208. [Google Scholar] [CrossRef]
- He, J.H. Homotopy perturbation method for solving boundary value problems. Phys. Lett. 2006, 350, 87–88. [Google Scholar] [CrossRef]
- Jafari, H.; Nazari, M.; Baleanu, D.; Khalique, C.M. A new approach for solving a system of fractional partial differential equations. Comput. Math. Appl. 2013, 66, 838–843. [Google Scholar] [CrossRef]
- Machado, J.; Baleanu, D.; Chen, W.; Sabatier, J. New trends in fractional dynamics. J. Vib. Control SAGE Public. 2014, 20, 963. [Google Scholar] [CrossRef]
- Baleanu, D.; Guvenc, Z.; Machado, J. New Trends in Nanotechnology and Fractional Calculus Applications; Springer: Dordrecht, The Netherlands, 2010. [Google Scholar]
- Maitama, S.; Zhao, W. New integral transform: Shehu transform a generalization of Sumudu and Laplace transform for solving differential equations. arXiv 2019, arXiv:1904.11370. [Google Scholar]
- Khan, H.; Farooq, U.; Shah, R.; Baleanu, D.; Kumam, P.; Arif, M. Analytical Solutions of (2+ Time Fractional Order) Dimensional Physical Models, Using Modified Decomposition Method. Appl. Sci. 2020, 10, 122. [Google Scholar] [CrossRef]
- Bokhari, A.; Baleanu, D.; Belgacem, R. Application of Shehu transform to Atangana-Baleanu derivatives. J. Math. Comput. Sci. 2019, 20, 101–107. [Google Scholar] [CrossRef]
- Belgacem, R.; Baleanu, D.; Bokhari, A. Shehu Transform and Applications to Caputo-Fractional Differential Equations. Int. J. Anal. Appl. 2019, 17, 917–927. [Google Scholar]
- Yıldırım, A.; Kelleci, A. Homotopy perturbation method for numerical solutions of coupled Burger’s equations with time-and space-fractional derivatives. Int. J. Numer. Methods Heat Fluid Flow 2010, 20, 897–909. [Google Scholar] [CrossRef]
- Maitama, S. A hybrid natural transform homotopy perturbation method for solving fractional partial differential equations. Int. J. Differ. Equ 2016, 2016, 9207869. [Google Scholar] [CrossRef]
- Prakash, A.; Verma, V.; Kumar, D.; Singh, J. Analytic study for fractional coupled Burger’s equations via Sumudu transform method. Nonlinear Eng. 2018, 7, 323–332. [Google Scholar]






| HPLTM | HPLTM | HPSTM | HPSTM | HPM [54] | HPM [54] | ||
|---|---|---|---|---|---|---|---|
| 1 | 8.19373 | 7.06835 | 8.19373 | 7.06835 | 8.19373 | 7.06835 | |
| 2 | 8.85419 | 7.63809 | 8.85419 | 7.63809 | 8.85419 | 7.63809 | |
| 0.1 | 3 | 1.37414 | 1.18540 | 1.37414 | 1.18540 | 1.37414 | 1.18540 |
| 4 | 7.36928 | 6.35714 | 7.36928 | 6.35714 | 7.36928 | 6.35714 | |
| 5 | 9.33742 | 8.05496 | 9.33742 | 8.05496 | 9.33742 | 8.05496 | |
| 1 | 1.40490 | 2.32077 | 1.40490 | 2.32077 | 1.40490 | 2.32077 | |
| 2 | 1.51814 | 2.50784 | 1.51814 | 2.50784 | 1.51814 | 2.50784 | |
| 0.2 | 3 | 2.35611 | 3.89208 | 2.35611 | 3.89208 | 2.35611 | 3.89208 |
| 4 | 1.26354 | 2.08726 | 1.26354 | 2.08726 | 1.26354 | 2.08726 | |
| 5 | 1.60100 | 2.64471 | 1.60100 | 2.64471 | 1.60100 | 2.64471 | |
| 1 | 1.92364 | 1.79300 | 1.92364 | 1.79300 | 1.92364 | 1.79300 | |
| 2 | 2.07869 | 1.93753 | 2.07869 | 1.93753 | 2.07869 | 1.93753 | |
| 0.3 | 3 | 3.22607 | 3.00698 | 3.22607 | 3.00698 | 3.22607 | 3.00698 |
| 4 | 1.73008 | 1.61259 | 1.73008 | 1.61259 | 1.73008 | 1.61259 | |
| 5 | 2.19214 | 2.04327 | 2.19214 | 2.04327 | 2.19214 | 2.04327 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qin, Y.; Khan, A.; Ali, I.; Al Qurashi, M.; Khan, H.; Shah, R.; Baleanu, D. An Efficient Analytical Approach for the Solution of Certain Fractional-Order Dynamical Systems. Energies 2020, 13, 2725. https://doi.org/10.3390/en13112725
Qin Y, Khan A, Ali I, Al Qurashi M, Khan H, Shah R, Baleanu D. An Efficient Analytical Approach for the Solution of Certain Fractional-Order Dynamical Systems. Energies. 2020; 13(11):2725. https://doi.org/10.3390/en13112725
Chicago/Turabian StyleQin, Ya, Adnan Khan, Izaz Ali, Maysaa Al Qurashi, Hassan Khan, Rasool Shah, and Dumitru Baleanu. 2020. "An Efficient Analytical Approach for the Solution of Certain Fractional-Order Dynamical Systems" Energies 13, no. 11: 2725. https://doi.org/10.3390/en13112725
APA StyleQin, Y., Khan, A., Ali, I., Al Qurashi, M., Khan, H., Shah, R., & Baleanu, D. (2020). An Efficient Analytical Approach for the Solution of Certain Fractional-Order Dynamical Systems. Energies, 13(11), 2725. https://doi.org/10.3390/en13112725






