A Comparison of the Risk Quantification in Traditional and Renewable Energy Markets

Abstract

The transition from traditional energy to cleaner energy sources has raised concerns from companies and investors regarding, among other things, the impact on financial downside risk. This article implements backtesting techniques to estimate and validate the value-at-risk (VaR) and expected shortfall (ES) in order to compare their performance among four renewable energy stocks and four traditional energy stocks from the WilderHill New Energy Global Innovation and the Bloomberg World Energy for the period 2005-2016. The models used to estimate VaR and ES are AR(1)-GARCH(1,1), AR(1)-EGARCH(1,1), and AR(1)-APARCH(1,1), all of them under either normal, skew-normal, Student’s t, skewed-t, Generalized Error or Skew-Generalized Error distributed innovations. Backtesting performance is tested through traditional Kupiec and Christoffersen tests for VaR, but also through recent backtesting ES techniques. The paper extends these tests to the skewed-t, skew-normal and Skew-Generalized Error distributions and applies it for the first time in traditional and renewable energy markets showing that the skewed-t and the Generalized Error distribution are an accurate tool for risk management in those markets. Our findings have important implications for portfolio managers and regulators in terms of capital allocation in renewable and traditional energy stocks, mainly to reduce the impact of possible extreme loss events.

1. Introduction

The demise of fossil fuels is imminent, as can be seen in the recent generation of electricity in the United States. In April 2019, for the first time, renewable sources generated more electricity than coal, according to Bloomberg News based on data from the Energy Information Administration [1]. Moreover, Saudi Arabia is keen to move towards clean energy development, recognizing the changing global agenda in energy resources [2]. This climate shift is leading to concerns among regulators and investors regarding financial downside risk. Consequently, risk quantification and management of financial assets related to traditional and renewable energy have become increasingly important in both academia and industry. This interest is triggered by different issues, such as the high energy price volatility or the demand for mitigation of climate change, which encourages the intensification of energy generation from renewable sources, among others.

In energy markets, it is known that renewable energy stocks are more volatile than traditional energy stocks; the annual volatility between 2005 and 2016 associated with the main traditional energy index, Bloomberg World Energy (BWEI), was 17%, while that of the main renewable energy index, WilderHill New Energy Global Innovation (NEX), was 35%. This difference in volatility can be explained by several factors that more aggressively affect renewable energy stocks; among them, weather conditions, inventory levels, geopolitical events, legislation and exchange rate movements [3]. As a result, investors participating in this market face higher risks in comparison to the traditional energy market.

Regarding investment opportunities, the global green economy represents market capitalization comparable to the fossil fuel sector as of December 2017, according to an FTSE Russell research [4]. Although the market share for each sector represents around 6% (USD 4 trillion), the green economy has been growing since 2013, and it could represent 7% by 2030 based on the current trend. The potential growth could be higher, considering that renewables (excluding hydropower) produce only 8% of the world’s electricity, and financial innovation is helping in developing new ways of investing in renewable energy, as stated in a report of the Economist Intelligence Unit [5]. On the other hand, there has been a decreasing tendency in fossil fuel share since 2011. However, there is a greater role to be played by governments in mitigating the effects of climate change. For instance [6], a Senator in Nebraska argued that renewable energy is very expensive, and replacing traditional energy sources is not foreseeable in the short term.

There are some other risk factors faced by investment in traditional or renewable energy. The performance of traditional energy investment depends greatly on the behavior of oil prices, which is conditional on the supply and demand of the commodity. Oil amounted to 46% of global energy supply during the Arab oil embargo in 1973. In 2014 the stranded assets (fossil fuels) still dominated the energy market, 31% for oil, 29% for coal, and 21% for natural gas, whereas the main renewable sources (wind, solar and geothermal energy) only accounted for around 1% of the market supply.

Additionally, oil companies are under pressure by European and American shareholders who ignore how these companies are going to deal with their business if regulation becomes more oriented to a “cleaner” world energy market. This raises concerns for financial regulators, especially for the current Governor of Bank of England (Mark Carney), about the financial instability potentially caused by the energy transition, since around 80% of fossil fuel reserves could be stranded [7]. Energy markets are becoming more volatile, and shares that were profitable in the past could return huge losses to investors. This is the case of stock prices of E.ON and RWE (the two largest German utilities companies), which declined by two thirds after Japan’s Fukushima nuclear disaster in 2011 [8].

For all the previously stated reasons, there is a need to assess potential losses adequately in traditional and renewable energy financial assets. More specifically, it is necessary to gauge the market risk posed by investments in such assets. To this end, our study implements validation tests on the recently proposed risk measure by the Basel Committee, expected shortfall (ES), which captures the tail risk more adequately than its predecessor, the Value-at-Risk measure. Nonetheless, the accuracy of the risk measure depends on the distribution assumed to fit the returns of the assets.

In this context, the purpose of this study is to provide a technical approach to quantifying market risk measures and compare its performance between traditional and renewable energy markets, considering the financial regulation changes by the BCBS combined with new ES backtesting techniques proposed in the literature. The dataset is composed of four traditional energy stocks, Epistar, Kingspan, Boralex, Nibe, and four traditional energy stocks, Exxon Mobil, Chevron, Total S.A., Schlumberger, the period is from January 2005 to December 2016, for a total of 2901 prices and 2900 log-returns.

Furthermore, we extend the analysis to the skew-normal, skewed-t, Generalized Error and Skew-Generalized Error distributions (GED and SGED henceforth, respectively) under a comprehensive analysis of AR-GARCH/EGARCH/APARCH processes to filter the returns of the analyzed stocks over the period 2005–2016. Our results indicate that the skewed-t and the SGED are the probability distributions that perform best in backtesting when the AR(1)-GARCH(1,1) model is used. In general, there are more VaR violations with renewable energy stocks than with traditional energy stocks; however, renewable energy stocks perform better in ES backtesting than traditional energy stocks. All this reveals the skewed-t and the SGED to be very accurate tools for quantifying ES and implementing risk management policies in energy markets. In terms of ES, the skew-t has better results in the traditional energy sector, and the SGED performs better in the renewable energy sector.

The remainder of this paper is structured as follows. Section 2 provides a literature review in risk quantification. Section 3 reviews the VaR and ES methodologies, as well as the AR-GARCH models. Section 4 presents the data. Section 5 shows an application of VaR and ES backtesting to traditional and renewable energy stocks and the results of the application, whereas Section 6 presents a discussion in light of the new regulation. Lastly, Section 7 summarizes the conclusions.

2. Literature Review: Risk Quantification

This study applies recent ES tests proposed by Acerbi and Székely [9,10] and extends these tests to the skewed Student’s t (skewed-t hereafter) and SGED distributions, which are flexible distributions with good performance for capturing risk in financial markets. We introduce this approach to measuring risk in the renewable energy market and present a comparison in terms of risk assessment with the traditional energy market. The paper aims to provide adequate tools for investors, portfolio and risk managers, and regulators to mitigate the negative impact of several risk factors on investments in traditional and renewable energy stocks.

Risk in energy markets has traditionally been quantified through Value-at-Risk (VaR) [11,12], which can be defined as the maximum expected loss at a given confidence level and time horizon. Statistically, VaR corresponds to a quantile of the asset return distribution. Despite its common use, this measure does not meet the ‘subadditivity’ property or diversification criteria, which means that it is not consistent with portfolio diversification, i.e., the risk of a diversified portfolio may be higher than that incurred independently by its components [13]. Additionally, it is argued that VaR is unable to adequately capture fat-tailed risk and thus performed poorly during the recent financial crisis. Consequently, in 2013, the Basel Committee on Banking Supervision (BCBS) decided to replace VaR at the 1% significance level with ES also known as Tail VaR (TVaR) or Conditional VaR (CVaR), at a 2.5% significance level as the appropriate measure to estimate the regulatory capital under Basel III. ES, defined as the expected loss given that losses have exceeded VaR, is a coherent risk measure [14]. This implies that it not only has better mathematical properties than VaR, but that it also captures the extreme loss events that impact the price of traditional and renewable energy stocks in periods of high instability. However, despite these improvements, ES has not been fully accepted due to criticisms regarding its implementation; these are mainly linked to the lack of ‘elicitability’ [15] and its implications for backtesting. The latter refers to the process of validating the estimates of the risk measure by verifying whether the realized losses, observed ex post, are in line with the ex-ante estimates or forecasts. Research, see, e.g., Acerbi and Szekely [9], Constanzino and Curran [16], Du and Escanciano [17], Fissler and Ziegel [18] and Fissler et al. [19] has demonstrated that elicitability affects the risk measure selection, but not its validation; therefore, backtesting techniques for ES can be performed.

Recent works have assessed expected shortfall in financial markets [20,21], but also in the energy field. For instance, Ref. [22] applied VaR and ES on energy markets, and the author recommended tougher guidelines for the proposal of Basel III; Ref. [23] also employed these risk measures for hedging comparison using future contracts. On the other hand, for systemic risk, marginal and component ES have been estimated to find that Energy and Industrial sectors are the main risk contributors in the Chinese stock markets [24]. Chinese energy stocks have also been examined for diversification purposes in [25]. The authors found that commodity futures could help to reduce the expected shortfall of the diversified portfolios. Expected shortfall or expected shortage was calculated in food, energy, water and environmental security worldwide data by [26]. Other authors [27] have proposed a risk-averse two-stage stochastic mixed-integer optimization model with Conditional Value-at-Risk or ES as a risk measure for power generation capacity expansion, while Ref. [28] applied the financial risk measures but in an energy security context for better understanding of energy accident risks. In related applications, Ref. [29] employed Bayesian CVaR super-quantile regression on the energy price dataset, whereas Ref. [30] used ES and VaR as risk measures in a real options context.

3. Materials and Methods

This section provides the definitions of VaR and ES with their respective closed expressions according to three probability density functions (pdfs): normal, skew-normal, Student’s t, skewed-t, GED and SGED. Subsequently, the complete VaR/ES measure for different mean-variance models is defined. Finally, the three tests proposed by Acerbi and Székely [9,10] for ES backtesting are presented.

3.1. Dynamics of VaR/ES with Mean and Variance Models

It is known that daily financial returns exhibit characteristics of leptokurtosis (fat-tailed risk), skewness, clustering, and persistence in the conditional volatility, in addition to long memory in stochastic shocks [31,32,33,34,35,36], among others. These returns have a predictable component in their conditional mean, which has traditionally been modeled with ARMA structures; in this case, the AR(1) model is used in accordance with most financial literature. The other standard features have traditionally been captured by different conditional volatility models, among them we chose the GARCH [37], EGARCH [38] and APARCH [39] models; the latter two can capture asymmetric effects on conditional volatility (the so-called ‘leverage effect’, which involves a higher severity of negative returns). From an empirical viewpoint, the combination of AR with these different GARCH models was selected according to their performance and accuracy criteria (e.g., AIC or BIC). The formal representation of the models for the conditional mean and the variance are:

$$\begin{gathered} AR\left(1\right) \\ {\mu }_t=\phi +\varphi {\mu }_{t-1}+{\epsilon }_t, \end{gathered}$$

(1)

where $-1<\varphi <1$ and $\phi >0$.

$$\begin{gathered} GARCH\left(1,1\right) \\ {\sigma }_t^2=\omega +\alpha {\epsilon }_{t-1}^2+\beta {\sigma }_{t-1}^2, \end{gathered}$$

(2)

where $\alpha >0,\beta >0,\alpha +\beta <1$ and $\omega >0$.

$$\begin{gathered} EGARCH\left(1,1\right) \\ \log \left({\sigma }_t^2\right)=\omega +\gamma \left(\left|Z_{t-1}\right|-\mathbb{E}\left|Z_{t-1}\right|\right)+\alpha Z_{t-1}+\beta \log \left({\sigma }_{t-1}^2\right), \end{gathered}$$

(3)

where $\omega >0$ and $\gamma \in ℝ$.

$$\begin{gathered} APARCH\left(1,1\right) \\ {\sigma }_t^{\delta }=\omega +\alpha {\left(\left|{\epsilon }_{t-1}\right|-\gamma {\epsilon }_{t-1}\right)}^{\delta }+\beta {\sigma }_{t-1}^{\delta }, \end{gathered}$$

(4)

where $\delta <0$ and $-1<\gamma <1$.

Standardized errors are modeled according to a certain parametric distribution,

$$Z_t=\frac{{\epsilon }_t}{{\sigma }_t}, ~ \mathrm{iid} F_{\theta }\left(Z_t\right),$$

(5)

where $Z_t$ represents independent and identically distributed (iid) innovations. The normal ($\theta =\left(\mu =0,\sigma =1\right)$), the skew-normal ($\theta =(\mu =0,\sigma =1, \xi$)), Student’s t ($\theta =\nu$), skewed-t ($\theta =\left(\nu ,\lambda \right)$), GED ($\theta =\eta$) and SGED ($\theta =\left(\eta ,\zeta \right)$) distributions are employed to characterize the innovations of GARCH models. Where $\xi$ stands for the skewness parameter in the skew-normal, $\nu$ stands for the degrees of freedom in Student’s t, $\lambda$ stands for skewness parameter in the skewed-t, $\eta$ stands for the shape parameter in GED, and $\zeta$ stands for the skew parameter in SGED.

In the empirical application, we estimate the two risk measures with a time horizon of one day, ${\widehat{ES}}_{t+1, 1-\alpha }^{}$ and ${\widehat{VaR}}_{t+1, 1-\alpha }^{}$, which are subject to the information available up to time t (${ℱ}_t$), which comprises a 500-day rolling window. The parameters of the pdfs associated with the innovations $Z_t$ and the AR(1)-GARCH(1,1), AR(1)-EGARCH(1,1) and AR(1)-APARCH(1,1) model parameters are jointly estimated through maximum likelihood (ML) method and used to estimate the dynamic VaR and ES as follows:

$${\widehat{VaR}}_{t+1,1-\alpha }^{}={\widehat{\mu }}_{t+1}+{\widehat{\sigma }}_{t+1}Va{R}_{1-\alpha }\left(Z_{t+1}\right),$$

(6)

$${\widehat{ES}}_{t+1, 1-\alpha }^{}={\widehat{\mu }}_{t+1}+{\widehat{\sigma }}_{t+1}E{S}_{1-\alpha }\left(Z_{t+1}\right),$$

(7)

where $Va{R}_{1-\alpha }\left(Z_{t+1}\right)$and $E{S}_{1-\alpha }\left(Z_{t+1}\right)$are computed according to Equations (8) and (9), respectively, depending on the distribution function.

3.2. Risk Measures under Different Distributions

Given the innovations, $Z_t \left(\forall t=1\dots T\right)$ with a cumulative distribution function (cdf) $F_Z$, the $Va{R}_{1-\alpha }\left(Z_t\right)$, and $E{S}_{1-\alpha }\left(Z_t\right)$ can be defined as:

$$Va{R}_{1-\alpha }\left(Z\right)=inf\left\{z \in ℝ: F_Z\left(z\right)\ge 1-\alpha \right\},$$

(8)

$$E{S}_{1-\alpha }\left(Z\right)=\frac{1}{\alpha }{\int }_0^{\alpha }Va{R}_{1-q}\left(Z\right)dq,$$

(9)

where $\alpha$ represents the significance level, which conforms to the regulation is set at 1% and 2.5% for the VaR and ES, respectively. According to this notation, VaR and ES are quantified in the left tail of the innovations (1% and 2.5%), and it is denoted VaR at 99% and ES at 97.5%. Equation (8) can be expressed as:

$$Va{R}_{1-\alpha }\left(Z\right)=F_Z^{-1}\left(\alpha \right),$$

(10)

where $F_Z^{-1}$ stands for the quantile function, which is represented by ${\Phi }^{-1}, {\Phi }_{\xi }^{-1}$, $t_{\nu }^{-1}$, $s{t}_{\nu ,\lambda }^{-1}$, $g_{\eta }^{-1}$ and $g_{\eta ,\zeta }^{-1}$ for the cases of the normal, skew-normal, Student’s t, skewed-t, GED and SGED, respectively. Based on Equation (9), and solving the integral, ES under a normal distribution is:

$$E{S}_{1-\alpha }\left(Z\right)=-\frac{\varphi \left({\Phi }^{-1}\left(\alpha \right)\right)}{\alpha },$$

(11)

where $\varphi$ represents the pdf of the standard normal distribution. For the skew-normal distribution, ES is:

$$E{S}_{1-\alpha }\left(Z\right)=e{s}_{1-\alpha }\left(\xi \right),$$

(12)

where $e{s}_{1-\alpha }\left(\xi \right)$ is estimated through numerical integration, using Equation (9) and the pdf of the skew-normal distribution following Fernández and Steel [40] in the general method to transform a unimodal symmetric distribution into a skew-symmetric distribution:

$$sn\left(z,\xi \right)=\{\begin{array}{c}-\frac{2}{\lambda +\frac{1}{\lambda }}\varphi \begin{array}{ccc}\left(\xi z\right)& for& z<0,\end{array}\\ \frac{2}{\lambda +\frac{1}{\lambda }}\varphi \begin{array}{ccc}\left(\frac{z}{\xi }\right)& for& z\ge 0\end{array},\end{array}$$

(13)

where $\xi$ is the skewness parameter ($\xi \in \left(0,\infty \right)$), and $\varphi \left(z\right)$ denotes the standard normal pdf.

For the Student’s t distribution, the ES [41] is expressed as:

$$E{S}_{1-\alpha }\left(Z\right)=-\frac{g_{\nu }\left(t_{\nu }^{-1}\left(\alpha \right)\right)}{\alpha }\left(\frac{\nu +{\left(t_{\nu }^{-1}\left(\alpha \right)\right)}^2}{\nu -1}\right),$$

(14)

where $\nu$ represents the degrees of freedom and $t_{\nu }$and $g_{\nu }$ denote the Student’s t cdf and pdf, respectively.

For the skewed-t distribution, ES is:

$$E{S}_{1-\alpha }\left(Z\right)=e{s}_{1-\alpha }\left(v,\lambda \right),$$

(15)

where $e{s}_{1-\alpha }\left(v,\lambda \right)$ is estimated through numerical integration, using Equation (9) and the pdf of the skewed-t distribution proposed by Fernández and Steel [40]:

$$st\left(z,\lambda \right)=\{\begin{array}{c}-\frac{2}{\lambda +\frac{1}{\lambda }}t\begin{array}{ccc}\left(\lambda z\right)& for& z<0,\end{array}\\ \frac{2}{\lambda +\frac{1}{\lambda }}t\begin{array}{ccc}\left(\frac{z}{\lambda }\right)& for& z\ge 0\end{array},\end{array}$$

(16)

where $\lambda$ is the skewness parameter ($\lambda \in \left(0,\infty \right)$), and $t\left(z\right)$ denotes the Student’s t pdf. For GED, the ES is:

$$E{S}_{1-\alpha }\left(Z\right)=e{s}_{1-\alpha }\left(\eta \right),$$

(17)

where $e{s}_{1-\alpha }\left(\eta \right)$ is estimated by numerical integration using Equations (9) and (18). The GED’s pdf as introduced in [38] is:

$$g\left(z\right)=\frac{\eta e^{\left[-\left(\frac{1}{2}\right){\left|\raisebox{1ex}{$z$}\!\left/ \!\raisebox{-1ex}{$\kappa $}\right.\right|}^{\eta }\right]}}{\kappa 2^{\left(1+\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$\eta $}\right.\right)}\mathsf{\Gamma }\left(\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$\eta $}\right.\right)},$$

(18)

where $\kappa ={\left[2^{\left(-2/\eta \right)}\mathsf{\Gamma }\left(1/\eta \right)/\mathsf{\Gamma }\left(3/\eta \right)\right]}^{1/2}$, and $\eta$ stands for the shape parameter ($\eta \in \left(0,\infty \right)$). For SGED, the ES is:

$$E{S}_{1-\alpha }\left(Z\right)=e{s}_{1-\alpha }\left(\eta ,\zeta \right),$$

(19)

where $e{s}_{1-\alpha }\left(\eta ,\zeta \right)$ is estimated throughout numerical integration using Equations (9) and (20), where Equation (20) stands for the SGED’s pdf:

$$sg\left(\eta ,\zeta \right)=\{\begin{array}{c}-\frac{2}{\zeta +\frac{1}{\zeta }}g\begin{array}{ccc}\left(\zeta z\right)& for& z<0,\end{array}\\ \frac{2}{\zeta +\frac{1}{\zeta }}g\begin{array}{ccc}\left(\frac{z}{\zeta }\right)& for& z\ge 0\end{array},\end{array}$$

(20)

where $\zeta$ is the skewness parameter ($\zeta \in \left(0,\infty \right)$), and $g\left(z\right)$ represents the GED’s pdf.

3.3. VaR Backtesting

The literature on VaR backtesting is broad; this article uses the tests by Kupiec [42] and the independence test of Christoffersen [43]. The first test is based on the observation of the VaR estimated with a significance level $\alpha$, and identifying the occasions when realized losses exceed the VaR during the backtesting period, which are called VaR exceptions. To validate the risk measure, the sequence of exceptions should follow an iid Bernoulli process with probability $\alpha \left(1-\alpha \right)$. This binomial test for the exceptions is known as an unconditional coverage test. The second test examines the independence of the exceptions. The period of both VaR and ES backtesting in the empirical application is $T=$ 2400, and the rolling window size is 500 observations.

3.4. ES Backtesting

Three tests have been proposed for ES backtesting; two of them were presented in [9], and the other was introduced in [10]. To the best of our knowledge, this is the first application of these three tests on traditional and renewable energy markets. To implement the tests, we assume that the model performance derives from a ‘true but unknown’ conditional distribution function $F_t$, which is unknown, but can be estimated by a ‘predictive’ probability distribution $P_t$. In our case, $P_t$ represents the normal, skew-normal, Student’s t, and skewed-t distributions. Following the same notation of the authors, the risk measure is denoted by $Va{R}_{1-\alpha }^F$ and $E{S}_{1-\alpha }^F$ when the variable X is distributed according to $F$. It is assumed that the return distribution is continuous and strictly increasing. Therefore, the ES can be expressed as:

$$E{S}_{1-\alpha }\left(X_t\right)=-\mathrm{E}\left[X_t|X_t+Va{R}_{1-\alpha ,t}<0\right].$$

(21)

For all three tests, 97.5%-VaR backtest is performed first, after which the exceptions are used to build the ES backtests. The null hypothesis assumes that the distribution employed to construct the risk measures is correct, and thus the alternative hypothesis implies risk misspecification.

3.4.1. Z₁ Test

The first test proposed by Acerbi and Székely [9] is based on the conditional expectation of the exceptions with VaR at 97.5%. From Equation (17), it follows that

$$\mathsf{E}\left[\frac{X_t}{E{S}_{1-\alpha ,t}}+1| X_t+Va{R}_{1-\alpha ,t}<0\right]=0,$$

(22)

Then, the $Z_1$ statistic is defined as

$$Z_1\left(\stackrel{\rightharpoonup }{X}\right)={\sum }_{t=1}^T\frac{\frac{X_t{I}_t}{E{S}_{1-\alpha ,t}}}{N_T}+1,$$

(23)

where $I_t$ is an indicator function that takes the value 1 if $X_t+Va{R}_{1-\alpha ,t}<0$, and is otherwise equal to 0. $N_t=\sum _{t=1}^T{I}_t$ is the sum of the exceptions at $Va{R}_{1-\alpha }$. $T$ is the backtesting period, which is 2400 in our empirical application. The null and alternative hypotheses being

$$H_0: P_t^{\left[\alpha \right]}=F_t^{\left[\alpha \right]}, \forall t,$$

(24)

$$\begin{gathered} H_1: E{S}_{1-\alpha }^F\ge E{S}_{1-\alpha ,t}, \forall t;\mathrm{and}\mathrm{greater}\mathrm{for}\mathrm{some} t, \\ Va{R}_{1-\alpha }^F=Va{R}_{1-\alpha ,t}, \forall t. \end{gathered}$$

(25)

In test $Z_1$, null hypothesis $H_0$ indicates that the ‘predictive’ probability distribution $P_t$, is correct, since it complies with the characteristics of the $F_t$ distribution to characterize financial returns. On the contrary, the alternative hypothesis $H_1$ indicates an underestimation of the ES, including when the VaR estimation is correct.

The $Z_1$ statistic reveals that $E{S}_{1-\alpha }$ is an appropriate risk measure when the result of the estimate is close to zero, more specifically, $E_{H_0}\left[Z_1|N_T>0\right]=0$. Conversely, when $E_{H_1}\left[Z_1|N_T>0\right]$is negative, it implies that $E{S}_{1-\alpha }$ is not a suitable risk measure. Algorithm 1, described in Section 3.4.4, is used to find the critical values of the three backtesting ES tests. These values are tabulated in Table 1, for different values of the parameters of the normal, skew-normal, student’s t, skewed-t, GED and SGED distributions, considering a backtesting period $T=$ 2400 and a 5% confidence level. The critical value at 5% for the normal, skew-normal, GED and SGED distributions is −0.03; for the Student’s t and skewed-t distributions, it is −0.05. The critical values are sensitive to the size $T$, as shown in [44], and also to the degrees of freedom parameter and shape parameter, but not to the skewness parameter of the skew-normal, skewed-t distributions and SGED. As $T$ increases, the critical value of the test increases until it stabilizes close to zero.

Table 1. Selection of critical values for Z₁, Z₂ y ZES tests, and different distributions. T = 2400 and significance level of 5%.

Panel A: Normal, Skew-Normal, t-Student and Skew t							Panel B: GED and SGED
Test Z1	Skew Parameter (λ,ξ)							Skew Parameter (ζ)
Degrees of freedom (ν)	0.6	0.8	0.9	1	1.1	1.2	Shape parameter (η)	0.6	0.8	0.9	1	1.1	1.2
3	−0.13	−0.13	−0.14	−0.14	−0.14	−0.14	1	−0.06	−0.06	−0.06	−0.06	−0.05	−0.05
5	−0.07	−0.07	−0.07	−0.08	−0.07	−0.08	1.2	−0.05	−0.05	−0.05	−0.05	−0.05	−0.05
7	−0.05	−0.06	−0.06	−0.06	−0.06	−0.06	1.4	−0.05	−0.05	−0.04	−0.04	−0.04	−0.04
10	−0.05	−0.05	−0.05	−0.05	−0.05	−0.05	1.6	−0.04	−0.04	−0.04	−0.04	−0.04	−0.04
Skew−Normal	−0.03	−0.03	−0.03	−0.03	−0.03	−0.03	1.8	−0.04	−0.04	−0.04	−0.03	−0.03	−0.03
Test Z2	Skew Parameter (λ,ξ)							Skew Parameter (ζ)
Degrees of freedom (ν)	0.6	0.8	0.9	1	1.1	1.2	Shape parameter (η)	0.6	0.8	0.9	1	1.1	1.2
3	−0.25	−0.26	−0.26	−0.26	−0.26	−0.26	1	−0.22	−0.22	−0.22	−0.22	−0.22	−0.22
5	−0.22	−0.23	−0.22	−0.23	−0.23	−0.22	1.2	−0.22	−0.22	−0.22	−0.22	−0.21	−0.22
7	−0.22	−0.21	−0.22	−0.22	−0.23	−0.22	1.4	−0.22	−0.22	−0.22	−0.22	−0.22	−0.21
10	−0.22	−0.22	−0.22	−0.22	−0.22	−0.22	1.6	−0.22	−0.22	−0.21	−0.22	−0.22	−0.22
Skew−Normal	−0.21	−0.21	−0.21	−0.21	−0.21	−0.21	1.8	−0.22	−0.22	−0.22	−0.21	−0.22	−0.22
Test ZES	Skew Parameter (λ,ξ)							Skew Parameter (ζ)
Degrees of freedom (ν)	0.6	0.8	0.9	1	1.1	1.2	Shape parameter (η)	0.6	0.8	0.9	1	1.1	1.2
3	−0.50	−0.51	−0.52	−0.52	−0.52	−0.52	1	−0.34	−0.33	−0.33	−0.32	−0.31	−0.30
5	−0.34	−0.35	−0.35	−0.36	−0.36	−0.37	1.2	−0.31	−0.30	−0.29	−0.29	−0.28	−0.27
7	−0.29	−0.30	−0.30	−0.30	−0.31	−0.31	1.4	−0.28	−0.28	−0.27	−0.26	−0.25	−0.24
10	−0.25	−0.26	−0.27	−0.27	−0.27	−0.28	1.6	−0.25	−0.25	−0.25	−0.24	−0.23	−0.22
Skew−Normal	−0.19	−0.20	−0.20	−0.20	−0.21	−0.21	1.8	−0.25	−0.23	−0.23	−0.22	−0.21	−0.21

Z₁ and Z₂ tests are proposed by Acerbi and Székely [9], while Z_ES is proposed in Acerbi and Székely [10]. Skew-normal, Skewed-t and SGED distributions collapse to standard normal, Student’s t and GED distribution, respectively, when the skew parameter is equal to 1.

3.4.2. Z₂ Test

ES can be expressed as the following unconditional expectation:

$$E{S}_{1-\alpha ,t}=\mathsf{E}\left[\frac{X_t{I}_t}{\alpha }\right].$$

(26)

The $Z_2$ statistic is defined as

$$Z_2\left(\stackrel{\rightharpoonup }{X}\right)={\sum }_{t=1}^T\frac{X_t{I}_t}{T\alpha E{S}_{1-\alpha ,t}}+1,$$

(27)

where the null and alternative hypotheses are:

$$H_0: P_t^{\left[\alpha \right]}=F_t^{\left[\alpha \right]},\forall t,$$

(28)

$$\begin{gathered} H_1: E{S}_{\alpha }^F\ge E{S}_{\alpha ,t}, \forall t;\mathrm{and}\mathrm{greater}\mathrm{for}\mathrm{some} t, \\ Va{R}_{\alpha }^F\ge Va{R}_{\alpha ,t}, \forall t. \end{gathered}$$

(29)

In test $Z_2$, null hypothesis $H_0$ indicates that the ‘predictive’ probability distribution $P_t$, is correct. On the contrary, the alternative hypothesis, $H_1$, indicates an underestimation of the VaR and the ES.

The $Z_2$ test indicates that $E{S}_{1-\alpha }$ is an appropriate risk measure when the result of the estimate is close to zero, i.e., ${\mathrm{E}}_{H_0}\left[Z_2| N_T>0\right]=0$. On the contrary, $E{S}_{1-\alpha }$ is not an appropriate risk measure when ${\mathrm{E}}_{H_1}\left[Z_2| N_T>0\right]<0$, since losses are underestimated. This test penalizes the $Va{R}_{1-\alpha }$ due to the number of exceptions; additionally, the alternative hypothesis rejects $Va{R}_{1-\alpha }$ and $E{S}_{1-\alpha }$. The critical value at 5% for the normal, skew-normal, GED and SGED distribution is −0.21; for the Student’s t and skewed-t distributions, it is −0.22 (see Table 1).

3.4.3. Z_ES Test

Tests $Z_1$ and $Z_2$ depend not only on the $E{S}_{1-\alpha }$ results, but also on the values of $Va{R}_{1-\alpha }$ because the latter needs to be backtested previously. Figure 1 illustrates how the critical value of the$Z_2$ (ordinate axis) at 5% increases as the value of $Va{R}_{1-\alpha }$ (abscissa axis) does. This is crucial, because it increases the possibility of committing a type II error $P\left(accept H_0| reject H_0\right)$. If the type II error occurs, a $E{S}_{1-\alpha }$ risk measure would be accepted, which is not suitable, and would leave the investment exposed to market risk.

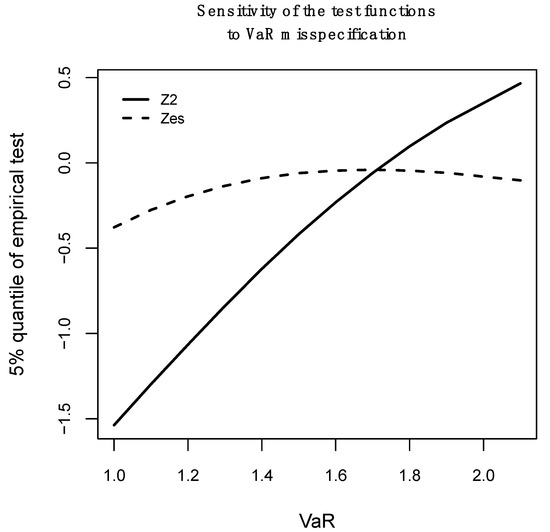
Figure 1. Sensitivity of the test Z₂ and Z_ES to VaR.

Given the above feature, Acerbi and Székely [10] proposed the $Z_{ES}$ test, which is not as sensitive to possible VaR values (see dotted dash line in Figure 1); therefore, this test is expected to be more powerful. From Equation (15) and following [14], $E{S}_{1-\alpha }$ is equivalent to:

$$E{S}_{1-\alpha ,t}=Va{R}_{1-\alpha ,t}-\frac{1}{\alpha }\mathsf{E}\left[\left(X_t+Va{R}_{1-\alpha ,t}\right)I_t\right].$$

(30)

Re-organizing the terms and performing the operations, the $Z_{ES}$ test becomes:

$$Z_{ES}\left(\stackrel{\rightharpoonup }{X}\right)={\displaystyle \sum }_{t=1}^T\frac{\alpha \left(E{S}_{1-\alpha }-Va{R}_{1-\alpha }\right)+\left(X_t+Va{R}_{1-\alpha }\right)I_t}{T\alpha E{S}_{1-\alpha ,t}}.$$

(31)

The null and alternative hypotheses are:

$$H_0: P_t^{\left[\alpha \right]}=F_t^{\left[\alpha \right]}, \mathrm{for}\mathrm{all} t,$$

(32)

$$\begin{gathered} H_1: E{S}_{1-\alpha }^F\ge E{S}_{1-\alpha ,t},\forall t \mathrm{and}\mathrm{lesser} \mathrm{for}\mathrm{some} t, \\ Va{R}_{1-\alpha ,t}~Va{R}_{1-\alpha ,t}^F \end{gathered}$$

(33)

The $Z_{ES}$ test, just like the other two tests, indicates that $E{S}_{1-\alpha }$ is a good risk measure when ${\mathrm{E}}_{H_0}\left[Z_{ES}\right]=0$; and when ${\mathrm{E}}_{H_1}\left[Z_{ES}\right]<0$, it indicates that $E{S}_{1-\alpha }$ is not a good risk measure. In this test, the alternative hypothesis indicates that $E{S}_{1-\alpha }$ is rejected, regardless of the value of $Va{R}_{1-\alpha }$. The critical value at 5% for the normal and skew-normal distributions is −0.20, for Student’s t and skewed-t distributions, it is −0.27, while for GED and SGED, it is −0.22 (see Table 1). The next subsection explains the algorithm used to delimit the rejection area of $Z_1$, $Z_2$, and $Z_{ES}$ tests, which is based on the computation of the critical values at 5% under the normal, skew-normal, Student’s t, skewed-t, GED and SGED distributions.

3.4.4. Algorithm 1: Critical Values for ES Backtesting under Student’s t Distributions

The critical values of the $Z_1,Z_2$, and $Z_{ES}$ tests are determined by generating random numbers from the normal, skew-normal, Student’s t, skewed-t, GED and SGED distributions. In Panel A of Table 1, the degrees of freedom and coefficient of skewness parameters are $\left(\xi ,\lambda \right)=\left\{0.6,0.8,0.9,1,1.1,1.2\right\}$, and $v=\left\{3,5,7,10\right\}$, respectively. In Panel B, the skewness parameters are $\left(\zeta \right)=\left\{0.6,0.8,0.9,1,1.1,1.2\right\}$, and the shape parameters are $\eta =\left\{1,1.2,1.4,1.6,1.8\right\}$. We choose the parameters according to the model results in Table A2, Table A3 and Table A4 for traditional and renewable energy markets.

Algorithm 1

1. Simulation of $X_t^i$ under normal, skew-normal, Student’s t, skewed -t, GED and SGED distributions, and M = 10,000 times. The $i$ value indicates the test ($i=1,2,ES$).

2. Calculation of the $Z_i=Z({\overrightarrow{X}}^i)$ statistics, using the data simulated in step 1.

3. Estimation of critical values (cv) at 5%, $Z_{cv}=F_{5\%}^{-1}\left(Z_i\right)$.

4. Resampling the critical values for the different skewness, degrees of freedom and shape parameters.

Table 1 shows the results of critical values.

If Algorithm 1 is applied with $T=$ 2400, it is found that the mean of the $Z_1$ test with a skewed-t distribution is −0.000318, and the confidence interval at 95% is [−0.05868; 0.05199]. With the $Z_2$ test, the mean is 0.001611, and the confidence interval at 95% is [−0.25791; 0.24852]. With the $Z_{ES}$ test, the mean is −0.203813, and the confidence interval at 95% is [−0.28459; −0.13449]. For the SGED, the mean of the $Z_1$ test is −0.000082, and the confidence interval at 95% is [−0.04253; 0.03816]. For the $Z_2$ test, the mean is −0.001122, and the confidence interval at 95% is [−0.27060; 0.24579]. With the $Z_{ES}$ test, the mean is −0.168741, and the confidence interval at 95% is [−0.23137; −0.11399]. The critical values do not vary consistently over skew-t and SGED distributions. Figure 2 shows these results and the empirical distributions of the three tests under skew-t, and also identifies in blue the critical value at 5%.

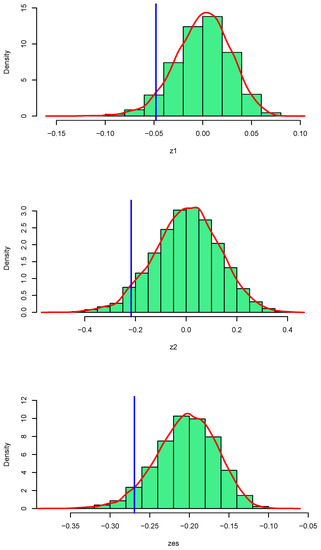
Figure 2. Critical values tests for skewed-t distribution.

4. Data

The dataset consists of the prices of four renewable energy stocks from WilderHill New Energy Global Innovation (NEX), and four traditional energy stocks from the Bloomberg World Energy index (BWEI). Appendix A gathers detailed information on the stocks. The prices are collected on a daily frequency basis from January 2005 to December 2016, for a total of 2900 observations. The logarithmic returns are calculated as $r_t=100\log \left(V_t/V_{t-1}\right)$, where $V_t$ represents the price of each share at a time $t$. The units of the variables are logarithmic returns in decimals.

Table 2 displays the descriptive statistics of the data. The typical characteristics of the daily returns are featured, such as mean reversion, positive excess kurtosis, and non-zero skewness. The average annual volatility of renewable energy stocks is 41%, while that of the traditional energy stocks is 19%. Renewable energy stocks have an average excess kurtosis of 10, while that of the traditional energy stocks is 13. The high kurtosis values imply that the empirical distributions of returns exhibit extreme values. The renewable energy stocks Epistar, Kingspan, and Nibe and the traditional energy stock Schlumberger have negative coefficients of skewness; this means that in these stocks, negative returns persist more than positive returns. This finding represents evidence supporting the fact that the analyzed renewable energy stocks are riskier than traditional energy stocks. These stylized facts are illustrated in Figure A1 and Figure A2 (see Appendix B), which depicts prices and log-returns of different energy stocks.

Table 2. Descriptive statistics of renewable and traditional energy stocks.

	Total Period (January 2005–December 2016)
Stock	Type	Mean	Median	Std. Dev.	Excess Kurtosis	Skewness	Min	Max	Obs
Epistar	Renewable	−0.0001	0.0007	0.030 (47.62%)	3.494	−0.014	−0.109	0.098	2900
Kingspan	Renewable	0.0003	0.0008	0.027 (42.86%)	11.997	−0.546	−0.254	0.179	2900
Boralex	Renewable	0.0004	0.0004	0.023 (36.51%)	13.677	0.062	−0.195	0.220	2900
Nibe	Renewable	0.0005	0.0002	0.024 (38.10%)	12.231	−0.119	−0.255	0.224	2900
Exxon Mobil	Traditional	0.0002	0.0003	0.016 (25.40%)	16.283	0.028	−0.150	0.159	2900
Chevron	Traditional	0.0003	0.0008	0.017 (26.99%)	15.495	0.086	−0.133	0.189	2900
Total S.A.	Traditional	0.0000	0.0004	0.019 (30.16%)	10.130	0.184	−0.113	0.162	2900
Schlumberger	Traditional	0.0003	0.0002	0.023 (36.51%)	10.806	−0.533	−0.203	0.139	2900
Annual volatility is presented in parentheses.

5. Empirical Results

5.1. Conditional Mean and Variance Models in Sample Estimations

The AR(1)-GARCH(1,1), AR(1)-EGARCH(1,1) and AR(1)-APARCH(1,1) models are used to standardize the returns with the conditional mean and conditional variance. The AR and GARCH orders were selected according to the significance of the coefficients, validation of the assumptions of each model, and information criteria. Each model is estimated jointly by ML method. Table A2, Table A3 and Table A4 (see Appendix B) gather the coefficients associated with each model for the six distributions: normal, skew-normal, Student’s t, skewed-t, GED and SGED. These tables also display the estimates of the conditional mean-variance models, either AR(1)-GARCH(1,1), AR(1)-EGARCH(1,1) or AR(1)-APARCH(1,1). In all cases, the coefficients associated with the AR(1) ($\varphi$) and GARCH(1,1) ($\alpha$ and $\beta$) processes are significant, both in traditional and renewable energy stocks. Similarly, the results of the coefficients of the skewness ($\xi$) of the skew-normal distribution, the degrees of freedom for the Student’s t distributions $\left(v\right)$, the skewness parameter of the skewed-t distributions $\left(\lambda \right)$, and the shape parameter $\left(\eta \right)$ from GED, and the skewness parameter from SGED $\left(\zeta \right),$are consistently significant. For the EGARCH model, the parameter that represents the asymmetry of stochastic shocks in the conditional volatility ($\gamma$) is positive and significant in all cases. In the APARCH model, the parameter that also represents the asymmetric effects of the stochastic shocks on conditional volatility is significant in all cases, and it is even higher than 1 for the renewable energy stocks Epistar and Boralex, and the traditional energy stocks Exxon, Chevron and Schlumberger.

Table A5 (see Appendix B) shows the results of the two-sample Kolmogorov-Smirnov test, where the null hypothesis indicates that standardized returns and standardized residuals for the models AR(1)-GARCH(1,1), AR(1)-EGARCH(1,1), AR(1)-APARCH(1,1) with the six distributions were drawn from the same continuous distribution. In addition to the estimate of the skewness parameters and excess kurtosis in the standardized residuals of the AR(1)-GARCH(1,1), AR(1)-EGARCH(1,1), AR(1)-APARCH(1,1) models, each fitted with normal, skew-normal, Student’s t, skewed-t, GED and SGED distributions. In the two-sample Kolmogorov-Smirnov test, the null hypothesis, is rejected for all stocks and models, except for Epistar, from the renewable energy market. Nonetheless, the best results were achieved with the skew-t and GED distributions in the AR(1)-EGARCH(1,1) model. In all models, the kurtosis coefficients are greater than three. Moreover, in the AR(1)-GARCH(1,1) model, all the skewness coefficients are negative, except that of the traditional energy stock Nibe, which is positive. In the AR(1)-EGARCH(1,1) model under the Student’s t, skewed-t, GED and SGED distributions, three renewable energy stocks present positive skewness coefficients: Epistar, Kingspan and Nibe. For the remaining stocks, the skewness coefficients are negative. In the AR(1)-APARCH(1,1) model under the Student’s t and skewed-t distributions, two renewable energy stocks have positive skewness coefficients: Kingspan and Nibe. For the remaining stocks, the skewness coefficients are negative. The kurtosis coefficient is consistently lower for the GED and SGED distributions in the AR(1)-APARCH(1,1) model. In summary, in all three models with the three innovation distributions, the standardized residuals still exhibit skewness and kurtosis after filtering the returns. Figure 3 shows the standardized returns and standardized residuals of the AR(1)-GARCH(1,1) model, under the skew-normal, skew-t and SGED distributions.

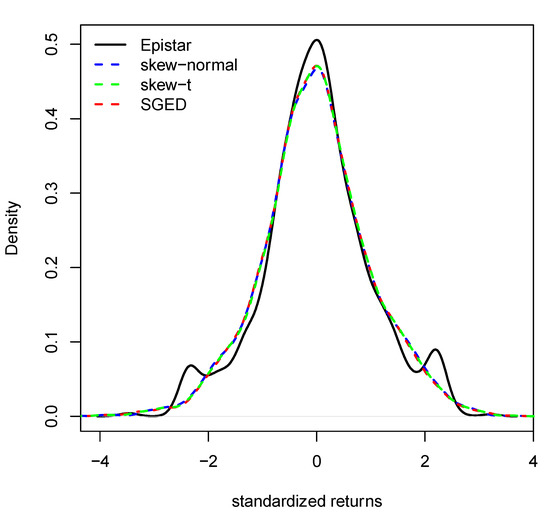
Figure 3. Epistar’s standardized returns and standardized residuals of the AR(1)-GARCH(1,1) model under the skew-normal, skew-t and SGED distributions.

Table A6 (see Appendix B) shows the Ljung-Box test results to detect autocorrelation of the standardized residuals from the AR(1)-GARCH(1,1), AR(1)-EGARCH(1,1), AR(1)-APARCH(1,1) models, with the different innovation distributions. Considering no seasonal effects in the daily returns included in the sample, it is suggested the number of lags $m=\ln \left(T\right)$ [45] provides better power performance. Accordingly, we choose $m=\ln \left(2900\right)\approx 8$. In addition, we added the twelfth and twentieth lags. There is no autocorrelation in any of the lags. This indicates that the proposed AR models are suitable for modeling renewable and traditional energy stock returns.

Table A7 (see Appendix B) shows the Ljung-Box test results to detect autocorrelation of the squared standardized residuals from the AR(1)-GARCH(1,1), AR(1)-EGARCH(1,1), AR(1)-APARCH(1,1) models with different innovation distributions. The Kingspan stock shows significant autocorrelation in the first five lags. The Boralex stock, from the renewable sector, evidences autocorrelation until the fifth lag; nonetheless, there is no evidence of autocorrelation for the AR(1)-GARCH(1,1) under the student’s t and skew-t distribution. The Chevron stock displays significant autocorrelation for lags in the orders two, three and four in the AR(1)-GARCH(1,1) model under all distributions; nevertheless, there is no statistical evidence of autocorrelation under all distributions for the AR(1)-EGARCH(1,1) and AR(1)-APARCH(1,1) models. The remaining stocks work well for all the models and distributions.

5.2. Backtesting of 99%-VaR

The results of the backtesting for 99%-VaR are presented in Table 3, including, for all the models and stocks, the observed and expected number of violations as well as the Kupiec and independence tests. Model performance is considered accurate if it simultaneously rejects the null hypothesis in both tests.

Table 3. 99%-VaR backtesting. Expected violations (EV) = 24.

	AR(1)-GARCH(1,1)
	Normal			Skew-Normal			t-Student			Skew-t			GED			SGED
	v	Kupiec Test	Ind. Test	v	Kupiec Test	Ind. Test	v	Kupiec Test	Ind. Test	v	Kupiec Test	Ind. Test	v	Kupiec Test	Ind. Test	v	Kupiec Test	Ind. Test
Epistar	36	4.57 (0.03)	4.92 (0.09)	36	5.25 (0.02)	5.58 (0.06)	24	0.02 (0.89)	1.45 (0.48)	27	0.21 (0.65)	1.28 (0.53)	25	0.04 (0.84)	1.30 (0.52)	28	0.64 (0.42)	1.56 (0.46)
Kingspan	39	7.10 (0.01)	9.14 (0.01)	44	13.51 (0.00)	14.82 (0.00)	20	0.97 (0.32)	7.70 (0.02)	27	0.21 (0.65)	4.68 (0.10)	25	0.04 (0.84)	4.97 (0.08)	24	0.00 (1.00)	5.23 (0.07)
Boralex	43	11.20 (0.00)	12.70 (0.00)	48	18.79 (0.00)	19.69 (0.00)	23	0.12 (0.73)	1.65 (0.48)	26	0.07 (0.80)	1.25 (0.54)	24	0.00 (1.00)	1.38 (0.50)	27	0.36 (0.55)	1.39 (0.50)
Nibe	31	1.50 (0.22)	5.00 (0.08)	38	7.01 (0.01)	9.12 (0.01)	17	2.73 (0.10)	5.35 (0.07)	27	0.21 (0.65)	4.68 (0.10)	21	0.40 (0.53)	6.64 (0.05)	27	0.36 (0.55)	4.73 (0.09)
Exxon Mobil	49	18.75 (0.00)	14.48 (0.00)	45	14.76 (0.00)	16.48 (0.00)	39	7.10 (0.01)	9.14 (0.01)	28	0.42 (0.51)	4.63 (0.10)	40	8.97 (0.00)	10.33 (0.01)	36	5.25 (0.02)	6.35 (0.04)
Chevron	46	14.78 (0.00)	15.92 (0.00)	34	3.73 (0.05)	4.70 (0.10)	31	1.50 (0.22)	5.00 (0.08)	17	2.73 (0.10)	5.35 (0.07)	40	8.97 (0.00)	10.33 (0.01)	27	0.36 (0.55)	0.98 (0.61)
Total S.A.	45	13.54 (0.00)	13.58 (0.00)	41	10.03 (0.00)	10.15 (0.01)	27	0.21 (0.65)	4.68 (0.10)	19	1.45 (0.23)	4.36 (0.08)	33	3.05 (0.08)	3.56 (0.17)	28	0.64 (0.42)	1.56 (0.46)
Schlumberger	39	7.10 (0.01)	7.31 (0.03)	39	7.96 (0.00)	9.25 (0.01)	23	0.12 (0.73)	1.65 (0.48)	26	0.07 (0.80)	1.25 (0.54)	31	1.89 (0.17)	2.70 (0.26)	30	1.40 (0.24)	2.16 (0.34)
	AR(1)-EGARCH(1,1)
	Normal			Skew-Normal			t-Student			Skew-t			GED			SGED
	v	Kupiec Test	Ind. Test	v	Kupiec Test	Ind. Test	v	Kupiec Test	Ind. Test	v	Kupiec Test	Ind. Test	v	Kupiec Test	Ind. Test	v	Kupiec Test	Ind. Test
Epistar	45	13.54 (0.00)	14.81 (0.00)	42	11.14 (0.00)	12.70 (0.00)	32	1.99 (0.16)	5.27 (0.07)	38	6.20 (0.01)	8.40 (0.02)	33	3.05 (0.08)	6.04 (0.05)	36	5.25 (0.02)	7.69 (0.02)
Kingspan	43	11.20 (0.00)	15.27 (0.00)	44	13.51 (0.00)	14.82 (0.00)	22	0.31 (0.58)	6.30 (0.04)	29	0.71 (0.40)	8.96 (0.01)	21	0.40 (0.53)	2.22 (0.33)	27	0.36 (0.55)	4.73 (0.09)
Boralex	52	23.11 (0.00)	23.74 (0.00)	50	21.68 (0.00)	21.68 (0.00)	27	0.42 (0.51)	4.63 (0.10)	26	0.07 (0.80)	1.25 (0.54)	28	0.64 (0.42)	1.56 (0.46)	31	1.89 (0.17)	2.54 (0.28)
Nibe	30	1.07 (0.30)	8.93 (0.01)	36	5.25 (0.02)	7.69 (0.02)	21	0.59 (0.44)	6.94 (0.03)	27	0.21 (0.65)	9.28 (0.01)	21	0.40 (0.53)	2.22 (0.33)	26	0.16 (0.69)	4.80 (0.09)
Exxon Mobil	58	32.85 (0.00)	36.45 (0.00)	42	11.14 (0.00)	12.64 (0.00)	46	14.78 (0.00)	15.94 (0.00)	32	1.99 (0.16)	2.60 (0.27)	42	11.14 (0.00)	12.64 (0.00)	37	6.10 (0.01)	7.26 (0.03)
Chevron	54	26.20 (0.00)	28.29 (0.00)	40	8.97 (0.00)	10.33 (0.01)	49	18.75 (0.00)	21.64 (0.00)	22	0.31 (0.58)	6.30 (0.04)	47	17.40 (0.00)	19.28 (0.00)	37	6.10 (0.01)	7.26 (0.03)
Total S.A.	49	18.75 (0.88)	18.75 (0.00)	40	8.97 (0.00)	9.12 (0.01)	38	6.20 (0.01)	6.45 (0.04)	28	0.42 (0.51)	4.63 (0.10)	39	7.96 (0.00)	8.15 (0.02)	33	3.05 (0.08)	3.97 (0.14)
Schlumberger	38	6.20 (0.01)	8.40 (0.00)	38	7.01 (0.01)	8.23 (0.01)	29	0.71 (0.40)	1.58 (0.45)	28	0.42 (0.51)	4.63 (0.10)	29	0.99 (0.32)	1.70 (0.43)	27	0.36 (0.55)	0.98 (0.61)
	AR(1)-APARCH(1,1)
	Normal			Skew-Normal			t-Student			Skew-t			GED			SGED
	v	Kupiec Test	Ind. Test	v	Kupiec Test	Ind. Test	v	Kupiec Test	Ind. Test	v	Kupiec Test	Ind. Test	v	Kupiec Test	Ind. Test	v	Kupiec Test	Ind. Test
Epistar	55	27.81 (0.00)	29.76 (0.00)	44	12.20 (0.00)	12.44 (0.00)	38	6.20 (0.01)	8.40 (0.02)	42	10.10 (0.00)	14.40 (0.00)	33	3.05 (0.08)	6.04 (0.05)	28	0.64 (0.42)	1.56 (0.46)
Kingspan	43	11.20 (0.00)	11.29 (0.00)	41	9.05 (0.00)	9.31 (0.00)	21	0.59 (0.44)	2.46 (0.29)	28	0.42 (0.51)	4.63 (0.10)	27	0.36 (0.55)	4.73 (0.09)	24	0.02 (0.89)	0.00 (0.99)
Boralex	40	8.05 (0.00)	8.22 (0.02)	45	11.20 (0.00)	13.13 (0.00)	22	0.31 (0.58)	6.30 (0.04)	24	0.02 (0.89)	0.00 (0.99)	24	0.02 (0.89)	0.00 (0.99)	24	0.02 (0.89)	0.00 (0.99)
Nibe	29	0.71 (0.40)	4.67 (0.10)	32	1.99 (0.16)	5.51 (0.08)	25	0.00 (0.95)	1.30 (0.52)	39	7.10 (0.01)	15.92 (0.00)	22	0.31 (0.58)	4.63 (0.10)	28	0.64 (0.42)	4.73 (0.09)
Exxon Mobil	56	29.45 (0.00)	30.23 (0.00)	43	11.20 (0.00)	12.41 (0.00)	46	14.78 (0.00)	16.82 (0.00)	28	0.42 (0.51)	4.63 (0.10)	42	11.14 (0.00)	12.64 (0.00)	44	13.51 (0.00)	14.82 (0.00)
Chevron	50	20.16 (0.00)	20.16 (0.00)	46	14.78 (0.00)	16.01 (0.00)	38	6.20 (0.01)	6.45 (0.04)	20	0.97 (0.32)	3.56 (0.08)	44	13.51 (0.00)	14.82 (0.00)	47	17.40 (0.00)	19.28 (0.00)
Total S.A.	51	21.61 (0.00)	22.32 (0.00)	40	8.97 (0.00)	11.46 (0.01)	33	2.54 (0.11)	5.52 (0.05)	25	0.00 (0.95)	1.23 (0.59)	38	6.20 (0.01)	8.40 (0.02)	37	6.10 (0.01)	7.26 (0.03)
Schlumberger	41	9.05 (0.00)	9.31 (0.00)	39	7.10 (0.01)	8.35 (0.00)	25	0.00 (0.95)	1.23 (0.59)	26	0.07 (0.80)	1.25 (0.54)	28	0.42 (0.51)	4.63 (0.10)	27	0.21 (0.65)	2.60 (0.27)

v stands for violations depending on the distribution (normal, Skew-normal,Student’s t, Skewed-t, GED and SGED). p-values for each test in parentheses. Bold figures represent adequate performance of the model for each test.

In the AR(1)-GARCH(1,1) model, the normal distribution does not perform accurately in any case; however, the renewable energy stock Nibe exceeds the Kupiec test. The model under the skew-normal only works well for Chevron. As for the Student’s t distribution, model performance is found to be accurate for four stocks: Epistar and Boralex for renewable energy and Total S.A. and Schlumberger for traditional energy. The model under skewed-t distribution performs well in all cases except with two traditional energy stocks—Chevron and Total S.A.—which do not reject the null hypothesis in the independence test. The null hypothesis is not rejected for any of the stocks in either test, except for Exxon Mobil and Chevron, from the traditional energy sector for the GED distribution. The model for the SGED distribution works well in all cases, except for Exxon Mobil.

For the AR(1)-EGARCH(1,1) model, the normal and skew-normal distributions are not appropriate in any case; however, as in the previous model for the normal, the renewable energy stock Nibe does not reject the null hypothesis in the Kupiec test. Regarding the Student’s t distribution, the model only works well in two cases, with the renewable energy stock Boralex and the traditional energy stock Schlumberger. The model under the skewed-t distribution performs accurately in four cases: renewable energy stock Boralex, and traditional energy stocks Exxon Mobil, Total S.A., and Schlumberger. For the GED distribution case, the null hypothesis is not rejected for all of the stocks in either of the tests, except for Exxon Mobil, Chevron and Total S.A. from the traditional energy industry. On the other hand, the null hypothesis is rejected for Epistar, Exxon Mobil and Chevron for the SGED distribution.

As far as the AR(1)-APARCH(1,1) model is concerned, under normal and skew-normal distributions, only the renewable energy stock Nibe performs well. Besides, the Student’s t distribution behaves adequately in three cases: Kingspan and Nibe for renewable energy and Schlumberger for traditional energy. The skewed-t model, however, presents adequate performance in six cases, two from renewable energy stocks (Kingspan and Boralex) and for all the four traditional energy stocks. For the GED and SGED distributions, both tests perform well in all cases, except for Exxon Mobil, Chevron and Total S.A. from the traditional energy sector.

5.3. Backtesting of 97.5%-VaR

Backtesting analyses for VaR are extended in Table 4 by considering 97.5%-VaR.

Table 4. 97.5%-VaR backtesting. Expected violations (EV) = 60.

	AR(1)-GARCH(1,1)
	Normal			Skew-Normal			t-Student			Skew-t			GED			SGED
	v	Kupiec Test	Ind. Test	v	Kupiec Test	Ind. Test	v	Kupiec Test	Ind. Test	v	Kupiec Test	Ind. Test	v	Kupiec Test	Ind. Test	v	Kupiec Test	Ind. Test
Epistar	81	5.60 (0.02)	8.98 (0.01)	79	5.62 (0.02)	9.16 (0.01)	66	0.29 (0.59)	1.05 (0.58)	77	3.57 (0.06)	7.73 (0.02)	74	3.12 (0.08)	4.26 (0.12)	78	5.07 (0.02)	7.09 (0.03)
Kingspan	73	1.98 (0.16)	3.33 (0.19)	84	8.77 (0.00)	10.07 (0.01)	61	0.01 (0.92)	1.23 (0.54)	67	0.44 (0.51)	1.13 (0.57)	61	0.02 (0.90)	1.15 (0.56)	64	0.27 (0.60)	2.67 (0.26)
Boralex	74	2.34 (0.13)	7.13 (0.03)	74	3.12 (0.08)	10.02 (0.01)	62	0.00 (0.98)	1.12 (0.57)	63	0.02 (0.87)	1.05 (0.59)	53	0.87 (0.35)	1.38 (0.50)	55	0.44 (0.51)	0.83 (0.66)
Nibe	61	0.01 (0.92)	0.16 (0.92)	67	0.81 (0.37)	1.42 (0.49)	57	0.39 (0.53)	0.71 (0.70)	78	4.04 (0.05)	6.22 (0.04)	51	1.46 (0.23)	2.11 (0.35)	63	0.15 (0.70)	0.22 (0.89)
Exxon Mobil	91	12.41 (0.00)	13.17 (0.00)	79	5.62 (0.02)	6.32 (0.04)	81	5.60 (0.02)	5.79 (0.06)	64	0.08 (0.78)	0.15 (0.93)	79	5.62 (0.02)	5.68 (0.06)	72	2.32 (0.13)	2.33 (0.31)
Chevron	87	9.39 (0.00)	9.84 (0.01)	70	1.62 (0.20)	2.31 (0.31)	79	4.53 (0.03)	4.66 (0.10)	43	6.54 (0.01)	6.62 (0.04)	85	9.48 (0.00)	9.89 (0.01)	64	0.27 (0.60)	0.63 (0.73)
Total S.A.	80	5.05 (0.02)	6.40 (0.04)	78	5.07 (0.02)	6.34 (0.04)	72	1.65 (0.20)	2.40 (0.30)	52	1.68 (0.20)	1.68 (0.43)	72	2.32 (0.13)	3.14 (0.21)	66	0.60 (0.44)	1.06 (0.59)
Schlumberger	66	0.29 (0.59)	0.32 (0.85)	67	0.81 (0.37)	0.82 (0.66)	53	1.34 (0.25)	1.90 (0.39)	53	1.34 (0.25)	1.90 (0.39)	61	0.02 (0.90)	0.14 (0.93)	60	0.00 (1.00)	0.16 (0.92)
	AR(1)-EGARCH(1,1)
	Normal			Skew-Normal			t-Student			Skew-t			GED			SGED
	v	Kupiec Test	Ind. Test	v	Kupiec Test	Ind. Test	v	Kupiec Test	Ind. Test	v	Kupiec Test	Ind. Test	v	Kupiec Test	Ind. Test	v	Kupiec Test	Ind. Test
Epistar	96	16.68 (0.00)	20.76 (0.00)	85	9.48 (0.00)	12.00 (0.00)	88	10.11 (0.00)	13.99 (0.00)	94	14.90 (0.00)	23.57 (0.00)	74	3.12 (0.08)	5.74 (0.06)	76	4.04 (0.04)	6.35 (0.04)
Kingspan	88	10.11 (0.00)	13.99 (0.00)	89	12.54 (0.00)	12.58 (0.00)	74	2.34 (0.13)	9.53 (0.01)	76	3.13 (0.08)	9.77 (0.01)	73	2.71 (0.10)	2.73 (0.26)	75	3.57 (0.06)	3.62 (0.16)
Boralex	87	9.39 (0.00)	11.80 (0.00)	80	6.20 (0.01)	6.40 (0.04)	74	2.34 (0.13)	7.13 (0.03)	73	1.98 (0.16)	7.00 (0.03)	65	0.42 (0.52)	0.45 (0.80)	67	0.81 (0.37)	0.82 (0.66)
Nibe	62	0.00 (0.98)	5.19 (0.07)	69	1.32 (0.25)	3.02 (0.22)	60	0.05 (0.82)	1.38 (0.50)	86	8.70 (0.00)	15.04 (0.00)	52	1.14 (0.28)	1.72 (0.42)	59	0.02 (0.90)	0.21 (0.90)
Exxon Mobil	96	16.68 (0.00)	19.19 (0.00)	74	3.12 (0.08)	3.16 (0.21)	91	12.41 (0.00)	14.26 (0.00)	70	1.08 (0.30)	4.56 (0.10)	80	6.20 (0.01)	6.24 (0.04)	69	1.32 (0.25)	1.32 (0.52)
Chevron	90	11.62 (0.00)	15.12 (0.00)	66	0.60 (0.44)	1.06 (0.59)	87	9.39 (0.00)	11.80 (0.00)	49	2.91 (0.09)	11.94 (0.00)	87	10.96 (0.00)	10.97 (0.00)	65	0.42 (0.52)	0.83 (0.66)
Total S.A.	98	18.55 (0.00)	18.86 (0.00)	79	5.62 (0.02)	5.98 (0.04)	86	8.70 (0.00)	9.92 (0.01)	66	0.29 (0.59)	1.05 (0.59)	78	5.07 (0.02)	5.15 (0.08)	72	2.32 (0.13)	2.63 (0.27)
Schlumberger	75	2.72 (0.59)	3.87 (0.14)	72	2.32 (0.13)	3.14 (0.21)	66	0.29 (0.59)	2.53 (0.28)	63	0.02 (0.87)	2.73 (0.26)	61	0.02 (0.90)	0.25 (0.88)	60	0.00 (1.00)	0.20 (0.91)
	AR(1)-APARCH(1,1)
	Normal			Skew-Normal			t-Student			Skew-t			GED			SGED
	v	Kupiec Test	Ind. Test	v	Kupiec Test	Ind. Test	v	Kupiec Test	Ind. Test	v	Kupiec Test	Ind. Test	v	Kupiec Test	Ind. Test	v	Kupiec Test	Ind. Test
Epistar	102	22.53 (0.00)	27.10 (0.00)	102	22.53 (0.00)	24.10 (0.00)	90	11.62 (0.00)	11.78 (0.00)	89	10.85 (0.00)	11.79 (0.00)	76	4.04 (0.04)	6.35 (0.04)	80	6.20 (0.01)	6.40 (0.04)
Kingspan	91	12.41 (0.00)	12.55 (0.00)	88	10.11 (0.00)	11.42 (0.00)	71	1.35 (0.25)	1.77 (0.41)	76	3.13 (0.08)	5.61 (0.06)	74	3.12 (0.08)	5.74 (0.06)	70	1.08 (0.30)	4.56 (0.10)
Boralex	81	5.60 (0.02)	5.79 (0.06)	80	5.05 (0.02)	6.51 (0.02)	68	0.62 (0.43)	0.63 (0.73)	69	0.84 (0.36)	0.84 (0.66)	65	0.42 (0.52)	0.83 (0.66)	69	1.32 (0.25)	1.32 (0.52)
Nibe	63	0.02 (0.87)	1.05 (0.59)	63	0.02 (0.87)	2.73 (0.26)	62	0.00 (0.98)	0.24 (0.89)	92	13.22 (0.00)	18.12 (0.00)	52	1.14 (0.28)	1.72 (0.42)	57	0.39 (0.53)	0.71 (0.70)
Exxon Mobil	101	21.50 (0.00)	21.87 (0.00)	80	6.20 (0.01)	6.40 (0.04)	92	13.22 (0.00)	13.28 (0.00)	71	1.35 (0.25)	1.35 (0.51)	80	6.20 (0.01)	6.40 (0.04)	73	1.98 (0.16)	1.05 (0.59)
Chevron	94	14.90 (0.00)	15.01 (0.00)	90	11.62 (0.00)	10.08 (0.00)	79	4.53 (0.03)	5.79 (0.06)	43	6.54 (0.01)	6.62 (0.04)	88	10.11 (0.00)	11.42 (0.00)	71	1.35 (0.25)	1.77 (0.41)
Total S.A.	90	11.62 (0.01)	11.78 (0.00)	90	11.62 (0.00)	13.22 (0.00)	82	6.17 (0.01)	6.20 (0.05)	64	0.08 (0.78)	4.80 (0.09)	80	6.20 (0.01)	6.40 (0.04)	74	3.12 (0.08)	3.16 (0.21)
Schlumberger	76	3.13 (0.82)	4.16 (0.12)	73	1.98 (0.16)	1.05 (0.59)	60	0.05 (0.82)	0.22 (0.90)	56	0.57 (0.45)	0.64 (0.73)	62	0.00 (0.98)	0.24 (0.89)	69	0.84 (0.36)	0.84 (0.66)
	102	22.53 (0.00)	27.10 (0.00)	102	22.53 (0.00)	24.10 (0.00)	90	11.62 (0.00)	11.78 (0.00)	89	10.85 (0.00)	11.79 (0.00)	63	0.02 (0.87)	2.73 (0.26)	60	0.05 (0.82)	1.38 (0.50)

v stands for violations depending on the distribution (normal, Skew-normal,Student’s t, Skewed-t, GED and SGED). p-values for each test in parentheses. Bold figures represent the adequate performance of the model for each test.

The AR(1)-GARCH(1,1) model under normal distribution performs well in three stocks: Kingspan and Nibe from the renewable energy sector, and Schlumberger from the traditional energy sector. The model under the skew-normal distribution performs well in Nibe, Exxon Mobil, and Schlumberger. All stocks pass the test with the Student’s t distribution, except two from the traditional power sector: Exxon Mobil and Chevron. The model performs accurately with the skewed-t distribution in five cases, but the renewable energy stocks Epistar and Nibe and the traditional energy stock Chevron reject the null hypothesis in the Kupiec and independence test. The model under the GED distribution does not reject both tests in any of the cases, except for Exxon Mobil and Chevron, from the traditional energy sector. Whereas for the SGED distribution, the model performs well in all cases except for Epistar, from the renewable energy sector.

The AR(1)-EGARCH(1,1) model under normal distribution is only satisfactory for the traditional energy stock Schlumberger. Under the skew-normal distribution, four stocks pass the tests: Nibe from the renewable sector, and Exxon Mobil, Chevron, and Schlumberger from the traditional energy sector. As for the Student’s t distribution, the model seems adequate in two cases, the renewable energy stock Nibe and the traditional energy stock Schlumberger. The renewable energy stocks do not pass the test for the skewed-t distribution. On the contrary, all the traditional energy stocks except for Chevron reject the null hypothesis in the Kupiec and independence test. The model under the GED distribution accurately exhibits results in all cases, except for Exxon Mobil, Chevron and Total S.A. In addition, for the SGED distribution, the model works well in all cases except for Epistar, from the renewable energy sector.

The AR(1)-APARCH(1,1) model performs well under normal and skew-normal distributions in two cases: with the renewable energy stock Nibe, and with the traditional energy stock Schlumberger. The model behaves adequately under the Student’s t distribution with the renewable energy stocks Kingspan, Boralex and Nibe, and the traditional energy stock Schlumberger. Under the skewed-t distribution, the model performs accurately with the renewable energy stock Boralex and with all the traditional energy stocks, with the exception of Chevron. The model under the GED distribution works well in all cases, except for Exxon Mobil, Chevron, and Total S.A. from the traditional energy sector. For the SGED distribution, the model works precisely in all cases except for Epistar from the renewable energy sector.

5.4. Backtesting of 97.5%-ES

Table 5 displays the results for the 97.5%-ES backtesting for the three tests (Z₁, Z₂ y Z_ES).

Table 5. 97.5%-ES backtesting. Values for Z₁, Z₂ y Z_ES statistics.

	AR(1)-GARCH(1,1)
	Normal			Skew-Normal			t-Student			Skew-t			GED			SGED
	Z1	Z2	ZES	Z1	Z2	ZES	Z1	Z2	ZES	Z1	Z2	ZES	Z1	Z2	ZES	Z1	Z2	ZES
Epistar	−0.09	−0.45	−0.32	−0.10	−0.44	−0.34	0.02	−0.17	−0.25	0.00	−0.37	−0.33	−0.02	−0.20	−0.20	−0.02	−0.32	−0.20
Kingspan	−0.10	−0.52	−0.36	−0.12	−0.57	−0.39	0.02	−0.05	−0.24	0.01	−0.22	−0.24	−0.03	−0.06	−0.10	−0.03	−0.11	−0.16
Boralex	−0.21	−0.35	−0.41	−0.19	−0.46	−0.43	0.03	0.08	−0.26	0.02	0.01	−0.23	−0.03	0.05	−0.22	−0.02	0.00	−0.19
Nibe	−0.18	−0.27	−0.37	−0.21	−0.35	−0.41	−0.04	0.03	−0.28	−0.01	−0.49	−0.42	−0.13	0.04	−0.28	−0.12	−0.18	−0.34
Exxon Mobil	−0.16	−0.72	−0.48	−0.14	−0.50	−0.40	−0.05	−0.48	−0.39	−0.05	−0.09	−0.29	−0.10	−0.45	−0.39	−0.09	−0.20	−0.34
Chevron	−0.11	−0.70	−0.41	−0.10	−0.28	−0.32	−0.05	−0.46	−0.37	−0.01	0.25	−0.16	−0.09	−0.54	−0.38	−0.08	−0.15	−0.28
Total S.A.	−0.09	−0.57	−0.36	−0.09	−0.41	−0.32	−0.02	−0.31	−0.30	0.00	0.05	−0.20	−0.02	−0.21	−0.22	−0.03	−0.15	−0.16
Schlumberger	−0.15	−0.36	−0.36	−0.15	−0.29	−0.35	−0.05	−0.05	−0.27	−0.06	−0.06	−0.25	−0.09	−0.11	−0.18	−0.09	−0.09	−0.18
	AR(1)-EGARCH(1,1)
	Normal			Skew-Normal			t-Student			Skew-t			GED			SGED
	Z1	Z2	ZES	Z1	Z2	ZES	Z1	Z2	ZES	Z1	Z2	ZES	Z1	Z2	ZES	Z1	Z2	ZES
Epistar	−0.08	−0.52	−0.34	−0.09	−0.54	−0.35	0.00	−0.28	−0.27	−0.05	−0.41	−0.36	−0.02	−0.21	−0.22	−0.01	−0.33	−0.19
Kingspan	−0.08	−0.60	−0.36	−0.10	−0.63	−0.38	0.03	−0.20	−0.26	0.01	−0.21	−0.26	−0.00	−0.19	0.21	−0.01	−0.26	−0.17
Boralex	−0.14	−0.52	−0.40	−0.16	−0.54	−0.42	0.03	−0.04	−0.28	0.02	−0.05	−0.27	−0.03	−0.13	−0.19	−0.03	−0.13	−0.10
Nibe	−0.19	−0.23	−0.37	−0.20	−0.38	−0.41	−0.05	0.02	−0.28	0.00	−0.42	−0.38	−0.12	0.03	−0.16	−0.14	−0.12	−0.18
Exxon Mobil	−0.18	−0.70	−0.49	−0.17	−0.44	−0.41	−0.10	−0.50	−0.43	−0.07	−0.11	−0.26	−0.13	−0.51	−0.43	−0.12	−0.19	−0.40
Chevron	−0.14	−0.63	−0.43	−0.12	−0.23	−0.32	−0.09	−0.62	−0.42	−0.07	0.22	−0.17	−0.11	−0.61	−0.41	−0.10	−0.19	−0.36
Total S.A.	−0.12	−0.58	−0.39	−0.10	−0.45	−0.34	−0.01	−0.42	−0.35	−0.01	−0.03	−0.22	−0.02	−0.40	−0.22	−0.03	−0.21	−0.20
	−0.15	−0.30	−0.35	−0.12	−0.35	−0.34	−0.07	−0.08	−0.28	−0.07	−0.01	−0.27	−0.09	−0.11	−0.19	−0.09	−0.09	−0.20
	AR(1)-APARCH(1,1)
	Normal			Skew-Normal			t-Student			Skew-t			GED			SGED
	Z1	Z2	ZES	Z1	Z2	ZES	Z1	Z2	ZES	Z1	Z2	ZES	Z1	Z2	ZES	Z1	Z2	ZES
Epistar	−0.11	−0.63	−0.29	−0.08	−0.52	−0.32	0.04	−0.21	−0.27	−0.02	−0.41	−0.36	−0.03	−0.21	−0.21	−0.03	−0.31	−0.17
Kingspan	−0.09	−0.49	−0.35	−0.11	−0.58	−0.36	0.01	−0.20	−0.26	0.01	−0.19	−0.22	−0.02	−0.18	0.15	−0.00	−0.28	−0.21
Boralex	−0.12	−0.72	−0.44	−0.12	−0.61	−0.40	0.05	−0.04	−0.25	0.02	−0.05	−0.24	−0.02	−0.11	−0.16	−0.03	−0.12	−0.14
Nibe	−0.21	−0.35	−0.36	−0.23	−0.42	−0.37	−0.03	0.02	−0.22	0.00	−0.42	−0.38	−0.12	0.03	−0.22	−0.12	−0.12	−0.17
Exxon Mobil	−0.11	−0.59	−0.47	−0.26	−0.51	−0.47	−0.10	−0.50	−0.43	−0.09	−0.11	−0.21	−0.15	−0.55	−0.39	−0.11	−0.17	−0.41
Chevron	−0.09	−0.45	−0.45	−0.14	−0.28	−0.36	−0.03	−0.62	−0.42	−0.02	0.22	−0.23	−0.10	−0.60	−0.41	−0.10	−0.18	−0.36
Total S.A.	−0.11	−0.69	−0.42	−0.11	−0.45	−0.38	−0.02	−0.42	−0.35	−0.01	−0.03	−0.25	−0.03	−0.41	−0.21	−0.01	−0.21	−0.22
Schlumberger	−0.18	−0.22	−0.35	−0.17	−0.35	−0.33	−0.12	−0.08	−0.25	−0.08	−0.01	−0.19	−0.09	−0.11	−0.17	−0.11	−0.11	−0.16

The critical value for Z1 test is -0.03 for normal, skew-normal, GED and SGED, -0.05 for Student’s t and skewed-t. The critical value for Z2 test is -0.21 for normal, skew-normal, GED and SGED, -0.22 for Student’s t and skewed-t. The critical value for ZES test is -0.20 for normal and skew-normal, -0.27 for Student’s t and skewed-t, and -0.22 for GED and SGED. Bold figures represent the adequate performance of the model for each test.

5.4.1. Z₁ Test

With the AR(1)-GARCH(1,1) model under normal and skew-normal distributions, all of the stocks reject the null hypothesis of the test. Under the Student’s t distribution, the test works well with the renewable energy stocks Epistar, Kingspan and Boralex, and the traditional energy stock Total S.A. The test presents satisfactory results under the skewed-t distribution; in all cases, the null hypothesis of the test is not rejected, except with the traditional energy stock Schlumberger. For the GED and SGED, the test works well for Epistar, Kingspan and Boralex from the renewable energy sector, and for Total S.A. from the traditional energy sector.

In the AR(1)-EGARCH(1,1) and AR(1)-APARCH(1,1) model under normal and skew-normal distributions, all of the stocks rejects the null hypothesis of the test. The four renewable energy stocks pass the test with the Student’s t and skewed-t distributions, and the traditional energy stocks Total S.A. and Chevron also pass, but the latter only passes the test in the AR(1)-APARCH(1,1) model. Under the GED and SGED, the test works well for Epistar, Kingspan and Boralex, and for Total S.A.

5.4.2. Z₂ Test

In the AR(1)-GARCH(1,1) model under normal and skew-normal distributions, all of the stocks reject the null hypothesis of the test. For the Student’s t distribution, the test performs well with all four renewable energy stocks and with the traditional energy stock Schlumberger. The results improve noticeably with the skewed-t distribution; none of the stocks reject the null hypothesis of the test except the renewable energy stocks Epistar and Nibe. Under the GED, the test performs well for all four stocks from the renewable sector, and for Total S.A. and Schlumberger from the traditional energy sector. In the case of SGED, the test presents satisfactory results for all the stocks, except for Epistar, from the renewable energy sector.

In the AR(1)-EGARCH(1,1) and AR(1)-APARCH(1,1) models under normal and skew-normal distributions, all of the stocks rejects the null hypothesis of the test. All the renewable energy stocks, except for Epistar in AR(1)-EGARCH(1,1), pass the test with the Student’s t distribution; Schlumberger from the renewable energy stocks also passes the test. None of the stocks reject the null hypothesis of the test under the skewed-t distribution, except the renewable energy stocks Epistar and Nibe. Under the GED, the test performs well for all the four stocks from the renewable sector, and for Schlumberger from the traditional energy sector. For the SGED, the test performs well for all the stocks, except for Epistar and Kingspan, from the renewable energy sector.

5.4.3. Z_ES Test

In the AR(1)-GARCH(1,1) model under normal and skew-normal distributions, all of the stocks reject the null hypothesis of the test. For the Student’s t distribution, the test works well with three renewable energy stocks (Epistar, Kingspan and Boralex) and with the traditional energy stock Schlumberger. With the skewed-t distribution, the null hypothesis of the test cannot be rejected for all the stocks, with the exception of the renewable energy stocks Epistar and Nibe and the traditional energy stock Exxon Mobil. Under the GED and the SGED, the test exhibits satisfactory results for Epistar, Kingspan, Boralex, Total S.A., and Schlumberger.

None of the stocks pass the test with the AR(1)-EGARCH(1,1) and AR(1)-APARCH(1,1) models under normal and skew-normal distributions. With the Student’s t distribution, however, none of the renewable energy stocks reject the null hypothesis of the test; nor does the traditional energy stock Schlumberger. Under the skewed-t distribution, all stocks pass the test except the renewable energy stocks Epistar and Nibe. Under the GED and SGED, the test works well in all cases, except for Exxon Mobil and Chevron from the traditional energy market.

In summary, the higher flexibility of the skewed-t and the SGED provides the best results for VaR and ES testing. The skewed-t has better results in the traditional energy sector; meanwhile, the SGED performs better in the renewable energy sector. Nevertheless, we recommend filtering the returns by employing AR(1)-GARCH(1,1), since the results are similar to other GARCH(1,1) family models tested in our application. Furthermore, $Z_{ES}$ statistic is proposed to validate ES quantities, since this test is more potent than Z₁ and Z₂ tests.

6. Discussion

The empirical analyses in the previous section shed light on the best techniques for risk management in energy markets, revealing the skewed-t distribution to be an accurate tool, but also the adequacy of ES as a new paradigm for regulatory capital. In this section, we present a discussion on the implications in terms of capital reserves of the shift in the risk measure from VaR_99% to ES_97.5% in renewable and traditional energy stocks considering skewed-t distribution for the innovations. Table 6 shows the daily VaR_99%, ES_97.5% and the difference between these two risk measures diff = ES_97.5% − VaR_99% calculated for the renewable and traditional energy stock returns with the AR(1)-GARCH(1,1), AR(1)-EGARCH(1,1) and AR(1)-APARCH(1,1) models in the analyzed sample. This difference (diff) represents the percentage of extra reserve capital that must be established in adopting ES.

Table 6. Capital requirements percentage for energy stocks under skewed-t innovations.

	Total Period (January 2005–December 2016)
Model	AR(1)-GARCH(1,1)			AR(1)-EGARCH(1,1)			AR(1)-APARCH(1,1)
Stock	VaR99%	ES97.5%	diff	VaR99%	ES97.5%	diff	VaR99%	ES97.5%	diff
Renewable
Epistar	−4.52166	−4.62706	0.10540	−4.50284	−4.60416	0.10131	−4.58420	−4.68796	0.10376
Kingspan	−5.68544	−5.93938	0.25394	−5.52422	−5.75760	0.23338	−5.29004	−5.51206	0.22202
Boralex	−3.74001	−3.99852	0.25851	−3.48382	−3.70996	0.22614	−3.85014	−4.10433	0.25420
Nibe	−4.58810	−4.79142	0.20332	−4.91927	−5.13077	0.21150	−4.71179	−4.91350	0.20171
Traditional
Exxon Mobil	−2.75996	−2.84387	0.08391	−2.43863	−2.50695	0.06832	−2.44536	−2.51313	0.06777
Chevron	−3.03334	−3.09445	0.06111	−3.06976	−3.11185	0.04209	−3.15134	−3.21426	0.06291
Total S.A.	−3.87745	−3.98049	0.10305	−3.93551	−4.03167	0.09616	−3.83333	−3.92498	0.09166
Schlumberger	−3.23484	−3.31588	0.08104	−3.08337	−3.15876	0.07540	−3.06615	−3.13985	0.07370

The table presents the differences in capital requirements from replacing VaR_99% with ES_97.5%, computed as diff = ES_97.5% − VaR_99%.

In Table 6, we can observe that VaR, ES, and diff values do not vary considerably between AR(1)-GARCH(1,1), AR(1)-EGARCH(1,1), and AR(1)-APARCH(1,1) models. On average, VaR and ES quantities are higher in renewable (−4.6338 and −4.8391, respectively) than in traditional energy stocks (−3.2264 and −3.3087), this can be attributed to the higher volatility faced in the renewable energy market. In addition, ES estimates in all cases are considerably higher than VaR. This is a result of extreme values that fatten the tail of the return distribution, which leads ES to assign higher regulatory capital when the skewed-t distribution is employed to fit the standardized residuals of stock returns. These findings have important implications for portfolio managers and regulators in terms of capital allocation in renewable and traditional energy stocks mainly to reduce the impact of possible extreme losses events.

To have a better understanding of the effects of switching the risk measures, we compute AR(1)-GARCH(1,1)-VaR and -ES for two stocks, Epistar (renewable energy) and Exxon Mobil (traditional energy), by employing a 500-day rolling window, and then we calculate the daily difference between the two risk measures. The results are illustrated in Figure 4. In this graph, it can be observed that, on average, the difference between both risk measures is much higher in Epistar (0.2402%) than in Exxon Mobil (0.1119%). Nevertheless, in 2008, within the context of the subprime crisis, differences for Exxon Mobil sharply rose to 1%, while those for Epistar remained at 0.25%. On the contrary, in relative calm periods such as in 2012 to 2013, the difference between the risk measures is around 0.2%. On the other hand, the difference between the two risk measures has increased consistently for Epistar since 2012, with a difference between 0.3% and 0.7% in 2014 and 0.6% in 2016.

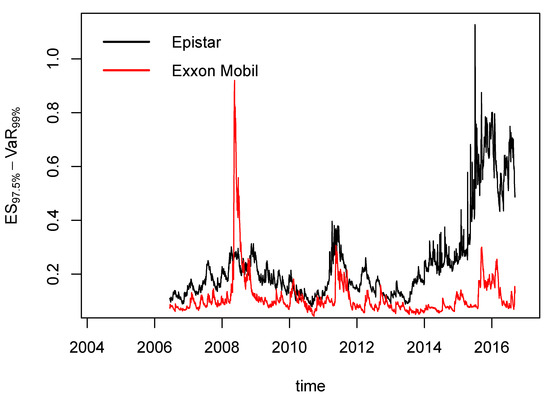
Figure 4. The difference in risk measures in Epistar and Exxon Mobil stock returns.

Figure 5 shows the difference between the 97.5%-ES and 99%-VaR, estimated with the AR(1)-GARCH(1,1) and the skewed-t distribution for innovations during the 2008 subprime crisis. Throughout this period, the ES was capable of adapting the extreme values and of allocating higher capital reserves than the VaR. This evidence emphasizes the need to search for the most accurate risk measures, especially in highly volatile scenarios. In these contexts, the use of ES with skewed-t distribution is advisable as a protection mechanism against extreme loss events in renewable energy stocks due to the capacity of skewed-t to adapt to potential volatility shocks and the asymmetric impact of market news.

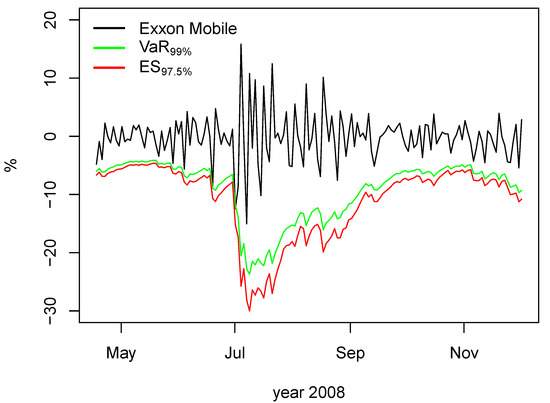
Figure 5. Estimated VaR-99% and ES-97.5% with the skewed-t distribution.

Our results support the ES as a suitable risk measure for renewable and traditional energy stocks in the context of periods of high volatility and turmoil when investors face extreme market risk. Consequently, this study helps energy market participants to have a better understanding of the market risk posed in renewable and traditional energy stock investments. Moreover, the efficient allocation of regulatory capital through accurate risk management techniques also helps regulators to fight against market instability and policymakers to decide on real investment decisions that might have a significant impact on the future of traditional and renewable energies.

7. Conclusions

The increasing demand for renewable energy and the high volatility of the prices of these energy sources have increased the need to accurately measure the risk of these markets. This is particularly important for the decision-making of firms, investors, and regulators and represents a cornerstone for the stability and sustainability of these markets with profound implications for the whole economy. This paper fits into this framework, implementing a rigorous methodology for risk management. This section summarizes the main contributions and results of the paper, which are enumerated below.

(1) The article studies the risk in traditional and renewable energy markets by examining four renewable energy stocks and four traditional energy stocks. The prices of these stocks exhibit the same features as other financial assets, particularly leptokurtosis and skewness, calling for the use of conditional mean-variance models and flexible non-normal distributions. The performance of three models—(AR(1)-GARCH(1,1), AR(1)-EGARCH(1,1) and AR(1)-APARCH(1,1))—with either normal, skew-normal, Student’s t, skewed-t, GED or SGED innovations are compared in terms of both VaR and ES backtesting techniques.

(2) The paper implements three tests proposed by Acerbi and Székely [9,10] to backtest 97.5%-ES. Backtesting of 99%-VaR and 97.5%-VaR is also carried out with Kupiec and independence tests. Our study contributes to the literature by extending the proposed ES tests to the skewed-t, GED and SGED distributions. A straightforward algorithm is proposed to compute critical values, and we tabulate them for different values of the skewed-t parameters. Furthermore, to the best of our knowledge, this is the first application of these tests to renewable and traditional energy stocks.

(3) The renewable energy stocks generally have higher price volatility than the traditional energy stocks, and thus the renewable energy stocks on average have more VaR violations than do the traditional energy stocks. The results indicate that the fitting of the normal distribution is weak in the three GARCH models for both traditional and renewable energy stocks. The best-fitting distribution in the backtests is the skewed-t, and AR(1)-GARCH(1,1) is the model that best fits the sample data.

(4) In the ES backtest, renewable energy stocks perform better than traditional energy stocks. We show that the tests proposed by Acerbi and Székely [9,10] are adequate for solving the drawback of the backtestability of ES, especially the $Z_{ES}$ test, which is more powerful. For this test, the skewed-t has better results in the traditional energy sector; meanwhile, the SGED performs better in the renewable energy sector. Consequently, we provide evidence on the appropriateness of ES, the new risk measure proposed by the last Basel Accords, for quantifying the risk of traditional and renewable energy stocks.

(5) Our results have important implications for the efficient allocation of regulatory capital, particularly in periods of high instability. The use of flexible distributions as the skewed-t and the SGED may help to provide accurate capital provisions in case of potential losses provoked by extreme events but also to free resources in more calm periods that can be used for undertaking real investments in traditional or renewable energies.

All in all, our results constitute a methodological framework with empirical evidence that can be used by regulators and investors to mitigate the market risk emerging from renewable and traditional energy markets.