A Compact Thermally Driven Cooling System Based on Metal Hydrides
Abstract
1. Introduction
- No consumption of electrical power, thus no dependency in driving range on AC operation;
- No moving parts leading to a quiet and low maintenance system;
- No environmentally unfriendly refrigerants are required (hydrogen as working fluid);
- Potentially small systems due to high thermal power density of MH based systems (this aspect is material intrinsic but its effect on the complete system depends highly on the available reactor design).
2. Experimental
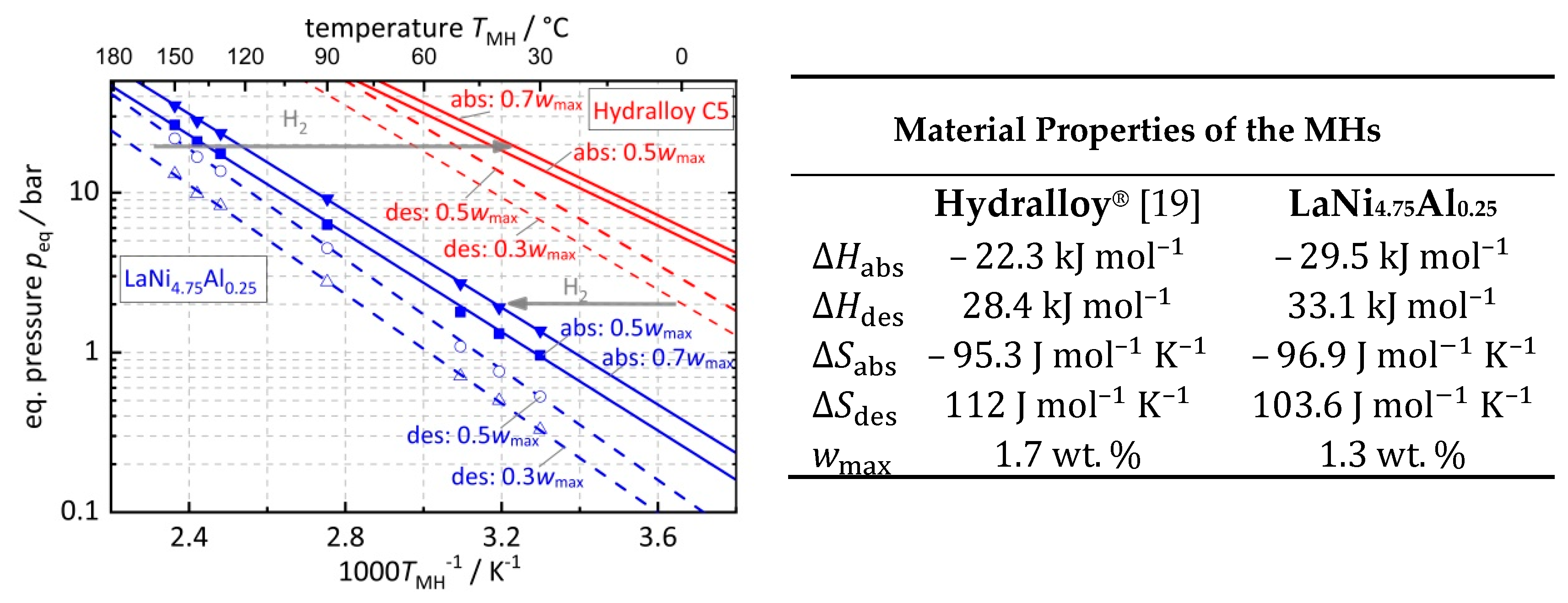
2.1. Metal Hydride Working Pair
2.2. Reactor Design
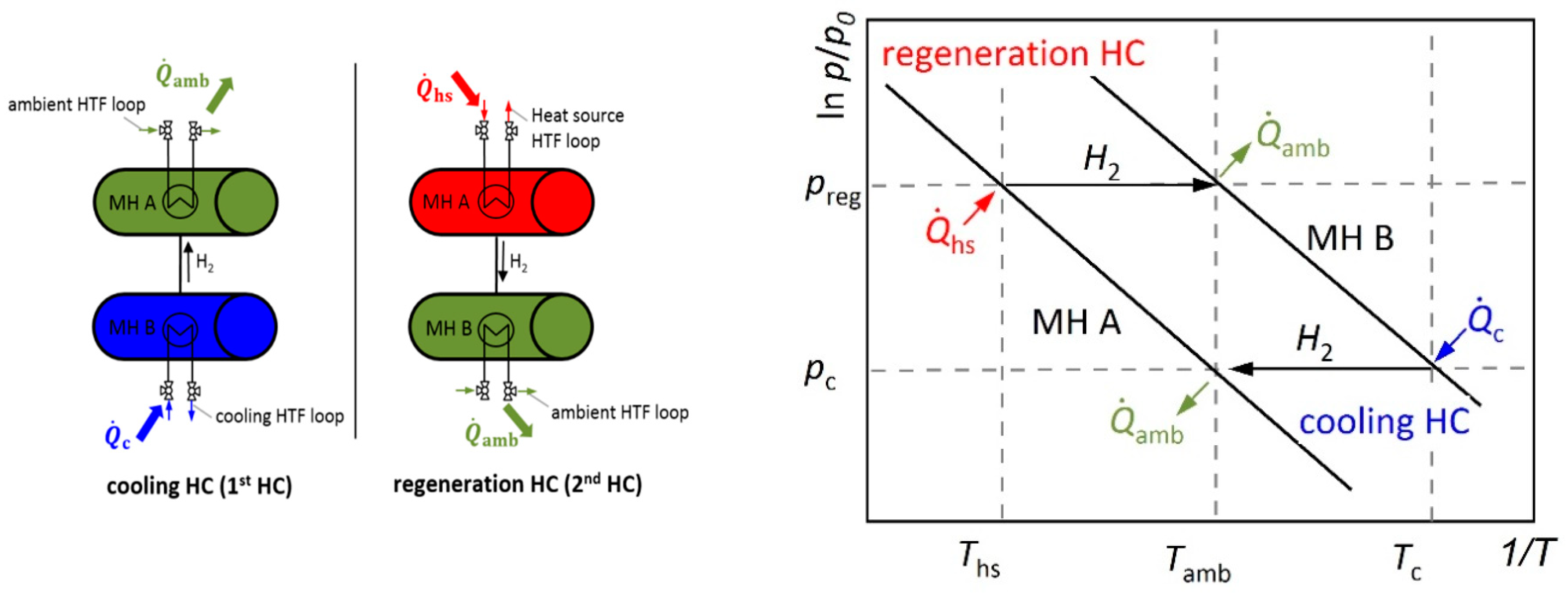
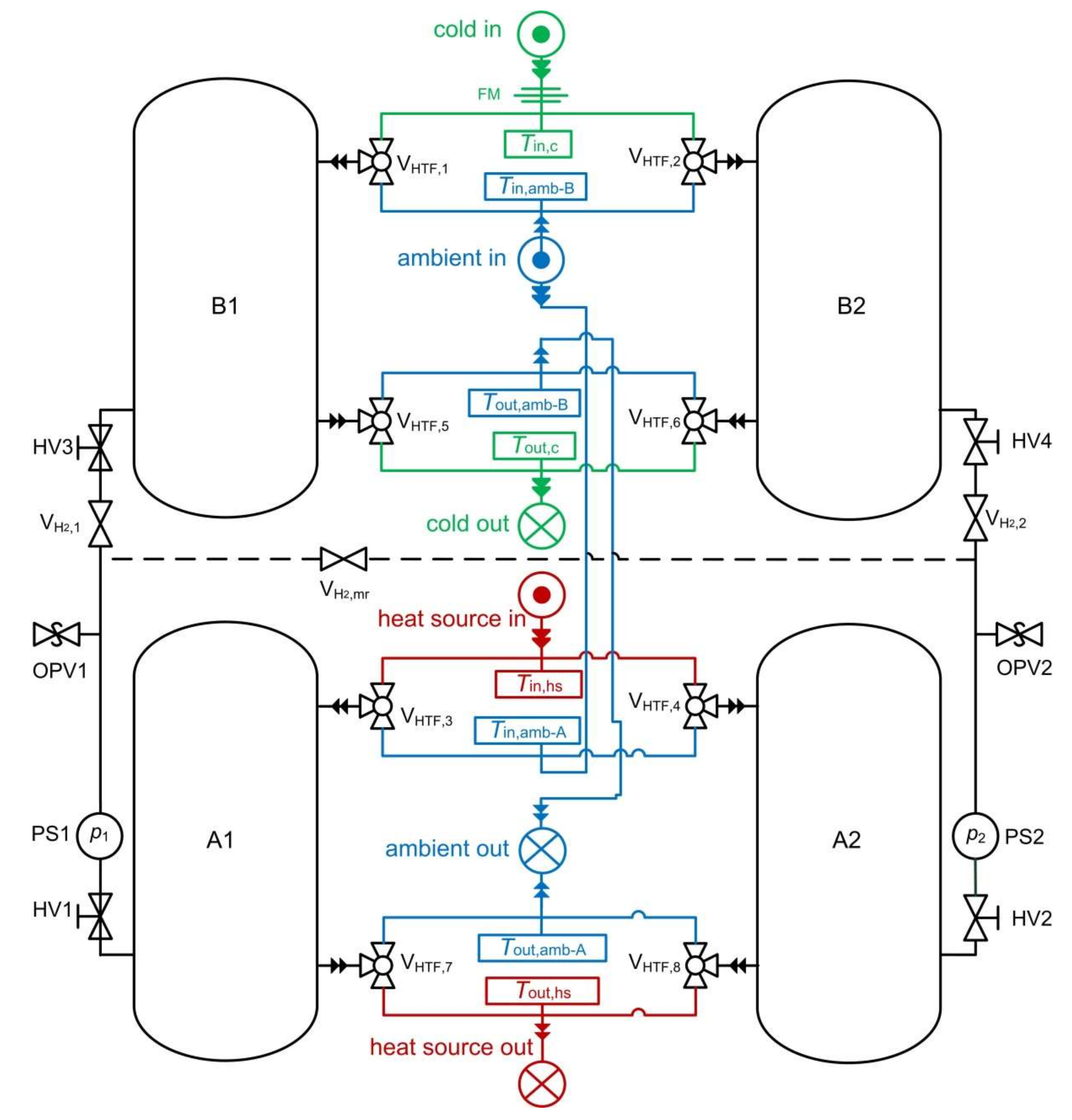
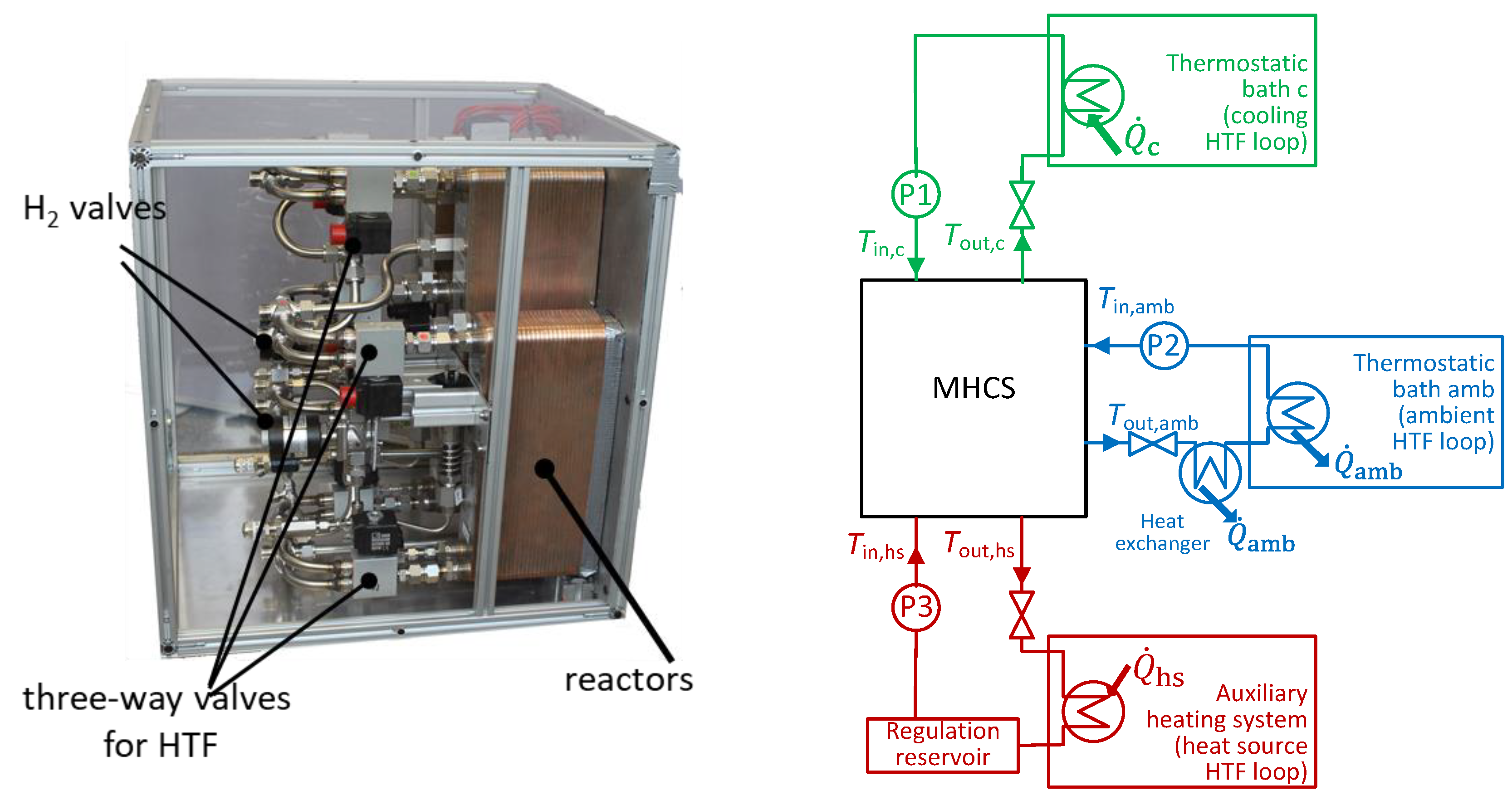
2.3. Description of the Modular MHCS
2.4. MHCS Operation and Optimization Strategy
3. Results and Discussion
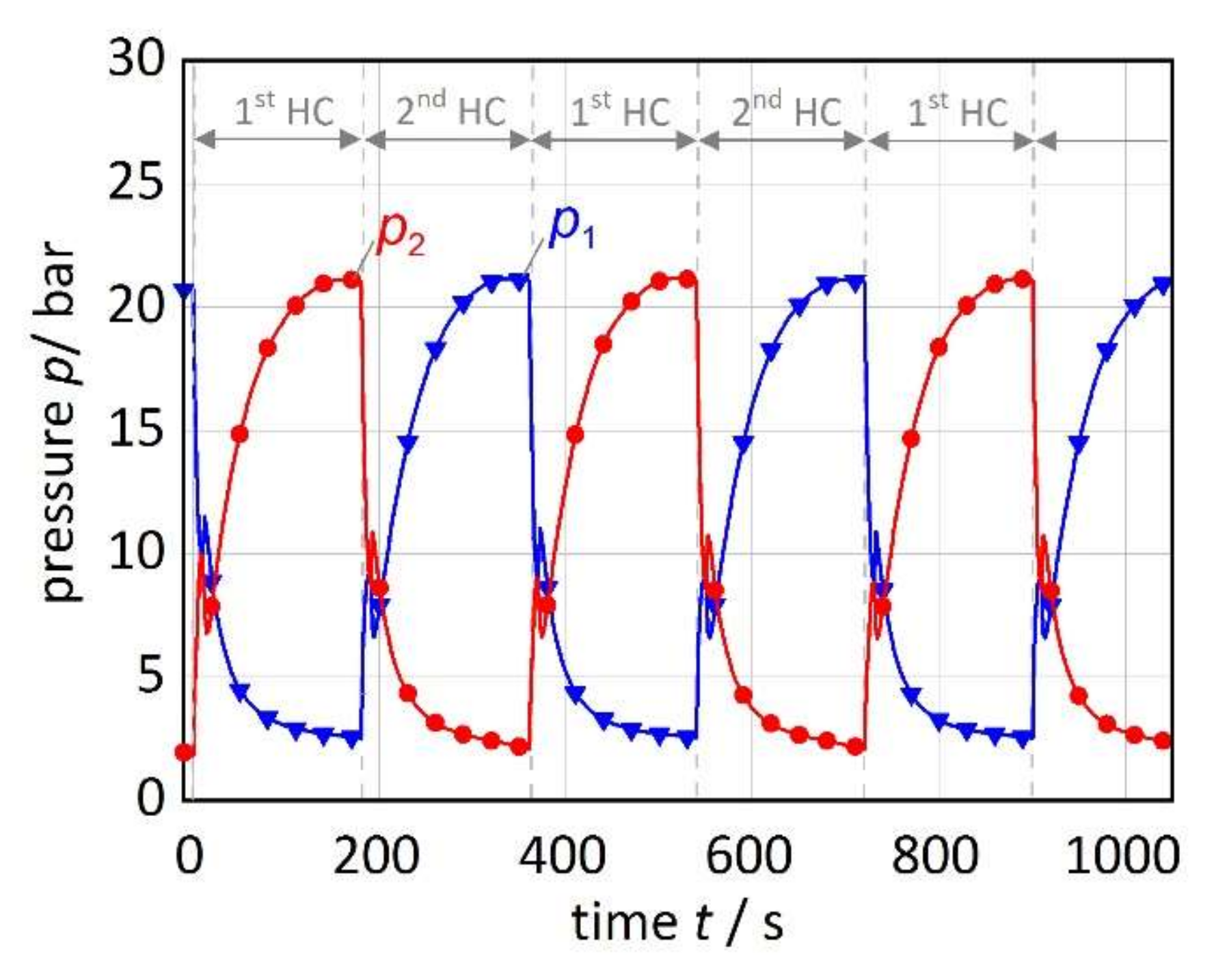
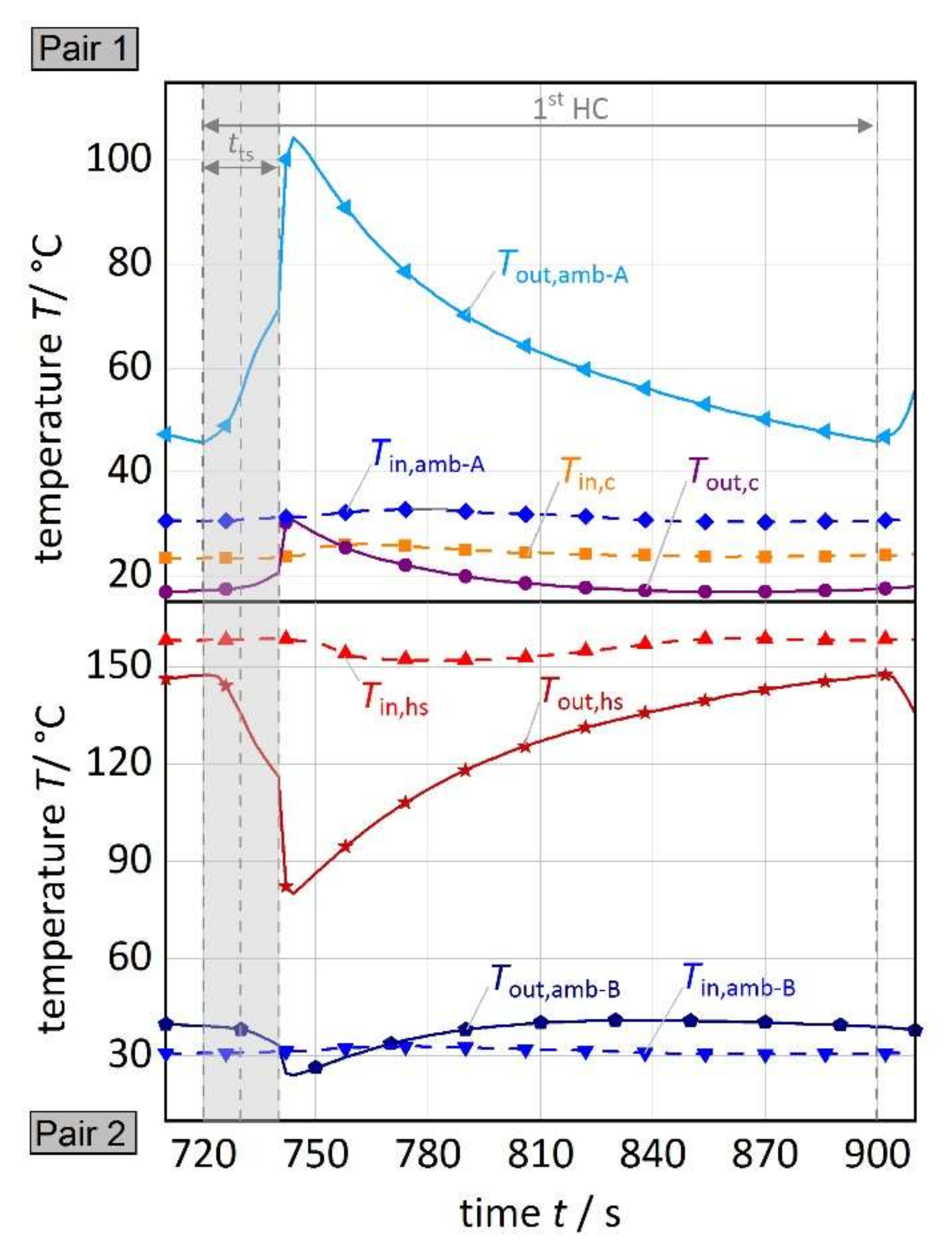
3.1. Results of the Reference Experiment
3.2. Sensitivity Study on Cooling Power
3.2.1. Temperature of the Heat Source
3.2.2. Ambient Temperature
- For lower in the regeneration HC, the absorption process in reactor B proceeds at a lower pressure leading to an improved desorption in reactor A at . Therefore, Δwmax is increased during the following cooling HC.
- For lower in the cooling HC, the pressure level is lower as well, leading to improved thermodynamic conditions for desorption at . This, again, leads to an increase in Δwmax.
- For lower additionally, the thermal losses in the cooling HC are reduced due to a smaller temperature difference ΔT = Tamb-Tc of reactor B, when the HCs are switched. As a consequence, Δwmax can be better utilized for effective cold generation.
3.2.3. Cooling Temperature
3.2.4. Cooling HTF Flow Rate
3.2.5. HC Time
3.2.6. Operation Optimization
3.2.7. Evaluation of Cooling Power, Specific Cooling Power and Efficiency for Ooptimal Experimental Conditions
3.3. Recommendations for System Improvement
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| AC | Air-conditioning |
| C | Connection |
| COP | Coefficient of Performance |
| FM | Flowmeter |
| FS | Full scale |
| FM | Flowmeter |
| HC | Half-cycle |
| HTF | Heat transfer fluid |
| HV | Hand valve |
| M | Metal |
| MH | Metal hydride |
| MHCS | Metal hydride cooling system |
| OPV | Overpressure valve |
| P | Pump |
| PS | Pressure sensor |
| repro | Reproduced experiment |
| Rd | Reading |
| TB | Thermostatic bath |
| V | Valve |
Nomenclature
| b | Reactor width, m |
| Reactor height, m | |
| Mass ratio, - | |
| Reactor length, m | |
| Molar weight | |
| Number, - | |
| Thermal Energy, J | |
| Entropy of reaction, J mol−1K−1 | |
Greek Letters
Subscripts
| abs | Absorption |
| amb | Ambient |
| avg | Average |
| c | Cooling |
| des | Desorption |
| eq | Equilibrium |
| H2 | Hydrogen |
| hs | Heat source |
| in | Inlet |
| max | Maximum |
| min | Minimum |
| mr | Mass recovery |
Appendix A
Uncertainty Analysis
| Description | Type |
|---|---|
| Hydrogen section | |
| Electromagnetic valves VH2,1–2 | Bürkert 0355-C |
| Hand valve HV1–4 | Swagelok SS-6P4T-MM-BK |
| Overpressure valve OPV1-2 | Swagelok SS-6R3A-MM |
| Pressure sensors PS1-2 | Wagner P-3278 0.5% FS) |
| HTF infrastructure section | |
| Electromagnetic three-valves VHTF,1–8 | Bürkert 0355-C |
| Impeller HTF flow meter FM | Meister DHGA-10 (A: 2% v.Rd) |
| Thermocouples | 1.5 K, temperature difference calibrated) |
| Control unit and data acquisition | |
| Control unit | Arduino Mega 2560 microcontroller |
| Data acquisition | Agilent 34970A |
| Testing infrastructure | |
| Auxiliary heating system | Webasto Thermo Pro 90, 24 V |
| HTF gear type pumps P1-P3 | Kracht KF6 RF 3 |
| Liquid-to-liquid heat exchanger | VAU VM 15/20 |
| Thermostatic bath TBc | Lauda Proline P8 |
| Thermostatic bath TBamb | Lauda Proline RP890 |
References
- Kambly, K.; Bradley, T. Geographical and temporal differences in electric vehicle range due to cabin conditioning energy consumption. J. Power Sources 2015, 275, 468–475. [Google Scholar] [CrossRef]
- Zhai, X.; Wang, R.; Wu, J.; Dai, Y.; Ma, Q. Design and performance of a solar-powered air-conditioning system in a green building. Appl. Energy 2008, 85, 297–311. [Google Scholar] [CrossRef]
- Tso, C.; Chan, K.C.; Chao, C.; Wu, C. Experimental performance analysis on an adsorption cooling system using zeolite 13X/CaCl2 adsorbent with various operation sequences. Int. J. Heat Mass Transf. 2015, 85, 343–355. [Google Scholar] [CrossRef]
- Sharafian, A.; Mehr, S.M.N.; Thimmaiah, P.C.; Huttema, W.; Bahrami, M. Effects of adsorbent mass and number of adsorber beds on the performance of a waste heat-driven adsorption cooling system for vehicle air conditioning applications. Energy 2016, 112, 481–493. [Google Scholar] [CrossRef]
- Palomba, V.; Dawoud, B.; Sapienza, A.; Vasta, S.; Frazzica, A. On the impact of different management strategies on the performance of a two-bed activated carbon/ethanol refrigerator: An experimental study. Energy Convers. Manag. 2017, 142, 322–333. [Google Scholar] [CrossRef]
- Regulation (EU) No 517/2014 of the European Parliament and of the Council of 16 April 2014 on Fluorinated Greenhouse Gases and Repealing Regulation (EC) No 842/2006 2014; European Parliament: Brussels, Belgium.
- Von Colbe, J.B.; Ares, J.-R.; Barale, J.; Baricco, M.; Buckley, C.; Capurso, G.; Gallandat, N.; Grant, D.M.; Guzik, M.N.; Jacob, I.; et al. Application of hydrides in hydrogen storage and compression: Achievements, outlook and perspectives. Int. J. Hydrog. Energy 2019, 44, 7780–7808. [Google Scholar] [CrossRef]
- Lototskyy, M.V.; Yartys, V.A.; Pollet, B.G.; Bowman, R. Metal hydride hydrogen compressors: A review. Int. J. Hydrog. Energy 2014, 39, 5818–5851. [Google Scholar] [CrossRef]
- Muthukumar, P.; Groll, M. Metal hydride based heating and cooling systems: A review. Int. J. Hydrog. Energy 2010, 35, 3817–3831. [Google Scholar] [CrossRef]
- Gruen, D.; Mendelsohn, M.; Sheft, I. Metal hydrides as chemical heat pumps. Sol. Energy 1978, 21, 153–156. [Google Scholar] [CrossRef]
- Ron, M. A hydrogen heat pump as a bus air conditioner. J. Less Common Met. 1984, 104, 259–278. [Google Scholar] [CrossRef]
- Linder, M. Automotive Cooling Systems based on Metal Hydrides. Ph.D. Thesis, University of Stuttgart, Stuttgart, Germany, 2010. [Google Scholar]
- Bhuiya, M.H.; Kumar, A.; Kim, K.J. Metal hydrides in engineering systems, processes, and devices: A review of non-storage applications. Int. J. Hydrog. Energy 2015, 40, 2231–2247. [Google Scholar] [CrossRef]
- Satheesh, A.; Muthukumar, P. Performance investigation of double-stage metal hydride based heat pump. Appl. Therm. Eng. 2010, 30, 2698–2707. [Google Scholar] [CrossRef]
- Willers, E.; Groll, M. The two-stage metal hydride heat transformer. Int. J. Hydrog. Energy 1999, 24, 269–276. [Google Scholar] [CrossRef]
- Muthukumar, P.; Patil, M.S.; Raju, N.N.; Imran, M. Parametric investigations on compressor-driven metal hydride based cooling system. Appl. Therm. Eng. 2016, 97, 87–99. [Google Scholar] [CrossRef]
- Park, J.-G.; Han, S.-C.; Jang, H.-Y.; Lee, S.-M. The development of compressor-driven metal hydride heat pump (CDMHHP) system as an air conditioner. Int. J. Hydrog. Energy 2002, 27, 941–944. [Google Scholar] [CrossRef]
- Linder, M.; Kulenovic, R. An energy-efficient air-conditioning system for hydrogen driven cars. Int. J. Hydrog. Energy 2011, 36, 3215–3221. [Google Scholar] [CrossRef]
- Herbrig, K.; Röntzsch, L.; Pohlmann, C.; Weissgaerber, T.; Kieback, B. Hydrogen storage systems based on hydride–graphite composites: Computer simulation and experimental validation. Int. J. Hydrog. Energy 2013, 38, 7026–7036. [Google Scholar] [CrossRef]
- Wanner, M.; Hoffmann, G.; Groll, M. Thermodynamic and Structural Changes of an Ab2-Laves-Phase Alloy (Ti0.98 Zr0.02 V0.43 Fe0.06 Cr0.05 Mn1.52) During Extended Thermal Cycling. Hydrog. Power Theor. Eng. Solut. 1998, 9, 257–262. [Google Scholar] [CrossRef]
- Friedlmeier, G.; Manthey, A.; Wanner, M.; Groll, M. Cyclic stability of various application-relevant metal hydrides. J. Alloy. Compd. 1995, 231, 880–887. [Google Scholar] [CrossRef]
- Kölbig, M.; Bürger, I.; Linder, M. Characterization of metal hydrides for thermal applications in vehicles below 0 °C. Int. J. Hydrog. Energy 2019, 44, 4878–4888. [Google Scholar] [CrossRef]
- Skripnyuk, V.; Ron, M. Hydrogen desorption kinetics in intermetallic compounds C2, C5 and C5 with Laves phase structure. Int. J. Hydrog. Energy 2003, 28, 303–309. [Google Scholar] [CrossRef]
- Yang, F.; Wang, G.; Zhang, Z.; Meng, X.; Rudolph, V. Design of the metal hydride reactors—A review on the key technical issues. Int. J. Hydrog. Energy 2010, 35, 3832–3840. [Google Scholar] [CrossRef]
- Weckerle, C.; Bürger, I.; Linder, M. Novel reactor design for metal hydride cooling systems. Int. J. Hydrog. Energy 2017, 42, 8063–8074. [Google Scholar] [CrossRef]
- Weckerle, C.; Bürger, I.; Linder, M. Experimental demonstration of a metal hydride air-conditioning system for fuel cell vehicles—Functional demonstration. Appl. Energy 2020, 259, 114187. [Google Scholar] [CrossRef]
- Weckerle, C.; Nasri, M.; Hegner, R.; Linder, M.; Bürger, I. A metal hydride air-conditioning system for fuel cell vehicles—Performance investigations. Appl. Energy 2019, 256, 113957. [Google Scholar] [CrossRef]
- Weckerle, C.; Bürger, I.; Linder, M. Numerical optimization of a plate reactor for a metal hydride open cooling system. Int. J. Hydrog. Energy 2019, 44, 16862–16876. [Google Scholar] [CrossRef]
- Li, T.; Wang, R.; Li, H. Progress in the development of solid–gas sorption refrigeration thermodynamic cycle driven by low-grade thermal energy. Prog. Energy Combust. Sci. 2014, 40, 1–58. [Google Scholar] [CrossRef]
- Cot-Gores, J.; Castell, A.; Cabeza, L.F. Thermochemical energy storage and conversion: A-state-of-the-art review of the experimental research under practical conditions. Renew. Sustain. Energy Rev. 2012, 16, 5207–5224. [Google Scholar] [CrossRef]





| Description | Value |
|---|---|
| Average channel thickness | 1.5 × 10−3 m |
| Empty reactor mass | 5.3 kg (without connections) |
| Free MH volume | 1.03 × 10−3 m3 |
| Mass ratio of reactor A1 and A2 | |
| Mass ratio of reactor B1 and B2 | |
| Max. permitted pressure | 30 bar |
| Max. permitted temperature | 195 °C |
| MH mass of reactor A1 and A2 | |
| MH mass of reactor B1 and B2 | |
| Number of HTF channels | |
| Number of MH channels | |
| Number of separating steel plates | |
| Reactor dimensions | 0.308 m × 0.072 m × 0.158 m |
| Reactor volume | 3.5 × 10−3 m3 |
| Reactor | A1 | B1 | A2 | B2 | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Operation Mode | 1st HC: Cooling HC 2nd HC: Regeneration HC | 1st HC: Regeneration HC 2nd HC: Cooling HC | ||||||||||
| HTF Valve Position | ||||||||||||
| Valve | 1st HC | 2nd HC | Valve | 1st HC | 2nd HC | Valve | 1st HC | 2nd HC | Valve | 1st HC | 2nd HC | |
| Phase 1 and Phase 2 | VHTF,3 | b-c | a-c | VHTF,1 | b-c | a-c | VHTF,4 | a-c | b-c | VHTF,2 | a-c | b-c |
| VHTF,7 | a-b | a-c | VHTF,5 | a-c | a-b | VHTF,8 | a-c | a-b | VHTF,6 | a-b | a-c | |
| Phase 3 | VHTF,3 | b-c | a-c | VHTF,1 | b-c | a-c | VHTF,4 | a-c | b-c | VHTF,2 | a-c | b-c |
| VHTF,7 | a-c | a-b | VHTF,5 | a-b | a-c | VHTF,8 | a-b | a-c | VHTF,6 | a-c | a-b | |
| H2 Valve Position | ||||||||||||
| Valve | 1st HC (H2 Flow) | 2nd HC (H2 Flow) | Valve | 1st HC (H2 Flow) | 2nd HC (H2 Flow) | |||||||
| Phase 1 | VH2,mr | Open (A1 A2) | Open (A2 A1) | VH2,mr | Open (A1 A2) | Open (A2 A1) | ||||||
| VH2,1 | closed | closed | VH2,1 | closed | closed | |||||||
| Phase 2 and Phase 3 | VH2,mr | closed | closed | VH2,mr | closed | closed | ||||||
| VH2,1 | Open (B1 A1) | Open (A1 B1) | VH2,1 | Open (A2 B2) | Open (B2 A2) | |||||||
| Parameter | Symbol | Reference Value | Range |
|---|---|---|---|
| Inlet temperature of the heat source HTF loop | 156.3 °C | 120–167 °C | |
| Inlet temperature of the ambient HTF loop | 31.4 °C | 29–40 °C | |
| Inlet temperature of the cooling HTF loop | 24.5 °C | 16–31 °C | |
| Volume flow of the cooling HTF loop | 6.3 × 10−3 m3 min−1 | 2.1–8.1 × 10−3 m3 min−1 | |
| Duration of the HC | 180 s | 120–420 s | |
| Duration of the time-shifted switching | 20 s | 0–40 s | |
| Duration of the mass recovery | 10 s | 0–20 s |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Weckerle, C.; Dörr, M.; Linder, M.; Bürger, I. A Compact Thermally Driven Cooling System Based on Metal Hydrides. Energies 2020, 13, 2482. https://doi.org/10.3390/en13102482
Weckerle C, Dörr M, Linder M, Bürger I. A Compact Thermally Driven Cooling System Based on Metal Hydrides. Energies. 2020; 13(10):2482. https://doi.org/10.3390/en13102482
Chicago/Turabian StyleWeckerle, Christoph, Marius Dörr, Marc Linder, and Inga Bürger. 2020. "A Compact Thermally Driven Cooling System Based on Metal Hydrides" Energies 13, no. 10: 2482. https://doi.org/10.3390/en13102482
APA StyleWeckerle, C., Dörr, M., Linder, M., & Bürger, I. (2020). A Compact Thermally Driven Cooling System Based on Metal Hydrides. Energies, 13(10), 2482. https://doi.org/10.3390/en13102482





