Heat and Mass Transfer in Hydromagnetic Second-Grade Fluid Past a Porous Inclined Cylinder under the Effects of Thermal Dissipation, Diffusion and Radiative Heat Flux

Abstract

Current disquisition is presented to excogitate heat and mass transfer features of second grade fluid flow generated by an inclined cylinder under the appliance of diffusion, radiative heat flux, convective and Joule heating effects. Mathematical modelling containing constitutive expressions by obliging fundamental conservation laws are constructed in the form of partial differential equations. Afterwards, transformations are implemented to convert the attained partial differential system into ordinary differential equations. An implicit finite difference method known as the Keller Box was chosen to extract the solution. The impact of the flow-controlling variables on velocity, temperature and concentration profiles are evaluated through graphical visualizations. Variations in skin friction, heat transfer and mass flux coefficients against primitive variables are manipulated through numerical data. It is inferred from the analysis that velocity of fluid increases for incrementing magnitude of viscoelastic parameter and curvature parameter whereas it reduces for Darcy parameter whereas skin friction coefficient decreases against curvature parameter. Assurance of present work is manifested by constructing comparison with previous published literature.

1. Literature Survey

Two types of fluids, namely Newtonian and non-Newtonian fluids, have changed the dynamics of today’s world. Initially Newtonian fluids gained pervasive focus from researchers, but due to the complexity and diversification in various fluid-dependent procedures, the essence of non-Newtonian fluids is rising. Non-Newtonian fluids have venerable significance and are required for different commercial, industrial, physiological, mechanical, physical, medicinal and technological purposes. 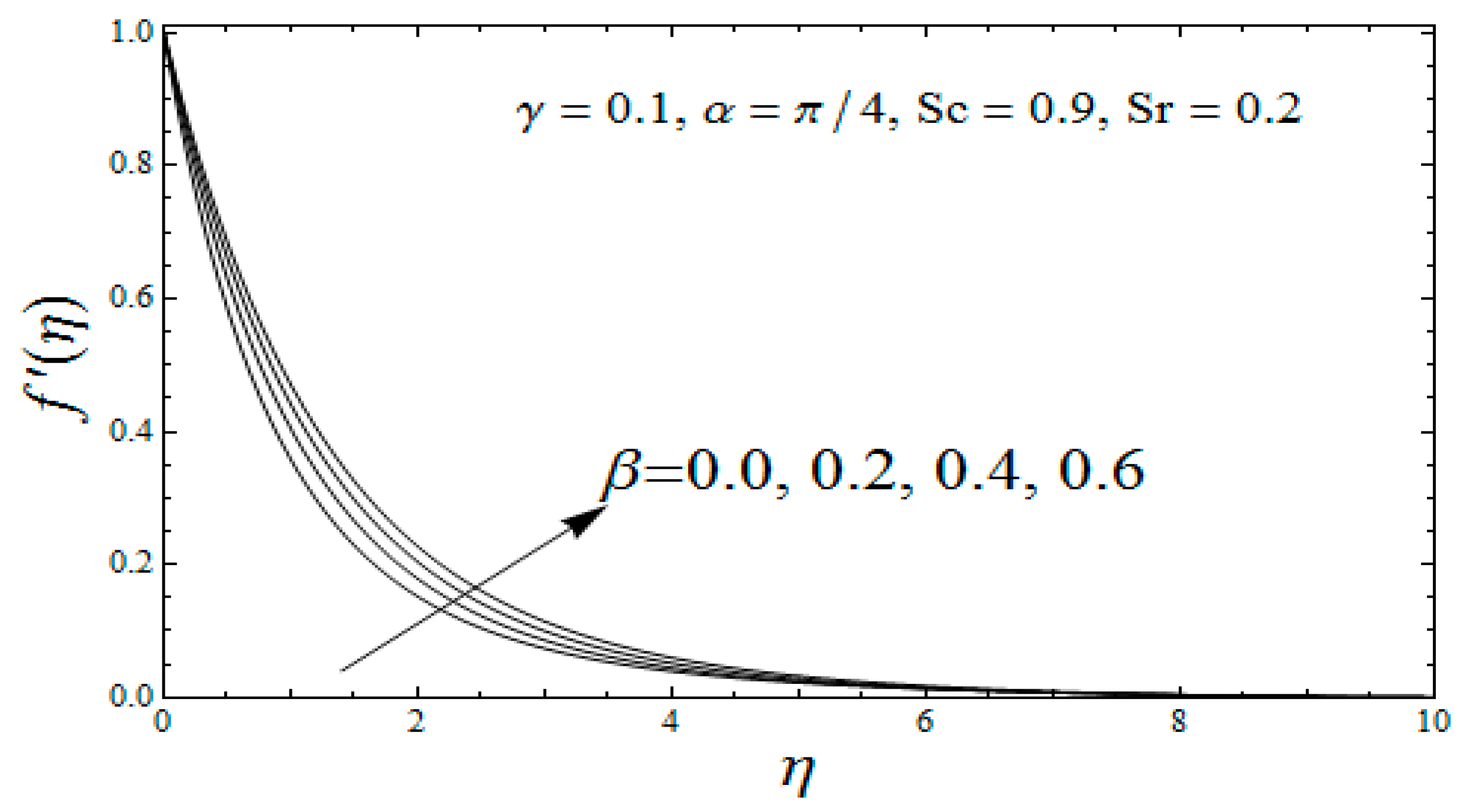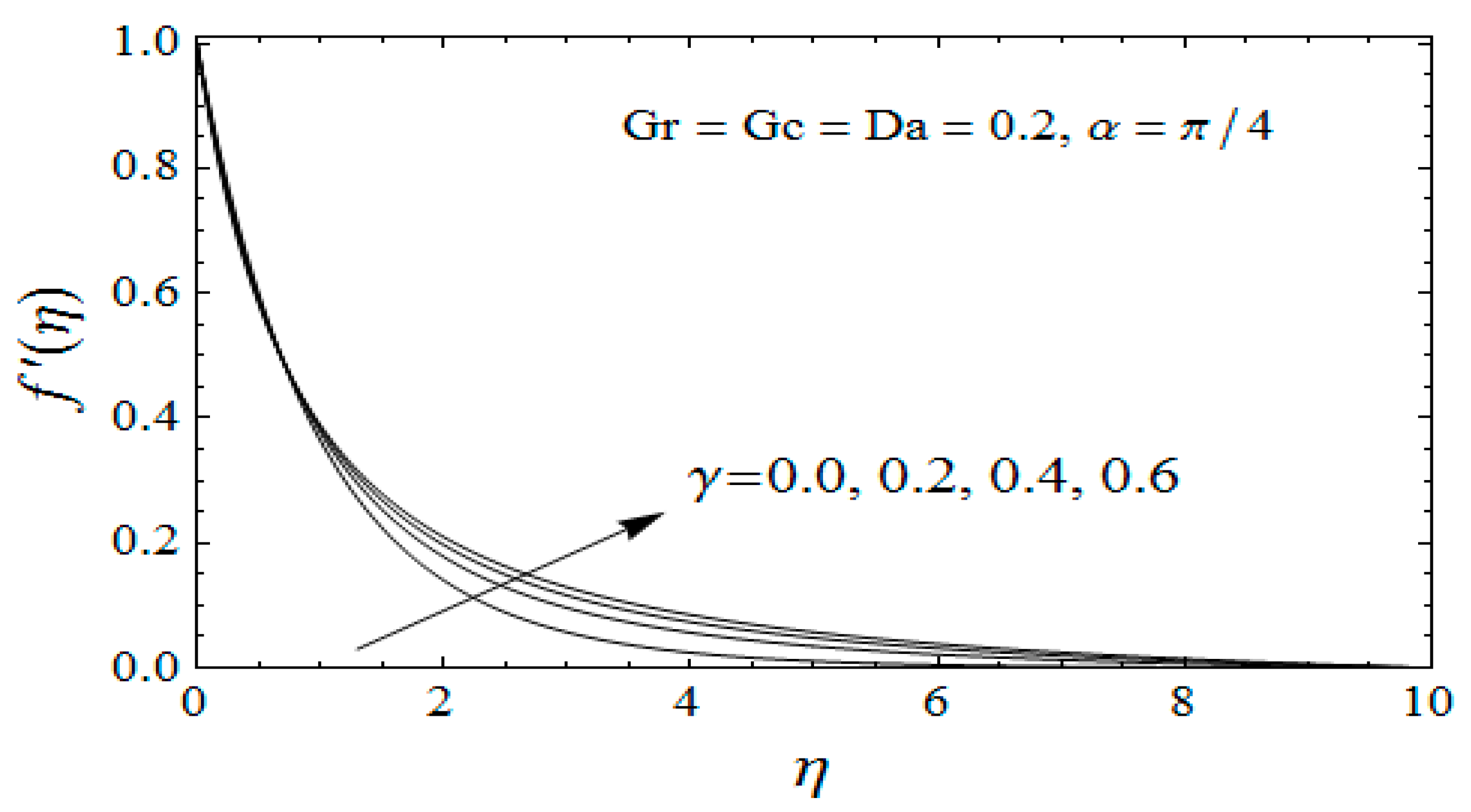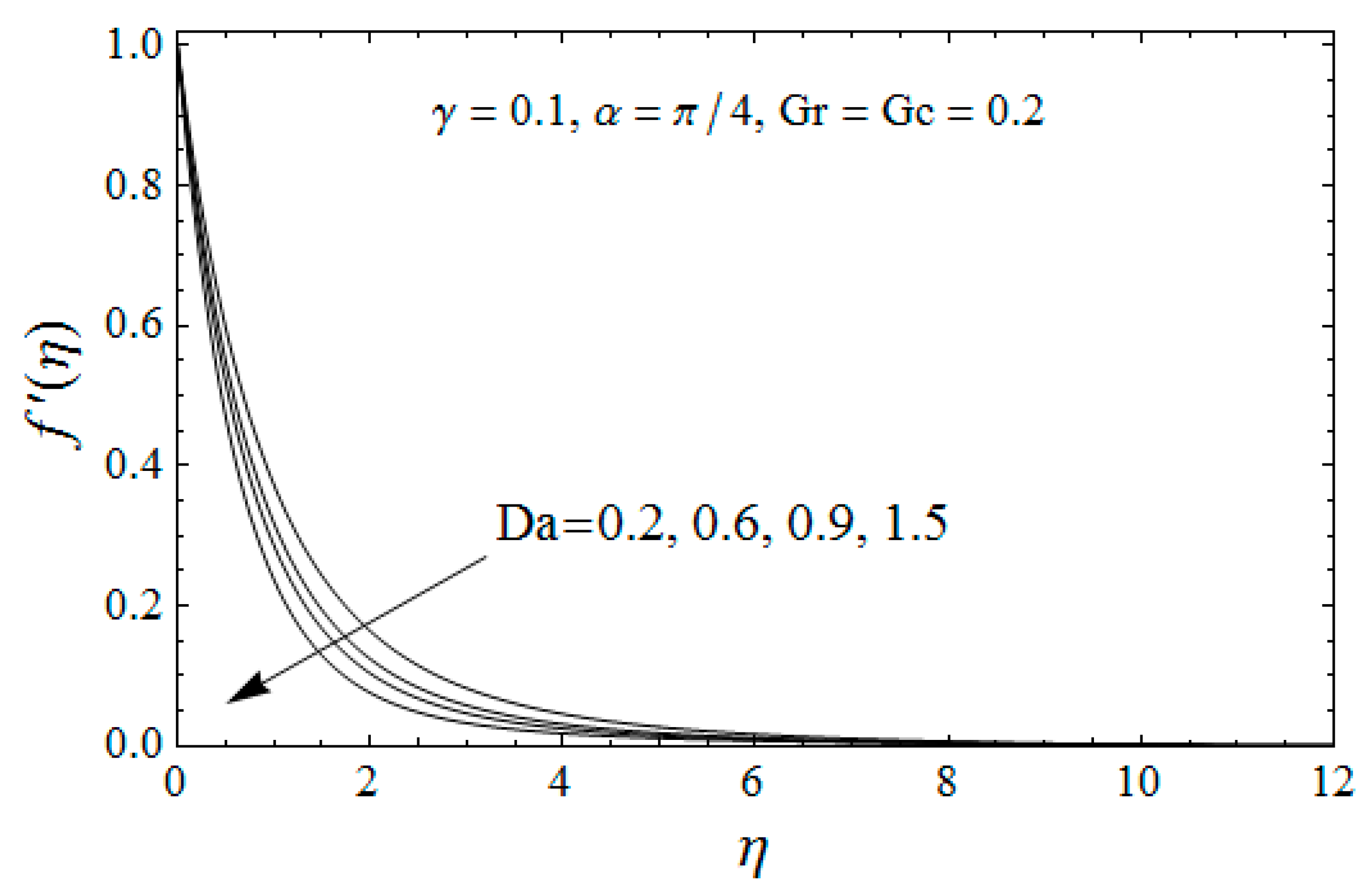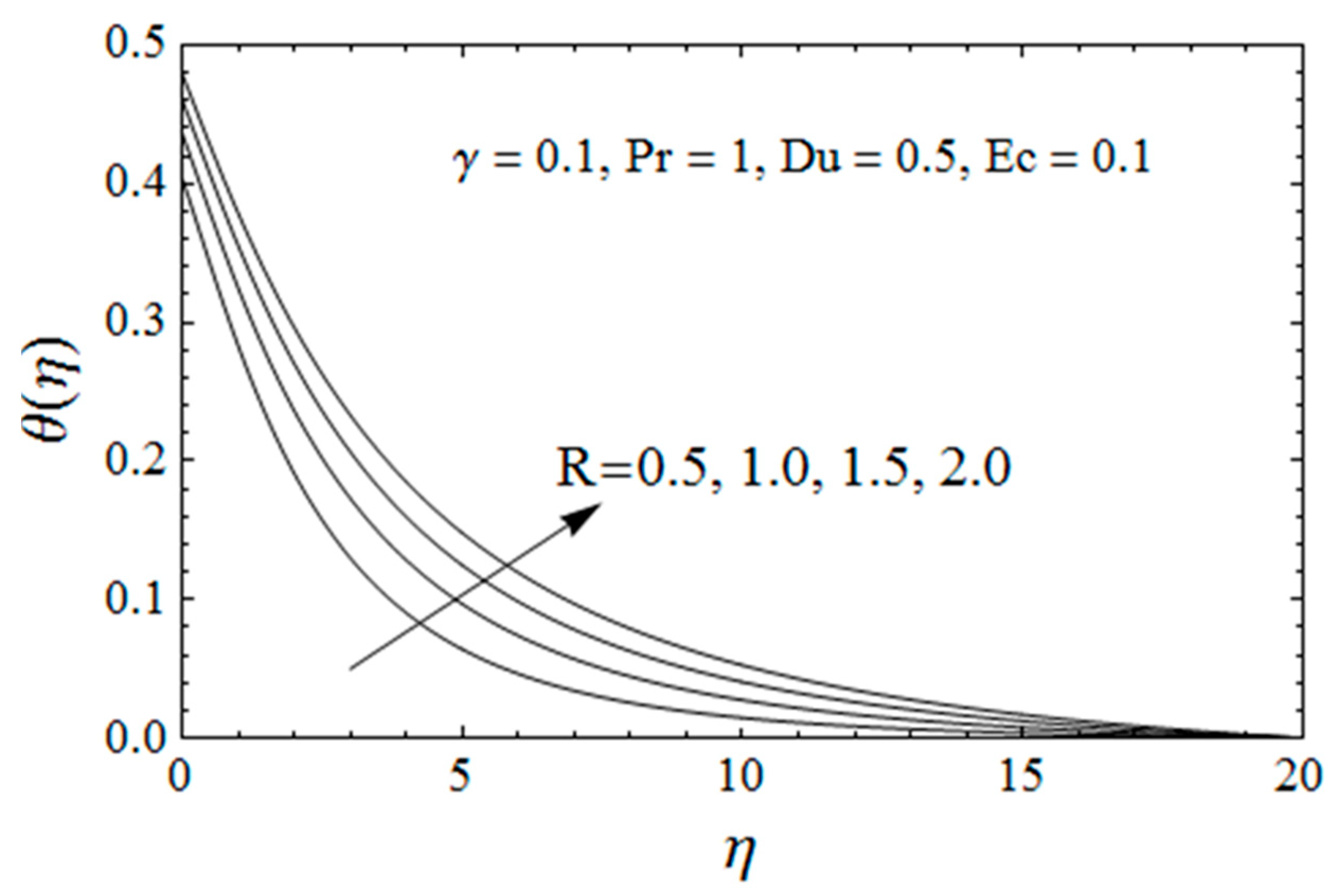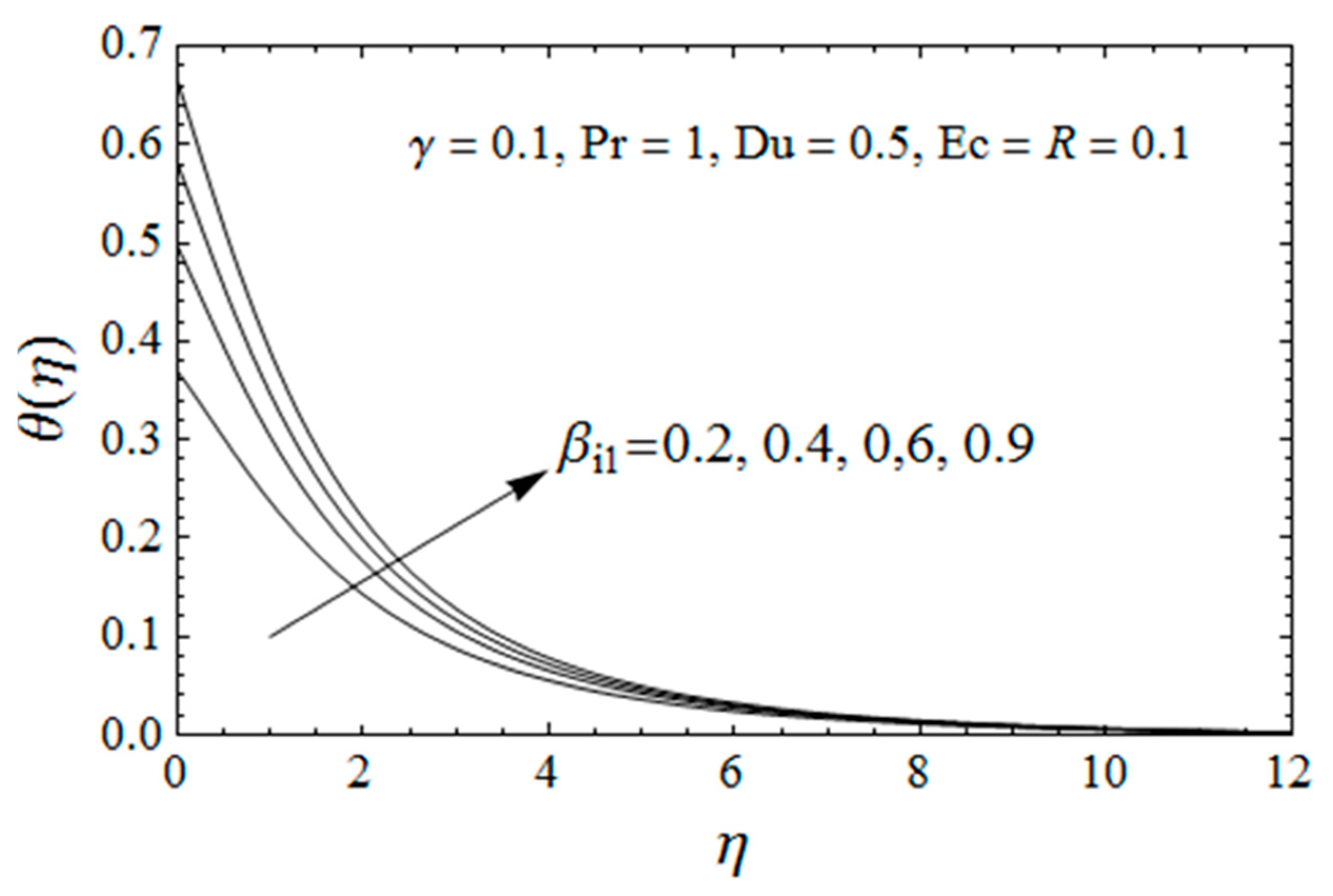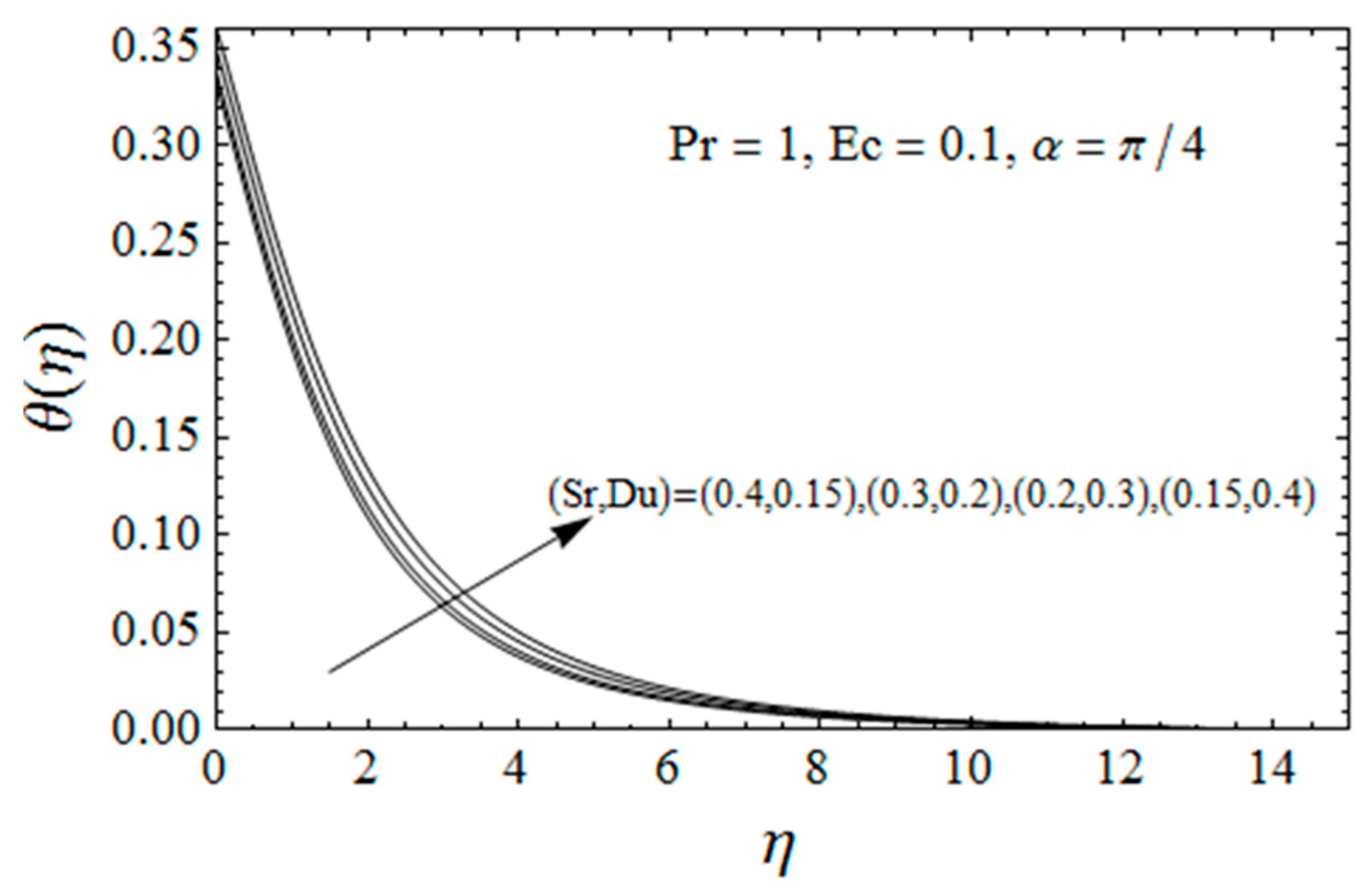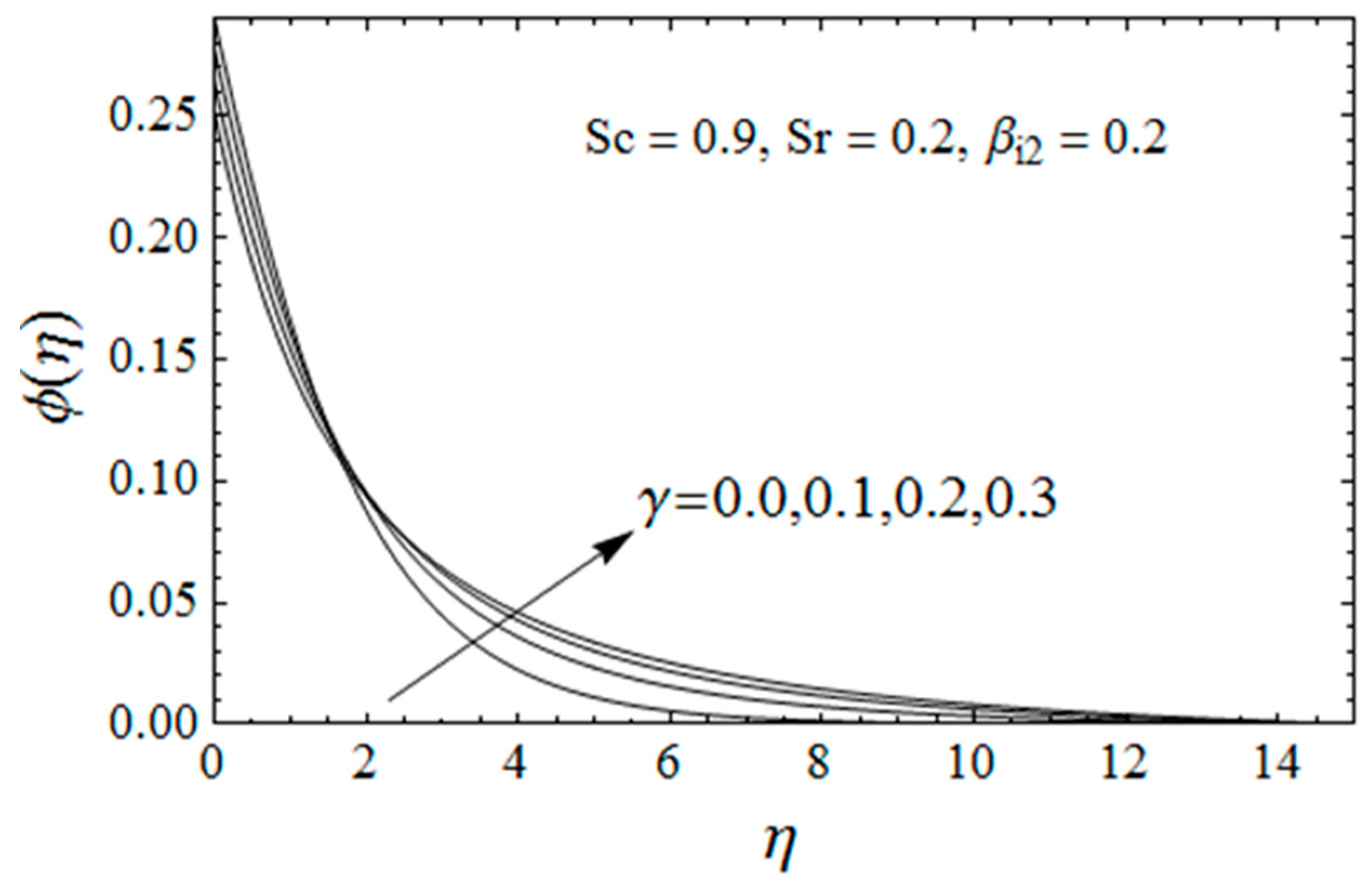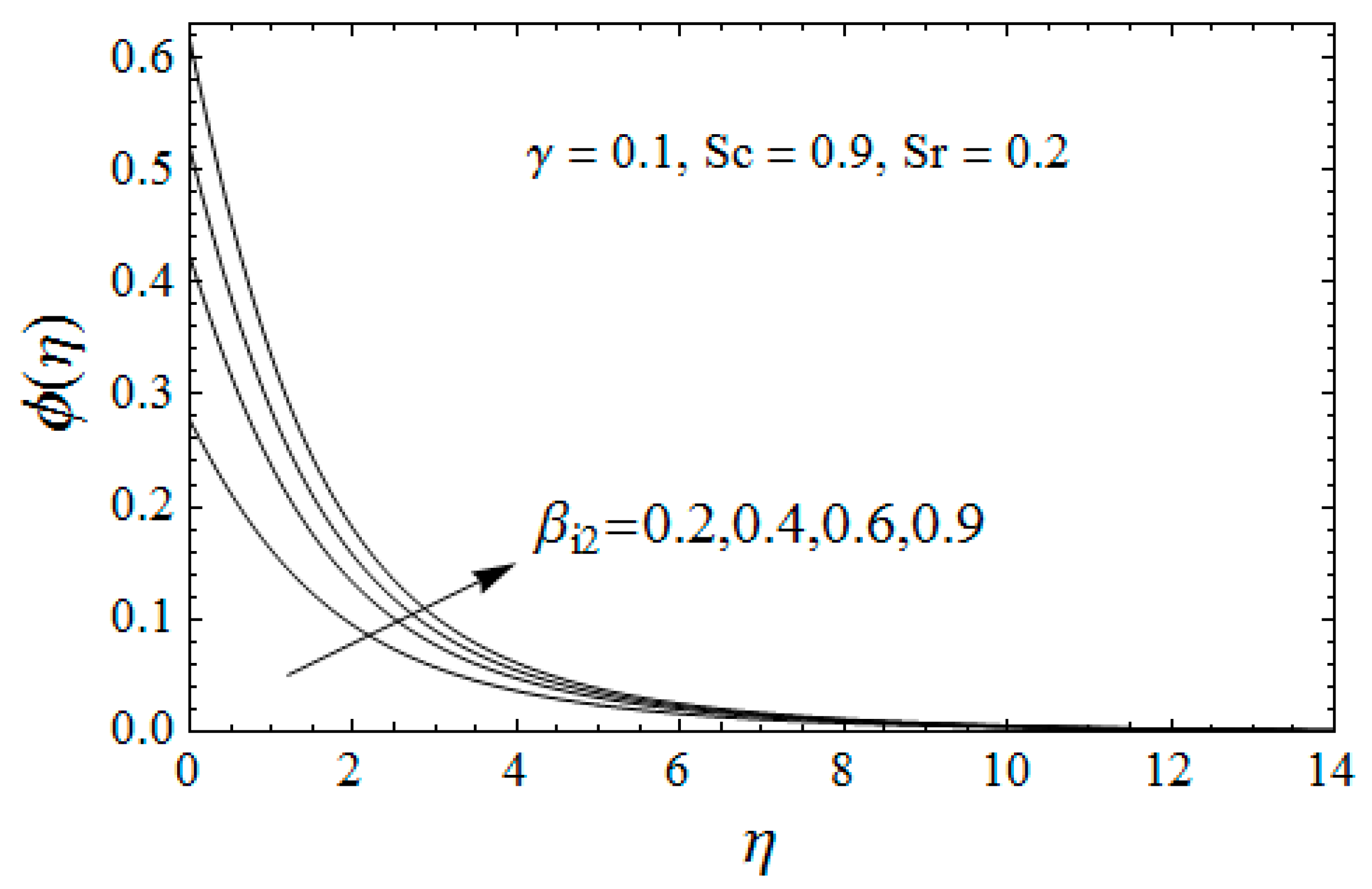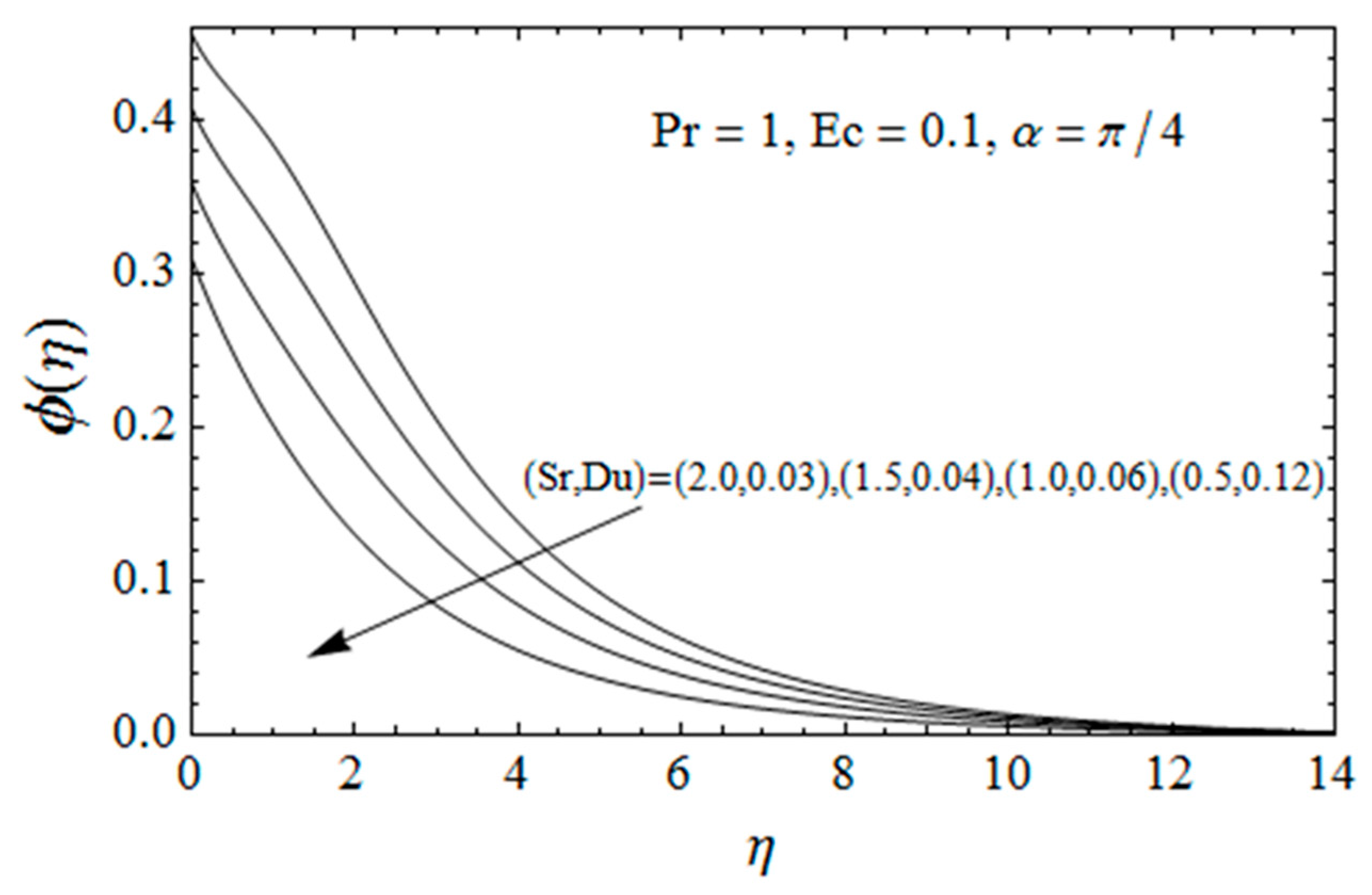So, for a better interpretation of such processes, narration of non-Newtonian fluids is essential. It can be done by comparing the properties of Newtonian and non-Newtonian fluids. One major difference between these two fundamental classes of fluids is that Newtonian fluid exhibits the linear relation among shear and strain rates whereas non-Newtonian fluids manifest a non-linear relationship. Due to such a relation, non-Newtonian fluids disclose intricate properties and are characterized into subdivisions like shear thinning, shear thickening, dilatant and thixotropic fluids. Rheologist’s have recognized that some fluid models which behave multiply under different conditions like second-grade fluid that explicates features of shear thinning, shear thickening and Newtonian fluid. Such dynamical features of second-grade fluid has made it notable and worthy among researchers. The thermal and dynamical analyses of second-grade fluid was done by Vejravelu and Roper [1]. Rajeswari and Rantha [2] capitalized the perturbation technique to discuss the dynamics of stagnant second-grade fluid. Garg and Rajagopal [3] followed the work conducted in Reference [2] and found total agreement with their findings. Fetecau and Fetecau [4] determined solution for second-grade fluids due to an oscillating circular cylinder by using Hankel transform method). A wealth of knowledge about the analysis of second-grade fluid over various physical configurations and conditions can be accessed through References [5,6,7,8].

Optimal production from the industrial sector requires appropriate collaboration of thermal and concentration fields. This can be done either by providing radiation, Newtonian heating, Dufour and Soret aspects, mixed convection, as well as many other ways. So, we discuss separately the abovementioned thermal aspects and their physical implications. Newtonian heating is defined as the process in which internal resistance is at a minute scale in comparison to the surface resistance. Newtonian heating is involved in thermal exchange procedures like heat exchangers, transferal of heat around fins, the oil and gas industry and many more. Merkin [9] performed premier work by considering different types of wall thermal conditions, and convective heating was one of them. Salleh et al. [10] probed changes in the thermal boundary layer and the associated heat transfer aspect by obliging Newtonian heating. Haq et al. [11] and Nadeem et al. [12] scrutinized the 2D and 3D flow of viscoelastic fluid under the existence of convective boundary sources. Innovative work in this direction is conducted and cited in [13,14,15,16,17].

In advance manufacturing and thermal procedures, the capability to generate chaotic energy emission is vital. Radiative energy flux has a conclusive impact on chaotic heat energy management in various engineering and physical processes. One of the latest investigations emphasizing the impact of radiation was conducted by Kothandapani and Parakash [18], who interpreted the impact of radiative heat transfer in peristaltic flow through tapered asymmetric arteries. The behavior of the pseudoplastic fluid model along with the suspended particles by obliging non-linearized radiative flux due to a stretchable surface was elucidated by Kumar et al. [19]. Khan et al. [20] disclosed the influence of radiative energy on a magnetized Carreau nano fluid over a convective thermal sheet. Waqas et al. [21] manipulated the modelling of a Carreau fluid by obliging the Roseland approximation. Goodarzi et al. [22] explicated the effect of radiative heat flux on laminar and turbulent mixed-convection heat transfer of a semitransparent medium in a square enclosure by implementing the finite volume method. Pordanjani et al. [23] studied the impact of radiation on the convection heat transfer rate and the nanofluid entropy generation within a diagonal rectangular chamber numerically, in the presence of a magnetic field. Aghaei et al. [24] scrutinized heat transfer aspects by placing horizontal and vertical elliptic baffles in the flow in the presence of entropy generation of multi wall carbon nano tubes MWCNTs-water nanofluid.

Thermal variations by way of radiation, viscous dissipation, convective heating across boundaries concentration and temperature gradients are generated, which yields mass/energy fluxes, respectively. An energy flux termed as diffusion-thermo (the Dufour effect) is produced due to a concentration gradient, whereas mass flux is known as thermo-diffusion (the Soret effect), and which is induced by way of temperature gradients. Such aspects are required in heat exchangers, cooling applications, steel industries and so forth. So, the investigation of flow processes under the effect of Dufour and Soret aspects are highly recommendable and relevant to researchers. In view of relevancy, a lot of information of such aspects has been gathered, which is viewed in the accompanied references. Hirshfelder et al. [25] measured the diffusion coefficient of mono atomic gases. Afify [26] investigated fluid flow generated by a stretching sheet in the presence of Dufour and Soret aspects. Bhattacharya et al. [27] investigated stagnant flow over an extendable sheet with diffusion effects. Similar to the analysis in [28], Awad et al. premediated the double diffusion (Dufour and Soret) effects over a stretching sheet by way of a computational scheme. For the power-law model, diffusion effects were elucidated by Goyal et al. [29]. Umar et al. [30] disclosed transportation of nano particles along with diffusion effects over a porous configuration. Hayat et al. [31] adumbrated the heat transfer of Newtonian fluids over an inclined stretching cylinder. Bagherzadeh et al. [32] experimentally verified the enhancement in heat transfer rate by jet injection of a nanofluid under a homogeneous magnetic field. Goshayeshi et al. [33] elaborated the effect of a ferro nanofluid on the enhancement of the thermal features of a flowing fluid within the heat pipe under the implication of a magnetic field. Goshayeshi et al. [34] experimentally justified the impact of a Fe₂O₃/kerosene nanofluid on fluid flow in a heated pipe to enhance the thermal performance as well as the heat transfer coefficient. Yousefzadeh et al. [35] probed laminar mixed-convection heat transfer inside an open square cavity with different heat transfer areas by finding a computational solution. Tian et al. [36] experimentally measured heat transfer in a silica DI water nano-fluid with three various surfactants on the surface of copper heaters at different concentrations at atmospheric pressure. Forced convection in a double-tube heat exchanger using nanofluids with constant and variable thermophysical properties was scrutinized by Bahman et al. [37].

The prime concern of this investigation is to anticipate the radiative flow of a second-grade fluid with Joule heating, as well as Dufour and Soret aspects over an inclined stretching cylinder with Newtonian heating. Model formulation is controlled through coupled partial differential equations and afterwards converted to ordinary differential equations by permissible transmutations. Findings are attained by implementing the Keller Box scheme. Tabular and pictorial representations regarding the impact of concerning parameters on sundry distributions are disclosed. To the best of the author′s knowledge, this work has not been done so far and it will serve as a reference study for upcoming research in this direction.

2. Mathematical Modelling

Let us consider the steady, axisymmetric and incompressible flow of a second-grade fluid flowing over an inclined stretchable cylinder under the appliance of a transverse magnetic field.

The tensor describing the flow analysis for concerning fluid is presented as follows:

$$T=-pI+\mu A_1+{\alpha }_1{A}_2+{\alpha }_2{A}_1^2.$$

(1)

In the above expression ${\alpha }_1$ and ${\alpha }_2$ are the material moduli and $A_2$ is given by

$$A_2=\frac{d{A}_1}{dt}+A_1\left(grad V\right)+{\left(grad V\right)}^T{A}_1,$$

(2)

where we can write

$$A_2=\left[\begin{array}{ccc}4{\left(\frac{\partial u}{\partial r}\right)}^2+2\frac{\partial v}{\partial r}\left(\frac{\partial u}{\partial x}+\frac{\partial w}{\partial r}\right)& 0& 2\frac{{\partial }^{2}u}{\partial r\partial x}+2\frac{{\partial }^{2}w}{\partial r\partial x}+\frac{\partial w}{\partial x}\left(\frac{\partial u}{\partial x}+\frac{\partial w}{\partial r}\right)+\frac{\partial u}{\partial r}\left(\frac{\partial u}{\partial x}+\frac{\partial w}{\partial r}\right)\\ 0& 4\frac{u^2}{r^2}& 0\\ 2\frac{{\partial }^{2}u}{\partial r\partial x}+2\frac{{\partial }^{2}w}{\partial r\partial x}+\frac{\partial w}{\partial x}\left(\frac{\partial u}{\partial x}+\frac{\partial w}{\partial r}\right)+\frac{\partial u}{\partial r}\left(\frac{\partial u}{\partial x}+\frac{\partial w}{\partial r}\right)& 0& 4{\left(\frac{\partial w}{\partial x}\right)}^2+2\frac{\partial u}{\partial x}\left(\frac{\partial u}{\partial x}+\frac{\partial w}{\partial r}\right)\end{array}\right].$$

(3)

Thus, the equations for motion, energy and concentration are expressed as

$$\begin{array}{ll}u\frac{\partial u}{\partial x}+w\frac{\partial u}{\partial r} =& \nu \left(\frac{{\partial }^{2}u}{\partial r^2}+\frac{1}{r} \frac{\partial u}{\partial r}\right)+g\beta \left(T-T_{\infty }\right)Cos\left(\alpha \right)+g{\beta }_c\left(C-C_{\infty }\right)Cos\left(\alpha \right)-\frac{\nu }{K}u\\ & +\frac{{\alpha }_1}{\rho }(w\frac{{\partial }^{3}u}{\partial r^3}+u\frac{{\partial }^{3}u}{\partial x{\partial }^{2}r}+\frac{\partial u}{\partial x}\frac{{\partial }^{2}u}{\partial r^2}-\frac{\partial u}{\partial r}\frac{{\partial }^{2}w}{\partial r^2}\\ & +\frac{1}{r}\left(w\frac{{\partial }^{2}u}{\partial r^2}+u\frac{{\partial }^{2}u}{\partial r\partial x}+\frac{\partial u}{\partial r}\frac{\partial u}{\partial x}-\frac{\partial u}{\partial r}\frac{\partial w}{\partial r}\right))-\frac{\sigma B_0{}^2}{\rho }u,\end{array}$$

(4)

$$\begin{gathered} u\frac{\partial T}{\partial x}+w\frac{\partial T}{\partial r} = {\alpha }^{\ast }\left(1+\frac{4}{3}R\right)\frac{1}{r}\frac{\partial }{\partial r}\left(r\frac{\partial T}{\partial r}\right)+\frac{\mu }{\rho c_p}{\left(\frac{\partial u}{\partial r}\right)}^2+\frac{D_m{k}_T}{c_p{c}_s}\frac{1}{r}\frac{\partial }{\partial r}\left(r\frac{\partial C}{\partial r}\right)+ \\ \frac{{\alpha }_1}{\rho c_p}\left(w\frac{\partial u}{\partial r}\frac{{\partial }^{2}u}{\partial r^2}+ u\frac{\partial u}{\partial r}\frac{{\partial }^{2}u}{\partial x\partial r}\right)+\frac{\sigma B_0{}^2}{\rho c_p}{u}^2, \end{gathered}$$

(5)

$$u\frac{\partial C}{\partial x}+w\frac{\partial C}{\partial r} = D_m\frac{1}{r}\frac{\partial }{\partial r}\left(r\frac{\partial C}{\partial r}\right)+\frac{ D_m{k}_T}{T_m} \frac{1}{r}\frac{\partial }{\partial r}\left(r\frac{\partial T}{\partial r}\right).$$

(6)

The present flow situation is subjected to the following boundary conditions,

$$\{\begin{array}{c}u = \frac{U_{o}x}{l},w=0, -k\frac{\partial T}{\partial r} = h\left(T_f-T\right),-D_m\frac{\partial C}{\partial r} = k_m\left(C_f-C\right), at r = a \\ u\to 0, T\to T_{\infty }, C\to C_{\infty }, as r\to \infty \end{array}.$$

(7)

Invoking the similarity variables,

$$\begin{array}{cccc}u = \frac{U_{o}x}{l}{f}^{\prime }\left(\eta \right),& w=-\sqrt{\left(\frac{\nu U_o}{l}\right)}f\left(\eta \right),& \theta \left(\eta \right)=\frac{T-T_{\infty }}{T_f-T_{\infty }},& \varphi \left(\eta \right)=\frac{C-C_{\infty }}{C_f-C_{\infty }},\\ & \eta =\frac{r^2-a^2}{2a}\sqrt{\frac{U_o}{\nu l}}.& & \end{array}$$

(8)

Employing the transformations, Equations (4)–(6) taken as the form, we get

$$\begin{gathered} \left(1+2\gamma \eta \right)f^{‴}+2\gamma f^{″}+f{f}^{″}-{f^{\prime }}^2-Da{f}^{\prime }+4\gamma \beta \left(f^{\prime }{f}^{″}-f{f}^{‴}\right)+\beta \left(1+2\gamma \eta \right) \\ \left(2f^{\prime }{f}^{‴}+{f^{″}}^2-f{f}^{⁗}\right)-H{a}^2{f}^{\prime }+Gr\theta Cos\left(\alpha \right)+Gc\varphi Cos\left(\alpha \right)=0, \end{gathered}$$

(9)

$$\begin{gathered} \left(1+\frac{4}{3}R\right)\left(\left(1+2\gamma \eta \right){\theta }^{″}+2\gamma {\theta }^{\prime }\right)+Prf{\theta }^{\prime }+Du\left(\left(1+2\gamma \eta \right){\varphi }^{″}+2\gamma {\varphi }^{\prime }\right)-PrEc\beta \gamma f{f^{″}}^2 \\ +PrEc\left(1+2\gamma \eta \right)\left({f^{″}}^2-\beta f{f}^{″}{f}^{‴}+\beta f^{\prime }{f^{″}}^2\right)+PrEcH{a}^2{f^{\prime }}^2=0, \end{gathered}$$

(10)

$$\left(1+2\gamma \eta \right){\varphi }^{″}+2\gamma {\varphi }^{\prime }+Scf{\varphi }^{\prime }+Sr\left(\left(1+2\gamma \eta \right){\theta }^{″}+2\gamma {\theta }^{\prime }\right)=0.$$

(11)

Here the derivatives of the function are indicated by a prime with respect to $\eta$, and $\beta =\frac{{\alpha }_{1U_o}}{\rho \nu l}$ and $Ha=\frac{\sigma B_0{}^{2}l}{\rho U_o}$ are the viscoelastic parameter and Hartmann number, respectively.

$$\{\begin{array}{c}f=0, f^{\prime }=1, {\theta }^{\prime }\left(0\right)=-B_{i1}\left(1-\theta \left(0\right)\right), {\varphi }^{\prime }\left(0\right)=-B_{i2}\left(1-\varphi \left(0\right)\right), at \eta =0\\ f^{\prime }=0, \theta =0, \varphi =0, at \eta =\infty . \end{array}$$

(12)

in which

$$\begin{array}{ll}\gamma =\sqrt{\frac{\nu l}{a^2{U}_o} },Gr=& \frac{g\beta \left(T_f-T_{\infty }\right)l^2}{x{U}_o^2},Gc=\frac{g{\beta }_c\left(C_f-C_{\infty }\right)l^2}{x{U}_o^2},Da=\frac{\nu l}{K{U}_o},Pr=\frac{\nu }{{\alpha }^{\ast }},\\ & Du=\frac{D_m{k}_T}{c_p{c}_s}\frac{\rho c_p}{k}\frac{C_f-C_{\infty }}{T_f-T_{\infty }},Sr=\frac{k_{T\left(T_f-T_{\infty }\right)}}{T_m\left(C_f-C_{\infty }\right)},Sc=\frac{\nu }{D_m},\\ & Ec=\frac{U_o^2{\left(\frac{x}{l}\right)}^2}{c_p\left(T_f-T_{\infty }\right)},B_{i1}=\frac{h}{k}\sqrt{\frac{\nu l}{U_o} },B_{i2}=\frac{k_m}{D_m}\sqrt{\frac{\nu l}{U_o}},R=\frac{4\sigma T^3}{k{k}^{\ast }},\end{array}$$

(13)

where $\gamma$ is the curvature parameter, $Da$ is the Darcy number, $Du$ is the Dufour number, $Sr$ is the Soret number, $Gr$ is the thermal Grashof number, $Gc$ is the solutal Grashof number, $R$ is the radiation parameter, and $B_{i1}$ and $B_{i2}$ are the thermal and concentration Biot numbers, respectively.

Nusselt and Sherwood mass flux coefficients are expressed as $N{u}_x$ and $S{h}_x$, and with the skin-friction co-efficient $C_{fx}$, are the physical quantities of interest expressed as

$$N{u}_x=\frac{x{q}_w}{k\left(T_f-T_{\infty }\right)}, q_w=-k\frac{\partial T}{\partial r}-\frac{16\sigma T_{\infty }^3}{3k^{\ast }}\frac{\partial T}{\partial r}{|}_{r=a},$$

(14)

$$S{h}_x=\frac{J_{w}x}{D_m\left(C_f-C_{\infty }\right)}, J_w=-D_m\frac{\partial C}{\partial r}{|}_{r=a},$$

(15)

$$C_{fx}=\frac{2{\tau }_w}{\rho u_w^2}, u_w=U_0\left(\frac{x}{l}\right) and {\tau }_w=\mu \frac{\partial u}{\partial r}{|}_{r=a}.$$

(16)

In dimensionless form

$$\frac{1}{2}{C}_{fx}R{e}_x^{1/2}=f^{″}\left(0\right),$$

(17)

$$N{u}_x/R{e}_x^{\frac{1}{2}}=-\left(1+\frac{4}{3}R\right){\theta }^{\prime }\left(0\right),$$

(18)

$$S{h}_x/R{e}_x^{\frac{1}{2}}=-{\varphi }^{\prime }\left(0\right).$$

(19)

3. Solution Methodology

The problem comprising Equations (9)–(11) is handled numerically by way of the Keller Box scheme. Firstly, Equations (9)–(11) are reduced to the initial value problem by utilizing a new variable given by

$$f^{\prime }=u, u^{\prime }=v, {\theta }^{\prime }=p, {\varphi }^{\prime }=g,$$

(20)

then, Equations (9)–(11) become

$$\left(1+2\gamma \eta \right)v^{\prime }+2\gamma v+fv-u^2-Da u+Gr\theta Cos\left(\alpha \right)+Gc\varphi Cos\left(\alpha \right)=0,$$

(21)

$$\left(1+\frac{4}{3}R\right)\left(\left(1+2\gamma \eta \right)p^{\prime }+2\gamma p\right)+Prfp+Du\left(\left(1+2\gamma \eta \right)g^{\prime }+2\gamma g\right)+PrEc\left(1+2\gamma \eta \right)v^2=0,$$

(22)

$$\left(1+2\gamma \eta \right)g^{\prime }+2\gamma g+Scfg+Sr\left(\left(1+2\gamma \eta \right)p^{\prime }+2\gamma p\right)=0,$$

(23)

along with the B. C′s

$$\{\begin{array}{c}f\left(0\right)=0, u\left(0\right)=1, p\left(0\right)=-B_{i1}\left(1-\theta \left(0\right)\right), g\left(0\right)=-B_{i2}\left(1-\varphi \left(0\right)\right),\\ u(\infty )=0, \theta (\infty )=0, \varphi (\infty )=0.\end{array}$$

(24)

By using the central difference gradients and the average at the mid points of the net derivatives, the following relation is approximated:

$$x^0=0, x^n=x^{n-1}+k_{n, } n=1,2,\dots ,J,$$

$${\eta }_0=0, {\eta }_j={\eta }_{j-1}+h_{j, } j=1,2,\dots ,J n_J=n_{\infty }.$$

Equations (20)–(23) then become

$$\frac{f_j-f_{j-1}}{h_j} =u_{j-\frac{1}{2}} ,\frac{u_j-u_{j-1}}{h_j} =v_{j-\frac{1}{2}} ,\frac{{\theta }_j-{\theta }_{j-1}}{h_j} =p_{j-\frac{1}{2}} ,\frac{{\varphi }_j-{\varphi }_{j-1}}{h_j} =g_{j-\frac{1}{2}},$$

(25)

$$\begin{gathered} \left(1+2\gamma \eta \right)\left(\frac{v_j-v_{j-1}}{h_j}\right)+2\gamma \left(v_{j-\frac{1}{2}}\right)+\left(f_{j-\frac{1}{2}}\right)\left(v_{j-\frac{1}{2}}\right)-{\left(u_{j-\frac{1}{2}}\right)}^2-Da\left(u_{j-\frac{1}{2}}\right) \\ +GrCos\left(\alpha \right)\left({\theta }_{j-\frac{1}{2}}\right)+GcCos\left(\alpha \right)\left({\varphi }_{j-\frac{1}{2}}\right)=0, \end{gathered}$$

(26)

$$\begin{gathered} \left(1+\frac{4}{3}R\right)\left(\left(1+2\gamma \eta \right)\left(\frac{p_j-p_{j-1}}{h_j}\right)+2\gamma \left(p_{j-\frac{1}{2}}\right)\right)+Pr\left(f_{j-\frac{1}{2}}\right)\left(p_{j-\frac{1}{2}}\right)+ \\ Du\left(\left(1+2\gamma \eta \right)\left(\frac{g_j-g_{j-1}}{h_j}\right)+2\gamma \left(g_{j-\frac{1}{2}}\right)\right)+PrEc\left(1+2\gamma \eta \right){\left(v_{j-\frac{1}{2}}\right)}^2=0, \end{gathered}$$

(27)

$$\begin{gathered} \left(1+2\gamma \eta \right)\left(\frac{g_j-g_{j-1}}{h_j}\right)+2\gamma \left(g_{j-\frac{1}{2}}\right)+Sc\left(f_{j-\frac{1}{2}}\right)\left(g_{j-\frac{1}{2}}\right)+ \\ Sr\left(\left(1+2\gamma \eta \right)\left(\frac{p_j-p_{j-1}}{h_j}\right)+2\gamma \left(p_{j-\frac{1}{2}}\right)\right)=0, \end{gathered}$$

(28)

where $f_{j-\frac{1}{2}}=\frac{f_j+f_{j-1}}{2}$, etc.

Equations (26)–(28) are in algebraic form and therefore have to be linear equations before the implementation of factorization. We write the Newton iterations in the following way:

$$f_j^{\left(i+1\right)}=f_j^{\left(i\right)}+\delta f_j^{\left(i\right)}, u_j^{\left(i+1\right)}=u_j^{\left(i\right)}+\delta u_j^{\left(i\right)}, v_j^{\left(i+1\right)}=v_j^{\left(i\right)}+\delta v_j^{\left(i\right)},$$

$${\theta }_j^{\left(i+1\right)}={\theta }_j^{\left(i\right)}+\delta {\theta }_j^{\left(i\right)}, {\varphi }_j^{\left(i+1\right)}={\varphi }_j^{\left(i\right)}+\delta {\varphi }_j^{\left(i\right)}, p_j^{\left(i+1\right)}=p_j^{\left(i\right)}+\delta p_j^{\left(i\right)}, g_j^{\left(i+1\right)}=g_j^{\left(i\right)}+\delta g_j^{\left(i\right)}.$$

By substituting these expressions into Equations (26)–(28) and neglecting the second-order and higher-order terms in $\delta$, a linear tri-diagonal system of equations will be found as follows:

$$\delta f_j-\delta f_{j-1}-\frac{h_j}{2}\left(\delta u_j+\delta u_{j-1}\right)={\left(r_1\right)}_{j-\frac{1}{2}},$$

(29)

$$\delta u_j-\delta u_{j-1}-\frac{h_j}{2}\left(\delta v_j+\delta v_{j-1}\right)={\left(r_5\right)}_{j-\frac{1}{2}},$$

(30)

$$\delta {\theta }_j-\delta f{\theta }_{j-1}-\frac{h_j}{2}\left(\delta p_j+\delta p_{j-1}\right)={\left(r_6\right)}_{j-\frac{1}{2}},$$

(31)

$$\delta {\varphi }_j-\delta {\varphi }_{j-1}-\frac{h_j}{2}\left(\delta g_j+\delta g_{j-1}\right)={\left(r_7\right)}_{j-\frac{1}{2}},$$

(32)

$$\begin{gathered} {\left({\xi }_1\right)}_j\delta f_j+{\left({\xi }_2\right)}_j\delta f_{j-1}+{\left({\xi }_3\right)}_j\delta u_j+{\left({\xi }_4\right)}_j\delta u_{j-1}+{\left({\xi }_5\right)}_j\delta v_j+{\left({\xi }_6\right)}_j\delta v_{j-1}+{\left({\xi }_7\right)}_j\delta {\theta }_j+ \\ {\left({\xi }_8\right)}_j\delta {\theta }_{j-1}+{\left({\xi }_9\right)}_j\delta {\varphi }_j+{\left({\xi }_{10}\right)}_j\delta {\varphi }_{j-1}={\left(r_2\right)}_{j-\frac{1}{2}}, \end{gathered}$$

(33)

$$\begin{gathered} {\left({\psi }_1\right)}_j\delta f_j+{\left({\psi }_2\right)}_j\delta f_{j-1}+{\left({\psi }_3\right)}_j\delta v_j+{\left({\psi }_4\right)}_j\delta v_{j-1}+{\left({\psi }_5\right)}_j\delta p_j+{\left({\psi }_6\right)}_j\delta p_{j-1} \\ +{\left({\psi }_7\right)}_j\delta g_j+{\left({\psi }_8\right)}_j\delta g_{j-1}={\left(r_3\right)}_{j-\frac{1}{2}}, \end{gathered}$$

(34)

$${\left({\lambda }_1\right)}_j\delta f_j+{\left({\lambda }_2\right)}_j\delta f_{j-1}+{\left({\lambda }_3\right)}_j\delta p_j+{\left({\lambda }_4\right)}_j\delta p_{j-1}+{\left({\lambda }_5\right)}_j\delta g_j+{\left({\lambda }_6\right)}_j\delta g_{j-1}={\left(r_4\right)}_{j-\frac{1}{2}}.$$

(35)

Subject to boundary conditions

$$\{\begin{array}{c}\delta f_0=0, \delta u_0=0,\delta p_0-B_{i1}\delta {\theta }_0=-p_0+B_{i1}\left({\theta }_0+1\right),\\ \delta g_0-B_{i2}\delta {\varphi }_0=-g_0+B_{i2}\left({\varphi }_0+1\right),\delta u_J=0, \delta {\theta }_J=0, \delta {\varphi }_J=0,\end{array}$$

(36)

where

$${\left({\xi }_1\right)}_j={\left({\xi }_2\right)}_j=\frac{h}{4}\left(v_j+v_{j-1}\right),$$

$${\left({\xi }_3\right)}_j={\left({\xi }_4\right)}_j=-\frac{h_j}{2}\left(Da+\left(u_j+u_{j-1}\right)\right),$$

$${\left({\xi }_5\right)}_j=1+\gamma \left({\eta }_j+{\eta }_{j-1}\right)+h_j\gamma +\frac{h_j}{4}(f_j+f_{j-1}),$$

$$\begin{gathered} {\left({\xi }_6\right)}_j=-1-\gamma \left({\eta }_j+{\eta }_{j-1}\right)+h_j\gamma +\frac{h_j}{4}(f_j+f_{j-1}), \\ {\left({\xi }_7\right)}_j={\left({\xi }_8\right)}_j=\frac{h_j}{2}GrCos\left(\alpha \right), \end{gathered}$$

$${\left({\xi }_9\right)}_j={\left({\xi }_{10}\right)}_j=\frac{h_j}{2}GcCos\left(\alpha \right),$$

$${\left({\psi }_1\right)}_j={\left({\psi }_2\right)}_j=\frac{Pr h_j}{4}\left(p_j+p_{j-1}\right),$$

$${\left({\psi }_3\right)}_j={\left({\psi }_4\right)}_j=PrEc\frac{h_j}{4}\left(1+\gamma \left({\eta }_j+{\eta }_{j-1}\right)\right)\left(v_j+v_{j-1}\right),$$

$${\left({\psi }_5\right)}_j=\mathrm{Pr}\frac{h_j}{4}\left(f_j+f_{j-1}\right)+\left(1+\frac{4}{3}R\right)\left(1+\gamma \left({\eta }_j+{\eta }_{j-1}\right)+h_j\gamma \right),$$

$${\left({\psi }_6\right)}_j=\mathrm{Pr}\frac{h_j}{4}\left(f_j+f_{j-1}\right)+\left(1+\frac{4}{3}R\right)\left(-1-\gamma \left({\eta }_j+{\eta }_{j-1}\right)+h_j\gamma \right),$$

$${\left({\psi }_7\right)}_j=Du\left(1+\gamma \left({\eta }_j+{\eta }_{j-1}\right)+h_j\gamma \right),$$

$${\left({\psi }_8\right)}_j=-Du\left(1+\gamma \left({\eta }_j+{\eta }_{j-1}\right)+h_j\gamma \right),$$

$${\left({\lambda }_1\right)}_j={\left({\lambda }_2\right)}_j=Sc\frac{h}{4}\left(g_j+g_{j-1}\right),$$

$${\left({\lambda }_3\right)}_j=Sr\left(1+\gamma \left({\eta }_j+{\eta }_{j-1}\right)+h_j\gamma \right),$$

$${\left({\lambda }_4\right)}_j=Sr\left(-1-\gamma \left({\eta }_j+{\eta }_{j-1}\right)+h_j\gamma \right),$$

$${\left({\lambda }_5\right)}_j=1+\gamma \left({\eta }_j+{\eta }_{j-1}\right)+h_j\gamma +Sc\frac{h}{4}\left(f_j+f_{j-1}\right),$$

$${\left({\lambda }_6\right)}_j=-1-\gamma \left({\eta }_j+{\eta }_{j-1}\right)+h_j\gamma +Sc\frac{h}{4}\left(f_j+f_{j-1}\right),$$

$$\begin{array}{ll}{\left(r_2\right)}_{j-\frac{1}{2}}=& -\left(1+\gamma \left({\eta }_j+{\eta }_{j-1}\right)\right)\left(v_j-v_{j-1}\right)-2\gamma h_j\left(v_{j-\frac{1}{2}}\right)-h_j\left(f_{j-\frac{1}{2}}\right)\left(v_{j-\frac{1}{2}}\right)\\ & +h_j{\left(u_{j-\frac{1}{2}}\right)}^2+Da h_j\left(u_{j-\frac{1}{2}}\right)-GrCos\left(\alpha \right)h_j\left({\theta }_{j-\frac{1}{2}}\right)\\ & -GcCos\left(\alpha \right)h_j\left({\varphi }_{j-\frac{1}{2}}\right),\end{array}$$

$$\begin{array}{ll}{\left(r_3\right)}_{j-\frac{1}{2}}=& -\left(1+\frac{4}{3}R\right)\left(\left(1+\gamma \left({\eta }_j+{\eta }_{j-1}\right)\right)\left(p_j-p_{j-1}\right)+2\gamma h_j\left(p_{j-\frac{1}{2}}\right)\right)\\ & -Pr{h}_j\left(f_{j-\frac{1}{2}}\right)\left(p_{j-\frac{1}{2}}\right)-Du\left(1+\gamma \left({\eta }_j+{\eta }_{j-1}\right)\right)\left(g_j-g_{j-1}\right)\\ & -2Du\gamma h_j\left(g_{j-\frac{1}{2}}\right)-PrEc\left(1+2\gamma \eta \right)h_j{\left(v_{j-\frac{1}{2}}\right)}^2,\end{array}$$

$$\begin{array}{ll}{\left(r_4\right)}_{j-\frac{1}{2}}=& -\left(1+\gamma \left({\eta }_j+{\eta }_{j-1}\right)\right)\left(g_j-g_{j-1}\right)-2\gamma h_j\left(g_{j-1/2}\right)-Sc{h}_j\left(f_{j-1/2}\right)\left(g_{j-1/2}\right)\\ & -Sr\left(\left(1+\gamma \left({\eta }_j+{\eta }_{j-1}\right)\right)\left(p_j-p_{j-1}\right)+2\gamma h_j\left(p_{j-\frac{1}{2}}\right)\right).\end{array}$$

In the matrix vector form, we can write

$$A\delta =r,$$

(37)

in which

$$A=\left[\begin{array}{ccccccc}\left[A_1\right]& \left[C_1\right]& & & & & \\ \left[B_2\right]& \left[A_2\right]& \left[C_2\right]& & & & \\ & & \ddots & \ddots & & & \\ & & \ddots & \ddots & \ddots & & \\ & & & \ddots & \ddots & & \\ & & & & \left[B_{J-1}\right]& \left[A_{J-1}\right]& \left[C_{J-1}\right]\\ & & & & & \left[B_J\right]& \left[A_J\right]\end{array}\right]$$

$$\delta =\left[\begin{array}{c}\left[{\mathsf{\delta }}_1\right]\\ \left[{\delta }_2\right]\\ \ddots \\ \left[{\delta }_{J-1}\right]\\ \left[{\delta }_J\right]\end{array}\right], r=\left[\begin{array}{c}\left[{\mathrm{r}}_1\right]\\ \begin{array}{c}\left[r_2\right]\\ \begin{array}{c}\ddots \\ \begin{array}{c}\left[r_{J-1}\right]\\ \left[r_J\right]\end{array}\end{array}\end{array}\end{array}\right].$$

where in Equation (37) the components are defined by

$$\left[A_1\right]=\left[\begin{array}{ccccccc}1& 0& 0& 0& 0& 0& 0\\ 0& 1& 0& 0& 0& 0& 0\\ 0& 0& 0& -B_{i1}& 1& 0& 0\\ 0& 0& 0& 0& 0& -B_{i2}& 1\\ 0& -1& -C_j& 0& 0& 0& 0\\ 0& 0& 0& -1& -C_j& 0& 0\\ 0& 0& 0& 0& 0& -1& -C_j\end{array}\right],c_j=\frac{1}{2}{h}_j,$$

$$\left[A_j\right]=\left[\begin{array}{ccccccc}1& -C_j& 0& 0& 0& 0& 0\\ {\left({\xi }_1\right)}_j& {\left({\xi }_3\right)}_j& {\left({\xi }_5\right)}_j& {\left({\xi }_7\right)}_j& 0& {\left({\xi }_9\right)}_j& \\ {\left({\psi }_1\right)}_j& 0& {\left({\psi }_3\right)}_j& 0& {\left({\psi }_5\right)}_j& 0& {\left({\psi }_7\right)}_j\\ {\left({\lambda }_1\right)}_j& 0& 0& 0& {\left({\lambda }_3\right)}_j& 0& {\left({\lambda }_5\right)}_j\\ 0& -1& -C_i& 0& 0& 0& 0\\ 0& 0& 0& -1& -C_j& 0& 0\\ 0& 0& 0& 0& 0& -1& -C_j\end{array}\right],2<j<J-1,$$

$$\left[A_J\right]=\left[\begin{array}{ccccccc}1& -C_J& 0& 0& 0& 0& 0\\ {\left({\xi }_1\right)}_J& {\left({\xi }_3\right)}_J& {\left({\xi }_5\right)}_J& {\left({\xi }_7\right)}_J& 0& {\left({\xi }_9\right)}_J& 0\\ {\left({\psi }_1\right)}_J& 0& {\left({\psi }_3\right)}_J& 0& {\left({\psi }_5\right)}_J& 0& {\left({\psi }_7\right)}_J\\ {\left({\lambda }_1\right)}_J& 0& 0& 0& {\left({\lambda }_3\right)}_J& 0& {\left({\lambda }_5\right)}_J\\ 0& 1& 0& 0& 0& 0& 0\\ 0& 0& 1& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 1& 0\end{array}\right],$$

$$\left[B_j\right]=\left[\begin{array}{ccccccc}-1& -C_j& 0& 0& 0& 0& 0\\ {\left({\xi }_2\right)}_j& {\left({\xi }_4\right)}_j& {\left({\xi }_6\right)}_j& {\left({\xi }_8\right)}_j& 0& {\left({\xi }_{10}\right)}_j& 0\\ {\left({\psi }_2\right)}_j& 0& {\left({\psi }_4\right)}_j& 0& {\left({\psi }_6\right)}_j& 0& {\left({\psi }_8\right)}_j\\ {\left({\lambda }_2\right)}_j& 0& 0& 0& {\left({\lambda }_4\right)}_j& 0& {\left({\lambda }_6\right)}_j\\ 0& 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& 0\end{array}\right],2<j<J,$$

$$\left[C_j\right]=\left[\begin{array}{ccccccc}0& 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& 0\\ 0& 1& -c_j& 0& 0& 0& 0\\ 0& 0& 0& 1& -c_j& 0& 0\\ 0& 0& 0& 0& 0& 1& -c_j\end{array}\right],1<j<J-1,$$

$$\left[{\delta }_j\right]=\left[\begin{array}{c}\delta f_j\\ \delta u_j\\ \delta v_j\\ \delta {\theta }_j\\ \delta p_j\\ \delta {\varphi }_j\\ \delta g_j\end{array}\right] , 1<j<J,$$

$$\left[r_j\right]=\left[\begin{array}{c}{\left(r_1\right)}_{j-1/2}\\ {\left(r_2\right)}_{j-1/2}\\ {\left(r_3\right)}_{j-1/2}\\ {\left(r_4\right)}_{j-1/2}\\ {\left(r_5\right)}_{j-1/2}\\ {\left(r_6\right)}_{j-1/2}\\ {\left(r_7\right)}_{j-1/2}\end{array}\right] , 1<j<J,$$

Now, we let

$$A=LU$$

(38)

where

$$L=\left[\begin{array}{ccccc}\left[a_1\right]& & & & \\ \left[B_2\right]& \left[a_2\right]& & & \\ & \ddots & \ddots & & & \\ & & & \ddots & \ddots & & \\ & & & & \left[B_J\right]& \left[a_J\right]\end{array}\right] ,$$

$$U=\left[\begin{array}{cccccc}\left[I\right]& \left[{\mathsf{\Gamma }}_1\right]& & & & \\ & \left[I\right]& \left[{\mathsf{\Gamma }}_1\right]& & & \\ & & \ddots & \ddots & & \\ & & & \ddots & \ddots & \\ & & & & \left[I\right]& \left[{\mathsf{\Gamma }}_{J-1}\right]\\ & & & & & \left[I\right]\end{array}\right] ,$$

where $\left[I\right]$ is the unit matrix while $\left[a_i\right]$ and $\left[{\mathsf{\Gamma }}_i\right]$ are $7\times 7$ matrices whose elements are found by the following expressions:

$$\left[a_i\right]=\left[A_1\right],$$

$$\left[A_1\right]\left[{\mathsf{\Gamma }}_1\right]=\left[C_1\right],$$

$$\left[a_j\right]=\left[A_j\right]-\left[B_j\right]\left[{\mathsf{\Gamma }}_{j-1}\right], j=2,3,\dots ..,J ,$$

$$\left[a_j\right]\left[{\mathsf{\Gamma }}_j\right]=\left[C_j\right], j=2,3,\dots ..,J-1.$$

Equation (38) can be substituted into Equation (37) to get

$$LU\delta =r.$$

(39)

Once the element of $\delta$ is found, Equation (38) can be used to find the $\left(i+1\right)\mathrm{th}$ iteration. The procedure described above is implemented in Mathematica and results are displayed in the next section.

4. Results Interpretation

To scrutinize the flow features of the second-grade fluid along with the effect of the magnetic field, radiative heat flux, viscous dissipation, and a double diffusion (Dufour and Soret) solution of Equations (9)–(11) is essential. Before getting to the solution of the coupled system, it is highly important to look at the nature and complexity of it. After sighting the system, it is clear that the momentum equation mentioned in Equation (9) is a third order equation, whereas Equations (10)–(11), i.e., the temperature and concentration equations, are second-order equations. So, there are various approaches (finite difference, finite element and finite volume) to get to the solution of these equations. Among them the best is the finite difference approach for such type of problems, so the Keller Box differencing scheme is implemented. Figure 1, Figure 2 and Figure 3 are displayed to portray the behavior of the velocity distribution against the relative parameters. To see the impacts of viscoelastic parameter $\beta$ on second grade velocity field SVF, Figure 1 is plotted. Variation in velocity against ($\beta )$ is measured for $\beta =0.0, 0.2, 0.4, 0.6$. An increasing trend in velocity is sketched against an increasing $\left(\beta \right)$. This behavior is justified by the mathematical representation of $\left(\beta =\frac{{\alpha }_{1U_o}}{\rho \nu l}\right)$ that by increasing the magnitude of $\left(\beta \right)$, viscosity decreases as a result of the velocity of the fluid mounts and chaotic behavior uplifts. Here, it is productive to mention that for $\beta =0.0$, the present problem reduces to the Newtonian case. From a boundary layer point of view, the thickness of the fluid increases with an increase in $\left(\beta \right)$. Figure 2 indicates the incrementing behavior of velocity against inciting the magnitude of the curvature parameter $(\gamma =0.0, 0.2, 0.4, 0.6,$). The reason is that by the increasing curvature parameter, bending of the surface as well as the radius decreases. Hence, less friction will be offered to fluid molecules by the surface and velocity uplifts. A declining trend in velocity is depicted against the Darcy parameter (Da) in Figure 3. Since the Darcy parameter (Da) represents the presence of a porous medium, suggests porosity creates a high resistance to fluid molecules and as an outcome velocity declines. Variation in the thermal profile against influencing parameters are disclosed in Figure 4, Figure 5 and Figure 6. Figure 4 is manifested to excogitate the impression of radiation parameter (R) on the thermal field. An increasing pattern in temperature is observed by choosing R = 0.5, 1.0, 1.5, 2.0 and by fixing $\gamma =0.1,\mathrm{Pr}=1, Du=0.5, Ec=0.1$. It is because of the fact that energy flux increases and consequently fluid temperature increases. In Figure 5, the effect of the thermal Biot number ($B_{i1 }$) on θ(η) is presented. By definition, the thermal Biot number is directly related to the heat transfer coefficient generated by the hot fluid. Thus, as the thermal Biot number increases, the convection due to the hot fluid raises and the temperature mounts. Impacts of the Dufour (Du) and Soret (Sr) aspects on the thermal field is disclosed in Figure 6. In the present graph, the values of (Du) and (Sr) are selected in such a way that their product will give a constant magnitude. By growing the Dufour number (i.e., by declining the Soret number) the thermal change between the hot and ambient fluid increases, which enhances the temperature. Figure 7, Figure 8 and Figure 9 are plotted to predict the changes in the concentration profile with respect to the involved parameters like $\gamma , B_{i2} , Du and Sr$. Figure 7 presents the impression of the curvature parameter γ on the concentration profile. Duality in concentration features are interpreted against the curvature parameter. For small values of η, i.e., (η < 2), the concentration decreases whereas it increases when η > 3. The upshot of the concentration Biot number $(B_{i2})$ on ϕ(η) is captured in Figure 8. From the drawn curves it is portrayed that by increasing the $(B_{i2})$ concentration field the associated boundary layer thickness increases. The joint conspiration of (Sr) and (Du) on the concentration field is divulged in Figure 9. It is interpreted that by decreasing (Sr) and increasing (Du) the strength of the intermolecular forces weakens and as a consequence the concentration field declines.

Table 1. Variation in the local Nusselt number $N{u}_x/R{e}_x^{1/2}$ for various parameters.

$\mathit{\gamma }$	$\mathit{G}\mathit{r}$	$\mathit{G}\mathit{c}$	$\mathit{\alpha }$	$\mathit{D}\mathit{a}$	$\mathit{P}\mathit{r}$	Hayat et al. [31]	Present Results
0.1	0.2	0.2	$\pi /4$	0.2	1	0.1427	0.142683
0.0						0.1397	0.139746
0.1						0.1427	0.142683
0.12						0.1433	0.143252
	0.1					0.1417	0.141627
	0.3					0.1436	0.143621
	0.5					0.1452	0.145236
		0.2				0.1427	0.142683
		0.4				0.1439	0.143921
		0.6				0.1450	0.145011
			$\pi /6$			0.1434	0.143397
			$\pi /4$			0.1427	0.142683
			$\pi /3$			0.1417	0.141653
				0.1		0.1445	0.144551
				0.3		0.1409	0.140885
				0.5		0.1376	0.137455
					0.9	0.1394	0.139384
					1.0	0.1427	0.142683
					1.2	0.1480	0.148027

,

Table 2. Variation in the local Sherwood number $S{h}_x/R{e}_x^{1/2}$ for various parameters.

$\mathit{R}$	${\mathit{B}}_{\mathit{i}1}$	${\mathit{B}}_{\mathit{i}2}$	$\mathit{D}\mathit{u}$	$\mathit{E}\mathit{c}$	$\mathit{S}\mathit{c}$	Hayat et al. [31]	Present Results
0.1	0.2	0.2	0.5	0.1	0.9	0.1427	0.142683
0.3						0.1712	0.171117
0.5						0.1983	0.198211
0.7						0.2049	0.224187
	0.3					0.1900	0.189984
	0.4					0.2278	0.227806
	0.5					0.2588	0.258763
		0.3				0.1391	0.139068
		0.4				0.1362	0.136198
		0.5				0.1339	0.133862
			0.3			0.1475	0.147474
			0.7			0.1379	0.137879
			1.1			0.1282	0.128200
				0.2		0.1310	0.130941
				0.3		0.1194	0.119422
				0.4		0.1081	0.108115
					0.7	0.1442	0.144269
					1.2	0.1411	0.141060
					1.6	0.1397	0.139623

and

Table 3. Variation in the skin-friction coefficient $C{f}_x/R{e}_x^{1/2}$ for various parameters.

$\mathit{\gamma }$	$\mathit{P}\mathit{r}$	$\mathit{R}$	${\mathit{B}}_{\mathit{i}1}$	${\mathit{B}}_{\mathit{i}2}$	$\mathit{D}\mathit{u}$	$\mathit{E}\mathit{c}$	$\mathit{S}\mathit{c}$	$\mathit{S}\mathit{r}$	Hayat et al. [31]	Present Results
0.1	1.0	0.1	0.2	0.2	0.5	0.1	0.9	0.2	0.1445	0.144411
0.0									0.1421	0.142061
0.1									0.1445	0.144411
0.12									0.1449	0.144864
	0.9								0.1447	0.144664
	1.0								0.1445	0.144411
	1.2								0.1441	0.144013
		0.3							0.1448	0.144730
		0.5							0.1451	0.145036
		0.7							0.1454	0.145323
			0.3						0.1432	0.143138
			0.4						0.1422	0.142127
			0.5						0.1413	0.141304
				0.3					0.1924	0.192309
				0.4					0.2307	0.230657
				0.5					0.2621	0.262084
					0.3				0.1441	0.144029
					0.6				0.1446	0.144601
					0.9				0.1452	0.145170
						0.3			0.1465	0.146412
						0.4			0.1475	0.147384
						0.5			0.1484	0.148338
							0.9		0.1445	0.144411
							1.2		0.1520	0.151954
							1.6		0.1586	0.158605
								0.4	0.1411	0.141043
								0.5	0.1395	0.139376
								0.6	0.1378	0.137719

are enumerated to record the variation in the Nusselt number ($Nu)$, Sherwood number $\left(Sh\right)$ and coefficient of skin-friction $\left(C_f\right)$ for numerous values of involved parameters. Excellent correlation is noticed between our results and findings made by Hayat et al. [31]. This comparison between attained figures assures the credibility of the current work.

5. Outcomes of Analysis

The current communication is devoted to explicate the flow features of magnetohydrodynamic boundary layer flow of a second-grade fluid over an inclined porous cylinder under the impacts of viscos dissipation, radiation, convective heating, and Dufour and Soret effects. The mathematical modelling is attained in the form of partial differential equations and converted into ordinary differential equations by employing compatible transformations. Afterwards the solution is accomplished by using an implicit finite difference method known as the Keller Box scheme. The impact of the involved variables on velocity, temperature and concentration profiles is excogitated through graphical visualizations. Assurance of the present findings is achieved by constructing comparative analysis with previously published literature. The key findings are summarized as follows:

(i)

Increasing aptitude of velocity within the boundary layer region is depicted against the curvature parameter;

(ii)

It is found that the velocity profile upsurges against the viscoelastic parameter whereas it declines by uplifting the Darcy parameter;

(iii)

The thermal Biot number raises the temperature profile and also enriches the magnitude of the Nusselt number;

(iv)

Concentration of the Biot number causes growth in the concentration profile and augments the mass flux coefficient;

(v)

Dufour and Soret effects enhance the temperature field and depreciate the concentration profile.