Stochastic Control for Intra-Region Probability Maximization of Multi-Machine Power Systems Based on the Quasi-Generalized Hamiltonian Theory
Abstract
1. Introduction
2. Intra-Region Probability and Transformation
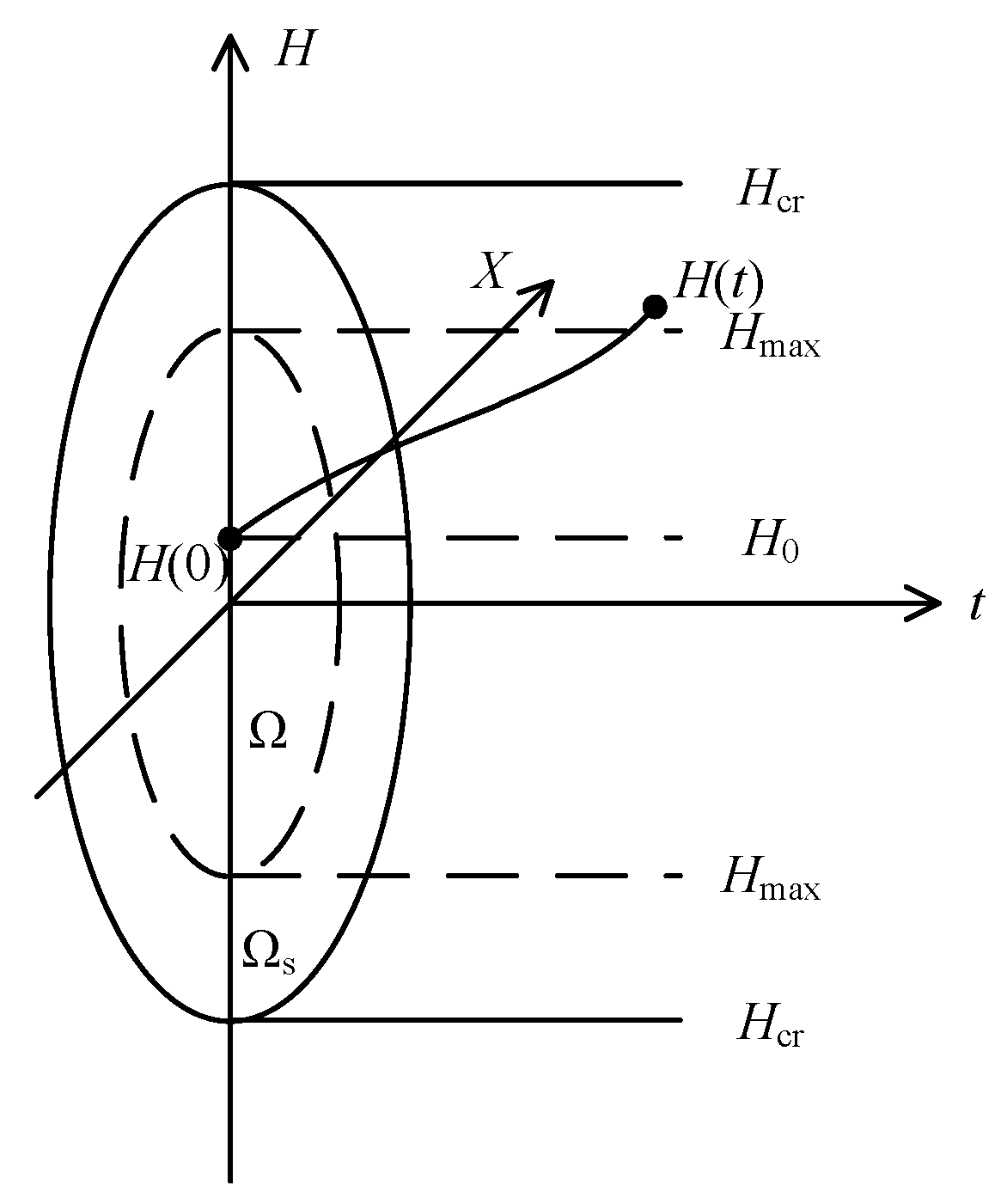
2.1. Intra-Region Probability Definition
2.2. Intra-Region Probability Transformation
3. SAM of Quasi-Generalized Hamiltonian Systems for Multi-Machine Power Systems
4. Stochastic Optimal Control for Maximizing Intra-Region Probability
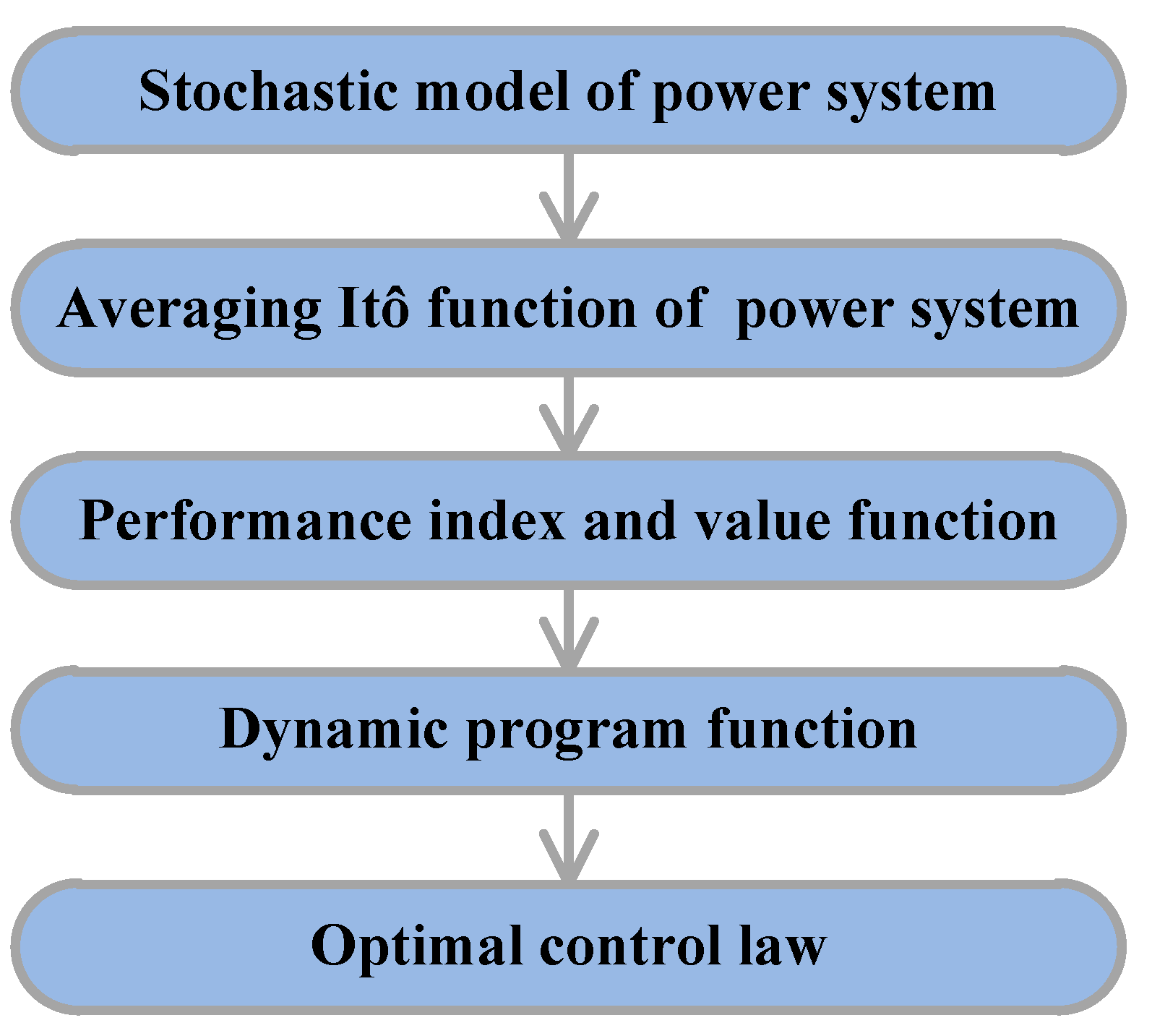
4.1. Procedure of the Stochastic Optimal Control
4.2. Performance Index
4.3. Stochastic Dynamic Programming Method
4.4. Conditional Intra-Region Probability Function
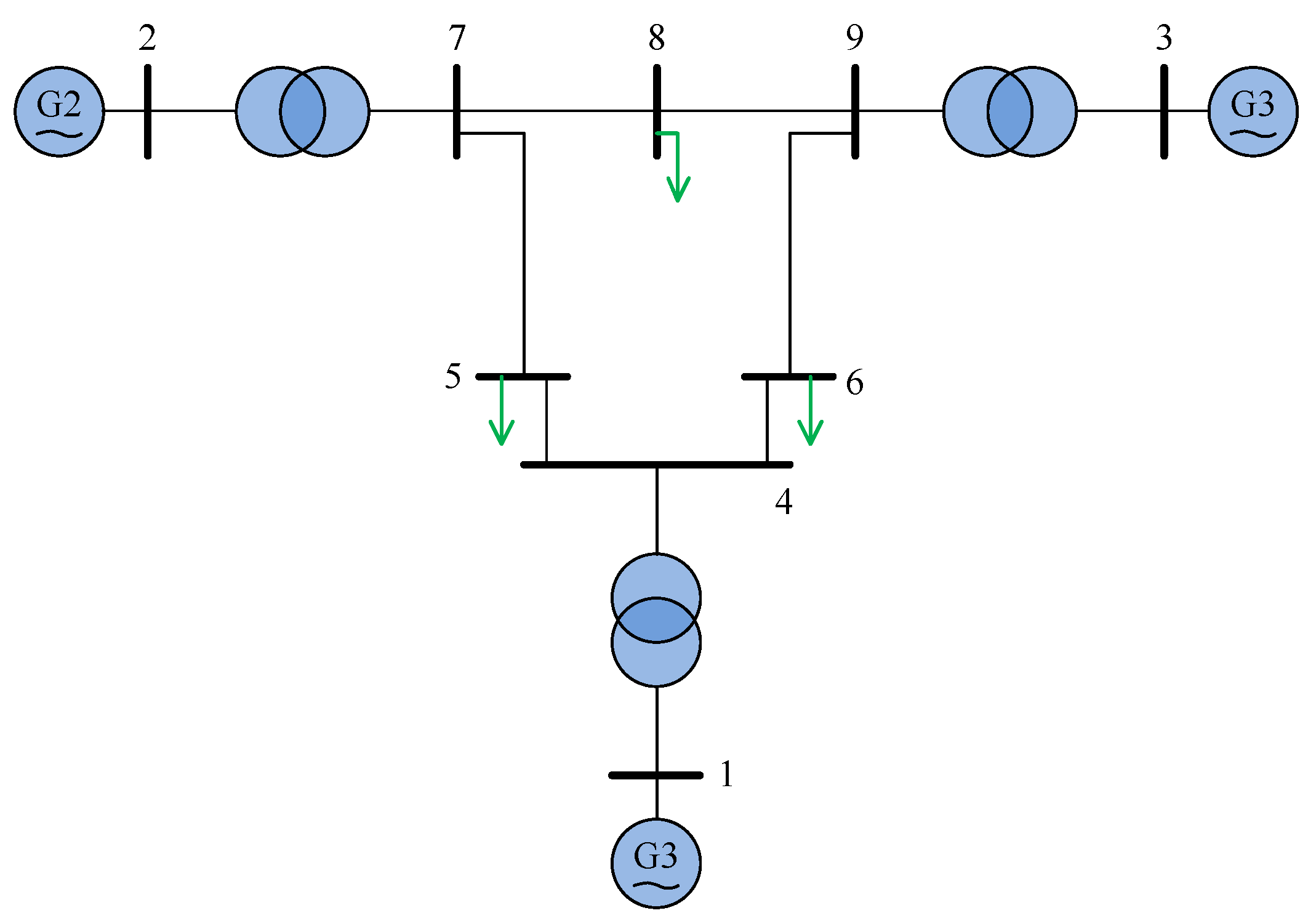
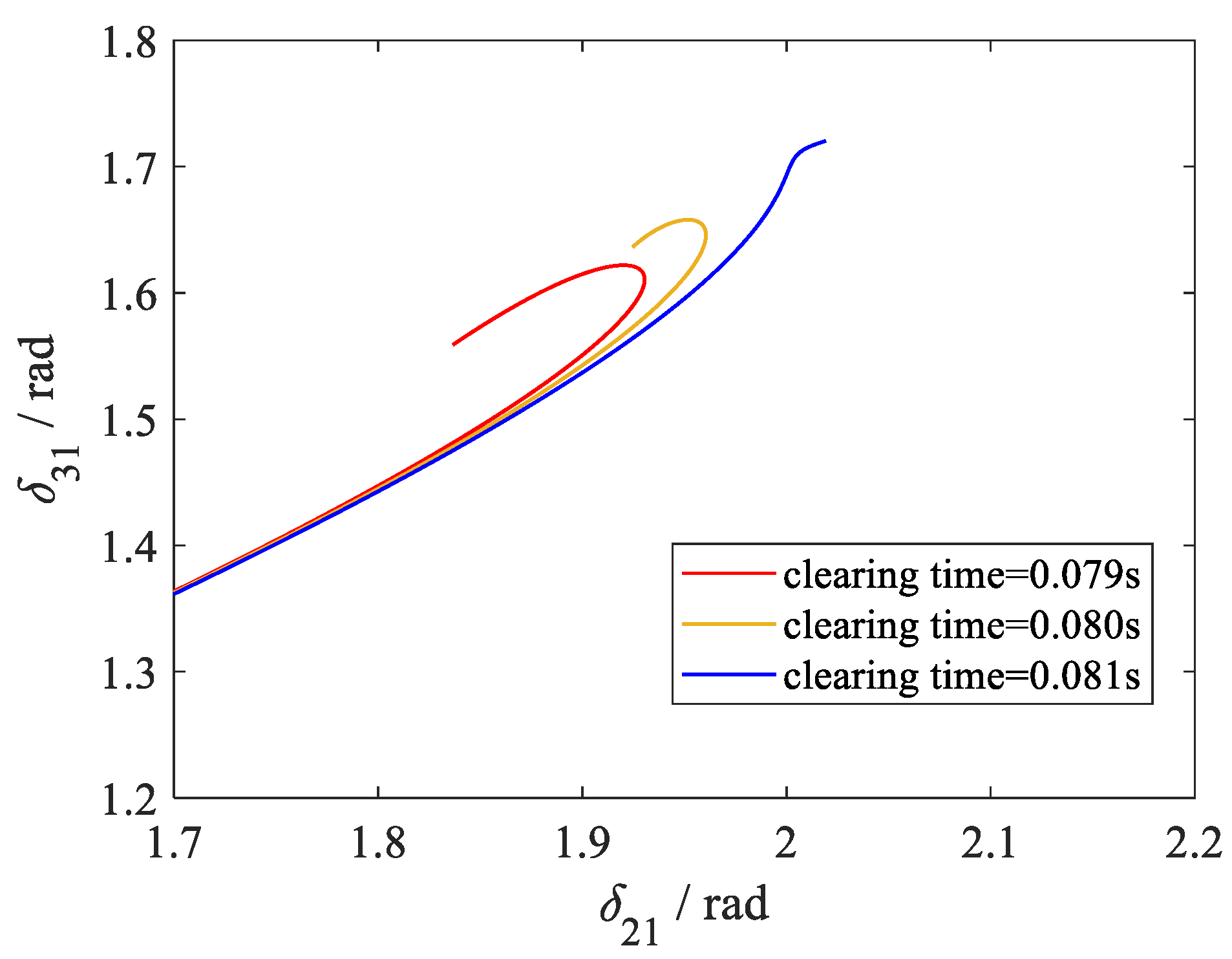
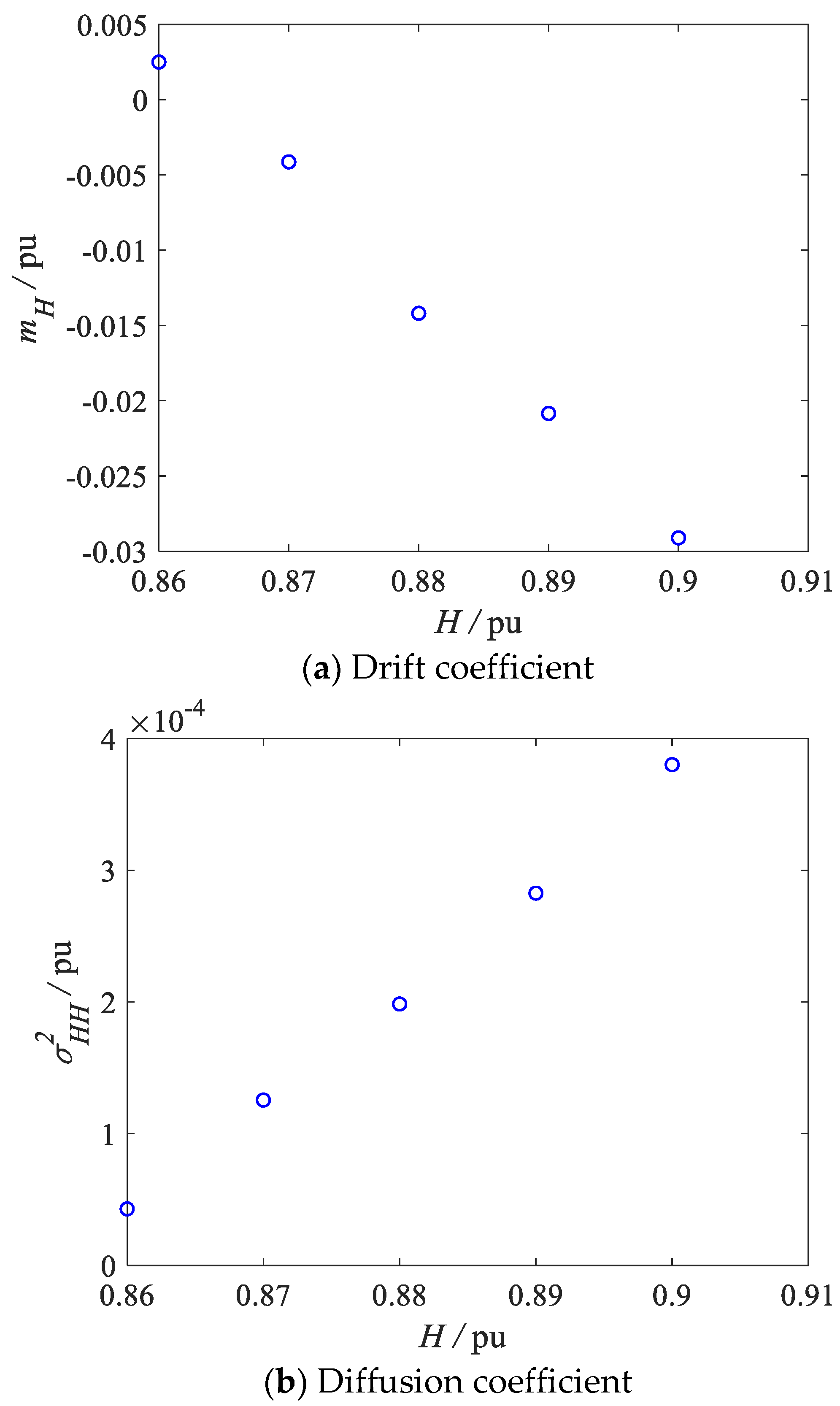
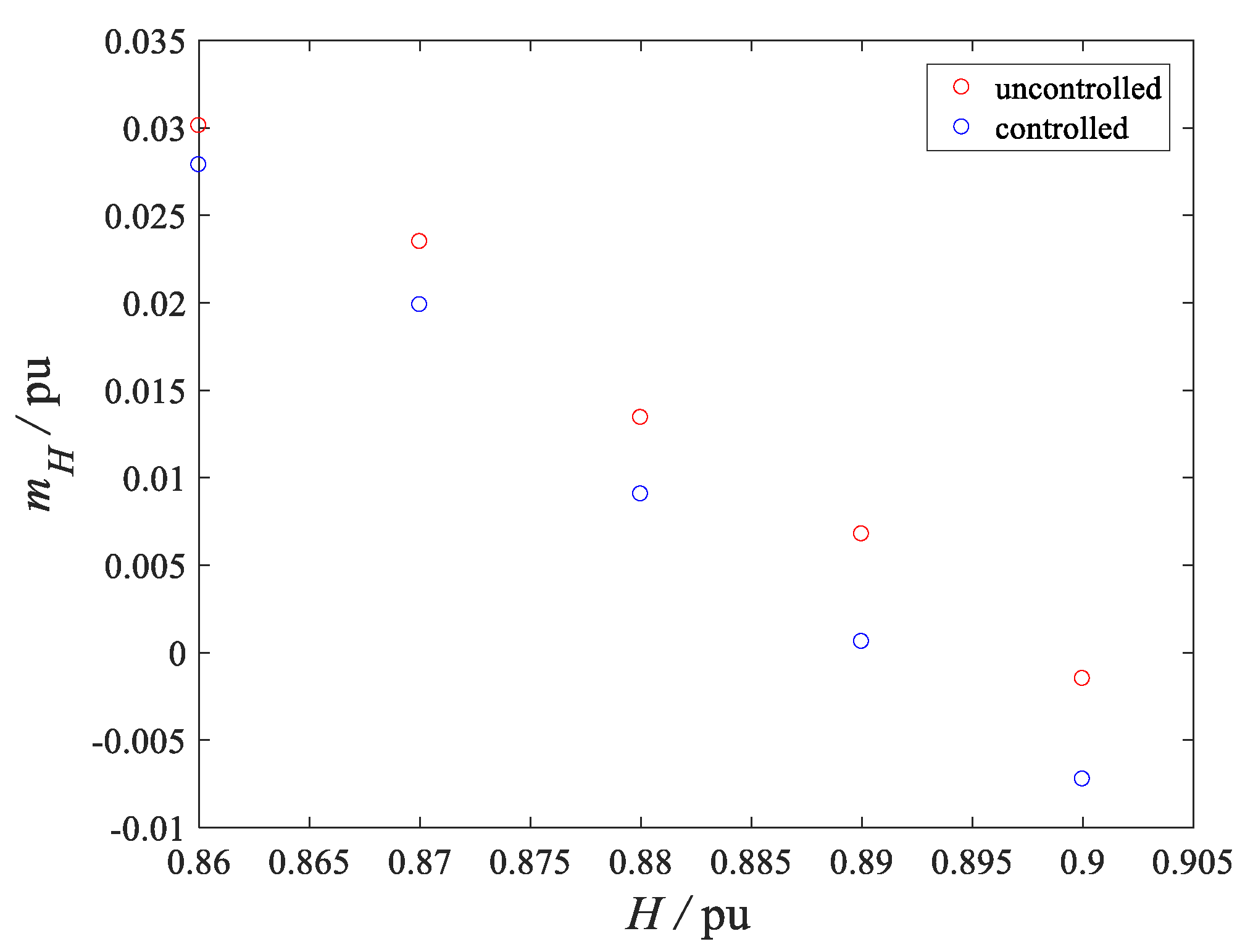
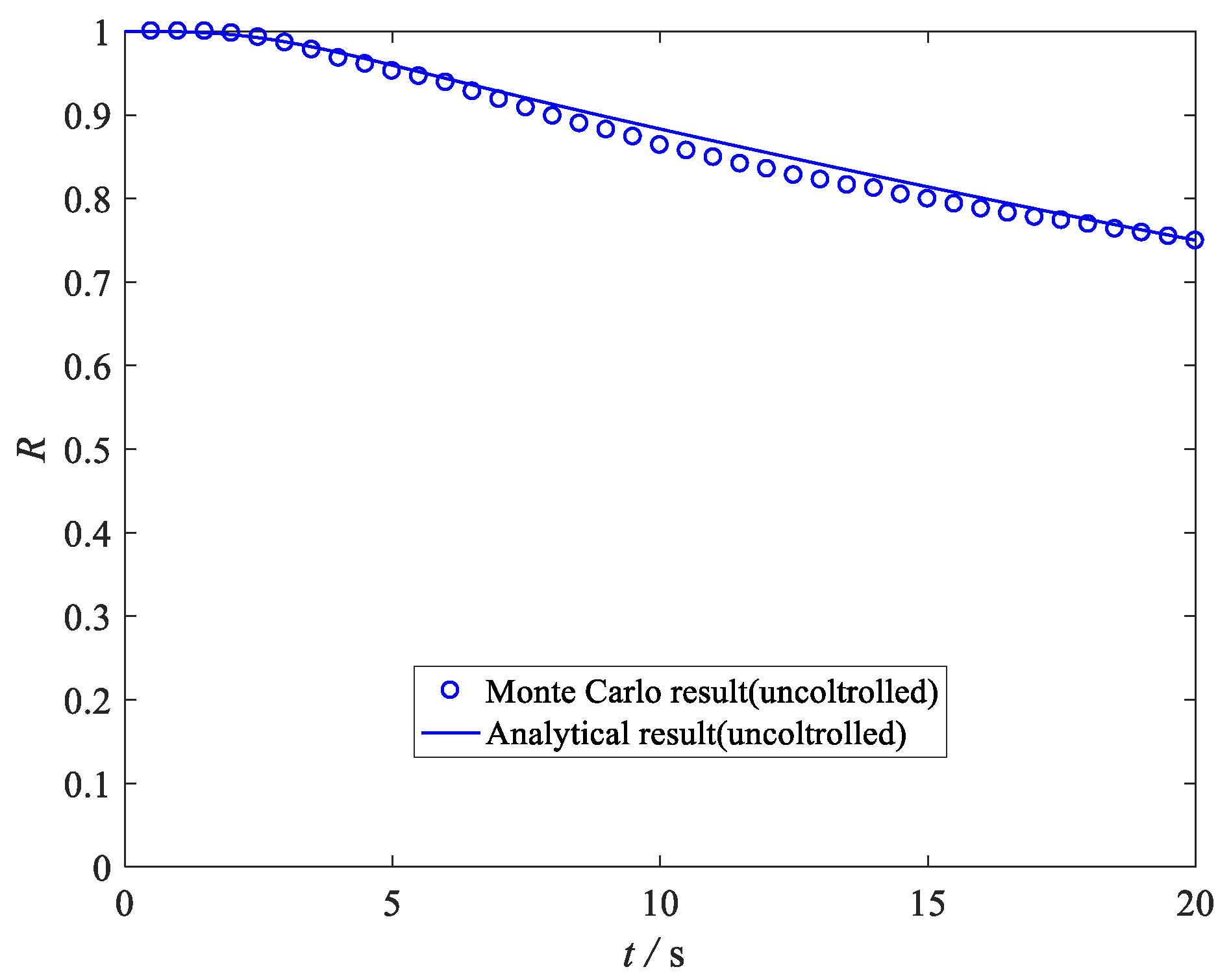
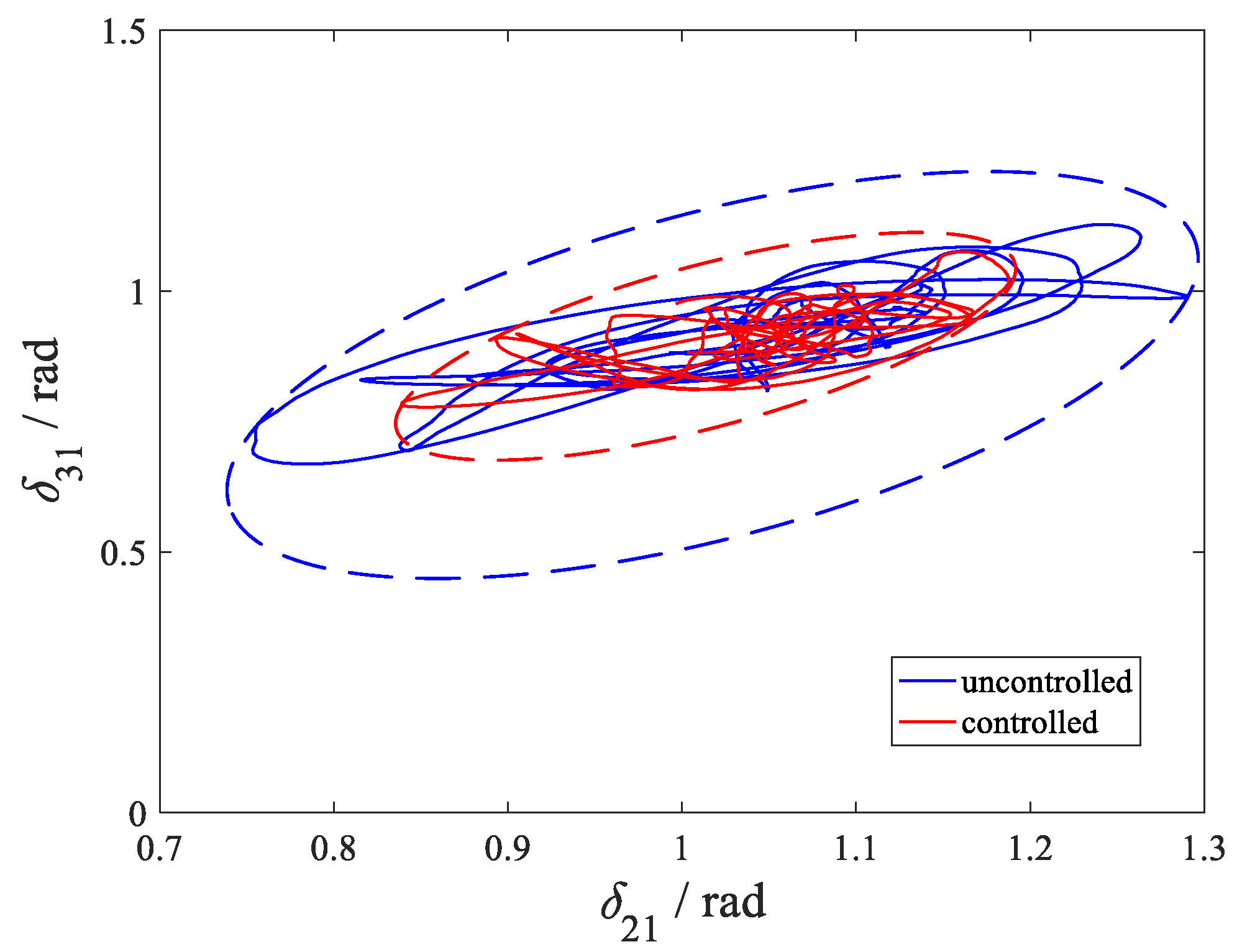
5. Case Study
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Ju, P.; Li, H.; Gan, C.; Liu, Y.; Yu, Y.; Liu, Y. Analytical Assessment for Transient Stability Under Stochastic Continuous Disturbances. IEEE Trans. Power Syst. 2018, 33, 2004–2014. [Google Scholar] [CrossRef]
- Li, H.; Ju, P.; Chen, X.; Sun, W.; Wu, F. Stochastic averaging method for quasi Hamiltonian system of multi-machine power systems. Sci. Sin. Technol. 2015, 45, 766. [Google Scholar]
- Ju, P.; Li, H.; Pan, X.; Gan, C.; Liu, Y. Stochastic Dynamic Analysis for Power Systems Under Uncertain Variability. IEEE Trans. Power Syst. 2018, 33, 3789–3799. [Google Scholar] [CrossRef]
- Deng, J.; Suo, J.; Yang, J.; Peng, S.; Chi, F.; Wang, T. Adaptive Damping Control Strategy of Wind Integrated Power System. Energies 2019, 12, 135. [Google Scholar] [CrossRef]
- Asghar, I.; Sarkar, B.; Kim, S. Economic Analysis of an Integrated Production–Inventory System under Stochastic Production Capacity and Energy Consumption. Energies 2019, 12, 3179. [Google Scholar] [CrossRef]
- Jamal, R.; Men, B.; Khan, N.H.; Zahoor Raja, M.A. Hybrid Bio-Inspired Computational Heuristic Paradigm for Integrated Load Dispatch Problems Involving Stochastic Wind. Energies 2019, 12, 2568. [Google Scholar] [CrossRef]
- Zhou, C.; Huang, G.; Chen, J. A Type-2 Fuzzy Chance-Constrained Fractional Integrated Modeling Method for Energy System Management of Uncertainties and Risks. Energies 2019, 12, 2472. [Google Scholar] [CrossRef]
- Ma, J.; Wang, S.; Qiu, Y.; Li, Y.; Wang, Z.; Thorp, J.S. Angle Stability Analysis of Power System with Multiple Operating Conditions Considering Cascading Failure. IEEE Trans. Power Syst. 2017, 32, 873–882. [Google Scholar] [CrossRef]
- Ntomaris, A.V.; Bakirtzis, A.G. Stochastic Scheduling of Hybrid Power Stations in Insular Power Systems with High Wind Penetration. IEEE Trans. Power Syst. 2016, 31, 3424–3436. [Google Scholar] [CrossRef]
- Papaefthymiou, G.; Kurowicka, D. Using Copulas for Modeling Stochastic Dependence in Power System Uncertainty Analysis. IEEE Trans. Power Syst. 2009, 24, 40–49. [Google Scholar] [CrossRef]
- Yuan, B.; Zhou, M.; Li, G.; Zhang, X.-P. Stochastic Small-Signal Stability of Power Systems with Wind Power Generation. IEEE Trans. Power Syst. 2015, 30, 1680–1689. [Google Scholar] [CrossRef]
- Li, H.; Ju, P.; Gan, C.; Tang, Y.; Yu, Y.; Liu, Y. Analytic Estimation Method of Forced Oscillation Amplitude under Stochastic Continuous Disturbances. IEEE Trans. Smart Grid 2018, 10, 4026–4036. [Google Scholar] [CrossRef]
- Li, H.; Ju, P.; Gan, C.; You, S.; Wu, F.; Liu, Y. Analytic Analysis for Dynamic System Frequency in Power Systems Under Uncertain Variability. IEEE Trans. Power Syst. 2019, 34, 982–993. [Google Scholar] [CrossRef]
- Liu, Y.; Ju, P.; Xue, Y.; Wu, F.; Zhang, J. Calculation analysis on power system characteristics under random excitation. Autom. Electr. Power Syst. 2014, 38, 137–142. [Google Scholar]
- Li, H.; Ju, P.; Yu, Y.; Huang, X.; Chen, X. Bounded fluctuations region and analytic method of intra-region probability in power system under stochastic excitations. Proc. CSEE 2015, 35, 3561–3568. [Google Scholar]
- Zhu, W.Q. Stochastic averaging of quasi-Hamiltonian systems. Sci. China Ser. A Math. Phys. Astron. 1996, 39, 97–107. [Google Scholar] [CrossRef]
- Huang, Z.L.; Zhu, W.Q. Stochastic averaging of quasi-generalized Hamiltonian systems. Int. J. Non-Linear Mech. 2009, 44, 71–80. [Google Scholar] [CrossRef]
- Zhu, W. Nonlinear Stochastic Dynamics and Control: Hamiltonian Theoretical Framework; Science Press: Beijing, China, 2003; pp. 206–457. [Google Scholar]
- Zhu, W.Q. Nonlinear Stochastic dynamics and control in Hamiltonian formulation. Appl. Mech. Rev. 2006, 59, 230–248. [Google Scholar] [CrossRef]
- Zhu, W.Q.; Yang, Y.Q. Stochastic averaging of quasi-nonintegrable-Hamiltonian systems. J. Appl. Mech. Trans. Asme 1997, 64, 157–164. [Google Scholar] [CrossRef]
- Gontijo, G.; Soares, M.; Tricarico, T.; Dias, R.; Aredes, M.; Guerrero, J. Direct Matrix Converter Topologies with Model Predictive Current Control Applied as Power Interfaces in AC, DC, and Hybrid Microgrids in Islanded and Grid-Connected Modes. Energies 2019, 12, 3302. [Google Scholar] [CrossRef]
- Corsini, A.; Cedola, L.; Lucchetta, F.; Tortora, E. Gen-Set Control in Stand-Alone/RES Integrated Power Systems. Energies 2019, 12, 3353. [Google Scholar] [CrossRef]
- Ali, K.; Khan, L.; Khan, Q.; Ullah, S.; Ahmad, S.; Mumtaz, S.; Karam, F.W.; Naghmash. Robust Integral Backstepping Based Nonlinear MPPT Control for a PV System. Energies 2019, 12, 3180. [Google Scholar] [CrossRef]
- Ouyang, J.; Li, M.; Zhang, Z.; Tang, T. Multi-Timescale Active and Reactive Power-Coordinated Control of Large-Scale Wind Integrated Power System for Severe Wind Speed Fluctuation. IEEE Access 2019, 7, 51201–51210. [Google Scholar] [CrossRef]
- Rouzbehi, K.; Yazdi, S.S.H.; Moghadam, N.S. Power flow control in multi-terminal HVDC grids using a serial-parallel DC power flow controller. IEEE Access 2018, 6, 56934–56944. [Google Scholar] [CrossRef]
- Chen, L.; Zhu, W.Q. First passage failure of quasi non-integrable generalized Hamiltonian systems. Arch. Appl. Mech. 2010, 80, 883–893. [Google Scholar] [CrossRef]
- Gan, C.B.; Zhu, W.Q. First-passage failure of quasi-non-integrable-Hamiltonian systems. Int. J. Non-Linear Mech. 2001, 36, 209–220. [Google Scholar] [CrossRef]
- Deng, M.L.; Hong, M.C.; Zhu, W.Q. Stochastic optimal control for the response of quasi non-integrable Hamiltonian systems. Acta Mech. Solida Sin. 2003, 16, 313–320. [Google Scholar]
- Zhu, W.Q. Feedback stabilization of quasi nonintegrable Hamiltonian systems by using Lyapunov exponent. Nonlinear Dyn. 2004, 36, 455–470. [Google Scholar] [CrossRef]
- Zhu, W.Q.; Deng, M.L. Optimal bounded control for minimizing the response of quasi non-integrable Hamiltonian systems. Nonlinear Dyn. 2004, 35, 81–100. [Google Scholar] [CrossRef]
- Zhu, W.Q.; Huang, Z.L. Stochastic stabilization of quasi non-integrable Hamiltonian systems. Int. J. Non-Linear Mech. 2004, 39, 879–895. [Google Scholar] [CrossRef]
- Zhu, W.Q.; Huang, Z.L.; Deng, M.L. Feedback minimization of first-passage failure of quasi non-integrable Hamiltonian systems. Int. J. Non-Linear Mech. 2002, 37, 1057–1071. [Google Scholar] [CrossRef]
- Zhu, W.Q.; Ying, Z.G. Optimal nonlinear feedback control of quasi-Hamiltonian systems. Sci. China Ser. A Math. Phys. Astron. 1999, 42, 1213–1219. [Google Scholar] [CrossRef]
- Lin, X.; Ju, P.; Sun, L. Maximization of reliability of stochastic multiple machines power system based on the quasi Hamiltonian system. In Proceedings of the 2017 IEEE Electrical Power and Energy Conference, Saskatoon, SK, Canada, 22–25 October 2017. [Google Scholar]
- Lin, X.; Sun, L.; Ju, P. Control of stochastic power system reliability maximization based on quasi-generalized Hamiltonian system. Dianli Zidonghua Shebei/Electr. Power Autom. Equip. 2017, 37, 173–178. [Google Scholar]
- Ni, Y.; Chen, S.; Zhang, B. Theory and Analysis of Dynamic Power System; Tsinghua University Press: Beijing, China, 2002; pp. 181–199. [Google Scholar]
- Sun, Y.; Jiao, X.; Shen, T. Power System Nonlinear Robust Control; Tsinghua University Press: Beijing, China, 2007; pp. 236–246. [Google Scholar]
- Zhang, B.; Zhao, Y. Stochastic Differential Equations in Science and Engineering; China Ocean Press: Beijing, China, 1980; pp. 162–180. [Google Scholar]
- Anderson, P.M. Power System Control and Stability, 2nd ed.; Wiley-IEEE Press: Hoboken, NJ, USA, 2003; pp. 37–39. [Google Scholar]



© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lin, X.; Sun, L.; Ju, P.; Li, H. Stochastic Control for Intra-Region Probability Maximization of Multi-Machine Power Systems Based on the Quasi-Generalized Hamiltonian Theory. Energies 2020, 13, 167. https://doi.org/10.3390/en13010167
Lin X, Sun L, Ju P, Li H. Stochastic Control for Intra-Region Probability Maximization of Multi-Machine Power Systems Based on the Quasi-Generalized Hamiltonian Theory. Energies. 2020; 13(1):167. https://doi.org/10.3390/en13010167
Chicago/Turabian StyleLin, Xue, Lixia Sun, Ping Ju, and Hongyu Li. 2020. "Stochastic Control for Intra-Region Probability Maximization of Multi-Machine Power Systems Based on the Quasi-Generalized Hamiltonian Theory" Energies 13, no. 1: 167. https://doi.org/10.3390/en13010167
APA StyleLin, X., Sun, L., Ju, P., & Li, H. (2020). Stochastic Control for Intra-Region Probability Maximization of Multi-Machine Power Systems Based on the Quasi-Generalized Hamiltonian Theory. Energies, 13(1), 167. https://doi.org/10.3390/en13010167






