Multi-Timescale-Based Partial Optimal Control of a Proton-Exchange Membrane Fuel Cell

Abstract

This paper presents a Proton-Exchange Membrane Fuel Cell (PEMFC) transient model in stack current cycling conditions and its partial optimal control. The derived model is used for a specific application of the recently published multistage control technique developed by the authors. The presented control-oriented transient PEMFC model is an extension of the steady-state control-oriented model previously established by the authors. The new model is experimentally validated for transient operating conditions on the Greenlight Innovation G60 testing station where the comparison of the experimental and simulation results is presented. The derived five-state nonlinear control-oriented model is linearized, and three clusters of eigenvalues can be clearly identified. This specific feature of the linearized model is known as the three timescale system. A novel multistage optimal control technique is particularly suitable for this class of systems. It is shown that this control technique enables the designer to construct a local LQR, pole-placement or any other linear controller type at the subsystem level completely independently, which further optimizes the performance of the whole non-decoupled system.

1. Introduction

Proton-Exchange Membrane Fuel Cells (PEMFC) are devices that convert the energy of electrochemical reactions to electrical energy. PEMFC is seen as a promising power source of the future, as an alternative to internal combustion engines and batteries, mainly because the only byproduct of the electrochemical reaction is water. Wide commercialization of such devices could reduce the greenhouse gas emissions, particularly associated with transportation. Those devices have a promising future in the automotive applications [1,2]. Even though the PEMFC have been extensively studied, they are still not even close to concur the market of power sources. The major bottlenecks for wider commercialization of PEMFC have cost and durability nature. Such systems operate sufficiently well on a fraction of their lifetime and then the performance decreases. Major reason for this is limited understanding of complex phenomena occurring during PEMFC operation and not controlling the system sufficiently well. There is an emerging need for taking a constructive control-oriented approach to PEMFC modeling and developing new control strategies.

PEMFC modeling and control is a multidisciplinary research area, because successful and efficient PEMFC operation implies deep understanding of various electrochemical, transport and material science phenomena. Over the years PEMFC have been studied from various aspects. Quite broad ongoing PEMFC research may be divided into two groups:

(i)

Examination of the fundamental electrochemical processes happening during PEMFC operation. The ones considered are thermo-electrochemistry [3,4,5], gas kinematics [6,7,8,9], membrane transport phenomena [10], capillary phenomena [11,12], etc.

(ii)

PEMFC systems engineering design. Research work has been done towards improvements of the cell stack design [13,14], choice of materials [15], gas supply pipeline and ejector [16], etc.

PEMFC modeling is the research area which represents the coupling between (i) and (ii). Physical PEMFC modeling uses the fundamental results of the group (i) research and lights the path which leads to a better design of cells, stacks, as outcome of the group (ii) PEMFC research. Numerous experimental, as well as theoretical studies have been conducted with a goal to explore the system’s performance and enhance efficiency. Review of the models present in the literature can be found in [17,18]. Some researchers focused on the system design and modeling the water content present in the PEMFC stack [19]. Study [20] focused on the effect of membrane water content during cold start. Studies such as [21] carried out a 3D non-isothermal multi-phase modeling and analysis. Common approaches in modeling are mechanistic approaches and empirically-based analysis [7,22,23,24,25]. In general, mechanistic approaches require specific parameters identification and empirically-based analysis relies heavily on experimental data which may be valid in a very narrow operating range. Also, those systems seem to be overparametrized [26], complicated and very challenging to control. In the current literature, to the authors’ best knowledge, there is not present a transient control-oriented model, suitable for further study and control systems design. Such a model is derived and experimentally validated in this paper.

PEMFC systems age with exploitation and performance of the stack deteriorates [27,28,29]. One of the main reasons that causes the aging effect is the oxygen starvation phenomenon. Study [30] summarizes about 15 possible reasons for gas starvation and suggests that more research effort should be put in the diagnostics of starvation and adequate control in the operating regime. Furthermore, PEMFC material degradation, and local heterogeneity, caused by nonuniform fueling, were discussed in [31], where some possible mitigation strategies were suggested. For example, study [31] states that hydrogen starvation problems could be reduced by shortening the hydrogen presence in front of anode bipolar plate channels, which will help in uniform distribution along the stack channels. Stack behavior under fuel starvation conditions is explored and experimentally documented in [32]. PEMFC assembly aging was experimentally shown [33], where analysis has shown that frequent gas starvation operating conditions present especially during transients, have significant impact on performance. For successful PEMFC operation there is a need for an adequate control strategy and the controller design. Comprehensive studies [17,34] review most recent research efforts and attempts to define and use of various control techniques for PEMFC systems. Despite all the efforts, the community needs more control-oriented models and classical control schemes such as [35,36]. On the other hand, physical variables (states in the control-oriented state space models) coupling and dependence among them is not explored well enough. Dynamic phenomena present in the PEMFC have been studied on the improved model presented in [37], where it is shown that they have an important influence on the PEMFC fuel cell control system design. Coupling analysis showed that some sort of the decoupling control strategy would optimize the system performance. The recent approach presented in [38,39,40], tackle the coupling interference between physical variables represented as states in the model, by investigating PEMFC subsystems as systems with multiple time scales. It was suggested and demonstrated in [41] that PEMFC has at least three distinct characteristic time scales, processes with response time less than $1s$, approximately $100s$ and more than $1000s$. This unique feature of PEMFC systems makes them particularly suitable for the application of the multistage multi-timescale controller technique.

This paper provides a control-oriented framework to study PEMFC and it is consisted of two parts:

• Development of the control-oriented dynamic PEMFC transient model. The transient model is developed from basic physics principles, where double layer charge effect is taken into account as well as the input delays due to gas starvation during transients. The transient model is specifically developed and experimentally validated for Greenlight Innovation TP50 (www.greenlightinnovation.com) fuel cell attached to the Greenlight Innovation G60${}^1$ testing station, currently operating at Villanova University research lab.
• Application of the multistage control technique to the developed transient model. This is a novel control technique recently developed by the authors, particularly suitable for multi-timescale systems.

2. Materials and Methods

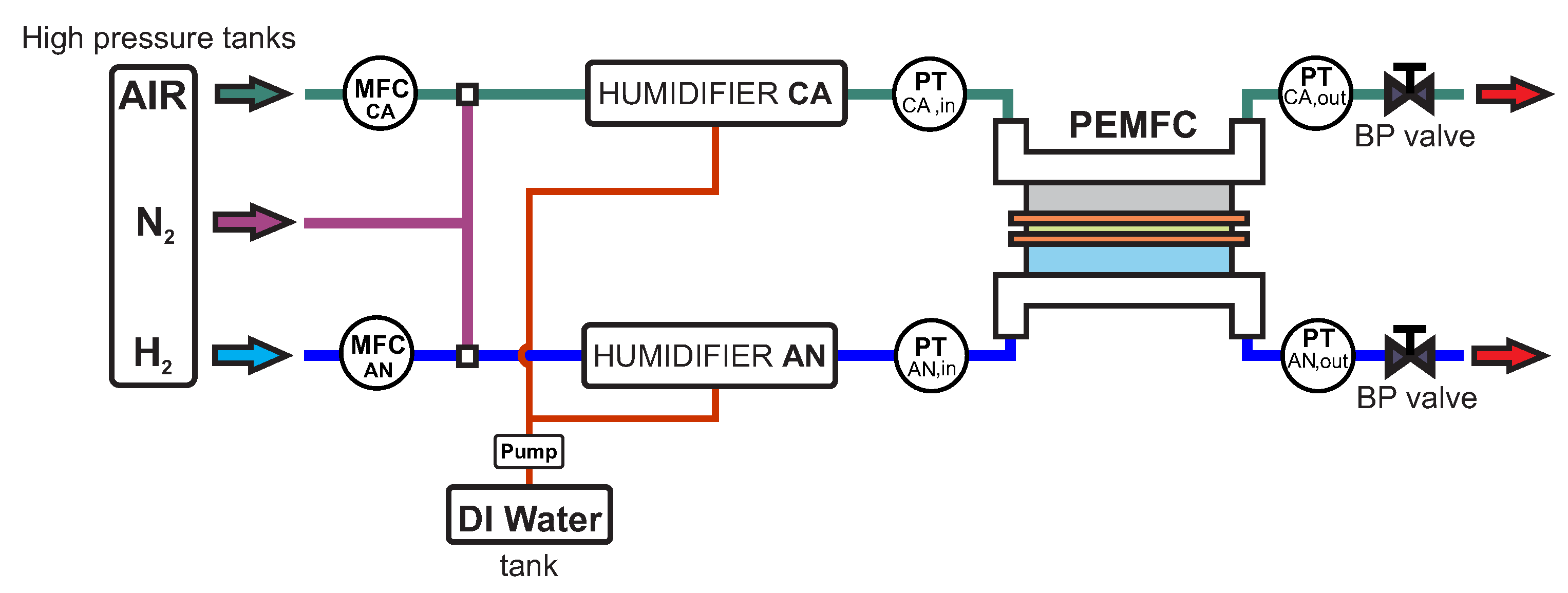
2.1. Experimental Setup

An experimental setup present in a Villanova University lab is consisted of: PEMFC testing station Greenlight Innovation G60 (Figure 1) and a Greenlight Innovation TP50 fuel cell stack (Figure 2). Model derivation in this paper assumes that the stack temperature during transients is constant (stack endplate heaters and external fan ensure operating temperature), so the thermal control loops are purposely omitted on the block diagram. Block diagram in Figure 3, shows only flow loops present in the system: fuel (Hydrogen) flow loop, oxidant (Air) flow loop, purging gas (nitrogen) flow loop, deionized (DI) water flow loop. As it can be seen input gases are driven through external humidifiers prior to entering the PEMFC stack.

In the model derivation the following assumptions were made:

• Inlet pressure is maintained constant during transient periods.
• All gases present are assumed to be single phase gases.
• Flow velocity is the same on the cathode (CA) and anode (AN) sides at all points where the gas flow is considered laminar, despite the fact that on the anode side during low stoic and pure $H_2$ condition this assumption might be violated. Since this assumption is used only for pressure calculation, non-uniformity of the flow on the anode side can be neglected in the developed model.
• Oxidant, in this case air is consisted of only oxygen $(78\%)$ and nitrogen $(21\%)$.
• Internal stack relative humidity never exceeds $100(\%)$. In this model, liquid water content (known as flooding) is not considered.
• CA and AN volumes are calculated as single lumped volume.
• Stack temperature is constant.

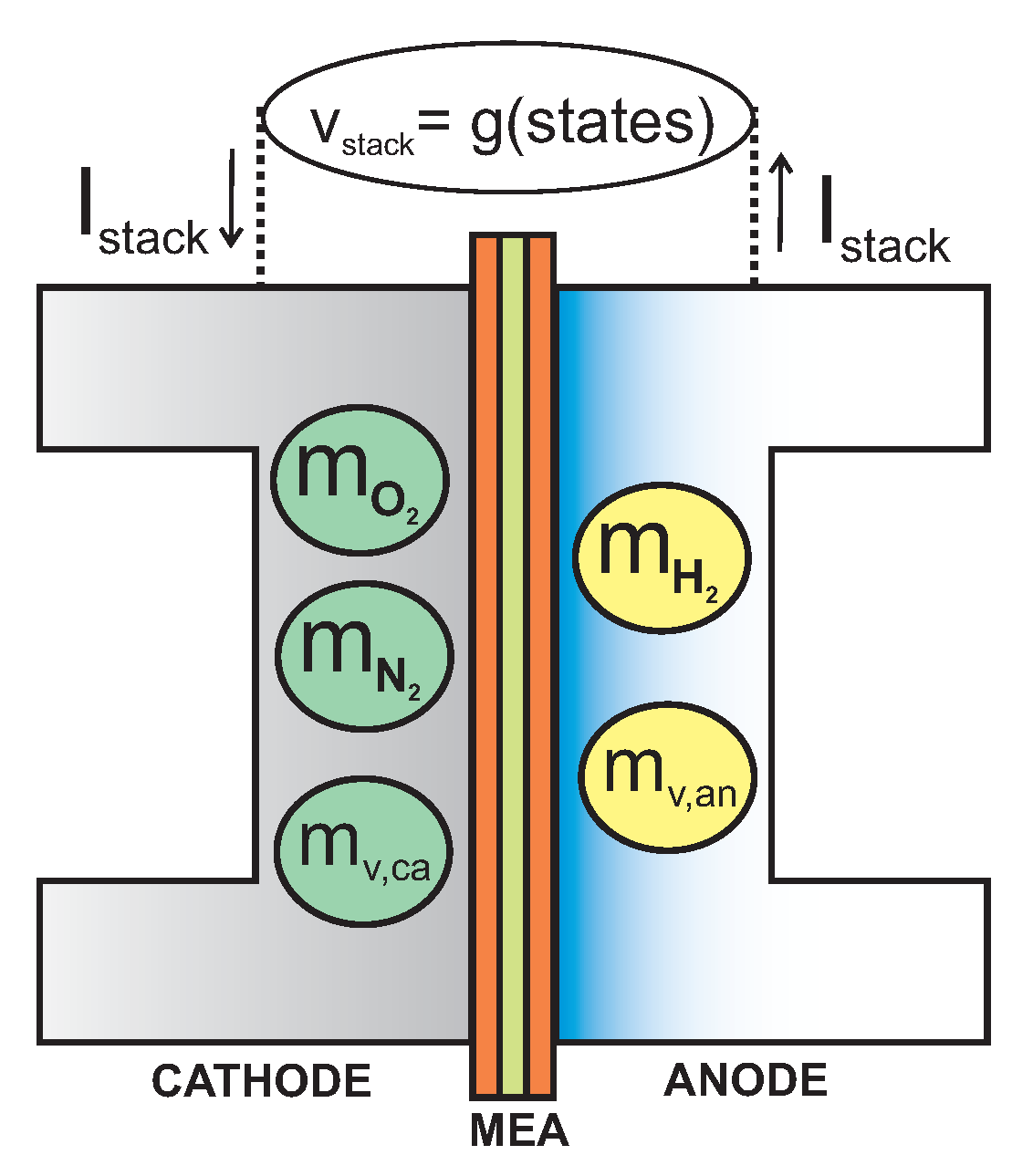
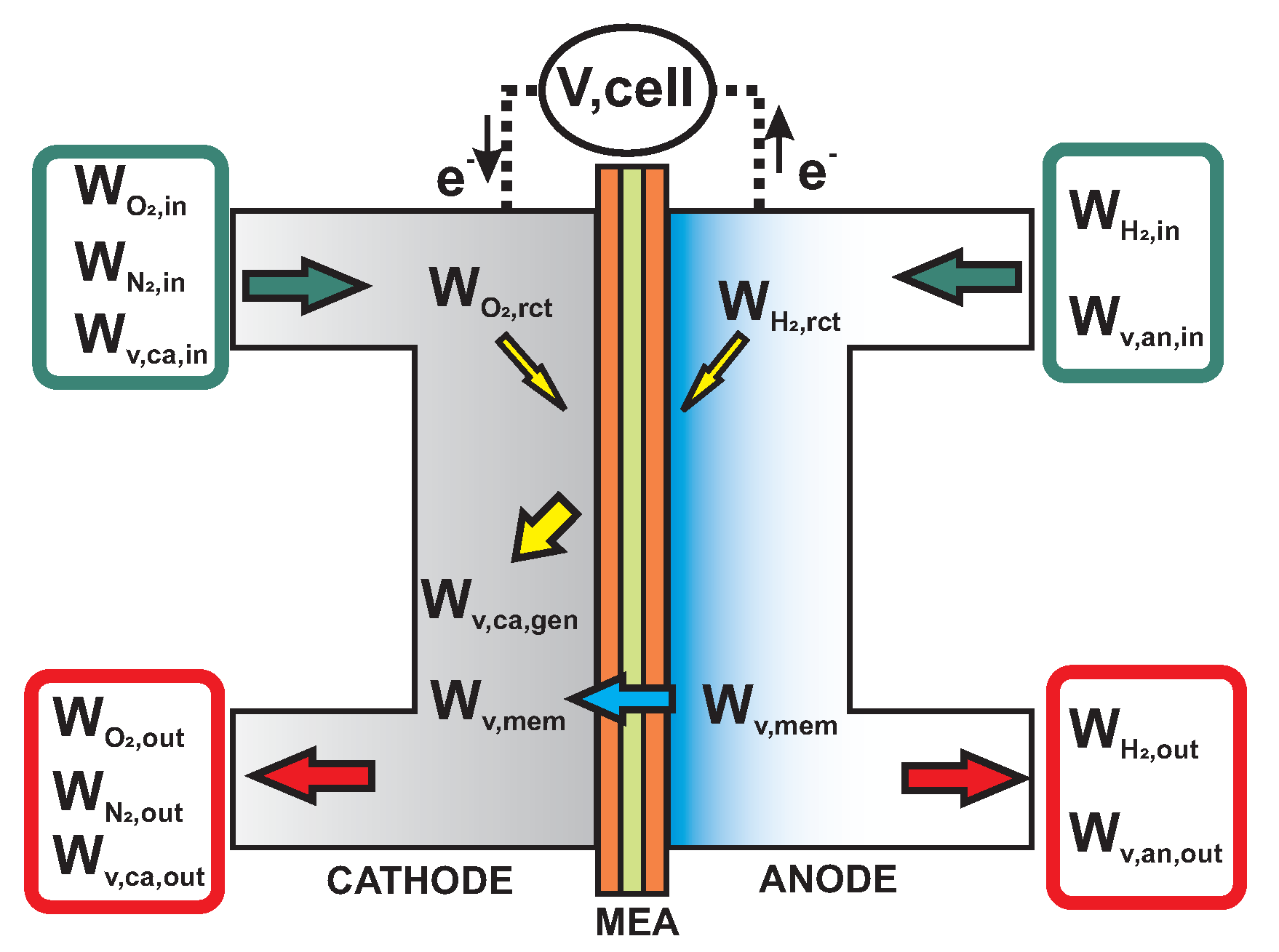
2.2. Control-Oriented Transient PEMFC Model: Derivation

The control-oriented PEMFC model is structured as

$$\left.\begin{array}{cc}\hfill \mathrm{State}\mathrm{equations}:& \dot{\mathbf{x}}\left(t\right)=\mathbf{f}\left(\mathbf{x}\left(t\right),\mathbf{u}\left(t\right),w\left(t\right)\right)\hfill \\ \hfill \mathrm{Input}:& \mathbf{u}\left(t\right)=\left[\begin{array}{c}{u}_1\left(t\right)\\ u_2\left(t\right)\end{array}\right]=\left[\begin{array}{c}{W}_{H_{2,an,in}}\left(t\right)\\ W_{a,ca,in}\left(t\right)\end{array}\right]\hfill \\ \hfill \mathrm{Input}\mathrm{disturbance}:& w\left(t\right)=I_{st}\left(t\right)\hfill \\ \hfill \mathrm{Output}:& u\left(t\right)=v_{st}\left(t\right)=g\left(\mathbf{x}\left(t\right)\right).\hfill \end{array}\right\}$$

(1)

In the rest of the paper, for convenience, explicit input, output, disturbance, and state time dependency will be omitted. The state space vector has five states, three in cathode (CA) and two in anode (AN), as outlined in Figure 4. CA and AN volumes are lumped volumes of serpentine distributed flow channels in CA and AN. The state vector is defined as

$$\mathbf{x}\left(t\right)={\left[\begin{array}{ccccc}{m}_{O_2}\left(t\right)& m_{N_2}\left(t\right)& m_{H_2}\left(t\right)& m_{v,an}\left(t\right)& m_{v,ca}\left(t\right)\end{array}\right]}^T$$

(2)

where $m_{O_2}\left(t\right)$, $m_{N_2}\left(t\right)$, $m_{v,ca}\left(t\right)$ are masses of oxygen, nitrogen and water vapor in CA in $\left[kg\right]$; and $m_{H_2}\left(t\right)$, $m_{v,an}\left(t\right)$ are masses of hydrogen and water vapor in AN in $\left[kg\right]$. Model inputs are: inlet mass flow of air on the CA side $W_{a,ca,in}$ in $\left[\frac{kg}{sec}\right]$, inlet mass flow of hydrogen on the AN side $\left[\frac{kg}{sec}\right]$ and stack current, treated as an input disturbance, in $\left[Amps\right]$. Output of the constructed model is stack voltage $v_{st}\left(t\right)$ in $\left[Volts\right]$.

Particular state equations take the following form

$$\begin{array}{cc}\hfill \mathrm{CA}:& \frac{d{m}_{O_2}}{dt}=W_{O_2,in}-W_{O_2,out}-W_{O_2,rct}\hfill \end{array}$$

(3)

$$\begin{array}{cc}\hfill \mathrm{CA}:& \frac{d{m}_{N_2}}{dt}=W_{N_2,in}-W_{N_2,out}\hfill \end{array}$$

(4)

$$\begin{array}{cc}\hfill \mathrm{AN}:& \frac{d{m}_{H_2}}{dt}=W_{H_2,in}-W_{H_2,out}-W_{H_2,rct}\hfill \end{array}$$

(5)

$$\begin{array}{cc}\hfill \mathrm{AN}:& \frac{d{m}_{v,an}}{dt}=W_{v,an,in}-W_{v,an,out}-W_{v,mem}\hfill \end{array}$$

(6)

$$\begin{array}{cc}\hfill \mathrm{CA}:& \frac{d{m}_{v,ca}}{dt}=W_{v,ca,in}-W_{v,ca,out}+W_{v,ca,gen}+W_{v,mem}\hfill \end{array}$$

(7)

where partial species present in CA or AN mass flow are denoted as W with subscripts $in$, $out$, $rct$, $gen$, $mem$ stand for inlet and outlet mass flows, reacted (depleted in electrochemical reaction) mass flow, generated species mass flow and mass flow through membrane respectively. Schematic of the mass flows present in the equations are provided in Figure 5. The derivations are procedure is split in four parts cathode, anode, outlet pressures and stack voltage.

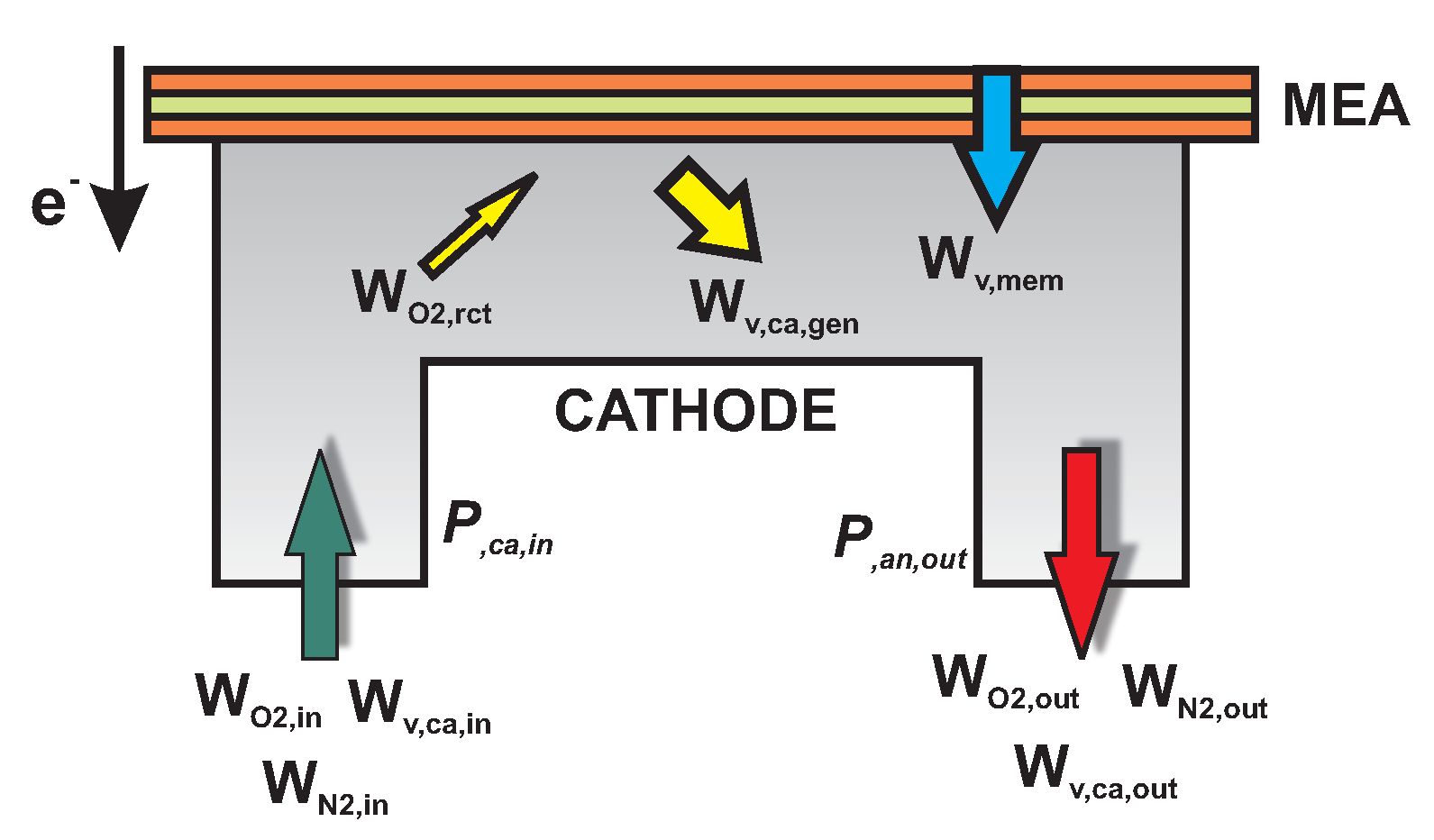
2.2.1. Cathode

This part focuses on Equations (3), (4) and (7). Particular mass flows considered are given in Figure 6. Cathode inlet components, mass flows of oxygen $W_{O_2,in}$, nitrogen $W_{N_2,in}$, and water vapor can be represented as mass fractions of the total CA inlet mass flow $W_{a,ca,in}$.

$$\begin{array}{cc}\hfill W_{O_2,in}& =x_{O_2}{W}_{a,ca,in}\hfill \end{array}$$

(8)

$$\begin{array}{cc}\hfill W_{N_2,in}& =x_{N_2}{W}_{a,ca,in}\hfill \end{array}$$

(9)

$$\begin{array}{cc}\hfill W_{v,ca,in}& =\frac{M_v}{M_a}\frac{p_{v,ca,in}}{p_{ca,in}-p_{v,ca,in}}{W}_{a,ca,in}\hfill \end{array}$$

(10)

where $M_a$ and $M_v$ are air and water vapor molar masses. Mass fraction coefficients $x_{O_2}$ and $x_{N_2}$ are defined as

$$\begin{array}{cc}\hfill x_{O_2}& =y_{O_2}\frac{M_{O_2}}{M_a}\hfill \end{array}$$

(11)

$$\begin{array}{cc}\hfill x_{N_2}& =(1-y_{O_2})\frac{M_{N_2}}{M_a}\hfill \end{array}$$

(12)

where $y_{O_2}=0.21$ is the oxygen mole fraction of the incoming air and $M_a$, $M_{N_2}$ are molar masses. In (10) externally controlled CA inlet pressure $p_{ca,in}$ is assumed to be constant, while the partial water vapor pressure depends on the incoming gas relative humidity ${\varphi }_{ca,in}$ and saturation pressure $p_{sat}^{T_{ca,in}}$ calculated at cathode inlet temperature $T_{ca,in}$ [42] as

$$\begin{array}{c}\hfill p_{v,ca,in}={\varphi }_{ca,in}{p}_{sat}^{T_{ca,in}}\end{array}$$

(13)

The saturation pressure defines an upper limit of water vapor partial pressure in the water-gas mixture. If this pressure is exceeded, condensation will occur. In transient conditions, delay between the stack current change and the net mass flow of oxygen $W_{O_2,net}$ can be represented by the first order differential equation

$$\begin{array}{c}\hfill {\tau }_{ca}\frac{d{W}_{O_2,net}}{dt}=\frac{i_{st}{M}_{O_2}}{4F}-W_{O_2,net}\end{array}$$

(14)

where the net flow is the difference between inlet and outlet oxygen mass flows, $W_{O_2,net}=W_{O_2,in}-W_{O_2,out}$. Coefficient ${\tau }_{ca}$ is a fitting parameter, with usual value of a couple of seconds. Next, CA outlet components are defined as

$$\begin{array}{cc}\hfill W_{O_2,out}& =\frac{m_{O_2}}{m_{ca}}{W}_{ca,out}\hfill \end{array}$$

(15)

$$\begin{array}{cc}\hfill W_{N_2,out}& =\frac{m_{N_2}}{m_{ca}}{W}_{ca,out}\hfill \end{array}$$

(16)

$$\begin{array}{cc}\hfill W_{v,ca,out}& =\frac{m_{v_{ca}}}{m_{ca}}{W}_{ca,out}\hfill \end{array}$$

(17)

where $m_{ca}=m_{O_2}+m_{N_2}+m_{v,ca}$ is the total mass present in the CA. Total outlet CA mass flow can be determined from $W_{ca,out}=k_{ca}\left(p_{ca}-p_{ca,out}\right)$, where $k_{ca}$ is the empirically determined orifice constant. The total pressure in the cathode is sum of all components partial pressures $p_{ca}=p_{O_2}+p_{N_2}+p_{v,ca}$, and $p_{ca,out}$ is the CA outlet pressure defined in subsection outlet pressures. Partial pressures at stack temperature $T_{st}$ present in the cathode can be calculated by using gas constants $R_{O_2}$, $R_{N_2}$ and CA volume $V_{ca}$ as: $p_{O_2}=\frac{R_{O_2}{T}_{st}}{V_{ca}}$, $p_{N_2}=\frac{R_{N_2}{T}_{st}}{V_{ca}}$ and $p_{v,ca}={\varphi }_{ca}{p}_{sat}^{T_{st}}$, where ${\varphi }_{ca}$ is the relative humidity in CA. Relative humidity inside CA depends on the state $m_{v,ca}$ as

$$\begin{array}{c}\hfill {\varphi }_{ca}=\frac{R{T}_{st}}{M_v{V}_{ca}{p}_{sat}^{T_{st}}}{m}_{v,ca}\end{array}$$

(18)

where $M_v$ is the water molar mass and R is the universal gas constant. Due to chemical reaction some portion of the oxygen is depleted on the CA side (represented by $-W_{O_2,rct}$ in (3)) and some water vapor is generated. For stack current $I_{st}$ and n cells present in the stack, the use of Faraday’s Law [43], leads to

$$\begin{array}{c}\hfill W_{O_2,rct}=M_{O_2}\frac{n{I}_{st}}{4F}\end{array}$$

(19)

$$\begin{array}{c}\hfill W_{v,ca,gen}=M_v\frac{n{I}_{st}}{2F}\end{array}$$

(20)

where F is the Faraday’s constant. Two phenomena dominate the membrane transport of water vapor: electro-osmotic drag and water back diffusion. The electro-osmotic drag occurs when $H^{+}$ ions dragged through membrane carry some water molecules as well. Also, due to new water vapor molecules excessive generation on the CA side a pressure gradient is present between CA and AN, so some molecules are being transferred back from CA to AN side. This process is called water back diffusion. On higher current densities, in a typical PEMFC working regime, water back diffusion is dominated by electro-osmotic drag, so the resulting net mass transfer of water vapor molecules is from AN to CA side. Mass transfer through membrane with active area $A_{fc}$ for stack with n cells and current density i has the following form [44]

$$\begin{array}{c}\hfill W_{v,mem}=M_v{A}_{fc}n\left(n_d\frac{i}{F}-D_w\frac{c_{v,ca}-c_{v,an}}{t_m}\right)\end{array}$$

(21)

where water concentrations in $\left[\frac{mol}{c{m}^3}\right]$ are determined by $c_{v,ca}=\frac{{\rho }_{m,dry}}{M_{m,dry}}{\lambda }_{ca}$ and $c_{v,an}=\frac{{\rho }_{m,dry}}{M_{m,dry}}{\lambda }_{an}$, for membrane dry density ${\rho }_{m,dry}$ in $\left[\frac{kg}{c{m}^3}\right]$, membrane equivalent weight $M_{m,dry}$ in $\left[\frac{kg}{mol}\right]$ and membrane thickness $t_m$ in $\left[cm\right]$. Water content coefficients ${\lambda }_{ca}$, ${\lambda }_{an}$ and ${\lambda }_m$ are fitted from experimental data taken from [45]. They are dependent on water activities $a_{ca}$ and $a_{an}$, which are calculated as ratio of the partial water vapor pressure $p_{v,ca}$ or $p_{v,an}$ and the saturation pressure at stack temperature as $a_{ca}=\frac{p_{v,ca}}{p_{sat}^{T_{st}}}$, $a_{an}=\frac{p_{v,an}}{p_{sat}^{T_{st}}}$ and $a_m=\frac{a_{ca}+a_{an}}{2}$. Water content coefficients are

$${\lambda }_k=\begin{array}{c}\{\begin{array}{cc}0.043+17.81a_k-39.85a_k^2+36a_k^3\hfill & 0<a_k\le 1\hfill \\ 14+1.4\left(a_k-1\right)\hfill & 1<a_k\le 3\hfill \end{array}\hfill \\ \mathrm{where}:k=ca,an,m(\mathrm{average}\mathrm{water}\mathrm{content})\hfill \end{array}$$

(22)

In Equation (21) electro-osmotic drag coefficient $n_d$ is defined as in [46]. It is a polynomial function of average water content ${\lambda }_m$

$$\begin{array}{c}\hfill n_d=0.0029{\lambda }_m^2+0.05{\lambda }_m-3.4\times {10}^{-19}\end{array}$$

(23)

Water diffusion coefficient $D_w$ in Equation (21) is given in [44]

$$\begin{array}{c}\hfill D_w=D_{\lambda }{e}^{\left(2416\left(\frac{1}{303}-\frac{1}{T_{st}}\right)\right)}\end{array}$$

(24)

where

$$D_{\lambda }=\{\begin{array}{cc}{10}^{-6},\hfill & {\lambda }_m<2\hfill \\ {10}^{-6}\left(1+2\left({\lambda }_m-2\right)\right),\hfill & 2\le {\lambda }_m\le 3\hfill \\ {10}^{-6}\left(3-1.67\left({\lambda }_m-3\right)\right),\hfill & 3\le {\lambda }_m<4.5\hfill \\ 1.25\times {10}^{-6},\hfill & {\lambda }_m\ge 4.5\hfill \end{array}$$

(25)

2.2.2. Anode

This modeling part focuses on Equations (5) and (6). Particular mass flows considered are given in Figure 7. Anode inlet components, hydrogen mass flow $W_{H_2,in}$ and water vapor mass flow $W_{v,an,in}$ are

$$\begin{array}{cc}\hfill W_{H_2,in}& =W_{H_2,in}\hfill \end{array}$$

(26)

$$\begin{array}{cc}\hfill W_{v,an,in}& =\frac{M_v}{M_{H_2}}\frac{p_{v,an,in}}{p_{an,in}-p_{v,an,in}}{W}_{H_2,an,in}\hfill \end{array}$$

(27)

where $M_{H_2}$ is hydrogen molar mass. In (27), AN inlet pressure $p_{an,in}$ is controlled externally, by the station and assumed to be constant during transients. Partial water vapor pressure depends on the incoming gas relative humidity ${\varphi }_{an,in}$ and saturation pressure $p_{sat}^{T_{an,in}}$ at anode inlet temperature

$$\begin{array}{c}\hfill p_{v,an,in}={\varphi }_{an,in}{p}_{sat}^{T_{an,in}}\end{array}$$

(28)

In transient conditions, delay between the stack current change and the net mass flow of hydrogen $W_{H_2,net}$ can be represented by the first order differential equation

$$\begin{array}{c}\hfill {\tau }_{an}\frac{d{W}_{H_2,net}}{dt}=\frac{i_{st}{M}_{H_2}}{4F}-W_{H_2,net}\end{array}$$

(29)

where the net flow is the difference between inlet and outlet hydrogen mass flows, $W_{H_2,net}=W_{H_2,in}-W_{H_2,out}$. Coefficient ${\tau }_{an}$ is a fitting parameter, with usual value of a couple of seconds. The outlet hydrogen mass flow $W_{H_2,out}$ and the outlet water vapor mass flow $W_{v,an,out}$ are mass fractions of the total mass in AN, $m_{an}=m_{H_2}+m_{v,an}$, given as

$$\begin{array}{cc}\hfill W_{H_2,out}& =\frac{m_{H_2}}{m_{an}}{W}_{an,out}\hfill \end{array}$$

(30)

$$\begin{array}{cc}\hfill W_{v,an,out}& =\frac{m_{v,an}}{m_{an}}{W}_{an,out}\hfill \end{array}$$

(31)

where the total outlet mass flow $W_{an,out}$ is proportional to pressure difference as $W_{an,out}=k_{an}\left(p_{an}-p_{an,out}\right)$, between total AN pressure $p_{an}$ and AN outlet pressure $p_{an,out}$ defined in subsection outlet pressures. AN orifice constant $k_{an}$ is determined empirically. The total AN pressure is sum of partial hydrogen pressure $p_{H_2}$ and partial water vapor pressure $p_{v,an}$, $p_{an}=p_{H_2}+p_{v,an}$, where partial pressures are given as $p_{H_2}=\frac{R_{H_2}{T}_{st}}{V_{an}}{m}_{H_2}$ and $p_{v,an}={\varphi }_{an}{p}_{sat}^{Tst}$, with the hydrogen gas constant $R_{H_2}$ and AN lumped volume $V_{an}$. Relative humidity inside AN, ${\varphi }_{an}$ is a function of the state variable $m_{v,an}$ as

$$\begin{array}{c}\hfill {\varphi }_{an}=\frac{R{T}_{st}}{M_v{V}_{an}{p}_{sat}^{T_{st}}}{m}_{v,an}\end{array}$$

(32)

In chemical reaction on the AN side some hydrogen is depleted, which is represented by term $-W_{H_2,rct}$ in (5) and defined by Faraday’s Law [43] as

$$\begin{array}{c}\hfill W_{H_2,rct}=M_{H_2}\frac{n{I}_{st}}{2F}\end{array}$$

(33)

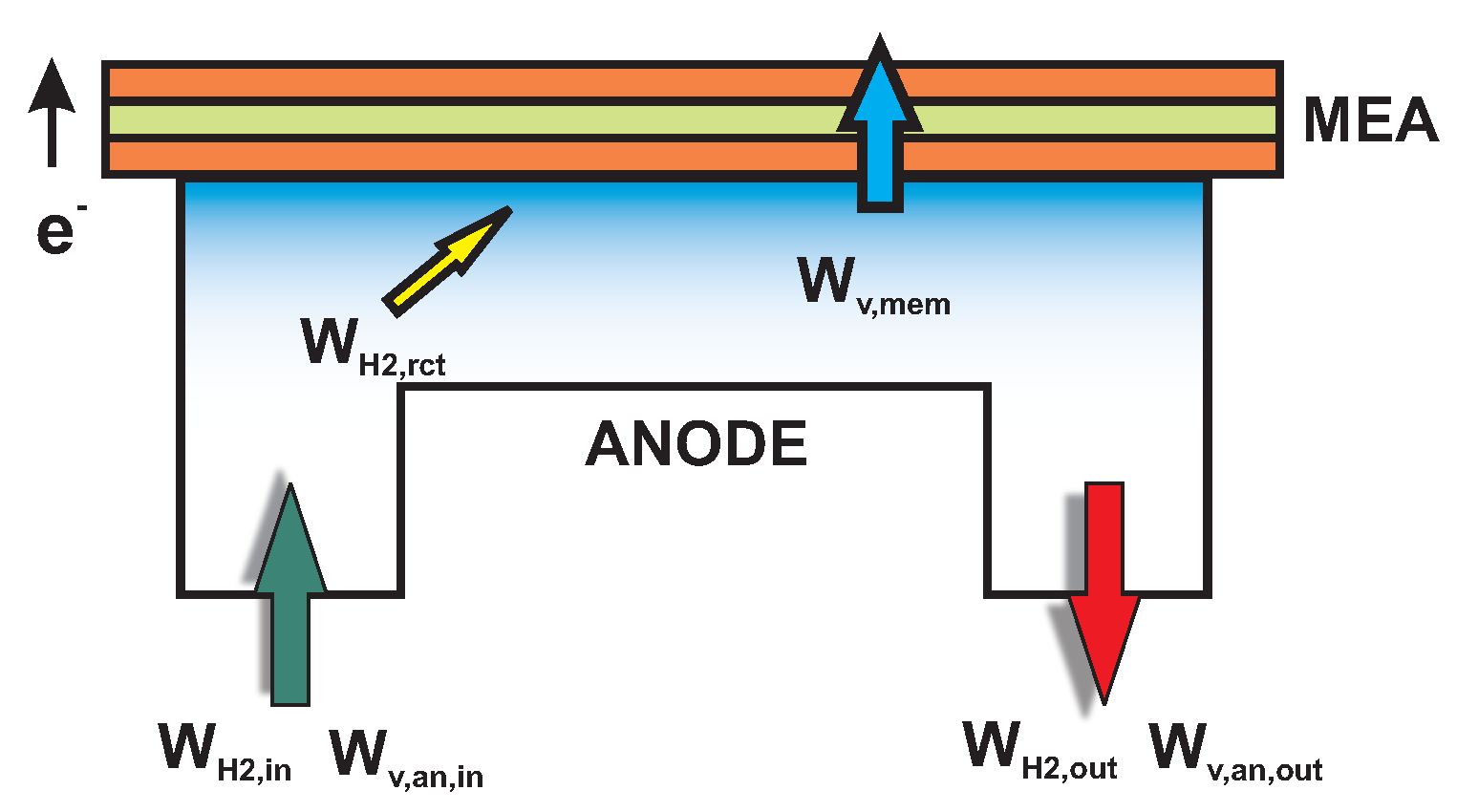
The water vapor mass flow through membrane $W_{v,mem}$ in Equation (6) is explained previously, but here has a negative sign $-W_{v,mem}$, because the direction of the flow is from AN side to CA side.

2.2.3. Outlet Pressures

Greenlight TP50 PEMFC present in the experimental setup has a serpentine flow pattern. This pattern causes significant pressure loss as the gas is traveling through the channels. Pressure difference between inlet and outlet pressures $p_{ca,in}$ and $p_{ca,out}$ on the CA side and $p_{an,in}$ and $p_{an,out}$ on the AN side is caused by three dominant losses:

• Friction losses. As flow is considered to be laminar at all times, this loss $\mathsf{\Delta }P$ can be modeled by Darcy’s Law as

  $$\begin{array}{c}\hfill \mathsf{\Delta }P=f_{d,j}\frac{L_j{\rho }_j}{2D_H}{v}_j^2,j=caoran\end{array}$$

  (34)

  where Darcy’s friction factor is given as $f_{d,j}=\frac{64}{R_{e_j}}$, with Reynolds number $R_{e_j}=\frac{{\rho }_j{L}_j}{{\mu }_j}{v}_j$ and flow velocity $v_j=\frac{{\rho }_j}{A_c}{W}_{j,in}$, which depends on the inlet mass flow $W_{j,in}$. In the previous expressions ${\rho }_j$ is fluid density, ${\mu }_j$ is fluid viscosity, $L_j$ is channel chord length, $D_H$ is hydraulic diameter of the rectangular flow channel, and $A_c$ stands for the channel cross sectional area.
• Channel bending losses. This pressure loss $\mathsf{\Delta }{P}_{bend,j}$ is a consequence of bends present in the serpentine channel pattern [47], dependable on flow velocity $v_j$

  $$\begin{array}{c}\hfill \mathsf{\Delta }{P}_{bend,j}=k_j\frac{{\rho }_j}{2}{v}_j^2,j=ca\mathrm{or}an\end{array}$$

  (35)

  where $k_j=k_{loc}+k_{fr,j}$ are friction coefficients defined as $k_{loc}=\frac{0.21}{{\left(\frac{R_0}{D_H}\right)}^{0.25}}$ (for a square duct) and $k_{fr,j}=0.0175\frac{R_0}{D_H}\delta {\lambda }_j$ (for $\delta ={90}^{°}$ bend angle) and ${\lambda }_j=32{\left(R{e}_j\sqrt{\frac{2R_0}{D_H}}\right)}^{-\frac{2}{3}}$ (for laminar flow).
• Chemical reaction pressure losses $\mathsf{\Delta }{P}_{rct}$ dependable on flow velocity $v_j$:

  $$\begin{array}{cc}\hfill \mathsf{\Delta }{P}_{rct,j}=& \left(a_{j,0}+a_{j,1}{I}_{st}+a_{j,2}{I}_{st}^2+a_{j,3}{I}_{st}^3\right)v_j^2\hfill \end{array}$$

  (36)
  Coefficient values can be found in Appendix A,

  Table A2. CA pressure drop coefficients.

  Symbol	Value
  $a_{ca,0}$	$2.8152$
  $a_{ca,1}$	$-0.3530$
  $a_{ca,2}$	$0.0123$
  $a_{ca,3}$	$-6.9846\times {10}^{-6}$

  and

  Table A3. AN press. drop coefficients.

  Symbol	Value
  $a_{an,0}$	$-26.7567$
  $a_{an,1}$	$-0.6225$
  $a_{an,2}$	$0.0544$
  $a_{an,3}$	$-7.267\times {10}^{-4}$

  .

Subtracting all three defined losses from inlet pressures $p_{j,in}$ leads to formula for outlet pressures $p_{j,out}$ on the CA side $(j=ca)$ and the AN side $(j=an)$

$$\begin{array}{cc}\hfill p_{j,out}=& p_{j,in}-\mathsf{\Delta }{P}_j-\mathsf{\Delta }{P}_{bend,j}-\mathsf{\Delta }{P}_{rct,j}\hfill \end{array}$$

(37)

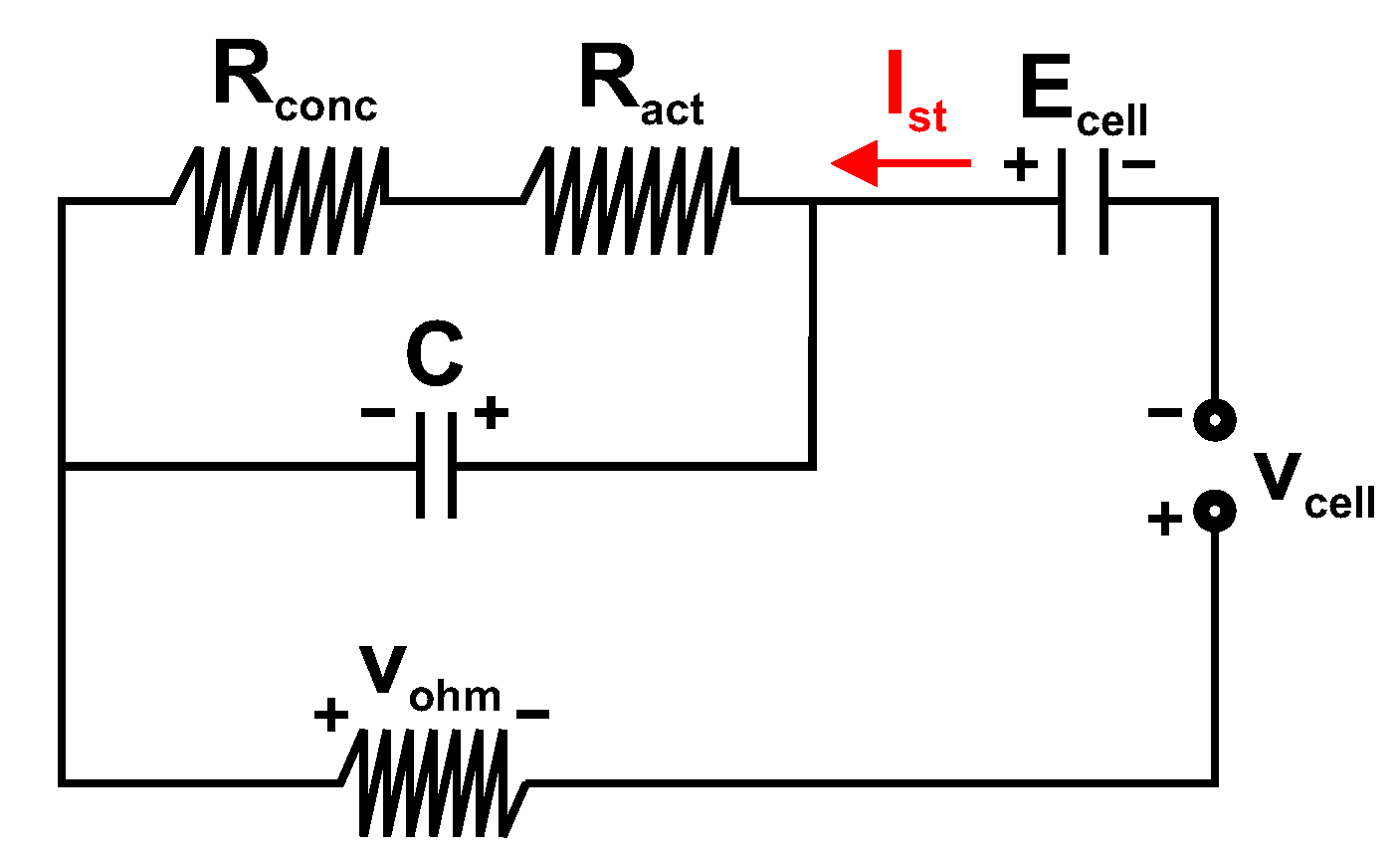
2.2.4. Stack Voltage

The actual stack output voltage consisted of n cells is the open circuit voltage $E_{cell}$ reduced by three quantities, in this work considered, voltage losses: [48], or ohmic voltage loss $v_{ohm}$, activation voltage loss $v_{act}$, and concentration voltage loss $v_{conc}$

$$\begin{array}{c}\hfill v_{st}=n\left(E_{cell}-v_{ohm}-v_{act}-v_{conc}\right)\end{array}$$

(38)

By following the principles of thermodynamic potentials [42,49], it is known that a negative change in Gibbs free energy directly corresponds to the maximum electrical work, seen as an open circuit voltage, at standard state conditions. Under nonstandard state conditions, the open circuit voltage $E_{cell}$ is a function of variations of pressures of the reactant species, in PEMFC case, oxygen pressure $p_{O_2}$ and hydrogen pressure $p_{H_2}$ and it is represented by the Nernst equation as

$$\begin{array}{c}\hfill E=E^o+\frac{\mathsf{\Delta }\widehat{s}}{nF}\left(T-T_0\right)+\frac{RT}{nF}\ln \left(p_{H_2}{P}_{O_2}^{0.5}\right)\end{array}$$

(39)

where $\mathsf{\Delta }\widehat{s}$ is the heat capacity change of the substance. At stack temperature $T=T_{st}$,with standard temperature $T_0=298.15\left[K\right]$ and with $\mathsf{\Delta }\widehat{s}$ taken from thermodynamic tables in [49], the final form of the open circuit voltage equation is

$$\begin{array}{c}\hfill E=1.229-8.5\times {10}^{-4}\left(T_{st}-298.15\right)+4.3085\times {10}^{-5}{T}_{st}\left[\ln \left(p_{H_2}\right)+0.5\ln \left(p_{O_2}\right)\right]\end{array}$$

(40)

For a membrane thickness $t_m$ and membrane conductivity ${\sigma }_m$, ohmic voltage loss $v_{ohm}$ is

$$\begin{array}{c}\hfill v_{ohm}=i{R}_{ohm}=i\frac{t_m}{{\sigma }_m}\end{array}$$

(41)

Membrane conductivity takes the following form [45]

$$\left.\begin{array}{c}\hfill {\sigma }_m=b_{1}exp\left(b_2\left(\frac{1}{303}-\frac{1}{T_{st}}\right)\right)\\ \hfill b_1=b_{11}{\lambda }_m-b_{12}\\ \hfill b_{11}=-5.8922\times {10}^{-6}\\ \hfill b_{12}=-0.018462\\ \hfill b_2=200\end{array}\right\}$$

(42)

where ${\lambda }_m$ is water content provided in Equation (22). Portion of the energy is consumed in the chemical reaction, where it is used to support chemical bonds breakage and electron transport. This energy consumption is the main reason for activation voltage losses $v_{act}$. This loss can be described by Tafel equation $v_{act}=A\times ln\left(\frac{i}{i_0}\right)$[48], where A is constant. This equation is valid for simulation only for the current densities $i=\frac{I_{st}}{A_{fc}}$ greater than the exchange current density $i_0$, as $i>i_0$. For simulation purposes, this equation is approximated with similar well-defined function

$$v_{act}=v_0+v_a\left(1-e^{-c_{1}i}\right)$$

(43)

where $v_0$ is the voltage drop at zero current density, $v_a$ values are taken from [44] and $c_1=20.8605$ is fitted to our experimental data. The voltage drop at zero current density is in the form

$$\left.\begin{array}{c}\hfill v_0=0.279-8.5\times {10}^{-4}(T_{st}-298.15)+4.308\times {10}^{-5}{T}_{st}\times \\ \hfill \times \left[\ln \left(p_{ca}-p_{sat}^{T_{st}}\right)+\frac{1}{2}\ln \left[0.1173(p_{ca}-p_{sat}^{T_{st}})\right]\right]\\ \hfill v_a=v_{a,1}{\left(\frac{p_{O_2}}{0.1173}+p_{sat}^{T_{st}}\right)}^2+v_{a,2}\left(\frac{p_{O_2}}{0.1173}+p_{sat}^{st}\right)+v_{a,3}\\ \hfill v_{a,1}=-1.618\times {10}^5{T}_{st}+1.618\times {10}^{-2}\\ \hfill v_{a,2}=1.8\times {10}^{-4}{T}_{st}-0.166\\ \hfill v_{a,3}=-5.8\times {10}^{-4}{T}_{st}+0.5736\end{array}\right\}$$

(44)

The concentration voltage drops dominate the voltage response of the stack at higher current densities. At stack current density i the voltage concentration drop takes the form

$$\begin{array}{c}\hfill v_{conc}=i{\left(c_2\frac{i}{i_{max}}\right)}^{c_3}\end{array}$$

(45)

where $c_2$ is taken from [44]

$$c_2=\{\begin{array}{cc}\hfill \begin{array}{cc}\hfill & \left(7.16\times {10}^{-4}{T}_{st}-0.622\right)\left(\frac{p_{O_2}}{0.1173}+p_{sat}\right)+\hfill \\ \hfill & +\left(-1.45\times {10}^{-3}{T}_{st}+1.68\right)\hfill \end{array}& \mathrm{if}:\left(\frac{p_{O_2}}{0.1173}+p_{sat}\right)<2.0265\mathrm{bar}\\ \hfill \begin{array}{cc}\hfill & \left(8.66\times {10}^{-5}{T}_{st}-0.068\right)\left(\frac{p_{O_2}}{0.1173}+p_{sat}\right)+\hfill \\ \hfill & +\left(-1.6\times {10}^{-4}{T}_{st}+0.54\right)\hfill \end{array}& \mathrm{if}:\left(\frac{p_{O_2}}{0.1173}+p_{sat}\right)\ge 2.0265\mathrm{bar}\end{array}$$

(46)

while parameters $c_3=4.4469$ and $i_{max}=0.96$ are fitted to match experimental data. Membrane Electrolyte Assembly (MEA) separates metal plates in space and allows positive $H^{+}$ ions to pass while electron flow is blocked. On the AN side there is a negative charge build up and on the CA side there is a positive charge build up. In this way, an electrochemical double layer is formed, and it is acting as a regular electrical capacitor, which can store some electrical energy. This phenomenon is incorporated in the model by introducing the equivalent electrical circuit [50], where equivalent electrical capacitance C needs to be determined. The stack voltage becomes

$$v_{st}=n\left(E_{cell}-v_{ohm}\underset{\mathrm{capacitor}:{\mathrm{V}}_{\mathrm{C}}}{\underbrace{-v_{conc}-v_{act}}}\right)=n\left(E_{cell}-v_{ohm}-V_C\right)$$

(47)

where governing equation for capacitor voltage $V_C$ for circuit provided in Figure 8 is

$$\begin{array}{c}\hfill V_C=\left(I_{st}-C\frac{d{V}_C}{dt}\right)\left(R_{act}+R_{conc}\right)\end{array}$$

(48)

where $R_{act}$ and $R_{conc}$ are equivalent resistances of the activation voltage loss $v_{act}$ given in (43) and the concentration voltage loss $v_{conc}$ given in (45).

2.3. Multistage Control Technique

The multistage control technique applied to a linear system in state space form can be split in two parts [40]: part 1 of the design transforms original system into the upper triangular form, and part 2 implements the multistage procedure where in each stage reduced order subsystem is decoupled from full-order system and a local controller is designed. A linear time invariant (LTI) continuous time dynamic system in a three-system partitioned form looks like

$$\begin{array}{c}\hfill \left[\begin{array}{c}{\dot{x}}_1\left(t\right)\\ {\dot{x}}_2\left(t\right)\\ {\dot{x}}_3\left(t\right)\end{array}\right]=\left[\begin{array}{ccc}{A}_{11}& A_{12}& A_{13}\\ A_{21}& A_{22}& A_{23}\\ A_{31}& A_{32}& A_{33}\end{array}\right]\left[\begin{array}{c}{x}_1\left(t\right)\\ x_2\left(t\right)\\ x_3\left(t\right)\end{array}\right]+\left[\begin{array}{c}{B}_{11}\\ B_{21}\\ B_{31}\end{array}\right]u\left(t\right)=Ax\left(t\right)+Bu\left(t\right)\end{array}$$

(49)

where state vector variables are $x\left(t\right)\in R^{n\times 1}$, $x_1\left(t\right)\in R^{n_1\times 1}$, $x_2\left(t\right)\in R^{n_2\times 1}$ and $x_3\left(t\right)\in R^{n_3\times 1}$, $n=n_1+n_2+n_3$, the control input vector $u\left(t\right)\in R^{1\times 1}$. State space matrices A and B are constant and submatrices $A_{ij}$ and $B_{ij}$ have appropriate dimensions, $i,j=1,2,3$. The diagonal blocks of matrix A, submatrices $A_{ii}$ define subsystems $x_1\left(t\right)$, $x_2\left(t\right)$, $x_3\left(t\right)$, with coupling between them determined by the non-diagonal elements $A_{ij}$, $i\ne j$. In the following presentation explicit time dependency of the state and input variables is omitted to simplify notation.

Part 1 derivation steps explained in [40] lead to a similarity transformation $\mathbf{L}$, which maps the original system (49) in x coordinates to the upper triangular form in $\eta$ coordinates as outlined bellow

$$\begin{array}{c}\hfill \mathbf{L}=\left[\begin{array}{ccc}I& 0& 0\\ L_3& I& 0\\ L_1& L_2& I\end{array}\right]\to \left[\begin{array}{c}{\eta }_1\\ {\eta }_2\\ {\eta }_3\end{array}\right]=\mathbf{L}\left[\begin{array}{c}{x}_1\\ x_2\\ x_3\end{array}\right],\left[\begin{array}{c}{x}_1\\ x_2\\ x_3\end{array}\right]={\mathbf{L}}^{-1}\left[\begin{array}{c}{\eta }_1\\ {\eta }_2\\ {\eta }_3\end{array}\right]\end{array}$$

(50)

Part 2 transform the upper triangular form of the system to lower-triangular block diagonal form, where intermediate coordinates $\eta$ are mapped to new $\zeta$ coordinates. Transformations between the original x, intermediate $\eta$ and final $\zeta$ coordinates are

$$\begin{array}{c}\hfill \left[\begin{array}{c}{\zeta }_1\\ {\zeta }_2\\ {\zeta }_3\end{array}\right]=T_2\left[\begin{array}{c}{\eta }_1\\ {\zeta }_2\\ {\zeta }_3\end{array}\right]=T_2{T}_1\left[\begin{array}{c}{\eta }_1\\ {\eta }_2\\ {\zeta }_3\end{array}\right]=T_2{T}_1\left[\begin{array}{c}{\eta }_1\\ {\eta }_2\\ {\eta }_3\end{array}\right]=\mathbf{P}\left[\begin{array}{c}{\eta }_1\\ {\eta }_2\\ {\eta }_3\end{array}\right]=\mathbf{PL}\left[\begin{array}{c}{x}_1\\ x_2\\ x_3\end{array}\right]\end{array}$$

(51)

where transformation matrices $T_2$, $T_1$ are defined as

$$\begin{array}{c}\hfill T_2=\left[\begin{array}{ccc}I& -P_1& -P_2\\ 0& I& 0\\ 0& 0& I\end{array}\right],T_1=\left[\begin{array}{ccc}I& 0& 0\\ 0& I& -P_3\\ 0& 0& I\end{array}\right]\end{array}$$

(52)

$\mathbf{L}$ and $\mathbf{P}$ transformations are similarity transformations, so when the system is transformed back to original coordinates x, the system eigenvalues are preserved. Carrying out derivations can be cumbersome and might blur the outline of the multistage design. For a quick reference, those equations are summarized in a table [p. 194] [40]. Solving nonlinear algebraic equations for $L_1,L_2$ is a very challenging task, if possible at all. To overcome this issue, this approach is specialized for three timescale singularly perturbed systems in the form

$$\left[\begin{array}{c}{\dot{x}}_1\\ {\dot{x}}_2\\ {\dot{x}}_3\end{array}\right]=\left[\begin{array}{ccc}\hfill {\widehat{A}}_{11}& \hfill {\widehat{A}}_{12}& \hfill {\widehat{A}}_{13}\\ \hfill \frac{1}{{\epsilon }_1}{\widehat{A}}_{21}& \hfill \frac{1}{{\epsilon }_1}{\widehat{A}}_{22}& \hfill \frac{1}{{\epsilon }_1}{\widehat{A}}_{23}\\ \hfill \frac{1}{{\epsilon }_2}{\widehat{A}}_{31}& \hfill \frac{1}{{\epsilon }_2}{\widehat{A}}_{32}& \hfill \frac{1}{{\epsilon }_2}{\widehat{A}}_{33}\end{array}\right]\left[\begin{array}{c}{x}_1\\ x_2\\ x_3\end{array}\right]+\left[\begin{array}{c}\hfill {\widehat{B}}_{11}\\ \hfill \frac{1}{{\epsilon }_1}{\widehat{B}}_{21}\\ \hfill \frac{1}{{\epsilon }_2}{\widehat{B}}_{31}\end{array}\right]u=x_{s\mathrm{p}}\left[\begin{array}{c}{x}_1\\ x_2\\ x_3\end{array}\right]+B_{s\mathrm{p}}\mathrm{u}$$

(53)

with small positive singular perturbation parameters ${\epsilon }_1\gg {\epsilon }_2\ge 0$. Matrices ${\widehat{A}}_{ij}$ and ${\widehat{B}}_{i1}$ are singularly perturbed matrix elements corresponding to original ones $A_{ij}$ and $B_{i1}$, $i,j=1,2,3$. State vector variables $x\in R^{n\times 1}$, $n=n_1+n_2+n_3$ are split as slow state variables: $x_1\in R^{n_1\times 1}$, fast state variables: $x_2\in R^{n_2\times 1}$, and very fast state variables: $x_3\in R^{n_3\times 1}$. For singularly perturbed system (53), resulting governing equations can be solved by iteration algorithm [40]. $\mathbf{L}$ similarity transformation (50) coefficients $L_1$, $L_2$ and $L_3$ can be determined from the following iterative equations

$$\left.\begin{array}{c}\hfill L_1^{\left(i+1\right)}={\widehat{A}}_{33}^{-1}\left[{\epsilon }_2{L}_1^{\left(i\right)}{\widehat{A}}_{11}+\frac{{\epsilon }_2}{{\epsilon }_1}{L}_2^{\left(i\right)}{\widehat{A}}_{21}+{\widehat{A}}_{31}-\left({\epsilon }_2{L}_1^{\left(i\right)}{\widehat{A}}_{13}+\frac{{\epsilon }_2}{{\epsilon }_1}{L}_2^{\left(i\right)}{\widehat{A}}_{23}\right)L_1^{\left(i\right)}\right]\\ \hfill L_2^{\left(i+1\right)}={\widehat{A}}_{33}^{-1}\left[{\epsilon }_2{L}_1^{\left(i\right)}{\widehat{A}}_{12}+\frac{{\epsilon }_2}{{\epsilon }_1}{L}_2^{\left(i\right)}{\widehat{A}}_{22}+{\widehat{A}}_{32}-\left({\epsilon }_2{L}_1^{\left(i\right)}{\widehat{A}}_{13}+\frac{{\epsilon }_2}{{\epsilon }_1}{L}_2^{\left(i\right)}{\widehat{A}}_{23}\right)L_2^{\left(i\right)}\right]\\ \hfill L_3^{(i+1)}={\left({\widehat{A}}_{22}-{\widehat{A}}_{23}{L}_2^f\right)}^{-1}\left[{\widehat{A}}_{21}-{\widehat{A}}_{23}{L}_1^f-{\epsilon }_1\left(L_3^{\left(i\right)}\left({\widehat{A}}_{12}-{\widehat{A}}_{13}{L}_2^f\right)L_3^{\left(i\right)}-L_3^{\left(i\right)}\left(A_{11}-A_{13}{L}_1^f\right)\right)\right]\end{array}\right\}$$

(54)

where $L_1^f$ and $L_2^f$ are final iteration values determined in the first two equations. $\mathbf{P}$ similarity transformation (52) is determined by solving for $P_1$, $P_2$ and $P_3$ coefficients, from the following iterative equations [40]

$$\left.\begin{array}{c}\hfill P_3^{(i+1)}=\left(\frac{{\epsilon }_2}{{\epsilon }_1}\right)\left({\widehat{A}}_{23}+{\widehat{A}}_2{P}_3^{\left(i\right)}+{\epsilon }_1{L}_3^f{\widehat{A}}_{13}-{\widehat{B}}_2{G}_3\right){\left({\widehat{A}}_3-{\widehat{B}}_3{G}_3\right)}^{-1}\\ \hfill P_2^{(i+1)}={\epsilon }_2\left({\widehat{\alpha }}_{13}+{\widehat{A}}_1{P}_2^{\left(i\right)}\right){\left({\widehat{A}}_3-{\widehat{B}}_3{G}_3\right)}^{-1}\\ \hfill P_1^{(i+1)}={\epsilon }_1\left[{\widehat{A}}_1{P}_1^{\left(i\right)}+{\widehat{\alpha }}_{12}-\frac{1}{{\epsilon }_2}{P}_2^f\left(-{\widehat{B}}_3{G}_2\right)\right]{\left({\widehat{A}}_2-{\widehat{\beta }}_2{G}_2\right)}^{-1}\end{array}\right\}$$

(55)

where $L_3^f$, $P_2^f$ are final iteration values obtained from previous equations. Terms ${\widehat{A}}_1$, ${\widehat{A}}_2$, ${\widehat{A}}_3$, ${\widehat{B}}_2$, ${\widehat{B}}_3$, ${\widehat{\alpha }}_{12}$, ${\widehat{\alpha }}_{13}$ and ${\widehat{\beta }}_2$ are spelled out in the Appendix A.2. Comments on the required computational power needed to solve those iterative equations and achieved precision and convergence rate are provided in [39].

Algorithm 1 Three stage technique implementation

input: Singularly perturbed matrices $A_{sp}$, $B_{sp}$, Equation (53)

output: Equivalent gain for feedback $G_{eq}$

solve for $L_1,L_2$ matrices (54);

solve for $L_3$ matrix (54);

set $G_3$ control gain law with very fast desired eigenvalues ${\lambda }_{veryfast}^d$;

solve for $P_3$ matrix (55);

set $G_2$ control gain law with fast desired eigenvalues $\frac{1}{{\epsilon }_1}{\lambda }_{fast}^d$;

solve for $P_2$ matrix (55);

solve for $P_1$ matrix (55);

set $G_1$ control gain law with slow desired eigenvalues $\frac{1}{{\epsilon }_2}{\lambda }_{slow}^d$;

set equivalent gain $G_{eq}=\left[\begin{array}{ccc}{G}_1& G_2& G_3\end{array}\right]{\mathbf{T}}_{\mathbf{2}}^{\mathbf{f}}{\mathbf{T}}_{\mathbf{1}}^{\mathbf{f}}{\mathbf{L}}^{\mathbf{f}}$;

→ feedback control: $u=-G_{eq}x$;

The presented approach assumes that the following matrices are non-singular (invertible):

• Matrix ${\widehat{A}}_{33}$. This is a standard assumption in singular perturbation analysis [51,52].
• Matrix ${\widehat{A}}_{22}-{\widehat{A}}_{23}{L}_2^f$. If this cannot be satisfied then $L_3$ equation in (54) can be solved iteratively as a sequence of algebraic Sylvester like equations

  $$\begin{array}{cc}\hfill {\widehat{f}}_{21}& ={\epsilon }_1{L}_3\left({\widehat{A}}_{11}-{\widehat{A}}_{13}{L}_1^f\right)+{\widehat{A}}_{21}-{\widehat{A}}_{23}{L}_1^f-{\widehat{A}}_2{L}_3=\hfill \\ \hfill & ={\epsilon }_1{L}_3\left({\widehat{A}}_{11}-{\widehat{A}}_{13}{L}_1^f\right)+{\widehat{A}}_{21}-{\widehat{A}}_{23}{L}_1^f-\left[{\epsilon }_1{L}_3\left({\widehat{A}}_{12}-{\widehat{A}}_{13}{L}_2^f\right)+\left({\widehat{A}}_{22}-{\widehat{A}}_{23}{L}_2^f\right)\right]L_3=0\hfill \end{array}$$

  with initial condition

  $$\begin{array}{c}\hfill \left({\widehat{A}}_{22}-{\widehat{A}}_{23}{L}_2^f\right)L_3^{\left(0\right)}-{\epsilon }_1{L}_3^{\left(0\right)}\left({\widehat{A}}_{11}-{\widehat{A}}_{13}{L}_1^f\right)={\widehat{A}}_{21}-{\widehat{A}}_{23}{L}_1^f\end{array}$$
  Coefficient matrices have eigenvalues of different order $\mathcal{O}\left(eig\left({\widehat{A}}_{22}-{\widehat{A}}_{23}{L}_2^f\right)\right)=\mathcal{O}\left(1\right)$ and $\mathcal{O}\left(eig\left({\widehat{A}}_{11}-{\widehat{A}}_{13}{L}_1^f\right)\right)=\mathcal{O}\left({\epsilon }_1\right)$. Since there are no common eigenvalues a unique solution for $L_3^{\left(0\right)}$ exists [53]. Iteration algorithm for Sylvester like equation is

  $$\begin{array}{c}\hfill \left({\widehat{A}}_{22}-{\widehat{A}}_{23}{L}_2^f\right)L_3^{(i+1)}-{\epsilon }_1{L}_3^{(i+1)}\left({\widehat{A}}_{11}-{\widehat{A}}_{13}{L}_1^f\right)={\widehat{A}}_{21}-{\widehat{A}}_{23}{L}_1^f-{\epsilon }_1{L}_3^{\left(i\right)}\left({\widehat{A}}_{12}-{\widehat{A}}_{12}{L}_2^f\right)L_3^{\left(i\right)}\end{array}$$
  Convergence rate of this algorithm is $\mathcal{O}\left({\epsilon }_1\right)$. After i iterations precision $\mathcal{O}\left({\epsilon }_1^i\right)$ can be achieved $\parallel L_3-L_3^{\left(i\right)}\parallel =\mathcal{O}\left({\epsilon }_1^i\right)$ [40].
• Matrices ${\widehat{A}}_3-{\widehat{B}}_3{G}_3$ and ${\widehat{A}}_2-{\widehat{\beta }}_2{G}_2$. Those matrices are asymptotically stable, so they are always invertible [54]. Feedback controller gains $G_3$ and $G_2$ are chosen such that this is satisfied.

3. Results

3.1. Control-Oriented Transient PEMFC Model: Experimental Validation

Nonlinear model simulation is run for stack current step from $I_{st}=25A$ to $I_{st}=30A$ and compared with experimental data-log for the same stack current step. Model transient response provides a good match overall with the experimental data, as observed in Figure 9 and Figure 10.

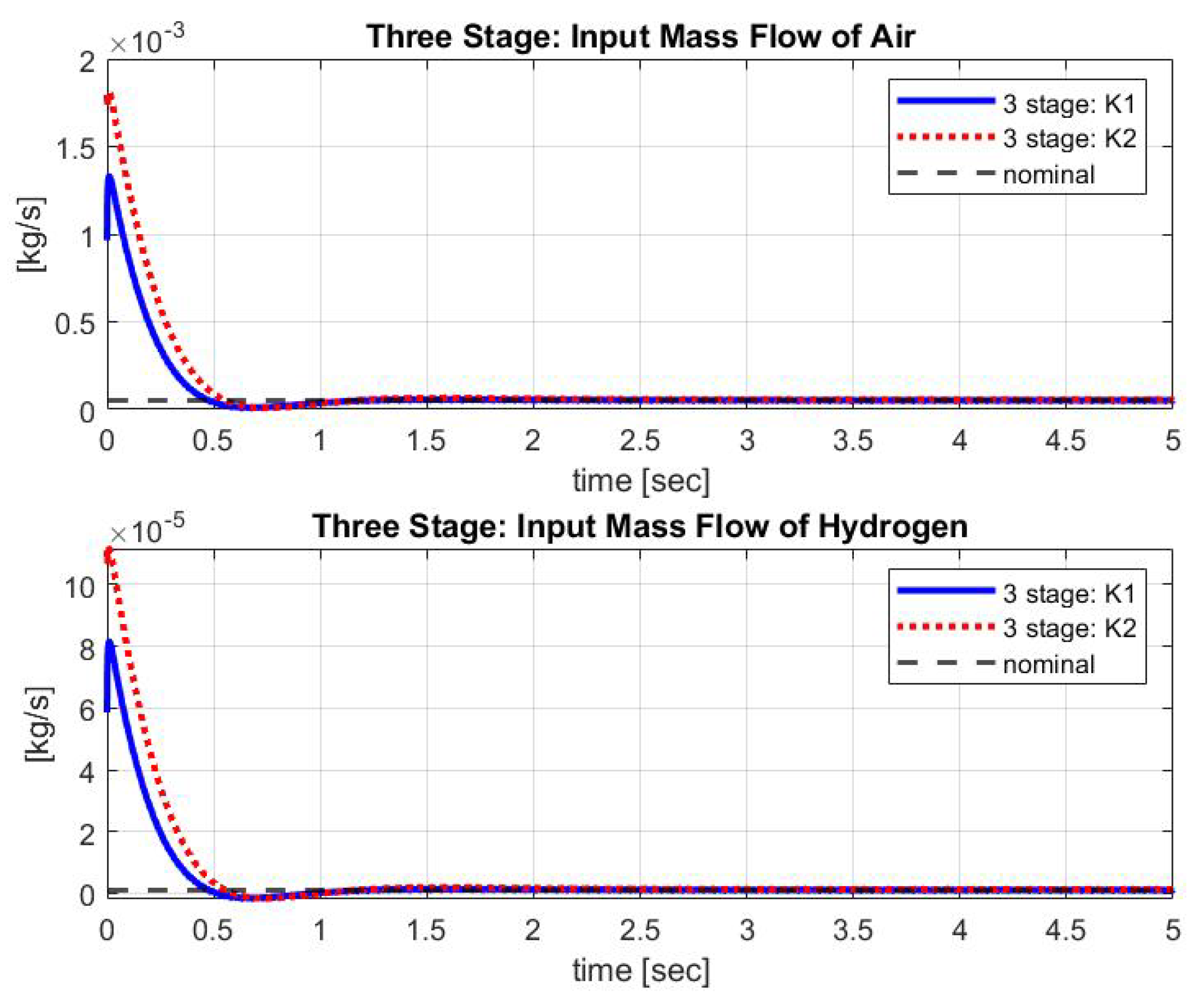
3.2. Multistage Control Technique Application: Simulation Results and Analysis

The developed five-state nonlinear model is linearized around nominal operating point with the following nominal inputs and disturbance values

$$\mathrm{nominal}\mathrm{inputs}:\left[\begin{array}{c}{u}_1^{nom}\\ u_2^{nom}\end{array}\right]=\left[\begin{array}{c}1.18\times {10}^{-6}\\ 5.4\times {10}^{-5}\end{array}\right]\left[\frac{kg}{s}\right]$$

(56)

$$\mathrm{nominal}\mathrm{disturbance}:w^{nom}=I_{st}=25A$$

(57)

The corresponding linear model takes the following standard state space form

$$\left.\begin{array}{c}\hfill \delta \dot{x}=A\delta x+\left[\begin{array}{ccc}{B}_{u_1}& B_{u_2}& B_w\end{array}\right]\left[\begin{array}{c}\delta u_1\\ \delta u_2\\ \delta w\end{array}\right]\\ \hfill \delta y=C_y\delta x+\left[\begin{array}{ccc}{D}_{u_1}& D_{u_2}& D_w\end{array}\right]\left[\begin{array}{c}\delta u_1\\ \delta u_2\\ \delta w\end{array}\right]\end{array}\right\}$$

(58)

The transient model is structured to have two inputs, but the multistage control technique is applicable to single input systems. A dual input system can be reduced for simulation purposes to a single input system as

$$\left.\begin{array}{c}\hfill \delta \dot{x}=A\delta x+B_{u_1}\delta u_1\\ \hfill \delta y=C_y\delta x+D_{u_1}\delta u_1\end{array}\right\}$$

(59)

System input $u_2$ is calculated from relation $u_2=c_{fit}·u_1$, where $c_{fit}$ is the fitting constant. Simulation results in Figure 11, Figure 12 and Figure 13 are obtained from the following model

$$\left.\begin{array}{c}\hfill \delta \dot{x}=A\delta x+\left[\begin{array}{cc}{B}_{u_1}& B_{u_2}\end{array}\right]\left[\begin{array}{c}\delta u_1\\ c_{fit}·\delta u_1\end{array}\right]\\ \hfill \delta y=C_y\delta x+\left[\begin{array}{cc}{D}_{u_1}& D_{u_2}\end{array}\right]\left[\begin{array}{c}\delta u_1\\ c_{fit}·\delta u_1\end{array}\right]\end{array}\right\}$$

(60)

where the state space matrices are given in Appendix A. Nominal states values for the linearization are

$$x^{nom}={\left[\begin{array}{ccccc}{m}_{O_2}^{nom}& m_{N_2}^{nom}& m_{H_2}^{nom}& m_{v,an}^{nom}& m_{v_{ca}}^{nom}\end{array}\right]}^T=$$

$$=\left[\begin{array}{ccccc}1.52·{10}^{-6}& 9.93·{10}^{-6}& 7.87·{10}^{-7}& 7.55·{10}^{-7}& 2.00·{10}^{-6}\end{array}\right]\left[kg\right]$$

(61)

Three Stage Control Technique

Original eigenvalues of the linearized system are

$$\begin{array}{c}\hfill \lambda =\left[-1.238,-2.827,-3.578,-193.830,-1179.733\right]\end{array}$$

(62)

This system has a three timescale structure. There are three clusters of eigenvalues present and grouped as

$$\begin{array}{c}\hfill \lambda =\left[\begin{array}{c}\underset{\mathrm{slow}}{\underbrace{-1.238}},\underset{\mathrm{fast}}{\underbrace{-2.827,-3.578}},\underset{\mathrm{very}\mathrm{fast}}{\underbrace{-193.830,-1179.733}}\end{array}\right]\end{array}$$

(63)

Small perturbation parameters are defined as

$$\begin{array}{c}\hfill {\epsilon }_1=\frac{|-1.238|}{|-2.827|}=0.4378,{\epsilon }_2=\frac{|-1.238|}{|-193.8303|}=0.0064\end{array}$$

(64)

Permutation matrix V puts the original system matrix A (given in the Appendix A) in the explicit singularly perturbed form provided in (53), where $A_{sp}=VA{V}^T$. One randomly chosen permutation matrix V solution has the following form

$$\begin{array}{c}\hfill V=\left[\begin{array}{ccccc}0& 0& 1& 0& 0\\ 1& 0& 0& 0& 0\\ 0& 0& 0& 0& 1\\ 0& 1& 0& 0& 0\\ 0& 0& 0& 1& 0\end{array}\right]\end{array}$$

(65)

Solving (54) for $L_1^f$, $L_2^f$ and $L_3^f$ provides

$$\left.\begin{array}{c}\hfill L_1^f=\left[\begin{array}{c}0.0006\\ 0.0030\end{array}\right],L_2^f=\left[\begin{array}{cc}0.8746& 1.5544\\ 0.0000& -0.3820\end{array}\right]\\ \hfill L_3^f=\left[\begin{array}{c}-0.0463\\ 0.2209\end{array}\right]\end{array}\right\}$$

(66)

Let us consider the pole-placement design of two possible controllers $K_1$ and $K_2$ design with no particular performance goal in mind. For controller $K_1$ desired eigenvalues positions are selected as

$$\begin{array}{c}\hfill {\lambda }_{des}=\left[\begin{array}{c}\underset{\mathrm{slow}\mathrm{desired}}{\underbrace{-4}},\underset{\mathrm{fast}\mathrm{desired}}{\underbrace{-6,-10}},\underset{\mathrm{very}\mathrm{fast}\mathrm{desired}}{\underbrace{-50,-100}}\end{array}\right]\end{array}$$

(67)

By using MATLAB place command, the following gains values are obtained

$$\left.\begin{array}{cc}\hfill \mathrm{slow}:G_1& =\mathrm{place}(A_1,{\beta }_1,\mathrm{slow}\mathrm{desired})=\left[\begin{array}{c}-151.1523\end{array}\right]\hfill \\ \hfill \mathrm{fast}:G_2& =\mathrm{place}\left(A_2,{\beta }_2,\frac{\mathrm{fast}\mathrm{desired}}{{\epsilon }_1}\right)=\left[\begin{array}{cc}-4.0862& -7.6311\end{array}\right]\hfill \\ \hfill \mathrm{very}\mathrm{fast}:G_3& =\mathrm{place}\left(A_3,B_3,\frac{\mathrm{very}\mathrm{fast}\mathrm{desired}}{{\epsilon }_2}\right)=\left[\begin{array}{cc}36.5238& -59.0113\end{array}\right]\hfill \end{array}\right\}$$

(68)

Solving (55) for $P_3^f$, $P_2^f$ and $P_1^f$ provides

$$P_1^f=\left[\begin{array}{cc}0.0319& 0.0388\end{array}\right],P_2^f=\left[\begin{array}{cc}-0.0001& -0.0012\end{array}\right],P_3^f=\left[\begin{array}{cc}0.2159& -1.4828\\ 0.0298& 0.5847\end{array}\right]$$

(69)

For controller $K_2$ the desired eigenvalues positions are chosen as

$$\begin{array}{c}\hfill {\lambda }_{des}=\left[\begin{array}{c}\underset{\mathrm{slow}\mathrm{desired}}{\underbrace{-3}},\underset{\mathrm{fast}\mathrm{desired}}{\underbrace{-20\pm 0.5·i}},\underset{\mathrm{very}\mathrm{fast}\mathrm{desired}}{\underbrace{-40,-80}}\end{array}\right]\end{array}$$

(70)

By using MATLAB place command, the following gains values are obtained

$$\left.\begin{array}{cc}\hfill \mathrm{slow}:G_1=& \mathrm{place}(A_1,{\beta }_1,\mathrm{slow}\mathrm{desired})=\left[\begin{array}{c}-516.0858\end{array}\right]\hfill \\ \hfill \mathrm{fast}:G_2=& \mathrm{place}\left(A_2,{\beta }_2,\frac{\mathrm{fast}\mathrm{desired}}{{\epsilon }_1}\right)=\left[\begin{array}{cc}-44.0928& -64.2397\end{array}\right]\hfill \\ \hfill \mathrm{very}\mathrm{fast}:G_3=& \mathrm{place}\left(A_3,B_3,\frac{\mathrm{very}\mathrm{fast}\mathrm{desired}}{{\epsilon }_2}\right)=\left[\begin{array}{cc}36.793& -73.9818\end{array}\right]\hfill \end{array}\right\}$$

(71)

Solving (55) for $P_3^f$, $P_2^f$ and $P_1^f$ provides

$$P_1^f=\left[\begin{array}{cc}0& 0\end{array}\right],P_2^f=\left[\begin{array}{cc}-3.354\times {10}^{-5}& -0.0031\end{array}\right],P_3^f=\left[\begin{array}{cc}0.239& -3.208\\ 0.012& 1.851\end{array}\right]$$

(72)

4. Discussion & Conclusions

4.1. Control-Oriented Transient PEMFC Model

Control-oriented state space PEMFC model development enables us to better understand the PEMFC modeled dynamics, get insight what are the operating challenges and to do in depth analysis. Model is set up in a standard state space form so that wider engineering and scientific community can use it as a framework for design and implement new control techniques that may lead to more efficient and more durable PEMFC systems. The control-oriented model features to be highlighted are:

• A complex physical system is represented by simple, but a realistic model, without overwhelming details. Following this modeling approach, scientist equipped with such a model can have full focus on designing a control strategies and controllers for the most dominant effects and study them theoretically and experimentally with less efforts.
• In this model setup stack current is treated as a measured disturbance. The stack current is the fastest physical variable and it can be used in various control designs, with accent on feedforward control approaches, which one possible future research direction.
• Since the inlet relative humidity is included in the model, it can be manipulated (controlled) to improve the water management in the stack, which is crucial for the correct operation of the fuel cell.
• The presented logic model can be easily expanded. Flexibility is important, because for example, if a researcher wants to focus on the analysis in the higher current densities operational range, one might want to consider adding extra states which represent liquid phase generated water.
• The system is in state space form, which enables us to perform controllability and observability analysis.

Future work: Future research directions would be derivation of aging dynamics and incorporating it in the presented model with the intention of developing a useful diagnostic tool for PEMFC stack health monitoring. Possible future work includes integration of the developed PEMFC stack model with the hydrogen gas processing system.

4.2. Multistage Control Technique Application

With the proposed multistage control technique developed and elaborated in detail in [40], different types of state feedback controllers may be designed to control different subsystems. These local feedback controllers can stabilize certain subsystems of interest only, while the rest of the subsystems are seamlessly not affected at all. The notable features of the proposed technique are:

• Similarity transformations $\mathbf{L}$ and $\mathbf{P}$ preserve the controllability/observability property of the full system. If the original full-order system is controllable/observable then local systems will also be controllable/observable.
• The original full-order system is decoupled in several subsystems, each with the unique timescale. A composite feedback controller applied to the full-order system is constructed with different state feedback controllers: eigenvalue assignment, optimal, robust, etc.
• Computational costs are significantly reduced because all calculations are done with reduced order matrices where numerical ill-conditioning of higher order matrices is completely avoided. Instead, very high accuracy can be achieved by using iteration algorithms to solve nonlinear algebraic equations.
• Partial full-state feedback and partial output feedback (for subsystem for which only the output is available for feedback) can be implemented through this design. If certain subsystem does not need to be controlled, the gain for that subsystem is set to zero. The gains of the other subsystems are set accordingly and combined in the composite feedback matrix.

The multistage control technique is a state feedback technique, so the states need to be available for feedback. The PEMFC derived system model has states which are not measurable, but observable and the state space form enables us to do the observability analysis. Due to multiple time scales nature it is a great challenge to design an adequate observer to estimate unavailable states, if the system is observable at all. Research in that direction, where linear observers for systems with slow and fast modes are considered, could be found in [55]. On the other hand, if multistage design technique is used, then observers could be constructed at subsystems level, which simplifies the design. In the review paper [30], some possible mitigation strategies are suggested: system intake control, nitrogen governing, purging strategy, etc. This approach in controlling large scale systems with multiple time scales is applied to nuclear reactors [56]. Future work: Our group specialized this design for 2 timescale systems [57] and expanded the work to 3 timescale systems [39,58]. The multistage design framework is quite universal and future research directions could include the possible expansion to 4 timescale systems, which is already outlined in [59]. Also, it will be interesting to study how observers affect optimality when optimal controllers are used at subsystem levels [60].