A Coupled-Inductor DC-DC Converter with Input Current Ripple Minimization for Fuel Cell Vehicles
Abstract
:1. Introduction
2. Topology
3. Analysis of Operating Principles and Characteristics
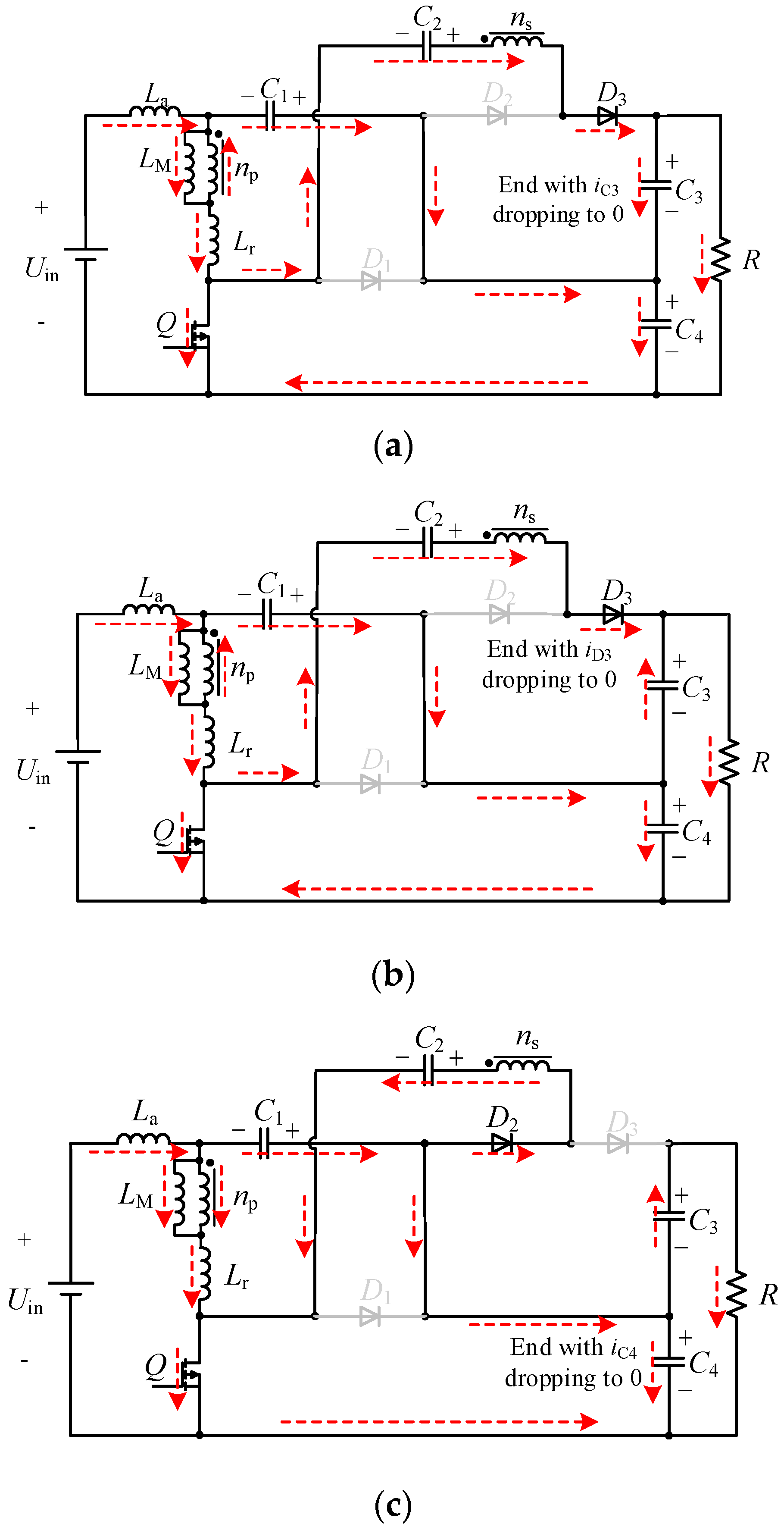
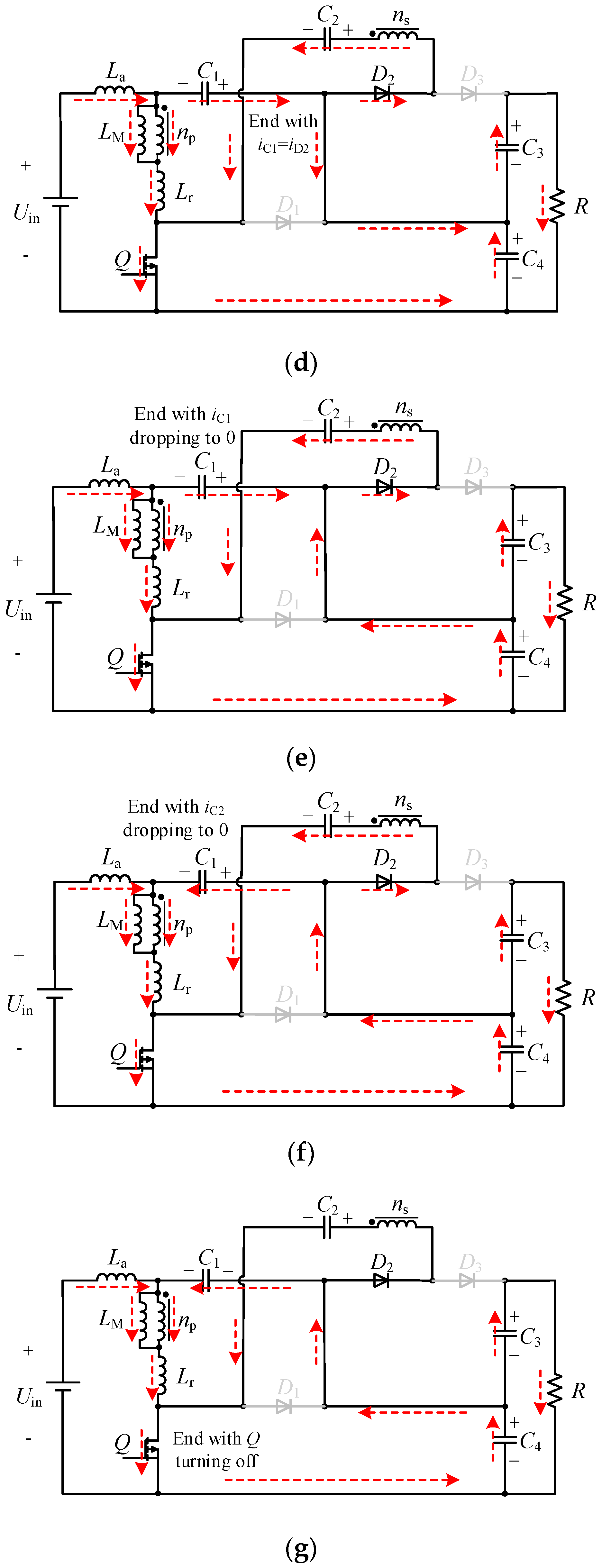
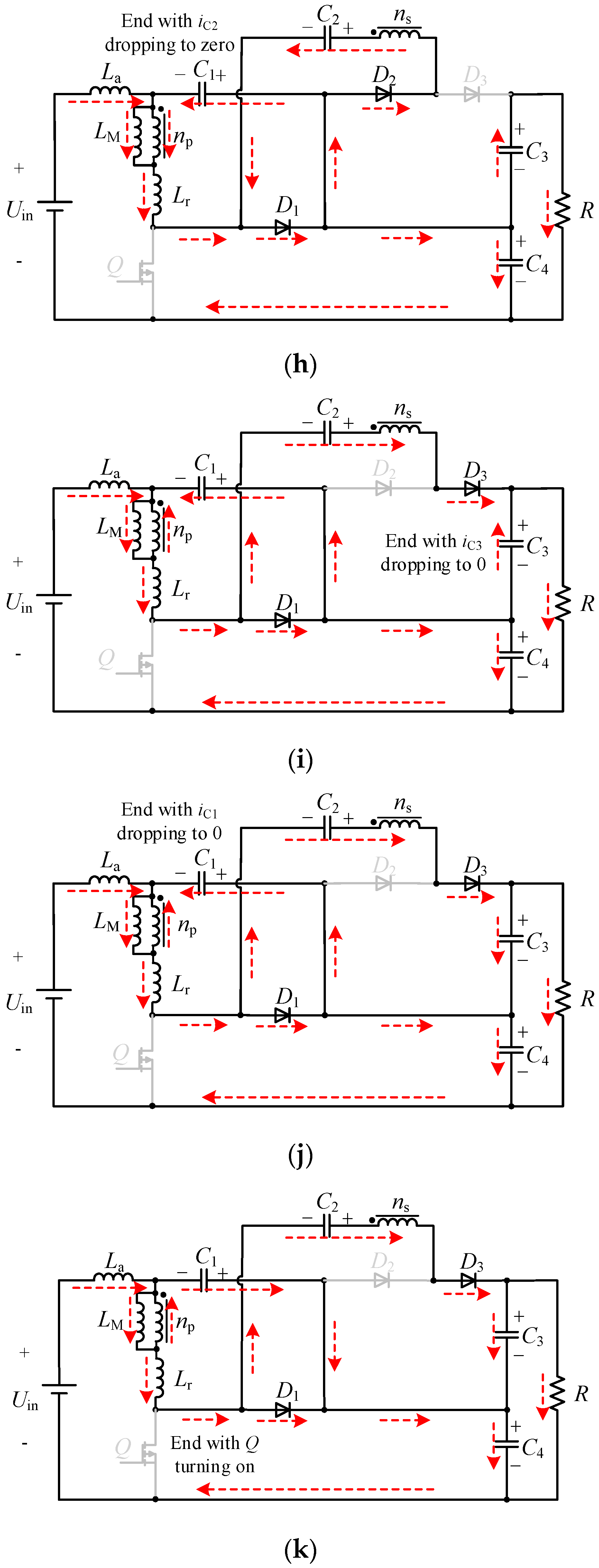
3.1. Operating Principles
3.2. Analysis of Ripple Minimization Characteristics
3.3. Voltage Gain Analysis
3.4. Analysis of Passive Lossless Clamping Circuit
4. Voltage and Current Stresses and Performance Comparisons
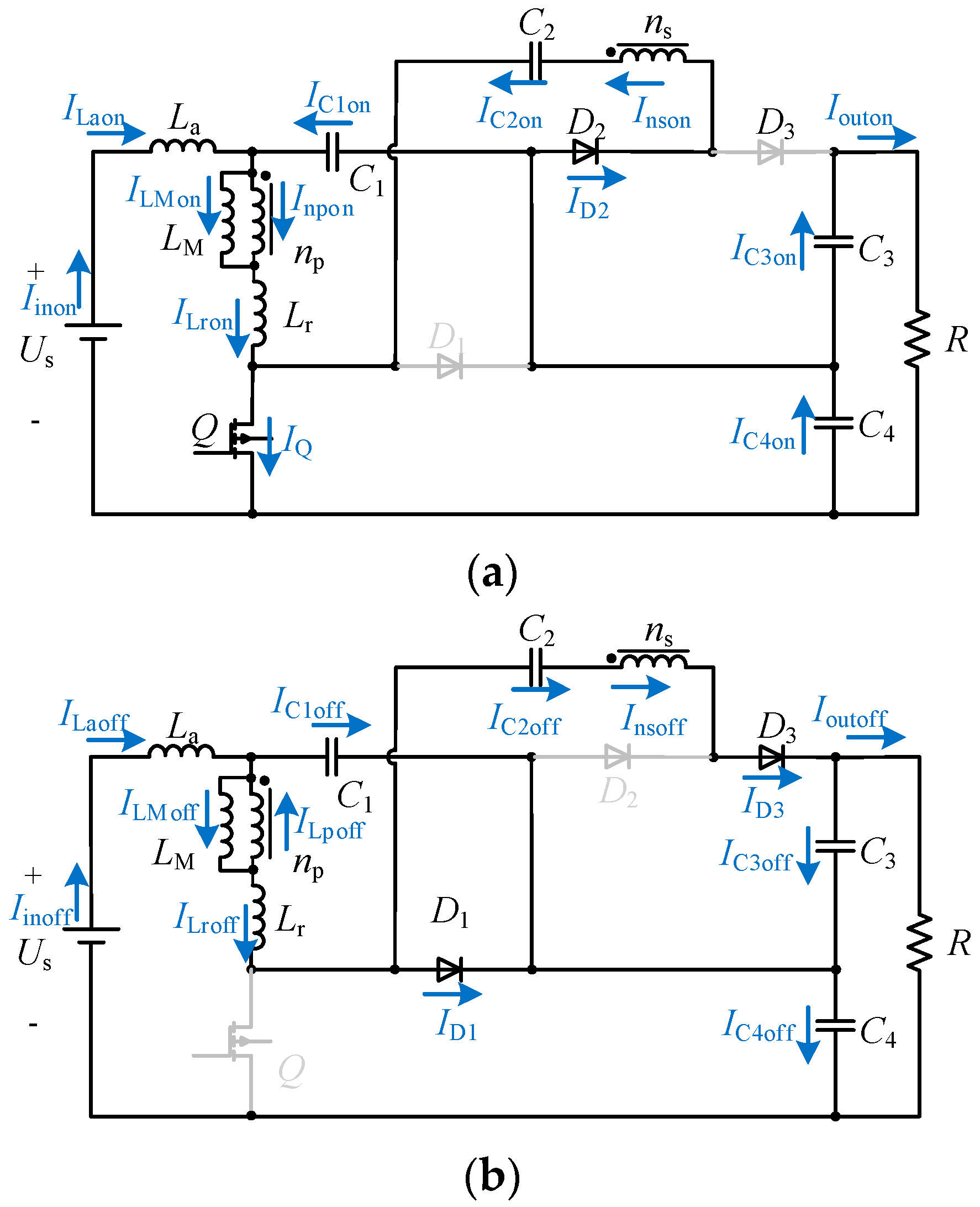
4.1. Voltage Stresses
4.2. Current Stresses
4.3. Performance Comparisons
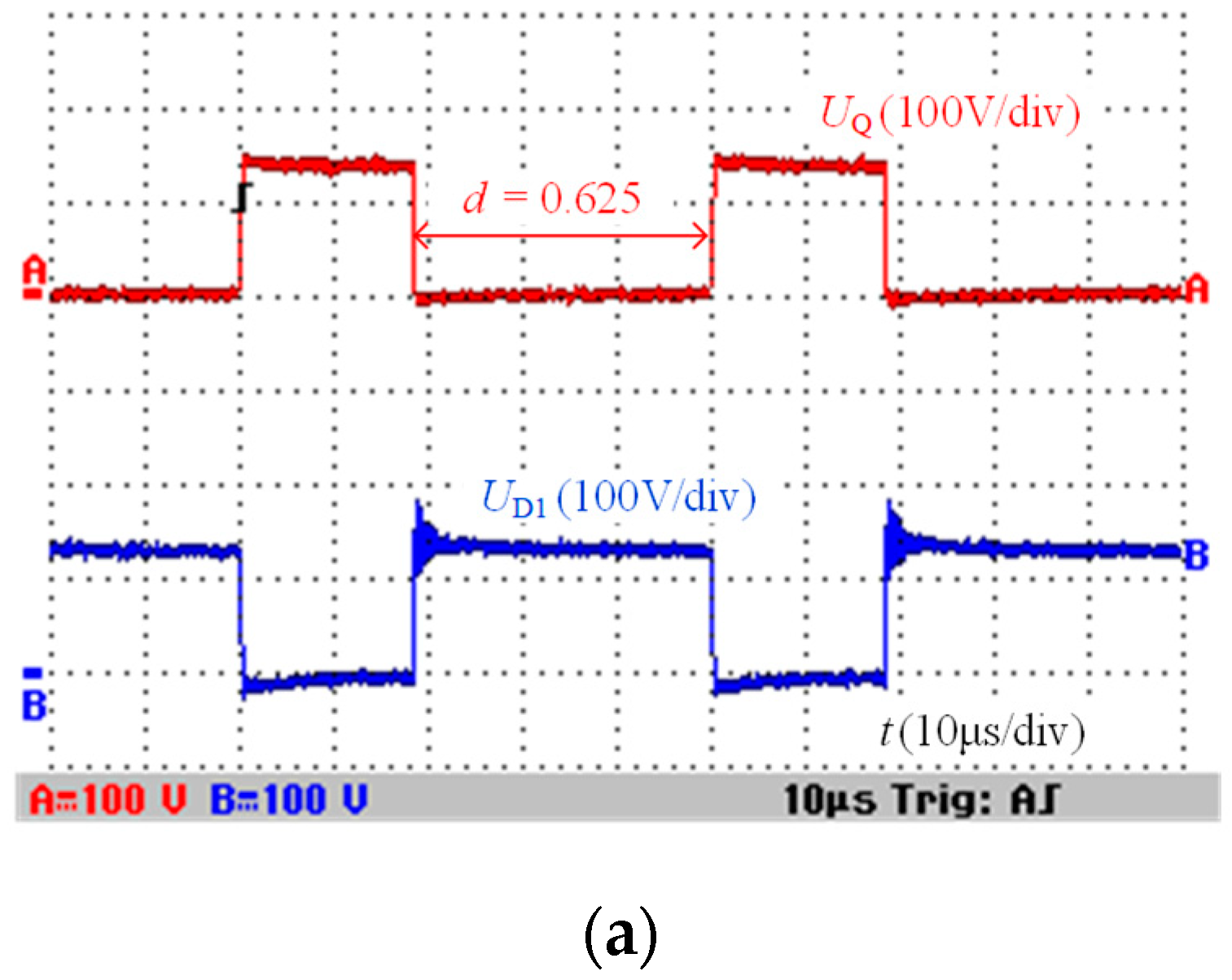
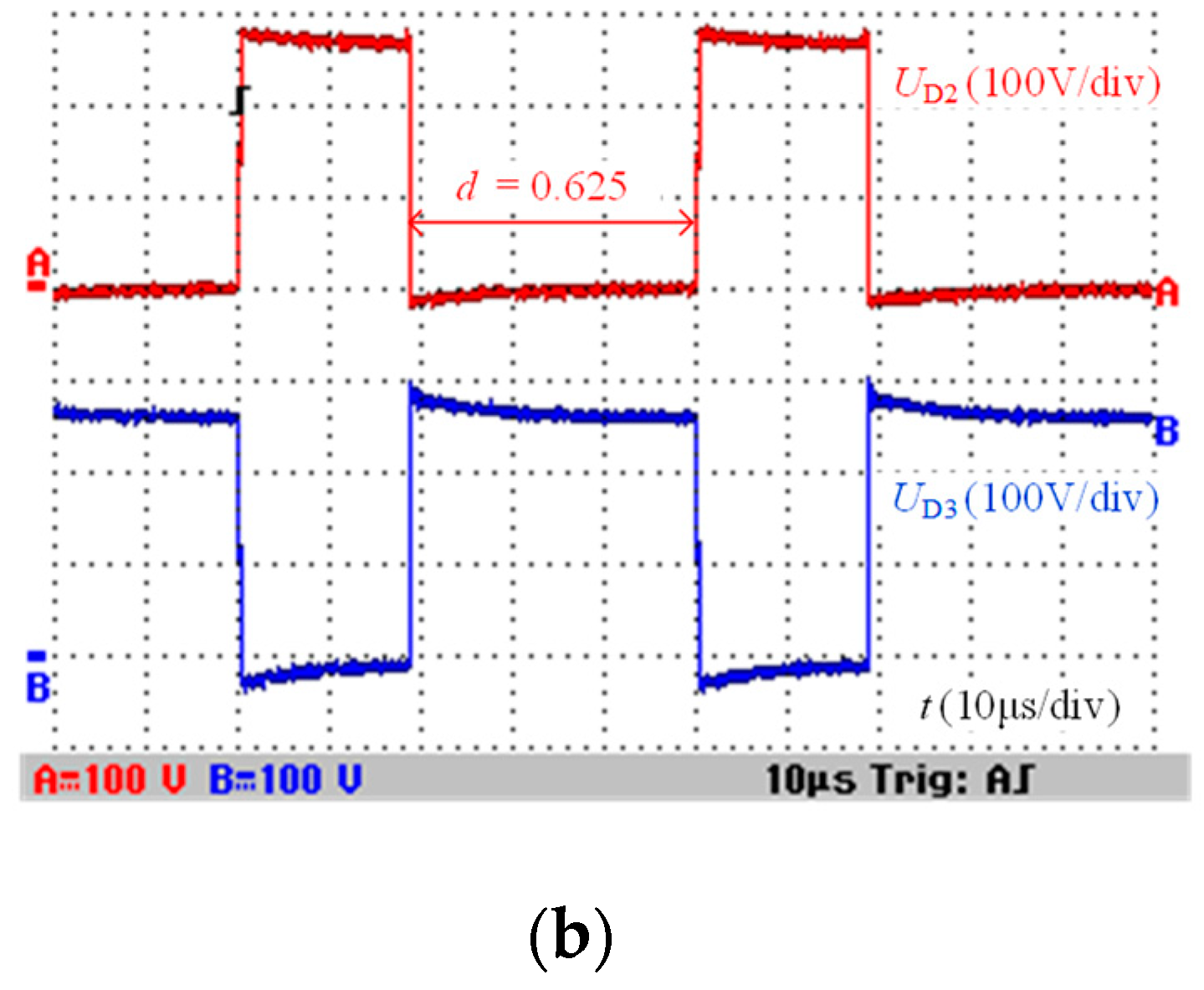
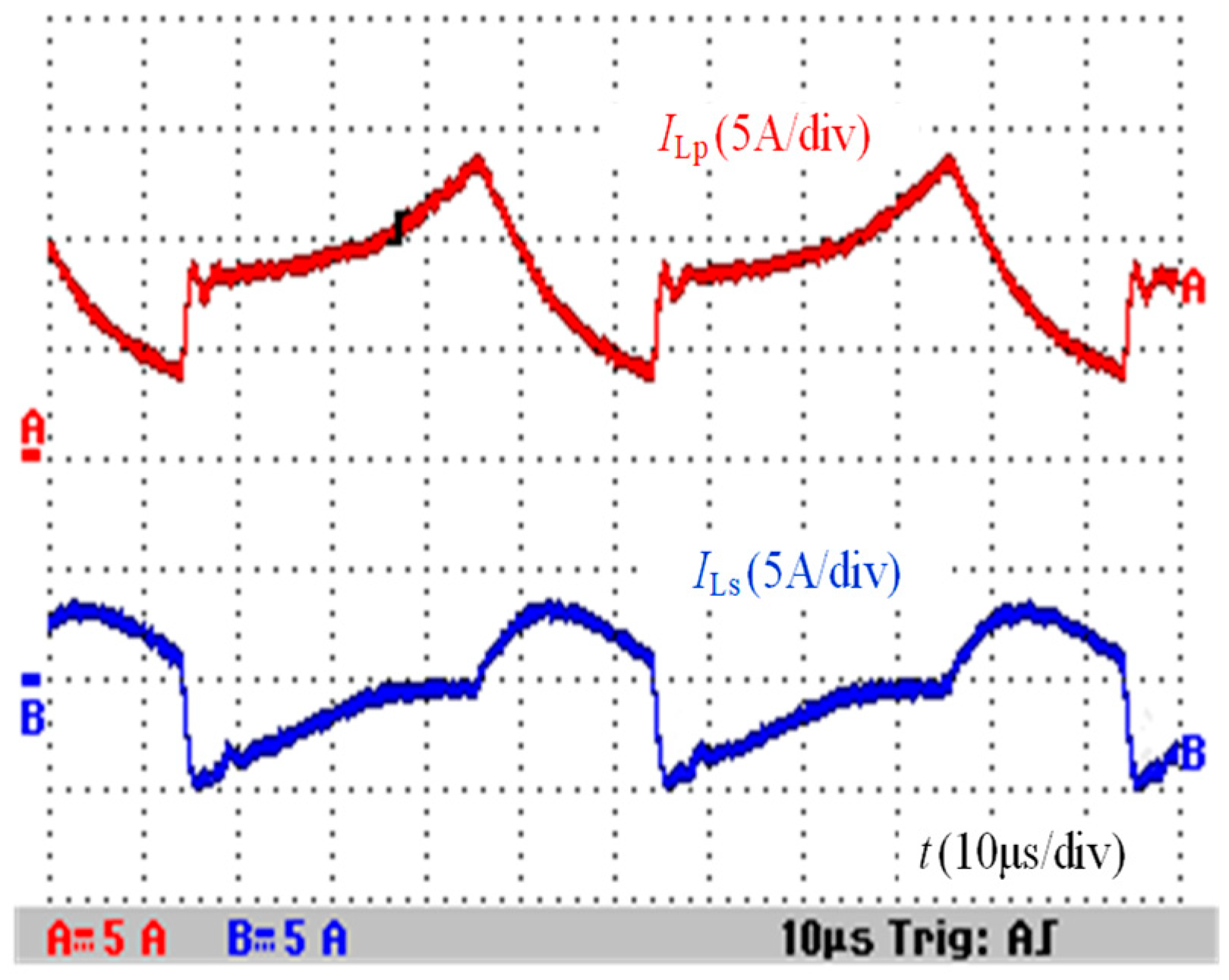
5. Experimental Results and Analysis
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Khaligh, A.; Li, Z. Battery, ultracapacitor, fuel cell, and hybrid energy storage systems for electric, hybrid electric, fuel cell, and plug-in hybrid electric vehicles: State of the art. IEEE Trans. Veh. Technol. 2016, 59, 2806–2814. [Google Scholar] [CrossRef]
- Bahroon, D.A.; Rahman, H.A. Performance evaluation of solar-fossil fuel-hybrid parabolic trough power plant in Yemen under different fuel types. In Proceedings of the 2014 IEEE Conference on Energy Conversion (CENCON), Johor Bahru, Malaysia, 13–14 October 2014; pp. 158–163. [Google Scholar]
- Zeng, B.; Zhang, J.; Yang, X.; Wang, J.; Dong, J.; Zhang, Y. Integrated planning for transition to low-carbon distribution system with renewable energy generation and demand response. IEEE Trans. Power Syst. 2014, 29, 1153–1165. [Google Scholar] [CrossRef]
- Boulanger, A.G.; Chu, A.C.; Maxx, S.; Waltz, D.L. Vehicle electri- fication: Status and issues. Proc. IEEE. 2011, 99, 1116–1138. [Google Scholar] [CrossRef]
- Li, K.; Chen, T.; Luo, Y.; Wang, J. Intelligent environment-friendly vehicles: concept and case studies. IEEE Trans. Intell. Transp. Syst. 2011, 13, 318–328. [Google Scholar] [CrossRef]
- Jin, J.X.; Chen, X.Y.; Wen, L.; Wang, S.C.; Xin, Y. Cryogenic power conversion for SMES application in a liquid hydrogen powered fuel cell electric vehicle. IEEE Trans. Appl. Supercond. 2015, 25, 1–11. [Google Scholar]
- Su, W.; Rahimi-Eichi, H.; Zeng, W.; Chow, M.-Y. A survey on the electrification of transportation in a smart grid environment. IEEE Trans Ind. Informat. 2012, 8, 1–10. [Google Scholar] [CrossRef]
- Jiang, W.; Fahimi, B. Active current sharing and source management in fuel cell-battery hybrid power system. IEEE Trans. Ind. Electron. 2010, 57, 752–761. [Google Scholar] [CrossRef]
- Restrepo, C.; Konjedic, T.; Guarnizo, C.; Aviñó-Salvadó, O.; Calvente, J.; Romero, A.; Giral, R. Simplified mathematical model for calculating the oxygen excess ratio of a PEM fuel cell system in real-time applications. IEEE Trans. Ind. Electron. 2014, 61, 2816–2825. [Google Scholar] [CrossRef]
- Rathore, A.K.; Bhat, A.K.S.; Oruganti, R. Analysis, design and experimental results of wide range ZVS active-clamped L-L type currentfed DC-DC converter for fuel cell to utility interface application. IEEE Trans. Ind. Electron. 2012, 59, 473–485. [Google Scholar] [CrossRef]
- Jang, M.; Agelidis, V.G. A boost-inverter-based, battery-supported, fuel-cell sourced three-phase stand-alone power supply. IEEE Trans. Power Electron. 2014, 29, 6472–6480. [Google Scholar] [CrossRef]
- Tseng, K.C.; Lin, J.T.; Huang, C.C. High step-up converter with three-winding coupled inductor for fuel cell energy source applications. IEEE Trans. Power Electron. 2015, 30, 574–581. [Google Scholar] [CrossRef]
- Wang, P.; Zhao, C.; Zhang, Y.; Li, J.; Gao, Y. A bidirectional three-level dc-dc converter with a wide voltage conversion range for hybrid energy source electric vehicles. J. Power Electron. 2017, 17, 334–345. [Google Scholar] [CrossRef]
- Qian, W.; Cao, D.; Cintron-Rivera, J.G.; Gebben, M.; Wey, D.; Peng, F.Z. A switched-capacitor DC-DC converter with high voltage gain and reduced component rating and count. IEEE Trans. Ind. Appl. 2012, 48, 1397–1406. [Google Scholar] [CrossRef]
- Wu, B.; Li, S.; Smedley, K.; Singer, S. A family of two-switch boosting switched-capacitor converters. IEEE Trans. Power Electron. 2015, 30, 5413–5424. [Google Scholar] [CrossRef]
- Wai, R.J.; Duan, R.Y. High step-up converter with coupled-inductor. IEEE Trans. Power Electron. 2005, 20, 1025–1035. [Google Scholar] [CrossRef]
- Yang, L.S.; Liang, T.J.; Lee, H.C.; Chen, J.F. Novel high step-up DC-DC converter with coupled-inductor and voltage-doubler circuits. IEEE Trans. Ind. Electron. 2011, 58, 4196–4206. [Google Scholar] [CrossRef]
- Ajami, A.; Ardi, H.; Farakhor, A. A novel high step-up DC/DC converter based on integrating coupled inductor and switched-capacitor techniques for renewable energy applications. IEEE Trans. Power Electron. 2015, 30, 4255–4263. [Google Scholar] [CrossRef]
- Dwari, S.; Parsa, L. An efficient high-step-up interleaved DC-DC converter with a common active clamp. IEEE Trans. Power Electron. 2011, 26, 66–78. [Google Scholar] [CrossRef]
- Zhao, Y.; Li, W.; Deng, Y.; He, X. High step-up boost converter with passive lossless clamp circuit for non-isolated high step-up applications. IET Trans. Power Electron. 2011, 4, 851–859. [Google Scholar] [CrossRef]
- Thounthong, P.; Sethakul, P.; Davat, B. Modified 4-phase interleaved fuel cell converter for high-power high-voltage applications. In Proceedings of the 2009 IEEE International Conference on Industrial Technology, Gippsland, VIC, Australia, 10–13 February 2009. [Google Scholar]
- Hu, X.; Gong, C. A high gain input-parallel output-series DC/DC converter with dual coupled inductors. IEEE Trans. Power Electron. 2015, 30, 1306–1317. [Google Scholar] [CrossRef]
- Tan, S.-C.; Kiratipongvoot, S.; Bronstein, S.; Ioinovici, A.; Lai, Y.M.; Tse, C.K. Adaptive mixed on-time and switching frequency control of a system of interleaved switched-capacitor converters. IEEE Trans. Power Electron. 2011, 26, 364–380. [Google Scholar] [CrossRef]
- Tseng, K.-C.; Huang, C.-C. High step-up high-efficiency interleaved converter with voltage multiplier module for renewable energy system. IEEE Trans. Ind. Electron. 2014, 61, 1311–1319. [Google Scholar] [CrossRef]
- Zhan, Y.; Guo, Y.; Zhu, J.; Li, L. Performance comparison of input current ripple reduction methods in UPS applications with hybrid PEM fuel cell/supercapacitor power sources. Int. J. Electr. Power Energy Syst. 2015, 64, 96–103. [Google Scholar] [CrossRef]
- Zhan, Y.; Guo, Y.; Zhu, J.; Li, L. Input current ripple reduction and high efficiency for PEM fuel cell power conditioning system. In Proceedings of the 2017 20th International Conference on Electrical Machines and Systems (ICEMS), Sydney, NSW, Australia, 11–14 August 2017. [Google Scholar]
- Paja, C.A.R.; Arango, E.; Giral, R.; Montesa, A.J.S.; Carrejo, C. DC/DC pre-regulator for input current ripple reduction and efficiency improvement. Elect. Power Syst. Res. 2011, 81, 2048–2055. [Google Scholar] [CrossRef]
- Shi, Y.; Liu, B.; Duan, S. Low-frequency input current ripple reduction based on load current feedforward in a two-stage single-phase inverter. IEEE Trans. Power Electron. 2016, 31, 7972–7985. [Google Scholar] [CrossRef]
- Chen, Z.; Xu, J. High boost ratio DC-DC converter with ripple-free input current. Electron. Lett. 2014, 50, 353–355. [Google Scholar] [CrossRef]







| Characteristics | Converter in [29] | Proposed Converter |
|---|---|---|
| Voltage Gain | ||
| Voltage Stress of power switch | ||
| Voltage Stress of diodes | ||
| Current Stress of power switch | ||
| Current Stress of diodes | ||
| Number of power switches | 1 | 1 |
| Number of diodes | 2 | 3 |
| Ripple-minimization input current | Yes | Yes |
| Parameters | Values |
|---|---|
| Rated power Pn | 400 W |
| Switching frequency fs | 20 kHz |
| Capacitor C1 | 270 μF |
| Capacitors C2, C3, and C4 | 540 μF |
| Inductor La | 241 μH |
| Magnetizing inductor LM | 368 μH |
| Leakage inductance Lr | 3.25 μH |
| Turns ratio np:ns | 1:1 |
| Output voltage Uout | 400 V |
| Input voltage Uin | 30–100 V |
| Power switch Q | IXTH88N30P |
| Diodes D1–D3 | DPG60C300HB |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yan, F.; Li, J.; Du, C.; Zhao, C.; Zhang, W.; Zhang, Y. A Coupled-Inductor DC-DC Converter with Input Current Ripple Minimization for Fuel Cell Vehicles. Energies 2019, 12, 1689. https://doi.org/10.3390/en12091689
Yan F, Li J, Du C, Zhao C, Zhang W, Zhang Y. A Coupled-Inductor DC-DC Converter with Input Current Ripple Minimization for Fuel Cell Vehicles. Energies. 2019; 12(9):1689. https://doi.org/10.3390/en12091689
Chicago/Turabian StyleYan, Fuwu, Jingyuan Li, Changqing Du, Chendong Zhao, Wei Zhang, and Yun Zhang. 2019. "A Coupled-Inductor DC-DC Converter with Input Current Ripple Minimization for Fuel Cell Vehicles" Energies 12, no. 9: 1689. https://doi.org/10.3390/en12091689
APA StyleYan, F., Li, J., Du, C., Zhao, C., Zhang, W., & Zhang, Y. (2019). A Coupled-Inductor DC-DC Converter with Input Current Ripple Minimization for Fuel Cell Vehicles. Energies, 12(9), 1689. https://doi.org/10.3390/en12091689






