Voltage Support under Grid Faults with Inherent Current Limitation for Three-Phase Droop-Controlled Inverters

Abstract

A novel nonlinear current-limiting controller for three-phase grid-tied droop-controlled inverters that is capable of offering voltage support during balanced and unbalanced grid voltage drops is proposed in this paper. The proposed controller introduces a unified structure under both normal and abnormal grid conditions operating as a droop controller or following the recent fault-ride-through requirement to provide voltage support. In the case of unbalanced faults, the inverter can further inject or absorb the required negative sequence real and reactive power to eliminate the negative sequence voltage at the point of common coupling (PCC) whilst ensuring at all times boundedness for the grid current. To accomplish this task, a novel and easily implementable method for dividing the available current into the two sequences (positive and negative) is proposed, suitably adapting the proposed controller parameters. Furthermore, nonlinear input-to-state stability theory is used to guarantee that the total grid current remains limited below its given maximum value under both normal and abnormal grid conditions. Asymptotic stability for any equilibrium point of the closed-loop system in the bounded operating range is also analytically proven for first time using interconnected-systems stability analysis irrespective of the system parameters. The proposed control concept is verified using an OPAL-RT real-time digital simulation system for a three-phase inverter connected to the grid.

1. Introduction

In the recent years, the smart inverter concept has attracted a lot of attention since its adaptability and plug and play properties enable the seamless integration of distributed energy resources (DERs) into the next generation smart grid [1]. In order to implement these features whilst ensuring a stable and reliable power system, the design of advanced control techniques for the inverter-interfaced DERs is of major significance.

Among the various control approaches for the inverter-interfaced DERs connected to the main grid, “droop control” represents the most widely used method since it provides support of the grid voltage and frequency and can be also used to achieve power sharing between several DERs [2]. However, the droop control approach introduces nonlinear dynamics due to the real and reactive power calculation and thus closed-loop system stability becomes a challenging task. To improve the stability of the system, a virtual impedance or resistance is usually considered in the control design [3,4] while small-signal modeling combined with root-locus analysis is usually employed to obtain theoretical stability results for the closed-loop system [5]. Nevertheless, the closed-loop system stability analysis of droop-controlled inverters without assuming knowledge of the grid and inverter parameters still represents a challenging problem for control and power system researchers.

Droop control and system stability are often analyzed in the literature under normal grid conditions. When sudden grid voltage drops occur, the raised overcurrents may harm the DERs or lead to instant tripping of the inverters. However, the tripping scenario is against the recent fault-ride-through (FRT) requirement that demands from the DERs to support the faulty grids [5,6,7,8]. Hence, current-limiting techniques should be embedded in the control design of every inverter-interfaced DER to allow maximum power injection and avoid undesired tripping [9,10,11]. In voltage-controlled inverters, saturated integrators in the inner control loops are usually employed to accomplish the desired current limitation; however these units may suffer from integrator wind-up and eventually lead to instability [10,12]. Other control techniques consider a switching to a different current-limiting controller under abnormal grid conditions. Nevertheless, such a switching operation can still result in integrator wind-up or force the controller to latch-up [13]. Since the virtual impedance or resistance concept offers a promising solution to overcome these instability issues and achieve a current limitation property [12,14], in [15,16] a current-limiting droop controller has been presented for single-phase and three-phase inverters, respectively, where no switching actions or saturated integrators are used for the current limitation.

Under balanced fault conditions, the limitation of the total current and the maximum power injection for supporting the grid are the two main tasks of the inverter. However, when unbalanced faults appear at the grid, the selection of the appropriate strategy to optimally provide grid support is a complicated problem [17,18]. Significant amount of research has addressed the inverter response through current controllers that inject both positive and negative sequence currents, in order to provide voltage support in terms of positive sequence voltage support and negative sequence voltage elimination [19,20]. The voltage support concept is thoroughly presented in [20], where current-controlled inverters are reviewed to employ symmetric sequence components and reduce the voltage unbalance factor (VUF). The way current limitation is achieved under unbalanced grid conditions still represents a challenging task, especially when droop controlled inverters are considered, since their task is to regulate the grid voltage and frequency. The authors in [6,21] have implemented controllers that ensure a balanced current provision under voltage sags. As explained in [6], this enhances the fault-ride-through capability in terms of injecting only positive sequence powers/current that comply with the FRT requirement, while current limitation at the steady-state is achieved through the controller reference powers. However these approaches do not deal with negative sequence voltage mitigation. In [5], a negative sequence droop controller is presented which manages to mitigate the voltage unbalance at the point of common coupling (PCC) under voltage drops. Nevertheless, current limitation is not considered in this control design; instead, saturation units are used in the negative sequence reference power generation unit. A current-limiting scheme in both sequences for voltage controllers is presented in [22,23] for microgrid and grid-connected applications respectively, where the novel theory from [24] is introduced and employed. However, the current limitation is performed through saturation units that can lead to instability, while the droop control concept is not considered in the control design.

In this paper, a novel current-limiting controller for three-phase grid-tied droop-controlled inverters is proposed. The main novelty of this paper is that a unified control structure is proposed that achieves: (i) voltage and frequency support (droop control) under normal grid conditions and compliance with the “voltage support concept” for balanced and unbalanced faulty grid conditions, with an inherent current limitation; (ii) a non-dynamic function for dividing the total current into the two sequences according to the grid conditions, during unbalanced grid faults and (iii) a rigorous stability analysis for the closed-loop system, regardless of the system parameters. According to the authors knowledge, this is the first time that the above properties are guaranteed in a unified control structure without switching to a different control scheme under faults. Compared to the current controllers that limit the inverter current on both sequences by limiting their reference values [11,18], or to the methods employing saturation units which can lead to instability under faults or power step changes, as showcased in [10,12,13], here a droop controller is proposed and grid current boundedness is guaranteed from the input-to-state stability (ISS) property of the closed-loop system. Furthermore, instead of using root-locus analysis to test the closed-loop system stability [5], asymptotic stability of any equilibrium point of the closed-loop system in the bounded operating range is proven without assuming knowledge of the system parameters. Extended real-time simulation results are provided in order to validate the performance of the proposed control approach.

2. System Modeling and Problem Formulation

2.1. Power System under Consideration

The system under consideration consists of a three-phase inverter connected to the grid through an $LCL$ filter and a line, as depicted in Figure 1. The capacitors of the filter are denoted as $C,$ while the inductors are denoted as L and $L_g$ with their parasitic resistances being r and $r_g$, respectively. The line-to-line inverter voltage between phases a and b is given as $v_{iab}$, while $v_{ia}$ represents the phase voltage of the inverter. The capacitor voltage is denoted as $v_{ca}$ while the PCC voltage is $v_a$ with $v_a=\sqrt{2}Vcos{\omega }_{g}t,$ where V is the RMS PCC voltage and ${\omega }_g$ is the angular PCC frequency. The grid voltage is denoted as $v_{ga}$ and is considered as unknown in this paper. The inverter and grid side currents are $i_a$ and $i_{ga},$ respectively. When considering a balanced system, the above voltage and current quantities match with the positive sequence components. However, in the presence of unbalanced grid conditions, both positive and negative sequence components appear, while zero sequence components can be neglected when considering a three-phase three-wire system. In order to obtain the dynamic model of the system in both sequences, the widely used synchronous reference framework (SRF) theory is considered together with the delay signal cancellation (DSC) sequence extraction method [25,26], as explained in the analysis that follows.

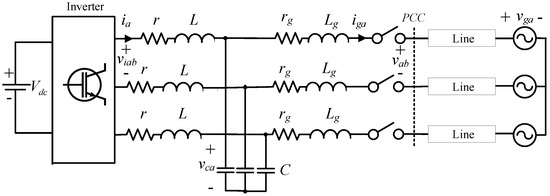
Figure 1. Three-phase inverter connected to the grid through an $LCL$ filter.

2.2. Dynamic Modeling in the SRF Using DSC Method

In this paper the clockwise SRF transformation is considered. In order to align phase a to the $\alpha$ axis, ${\theta }_a$ can be selected as $0^{°}$ in the generic $\alpha \beta$ transformation presented in [27]

$$T_{\alpha \beta }=\frac{2}{3}\left[\begin{array}{ccc}\cos {\theta }_a& \cos ({\theta }_a-120)& \cos ({\theta }_a+120)\\ \sin {\theta }_a& \sin ({\theta }_a-120)& \sin ({\theta }_a+120)\\ 0.5& 0.5& 0.5\end{array}\right].$$

Following to the $T_{\alpha \beta }$ transformation, the sequential transformation for the clockwise SRF takes the form:

$$T_{+-}=\frac{1}{2}\left[\begin{array}{cccccc}1& 0& 0& 0& 1& 0\\ 0& 1& 0& -1& 0& 0\\ 0& 0& 1& 0& 0& 0\\ 1& 0& 0& 0& -1& 0\\ 0& 1& 0& 1& 0& 0\\ 0& 0& 0& 0& 0& 1\end{array}\right].$$

The matrix $T_{+-}$ occurs from the DSC method which is preferred in this paper because it is faster compared to the methods using low-pass filters [5]. Note that this matrix is different when anti-clockwise SRF is employed while for details on obtaining this matrix and a comparison with the low pass filtering method, the reader is referred to [28]. $T_{+-}$ is then followed by the rotating transformation

$$T_{dq}^{+-}=\left[\begin{array}{ccc}\cos {\theta }_g^{+-}& -\sin {\theta }_g^{+-}& 0\\ \sin {\theta }_g^{+-}& \cos {\theta }_g^{+-}& 0\\ 0& 0& 1\end{array}\right],$$

where ${\theta }_g^{+}={\omega }_{g}t$ for the positive sequence and ${\theta }_g^{-}=-{\omega }_{g}t$ for the negative sequence. Hence, considering $T\left(t\right)={\tilde{T}}_{dq}{T}_{+-}{\tilde{T}}_{\alpha \beta }$ with ${\tilde{T}}_{\alpha \beta }=\left[\begin{array}{cc}{T}_{\alpha \beta }& 0_{3x3}\\ 0_{3x3}& T_{\alpha \beta }\end{array}\right]$ and ${\tilde{T}}_{dq}=\left[\begin{array}{cc}{T}_{dq}^{+}& 0_{3x3}\\ 0_{3x3}& T_{dq}^{-}\end{array}\right],$ then the complete transformation can be described for a cosinusoidal three-phase voltage variable $v_{abc}$ from the equation

$$\left[\begin{array}{c}{v}_d^{+}\\ v_q^{+}\\ v_0^{+}\\ v_d^{-}\\ v_q^{-}\\ v_0^{-}\end{array}\right]=T\left(t\right)\left[\begin{array}{c}{v}_a\left(t\right)\\ v_b\left(t\right)\\ v_c\left(t\right)\\ v_a(t-T)\\ v_b(t-T)\\ v_c(t-T)\end{array}\right]=\left[\begin{array}{c}\frac{\sqrt{2}}{3}\left(V_a+V_b+V_c\right)\\ 0\\ \frac{1}{6}\left(v_a\left(t\right)+v_b\left(t\right)+v_c\left(t\right)\right)\\ \frac{\sqrt{2}}{3}\left(V_a-0.5V_b-0.5V_c\right)\\ \frac{1}{\sqrt{6}}\left(V_b-V_c\right)\\ \frac{1}{6}\left(v_a\left(t-T\right)+v_b\left(t-T\right)+v_c\left(t-T\right)\right)\end{array}\right],$$

(1)

where $T=\frac{1}{4f}$ and $f=\frac{{\omega }_g}{2\pi }.$ By applying the above transformation to the three-phase current and voltage quantities of the system, the SRF-based dynamic equations of the three-phase grid-tied inverter are obtained as

$$\begin{array}{ccc}\hfill L\frac{d{i}_d^{+-}}{dt}& =& v_{id}^{+-}-v_{cd}^{+-}-r{i}_d^{+-}\mp {\omega }_{g}L{i}_q^{+-}\hfill \end{array}$$

(2)

$$\begin{array}{ccc}\hfill L\frac{d{i}_q^{+-}}{dt}& =& v_{iq}^{+-}-v_{cq}^{+-}-r{i}_q^{+-}\pm {\omega }_{g}L{i}_d^{+-}\hfill \end{array}$$

(3)

$$\begin{array}{ccc}\hfill L_g\frac{d{i}_{gd}^{+-}}{dt}& =& v_{cd}^{+-}-v_d^{+-}-r_g{i}_{gd}^{+-}\mp {\omega }_g{L}_g{i}_{gq}^{+-}\hfill \end{array}$$

(4)

$$\begin{array}{ccc}\hfill L_g\frac{d{i}_{gq}^{+-}}{dt}& =& v_{cq}^{+-}-v_q^{+-}-r_g{i}_{gq}^{+-}\pm {\omega }_g{L}_g{i}_{gd}^{+-}\hfill \end{array}$$

(5)

$$\begin{array}{ccc}\hfill C\frac{d{v}_{cd}^{+-}}{dt}& =& i_d^{+-}-i_{gd}^{+-}\mp {\omega }_{g}C{v}_{cq}^{+-}\hfill \end{array}$$

(6)

$$\begin{array}{ccc}\hfill C\frac{d{v}_{cq}^{+-}}{dt}& =& i_q^{+-}-i_{gq}^{+-}\pm {\omega }_{g}C{v}_{cd}^{+-},\hfill \end{array}$$

(7)

where $v_{id}^{+-}$ and $v_{iq}^{+-}$ are the positive and negative sequence $dq$-axis components of the inverter voltage and represent the control inputs of the system. For the ± and ∓ signs that appear in the coupling terms in Equations (2)–(7), the top operator corresponds to the positive sequence and the bottom one to the negative sequence. The instantaneous real and reactive power injected to the grid can be calculated from

$$p=P^{+}+P^{-}+\tilde{p},q=Q^{+}+Q^{-}+\tilde{q},$$

where

$$\begin{array}{ccc}\hfill P^{+}& =& \frac{3}{2}{v}_d^{+}{i}_{gd}^{+},P^{-}=\frac{3}{2}(v_d^{-}{i}_{gd}^{-}+v_q^{-}{i}_{gq}^{-})\hfill \end{array}$$

(8)

$$\begin{array}{ccc}\hfill Q^{+}& =& \frac{3}{2}{v}_d^{+}{i}_{gq}^{+},Q^{-}=\frac{3}{2}(v_d^{-}{i}_{gq}^{-}-v_q^{-}{i}_{gd}^{-})\hfill \end{array}$$

(9)

since $v_q^{+}$ is always zero from Equation (1) while $\tilde{p},\tilde{q}$ are oscillation terms with zero average value [5,6,9]. The VUF can be defined now at the PCC as

$$VUF=\frac{V^{-}}{V^{+}}=\frac{\sqrt{v_d^{-2}+v_q^{-2}}}{\sqrt{v_d^{+2}+v_q^{+2}}}$$

while $VU{F}_{grid}$ is equivalently derived for the grid side [29,30].

2.3. Problem Formulation

The main goal in this paper is to design a controller that provides support to the grid, under both normal conditions (droop control concept) and faulty conditions (voltage support concept) while boundedness should be proven for the grid current at all times, even during transients. A novel control concept was recently proposed in [15], where droop control is considered in order to mimic the dynamic response of synchronous generators and support the grid voltage and frequency regulation. Furthermore, an inherent current limitation is achieved at all times without using any saturation units but based on the ISS property of the closed-loop system. However, apart from the desired current limitation, according to the voltage support concept, a grid-connected inverter should have support capability when faults occur at the grid in terms of positive sequence voltage increase and negative sequence voltage elimination, aiming to restore the voltage to its pre-fault conditions [18,20]. Since controlling the negative sequence powers is inevitable to mitigate the negative sequence voltage at the PCC under unbalanced faults, a current limitation should be also applied at the negative sequence current while a more sophisticated algorithm is required to optimally allocate the maximum current of each sequence. To address the stated problem, a new droop control structure for three-phase inverters is proposed in the sequel to guarantee a limit for the total grid current and closed-loop asymptotic stability while maximizing the voltage support under both balanced and unbalanced faults.

3. The Proposed Controller

The proposed controller consists of two inner-loop controllers, i.e. current and voltage control, designed in the $\alpha \beta$ frame and two novel outer-loop controllers in the SRF (in the positive and negative sequence), which include the droop control concept and inherently limit the grid current in both sequences.

3.1. Inner-Loop Controllers

The current controller of the inner control loop takes the form

$$\begin{array}{ccc}\hfill v_{i\alpha }& =& v_{c\alpha }+\left(k_{PCC}+k_{RCC}\frac{s}{s^2+{\omega }_g^2}\right)(i_{\alpha }^{ref}-i_{\alpha })\hfill \end{array}$$

(10)

$$\begin{array}{ccc}\hfill v_{i\beta }& =& v_{c\beta }+\left(k_{PCC}+k_{RCC}\frac{s}{s^2+{\omega }_g^2}\right)(i_{\beta }^{ref}-i_{\beta })\hfill \end{array}$$

(11)

where PR controllers are applied to regulate $i_{\alpha }$ to $i_{\alpha }^{ref}$ and $i_{\beta }$ to $i_{\beta }^{ref}.$ Similarly, the voltage controller, from which $i_{\alpha }^{ref}$ and $i_{\beta }^{ref}$ are obtained, is described through the equations

$$\begin{array}{ccc}\hfill i_{\alpha }^{ref}& =& i_{g\alpha }+\left(k_{PVC}+k_{RVC}\frac{s}{s^2+{\omega }_g^2}\right)(v_{c\alpha }^{ref}-v_{c\alpha })\hfill \end{array}$$

(12)

$$\begin{array}{ccc}\hfill i_{\beta }^{ref}& =& i_{g\beta }+\left(k_{PVC}+k_{RVC}\frac{s}{s^2+{\omega }_g^2}\right)(v_{c\beta }^{ref}-v_{c\beta })\hfill \end{array}$$

(13)

where the reference values $v_{c\alpha }^{ref}$ and $v_{c\beta }^{ref}$ are defined from the values $v_{cd}^{ref+},v_{cd}^{ref-}$ and $v_{cq}^{ref+},v_{cq}^{ref-}$ (generated by the positive and negative sequence outer-loop controllers) transformed to $\alpha \beta$. Note that as in typical multi-loop controller applications, the PR controller gains can be suitably selected such that the current controller settles much faster than the voltage controller which settles much faster than the outer-loop controllers. Thus, for the outer-loop controllers design, which operate in a slower time scale, it is reasonable to assume that $v_{c\alpha }$ and $v_{c\beta }$ quickly track $v_{c\alpha }^{ref}$ and $v_{c\beta }^{ref}$. This is a common assumption for the inner-loop controllers used in DERs applications and further analysis can be found in [26].

3.2. Positive Sequence Current-Limiting Droop Control

The positive sequence outer-loop controller consists of a droop-based power controller to support the grid. Since apart from the droop operation, a grid current limitation should be embedded through the power controller, inspired by [15], a virtual resistance should be introduced through the control design. Furthermore, to realize current limitation, the controller states should be bounded in a range set by the operator. In order to avoid the possible instability issues that may occur when using saturation units, for the boundedness of the controller states, the BIC structure from [31] is adopted here. Following the introduction of the inner-loop controller in the previous subsection, the power controller will be directly applied to the capacitor voltage of the $LCL$ filter through controlling the reference capacitor voltage values $v_{cd}^{ref+}$ and $v_{cq}^{ref+}$. The proposed controller is described by the following equations

$$\begin{array}{ccc}\hfill v_{cd}^{ref+}& =& v_d^{+}+E_d^{+}-r_v^{+}{i}_{gd}^{+}+{\omega }_g{L}_g{i}_{gq}^{+}\hfill \end{array}$$

(14)

$$\begin{array}{ccc}\hfill v_{cq}^{ref+}& =& v_q^{+}+E_q^{+}-r_v^{+}{i}_{gq}^{+}-{\omega }_g{L}_g{i}_{gd}^{+}\hfill \end{array}$$

(15)

where $r_v^{+}$ is a constant virtual resistance and $E_d^{+},E_q^{+}$ are virtual voltages applied to each axis which change according to the expressions

$$\begin{array}{ccc}\hfill {\dot{E}}_d^{+}& =& c_{pd}f\left({\mathcal{P}}^{+}\right){\left(E_{dq}^{+}\right)}^2-k_{we}\left(\frac{{\left(E_d^{+}\right)}^2}{{\left(E_{max}^{+}\right)}^2}+{\left(E_{dq}^{+}\right)}^2-1\right)E_d^{+}\hfill \\ \hfill {\dot{E}}_{dq}^{+}& =& -\frac{c_{pd}{E}_d^{+}{E}_{dq}^{+}}{{\left(E_{max}^{+}\right)}^2}f\left({\mathcal{P}}^{+}\right)-k_{we}\left(\frac{{\left(E_d^{+}\right)}^2}{{\left(E_{max}^{+}\right)}^2}+{\left(E_{dq}^{+}\right)}^2-1\right)E_{dq}^{+}\hfill \end{array}$$

(16)

$$\begin{array}{ccc}\hfill {\dot{E}}_q^{+}& =& c_{pq}g\left({\mathcal{Q}}^{+}\right){\left(E_{qq}^{+}\right)}^2-k_{we}\left(\frac{{\left(E_q^{+}\right)}^2}{{\left(E_{max}^{+}\right)}^2}+{\left(E_{qq}^{+}\right)}^2-1\right)E_q^{+}\hfill \\ \hfill {\dot{E}}_{qq}^{+}& =& -\frac{c_{pq}{E}_q^{+}{E}_{qq}^{+}}{{\left(E_{max}^{+}\right)}^2}g\left({\mathcal{Q}}^{+}\right)-k_{we}\left(\frac{{\left(E_q^{+}\right)}^2}{{\left(E_{max}^{+}\right)}^2}+{\left(E_{qq}^{+}\right)}^2-1\right)E_{qq}^{+}\hfill \end{array}$$

(17)

where $c_{pd},c_{pq},k_{we},E_{max}^{+}$ are positive constants and

$$\begin{array}{ccc}\hfill f\left({\mathcal{P}}^{+}\right)& =& n(P_{set}^{+}-{\mathcal{P}}^{+})+E_{rms}^{+}-V^{+}\hfill \end{array}$$

(18)

$$\begin{array}{ccc}\hfill g\left({\mathcal{Q}}^{+}\right)& =& m(Q_{set}^{+}-{\mathcal{Q}}^{+})-{\omega }^{*}+{\omega }_g\hfill \end{array}$$

(19)

where $E_{rms}^{+}$ is the RMS nominal voltage in the positive sequence, n, m are the droop coefficients, while the powers are being measured from ${\mathcal{P}}^{+}=\frac{3v_d^{+}{E}_d^{+}}{2r_v^{+}}$ and ${\mathcal{Q}}^{+}=\frac{3v_d^{+}{E}_q^{+}}{2r_v^{+}}$ by using the steady-state current values (this will be further explained in Section 3.4). Hence, at the steady-state ${\mathcal{P}}^{+}=P^{+}$ and ${\mathcal{Q}}^{+}=Q^{+},$ thus achieving the desired droop control operation, while the expressions of ${\mathcal{P}}^{+}$ and ${\mathcal{Q}}^{+}$ are used to facilitate the stability analysis, as explained in the sequel. The positive sequence reference real and reactive power are denoted as $P_{set}^{+}$ and $Q_{set}^{+}$ respectively. It should be highlighted that due to the virtual resistance $r_v^{+}$ introduced by the proposed controller, the $P\sim V$ and $Q\sim -\omega$ droop expressions are adopted here. Through the functions (18) and (19), the PQ-set and PQ-droop control modes are inherited in the control system. In these two control modes, the inverter either regulates the real and reactive power to their reference values $P_{set}^{+}$, $Q_{set}^{+}$, when the terms $E_{rms}^{+}-V^{+}$ and $-{\omega }^{*}+{\omega }_g$ are removed from (18) and (19), respectively, or supports the grid voltage and frequency regulation through droop control. For the dynamics of the virtual voltages $E_d^{+}$ and $E_q^{+}$ in Equations (14) and (15), the bounded integral controller (BIC), proposed in [31], is adopted in order to guarantee the boundedness of $E_d^{+}$ and $E_q^{+}$ without using any saturated integrators that could drive the system to instability. It is noteworthy that in this paper the terms $-k_{we}\left(\frac{{\left(E_d^{+}\right)}^2}{{\left(E_{max}^{+}\right)}^2}+{\left(E_{dq}^{+}\right)}^2-1\right)E_d^{+}$ and $-k_{we}\left(\frac{{\left(E_q^{+}\right)}^2}{{\left(E_{max}^{+}\right)}^2}+{\left(E_{qq}^{+}\right)}^2-1\right)E_q^{+}$ have been added in (16) and (17) to guarantee attractiveness of the controller states to a desired ellipse on the phase plane. To further explain this, consider the lower bounded function

$$W=\frac{1}{4}{\left(\frac{{\left(E_d^{+}\right)}^2}{{\left(E_{max}^{+}\right)}^2}+{\left(E_{dq}^{+}\right)}^2-1\right)}^2$$

for the system in Equation (16). The time derivative of W takes the form

$$\dot{W}=\frac{1}{2}\left(\frac{{\left(E_d^{+}\right)}^2}{{\left(E_{max}^{+}\right)}^2}+{\left(E_{dq}^{+}\right)}^2-1\right)\left(\frac{2E_d^{+}{\dot{E}}_d^{+}}{{\left(E_{max}^{+}\right)}^2}+2E_{dq}^{+}{\dot{E}}_{dq}^{+}\right)$$

which by substituting ${\dot{E}}_d^{+}$ and ${\dot{E}}_{dq}^{+}$ from Equation (16), becomes

$$\dot{W}=-k_{we}{\left(\frac{{\left(E_d^{+}\right)}^2}{{\left(E_{max}^{+}\right)}^2}+{\left(E_{dq}^{+}\right)}^2-1\right)}^2\left(\frac{{\left(E_d^{+}\right)}^2}{{\left(E_{max}^{+}\right)}^2}+{\left(E_{dq}^{+}\right)}^2\right)\le 0.$$

(20)

Furthermore, one can easily show that $\ddot{W}$ is bounded. Hence, according to the “Lyapunov-Like Lemma” (Lemma 4.3 in [32]), $\dot{W}\to 0$ as $t\to \infty .$ It is clear from (20) that $\dot{W}=0$ holds at the set $E=\left\{E_d^{+},E_{dq}^{+}\in R:\frac{{\left(E_d^{+}\right)}^2}{{\left(E_{max}^{+}\right)}^2}+{\left(E_{dq}^{+}\right)}^2=1\right\}$ and at the origin. However, regarding the origin, where $E_d^{+}=0$ and $E_{dq}^{+}=0,$ it can be easily proven that it is an unstable equilibrium point, from Theorem 4.4 in [32], by considering the continuously differentiable function $\overline{W}=\frac{{\left(E_d^{+}\right)}^2}{{\left(E_{max}^{+}\right)}^2}+{\left(E_{dq}^{+}\right)}^2.$ Thus, starting from any initial conditions $E_{d0}^{+}$ and $E_{dq0}^{+}$ inside or on the ellipse $E,$ except from the origin, the states $E_d^{+}$ and $E_{dq}^{+}$ will be quickly attracted on E and remain on the curve thereafter ensuring that $E_d^{+}\in \left[-E_{max}^{+},E_{max}^{+}\right],\forall t\ge 0.$ Note that the positive parameter $E_{max}^{+}$ represents the horizontal radius of the ellipse E and when it varies, it becomes clear from (20), that $E_d^{+}$ and $E_{dq}^{+}$ will quickly converge to a new ellipse. The larger the $k_{we},$ the faster the convergence. This enables an adaptation of the upper and lower bounds of $E_d^{+}.$ A similar analysis holds for $E_q^{+}$ and $E_{qq}^{+}$ guaranteeing that $E_q^{+}\in \left[-E_{max}^{+},E_{max}^{+}\right],\forall t\ge 0.$

3.3. Negative Sequence Current-Limiting Control

The proposed current-limiting controller in the negative sequence is designed in a similar form and aims at regulating the negative sequence grid current. Hence it can be obtained as follows

$$\begin{array}{ccc}\hfill v_{cd}^{ref-}& =& v_d^{-}+E_d^{-}-r_v^{-}{i}_{gd}^{-}-{\omega }_g{L}_g{i}_{gq}^{-}\hfill \end{array}$$

(21)

$$\begin{array}{ccc}\hfill v_{cq}^{ref-}& =& v_q^{-}+E_q^{-}-r_v^{-}{i}_{gq}^{-}+{\omega }_g{L}_g{i}_{gd}^{-}\hfill \end{array}$$

(22)

where similarly to the positive sequence controller, $r_v^{-}$ is a constant virtual resistance and $E_d^{-},E_q^{-}$ are virtual voltages applied to each axis which change according to the expressions

$$\begin{array}{ccc}\hfill {\dot{E}}_d^{-}& =& c_{nd}\left(i_{gd}^{ref-}-\frac{E_d^{-}}{r_v^{-}}\right){\left(E_{dq}^{-}\right)}^2-k_{we}\left(\frac{{\left(E_d^{-}\right)}^2}{{\left(E_{max}^{-}\right)}^2}+{\left(E_{dq}^{-}\right)}^2-1\right)E_d^{-}\hfill \\ \hfill {\dot{E}}_{dq}^{-}& =& -\frac{c_{nd}{E}_d^{-}{E}_{dq}^{-}}{{\left(E_{max}^{-}\right)}^2}\left(i_{gd}^{ref-}-\frac{E_d^{-}}{r_v^{-}}\right)-k_{we}\left(\frac{{\left(E_d^{-}\right)}^2}{{\left(E_{max}^{-}\right)}^2}+{\left(E_{dq}^{-}\right)}^2-1\right)E_{dq}^{-}\hfill \end{array}$$

(23)

$$\begin{array}{ccc}\hfill {\dot{E}}_q^{-}& =& c_{nq}\left(i_{gq}^{ref-}-\frac{E_q^{-}}{r_v^{-}}\right){\left(E_{qq}^{-}\right)}^2-k_{we}\left(\frac{{\left(E_q^{-}\right)}^2}{{\left(E_{max}^{-}\right)}^2}+{\left(E_{qq}^{-}\right)}^2-1\right)E_q^{-}\hfill \\ \hfill {\dot{E}}_{qq}^{-}& =& -\frac{c_{nq}{E}_q^{-}{E}_{qq}^{-}}{{\left(E_{max}^{-}\right)}^2}\left(i_{gq}^{ref-}-\frac{E_q^{-}}{r_v^{-}}\right)-k_{we}\left(\frac{{\left(E_q^{-}\right)}^2}{{\left(E_{max}^{-}\right)}^2}+{\left(E_{qq}^{-}\right)}^2-1\right)E_{qq}^{-}\hfill \end{array}$$

(24)

where $i_{gd}^{ref-}=\frac{2\left(P_{set}^{-}{v}_d^{-}-Q_{set}^{-}{v}_q^{-}\right)}{3\left(v_d^{-2}+v_q^{-2}\right)}$ and $i_{gq}^{ref-}=\frac{2\left(P_{set}^{-}{v}_q^{-}+Q_{set}^{-}{v}_d^{-}\right)}{3\left(v_d^{-2}+v_q^{-2}\right)}$ are the current reference values which, can be realized by equating the $P^{-}$ and $Q^{-}$ formulas from Equations (8) and (9) with their reference values $P_{set}^{-}$ and $Q_{set}^{-},$ while $c_{nd},c_{nq},E_{max}^{-}$ are positive constants. As one can see, through the proposed controller, the expressions $\frac{E_d^{-}}{r_v^{-}}$ and $\frac{E_q^{-}}{r_v^{-}},$ which represent a good approximation of the steady-state negative sequence current values (see Section 3.4) can be regulated to the reference values $i_{gd}^{ref-}$ and $i_{gq}^{ref-}.$ Through this control structure, $P^{-}$ and $Q^{-}$ can track their reference values which can be computed to optimally eliminate the negative sequence voltage. Following a similar analysis to the positive sequence controller, it can be proven that $E_d^{-},E_q^{-}\in [-E_{max}^{-},E_{max}^{-}],\forall t\ge 0,$ which facilitates the desired current limitation. The methodology for generating $P_{set}^{-}$ and $Q_{set}^{-}$ and the current-limiting property are explained in the sequel.

3.4. Current-Limiting Property

By substituting the proposed controller (14), (15), (21) and (22) into the system dynamics (4) and (5), the closed-loop system takes the form

$$\begin{array}{ccc}\hfill L_g\frac{d{i}_{gd}^{+-}}{dt}& =& E_d^{+-}-\left(r_v^{+-}+r_g\right)i_{gd}^{+-}\hfill \end{array}$$

(25)

$$\begin{array}{ccc}\hfill L_g\frac{d{i}_{gq}^{+-}}{dt}& =& E_q^{+-}-\left(r_v^{+-}+r_g\right)i_{gq}^{+-}.\hfill \end{array}$$

(26)

The Equations (25) and (26) are the derived dynamics of the grid current in both sequences. From (25) and (26) the steady-state value of the grid currents can be approximated from $i_{gde}^{+-}\approx E_d^{+-}/r_v^{+-}$ and $i_{gqe}^{+-}\approx E_q^{+-}/r_v^{+-}$ considering that $r_v^{+-}\gg r_g,$ which can be achieved by appropriately selecting the virtual resistances $r_v^{+-},$ which represent controller parameters. This is why the previous expressions are used in Equations (18), (19), (23) and (24). Taking into account that $E_d^{+-},E_q^{+-}\in [-E_{max}^{+-},E_{max}^{+-}],\forall t\ge 0,$ let us consider the continuous differentiable function

$$V=\frac{1}{2}{L}_g{i}_{gd}^{+-2}$$

for the system in Equation (25).

The time derivative of V becomes

$$\dot{V}=-\left(r_g+r_v^{+-}\right){\left(i_{gd}^{+-}\right)}^2+i_{gd}^{+-}{E}_d^{+-}\le -\left(r_g+r_v^{+-}\right){\left(i_{gd}^{+-}\right)}^2+\left|i_{gd}^{+-}\right|\left|E_d^{+-}\right|.$$

Thus,

$$\dot{V}\le -r_g{\left(i_{gd}^{+-}\right)}^2,\forall \left|i_{gd}^{+-}\right|\ge \frac{\left|E_d^{+-}\right|}{r_v^{+-}}$$

which proves that system (25) is input-to-state stable (ISS) by considering $E_d^{+-}$ as the input. Since it is proven that $\left|E_d^{+-}\right|\le E_{max}^{+-},\forall t\ge 0,$ then $i_{gd}^{+-}$ will be bounded for all $t\ge 0.$ More precisely, it will hold that

$$\left|i_{gd}^{+-}\right|\le \frac{E_{max}^{+-}}{r_v^{+-}},\forall t\ge 0,$$

with the condition that initially $\left|i_{gd}^{+-}\left(0\right)\right|\le \frac{E_{max}^{+-}}{r_v^{+-}}.$ This holds true because the set $\mathrm{\Omega }=\left\{i_{gd}^{+-}\in R,\left|i_{gd}^{+-}\right|\le \frac{E_{max}^{+-}}{r_v^{+-}}\right\}$ is invariant. Hence, if $E_{max}^{+}$ and $E_{max}^{-}$ are selected as $E_{max}^{+}=\sqrt{2}{r}_v^{+}{I}_{grms}^{max+}$ and $E_{max}^{-}=r_v^{-}{I}_{grms}^{max-},$ then $\left|i_{gd}^{+}\right|\le \sqrt{2}{I}_{grms}^{max+}$ and $\left|i_{gd}^{-}\right|\le I_{grms}^{max-}.$ Since the same analysis and same result holds for the q axis current as well, it is concluded that

$$\begin{array}{ccc}\hfill I_{grms}^{+}& =\frac{\sqrt{{\left(i_{gd}^{+}\right)}^2+{\left(i_{gq}^{+}\right)}^2}}{\sqrt{2}}\le & \sqrt{2}{I}_{grms}^{max+}\hfill \\ \hfill I_{grms}^{-}& =\frac{\sqrt{{\left(i_{gd}^{-}\right)}^2+{\left(i_{gq}^{-}\right)}^2}}{\sqrt{2}}\le & I_{grms}^{max-}.\hfill \end{array}$$

The reason $\sqrt{2}$ is used in $E_{max}^{+}$ and the way $I_{grms}^{max+}$ and $I_{grms}^{max-}$ are selected online, are further explained in Section 4.2.

4. Voltage Support Concept-Based Operation under Grid Faults

4.1. Fault-Ride-Through Operation

Fault-ride-through guidelines have been recently proposed in order to standardize the way DERs should provide support under grid faults. In particular, during grid voltage drops, DERs should provide voltage support through reactive power injection instead of getting disconnected due to tripping of the inverter. In a wider manner, the most common support technique is the “voltage support concept” where maximum available power is injected to the grid in order to increase the voltage level at the PCC [20]. To understand this, consider the voltage difference between the PCC and the grid $\mathrm{\Delta }{V}^{+}=V^{+}-V_g^{+}$ and assuming a resistive-inductive line with resistance $r_l$ and inductance $L_l,$ let us use the approximation of this voltage difference as it is commonly presented in the literature [33,34]

$$\mathrm{\Delta }{V}^{+}=\frac{P^{+}{r}_l+Q^{+}{x}_{L_l}}{3V^{+}}.$$

(27)

Interested readers can obtain this approximation by using the equations that relate the magnitudes of the PCC and grid voltages according to the current real and reactive components, as shown in [18,35,36].

Since power lines are most of the times considered as predominantly inductive, it can be understood from Equation (27) that reactive power affects more drastically the PCC voltage and thus, by injecting reactive power we can increase the PCC voltage level compared to the faulty grid voltage. In case only resistive or only inductive impedance is considered between the PCC and the grid, the relations between the amplitudes are simplified as presented in [20], thus requiring the injection of only real or reactive power respectively to support PCC by increasing $\mathrm{\Delta }{V}^{+}.$ The most commonly used FRT guidelines are those from the German grid code [7] which take the form:

$$I_{grmsQ}^{+}=\left\{\begin{array}{c}\begin{array}{cc}0,& V^{+}\ge 0.9E_{rms}^{+}\\ \left(1-\frac{V^{+}}{E_{rms}^{+}}\right)k{I}_{grms}^{max+},& 0.5E_{rms}^{+}<V^{+}<0.9E_{rms}^{+}\\ I_{grms}^{max+},& V^{+}\le 0.5E_{rms}^{+}\end{array}\hfill \end{array}\right.$$

(28)

where $I_{grmsQ}^{+}$ is the reactive component of the positive sequence grid current and k is the FRT gain $\left(k\ge 2\right)$ with $\left(1-\frac{V^{+}}{E_{rms}^{+}}\right)k\le 1.$ According to Equation (28), it is concluded that $P_{set}^{+}=\sqrt{{\left(S_{max}^{+}\right)}^2-{\left(Q_{set}^{+}\right)}^2}$ and $Q_{set}^{+}=\left(1-\frac{V^{+}}{E_{rms}^{+}}\right)k{S}_{max}^{+},$ where $S_{max}^{+}$ represents the amount of apparent power assigned to the positive sequence controller during faults, in the case where $0.5E_{rms}^{+}<V^{+}<0.9E_{rms}^{+}.$

Regarding the negative sequence voltage (which is a crucial part of the voltage support concept as well), according to the literature, it can be eliminated by increasing the negative sequence reactive power and decreasing the negative sequence real power. This can be understood either from [18], where equations that involve the magnitude of the PCC voltage are shown to explain the negative sequence voltage elimination concept or from the phasor analysis in [5]. For the calculation of the negative sequence reference powers during unbalanced grid faults, in this paper, a PI controller is applied to generate $Q_{set}^{-},$ i.e.,

$$Q_{set}^{-}=\left(k_{PVU}+\frac{k_{IVU}}{s}\right)\left(V^{-}-E_{rms}^{-}\right)$$

(29)

while

$$P_{set}^{-}=-\frac{r_l}{{\omega }_g{L}_l}{Q}_{set}^{-},$$

(30)

where $E_{rms}^{-}$ is a constant and $k_{PVU},k_{IVU}$ are the proportional and integral gains of the PI controller. Note that Equation (30) represents a decoupling solution based on the line impedance parameters [5,37]. However, accurate knowledge of $r_l$ and $L_l$ is not essential since an estimation of the term $\frac{r_l}{L_l}$ is enough. Through Equations (29) and (30), the required negative sequence reference powers to eliminate the PCC negative sequence voltage are acquired. As it is obvious from (29) and (30), considering initially a balanced system, as long as there is no negative sequence voltage at the PCC (balanced system), $Q_{set}^{-}=P_{set}^{-}=0$ and thus the inverter injects only positive sequence power. Note that a superiority of the proposed controller compared to existing approaches, is that when the capacity is not enough to track $P_{set}^{-}$ and $Q_{set}^{-},$ priority is given to the current limitation property proven in Section 3.4, without switching to different control dynamics or suffering from integrator wind-up issues.

It should be highlighted that methodologies that take into account the line impedance have been also applied for positive sequence voltage support, see for example [18,36]. In this case, decoupling based on the line impedance parameters is achieved in the positive sequence as well and thus, Equation (27) does not represent an assumption since it expresses accurately the voltage difference. However, since the FRT is an essential standard in most of the grid codes nowadays, it is adopted for the positive sequence voltage support in this paper, as in [5]. Note though that if required, $P_{set}^{+}$ and $Q_{set}^{+}$ formulas can be easily modified and be determined according to $r_l$ and $L_l$ instead of the FRT guidelines.

4.2. Online Adaptation of $I_{grms}^{max+}$ and $I_{grms}^{max-}$

In this paper, the grid current limitation is inherently applied through the outer-loop controllers and not through saturated integrators in the inner loop. Thus, a proper selection of the maximum available current in each sequence needs to take place by proposing an algorithm that defines the values $I_{grms}^{max+}$ and $I_{grms}^{max-}.$ To realize the current allocation, priority is given to the positive sequence voltage regulation by means of supporting the positive sequene capacitor voltage $V_c^{+}$ so that when $V^{+}<0.9E_{rms}^{+},$ we can achieve $V_c^{+}\ge 0.9E_{rms}^{+}$ or $V_c^{+}-V^{+}\ge 0.9E_{rms}^{+}-V^{+}$ which through Equation (27) can be written as

$$\frac{P^{+}{r}_g+Q^{+}{x}_{L_g}}{3V_c^{+}}\ge 0.9E_{rms}^{+}-V^{+},$$

(31)

if the voltage difference is selected as $V_c^{+}-V^{+}.$ This methodology is employed since in contrary to [24], the aim here is to provide a non dynamic method of adjusting the positive and negative sequence maximum currents and furthermore, $V_g^{+}$ is considered unknown. Otherwise the positive sequence voltage support could be applied at the PCC voltage. By recalling the $P_{set}^{+}$ and $Q_{set}^{+}$ formulas derived from (28), expression (31) results to

$$I_{grms}^{max+}\ge \frac{E_{rms}^{+}\left(\rho -0.1\right)}{\sqrt{1-k^2{\rho }^2}{r}_g+k\rho {\omega }_g{L}_g}.$$

Thus, we can select

$$I_{grms}^{max+}=\frac{E_{rms}^{+}\left(\rho -0.1\right)}{\sqrt{1-k^2{\rho }^2}{r}_g+k\rho {\omega }_g{L}_g}$$

(32)

where $\rho$ is the p.u. voltage drop of the RMS voltage at the PCC. Note that Equation (32) is valid only when $0.5\ge \rho \ge 0.1$ (from Equation (28)) and $V^{-}>E_{rms}^{-}$ since in the absence of negative sequence voltage, all the available current is assigned to the positive sequence. $I_{grms}^{max+}$ is then passed through a saturator that ensures that $I_{grms}^{max+}\in \left[0,I_{grms}^{max}\right].$ Opposed to conventional current-limiting control schemes that apply a saturator on the current dynamics, here the function being saturated is not dynamic and thus does not suffer from integrator wind-up. Then, according to the theory presented in [22,23], which shows that the total current of any phase has a maximum value $I_{grms}^{max}\le I_{grms}^{+}+I_{grms}^{-}$ even if unbalanced current is injected to the grid, $I_{grms}^{max-}$ can be set as

$$I_{grms}^{max-}=I_{grms}^{max}-I_{grms}^{max+}.$$

(33)

When current allocation has taken place, the value $S_{max}^{+}$ can be easily selected as $3V^{+}{I}_{grms}^{max+}$ and the positive sequence reference powers can be calculated according to the FRT guidelines in Equation (28), while when $I_{grms}^{max+}=I_{grms}^{max}$ from Equation (32) or due to the saturator, then $S_{max}^{+}=S_{max}$ and $I_{grms}^{max-}=0.$ Since the maximum current for each sequence is now defined according to the voltage drop, the proposed controller dynamics in (16), (17), (23) and (24) can be adapted online through the expressions $E_{max}^{+}=\sqrt{2}{r}_v^{+}{I}_{grms}^{max+},E_{max}^{-}=r_v^{-}{I}_{grms}^{max-}.$ Opposed to the work presented in [15,38], here the proposed design enables the adaptation of the controller parameters $E_{max}^{+}$ and $E_{max}^{-},$ and the controller states are attracted on any ellipse E with varying horizontal radius ($E_{max}^{+}$ or $E_{max}^{-}$) as analytically proven in Section 3.2. The positive sequence maximum current is set as the amplitude and not the RMS value in order to allow $P,Q\in \left[0,S_{max}^{+}\right]$ for the FRT. However, since it holds that $P_{set}^{+}=\sqrt{{\left(S_{max}^{+}\right)}^2-{\left(Q_{set}^{+}\right)}^2},$ the maximum RMS current will never be violated at the steady-state, while during transients, through the input-to-state stability property of the closed-loop current dynamics, it is proven that it remains below the value $\sqrt{2}{I}_{grms}^{max}=1.4I_{grms}^{max}$ (worst-case scenario), which commercial inverters can handle [39]. Finally, during normal grid conditions, $I_{grms}^{max+}$ can be simply selected as $I_{grms}^{max}/\sqrt{2}$ to ensure current limitation under the value $I_{grms}^{max}$ at all times. The implementation of the proposed control approach is depicted in Figure 2, where the control part generating the positive and negative sequence reference powers and the maximum currents is denoted as the FRT block, which is shown in Figure 3.

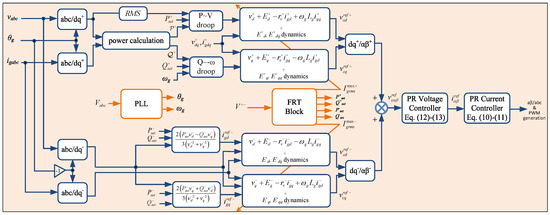
Figure 2. Implementation diagram of the proposed controller.

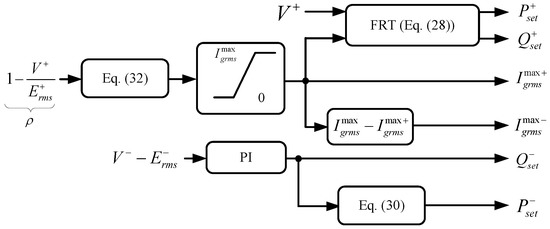
Figure 3. Fault-ride-through (FRT) Block.

5. Stability Analysis

After applying the proposed controller into the three-phase inverter system, the closed-loop dynamics are given by (16), (17), (23)–(26). The state vector of the closed-loop system, for both sequences, takes the form $x^{+-}={\left[{\left(x_1^{+-}\right)}^T{\left(x_2^{+-}\right)}^T\right]}^T,$ where $x_1^{+-}={\left[\begin{array}{cc}{i}_{gd}^{+-}& i_{gq}^{+-}\end{array}\right]}^T,$ $x_2^{+-}={\left[\begin{array}{cccc}{E}_d^{+-}& E_{dq}^{+-}& E_q^{+-}& E_{qq}^{+-}\end{array}\right]}^T.$ Consider now any steady-state equilibrium point $x_e^{+-}={\left[{\left(x_{1e}^{+-}\right)}^T{\left(x_{2e}^{+-}\right)}^T\right]}^T$ $={\left[i_{gde}^{+-}{i}_{gqe}^{+-}{E}_{de}^{+-}{E}_{dqe}^{+-}{E}_{qe}^{+-}{E}_{qqe}^{+-}\right]}^T$ with $E_{de}^{+-},E_{qe}^{+-}\in \left(-E_{max}^{+-},E_{max}^{+-}\right),$ i.e., $E_{dqe}^{+-},E_{qqe}^{+-}\in \left(0,1\right],$ where the voltage and frequency at the PCC are assumed constant (not necessarily equal to their rated values). By defining ${\tilde{x}}_1^{+-}=x_1^{+-}-x_{1e}^{+-}$ and ${\tilde{x}}_2^{+-}=x_2^{+-}-x_{2e}^{+-},$ then the closed-loop dynamics (16), (17), (23)–(26) can be written in the following interconnected system form

$$\begin{array}{ccc}\hfill {\dot{\tilde{x}}}_1^{+-}& =& f_1\left({\tilde{x}}_1^{+-},{\tilde{x}}_2^{+-}\right)\hfill \end{array}$$

(34)

$$\begin{array}{ccc}\hfill {\dot{\tilde{x}}}_2^{+-}& =& f_2\left({\tilde{x}}_2^{+-}\right),\hfill \end{array}$$

(35)

where the equilibrium has been shifted at the origin. According to Lemma 5.6 in [40], if the system (34) with the ${\tilde{x}}_2^{+-}$ as input, is locally input-to-state stable and the origin of the system (35) is asymptotically stable, then the origin of the interconnected systems (34) and (35) is asymptotically stable.

System (34) is linear and can be written from (25) and (26) as

$$\left[\begin{array}{c}{\dot{\tilde{i}}}_{gd}^{+-}\\ {\dot{\tilde{i}}}_{gq}^{+-}\end{array}\right]=\left[\begin{array}{cc}-\frac{r_g+r_v^{+-}}{L_g}& 0\\ 0& -\frac{r_g+r_v^{+-}}{L_g}\end{array}\right]\left[\begin{array}{c}{\tilde{i}}_{gd}^{+-}\\ {\tilde{i}}_{gq}^{+-}\end{array}\right]+\left[\begin{array}{c}\frac{{\tilde{E}}_d^{+-}}{L_g}\\ \frac{{\tilde{E}}_q^{+-}}{L_g}\end{array}\right].$$

Since the characteristic matrix of the grid current dynamics is diagonal with all elements being negative, then the system (34) is bounded-input bounded state stable with respect to the input ${\left[\frac{{\tilde{E}}_d^{+-}}{L_g}\frac{{\tilde{E}}_q^{+-}}{L_g}\right]}^T,$ which means that (34) is ISS. Then, for the dynamics of the control systems (16), (17), (23) and (24), the Jacobian matrix of (35) becomes

$$A^{+-}=\left[\begin{array}{cc}{A}_1^{+-}& 0_{2x2}\\ 0_{2x2}& A_2^{+-}\end{array}\right],$$

where

$$\begin{array}{ccc}\hfill A_1^{+-}& =& \left[\begin{array}{cc}-{\alpha }^{+-}{\left(E_{dqe}^{+-}\right)}^2-2k_{we}\frac{{\left(E_{de}^{+-}\right)}^2}{{\left(E_{max}^{+-}\right)}^2}& -2k_{we}{E}_{dqe}^{+-}{E}_{de}^{+-}\hfill \\ \frac{{\alpha }^{+-}{E}_{de}^{+-}{E}_{dqe}^{+-}-2k_{we}{E}_{de}^{+-}{E}_{dqe}^{+-}}{{\left(E_{max}^{+-}\right)}^2}& -2k_{we}{\left(E_{dqe}^{+-}\right)}^2\hfill \end{array}\right]\hfill \\ \hfill A_2^{+-}& =& \left[\begin{array}{cc}-{\beta }^{+-}{\left(E_{qqe}^{+-}\right)}^2-2k_{we}\frac{{\left(E_{qe}^{+-}\right)}^2}{{\left(E_{max}^{+-}\right)}^2}& -2k_{we}{E}_{qqe}^{+-}{E}_{qe}^{+-}\hfill \\ \frac{{\beta }^{+-}{E}_{qe}^{+-}{E}_{qqe}^{+-}-2k_{we}{E}_{qe}^{+-}{E}_{qqe}^{+-}}{{\left(E_{max}^{+-}\right)}^2}& -2k_{we}{\left(E_{qqe}^{+-}\right)}^2\hfill \end{array}\right]\hfill \end{array}$$

with ${\alpha }^{+}=\frac{c_{pd}3n{v}_d^{+}}{2r_v^{+}},$ ${\beta }^{+}=\frac{c_{pq}3m{v}_d^{+}}{2r_v^{+}},$ ${\alpha }^{-}=\frac{c_{nd}}{r_v^{-}}$ and ${\beta }^{-}=\frac{c_{nq}}{r_v^{-}}.$ Since $A^{+-}$ is a block diagonal matrix, we can investigate the system matrices $A_1^{+-}$ and $A_2^{+-}$ independently. The characteristic polynomials of these two matrices take the form

$$\begin{array}{ccc}{\lambda }^2+\left(2k_{we}+{\alpha }^{+-}{\left(E_{dqe}^{+-}\right)}^2\right)\lambda +2k_{we}{\left(E_{dqe}^{+-}\right)}^4{\alpha }^{+-}+\frac{2k_{we}{\left(E_{de}^{+-}\right)}^2{\left(E_{dqe}^{+-}\right)}^2{\alpha }^{+-}}{{\left(E_{max}^{+-}\right)}^2}& =& 0\\ {\lambda }^2+\left(2k_{we}+{\beta }^{+-}{\left(E_{qqe}^{+-}\right)}^2\right)\lambda +2k_{we}{\left(E_{qqe}^{+-}\right)}^4{\beta }^{+-}+\frac{2k_{we}{\left(E_{qe}^{+-}\right)}^2{\left(E_{qqe}^{+-}\right)}^2{\beta }^{+-}}{{\left(E_{max}^{+-}\right)}^2}& =& 0.\end{array}$$

Hence, the condition to guarantee asymptotic stability for any equilibrium point $x_e^{+-}$ of the closed-loop system in the bounded operating range $E_{de}^{+-},E_{qe}^{+-}\in \left(-E_{max}^{+-},E_{max}^{+-}\right),$ is

$${\alpha }^{+},{\alpha }^{-},{\beta }^{+},{\beta }^{-}>0,$$

which is always true regardless of the voltage level. Opposed to the majority of the conventional approaches that use root locus analysis and guarantee stability of a given equilibrium point under the specific parameters of the inverter and the grid, here the proposed controller guarantees asymptotic stability of any equilibrium point $x_e^{+-}$ in the bounded operating range. In addition, an inherent current-limiting property and an enhanced operation under grid faults is achieved in a unified control structure, which highlights the novelty of the proposed control scheme.

6. Validation through Real-Time Results

In order to validate the proposed control approach, a three-phase inverter connected to the grid, as shown in Figure 1, and equipped with the controller proposed in this paper, is tested using an OPAL-RT OP4500 real-time digital simulator. The parameters of the controller and the power system are given in Table 1. In the next subsections, the performance of the proposed controller will be showcased under various normal and abnormal grid conditions.

Table 1. System and controller parameters.

Parameter	Value	Parameter	Value
$L,L_g$	$2.2\mathrm{mH}$	$Z_l$	$0.9+1.256j\mathrm{\Omega }$
$r,r_g$	$0.5\mathrm{\Omega }$	$V_{dc}$	$400\mathrm{V}$
C	$1\mathsf{\mu }\mathrm{F}$	$S_{max}$	$3.3\mathrm{KVA}$
$E_{rms}^{+}$	$110\mathrm{V}$	$I_{grms}^{max}$	$10\mathrm{A}$
$E_{rms}^{-}$	$0\mathrm{V}$	${\omega }^{*}$	$314.15\mathrm{rad}/\mathrm{s}$
${\omega }_g$	$314.03\mathrm{rad}/\mathrm{s}$	$k_{we}$	1000
n	0.00333	m	0.0019
$r_v^{+}$	$30\mathrm{\Omega }$	$r_v^{-}$	$10\mathrm{\Omega }$
$c_{pd}$	780	$c_{pq}$	3415
$c_{nd}$	250	$c_{nq}$	125
$k_{PVU}$	2	$k_{IVU}$	20
$k_{PCC}$	0.2	$k_{RCC}$	2
$k_{PVC}$	1.5	$k_{RVC}$	15

6.1. Balanced Operation

Firstly, the operation of the grid-connected inverter equipped with the proposed controller will be tested under balanced grid conditions. The switch between the $LCL$ filter and the PCC is initially open, and then closes at $t=0.1\mathrm{s}$, while at the same time the controller is enabled with the reference values $P_{set}^{+}$ and $Q_{set}^{+}$ having the values of $600\mathrm{W}$ and $0\mathrm{Var},$ respectively. The controller operates initially in the PQ-set mode and regulates $P^{+}$ and $Q^{+}$ to their desired values, as shown in Figure 4. In the same figure, $V_c^{+}$ and $I_{grms}^{+}$ can be observed as well. At $t=1\mathrm{s},$ $Q_{set}^{+}$ is changed to $50\mathrm{Var}$ and the reactive power injection is accordingly modified while at $t=2\mathrm{s},$ $P_{set}^{+}$ is set as $800\mathrm{W}.$ Since the PQ-set operation is now verified, at $t=4\mathrm{s}$ and $t=5\mathrm{s},$ the real and reactive power droop control modes are enabled respectively. One can see that both the real and the reactive power drop since at that time, the grid operates with a slightly higher value of RMS grid voltage compared to the nominal ($110.4\mathrm{V}$) and a slightly lower than the nominal grid frequency ($49.98\mathrm{Hz}$). At $t=6\mathrm{s},$ a balanced grid voltage drop of $0.4\mathrm{p}.\mathrm{u}.$ is applied in order to test the operation under faulty grid conditions. At the initial transient, it can be observed in Figure 4, that $I_{grms}^{+}$ reaches the value of $11\mathrm{A}$ while it never violates the ultimate bound of $\sqrt{2}{I}_{grms}^{max}=14\mathrm{A}.$

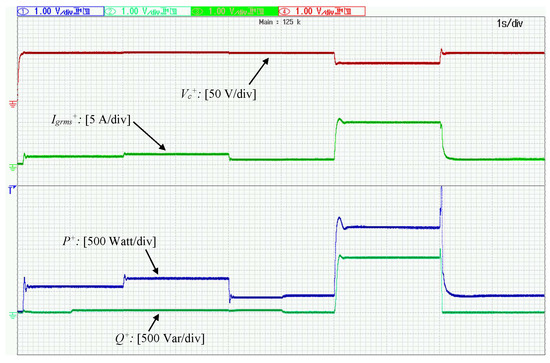
Figure 4. Operation under balanced conditions with a $0.4\mathrm{p}.\mathrm{u}.$ balanced voltage drop at 6 s.

Following to the transient, the RMS value of the grid current is regulated to its maximum value of $10\mathrm{A},$ as it has been analytically proven in this paper, while $P^{+}$ and $Q^{+}$ are regulated according to the FRT, thus achieving grid support and inverter protection simultaneously. When the fault is self-cleared at $t=8\mathrm{s},$ $P^{+}$ and $Q^{+}$ return smoothly to their original values according to the droop control.

6.2. Operation under Single-Phase Voltage Sag

In order to test the operation of the proposed controller under unbalanced faults, a single-phase voltage sag is applied on $v_{ga},$ with its RMS value dropping by $0.65\mathrm{p}.\mathrm{u}.$ which leads to $V_g^{+}\approx 0.78\mathrm{p}.\mathrm{u}.,$ while the inverter is operating with droop control. As it can be observed in Figure 5, the current allocation algorithm leads the RMS currents to the values $I_{grms}^{+}=6.75\mathrm{A}$ and $I_{grms}^{-}=3.15\mathrm{A}$. It should be noted that according to the proposed controller operation, the components $I_{grms}^{+}$ and $I_{grms}^{-}$ are tracking their maximum values from Equations (32) and (33) during voltage drops (unless the desired $V^{-}=E_{rms}^{-}$ regulation has been achieved with less than the maximum negative sequence current). Hence, the total current is regulated close to its maximum value $I_{grms}^{max}$ but without exceeding it. The primary objective of the proposed controller is achieved since as it is depicted in Figure 5, $V_c^{+}$ is regulated to $0.9E_{rms}^{+}.$ This verifies the proper selection of the value $I_{grms}^{max+}$ which further leads to the $S_{max}^{+}$ calculation, while the rest of the available inverter capacity is assigned to negative sequence current controller so that $V^{-},$ shown in Figure 5, is eliminated as much as possible. The real and reactive power components injected to the grid according to Equation (28) and Equations (29) and (30) are depicted in Figure 6 while, even if the proposed controller does not deal directly with the VUF but aims to increase the positive sequence voltage and eliminate the negative sequence voltage, in this certain scenario, it can be seen in Figure 7 that $VUF$ at the PCC is eliminated by 7% when compared to $VU{F}_{grid}.$ At the steady-state, $P_{set}^{-}$ and $Q_{set}^{-}$ are not tracked since priority is given to the current-limiting property. However, if greater capacity was available, such that $V^{-}=E_{rms}^{-},$ $P^{-}$ and $Q^{-}$ would be regulated to their reference values. After $1.5\mathrm{s},$ the fault is self-cleared and the positive sequence components are driven to their initial values according to droop control while the negative sequence components are driven to 0.

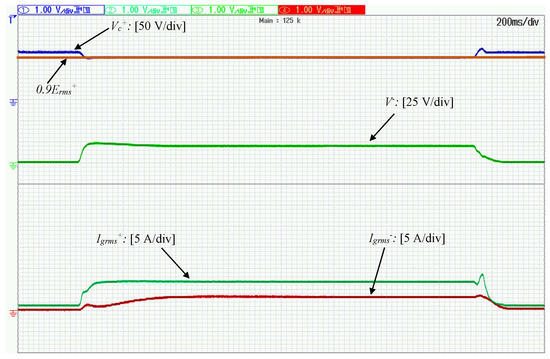
Figure 5. Operation under single-phase voltage drop ($V_{ga}=0.35\mathrm{p}.\mathrm{u}.$): Positive and negative sequence RMS voltages and currents.

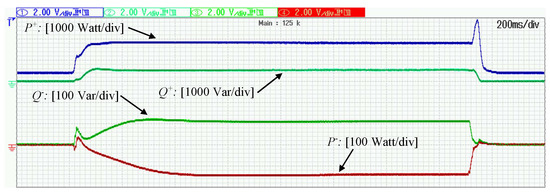
Figure 6. Operation under single-phase voltage drop ($V_{ga}=0.35\mathrm{p}.\mathrm{u}.$): Injected powers.

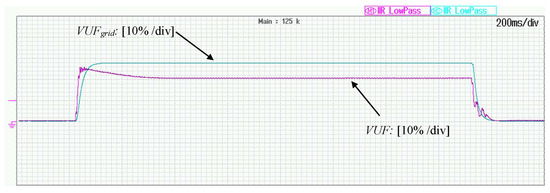
Figure 7. Operation under single-phase voltage drop ($V_{ga}=0.35\mathrm{p}.\mathrm{u}.$): Voltage unbalance factors.

Note that during the clearing transient, the value $I_{grms}^{+}+I_{grms}^{-}$ reaches the value $12\mathrm{A}$ for $10\mathrm{ms},$ however, it never exceeds its ultimate bound during transients set at $14\mathrm{A},$ as proven in the theoretic analysis presented in this paper.

6.3. Operation under Two-Phase Voltage Sag

To further demonstrate the operation of the proposed controller under unbalanced faults, a two-phase voltage sag is now applied, with the RMS values of $v_{ga}$ and $v_{gc}$ dropping so that $V_{ga}=0.73\mathrm{p}.\mathrm{u}.$ and $V_{gc}=0.65\mathrm{p}.\mathrm{u}.$ leading to $V_g^{+}\approx 0.8\mathrm{p}.\mathrm{u}.,$ while the inverter is operated in the droop control mode. As mentioned before, the maximum current assigned to the positive sequence controller is tracked by the controller leading to $I_{grms}^{+}=6.1\mathrm{A}$ in order to optimize the support operation and thus, $V_c^{+}$ is regulated to $0.9E_{rms}^{+},$ as shown in Figure 8. The the rest of the available current, is assigned to the negative sequence current controller which leads to $I_{grms}^{-}=3.7\mathrm{A}$ thus, managing to eliminate the negative sequence voltage, shown in Figure 8. Hence, the total current never violates its maximum value $I_{grms}^{max}=10\mathrm{A}.$ The powers injected to the grid in both sequences can be observed in Figure 9 while the $VUF$ is eliminated by 7% compared to the $VU{F}_{grid},$ as depicted in Figure 10. After $1.5\mathrm{s},$ the fault is self-cleared and the positive sequence components are driven to their initial values according to droop control while the negative sequence components are driven to 0. It is underlined that during the clearing transient, the addition $I_{grms}^{+}+I_{grms}^{-},$ reaches the value of $11.5\mathrm{A}$ for less than $10\mathrm{ms}$ without ever violating the ultimate bound for transient currents, set at $14\mathrm{A}.$

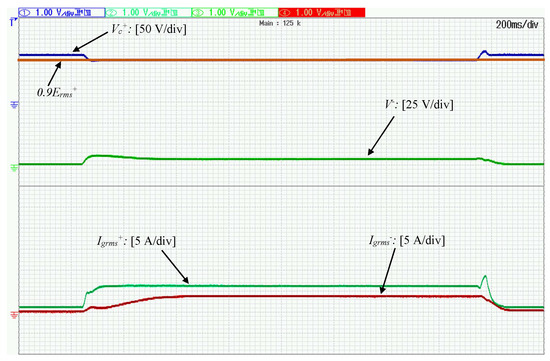
Figure 8. Operation under two-phase voltage drop ($V_{ga}=0.73\mathrm{p}.\mathrm{u}.$ and $V_{gc}=0.65\mathrm{p}.\mathrm{u}.$): Positive and negative sequence RMS voltages and currents.

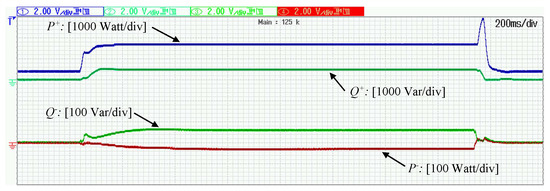
Figure 9. Operation under two-phase voltage drop ($V_{ga}=0.73\mathrm{p}.\mathrm{u}.$ and $V_{gc}=0.65\mathrm{p}.\mathrm{u}.$): Injected powers.

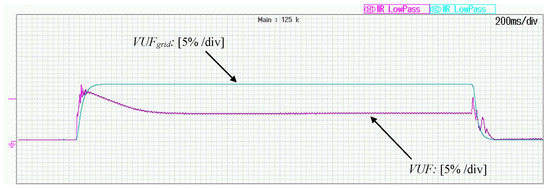
Figure 10. Operation under two-phase voltage drop ($V_{ga}=0.73\mathrm{p}.\mathrm{u}.$ and $V_{gc}=0.65\mathrm{p}.\mathrm{u}.$): Voltage unbalance factors.

7. Conclusions

In this paper, a new control concept that offers an inherent current limitation at all times is proposed for three-phase grid-tied droop-controlled inverters. The proposed controller complies with the latest grid code requirements and apart from droop control, voltage support through maximum power injection is achieved under both balanced and unbalanced grid faults. To accomplish this, two novel outer-loop controllers are applied to both positive and negative sequence while boundedness of the grid current is achieved during transients without the need of saturation units. A new way of dividing the available current into the positive and negative sequence is proposed so that positive sequence voltage is increased and the negative sequence voltage is eliminated. Asymptotic stability of any equilibrium point of the closed-loop system within the bounded operating range is proven without assuming knowledge of the system parameters. The proposed control approach is verified through extensive real-time simulation results.

Future research will focus on the experimental validation of the proposed control approach and the comparison with other techniques that aim to implement the voltage support concept under balanced and unbalanced grid faults.