Photovoltaic Power Converter Management in Unbalanced Low Voltage Networks with Ancillary Services Support
Abstract
1. Introduction
1.1. Generally Known Information about the Topic
1.2. Prior Studies’ Historical Context to the Research
1.3. Hypothesis and an Overview of the Results
1.4. Article Organization
2. PV Inverters Topology and Control
3. Proposed PV Inverter Control Strategy
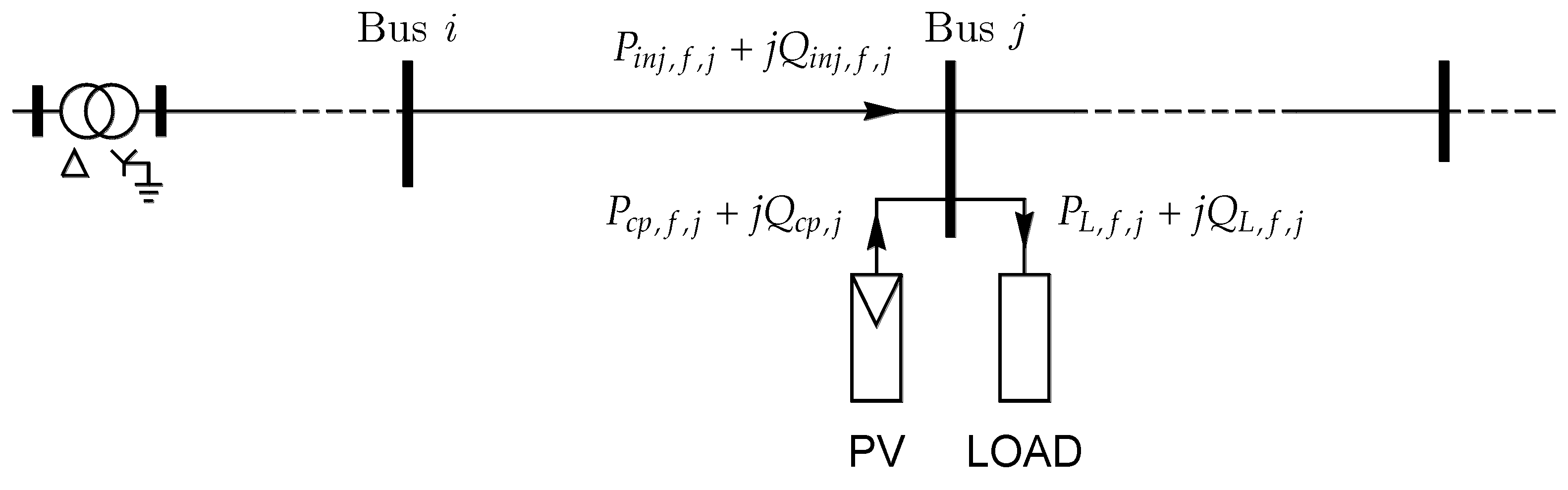
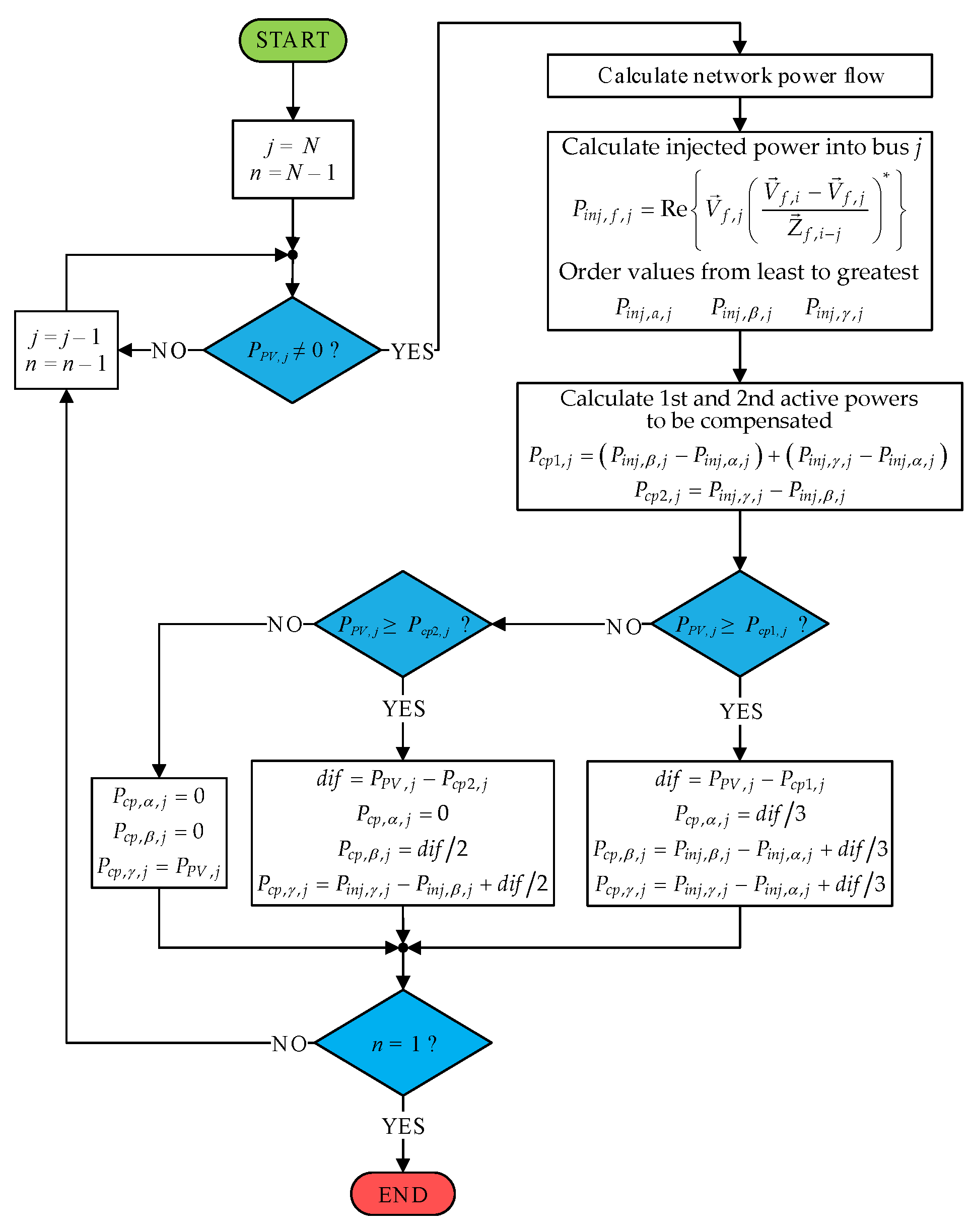
3.1. Proposed Imbalance Compensation Algorithm
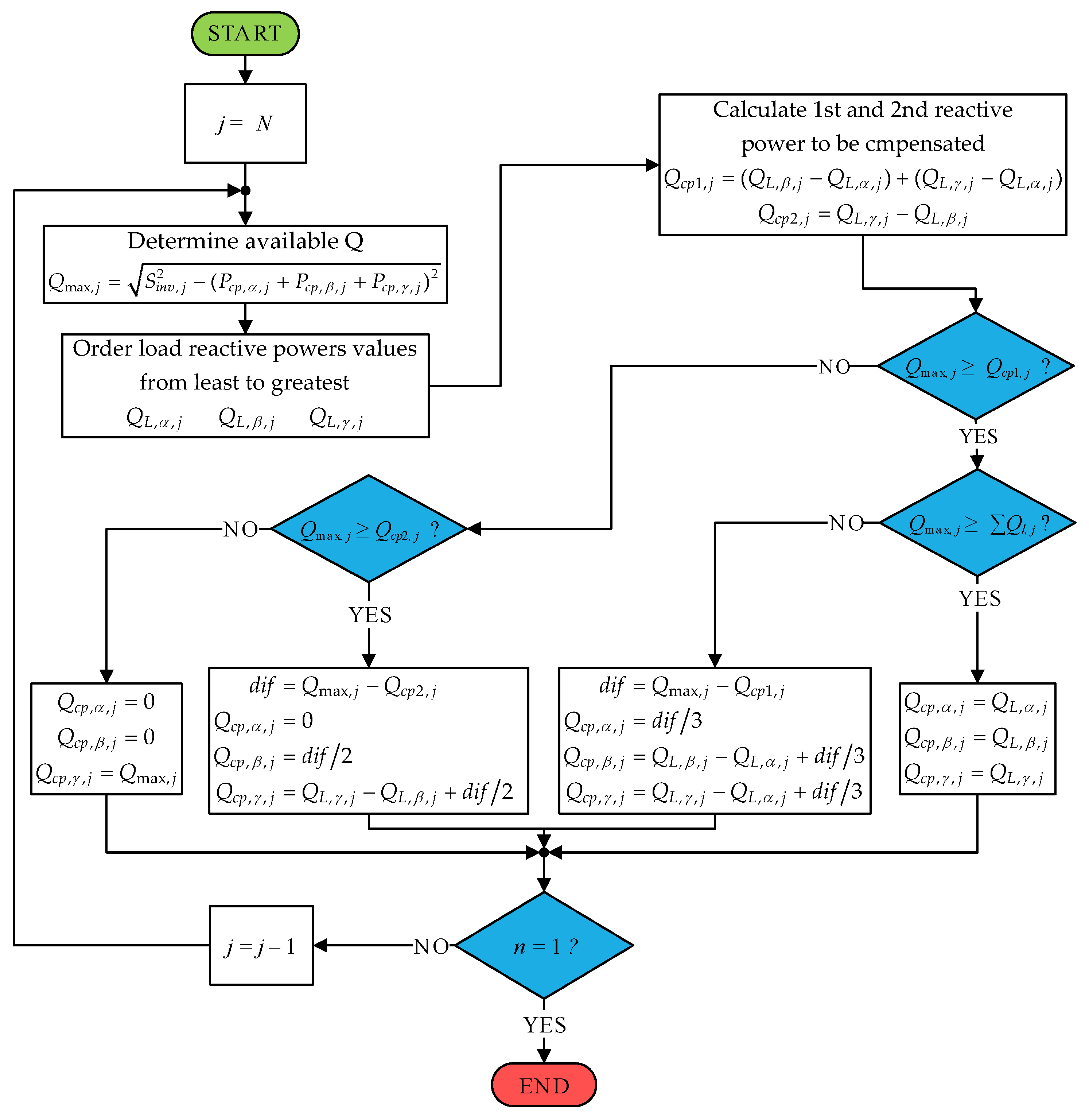
3.2. Proposed Reactive Power Compensation Algorithm.
4. Simulation Results and Analysis
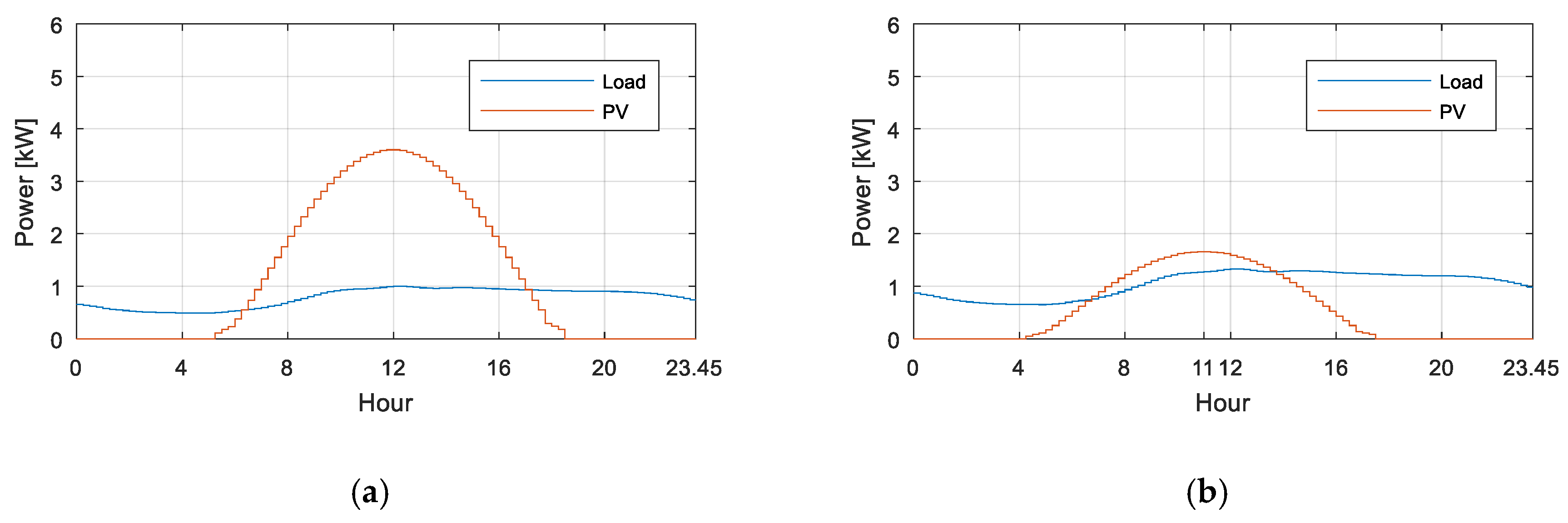
4.1. Test Network
4.2. Simulated Case Studies
- Scenario 0: No PV production;
- Scenario 1: PV production, no imbalance compensation and no reactive power compensation;
- Scenario 2: PV production, imbalance compensation and no reactive power compensation;
- Scenario 3: PV production, imbalance and reactive power compensation.
4.3. Scenario 0. No Photovoltaic Production
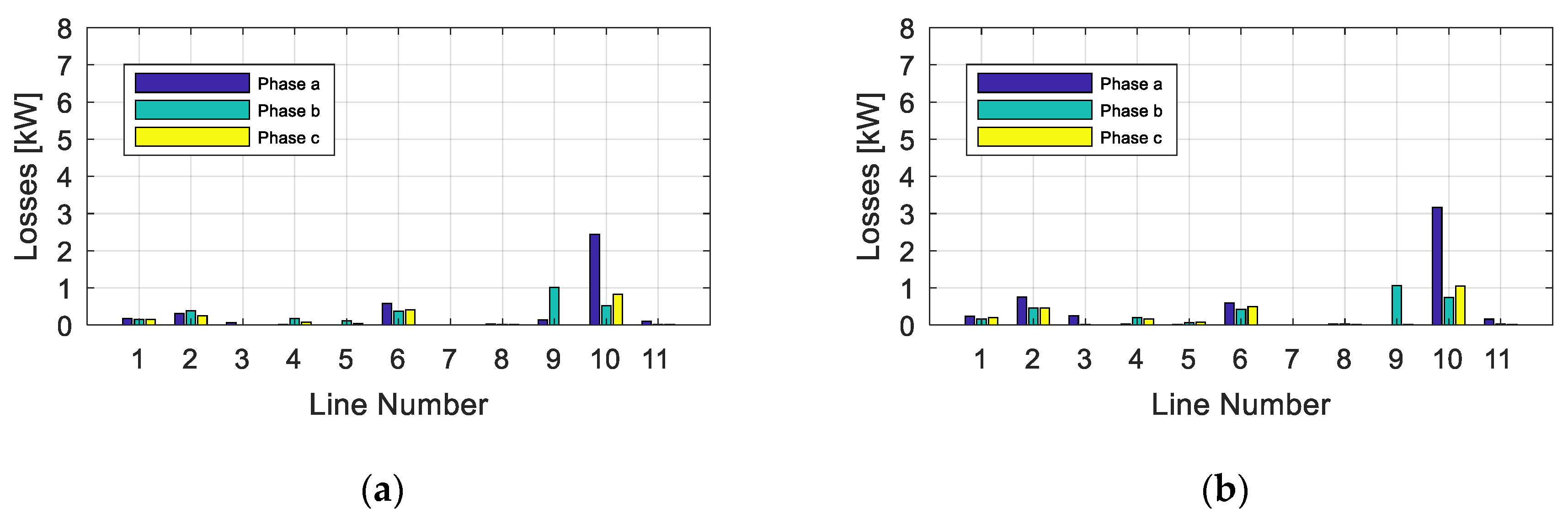
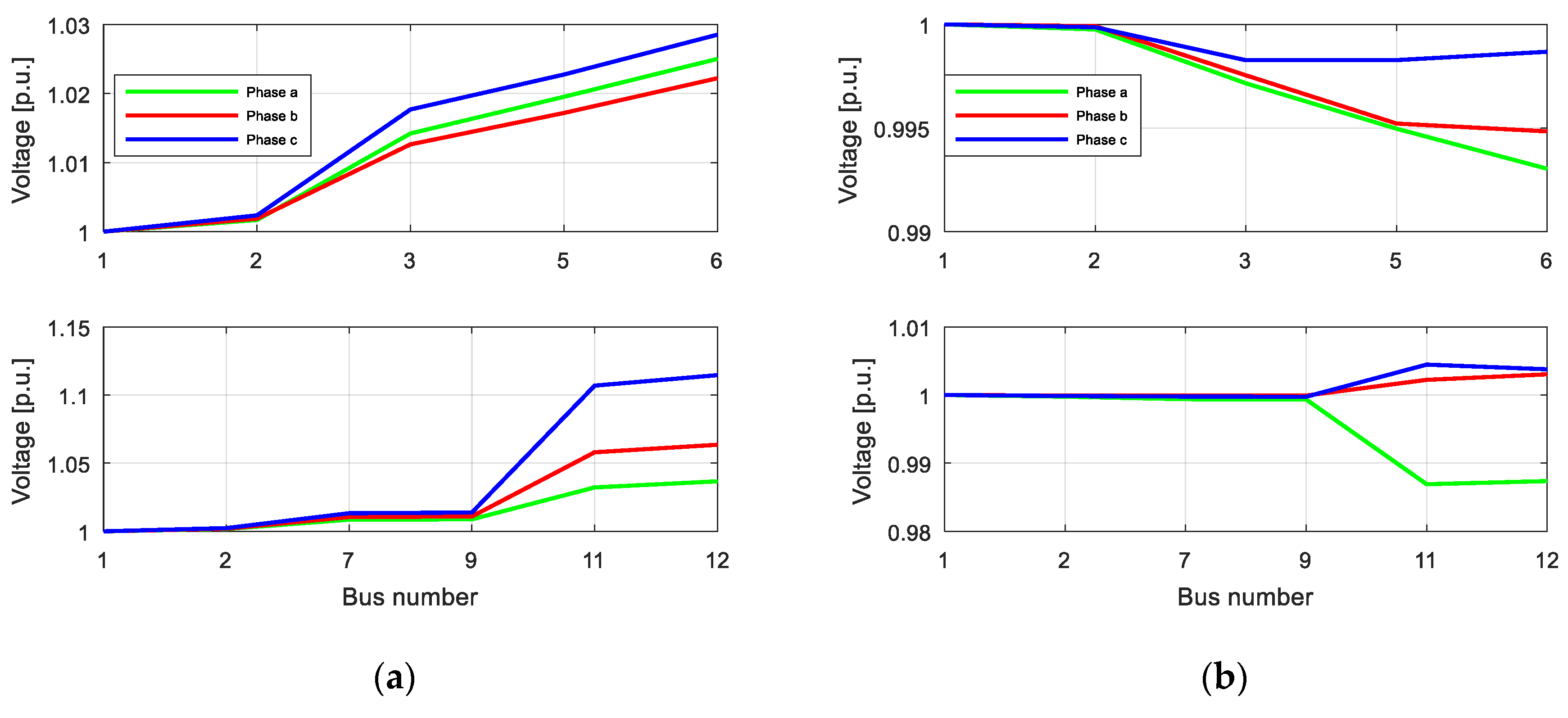
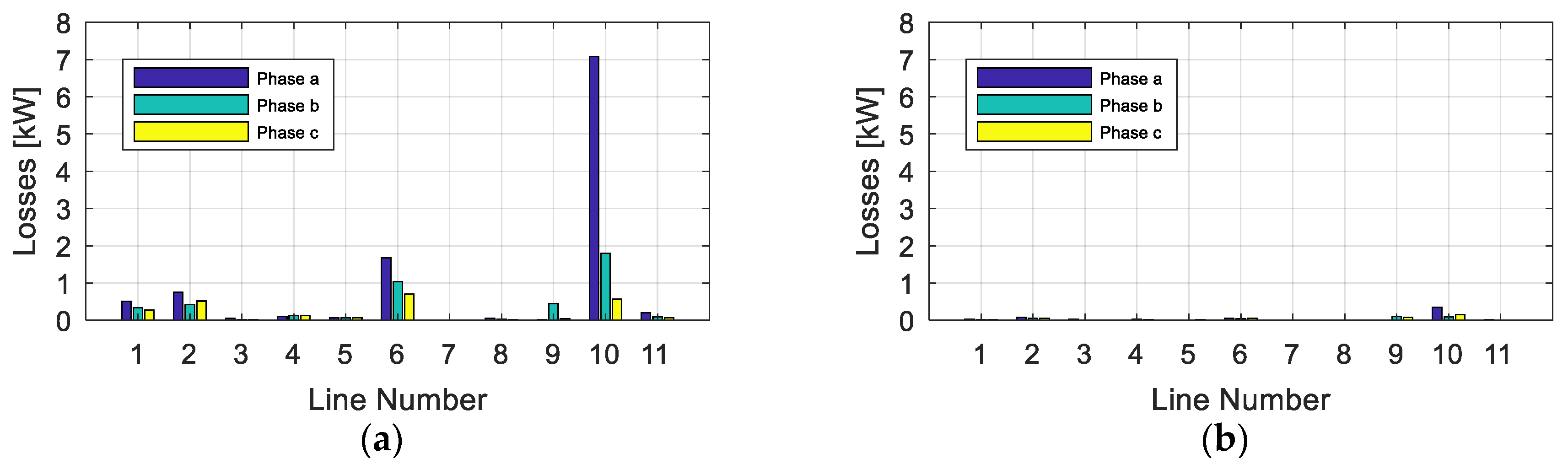
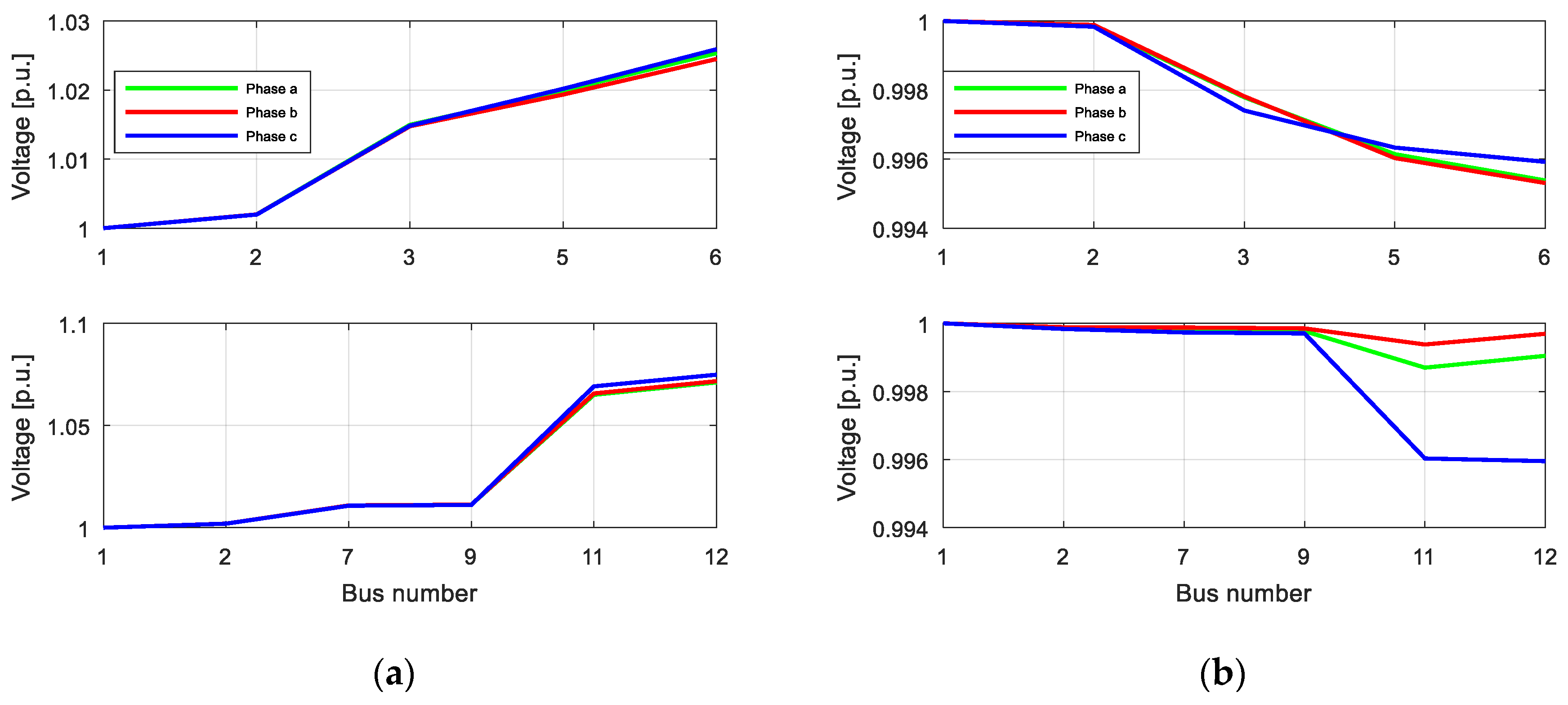
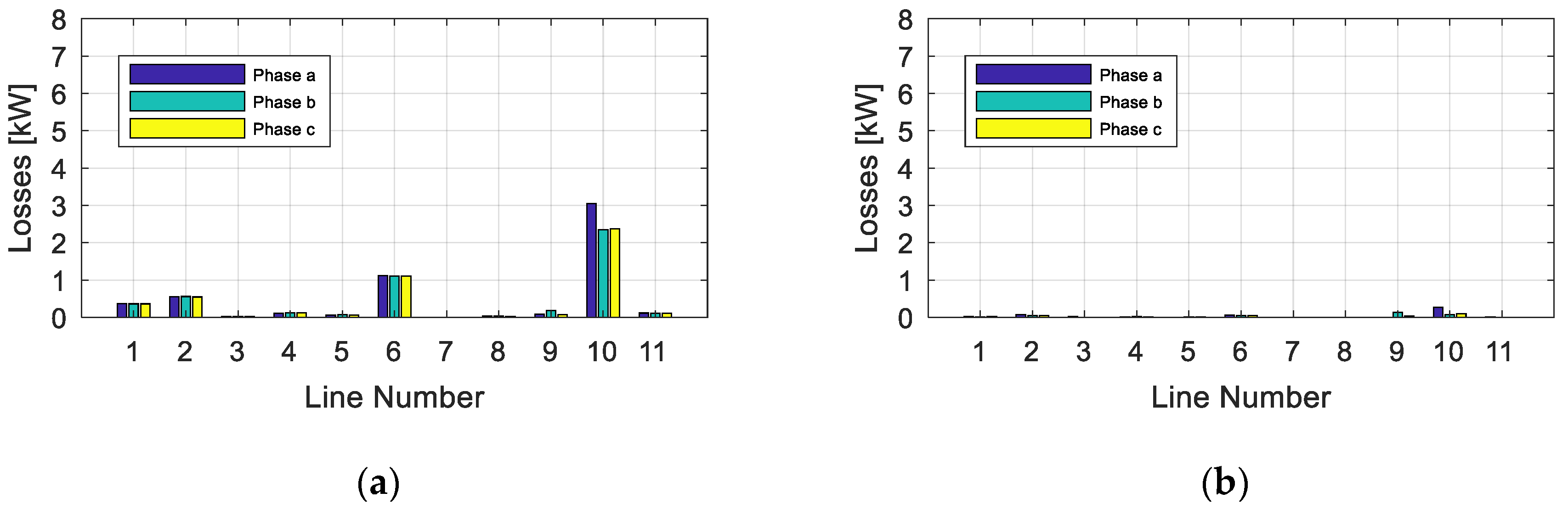
4.4. Scenario 1: PV Production, No Imbalance Compensation and No Reactive Power Compensation
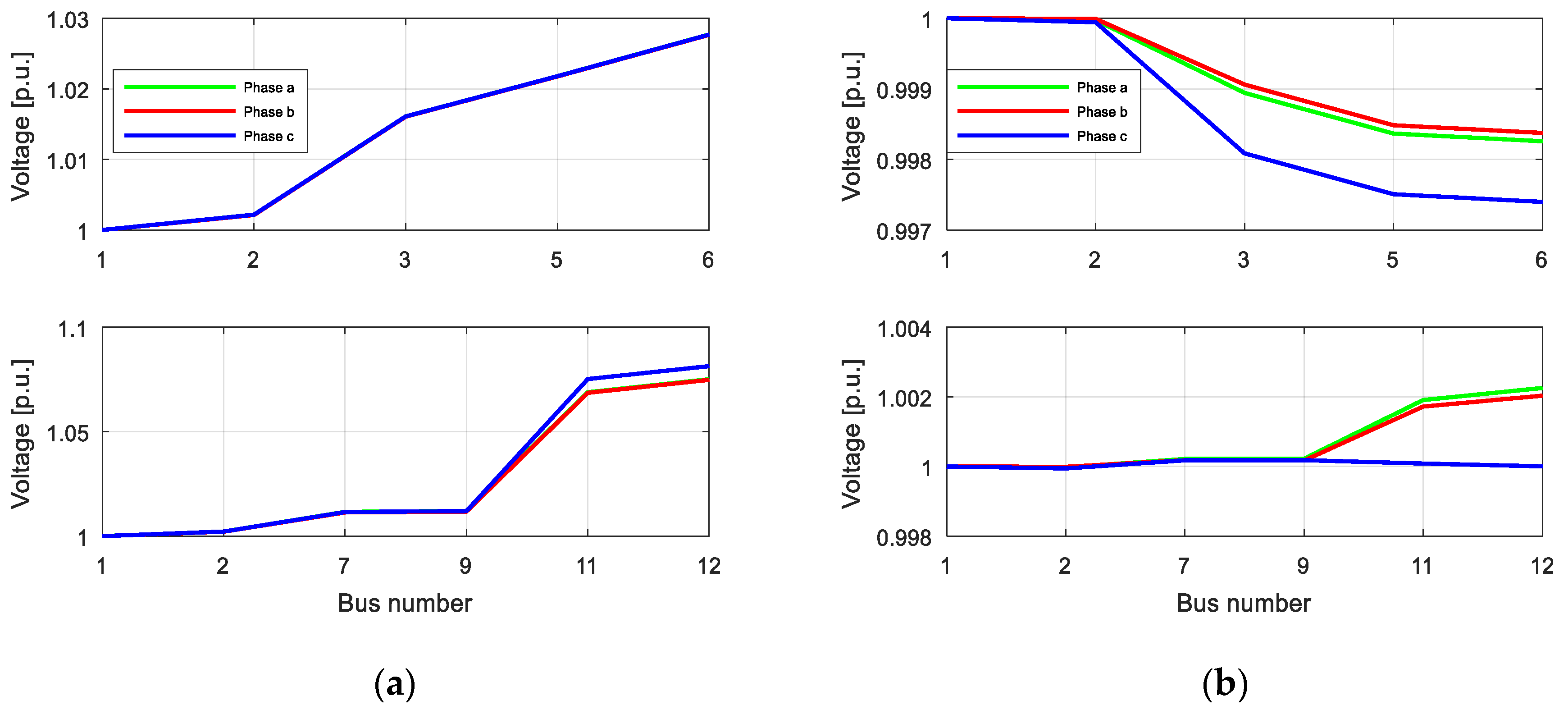
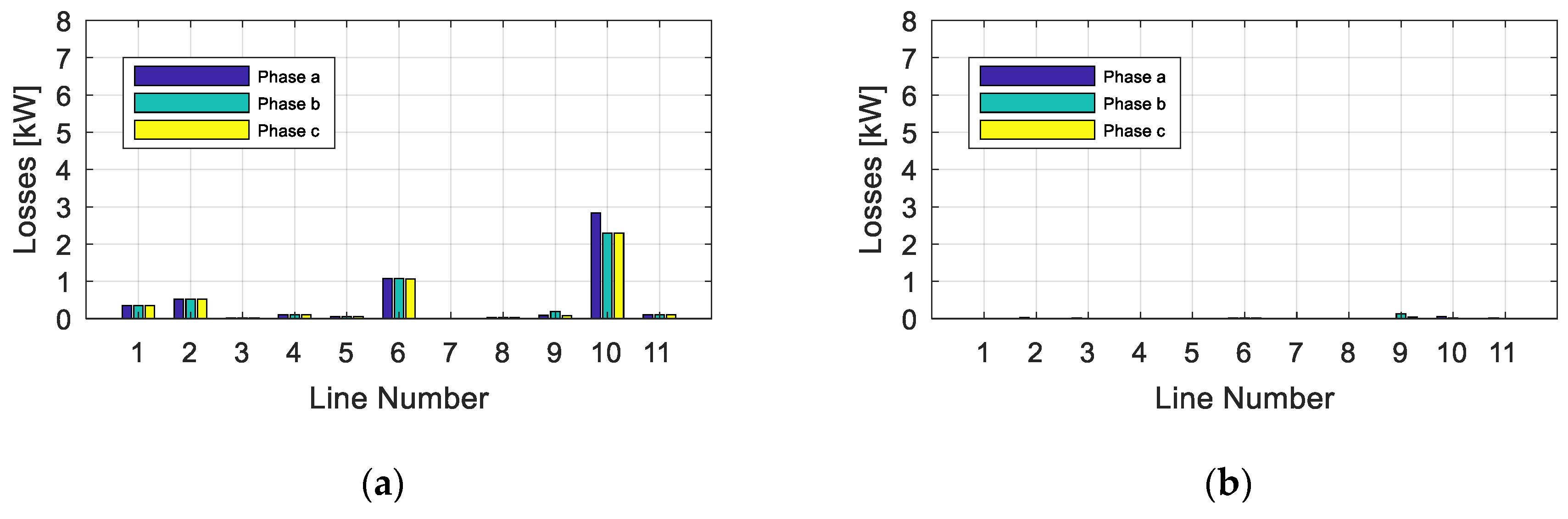
4.5. Scenario 2: PV Production, Imbalance Compensation and No Reactive Power Compensation
4.6. Scenario 3: PV Production, Imbalance and Reactive Power Compensation
4.7. Comparative Analysis
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Bellekom, S.; Arentsen, M.J.; van Gorkum, K. Prosumption and the distribution and supply of electricity. Energy Sustain. Soc. 2016, 6, 1–17. [Google Scholar] [CrossRef]
- Postigo Marcos, F.; Mateo Domingo, C.; Gómez San Román, T.; Palmintier, B.; Hodge, B.; Krishnan, V.; de Cuadra García, F.; Mather, B. A Review of Power Distribution Test Feeders in the United States and the Need for Synthetic Representative Networks. Energies 2017, 10, 1896. [Google Scholar] [CrossRef]
- Schneider, K.P.; Mather, B.A.; Pal, B.C.; Ten, C.W.; Shirek, G.J.; Zhu, H.; Fuller, J.C.; Pereira, J.L.R.; Ochoa, L.F.; de Araujo, L.R.; et al. Analytic Considerations and Design Basis for the IEEE Distribution Test Feeders. IEEE Trans. Power Syst. 2018, 33, 3181–3188. [Google Scholar] [CrossRef]
- Mateo, C.; Prettico, G.; Gómez, T.; Cossent, R.; Gangale, F.; Frías, P.; Fulli, G. European representative electricity distribution networks. Int. J. Electr. Power Energy Syst. 2018, 99, 273–280. [Google Scholar] [CrossRef]
- Teodorescu, R.; Liserre, M.; Rodríguez, P. Grid Converters for Photovoltaic and Wind Power Systems, 1st ed.; Wiley: Chichester, UK, 2011. [Google Scholar]
- Matos, D.; Catalão, J.P.S. Geração Distribuída e os seus Impactes no Funcionamento da Rede Elétrica: Parte 1. In Proceedings of the International Conference on Engineering, Covilhã, Portugal, 27–29 November 2013. [Google Scholar]
- Röhrig, C.; Rudion, K.; Styczynski, Z.A.; Nehrkorn, H.J. Fulfilling the standard EN 50160 in distribution networks with a high penetration of renewable energy system. In Proceedings of the 2012 3rd IEEE PES Innovative Smart Grid Technologies Europe (ISGT Europe), Berlin, Germany, 14–17 October 2012. [Google Scholar]
- Masoum, A.S.; Moses, P.S.; Masoum, M.A.S.; Abu-Siada, A. Impact of rooftop PV generation on distribution transformer and voltage profile of residential and commercial networks. In Proceedings of the 2012 IEEE PES Innovative Smart Grid Technologies (ISGT), Washington, DC, USA, 16–20 January 2012. [Google Scholar]
- Rodriguez-Calvo, A.; Cossent, R.; Frías, P. Integration of PV and EVs in unbalanced residential LV networks and implications for the smart grid and advanced metering infrastructure deployment. Int. J. Electr. Power Energy Syst. 2017, 91, 121–134. [Google Scholar] [CrossRef]
- CENELEC. Voltage Characteristics of Electricity Supplied by Public Distribution Systems; European Standard EN50160; CENELEC: Brussels, Belgium, 2015. [Google Scholar]
- Yu, H.; Pan, J.; Xiang, A. A multi-function grid-connected PV system with reactive power compensation for the grid. Sol. Energy 2005, 79, 101–106. [Google Scholar] [CrossRef]
- Piegari, L.; Tricoli, P. A control algorithm of power converters in smart-grids for providing uninterruptible ancillary services. In Proceedings of the 14th International Conference on Harmonics and Quality of Power—ICHQP 2010, Bergamo, Italy, 26–29 September 2010. [Google Scholar]
- Pires, V.F.; Martins, J.F.; Silva, J.F. A control structure for a photovoltaic supply system with power compensation characteristics suitable for smart grid topologies. In Proceedings of the 2013 International Conference-Workshop Compatibility and Power Electronics, Ljubljana, Slovenia, 5–7 June 2013. [Google Scholar]
- Fernao Pires, V.; Husev, O.; Vinnikov, D.; Martins, J.F. A control strategy for a grid-connected PV system with unbalanced loads compensation. In Proceedings of the 2015 9th International Conference on Compatibility and Power Electronics (CPE), Costa da Caparica, Portugal, 24–26 June 2015. [Google Scholar]
- Kim, E.; Kim, G.; Hwang, C.; Jeon, J.; Ahn, J. A novel three-phase four-leg inverter based load unbalance compensator for stand-alone microgrid. Int. J. Electr. Power Energy Syst. 2015, 65, 70–75. [Google Scholar] [CrossRef]
- Shahnia, F.; Wolfs, P.J.; Ghosh, A. Voltage Unbalance Reduction in Low Voltage Feeders by Dynamic Switching of Residential Customers Among Three Phases. IEEE Trans. Smart Grid 2014, 5, 1318–1327. [Google Scholar] [CrossRef]
- Su, X.; Masoum, M.A.S.; Wolfs, P.J. Optimal PV Inverter Reactive Power Control and Real Power Curtailment to Improve Performance of Unbalanced Four-Wire LV Distribution Networks. IEEE Trans. Sustain. Energy 2014, 5, 967–977. [Google Scholar] [CrossRef]
- Gagrica, O.; Nguyen, P.H.; Kling, W.L.; Uhl, T. Microinverter Curtailment Strategy for Increasing Photovoltaic Penetration in Low-Voltage Networks. IEEE Trans. Sustain. Energy 2015, 6, 369–379. [Google Scholar] [CrossRef]
- Su, X.; Masoum, M.A.S.; Wolfs, P.J. Multi-Objective Hierarchical Control of Unbalanced Distribution Networks to Accommodate More Renewable Connections in the Smart Grid Era. IEEE Trans. Power Syst. 2016, 31, 3924–3936. [Google Scholar] [CrossRef]
- Jin, P.; Li, Y.; Li, G.; Chen, Z.; Zhai, X. Optimized hierarchical power oscillations control for distributed generation under unbalanced conditions. Appl. Energy 2017, 194, 343–352. [Google Scholar] [CrossRef]
- Alam, M.J.E.; Muttaqi, K.M.; Sutanto, D. Community Energy Storage for Neutral Voltage Rise Mitigation in Four-Wire Multigrounded LV Feeders with Unbalanced Solar PV Allocation. IEEE Trans. Smart Grid 2015, 6, 2845–2855. [Google Scholar] [CrossRef]
- Brandao, D.I.; de Araújo, L.S.; Caldognetto, T.; Pomilio, J.A. Coordinated control of three- and single-phase inverters coexisting in low-voltage microgrids. Appl. Energy 2018, 228, 2050–2060. [Google Scholar] [CrossRef]
- Unigwe, O.; Okekunle, D.; Kiprakis, A. Economical distributed voltage control in low-voltage grids with high penetration of photovoltaic. CIRED Open Access Proc. J. 2017, 2017, 1722–1725. [Google Scholar] [CrossRef]
- Olivier, F.; Aristidou, P.; Ernst, D.; Van Cutsem, T. Active Management of Low-Voltage Networks for Mitigating Overvoltages Due to Photovoltaic Units. IEEE Trans. Smart Grid 2016, 7, 926–936. [Google Scholar] [CrossRef]
- Fang, Y.; Li, R.; Wang, L.; Song, B.; Li, E.; Zhang, Q. Research of active load regulation method for distribution network considering distributed photovoltaic and electric vehicles. J. Eng. 2017, 2017, 2444–2448. [Google Scholar] [CrossRef]
- Exposto, B.; Monteiro, V.; Pinto, J.G.; Pedrosa, D.; Meléndez, A.A.N.; Afonso, J.L. Three-phase current-source shunt active power filter with solar photovoltaic grid interface. In Proceedings of the 2015 IEEE International Conference on Industrial Technology (ICIT), Seville, Spain, 17–19 March 2015. [Google Scholar]
- Dai, X.; Chao, Q. The research of photovoltaic grid-connected inverter based on adaptive current hysteresis band control scheme. In Proceedings of the 2009 International Conference on Sustainable Power Generation and Supply, Nanjing, China, 6–7 April 2009. [Google Scholar]
- Blorfan, A.; Wira, P.; Flieller, D.; Sturtzer, G.; Mercklé, J. A three-phase hybrid active power filter with photovoltaic generation and hysteresis current control. In Proceedings of the IECON 2011—37th Annual Conference of the IEEE Industrial Electronics Society, Melbourne, Australia, 7–10 November 2011. [Google Scholar]
- Feng, W.; Sun, K.; Guan, Y.; Guerrero, J.M.; Xiao, X. Active Power Quality Improvement Strategy for Grid-Connected Microgrid Based on Hierarchical Control. IEEE Trans. Smart Grid 2018, 9, 3486–3495. [Google Scholar] [CrossRef]
- Milanes-Montero, M.I.; Barrero-Gonzalez, F.; Pando-Acedo, J.; Gonzalez-Romera, E.; Romero-Cadaval, E.; Moreno-Munoz, A. Active, reactive and harmonic control for distributed energy micro-storage systems in smart communitie homes. Energies 2017, 10, 448. [Google Scholar] [CrossRef]
- Milanes-Montero, M.I.; Barrero-Gonzalez, F.; Pando-Acedo, J.; Gonzalez-Romera, E.; Romero-Cadaval, E.; Moreno-Munoz, A. Smart Community Electric Energy Micro-Storage Systems with Active Functions. IEEE Trans. Ind. Appl. 2018, 54, 1975–1982. [Google Scholar] [CrossRef]
- Fernão Pires, V.; Romero-Cadaval, E.; Vinnikov, D.; Roasto, I.; Martins, J.F. Power converter interfaces for electrochemical energy storage systems—A review. Energy Convers. Manag. 2014, 86, 453–475. [Google Scholar] [CrossRef]
- Camilo, F.M.; Castro, R.; Almeida, M.E.; Pires, V.F. Self-consumption and storage as a way to facilitate the integration of renewable energy in low voltage distribution networks. IET Gener. Transm. Distrib. 2016, 10, 1741–1748. [Google Scholar] [CrossRef]
- Caracterização da procura de energia elétrica em 2018. Entidade Reguladora dos Serviços Energéticos de Portugal. Available online: www.erse.pt (accessed on 30 September 2018).
- PVGIS. Photovoltaic Geographical Information System—Interactive Maps. Available online: http://re.jrc.ec.europa.eu/pvgis/apps4/pvest.php# (accessed on 30 September 2018).
- Liu, X.; Shahidehpour, M.; Li, Z.; Liu, X.; Cao, Y.; Tian, W. Protection Scheme for Loop-Based Microgrids. IEEE Trans. Smart Grid 2017, 8, 1340–1349. [Google Scholar] [CrossRef]
- Tekpeti, B.S.; Kang, X.; Huang, X. Fault analysis of solar photovoltaic penetrated distribution systems including overcurrent relays in presence of fluctuations. Int. J. Electr. Power Energy Syst. 2018, 100, 517–530. [Google Scholar] [CrossRef]

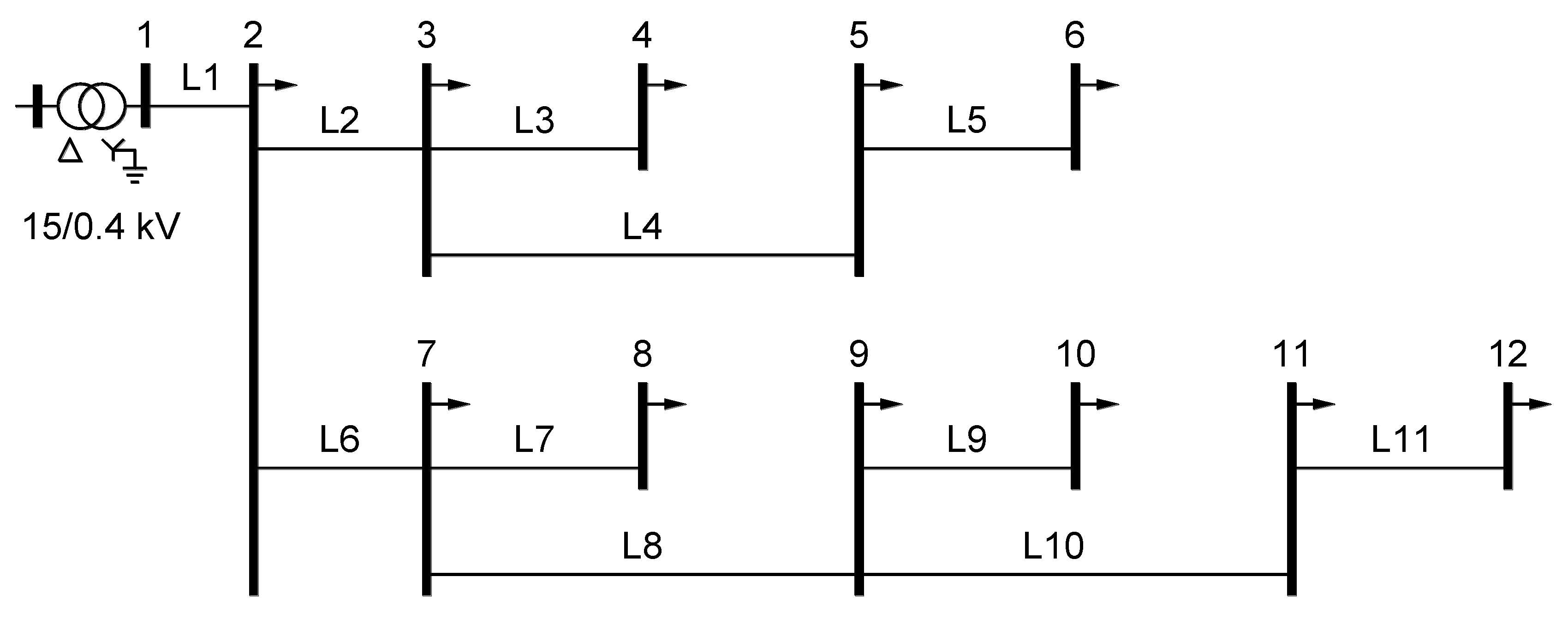

| Line | L1 | L2 | L3 | L4 | L5 | L6 | L7 | L8 | L9 | L10 | L11 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| R (Ω) | 0.00074 | 0.01974 | 0.02547 | 0.01589 | 0.03056 | 0.00446 | 0.00213 | 0.00043 | 0.05795 | 0.07513 | 0.01891 |
| X (Ω) | 0.00033 | 0.00630 | 0.00813 | 0.00796 | 0.00975 | 0.00142 | 0.00107 | 0.00021 | 0.01780 | 0.02397 | 0.00581 |
| Scenario Number | Highest Radiation Day | Lowest Radiation Day | ||
|---|---|---|---|---|
| (kW) | (kW) | (kW) | (kW) | |
| Scenario 0 (Baseline) | 8.50138 | 304.20365 | 10.96334 | 353.68494 |
| Scenario 1 | 17.23334 | −471.07305 | 1.24492 | −15.10588 |
| Scenario 2 | 15.23509 | −473.0713 | 1.08481 | −15.26599 |
| Scenario 3 | 14.56905 | −473.73734 | 0.41763 | −15.93317 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Barrero-González, F.; Pires, V.F.; Sousa, J.L.; Martins, J.F.; Milanés-Montero, M.I.; González-Romera, E.; Romero-Cadaval, E. Photovoltaic Power Converter Management in Unbalanced Low Voltage Networks with Ancillary Services Support. Energies 2019, 12, 972. https://doi.org/10.3390/en12060972
Barrero-González F, Pires VF, Sousa JL, Martins JF, Milanés-Montero MI, González-Romera E, Romero-Cadaval E. Photovoltaic Power Converter Management in Unbalanced Low Voltage Networks with Ancillary Services Support. Energies. 2019; 12(6):972. https://doi.org/10.3390/en12060972
Chicago/Turabian StyleBarrero-González, Fermín, Victor Fernão Pires, José L. Sousa, João F. Martins, María Isabel Milanés-Montero, Eva González-Romera, and Enrique Romero-Cadaval. 2019. "Photovoltaic Power Converter Management in Unbalanced Low Voltage Networks with Ancillary Services Support" Energies 12, no. 6: 972. https://doi.org/10.3390/en12060972
APA StyleBarrero-González, F., Pires, V. F., Sousa, J. L., Martins, J. F., Milanés-Montero, M. I., González-Romera, E., & Romero-Cadaval, E. (2019). Photovoltaic Power Converter Management in Unbalanced Low Voltage Networks with Ancillary Services Support. Energies, 12(6), 972. https://doi.org/10.3390/en12060972







