Hybrid Empirical Mode Decomposition with Support Vector Regression Model for Short Term Load Forecasting
Abstract
1. Introduction
2. The Proposed H-EMD-SVR-PSO Model
2.1. The Empirical Mode Decomposition (EMD) Technique
2.2. The Hybrid Support Vector Regression with Particle Swarm Optimization (SVR-PSO) Model
2.3. The Full Procedure of the Proposed H-EMD-PSO-SVR Model
3. Experimental Examples
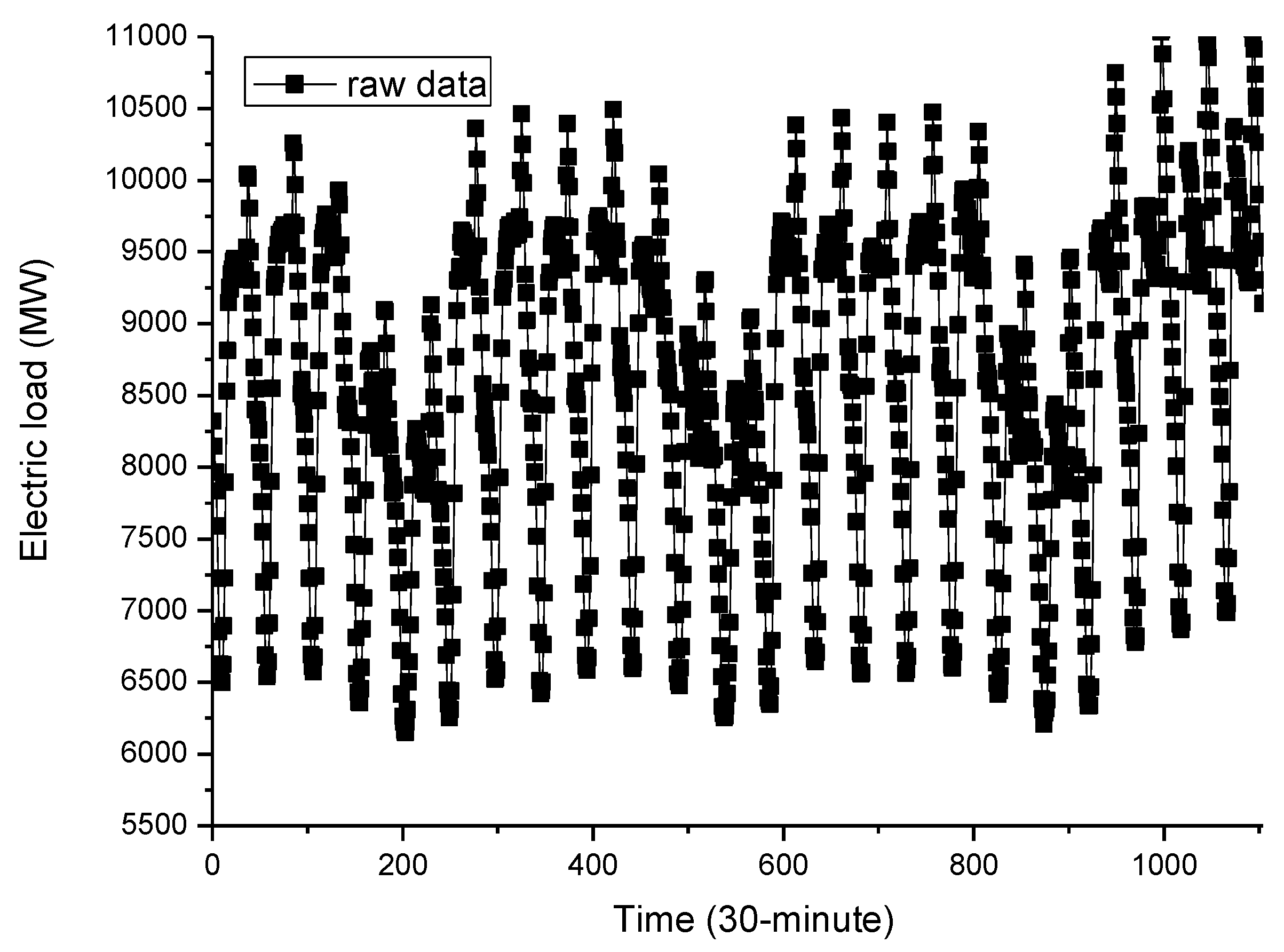
3.1. Data Sets of Experimental Examples
3.2. Parameter Settings of the SVR-PSO Model
3.3. Forecasting Accuracy Indexes
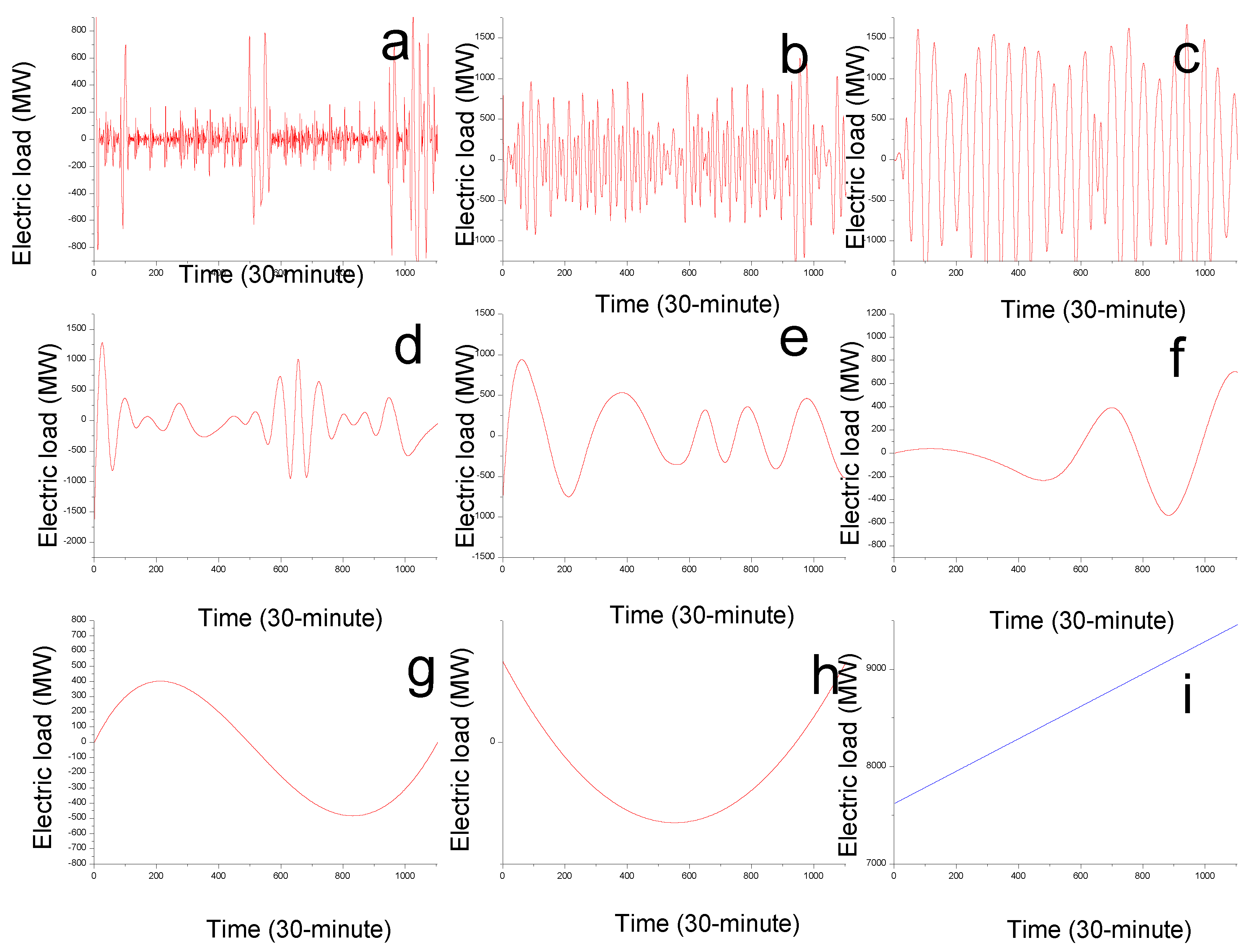
3.4. Decomposition Results after EMD
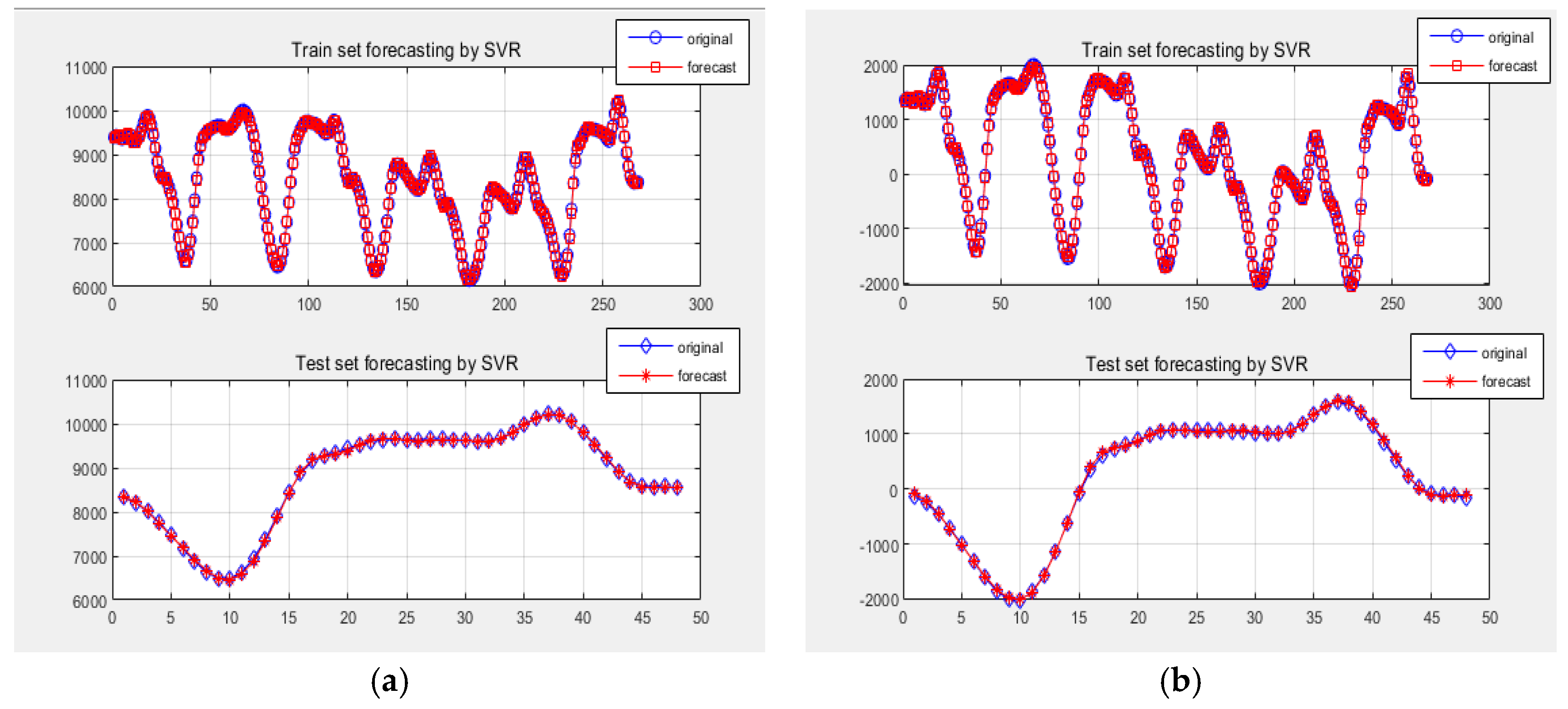
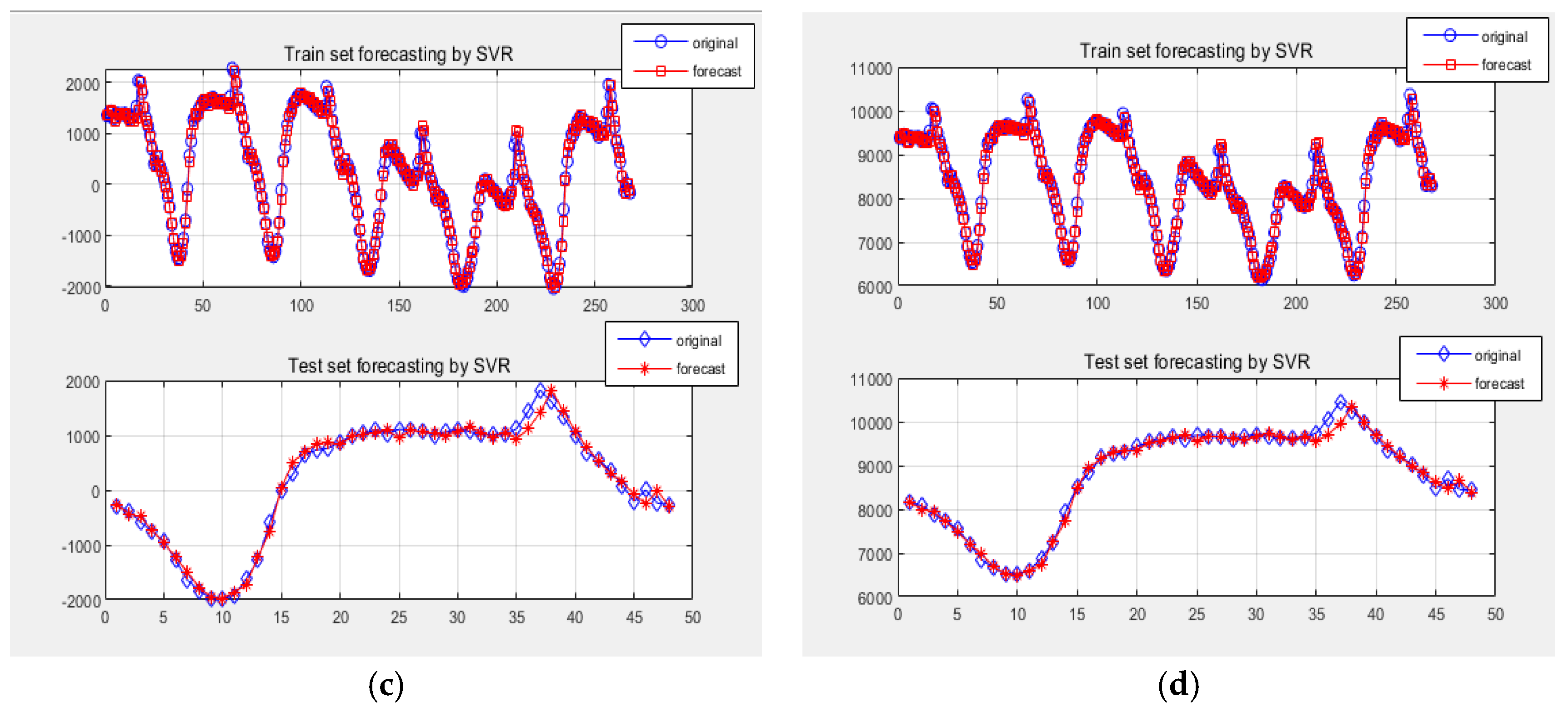
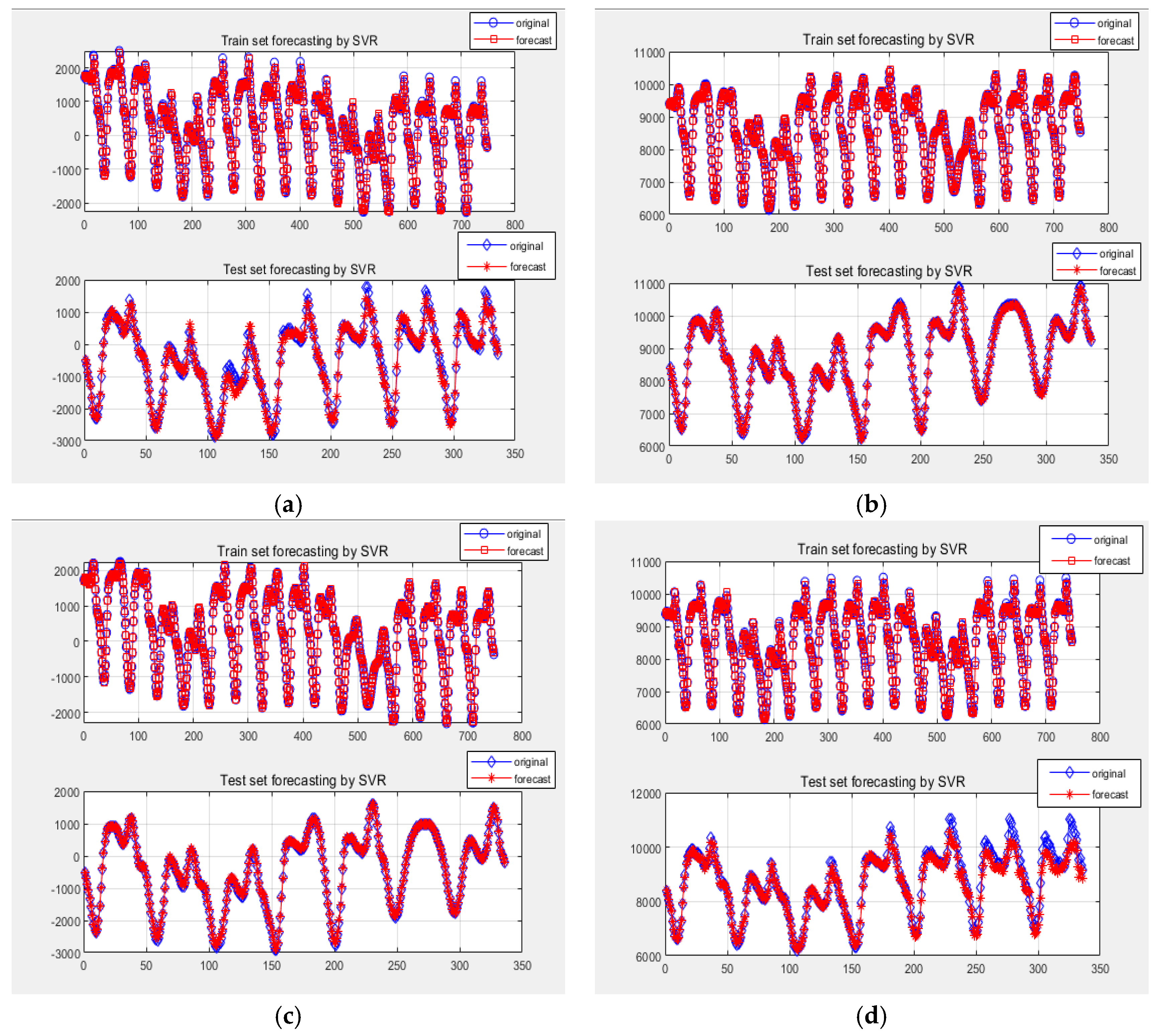
3.5. Forecasting Results by the SVR-PSO Model for Three Defined Items
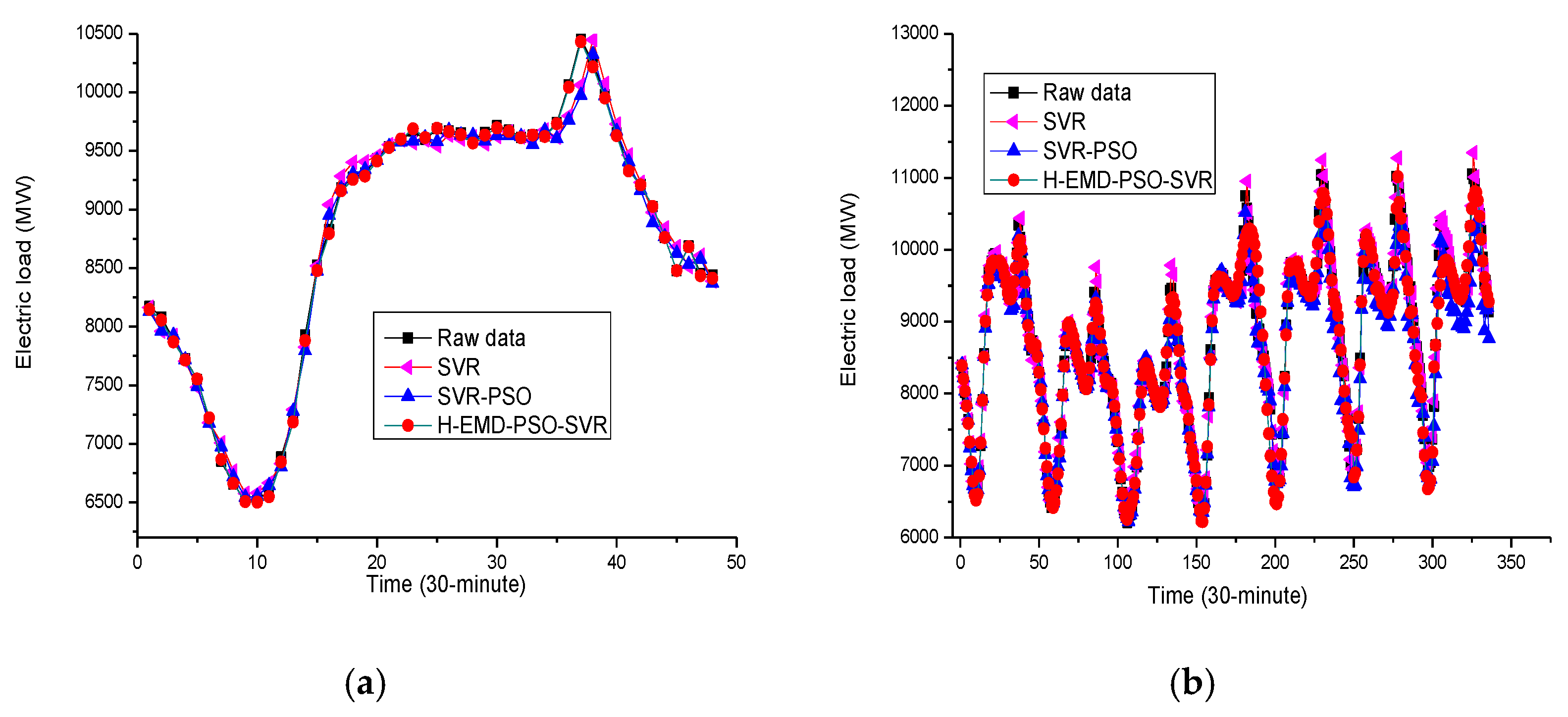
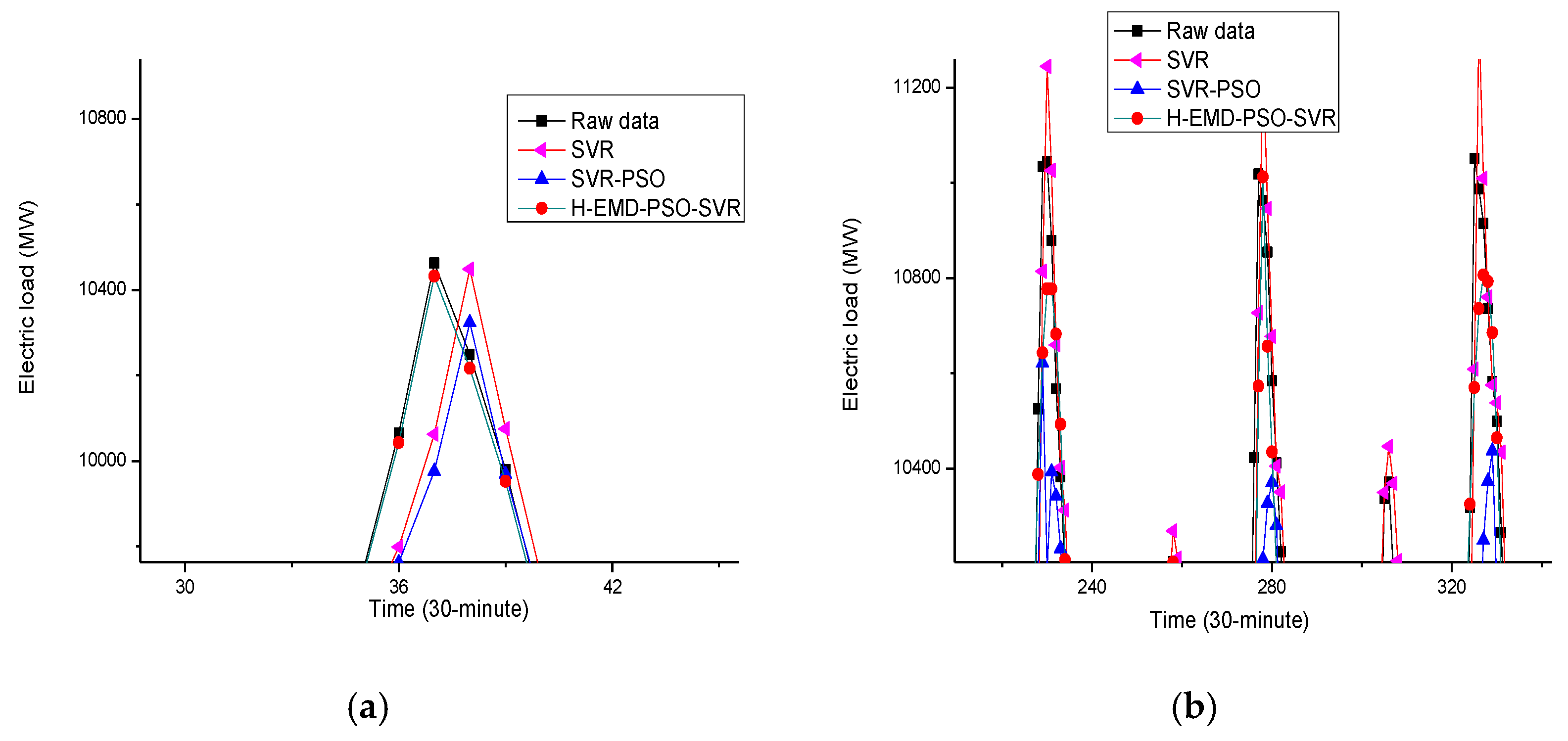
3.6. Analyses of Forecasting Accuracy and the Relevant Applications
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Xiao, L.; Shao, W.; Liang, T.; Wang, C. A combined model based on multiple seasonal patterns and modified firefly algorithm for electrical load forecasting. Appl. Energy 2016, 167, 135–153. [Google Scholar] [CrossRef]
- Hussain, A.; Rahman, M.; Memon, J.A. Forecasting electricity consumption in Pakistan: The way forward. Energy Policy 2016, 90, 73–80. [Google Scholar] [CrossRef]
- Tarsitano, A.; Amerise, I.L. Short-term load forecasting using a two-stage sarimax model. Energy 2017, 133, 108–114. [Google Scholar] [CrossRef]
- Boroojeni, K.G.; Amini, M.H.; Bahrami, S.; Iyengar, S.S.; Sarwat, A.I.; Karabasoglu, O. A novel multi-time-scale modeling for electric power demand forecasting: From short-term to medium-term horizon. Electr. Power Syst. Res. 2017, 142, 58–73. [Google Scholar] [CrossRef]
- Dudek, G. Pattern based local linear regression models for short term load forecasting. Electr. Power Syst. Res. 2016, 130, 139–147. [Google Scholar] [CrossRef]
- Vu, D.H.; Muttaqi, K.M.; Agalgaonkar, A.P. A variance inflation factor and backward elimination based robust regression model for forecasting monthly electricity demand using climatic variables. Appl. Energy 2015, 140, 385–394. [Google Scholar] [CrossRef]
- Wu, J.; Wang, J.; Lu, H.; Dong, Y.; Lu, X. Short term load forecasting technique based on the seasonal exponential adjustment method and the regression model. Energy Convers. Manag. 2013, 70, 1–9. [Google Scholar] [CrossRef]
- Maçaira, P.M.; Souza, R.C.; Oliveira, F.L.C. Modelling and forecasting the residential electricity consumption in Brazil with pegels exponential smoothing techniques. Procedia Comput. Sci. 2015, 55, 328–335. [Google Scholar] [CrossRef]
- Dong, Z.; Yang, D.; Reindl, T.; Walsh, W.M. Short-term solar irradiance forecasting using exponential smoothing state space model. Energy 2013, 55, 1104–1113. [Google Scholar] [CrossRef]
- De Oliveira, E.M.; Oliveira, F.L.C. Forecasting mid-long term electric energy consumption through bagging ARIMA and exponential smoothing methods. Energy 2018, 144, 776–788. [Google Scholar] [CrossRef]
- Takeda, H.; Tamura, Y.; Sato, S. Using the ensemble Kalman filter for electricity load forecasting and analysis. Energy 2016, 104, 184–198. [Google Scholar] [CrossRef]
- Scarpa, F.; Bianco, V. Assessing the quality of natural gas consumption forecasting: An application to the Italian residential sector. Energies 2017, 10, 1879. [Google Scholar] [CrossRef]
- Niu, D.X.; Shi, H.F.; Wu, D.D. Short-term load forecasting using Bayesian neural networks learned by hybrid Monte Carlo algorithm. Appl. Soft Comput. 2012, 12, 1822–1827. [Google Scholar] [CrossRef]
- Hippert, H.S.; Taylor, J.W. An evaluation of Bayesian techniques for controlling model complexity and selecting inputs in a neural network for short-term load forecasting. Neural Netw. 2010, 23, 386–395. [Google Scholar] [CrossRef] [PubMed]
- Bianco, V.; Cascetta, F.; Marino, A.; Nardini, S. Understanding energy consumption and carbon emissions in Europe: A focus on inequality issues. Energy 2019, 170, 120–130. [Google Scholar] [CrossRef]
- Kelo, S.; Dudul, S. A wavelet Elman neural network for short term electrical load prediction under the influence of temperature. Int. J. Electr. Power Energy Syst. 2012, 43, 1063–1071. [Google Scholar] [CrossRef]
- Ghofrani, M.; Ghayekhloo, M.; Arabali, A.; Ghayekhloo, A. A hybrid short-term load forecasting with a new input selection framework. Energy 2015, 81, 777–786. [Google Scholar] [CrossRef]
- Singh, P.; Dwivedi, P. Integration of new evolutionary approach with artificial neural network for solving short term load forecast problem. Appl Energy 2018, 217, 537–549. [Google Scholar] [CrossRef]
- Khwaja, A.S.; Zhang, X.; Anpalagan, A.; Venkatesh, B. Boosted neural networks for improved short-term electric load forecasting. Electr. Power Syst. Res. 2017, 143, 431–437. [Google Scholar] [CrossRef]
- Duan, Q.; Liu, J.; Zhao, D. Short term electric load forecasting using an automated system of model choice. Int. J. Electr. Power Energy Syst. 2017, 91, 92–100. [Google Scholar] [CrossRef]
- Karimi, M.; Karami, H.; Gholami, M.; Khatibzadehazad, H.; Moslemi, N. Priority index considering temperature and date proximity for selection of similar days in knowledge-based short term load forecasting method. Energy 2018, 144, 928–940. [Google Scholar] [CrossRef]
- Chaturvedi, D.K.; Sinha, A.P.; Malik, O.P. Short term load forecast using fuzzy logic and wavelet transform integrated generalized neural network. Int. J. Electr. Power Energy Syst. 2015, 67, 230–237. [Google Scholar] [CrossRef]
- Sadaei, H.J.; Guimarães, F.G.; da Silva, C.J.; Lee, M.H.; Eslami, T. Short-term load forecasting method based on fuzzy time series, seasonality and long memory process. Int. J. Approx. Reason. 2017, 83, 196–217. [Google Scholar] [CrossRef]
- Efendi, R.; Ismail, Z.; Deris, M.M. A new linguistic out-sample approach of fuzzy time series for daily forecasting of Malaysian electricity load demand. Appl. Soft Comput. 2015, 28, 422–430. [Google Scholar] [CrossRef]
- Hooshmand, R.A.; Amooshahi, H.; Parastegari, M. A hybrid intelligent algorithm based short-term load forecasting approach. Int. J. Electr. Power Energy Syst. 2013, 45, 313–324. [Google Scholar] [CrossRef]
- Lou, C.W.; Dong, M.C. A novel random fuzzy neural networks for tackling uncertainties of electric load forecasting. Int. J. Electr. Power Energy Syst. 2015, 73, 34–44. [Google Scholar] [CrossRef]
- Niu, M.; Sun, S.; Wu, J.; Yu, L.; Wang, J. An innovative integrated model using the singular spectrum analysis and nonlinear multi-layer perceptron network optimized by hybrid intelligent algorithm for short-term load forecasting. Appl. Math. Model. 2016, 40, 4079–4093. [Google Scholar] [CrossRef]
- Zhao, J.; Liu, X. A hybrid method of dynamic cooling and heating load forecasting for office buildings based on artificial intelligence and regression analysis. Energy Buildings 2018, 174, 293–308. [Google Scholar] [CrossRef]
- Yu, F.; Xu, X. A short-term load forecasting model of natural gas based on optimized genetic algorithm and improved BP neural network. Appl. Energy 2014, 134, 102–113. [Google Scholar] [CrossRef]
- Liu, N.; Tang, Q.; Zhang, J.; Fan, W.; Liu, J. A hybrid forecasting model with parameter optimization for short-term load forecasting of micro-grids. Appl. Energy 2014, 129, 336–345. [Google Scholar] [CrossRef]
- Fan, G.-F.; Peng, L.-L.; Hong, W.-C. Short term load forecasting based on phase space reconstruction algorithm and bi-square kernel regression model. Appl. Energy 2018, 224, 13–33. [Google Scholar] [CrossRef]
- Fan, G.; Wang, H.; Qing, S.; Hong, W.-C.; Li, H.-J. Support vector regression model based on empirical mode decomposition and auto regression for electric load forecasting. Energies 2013, 6, 1887–1901. [Google Scholar] [CrossRef]
- Geng, J.; Huang, M.L.; Li, M.W.; Hong, W.C. Hybridization of seasonal chaotic cloud simulated annealing algorithm in a SVR-based load forecasting model. Neurocomputing 2015, 151, 1362–1373. [Google Scholar] [CrossRef]
- Hong, W.-C.; Dong, Y.; Lai, C.-Y.; Chen, L.-Y.; Wei, S.-Y. SVR with hybrid chaotic immune algorithm for seasonal load demand forecasting. Energies 2011, 4, 960–977. [Google Scholar] [CrossRef]
- Fan, G.-F.; Peng, L.-L.; Zhao, X.; Hong, W.-C. Applications of hybrid EMD with PSO and GA for an SVR-based load forecasting model. Energies 2017, 10, 1713. [Google Scholar] [CrossRef]
- Hong, W.-C.; Dong, Y.; Zhang, W.; Chen, L.-Y.; Panigrahi, B.K. Cyclic electric load forecasting by seasonal SVR with chaotic genetic algorithm. Int. J. Electr. Power Energy Syst. 2013, 44, 604–614. [Google Scholar] [CrossRef]
- Ju, F.-Y.; Hong, W.-C. Application of seasonal SVR with chaotic gravitational search algorithm in electricity forecasting. Appl. Math. Model. 2013, 37, 9643–9651. [Google Scholar] [CrossRef]
- Li, M.; Hong, W.-C.; Kang, H. Urban traffic flow forecasting using Gauss-SVR with cat mapping, cloud model and PSO hybrid algorithm. Neurocomputing 2013, 99, 230–240. [Google Scholar] [CrossRef]
- Chen, R.; Liang, C.; Hong, W.-C.; Gu, D. Forecasting holiday daily tourist flow based on seasonal support vector regression with adaptive genetic algorithm. Appl. Soft Comput. 2015, 26, 435–443. [Google Scholar] [CrossRef]
- Huang, B.; Kunoth, A. An optimization based empirical mode decomposition scheme. J. Comput. Appl. Math. 2013, 240, 174–183. [Google Scholar] [CrossRef]
- An, X.; Jiang, D.; Zhao, M.; Liu, C. Short-term prediction of wind power using EMD and chaotic theory. Commun. Nonlinear Sci. Numer. Simul. 2012, 17, 1036–1042. [Google Scholar] [CrossRef]
- Fan, G.; Qing, S.; Wang, S.Z.; Hong, W.C.; Dai, L. Study on apparent kinetic prediction model of the smelting reduction based on the time series. Math. Probl. Eng. 2012, 720849. [Google Scholar] [CrossRef]
- Premanode, B.; Toumazou, C. Improving prediction of exchange rates using Differential EMD. Expert Syst. Appl. 2013, 40, 377–384. [Google Scholar] [CrossRef]
- Dong, Y.; Zhang, Z.; Hong, W.-C. A hybrid seasonal mechanism with a chaotic cuckoo search algorithm with a support vector regression model for electric load forecasting. Energies 2018, 11, 1009. [Google Scholar] [CrossRef]
- Derrac, J.; García, S.; Molina, D.; Herrera, F. A practical tutorial on the use of nonparametric statistical tests as a methodology for comparing evolutionary and swarm intelligence algorithms. Swarm Evol. Comput. 2011, 1, 3–18. [Google Scholar] [CrossRef]

| Sample Size/Defined Items | The Parameters of an SVR Model | ||
|---|---|---|---|
| C | |||
| The small sample data | |||
| Item A: the random term + the middle term | 0.14 | 89 | 0.0022 |
| Item B: the middle term + the trend (residual) term | 0.14 | 88 | 0.0020 |
| Item C: the middle term | 0.15 | 91 | 0.0025 |
| Item D: A + B − C (all IMFs, i.e., complete decomposed effects) | 0.15 | 92 | 0.0025 |
| The large sample data | |||
| Item A: the random term + the middle term | 0.18 | 95 | 0.0011 |
| Item B: the middle term + the trend (residual) term | 0.18 | 96 | 0.0011 |
| Item C: the middle term | 0.20 | 98 | 0.0013 |
| Item D: A + B − C (all IMFs, i.e., complete decomposed effects) | 0.20 | 98 | 0.0012 |
| Forecasting Accuracy Indexes | The Defined Items | ||||
|---|---|---|---|---|---|
| Item A (by SVR-PSO) | Item B (by SVR-PSO) | Item C (by SVR-PSO) | Item D (by SVR-PSO) | Item D (by SVR) | |
| The Small Sample | |||||
| (training stage) | 0.0001936 | 0.0001635 | 0.0029 | 0.0009 | 0.0021 |
| (testing stage) | 0.0001806 | 0.0001641 | 0.0033 | 0.0011 | 0.0026 |
| R (training stage) | 0.9993 | 0.9995 | 0.9888 | 0.9884 | 0.9871 |
| R (testing stage) | 0.9994 | 0.9995 | 0.9867 | 0.9881 | 0.9890 |
| The Large Sample | |||||
| (training stage) | 0.0001280 | 0.0001090 | 0.0007 | 0.0007 | 0.0012 |
| (testing stage) | 0.0002281 | 0.0002814 | 0.0033 | 0.0096 | 0.0099 |
| R (training stage) | 0.9994 | 0.9994 | 0.9962 | 0.9965 | 0.9916 |
| R (testing stage) | 0.9992 | 0.9991 | 0.9982 | 0.9756 | 0.9912 |
| Compared Models | MAPE | RMSE | MAE | Running Time (s) |
|---|---|---|---|---|
| The Small Sample | ||||
| Original SVR [32] | 11.70 | 145.87 | 10.92 | 180.4 |
| SVR-PSO [32] | 11.41 | 145.69 | 10.67 | 165.2 |
| PSO–BP [32] | 10.91 | 142.26 | 10.14 | 159.9 |
| SVR-GA [35] | 13.52 | 150.38 | 11.88 | 171.3 |
| EMD-SVR-AR [32] | 9.86 | 117.16 | 9.10 | 80.7 |
| EMD-PSO-GA-SVR [35] | 9.09 | 123.38 | 9.19 | 135.7 |
| H-EMD-SVR-PSO | 10.01 | 125.38 | 9.75 | 120.5 |
| The Large Sample | ||||
| Original SVR [32] | 12.88 | 181.62 | 12.05 | 116.8 |
| SVR-PSO [32] | 13.50 | 271.43 | 13.07 | 192.7 |
| PSO–BP [32] | 12.24 | 175.24 | 11.36 | 163.1 |
| SVR-GA [35] | 14.31 | 183.57 | 15.31 | 195.7 |
| EMD-SVR-AR [32] | 5.10 | 134.20 | 9.82 | 162.0 |
| EMD-PSO-GA-SVR [35] | 3.92 | 142.41 | 9.04 | 179.1 |
| H-EMD-SVR-PSO | 5.83 | 130.17 | 9.56 | 167.4 |
| Compared Models | Wilcoxon Signed-Rank Test | |
|---|---|---|
| α = 0.025; W = 4 | α = 0.05; W = 6 | |
| The Small Sample | ||
| H-EMD-SVR-PSO vs. Original SVR | 3 * | 3 * |
| H-EMD-SVR-PSO vs. SVR-PSO | 2 * | 2 * |
| H-EMD-SVR-PSO vs. PSO–BP | 2 * | 3 * |
| H-EMD-SVR-PSO vs. SVR-GA | 2 * | 3 * |
| H-EMD-SVR-PSO vs. EMD-SVR-AR | 6 | 4 * |
| H-EMD-SVR-PSO vs. EMD-PSO-GA-SVR | 6 | 8 |
| The Large Sample | ||
| H-EMD-SVR-PSO vs. Original SVR | 3 * | 2 * |
| H-EMD-SVR-PSO vs. SVR-PSO | 3 * | 2 * |
| H-EMD-SVR-PSO vs. PSO–BP | 3 * | 2 * |
| H-EMD-SVR-PSO vs. SVR-GA | 3 * | 2 * |
| H-EMD-SVR-PSO vs. EMD-SVR-AR | 6 | 2 * |
| H-EMD-SVR-PSO vs. EMD-PSO-GA-SVR | 6 | 4 * |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hong, W.-C.; Fan, G.-F. Hybrid Empirical Mode Decomposition with Support Vector Regression Model for Short Term Load Forecasting. Energies 2019, 12, 1093. https://doi.org/10.3390/en12061093
Hong W-C, Fan G-F. Hybrid Empirical Mode Decomposition with Support Vector Regression Model for Short Term Load Forecasting. Energies. 2019; 12(6):1093. https://doi.org/10.3390/en12061093
Chicago/Turabian StyleHong, Wei-Chiang, and Guo-Feng Fan. 2019. "Hybrid Empirical Mode Decomposition with Support Vector Regression Model for Short Term Load Forecasting" Energies 12, no. 6: 1093. https://doi.org/10.3390/en12061093
APA StyleHong, W.-C., & Fan, G.-F. (2019). Hybrid Empirical Mode Decomposition with Support Vector Regression Model for Short Term Load Forecasting. Energies, 12(6), 1093. https://doi.org/10.3390/en12061093






